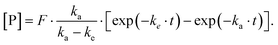Towards therapeutic drug monitoring of antibiotic levels – analyzing the pharmacokinetics of levofloxacin using DUV-resonance Raman spectroscopy

Abstract

Therapeutic drug monitoring (TDM) plays an important role in clinical practice. Here, pharmacokinetics has a decisive influence on the effective antibiotic concentration during treatment. Moreover, different kinetics exist for different administration forms. Accordingly, adjusting the correct concentration depends, in addition to gender, age, weight, clinical picture, etc., on the dosage form of the antibiotic. This study investigates the capability of deep UV resonance Raman spectroscopy (DUV-RRS) to simulate the pharmacokinetics of fluoroquinolone levofloxacin after two different administration forms (intravenous and oral). Three different pre-processing methods were applied, and the best agreement with the simulation was achieved using the extended multiplicative scatter correction. The resulting spectra were used for partial least squares (PLS) regression and ordinary least squares (OLS) regression. The kinetic parameters were compared with the simulated data, with PLS showing the best performance for intravenous administration and a comparable result to OLS for oral administration, while the errors are smaller. The acquired results show the potential of DUV-RRS in combination with PLS regression as a promising supportive method for TDM.

---

Introduction

Studies suggest that up to 50% of critically ill patients are underdosed with fixed-dose antibiotic regimens due to grossly altered pharmacokinetics in critical illness and failure of target attainment is associated with worse clinical outcomes.¹ Therapeutic drug monitoring (TDM) guided antibiotic therapy may be an appropriate strategy to overcome this pharmacokinetic variability and the problem of underdosing. In this process, serum antibiotic exposure is measured and dosing can be adapted during therapy to ensure optimal exposure.² In this context, today's well-established robust methods are mainly chromatography-based^3–7 and ensure sensitive detection of a specific group of drugs or a single antibiotic.^8–12

However, these techniques are time-consuming and labor-intensive, require large volumes for sample preparation and processing and consume high amounts of organic solvents.^13,14 In addition, in some cases, samples must be forwarded to a central laboratory for analysis, which may delay the required results.^15,16 An all-encompassing application requires a rapid method with low sample demand and the ability for multicomponent detection.

In this respect, Raman spectroscopy^17,18 is a very promising technique,^19–25 as it is label-free and non-invasive,^26–28 fast and sensitive,^29–32 and provides an extremely high chemical selectivity^33–41 and potential as a point-of-care technique. For the evaluation of complex samples, e.g., human body fluids, a simple ordinary least squares (OLS) analysis may lead to insufficient results, and therefore multivariate data analysis may be helpful. The most widely used techniques in chemometrics for this task are principal component regression (PCR) and partial least squares (PLS) regression.^{21,25,42–44}

Another important piece of information resulting from TDM is the time-dependent aspect of drug interaction in the host body, known as pharmacokinetics.⁴⁵ Depending on drug administration, specific kinetic models can be assumed, which, in addition to kinetic time constants, provide deeper insight into important parameters such as the bioavailability, dose, and volume of distribution of antibiotics.^46,47 These variables can be used to model the time-dependent interaction of drugs, which in turn can be used to adjust and improve antibiotic therapy. However, the pathology of critically ill patients may cause physiological changes that alter their pharmacokinetics^48,49 and complicate the prediction of drug exposure.^50,51 These physiological changes may lead to under- or overdosage, which carries the risk of treatment failure in the case of underdosage and the risk of drug accumulation and toxic side effects in the case of overdosage. Above all, in vitro data show that sub-inhibitory antibiotic concentrations can foster multidrug resistance.^52–54 This necessitates robust, rapid, and sensitive spectroscopic and analytical methods.

This work therefore aims to demonstrate the potential of deep UV resonance Raman spectroscopy (DUV-RRS) in combination with PLS regression for monitoring of antibiotic pharmacokinetics.

Materials and methods

Sample preparation

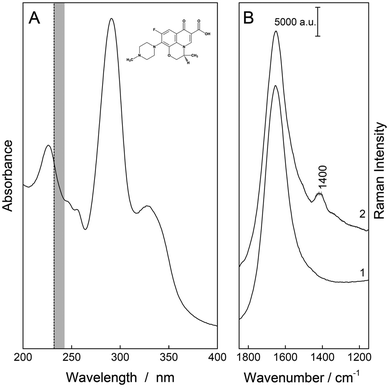
The fluoroquinolone levofloxacin (levofloxacin hydrochloride, Santa Cruz Biotechnology Inc., Dallas, Texas USA, see Fig. 1) was used without further purification. Starting from a 1 mM stock solution, a dilution series of 0 μM–50 μM (hereafter referred to as c_cal) was prepared using ultra-clear water from a feed system [SG Water GmbH, (Siemens, Barsbüttel, Germany) with κ > 0.06 μS cm⁻¹], followed by several concentrations from 0 μM to 26.37 μM (c_sim,int) and 21.97 μM (c_sim,o). These samples were used for the calibration (c_cal) and simulation of two different kinetics (c_sim,int and c_sim,o), respectively. Here, 15 and twelve different concentration values representing specific time points were taken from pharmacokinetic studies of 750 mg levofloxacin after intravenous⁵⁵ and oral administration,⁵⁶ respectively. All standard compounds are >95% pure as determined by HPLC analysis.

Fig. 1 Absorption spectrum of 0.1 mM aqueous solutions of levofloxacin (A). The applied laser excitation wavelength λ_exc. = 232 nm and the collected region of the Raman spectra are depicted as a vertical line and a shaded portion, respectively. Resonance Raman spectra (B) of water (1) and the highest concentration of levofloxacin used for calibration (50 μM, 2) with its marker band at about 1400 cm⁻¹.

Spectroscopy

The deep UV resonance Raman spectra were acquired with a Raman spectrometer (IsoPlane, Teledyne Princeton Instrument, Trenton, USA) equipped with a UV laser. An excitation wavelength of λ_exc. = 232 nm was applied (laser power: 42 mW at the sample). A 2400 g mm⁻¹ grating and an exposure time of 7.5 s (four accumulations) were used to measure five replicate repetitions of each sample. To avoid any photo-degradation during the measurements, the samples were constantly stirred in a rotational cuvette.

The absorption spectrum was recorded from a 0.1 mM aqueous solution of the antibiotic using a Cary 5000 system (Varian, Darmstadt, Germany) with a step size of 1 nm and the Fourier transform (FT) Raman spectrum of the solid was recorded with a resolution of 4 cm⁻¹ using a Nd:YAG laser with an excitation wavelength of λ_exc. = 1064 nm, a laser power of 500 mW, and 256 scan exposures, in combination with a Ram II spectrometer (Bruker, Bremen, Germany).

Data preprocessing

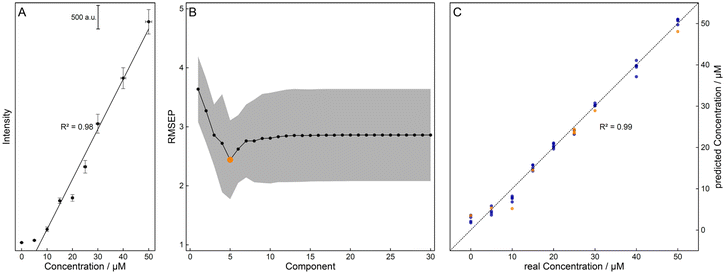
All preprocessing and analysis of the raw Raman data were performed with statistical programming GnuR 3.6.1.⁵⁷ The packages ‘signal’,⁵⁸ ‘EMSC’,⁵⁹ ‘Peaks’,⁶⁰ ‘minpack.lm’,⁶¹ and ‘pls’⁶² were utilized and their functions were complemented by an in-house written procedure. First, the Raman data were truncated to the wavenumber region of interest (2000 cm⁻¹–1000 cm⁻¹), and a median filter (window = 3) was applied for spike removal. Then, different algorithms were tested for their results in predicting the sample concentration. The treated Raman spectra were either baseline corrected using the SNIP algorithm⁶³ (iterations = 18, order = 2) and normalized to the water band or scatter corrected using extended multiplicative scatter correction (EMSC)^64,65 (degree = 1) with the median spectra of water as a reference or processed using a combination of both methods.

For quantification, the difference spectra were calculated using the median water spectra as a reference and a Gaussian peak profile was fitted to the marker band at about 1400 cm⁻¹. The resulting peak intensities of the calibration samples were correlated with the corresponding concentration (c_cal), showing a linear relationship (see Fig. 2A) that was used to predict the simulated concentration (c_sim,int and c_sim,o). A representation of the preprocessing workflow can be found in the ESI (see Fig. S1†).

Fig. 2 The calibration curve using the intensity of the Raman marker band of levofloxacin at about 1400 cm⁻¹ showed a good correlation with the concentration of the samples (c_cal, A). For the prediction of the simulated concentrations via OLS regression, concentrations from 5 μM to 50 μM were used. The PLS regression model was optimized by calculating the minimum error via 100-fold cross-validation, resulting in an an optimum number of five components (big dot) for the prediction of the test data (c_cal,test, B). With this value, a good relationship between the concentrations of the training (c_cal,train) and test data (c_cal,test) could be achieved, with the respective values depicted in blue and orange (C).

Furthermore, the preprocessed data were vector normalized and partial least squares (PLS) regression⁶⁶ was applied. The optimal number of five components was calculated minimizing the root-mean-square error of prediction (RMSEP) via 100-fold cross-validation using the concentrations of the calibration (c_cal, see Fig. 2B). Here, the data were divided into train (c_cal,train, 80%) and test (c_cal,test, 20%) data sets, showing a good correlation (see Fig. 2C). This regression model was then used for the prediction of the concentrations of the pharmacokinetic simulations c_sim,int and c_sim,o, referred to as c_pred,int and c_pred,o in the following.

Density functional theory calculation for vibrational assignment of Raman marker bands

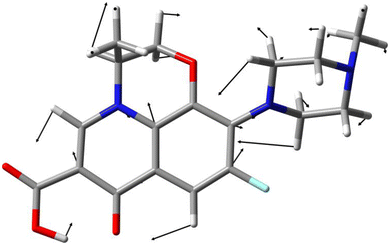
For a better understanding of the assignment and an interpretation of the Raman marker bands used for the quantification, the molecular structures were optimized and the vibrational modes and Raman activities were calculated with density functional theory (DFT) using Gaussian 09.⁶⁷ The hybrid exchange–correlation functional with Becke's three-parameter exchange functional (B3)⁶⁸ slightly modified by Stephens et al.⁶⁹ coupled with the correlation part of the functional from Lee, Yang, and Parr (B3LYP)⁷⁰ and Dunning's triple correlation consistent basis sets of contracted Gaussian functions with polarized and diffuse functions (cc-pVTZ)⁷¹ were applied. For alignment, the wavenumber positions of the FT-Raman peaks (threshold: 20% of the maximum intensity) were scaled to the vibrational frequencies of the calculation. The frequency scaling factor was calculated by minimizing the mean average error (MAE), and an intensity correction was applied to the scattering activities.⁷² Finally, the scaled scattering activities were fitted with a Gaussian peak profile with the median value of the full width at half maximum (FWHM) of all experimental peaks investigated to simulate Raman bands with finite resolution (see Fig. S2†).

Results and discussion

Resonance Raman spectroscopy for simulation of pharmacokinetic models

The excitation wavelength λ_exc. = 232 nm enables strong resonance and sensitive detection of the fluoroquinolone levofloxacin (see Fig. 1). As a proof-of-principle measurement, the pharmacokinetics of an intravenous and an oral 750 mg dose of levofloxacin were simulated with aqueous solutions of various antibiotic concentrations c_sim,int and c_sim,o. First, the best preprocessing routine had to be selected, i.e., baseline correction, EMSC correction, or their combination, followed by two different quantification approaches: OLS and PLS regression.

For the first regression model, the marker band was examined with a Gaussian peak profile. For a better understanding of this Raman signal, DFT calculations were aligned with the experimental FT-Raman spectra and their vibrational modes were assigned. For levofloxacin, the vibration at about 1400 cm⁻¹ can be construed as a combination of CH₂-wagging of the piperazine system and CH-bending vibration of the quinolone ring (see Fig. 3). In this case, the fitted peak intensity of the marker band of the dilution series was correlated with their concentration, and the resulting linear regression model was used to quantify the concentration of the simulated samples (see Fig. 2A).

Fig. 3 Assignment of the vibrational mode of the Raman marker band used for ordinary least squares analysis. The atomic displacement vectors of the Raman band of levofloxacin at 1400 cm⁻¹ are shown and can be assigned to a combination of CH₂-wagging of the piperazine system and CH-bending vibration of the quinolone ring. The color code for the individual atoms is: hydrogen, white; carbon, grey; oxygen, red; nitrogen, blue; and fluorine, cyan.

For the PLS regression model, the dimensions of the calibration data set were reduced via the minimization of the RMSEP. Then, the spectral data were divided into train (c_cal,train) and test (c_cal,test) data sets. The error between the predicted (from regression with the training data) and the test data set was calculated via 100-fold cross-validation, resulting in an optimal number of five components (see Fig. 2B). When correlating the predicted concentrations of the test set with the adjusted concentrations, a good linear relationship was obtained (see Fig. 2C). With this optimized model, the concentrations of the simulated samples could be predicted.

As a marker for the ‘best’ model of the selection presented, the RMSEP was calculated for the simulated sample concentrations c_sim,int and c_sim,o and their prediction resulting from the regression model (c_pred,int and c_pred,o, see Table 1). It is evident that the prediction of the intravenous model is superior to that of the oral model, regardless of the regression model and data treatment, and the OLS regression shows an overall worse performance than the PLS regression. In addition, the concentration of the EMSC data shows higher similarities to the adjusted data, but the baseline correction has a greater impact on the calibration and prediction result, as the combined data treatment differs only slightly from the baseline-corrected one. Therefore, in further evaluation, the focus is on the EMSC data.

Table 1 Evaluation of the different models for preprocessing and prediction. The RMSEP for the baseline and EMSC correction and their combination were calculated using the simulated (c_sim,int and c_sim,o) and predicted (c_pred,int and c_pred,o) sample concentrations for both pharmacokinetics. The OLS regression shows overall poorer performance than the PLS regression, and the concentrations of the intravenous model are better predicted than those of the oral ones. In addition, the concentrations of the EMSC-corrected data show higher similarities to the simulated ones, but the baseline correction has a greater impact on the calibration and prediction results since the combined data treatment differs only slightly from the baseline correction

		Pre-processing method
		Baseline correction	EMSC correction	Combination
OLS regression	RMSEP (iv)/μM	3.20	1.96	3.11
	RMSEP (o)/μM	4.10	2.29	4.04
	LoD/μM (mg L^−1)	8.78 (3.49)	5.54 (2.20)	8.70 (3.46)
PLS regression	RMSEP (iv)/μM	1.95	1.27	1.69
	RMSEP (o)/μM	2.71	1.66	2.01
	LoD/μM (mg L^−1)	6.39 (2.54)	4.50 (1.79)	5.01 (1.99)

---

The limit of detection (LoD) may provide a possible explanation for the differences in the performance of the models. According to the IUPAC definition,⁷³ the LoD is calculated from the mean (c̄_bl) and the standard deviation (σ_bl) of the blank sample concentration:

LoD = c̄_bl + 3·σ_bl.

The LoD of the blank values of the PLS model is significantly lower than that of the OLS model (see Table 1). Therefore, the lower sample concentrations could not be satisfactorily determined for the latter, resulting in poorer performance.

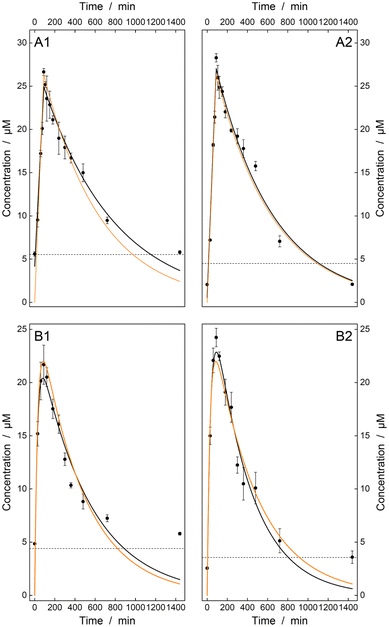
Various kinetic parameters can be derived from the time-dependent concentration profile resulting from a pharmacokinetic study. Two different kinetic models were simulated (vide supra). Intravenous treatment can be expressed as linear absorption and first-order elimination

[E] = [E]₀·exp(−k_e·t),

where [E] and [E]₀ are the concentrations of the educts at any time point t and at the starting point t₀, respectively, and k_e is the kinetic time constant of the elimination. Oral administration follows Bateman kinetics,⁷⁴ in which the absorption, resorption, and elimination of the antibiotics take place:

Here, [P] is the product concentration at any time point t, 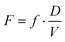is a factor representing the relationship between the bioavailability f, dose D, and volume of distribution V, and k_a and k_e are the kinetic time constants for absorption and elimination, respectively.

As an additional indicator of the quality of the algorithm used, these pharmacokinetic models were fitted to the predicted concentration profiles and their results were compared with the simulated values (see Fig. 4 and Table 2). Here, the PLS regression yields a near-perfect agreement for the intravenous model and provides values of the same order of magnitude for the oral administration model. For the latter, the OLS model is slightly better than the PLS model but has higher errors. Thus, the experiments performed demonstrate the potential of resonance Raman spectroscopy in combination with PLS regression as a promising method providing reliable results for TDM.

Fig. 4 Concentration profile after the intravenous (A) and oral (B) administration of 750 mg levofloxacin. Simulated concentrations (c_sim,int and c_sim,o, orange solid line) were compared with their predicted values (c_pred,int and c_pred,o) using either OLS (1) or PLS (2) regression. First-order (A) or Batman kinetics (B) were fitted (black solid line). Concentrations below the limit of detection (dashed horizontal line) were not satisfactorily determined. Therefore, the resulting concentrations are too high for both models, but the PLS regression shows better overall agreement with the simulated data.

Table 2 Evaluation of the different regression models for both forms of administration. The PLS regression shows the best agreement with the intravenous treatment, while the OLS regression deviates less from the oral treatment. Here, the PLS model is slightly worse but shows lower errors

		Regression model
		Simulation	OLS	PLS
Parameter (iv)	[E]0/μM	30.9	28.3 ± 0.8	31.7 ± 1.0
	k e/10^−3 min^−1	1.76	1.42 ± 0.12	1.76 ± 0.14
	R ^2	1.00	0.97	0.98
Parameter (o)	F/μM	394	468 ± 202	305 ± 84
	k a/10^−3 min^−1	2.28	1.97 ± 0.45	2.74 ± 0.43
	k e/10^−3 min^−1	33.6	38.4 ± 13.1	28.6 ± 6.1
	R ^2	1.00	0.86	0.95

---

Conclusion

In this work, the potential of deep UV resonance Raman spectroscopy in combination with PLS regression could be shown for two different administration forms of the antibiotic levofloxacin. The stable regression model enables good agreement of important kinetic parameters with the simulated data. These additionally provide important information on pharmacokinetics, which can further be used for better antibiotic dose adjustment. For the antibiotic quantification with deep UV resonance Raman spectroscopy, only a small sample volume (200 μL) and a short integration time (7.5 s) were required for sufficient results.

The measurements carried out in this study can be applied to body fluids, such as blood plasma, without significant modifications. Using a precisely selected wavelength in the DUV range, no fluorescence appears in the Raman spectrum and the analyte signals are resonantly enhanced. The complex composition of body fluids will result in several signals in the Raman spectrum, which may cause poorer results with OLS regression since the antibiotic marker band could be overlaid by the signals of the body fluid. However, the PLS regression could be applied to quantify antibiotic levels in body fluids comparatively well, as a larger spectral range is utilized in comparison with the OLS regression.

In summary, the UV resonance Raman experiments performed show high potential for the quantification of the levofloxacin pharmacokinetics and provide the foundation for future TDM studies.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Funding from the German Federal Ministry of Education and Research (Foerderprogramm “Innovative medizintechnische Loesungen zur Praevention und Versorgung nosokomialer Infektionen“, FKZ: 33GW0425E) and from the Deutsche Forschungsgemeinschaft (INST 275/334-1 FUGG and INST 275/363-1 FUGG, EXC 2051 Project-ID 390713860) is acknowledged.

References

1. J. A. Roberts, M. Paul Sk Fau-Akova, M. Akova M Fau-Bassetti, J. J. Bassetti M Fau-De Waele, G. De Waele Jj Fau-Dimopoulos, K.-M. Dimopoulos G Fau-Kaukonen, D. Kaukonen Km Fau-Koulenti, C. Koulenti D Fau-Martin, P. Martin C Fau-Montravers and J. Montravers P Fau-Rello, et al., DALI: defining antibiotic levels in intensive care unit patients: are current β-lactam antibiotic doses sufficient for critically ill patients?, Clin. Infect. Dis., 2014, 58(8), 1072–1083.
2. J.-S. Kang and M.-H. Lee, Overview of therapeutic drug monitoring, Korean J. Intern. Med., 2009, 24(1), 1.
3. S. A. Helmy, Simultaneous quantification of linezolid, tinidazole, norfloxacin, moxifloxacin, levofloxacin, and gatifloxacin in human plasma for therapeutic drug monitoring and pharmacokinetic studies in human volunteers, Ther. Drug Monit., 2013, 35(6), 770–777.
4. P. Sistik, R. Urinovska, H. Brozmanova, I. Kacirova, P. Silhan and K. Lemr, Fast simultaneous LC/MS/MS determination of 10 active compounds in human serum for therapeutic drug monitoring in psychiatric medication, Biomed. Chromatogr., 2016, 30(2), 217–224.
5. A. S. Abdul Keyon, M. Miskam, N. S. Ishak, N. A. Mahat, M. A. Mohamed Huri, R. Abdul Wahab, S. Chandren, F. I. Abdul Razak, N. T. Ng and T. G. Ali, Capillary electrophoresis for the analysis of antidepressant drugs: A review, J. Sep. Sci., 2019, 42(4), 906–924.
6. W. Thormann, Capillary electrophoresis for the determination of drugs in biological fluids, in Handbook of Analytical Separations, Elsevier, 2020, vol. 7, pp. 81–96.
7. T. N. M. Pham, T. B. Le, D. D. Le, T. H. Ha, N. S. Nguyen, T. D. Pham, P. C. Hauser, T. A. H. Nguyen and T. D. Mai, Determination of carbapenem antibiotics using a purpose-made capillary electrophoresis instrument with contactless conductivity detection, J. Pharm. Biomed. Anal., 2020, 178, 112906.
8. M.-C. Verdier, O. Tribut, P. Tattevin, Y. Le Tulzo, C. Michelet and D. Bentué-Ferrer, Simultaneous determination of 12 β-lactam antibiotics in human plasma by high-performance liquid chromatography with UV detection: application to therapeutic drug monitoring, Antimicrob. Agents Chemother., 2011, 55(10), 4873–4879.
9. J. J. Lee, J. H. Beumer and E. Chu, Therapeutic drug monitoring of 5-fluorouracil, Cancer Chemother. Pharmacol., 2016, 78(3), 447–464.
10. N. Pinder, T. Brenner, S. Swoboda, M. A. Weigand and T. Hoppe-Tichy, Therapeutic drug monitoring of beta-lactam antibiotics–Influence of sample stability on the analysis of piperacillin, meropenem, ceftazidime and flucloxacillin by HPLC-UV, J. Pharm. Biomed. Anal., 2017, 143, 86–93.
11. D. Moreno–González, M. Krulišová, L. Gámiz–Gracia and A. M. García–Campaña, Determination of tetracyclines in human urine samples by capillary electrophoresis in combination with field amplified sample injection, Electrophoresis, 2018, 39(4), 608–615.
12. Y. Zheng, Z. Wang, G. Lui, D. Hirt, J. M. Treluyer, S. Benaboud, R. Aboura and I. Gana, Simultaneous quantification of levofloxacin, pefloxacin, ciprofloxacin and moxifloxacin in microvolumes of human plasma using high–performance liquid chromatography with ultraviolet detection, Biomed. Chromatogr., 2019, 33(5), e4506.
13. Z. Yang and S. Wang, Recent development in application of high performance liquid chromatography-tandem mass spectrometry in therapeutic drug monitoring of immunosuppressants, J. Immunol. Methods, 2008, 336(2), 98–103.
14. K. Sharma and R. Mullangi, A concise review of HPLC, LC–MS and LC–MS/MS methods for determination of azithromycin in various biological matrices, Biomed. Chromatogr., 2013, 27(10), 1243–1258.
15. D. Andes, A. Pascual and O. Marchetti, Antifungal therapeutic drug monitoring: established and emerging indications, Antimicrob. Agents Chemother., 2009, 53(1), 24–34.
16. H. R. Ashbee, R. A. Barnes, E. M. Johnson, M. D. Richardson, R. Gorton and W. W. Hope, Therapeutic drug monitoring (TDM) of antifungal agents: guidelines from the British Society for Medical Mycology, J. Antimicrob. Chemother., 2014, 69(5), 1162–1176.
17. D. A. Long, The Raman effect: a unified treatment of the theory of Raman scattering by molecules, John Wiley & Sons, Inc., 2002.  DOI:10.1002/0470845767.
18. T. Frosch, A. Knebl and T. Frosch, Recent advances in nano-photonic techniques for pharmaceutical drug monitoring with emphasis on Raman spectroscopy, Nanophotonics, 2020, 9(1), 19–37,  DOI:10.1515/nanoph-2019-0401 , review.
19. C. Domes, R. Domes, J. r. Popp, M. W. Pletz and T. Frosch, Ultrasensitive detection of antiseptic antibiotics in aqueous media and human urine using deep UV resonance raman spectroscopy, Anal. Chem., 2017, 89(18), 9997–10003.
20. D. Yan, J. r. Popp, M. W. Pletz and T. Frosch, Highly sensitive broadband Raman sensing of antibiotics in step-index hollow-core photonic crystal fibers, ACS Photonics, 2017, 4(1), 138–145.
21. A. G. Berger, S. M. Restaino and I. M. White, Vertical-flow paper SERS system for therapeutic drug monitoring of flucytosine in serum, Anal. Chim. Acta, 2017, 949, 59–66.
22. S. Fornasaro, A. Bonifacio, E. Marangon, M. Buzzo, G. Toffoli, T. Rindzevicius, M. S. Schmidt and V. Sergo, Label-free quantification of anticancer drug imatinib in human plasma with surface enhanced Raman spectroscopy, Anal. Chem., 2018, 90(21), 12670–12677.
23. D. R. Parachalil, J. McIntyre and H. J. Byrne, Potential of Raman spectroscopy for the analysis of plasma/serum in the liquid state: recent advances, Anal. Bioanal. Chem., 2020, 1–15.
24. D. Yan, J. Popp, M. W. Pletz and T. Frosch, Fiber enhanced Raman sensing of levofloxacin by PCF bandgap-shifting into the visible range, Anal. Methods, 2018, 10(6), 586–592,  10.1039/c7ay02398g.
25. S. Wolf, T. Frosch, J. Popp, M. W. Pletz and T. Frosch, Highly Sensitive Detection of the Antibiotic Ciprofloxacin by Means of Fiber Enhanced Raman Spectroscopy, Molecules, 2019, 24(24), 1–11,  DOI:10.3390/molecules24244512.
26. R. Keiner, M. C. Gruselle, B. Michalzik, J. Popp and T. Frosch, Raman spectroscopic investigation of 13CO 2 labeling and leaf dark respiration of Fagus sylvatica L. (European beech), Anal. Bioanal. Chem., 2015, 407(7), 1813–1817,  DOI:10.1007/s00216-014-8446-8.
27. A. Sieburg, T. Jochum, S. E. Trumbore, J. Popp and T. Frosch, Onsite cavity enhanced Raman spectrometry for the investigation of gas exchange processes in the Earth's critical zone, Analyst, 2017, 142(18), 3360–3369,  10.1039/c7an01149k.
28. A. Knebl, R. Domes, S. Wolf, C. Domes, J. Popp and T. Frosch, Fiber-Enhanced Raman Gas Spectroscopy for the Study of Microbial Methanogenesis, Anal. Chem., 2020, 92(18), 12564–12571,  DOI:10.1021/acs.analchem.0c02507 , from NLM Medline.
29. S. Wolf, J. Popp and T. Frosch, Multifocal hyperspectral Raman imaging setup for multi-well plates, Sens. Actuators, B, 2023, 375, 132949,  DOI:10.1016/j.snb.2022.132949.
30. T. Frosch, T. Meyer, M. Schmitt and J. Popp, Device for Raman difference spectroscopy, Anal. Chem., 2007, 79(16), 6159–6166,  DOI:10.1021/ac070440+.
31. S. Wolf, R. Domes, A. Merian, C. Domes and T. Frosch, Parallelized Raman Difference Spectroscopy for the Investigation of Chemical Interactions, Anal. Chem., 2022, 94(29), 10346–10354,  DOI:10.1021/acs.analchem.2c00222 , from NLM Medline.
32. T. Frosch, E. Wyrwich, D. Yan, C. Domes, R. Domes, J. Popp and T. Frosch, Counterfeit and Substandard Test of the Antimalarial Tablet Riamet((R)) by Means of Raman Hyperspectral Multicomponent Analysis, Molecules, 2019, 24(18), 1–14,  DOI:10.3390/molecules24183229.
33. A. Sieburg, A. Knebl, J. M. Jacob and T. Frosch, Characterization of fuel gases with fiber-enhanced Raman spectroscopy, Anal. Bioanal. Chem., 2019, 411(28), 7399–7408,  DOI:10.1007/s00216-019-02145-x.
34. D. Yan, J. Popp and T. Frosch, Analysis of Fiber-Enhanced Raman Gas Sensing Based on Raman Chemical Imaging, Anal. Chem., 2017, 89(22), 12269–12275,  DOI:10.1021/acs.analchem.7b03209.
35. A. Knebl, C. Domes, R. Domes, S. Wolf, J. Popp and T. Frosch, Hydrogen and C2-C6 Alkane Sensing in Complex Fuel Gas Mixtures with Fiber-Enhanced Raman Spectroscopy, Anal. Chem., 2021, 93(30), 10546–10552,  DOI:10.1021/acs.analchem.1c01500 , from NLM Medline.
36. T. Frosch, E. Wyrwich, D. Yan, J. Popp and T. Frosch, Fiber-Array-Based Raman Hyperspectral Imaging for Simultaneous, Chemically-Selective Monitoring of Particle Size and Shape of Active Ingredients in Analgesic Tablets, Molecules, 2019, 24(23), 1–15,  DOI:10.3390/molecules24234381.
37. T. Frosch and J. Popp, Structural analysis of the antimalarial drug halofantrine by means of Raman spectroscopy and density functional theory calculations, J. Biomed. Opt., 2010, 15(4), 041516,  DOI:10.1117/1.3432656.
38. T. Frosch, M. Schmitt and J. Popp, Raman spectroscopic investigation of the antimalarial agent mefloquine, Anal. Bioanal. Chem., 2007, 387(5), 1749–1757,  DOI:10.1007/s00216-006-0754-1.
39. T. Frosch, M. Schmitt, T. Noll, G. Bringmann, K. Schenzel and J. Popp, Ultrasensitive in situ tracing of the alkaloid dioncophylline A in the tropical liana Triphyophyllum peltatum by applying deep-UV resonance Raman microscopy, Anal. Chem., 2007, 79(3), 986–993,  DOI:10.1021/ac061526q.
40. T. Frosch, M. Schmitt, K. Schenzel, J. H. Faber, G. Bringmann, W. Kiefer and J. Popp, In vivo localization and identification of the antiplasmodial alkaloid dioncophylline A in the tropical liana Triphyophyllum peltatum by a combination of fluorescence, near infrared Fourier transform Raman microscopy, and density functional theory calculations, Biopolymers, 2006, 82(4), 295–300,  DOI:10.1002/bip.20459.
41. T. Frosch, B. Küstner, S. Schlücker, A. Szeghalmi, M. Schmitt, W. Kiefer and J. Popp, In vitro polarization-resolved resonance Raman studies of the interaction of hematin with the antimalarial drug chloroquine, J. Raman Spectrosc., 2004, 35(10), 819–821,  DOI:10.1002/jrs.1252.
42. S. Fornasaro, S. Dalla Marta, M. Rabusin, A. Bonifacio and V. Sergo, Toward SERS-based point-of-care approaches for therapeutic drug monitoring: the case of methotrexate, Faraday Discuss., 2016, 187, 485–499.
43. D. Yan, T. Frosch, J. Kobelke, J. r. Bierlich, J. r. Popp, M. W. Pletz and T. Frosch, Fiber-enhanced Raman sensing of cefuroxime in human urine, Anal. Chem., 2018, 90(22), 13243–13248.
44. J. Xu, T. Jiao, S. S. Arumugam, P. He, J. Zhu, H. Li and Q. Chen, Quantitative analysis of docetaxel by surface-enhanced Raman spectroscopy (SERS) combined with chemometric models and Ag@ ZnO nanoparticles substrates, Elsevier, 2019.
45. L. Z. Benet and P. Zia-Amirhosseini, Basic principles of pharmacokinetics, Toxicol. Pathol., 1995, 23(2), 115–123.
46. R. S. Obach, F. Lombardo and N. J. Waters, Trend analysis of a database of intravenous pharmacokinetic parameters in humans for 670 drug compounds, Drug Metab. Dispos., 2008, 36(7), 1385–1405.
47. S. Shugarts and L. Z. Benet, The role of transporters in the pharmacokinetics of orally administered drugs, Pharm. Res., 2009, 26(9), 2039–2054.
48. J. A. Roberts and J. Lipman, Pharmacokinetic issues for antibiotics in the critically ill patient, Crit. Care Med., 2009, 37(3), 840–851.
49. J. A. Roberts, Using PK/PD to optimize antibiotic dosing for critically ill patients, Curr. Pharm. Biotechnol., 2011, 12(12), 2070–2079.
50. J. Gonçalves-Pereira and P. Póvoa, Antibiotics in critically ill patients: a systematic review of the pharmacokinetics of β-lactams, Crit. Care, 2011, 15(5), R206.
51. F. B. Sime, M. S. Roberts, S. L. Peake, J. Lipman and J. A. Roberts, Does beta-lactam pharmacokinetic variability in critically ill patients justify therapeutic drug monitoring? A systematic review, Ann. Intensive Care, 2012, 2(1), 35.
52. C. Ching and M. H. Zaman, Development and selection of low-level multi-drug resistance over an extended range of sub-inhibitory ciprofloxacin concentrations in Escherichia coli, Sci. Rep., 2020, 10(1), 8754,  DOI:10.1038/s41598-020-65602-z.
53. J. F. Barletta, A. J. Mangram, M. Byrne, A. K. Hollingworth, J. F. Sucher, F. R. Ali-Osman, G. R. Shirah and J. K. Dzandu, The importance of empiric antibiotic dosing in critically ill trauma patients: Are we under-dosing based on augmented renal clearance and inaccurate renal clearance estimates?, J. Trauma Acute Care Surg., 2016, 81(6), 1115–1121.
54. B. Jung, M. Mahul, D. Breilh, R. Legeron, J. Signe, H. Jean-Pierre, A.-C. Uhlemann, N. Molinari and S. Jaber, Repeated Piperacillin-Tazobactam Plasma Concentration Measurements in Severely Obese Versus Nonobese Critically Ill Septic Patients and the Risk of Under–and Overdosing, Crit. Care Med., 2017, 45(5), e470–e478.
55. A. T. Chow, C. Fowler, R. R. Williams, N. Morgan, S. Kaminski and J. Natarajan, Safety and pharmacokinetics of multiple 750-milligram doses of intravenous levofloxacin in healthy volunteers, Antimicrob. Agents Chemother., 2001, 45(7), 2122–2125.
56. S.-C. Chien, F. A. Wong, C. L. Fowler, S. V. Callery-D'Amico, R. R. Williams, R. Nayak and A. T. Chow, Double-blind evaluation of the safety and pharmacokinetics of multiple oral once-daily 750-milligram and 1-gram doses of levofloxacin in healthy volunteers, Antimicrob. Agents Chemother., 1998, 42(4), 885–888.
57. R: A Language and Environment for Statistical Computing, 2019. https://www.R-project.org/(accessed).
58. signal: Signal processing, 2014. https://r-forge.r-project.org/projects/signal/(accessed).
59. EMSC: Extended Multiplicative Signal Correction, 2017. https://CRAN.R-project.org/package=EMSC (accessed).
60. Peaks: Peaks, 2012. https://CRAN.R-project.org/package=Peaks (accessed).
61. minpack.lm: R Interface to the Levenberg-Marquardt Nonlinear Least-Squares Algorithm Found in MINPACK, Plus Support for Bounds, 2016. https://CRAN.R-project.org/package=minpack.lm (accessed).
62. pls: Partial Least Squares and Principal Component Regression, 2019. https://CRAN.R-project.org/package=pls (accessed).
63. C. Ryan, E. Clayton, W. Griffin, S. Sie and D. Cousens, SNIP, a statistics-sensitive background treatment for the quantitative analysis of PIXE spectra in geoscience applications, Nucl. Instrum. Methods Phys. Res., Sect. B, 1988, 34(3), 396–402.
64. H. Martens and E. Stark, Extended multiplicative signal correction and spectral interference subtraction: new preprocessing methods for near infrared spectroscopy, J. Pharm. Biomed. Anal., 1991, 9(8), 625–635.
65. J. Skogholt, K. H. Liland and U. G. Indahl, Preprocessing of spectral data in the extended multiplicative signal correction framework using multiple reference spectra, J. Raman Spectrosc., 2019, 50(3), 407–417.
66. R. Wehrens and B.-H. Mevik, The pls package: principal component and partial least squares regression in R, 2007.
67. M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Revision A. 02, Gaussian. Inc., Wallingford, CT, 2009, pp. 200.
68. A. Becke, Density–functional thermochemistry. II. The effect of the Perdew–Wang generalized–gradient correlation correction, J. Chem. Phys., 1992, 97(12), 9173–9177.
69. P. Stephens, F. Devlin, C. Chabalowski and M. Frisch, Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields, J. Phys. Chem., 1994, 98(45), 11623–11627.
70. C. Lee, W. Yang and R. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785.
71. T. Dunning, A road map for the calculation of molecular binding energies, J. Phys. Chem. A, 2000, 104(40), 9062–9080.
72. P. Polavarapu, Ab initio vibrational Raman and Raman optical activity spectra, J. Phys. Chem., 1990, 94(21), 8106–8112.
73. Iupac, IUPAC Gold Book, 2014. https://goldbook.iupac.org/terms/view/L03540 (accessed).
74. E. R. Garrett, Simplified methods for the evaluation of the parameters of the time course of plasma concentration in the one-compartment body model with first-order invasion and first-order drug elimination including methods for ascertaining when such rate constants are equal, J. Pharmacokinet. Biopharm., 1993, 21(6), 689–734.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3an00402c

---