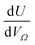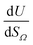Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Brute force determination of the optimum pore sizes for CO2 uptake in turbostratic carbons†
L. Scott
Blankenship
 *a,
Nawaf
Albeladi‡
*a,
Nawaf
Albeladi‡
 ab,
Thria
Alkhaldi‡
ab,
Thria
Alkhaldi‡
 ac,
Asma
Madkhali‡
ac,
Asma
Madkhali‡
 ad and
Robert
Mokaya
ad and
Robert
Mokaya
 a
a
aSchool of Chemistry, University of Nottingham, University Park, Nottingham, NG7 2RD, UK. E-mail: leo.blankenship@nottingham.ac.uk
bChemistry Department, Faculty of Sciences Yanbu, Taibah University, Yanbu Al Bahr, 46423, Saudi Arabia
cDepartment of Chemistry, Jeddah University, Jeddah 23442, Saudi Arabia
dDepartment of Chemistry, University College in Samtah, Jazan University, Samtah 86736, Saudi Arabia
First published on 24th October 2022
Abstract
Porosity, and in particular pore size is one of the most important considerations in the development of porous carbons for CO2 capture. Current methods for determining the optimum pore size for adsorption of gases either make very broad assumptions (in computational studies), or are not sufficiently exhaustive (in experimental studies). Herein we present a piece of software known as the python Porosity Uptake Correlator (pyPUC) which employs a brute force, first principles method for determining the range of pore sizes, Ω, best suited to adsorption of a given sorptive at a range of pressures. As an initial test, pyPUC is used to determine Ω for CO2 in a broad pressure range according to N2 porosimetry. The analysis is then extended to other porosimetric sorptives and combinations thereof to assess their efficacy in determining Ω for CO2, and we find that traditional N2 porosimetry is insufficient for determining the relationship between pore size and CO2 uptake in ultramicroporous turbostratic carbons. While pyPUC is not meant as a predictive tool, it facilitates a more robust and thorough investigation of the relationship between porosity and adsorbate uptake capacity than current methods, and provides a method for understanding such relationships more generally.
1 Introduction
Porous carbons have been extensively investigated for their potential use in gas storage and/or capture applications, in particular related to energy storage applications including for alternative fuels such as H2 and CH4 or for CO2 capture.1–9 A material's storage capacity for a particular sorptive is known to be related to the porosity of the material, and in particular the pore width plays an important role.5,10–21 Pore entrances for sorption of some gas at a given pressure and temperature must be large enough for the molecule in question can diffuse into it. This lower limit to the so-called pore size range is not necessarily solely determined by the size of the molecule; for example while N2 has a nominal kinetic diameter (dk) of 3.60 Å, it has been observed that at −196 °C in biochars this molecule diffuses extremely slowly into pores of width 4 Å.22–24 On the other hand, adsorption can be improved by optimising the interactions between parallel pore walls and adsorptive molecules. That is, when the distance between pore walls is sufficiently small, adsorbed molecules are affected by physical attraction to both walls, which increases the heat of adsorption and thus the retention of molecules within the pores.25,26 This is particularly significant at low pressures where the adsorbate–adsorbent interactions dominate.13,15,27–34 It follows therefore, that there is a range of optimum pore sizes for adsorption of any given molecule at some pressure and temperature.There have been several attempts to determine the optimum pore size for given sorptives under some conditions. In general, the approach to this has been to either identify the ‘ideal’ pore size, i.e. a single width such as 6 Å for H2 with slight variations depending on temperature and pressure.12,28 An alternative method is to propose larger regions, i.e. an optimum pore size range (herein referred to as Ω);15,35,36 for H2 it has been reported that ultramicropores, i.e. pores of width <7 Å are ideal.20,31 Sdanghi et al. expanded on this, finding that pores narrower than 6.0 Å are essential for maximising H2 storage at pressures below 1 bar, while broader PSDs are more relevant at higher pressures.37 In practice, these regions or single widths are determined via purely computational methods or from experimentally determined uptakes and pore size distributions (PSDs). Computational methods attempt to determine the uptake of the sorptive in an idealised sorbent with pores of a single width via Density Functional Theory (DFT) or Grand Canonical Monte Carlo (GCMC) methods.5,12,38 Whereas experimental data can be used to performing linear regressions of uptake at a given pressure against pore volume in a certain range (usually all pores below some maximum).11,13,15,17,35,39 By the latter method, Presser et al. determined (N = 24) that at 1.0 bar, pores in activated carbons of width <8 Å are most strongly associated with gravimetric CO2 uptake, while this reduced to 5 Å for uptake at 0.1 bar. Pores larger than 10 Å, as well as the oft-used parameter of average pore size were shown to be poor predictors of uptake at these low pressures.13 Average pore size can however be useful when compared against so-called uptake density (uptake per unit surface area). For example, Masika et al. found that uptake density of H2 (1 bar, −196 °C) reduced drastically as average pore width increased from 10 to 20 Å.16
Current experimental approaches to determining Ω are limited in that they typically only consider a small set of possible Ωs, which is informed by theoretical data, and only at one or two pressures. Furthermore, the lower limit of the Ω is not typically varied – the assumption being that pores larger than the diameter of the sorptive will always be strong contributors to sorptive uptake under all conditions. As for computational studies, not only is the use of materials having a single pore width unrealistic for amorphous porous carbon, it is difficult to account for factors such as surface chemical and energetic heterogeneity and variation in pore geometry. Thus we present herein the python Porosity Uptake Correlator (pyPUC); a combined, iterative experimental and computational approach to Ω determination. Regressions are performed using experimental data between all possible Ωs at a large range of pressures and used to determine the Ω at each pressure. Both the range and increment of the possible Ωs and pressures can be easily adjusted to give an extremely fine level of detail. As a demonstration, pyPUC is applied to the determination of Ω for CO2 uptake in amorphous carbons at 25 °C where porosity is determined from N2 sorption isotherms obtained at −196 °C. The relative efficacy of H2, O2, and N2 (−196 °C) isothermal porosimetry as well as dual fit N2/H2 and O2/H2 analyses is then assessed for their ability to predict Ω for CO2 in highly ultramicroporous carbons.
2 Methods
2.1 pyPUC
The pyPUC software requires both total gravimetric uptake isotherms (υ) for the adsorptive in question, and cumulative PSDs (π) for a set of porous samples. Firstly, a model isotherm is fit to each experimental isotherm in υ using the pyGAPS adsorption isotherm processing framework, via the modelling package initially developed in pyIAST.40,41 These model isotherms are converted to point isotherms according to some user-defined pressure range and increment. Thus, discrete loadings are determined for all samples at identical pressures, and are stored in the loading DataFrame (Dυ).Next, from π the apparent pore volume (V) or surface area (S) of each sample between the minimum and maximum pore width (wmin and wmax, respectively) is determined via;
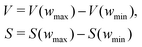 | (1) |
This is repeated across all pairs of wmax and wmin prescribed by the user, thus generating a parameter DataFrame (Dπ). The number of parameters calculated Nπ is thus related to the number of pore widths defined in the calculation Nw by;
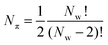 | (2) |
Thereafter, linear regressions are determined between every row of Dυ and Dπ to give the correlation DataFrame (Dc), i.e. Dc shows how well porosity (in terms of V or S) within each pore width range in Dπ correlates to the loading of the sorptive on the samples at each pressure in Dυ. Each row of Dc contains the Pearson coefficient (r2),42 slope (m) and intercept (c) of the regression. Finally, the best correlation at each pressure may be found simply by selecting the maximum r2 value for a given pressure after the exclusion of regressions giving a negative slope. This is repeated for all pressures, giving the Ω associated with uptake of the sorptive at each pressure.
2.2 Carbon synthesis
Carbons were synthesised by pyrolysis of various biomasses and synthetic polymers either alone or with the aid of a porogen. In all cases they were washed after synthesis to remove any non-carbonaceous matter. Synthetic summaries are provided in for DataSet 1 (33 samples) and DataSet 2 (12 samples) in Tables S1.1 and S2.1 (ESI†) respectively. DataSet 1 was selected to give a large variety of PSDs that are representative of so-called activated carbons in general; that is samples in this group have either solely microporous, solely mesoporous or hierarchical (i.e. mixed) PSDs. DataSet 2 contains principally microporous materials, especially those containing a large proportion of so-called ultramicropores (w < 7).2.3 Isotherm measurement and processing
All raw experimental isotherms measured as described below are available in the electronic ESI,† as human- and machine-readable .aif files.43 N2, O2, and H2 isotherms for determination of PSDs were measured at −196 °C on a Micromeritics 3flex porosimeter at pressures up to P0 for N2 and O2 and 1013 mbar for H2. PSDs were determined using the SAIEUS software with the appropriate 2D-NLDFT heterogeneous surface kernel(s), in order to adequately account for chemical and energetic heterogeneity. Within SAIEUS it is possible to select an appropriate fitting parameter, λ44–46 which controls the roughness of the PSD. λ was selected to provide the most realistic differential PSD based on known properties of carbons, and in all cases was between 2.5 and 5.0 and kept constant for carbons derived from the same precursor (see Tables S1.1 and S2.1, ESI†). Isotherms and derived PSDs can be found in Fig. S1.6–S1.10 and S2.4–S2.12 (ESI†).Gravimetric CO2 uptakes were measured on gravimetric analysers provided by Hiden; either the XEMIS analyser at 25 °C (0–40 bar) or the IGA at 18 °C (0–20 bar) for DataSet 1 and 2 respectively. Fits were attempted with Langmuir,47,48 Double Site Langmuir (DSLangmuir),48 Triple Site Langmuir (TSLangmuir),48 Guggenheim–Anderson–de Boer (GAB),49–51 Freundlich,52 Dubinin–Raduschkevich (DR)53 and Toth54 theoretical isotherms using pyGAPS (see Section 2.1). The best fit was then selected by minimum root mean square error (RMSE). CO2 isotherms as well as their best fits and details thereof can be found in Fig. S1.1–S1.5 and S2.1–S2.3 (ESI†).
3 Results and discussion
3.1 From N2 isotherms only
We first present the use of pyPUC to determine Ω according to porosity derived from isotherms of the “traditional” porosimetric molecule, N2. This is to establish the validity of this brute force method and to compare results derived in this way to those reported in the literature. A set of 33 carbon samples were used in this section.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 linear regressions, which were used to determine the Ω at each of the 40 pressures defined in Dυ in terms of V and S i.e. ΩV and ΩS respectively. A more detailed calculation, using a Dπ of 500 values between 3.6 and 500 Å was also performed in order to ascertain the effect of increasing the granularity of detail used in the input data on the calculated Ω. This calculation took almost 7 days each for ΩV and ΩS compared to the original calculation which was completed within 24 h and results are not significantly different. As such this data was not used as the basis of the study. A comparison can be seen in Fig. S1.11 (ESI†).
000 linear regressions, which were used to determine the Ω at each of the 40 pressures defined in Dυ in terms of V and S i.e. ΩV and ΩS respectively. A more detailed calculation, using a Dπ of 500 values between 3.6 and 500 Å was also performed in order to ascertain the effect of increasing the granularity of detail used in the input data on the calculated Ω. This calculation took almost 7 days each for ΩV and ΩS compared to the original calculation which was completed within 24 h and results are not significantly different. As such this data was not used as the basis of the study. A comparison can be seen in Fig. S1.11 (ESI†).
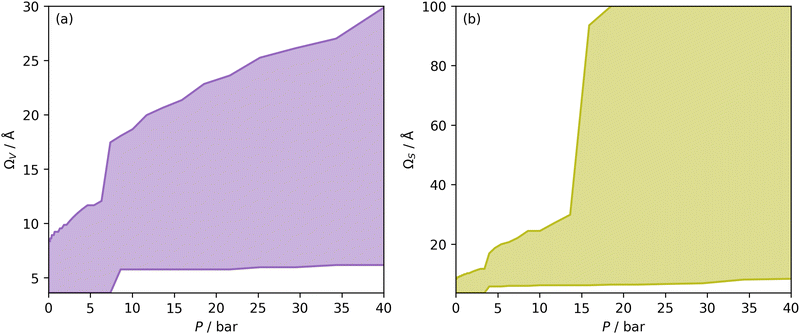 | ||
| Fig. 1 Ω V (a) and ΩS (b) at each pressure, i.e. optimum wmax and wmin plotted against pressure. The shaded area is thus the Ω in each case. | ||
Once Ω begins to exclude ultramicropores, there is a sharp increase in wmax. As a result, ΩS includes both supermicropores and small mesopores after 6 bar. Conversely, ΩV remains strictly in the supermicropore region until 13 bar. Again, this seems to be an indication of the difference in the how surface area vs. pore volume improve adsorption of CO2. That is smaller pores result in improved sorptive–sorptive interactions, while larger pores provide more surface for CO2 to interact with. This is further exhibited by the large increase in wmax up to 100 Å for ΩS at 16 bar which does not exist for ΩV. Of course, this upper limit for ΩS is not real but represents the upper limit of wmax established in the determination of Dπ. Nevertheless, these results may inform design of porous carbons for different applications; for example a carbon with high porosity below 8.0 Å is best suited for low pressure capture of CO2, whereas carbons for so-called pressure-swing adsorption (PSA) should have hierarchical micro-mesoporous PSDs with minimal porosity below 8.0 Å. This confirms previous reports.13,15,27,55,56
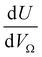 or
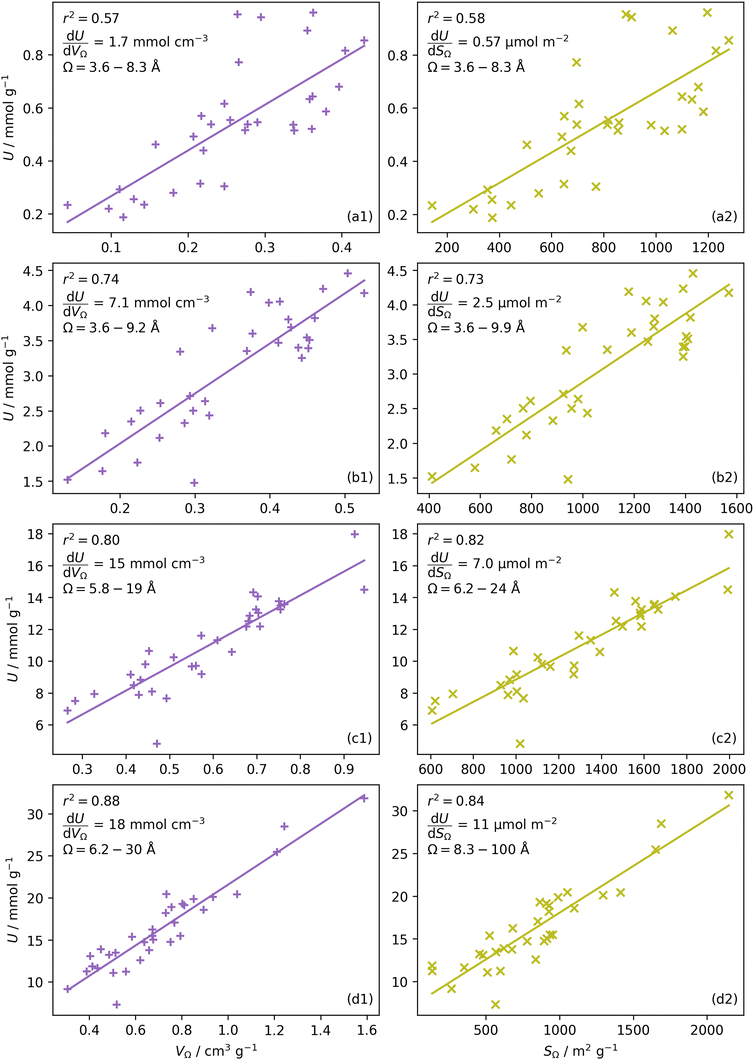
or 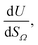 as derived from the linear regression. It is thus possible to predict the effect of increasing pore volume within the Ω on CO2 uptake at that pressure, i.e. increasing volume of pores of width 3.6–8.3 Å by 1 cm3 g−1 ought to result in an increase in uptake of 1.7 mmol g−1 CO2 at 0.1 bar, whereas the same increase in pore volume in the range 6.2–30 Å (approximately the supermicropore and small mesopore region) results in an improvements in CO2 uptake at 40 bar of 18 mmol g−1. If we examine slopes of fits in Fig. 2, (column b), a similar pattern appears, with an increase in surface area of 1000 m2 g−1 in pores between 3.6 and 8.3 Å corresponding to a meager 0.57 mmol g−1 improvement in CO2 uptake at 0.1 bar compared with an increase in uptake of 11 mmol g−1 at 40 bar when surface area in pores of width 8.3–100 Å increases by the same amount.
as derived from the linear regression. It is thus possible to predict the effect of increasing pore volume within the Ω on CO2 uptake at that pressure, i.e. increasing volume of pores of width 3.6–8.3 Å by 1 cm3 g−1 ought to result in an increase in uptake of 1.7 mmol g−1 CO2 at 0.1 bar, whereas the same increase in pore volume in the range 6.2–30 Å (approximately the supermicropore and small mesopore region) results in an improvements in CO2 uptake at 40 bar of 18 mmol g−1. If we examine slopes of fits in Fig. 2, (column b), a similar pattern appears, with an increase in surface area of 1000 m2 g−1 in pores between 3.6 and 8.3 Å corresponding to a meager 0.57 mmol g−1 improvement in CO2 uptake at 0.1 bar compared with an increase in uptake of 11 mmol g−1 at 40 bar when surface area in pores of width 8.3–100 Å increases by the same amount.
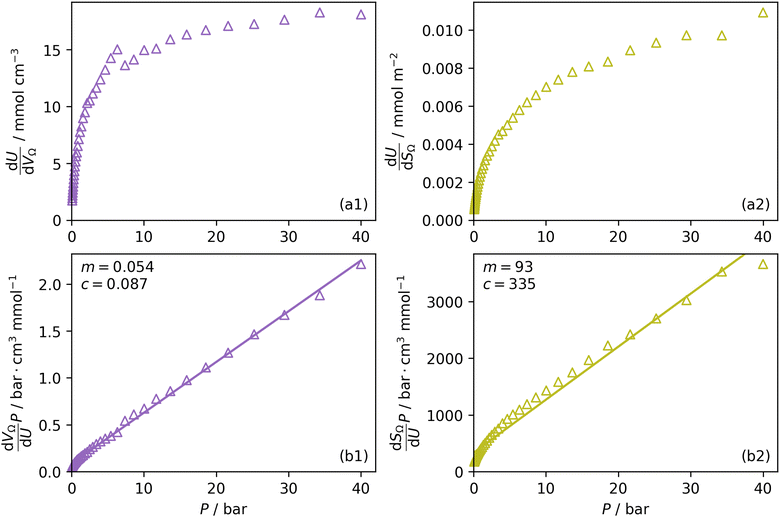
Furthermore, a clear positive, semi-logarithmic trend is observed between 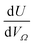 and P, i.e. it takes the form of a gas adsorption isotherm (see Fig. 3). A similar transform to that used in determination of a Langmuir isotherm47 demonstrates a strong relationship of the form;
and P, i.e. it takes the form of a gas adsorption isotherm (see Fig. 3). A similar transform to that used in determination of a Langmuir isotherm47 demonstrates a strong relationship of the form;
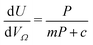 | (3) |
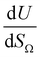 by the same treatment as in eqn (3), where m = 93 m2 mmol−1. However the relationship between
by the same treatment as in eqn (3), where m = 93 m2 mmol−1. However the relationship between 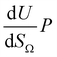 and P is not exactly linear. Nevertheless, it is clear that with increasing pressure, improvements in ΩV or ΩS correspond to rapid improvements in U at low pressures, but these improvements diminish at higher pressures. This is likely a result of a reduction in enthalpy of adsorption with increasing adsorbate loading.
and P is not exactly linear. Nevertheless, it is clear that with increasing pressure, improvements in ΩV or ΩS correspond to rapid improvements in U at low pressures, but these improvements diminish at higher pressures. This is likely a result of a reduction in enthalpy of adsorption with increasing adsorbate loading.
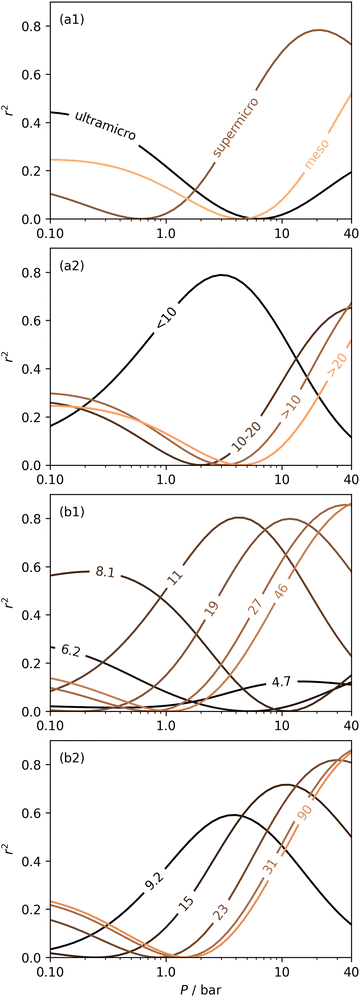
In Section 3.1.2 and Fig. 1 we see that at lower pressures Ω is approximately 3.6–10 Å. Therefore, a reasonable alternative to the traditional subdivision of micropores at 7 Å could be at 10 Å. As shown in Fig. 4(a2), pores of width <10 Å do indeed show improved correlation with CO2 uptake at relatively low pressures with r2 reaching 0.79 at 2.9 bar. Conversely the larger subdivision, i.e. between 10 and 20 Å does not show improvements relative to the supermicropore designation, and has much poorer correlations at high pressures. Expanding this pore size region to include all pores above 10 Å does not significantly improve r2 values in the pressure range used in this study. In other words it appears that pore size regions to target for high (10–40 bar) and medium (<10 bar) pressure uptake overlap, with the former being pores above 7 Å, and the latter below 10 Å. Low pressures (<1 bar) require even smaller pores of widths less than 8–9 Å (see Fig. 1 and 2(a1-2, b1-2)).
Fig. 4(b1 and b2) show the effect of a broadening pore size region on the relationship between r2 and P, with a fixed lower limit of 3.6 and 7.0 Å respectively. These lower limits correspond to the two values of wmin mentioned in 3.1.2. In both cases small increases in wmax have a strong affect on the pressure at which correlation is strongest for the pore size region. However at higher values of wmax, this discrepancy is reduced. For example pores of width 7.0–31 and 7.0–90 Å have their strongest association (r2 ≈ 0.85) with CO2 uptake at 40 bar. This corresponds roughly to ΩV at 40 bar (Fig. 2(d1)) and shows that at high pressures larger pores may not significantly effect adsorption of CO2. It is interesting to note that very narrow pore size ranges i.e. 3.6–4.7 and 3.6–6.2 Å (Fig. 4(b1)) do not show any significant relationship to CO2 uptake, in fact r2 never exceeds 0.27 for either of these pore size regions, so any variation in r2 here is of limited interpretation. That is, there appears to be a lower limit to pore size that positively affects uptake at pressures of 0.10 bar and greater which is around 8.1 Å.
3.2 Highly ultramicroporous carbons
We recently reported on relative improvements in the precision of PSDs determination by use of dual fits of DFT kernels to O2 and H2 isotherms relative to using N2 and H2.34 This was particularly relevant to so-called biochars and carbons activated with small amounts of porogen, both having a high proportion of ultramicropores. The rationale being that N2's poor diffusion into ultramicropores meant that PSDs, especially at the smaller end of the micropore region, are imprecise. In addition, when NLDFT kernels were fit to N2, O2 and H2 isotherms individually there were notable discrepancies in derived PSDs, which were more evident for the more ultramicroporous carbons.34 In the previous section it was noted that the Pearson coefficient for Ω was very low at low pressures, which may be a result of imprecise PSDs for DataSet 1 in the ultramicropore region. It is useful therefore to examine the relative results of Ω determination using PSDs from single N2, O2 and H2 isotherms as well as from dual kernel fitting. The following sections examine PSDs from these sorptives and combinations thereof in the determination of optimum porosity in the 12 carbons in DataSet 2. Synthetic details for these samples can be found in Table S2.1 (ESI†).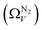 isotherms (Fig. 5(a1)) gives the unreasonable conclusion that up to 2.1 bar
isotherms (Fig. 5(a1)) gives the unreasonable conclusion that up to 2.1 bar 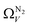 is constant at around 5.8–6.3 Å. This is both a surprisingly narrow range, and it is unlikely that there would be effectively no broadening of
is constant at around 5.8–6.3 Å. This is both a surprisingly narrow range, and it is unlikely that there would be effectively no broadening of 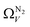 with increasing P up to this point. Similarly, after 2.1 bar
with increasing P up to this point. Similarly, after 2.1 bar 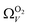 (Fig. 5(a2)) drops to a very narrow, relatively constant range (approximately 10–11 Å). This may simply be an effect of the minimal increases in CO2 uptake for these carbons above 2 bar (see Fig. S2.1–S2.3, ESI†), which is attributable to the very low porosity of these carbons in the supermicropore and mesopore regions (see Fig. S2.4–S2.6, ESI†).34 As such discussions of these analyses are best limited to uptakes at P < 2.0 bar.
(Fig. 5(a2)) drops to a very narrow, relatively constant range (approximately 10–11 Å). This may simply be an effect of the minimal increases in CO2 uptake for these carbons above 2 bar (see Fig. S2.1–S2.3, ESI†), which is attributable to the very low porosity of these carbons in the supermicropore and mesopore regions (see Fig. S2.4–S2.6, ESI†).34 As such discussions of these analyses are best limited to uptakes at P < 2.0 bar.
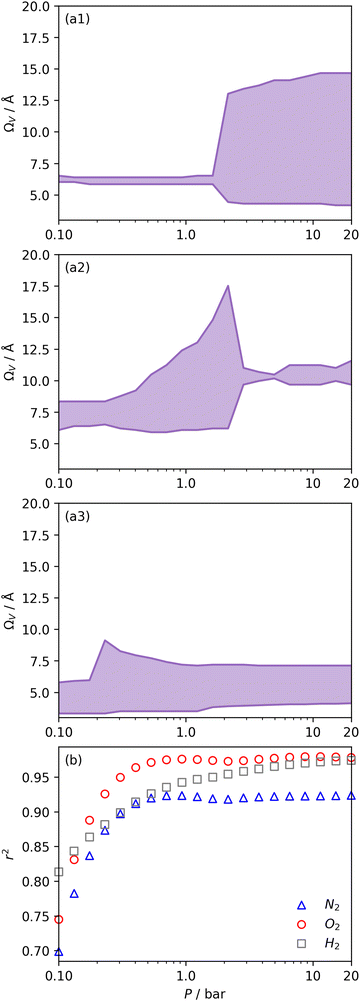 | ||
| Fig. 5 Ω V calculated from DataSet 2 using PSDs derived from N2 (a1), O2 (a2), and H2 (a3) isotherms as well as corresponding r2 values (b). | ||
For analyses using both O2 and H2 there is a broadening in ΩV with increasing P at relatively low pressures which is not present according to N2 analysis. In addition, as shown in Fig. 5(b), r2 is lower at all pressures for correlations derived using 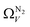 data compared to
data compared to 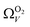 and
and 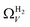 . While
. While 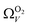 data shows the best correlations in general, r2 from
data shows the best correlations in general, r2 from 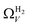 data is greater at 0.10 and 0.13 bar. In other words, for this set of carbons, porosity accessible to CO2 is best determined using H2 isotherms up to 0.13 bar, and thereafter (up to around 2.0 bar) using O2 isotherms. This follows from the standpoint of H2 having access to – and thus predicting the presence of – pores of widths as small as 3.0 Å, while the lower limit for O2 is 3.6 Å. Thus the contribution of pores of widths less than 3.6 Å to low pressure CO2 uptake can only be accounted for using H2 porosimetry, yielding
data is greater at 0.10 and 0.13 bar. In other words, for this set of carbons, porosity accessible to CO2 is best determined using H2 isotherms up to 0.13 bar, and thereafter (up to around 2.0 bar) using O2 isotherms. This follows from the standpoint of H2 having access to – and thus predicting the presence of – pores of widths as small as 3.0 Å, while the lower limit for O2 is 3.6 Å. Thus the contribution of pores of widths less than 3.6 Å to low pressure CO2 uptake can only be accounted for using H2 porosimetry, yielding 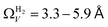 . At 0.17 bar and above, pores above 6.0 Å appear to become more heavily utilised for CO2 adsorption according to relative magnitudes of r2. The upper limit of porosity measurable by H2 at −196 °C is unknown, however it is usually said to be between 8.0–10 Å.22,24 This explains why results for
. At 0.17 bar and above, pores above 6.0 Å appear to become more heavily utilised for CO2 adsorption according to relative magnitudes of r2. The upper limit of porosity measurable by H2 at −196 °C is unknown, however it is usually said to be between 8.0–10 Å.22,24 This explains why results for 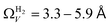 become less reasonable at pressures above 0.3 bar; H2 porosimetry is unsuitable for prediction of CO2 uptake at these pressures. Indeed, in determination of PSDs from fitting of the DFT kernel to H2 isotherms, wmax was set to 10 Å.
become less reasonable at pressures above 0.3 bar; H2 porosimetry is unsuitable for prediction of CO2 uptake at these pressures. Indeed, in determination of PSDs from fitting of the DFT kernel to H2 isotherms, wmax was set to 10 Å.
Fig. 6 presents further information on the relative efficacy of the three sorptives in measuring pores of widths below some limit (wmax), and the relationship between pores of these widths and CO2 uptake between 0.10 and 2.0 bar. It is striking that when wmax is set at 5.0 or 6.0 Å, only H2 porosimetry provides reasonable correlations (r2 > 0.60) at any pressure. Indeed, in the case of O2 (see Fig. 6(b)) r2 is zero at all pressures and thus cannot be displayed within the figure. Strong correlations only begin to be shown when wmax is set to 10. PSDs derived from O2 isotherms do show porosity in the ultramicropore region, thus it may be concluded that the ultramicropores accessible to O2 are not important for CO2 uptake, while those ultramicropores accessible to H2 do contribute to CO2 uptake. The latter statement can be accounted for by the fact that H2 has access to pores undetectable by O2. Similar rationale can be applied to the plot for N2 (Fig. 6(a)). When wmax is increased past 10 Å, r2vs. P plots become very similar in the case of calculations made using both N2 and O2 derived PSDs. This indicates that there is little measurable improvement in CO2 adsorption (under 2.0 bar) by broadening the PSD past 10 Å, however this may simply be a result of the relatively narrow PSDs present in these samples.
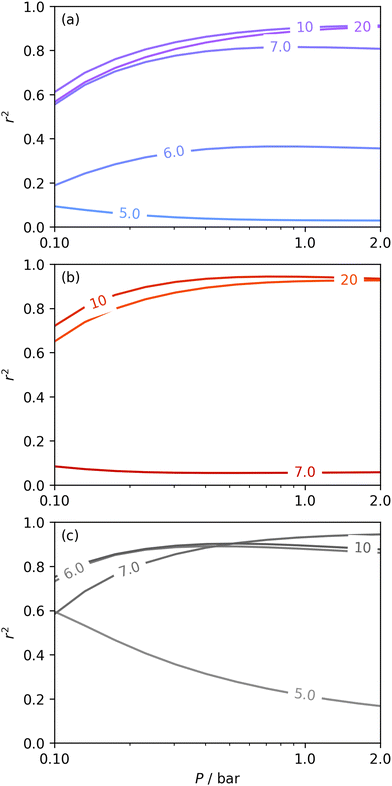 | ||
| Fig. 6 Comparison of dependence of r2 on pressure with increasing wmax as determined using PSDs from N2 (a), O2 (b), and H2 (c) isotherms. | ||
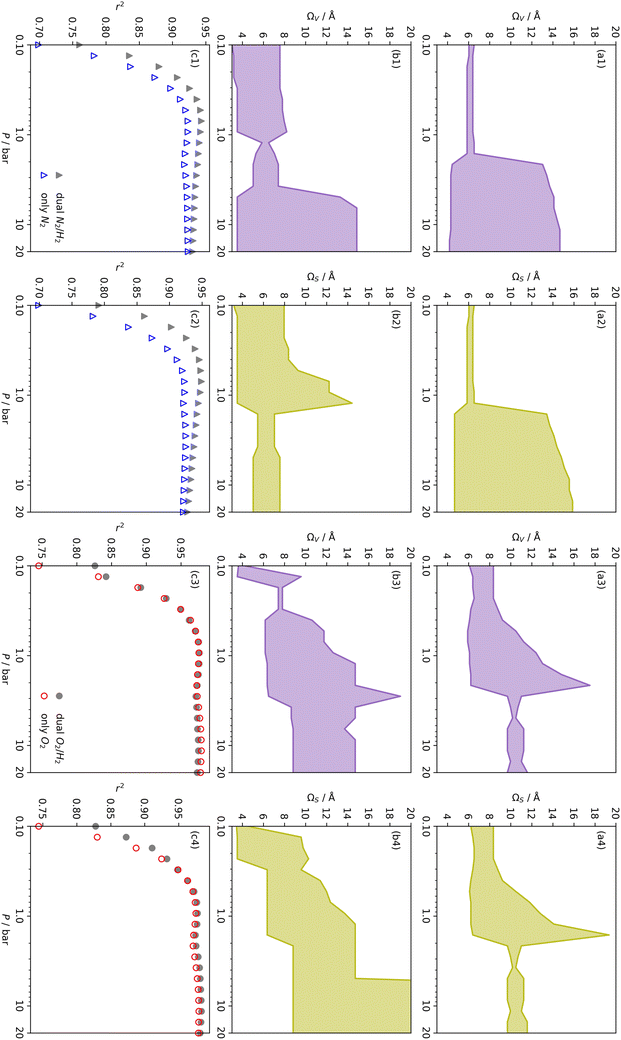
In summary, examination of Dc for DataSet 2 with each of the three porosimetric sorptives shows that low pressure (<2.0 bar) CO2 uptake is improved by increasing volume in pores below 10 Å. In addition, N2 is consistently outperformed by O2 and/or H2 at measuring porosity appropriate for CO2 uptake. However, while porosity as determined by O2 improves CO2 uptake at pressures above 0.13 bar, H2 is needed to determine optimum porosity for uptake at ultra-low pressures. It is therefore logical to consider PSDs as determined via dual isotherm analysis as a way to extend the range of pressures at which optimum pore size for CO2 can be accurately determined.
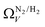 the improvement over single fit is principally in that the breadth of pore sizes (approx. 3.0–8.0 Å) in
the improvement over single fit is principally in that the breadth of pore sizes (approx. 3.0–8.0 Å) in 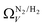 below 1.0 bar is much more realistic than for
below 1.0 bar is much more realistic than for 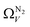 . There is however no broadening within this region with increasing pressure, unlike for
. There is however no broadening within this region with increasing pressure, unlike for 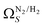 which may be a result of the difference in nature of adsorbate–adsorbent as compared with adsorbate–adsorbate interactions as highlighted in Section 3.1.2. In addition to the relationship between Ω and P being more realistic in terms of both surface area and pore volume, the r2 is consistently better for both
which may be a result of the difference in nature of adsorbate–adsorbent as compared with adsorbate–adsorbate interactions as highlighted in Section 3.1.2. In addition to the relationship between Ω and P being more realistic in terms of both surface area and pore volume, the r2 is consistently better for both 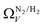 (c1) and
(c1) and 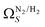 (c2) than their single-isotherm PSD counterparts. That is to say, that extending the range of accurate, measurable porosity well into the ultramicropore region yields improved certainty in the determination of optimum porosity for CO2 uptake.
(c2) than their single-isotherm PSD counterparts. That is to say, that extending the range of accurate, measurable porosity well into the ultramicropore region yields improved certainty in the determination of optimum porosity for CO2 uptake.
r
2 values for 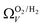 and
and 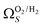 only shows noticeable improvements at pressures below 0.30 bar compared to their single isotherm counterparts (Fig. 7(c3 and c4)). This again indicates the importance of porosity penetrable by H2 alone in the adsorption of CO2 at low pressures. For
only shows noticeable improvements at pressures below 0.30 bar compared to their single isotherm counterparts (Fig. 7(c3 and c4)). This again indicates the importance of porosity penetrable by H2 alone in the adsorption of CO2 at low pressures. For 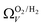 (Fig. 7(b3)) this corresponds to a significantly smaller range at low pressures, with pores in the range 3.6–4.2 Å being most associated with CO2 uptake at 0.10 bar, compared to 6.1–8.3 Å for
(Fig. 7(b3)) this corresponds to a significantly smaller range at low pressures, with pores in the range 3.6–4.2 Å being most associated with CO2 uptake at 0.10 bar, compared to 6.1–8.3 Å for 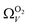 (Fig. 7(a3)). Broadening in
(Fig. 7(a3)). Broadening in 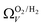 is also briefly apparent as P increases to 0.13 bar, but falls to an unrealistically narrow range again quickly. On the other hand
is also briefly apparent as P increases to 0.13 bar, but falls to an unrealistically narrow range again quickly. On the other hand 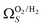 (Fig. 7(b4)) gives the most physically reasonable result as it broadens consistently with increasing P. Furthermore, we see three distinct values of wmin of 3.5, 6.3, and 8.8 Å. The latter two values reflect the results shown in Fig. 1, indicating that the use of dual O2/H2 isotherms gives information on the pressures at which the influence of the smallest of ultramicropores on CO2 uptake is greatest, that is below 0.30 bar.
(Fig. 7(b4)) gives the most physically reasonable result as it broadens consistently with increasing P. Furthermore, we see three distinct values of wmin of 3.5, 6.3, and 8.8 Å. The latter two values reflect the results shown in Fig. 1, indicating that the use of dual O2/H2 isotherms gives information on the pressures at which the influence of the smallest of ultramicropores on CO2 uptake is greatest, that is below 0.30 bar.
The utility of dual isotherm porosimetry with H2 as one of the probes in CO2 porosity uptake correlations is further emphasised on examination of the dependency of r2 on P with broadening PSDs (see Fig. 8). In the case of the corresponding plots for single isotherm fits (Fig. 6) H2 was the only probe molecule that provided strong correlations where wmax is 5.0 or 6.0 Å. While dual N2/H2 porosimetry (Fig. 8(a)) provides some improvements for these narrow pore width ranges compared to single isotherm N2 (Fig. 6(a)), the most significant improvements are for O2/H2 relative to O2. Indeed, for all values of wmax between 5.0 and 7.0 Å there are reasonable r2 values (>0.50) (Fig. 8(b)) at some pressure, with wmax = 5.0 Å showing the greatest improvement relative to the its single isotherm counterpart. In fact, the plot for 5.0 Å shows improvement even relative to its corresponding plot from single isotherm H2 porosimetry (Fig. 6(c)), as r2 does not fall below 0.50 at pressures below 5.0 bar. In other words, while H2 porosimetry shows that pores of width less than 5.0 Å have a reasonable association with CO2 uptake at 0.10 bar only, combined O2/H2 porosimetry shows that this continues to much higher pressures.
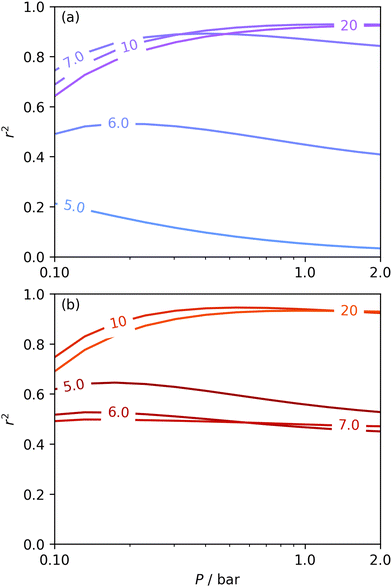 | ||
| Fig. 8 Comparison of dependence of r2 on pressure with increasing wmax as determined using PSDs from dual N2/H2 (a) and O2/H2 (b) isotherms. | ||
It appears therefore that dual O2/H2 porosimetry may give a more nuanced and reasonable picture of porosity relevant to CO2 uptake within samples in DataSet 2 as compared to both dual N2/H2 analysis as well as PSDs from single sorptives. In particular, if we compare results from O2/H2 analysis to the traditional N2 analysis it is interesting that the presence of micropores of width <5.0 Å according to the former (Fig. 8(b)) are at least as important as micropores in general according to the latter for CO2 uptake at very low pressures (see Fig. 8(b) and 6(a), respectively). While more investigation is necessary to determine the precise reasons for the differences in results given by dual isotherm O2/H2 and the other methods measurement of the porosity most relevant to CO2 uptake in highly ultramicroporous carbons, it remains clear that both the certainty of these results from the former and their correspondence with accepted theory of gas adsorption in pores is better.
4 Conclusions
pyPUC shows promise in its ability to thoroughly and definitively elucidate the relationship between porosity within some pore size range, and uptake of a gas at some pressure. We have examined its utility in determining the optimum pore size region in terms of pore volume or surface area (ΩV or ΩS) for CO2 capture in turbostratic carbons at pressures between 0.10 and 40 bar. More than broadly confirming reports by previous experimental and theoretical studies, this work gives a much higher level of precision concerning the relationship between Ω and P. Furthermore, it is possible to approximately predict the increase in CO2 uptake achieved by increasing porosity within the Ω. Apart from optimum pore sizes ranges, we also find the relationship between pores within arbitrary width ranges on CO2 uptake.In addition this method allows facile, comprehensive comparison of such results using different isothermal porosimetric methods for PSD determination. This is particularly relevant to highly ultramicroporous carbons, wherein the utility of N2 has been called into question. Here, we show that dual isotherm analysis, and in particular O2/H2 analysis improves our predictions of CO2 uptake especially at very low pressures.
The pyPUC method can be easily expanded to be used for calculations related to the uptake of other sorptives, adsorbents, under different conditions, and with other variables (e.g. surface chemistry) accounted for. Results from our methods may help improve the design of porous materials for a wide range of adsorption applications.
Author contributions
L. Scott Blankenship: conceptualization, methodology, software, formal analysis, data curation, investigation, writing – original draft, visualization. Nawaf Albeladi: investigation. Thria Alkhaldi: investigation. Asma Madkhali: investigation. Robert Mokaya: validation, resources, writing – review & editing, funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
We are thankful to the EPSRC (Low-Dimensional Materials & Interfaces DTP) for a studentship for L. S. B. In addition, L. S. B. thanks Paul Iacomi for the development of pyGAPS, and assistance with implementation of some of its features in pyPUC as well as to Hassan Akhtar who assisted and advised on some of the code. The use of the University of Nottinghams Augusta HPC service was essential to the completion of this work. We thank the government of the Kingdom of Saudi Arabia for funding PhD studentships for N. A., T. A. and A. M. R. M. thanks the Royal Society for a Royal Society Wolfson Research Merit Award.Notes and references
- M. Sevilla and R. Mokaya, Energy Environ. Sci., 2014, 7, 1250–1280 RSC.
- T. C. Drage, J. M. Blackman, C. Pevida and C. E. Snape, Energy Fuels, 2009, 23, 2790–2796 CrossRef CAS.
- M. G. Plaza, S. Garcia, F. Rubiera, J. J. Pis and C. Pevida, Chem. Eng. J., 2010, 163, 41–47 CrossRef CAS.
- A. Altwala and R. Mokaya, Energy Environ. Sci., 2020, 13, 2967–2978 RSC.
- S. Biloé, V. Goetz and A. Guillot, Carbon, 2002, 40, 1295–1308 CrossRef.
- M. Beckner and A. Dailly, Appl. Energy, 2016, 162, 506–514 CrossRef CAS.
- J. Juan-Juan, J. Marco-Lozar, F. Suárez-García, D. Cazorla-Amorós and A. Linares-Solano, Carbon, 2010, 48, 2906–2909 CrossRef CAS.
- K.-S. Lin, A. K. Adhikari, K.-C. Chang, C.-L. Chiang and C.-H. Wang, J. Nanosci. Nanotechnol., 2014, 14, 2700–2708 CrossRef CAS PubMed.
- Q. Zhao, F. Wu, K. Xie, R. Singh, J. Zhao, P. Xiao and P. A. Webley, Chem. Eng. J., 2018, 336, 659–668 CrossRef CAS.
- J. Alcaniz-Monge, M. A. de la Casa-Lillo, D. Cazorla-Amorós and A. Linares-Solano, Carbon, 1997, 35, 291–297 CrossRef CAS.
- D. Lozano-Castello, D. Cazorla-Amoros, A. Linares-Solano and D. F. Quinn, Carbon, 2002, 40, 989–1002 CrossRef CAS.
- I. Cabria, M. J. López and J. A. Alonso, Carbon, 2007, 45, 2649–2658 CrossRef CAS.
- V. Presser, J. McDonough, S.-H. Yeon and Y. Gogotsi, Energy Environ. Sci., 2011, 4, 3059–3066 RSC.
- W. Zhao, V. Fierro, C. Zlotea, E. Aylon, M. Izquierdo, M. Latroche and A. Celzard, Int. J. Hydrogen Energy, 2011, 36, 11746–11751 CAS.
- M. Sevilla, J. B. Parra and A. B. Fuertes, ACS Appl. Mater. Interfaces, 2013, 5, 6360–6368 CrossRef CAS PubMed.
- E. Masika and R. Mokaya, J. Phys. Chem. C, 2012, 116, 25734–25740 CrossRef CAS.
- Z. Geng, C. Zhang, D. Wang, X. Zhou and M. Cai, J. Energy Chem., 2015, 24, 1–8 CrossRef.
- B. Adeniran and R. Mokaya, Chem. Mater., 2016, 28, 994–1001 CrossRef CAS.
- Y.-K. Choi and S.-J. Park, Bull. Korean Chem. Soc., 2016, 37, 830–834 CrossRef CAS.
- G. Sethia and A. Sayari, Carbon, 2016, 99, 289–294 CrossRef CAS.
- T. K. Das, S. Banerjee, P. Sharma, V. Sudarsan and P. U. Sastry, Int. J. Hydrogen Energy, 2018, 43, 8385–8394 CrossRef CAS.
- J. Jagiello, J. Kenvin, A. Celzard and V. Fierro, Carbon, 2019, 144, 206–215 CrossRef CAS.
- D. Grau-Marin, J. Silvestre-Albero, E. O. Jardim, J. Jagiello, W. R. Betz and L. E. Peña, Carbon, 2020, 157, 495–505 CAS.
- J. Jagiello, J. Kenvin, C. O. Ania, J. B. Parra, A. Celzard and V. Fierro, Carbon, 2020, 160, 164–175 CrossRef CAS.
- D. H. Everett and J. C. Powl, J. Chem. Soc., Faraday Trans. 1, 1976, 72, 619–636 RSC.
- J. Jagiello and M. Thommes, International Conference on Carbon for Energy Storage and Environment Protection, 2005 Search PubMed.
- N. P. Wickramaratne and M. Jaroniec, J. Mater. Chem. A, 2013, 1, 112–116 RSC.
- M. De la Casa-Lillo, F. Lamari-Darkrim, D. Cazorla-Amoros and A. Linares-Solano, J. Phys. Chem. B, 2002, 106, 10930–10934 CrossRef CAS.
- K. R. Matranga, A. Stella, A. L. Myers and E. D. Glandt, Sep. Sci. Technol., 1992, 27, 1825–1836 CAS.
- S. Reljic, E. Jardim, C. Cuadrado-Collados, M. Bayona, M. Martinez-Escandell, J. Silvestre-Albero and F. Rodríguez-Reinoso, CO2 Adsorption in Activated Carbon Materials, Springer, 2021, pp. 139–152 Search PubMed.
- N. Texier-Mandoki, J. Dentzer, T. Piquero, S. Saadallah, P. David and C. Vix-Guterl, Carbon, 2004, 42, 2744–2747 CrossRef CAS.
- Z. Tan and K. E. Gubbins, J. Phys. Chem., 1990, 94, 6061–6069 CrossRef CAS.
- C. M. Simon, J. Kim, D. A. Gomez-Gualdron, J. S. Camp, Y. G. Chung, R. L. Martin, R. Mercado, M. W. Deem, D. Gunter and M. Haranczyk, Energy Environ. Sci., 2015, 8, 1190–1199 RSC.
- L. S. Blankenship, J. Jagiello and R. Mokaya, Mater. Adv., 2022, 3, 3961–3971 RSC.
- J. Li, B. Michalkiewicz, J. Min, C. Ma, X. Chen, J. Gong, E. Mijowska and T. Tang, Chem. Eng. J., 2019, 360, 250–259 CrossRef CAS.
- S.-Y. Lee and S.-J. Park, J. Colloid Interface Sci., 2013, 389, 230–235 CrossRef CAS PubMed.
- G. Sdanghi, R. L. Canevesi, A. Celzard, M. Thommes and V. Fierro, Characterization of Carbon Materials for Hydrogen Storage and Compression, C – Journal of Carbon Research, 2020, 6(3), 46 CrossRef CAS.
- S. Hlushak, Phys. Chem. Chem. Phys., 2018, 20, 872–888 RSC.
- G. Sethia and A. Sayari, Carbon, 2015, 93, 68–80 CrossRef CAS.
- P. Iacomi and P. L. Llewellyn, Adsorption, 2019, 25, 1533–1542 CrossRef CAS.
- C. M. Simon, B. Smit and M. Haranczyk, Comput. Phys. Commun., 2016, 200, 364–380 CrossRef CAS.
- K. Pearson, Proc. R. Soc. London, 1895, 58, 240–242 CrossRef.
- J. D. Evans, V. Bon, I. Senkovska and S. Kaskel, Langmuir, 2021, 37, 4222–4226 CAS.
- P. C. Hansen, SIAM Rev., 1992, 34, 561–580 CrossRef.
- P. C. Hansen and D. P. OLeary, SIAM J. Sci. Comput., 1993, 14, 1487–1503 CrossRef.
- P. Hansen, in The L-curve and its use in the numerical treatment of inverse problems, ed. P. Johnston, WIT Press, Southampton, 2001, pp. 119–142 Search PubMed.
- I. Langmuir, J. Am. Chem. Soc., 1916, 38, 2221–2295 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361–1403 CAS.
- E. A. Guggenheim, Applications of Statistical Mechanics, Oxford Clarendon Press, 1966 Search PubMed.
- R. B. Anderson, J. Am. Chem. Soc., 1946, 68, 686–691 CrossRef CAS.
- J. H. de Boer, The Dynamical Character of Adsorption, Oxford Clarendon Press, 1953, vol. 76 Search PubMed.
- H. Freundlich, Zeitschrift für Physikalische Chemie, 1907, 57, 385–470 CrossRef CAS.
- B. Bering, M. Dubinin and V. Serpinsky, J. Colloid Interface Sci., 1966, 21, 378–393 CrossRef CAS.
- J. Tóth, J. Colloid Interface Sci., 1994, 163, 299–302 CrossRef.
- M. E. Casco, M. Martínez-Escandell, J. Silvestre-Albero and F. Rodríguez-Reinoso, Carbon, 2014, 67, 230–235 CrossRef CAS.
- M. Sevilla, A. S. M. Al-Jumialy, A. B. Fuertes and R. Mokaya, ACS Appl. Mater. Interfaces, 2018, 10, 1623–1633 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Supplementary figures and tables; raw (.aif) isotherms; PSD and modelling analysis summaries as.csv; and raw outputs of Dυ, Dπ, and Dc for each DataSet (.csv) available at https://github.com/sblanky/pyPUC_si; source code available on https://github.com/sblanky/pyPUC. See DOI: https://doi.org/10.1039/d2ya00149g |
| ‡ These authors contributed equally to this work. |
| § In the more detailed calculation (see Fig. S1.11, ESI†) this limit is found to be slightly lower. |
| ¶ Results for ΩsorptiveS are sufficiently similar to not require a separate discussion here. A comparison is displayed in Fig. S2.13 (ESI†). |
| This journal is © The Royal Society of Chemistry 2022 |