A feasible pathway to stabilize monoclinic and tetragonal phase coexistence in barium titanate-based ceramics

Abstract

Multiphase coexistence has attracted significant interest in recent years because its control has entailed a significant breakthrough for the piezoelectric activity enhancement of lead-free piezoelectric oxides. However, the comprehension of phase coexistence still has many controversies including an adequate synthesis process and/or the role played by crystalline phases in functional properties. In this study, functional barium titanate [BaTiO₃, (BTO)]-based materials with tunable functional properties were obtained by compositional modification via Bismuth (Bi) doping. Towards this aim, we systematically synthesized BTO-based materials by a sol–gel method, focusing on the control of Bi substitution in the BaTiO₃ structure. In particular, we found that the substitution of Bi⁺³ leads to the stabilization of a monoclinic–tetragonal (M–T) phase boundary close to room temperature, which facilities the polarization process of the system. As a surprising result, we believe that the simple and cost-effective strategy and design principles described in this work open up the possibility of obtaining BTO-based lead-free ceramics with enhanced properties induced by the stabilization of the phase coexistence, expanding their application range.

---

1. Introduction

BaTiO₃-based complex perovskites are considered smart materials since they are highly versatile and multifunctional, mainly due to their good and interesting dielectric and ferroelectric properties.¹ The range of technological and industrial applicability is immense as can be the degradation of bacteria by ferrocatalysis,² the variation of their ferroelectric properties by the application of polarized light,³ photocatalysis,⁴ thermoelectrics,^5,6 piezotronics,⁷ high energy storage,⁸ multilayer chip thermistors,⁹ multiferroics,¹⁰ or electromagnetic shielding,^11–13 among others. One of the key factors to exploit their multidisciplinary nature belongs to their high capacity to incorporate other atomic elements in their crystal structure, generating slight crystalline deformations. Moreover, they may also induce metastable polymorphs that generate significant singularities in their dielectric properties, which can boost their technological applicability.^9,10,14–17

Among the various possibilities of available dopants, Bi with 6s² lone-pair electrons can be considered as a potential candidate that induces local structural distortions in BaTiO₃.^18,19 The existence of 6s² lone-pair electrons is considered to be one of the main factors leading to the difference in ferroelectric characteristics compared to the PbTiO₃ system (having Pb²⁺ with 6s² lone-pair electrons) and BaTiO₃ (Ba²⁺ without lone-pair electrons).²⁰ Regarding the synthesis of BaTiO₃-based ceramics, chemical routes such as sol–gel method,^5,10,21–27 hydrothermal method,²⁸ solvothermal method,¹³ chemical co-precipitation,²⁹ and microwave heating³⁰ are employed as effective methods. Among them, the sol–gel technology stands out because of its mild reaction conditions and excellent properties such as high purity, excellent particle distribution, control substitution composition and homogeneity of the obtained powders and coatings.^31–33

The formation and synthesis of stable BaTiO₃ polymorphs is of high interest since new polarization rotation mechanisms are provided, mainly favored by the mobility of Ti⁴⁺.^5,14 In this line, superposition of orthorhombic and tetragonal phases is obtained^34–36 and there are interesting works where the coexistence of morphotropic phase boundaries between cubic and tetragonal phases,³⁷ the formation of polymorphic phase boundaries³⁸ or monoclinic and/or orthorhombic phases induced by poling³⁵ are demonstrated. These are clear examples of the remarkable versatility of the perovskite structure of BaTiO₃ to form metastable structures that possess interesting dielectric properties and can be competitive to those commonly found in lead-based ceramics series.³⁹ Unfortunately, to the best of our knowledge, there are no experimental works that faithfully reproduce the formation of monoclinic structures with the Pm space group. Therefore, the stabilization of the monoclinic polymorph at room temperature (RT) and in unpoled samples represents a breakthrough in the synthesis of multiphases in BaTiO₃-based materials because it can provide a new stable and reversible pathway for polarization rotation, unveiling outstanding dielectric and ferroelectric properties.^35,40

In this work, we aimed to synthesize BaTiO₃-based (BTO) lead-free piezoceramics by replacing the A-sites with Bi³⁺ ions, thereby engendering an evolution of the polymorphic behavior containing a monoclinic (M) and tetragonal (T) phase boundary close to RT. For that, novel sol–gel approaches based on the simultaneous assistance of water and ethanol on nitrate-based precursors are effective in obtaining Ba_1−xBi_xTiO₃ ceramics, employing concentrations of x = 0.000, 0.050, and 0.075. Interestingly, the coexistence of the monoclinic phase (space group Pm)³⁵ with the tetragonal phase (P4mm)²⁵ was achieved for the concentration of x = 0.050, improving enormously the dielectric properties as a function of temperature and frequency in comparison with the pure BaTiO₃ samples. By contrast, the purely tetragonal phase attained a higher degree of Bi substitution with x = 0.075, highlighting that the compositional window to obtain different polymorphs owing to the addition of Bi is very narrow.

2. Experimental procedure and characterization techniques

2.1. Sol–gel methods to obtain Ba_1−xBi_xTiO₃ (x = 0.000, 0.050, and 0.075) ceramics

Fig. 1 shows the chemical steps followed to obtain bismuth-based barium titanate (Ba_1−xBi_xTiO₃ with x = 0.000, 0.050, and 0.075) ceramics. The powders were synthesized by a sol–gel method using Ba(NO₃)₂ (Sigma Aldrich, 99%) and Bi(NO₃)₃·5H₂O (Sigma-Aldrich, 98%) as precursor materials dissolved in ethanol absolute (Labkem, 99%) and distilled water. Then, the mixture was homogenized by magnetic stirring until achieving complete dissolution at RT (Fig. 1, step i). Afterwards, the temperature was increased up to 60 °C to promote the hydrolysis and polycondensation processes, and Ti{OCH(CH₃)₂}₄ (Sigma Aldrich, 99%) was subsequently added dropwise (Fig. 1, step ii). In addition, nitric acid was incorporated as a catalyst to favor the sol–gel kinetics and stirring was continued for 1 h (Fig. 1, step iii). Next, the resulting solution was dried at 85 °C for 24 h, obtaining a densified powder (Fig. 1, step iv). Finally, the xerogel was densified in an air environment at different temperatures ranging from 800 to 1000 °C for 2 h at a heating rate of 5 °C min⁻¹ (Fig. 1, step v).

Fig. 1 Scheme of the synthesis process of the Ba_1−xBi_xTiO₃ system via a sol–gel route. Water-assisted sol–gel synthesis for obtaining Ba_1−xBi_xTiO₃ powders with x = 0.000, 0.050, and 0.075.

2.2. Thermal evolution

Differential thermal analysis–thermogravimetric analyses (DTA–TGA) were performed simultaneously using TA Instruments in the DSC/DTA/TGA Q600 module at a rate of 5 °C min⁻¹ in an air atmosphere.

2.3. X-Ray diffraction (XRD)

The crystal structure and phase formation were studied by X-ray diffraction using a PANalytical X-ray diffractometer (Empyrean) with Cu Kα radiation (1.5406 Å). The measurements were performed at RT in a continuous mode in the 2θ range between 20 and 85° with an angle step of 0.04°. The data were analyzed by the Rietveld refinement using the Full Proof program.⁴¹

2.4. Electron microscopy

The microstructure and morphological aspects were examined by scanning electron microscopy (SEM) using a JEOL JSM 6400 instrument.

2.5. Relative density (ρ_r)

The ρ_r value of the sintered ceramics was obtained by the Archimedes method (theoretical density – ρ_t, 6.02 g cm⁻³).⁴²

2.6. Electrical properties

For the dielectric measurements, pre-densified ceramic powders at 1000 °C were pressed into pellets at 5 tons for 5 min. Subsequently, the pellets were sintered at 1350 °C for 3 h in an air environment. Next, a silver paint capping was deposited to ensure a good ohmic contact. The dielectric analysis was performed using an impedance analyzer (Agilent hp4294A) by the parallel plate technique as a function of temperature between 25 and 200 °C at a heating rate of 1 °C min⁻¹ in the frequency range of 10³–10⁹ Hz. The dielectric parameters such as dielectric constant, ε_r, and dielectric loss tangent, tan δ, were obtained. Finally, the polarization–electric field (P–E) hysteresis loops were measured in a silicon oil bath using a hysteresis meter (RT 6000 HVS, RADIANT Technologies).

3. Results and discussion

3.1. Growth, structure and morphological features of Ba_1−xBi_xTiO₃ compositions (x = 0.000, 0.050, and 0.075)

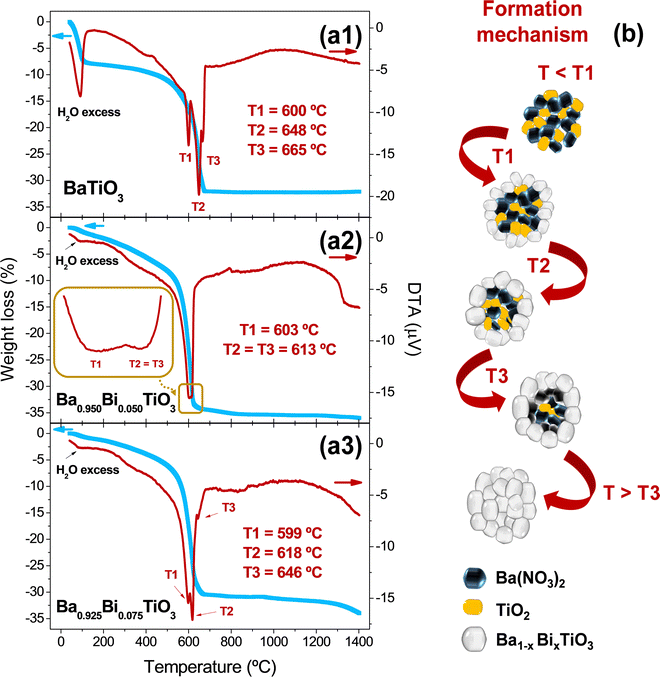
To identify clearly the thermal evolution of the Ba_1−xBi_xTiO₃ system as a function of the Bi³⁺ content, the TGA–DTA curves were measured to unveil the influence of Bi³⁺ content on the formation of Ba_1−xBi_xTiO₃ for samples prepared with x = 0.000, 0.050, and 0.075. As shown in TGA curves (blue curves in Fig. 2a1–a3), there is a decrease in weight up to 100 °C corresponding to the loss of water and alcoholic groups formed during the hydrolysis and polycondensation processes.²² Then, a gradual loss is observed with temperature up to 400 °C,⁴³ which is associated with the combustion of the organic compounds, with mass losses of about 10%. Above that temperature, there is a pronounced change in the TGA curve slopes up to 600 °C, where the material drastically undergoes decomposition of nitrates used to form the perovskite with a weight loss between 32 and 35%. From 650 °C onwards, no substantial weight losses occur in the samples up to 1300 °C, confirming the formation of thermodynamic stable phases.

Fig. 2 Determination of the thermal conditions and the chemical mechanism of the Ba_1−xBi_xTiO₃ system. TGA (blue) and DTA (red) curves for Ba_1−xBi_xTiO₃ with (a1) x = 0.000, (a2) x = 0.050, (a3) and x = 0.075. Additionally, the inset in panel a2 shows the detail of the DTA curve for the composition with x = 0.050 in the temperature range from 595 to 620 °C. (b) Chemical mechanism proposed for the formation of Bi-based BaTiO₃ compositions.

The DTA curves (red curves in Fig. 2a1–a3) of the three compositions also display similar behaviors with relatively small endothermic contributions below 150 °C corresponding to the evaporation of alcoholic groups and excess water.²² Between 150 and 400 °C, there are also small endothermic transformations due to the decomposition of organic compounds formed,⁴³ and differences were found between the compositions around 600–670 °C. In that range, corresponding to the decomposition of nitrates, the DTA curves provide information on the chemical reactions that occur repeatedly in the form of Ba(NO₃)₂ + TiO₂ → BaTiO₃ + 2NO₂ + ½ O₂.⁴⁴ The reaction takes place at a temperature above the melting point of Ba(NO₃)₂⁴⁵ and, therefore, it is a liquid–solid reaction.⁴⁶ Different works report one sharp endothermic peak,⁴⁴ two peaks,⁴⁷ or three contributions,⁴⁸ attributed to the same reaction occurring several times at different temperatures up to the complete formation of BaTiO₃.

In short, the samples prepared in this work exhibit three endothermic temperatures (T1–3), which are detected for BaTiO₃ and Bi_0.075Ba_0.925TiO₃, and two contributions for Bi_0.050Ba_0.950TiO₃. The reason for these variations in temperature probably comes from the size of the micelle precursors of Ba_1−xBi_xTiO₃ when the material reaches the melting point of Ba(NO₃)₂.⁴⁵ Below T1, Ba(NO₃)₂ and TiO₂ are mixed together and no reaction has occurred. Above T1, the reaction begins; however, a certain amount of Ba(NO₃)₂ and TiO₂ remain unreacted. The non-reacted Ba(NO₃)₂ and TiO₂ samples persist even after T2 and T3. Above T3, the reaction gets completed, leading to the formation of Ba_1−xBi_xTiO₃. Subsequently, slight exothermic contributions are found with a relatively broad peak around 1000–1100 °C, which may be due to recrystallizations of BaTiO₃. Finally, the melting point of BaTiO₃ is around ∼1618 °C,⁴⁹ and the associated thermodynamic changes above that value are out of analyses. The schematic procedure of the involved chemical mechanisms is shown in Fig. 2b.

The structural properties and phase composition were evaluated by XRD to reveal the crystalline compounds formed after the large endothermic peak observed in the compositions BaTiO₃ (bottom region), Ba_0.950Bi_0.050TiO₃ (central region), and Ba_0.925Bi_0.075TiO₃ (upper region) densified at 800, 900, and 1000 °C (Fig. 3a). The three compositions exhibit similar structural characteristics to the BaTiO₃-based compounds¹ without secondary impurity phases, confirming the feasibility of the proposed sol–gel synthesis, including small Bi substitutions of x = 0.050 and 0.075. However, the crystal structure and phase evolution are clearly affected by the degree of Bi substitution. First, it can be observed that the BaTiO₃ sample treated at 800 °C already presented high evidence of tetragonality by showing a clear splitting corresponding to the reflections (002) and (200) (inset magnification in Fig. 3a). This temperature is slightly lower than that obtained in other works combining sol–gel and solid-state methods, where the tetragonality was achieved at 900 °C.²⁷ In contrast, the double contribution between 44 and 46° disappears, establishing a single contribution at 800 °C when Bi is introduced for x = 0.050 and 0.075 concentrations. The single contribution could be due to the prevalence of the cubic phase⁵⁰ and the higher temperature required to obtain the tetragonality in the presence of small amounts of Bi.⁵¹ In addition, the width of the peak is much larger, indicating a decrease in the crystalline domain size compared to the BaTiO₃ sample treated at the same temperature. Nevertheless, the results confirm a good substitution of Bi in the crystal structure of BaTiO₃ in the cationic positions of Ba²⁺ since its ionic radius is 1.61 Å and that of Bi³⁺ is 1.17 Å.²⁴

Fig. 3 Basic identification of the crystal structure of the Ba_1−xBi_xTiO₃ system by XRD: (a) experimental XRD pattern evolution of BaTiO₃ (bottom region), Ba_0.950Bi_0.050TiO₃ (central region), and Ba_0.925Bi_0.075TiO₃ (upper region) densified at 800, 900, and 1000 °C, respectively. The inset in the right part of panel a shows magnification in the 2θ range indicated with a red rectangle. Comparison of different 2θ ranges between samples prepared at 1000 °C for expected tetragonal reflections (b) (101) and (110), (c) (111), and (d) (200) and (002). Rietveld refinement using the tetragonal space group P4mm for (e) BaTiO₃, (f) Ba_0.950Bi_0.050TiO₃, and (g) Ba_0.925Bi_0.075TiO₃ samples prepared at 1000 °C.

Different behaviors are also noticed when the temperature is increased to 900 and 1000 °C for the concentration of x = 0.050 and for x = 0.075. For x = 0.075, the width of the peak narrows and tetragonality features are detected, being more noticeable at 1000 °C. On the contrary, for x = 0.050, the shape of the peak is maintained with a single contribution at 1000 °C and a shift towards higher 2θ is observed, evidencing a slight compression of the crystal lattice. Particularly, the width of the peak increases with the temperature in that sample, being a strange behavior if it is the same crystalline phase, as the temperature increases.⁴³ Therefore, the results indicate the emergence of a phase different from the tetragonal one.^35,52

To corroborate our hypothesis, the morphology and number of contributions of other plane families such as (101)/(110) and (111) were examined, comparing with the (002)/(200) reflections treated at 1000 °C for the three compositions taking the P4mm space group as reference³⁷ (Fig. 3b–d, respectively). The diffraction peaks displayed in Fig. 3b show a certain degree of asymmetry in the three compositions corresponding to the (101)/(110) contributions of the P4mm space group, resulting in significantly more separated contributions for the case of x = 0.050. In principle, these features could be compatible only with the tetragonal phase and other reflections should be investigated. However, Fig. 3c related to the (111) plane family should exhibit only a single contribution, and a double peak is observed for the composition x = 0.050, demonstrating the existence of another stable phase with temperature (Fig. 3c). Finally, the comparison of the samples with the (002) and (200) reflections also shows inconsistencies with the pure tetragonality model by having only one broad peak, which could hide a larger number of contributions (Fig. 3d).

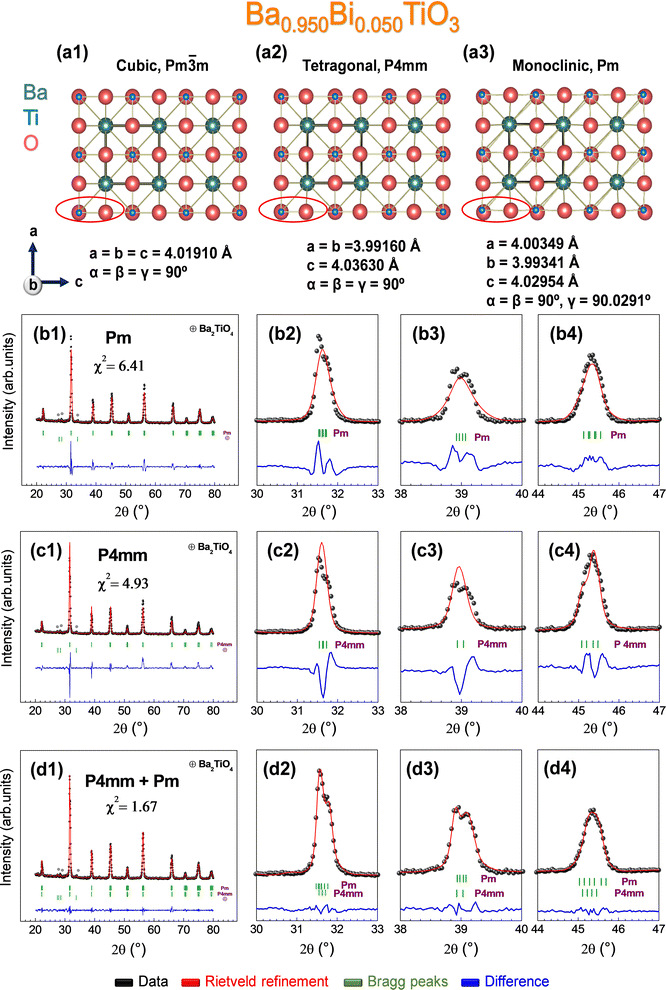
To validate these findings, the Rietveld refinement was performed taking into account only a tetragonal model, and the results are presented in Fig. 3e–g respectively for BaTiO₃, Ba_0.950Bi_0.050TiO₃, and Ba_0.925Bi_0.075TiO₃. Although the three refinements are compatible with the tetragonal model, there is a major error of χ² = 4.93 for x = 0.050, suggesting that there are contributions within the XRD pattern that go beyond the purely tetragonal model. Instead, the tetragonal simulation converges well for x = 0.000 and x = 0.075, obtaining χ² values of 1.69 and 2.30, respectively, being reliable for a good fit.^35,53 In addition to the BaTiO₃-based compounds, residual contributions of Ba₂TiO₄ at 1000 °C were noted with percentages of 1.8(7)%, 0.9(3)%, and 2.1(9)% for x = 0.000, 0.050, and 0.075, respectively. These compounds are considered transient as they tend to vanish with the densification temperature.

The existence of other stable polymorphs of BaTiO₃ is known as a function of temperature with rhombohedral structures below −90 °C (R3m),⁵⁴ orthorhombic structures between −90 and 0 °C (Amm2),³⁴ tetragonal structures between 0 and 120 °C (P4mm),⁵⁵ and cubic structures above 120 °C (Pm3̄m).³⁷ The cubic phase is paraelectric while the other three are ferroelectric, exhibiting large increases in the dielectric constant at temperatures close to the above-mentioned structural transition temperatures.⁵⁶ Interestingly, the stabilization of phases with unique polarization properties operating at RT is of potential applicability.¹ In reference to other systems, in lead-based compounds, the existence of a monoclinic phase as a morphotropic phase boundary is accepted, which is the explanation for the high piezoelectric response observed in lead zirconate titanate Pb(Ti, Zr)O₃ (PZT).³⁸ (K, Na)NbO₃ (KNN) compounds also display a relatively high depolarization temperature based on a specific substitution,⁵⁷ not only due to the presence of MPBs but also due to polymorphic phase boundaries (PPBs) that structurally correspond to monoclinic regions.^38,58 Therefore, the possibility of a monoclinic stable phase in BaTiO₃-based materials could be considered.

In this line, there are several theoretical studies corroborating such distortion based on the Devonshire theory^59,60 with an extension up to eight orders for describing a monoclinic phase (Mc),⁶¹ but experimental evidence of its existence is very scarce.^{34,35,52,62–66} Considering these premises, the possibility of the occurrence of the monoclinic phase Pm in the sample prepared at 1000 °C with composition x = 0.050 is addressed, since the monoclinic crystal structure possesses extra reflections to the purely tetragonal one and could explain the structural evolution with temperature for that composition. Concretely, the refinement parameters obtained from an interesting experimental study enable us to solve the monoclinic structure Pm obtained irreversibly by the application of an electric induction field, coexisting with the tetragonal phase P4mm.³⁵ To visually materialize the structural variations that can be expected, the cubic Pm3̄m, tetragonal P4mm, and monoclinic Pm structures are represented along the b-axis simulated using the VESTA software⁶⁷ (Fig 4a1–a3). The red ellipse illustrates the main differences between the structures of Ti and O (mainly) in the projection along the b-axis, showing a higher distortion for Ti in the case of the monoclinic structure. In detail, Rietveld refinements were performed according to a purely monoclinic Pm (Fig 4b1–b4), purely tetragonal P4mm (Fig 4c1–c4), and a combination of Pm and P4mm structures (Fig 4d1–d4). The fits reveal that the experimental curve fits correctly for the combination of Pm and P4mm with goodness fit χ² = 1.67, being an unstable model for the treatment of the pure phases separately. Therefore, the synthesis of a monoclinic phase and its stabilization at RT is demonstrated with no external induction of polarization.³⁵ Thus, the mobility of Ti is favored by substituted Bi with concentration x = 0.050 in the crystal lattice as the densification temperature increases, providing new polarization mechanisms that can adopt any direction in the (110) plane.³⁵ The results of the Rietveld refinements for the sample prepared at 1000 °C with x = 0.050, taking into account the combination of Pm + P4mm, together with the rest of the samples considering the P4mm structure, are listed in Table 1.

Fig. 4 Identification of phase coexistence on the Ba_1−xBi_xTiO₃ system by the Rietveld refinement for X-ray. (a1) Schematic representation of BaTiO₃ along the b axis belonging to the space group (a1) Pm3̄m, (a2) P4mm, and (a3) Pm. Rietveld refinement of the composition Ba_0.950Bi_0.050TiO₃ using (b1) monoclinic space group Pm, (c1) tetragonal space group P4mm, and (d1) a combination of monoclinic and tetragonal space group (Pm + P4mm). Magnifications of different 2θ ranges (b2–d2) 30–33°, (b3–d3) 38–40°, and (b4–d4) 44–47° related to their corresponding space groups fitting, respectively.

Table 1 Densification temperature (T), lattice parameters (a, c), tetragonality ratio (c/a), unit cell volume (V), phase composition percentage (CP), crystalline domain size (d), and strain (S) for BaTiO₃ and Bi-substituted BaTiO₃ ceramics. Corresponding errors are indicated in parentheses

x	T (°C)	a (Å)	c (Å)	c/a	V (Å^3)	d (nm)		S (10^−3)	CP (%)
									BaTiO3		Ba2TiO4	TiO2
									P4mm	Pm
0.000	800	3.99638 (0.00012)	4.02904 (0.00037)	1.00817 (0.00012)	64.34803 (0.00977)	34.76 (0.33)		3.21	93.92 (1.13)	—	5.59 (0.83)	0.49 (0.01)
	900	3.99681 (0.00024)	4.03126 (0.00015)	1.00862 (0.00009)	64.39758 (0.01013)	34.94 (0.58)		3.30	97.72 (2.35)	—	2.28 (0.54)	—
	1000	3.99695 (0.00018)	4.03435 (0.00027)	1.00936 (0.00011)	64.45149 (0.01012)	37.38 (0.47)		3.20	98.16 (2.35)	—	1.84 (0.72)	—
0.050	800	4.00495 (0.00046)	4.02120 (0.00057)	1.00406 (0.00025)	64.49863 (0.02396)	28.07 (0.83)		3.98	92.32 (1.63)	—	7.52 (0.76)	0.16 (0.03)
	900	4.00318 (0.00087)	4.02258 (0.00073)	1.00485 (0.00040)	64.46380 (0.03972)	29.09 (1.03)		3.91	96.65 (0.33)	—	3.35 (0.12)	—
	1000	3.99974 (0.00094)	4.01890 (0.00068)	1.00479 (0.00041)	64.29415 (0.04110)	P4mm	Pm	5.03	89.57 (0.24)	9.57 (0.23)	0.86 (0.26)	—
						24.82 (1.22)	19.45 (0.93)
0.075	800	4.00678 (0.00022)	4.02419 (0.00043)	1.00434 (0.00016)	64.60569 (0.01400)	24.90 (0.45)		4.66	88.38 (2.43)	—	11.43 (0.33)	0.19 (0.03)
	900	4.00486 (0.00031)	4.02599 (0.00024)	1.00527 (0.00013)	64.57266 (0.01385)	28.81 (0.53)		3.96	94.11 (1.76)	—	5.89 (0.81)	—
	1000	4.00294 (0.00045)	4.02391 (0.00037)	1.00524 (0.00021)	64.47756 (0.02043)	30.93 (0.33)		3.63	97.86 (0.85)	—	2.14 (0.92)	—

---

One of the parameters to venture good ferroelectric properties is the tetragonality ratio of the BaTiO₃-based ceramics (c/a) and its standard value should be close to 1.010.^44,68 In turn, the tetragonality ratio is a function of synthesis temperature and particle size⁶⁸ and for the composition x = 0.000 densified at 1000 °C, a value of 1.00936 was obtained. To contextualize with other works, the tetragonality ratios of 1.0092 were obtained after sintering at temperatures over 1300 °C⁴⁴ and of 1.0105 at a temperature of 1000 °C following a two-step thermal processing.⁶⁸ Thus, the values obtained in this work are competitive for pure BaTiO₃ samples. The tetragonality ratio for samples with Bi substitutions decreases compared to composition x = 0.000, obtaining a maximum value of 1.00524 for the composition x = 0.075. Consequently, the addition of Bi has a strong impact on the tetragonality ratio of BaTiO₃ and slightly decreases for the sample of composition x = 0.050 treated at 1000 °C up to a value of 1.00479, probably due to the degree of Bi substitution and to the stabilization and/or interaction with the monoclinic phase.

The crystalline domain sizes of the tetragonal phase show similar values of a few tens of nanometers for the three compositions densified between 800 and 1000 °C, which are slightly higher for the sample with x = 0.000. This result is typical for samples with additions of other elements such as Bi,²⁴ Sn,¹⁵ Sm,¹⁶ and Zr.¹⁷ Moreover, this value increases with temperature except for the sample x = 0.050 densified at 1000 °C. The crystalline domain decreases here and the reason could be the emergence of the coexisting monoclinic phase. The effect on the local strain could also be an indicator of a phase transition with a maximum value of 5.03 × 10⁻³.¹⁶ In relation to the percentage of synthesized phases, high purities are observed for all samples, obtaining ∼10% of monoclinic phase stable at RT for the composition x = 0.050. Rietveld refinement also shows the occurence of TiO₂ and Ba₂TiO₄ as residual phases below 8% at 800 °C and values close to 2% at higher temperatures (Table 1).

The crystallographic nature of the system plays a relevant role in the functional properties of ferroelectric materials. However, it is also relevant to consider the morphological features of piezoelectric materials because controlling the grain size is also an effective method to improve the electrical properties of piezoceramics.⁶⁹ From this perspective, the relationships between the morphology and the crystallographic nature of the system were studied here by FE-SEM, as shown in Fig. 5. The particle size, its distribution, and morphological aspects were examined by SEM analyses to study their evolution with temperature between 800 and 1000 °C for each Ba_1−xBi_xTiO₃ composition. The analyses show a remarkable modification of the particle size and morphology with temperature as a function of the Bi substitution (Fig. 5).

Fig. 5 Identification of the morphology and crystal structure of the Ba_1−xBi_xTiO₃ system. SEM images and particle size distribution (overlapped) of (a–c) BaTiO₃, (d–f) Ba_0.950Bi_0.050TiO₃, and (g–i) Ba_0.925Bi_0.075TiO₃ compositions densified between 800 and 1000 °C, respectively.

From a general point of view and common to all samples, the particle size distributions are relatively narrow and lie in the sub-microscale. Moreover, they follow a log-normal distribution considering an analysis with a sampling of at least 200 particles (Fig. 5). Such distributions are typical of sol–gel synthesized samples⁷⁰ and because the particle size is much larger than the crystalline domain size (Table 1), the particles in all samples are polycrystalline. Specifically, the particle size distribution displays decreasing mean values ranging from 0.70(1) to 0.58(3) μm for BaTiO₃ and from 0.48(3) to 0.40(1) μm for the composition Ba_0.950Bi_0.050TiO₃ with densification temperatures of 800 and 1000 °C, respectively. On the contrary, the trend is completely opposite for the Ba_0.925Bi_0.075TiO₃ composition, showing an increasing evolution with the densification temperature from 0.28(1) μm for 800 °C to 0.47(1) μm. The explanation for these effects may be due to several factors or a combination of them. First, related to the pure composition of BaTiO₃, it is well known that an increase in the tetragonality ratio is accompanied by an increase in the crystalline domain size with the densification temperature.^27,71 The mobility of the Ti⁴⁺ ions belonging to the octahedron undergoes slight modifications in the cubic polymorph due to the larger ionic radius of Ba²⁺, altering the crystal structure of BaTiO₃ and promoting the tetragonality ratio.^27,68,71 This effect is found in the previous XRD analyses (Fig. 3) for the three compositions studied. However, the relationship is not extrapolated for the particle size in the present work and there may be strong dependence on the microstructure evolving with temperature. For the BaTiO₃ composition, the particles have different geometric shapes with well-defined cubic and rectangular axes (Fig. 5a–c), as observed in other works.^26,27,72 In ref. 27, the samples were synthesized by a combination of sol–gel and solid-state reactions and the morphological evolution encompasses microparticles with cubic and whisker shapes synthesized at 700 °C, transforming into smaller cubic structures at 900 °C. Thus, the resulting morphology and sizes are highly dependent on the method and approach established in the synthesis method. The effects of organic remnants from the sol–gel synthesis are excluded since no weight loss is observed from the formation of BaTiO₃ above 646 °C (Fig. 2a1). At the same time, a gradual coarsening is also noticed with the increase in temperature, and the degree of agglomeration between particles is enhanced. This is due to the increase in the mobility of the material at the grain boundaries with temperature leading to such morphologies produced by gradual coarsening.^26,72 When Bi³⁺ ions are substituted at the Ba²⁺ sites, it also produces strong modifications in the particle size, gradually decreasing with the increase in substituted Bi (Fig. 5d–i). This effect is observed in other studies with substitutions of Bi²⁴ and other elements such as Zr,¹⁷ Sn,¹⁵ and Sm.¹⁶ In addition, the particles lose their polygonal character and round shapes are promoted with a high degree of agglomeration and coarsening that increases with the densification temperature. This agglomeration and coarsening does result in an increase in the particle size for the case of Ba_0.925Bi_0.025TiO₃. However, it still maintains the trend with the temperature of pure BaTiO₃ for the Ba_0.950Bi_0.050TiO₃ composition samples, but with a lower particle size starting point from 800 °C.

3.2. Dielectric properties of Ba_1−xBi_xTiO₃ (x = 0.000, 0.050, and 0.075) sintered samples

The dielectric properties and the influence of the degree of Bi substitution on the crystal structure of the chosen compositions were evaluated, as well as the coexistence effect of the monoclinic and tetragonal phase. Fig. 6 shows the evolution of the relative permittivity ε_r of the Ba_1−xBi_xTiO₃ ceramics (x = 0.000, 0.050 and 0.075) as a function of temperature in the range between 25 and 200 °C at several fixed frequencies from 1 kHz to 1 MHz. As anticipated, it is well known that in the BTO-based system, there are four polymorphic phases, namely, rhombohedral (R), orthorhombic (O), tetragonal (T), and cubic (C) phases with the increase in temperature. Therefore, the transition temperatures are correspondingly defined as T_R–O, T_O–T, and T_C (or Curie temperature). The curves corresponding to ceramics with 0.000 ≤ x ≤ 0.075 present two transitions (see the curves in the Fig. 6a–c), which are associated with corresponding T_O–T and T_C, respectively. In the temperature-dependent real part of permittivity (ε′–T) curves (Fig. 6a–c), ε′ shows a diffused and broadened transition with strong frequency dependence close to MPB around RT, with the maximum ε′ increasing and shifting to higher temperatures with frequency. Considering the results of both XRD patterns and ε′–T curves (see Fig. 4 and 6), two situations can be identified depending on the doping content: first, for a high doping range as well as for undoped samples, the ceramics belong to O and T phase coexistence close to RT (see grey regions marked in Fig. 6a and c); and second, for an optimum doping range (that is, x = 0.050), the O–T phase boundary is suppressed in favour of a new M–T phase transition (see blue region indicated in Fig. 6b). Noteworthy, the dielectric constant at RT increases with the doping amount, while the dielectric losses remain low, reaching a minimum at x = 0.050 (see at bottom of each panel of the Fig. 6a–c). The coexistence of M–T phases increases the charge accumulation of the system. This behaviour is similar to the one that occurs at the MPB in the PZT system. This fact anticipates the improvement of the piezoelectric properties.

Fig. 6 Identification and Influence of the Bi³⁺ content on phase transitions: temperature-dependent real permittivity and its frequency dependence in Ba_1−xBi_xTiO₃ sintered ceramics in the temperature range from 25 to 200 °C, where x takes values of 0.000 (a), 0.050 (b) and 0.075 (c). The red arrows marked on the panel correspond to T_C. The maximum value of the dielectric constant appears at the Curie temperature (T_C) corresponding to the tetragonal (ferroelectric phase)–cubic (paraelectric phase) phase transition. Another maximum, much weaker, appears near RT, indicating the orthorhombic (ferroelectric phase)–tetragonal (ferroelectric phase) phase transition (T_O–T) for composition where x takes values of 0.000 (a) and 0.075 (c), which is represented by grey area in the panels (a and c). By contrast, for composition with x = 0.050 (c), the phase transition is different because it occurs between a monoclinic phase (ferroelectric phase)–tetragonal (ferroelectric phase) phase transition (T_M–T), being indicated by blue area in panel (b). Additionally, at the bottom of each panel (a–c) are represented the temperature-dependent tan δ (dielectric losses) and its frequency dependence in Ba_1−xBi_xTiO₃ sintered ceramics. The black color marked on the panel indicates the evolution of real permittivity and tan δ with the frequency, in the frequency range from 1 kHz to 1 MHz.

However, we also focus on the variation in T_C with the Bi⁺³ content, and this is plotted in Fig. 6a–c. As compared with the Ba_1−xBi_xTiO₃ ceramics without Bi³⁺, we can notice that the ceramics with Bi³⁺ have a higher T_C. Moreover, the dielectric constant value at T_C increases with the Bi⁺³ doping, reaching a maximum at x = 0.050. This phenomenon is consistent with previously reported results in a BTO-based system with the addition of other A-site doping.²⁴ Therefore, Bi ions are occupying the Ba positions in the crystal lattice of BaTiO₃, providing an extra positive charge and it is compensated for this contribution by an electron and/or Ba vacancies.^24,51 In turn, this structural modification causes modifications in the positions of the Ti–O ligands of the octahedron, leading to changes in the dielectric properties.

Considering the nature of coexistence of monoclinic and tetragonal phases related to the composition Ba_0.950Bi_0.050TiO₃ and a pure tetragonal phase of the composition Ba_0.925Bi_0.075TiO₃, it was found that the Bi ions should occupy similar positions in the crystal lattice, and although a higher degree of deformation is obtained in the case of the monoclinic one, it has no effect on the position of the Curie transition. The result is in contradiction with the results of other works, where a shift towards higher values of the Curie temperature was observed as the Bi content increased.²⁴ Moreover, there is a rather widespread concept that when BaTiO₃ is substituted or doped with other elements such as Pr,⁷³ Sr,⁷⁴ or Sm¹⁶ (among others), a diffusive behavior is induced by attenuating the transition and widening it in temperature. The diffusivity-inducing structural mechanism also appears when Bi is substituted, as reported in other studies²⁴ since this element is one of the cornerstones for obtaining lead-free relaxor ceramic materials with a high technological applicability.^8,39 The origin of the diffusion capacity provided by Bi lies in the structural variations and/or crystallographic defects that may lead to different atomic distributions at different Curie temperatures in the same sample.²⁴ However, the chemical approach established in our investigations using the sol–gel technique produces accentuated and sharp transitions obtaining the same Curie temperatures as a function of the frequencies considered for the two compositions of Ba_0.950Bi_0.050TiO₃ and Ba_0.925Bi_0.075TiO₃ (Fig. 6b and c).

Interestingly, the value of the dielectric constant is considerably enhanced in the sintered samples with Bi substitutions (ε_r,Bi=0.050 = 2348 and ε_r,Bi=0.075 = 1720 for 1 MHz), with respect to the pure BaTiO₃ composition (ε_r,Bi=0 = 1052) and anomalies are observed at the maximum of the permittivity as a function of frequency (Fig. 6b). First of all, the improvement in the dielectric constant values as a function of temperature is reported as a single dopant when Bi is substituted or doped in the BaTiO₃ crystal structure,^24,51 and in relaxor ferroelectrics with solid solutions containing Na and Nb substitutions.^75,76 Notably, an increase of 5% was obtained for Bi substitutions at the Ti⁴⁺ positions for every 0.01 mol% of Bi in reference⁵¹ and similar values of maximum permittivity when the Bi substitutions occur in the Ba²⁺ positions.^24,51 In the present investigation, an enhancement of 24.4% was obtained from the Ba_0.950Bi_0.050TiO₃ composition and 8.4% for the Ba_0.925Bi_0.075TiO₃ composition corresponding to each 0.01 mol% of Bi (Fig. 6b and c, respectively). Therefore, the synthesis and processing of Ba_1−xBi_xTiO₃ developed in this work presents a substantial improvement in ferroelectrics with a single-substitution. There are possible reasons for the composition with x = 0.050 being a strong enhancement in the maximum value of the dielectric constant with respect to Ba_0.925Bi_0.075TiO₃. Such causes could be related to excessive doping,¹⁶ the replacement of Ti ions in B-sites with larger Bi³⁺ ions, as it is observed in other ABO₃ systems,³⁸ and/or the purely tetrahedral character of the composition of x = 0.075. Furthermore, the additional degree of rotational freedom of polarization in the crystal structure of BaTiO₃ with the stabilization of the monoclinic phase together with the tetragonal one regarding the composition Ba_0.950Bi_0.050TiO₃, it becomes a consistent explanation and its improved and unique properties can be contrasted with the formation of morphotropic phase boundaries.^37,39,77 In this line, the change in the trend of maximum permittivity as a function of frequency with an inflection point around 200 kHz is remarkable (Fig. 6b), common for all the samples even for pure BaTiO₃. The observed phenomenon becomes more pronounced as the Bi content increases and reaches a maximum for the x = 0.050 composition. Such effect presents a great anomaly in charge carriers since generally when the frequency increases, the maximum value of the dielectric constant decreases.^16,74 Finally, regarding the dielectric losses (tan δ), a maximum at the Curie transition for the three compositions can be noted (see at the bottom of each panel in Fig. 6a–c). For pure BaTiO₃, tan δ is extremely high at temperatures above the Curie transition, indicating a huge dielectric dispersion and a high conductivity. On the contrary, the losses remain low for the two other Bi-substituted composition located at the same temperature range. The result can be explained by the difference in density between the three samples since the porosity is higher for the BaTiO₃ pellet (ρ_r,x=0.000 = 95.40%) than for x = 0.050 (ρ_r,x=0.050 = 97.22%) and x = 0.075 (ρ_r,x=0.075 = 96.87%), which increases the dielectric losses (at the bottom of Fig. 7a). Materials are considered as good dielectrics when their losses do not exceed 8%.⁷⁸ These dielectric losses are indicators of the amount of energy dissipated as heat,¹⁶ and an enhanced response of the material is expected with low dielectric losses as a function of frequency and temperature. Specific to this work, the dielectric losses are between 8 and 10% for the x = 0.050 substitution and between 4 and 8% for the x = 0.075 substitution. Therefore, the loss tangent decreases progressively with the amount of substituted Bi and represents a great improvement in dielectric properties and porosity with respect to BaTiO₃, displaying symmetric and stable behaviors around the Curie temperature for x = 0.050 and with a more diffusive and asymmetric character for x = 0.075.

Fig. 7 Ferroelectric behaviours and their relation to functional properties of the Ba_1−xBi_xTiO₃ ceramics: P–E loops of the ceramics as a function of x, where x takes values of 0.000 (a), 0.050 (b) and 0.075 (c). The red dot and grey dot show the evolution of both the remnant polarization (P_r) and the coercive field (E_c), respectively. (d) Remanent polarization (P_r) and (e) coercive field (E_C) values of the Ba_1−xBi_xTiO₃ ceramics as a function of x. Panel (f) shows the product ε_rP_rversus Bi³⁺ content.

3.3. Influence of the phase transition at RT on the functional properties of the Ba_1−xBi_xTiO₃ ceramics

From a functional viewpoint, the design and control of new phase coexistence were used to attain a significant enhancement in the piezoelectric activity of piezoelectric oxides. In this context, supplementary information concerning the effects of Bi³⁺ doping on the phase transformations of the Ba_1−xBi_xTiO₃ system can be attained from the ferroelectric features.

For a better understanding of the relationship between observed structural evolution and functional properties of the ceramics, the dependence polarization (P–E) loops as a function of Bi³⁺ content were measured, as displayed in Fig. 7a–c. From Fig. 7a–c, we can observe that all the ceramics exhibit good square hysteresis loops at RT, revealing their ferroelectric behavior. As observed in Fig. 7a–c, the coercive field (E_c) decreases with the Bi⁺³ content, evidencing that the ferroelectricity is clearly sensitive to the Bi⁺³ content. To make clear the effects of Bi⁺³ content on the ferroelectric behavior of the system, the remnant polarization (P_r) and coercive field (E_c) of each sample derived from Fig. 7a–c are represented in Fig. 7d and e. In Fig. 7e, it is observed that E_c decreases as the Bi⁺³ content increases, indicating that the addition of Bi⁺³ facilitates the movement of ferroelectric domain and made the polarization switching easier.⁷⁹ By contrast, P_r increases as the Bi⁺³ content increases because the coexistence of monoclinic-tetragonal phases begins to appear, reaching a maximum at x = 0.050 and then decreases again as the Bi⁺³ content increases (that is, at x = 0.075).

P _r, and consequently the dielectric behavior (Fig. 6), seems to be definitively related to the stabilization of the monoclinic and tetragonal phase coexistence. From this perspective, enhanced dielectric and ferroelectric properties are desirable; it is well known that dielectric and ferroelectric behaviors determine the piezoelectric properties, remembering that the d₃₃ piezoelectric constant is proportional to the ε_rP_r product.^69,80 Consequently, an enhancement of the piezoelectric properties is possible for higher P_r (in particular for composition at x = 0.05), even though ε_r remains constant at RT. In this context, the ε_rP_r product is plotted as a function of the Bi³⁺ content, as shown in Fig. 7f. A similar changing tendency in ε_rP_r evolution occurs in all compositions, i.e., ε_rP_r first increases and then decreases as x increases, reaching a peak for x = 0.050. Specifically, the high dielectric permittivity is related to the coexistence of the M–T phases, which make the system (for composition at x = 0.050) more polarizable due to the existence of more directions for the polarization orientation, and more importantly, it provides the rotation path for the enhanced piezoelectric properties near the phase boundary.⁸¹ This fact is highly remarked by the appearance of large P_r values for the compositions having monoclinic-tetragonal coexistence at RT. Large P_r and the lower values of E_c indicate a high domain mobility characteristic of the Ba_1−xBi_xTiO₃ system.

In summary, the stabilization of this phase coexistence induces a high degree of polarization in the system close to RT, associated with the spontaneous polarization reorientation on the [010]_c and [001]_c directions for the monoclinic (M) and a tetragonal (T) phases, respectively.⁸² Thus, the M–T phase coexistence at RT produces a lattice deformation associated with the high degree of the polarization directions that contribute to the domain mobility and, therefore, to the enlargement of the functional properties.

4. Conclusions

In this study, a novel sol–gel approach has been designed with the objective of obtaining thermodynamically stable phases at RT that offer new polarization mechanisms in the crystallographic structure of the BaTiO₃-based system, significantly improving the functional properties. For that, we systematically focused on the control of the Bi⁺³ substitution in the Ba_1−xBi_xTiO₃ structure, finding that the replacement of the A-sites with Bi ions in the perovskite structure leads to the stabilization of the Monoclinic–Tetragonal (M–T) phase boundary close to RT. This phase coexistence causes an elevated degree of polarization direction close to RT, facilitating the polarization process of the system. We are convinced that the present research opens up new avenues for chemical synthesis by a sol–gel method with the aim of achieving stable polymorphs to further enhance the interesting ferroelectric properties offered by BaTiO₃-based compounds.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The present work has been supported by the Ministerio Español de Ciencia e Innovación (MICINN) through the projects: RTI2018-095856-B-C21 and RTI2018-095303-A-C52; Ministerio de Asuntos Económicos y Transformación Digital (MINECO) by PID2020-114192RB-C41; and Comunidad de Madrid, Spain, by S2018/NMT-4321 NANOMAGCOST and “Doctorados Industriales” project (IND2020/IND-17375), which is co-financed by the European Social Fund. A. S. acknowledges the financial support from the Comunidad de Madrid for an “Atracción de Talento Investigador” contract (2017-t2/IND5395). A. P. received funding from grant PRE2019-0875001234, Ministerio de Ciencia e Innovación (MICINN), Spain. R. E. Rojas-Hernandez acknowledges financial support from the Estonian Research Council (grants PSG-466).

References

1. B. Jiang, J. Iocozzia, L. Zhao, H. Zhang, Y. W. Harn, Y. Chen and Z. Lin, Chem. Soc. Rev., 2019, 48, 1194–1228.
2. S. Kumar, M. Sharma, S. Powar, E. N. Kabachkov and R. Vaish, J. Eur. Ceram. Soc., 2019, 39, 2915–2922.
3. F. Rubio-Marcos, A. Del Campo, P. Marchet and J. F. Fernández, Nat. Commun., 2015, 6, 6594.
4. C. Chao, Y. Zhou, T. Han, Y. Yang, J. Wei, H. Li and W. He, J. Alloys Compd., 2020, 825, 154060.
5. S. Ram, A. Jana and T. K. Kundu, J. Appl. Phys., 2007, 102, 054107.
6. C. Mallada, J. L. Menéndez, O. J. Dura, M. A. López de la Torre, R. Menéndez and R. Santamaría, J. Eur. Ceram. Soc., 2017, 37, 3741–3746.
7. S. Xu, Z. Liu, M. Zhang and L. Guo, J. Alloys Compd., 2019, 801, 483–488.
8. H. Yang, F. Yan, Y. Lin, T. Wang, F. Wang, Y. Wang, L. Guo, W. Tai and H. Wei, J. Eur. Ceram. Soc., 2017, 37, 3303–3311.
9. L. Yan, Q. Fu, D. Zhou, M. Wang, Z. Zheng, W. Luo and G. Wang, Ceram. Int., 2019, 45, 19113–19119.
10. D. Karoblis, A. Zarkov, K. Mazeika, D. Baltrunas, G. Niaura, A. Beganskiene and A. Kareiva, Ceram. Int., 2020, 46, 16459–16464.
11. Q. Yuchang, W. Qinlong, L. Fa, Z. Wancheng and Z. Dongmei, J. Mater. Chem. C, 2016, 4, 371–375.
12. Y. F. Zhu, L. Zhang, T. Natsuki, Y. Q. Fu and Q. Q. Ni, ACS Appl. Mater. Interfaces, 2012, 4, 2101–2106.
13. C. Bi, M. Zhu, Q. Zhang, Y. Li and H. Wang, Mater. Chem. Phys., 2011, 126, 596–601.
14. J. Wang, Y. Liu, Q. Li, K. Lau, R. L. Withers, Z. Li and Z. Xu, Appl. Phys. Lett., 2013, 103, 042910.
15. M. Selvaraj, R. Venkatesan, J. Mayandi and V. Venkatachalapathy, Mater. Today: Proc., 2019, 35, 13–16.
16. A. Kumari, K. Kumari, F. Ahmed, A. Alshoaibi, P. A. Alvi, S. Dalela, M. M. Ahmad, R. N. Aljawfi, P. Dua, A. Vij and S. Kumar, Vacuum, 2021, 184, 109872.
17. M. Aghayan, A. Khorsand Zak, M. Behdani and A. Manaf Hashim, Ceram. Int., 2014, 40, 16141–16146.
18. R. Seshadri and N. A. Hill, Chem. Mater., 2001, 13, 2892–2899.
19. D. S. Keeble, E. R. Barney, D. A. Keen, M. G. Tucker, J. Kreisel and P. A. Thomas, Adv. Funct. Mater., 2013, 23, 185–190.
20. R. E. Cohen, Nature, 1992, 358, 136–138.
21. Z. M. Wang, K. Zhao, X. L. Guo, W. Sun, H. L. Jiang, X. Q. Han, X. T. Tao, Z. X. Cheng, H. Y. Zhao, H. Kimura, G. L. Yuan, J. Yin and Z. G. Liu, J. Mater. Chem. C, 2013, 1, 522–530.
22. M. García-Hernández, A. García-Murillo, F. De, J. Carrillo-Romo, D. Jaramillo-Vigueras, G. Chadeyron, E. De La Rosa and D. Boyer, Int. J. Mol. Sci., 2009, 10, 4088–4101.
23. M. Liu, H. Hao, Y. Zhen, T. Wang, D. Zhou, H. Liu, M. Cao and Z. Yao, J. Eur. Ceram. Soc., 2015, 35, 2303–2311.
24. N. Sareecha, W. A. Shah, M. L. Mirza, A. Maqsood and M. S. Awan, Phys. B, 2018, 530, 283–289.
25. F. A. Rabuffetti and R. L. Brutchey, J. Am. Chem. Soc., 2012, 134, 9475–9487.
26. X. Zhang, B. Cui, J. Wang and Q. Jin, Ceram. Int., 2019, 45, 10626–10632.
27. L. Mi, Q. Zhang, H. Wang, Z. Wu, Y. Guo, Y. Li, X. Xiong, K. Liu, W. Fu, Y. Ma, B. Z. Wang and X. W. Qi, Ceram. Int., 2020, 46, 10619–10633.
28. A. Testino, V. Buscaglia, M. T. Buscaglia, M. Viviani and P. Nanni, Chem. Mater., 2005, 17, 5346–5356.
29. S. K. Lee, T. J. Park, G. J. Choi, K. K. Koo and S. W. Kim, Mater. Chem. Phys., 2003, 82, 742–749.
30. S. H. Jhung, J. H. Lee, J. W. Yoon, Y. K. Hwang, J. S. Hwang, S. E. Park and J. S. Chang, Mater. Lett., 2004, 58, 3161–3165.
31. J. López-Sánchez, A. Serrano, A. del Campo, M. Abuín, E. Salas-Colera, A. Muñoz-Noval, G. R. Castro, J. de la Figuera, J. F. Marco, P. Marín, N. Carmona and O. Rodríguez de la Fuente, RSC Adv., 2019, 9, 17571–17580.
32. J. López-Sánchez, A. Muñoz-Noval, A. Serrano, M. Abuín, J. de la Figuera, J. F. Marco, L. Perez, N. Carmona and O. Rodríguez de la Fuente, RSC Adv., 2016, 6, 46380.
33. J. López-Sánchez, A. Muñoz-Noval, C. Castellano, A. Serrano, A. del Campo, M. Cabero, M. Varela, M. Abuín, J. de la Figuera, J. F. Marco, G. R. Castro, O. Rodriguez de la Fuente and N. Carmona, J. Phys.: Condens. Matter, 2017, 29, 485701.
34. C. Eisenschmidt, H. T. Langhammer, R. Steinhausen and G. Schmidt, Ferroelectrics, 2012, 432, 103–116.
35. A. K. Kalyani, D. K. Khatua, B. Loukya, R. Datta, A. N. Fitch, A. Senyshyn and R. Ranjan, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 1–12.
36. N. Horchidan, L. Padurariu, C. E. Ciomaga, L. Curecheriu, M. Airimioaei, F. Doroftei, F. Tufescu and L. Mitoseriu, J. Eur. Ceram. Soc., 2020, 40, 1258–1268.
37. J. M. Rosso, J. A. Burato, V. F. Freitas, D. M. Silva, E. A. Volnistem, G. M. Santos, T. G. M. Bonadio, G. S. Dias, L. F. Cótica and I. A. Santos, Mater. Chem. Phys., 2019, 237, 121794.
38. J. E. García and F. Rubio-Marcos, J. Appl. Phys., 2020, 127, 131102.
39. A.-B. M. A. Ibrahim, R. Murgan, M. K. Abd Rahman and J. Osm, in Ferroelectrics – Physical Effects, InTech, 2011.
40. J. Gao, D. Xue, W. Liu, C. Zhou and X. Ren, Actuators, 2017, 6, 24.
41. J. Rodriguez-Carvajal, Phys. B, 1993, 192, 55–69.
42. P. Duran, D. Gutierrez, J. Tartaj and C. Moure, Ceram. Int., 2002, 28, 283–292.
43. J. López-Sánchez, A. Serrano, A. del Campo, Á. Muñoz-Noval, E. Salas-Colera, M. Cabero, M. Varela, M. Abuín, G. R. Castro, J. Rubio-Zuazo, Ó. Rodríguez de la Fuente and N. Carmona, J. Alloys Compd., 2022, 892, 162061.
44. M. J. Ansaree and S. Upadhyay, Process. Appl. Ceram., 2015, 9, 181–185.
45. G. W. Gokel, Dean’S Handbook Of Organic Chemistry, McGraw-Hill Education, 2nd edn, 2004.
46. M. J. Ansaree and S. Upadhyay, Integr. Ferroelectr., 2016, 176, 184–201.
47. H. Tagawa and J. Ohashi, Thermochim. Acta, 1985, 88, 307–312.
48. K. Othman, BaTiO3 ferroelectric material Synthesis and characterization, Lap Lambert Academic Publishing, 2019.
49. D. Fang and J. Liu, in Fracture Mechanics of Piezoelectric and Ferroelectric Solids, eds., D. Fang and J. Liu, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, pp. 33–76.
50. M. Shandilya, R. Rai, A. Zeb and S. Kumar, Ferroelectrics, 2017, 520, 93–109.
51. S. Liu, H. Zhang, L. Sviridov, L. Huang, X. Liu, J. Samson, D. Akins, J. Li and S. O’Brien, J. Mater. Chem., 2012, 22, 21862–21870.
52. H. Cao, C. P. Devreugd, W. Ge, J. Li, D. Viehland, H. Luo and X. Zhao, Appl. Phys. Lett., 2009, 94, 1–4.
53. J. López Sánchez, E. Navarro, A. Serrano, C. Granados-Miralles, A. Del Campo, A. Quesada and P. Marín, ACS Appl. Electron. Mater., 2020, 2, 1484–1496.
54. A. W. Hewat, Ferroelectrics, 1973, 6, 215–218.
55. K. L. Ying and T. E. Hsieh, Mater. Sci. Eng., B, 2007, 138, 241–245.
56. J. Su and J. Zhang, J. Mater. Sci.: Mater. Electron., 2019, 30, 1957–1975.
57. Y. Saito, H. Takao, T. Tani, T. Nonoyama, K. Takatori, T. Homma, T. Nagaya and M. Nakamura, Nature, 2004, 432, 84–87.
58. W. Ge, Y. Ren, J. Zhang, C. P. Devreugd, J. Li and D. Viehland, J. Appl. Phys., 2012, 111, 3–9.
59. A. F. Devonshire, London, Edinburgh, Dublin Philos. Mag. J. Sci., 1949, 40, 1040–1063.
60. A. F. Devonshire, London, Edinburgh, Dublin Philos. Mag. J. Sci., 1951, 42, 1065–1079.
61. D. Vanderbilt and M. H. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 1–9.
62. J. Paul, T. Nishimatsu, Y. Kawazoe and U. V. Waghmare, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 1–6.
63. S. E. Park and T. R. Shrout, J. Appl. Phys., 1997, 82, 1804–1811.
64. K. Tsuda, R. Sano and M. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 2–6.
65. H. Fu and R. E. Cohen, Nature, 2000, 403, 281–283.
66. M. Budimir, D. Damjanovic and N. Setter, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 1–6.
67. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
68. D. H. Yoon, J. Ceram. Process. Res., 2006, 7, 343–354.
69. X. Lv, J. Zhu, D. Xiao, X. X. Zhang and J. Wu, Chem. Soc. Rev., 2020, 49, 671–707.
70. J. López-Sánchez, A. Serrano, A. Del Campo, M. Abuín, O. Rodríguez de la Fuente and N. Carmona, Chem. Mater., 2016, 28, 511–518.
71. T.-C. Huang, M.-T. Wang, H.-S. Sheu and W.-F. Hsieh, J. Phys.: Condens. Matter, 2007, 19, 476212.
72. X. Wang, S. Liu, L. Zhang, J. Wang and Y. Zhao, Ceram. Int., 2018, 44, S216–S219.
73. R. Sagar, S. Madolappa, N. Sharanappa and R. L. Raibagkar, Mater. Chem. Phys., 2013, 140, 119–125.
74. A. M. Henaish, M. Mostafa, I. Weinstein, O. Hemeda and B. Salem, Magnetism, 2021, 1, 22–36.
75. Y. Liu, B. Cui, Y. Wang, R. Ma, M. Shangguan, X. Zhao, S. Wang, Q. Li and Y. Wang, J. Am. Ceram. Soc., 2016, 99, 1664–1670.
76. Y. Chen, H. Fan, D. Hou, Y. Jia, A. Zhang and W. Wang, Ceram. Int., 2022, 48, 26894–26903.
77. K. Pengpat, S. Hanphimol, S. Eitssayeam, U. Intatha, G. Rujijanagul and T. Tunkasiri, J. Electroceramics, 2006, 16, 301–305.
78. L. Curecheriu, V. A. Lukacs, L. Padurariu, G. Stoian and C. E. Ciomaga, Materials, 2020, 13, 3324.
79. F. Rubio-Marcos, J. F. Fernandez, D. A. Ochoa, J. E. García, R. E. Rojas-Hernandez, M. Castro and L. Ramajo, J. Eur. Ceram. Soc., 2017, 37, 3501–3509.
80. B. Zhang, J. Wu, X. Cheng, X. Wang, D. Xiao, J. Zhu, X. Wang and X. Lou, ACS Appl. Mater. Interfaces, 2013, 5, 7718–7725.
81. F. Rubio-Marcos, R. López-Juárez, R. E. Rojas-Hernandez, A. Del Campo, N. Razo-Pérez and J. F. Fernandez, ACS Appl. Mater. Interfaces, 2015, 7, 23080–23088.
82. Z. Chen, Z. Luo, C. Huang, Y. Qi, P. Yang, L. You, C. Hu, T. Wu, J. Wang, C. Gao, T. Sritharan and L. Chen, Adv. Funct. Mater., 2011, 21, 133–138.

---

Footnote

† These authors contributed equally this work.

---