Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Combining two-photon photoemission and transient absorption spectroscopy to resolve hot carrier cooling in 2D perovskite single crystals: the effect of surface layer†
Weihua
Lin‡
 a,
Mingli
Liang‡
ab,
Yuran
Niu
c,
Zhesheng
Chen
d,
Marie
Cherasse
de,
Jie
Meng
a,
Mingli
Liang‡
ab,
Yuran
Niu
c,
Zhesheng
Chen
d,
Marie
Cherasse
de,
Jie
Meng
 ab,
Xianshao
Zou
a,
Qian
Zhao
b,
Huifang
Geng
f,
Evangelos
Papalazarou
g,
Marino
Marsi
g,
Luca
Perfetti
d,
Sophie E.
Canton
*bh,
Kaibo
Zheng
*ab and
Tönu
Pullerits
ab,
Xianshao
Zou
a,
Qian
Zhao
b,
Huifang
Geng
f,
Evangelos
Papalazarou
g,
Marino
Marsi
g,
Luca
Perfetti
d,
Sophie E.
Canton
*bh,
Kaibo
Zheng
*ab and
Tönu
Pullerits
 *a
*a
aChemical Physics and NanoLund, Lund University, Box 124, 22100 Lund, Sweden. E-mail: tonu.pullerits@chemphys.lu.se; kaibo.zheng@chemphys.lu.se
bDepartment of Chemistry, Technical University of Denmark, DK-2800 Kongens Lyngby, Denmark
cMAX IV Laboratory, Lund University, P.O. Box 118, 22100 Lund, Sweden
dLaboratoire des Solides Irradiés, CEA/DRF/IRAMIS, CNRS, Ecole polytechnique, Institut Polytechnique de Paris, 91120 Palaiseau, France
eFritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany
fUltrafast Electron Microscopy Laboratory, The MOE Key Laboratory of Weak-Light Nonlinear Photonics, School of Physics, Nankai University, Tianjin 300071, China
gLaboratoire de Physique des Solides, CNRS, Université Paris Saclay, Orsay 91405, France
hEuropean XFEL, Holzkoppel 4, 22869 Schenefeld, Germany. E-mail: sophie.canton@xfel.eu
First published on 25th October 2022
Abstract
We investigate hot carrier (HC) cooling in two-dimensional (2D) perovskite single crystals by applying two complementary ultrafast spectroscopy techniques – transient absorption (TA) and time-resolved two-photon photoemission (TR-2PPE) spectroscopies. TR-2PPE directly maps the hot electron distribution and its dynamics in the conduction band to the detected photoelectron distribution. While TR-2PPE selectively probes the upper layer of the material, TA provides information on the whole bulk. Two cooling regimes are resolved in both techniques. The fast timescale of 100–200 fs is related to the electron scattering by longitudinal optical (LO) phonons and the slow timescale of 3–4 ps corresponds to the LO phonon relaxation. The HC cooling dynamic of TA measurement has faster initial stage and higher starting temperature for the slower stage than in TR-2PPE measurements. Conclusions about spatial sensitivity of the cooling dynamics across the 2D perovskite single crystals constitute valuable information that can guide the future development of HC solar cells and thermoelectric applications based on 2D perovskites.
Introduction
Organic–inorganic hybrid perovskites have numerous photo-physical properties, which make them promising for optoelectronic and thermoelectric applications.1–3 They are particularly famous as active materials for solar cells achieving power conversion efficiencies (PCE) exceeding 25%.4–6 This value is not so far from the Shockley–Queisser limit of the conventional single-junction photovoltaic devices,7 and further improvements need a principally different methodology. One approach is to establish a tandem cell structure combining the photoactive layers of alternating spectral coverage.8 Another very promising but not yet practically demonstrated concept is the hot carrier solar cell (HCSC) with theoretical maximum efficiency of 66% under one sun illumination.9 In HCSC,10–12 the inhibited cooling of the photo-generated hot carriers (HC) elevates the equilibrium carrier temperature collected by the electrodes, thus reducing the heat loss during the light-to-electricity conversion process. Recently the potential of three-dimensional (3D) hybrid perovskites in the application of HCSC has attracted increasing attention.13–16 Firstly, the small effective mass of the charge carriers leads to slower HC relaxation by diminishing the possible intraband Auger-type energy transfer that promotes energy losses.17,18 Secondly, the large phonon bandgap between longitudinal optical (LO) and longitudinal acoustic (LA) phonon branches of halide perovskite suppresses the pathways in the phonon decay, thereby enhancing the hot phonon bottleneck effect.18,19 Thirdly, polarons are generated due to the strong polar Fröhlich interactions between the charge carriers and the LO phonons. Such strongly-coupled polarons further decelerate the cooling of the HC via screening the Coulomb interaction responsible for the carrier scattering with the LO phonons.20 Long-lived HCs with lifetime reaching 100 picoseconds in hybrid halide perovskites have been reported by several groups based on spectroscopic techniques,20,21 such as ultrafast transient absorption microscopy and time-resolved photoluminescence spectroscopy. However, the standard analyses method based on the assumption of the exponential high energy tail of the spectrum due to the Boltzmann distribution, is sometimes problematic. For example, the resulting HC cooling temperatures significantly depend on the energy range chosen for the analyses.22 Clearly, a technique is needed where the hot carrier energies in conduction band could be directly observed and compared for different samples.The emerging two-dimensional (2D) derivatives of the organic-inorganic hybrid perovskites are expected to be even more promising building blocks for realizing the HCSCs due to their unique electronic and phononic structures that could further hinder the HC cooling process and promote a long-lived hot quasi-equilibrium state. The 2D lead halide perovskites are denoted as (B)2(A)n−1PbnX3n+1, where n inorganic octahedra layers are sandwiched between two long-chain organic spacing cation (B-site) layers, while the small cations (A-site) fill the inorganic perovskite cages. On one hand, the soft and long-chain spacing cations can significantly reduce the group velocity and propagation length of the acoustic phonons slowing down the heat dissipation.23 Furthermore, the natural multiple-quantum-well (MQW) structure might stimulate hot phonon bottleneck effects similar to what can occur in traditional semiconductor quantum well superlattices (QWSL).24,25 QW structure may hinder the diffusion of HCs and propagation of acoustic phonons at the interface. The emitted zone-centre LO phonons might be reflected by the barrier. Furthermore, a phononic bandgap between LO phonons and acoustic phonons might be opened up due to MQW structure.26,27 All these effects can increase the hot phonon bottleneck effect and significantly slow down the HC cooling process. Earlier studies based on transient reflectance experiments have reported a HC cooling within sub-ps timescale in 2D perovskites.28 However, the fundamental photophysical mechanism of the cooling is yet to be clarified. In particular, the QW layers in the 2D perovskites are isolated by the organic spacing cations that modify the vibrational modes in both optical and acoustic branches. Such additional phonon modes might influence the HC cooling dynamics.
In order to elucidate the possible causal connection between the structure of the 2D perovskite and the cooling dynamics, a highly ordered single-crystal sample is preferable compared to the films with numerous grain boundaries and long-range disorder. In this article, we target the HC cooling dynamics on exfoliated (BA)2(MA)2Pb3I10 single-crystal flakes (BA = Butylammonium; CH3(CH2)3NH3+, MA = Methylammonium; CH3NH3+). To obtain a clear insight on the cooling mechanisms in the 2D perovskite crystalline flake, we compare the HC cooling dynamics monitored by transient absorption (TA) and time-resolved two-photon photoemission (TR-2PPE) spectroscopies. With the TA technique, the HC temperature is extracted by fitting the high-energy tail of photobleaching signals using the Boltzmann distribution function.29,30 The uncertainties of the fitting procedure are reduced by simultaneous analyses of many excitation intensities and by exploring multiple fitting models as described below. The other used method, TR-2PPE, enables direct mapping of the distribution of the measured kinetic energies of the emitted photoelectrons into the electron energy distribution in the conduction band (CB). Therefore, in this technique the HC temperature (energy) is directly available as a function of the probe delay time allowing to follow the cooling dynamics (relaxation). All in all, combing the straightforward interpretation of the TR-2PPE analysis with TA results, allows a more comprehensive study on HC cooling in 2D perovskites.
Since the photoelectrons in TR-2PPE originate only from the top layer of the sample whereas TA probes the whole bulk, we can relate the differences in the cooling dynamics to the details of the material properties at the surface and in the bulk of the crystal.
In general, the HC cooling dynamics extracted from these two techniques exhibit two stages, where the fast one (Stage I) is caused by the efficient electron – LO phonon (e-ph) scattering after which a thermal quasi-equilibration between hot electrons and LO phonons is reached.31,32 The following slower dynamics (Stage II) corresponds to the LO phonon relaxation due to the coupling to the acoustic phonons.18,33,34 We found that the dynamics obtained from TA measurement has faster cooling in Stage I and higher initial temperature of Stage II than in TR-2PPE measurements. There are three main possible explanations for this result.
First, the deviation in HC cooling dynamics can be attributed to the different probing depth of the two techniques – while the TA probes the whole sample, the photoelectrons in the TR-2PPE experiments are emitted only from the outermost layer. Thereby, the different local structure at the surface and in the bulk can cause the observed differences of the dynamics. In particular, the strain accumulation is released on the surface layer by both the in-plane and out-of-plane tilting which can lead to the weakened carrier–phonon coupling.35 In addition, the tilting of the octahedra at the surface of the exfoliated sample can modify the phononic features that HCs couple to.36 The spacing cation on the exfoliated surface sheet is softer, which could possibly decrease the e-ph coupling and slow down the cooling in Stage I.23,37 Second, the environmental temperature in these two measurements is different, which will cause the different LO phonon population which affects the cooling efficiency in the first stage. Third, only the electrons are probed in TR-2PPE measurements,18,38 while both excited electrons and holes contribute to the TA signals. The performed TA analyses provide an averaged effective cooling rate which is faster than the result for the electrons only. However, because the Fröhlich coupling strength is proportional to the square root of effective mass which is not so different for the electron and hole, it is unlikely to be the main source for the faster cooling in Stage I in the TA analysis. In Stage II, the obtained HC cooling dynamics share similar rate from two techniques, but the higher starting temperature in TA measurement indicates stronger hot phonon bottleneck effect in the bulk compared to the surface.39 Our findings reveal that the HC cooling dynamics on the crystal surface and in the bulk are different. The results suggest that the spacing cations have a significant role in the details of the cooling processes in 2D perovskites.
Results and discussion
2D perovskite single-crystal thin flakes with a diameter of around 100 μm were prepared by the mechanical exfoliation with Scotch tape from a bulk single crystal in the glove box.40 Such a procedure can provide flakes with a pure phase and an atomically flat surface (for the experimental details, see Methods and S1, ESI†). The steady state absorption spectrum of 2D perovskite (BA)2(MA)2Pb3I10 single crystal bulk is shown in Fig. S1 (ESI†), where the optical microscope image in the inset shows a 2D perovskite flake. The thickness of the flake is characterized in SEM measurement to be around 100 nm, see Fig. S2 (ESI†). Fig. 1a shows a typical TA spectrogram of 2D perovskite flake excited with 3.1 eV photon (i.e. 400 nm) at an intensity of 30 μJ cm−2 per pulse, which corresponds to an initial carrier density n0 = 6 × 1018 cm−3. A single ground state bleach (GSB) signal (ΔA < 0) due to the filling of band-edge states appears at around 2 eV and is consistent with the ground state absorption band-edge position in Fig. S1 (ESI†), as well as with the excitonic absorption peak of the similar samples in earlier study.41 In addition, there is an evolution of photo-induced absorption (PIA) signal (ΔA > 0) at the red-side of the band-edge (1.95 eV in Fig. 1a) into a photobleaching signal since the lowest-energy states at the band edge are quickly (∼0.1 ps) populated by the cooled carriers.42 We point out that the 2D perovskite phases with other n-value (i.e. (BA)2PbI4 as n = 1 or (BA)2(MA)Pb2I7 as n = 2 in Fig. S3, ESI†), which are unavoidable in film samples, are not present here, demonstrating the high purity of (BA)2(MA)2Pb3I10 single-crystal flakes.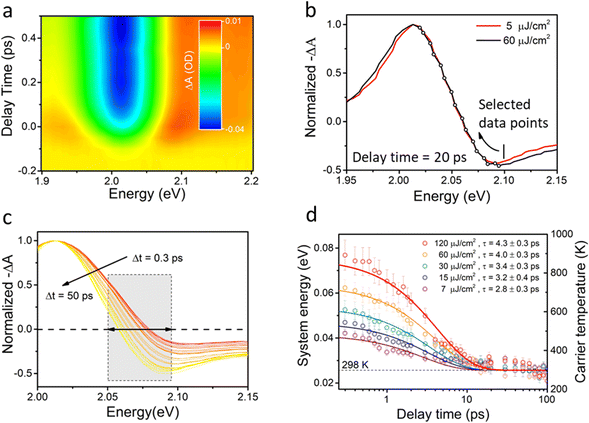 | ||
| Fig. 1 TA spectra and HC cooling dynamics of a 2D perovskite flake. (a) Pseudo-color representative TA spectrogram of the flake excited at 3.1 eV (400 nm) with excitation intensity of 30 μJ cm−2. (b) TA spectra of flake with excitation intensity of 5 and 60 μJ cm−2, the inserted line represents end point (∼2.10 eV) of the fitting range. (c) Normalized TA spectra extracted from (a) with the time delay range from 0.3 to 50 ps. The shaded rectangle with a two-headed black arrow marks the fitting range of the high energy tails of the ground state bleach used for obtaining the hot carrier temperature. (d) Photo-generated hot carrier temperature decay kinetics with 400 nm excitation at different excitation intensities (I1 = 120 μJ cm−2, I2 = 60 μJ cm−2, I3 = 30 μJ cm−2, I4 = 15 μJ cm−2, I5 = 7 μJ cm−2, corresponding to initial carrier density n0 = 2.4 × 1019, 1.2 × 1019, 6 × 1018, 3 × 1018, 1.4 × 1018 cm−3 respectively, see ESI,† S2 and S3). The temperature decays are individually fitted with single exponential function. | ||
First we analyze time-dependent carrier temperature based on the analysis of the TA spectra. As the ΔA reflects the population of excited carriers, we can fit the high energy tail of GSB signal by the Boltzmann distribution of HCs to extract the temperature. The approach has been widely reported in literature.18,29,43 The details of the implementation vary from study to study. Our procedure starts from verifying that the long-time line-shapes of the spectra under different excitation intensities are the same thereby showing consistency with the expected asymptotic approach to the ambient conditions. As shown in Fig. 1b, the TA spectra under more than an order of magnitude different excitation intensities coincide, showing that the hot carriers have cooled to the same level within 20 ps reaching equilibrium with the environment. Based on this, we choose spectra at 100 ps under the lowest excitation intensity and assumed the ambient (298 K) carrier temperature.
Clearly, the TA spectra as in Fig. 1. cannot be directly fitted by an exponential Boltzmann distribution since the curves cross zero and resemble exponential only in a limited region. Therefore, the spectra need to be shifted up by an offset and we have to establish a way to determine which part of the spectrum should be used for the fitting.
The TA spectrum as shown in Fig. 1 changes the sign because of the contributions with opposite signs to the spectrum. In the chosen representation the bleach signal is positive and the excited state absorption negative. This is chosen for visual convenience to recognize the exponential tail of the bleach while the usual convention in TA spectroscopy is opposite to this. Not much is known about the spectral shape of the excited state absorption. In semiconductors it should be largely determined by the density of states and since the latter is constant for the 2D materials, we have chosen constant offset in our analyses. We used the following expression to fit the exponential tail of the spectrum:
 | (1) |
Considering the similar effective masses of electrons (0.097 × m0) and hole (0.141 × m0),38,44 their contributions to the TA signals are similar. Therefore, Tc should represent the average temperature of both hot electrons and holes. We have tested also the square root dependent offset (density of states in 3D)45 leading only to minor changes in the outcome, see ESI,† S4.
In Fig. 1b we see that at about 2.1 eV the spectrum turns upwards and clearly does not follow the exponent. This sets the end point for the fitting range. To find the appropriate starting point, we gradually increased the number of the points used for the fitting and evaluated R-square and the sum of the absolute values of residuals (see Fig. S7, ESI†). The R-square reaches a relatively flat plateau when including 8–9 points while the sum of the absolute value of residuals starts rapidly increasing after including 12 points. We plot the TA spectra with Y-axis in log scale in Fig. S9 (ESI†) and from this we establish the optimal number of data points as 10. In order to find appropriate offset we fixed the long-time temperature as 298 K and found the offset level which gave the best fit. The range of the fitted high-energy tails of the GSB signals is marked in Fig. 1c. After the photoexcitation, the initially highly non-equilibrated HCs undergo a rapid energy redistribution reaching a quasi-thermal distribution. The HC temperature is a valid measure only after such distribution has been established. Since the TA analyses in terms of HC temperature relies on the thermal distribution of the carriers, the question rises, when can we start assigning temperature to the HCs based on the TA spectra. Here we analyzed the line-shapes of TR-2PPE spectra and concluded that at 0.3 ps the quasi-thermal distribution is achieved. For the details we refer to the ESI,† S5.
Visual inspection of the TA spectra shown in ESI,† S6, reveals qualitative trends of the cooling dynamics. The slope of the high-energy tail increases with the time until tens of picoseconds, indicating the decay of the HC temperature. The slope of the tail at an early timescale (up to about 0.5 ps) becomes smaller with increasing excitation intensity in Fig. S12 (ESI†), which represents higher HC temperature. In addition, the larger slope changes at high excitation intensity indicate longer HC cooling time towards its final temperature. Fig. 1d shows the time dependence of the carrier temperature at various excitation densities. The cooling process is well described by a single exponential function. At higher excitation intensity, the HC cooling is slowed down. After a rapid relaxation, the HCs cool to reach room temperature with a lifetime of a few ps (lifetime summarized in Fig. 1d). These cooling times are within the same order of magnitude as the ones reported for 3D perovskite (for a detailed comparison, see ESI,† Table S2).18,29,30,43,46 To confirm reproducibility of the method, we measured another sample with similar thickness and the analysis gives comparable dynamics, as shown in ESI,† S7.
In the following we use TR-2PPE, which directly probes electron distribution in the conduction band.47–49 The technique is demanding and has not been used as frequently as TA for the studies of hot carrier cooling. The pump pulse in the two experiments is very similar exciting the electrons into high energy states in the CB. In TR-2PPE, after a certain time delay, the electrons are excited from the CB to vacuum (i.e. photo-emitted) by the middle ultraviolet (MUV) probe pulse. The emitted photoelectrons are collected and analyzed in terms of both energy and momentum. Fig. 2a illustrates the detailed configuration of the TR-2PPE measurement of our 2D perovskite single-crystal flake, which is cleaved under a high vacuum to generate an atomically flat surface. Fig. 2b shows a TR-2PPE spectrogram of a 2D perovskite flake that displays the intensity of the photoelectron signal as a function of their kinetic energy as well as time. The detailed energy distribution curves (EDC) at representative time delays are shown in Fig. S17 (ESI†). At early delays the probe pulse creates an intense distribution of photoexcited electrons with kinetic energy peaking around 1.30 eV and mapping out the corresponding early hot electron distribution in the CB created by the pump pulse. Later a broader band peaked around 0.95 eV appears, indicating that the energy of initial excited hot electrons is redistributed to a pool of quasi-thermalized electrons with lower energy. The detailed fitting and discussion on dynamics at different excess energy states can be found in ESI,† S8.
 | ||
| Fig. 2 (a) Scheme of the TR-2PPE measurements. (b) Pseudocolor TR-2PPE spectrogram where the sample is pumped with 3.1 eV at 100 μJ cm−2 and probed at 4.65 eV of incident MUV photon energy. (c) Average excess energy decay of hot electrons in TR-2PPE measurements based on eqn (2). Sample is kept at close to the 135 K with liquid nitrogen during the measurement. | ||
In the next step, we calculate the average excess energy Ex(t) as a function of time delay by integrating the overall excess energy distribution of the HCs as50
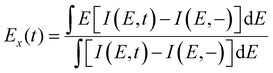 | (2) |
To have a meaningful discussion on the sub-picosecond dynamics of the TA and TR-2PPE measurements, as shown in Fig. 3, we use the term ‘system energy’ instead of carrier temperature since the temperature of carriers can only be evaluated after thermalization but the energy is there all the time.
As shown in Fig. 3a, the HC cooling dynamics from TR-2PPE can be fitted by bi-exponential decay function with lifetimes of 0.2 and 3 ps. The long component is the result of the hot phonon bottleneck. The fast component matches well with the short lifetime of hot electrons in Fig. S18 (ESI†). TR-2PPE measurements can directly monitor the hot electron distributions, which reflects system energy straightforwardly as excess energy. This is not the case in TA analysis. TA results contain abundant information of the system in a more general way with less experimental demands than TR-2PPE, but the high energy tail of bleaching signal needs to be fitted to obtain the system energy. It means that TA cannot quantify the system energy before the measured bleach tail follows the Boltzmann distribution. We confirm the timescale of this limitation (∼0.3 ps) by fitting the TR-2PPE spectra with Boltzmann distribution at different delays in Fig. S11 (ESI†).
We cannot consistently use the first 0.3 ps of the TA data for analyzing the cooling dynamics. This is why in Fig. 1d a single exponential fit starting at 0.3 ps was used, but we know that the initial excitation in two experiments is the same. Thus, we can adopt the initial system energy value from TR-2PPE as the starting point in TA analysis. The adopted value is close to the initial excess energy of hot carriers (∼4200 K) with thermal motion in 3D. This corresponds to a physical picture where the carriers can efficiently jump from layer to layer. More detailed discussion about determining the initial system energy can be found in ESI,† S10.
With this ‘starting temperature’, we can obtain a glance on the cooling dynamics, or relaxation, before the carrier temperature can be evaluated (<0.3 ps). The two time constants of the HC cooling based on the TA data are ≤0.1 ps and 4.3 ps – the first cooling stage is significantly faster than in TR-2PPE while the second stage has a comparable rate. At the same time the second cooling stage in TA has a higher amplitude. In Fig. 3b we demonstrate that the longer initial decay times severely deviate from the data points, meaning that the 0.1 ps has to be taken as the upper limit for the fast decay component.
The reason why there are two stages of the carrier cooling is the so called hot phonon bottleneck – the hot carriers warm up the LO phonons and reach equilibrium where the energy flow from hot carriers to LO phonons is equal to the backwards flow. Once the equilibrium is reached, the further cooling corresponds to the energy flow from LO phonons to the acoustic phonons. Apparently this stage has own bottleneck behavior revealed by the slowing down at higher excitation intensities, see Fig. 1d. This behavior has been earlier reported in other studies and also called the hot phonon bottleneck.17,29 However, there are subtle differences between these two bottleneck behaviors – the equilibrium at the first case is between the hot carriers and the LO phonons while in the second case the effect is more likely between the LO and acoustic phonons. The possible explanation of the latter can be the low thermal conductivity of the sample caused by the hindered acoustic phonon propagation.46
Let us now compare the HC cooling in Stage I in the two measurements. An important difference between the TA and TR-2PPE is the probing depth of the photo-generated species. Noteworthy, the samples are both pumped with 400 nm laser with similar fluence, meaning that the excitation concentrations are comparable in the two experiments. The mean escape depth of the photoelectrons due to the photon energy used in TR-2PPE is about 3 nm.51 This means that the signal in the TR-2PPE measurement is predominantly contributed by the first inorganic Pb–I octahedral layer plus the attached long-chain spacing cation with a thickness of 2.61 nm according to the lattice structure shown in Fig. 3c. On the other hand, the optical density (O.D.) of the single crystal flake in the TA measurement is 0.07, which ensures the transmittance of 86% of the incident light through the whole 2D perovskite flake containing 40 inorganic layers with a thickness of 100 nm. This means that the HC dynamics measured in TA, with the probing depth significantly longer than the flake thickness, contain information about the bulk.
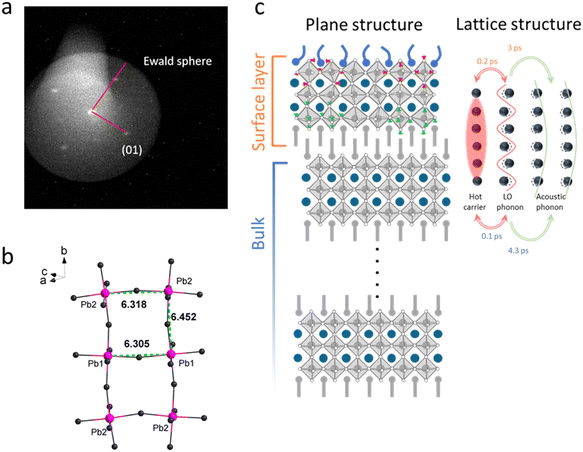
The initial HC relaxation is driven by the carrier-LO phonon coupling. In this context, the faster cooling rate may mean stronger coupling strength or the larger density of LO phonon states in the bulk. The Pb–I stretching mode of the octahedral cage provides the most important contribution to the LO phonons that cause the HC cooling in the 3D perovskite.31,32 If the Pb–I bond vibration on the surface of the 2D perovskite flake would be different from the analogous nuclear motions in the inner bulk, that could be a source of the differences in the cooling process in the two experiments. From the low-energy electron diffraction (LEED) measurements as seen in Fig. 4a, we found the distance between neighboring Pb atoms at the 2D perovskite surface (6.2 Å) to be very close to the value in the bulk (6.3 Å) as shown in Fig. 4b. The detailed calculation based on LEED pattern is discussed in ESI,† S11. The similar bond configuration suggests that the surface layer structure does not change much, and the spacer still exists on the very surface. Recently, surface octahedral tilting in the exfoliated 2D perovskite was reported based on a scanning tunneling microscopy (STM) study,36 indicating that surface lattice distortion is different from the bulk area. Our previous study revealed that the e-ph coupling strength of a 2D perovskite single crystal varies significantly between in-plane facet and facet perpendicular to the 2D layers.35 The e-ph coupling is enhanced in the strain-accumulated area at perpendicular facets while weakened in the strain-relaxed area at in-plane facet, which is the target facet in our measurements. This suggests that in our case the e-ph coupling is weakened in the surface layer where the steric hindrance is relaxed. In addition, the STM work shows that the spacing cation on the surface sheet is more flexible and softened by exfoliation (which is visualized via the increased octahedral tilting angle). Therefore, less ‘regular’ phonon modes may appear. In other words, there will be fewer decay channels for HC to be coupled to, which will reduce the efficiency of HC cooling on the surface layer in the first cooling stage.
Based on the above discussion, we propose that the e-ph coupling strength and amount of available LO phonons at the surface and bulk area are different due to the release of strain at exfoliated surface layer explaining the differences in the initial carrier relaxation dynamics at the surface and in the bulk.
Another difference between the two experiments is the environmental temperature – while the TA experiments were carried out at room temperature, in the TR-2PPE measurements were conducted at cryogenic conditions with temperature of the sample about 135 K. Can the faster HC cooling at higher environmental temperature be due to the increased population of acoustic phonons and leads to a more efficient phonon–phonon scattering?52 The interpretation fits our observation, but the associated timescale is much longer than our target since the phonon decay is involved.
A more likely explanation involves thermal population of LO phonons. In the Fröhlich model of electron–phonon interaction, the charge carriers are Coulomb coupled to the macroscopic electric field induced by the collective counter phase LO phonon motion of the oppositely charged ions. This coupling leads to hot electron dynamics via emitting or absorbing a LO phonon. The corresponding downwards (phonon emission) and upwards (phonon absorption) rates Wem and Wab can be expressed as:53,54
| Wem ∼ α[N(ωLO) + 1]ρ(ωLO) | (3) |
| Wab ∼ αN(ωLO)ρ(ωLO) | (4) |
Here ρ(ωLO) is LO phonon density of states, N(ωLO) is the Bose–Einstein distribution
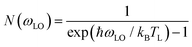 | (5) |
 | (6) |
The LO phonon here mostly corresponds to the stretching motion of the [PbI3]− network having frequency of about 100 cm−1 (corresponding to 12.4 meV or kB × 145 K).55 This mean that the LO phonon population at room temperature is much higher than at 135 K. The calculation based on eqn (5) gives values for the downwards relaxation “stimulation” factors N(ωLO) + 1 at room temperature and at 135 K as 2.6 and 1.5, respectively. The ratio
 | (7) |
The other possible reason for observing different HC cooling dynamics with TR-2PPE and TA is that the former can only probe the population of hot electrons, while the latter detects both hot electrons and holes. Taking the energy of LO phonon and the initial energy of the HC (i.e. directly after carrier excitation and before any energy transfer processes) as constants, the power loss rate is proportional to the Fröhlich coupling constant α and thereby further to the square root of the effective mass m of carriers, as shown in eqn (6).53,54 The effective mass of electrons is lighter than the effective mass of holes in 2D perovskite.38 Therefore the hot electrons should exhibit a lower power loss rate due to the e-ph coupling. However, the difference of the effective masses is small,38,44 and the square root further reduces the corresponding difference in the Fröhlich constant. Therefore, effective mass, should not be a dominating reason for the faster cooling rate in TA measurements. Though, the polaron formation can influence the electron and hole effective masses differently,61,62 we do not extend this discussion further.
As the result of the differences in two experiments, the hot electron temperature at the surface layer in the TR-2PPE measurements cools slower (0.2 ps) than the temperature in the whole bulk volume in the TA measurements (0.1 ps).
As for Stage II (thermal equilibration between LO phonons and acoustic phonons), the cooling time of the surface layer extracted from TR-2PPE data is 3 ps, while for bulk area extracted TA data it is 4.3 ps. These times are comparable. However, what is clear is that the initial temperature of the second stage, the hot phonon bottleneck temperature, is higher in TA measurement than TR-2PPE measurement. This difference is larger than the ambient temperature difference in the two experiments. We can speculate that if the density of states of LO phonons is higher in the surface area, the LO phonons could accommodate more energy and the hot phonon bottleneck would occur at lower temperature than in the bulk area. However, more work is needed before the explanation can be put forward with certainty.
Conclusion
We have studied photo-induced HC cooling dynamics in 2D perovskite single crystal flakes using TA and TR-2PPE spectroscopies. In the TA analysis, the high-energy tails of the bleaching signals are fitted by Boltzmann distribution. The analyses are applicable starting from 0.3 ps when the electron distribution has reached the quasi-equilibrium. The carrier temperature obtained from TA analysis strongly depends on the offset and the fitting range. The uncertainty is minimized by statistical analyses of the results and assuming long-time convergence of the temperature supported by direct line shape comparison of the spectra measured with wide range of intensities. By adopting the initial system energy from the TR-2PPE, the bi-exponential analysis of the TA temperature decay provides two lifetimes, ≤0.1 ps (upper limit for the fast component) and 4.3 ps. In the TR-2PPE analysis, we convert the average excess energy to system energy and fit it with a bi-exponential decay function (0.2 and 3 ps). All in all, compared to the TA results the cooling rates observed in TR-2PPE are slower in the first stage and the initial temperature in the second stage is lower. There are several possible origins of the differences in the two experiments. First of all, the probing depth is drastically different – TR-2PPE only “sees” the upper layer of the sample while the TA probes the whole. We also discuss the different temperatures of the environment and the contribution of the hole signal as the possible sources of the differences.The different probing depths speak for the influence of local structure on the HC cooling mechanisms. On the surface sheet, the local lattice structure is more distorted, and the attached spacing cations are more flexible and softer, which can modify the phononic features and decrease the e-ph coupling efficiency. Based on the temperature dependence of LO phonon population, the difference in the fast initial relaxation can partially be explained by different phonon populations. We also point out that only the electrons can be detected in TR-2PPE, and the lighter effective mass will lead to slower carrier temperature decay than what the holes have. However, the expected dependence is small and the effective mass difference alone cannot be the explanation. We conclude that the modification of the LO-phonon structure possibly combined with the other two factors, temperature difference and insensitivity to the holes, is responsible for the prolonged HC lifetime in Stage I observed in the TR-2PPE measurements. As for the lower initial temperature of Stage II in TR-2PPE measurement, possibly the hot phonon bottleneck effect is weakened due to the higher density of states of LO phonons. More investigations on the spatial profile of phonons are needed for the clearer understanding and identification of involved mechanisms.
Our work indicates a spatial dependency of the cooling process in 2D crystals. It also rationalizes the origins of HC cooling in 2D perovskites, which may benefit the future applications of hot carriers. In addition, we show the TR-2PPE technique is a powerful tool for investigating the HC properties allowing clear visualization of the cooling stages.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We acknowledge financial support from Swedish Research Council, Swedish Energy Agency, the Knut and Alice Wallenberg Foundation (Project 2016.0089), the ANR project 2D-Hype (Nr. ANR-21-CE30-0059-01). This work was supported by Chinese Scholarship Council for the PhD scholarship to W. L., M. L., J. M., X. Z., Q. Z, and the DAAD Scholarship for the PhD Scholarship of M.C.References
- H. J. Snaith, J. Phys. Chem. Lett., 2013, 4, 3623–3630 CrossRef CAS.
- Y. Fang, Q. Dong, Y. Shao, Y. Yuan and J. Huang, Nat. Photonics, 2015, 9, 679–686 CrossRef CAS.
- M. Yuan, L. N. Quan, R. Comin, G. Walters, R. Sabatini, O. Voznyy, S. Hoogland, Y. Zhao, E. M. Beauregard, P. Kanjanaboos, Z. Lu, D. H. Kim and E. H. Sargent, Nat. Nanotechnol., 2016, 11, 872–877 CrossRef CAS PubMed.
- L. Dou, A. B. Wong, Y. Yu, M. Lai, N. Kornienko, S. W. Eaton, A. Fu, C. G. Bischak, J. Ma, T. Ding, N. S. Ginsberg, L.-W. Wang, A. P. Alivisatos and P. Yang, Science, 2015, 349, 1518–1521 CrossRef CAS PubMed.
- M. Saliba, T. Matsui, J.-Y. Seo, K. Domanski, J.-P. Correa-Baena, M. K. Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate, A. Hagfeldt and M. Grätzel, Energy Environ. Sci., 2016, 9, 1989–1997 RSC.
- J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Nature, 2013, 499, 316–319 CrossRef CAS.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- A. Rajagopal, Z. Yang, S. B. Jo, I. L. Braly, P. W. Liang, H. W. Hillhouse and A. K. Y. Jen, Adv. Mater., 2017, 29, 1702140 CrossRef.
- R. T. Ross and A. J. Nozik, J. Appl. Phys., 1982, 53, 3813–3818 CrossRef CAS.
- G. Conibeer, N. Ekins-Daukes, J.-F. Guillemoles, D. Kőnig, E.-C. Cho, C.-W. Jiang, S. Shrestha and M. Green, Sol. Energy Mater. Sol. Cells, 2009, 93, 713–719 CrossRef CAS.
- Y. Takeda, T. Motohiro, D. König, P. Aliberti, Y. Feng, S. Shrestha and G. Conibeer, Appl. Phys. Express, 2010, 3, 104301 CrossRef.
- A. J. Nozik, Nat. Energy, 2018, 3, 170–171 CrossRef.
- Z. Nie, X. Gao, Y. Ren, S. Xia, Y. Wang, Y. Shi, J. Zhao and Y. Wang, Nano Lett., 2020, 20, 4610–4617 CrossRef CAS.
- Q. Sun, J. Gong, X. Yan, Y. Wu, R. Cui, W. Tian, S. Jin and Y. Wang, Nano Lett., 2022, 22, 2995–3002 CrossRef CAS.
- J. Meng, Z. Lan, W. Lin, M. Liang, X. Zou, Q. Zhao, H. Geng, I. E. Castelli, S. E. Canton, T. Pullerits and K. Zheng, Chem. Sci., 2022, 13, 1734–1745 RSC.
- J. M. Frost, L. D. Whalley and A. Walsh, ACS Energy Lett., 2017, 2, 2647–2652 CrossRef CAS PubMed.
- M. Li, S. Bhaumik, T. W. Goh, M. S. Kumar, N. Yantara, M. Gratzel, S. Mhaisalkar, N. Mathews and T. C. Sum, Nat. Commun., 2017, 8, 14350 CrossRef CAS PubMed.
- J. Fu, Q. Xu, G. Han, B. Wu, C. H. A. Huan, M. L. Leek and T. C. Sum, Nat. Commun., 2017, 8, 1300 CrossRef PubMed.
- G. Ghosh, R. K. Biswas, K. Marjit, S. Ghosh, A. Ghosh, S. K. Pati and A. Patra, Adv. Opt. Mater., 2022, 10, 2200030 CrossRef CAS.
- H. Zhu, K. Miyata, Y. Fu, J. Wang, P. P. Joshi, D. Niesner, K. W. Williams, S. Jin and X.-Y. Zhu, Science, 2016, 353, 1409–1413 CrossRef CAS.
- Z. Guo, Y. Wan, M. Yang, J. Snaider, K. Zhu and L. Huang, Science, 2017, 356, 59–62 CrossRef CAS PubMed.
- J. W. M. Lim, D. Giovanni, M. Righetto, M. Feng, S. G. Mhaisalkar, N. Mathews and T. C. Sum, J. Phys. Chem. Lett., 2020, 11, 2743–2750 CrossRef CAS.
- P. Guo, C. C. Stoumpos, L. Mao, S. Sadasivam, J. B. Ketterson, P. Darancet, M. G. Kanatzidis and R. D. Schaller, Nat. Commun., 2018, 9, 2019 CrossRef.
- M. Liang, W. Lin, Z. Lan, J. Meng, Q. Zhao, X. Zou, I. E. Castelli, T. Pullerits, S. E. Canton and K. Zheng, ACS Appl. Electron. Mater., 2020, 2, 1402–1412 CrossRef CAS.
- G. Conibeer, S. Shrestha, S. Huang, R. Patterson, H. Xia, Y. Feng, P. Zhang, N. Gupta, M. Tayebjee, S. Smyth, Y. Liao, S. Lin, P. Wang, X. Dai and S. Chung, Sol. Energy Mater. Sol. Cells, 2015, 135, 124–129 CrossRef CAS.
- L. Brillouin, Wave Propagation In Periodic Structures, Mcgraw-hil Book Company, Inc., New York, 1946.
- V. Narayanamurti, H. L. Störmer, M. A. Chin, A. C. Gossard and W. Wiegmann, Phys. Rev. Lett., 1979, 43, 2012–2016 CrossRef CAS.
- J. Yin, P. Maity, R. Naphade, B. Cheng, J.-H. He, O. M. Bakr, J.-L. Brédas and O. F. Mohammed, ACS Nano, 2019, 13, 12621–12629 CrossRef CAS.
- Y. Yang, D. P. Ostrowski, R. M. France, K. Zhu, J. van de Lagemaat, J. M. Luther and M. C. Beard, Nat. Photonics, 2015, 10, 53–59 CrossRef.
- M. B. Price, J. Butkus, T. C. Jellicoe, A. Sadhanala, A. Briane, J. E. Halpert, K. Broch, J. M. Hodgkiss, R. H. Friend and F. Deschler, Nat. Commun., 2015, 6, 8420 CrossRef CAS.
- K. Miyata, D. Meggiolaro, M. T. Trinh, P. P. Joshi, E. Mosconi, S. C. Jones, F. De Angelis and X. Y. Zhu, Sci. Adv., 2017, 3, e1701217 CrossRef.
- X. Lao, Z. Yang, Z. Su, Y. Bao, J. Zhang, X. Wang, X. Cui, M. Wang, X. Yao and S. Xu, J. Phys. Chem. C, 2019, 123, 5128–5135 CrossRef CAS.
- S. Kahmann and M. A. Loi, J. Mater. Chem. C, 2019, 7, 2471–2486 RSC.
- P. G. Klemens, Phys. Rev., 1966, 148, 845–848 CrossRef CAS.
- M. Liang, W. Lin, Q. Zhao, X. Zou, Z. Lan, J. Meng, Q. Shi, I. E. Castelli, S. E. Canton, T. Pullerits and K. Zheng, J. Phys. Chem. Lett., 2021, 12, 4965–4971 CrossRef CAS.
- Y. Shao, W. Gao, H. Yan, R. Li, I. Abdelwahab, X. Chi, L. Rogée, L. Zhuang, W. Fu, S. P. Lau, S. F. Yu, Y. Cai, K. P. Loh and K. Leng, Nat. Commun., 2022, 13, 138 CrossRef CAS.
- P. Maity, J. Yin, B. Cheng, J.-H. He, O. M. Bakr and O. F. Mohammed, J. Phys. Chem. Lett., 2019, 10, 5259–5264 CrossRef CAS PubMed.
- C. C. Stoumpos, D. H. Cao, D. J. Clark, J. Young, J. M. Rondinelli, J. I. Jang, J. T. Hupp and M. G. Kanatzidis, Chem. Mater., 2016, 28, 2852–2867 CrossRef CAS.
- N. S. Dahod, A. France-Lanord, W. Paritmongkol, J. C. Grossman and W. A. Tisdale, J. Chem. Phys., 2020, 153, 044710 CrossRef CAS PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- J. C. Blancon, A. V. Stier, H. Tsai, W. Nie, C. C. Stoumpos, B. Traore, L. Pedesseau, M. Kepenekian, F. Katsutani, G. T. Noe, J. Kono, S. Tretiak, S. A. Crooker, C. Katan, M. G. Kanatzidis, J. J. Crochet, J. Even and A. D. Mohite, Nat. Commun., 2018, 9, 2254 CrossRef.
- H. Chung, S. I. Jung, H. J. Kim, W. Cha, E. Sim, D. Kim, W. K. Koh and J. Kim, Angew. Chem., 2017, 56, 4160–4164 CrossRef CAS.
- J. Chen, M. E. Messing, K. Zheng and T. Pullerits, J. Am. Chem. Soc., 2019, 141, 3532–3540 CrossRef CAS PubMed.
- M. Dyksik, H. Duim, X. Zhu, Z. Yang, M. Gen, Y. Kohama, S. Adjokatse, D. K. Maude, M. A. Loi, D. A. Egger, M. Baranowski and P. Plochocka, ACS Energy Lett., 2020, 5, 3609–3616 CrossRef CAS.
- S. D. Verma, Q. Gu, A. Sadhanala, V. Venugopalan and A. Rao, ACS Energy Lett., 2019, 4, 736–740 CrossRef CAS.
- J. Yang, X. Wen, H. Xia, R. Sheng, Q. Ma, J. Kim, P. Tapping, T. Harada, T. W. Kee, F. Huang, Y. B. Cheng, M. Green, A. Ho-Baillie, S. Huang, S. Shrestha, R. Patterson and G. Conibeer, Nat. Commun., 2017, 8, 14120 CrossRef CAS.
- B. Lv, T. Qian and H. Ding, Nat. Rev. Phys., 2019, 1, 609–626 CrossRef.
- D. Niesner, H. Zhu, K. Miyata, P. P. Joshi, T. J. Evans, B. J. Kudisch, M. T. Trinh, M. Marks and X. Y. Zhu, J. Am. Chem. Soc., 2016, 138, 15717–15726 CrossRef CAS PubMed.
- E. Jung, K. Budzinauskas, S. Öz, F. Ünlü, H. Kuhn, J. Wagner, D. Grabowski, B. Klingebiel, M. Cherasse, J. Dong, P. Aversa, P. Vivo, T. Kirchartz, T. Miyasaka, P. H. M. Van Loosdrecht, L. Perfetti and S. Mathur, ACS Energy Lett., 2020, 5, 785–792 CrossRef CAS.
- Z. Chen, J. Sjakste, J. Dong, A. Taleb-Ibrahimi, J. P. Rueff, A. Shukla, J. Peretti, E. Papalazarou, M. Marsi and L. Perfetti, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 21962–21967 CrossRef CAS.
- M. P. Seah and W. A. Dench, Surf. Interface Anal., 1979, 1, 2–11 CrossRef CAS.
- I. Chatzakis, H. Yan, D. Song, S. Berciaud and T. F. Heinz, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205411 CrossRef.
- S. Das Sarma, J. K. Jain and R. Jalabert, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 6290–6296 CrossRef CAS PubMed.
- S. D. Sarma, J. K. Jain and R. Jalabert, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 3561–3571 CrossRef PubMed.
- M. A. Pérez-Osorio, Q. Lin, R. T. Phillips, R. L. Milot, L. M. Herz, M. B. Johnston and F. Giustino, J. Phys. Chem. C, 2018, 122, 21703–21717 CrossRef.
- F. Brivio, J. M. Frost, J. M. Skelton, A. J. Jackson, O. J. Weber, M. T. Weller, A. R. Goñi, A. M. A. Leguy, P. R. F. Barnes and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 144308 CrossRef.
- H. G. Duan, V. Tiwari, A. Jha, G. R. Berdiyorov, A. Akimov, O. Vendrell, P. K. Nayak, H. J. Snaith, M. Thorwart, Z. Li, M. E. Madjet and R. J. D. Miller, J. Am. Chem. Soc., 2020, 142, 16569–16578 CrossRef CAS PubMed.
- L. N. Quan, Y. Park, P. Guo, M. Gao, J. Jin, J. Huang, J. K. Copper, A. Schwartzberg, R. Schaller, D. T. Limmer and P. Yang, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104425118 CrossRef CAS.
- Y. Zhang, R. Wang, Y. Li, Z. Wang, S. Hu, X. Yan, Y. Zhai, C. Zhang and C. Sheng, J. Phys. Chem. Lett., 2019, 10, 13–19 CrossRef CAS.
- Z. Zhang, W. H. Fang, M. V. Tokina, R. Long and O. V. Prezhdo, Nano Lett., 2018, 18, 2459–2466 CrossRef CAS PubMed.
- M. Sendner, P. K. Nayak, D. A. Egger, S. Beck, C. Müller, B. Epding, W. Kowalsky, L. Kronik, H. J. Snaith, A. Pucci and R. Lovrinčić, Mater. Horiz., 2016, 3, 613–620 RSC.
- C. Liu, H. Tsai, W. Nie, D. J. Gosztola and X. Zhang, J. Phys. Chem. Lett., 2020, 11, 6256–6261 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: The following files are available free of charge. Characterization of 2D perovskite single crystals; absorption coefficient and carrier density calculations of 2D perovskite flake; absorption coefficient of 2D perovskite thin film; determination of energy window and offset for TA analysis; quasi-equilibrium timescale; excitation dependent TA spectra and time dependent HC temperature; comparison to other flakes; time dependent energy distribution curve (EDC) of TR-2PPE measurements; calculation of excess energy from TR-2PPE spectrogram; initial system energy and fast component analysis for TA results; low-energy electron diffraction (LEED) measurements; 2D perovskite flake preparation and position-selective TA measurements; estimation of lattice temperature and hot phonon bottleneck temperature; calculation of binding energy based on temperature dependent photoluminescence measurements (PDF). See DOI: https://doi.org/10.1039/d2tc03111f |
| ‡ W. L. and M. L. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |