Phase transitions and optical properties of the trigonal perovskite (CH₃NH₃)₂TeCl₆

Abstract

Vacancy-ordered double perovskites A₂BX₆ are attracting attention due to the isolated octahedra making them an ideal playground for studying perovskite structure-property relationships. MA₂TeCl₆ single crystals have been successfully grown from solution. X-ray structure experiments as a function of temperature have demonstrated two structural phase transitions: from cubic Fm3̄m (high temperature, phase I) to trigonal P3̄m1 (intermediate temperature, phase II) at 460 K and then to trigonal P3̄1c (low temperature, phase III) at 200 K. Intriguingly, we observe a negative thermal expansion for the c-axis in phase II believed to caused by dynamic tilting of the C–N bond in the MA⁺ ion. We have modified and extended the calculation of the Brown radii ratio in the perovskites to include hybrid A₂BX₆ compounds by selecting the shortest A–X distance for the ratio equation. We find that for ratios between 0.89 and 1.17, typically the Fm3̄m cubic structure is observed, while for ratios above 1.17, mostly distorted structures are found.

---

Introduction

Perovskite materials have received a great amount of attention in the photovoltaic field; however, chemical instability and toxicity issues are driving the demand for stable lead-free alternatives to the commonly used lead containing formulations. Vacancy-ordered double-perovskites A₂BX₆ with B equal to a Group 16 metal offer a new avenue to replace hybrid lead iodide perovskites in photovoltaic applications due to improved air and moisture stability whilst retaining similar properties to the perovskite ABX₃ compounds. The double-perovskite structure is obtained by replacing half of the B-site cations with vacancies in an ordered fashion, which leads to doubling of the lattice parameter. This extended unit cell allows for greater flexibility in compositional modification.^1–3 Vibrations of the organic cations and octahedra contribute significantly to the lattice dynamics, which, in turn, play an essential role in the material properties.⁴ Hence, it is interesting to study the influence of the organic cations on the structure–property relationships to further understand these materials.^2,5

Recently, tellurium-based double perovskites have been identified as potential lead-free solar cell materials with good electronic attributes and chemical stability.⁶ In this study, we have added to this new field by investigating the crystal structure of (CH₃NH₃)₂TeCl₆ (or MA₂TeCl₆) from 120 K to 500 K by variable temperature powder and single-crystal X-ray diffraction and neutron powder diffraction. Three phases were observed across the temperature range for MA₂TeCl₆; this contrasts with some other tellurium halides, for example Cs₂TeCl₆ where no phase transitions were previously reported. We report a complete structure solution for each crystallographic phase. The cation dynamics of MA₂TeCl₆ are notably different from other compounds in the series such as MA₂SnCl₆, which drives the necessity to study its structure-property relationship. The crystal structures analysed in our work, combined with other experiments to identify the phase-transition mechanism, will be helpful for further property investigations.⁷ Finally, we have extended the Brown radii-ratio calculation for perovskites to include the hybrid A₂BX₆ perovskites and have demonstrated an improved method to describe the lattice distortion that uses the shortest distance between the A-site and X-site atoms to calculate the radius ratio.

Experimental

Tellurium oxide and aqueous methylamine were separately reacted with 12 M hydrochloric acid to form TeCl₄ and methylammonium chloride (MACl) solutions. The acidic TeCl₄ and MACl solutions were mixed at room temperature and the resulting suspension was then filtered and dried to obtain MA₂TeCl₆ as a microcrystalline powder. MA₂TeCl₆ single crystals were grown by redissolving this MA₂TeCl₆ powder in 12 M HCl at 60 °C to obtain a saturated clear MA₂TeCl₆ solution, which was then slowly cooled to room temperature over 5 h to encourage crystal growth.

Single-crystal X-ray diffraction (SXD) measurements were made on MA₂TeCl₆ using an Agilent SuperNova diffractometer between 90 K and 295 K. Full spheres of data were measured with Mo Kα radiation in around 1 to 2 hours depending on temperature.

A room temperature powder X-ray diffraction (PXRD) pattern was obtained using a Stoe Stadi-P X-ray diffractometer in thin-foil transmission mode with Mo radiation. Subsequently, variable temperature powder X-ray diffraction (VT-PXRD) patterns were obtained using a Stoe Stadi-P X-ray diffractometer in capillary mode with Cu radiation. An Oxford Instruments CryojetHT was used to cool the sample to 120 K and then heat it in increments of 20 K to 500 K with PXRD patterns obtained at each temperature.

Room temperature neutron powder diffraction (NPD) was used to provide additional information on the light atom positions as carbon and nitrogen can be hard to distinguish reliably by X-rays in the presence of heavy atoms. Time-of-flight data were collected from MA₂TeCl₆ using the Polaris at the ISIS Muon and Neutron Spallation Source, U.K.

Variable temperature optical absorption spectra were collected using an Agilent Cary 4000 UV Vis Spectrometer over the wavelength range 175 to 900 nm from 175 K to 500 K in increments of 25 K.

Further experimental details are available in the ESI.†

Results and discussion

Crystal structure

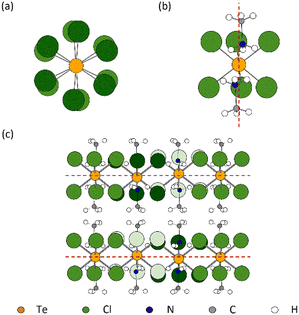
A light yellow hexagonal single crystal was selected for SXD measurements, as shown in Fig. S1 (ESI†); the sample has a plate-like morphology with its width around ten times greater than its thickness. The crystal structures of the different phases of MA₂TeCl₆ are shown in Fig. 1. From the SXD analysis, the crystal system of MA₂TeCl₆ at room temperature (295 K) is trigonal, space group symmetry P3̄m1 with lattice parameters a = 7.3565(4) Å, c = 7.0812(7) Å, and Z = 1, which is in agreement with the literature.⁸ We denote this as phase II where the [TeCl₆]²⁻ octahedra occupy the corners of the hexagonal unit cell while the MA⁺ cations lie between the octahedral units. Thus, the material consists of layers of [TeCl₆]²⁻ − MA⁺ − MA⁺ − [TeCl₆]²⁻ stacked along the c axis with one formula unit per unit cell and with the axis of the MA⁺ cations aligned parallel to c. The MA⁺ cations are orientated such the NH₃⁺ ionic head group points towards the Cl of three [TeCl₆]²⁻ anions with the non-polar –CH₃ groups lying in a plane formed by opposing MA⁺ cations.

Fig. 1 The crystal structure of MA₂TeCl₆ in (a) phase I at 500 K seen down the a-axis shown (upper) and obliquely (lower) in which a single N atom represents the whole MA⁺ cation due to the dynamical free rotation; (b) phase II at 295 K seen along the c-axis (upper) and down the a-axis (lower); and (c) phase III at 200 K seen along the c-axis (upper) and down the a-axis (lower).

As the temperature is lowered from room temperature to 200 K, jump rotations of the cation about its long axis are reduced in frequency, and a second-order transition to phase III occurs with frozen-in orientations of the MA⁺ cation. Phase III has space group symmetry P3̄1c with a = 12.6147(4) Å, c = 14.1897(6) Å, and Z = 6. It is related to phase II by a doubling of the unit along c and a increase in a (Fig. S2, ESI†). As illustrated in Fig. 1(c), [TeCl₆]²⁻ octahedra still occupy the corners of the unit cell, but there is a second crystallographic [TeCl₆]²⁻ unit within the enlarged unit cell. The loss of mirror symmetry in going from space group symmetry P3̄m1 in phase II to P3̄1c in phase III provides a greater freedom to the structure. Thus, to accommodate the MA⁺ cations, the [TeCl₆]²⁻ octahedra rotate slightly about the c-axis with respect to the layers above and below (Fig. 2(a)). At 90 K, there is a noticeable rotation of ca. 8.45° for the Te(1) octahedron in contrast to the Te(2) octahedron where the rotation is only 2.96° (Fig. S3, ESI†). This difference leads to a reduction in the cavity size surrounding the MA⁺ ion. Consequently, as supported by NMR results, a minor tilting of the C–N axis is observed in phase III (Fig. 2(b)).⁹ Thus, the combination of anion and cation tilts improves the coordination of the –NH₃⁺ group by the Cl⁻ of [TeCl₆]²⁻. As shown in Fig. 2(c), in addition to rotational movement, there is a slight positional change of the octahedra in each layer, which are no longer constrained to lie by symmetry within the same ab plane.

Fig. 2 Schematic of MA₂TeCl₆ (III) showing (a) the rotational twist about the c-axis of the [Te(1)Cl₆]²⁻ anions from one octahedral layer to the next layer; (b) the minor tilting of the C–N axis of the MA⁺ cation relative to the c-axis (shown as dashed red line); and (c) the slight positional offset of the octahedra in each layer, where red dashed lines represent ab planes at c = 0 and c = 1/2. The green colour shades are used to distinguish the Cl atoms belonging to different octahedra.

Curiously, calorimetric studies suggest additional low temperature phases of MA₂TeCl₆,^7,10 but no new phases were observed by SXD in the range 90 K to 295 K. The origin of this discrepancy is unclear and might be because calorimetry detects more subtle transitions (e.g. ferroelectric transitions), which are not easily observed in our SXD experiments. To confirm our observation of just two phases by SXD in the range 90 K to 295 K, VT-PXRD was performed. Initially, the purity of the MA₂TeCl₆ powder at room temperature was verified by Rietveld refinement using GSAS II¹¹ as shown in Fig. S4 (ESI†); all of the observed peaks in the data are accounted for in our structural model demonstrating the high quality of the powder. The CIF file, obtained from the SXD results, was used as the starting point for the refinement and R_wp = 9.19% was achieved.

Our VT-PXRD data as a function of temperature is shown in Fig. 3. Two phase transitions were detected in MA₂TeCl₆, a first-order phase transition on heating between 440 K and 460 K (phase II to phase I) and a second-order phase transition on heating between 200 K and 220 K (phase III to phase II). Focussing on the phase I structure at high temperature, it has been reported previously that the high-temperature phases of MA₂TeX₆ (X = Br, I) are cubic with space group symmetry Fm3̄m. The high-temperature phase I of MA₂TeCl₆ seen in a calorimetric study was assumed to be cubic too, but this was not confirmed by X-ray diffraction.^7,10 From our data, we can conclusively show that MA₂TeCl₆ is isomorphic to MA₂TeX₆ (X = Br, I) above 460 K, in agreement with the isotropic result from polarised light microscopy.¹⁰ We note that, at 460 K, the VT-PXRD pattern shows the coexistence of phases I and II; this is likely due to the relatively short wait time between changing temperatures and starting the next PXRD measurement in our study.

Fig. 3 Background subtracted VT-PXRD data collected on MA₂TeCl₆ over the temperature range 120–500 K displayed as a surface plot. Diffraction intensity is represented using a red (high) to white (low) colour scale. Dotted lines indicate the temperatures of the two phase transitions. The transition from phase III to phase II is not obvious from this plot given the low intensity of the additional peaks that characterise phase III (see Fig. S5, ESI†).

Next, we consider the low temperature phases II and III of MA₂TeCl₆ seen in Fig. 3. Consistent with a second-order transition, the position of the peaks changes smoothly as a function of temperature down to our lowest temperature of 120 K. Below the transition temperature to phase III, we observe the appearance of several additional weak peaks (see Fig. S5, ESI†) congruous with a phase transition to a lower symmetry trigonal structure with a larger unit cell. This transition is in agreement with the calorimetric study.¹⁰ As the temperature is increased from the base temperature (120 K), most of the peaks shift to lower angles consistent with thermal expansion but, in phase II, several peaks shift to higher angles, this is due to a shortening of the c-axis.

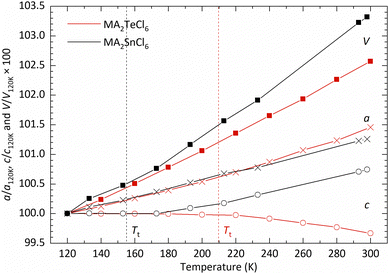
In Fig. 4, we show the temperature dependence of the lattice parameters and unit cell volume. For comparative purposes, the unit cell volume V is normalised by the number of formula units Z in each phase; for phase III, the lattice constant a is divided by and c is divided by 2. The sudden change in volume between phase II and phase I is evidence of first-order behaviour. In contrast, no discontinuous change in the lattice parameters at the phase II–III boundary is observed, consistent with the second-order transition reported previously.¹⁰

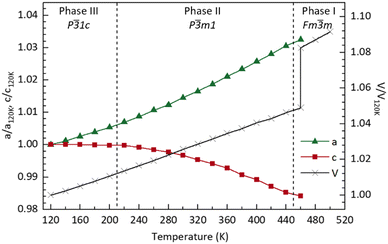Fig. 4 Plot showing the variation (compared with T = 120 K) in lattice parameter and volume as a function of temperature obtained from fits to the data using GSAS II.¹¹ Values are given in Table S1 (ESI†). Lines joining the data points are a guide to the eye.

SXD may struggle to accurately determine the positions of low atomic number atoms in a crystal structure containing heavy atoms. Hence, to complete the characterisation of the room temperature structure (phase II), a complementary neutron powder diffraction (NPD) study was performed to confirm the orientation of the MA⁺ cation. Fig. S6 (ESI†) shows the refinement results without and with the MA+ cation included in the structure. From previous studies, ¹H and ¹⁴N NMR data indicate that there is a continuous rotation of the methyl and ammonium groups about a non-static C–N axis spreading around a cone with a half angle of 22 ± 1° at 293 K,⁷ while the ³⁵Cl NQR relaxation time indicates a hindered rotation of the [TeCl₆]²⁻ octahedra at room temperature.⁹ It should be noted that our model of phase II has the MA⁺ cation aligned along the 3-fold symmetry axis: the d-spacing resolution in both SXD and NPD experiments do not allow us to distinguish between atoms lying on the axis and just off the axis with six-fold disorder (see Fig. S7, ESI†). The model with the MA⁺ cation aligned on the axis uses fewer parameters but results in an apparently shortened C–N bond length consistent with rotation about a cone. For comparison in MAPbI₃, the MA⁺ cations are fully ordered below 100 K, have fourfold disorder in the tetragonal structure at room temperature, and become isotropically disordered in the cubic phase above 352 K.¹²

The bandgap of MA₂TeCl₆ as a function of temperature, as determined from the Tauc plot of the absorption spectra, is shown in Fig. 5. As the temperature increases, a red shift is induced such that the bandgap decreases linearly within phases III and II (with a temperature dependence of −8.7(1) × 10⁻⁴ eV K⁻¹). The band gap shows an obvious drop after the transition to phase I. The data demonstrates that the cubic phase perovskite has a lower bandgap than trigonal structure, despite the larger volume of the cubic phase. Secondly, the first-order phase transition has a marked effect on the bandgap. The bandgap of MA₂TeCl₆ decreases as a function of temperature to a larger extent than that seen in Cs₂AgBiBr₆,¹³ which may due to differences in the crystal structure, but the temperature dependence has a similar value to that observed for other semiconductors.¹⁴ This thermochromic effect may lead to new applications for MA₂TeCl₆.

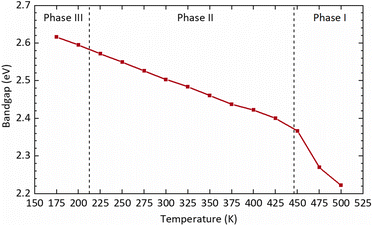Fig. 5 Optical bandgap of MA₂TeCl₆ calculated as a function of temperature from the Tauc plot shown in Fig. S8 (ESI†).

Comparison of MA₂TeCl₆ and MA₂SnCl₆

The structure of MA₂TeCl₆ is notably different from other MA₂BCl₆ (B = Sn, Pt, Se, Pd and Pb) compounds, all of which exhibit rhombohedral structures at room temperature with space-group symmetry R3̄m. These other compounds all undergo a structural phase transition to space group R3̄ at temperatures, T_t, between 100 and 200 K.^10,15 For example, the crystal structure of MA₂SnCl₆, shown in Fig. S9 (ESI†) has symmetry R3̄m at room temperature, and transforms to R3̄ below 156 K.¹⁵ Similar to the MA₂TeCl₆ room temperature phase, the octahedral [SnCl₆]²⁻ anions occupy the corners of a trigonal unit cell, while MA⁺ cations separate the layers of [SnCl₆]²⁻ anions. However, along the c-axis direction in MA₂TeCl₆, planes of [TeCl₆]²⁻ anions lie directly above each other, whereas in MA₂SnCl₆ the layer at z = ⅓ is displaced relative to the layer at z = 0 by 2/3 and 1/3 in a and b, respectively (see Fig. S9, ESI†).

In MA₂SnCl₆, it has been demonstrated that the MA⁺ cation rotates freely about the C–N axis far below T_t, indicating that the hydrogen bonding between cations and anions is too weak to drive the phase transition.^15,16 Furthermore, NMR studies indicate that the motion of the MA⁺ cations makes a smaller contribution to the phase transition compared to the rotation of the octahedra about the c-axis; also, NQR suggests that the phase transition may be driven by a soft rotary mode of the [SnCl₆]²⁻ anion.¹⁷ In the high temperature R3̄m phase, the anions perform a hindered rotation, but their motion is restricted in the low-temperature R3̄ phase and they can only vibrate. Consequently, the loss of mirror symmetry and slight rotation of the octahedra are expected to drive the phase transition in MA₂SnCl₆. Intriguingly, X-rays experiments did not detect this rotation. The softening of an acoustic mode at the zone centre may be considered the cause of transition, as supported by the non-observation of a soft mode in Raman spectroscopy.^{15,16,18–20} The situation concerning the anions in MA₂TeCl₆ is expected to be similar as there is also a loss of mirror symmetry in going from P3̄m1 in phase II to P3̄1c in phase III. However, although the MA⁺ cation has 3m symmetry in both the R3̄m phase of MA₂SnCl₆ and the P3̄m1 phase of MA₂TeCl₆, there is a distinct difference in the low temperature phase of each: the threefold symmetry of the MA⁺ cation is retained in MA₂SnCl₆. In contrast, the symmetry of the cation is lost entirely in MA₂TeCl₆ due to the tilt ordering of the C–N axis. We, therefore, expect the phase transition in MA₂TeCl₆ to be strongly affected by the order-disorder change of the cation.

Further insight into the nature of the structure and the phase transition can be gleaned from a comparison of the coefficients of thermal expansion in MA₂SnCl₆ and MA₂TeCl₆. As illustrated in Fig. 6, the c-axis length of MA₂SnCl₆ remains almost unchanged below 180 K; above this temperature, it increases with a thermal expansion coefficient of about 0.6 × 10⁻⁴ K⁻¹, while a expands steadily with a coefficient of 0.7 × 10⁻⁴ K⁻¹ in both phases.²¹ Similarly, based on the PXRD data, MA₂TeCl₆ exhibits a steady increase in a with increasing temperature (Fig. 6) with a thermal expansion coefficient of 0.9 × 10⁻⁴ K⁻¹, which is greater than for the tin compound. As in the case of MA₂SnCl₆, the c parameter of MA₂TeCl₆ remains unchanged in phase III but then decreases in phase II with a negative thermal expansion coefficient of −0.4 × 10⁻⁴ K⁻¹. These results demonstrate that temperature has a more dramatic effect on the c parameter compared with the a parameter.

Fig. 6 Variation of the lattice parameters (a and c) and unit cell volume (V) of MA₂TeCl₆ and MA₂SnCl₆ as a function of temperature relative to 120 K highlighting the difference in the behaviour of c for the two compounds. The vertical lines shown in red and black mark the phase transition boundary T_t for the lower temperature phases of MA₂TeCl₆ and MA₂SnCl₆, respectively.

The thermal expansion below T_t can be understood by considering the librational motion of the molecular ions. Previous work has discussed the effect of librational motion of both the MA⁺ and [SnCl₆]²⁻ ions. With librational motion about the c-axis, then with increasing temperature, the molecular ions are forced apart in the ab-plane, which has the effect of increasing a, but leaving c essentially unchanged. The behaviour of the a and c lattice parameters in phase III of MA₂TeCl₆ is seen to be similar. Vibrations of the ions would typically result in expansion along c, but this may be offset by an increased off-axis rotation of the MA⁺ cations with increasing temperature, effectively shortening the projection of the C–N bond length on the c-axis: 1.468(7) Å at 90 K versus 1.407(8) Å at 295 K. This apparent shortening was also noted in the X-ray study on MA₂SnCl₆ (1.522(25) Å at 120 K versus 1.487(30) Å at 298 K) and was also seen in the later neutron diffraction study on a deuterated sample.^21,22

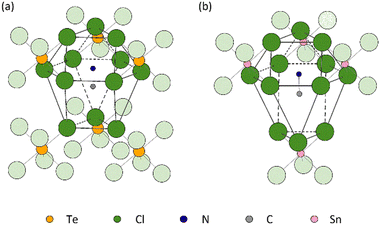
The distinct difference in the behaviour of the lattice parameter c above T_t in MA₂TeCl₆versus MA₂SnCl₆ may be due to the different stacking sequences of the MA⁺ − [Cl₃BCl₃]²⁻ − MA⁺ layers. While the immediate coordination environment of the MA⁺ cations is similar in both cases, i.e. they each have 12 Cl neighbours, these 12 Cl ions originate from different numbers of [BCl₆]²⁻ octahedral units: the MA⁺ cations are coordinated to 4 [SnCl₆]²⁻ anions in the tin compound, but to 6 [TeCl₆]²⁻ anions in the tellurium one (Fig. 7). The larger size of a 6-coordinate cavity permits a greater degree of motion of the MA⁺ cations. Further, in the low temperature phase transition of MA₂TeCl₆, the MA⁺ cations tilt with respect to the c-axis (see Fig. 2) in contrast to MA₂SnCl₆, where the cations remain co-linear with respect to the c-axis. On heating MA₂TeCl₆ through the III–II phase transition, it is likely that the increase in temperature results in the MA⁺ cations having an increased tilt (despite our model, see Fig. S7, ESI†): thus, the dynamically-disordered C–N axis forms a cone with an increased cone angle about the threefold axis and, consequently, a decrease in the lattice parameter c is observed.

Fig. 7 Schematic diagram of the MA⁺ cations located in (a) a cavity coordinated by 6 [TeCl₆]²⁻ anions in MA₂TeCl₆ and (b) the cavity formed by only 4 [SnCl₆]²⁻ anions in MA₂SnCl₆. For clarity, hydrogen atoms are not shown.

To understand the reasons for the constant c-axis below T_t, the magnitude of c can be broken down into the component distances between cation and anion layers, i.e., the C–N bond length, the ‘height’ of the octahedron (Cl–Cl), the intermolecular distance between chlorine ions from different octahedra (Cl⋯Cl), etc., as shown schematically in Fig. S10 (ESI†). These intermolecular distances and bond lengths are calculated from the atomic coordinates derived from the variable temperature SXD results and are summarised in Fig. 8 and Table S2 (ESI†), where, for comparative purposes, changes in both a and c are included.

Fig. 8 Percentage interatomic distance changes, d/d_90 K, as projected in a and c for a variety of atoms in MA₂TeCl₆ as a function of temperature relative to the structure at 90 K; the values are derived from SXD. Although there is a significant percentage increase in N⋯Cl with respect to c, in absolute terms, this contributes only a small to expansion in c. The error bar is smaller than the symbol; all error values can be found in Table S2 and S3 (ESI†).

The chloride anion distances (as projected along a) both inside and between octahedra seem to contribute similarly to a in that both distances increase with increasing temperature, which is due to thermal expansion and the small rotation of the octahedra about their 3-fold axes. However, along the c direction, although the intermolecular distances, as projected on c, for C⋯C and Cl⋯Cl increase, the contraction of the projection of the C–N bond length along c and the reduction in octahedra ‘height’ (Cl–Cl) due to librational motion offset the lattice expansion; thus the length of c-axis stays approximately constant in phase III. The apparent shortening of C–N bond length has been discussed already.

For the same reason, the increased librational motion of the [TeCl₆]²⁻ octahedra results in an apparent contraction of the Te–Cl bond and a reduction in its size. ‘N⋯Cl’ represents the interleaved distance between MA⁺ and octahedron layers, decreasing with increasing temperature. However, because of the overlap between layers, the decrease of distance will positively affect c, which is the reason for a positive slope in Fig. 8. The lack of SXD results makes it challenging to analyse MA₂SnCl₆ similarly. However, based on the observation in MA₂TeCl₆, the constant c in MA₂SnCl₆ in its low temperature phase is likely to be caused by the offset from increased thermal vibration of molecules. Further evidence is needed to prove the impact of corresponding interatomic distances.

The cation cavity

Geometric structure stability conditions in lattices are helpful to chemists as it allows them to quantify lattice-class stability and distortions easily. A classic example is the cation radius ratios and tolerance factors in perovskites.²³ A similar approach was proposed for cubic A₂BX₆ halide perovskites by Brown in 1964, who used the radius ratio (R) of the cation size (r_A) to the cavity size (r_cavity), given in eqn (1), to describe the distortion of the structure in A₂BX₆ crystals.²⁴

It has been suggested that the distortion of high-symmetry crystal structures are driven by the packing of large anions with small cations.²⁵ Hence, the definition of the cavity is crucial, for example, in MA₂TeCl₆ where the MA⁺ cation is surrounded by 12 chloride ions as shown in Fig. 7(a), with the 12 chloride ions provided by 6 octahedra. Three of the 6 octahedra are face-coordinated, with the remaining three being vertex coordinated. As the temperature decreases, the rotation of the octahedra leads to a distortion of the MA⁺ cavity, which drives the observed phase transition. However, the precise size of the cavity is difficult to define. Brown applied the halogen–halogen contacts as the size of the cavity eqn (2), where d_X–X is defined as the average value of interionic and intraionic halogen–halogen distances and r_X is the radius of halogen anion.

r_cavity = d_X–X − r_X (2)

However, the corresponding radius ratio is insufficient to distinguish the Fm3̄m cubic structure from other structures. This might be because eqn (2) is most applicable to the K₂PtCl₆ cubic structure type, where the distance between the spherical A⁺ cation and halogen roughly equals the halogen–halogen contact distance. However, the distance between cation and halogen can vary significantly for a distorted structure. We can improve the estimate of the cavity size by calculating the average distance from the centre of mass of the cation to the coordinate halogen atom d_A–X as given in eqn (3). Yet this does not wholly capture the variations from a distorted structure either due to the wide variation in contact distances.

r_cavity = d_A–X − r_X (3)

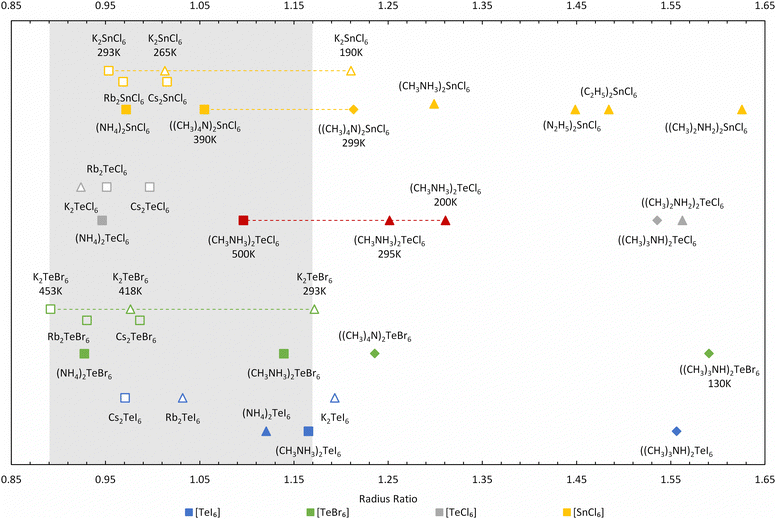
Further improvement can be made to the calculation by only considering the smallest r_cavity length, which is less sensitive to the spread of the contact distances but still captures the magnitude of the distortion. This approach makes more logical sense because in hybrid compounds, the A site cavity contains an organic cation, which are generally not only much larger than the inorganic cations but also behave non-spherically at low temperatures. Using the shortest d_A–X for the radius ratio calculations, a larger variation in R occurs, as shown in Fig. 9, in contrast to using the shortest d_X–X distance (see Table S4 and Fig. S11, ESI†). Our radius ratio range is larger than Brown's work (0.89 < R < 0.98), which did not consider hybrid compounds. Essentially, octahedral tilting in the hybrid compounds leads to lower symmetry structures with larger R values, which we capture in our modified equation allowing a more diverse range of materials to be compared.

Fig. 9 Radius ratio for A₂TeX₆ and A₂SnCl₆ compounds calculated from the shortest d_A–X values. The MA₂TeCl₆ phases determined in this work are highlighted in red. Fm3̄m cubic structures are found in the range 0.89–1.17 as picked out in grey. (Square, diamond, and triangle symbols represent the Fm3̄m cubic structure, other cubic structures, and non-cubic structures respectively; solid symbols represent organic cation structures and hollow symbols represent inorganic ones).

We have extended and updated the radius ratio calculation of Brown to include new hexahalotellurate and hexachlorostannate (IV) complexes obtained from the Inorganic Crystal Structure Database (ICSD)^26,27 as shown in Fig. 9 and Table S4 (ESI†). The coordination number of the A-site cation by halide ions remains 12 across all compounds. The ionic radii of halogen and metal are taken from Shannon radii,²⁸ and the radii of the complete isocharge density sphere are used as effective radii of organic cations.²⁹ The grey region picked out in Fig. 9 covers the ratio range 0.89 < R < 1.17, and this ratio R shows an improved ability to distinguish between high-symmetry (Fm3̄m) cubic phases (depicted as squares in Fig. 9) and other structures compared (diamonds and triangles in Fig. 9) to using the average d_X–X distance (see Table S4, ESI†). The highest temperature cubic phase of MA₂TeCl₆ (500 K) is clearly located inside the 0.89 < R < 1.17 range, whilst the other two phases fall above this range.

Most of the surveyed compounds follow a similar trend as MA₂TeCl₆: the cubic structure is stable in the lower R range while the lower symmetry structures tend to fall in the higher R regime. However, there are clear outliers in Fig. 9, e.g., Rb₂TeI₆ (P4/mnc), (NH₄)₂TeI₆ (P2₁/n), K₂TeBr₆ (P4/mnc), K₂TeCl₆ (I2/m) and K₂SnCl₆ (P4/mnc). These compounds have relatively small cations, so the cavity distorts more heavily to accommodate them, which suggests that our definitions could be further refined to include, for example, the shortest distance between the octahedra. However, this is beyond the scope of this work. K₂TeBr₆ and K₂SnCl₆ transform upon cooling from their high temperature cubic (Fm3̄m) phase to tetragonal (P4/mnc) and then to a monoclinic (P2₁/n) phase, unlike the large cation compound MA₂TeBr₆, which follows a similar trend to our material. Again, the reason for this behaviour is likely related to the A-site ion radius. Although only the room temperature phases of (NH₄)₂TeI₆ and K₂TeCl₆ are included in the ICSD, their highest temperature structures were reported as pseudo-cubic or cubic.^30,31

For those compounds with multiple phases as a function of temperature, the radius ratio increases as the temperature decreases, reflecting the well understood relationship of crystal symmetry and temperature. One source of error in this method may come from the calculated cation radii, which we have assumed to be temperature independent but will likely increase at elevated temperatures. Thus, as the cavity size is known, the higher temperature phase's radius ratio would be under-estimated (with a larger ionic radii), whereas the lower temperature phase's radius ratio should be over-estimated (with a smaller ionic radii).

Conclusions

Single crystals of MA₂TeCl₆ have been successfully grown by a slow cooling solvent method in HCl. VT-PXRD clearly identifies three phases from 120 K to 500 K. We corroborate that phase I (high temperature) is cubic structure (Fm3̄m), while single crystal XRD has determined the low temperature phase III structure as P3̄1c at 200 K. Lattice distortions upon cooling were analysed, and the increased C–N axis length, which is related to the softening of molecule libration, is believed to be the main driver of the constant length of c-axis below the second phase transition temperature. We propose a new radius ratio (R) beyond Brown's work calculated using the shortest distance between A-site cation and halogen atom, which captures the distortion of MA cavity more effectively. The calculation of radius ratio was extended to hybrid A₂BX₆ compounds, and we found that Fm3̄m cubic structure generally locates in the range of 0.89 < R < 1.17.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Y. L. thanks the UCL-CSC scholarship scheme for PhD funding. We acknowledge support from EPSRC for the funding of the X-ray diffractometers (grant reference EP/K03930X/1). We acknowledge ISIS Neutron and Muon Source for beamtime on Polaris. Data is available here: https://doi.org/10.5286/ISIS.E.RB2090007-1 and we thank Ron Smith for collecting the neutron data.

References

1. R. Sa, Y. Wei, W. Zha and D. Liu, Chem. Phys. Lett., 2020, 754, 137538.
2. A. E. Maughan, A. M. Ganose, D. O. Scanlon and J. R. Neilson, Chem. Mater., 2019, 31, 1184–1195.
3. D. Li, J. Shi, Y. Xu, Y. Luo, H. Wu and Q. Meng, Natl. Sci. Rev., 2018, 5, 559–576.
4. J.-W. Lee, S. Tan, S. Il Seok, Y. Yang and N.-G. Park, Science, 2022, 375 DOI:10.1126/SCIENCE.ABJ1186.
5. A. E. Maughan, A. A. Paecklar and J. R. Neilson, J. Mater. Chem. C, 2018, 6, 12095–12104.
6. D. Ju, X. Zheng, J. Yin, Z. Qiu, B. Türedi, X. Liu, Y. Dang, B. Cao, O. F. Mohammed, O. M. Bakr and X. Tao, ACS Energy Lett., 2019, 4, 228–234.
7. M. R. MacIntosh, M. L. H. Gruwel, K. N. Robertson and R. E. Wasylishen, Can. J. Chem., 1992, 70, 849–855.
8. Y. Kume, R. Ikeda and D. Nakamura, J. Phys. Chem., 1978, 82, 1926–1930.
9. Y. Furukawa, H. Kiriyama and R. Ikeda, Bull. Chem. Soc. Jpn., 1981, 54, 103–108.
10. N. Onoda, T. Matsuo and H. Suga, Philos. Mag. A, 1988, 57, 245–260.
11. B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549.
12. M. T. Weller, O. J. Weber, P. F. Henry, A. M. Di Pumpo and T. C. Hansen, Chem. Commun., 2015, 51, 4180–4183.
13. W. Ning, X. G. Zhao, J. Klarbring, S. Bai, F. Ji, F. Wang, S. I. Simak, Y. Tao, X. M. Ren, L. Zhang, W. Huang, I. A. Abrikosov and F. Gao, Adv. Funct. Mater., 2019, 29, 1807375.
14. Y. Cho, A. Yamaguchi, R. Uehara, S. Yasuhara, T. Hoshina and M. Miyauchi, J. Chem. Phys., 2020, 152, 231101.
15. Y. Kume, R. Ikeda and D. Nakamura, J. Magn. Reson., 1979, 33, 331–344.
16. Y. Furukawa, H. Kiriyama and R. Ikeda, Bull. Chem. Soc. Jpn., 1977, 50, 1927–1929.
17. R. Ikeda, Y. Kume, D. Nakamura, Y. Furukawa and H. Kiriyama, J. Magn. Reson., 1976, 24, 9–20.
18. Y. Kume, R. Ikeda and D. Nakamura, J. Magn. Reson., 1975, 20, 276–278.
19. J. R. Shi, Y. Kume, J. Pelzl, Y. C. Xu and X. Wu, J. Raman Spectrosc., 1998, 29, 149–151.
20. W. I. F. David, W. T. A. Harrison, R. C. Ward, A. J. Leadbetter, T. Matsuo and H. Suga, Phys. B Phys. Condens. Matter, 1989, 156–157, 96–98.
21. K. Kitahama, H. Kiriyama and Y. Baba, Bull. Chem. Soc. Jpn., 1979, 52, 324–328.
22. O. Yamamuro, T. Matsuo, H. Suga, W. I. F. David, R. M. Ibberson and A. J. Leadbetter, Phys. B Phys. Condens. Matter, 1995, 213–214, 414–416.
23. G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2015, 6, 3430–3433.
24. I. D. Brown, Can. J. Chem., 1964, 42, 2758–2767.
25. Y. Akahama, M. Kobayashi and H. Kawamura, Phys. Rev. B – Condens. Matter Mater. Phys., 1999, 59, 8520–8525.
26. G. Bergerhoff, R. Hundt, R. Sievers and I. D. Brown, J. Chem. Inf. Comput. Sci., 1983, 23, 66–69.
27. D. Zagorac, H. Muller, S. Ruehl, J. Zagorac and S. Rehme, J. Appl. Crystallogr., 2019, 52, 918–925.
28. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
29. M. Becker, T. Klüner and M. Wark, Dalton Trans., 2017, 46, 3500–3509.
30. H. Henke, J. Appl. Crystallogr., 1980, 13, 305–307.
31. Y. Furukawa and D. Nakamura, Berichte der Bunsengesellschaft für Phys. Chemie, 1989, 93, 13–18.

---

Footnote

† Electronic supplementary information (ESI) available: Additional experimental detail, crystallographic tables, and additional supporting figures are supplied. CIF files have been deposited at the Cambridge Crystallographic Data Centre with REFCODES 2142618 (90 K), 2142619 (120 K), 2142620 (160 K), 2142621 (200 K), 2142622 (250 K) and 2142623 (295 K). Neutron powder diffraction data is available with https://doi.org/10.5286/ISIS.E.RB2090007-1. See DOI: https://doi.org/10.1039/d2tc02372e

---