Getting the details right: optical, dielectric, and vibrational outcomes of structural phase transition in one-dimensional pyrrolidinium lead iodide and the role of defects

Abstract

One-dimensional hybrid organic–inorganic halide perovskites have recently come under the spotlight of research due to their unique optical properties, including strong light absorption and other physicochemical characteristics relevant to energy conversion applications. Exchanging organic cations in the perovskite lattice is known to strongly affect the optical and dielectric properties of the material along with structural stability, stimulating investigations of new organic cations favoring the formation of low-dimensional phases. Herein, we report the synthesis, dielectric and Raman spectroscopy, calorimetric properties, and linear and nonlinear optical behavior of 1D hybrid organic–inorganic lead iodide with the pyrrolidinium cation (C₄H₈NH₂PbI₃, PyrPbI₃). To the best of our knowledge, our results are the first showing the phase transition (PT) in this compound, which allowed us to determine its behavior in both phases. The material undergoes a first-order structural PT at 266.0 K (262.2 K) on heating (cooling). As a result of the structural PT, an abrupt rise in the dielectric permittivity, characteristic of dielectrically switchable materials, was observed. Temperature-dependent Raman spectra showed that the mechanism of the occurring PT is mainly associated with the sudden freezing of the Pyr⁺ cations. In addition, using independent optical methods such as photoacoustic and photothermal deflection spectroscopy, photoluminescence and third harmonic generation measurements, we determined the band gap energy of 2.6 eV. Thanks to in-depth optical measurements, we further the understanding of the photoluminescence emission origin in PyrPbI₃ and question the generality of the attribution of broad band emission to self-trapped excitons.

---

Introduction

In recent years, tremendous efforts have been devoted to the study of hybrid organic–inorganic perovskites (HOIPs) due to their significant contribution to the development of optoelectronic devices, including photovoltaic cells, light emitting diodes, and optically pumped lasers.^1–9 The bulk of the existing research on HOIPs largely focused on lead(II) halide perovskites (LHPs), in which the lead perovskite crystal lattice is usually defined as a network of corner-sharing [PbX₆]⁴⁻ octahedra, with a general APbX₃ or A₂PbX₄ stoichiometry, wherein A and X denote a monovalent organic cation and a halogen anion (Cl⁻, Br⁻, I⁻, or a mixture thereof), respectively. HOIPs not only offer rich chemistry e.g. in terms of the organic cation diversity, but also extend to the spatial arrangement of all inorganic and organic components involved, creating three-, two-, one-, or even zero-dimensional structures. Such reduced dimensionality of the inorganic subnetwork has a significant impact on the optical and electronic properties of HOIPs through the dielectric and quantum confinement of charge carriers.^10–16 Management of this property has promoted tremendous interest in three-dimensional (3D) and two-dimensional (2D) HOIPs and resulted in the demonstration of structure–property relationships, as well as helped to establish merits and drawbacks of respective HOIP subclasses for light harvesting and photoluminescence applications.^11,17–19 Low-dimensional counterparts, such as one-dimensional (1D) HOIPs constructed from single chains of [PbX₆]⁴⁻ octahedra, have captured much less attention of the perovskite community. This has changed only recently, since 1D HOIPs have earned growing publicity as a separate category of HOIPs, thanks to the possible capacity for enhanced quantum and dielectric confinements favourable for practical applications.²⁰ In a similar manner to 2D structures, a large diversity of available ‘A’-site organic cations offers enormous opportunities for tuning the structural, physical, and optical properties of 1D compounds. Quantum confinement in 1D perovskite structures offers additional tuning of their optical properties, relevant to both light-absorbing (tandem solar cells, spectrally-selective²¹ or polarization-sensitive²² photodetectors) and -emitting devices. Strong electron (exciton)–phonon interaction combined with high exciton binding energy gives rise to a plethora of unique effects; for instance, it has been shown that a 1D structure is favourable for exciton self-trapping to produce highly efficient below-gap broadband luminescence useful for white-light-emitting diodes.^23–25 In addition, a highly enhanced non-linear optical (NLO) response in the form of third harmonic generation (THG) was noticed, which can be further exploited to understand the excited states of such systems.^26,27

In recent time, research on compounds that exhibit a broad and strongly Stokes-shifted emission band has attracted a lot of attention. It has become a common practice in the scientific community to attribute this behaviour to emissions from so-called self-trapped excitons (STEs) created by the strong carrier–phonon interaction in the soft crystal lattice of perovskite materials. However, more often than not, the actual role of STEs in these materials is unclear, and the question remains whether they are responsible for broadening the emission band in all cases. To resolve these uncertainties, theoretical first-principles calculations are performed, and/or a combination of optical techniques is used, including ultrafast spectroscopy to investigate the dynamics of the observed processes.^28–32 Studying single crystals rather than common solution-processed thin layers is crucial to exclude grain boundaries of the tested materials. It is important to stress that although halide perovskites and their related compounds generally exhibit impressive optoelectronic performance metrics, some of their relevant photophysical characteristics are governed by defects.^33,34 Hence, detailed investigation into broad-emission perovskite compounds with high quantum efficiency has to be undertaken to distinguish between these effects.

Bearing the mentioned above in mind, we closely examine the behaviour of 1D hybrid organic–inorganic lead iodide with the pyrrolidinium as the ‘A’-site cation (C₄H₈NH₂PbI₃, PyrPbI₃). In the past, only a few reports describing the structure and optical properties of the PyrPbI₃ compound have been published.^35–38 Xu et al. showed that the compound has a bandgap allowing broad visible light absorption and crystallizes in the hexagonal P6₃/mmc space group (273 K),³⁸ while the Pnma orthorhombic phase is observed at lower temperatures (173 K).³⁹ So far, none of the previous studies addressed the topic of phase transition (PT) and its influence on material properties. In order to fill that knowledge gap, we determined the PT temperature of PyrPbI₃, described its switchable dielectric attributes as well as vibrational features of phases at either side of the PT. Moreover, we determined the band gap energy by employing independent optical methods, such as photoacoustic and photothermal deflection spectroscopies, photoluminescence, and THG measurements. Additionally, based on the lifetime of photoexcited carriers, we explained the nature of photoluminescence emission of the material.

Experimental

Synthetic procedures

PbI₂ (99%, Sigma-Aldrich), pyrrolidine (98%, Sigma-Aldrich), hydroiodic acid stabilized with H₃PO₂ (57 wt% in H₂O, Sigma-Aldrich), and N,N-dimethylformamide (DMF, 99.8%, Sigma-Aldrich) were commercially available and used without further purification. In order to grow single crystals of PyrPbI₃, 1 mmol of PbI₂ was dissolved in 3 mL of DMF under stirring at 50 °C. Then 1 mmol of pyrrolidine (0.083 mL) was added and the mixture was neutralized by HI. The solution was left at room temperature (RT) and the yellow single crystals of PyrPbI₃, which grew at the bottom of the glass vial, were separated from the mother liquid, washed with DMF, and dried at RT. The comparison of the powder XRD pattern of PyrPbI₃ with the calculated ones based on the room-temperature single-crystal data reported previously³⁸ (space group P6₃/mmc) confirmed the phase purity of powdered samples (Fig. S1 in the ESI†).

X-ray powder diffraction

Powder XRD patterns were measured in the reflection mode on an X’Pert PRO X-ray diffraction system equipped with a PIXcel ultrafast line detector and Soller slits for Cu Kα1 radiation (λ = 1.54056 Å).

Differential scanning calorimetry (DSC)

Heat capacity was measured using a Mettler Toledo DSC-1 calorimeter with a high resolution of 0.4 μW. The DSC thermograms were measured dynamically for the cooling and heating cycles with different temperature rates (1, 2, 5, 10 K min⁻¹) to determine thermal hysteresis. Nitrogen was used as a purging gas. The mass of the measured sample was 27.78 mg. The excess heat capacity associated with the phase transition was calculated by subtracting from the data the baseline representing the system variation in the absence of phase transitions.

Raman spectroscopy

Temperature-dependent Raman spectra in the 80–3500 cm⁻¹ range (with the resolution of 2 cm⁻¹) were measured in a back-scattering geometry using a Bruker RFS 100/S FT-Raman spectrometer operating at 1064 nm (Nd:YAG); the laser power used was 450 mW. For temperature controlling, the powdered and pelletized sample was placed in a Linkam THMS600 cryostat cell equipped with quartz windows.

Broadband dielectric spectroscopy

Dielectric measurements of the examined samples were carried out using a broadband impedance Novocontrol Alpha analyser. Since the obtained single crystals were not large enough to perform single-crystal dielectric measurements, pellets made of well-dried samples were used instead. The powder was pressed into cylindrical pellets of 5 mm in diameter and 0.5 mm in thickness. Silver paste was coated on both parallel surfaces of the sample to ensure good electrical contact. A sinusoidal voltage with an amplitude of 1 V and frequency in the range of 1 Hz–1 MHz were applied across the sample. The measurements were taken every 1 K in the temperature range of 150–325 K, and the temperature stability of the sample was better than 0.1 K. The temperature was stabilized by means of nitrogen gas using the Novocontrol Quattro system.

Photoacoustic spectroscopy

A 150 W quartz tungsten halogen (QTH) lamp coupled to a 320 mm focal length grating monochromator (Horiba iHR320) through a set of lenses was used as a tuneable light source for photoacoustic experiments. The pumping beam was mechanically chopped at 10 Hz and focused on the sample mounted inside a measurement chamber sealed with a quartz transmission window. The thermally excited acoustic waves were detected using an electret condenser microphone, producing a voltage signal further demodulated with a lock-in amplifier (EG&G 7260). Spectral resolution, determining the transition uncertainty, is 10 meV in the presented spectral range.

Photothermal deflection spectroscopy

In a similar manner to photoacoustic spectroscopy, a tuneable light source consisting of a 250 W QTH lamp and a 250 mm grating monochromator was used for exciting the sample, with the beam modulated with a mechanical chopper at 10 Hz. The sample was mounted in a quartz cuvette filled with a thermooptic medium (Fluorinert FC-72, 3M). A probing laser beam (670 nm) was passed close to the sample surface, where the pumping beam is focused with a lens to form a spot ∼0.2 mm in size. Absorption-related periodic material heating caused probing beam deflection, measured with a quadrant photodiode and demodulated with a lock-in amplifier (Stanford Research Systems SR830) to ensure a high signal dynamic range.

Steady-state photoluminescence measurements

Photoluminescence (Stokes emission) measurements were performed in the backscattering configuration, using a 375 nm diode laser (Omicron QuixX 375-70 PS) operating in the continuous-wave mode used for exciting the material (laser optical power given in relevant places). The emission spectra were analysed using a thermoelectrically cooled Si CCD array detector (Avantes, AvaSpec-HSC1024x58TEC-EVO). A 400 nm longpass filter was placed in front of a fibre coupler to attenuate residual laser light scattered by the sample. For temperature-dependent measurements, either above room temperature (RT) or down in the cryogenic temperature range, a liquid nitrogen cooled microscopic stage with a quartz optical transmission window (Linkam FTIR600) was utilized.

Time-resolved photoluminescence measurements

The luminescence kinetics of PyrPbI₃ was investigated using the time-correlated single-photon counting (TCSPC) method. We used a Becker & Hickl system (Berlin, Germany) constructed from a TCSPC Module (SPC-130-EM) and a hybrid photomultiplier detector (HPM-100-06) powered and controlled with a dedicated card (DCC 100), mounted on the exit slit of an Acton SpectraPro-2300i monochromator (Princeton Instruments, Trenton, NJ, USA). The sample was excited using a 375 nm BDL-377-SMC picosecond laser diode (20 MHz repetition rate, average power 6 mW), whereas the luminescence was passed through the monochromator to monitor 660 nm wavelength. The average luminescence lifetime values and their components were obtained from the fitting of data to biexponential functions, after the deconvolution of the instrument response function (IRF) which is ca. 200 ps. The average lifetime has been calculated using the following formula
in which τ₁ and τ₂ are the decay components, A₁ and A₂ are their weights, and τ_av is the average decay time.

Temperature control of the sample was performed using a Linkam LTS420 heating/freezing stage employing liquid nitrogen cooling.

Spectrally-resolved THG measurements

SR-THG measurements were performed using a laser system consisting of a Coherent Astrella Ti:Sapphire regenerative amplifier, providing 800 nm pulses (75 fs pulse duration, 1 kHz repetition rate) driving a wavelength-tuneable TOPAS Prime optical parametric amplifier (OPA). The output of the OPA was set in a range from 1200 nm to 1625 nm, using a 25 nm step. Prior to the measurements, the single crystals of PyrPbI₃ and those of potassium dihydrogen phosphate (KDP) were crushed using a spatula and sieved through a mini-sieve set (Aldrich), collecting a microcrystal size fraction of 125–177 μm. Next, size-graded samples of PyrPbI₃ and KDP were fixed in between microscope glass slides (forming tightly packed layers), sealed and mounted to the horizontally-aligned sample holder. No refractive index matching oil was used.

The employed SR-THG measurement setup operates in the reflection mode. Specifically, the laser beam was directed onto the sample at 45 degrees to the sample surface and was unfocused. Emission collecting optics consisted of Ø25.0 mm plano-convex lens of focal length 25.4 mm (Thorlabs) coupling light into a 400 μm, 0.22 NA glass optical fibre (Ocean Optics) and was placed along the normal to the sample surface. The distance between the collection lens and the sample was 30 mm. Scattered pumping radiation was suppressed with the use of a 1000 nm or 1200 nm shortpass dielectric filter (FESH1000 and FESH1200, Thorlabs), depending on the applied pumping wavelength.

Note that the geometry of the SR-THG experimental setup and the intensity of the pumping laser beam were strictly the same for both samples at a given wavelength. This allows us to demonstrate the wavelength spectrum of the relative THG efficiency of PyrPbI₃versus KDP standard and eliminates the need for adjustment of the pumping laser intensity to a constant power across all the investigated wavelength range. Stabilization of the samples’ temperature was done using a Linkam LTS420 heating/freezing stage. The emission spectra collected were recorded using an Ocean Optics Flame T spectrograph.

Results and discussion

Thermal properties

In order to identify the temperature-controlled phase stability, the differential scanning calorimetry (DSC) measurements were performed. From the DSC thermogram, it was possible to identify the temperatures of the PTs occurring in the investigated material, which were lacking in the previous studies. The conducted calorimetric investigations show a single, repetitive PT observed at T = 266.0 K (262.2 K) during the heating (cooling) cycle (Fig. 1 and Fig. S2, ESI†). The observed thermal hysteresis between heating and cooling cycles depends on the rate of temperature change (Fig. S2, ESI†). Under the conditions of complete thermodynamic equilibrium in the system (quasi-static), which is infeasibly realized under real experimental conditions, the material would undergo a PT at the temperature corresponding to the condition of equality of the specific thermodynamic potentials. The thermal hysteresis occurring in this compound between heating and cooling cycles indicates the first-order type of PT. The heat capacity peaks associated with PT are symmetrical and sharp because the positions of atoms at the point of first-order phase transition are changed in a jumpwise manner. This is also confirmed by the accompanying discontinuous change in the entropy (ΔS) (see the inset in Fig. 1). The estimated value of the ΔS (∼8 J mol⁻¹ K⁻¹) is associated with the structural transformation from the high-temperature (HT) hexagonal P6₃/mmc to the low-temperature orthorhombic Pnma phase.^38,39

Fig. 1 Temperature dependence of excess heat capacity, ΔC_p, obtained for heating and cooling cycles of PyrPbI₃ with the rates equal to 5 K min⁻¹. The inset shows the corresponding change of entropy, ΔS, measured under the same conditions.

Raman spectroscopy

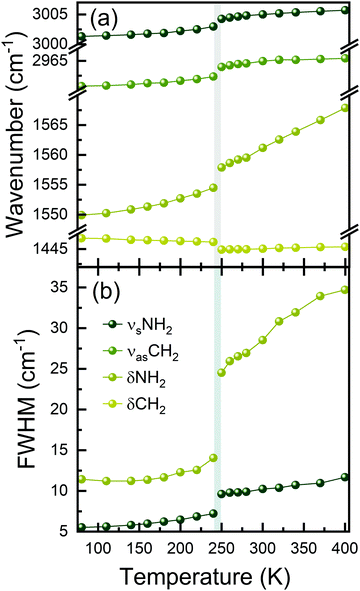
To elucidate the molecular mechanism of the occurring PT, Raman spectra were measured as a function of temperature (Fig. 2). The tentative peak assignment, based on the literature data, is shown in Table S1 (ESI†).^40–42 At RT, the number of observed Raman bands is much lower than that predicted by factor group analysis for the HT phase adopting the hexagonal P6₃/mmc space group.^38,43 This phase is expected to have 114 vibrational modes, which is far from the observation. This means that Davydov splitting is weak in the HT phase, and the individual modes are strongly overlapped. As a result of dynamical disorder, Raman bands are very broad at RT.⁴⁴ The gradual lowering of temperature causes a sudden narrowing of all bands below 250 K, in line with abrupt freezing of the disordered Pyr⁺ cations upon the first-order PT. The temperature of this transformation is slightly lower than that extracted from DSC data because of the partial and local overheating of the crystal by the infrared laser beam.

Fig. 2 Temperature-dependent Raman spectra measured for PyrPbI₃.

The LT phase of PyrPbI₃ is orthorhombic (Pnma symmetry).⁴³ Since the cell volume of this phase is doubled, the number of expected modes should also be duplicated to 228. Obviously, the splitting of bands is barely seen during cooling; thus, the Davydov splitting remains weak in the LT phase as well. It is worth noting that the majority of bands exhibit a strong increase in intensity during cooling (Fig. 2), and some of them become visible only below 250 K. This effect is especially pronounced for bands corresponding to the NH₂ groups involved in the creation of the N–H⋯I hydrogen bonds (HBs). Furthermore, bands corresponding to υ_sNH₂, υ_asNH₂, and δNH₂, which are considered as indicators of HB strength, downshift by 66, 15, and 10 cm⁻¹ when the temperature is lowered from 300 to 80 K (phonon softening).

Such large offsets and increase of intensity are consistent with a strong rearrangement of the HB network and freezing of Pyr⁺ cations when the HT phase transforms to the LT one. This freezing is caused by strengthening of the HBs, as evidenced by the decrease of the shortest N⋯I (H⋯I) contacts from 4.0396 Å (3.2262 Å) at 297 K (HT phase)³⁸ to 3.5721–3.6552 Å (2.7668–2.7918 Å) in the LT phase.

Fig. 3 and Fig. S3 (ESI†) show the results of Raman bands’ fitting using Lorentz curves, such as changes in the positions (Fig. 3(a)) and full-width-at-half-maximum (FWHM, Fig. 3(b)) values. It can be clearly seen that nearly all bands exhibit sudden narrowing and shifts at the PT temperature. Such pronounced thermal effects on Raman spectra, reported previously also for Pyr₂KM^III(CN)₆ (M^III = Co, Fe), Pyr₂(H₃O)Co(CN)₆, and CH₃NH₃PbX₃ (X = I, Br),^40,41,45 suggest that the PT affects geometry and confinement of the Pyr⁺ cations. Indeed, according to the crystallographic data, the volume available for a formula unit decreases from 304.4 ų at 297 K (HT phase) to 291.3 ų at 173 K (LT phase).³⁸ Furthermore, ordering of Pyr⁺ cations leads to the increase of HB strength, and a slight decrease in the Pb–I lengths and Pb–Pb distances within and between parallel chains.⁴⁶ The PT into the ordered structure and subsequent changes in the Pb–I bond lengths, as well as distortion of the [PbI₆]⁴⁻ octahedra, are reflected in the Raman spectra by the strong narrowing and shift of the low-wavenumber Raman bands (below 150 cm⁻¹, Fig. 2 and Fig. S3, ESI†), which correspond to Pb–I stretching and bending modes.

Fig. 3 Energy (a) and broadening (FWHM, b) thermal dependencies of selected Raman bands.

Dielectric studies

In order to describe more deeply the mechanism of the observed structural PT, broadband dielectric spectroscopy measurements were performed. Fig. 4(a) shows a temperature dependence of the real part of dielectric permittivity ε′(T), where a step-like anomaly with small thermal hysteresis at approximately 261 K is observed. Such behaviour indicates the first-order character of the observed PT, which is consistent with the results observed in both DSC and Raman spectra. In addition, the shape of this anomaly is characteristic of dielectrically switchable materials, with Δε equal to 4 at the PT temperature (inset Fig. 4(a)).^41,47–49 To check the phase stability after several phase switching between On/Off states, the dielectric permittivity was measured as a function of time and temperature. Each switching cycle consisted of a temperature change between 250 and 280 K at the rate of 5 K min⁻¹, and after reaching the set temperature (250 or 280 K), the material was dwelled for 30 min (Fig. 4(b)). These results indicate the reversibility and stability of the investigated materials subjected to multiple temperature switching.

Fig. 4 (a) Temperature dependence of the dielectric permittivity of PyrPbI₃ pellets measured upon heating. The representative curves are plotted in frequency decades between 1 Hz and 1 MHz. The changes of dielectric permittivity for 0.2 MHz during heating and cooling cycles were enlarged and are presented in the inset. (b) Several cycles of the temperature-induced dielectric switching of PyrPbI₃ for a frequency of 0.05 MHz.

The observed frequency dispersion above the PT temperature confirms the structural Pyr⁺ cation disorder induced by temperature. Moreover, characteristic of this type of material, the temperature-induced ionic conductivity process may influence the dielectric permittivity values at higher temperatures.^47,50

Photoacoustic and photothermal spectroscopy

We have performed optical spectroscopy experiments to evaluate the optoelectronic potential of PyrPbI₃, with photoacoustic spectroscopy (PAS) used to reveal absorption properties of the materials. Photoacoustic spectroscopy, due to its inherent dependence on nonradiative recombination processes and non-optical detection of the signal approximating optical absorption coefficient, is a unique experimental technique for studying optical transitions in both thick bulk crystals and powdered materials in the same system, overcoming the limitations caused by transmittance saturation and light scattering in regular absorbance measurements.^51,52Fig. 5(a) shows amplitude photoacoustic spectra of a bulk (0.5 × 3 mm, comparable with the excitation beam size) PyrPbI₃ crystal and powdered sample, ground to grains of around 10 μm in size, as confirmed by dark-field optical microscopy. Overall, the signal amplitude for the powdered material is about 2.5 times higher across the entire spectrum, meaning that grinding increases the absorption cross section and effectively increases the solid–gas heat exchange interface area, improving the signal, so all features seen in the spectra come from the bulk properties. In both cases, we observed a signal amplitude rise starting at 2.2 eV, forming a broad absorption edge and signal saturation at around 2.8 eV. No absorption features below 2 eV, down to the near infrared range can be observed, with the signal amplitude remaining at the noise level of the system. Such results are expected for a material yellow in colour (see the photograph in Fig. 5(a)).

Fig. 5 (a) Amplitude photoacoustic (PAS, bulk and powder) and photothermal deflection (PDS, bulk) spectra of PyrPbI₃, revealing visible range absorbance. Straight lines represent Urbach edge fitting. The inset shows the photography of single crystals. (b) Tauc plots for direct band gaps based on photoacoustic spectra presented in panel (a). The inset shows spectral dependence of photoacoustic signal phase, with an extremum coinciding with the determined band gap energy.

Assuming linear dependence between photoacoustic signal amplitude and optical absorption coefficient in the spectral range below signal saturation, we used Tauc plots for direct allowed transition,⁵³ presented in Fig. 5(b), to determine band gap energy of PyrPbI₃. The obtained energy gaps are in good agreement with each other, with 2.62 eV (∼473 nm) for powder and 2.60 eV (∼476 nm) for bulk crystal, respectively. The inflection point in photoacoustic phase spectra lies at the same spectral position as the determined band gap, further confirming a rapid change in optical penetration depth reflected by thermal modulation closer to the material surface.⁵⁴

Our observations differ from some of the previous reports showing a local extremum at 1.8 eV superimposed on the main absorption edge, with no precise interpretation proposed.^38,55 Not only does it appear in the same spectral range as photoluminescence emission (might be detected in the spectrometer setup if high-energy illumination is used), but it also affects the band gap determination from the Tauc plot, coincidently also derived at 1.8 eV. The following publication³⁷ includes absorption results obtained on spin-coated thin layers which are more similar to ours, revealing a clear edge and a peak around 500 nm, with no significant absorption at energies below that. Pham et al.³⁶ reported a slightly higher direct band gap energy of 2.7 eV, though with clear influence of sub-gap absorption on the fitting procedure using the Tauc plot.

Linear absorption dependence in logarithmic scale within a certain spectral range below the band gap indicates the contribution of material disorder in the optical absorption spectrum, represented by the Urbach tail.^56,57 We have fitted the photoacoustic amplitude spectra to the Urbach formula, with band gap energies used as input parameters (see curves in Fig. 5(a)). The obtained Urbach energies are the same within their uncertainties, which are equal to 202 ± 5 meV for the bulk crystal and 202 ± 3 meV for the powdered sample, suggesting no influence of grinding the material on short range disorder. The photothermal deflection spectrum (PDS) on single bulk crystal PyrPbI₃ shows that PDS offers a better dynamic range (possibility to probe lower relative absorbance) than PAS in the below-gap region due to higher method sensitivity, further confirming the presence of a strong absorption tail. Fitting the data in a much broader spectral range than for PAS (down to 1.8 eV) reveals a slightly higher Urbach energy of 212 ± 1 meV. Such large Urbach energy at room temperature is typical for highly disordered or amorphous materials^58–61 in semiconductors, often representing the activity of defects forming energy levels close to band edges.^62,63

The obtained band gap energy is higher than that for regular 3D lead-halide perovskites, and closer to that typically found for low-dimensional structures, such as Ruddlesden–Popper perovskites. The importance of residual optical absorption down to 2 eV lies in the potential applications as absorbers for indoor photovoltaics, optimized for artificial light sources rather than the sun in terms of the maximum efficiency bandgap elucidated from the Shockley–Queisser limit.^8,9,64 Its potential as an energy conversion material could also be exploited in hydrogen generation by photocatalytic water splitting.^65–67 Most organic–inorganic lead halide perovskites offer exceptionally beneficial optical properties for that application due to band gaps above 1.23 eV (allowing the generation of photoexcited carriers having energy sufficient for the reaction) and strong light absorption when compared to classic inorganic semiconductors, but previous efforts on exploring their photocatalytic utility were impeded by rapid material degradation upon exposure to water.^68,69 PyrPbI₃, despite having a larger band gap than the recommended maximum to obtain desirable apparent quantum yield with sunlight illumination (2.36 eV),⁷⁰ has been shown to be highly water-resistant.³⁸ It is also worth mentioning that the issue of water-assisted degradation can be overcome by using different hydrogen-rich reactants, with hydrohalic acids (like hydrogen iodide, HI) proven to be promising competitors.^69,71 To fully evaluate the photocatalytic potential of PyrPbI₃, further research on absolute energy level positions with respect to a vacuum (band alignment) is necessary.

Determination of band gap energy using spectrally-resolved THG data

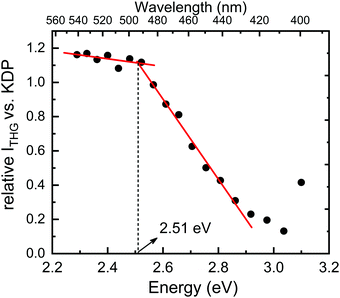
Next, we proceeded to the investigation of optical properties of the PyrPbI₃ material by means of spectrally-resolved THG measurements; however, the use of this technique needs a word of explanation. Specifically, in the past for several coordination polymers, we investigated the spectral intensity of the harmonic generation phenomena by monitoring the intensity of SHG and THG signals as a function of pumping laser wavelength.^72,73 Resulting spectrally-resolved spectra, which were essentially the excitation spectra of harmonic responses, demonstrated that the intensity of SHG and THG signals is attenuated by the presence of one-photon absorption bands not only at the fundamental (pumping) wavelength (λ), but also at the wavelength corresponding to the harmonic of radiation (λ/2, λ/3). In fact, attenuation of the harmonic radiation due to the self-absorption of SHG or THG seems to have a much stronger effect than the self-absorption of radiation at the fundamental wavelength.⁷² This property allowed us to draw a qualitative relationship between the relative strength of harmonic generation and the one-photon absorption spectra of the studied coordination polymers. Indeed, spectral areas with the lowest absorption coefficients featured the highest relative SHG and THG efficiencies, hence they were referred to as “optical transparency windows”. This, in turn, led us to the idea that a simple examination of absorption or reflectance spectra of coloured samples could be used for an assessment of which pumping wavelength the harmonic generation is expected to be the highest. From this perspective, quite interesting seems to be the prospect for a reverse approach – in which the excitation spectra of harmonic generation could be used to assess the approximate value of the optical energy band gap of a material. To the best of our knowledge, such a measurement technique has not been used so far to assess the optical band gap. Accordingly, following results are our very first take on this topic.

Fig. 6 presents the THG excitation spectrum measured for PyrPbI₃ at RT, i.e. relative THG efficiencies (expressed as fraction of KDP efficiency), for the excitation range from 1200 nm to 1625 nm, corresponding to THG maxima in between 400 nm and 541 nm. Experimental spectra of the obtained nonlinear emissions for PyrPbI₃ and KDP are provided in Fig. S4 (ESI†). In the former case, spectra show the presence of THG response only, confirming the assignment of a centrosymmetric space group.

Fig. 6 THG excitation spectrum for PyrPbI₃ as a function of energy of the produced THG response. Red lines are led through the points as a guide to assess the inflection point of an experimental curve. It is apparent that for pumping wavelengths higher than 1475 nm (i.e. THG intensities higher than 491 nm), the relative THG intensities do not significantly increase.

It is apparent that the THG excitation spectrum of PyrPbI₃ features two distinct ranges. The first range covers THG responses from 408 nm (3.04 eV) to 492 nm (2.52 eV), in which the relative efficiency of THG steadily rises from 0.13 to 1.12 compared to that of KDP. Beyond that point, a second region is apparent up to THG located at 542 nm (2.29 eV). Here, the relative efficiencies of THG rise slowly. A plot formed in this way thus features a clear inflection point, whose position is estimated to be at ca. 2.51 eV, as estimated by simple linear regression through adjacent points. We attribute that value to the energy of the optical bandgap of PyrPbI₃, especially in the context of the reference value of 2.62 eV obtained from photoacoustic measurement.

There is one intrinsic limitation to the proposed method of determining the optical bandgap from SR-THG data that needs to be mentioned. Namely, for the femtosecond laser, pulses show a significant broadening due to chromatic dispersion.⁷⁴ Because of that, broad NIR laser pulses are converted to THG response that probes a relatively wide spectral range. For example, in our case, the FWHM of the obtained THG emissions is about 25–30 nm, hence dense probing of the optical band gap cannot increase the resolution of the bandgap due to the overlap between consecutive measurement points. The FWHM of THG corresponds to ca. 0.1 eV near 500 nm, and we consider this value as the primary source of uncertainty of optical band gap determination using femtosecond SR-THG measurements. Indeed, if one compares E_g determined from SR-THG (2.51 eV) and that determined from photoacoustic measurement for the powder (2.62 eV), it becomes apparent that those values match well within the assumed uncertainty range.

The above results also provide an additional argument into the discussion whether observed emission of PyrPbI₃ has excitonic or defect-related character. Namely, it has been previously reported for 2D Ruddlesden–Popper perovskites that THG response can be resonantly enhanced if the third harmonic of radiation falls into the edge of the excitonic energy band gap.⁷⁵ Resonance enhancement is reflected in the excitation spectrum of relative THG intensity, which takes a Gauss (Bell) shape. It was also shown that the position of the excitonic bandgap of 2D RP perovskites could be regulated by the thickness of inorganic slabs as well as counterions (bromide, iodide).⁷⁵ In either case, the same bell-shaped spectral feature in THG excitation spectra has been noted. Very recently, analogous behaviour of SR-THG responses was noted for 1D lead halide perovskites of pyridinium lead iodide (PyPbI₃), which displayed self-trapped excitonic emission.²⁶ As opposed to these examples, results collected for PyrPbI₃ demonstrate no resonant enhancement of THG at the edge of the band gap, but stabilization of relative THG intensity is observed once third harmonic signals move away from the one-photon absorption band. In other words, the observed wavelength dependence of THG can be predominantly ascribed to harmonic self-absorption and the apparent lack of resonance enhancement of THG that we take as an additional hint that observed broad emission comes from defect-induced states.

Photoluminescence measurements

Further optical characterization of PyrPbI₃ involved photoluminescence (PL) measurements. Fig. 7 shows room temperature PL spectra measured at excitation powers of a 375 nm beam (Stokes emission) covering two orders of magnitude (0.1 to 10 mW). All spectra consist of a single peak centred around 680 nm (∼1.82 eV), exhibiting huge broadening with the FWHM of ∼200 nm, corresponding to 1.3 eV in this spectral range (not changing significantly with the excitation power), and emission tails reaching beyond the spectral range of our measurement system. It is important to mention that the broad emission may in fact be composed of multiple phonon-coupled peaks, which is expected for all low-dimensional perovskites exhibiting strong electron–phonon coupling. When compared to other lead-halide perovskites, either in the form of single crystals or thin layers, PyrPbI₃ has considerably lower photoluminescence quantum yield, judging by a typical excitation optical power range necessary to observe intense emission using state-of-the-art spectrometers. That, combined with large Stokes shift of the emission (0.8 eV), calls for deeper analysis, potentially revealing the nature of PL in PyrPbI₃. Our PL data cover a spectral range superior to previous reports^38,55 with overall good agreement on the spectral position and shape. It is also important to highlight that no interpretation for such PL behaviour has been proposed so far.

Fig. 7 Photoluminescence spectra of a bulk PyrPbI₃ crystal obtained across a wide range of excitation powers. The inset shows integrated emission intensity as a function of the excitation power along with best fits to exponential and asymptotic functions.

Power dependence of emission intensity is sublinear at low intensity excitation, with the exponent of 0.85 determined from the fitting procedure. At powers higher than 1 mW, we observed the saturation of emission intensity, which can be approximated by an asymptotic function. Sublinear power dependence is typically observed for defect-related emission rather than excitonic one, often expected for hybrid perovskites, even at room temperature. Intensity saturation has been previously observed on the archetypical hybrid perovskite, CH₃NH₃PbI₃, serving as evidence for the recombination of donor–acceptor pairs.⁷⁶ Such interpretation would also explain the observed Stokes shift and extraordinary emission broadening.⁷⁷

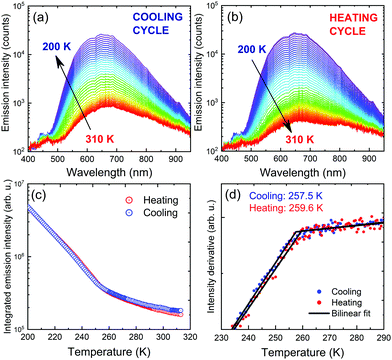
Temperature-dependent photoluminescence in Stokes configuration (375 nm excitation) has been used to assess the influence of PTs observed in DSC measurements on optical activity of the material. Fig. 8(a and b) show two separate measurement series corresponding to cooling the sample down from 310 K to 200 K followed by heating back to 310 K. Intense orange luminescence from the sample can be easily observed with the naked eye at cryogenic temperatures. Spectral position of the emission does not change in the covered temperature range, while emission intensity increases upon cooling. Given the broad temperature range covered during the experiment, such behaviour deviates from typical trends expected for either classic semiconductors^78,79 or lead-halide perovskites.^80,81 That observation further confirms our predictions of extrinsic nature of PyrPbI₃ emission shown here and in previous reports.

Fig. 8 Temperature dependence of photoluminescence emission spectra upon cooling (a) and heating (b) cycles. Total emission intensity obtained by integrating the emission curve has been determined for each series, summarized in (c). Derivatives of the intensity curves reveal PT temperatures (d).

Further analysis of the spectra involved tracing emission intensity across the covered temperature range by numerical integration of the spectra in the full range, as summarized in Fig. 8(c). A significant change in the emission slope is observed in the 240–260 K range, consistent with the obtained PT temperatures revealed by DSC. For a more precise evaluation, derivatives of the intensity traces were calculated, and were further approximated using a bilinear function, all presented in Fig. 8(d). The transition temperatures, taken at the intersection of two lines, are 257.5 and 259.6 K for cooling and heating cycles, respectively. This result proves that although photoluminescence emission is rather defect-related, it can still serve as an indication of material disorder and phase transitions.

Next, we examined time-resolved spectroscopic properties of PyrPbI₃ as a function of temperature. In particular, we were interested to what extent the temperature-induced PT is reflected in dynamics of excited states. Time-resolved luminescence decay data were found to have two decay components (Fig. S5 and S6 in ESI†), hence average decay times τ_av have been calculated after fitting to biexponential decay models, as indicated in the Experimental section. Fig. 9 presents the calculated τ_av values for cooling and heating runs. One sees that the average lifetimes are generally short, at maximum ca. 1.5 ns at 243 K.

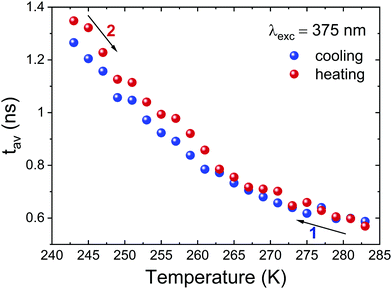Fig. 9 Plot of average luminescence decay lifetimes for PyrPbI₃ for cooling (black squares) and heating runs (red circles).

Even more importantly, there are no apparent signatures of structural PT in average luminescence decay lifetimes at around 265 K. These are reflected in time-resolved data only if one looks at traces of individual τ components, as seen in Fig. S6 in the ESI.† In particular, it is the long-lifetime component τ₁ that displays a temperature anomaly due to PT; also, its relative weight exponentially decreases with increasing temperature. By contrast, the short component τ₂ is practically insensitive to structural modification due to PT. All in all, these results demonstrate that structural phase transition brings minor changes in time-resolved emission characteristics of PyrPbI₃. It also reinforces our interpretation that the probed photoluminescence originates from defect states rather than from exciton recombination.

Conclusions

As research on hybrid organic–inorganic lead halides expands, standardization of both research methodologies and characterization techniques becomes critical to accurate reporting and ultimately helps to develop and discover potential applications of emerging materials. We presented the fundamental characterization of 1D hybrid organic–inorganic lead halide with the pyrrolidinium cation (PyrPbI₃) and identified a first-order PT occurring in this material. PyrPbI₃ also exhibits switchable dielectric properties at 261 K associated with the structural PT. Temperature-dependent Raman spectra showed that the mechanism of the occurring PT upon cooling is mainly associated with the sudden freezing of the Pyr⁺ cation, inducing the shrinkage of the volume available for the cation, subsequent re-arrangement, and strengthening of HBs and the subsequent bond length distortion of [PbI₆]⁴⁻ octahedral units. The lifetime of photoexcited carriers indicates that the observed emission of PyrPbI₃ has a defect-related character. Independent optical measurements confirmed that the band gap is approximately 2.5–2.6 eV. Due to the revealed properties, our work paves the way for potential application in water splitting and indoor photovoltaics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. J. Z. acknowledges the support from the Polish National Agency for Academic Exchange within the Bekker programme (grant no. PPN/BEK/2020/1/00264/U/00001). J. K. Z. acknowledges the financial support from Wroclaw University of Science and Technology.

References

1. M. Ptak, A. Sieradzki, M. Šimėnas and M. Maczka, Coord. Chem. Rev., 2021, 448, 214180.
2. Z.-K. Tan, R. S. Moghaddam, M. L. Lai, P. Docampo, R. Higler, F. Deschler, M. Price, A. Sadhanala, L. M. Pazos, D. Credgington, F. Hanusch, T. Bein, H. J. Snaith and R. H. Friend, Nat. Nanotechnol., 2014, 9, 687–692.
3. G. Xing, N. Mathews, S. S. Lim, N. Yantara, X. Liu, D. Sabba, M. Grätzel, S. Mhaisalkar and T. C. Sum, Nat. Mater., 2014, 13, 476–480.
4. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051.
5. W. Li, Z. Wang, F. Deschler, S. Gao, R. H. Friend and A. K. Cheetham, Nat. Rev. Mater., 2017, 2, 16099.
6. X. Zhao, J. D. A. Ng, R. H. Friend and Z.-K. Tan, ACS Photonics, 2018, 5, 3866–3875.
7. S. D. Stranks and H. J. Snaith, Nat. Nanotechnol., 2015, 10, 391–402.
8. H. S. Ryu, S. Y. Park, T. H. Lee, J. Y. Kim and H. Y. Woo, Nanoscale, 2020, 12, 5792–5804.
9. M. Li, F. Igbari, Z. Wang and L. Liao, Adv. Energy Mater., 2020, 10, 2000641.
10. D. Drozdowski, A. Gągor and M. Mączka, J. Mol. Struct., 2022, 1249, 131660.
11. Y. Han, S. Yue and B. Cui, Adv. Sci., 2021, 8, 2004805.
12. M. Mączka, J. K. Zaręba, A. Gągor, D. Stefańska, M. Ptak, K. Roleder, D. Kajewski, A. Soszyński, K. Fedoruk and A. Sieradzki, Chem. Mater., 2021, 33, 2331–2342.
13. M. Mączka, M. Ptak, A. Gągor, D. Stefańska and A. Sieradzki, Chem. Mater., 2019, 31, 8563–8575.
14. J.-C. Blancon, A. V. Stier, H. Tsai, W. Nie, C. C. Stoumpos, B. Traoré, L. Pedesseau, M. Kepenekian, F. Katsutani, G. T. Noe, J. Kono, S. Tretiak, S. A. Crooker, C. Katan, M. G. Kanatzidis, J. J. Crochet, J. Even and A. D. Mohite, Nat. Commun., 2018, 9, 2254.
15. P. Gao, A. R. Bin Mohd Yusoff and M. K. Nazeeruddin, Nat. Commun., 2018, 9, 5028.
16. R. L. Z. Hoye, J. Hidalgo, R. A. Jagt, J. Correa-Baena, T. Fix and J. L. MacManus-Driscoll, Adv. Energy Mater., 2022, 12, 2100499.
17. X. Li, J. M. Hoffman and M. G. Kanatzidis, Chem. Rev., 2021, 121, 2230–2291.
18. E.-B. Kim, M. S. Akhtar, H.-S. Shin, S. Ameen and M. K. Nazeeruddin, J. Photochem. Photobiol., C, 2021, 48, 100405.
19. W. Fu, H. Chen and A. K.-Y. Jen, Mater. Today Nano, 2021, 14, 100117.
20. Q. A. Akkerman and L. Manna, ACS Energy Lett., 2020, 5, 604–610.
21. J. Yang, W. Kang, Z. Liu, M. Pi, L.-B. Luo, C. Li, H. Lin, Z. Luo, J. Du, M. Zhou and X. Tang, J. Phys. Chem. Lett., 2020, 11, 6880–6886.
22. W. Zhang, M. Hong and J. Luo, J. Am. Chem. Soc., 2021, 143, 16758–16767.
23. A. Biswas, R. Bakthavatsalam, S. R. Shaikh, A. Shinde, A. Lohar, S. Jena, R. G. Gonnade and J. Kundu, Chem. Mater., 2019, 31, 2253–2257.
24. L. Mao, P. Guo, M. Kepenekian, I. Hadar, C. Katan, J. Even, R. D. Schaller, C. C. Stoumpos and M. G. Kanatzidis, J. Am. Chem. Soc., 2018, 140, 13078–13088.
25. Z. Yuan, C. Zhou, Y. Tian, Y. Shu, J. Messier, J. C. Wang, L. J. van de Burgt, K. Kountouriotis, Y. Xin, E. Holt, K. Schanze, R. Clark, T. Siegrist and B. Ma, Nat. Commun., 2017, 8, 14051.
26. S. Maqbool, T. Sheikh, Z. Thekkayil, S. Deswal, R. Boomishankar, A. Nag and P. Mandal, J. Phys. Chem. C, 2021, 125, 22674–22683.
27. T. Sheikh, S. Maqbool, P. Mandal and A. Nag, Angew. Chem., Int. Ed., 2021, 60, 18265–18271.
28. J. Luo, S. Li, H. Wu, Y. Zhou, Y. Li, J. Liu, J. Li, K. Li, F. Yi, G. Niu and J. Tang, ACS Photonics, 2018, 5, 398–405.
29. J. Yu, J. Kong, W. Hao, X. Guo, H. He, W. R. Leow, Z. Liu, P. Cai, G. Qian, S. Li, X. Chen and X. Chen, Adv. Mater., 2018, 1806385.
30. B. Ke, R. Zeng, Z. Zhao, Q. Wei, X. Xue, K. Bai, C. Cai, W. Zhou, Z. Xia and B. Zou, J. Phys. Chem. Lett., 2020, 11, 340–348.
31. X. Wang, Q. Shen, Y. Chen, N. Ali, Z. Ren, G. Bi and H. Wu, Nanoscale, 2021, 13, 15285–15291.
32. S. Kahmann, E. K. Tekelenburg, H. Duim, M. E. Kamminga and M. A. Loi, Nat. Commun., 2020, 11, 2344.
33. Y. Liu, H. Xiao and W. A. Goddard, Nano Lett., 2016, 16, 3335–3340.
34. S. G. Motti, D. Meggiolaro, S. Martani, R. Sorrentino, A. J. Barker, F. De Angelis and A. Petrozza, Adv. Mater., 2019, 31, 1901183.
35. A. F. Xu, R. T. Wang, L. W. Yang, E. E. Liu and G. Xu, Crystals, 2020, 10, 272.
36. N. D. Pham, Y. Yang, M. T. Hoang, T. Wang, V. T. Tiong, G. J. Wilson and H. Wang, Energy Technol., 2020, 8, 1900918.
37. F. Xu, Y. Li, N. Liu, Y. Han, M. Zou and T. Song, Crystals, 2021, 11, 241.
38. A. F. Xu, R. T. Wang, L. W. Yang, V. Jarvis, J. F. Britten and G. Xu, Chem. Commun., 2019, 55, 3251–3253.
39. Y. Miao, H. Fan, P. Wang, Y. Zhang, C. Gao, L.-M. Yang, Y. Song, C. Yang, C.-M. Liu and K. Jiang, Energy Technol., 2020, 8, 2000148.
40. C. S. de Medeiros, M. Ptak, A. Gągor and A. Sieradzki, J. Mol. Struct., 2022, 1252, 132143.
41. M. Trzebiatowska, M. Mączka, A. Gagor and A. Sieradzki, Inorg. Chem., 2020, 59, 8855–8863.
42. L. Carballeira and I. Pérez-Juste, J. Chem. Soc., Perkin Trans. 2, 1998, 1339–1346.
43. Y.-Y. Guo and P. Lightfoot, Dalton Trans., 2020, 49, 12767–12775.
44. M. Mączka, A. Gągor, B. Macalik, A. Pikul, M. Ptak and J. Hanuza, Inorg. Chem., 2014, 53, 457–467.
45. K. Nakada, Y. Matsumoto, Y. Shimoi, K. Yamada and Y. Furukawa, Molecules, 2019, 24, 626.
46. A. Z. Szeremeta, A. Nowok, S. Pawlus, K. Fedoruk, M. Trzebiatowska, M. Mączka, J. Symonowicz, M. Paluch and A. Sieradzki, Appl. Mater. Today, 2021, 22, 100957.
47. L.-S. Li, Y.-H. Tan, W.-J. Wei, H.-Q. Gao, Y.-Z. Tang and X.-B. Han, ACS Appl. Mater. Interfaces, 2021, 13, 2044–2051.
48. J. A. Zienkiewicz, D. A. Kowalska, K. Fedoruk, M. Stefanski, A. Pikul and M. Ptak, J. Mater. Chem. C, 2021, 9, 6841–6851.
49. H. Peng, Y.-H. Liu, X.-Q. Huang, Q. Liu, Z.-H. Yu, Z.-X. Wang and W.-Q. Liao, Mater. Chem. Front., 2021, 5, 4756–4763.
50. M. Maczka, M. Ptak, A. Gagor, D. Stefańska, J. K. Zareba and A. Sieradzki, Chem. Mater., 2020, 32, 1667–1673.
51. T. Toyoda, H. Kawano, Q. Shen, A. Kotera and M. Ohmori, Jpn. J. Appl. Phys., 2000, 39, 3160–3163.
52. A. Rosencwaig, Opt. Commun., 1973, 7, 305–308.
53. J. Tauc, R. Grigorovici and A. Vancu, Phys. Status Solidi, 1966, 15, 627–637.
54. P. Poulet, J. Chambron and R. Unterreiner, J. Appl. Phys., 1980, 51, 1738–1742.
55. A. F. Xu, R. T. Wang, L. W. Yang, N. Liu, Q. Chen, R. LaPierre, N. Isik Goktas and G. Xu, J. Mater. Chem. C, 2019, 7, 11104–11108.
56. Q. Shen, Y. Ogomi, J. Chang, T. Toyoda, K. Fujiwara, K. Yoshino, K. Sato, K. Yamazaki, M. Akimoto, Y. Kuga, K. Katayama and S. Hayase, J. Mater. Chem. A, 2015, 3, 9308–9316.
57. F. Urbach, Phys. Rev., 1953, 92, 1324.
58. V. R. Akshay, B. Arun, G. Mandal and M. Vasundhara, Phys. Chem. Chem. Phys., 2019, 21, 12991–13004.
59. Z. A. Garmaroudi, M. Abdi-Jalebi, M. R. Mohammadi and R. H. Friend, RSC Adv., 2016, 6, 70895–70901.
60. S. M. Menke, A. Cheminal, P. Conaghan, N. A. Ran, N. C. Greehnam, G. C. Bazan, T.-Q. Nguyen, A. Rao and R. H. Friend, Nat. Commun., 2018, 9, 277.
61. E. Feizi and A. K. Ray, J. Mater. Sci.: Mater. Electron., 2015, 26, 4691–4697.
62. M. Beaudoin, A. J. G. DeVries, S. R. Johnson, H. Laman and T. Tiedje, Appl. Phys. Lett., 1997, 70, 3540–3542.
63. S. R. Johnson and T. Tiedje, J. Appl. Phys., 1995, 78, 5609–5613.
64. Y. Peng, T. N. Huq, J. Mei, L. Portilla, R. A. Jagt, L. G. Occhipinti, J. L. MacManus-Driscoll, R. L. Z. Hoye and V. Pecunia, Adv. Energy Mater., 2021, 11, 2002761.
65. X. Li, J. Yu, J. Low, Y. Fang, J. Xiao and X. Chen, J. Mater. Chem. A, 2015, 3, 2485–2534.
66. T. Hisatomi, J. Kubota and K. Domen, Chem. Soc. Rev., 2014, 43, 7520–7535.
67. A. Kudo, H. Kato and I. Tsuji, Chem. Lett., 2004, 33, 1534–1539.
68. K. A. Huynh, D. L. T. Nguyen, V. Nguyen, D. N. Vo, Q. T. Trinh, T. P. Nguyen, S. Y. Kim and Q. Van Le, J. Chem. Technol. Biotechnol., 2020, 95, 2579–2596.
69. H. Huang, B. Pradhan, J. Hofkens, M. B. J. Roeffaers and J. A. Steele, ACS Energy Lett., 2020, 5, 1107–1123.
70. S. Chen, T. Takata and K. Domen, Nat. Rev. Mater., 2017, 2, 17050.
71. S. Park, W. J. Chang, C. W. Lee, S. Park, H.-Y. Ahn and K. T. Nam, Nat. Energy, 2017, 2, 16185.
72. J. K. Zaręba, J. Janczak, M. Samoć and M. Nyk, Dalton Trans., 2017, 46, 9349–9357.
73. J. K. Zaręba, M. J. Białek, J. Janczak, M. Nyk, J. Zoń and M. Samoć, Inorg. Chem., 2015, 54, 10568–10575.
74. C.-A. Bunge, M. Beckers and B. Lustermann, Polymer Optical Fibres, Elsevier, 2017, pp. 47–118.
75. I. Abdelwahab, G. Grinblat, K. Leng, Y. Li, X. Chi, A. Rusydi, S. A. Maier and K. P. Loh, ACS Nano, 2018, 12, 644–650.
76. W. Kong, Z. Ye, Z. Qi, B. Zhang, M. Wang, A. Rahimi-Iman and H. Wu, Phys. Chem. Chem. Phys., 2015, 17, 16405–16411.
77. T. Schmidt, K. Lischka and W. Zulehner, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 8989–8994.
78. K. P. O’Donnell and X. Chen, Appl. Phys. Lett., 1991, 58, 2924–2926.
79. Y. P. Varshni, Physica, 1967, 34, 149–154.
80. M. I. Dar, G. Jacopin, S. Meloni, A. Mattoni, N. Arora, A. Boziki, S. M. Zakeeruddin, U. Rothlisberger and M. Grätzel, Sci. Adv., 2016, 2, e1601156.
81. K. Wu, A. Bera, C. Ma, Y. Du, Y. Yang, L. Li and T. Wu, Phys. Chem. Chem. Phys., 2014, 16, 22476–22481.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S6: powder X-ray diffractogram, DSC traces, Raman wavenumbers and FWHM values, THG response, luminescence decay, and Table S1: Raman bands. See DOI: https://doi.org/10.1039/d2tc01523d

---