Excimer or aggregate? Near infrared electro- and photoluminescence from multimolecular excited states of N^C^N-coordinated platinum(II) complexes

Abstract

We present an experimental and theoretical study of aggregate excited states formed by complexes of the type Pt(N^C^N)Cl, which display near-infrared (NIR) photoluminescence in film and NIR electroluminescence in OLED devices. Here, N^C^N represents a tridentate cyclometallating ligand binding through a central benzene ring and two lateral N-heterocycles. A simple theoretical model for the bimolecular excited states of these complexes accounts for the observed behaviour in terms of metal–metal-to-ligand charge-transfer (MMLCT). Detailed photophysical study provides insight into the kinetic properties of Pt–Pt excimers in solution, in films processed from solution, and in vacuum-deposited films. A clear distinction between emission from dimers and higher oligomers (e.g., trimers and tetramers) is evident. We also demonstrate an alternative approach to the architecture of OLEDs based on aggregate states of Pt(II) complexes. An emissive layer (EML) as thin as 1 to 2 nm can be employed, without compromising the efficiency, while reducing the use of the precious-metal compound by >90% compared to typical devices using EMLs of ∼20–40 nm thickness. For example, OLEDs obtained with an EML of 2 nm thickness display an EQE of 1.2% with λ_EL = 817 nm and a maximum radiosity of 1.46 mW cm⁻². As for the photoluminescence of films, the longest-wavelength electroluminescence from devices employing pristine films of emitter is also attributed to trimers and tetramers.

---

Introduction

Near infrared (NIR) photo- and electroluminescence has widespread applications in modern technology. NIR radiation is invisible to the human eye, but low-cost photodetectors that operate in this region of the spectrum have become increasingly available. The NIR region offers important advantages for multiple applications,¹ for example, in night vision, sensing and light-based data transfer technology.² Meanwhile, biological tissue is relatively transparent to NIR radiation, especially in the 700–1400 nm region. Luminescence over such wavelengths can thus be applied to in vivo bioimaging and photodynamic therapy.^3–5

Organometallic complexes have become popular OLED emitters due to their reliability, stability and ease of colour tuning, coupled with the enhanced efficiency they offer through the harnessing of otherwise non-emissive triplet states.^6–9 While iridium(III) compounds remain the industry standard for visible light displays,^10,11 excimer/aggregate-forming platinum(II) complexes are widely recognised as having an important role to play in near infrared (NIR) OLEDs.^12–20 The d⁸ electron configuration of Pt(II) strongly favours a square-planar orientation of the surrounding ligands leading to an overall flat geometry to the complexes it forms.^21,22 This property allows for the stacking of molecules in a face-to-face manner, such that stabilising interactions between metal orbitals and/or π orbitals of conjugated aromatic ligands can occur. Of particular importance are the interactions that can occur between filled d_z² orbitals as they approach one another, which give rise to metal–metal-to-ligand charge-transfer (MMLCT) in the excited and/or ground state.^22–26 Such interactions account for the ease with which platinum(II) complexes may form excimers, dimers and larger aggregates (oligomers) in concentrated solution and in the solid state.^13,26–28 The excited states that originate from these bimolecular species often display long-wavelength photoluminescence, which may fall within the red and NIR regions of the spectrum.^29,30 Recent studies have also implicated larger aggregates (i.e., involving >2 coordinated metal units) in generating efficient NIR emission.^13,25 Meanwhile, intra molecular Pt–Pt interactions can also be observed within a single molecule featuring two coordinated Pt(II) units, if the two metal centres are oriented in a way that allows for a short contact between them in the ground and/or excited state.^31,32

Several classes of platinum(II) complexes have been explored as OLED emitters, based on the architecture of the chelating ligands around the metal centre, such as: (1) homo- and heteroleptic complexes of bidentate N^N¹⁹ and C^N³³ ligands (often with bidentate co-ligands), (2) complexes of N^N^C ligands, notably those where the coordination sphere is completed by an acetylide ligand,³⁴ (3) complexes of tridentate N^C^N ligands with halogen²⁹ and pseudohalogen³⁵ ancillary ligands, and (4) complexes of tetradentate O^N^C^N ligands, related to (3) but where the coordination is completed by a phenolate linked to the N^C^N unit.¹⁵

Despite recent impressive achievements in the application of bimolecular Pt–Pt excited states as NIR OLED emitters, there remain unanswered questions related to their design, as well as limitations in the understanding of fundamental effects, both molecularly and in the device. Most of the detailed studies, for example, in the pioneering work of Chi and co-workers, have focused on bidentate complexes of type (1).^12,30 In this contribution, we study four examples of N^C^N-coordinated complexes of type (3) (Fig. 1), probing the formation of NIR excimers in solution and aggregates in solid film. We account for experimental trends in MMLCT luminescence through TD-DFT models that consider the relative orientation of the two complex units in the bimolecular species.

Fig. 1 Structures of the Pt(II) complexes 1–4 studied in this work.

We also describe an improved, material-efficient design of OLED architectures based on Pt–Pt NIR emitters, where the thickness of a pristine film of the platinum(II) complex as the emissive layer (EML) can be reduced from the typical ∼20–30 nm to only 1–2 nm, without compromising the efficiency. This important advance reduces the use of the heavy metal complex in the OLED structure by 90–95% in comparison with typical OLED architectures. The OLEDs obtained with the 2 nm thick EML reach 1.2% external quantum efficiency (EQE) at λ_EL = 817 nm, with a maximum radiosity of 1.46 mW cm⁻². These results are competitive with existing NIR OLEDs showing EL in this region but which employ EMLs that are an order of magnitude thicker, ∼20–30 nm.^13,36 The PL and EL in the 800 nm region in pristine films is shown to be most likely due to the formation of trimers and tetramers.

Results and discussion

Complexes selected and their synthesis

The parent unsubstituted complex Pt(dpyb)Cl (1) has been widely investigated. It efficiently forms excimers that emit at around 700 nm in PL and EL with high quantum yield. We selected three other N^C^N complexes with a view to generating emission further into the NIR. Previous work has shown that the introduction of electron-withdrawing CF₃ groups into the pyridyl rings red-shifts both the unimolecular and excimer emission relative to 1, though the solubility of that derivative was rather poor.³⁶ We therefore identified the complex 2 as a suitable candidate for study, in which the appended t-butyl group was expected to improve the solubility. Complex 4 was selected on the grounds that the change to pyrimidine rings might have a similarly stabilising effect on the excimer/aggregate. Finally, the unimolecular emission of the isoquinolyl derivative 3 is known³⁷ to be red-shifted relative to 1 (λ_max = 592 versus 490 nm in CH₂Cl₂, see Table S5.1 in the ESI‡) though there is no reported information about excimer formation, so this complex was of interest too.

The two new complexes 2 and 4 were obtained from the corresponding N^CH^N proligands upon treatment with K₂PtCl₄ in refluxing acetic acid, as summarised in Scheme 1. The requisite proligands were synthesised by Suzuki cross-coupling of 3,5-bis-boronated tert-butylbenzene (in turn obtained from 1,3-dibromo-5-tert-butylbenzene) with either 2-bromopyrimidine (for 4), or 2-chloro-4-trifluoromethylpyridine (for 2). Experimental details and characterisation data for the new compounds are provided in the ESI.‡

Scheme 1 The synthetic route to complexes 2 and 4via Suzuki coupling of a mutually common intermediate obtained from 1,3-dibromo-5-tert-butylbenzene.

The molecular and crystal structures of 2, 3, and 4 in the solid state have been determined by X-ray diffraction (Fig. 2). Figures and experimental details are provided in the ESI.‡ The structure of 1 is already reported in the literature.³⁸ Two different crystalline forms of 2 were isolated, one a chloroform solvate and the other a methanol solvate (reflecting the solvent from which the crystals were obtained; yellow and red in colour respectively). Crystals of complex 3 suitable for diffraction analysis were obtained from a solution in DMF, whilst crystals of complex 4 were isolated by slow evaporation of a solution in a mixture of dichloromethane and methanol. All the molecular structures show the expected, roughly planar, geometries around the Pt(II) centres and of the constituent aromatic rings relative to one another. In terms of the packing of molecules in the crystal, 2-CHCl₃, 3 and 4 display a head-to-tail arrangement of the complexes within the slanted stacks. The interplanar distances are 3.638(18), 3.582(3) and 3.399(12) Å, respectively, but the slightly offset arrangement of neighbouring molecules relative to one another leads to longer Pt⋯Pt distances: 5.7896(5), 5.1914(7) and 4.3927 (11) Å, respectively. These separations are too long for there to be any significant Pt⋯Pt interactions, though the molecules are sufficiently close for some weak π–π stacking to be implicated. On the other hand, 2-MeOH shows a head-to-head packing of adjacent molecules, with close Pt⋯Pt contacts of 3.2137(3) Å. The difference in the crystal packing in the two forms of 2 highlights how different arrangements of molecules may have very similar energies. Effects favouring one over another may be subtle. For example, we note that 2 forms a yellow solid upon fast evaporation but a red solid on slower evaporation, perhaps reflecting the two different types of arrangement, found in the chloroform and methanol solvates respectively, and suggesting that both kinetic crystallisation and thermodynamic effects may be at work. From the behaviour of 2-MeOH we can probably also conclude that the absence of Pt⋯Pt interactions in 3 and 4 does not mean that they are not possible under subtly different conditions, a point we return to later.

Fig. 2 The packing of molecules of 2 in the two isolated solvates: head-to-tail in the chloroform solvate (top) and head-to-head in the methanol solvate (bottom).

Solution-state photophysics

Steady-state absorption and emission spectra. The absorption and PL spectra of the complexes in CH₂Cl₂ are shown in Fig. 3 and corresponding numerical data are summarised in Table S5.1 (ESI‡). In dilute solution (around 10⁻⁵ M), the complexes display vibrationally structured spectra, wherein the (0,0) component is most intense, emanating from unimolecular excited states. The trend in PL λ_max is: 1 < 4 < 2 < 3. In more concentrated solutions, an additional band appears at longer wavelength in each case due to the formation and subsequent emission of excimers, as previously interpreted for such N^C^N complexes.^39,40 The broad, structureless profile of these bands is typical of excimers with their shallow potential energy surfaces and the dissociative nature upon relaxation to the ground state. We return to this point later to confirm that this emission is indeed due to excimers rather than dimers that pre-exist in the ground state. The excimer band is least obvious for 3, where it apparently overlaps with the (0,4) component of the unimolecular emission, which is also rather broader. The λ_max for the excimer follows the same trend as that of the respective unimolecular species, a point that will be discussed further in Section DFT and TD-DFT calculations.

Fig. 3 Absorption (blue dashed lines) and PL spectra of complexes 1–4 in CH₂Cl₂: dilute solution, c = 10⁻⁵ M (black continuous lines); concentrated solution, c = 3 × 10⁻⁴ M (red dashed lines). The PL spectra of the excimers (purple dotted lines) were obtained by subtracting the photoluminescence spectrum obtained at lower concentration from that obtained at higher concentration after normalisation at λ_max.

Excimer formation mechanism. Excimer formation arises from the interaction between an excited-state molecule M* and a second molecule in the ground state M, as described by Birks’ scheme⁴¹ (Fig. 4 and discussed in the ESI,‡ Section 8).

Fig. 4 Schematic view of excimer formation.

This classic mechanism fully describes the formation of excimers of 1–4 as a dynamic quenching phenomenon in the excited state. The “monomer” excited-state population (M*) is depleted through collisions with ground-state molecules (M), resulting in shorter PL lifetimes of the unimolecular emission (τ_M) with increasing concentration, as described by the Stern–Volmer relationship (eqn (1) below). The lifetime at infinite dilution is τ₀, k_Q is the bimolecular rate constant of quenching through excimer formation, and k_−Q is the excimer dissociation rate constant regenerating the monomer. The excimer lifetime τ_E is k_E⁻¹. For 1–4, the unimolecular emission normally follows a single exponential decay (eqn (2)), indicating that the dissociation of excimers, k_−Q, can probably be neglected. Interestingly, however, we observe that 1 decays biexponentially at the highest concentrations investigated (3 × 10⁻⁴ M), (Fig. S5.5, ESI‡) which may be indicative of excimer dissociation regenerating M*, i.e., the assumption that k_−Q can be neglected may not be met in this instance due to large overall concentrations of generated excimers. For this case only, then, the biexponential decay is fitted to eqn (3).

The temporal dependence of the long-wavelength excimer PL on a microsecond timescale initially shows a rise in intensity, reflecting the formation of excimers by interaction between M* and M, as opposed to direct excitation of a ground-state bimolecular species.⁴² This grow-in of excimer PL is followed by monoexponential decay (Fig. 5). The overall variation of intensity with time is thus fitted to a sum of two exponential terms, one of which has a negative pre-exponential amplitude (eqn (4)). At t = 0, the excimers do not yet exist so the pre-exponential factors in eqn (4) need to be equal (of absolute value A′) but with opposite signs to meet this condition. When k_E >> k_M, as expected in this instance, the excimer emission first rises with a time constant equal to the excimer lifetime, and subsequently decays with a rate constant equal to the monomer decay rate.

Fig. 5 Photoluminescence decay traces for complex 4 at different concentrations in CH₂Cl₂.

Eqn (1)–(4) readily explain the photoluminescence decay of complexes 1–4, confirming the excimer formation in these compounds to be compatible with Birks’ kinetic mechanism.

Solid state photophysics

(i) Films in PVK and pristine films deposited from solution. We now consider the photoluminescence properties of complexes 2, 3 and 4 in the solid state, where the behaviour is more relevant to OLED devices. The PL and EL of parent complex 1 in film have already been reported.^29,43 We chose poly(N-vinylcarbazole) (PVK) as the polymer host due to its chemical similarity with hosts used in OLEDs (Fig. 6). In earlier work,^27,44 we noted that the mechanism for excimer formation is different in the solid state from that in solution. In solution, excimers can be recognised by their distinctive kinetic behaviour (i.e., biexponential decay and rise time), but in solid film, the mono- and bimolecular excited states behave as if they were not forming an equilibrium and decay independently of each other. As molecules have severely limited mobility in the solid phase, short intermolecular distances are necessary in the ground state in order to generate excimer-like species emitting at long wavelengths, giving a similar picture to aggregation. We will consider the photophysical behaviour of complexes 2 to 4 in PVK in the context of the above findings. Given the kinetic picture (Fig. S5.8, ESI‡) of the long wavelength luminescence arising from MMLCT states of complexes 2 to 4 in film resembling aggregation rather than typical excimer formation, we will use the term “aggregate” for the purpose of discussion in this section.

Fig. 6 PL spectra of complexes 2, 3 and 4 in solution-processed film: 5% load in PVK (black continuous line); 20% load in PVK (red dashed line); pristine prepared from solution (blue dashed line). The excimer PL spectra in solution (green continuous line) from Fig. 3 are displayed again here for comparison.

The PL spectrum of complex 3 in film resembles that in dilute solution, irrespective of the loading: 5, 10 or 100% (Fig. 6). There is almost no evidence of a longer-wavelength excimer/aggregate band, despite this complex showing excimer emission – unequivocally in the NIR – when in concentrated solution. Presumably, in the solid state, the molecules are not able to establish the short contacts that are necessary, ruling out this compound for use in NIR OLEDs.

In contrast, 2 and 4 show a large increase in the long-wavelength band (λ_max approx. 740 and 700 nm respectively) at 20% concentration in PVK films, relative to the structured shorter-wavelength emission that dominates at 5% loading (Fig. 6). The resemblance of the long wavelength band to the excimer PL in CH₂Cl₂ (Fig. 3) suggests a similar, bimolecular nature to the excited state responsible in film.

In pristine films, the behaviour is different again. For 2, the difference is subtle: there is a small red shift of the long wavelength band relative to that at 20% in PVK (λ_max = 742 versus 735 nm respectively). But, for 4, there is a large shift: (λ_max = 820 nm in neat film versus λ_max = 701 nm in 20% PVK film). The occurrence of such a profound red shift with increasing concentration in the film is highly suggestive of the formation of new emissive species in neat film, comprising of more than two molecules, i.e. trimers, tetramers, etc., that are not present in significant amounts at lower loadings. Such larger aggregates thus apparently dominate the PL spectra of 4. We explore the subject computationally below. We also note that the findings of another recent study on Pt(II) NIR OLED emitters have also implicated aggregates comprising more than two molecules in the generation of long-wavelength PL and EL.¹³

(ii) Vacuum-deposited pristine films. The absorption and PL spectra of vacuum-deposited films are shown in Fig. 7. The slight differences in λ_max of 4 compared to the solution-processed film (Fig. 6) most likely reflects subtly different proportions of trimers and tetramers in the films formed by the two methods. The absorption spectra of 2 and 4 in films clearly display an additional long-wavelength absorption band, λ_abs ∼500–650 nm, compared to the spectra in solution. Such bands can be attributed to the Pt–Pt MMLCT transition of ground state dimers or aggregates. The notable overlap between absorption and PL in the ∼600–650 nm region may, at first sight, seem inconsistent with a triplet emitter. In certain recently reported diplatinum(II) complexes, such overlap was a hallmark of thermally activated delayed fluorescence due to a small ΔE_S–T gap.^44,45 In the present instance, however, it is likely that the absorption spectra of higher level aggregates – such as trimers and tetramers, which will have relatively smaller energy gaps – will overlap with the PL of dimers, for example. In order to verify this, the emission spectra have been recorded over a range of excitation wavelengths (Fig. 8). For λ_ex < 500 nm, the PL spectra are identical, which is consistent with direct excitation of individual Pt(II) units within the oligomer (aggregate). In contrast, longer wavelength excitation leads to a progressive red shift of the emission spectrum, which indicates that lower energy emissive excited states are associated with those species displaying longer-wavelength absorption bands. This observation supports the notion that different sizes of aggregates are present in the film.

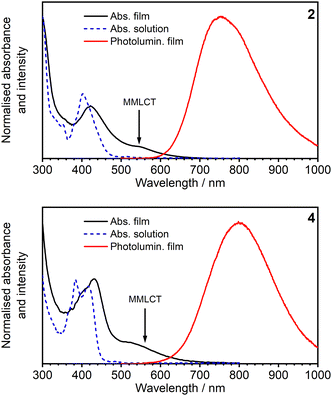Fig. 7 Absorption and PL spectra of complexes 2 and 4 in vacuum-deposited pristine films. The absorption spectra in diluted CH₂Cl₂ solution are overlaid for reference.

Fig. 8 The variation of the PL spectra of complexes 2 and 4 in pristine vacuum-deposited films according to λ_ex. Note how the low energy excited states dominate the PL spectra when longer wavelength excitation is used.

(iii) Variable-temperature studies. To gain further insight, we recorded the PL spectra and emission decays of the vacuum-deposited films of 2 and 4 over a range of temperatures between 300 and 80 K (Fig. 9 and Fig. S5.10–16; Table S5.2, ESI‡). Significant changes are observed. They are reversible with temperature (Fig. S5.17, ESI‡), confirming that the films are stable. Moreover, when dissolved in CH₂Cl₂, the films give PL and absorption spectra identical to those of the originally synthesised compounds (Fig. S5.7, ESI‡), confirming that the molecular structures are unchanged in the films.

Fig. 9 Normalised photoluminescence spectra of complexes 2 and 4 in pristine vacuum-deposited films recorded over the temperature range 300–80 K.

Complex 2 displays a progressive narrowing of its PL spectrum on lowering the temperature (intensity-normalised spectra in Fig. 9), with a concomitant large increase in PL intensity and decay lifetime (Fig. S5.12 and S5.14, ESI‡). The decays remain predominantly mono-exponential for all temperatures (Table S5.2, ESI‡), implying that the PL is dominated by one luminescent species, presumably dimers. Given the large increase in PL intensity and decay lifetime on going from 300 to 80 K, (τ = 0.12 and 1.26 μs respectively), non-radiative decay is evidently highly competitive with emission at room temperature.

Contrary to complex 2, the pristine film of complex 4 does not show any significant change in the overall PL intensity upon cooling, while the decay lifetime increases to a much lesser extent. We estimate the radiative rate constant k_r of complexes 2 and 4 in film at ≈2–3 × 10⁵ s⁻¹. Most interestingly, however, two distinct emission bands become resolved at temperatures near 80 K (λ_em = 734, 840 nm), compared to just one single band at 300 K (λ_em = 804 nm). In parallel, the decay becomes visibly biexponential at lower temperatures: a shorter-lived component emerges in the 700–800 nm region of the spectrum, but not at 850 nm (Fig. S5.16, ESI‡). Meanwhile, at 300 K, a rise time in the PL at 800 nm can be noted within the first 150 ns of excitation, but not at 750 nm (Fig. S5.16, ESI‡). These observations are consistent with the earlier tentative conclusion of at least two different luminescent species being present in the pristine film of 4. These species are most likely to be different oligomers of the complex, such as dimer, trimer and tetramer.

Different oligomers of 4 present in film will, in effect, behave as different compounds, each with their own singlet and triplet energy. In that case, the larger oligomers – presumably with the lowest lying T₁ – will act as traps for the triplet states of the smaller aggregates, with higher T₁ energies, through Dexter energy transfer.^46–48 At 300 K, the build-up of PL intensity at λ_em = 800 nm is a reflection of this process. As the temperature decreases, triplet energy transfer becomes slower^49,50 and can no longer be recognised in the time dependence as a build-up prior to decay. Simultaneously, a new short-lived component at ∼750 nm becomes present in the decay traces, consistent with the new luminescent band emerging to shorter wavelength. Radiative decay of the species associated with this band can outcompete triplet transfer at lower temperatures. The species responsible is most likely dimers, given the similar λ_max to that of the excimer (λ_em = 701 nm in solution). The short lifetime of this band is a result of competition between radiative decay and triplet energy transfer to populate the excited state of higher oligomers (trimer/tetramer).

The lack of significant increase of the PL intensity upon cooling 4 in neat film appears surprising, especially when contrasted with the large increase displayed by 2 (Fig. S5.12, ESI‡). The intensity does initially increase from 300 to 250 K, but then decreases as the new luminescent band emerges at λ_em = 734 nm. This behaviour suggests that the band at λ_em = 734 nm demonstrates a significantly smaller PLQY than that at λ_em = 840 nm. While triplet transfer processes are slowed down, this energetically higher, but lower-efficiency, luminescence channel apparently limits the overall emission efficiency achievable. This apparent contradiction of the energy gap law⁵¹ can be explained by exciton-vibration decoupling in the larger aggregates.¹³

DFT and TD-DFT calculations

In order to understand the fundamental connection between complex structure and excimer luminescence, we have studied model bimolecular systems using density functional theory (DFT) and time-dependent DFT (TD-DFT) computations using the ORCA 4.2.1 software.^52–54 In addition to complexes 1-4, complex 5 (Fig. S4.1, ESI‡) was also included, as it is offers an example of a derivative of 1 that displays blue-shifted excimer emission relative to the parent and thus offers an opportunity to cross-check the reliability of the modelling.⁴⁴ Since metallophilic Pt–Pt interactions have generally been considered central to the formation of excimers or aggregates of Pt(II) complexes,^{7,12,32,55,56} our model comprises molecules disposed parallel to each other and with the metal centres positioned on the z-axis (Fig. 10). Given the C₂ symmetry of the complexes 1–5 in the ground state, we have considered two possible starting geometries: one with the ancillary chloride ligands on the same side (a head-to-head arrangement or syn), and the other with the chlorides on opposite sides (head-to-tail or anti). These initial configurations were then optimised for the T₁ state geometry using the BP86/def2-SVP level of theory and the excited state energy was then calculated using B3LYP/def2-SVP. The approach of using BP86 instead of B3LYP for the geometry optimisation has been found to offer good accuracy while significantly reducing calculation times.⁵⁷

Fig. 10 Structural geometry and frontier molecular orbital contour plots for excimers of platinum(II) complex 4. The energy-minimised T₁ geometry of the excimer was evaluated using BP86/def2-SVP with subsequent single-point energy calculation using B3LYP/def2-SVP/CPCM(CH₂Cl₂).

The results suggest that distinctive syn and anti geometries of the excited state are possible in all cases (Fig. 10 and Fig. S4.2–6, ESI‡), as indeed observed experimentally for 2 (Fig. 2 above). In the syn geometry, the ancillary halogens in neighbouring molecules form an acute angle of 16.0–54.2° relative to one another (measured as the Cl–Pt–Pt–Cl dihedral angle). In the anti geometry, the chlorides form an obtuse angle, the value of which appears to depend on the steric hindrance associated with the lateral groups of the N^C^N ligand. For complexes 1 and 4, the angle is in the range of 131.7–137.9°, while for 3 it is 105.6°. Where additional peripheral tert-butyl and –CF₃ groups are present, as in 2 and 5, the two molecules are nearly anti-parallel with the angle being in the range of 163.9–169.2°. We recognise that the syn and anti geometries give a slightly different energy of the excited T₁ state (considered as the emissive state in these systems). To probe which geometry better accounts for the experimental results, we look for correlations between experimental and theoretical excimer energy, taking into account both λ_max and the excimer emission onset as indicative of excimer energy (Fig. 11). The differences in T₁ energy between the two geometries are affected by steric effects. Whilst the syn geometry gives a roughly correct estimation for excimer energy, the match is excellent for the anti configuration, and so we will limit further discussion to the latter.

Fig. 11 Correlating experimental and calculated excimer energy in the SYN and ANTI configurations. Syn: A = 0.6 ± 0.1, B = 1.4 ± 0.1 (onset); A = 0.6 ± 0.1, B = 0.9 ± 0.1 (maximum). Anti: A = 0.54 ± 0.02, B = 1.37 ± 0.03 (onset); A = 0.60 ± 0.05, B = 0.99 ± 0.06 (maximum). Owing to the superior correlation for the ANTI arrangement, this configuration is assumed in the subsequent discussion.

The d_z² orbitals of the Pt centres and the p_z orbitals of the ancillary chlorides dominate the HOMO in all the bimolecular states. The LUMO is delocalised over the N^C^N ligands of both contributing molecules. The distribution of the LUMO in a single complex is somewhat similar to that in the bimolecular state (Fig. S4.6, ESI‡). Such HOMO–LUMO distribution, as presented in Fig. 10, is an indication of clear metal–metal-to-ligand charge-transfer (MMLCT) character to S₁ and T₁.

The HOMO and LUMO energies of the simulated bimolecular species show the same trend as those of the individual molecules (Fig. 12a). This behaviour can be explained by the somewhat similar spatial distribution of the frontier molecular orbitals in both cases (Fig. 12b and Fig. S4.6, ESI‡). Electron withdrawing groups (EWGs) located on the outer periphery of the pyridine rings – such as –CF₃ in 2 or the additional heterocyclic nitrogen atom in 4 – stabilise the LUMO of the excimer, while a similar stabilising effect can be achieved by extending the conjugation, as in 3. On the other hand, the replacement of the –CF₃ group by tert-butyl in 5 leads to destabilisation of the LUMO.

Fig. 12 (a) HOMO and LUMO energy calculated for the isolated molecules (labelled mon.) and the excimers (exc.); (b) schematic representation of localisation of HOMO and LUMO in both the excimers and isolated molecules.

Given that the excimers formed by 2 and 4 in solid film (at 20% loading) have similar PL to those in solution, the theoretical model established for excimers in solution may offer a good starting approximation of behaviour in solid film. For 4, we use a related model comprising three or four molecules, given the earlier conclusion that the PL in neat film is probably due to such higher aggregates.^58,59 In this case, by using the empirical relation presented in Fig. 11, we find that the anti-trimer and anti-tetramer (Fig. 13) of molecule 4 yield photoluminescence maxima at 787 nm (onset 652 nm) and 823 nm (onset 676 nm), respectively – close to the experimental PL and EL maxima (804 and ∼820 nm, respectively). The HOMO and LUMO in these aggregates (Fig. 13) resemble those in the respective excimers (Fig. 10), but with visibly lesser contribution of the p_z orbital of chlorine to the HOMO. In both structures, the molecules are rotated one to another by ∼130–140°, resembling the anti geometry of the model excimer. In such a geometry, the relatively electron-rich ancillary chlorides are localised opposite to the electron-deficient pyrimidine units at a shortest distance of 3.4 Å. Such halide-to-π* electrostatic interaction, in conjunction with negligible steric hindrance, is likely to facilitate aggregation of 4 in the solid state. Aggregates should also contribute to the PL in pristine films of 2 (Fig. 6 and 7), but they appear to not form as easily as with complex 4 and give only a minor contribution to the overall luminescence spectrum. This is most likely due to the steric hindrance associated with the –CF₃ groups.

Fig. 13 Structural geometry and frontier molecular orbital contour plots for anti-trimer and anti-tetramer of 4 at T₁ geometry. Geometry optimised at BP86/def2-SVP level with subsequent single point energy calculation using B3LYP/def2-SVP/CPCM(CH₂Cl₂) level of theory.

OLED devices

Complexes 2 and 4 were selected for testing in NIR OLEDs due to their long wavelength photoluminescence in neat films. In order to achieve an optimal balance between holes and electrons in the emissive layer (EML), a device architecture was used in which the EML was sandwiched between layers of hole-blocking PO-T2T {2,4,6-tris[3-(diphenylphosphinyl)-phenyl]-1,3,5-triazine} and electron-blocking TSBPA {4,4′-(diphenylsilanediyl)bis(N,N-diphenylaniline)}. These materials have HOMO and LUMO energies close to the respective energy levels of the emitters (Fig. 14, Fig. S6.1 and Table S6.1, ESI‡). The device structure was ITO | HAT-CN (10 nm) | TSBPA (35 nm) | 2 or 4 (x nm) | PO-T2T (50 nm) | LiF (0.8 nm) | Al (100 nm). The material HAT-CN {dipyrazino[2,3-f:2′,3′-h]quinoxaline-2,3,6,7,10,11-hexacarbonitrile} is the hole injection layer, while the thin layer of LiF facilitates electron injection. The EL characteristics of the OLED devices are presented in Table 1 and Fig. 14, while the J–V and luminance–V plots are shown in the ESI‡ (Fig. S7.2–3).

Fig. 14 (a) Structure of devices 1–6 where the EML is indicated either as a filled brown rectangle (complex 4) or dashed red rectangle (complex 2). The width of rectangles roughly represents the relative thickness of each layer. Electroluminescence spectra of Devices 1–3 containing 2 as EML (b) and of Devices 4–6 containing 4 as EML (d). The corresponding EQE of the devices as a function of current density (c and e).

Table 1 Characteristics of OLED devices fabricated with complexes 2 and 4 as emitters. Device structure: ITO | HAT-CN (10 nm) | TSBPA (35 nm) | 2 or 4 (x nm) | PO-T2T (50 nm) | LiF (0.8 nm) | Al (100 nm)

Device	Complex	Φ PL	EML thickness x^b, nm	λ EL , nm	% λ > 700 nm^d	EQEmax^e, %	Max. radiosity, mW cm^−2
a Photoluminescence quantum yield of the emissive layer in nitrogen. b Emissive layer (EML) thickness. c Electroluminescence maxima. d Percent of spectral power at wavelengths above 700 nm. e Device maximum external quantum efficiency.
Dev 1	2	0.02 ± 0.01	1	541, 734	67	0.9 ± 0.1	1.54
Dev 2			2	765	89	0.8 ± 0.1	1.04
Dev 3			10	790	97	0.9 ± 0.1	1.19
Dev 4	4	0.03 ± 0.01	1	819	96	1.1 ± 0.1	1.33
Dev 5			2	817	95	1.2 ± 0.1	1.46
Dev 6			10	820	97	1.2 ± 0.1	1.31

---

The EML thickness used in NIR OLEDs involving neat films of platinum(II) complexes is typically ∼20–40 nm or more.^{12,13,19,25,29,33,60} We reasoned that, where the complex does not show sufficient charge carrier mobility for optimal performance, the use of a thinner EML could contribute to an increased device current, as well as reducing consumption of the precious metal-containing material. Devices featuring three different thicknesses of EML were therefore studied for each complex: 10, 2 and 1 nm. For both 2 and 4 as emitters, the resulting EL characteristics of the 10 and 2 nm OLEDs are very similar to one another, demonstrating the same efficiency and nearly identical spectra, as shown in Table 1 and Fig. 14. Indeed, amongst the three devices made using 4 as the emitter (Dev 4–6), even Device 4 with an EML of only 1 nm demonstrates similar characteristics to those of the other two (Devices 5 and 6 with 2 and 10 nm EMLs). These results suggest that the minimum practical EML thickness can be as low as 1–2 nm in this case. Such a strategy allows a reduction in the amount of platinum complex required of >90%, without compromising on efficiency and EL spectrum. The external quantum efficiency (EQE) of devices using complex 4 reaches 1.2 ± 0.1% at λ_EL = 817 nm with a maximum radiosity of 1.46 mW cm⁻² (Device 5). We note also that Devices 5 and 6 demonstrate negligible roll-off, with the EQE only dropping marginally to 0.90% at ∼100 mA cm⁻².

While there is very little variation in the EL spectra of the three devices made using complex 4 as the EML (i.e., Devices 4–6), those made using complex 2 as the emitter (Devices 1–3) show a substantial change in the EL spectrum with EML thickness. The PL spectra of Devices 2 and 3, with 2 and 10 nm EML, respectively, are similar to the EL spectrum of 2 in neat film. In contrast, for Device 1, with a 1 nm thick EML, the EL of the main NIR band is significantly blue shifted: λ_EL = 780, 765 and 734 nm for Devices 3, 2 and 1 respectively. Moreover, a new band emerges in Device 1 at λ_EL = 541 nm. The band at λ_EL = 734 nm in Device 1 closely matches the PL spectrum of 2 in PVK at 20% loading and is similar to the excimer PL in solution (Fig. 3 and 6), so we attribute it to a bimolecular excited species. The λ_EL = 541 nm band, however, does not match the unimolecular PL band observed in PVK films or in solution. An additional device (Device 7) was prepared using 5% 2 in mCP {1,3-bis(carbazol-9-yl)benzene} as the EML (Fig. S7.1, ESI‡), and similarly shows a band at λ_EL = 541 nm. We conclude that this band is indeed due to unimolecular emission of complex 2, but the difference between solution/PVK film and OLED may be related to the way 2 packs and interacts with mCP in a blend and at the TSBPA/PO-T2T interfaces in a vacuum-deposited film (finally, the shoulder at ∼500 nm in the electroluminescence spectrum of Device 1 is consistent with the known EL of the TSBPA:PO-T2T exciplex⁶¹).

The variation of the EL of devices containing different thicknesses of 2 can be rationalised as follows. We first note that all layers were deposited at a low evaporation rate of ∼0.1–0.3 Å s⁻¹, which effectively excludes the possibility of macroscopic heterogeneity of the layer (i.e., uneven coverage). However, while a 10 nm film thickness guarantees a full coverage of the underlying film, such an assumption becomes less reliable at an average thickness as low as 1–2 nm. Given the molecular dimensions of the studied platinum complexes of around 1 × 1 × 0.4 nm, it can be expected that mono- or bimolecular coverage should be the dominating mode in a 1–2 nm thick film, unless aggregation offers sufficient energetic advantage. With the thinning of the EML, it becomes less likely that the vacuum-deposited films of 2 will contain aggregates larger than dimers. Extending this reasoning, one would anticipate a smaller proportion of the higher aggregates in a 2 nm EML compared to one of 10 nm, and this prediction is indeed consistent with the blue shift of the EL λ_max in Device 2 vs. Device 3 (Table 1). In Device 1, the average layer thickness is so small that probably only bi- and monomolecular excited states can be formed. In areas between molecules of 2 in the film, direct contact between TSBPA and PO-T2T layers may become possible, leading to a small contribution of the aforementioned exciplex to the EL spectrum. On the other hand, complex 4 shows such a strong propensity to aggregation that preferential formation of aggregates probably occurs at any [average] layer thickness, leading to the EL spectrum being invariant with EML thickness.

Conclusions

Photoluminescence studies of complexes 1–4 in solution performed in this work give an insight into excimer kinetics, which is clearly important for further understanding and description of such systems when applied to OLED devices. TD-DFT calculations account for the experimental PL behaviour of excimers of the Pt(N^C^N)Cl class of complexes. In particular, they rationalise the hitherto purely empirical strategies for red- or blue-shifting the excimer PL. The similarity between trends in the excimer and unimolecular luminescence is explained by the HOMO and LUMO in the dimers, which show broadly similar localisation to those in the isolated molecules. The model also suggests that the molecules adopt an anti geometry in the excimer. Using the established theoretical model, we simulate T₁ geometry of trimer and tetramer of complex 4, which agree with the experimental PL in film. Our findings are likely to facilitate design of new excimer/dimer systems with a desired luminescence wavelength.

In terms of device fabrication, we propose the use of an extremely thin, 2 nm emissive layer as an alternative to the typical ∼20 nm thickness, to reduce the consumption of the platinum(II) complex in NIR OLEDs by >90%. This approach is especially important for aggregate emitters, where the long-wavelength PL and EL rely on pristine films of the organometallic compound. Efficient NIR OLEDs with EQE of 1.2% at λ_EL = 817 nm are obtained using complex 4 in 2 nm neat film as the EML, comparable to previous reports that utilised layers of ∼20–40 nm thickness. EML thickness is shown to be a powerful tool for controlling aggregation of emitter molecules: it offers an additional degree of flexibility in tuning device electroluminescence spectra.

Author contributions

P. P. – conceptualization, formal analysis, investigation, visualization, writing – original draft, writing – review & editing; A. S. – investigation (synthesis); R. J. S. – investigation (synthesis); C. W. H. – investigation (synthesis); M. T. W. – investigation (synthesis); D. Y. – investigation (X-ray diffraction); J. A. G. W. – conceptualization, funding acquisition, project administration, supervision, writing – review & editing; F. B. D. – funding acquisition, project administration, resources, validation, writing – original draft, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported, in part, by EPSRC, grant ref EP/S012788/1. We thank Durham University for additional support. Calculations have been carried out using resources provided by Wroclaw Centre for Networking and Supercomputing (https://wcss.pl), grant No. 555. This work made use of the facilities of the Hamilton HPC Service of Durham University.

Notes and references

1. A. Zampetti, A. Minotto and F. Cacialli, Adv. Funct. Mater., 2019, 29, 1807623.
2. M. Vasilopoulou, A. Fakharuddin, F. P. García de Arquer, D. G. Georgiadou, H. Kim, A. R. bin Mohd Yusoff, F. Gao, M. K. Nazeeruddin, H. J. Bolink and E. H. Sargent, Nat. Photonics, 2021, 15, 656–669.
3. A. K. East, M. Y. Lucero and J. Chan, Chem. Sci., 2021, 12, 3393–3405.
4. J. Huang and K. Pu, Chem. Sci., 2021, 12, 3379–3392.
5. Y. Liu, W. Hou, L. Xia, C. Cui, S. Wan, Y. Jiang, Y. Yang, Q. Wu, L. Qiu and W. Tan, Chem. Sci., 2018, 9, 7505–7509.
6. H. Xu, R. Chen, Q. Sun, W. Lai, Q. Su, W. Huang and X. Liu, Chem. Soc. Rev., 2014, 43, 3259–3302.
7. K. Li, G. S. Ming Tong, Q. Wan, G. Cheng, W.-Y. Tong, W.-H. Ang, W.-L. Kwong and C.-M. Che, Chem. Sci., 2016, 7, 1653–1673.
8. H. Yersin, A. F. Rausch, R. Czerwieniec, T. Hofbeck and T. Fischer, Coord. Chem. Rev., 2011, 255, 2622–2652.
9. Y. Zhang, Q. Li, M. Cai, J. Xue and J. Qiao, J. Mater. Chem. C, 2020, 8, 8484–8492.
10. B. Geffroy, P. le Roy and C. Prat, Polym. Int., 2006, 55, 572–582.
11. The Display Market, https://oled.com/oled-markets/oled-displays/, (accessed 19 October 2021).
12. K. Tuong, Ly, R. W. Chen-Cheng, H. W. Lin, Y. J. Shiau, S. H. Liu, P. T. Chou, C. S. Tsao, Y. C. Huang and Y. Chi, Nat. Photonics, 2017, 11, 63–68.
13. Y.-C. Wei, S. F. Wang, Y. Hu, L.-S. Liao, D.-G. Chen, K.-H. Chang, C.-W. Wang, S.-H. Liu, W.-H. Chan, J.-L. Liao, W.-Y. Hung, T.-H. Wang, P.-T. Chen, H.-F. Hsu, Y. Chi and P.-T. Chou, Nat. Photonics, 2020, 14, 570–577.
14. M. Ibrahim-Ouali and F. Dumur, Molecules, 2019, 24, 1412.
15. G. Cheng, Q. Wan, W. H. Ang, C. L. Kwong, W. P. To, P. K. Chow, C. C. Kwok and C. M. Che, Adv. Opt. Mater., 2019, 7, 1–7.
16. C. Cebrián and M. Mauro, Beilstein J. Org. Chem., 2018, 14, 1459–1481.
17. M. Z. Shafikov, R. Daniels, P. Pander, F. B. Dias, J. A. G. Williams and V. N. Kozhevnikov, ACS Appl. Mater. Interfaces, 2019, 11, 8182–8193.
18. K. R. Graham, Y. Yang, J. R. Sommer, A. H. Shelton, K. S. Schanze, J. Xue and J. R. Reynolds, Chem. Mater., 2011, 23, 5305–5312.
19. S. F. Wang, Y. Yuan, Y. C. Wei, W. H. Chan, L. W. Fu, B. K. Su, I. Y. Chen, K. J. Chou, P. T. Chen, H. F. Hsu, C. L. Ko, W. Y. Hung, C. S. Lee, P. T. Chou and Y. Chi, Adv. Funct. Mater., 2020, 30, 1–9.
20. J. R. Sommer, R. T. Farley, K. R. Graham, Y. Yang, J. R. Reynolds, J. Xue and K. S. Schanze, ACS Appl. Mater. Interfaces, 2009, 1, 274–278.
21. X. Yang, C. Yao and G. Zhou, Platinum Met. Rev., 2013, 57, 2–16.
22. K. Li, G. S. Ming Tong, Q. Wan, G. Cheng, W.-Y. Tong, W.-H. Ang, W.-L. Kwong and C.-M. Che, Chem. Sci., 2016, 7, 1653–1673.
23. D. Kim and J. L. Brédas, J. Am. Chem. Soc., 2009, 131, 11371–11380.
24. C. Sukpattanacharoen, P. Kumar, Y. Chi, N. Kungwan and D. Escudero, Inorg. Chem., 2020, 59, 18253–18263.
25. W. Chen, C. Sukpattanacharoen, W. Chan, C. Huang, H. Hsu, D. Shen, W. Hung, N. Kungwan, D. Escudero, C. Lee and Y. Chi, Adv. Funct. Mater., 2020, 30, 2002494.
26. Y. J. Cho, S. Y. Kim, H. J. Son, D. W. Cho and S. O. Kang, Phys. Chem. Chem. Phys., 2017, 19, 5486–5494.
27. M. T. Walden, P. Pander, D. S. Yufit, F. B. Dias and J. A. G. Williams, J. Mater. Chem. C, 2019, 7, 6592–6606.
28. M. Hruzd, N. le Poul, M. Cordier, S. Kahlal, J.-Y. Saillard, S. Achelle, S. Gauthier and F. Robin-le Guen, Dalton Trans., 2022, 51, 5546–5560.
29. M. Cocchi, J. Kalinowski, D. Virgili and J. A. G. Williams, Appl. Phys. Lett., 2008, 92, 113302.
30. S. F. Wang, L.-W. Fu, Y.-C. Wei, S.-H. Liu, J.-A. Lin, G.-H. Lee, P.-T. Chou, J.-Z. Huang, C.-I. Wu, Y. Yuan, C.-S. Lee and Y. Chi, Inorg. Chem., 2019, 58, 13892–13901.
31. S. Develay and J. A. G. Williams, Dalton Trans., 2008, 4562.
32. W. Xiong, F. Meng, H. Tan, Y. Wang, P. Wang, Y. Zhang, Q. Tao, S. Su and W. Zhu, J. Mater. Chem. C, 2016, 4, 6007–6015.
33. X. Yang, H. Guo, X. Xu, Y. Sun, G. Zhou, W. Ma and Z. Wu, Adv. Sci., 2019, 6, 1801930.
34. W. Lu, B.-X. Mi, M. C. W. Chan, Z. Hui, C.-M. Che, N. Zhu and S.-T. Lee, J. Am. Chem. Soc., 2004, 126, 4958–4971.
35. E. Rossi, A. Colombo, C. Dragonetti, D. Roberto, F. Demartin, M. Cocchi, P. Brulatti, V. Fattori and J. A. G. Williams, Chem. Commun., 2012, 48, 3182–3184.
36. E. Rossi, L. Murphy, P. L. Brothwood, A. Colombo, C. Dragonetti, D. Roberto, R. Ugo, M. Cocchi and J. A. G. Williams, J. Mater. Chem., 2011, 21, 15501–15510.
37. Z. Wang, E. Turner, V. Mahoney, S. Madakuni, T. Groy and J. Li, Inorg. Chem., 2010, 49, 11276–11286.
38. D. J. Cárdenas, A. M. Echavarren and M. C. Ramírez de Arellano, Organometallics, 1999, 18, 3337–3341.
39. S. J. Farley, D. L. Rochester, A. L. Thompson, J. A. K. Howard and J. A. G. Williams, Inorg. Chem., 2005, 44, 9690–9703.
40. D. L. Rochester, S. Develay, S. Záliš and J. A. G. Williams, Dalton Trans., 2009, 1728.
41. J. B. Birks, D. J. Dyson and I. H. Munro, Proc. R. Soc. London, Ser. A, 1963, 275, 575–588.
42. A. Iwakiri, Y. Konno and K. Shinozaki, J. Lumin., 2019, 207, 482–490.
43. M. Cocchi, J. Kalinowski, V. Fattori, J. A. G. Williams and L. Murphy, Appl. Phys. Lett., 2009, 94, 073309.
44. P. Pander, A. V. Zaytsev, A. Sil, J. A. G. Williams, P.-H. Lanoe, V. N. Kozhevnikov and F. B. Dias, J. Mater. Chem. C, 2021, 9, 10276–10287.
45. P. Pander, R. Daniels, A. V. Zaytsev, A. Horn, A. Sil, T. J. Penfold, J. A. G. Williams, V. N. Kozhevnikov and F. B. Dias, Chem. Sci., 2021, 12, 6172–6180.
46. H. Nakanotani, T. Higuchi, T. Furukawa, K. Masui, K. Morimoto, M. Numata, H. Tanaka, Y. Sagara, T. Yasuda and C. Adachi, Nat. Commun., 2014, 5, 4016.
47. O. V. Mikhnenko, P. W. M. Blom and T.-Q. Nguyen, Energy Environ. Sci., 2015, 8, 1867–1888.
48. D. Zhang, X. Song, M. Cai and L. Duan, Adv. Mater., 2018, 30, 1705250.
49. P. Pander, R. Bulmer, R. Martinscroft, S. Thompson, F. W. Lewis, T. J. Penfold, F. B. Dias and V. N. Kozhevnikov, Inorg. Chem., 2018, 57, 3825–3832.
50. P. Pander, S. Gogoc, M. Colella, P. Data and F. B. Dias, ACS Appl. Mater. Interfaces, 2018, 10, 28796–28802.
51. R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164.
52. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(e1327), 1.
53. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
54. S. Lehtola, C. Steigemann, M. J. T. Oliveira and M. A. L. Marques, SoftwareX, 2018, 7, 1–5.
55. W. Lu, M. C. W. Chan, N. Zhu, C.-M. Che, C. Li and Z. Hui, J. Am. Chem. Soc., 2004, 126, 7639–7651.
56. S. Chakraborty, A. Aliprandi and L. De Cola, Chem. – Eur. J., 2020, 26, 11007–11012.
57. J. M. Younker and K. D. Dobbs, J. Phys. Chem. C, 2013, 117, 25714–25723.
58. J. Kang, X. Zhang, H. Zhou, X. Gai, T. Jia, L. Xu, J. Zhang, Y. Li and J. Ni, Inorg. Chem., 2016, 55, 10208–10217.
59. A. J. Goshe, I. M. Steele and B. Bosnich, Inorg. Chim. Acta, 2004, 357, 4544–4551.
60. J. Kalinowski, M. Cocchi, L. Murphy, J. A. G. Williams and V. Fattori, Chem. Phys., 2010, 378, 47–57.
61. M. Chapran, P. Pander, M. Vasylieva, G. Wiosna-Salyga, J. Ulanski, F. B. Dias and P. Data, ACS Appl. Mater. Interfaces, 2019, 11, 13460–13471.

---

Footnotes

† Our supporting research data is available from the Durham Research Online DATAsets Archive (DRO-DATA) open data repository. DOI: http://doi.org/10.15128/r1mc87pq328

‡ Electronic supplementary information (ESI) available: Synthetic details and characterisation of new materials; X-ray diffraction and crystal data; further information on the equipment and methods for theory, photophysical characterisation, electrochemistry, and OLED devices. CCDC 2063390 (2-CHCl₃) and 2164616–2164618. (2-MeOH, 3, and 4). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2tc01511k

---