Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Discovery of superconductivity in Nb4SiSb2 with a V4SiSb2-type structure and implications of interstitial doping on its physical properties†
Manuele D.
Balestra
 ab,
Omargeldi
Atanov
ab,
Omargeldi
Atanov
 c,
Robin
Lefèvre
c,
Robin
Lefèvre
 b,
Olivier
Blacque
b,
Olivier
Blacque
 b,
Yat Hei
Ng
c,
Rolf
Lortz
c and
Fabian O.
von Rohr
b,
Yat Hei
Ng
c,
Rolf
Lortz
c and
Fabian O.
von Rohr
 *a
*a
aDepartment of Quantum Matter Physics, University of Geneva, CH-1211 Geneva, Switzerland. E-mail: fabian.vonrohr@unige.ch
bDepartment of Chemistry, University of Zürich, CH-8057 Zürich, Switzerland
cDepartment of Physics, The Hong Kong University of Science and Technology, Clear Water Bay Kowloon, Hong Kong
First published on 29th July 2022
Abstract
We report on the discovery, structural analysis, and the physical properties of Nb4SiSb2 – a hitherto unknown compound crystallizing in the V4SiSb2-type structure with the tetragonal space group I4/mcm and unit cell parameters a = 10.3638(2) Å and c = 4.9151(2) Å. We find Nb4SiSb2 to be a metal undergoing a transition to a superconducting state at a critical temperature of Tc ≈ 1.6 K. The bulk nature of the superconductivity in this material is confirmed by the observation of a well defined discontinuity in specific heat with a normalized specific heat jump of ΔC(Tc)/γTc = 1.33 mJ mol−1 K−2. We find that for Nb4SiSb2, the unoccupied sites on the 4b Wyckoff position can be partially occupied with Cu, Pd, or Pt. Low-temperature resistivity measurements show transitions to superconductivity for all three compounds at Tc ≈ 1.2 K for Nb4Cu0.2SiSb2, and Tc ≈ 0.8 K for Nb4Pd0.2SiSb2 as well as for Nb4Pt0.14SiSb2. The addition of electron-donor atoms into these void positions, henceforth, lowers the superconducting transition temperature in comparison to the parent compound.
1 Introduction
A promising approach for the discovery of new superconducting materials is based on the substitution or incorporation of elements into existing structures with crystallographic void positions. Substituting or incorporating atoms into a structure allows for the precise chemical modification of the density of electronic states at the Fermi-level. This may induce superconductivity or tune superconducting properties.1–5 Recent examples of this include the increase in the superconducting transition temperature of Nb5Ge3 – in the tetragonal Cr5B3 type-structure – from Tc ≈ 0.7 K to 15.3 K by the incorporation of carbon atoms into void positions,6 or the stabilization of η-carbide superconductors in a filled Ti2Ni-type structure, with remarkably high upper critical fields.4,7The results presented in this paper refer to structures, crystallizing in a defect variant of the W5Si3-type structure, commonly known as the V4SiSb2 structure. The W5Si3 structure itself exhibits the tetragonal space group I4/mcm8 and is a bulk superconductor with a critical temperature of Tc = 2.7 K.9 Other compounds crystallizing in the same structure-type and exhibiting superconducting properties are Nb5Si3 with a critical temperature of Tc = 0.7 K,10 and the ternary W5Si3-type compounds Nb5Sn2Ga, Ta5SnGa2, and Zr5Sb2.36Ru0.36 with critical temperatures of Tc ≈ 1.8 K, 1.8 K, and 5 K, respectively.11–13 In the V4SiSb2 structure, the 4b Wyckoff position of the W5Si3 structure is unoccupied, forming void channels along the c-direction. These channels are filled by Sb centred, essentially unhybridized 5p orbitals forming a 2D net stacking along the c-direction leading to “electron-filled” voids.14 The prospect of intercalating these voids with electrophilic species has been theoretically proposed by Rytz et al.14
To date, only six compounds have been reported to crystallize in this structure-type, namely V4SiSb2 and the compound series of Ti4TBi2 with (T = Cr, Mn, Fe, Co, Ni). All of these compounds are known to be non-magnetic metals.15,16 Furthermore, 5 pseudo-quaternary antimonides with the general formula Nb4Pd0.5ZSb2 with Z = Cr, Fe, Co, Ni, Si have been reported.17 These compounds contain three transition metals in an ordered arrangement; hence they are isostructural to each other and crystallize in substitutional variants of the W5Si3-type structure, or alternatively, they can be interpreted as V4SiSb2-type compounds with half occupied channels.
Here, we report on the discovery of the compound Nb4SiSb2, which crystallizes in a V4SiSb2-type structure with the tetragonal space group I4/mcm. We show that this material exhibits bulk superconductivity at a critical temperature of Tc ≈ 1.6 K. Furthermore, we find that the 4b Wyckoff void position can be partially occupied by the transition metals Cu, Pd or Pt, leading to the compounds Nb4Cu0.2SiSb2, Nb4Pd0.2SiSb2, and Nb4Pt0.14SiSb2. All three compounds are bulk superconductors with critical temperatures of Tc ≈ 1.2 K, 0.8 K, and 0.8 K, respectively.
2 Experimental
Synthesis
Polycrystalline samples of all compounds were obtained by solid state reaction of the pressed elemental powders at high temperatures. These were synthesized using pure elements as received and stored in air of niobium (powder, 99.99%, Alfa Aesar), silicon (pieces, 99.95%, Alfa Aesar), antimony (shots, 99.999%, Alfa Aesar), copper (powder, 99.7%, Merck), palladium (powder, 99.999%, Acros Organics) and platinum (powder, 99.999%, Acros Organics). The elements were thoroughly mixed and ground in their stoichiometric ratios, then pressed into pellets, and subsequently sealed in quartz ampoules under 400 mbar of Ar. The quartz ampoules were heated to T = 1100 °C with a heating rate of 180 °C h−1, and annealed at this temperature for 7 days.Diffraction
Single crystal X-ray diffraction (SXRD) data were collected at T = 160(1) K on a Rigaku XtaLAB Synergy, Dualflex, Pilatus 200K diffractometer using a monochromatic X-ray source (Cu Kα1 radiation: λ = 1.54184 Å) from a micro-focus sealed X-ray tube and cooled using an Oxford liquid–nitrogen Cryostream device. The selected suitable single crystals were mounted using polybutene oil. Pre-experiment, data collection, data reduction and analytical absorption correction18 were performed with the program suite CrysAlisPro. Using Olex2,19 the structure was solved with the SHELXT20 small molecule structure solution program and refined with the SHELXL2018/3 program package21 by full-matrix least-squares minimization on F2. PLATON22 was used to check the result of the X-ray analysis. CCDC 2166026 (for Nb4Cu0.2SiSb2), 2166027 (for Nb4Pd0.2SiSb2), 2166028 (for Nb4Pt0.14SiSb2) and 2166029 (for Nb4SiSb2).†Powder X-ray diffraction (PXRD) measurements were performed on a Rigaku SmartLab diffractometer using a Cu X-ray source (Kα1 = 1.540600 Å, Kα2 = 1.544430 Å) with CuKβ filter and collected using a 2θ range of 5–100°. The machine is equipped with a 3 kW sealed X-ray tube, CBO optics and a D/teX Ultra 250 silicon strip detector. Data was recorded using the SmartLab Studio II software. Rietveld refinements were performed using the FULLPROF software package23 and fitting of the diffracted data was done using the Thompson-Cox-Hastings pseudo-Voigt function with asymmetry correction.24
Physical properties
Physical property measurements were carried out on sintered, flat pellets. Temperature-dependent resistivity measurements were performed with a Quantum Design Physical Property Measurement System (PPMS) using a He-3 insert for temperature measurements down to 500 mK. A four-point resistivity measurement method, using silver wires (50 μm diameter) was employed.Specific heat measurements were performed from 300 mK to 2 K in a He-3 15 T magnet cryostat with a custom-developed modulated-temperature AC calorimetry technique using an SR830 digital lock-in amplifier, and from 2–10 K with a long relaxation technique in a He-4 cryostat. For the latter, each relaxation provides about 1000 data points over a temperature interval of 30–40% of the base temperature, which has been varied between 2 K and 10 K. The relaxation technique provides a high precision up to 1% while the AC technique is less accurate but provides high resolutions of ΔC/C of 10−5 at a high density of data points.25 Temperature-dependent magnetization measurements were performed using a Quantum Design Magnetic Properties Measurement System (MPMSXL) equipped with a reciprocating sample option (RSO) and a 7 T magnet.
3 Results and discussion
3.1 Crystal Structure of Nb4SiSb2
In Fig. 1a and b, we present the crystal structure and the unit cell of the single-crystal refinement of Nb4SiSb2, shown along the c-direction and along the b-direction, respectively. The structure of Nb4SiSb2 was determined by means of single crystal X-Ray diffraction (SXRD) at 160 K and the elemental composition was confirmed using EDX analysis at ambient temperature (ESI†).We find Nb4SiSb2 to crystallize in the tetragonal space group I4/mcm with the lattice parameters a = b = 10.3638(2) Å and c = 4.9151(2) Å with the corresponding calculated cell volume of V = 527.92(3) Å3. Hence, it is found to adopt the same centrosymmetric structure type that was previously reported for V4SiSb2.15,16 The crystallographic data and the details of the structure refinement are summarised in Table 1. All crystallographic positions as well as the anisotropic displacement parameters are presented in Table 2.
| Parameters | Nb4SiSb2 | Nb4Cu0.2SiSb2 | Nb4Pd0.2SiSb2 | Nb4Pt0.14SiSb2 |
|---|---|---|---|---|
| Crystal system | Tetragonal | Tetragonal | Tetragonal | Tetragonal |
| Structure-type | V4SiSb2 | W5Si3(defect) | W5Si3(defect) | W5Si3(defect) |
| Space group | I4/mcm (No. 140) | I4/mcm (No. 140) | I4/mcm (No. 140) | I4/mcm (No. 140) |
| Absorption correction method | Analytical | Analytical | Spherical | Analytical |
| Temperature [K] | 160(1) | 160(1) | 160(1) | 160(1) |
| Lattice parameters [Å] | a = 10.3638(2) | a = 10.3954(2) | a = 10.3991(2) | a = 10.3803(2) |
| c = 4.9151(2) | c = 4.9233(2) | c = 4.93619(16) | c = 4.9348(2) | |
| Cell volume [Å3] | 527.92(3) | 532.03(3) | 533.81(3) | 531.73(3) |
| Formula unit/cell | 4 | 4 | 4 | 4 |
| ρ calcd [g cm−3] | 8.093 | 8.189 | 8.268 | 8.376 |
| μ [mm−1] | 149.393 | 532.03(3) | 153.021 | 155.001 |
| Crystal size [mm] | 0.018 × 0.016 × 0.013 | 0.005 × 0.003 × 0.002 | 0.01 × 0.01 × 0.01 | 0.015 × 0.015 × 0.01 |
| F(000) | 1120.0 | 1143.0 | 1157.0 | 1164.0 |
| Radiation type | Cu Kα (λ = 1.54184) | Cu Kα (λ = 1.54184) | Cu Kα (λ = 1.54184) | Cu Kα (λ = 1.54184) |
| 2Θ range [°] | 12.078 to 146.58 | 12.04 to 148.58 | 12.036 to 147.576 | 12.058 to 147.716 |
| Index range | h[−9,12] | h[−11,9] | h[−11,12] | h[−12,12] |
| k[−12,12] | k[−12,12] | k[−12,12] | k[−12,12] | |
| l[−5,6] | l[−6,6] | l[−6,5] | l[−6,5] | |
| Observed reflections | 1466 | 838 | 2368 | 2381 |
| Independent reflections (2σ) | 165 | 166 | 166 | 167 |
| R int | 0.0278 | 0.0385 | 0.0312 | 0.0298 |
| R σ | 0.0127 | 0.0314 | 0.0107 | 0.0117 |
| Refined parameters | 14 | 16 | 16 | 17 |
| GOF | 1.363 | 1.142 | 1.252 | 1.240 |
| R 1 (all data) (%) | 1.69 | 3.33 | 1.64 | 1.60 |
| wR1 (≥2σ) (%) | 1.69 | 2.96 | 1.62 | 1.57 |
| wR2 (all data) (%) | 4.32 | 7.53 | 3.71 | 3.67 |
| wR2 (≥2σ) (%) | 4.33 | 7.37 | 3.71 | 3.66 |
| Max/min residual electron density [e Å−3] | 1.41/−0.94 | 1.12/−1.52 | 0.97/−0.98 | 1.13/−0.85 |
| Atom | Wyckoff symbol | x | y | z | U(eq) [Å2] | U 11/U22 | U 33 | U 12 | Occ. |
|---|---|---|---|---|---|---|---|---|---|
| Nb4SiSb2 | |||||||||
| Nb | 16k | 0.29305(6) | 0.58530(6) | 1/2 | 0.0111(3) | 10.6(4)/10.9(4) | 11.8(4) | 0.2(2) | 4.00 |
| Si | 4a | 1/2 | 1/2 | 3/4 | 0.0122(3) | 10.1(11)/10.1(11) | 16(2) | 0 | 1.00 |
| Sb | 8h | 0.14037(5) | 0.35963(5) | 1/2 | 0.0119(9) | 11.8(3)/11.8(3) | 13.0(5) | −1.5(3) | 2.00 |
| Nb4Cu0.2SiSb2 | |||||||||
| Nb | 16k | 0.29297(9) | 0.41603(9) | 1/2 | 0.0080(4) | 6.2(6)/6.4(6) | 11.4(6) | 0.3(4) | 4.00 |
| Cu | 4b | 0 | 1/2 | 3/2 | 0.021(7) | 24(8)/24(8) | 16(12) | 0 | 0.199(16) |
| Si | 4a | 1/2 | 1/2 | 3/2 | 0.0063(12) | 3.2(17)/3.2(17) | 12(3) | 0 | 1.00 |
| Sb | 8h | 0.14385(8) | 0.35615(2) | 1/2 | 0.0110(4) | 8.8(5)/8.8(5) | 15.3(7) | 2.3(4) | 2.00 |
| Nb4Pd0.2SiSb2 | |||||||||
| Nb | 16k | 0.29305(4) | 0.58369(4) | 1/2 | 0.0125(2) | 12.1(3)/12.8(3) | 12.7(3) | −0.01(17) | 4.00 |
| Pd | 4b | 0 | 1/2 | 1/4 | 0.0147(15) | 13.6(16)/13.6(16) | 17(2) | 0 | 0.199(5) |
| Si | 4a | 1/2 | 1/2 | 3/2 | 0.0131(6) | 13.1(8)/13.1(8) | 13.0(14) | 0 | 1.00 |
| Sb | 8h | 0.14470(4) | 0.35530(4) | 1/2 | 0.0170(2) | 15.8(2)/15.8(2) | 19.5(3) | −3.5(2) | 2.00 |
| Nb4Pt0.14SiSb2 | |||||||||
| Nb | 16k | 0.58429(5) | 0.29284(5) | 1/2 | 0.0063(2) | 6.3(3)/6.2(3) | 6.5(4) | −0.08(18) | 4.00 |
| Pt | 4b | 1/2 | 0 | 3/2 | 0.0122(5) | 12.5(17)/12.5(17) | 12(3) | 0 | 0.140(3) |
| Si | 4a | 1/2 | 1/2 | 3/2 | 0.0020(6) | 2.7(8)/2.7(8) | 0.7(16) | 0 | 1.00 |
| Sb | 8h | 0.35697(4) | 0.14303(4) | 1/2 | 0.0101(3) | 9.0(3)/9.0(3) | 12.5(4) | −3.1(2) | 2.00 |
In the structure of Nb4SiSb2 each atom occupies one atomic site: the niobium atoms are located at the 16k Wyckoff position, silicon occupies the 4a and antimony the 8h Wyckoff positions. Silicon forms thereby columns which can be interpreted as ∞[Nb8/2Si] chains along the c-direction as shown in Fig. 1(c). The Si–Si bonding distance in Nb4SiSb2 within the columns is 2.4576(1) Å, which is in good agreement with the ones found in V4SiSb215 and comparable to Si–Si bond distances in similar structures.17,26 Each Si atom is surrounded by eight Nb atoms with a distance of 2.6252(6) Å forming antiprisms with the surrounding neighbour atoms. Nb has a coordination number (CN) of 13 consisting of six Nb neighbours located in the ∞[Nb8/2Si] column, one Nb in the adjacent ∞[Nb8/2Si] column, two Si, and four Sb neighbours located in between the two columns. The Nb–Nb distances range from 3.0275(8) to 3.2807(9) Å. These distances, together with the relatively short intercolumn distance between two Nb atoms of 3.0449(13) Å are in good agreement with distances found in comparable structures.27,28 Also, the Nb-Sb distance ranging from 2.8238(7) Å to 2.9781(4) Å is in good agreement with the distances found in the related compounds, such as e.g. in Nb5Sb4.28 Each Sb has eight Nb neighbours and therefore a CN of 8. Another feature of this structure are the voids at the 4b Wyckoff position. These void positions are surrounded by four Sb atoms. These form void channels along the c-direction. If these void positions were fully occupied, then the V4SiSb2 structure would be equivalent to the W5Si3 structure.15
The validity of the structural model, the phase purity, and the homogeneity of the sample were confirmed by means of PXRD at ambient temperature and SXRD at 160 K. The reliability factors of the SXRD refinement can be found in the ESI.† In Fig. 3(d) the PXRD pattern of the polycrystalline sample is shown, with its respective Rietveld refinement. We find the lattice parameters of a = b = 10.3686(4) Å, and c = 4.9193(2) Å, as well as a calculated cell volume of V = 528.86(3) Å3. Hence, the SXRD and PXRD refinements and structural solutions are in excellent agreement with each other (ESI†).
3.2 Superconducting properties of Nb4SiSb2
In Fig. 2(a), we show the temperature-dependant resistivity of Nb4SiSb2 in zero field μ0H = 0T as ρ(T) between T = 300 K and 500 mK (inset) and in the vicinity of the superconducting transition. A sharp drop in the resistivity is observed at low temperature, corresponding to a transition to a superconducting state. The transition midpoint of Tc,mid ≈ 1.65 K and reaches a state of zero resistance at Tzero ≈ 1.56 K. The transition is comparably sharp with a transition width of ΔT = 0.18 K in the resistivity. The residual resistivity ρ(1.8 K) = 0.14 mΩ cm at 1.8 K and the room temperature resistivity value of ρ(300 K) = 2.06 mΩ cm, result in a residual resistivity ratio (RRR) here defined as RRR = ρ(300 K)/ρ(1.8 K) = 14.96. This RRR value corresponds to the value of a good metal.The bulk nature of the superconductivity in Nb4SiSb2 is confirmed by low-temperature specific-heat measurements. Temperature-dependent specific-heat measurements are of particular importance to prove the bulk nature of a superconductor.29,30
In Fig. 2(b), we present the temperature-dependent specific heat C(T)/T of Nb4SiSb2 in a temperature range between T = 600 mK and 2 K. We find a clearly pronounced discontinuity in the specific heat, resulting from the superconducting transition. The data was fitted using the α-model.31,32 Thereby, an entropy conserving construction was used to determine the critical temperature, Tc ≈ 1.6 K. This value is in good agreement with the critical temperature from the resistivity measurement. From the α-model fit, we obtained α = 1.7 and the Sommerfeld constant of γ = 9.00 mJ mol−1 K−2. We find a ratio for the normalized specific-heat jump of ΔC/γTc = 1.33 mJ mol−1 K−2, which confirms the bulk nature of the superconductivity, as this value is close to the weak-coupling BCS ratio of 1.43. This corresponds to a value of the superconducting gap of 2Δ(0) = 3.4kBTc.
Under the assumption of a degenerate electron gas of non-interacting particles, the electronic contribution to the heat capacity in a solid at low temperatures is proportional to the density of states at the Fermi level D(EF) and linear in T. With the previously determined value of γ = 9.00 mJ mol−1 K−2, the density of states at the Fermi level can be calculated as described by F. Heiniger et al.33 according to
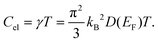 | (1) |
We obtain for Nb4SiSb2 a density of states at the Fermi level of D(EF) = 3.8 states eV−1.
Magnetic susceptibility measurements of Nb4SiSb2 were conducted in the normal-state, i.e. in a temperature range between T = 10 K to 300 K, in an external field of μ0H = 1 T. The observed temperature-independent positive magnetic moment corresponds to a Pauli-paramagnet (see ESI†). A summary of all obtained physical parameters can be found in Table 3.
| Parameter | Units | Nb4SiSb2 | Nb4Cu0.2SiSb2 | Nb4Pd0.2SiSb2 | Nb4Pt0.14SiSb2 |
|---|---|---|---|---|---|
| T c,resistivity | K | 1.65 | 1.16 | 0.76 | 0.84 |
| T c,specificheat | K | 1.59 | — | — | — |
| RRR | — | 14.96 | 4.54 | 1.56 | 1.70 |
| ρ(300) | mJ Ω cm | 2.06 | 0.70 | 8.46 | 2.49 |
| ρ 0 | mJ Ω cm | 0.13 | 0.15 | 5.43 | 1.46 |
| Type of magnetism | — | Pauli-paramagnetic | Pauli-paramagnetic | Pauli-paramagnetic | Pauli-paramagnetic |
| γ | mJ mol−1 K−2 | 9.00 | 7.5 | — | |
| ΔC/Tcγ | — | 1.33 | 1.2 | — | |
| 2Δ(0) | meV | 0.47 | 12 | — | |
| D(EF) | States eV−1 per f.u. | 3.82 | 3.18 | — |
3.3 Crystal Structures of Nb4Cu0.2SiSb2, Nb4Pd0.2SiSb2, and Nb4Pt0.14SiSb2
We have synthesized the three compounds Nb4Cu0.2SiSb2, Nb4Pd0.2SiSb2, and Nb4Pt0.14SiSb2. Here, the void 4b Wyckoff positions in Nb4SiSb2 are partially filled with a transition metal M = Cu, Pd, or Pt, respectively. In Fig. 3, we show a schematic representation of the unit cell along the c-direction and a high symmetry-direction of Nb4MxSiSb2, where M = Cu, Pt and Pd with x = 0.2, 0.14 and 0.2. The crystal structures of all three compounds were determined using SXRD at 160 K and PXRD diffraction at room temperature.All samples were found to be single phase by means of PXRD measurements and corresponding Rietveld refinements (ESI†). Atomic compositions were confirmed using EDX analysis (ESI†).
All three structures are in good agreement with the previously reported structure for Nb4Pd0.5ZSb2 with Z = Cr, Fe, Co, Ni, Si, where it was thought that a half-occupied Pd 4b site was necessary to stabilize these compounds.17 In contrary to this previous assumption, we found here that the channels were in our case either unoccupied or filled with 0.2 or 0.14 respectively (in case of Pt), independent of the initially used starting stoichiometry. These results indicate that, with improved synthesis methodologies, the continuous solid solution might be accessible in the future. All information regarding the lattice parameters, crystallographic data, and details of the structure refinements are summarized in Table 1.
3.4 Electronic properties of Nb4Cu0.2SiSb2, Nb4Pd0.2SiSb2 and Nb4Pt0.14SiSb2
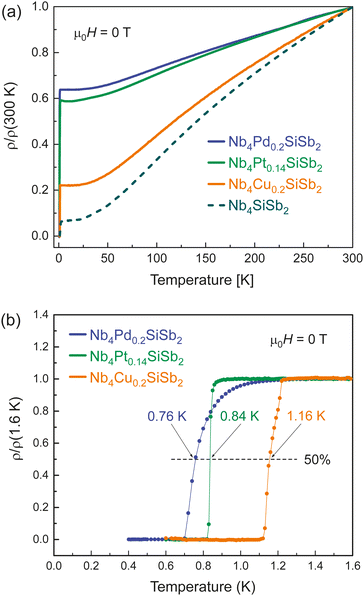
In Fig. 4 we present the temperature-dependent resistivity and the normalized low-temperature resistivity ρ(T)/ρ(1.6K) in a temperature range between T = 400 mK and 1.6 K for Nb4Cu0.2SiSb2, Nb4Pd0.2SiSb2 and Nb4Pt0.14SiSb2, measured in zero field μ0H = 0 T.We find all three compounds to undergo a transition to a superconducting state at low temperatures. The critical temperature midpoints are determined as Tc,mid ≈ 1.16 K for Nb4Cu0.2SiSb2, Tc,mid ≈ 0.76 K for Nb4Pd0.2SiSb2 and Tc,mid ≈ 0.84 K for Nb4Pt0.14SiSb2. All three compounds with atoms in the void position of Nb4SiSb2 have lower transition temperatures than the parent compound.
For comparison, we have performed specific heat measurements in the normal state of Nb4SiSb2 and Nb4Pt0.14SiSb2 (shown in the ESI†). For Nb4SiSb2 we find values for γn and β of 8.40 mJ mol−1 K−2 and 0.16 mJ mol−1 K−4, respectively. The γn value of this fit is in good agreement with the more accurate low-temperature value discussed above. For Nb4Pt0.14SiSb2 we find values for γn and β of 9.10 mJ mol−1 K−2 and 0.31 mJ mol−1 K−4, respectively. We note that the values for γn differ only slightly, indicating a small change of the electronic properties upon void position filling. We find, however, that β changes quite strongly. These findings indicate that the decrease of the superconducting transition temperature is likely caused by a change in the phonons, and the vibrations, respectively.
Nb4Pd0.2SiSb2 has the lowest critical temperature of the doped compounds, as well as the lowest RRR value of RRR = ρ(300 K)/ρ(1.8 K) = 1.56. Nb4Cu0.2SiSb2 with RRR = 4.54 and Nb4Pt0.14SiSb2 with RRR = 1.70 follow the descending trend observed for the critical temperatures accordingly. These low RRR values correspond to a poor metallic behaviour and are 3 to 24 times smaller than the RRR of the parent compound Nb4SiSb2. The pronounced effect on the physical properties on void position doping becomes clearly apparent in the large change of the RRR values. The nature of the change is, however, not only affected by the electronic states, but also by the phonons and by impurity state scattering.
4 Conclusion
We have reported on the discovery of the centrosymmetric structure compound Nb4SiSb2. This phase was found to crystallize in the tetragonal V4SiSb2-type structure. We found Nb4SiSb2 to undergo a transition to a superconducting state at a critical temperature of Tc ≈ 1.6 K. The bulk nature of the superconducting transition was evidenced by a clear discontinuity in specific heat, with a normalized specific heat jump of ΔC(Tc)/γTc = 1.33 mJ mol−1 K−2, close to the weak-coupling BCS value. Furthermore, we have shown that the unoccupied 4b Wyckoff site in Nb4SiSb2 can be partially occupied with the transition metals Cu, Pd, or Pt.These compounds crystallize in a tetragonal variant of the W5Si3-type structure with partially occupied channels, extending along the c-direction. All three compounds were found to be superconductors with transitions temperatures of Tc ≈ 1.2 K for Nb4Cu0.2SiSb2, Tc ≈ 0.8 K for Nb4Pd0.2SiSb2 and Tc ≈ 0.8 K for Nb4Pt0.14SiSb2. We find that the insertion of a host atom into the void positions strongly affects the electronic and superconducting properties of this material.
Hence, our results indicate that this and related compounds might be promising host structures for the discovery of new superconducting materials, as they allow for a controlled manipulation of the electronic and phononic properties by chemical manipulation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Swiss National Science Foundation under Grant No. PCEFP2_194183 and by grants from the Research Grants Council of the Hong Kong Special Administrative Region, China (GRF-16302018 & C6025-19G-A).Notes and references
- D. Yazici, K. Huang, B. D. White, I. Jeon, V. W. Burnett, A. J. Friedman, I. K. Lum, M. Nallaiyan, S. Spagna and M. B. Maple, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, B 87, 1–8 Search PubMed.
- Y. Zhang, B. Wang, Z. Xiao, Y. Lu, T. Kamiya, Y. Uwatoko, H. Kageyama and H. Hosono, npj Quantum Mater., 2017, 2, 45 CrossRef.
- J. Akimitsu, Proc. Jpn. Acad. Ser. B Phys. Biol. Sci., 2019, 95, 321–342 CrossRef CAS PubMed.
- K. Ma, K. Gornicka, R. Lefèvre, Y. Yang, H. M. Rønnow, H. O. Jeschke, T. Klimczuk and F. O. von Rohr, ACS Mater. Au, 2021, 1, 55–61 CrossRef CAS.
- B. Wang, Y. Zhang, S. Xu, K. Ishigaki, K. Matsubayashi, J.-G. Cheng, H. Hosono and Y. Uwatoko, Chin. Phys. B, 2019, 28, 107401 CrossRef CAS.
- A. D. Bortolozo, C. A. Dos Santos, R. F. Jardim, C. Ritter, A. Devishvili, M. Rotter, F. G. Gandra and A. J. MacHado, J. Appl. Phys., 2012, 111, 1–6 CrossRef.
- K. Ma, R. Lefèvre, K. Gornicka, H. O. Jeschke, X. Zhang, Z. Guguchia, T. Klimczuk and F. O. von Rohr, Chem. Mater., 2021, 33, 8722–8732 CrossRef CAS.
- B. Aronsson, O. Tjomsland, R. Lundén and H. Prydz, Acta Chem. Scand., 1955, 9, 1107–1110 CrossRef CAS.
- K. Kawashima, T. Muranaka, Y. Kousaka, S. Akutagawa and J. Akimitsu, J. Phys.: Conf. Ser., 2009, 150, 1–4 CrossRef.
- J. O. Willis, J. Appl. Phys., 1979, 50, 2863–2865 CrossRef CAS.
- T. Shishido, K. Ukei, N. Toyota, T. Sasaki, Y. Watanabe, K. Motai, T. Fukuda, H. Takeya and H. Takei, J. Cryst. Growth, 1989, 96, 1–6 CrossRef CAS.
- T. Shishido, J. Ye, N. Toyota, K. Ukei, T. Sasaki, H. Horiuchi and T. Fukuda, Jpn. J. Appl. Phys., 1989, 28, 1519–1520 CrossRef CAS.
- W. Xie, H. Luo, B. F. Phelan and R. J. Cava, J. Mater. Chem. C, 2015, 3, 8235–8240 RSC.
- R. Rytz and R. Hoffmann, Inorg. Chem., 1999, 38, 1609–1617 CrossRef CAS.
- P. Wollesen and W. Jeitschko, J. Alloys Compd., 1996, 243, 67–69 CrossRef CAS.
- G. C. Richter, W. Jeitschko, B. Künnen and H. M. Gerdes, Inorg. Chem., 1997, 133, 400–406 Search PubMed.
- M. Wang, W. C. Sheets, R. McDonald and A. Mar, Inorg. Chem., 2001, 40, 5199–5205 CrossRef CAS PubMed.
- R. Clark and J. Reid, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 887–897 CrossRef.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct, Chem., 2015, 71, 3–8 Search PubMed.
- A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed.
- J. Rodrguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef.
- L. Finger, D. Cox and A. Jephcoat, J. Appl. Crystallogr., 1994, 27, 892–900 CrossRef CAS.
- H. K. Mak, P. Burger, L. Cevey, T. Wolf, C. Meingast and R. Lortz, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 214523 CrossRef.
- M. E. Badding and F. J. DiSalvo, Inorg. Chem., 1990, 29, 3952–3954 CrossRef CAS.
- S. Janger and S. E. Rasmussen, Acta Crystallogr., 1975, B31, 2881–2883 Search PubMed.
- Y. F. Lomnytska and Y. B. Kuz'ma, J. Alloys Compd., 2006, 413, 114–117 CrossRef CAS.
- E. M. Carnicom, W. Xie, Z. Yang, K. Górnicka, T. Kong, T. Klimczuk and R. J. Cava, Chem. Mater., 2019, 31, 2164–2173 CrossRef CAS.
- C. Witteveen, K. Górnicka, J. Chang, M. Månsson, T. Klimczuk and F. O. von Rohr, Dalton Trans., 2021, 50, 3216–3223 RSC.
- H. Padamsee, J. E. Neighbor and C. A. Shiffman, J. Low Temp. Phys., 1973, 12, 387–411 CrossRef CAS.
- D. C. Johnston, Supercond. Sci. Technol., 2013, 26, 1–19 CrossRef.
- F. Heiniger, E. Bucher and J. Muller, Phys. der Kondens. Mater., 1966, 5, 243–284 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2166026–2166029. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2tc01510b |
| This journal is © The Royal Society of Chemistry 2022 |