Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pressure-induced non-radiative losses in halide perovskite light-emitting diodes†‡
Young-Kwang
Jung§
 a,
Mayami
Abdulla§
b,
Richard H.
Friend§
b,
Samuel D.
Stranks§
a,
Mayami
Abdulla§
b,
Richard H.
Friend§
b,
Samuel D.
Stranks§
 *bc and
Aron
Walsh
*bc and
Aron
Walsh
 *d
*d
aDepartment of Materials Science and Engineering, Yonsei University, Seoul 03722, Korea. E-mail: sds65@cam.ac.uk
bCavendish Laboratory, University of Cambridge, JJ Thompson Avenue, Cambridge CB3 0HE, UK
cDepartment of Chemical Engineering & Biotechnology, University of Cambridge, Philippa Fawcett Drive, Cambridge, CB3 0AS, UK
dDepartment of Materials, Imperial College London, Exhibition Road, London, SW7 2AZ, UK. E-mail: a.walsh@imperial.ac.uk
First published on 12th August 2022
Abstract
The control of non-radiative losses in light-emitting diodes (LEDs) based on metal halide perovskites is crucial to improve device efficiency. Recent studies have shown a correlation between lattice strain and electron–hole recombination. To consolidate the concept, we investigate how external pressure (strain) affects the crystal structure, electronic properties, point defect concentration, and luminescence efficiency of CH3NH3PbBr3. Relativistic first-principles calculations reveal enhanced Rashba splitting and Schottky defect disorder under compression, which produce a pronounced decrease in the electroluminescence peak energy and intensity in operating CH3NH3PbBr3 LEDs. The resulting model sheds light on the factors underpinning the intricate strain–property relationships in soft crystalline semiconductors.
Applications of halide perovskite semiconductors have ranged from photovoltaic (PV) to light-emitting diodes (LED) applications.1–4 Although both power conversion efficiency of perovskite PV and external quantum efficiency of LEDs have reached over 20%,5–8 these are still well below their theoretical limits. Non-radiative carrier recombination – which generates heat rather than light – in the active perovskite layer is one of the key factors that diminishes the efficiency of both LED and PV devices.9 Non-radiative recombination has several origins; for instance, indirect band to band transitions or defect mediated recombination (i.e. Shockley–Read–Hall recombination).10
There have been recent insights into how the strain present in halide perovskite films affects non-radiative recombination and luminescence efficiency.11,12 Strain – which can develop within the film during the growth and crystallization process – exhibits complex heterogeneity patterns that extend across multiple length scales in perovskite films and is demonstrated by spatial variation in luminescence.13 Spacial correlation between lattice strain and photoluminescence (PL) lifetime was directly revealed even in high-quality perovskite thin films.14 A recent study by Kim et al.15 reported that relieving the strain by cation exchange could reduce trap density and suppress non-radiative recombination, which results in higher open-circuit voltage of perovskite PV devices. Another study by Ye et al.16 also has demonstrated that strain relaxation in perovskite solar cells displayed an 1.2 times higher PCE and considerably longer stability than control groups. Nonetheless, the defect species that strongly couple with the strain in halide perovskites, and the other factors that could lead to non-radiative recombination, are poorly understood.
Herein, we aim to better understand the relationship between strain and carrier recombination. We set pressure as the sole control variable as it is a thermodynamic parameter that can directly induce strain in materials and tune their properties. Operando experiments of CH3NH3PbBr3 (or MAPbBr3) perovskite LED were performed to probe the change in the device properties (i.e. electroluminescence, EL) under hydrostatic pressure. The measurements were performed with the device immersed in an inert fluid (Fluorinert) acting as a pressure transmitting inside a capillary high-pressure cell. Next, complementary first-principles density functional theory (DFT) calculations were performed to demonstrate a change in material properties (atomic structure and electronic structure) at each pressure point. Finally, we adopted a statistical thermodynamic model to describe how defect concentration (including Schottky and Frenkel disorders) changes as pressure is applied. Our unique approach employs the pressure dependence of EL in perovskite devices to elucidate the pressure-carrier recombination relationship. The analysis provides insights into the strain–structure–property relationships of halide perovskites.
Results and discussion
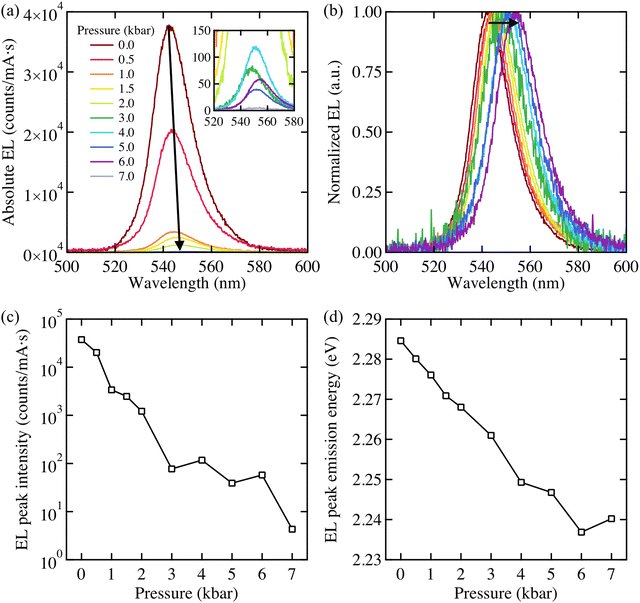
The EL evolution of a MAPbBr3 device measured under the application of various external hydrostatic pressures is shown in Fig. 1. All EL spectra are normalised to the number of counts per second per mA and were collated at room temperature. The MAPbBr3 LED is fabricated following Ref. 17 which under ambient conditions (T ≅ 298 K, P ≅ 1 atm) demonstrates green EL with a peak wavelength of λmax = 540 nm (see Methods for device stack). The evolution of the LED EL intensity with varying pressure is depicted in Fig. 1a. These results demonstrate that the intensity is impaired as the pressure rises; however EL intensity rapidly diminishes with the first increment of pressure. The reduction in EL intensity confirms that pressure adversely impacts the output of the MAPbBr3 LEDs. The fact there is no significant inhibition in charge injection to the device when the pressure is applied (see Fig. S1, ESI‡) allows us to assume that an increase in non-radiative recombination is the main cause of the EL reduction.The EL spectra have been normalised to the intensity value at the emission peak in Fig. 1b. The peak energy gradually shifts to longer wavelengths (lower energies) at a rate of 7 meV kbar−1 as the sample was compressed. Fig. 1c and d, demonstrate that the EL emission peak is negatively correlated with the applied pressure, indicating a pressure-induced band gap reduction. These results are consistent with previous studies of thin films and crystals of perovskite materials18–21 that have shown the same trend in band gap pressure relation. In our case and within the studied range of pressure, the MAPbBr3 LED proved to be considerably flexible in terms of band gap where the emission peak wavelength exhibited a gradual shift back to shorter wavelengths as the sample was decompressed slowly (see Fig. S2, ESI‡).
In our experimental settings, it is beyond our capabilities to obtain material specific properties such as change in crystal structure and defect concentration. Moreover, to attain insights into the causes of the observed quenching in EL intensity, it is necessary to decipher the origin of carrier recombination behavior at an atomic level; therefore, we performed first-principle DFT calculations. These are used to provide insights into the pressure-induced structural changes, as well as the impact of compression on defect formation to link with the macroscopic observation of EL quenching.
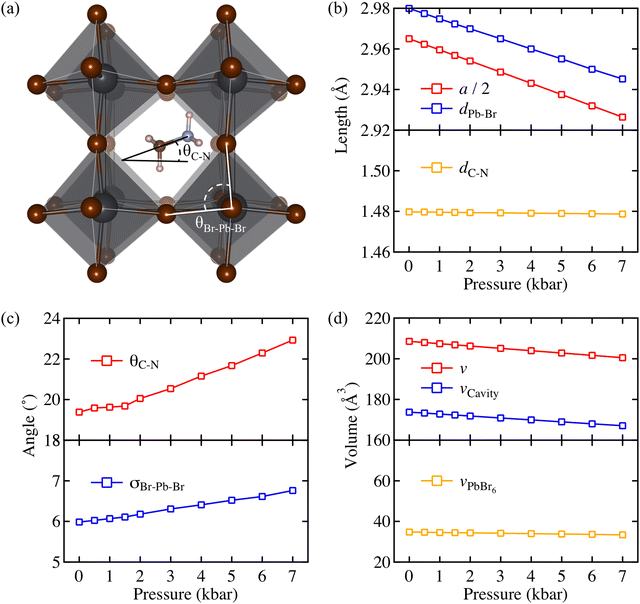
The optimised crystal structure of MAPbBr3 is shown in Fig. 2a. The calculated lattice constant of a0 = 5.93 Å coincides well with previously reported values of 5.91 Å (calculated)22 and 5.94 Å (measured).23 From fitting to the third-order Birch–Murnaghan equation-of-state,24 a bulk modulus of B0 = 18.2 GPa is obtained, which implies hybrid MAPbBr3 is softer than inorganic CsPbBr3 (B0 = 21.5 GPa).25 A report of B0 = 16.8 GPa measured from Brillouin scattering is in good agreement.26 Based on the calculated a0 and B0, the unit cell volume (ν) as a function of pressure is obtained following
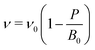 | (1) |
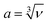 ) and fully relaxed the internal coordinates of all atoms. Changes of structural parameters as a function of pressure are plotted in Fig. 2b.
) and fully relaxed the internal coordinates of all atoms. Changes of structural parameters as a function of pressure are plotted in Fig. 2b.
Unlike the ideal perovskite structure (e.g. cubic CsPbBr3) where the Pb–Br bond length is half of its lattice constant, the averaged Pb–Br bond length of MAPbBr3 (dPb–Br) in MAPbBr3 is larger than a/2. This is because the MA+ molecular cation allows internal distortion of PbBr6 octahedron in MAPbBr3. While dPb–Br shortens as more pressure is applied, the C–N bond length of MA+ (dC–N) remains constant, which means that the applied pressure mainly affects the 3-dimensional PbBr6 octahedral networks and leaves the molecular cation unperturbed due to its stiffer bond. As a result, internal distortion of the PbBr6 octahedron becomes severe. A quantitative measure, the standard deviation of the octahedral angles (σBr–Pb–Br) defined by eqn (2),27,28 is plotted as a function of pressure in Fig. 2c.
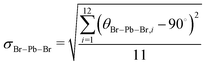 | (2) |
It confirms that pressure distorts the octahedra and consequently MA+ rotates to fit in the cavity. It is notable that the volume of PbBr6 is kept constant while the volume of the cavity shrinks under the pressure (see Fig. 2d). This could explain the microscopic origin of the organic cations locking under pressure that have been observed.29
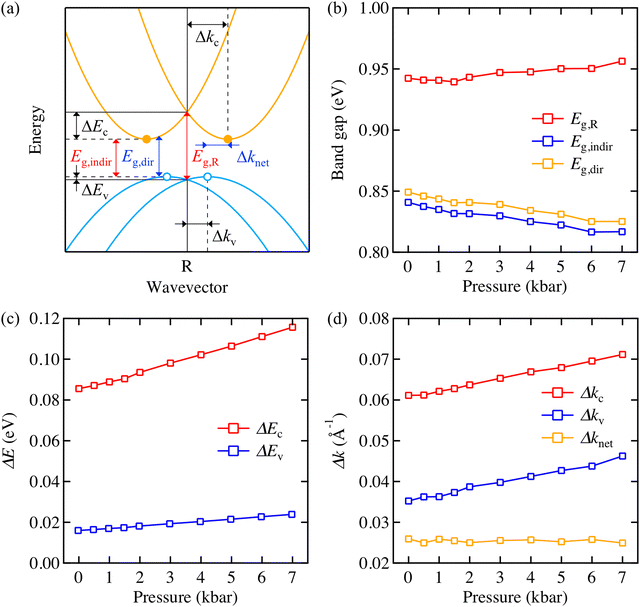
Hybrid lead halide perovskites are known to exhibit Rashba splitting in their band dispersion due to a break of the centrosymmetry by the presence of the molecular cation.30,31 To assess the impact of pressure on the electronic structure of MAPbBr3 including its Rashba splitting, we sampled a dense 3D k-point mesh near the R point in the momentum space. Fig. 3a depicts the band structure of MAPbBr3 and physical quantities that can make quantitative analysis of Rashba splitting available. The evolution of actual band structures is plotted in Fig. S4 and S5 (ESI‡). Band gap values shown in Fig. 3b are underestimated with respect to our measurement due to the level of theory. The use of the generalised gradient approximation with relativistic corrections can capture correct trends in relative changes of atomic and electronic structures for halide perovskites.28
Both the indirect and direct band gap of MAPbBr3 (Eg,indir) and (Eg,dir) decrease under applied pressure, Fig. 3b. This positive volume deformation potential (negative pressure coefficient) of the band gap arises through contributing the Pb 6s orbitals to the band structure.32 The band gap shrinkage of ∼25 meV at 7 kbar from our calculation is in the same order as the EL peak shift of our device (∼45 meV) at 7 kbar. When the band gap is simply measured right at the R point (Eg,R), it exhibits an opposite (increasing) trend as a function of the pressure, which means that sampling k-mesh properly near the high symmetry point is necessary to capture the Rashba splitting. We also note that the Rashba splitting mitigates band gap shrinkage (see Fig. S3, ESI‡).
We further analysed how the shape of the Rashba pockets evolves under pressure as the shape of band structure could impact charge carrier recombination dynamics.21,33,34Fig. 3c and d display that the actual band extrema drift apart from the R point both on the energy axis and momentum (wavevector) axis as pressure is applied, which indicates the Rashba pockets on the upper valence band and lower conduction band become deeper and wider under pressure. Exact band extrema positions in the reciprocal space and values used to plot Fig. 3c and d are tabulated in Table S1 (ESI‡). We attribute the shift of ΔE and Δk to the distortion of PbBr6 octahdera under pressure, as the correlation between octahedral distortion and spin–orbit coupling has been previously reported in halide perovskite systems.28,35,36 Nonetheless, it is important that the k-space separation between electrons and holes (represented by Δknet) remains constant, since it implies a change in band structure does not result in the enhancement of phonon-assisted indirect recombination that is a result of momentum mismatch. We conclude that the primary origin of the EL intensity decrease observed in our experiment is not related to the change of electronic structure. An interesting point is that no indirect to direct band gap transition occurs in MAPbBr3 unlike previous reports from MAPbI3.21
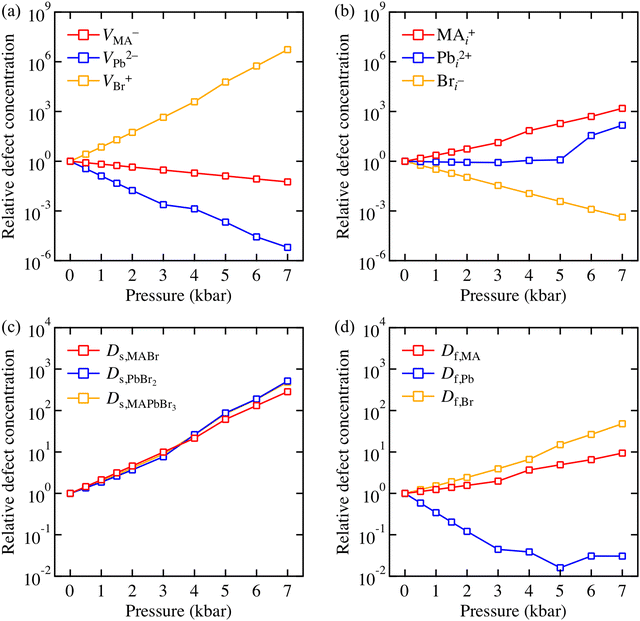
A correlation between strain and non-radiative recombination has been reported, where local defect density plays an important role.14 To assess this effect, we sampled 6 charged vacancies and interstitials (i.e. VMA−, VPb2−, VBr+, MAi+, Pbi2+, and Bri−) that can be found in MAPbBr3. To quantify how applied pressure can affects defect population, we predicted a change in relative defect concentration of all vacancies and interstitials as a function of applied pressure following eqn (7). In Fig. 4a, concentration of Br anion vacancy is expected to increase (∼107 times at 7 kbar), while the concentration of MA and Pb cation vacancies is expected to decrease. In Fig. 4b, interstital defects exhibit opposite tendencies, i.e. concentration of Br anion interstitial is predicted to decrease and concentration of the other cation interstitials are predicted to increase. Here, it is found that VBr+ is the most pressure-sensitive defect species.
The predictions shown in Fig. 4a and b assume local equilibrium at each pressure point, which is reasonable considering the relatively high ion mobility at in these materials at room temperature. Once an ion escapes from its lattice site and forms a vacancy, this ion can induce another vacancy to compensate the charge (Schottky disorder) or form an interstitial (Frenkel disorder).37 Possible balanced defect reactions are summarised in Table 1. The partial and full Schottky defect formation energies of MAPbBr3 are similar to previously reported values of MAPbI3,38 which implies that Schottky disorder is common in bromide perovskites, as well as iodide perovskites. Interestingly, MA and Br Frenkel disorder is found to be as accessible as Schottky disorder, whilst Pb Frenkel disorder is energetically unfavourable.
| Reaction | ΔHd (eV defect−1) | |
|---|---|---|
| Schottky | Nil → VMA− + VBr+ + MABr | 0.14 |
| Disorder | Nil → VPb2− + 2 VBr++ PbBr2 | 0.24 |
| Nil → VMA− +VPb2− + 3VBr++ MAPbBr3 | 0.20 | |
| Frenkel | Nil → VMA− + MAi+ | 0.07 |
| Disorder | Nil → VPb2− + Pbi2+ | 2.15 |
| Nil → VBr++ Bri− | 0.24 |
The variation of defect concentrations under pressure is shown in Fig. 4c and d, respectively. Schottky disorder is expected to increase up to 1000 times at 7 kbar. MA and Br Frenkel disorder is also predicted to increase, whereas Pb Frenkel disorder is predicted to decrease. The driving force behind the enhancement of Schottky and Br Frenkel disorders is stabilisation of Br anion vacancy under compression – in other words, reduction of VBr+ formation energy overcomes the rise of VMA−, VPb2−, and Bri− formation energies. On the other hand, the driving force behind the enhancement of MA Frenkel disorder is stabilisation of the MA interstitial.
An increase in crystal disorder, with a distribution of charged defect centres, will enhance carrier trapping due to band edge fluctuations in the semiconducting crystal. Furthermore, both the Br vacancy and interstitial introduce trap states within the band gap.39,40 These effects, which arise from enhanced Schottky disorder and Br Frenkel disorder under pressure, will lead to non-radiative pathways that lower the LED efficiency. In addition to bulk processes, pressure-induced changes at surfaces,41 interfaces, and42,43 grain boundaries can may also play a role, but are beyond the scope of this investigation.
Conclusions
The change in optoelectronic and material properties of MAPbBr3, probed using a combination of simulation techniques and experimental measurements, highlights that: (i) pressure distorts PbBr6 octahedra in the MAPbBr3 crystal, which results in larger relativistic Rashba splitting with electron and hole pockets near the R point that are deeper and wider; (ii) the band gap is reduced under hydrostatic pressure with indirectness of the band gap unchanged, which explains the red-shifted EL observed in MAPbBr3 LEDs; (iii) both Schottky and Frenkel disorder is enhanced under hydrostatic pressure, which leads to an increase in charged defect populations and a decrease in EL intensity. The same processes that we observe for pressure-induced behaviour are expected to be relevant for strain effects in general where the local structure is expanded or compressed, including carrier recombination phenomena related to photostriction,44,45 phase transitions,14,46 and compositional gradients.47,48Experimental methods
Sample preparation
The following chemicals were supplied from MABr and PbBr2 (>99%, Sigma-Aldrich), and F8 was provided by Cambridge Display Technology (CDT) Ltd. All materials were used as received from their sources without further purification. For the methylammonium lead tribromide (CH3NH3PbBr3, MAPbBr3) perovskite precursor solution (37.8 wt%), MABr and PbBr2 with a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were dissolved in a cosolvent of N,N-dimethylformamide (DMF) with 6 vol% of an aqueous hydrobromic acid (HBr) (48 wt%). The LED device was fabricated according to the recipe given in ref. 17. The LED was fabricated on a pre-patterned indium tin oxide (ITO) substrate that was cleaned in an ultrasonic bath with acetone, 2-propanol and followed by treatment in an oxygen-plasma etcher for 10 min, sequentially. A thin layer of poly(3,4-ethylenedioxythiophene) polystyrene sulfonic acid (PEDOT:PSS) was used as the hole transport layer (HTL) which was spun coated at 5000 rpm for 45 s on the substrate and then baked at 140 °C for 10 min under nitrogen atmosphere. Subsequently, the MAPbBr3 precursor solution was spun coated onto the PEDOT:PSS layer at 3000 rpm for 60 s and followed by annealing at 100 °C for 2 h. The Poly(9,9-di-n-octylfluorenyl-2,7-diyl) (F8) polymer solution with a concentration of (0.8 mg ml−1 in chlorobenzene) was spun coated onto the perovskite layer at 3000 rpm for 60 s. The device fabrication is concluded by thermally evaporating approximately 1 nm of LiF, followed by 80 nm of Ag. The device was fabricated, had wires attached to it, was encapsulated inside a N2-filled glove-box, and had an active area of 1 mm2 which was defined using a mask. Schematic of the device is shown in Fig. 5.
1 were dissolved in a cosolvent of N,N-dimethylformamide (DMF) with 6 vol% of an aqueous hydrobromic acid (HBr) (48 wt%). The LED device was fabricated according to the recipe given in ref. 17. The LED was fabricated on a pre-patterned indium tin oxide (ITO) substrate that was cleaned in an ultrasonic bath with acetone, 2-propanol and followed by treatment in an oxygen-plasma etcher for 10 min, sequentially. A thin layer of poly(3,4-ethylenedioxythiophene) polystyrene sulfonic acid (PEDOT:PSS) was used as the hole transport layer (HTL) which was spun coated at 5000 rpm for 45 s on the substrate and then baked at 140 °C for 10 min under nitrogen atmosphere. Subsequently, the MAPbBr3 precursor solution was spun coated onto the PEDOT:PSS layer at 3000 rpm for 60 s and followed by annealing at 100 °C for 2 h. The Poly(9,9-di-n-octylfluorenyl-2,7-diyl) (F8) polymer solution with a concentration of (0.8 mg ml−1 in chlorobenzene) was spun coated onto the perovskite layer at 3000 rpm for 60 s. The device fabrication is concluded by thermally evaporating approximately 1 nm of LiF, followed by 80 nm of Ag. The device was fabricated, had wires attached to it, was encapsulated inside a N2-filled glove-box, and had an active area of 1 mm2 which was defined using a mask. Schematic of the device is shown in Fig. 5.
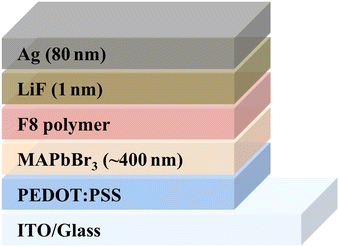 | ||
| Fig. 5 Schematic device structure of MAPbBr3 based LED, with (ITO/PEDOT:PSS/MAPbBr3/LiF/Ag) architecture. The active area of the device was 1 mm2. | ||
EL Measurement under hydrostatic pressure
The measurements of EL spectra as a function of pressure dependence were carried out at room temperature using the capillary-fed piston-cylinder cell pressure system with a manganin coil acting as a pressure gauge.49 The LED was immersed within the cell in 3MTM FluorinertTM (FC-77) liquid, which is characterised by being very inert with high electrical resistivity (1.9 × 1015 Ω cm) and is employed as a hydrostatic pressure transferring medium.50 The electroluminescence (EL) spectra emitted from the LED were recorded using a spectrometer positioned outside the pressure cell. During the measurements, the device was operated at a constant current while the light emitted was simultaneously collected and transmitted through an optical fiber from the device within the cell to the spectrometer. The collection of light emitted vertically to the substrate was achieved through having one port of thefibre located close to the sample. The pressure was increased gradually from ambient to 8 kbar in steps of 0.5 kbar. The EL was recorded using a fiber-coupled USB2000 Spectrometer with SpectraSuite software from Ocean Optics, while driving the LED at a constant current using a Keithley 2400 source measurement unit.Bulk structure calculations
Calculations were performed based on Kohn–Sham density-functional theory51 for a series of 10 pressures. The Vienna Ab Initio Simulation Package (VASP)52,53 was used with projector augmented-wave (PAW)54,55 scalar-relativistic potentials. The valence states of H, C, N, Br, and Pb are treated explicitly by 1(1s1),4 (2s22p2), 5(2s22p3), 7(4s24p5), and 14(5d106s26p2) electrons, respectively. For structure optimization, the Perdew–Burke–Ernzerhof exchange-correlation functional revised for solids (PBEsol)56 was employed with the plane-wave kinetic cutoff energy of 700 eV. High convergence criteria of 10−6 eV for total energy in the unit cell and 10−3 eV Å−1 for forces on each atom were set to properly describe the change in atomic structures under small volume changes.For the primitive unit cell, a Γ-centred k-point grid of 8 × 8 × 8 was used. To obtain accurate values of valence band maximum (VBM) and conduction band minimum (CBM) in energy-momentum space, a fine k-point mesh near the R point (0.5,0.5,0.5) was sampled in two steps: (i)13 × 13 × 13 mesh within |ki–R| ≤ 0.06[2π/a0], where i = x, y, and z; (ii) 13 × 13 × 13 mesh within |ki − R′| ≤ 0.006[2π/a0], where R' is the point that has minimum (maximum) eigenvalue from the first step. The rest of the Brillouin zone was sampled on 8 × 8 × 8 mesh. Spin–orbit coupling (SOC) was included to describe the splitting of band edges.
Defect thermodynamics
Within the modern theory of point defects in crystals, the enthalpy of defect formation (ΔHdefectα,q (μi, EF)) be calculated as a function of chemical potential (μi) and Fermi level (EF) following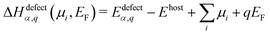 | (3) |
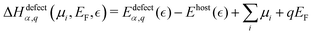 | (4) |
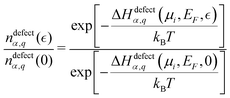 | (5) |
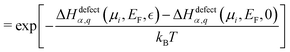 | (6) |
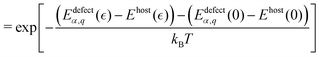 | (7) |
Author contributions
Y.-K. J. and A. M. equally contributed to this work and performed the primary modelling and measurements, respectively. All authors contributed to discussing the results and writing the manuscript.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
We thank Bo Ram Lee for sharing the device fabrication method. This research was supported by Young Researcher Program and Creative Materials Discovery Program through the National Research Foundation of Korea (NRF) funded by Ministry of Science and ICT (2018R1C1B6008728 and 2018M3D1A1058536). Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the ARCHER UK National Supercomputing Service (https://www.archer.ac.uk).References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- H.-S. Kim, C.-R. Lee, J.-H. Im, K.-B. Lee, T. Moehl, A. Marchioro, S.-J. Moon, R. Humphry-Baker, J.-H. Yum and J. E. Moser, et al., Lead iodide perovskite sensitized all-solid-state submicron thin film mesoscopic solar cell with efficiency exceeding 9%, Sci. Rep., 2012, 2, 1–7 Search PubMed.
- Z.-K. Tan, R. S. Moghaddam, M. L. Lai, P. Docampo, R. Higler, F. Deschler, M. Price, A. Sadhanala, L. M. Pazos and D. Credgington, et al., Bright light-emitting diodes based on organometal halide perovskite, Nat. Nanotechnol., 2014, 9, 687–692 CrossRef CAS PubMed.
- L. N. Quan, B. P. Rand, R. H. Friend, S. G. Mhaisalkar, T.-W. Lee and E. H. Sargent, Perovskites for Next-Generation Optical Sources, Chem. Rev., 2019, 119, 7444–7477 CrossRef CAS PubMed.
- NREL, Best Research-Cell Efficiencies. https://www.nrel.gov/pv/cell-efficiency.html, (accessed March 16, 2022).
- M. Jeong, I. W. Choi, E. M. Go, Y. Cho, M. Kim, B. Lee, S. Jeong, Y. Jo, H. W. Choi and J. Lee, et al., Stable perovskite solar cells with efficiency exceeding 24.8% and 0.3-V voltage loss, Science, 2020, 369, 1615–1620 CrossRef CAS PubMed.
- K. Lin, J. Xing, L. N. Quan, F. P. G. de Arquer, X. Gong, J. Lu, L. Xie, W. Zhao, D. Zhang and C. Yan, et al., Perovskite light-emitting diodes with external quantum efficiency exceeding 20 per cent, Nature, 2018, 562, 245–248 CrossRef CAS PubMed.
- B. Zhao, S. Bai, V. Kim, R. Lamboll, R. Shivanna, F. Auras, J. M. Richter, L. Yang, L. Dai and M. Alsari, et al., High-efficiency perovskite–polymer bulk heterostructure light-emitting diodes, Nat. Photonics, 2018, 12, 783–789 CrossRef CAS.
- S. D. Stranks, Nonradiative Losses in Metal Halide Perovskites, ACS Energy Lett., 2017, 2, 1515–1525 CrossRef CAS.
- J.-S. Park, S. Kim, Z. Xie and A. Walsh, Point defect engineering in thin-film solar cells, Nat. Rev. Mater., 2018, 3, 194–210 CrossRef CAS.
- J. N. Wilson, J. M. Frost, S. K. Wallace and A. Walsh, Dielectric and ferroic properties of metal halide perovskites, APL Mater., 2019, 7, 010901 CrossRef.
- D. Liu, D. Luo, A. N. Iqbal, K. W. Orr, T. A. Doherty, Z.-H. Lu, S. D. Stranks and W. Zhang, Strain analysis and engineering in halide perovskite photovoltaics, Nat. Mater., 2021, 20, 1337–1346 CrossRef CAS PubMed.
- D. W. de Quilettes, S. M. Vorpahl, S. D. Stranks, H. Nagaoka, G. E. Eperon, M. E. Ziffer, H. J. Snaith and D. S. Ginger, Impact of microstructure on local carrier lifetime in perovskite solar cells, Science, 2015, 348, 683–686 CrossRef CAS PubMed.
- T. W. Jones, A. Osherov, M. Alsari, M. Sponseller, B. C. Duck, Y.-K. Jung, C. Settens, F. Niroui, R. Brenes and C. V. Stan, et al., Lattice strain causes non-radiative losses in halide perovskites, Energy Environ. Sci., 2019, 12, 596–606 RSC.
- G. Kim, H. Min, K. S. Lee, S. M. Yoon and S. I. Seok, Impact of strain relaxation on performance of α -formamidinium lead iodide perovskite solar cells, Science, 2020, 370, 108–112 CrossRef CAS PubMed.
- T. Ye, K. Wang, S. Ma, C. Wu, Y. Hou, D. Yang, K. Wang and S. Priya, Strain-relaxed tetragonal MAPbI3 results in efficient mesoporous solar cells, Nano Energy, 2021, 83, 105788 CrossRef CAS.
- J. C. Yu, D. B. Kim, E. D. Jung, B. R. Lee and M. H. Song, High-performance perovskite light-emitting diodes via morphological control of perovskite films, Nanoscale, 2016, 8, 7036–7042 RSC.
- K. Matsuishi, T. Ishihara, S. Onari, Y. Chang and C. Park, Optical properties and structural phase transitions of lead-halide based inorganic-organic 3D and 2D perovskite semiconductors under high pressure, Phys. Status Solidi B, 2004, 241, 3328–3333 CrossRef CAS.
- A. Jaffe, Y. Lin, C. M. Beavers, J. Voss, W. L. Mao and H. I. Karunadasa, High-pressure single-crystal structures of 3D lead-halide hybrid perovskites and pressure effects on their electronic and optical properties, ACS Cent. Sci., 2016, 2, 201–209 CrossRef CAS PubMed.
- X. Lü, W. Yang, Q. Jia and H. Xu, Pressure-induced dramatic changes in organic-inorganic halide perovskites, Chem. Sci., 2017, 8, 6764–6776 RSC.
- T. Wang, B. Daiber, J. M. Frost, S. A. Mann, E. C. Garnett, A. Walsh and B. Ehrler, Indirect to direct bandgap transition in methylammonium lead halide perovskite, Energy Environ. Sci., 2017, 10, 509–515 RSC.
- F. Brivio, C. Caetano and A. Walsh, Thermodynamic Origin of Photoinstability in the CH3NH3 Pb(I1−xBrx) 3 Hybrid Halide Perovskite Alloy, J. Phys. Chem. Lett., 2016, 7, 1083–1087 CrossRef CAS PubMed.
- G. Kieslich, J. M. Skelton, J. Armstrong, Y. Wu, F. Wei, K. L. Svane, A. Walsh and K. T. Butler, Hydrogen Bonding versus Entropy: Revealing the Underlying Thermodynamics of the Hybrid Organic–Inorganic Perovskite [CH3NH3]PbBr3, Chem. Mater., 2018, 30, 8782–8788 CrossRef CAS.
- F. Birch, Finite Elastic Strain of Cubic Crystals, Phys. Rev., 1947, 71, 809–824 CrossRef CAS.
- Y.-K. Jung, K. T. Butler and A. Walsh, Halide Perovskite Heteroepitaxy: Bond Formation and Carrier Confinement at the PbS–CsPbBr3 Interface, J. Phys. Chem. C, 2017, 121, 27351–27356 CrossRef CAS.
- A. C. Ferreira, A. Létoublon, S. Paofai, S. Raymond, C. Ecolivet, B. Rufflé, S. Cordier, C. Katan, M. I. Saidaminov and A. A. Zhumekenov, et al., Elastic Softness of Hybrid Lead Halide Perovskites, Phys. Rev. Lett., 2019, 121, 085502 CrossRef PubMed.
- K. Robinson, G. V. Gibbs and P. H. Ribbe, Quadratic Elongation: A Quantitative Measure of Distortion in Coordination Polyhedra, Science, 1971, 172, 567–570 CrossRef CAS PubMed.
- X. Zhang, J.-X. Shen, W. Wang and C. G. Van de Walle, First-Principles Analysis of Radiative Recombination in Lead-Halide Perovskites, ACS Energy Lett., 2018, 3, 2329–2334 CrossRef CAS.
- A. Francisco-López, B. Charles, O. J. Weber, M. I. Alonso, M. Garriga, M. Campoy-Quiles, M. T. Weller and A. R. Goñi, Pressure-Induced Locking of Methylammonium Cations versus Amorphization in Hybrid Lead Iodide Perovskites, J. Phys. Chem. C, 2018, 122, 22073–22082 CrossRef.
- D. Niesner, M. Wilhelm, I. Levchuk, A. Osvet, S. Shrestha, M. Batentschuk, C. Brabec and T. Fauster, Giant Rashba Splitting in CH3NH3PbBr3 Organic-Inorganic Perovskite, Phys. Rev. Lett., 2016, 117, S156 CrossRef PubMed.
- L. D. Whalley, J. M. Frost, Y.-K. Jung and A. Walsh, Perspective: Theory and simulation of hybrid halide perovskites, J. Chem. Phys., 2017, 146, 220901–220912 CrossRef PubMed.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde and A. Walsh, Atomistic Origins of High-Performance in Hybrid Halide Perovskite Solar Cells, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS PubMed.
- S. D. Stranks and P. Plochocka, The influence of the Rashba effect, Nat. Mater., 2018, 17, 381–382 CrossRef CAS PubMed.
- X. Zhang, J.-X. Shen and C. G. Van de Walle, First-Principles Simulation of Carrier Recombination Mechanisms in Halide Perovskites, Adv. Energy Mater., 2019, 10, 1902830 CrossRef.
- A. Amat, E. Mosconi, E. Ronca, C. Quarti, P. Umari, M. K. Nazeeruddin, M. Grätzel and F. De Angelis, Cation-Induced Band-Gap Tuning in Organohalide Perovskites: Interplay of Spin–Orbit Coupling and Octahedra Tilting, Nano Lett., 2014, 14, 3608–3616 CrossRef CAS PubMed.
- Y.-K. Jung, J.-H. Lee, A. Walsh and A. Soon, Influence of Rb/Cs Cation-Exchange on Inorganic Sn Halide Perovskites: From Chemical Structure to Physical Properties, Chem. Mater., 2017, 29, 3181–3188 CrossRef CAS PubMed.
- E. Mosconi, D. Meggiolaro, H. J. Snaith, S. D. Stranks and F. De Angelis, Light-induced annihilation of Frenkel defects in organo-lead halide perovskites, Energy Environ. Sci., 2016, 9, 3180–3187 RSC.
- A. Walsh, D. O. Scanlon, S. Chen, X.-G. Gong and S.-H. Wei, Self-regulation mechanism for charged point defects in hybrid halide perovskites, Angew. Chem., Int. Ed., 2015, 54, 1791–1794 CrossRef CAS PubMed.
- A. Mannodi-Kanakkithodi, J.-S. Park, A. B. Martinson and M. K. Chan, Defect Energetics in Pseudo-Cubic Mixed Halide Lead Perovskites from First-Principles, J. Phys. Chem. C, 2020, 124, 16729–16738 CrossRef CAS.
- X. Zhang, M. E. Turiansky, J.-X. Shen and C. G. Van de Walle, Iodine interstitials as a cause of nonradiative recombination in hybrid perovskites, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 101, 140101 CrossRef CAS.
- Y. Fang, Q. Dong, Y. Shao, Y. Yuan and J. Huang, Highly narrowband perovskite single-crystal photodetectors enabled by surface-charge recombination, Nat. Photonics, 2015, 9, 679–686 CrossRef CAS.
- K. K. Wong, A. Fakharuddin, P. Ehrenreich, T. Deckert, M. Abdi-Jalebi, R. H. Friend and L. Schmidt-Mende, Interface-Dependent Radiative and Nonradiative Recombination in Perovskite Solar Cells, J. Phys. Chem. C, 2018, 122, 10691–10698 CrossRef CAS.
- C. M. Wolff, P. Caprioglio, M. Stolterfoht and D. Neher, Nonradiative Recombination in Perovskite Solar Cells: The Role of Interfaces, Adv. Mater., 2019, 31, 1902762 CrossRef CAS PubMed.
- Y. Zhou, S. Wang, Z. Ku, H. Fan, D. Schmidt, A. Rusydi, L. Chang, L. Wang, P. Ren and L. Chen, et al., Giant photostriction in organic–inorganic lead halide perovskites, Nat. Commun., 2016, 7, 1–8 Search PubMed.
- H. Tsai, R. Asadpour, J. C. Blancon, C. C. Stoumpos, O. Durand, J. W. Strzalka, B. Chen, R. Verduzco, P. M. Ajayan and S. Tretiak, et al., Light-induced lattice expansion leads to high-efficiency perovskite solar cells, Science, 2018, 360, 67–70 CrossRef CAS PubMed.
- I. M. Hermes, S. A. Bretschneider, V. W. Bergmann, D. Li, A. Klasen, J. Mars, W. Tremel, F. Laquai, H. J. Butt and M. Mezger, et al., Ferroelastic Fingerprints in Methylammonium Lead Iodide Perovskite, J. Phys. Chem. C, 2016, 120, 5724–5731 CrossRef CAS.
- D. P. McMeekin, Z. Wang, W. Rehman, F. Pulvirenti, J. B. Patel, N. K. Noel, M. B. Johnston, S. R. Marder, L. M. Herz and H. J. Snaith, Crystallization Kinetics and Morphology Control of Formamidinium-Cesium Mixed-Cation Lead Mixed-Halide Perovskite via Tunability of the Colloidal Precursor Solution, Adv. Mater., 2017, 29, 1607039 CrossRef PubMed.
- C. Zhu, X. Niu, Y. Fu, N. Li, C. Hu, Y. Chen, X. He, G. Na, P. Liu and H. Zai, et al., Strain engineering in perovskite solar cells and its impacts on carrier dynamics, Nat. Commun., 2019, 10, 1–11 CrossRef PubMed.
- D. Guy and R. Friend, Temperature measurement in high pressure cells using a rhodium +0.5% iron-chromel thermocouple pair, J. Phys. E: Sci. Instrum., 1986, 19, 430 CrossRef CAS.
- T. Varga, A. P. Wilkinson and R. J. Angel, Fluorinert as a pressure-transmitting medium for high-pressure diffraction studies, Rev. Sci. Instrum., 2003, 74, 4564–4566 CrossRef CAS.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of Ab- Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the density-gradient expansion for exchange in solids and surfaces, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, First-principles calculations for point defects in solids, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- A. Walsh and A. Zunger, Instilling defect tolerance in new compounds, Nat. Mater., 2017, 16, 964–967 CrossRef CAS PubMed.
Footnotes |
| † The crystal structure files for the optimised pristine and defective materials have been made available in an on-line repository at https://doi.org/10.5281/zenodo.7006160 |
| ‡ Electronic supplementary information (ESI) available: J–V curves of a device under pressure, EL spectra while pressure is released, changes in deformation potential, 3D band structure, and charge correction term as a function of pressure. See DOI: https://doi.org/10.1039/d2tc01490d |
| § Contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |