Phase control of sputter-grown large-area MoTe2 films by preferential sublimation of Te: amorphous, 1T′ and 2H phases

Abstract

Sputter-grown amorphous Mo–Te films were annealed to obtain the crystalline phase. Although as-deposited films exhibited an off-stoichiometric Te-rich composition, optimized annealing conditions enabled the elimination of excess Te by a preferential sublimation process. Owing to their similar local structure, the disordered amorphous phase first crystallized into a high temperature phase, 1T′, followed by a phase transition to the 2H structure upon further annealing. To realize 2D MoTe₂-based novel devices, understanding the crystallization mechanism of amorphous Mo–Te films is critical. Furthermore, the robustness of the fabrication method, i.e., the establishment of a method to realize MoTe₂ single-phase formation, which does not require the initial composition of the as-deposited amorphous film to be exactly stoichiometric, will greatly contribute to the deposition of large-area MoTe₂ films essential for industrial applications.

---

1. Introduction

Layered materials and their 2D monolayer analogues have been extensively studied since the discovery that graphene could be exfoliated from bulk graphite, due to their superior and exotic physical and chemical properties, some of which do not exist in their bulk counterparts. Moreover, their scalability down to the atomic level offers great potential for the realization of ultimately integrated devices. For instance, the International Roadmap for Devices and Systems (IRDS) 2021 states that channel materials for transistors beyond the current Si technology for More Moore scaling will be 2D materials.¹ Therefore, the development of a reliable synthesis technique for depositing high-quality 2D materials over large areas is urgently required, in particular, for transition metal dichalcogenides (TMDs), consisting of transition metals such as M (Mo, W, etc.) and chalcogens X (S, Se, and Te) to form MX₂ compounds; these materials are the most promising candidates for channel materials as they form semiconductor phases depending on the composition and the crystal structure.²

A variety of thin film growth techniques have been proposed for the synthesis of TMDs.³ Chemical-based methods including chemical vapor deposition (CVD),⁴ atomic layer deposition (ALD),⁵ and liquid metal (LM) synthesis⁶ have been the most widely investigated techniques. Recently, physical vapor deposition (PVD) techniques such as molecular beam epitaxy (MBE)^7,8 and pulsed laser deposition (PLD)⁹ have also drawn attention. Although sputtering is a mature PVD growth method in the semiconductor industry, the number of papers reporting the growth of TMDs by sputtering is limited.^10–13 When TMD films are fabricated by sputtering at room temperature, the as-deposited film forms an atomically disordered phase i.e., amorphous. Therefore, in order to obtain the desired layered crystal structure, annealing is required. Furthermore, particularly for sulfides, additional S must be supplied to compensate for the evaporation of S during the annealing process as S readily evaporates at the elevated temperatures used.¹⁴ Moreover, understanding the crystallization behavior of amorphous films is important not only for fundamental science but also for applications as can be seen in the progress of chalcogenide-based phase-change materials used in rewritable optical discs and non-volatile memory devices that were accelerated by pioneering work regarding the understanding of the switching mechanism of the well-known phase-change material Ge₂Sb₂Te₅.¹⁵

We focus on the crystallization mechanism occurring in Mo–Te films. 2H-MoTe₂ is a semiconductor possessing a band gap similar to Si (∼1 eV) and exhibits an indirect–direct band structure transition as the thickness approaches the monolayer limit.¹⁶ Due to its intriguing physical properties, MoTe₂ has drawn increased attention for a wide variety of applications including transistors,^17,18 non-volatile memory,^19–22 ferroelectric phase-change transistors,²³ LEDs and photodetectors,^24,25 photovoltaic cells,²⁶ and catalysts for hydrogen generation.²⁷ One of the pronounced features of MoTe₂ is that the differences in free energy between the different crystalline phases are small compared to other TMDs leading to the existence of several different polymorphs including the 2H (semiconducting), 1T′ (metallic),²⁸ and Td (Weyl semimetal) phases^29,30 depending on the temperature. The presence of multiple competing crystalline phases potentially makes the crystallization process of the amorphous phase more complicated.

In this work, it was found that a sputter-deposited amorphous Mo–Te film grown using a MoTe₂ alloy target had a Te-rich composition instead of the stoichiometric MoTe₂ (Mo_33.3Te_66.7) composition. Nevertheless, the controlled sublimation of excess Te atoms under vacuum conditions enabled the successful growth of single phase 1T′ or 2H, and even mixed phases by the control of the annealing temperature and/or time. A detailed structural analysis revealed the similarity of the local structure between the amorphous and high-temperature 1T′ phases. This simple but useful process will offer strong advantages in the fabrication of functional MoTe₂ films on an industrial scale for future electronics applications.

2. Experimental

Fabrication of samples

Thin films were grown by RF-sputtering (QAM-4, ULVAC KYUSYU Corp.) using a MoTe₂ alloy target. Quartz (SiO₂) (2 inch) and Si/SiO₂ (300 nm) (4 inch) were used as substrates. After the growth of the 50 nm-thick MoTe₂ film, a SiO₂ capping layer (50 nm) was deposited in the same sputtering chamber without breaking the vacuum at room temperature. After growth, the as-deposited samples were cut into 1 × 1 cm pieces and subsequently annealed at different temperatures in a vacuum furnace. The annealing ambient was either vacuum (<5 × 10⁻³ Pa) or Ar atmospheric pressure (1 × 10⁵ Pa).

Characterization

The temperature dependence of the electrical resistance of the as-deposited Mo–Te film was measured using a two-point probe method under an Ar atmosphere at a heating rate of 10 °C min⁻¹.

X-Ray diffraction (XRD) measurements were carried out using Cu-Kα (λ = 0.1542 nm) radiation in a Bragg–Brentano geometry to determine the out-of-plane orientation of the film (θ/2θ symmetric scan) (Ultima IV, Rigaku Corp.).

The composition of the film was analyzed using inductively coupled plasma optical emission spectroscopy (ICP-OES) (PS3520VDD II, Hitachi High-Tech Corp.). The composition of the as-deposited film fabricated from a stoichiometric MoTe₂ target was found to be Mo_21.1Te_78.9, a significantly Te-rich composition. This could be due to a large difference in the sputtering rate of Mo and Te; the vaporization temperature of Te is significantly lower than the melting point of Mo. Consequently, even when a stoichiometric compound target is used, Te is sputtered more efficiently than Mo, resulting in a Te-rich composition in the as-grown film.

Raman spectroscopy was carried out using a spectrometer equipped with a 488 nm laser at temperatures ranging from 300 K down to 100 K in a vacuum (inVia, Renishaw plc).

Transmission electron microscopy (TEM) was carried out to obtain cross-sectional images of the films (ARM200F, JEOL). TEM samples were prepared by mechanical polishing followed by Ar ion milling (PIPS, Gatan).

X-Ray absorption fine structure spectroscopy (XAFS)

X-Ray absorption fine structure (XAFS) measurements were carried out at SPring-8 beamline BL01B1. Both Mo and Te K-edge spectra were recorded in fluorescence mode at 10 K. The extended X-ray absorption fine structure (EXAFS) data were analyzed using the FEFF and IFEFFIT software packages (Athena and Artemis).³¹ The details of the XAFS analysis have been reported elsewhere.³²

3. Results and discussion

First, the effects of the annealing temperature on the crystallization behavior of amorphous Mo–Te films were studied. Fig. 1(a) shows the temperature dependence of the electrical resistance for the as-deposited Mo–Te film. The initial resistance was about 10 kΩ and was found to exponentially decrease with temperature, suggesting semiconductor behavior. When the temperature reached about 350 °C, the resistance sharply decreased by about one order of magnitude. After heating the sample to a maximum temperature of 550 °C followed by cooling to room temperature, the resistance remained at a low value. This resistance change behavior is typical of Te-based phase change materials such as Ge–Sb–Te,³³ where the resistance drop corresponds to the crystallization of the as-deposited amorphous film. Fig. 1(b) shows XRD patterns after annealing at different temperatures for 1 minute. Note that a SiO₂ capping layer was deposited on all samples to prevent oxidation, and annealing was carried out under an Ar atmosphere of 1 × 10⁵ Pa. It was found that crystalline Te peaks appear for the 300 °C-annealed sample even before the resistance drop could be observed as can be seen in Fig. 1(a). Further annealing to 400 °C resulted in crystallization into both MoTe₂ and Te, and only MoTe₂ peaks were found to increase in intensity after annealing at 500 °C while the Te peak intensities remain unchanged. Moreover, only 00l peaks were observed whose peak positions matched with those of the 1T′ phase and not the room temperature stable 2H phase. These results suggest that the resistance drop was a consequence of crystallization into the 1T′-MoTe₂ phase consistent with literature reports that the 1T′ phase is metallic.²⁸

Fig. 1 (a) Resistance–temperature curves of the as-deposited Mo–Te film. (b) XRD patterns of Mo–Te films annealed at 300, 400, and 500 °C in an Ar atmosphere of 1 × 10⁵ Pa after evacuation. A SiO₂ (50 nm) capping layer was deposited on all samples. (c) XRD patterns of Mo–Te films annealed at 600 °C for 1 min under three different conditions: (blue) without a capping layer under an Ar atmosphere of 1 × 10⁵ Pa, (green) the same condition as (blue) but a SiO₂ (50 nm) capping layer, and (red) with a SiO₂ (50 nm) capping layer in a vacuum of below 5 × 10⁻³ Pa.

Next, the effect of the annealing atmosphere on the crystallization behavior of amorphous Mo–Te films was studied. Fig. 1(c) shows the XRD patterns of MoTe₂ films at 600 °C annealed for 1 minute under the three different conditions: (blue) a thin film sample without a SiO₂ capping layer annealed under an Ar atmosphere of 1 × 10⁵ Pa, (green) with a 50 nm-thick SiO₂ capping layer under an Ar atmosphere of 1 × 10⁵ Pa, and (red) with a 50 nm-thick SiO₂ capping layer under evacuation at a pressure of below 5 × 10⁻³ Pa during annealing. The XRD pattern of the amorphous Mo–Te film annealed without a SiO₂ capping layer exhibited a single weak XRD peak around 12° originating from the 002 plane (a), implying poor crystallinity. On the other hand, the film with a SiO₂ capping layer deposited displayed relatively sharp 002 and 004 peaks from the 1T′-MoTe₂ phase shown in green together with the Te 101 peak at around 28°. When the amorphous Mo–Te film was capped with SiO₂ and annealed under vacuum, a negligible Te peak was observed as can be seen in the red curve. Moreover, 1T′-MoTe₂ 00l (l: 2, 4, 6, and 8) peaks with significantly increased intensities were obtained, indicating that the SiO₂ cover layer and the annealing condition affect the crystallization behavior of the Mo–Te films. The effects of the cover layer and pressure can be understood as follows. It is known that MoTe₂, especially Mo, is easily oxidized to form MoO₂ and other Mo oxides,³⁴ thus even though the sample was annealed under an Ar atmosphere, residual oxygen may react with Mo for the case of the non-capped sample (blue), leading to poor crystallinity MoTe₂. In addition, it was found that if the non-capped sample was annealed under vacuum, no XRD peaks were observed (data not shown), suggesting that all constituent elements evaporated in the form of Mo oxide and pure Te. This situation can be improved by the deposition of a SiO₂ capping layer on the top of the Mo–Te film, but the presence of excess Te crystalline grains hinders the growth of the MoTe₂ crystalline phase resulting in the peak intensities remaining weak (green). When the SiO₂-covered sample was annealed in a vacuum of <5 × 10⁻³ Pa, oxidation was avoided, and the intensity of the Te peaks was greatly reduced (red). We assume that this can be attributed to the preferential sublimation of Te in the high-temperature vacuum atmosphere. It should be noted that even though the thin film sample was capped with the SiO₂ layer, cracks may form after annealing at elevated temperatures through which the excess Te can evaporate. Therefore, hereafter, all samples were capped with the SiO₂ layer and annealed in a vacuum.

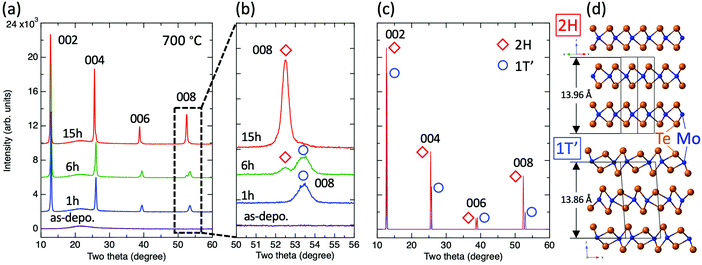
The above results suggest that the use of higher annealing temperatures can promote the evaporation of excess Te more effectively; thus, the annealing temperature was fixed at 700 °C to allow for sufficient crystallization of the films. Fig. 2(a) shows the XRD patterns of Mo–Te films annealed for 1, 6, and 15 hours and the as-deposited film. The XRD patterns of the as-deposited film show no apparent peaks suggesting that the film is amorphous. At first glance, all annealed films seem to be well-crystallized with a strong preferred c-axis orientation characterized by strong 00l peaks and the absence of other orientation peaks. On the other hand, the peak positions were found to slightly vary with annealing time. Fig. 2(b) shows an enlarged view of the dashed area in (a) that focuses on the 008 peak. The 1 h and 15 h annealed samples exhibit a single peak at higher and lower two theta positions, respectively, while the 6 h sample displays both peaks. Fig. 2(c) shows the simulated XRD patterns for the 2H- and 1T′-MoTe₂ crystal structures under the assumption of the strong c-axis preferred orientation.³⁵ As illustrated in Fig. 2(d), the 2H phase is reported to possess a slightly larger lattice constant c than 1T′, resulting in a peak shift toward lower angles.²⁸ Note that the difference in peak positions becomes more salient with increasing scattering angle, namely, the 002 peak appears to be essentially a single peak regardless of the existing phase due to a negligible difference of peak positions, while the 008 peaks can be clearly distinguishable from each other as can be seen in experimental results shown in Fig. 2(b). Summarizing Fig. 2, we found that the obtained phase can be controlled by optimizing the annealing time and that the 1 h, 6 h, and 15 h annealed samples correspond to 1T′, 1T′ + 2H (mixed), and 2H phases, respectively. This trend is consistent with a previous report.¹²

Fig. 2 (a) XRD patterns of Mo–Te films annealed at 700 °C for 1, 6, and 15 hours in a vacuum and for the as-deposited film. (b) Enlargement of the two theta range in the vicinity of the 008 peak. (c) Simulated XRD patterns of the 2H- and 1T′-MoTe₂ phases with a 001 preferred orientation. (d) Crystal structures of the 2H- and 1T′-MoTe₂ phases. Black lines indicate the unit cell of each structure.

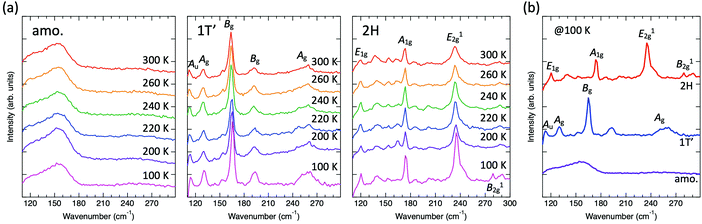
Raman spectroscopy was carried out to further confirm the phase of each sample with respect to the local structure. Fig. 3(a) shows the temperature dependence of the Raman spectra from 300 K down to 100 K for all three different phases. The amorphous (as-deposited) sample shows no clear peaks and is characterized by a broad peak at all measured temperatures. We attribute this to the presence of a disordered structure in the amorphous phase. Nevertheless, the broad peak consists of multiple sub-peaks, which correspond to different local structural arrangements existing within the amorphous sample. Therefore, although the peak is broad, the peak can be thought of as the superposition of sub-peaks that resemble those of the crystalline phase to some extent. Based on this assumption, we note that the maximum intensity of the amorphous phase is observed at a wavenumber of about 160 cm⁻¹. The Raman peaks of the 1 h-annealed (1T′) and 15 h-annealed (2H) samples exhibit good agreement with reported vibrational modes^36–38 and did not change as a function of temperature. Note that the 1T′ phase was reported to show a phase transition to the Td phase at around 260 K.^39,40 On the other hand, the Raman spectra of the 1T′ sample in this work (Fig. 3(a) middle) did not show any evidence for such a phase transition, which is characterized by the splitting of the A_g peak at around 130 cm⁻¹ into two peaks. The phase transition between the 1T′ and Td phases can be described as the relative sliding of sublayers parallel to the van der Waals gaps without changing the local structure of each sublayer.³⁷ In this study, a 1T′ film was obtained from the disordered amorphous phase suggesting the existence of many defects even in the vdW gaps that may play a role in suppressing the sublayer movement. Fig. 3(b) shows three different phases measured at 100 K. Note that the main peak position of the 1T′ phase is around 165 cm⁻¹, which resembles the maximum intensity region in the amorphous phase. On the other hand, the 2H phase shows an A_1g peak at around 174 cm⁻¹. These results suggest that the amorphous phase is rather similar to the 1T′ phase with respect to the local structure such as bond lengths instead of the 2H phase, although the 2H phase is the thermodynamically stable phase at room temperature, while the 1T′ phase is a high-temperature phase.

Fig. 3 (a) Raman spectra of as-deposited amorphous (amo.), 1T′ (700 °C, 1 h), and 2H (700 °C, 15 h) MoTe₂ films at different temperatures. (b) Comparison of the Raman spectra of different phases measured at 100 K.

The local structure of the fabricated film samples is further discussed based on EXAFS measurements. Fig. 4(a) compares the experimental and simulated k³-weighted EXAFS spectra of the as-deposited amorphous Mo–Te film at the Te and Mo K-edges. Experimental spectra were well-fit by the simulated curves. Fourier-transformed Te K-edge and Mo K-edge EXAFS spectra are shown in Fig. 4(b). Both edges were found to have a single peak between 2 and 3 Å corresponding to the first-nearest neighbor peak, while the second-nearest neighbor peak was absent, suggesting that the as-deposited film has only short-range order and does not have significant medium and long-range atomic order consistent with the XRD and Raman spectroscopy results. Note that the peak position in Fig. 4(b) is shorter than the actual bond length due to the effects of a phase shift originating from the different atomic potentials; this phase shift was taken into account during the fitting process. The local structure information, such as coordination numbers and bond lengths, obtained from fitting is summarized in Table 1. The coordination numbers of Mo coordinated by Te and Te coordinated by Mo are found to be 5.2 and 1.8, respectively, both values are smaller than those of the ideal crystalline phases of 6 and 3. Moreover, Te–Te wrong bonds were found to be present in the amorphous phase, while a negligible contribution of the Mo–Mo bonds was found. The Mo–Te bond length was 2.76 Å while the Te–Te bond length was found to be 2.80 Å. The 2H phase has higher symmetry than the 1T′ phase. The former has six equivalent Mo–Te bonds of length 2.68 Å, while the latter possesses three shorter (2.70 Å) and three longer (2.79 Å) first neighbor bonds (see Fig. 2(d) and Table 1). It should be noted that the local structure of the amorphous phase resembles that of the 1T′ phase in terms of the bond length, namely, the bond length in the amorphous phase is 2.76 Å, a value nearly midway between that of the shorter and longer bonds of the 1T′ phase. This trend is consistent with the Raman spectra shown in Fig. 3. It is assumed that, since the amorphous phase has a disordered structure, it would be energetically reasonable for it to transform into a crystalline phase with a lower symmetry (1T′ in this case) even though the phase is a metastable phase at room temperature.

Fig. 4 (a) k³-Weighted EXAFS oscillations and (b) Fourier transformed EXAFS spectra of the amorphous Mo–Te film for the Te and Mo edges. In both figures, open circles and solid lines indicate the experimental data and the corresponding fit, respectively.

Table 1 Estimated coordination numbers and bond lengths of an amorphous Mo–Te film. The reference data for the ideal 1T′ and 2H structures are also shown

	Scattering path: i–j	Coordination number	Bond length (Å)
Amorphous	Mo–Te	5.2 ± 0.4	2.76 ± 0.003
	Te–Mo	1.8 ± 0.3	2.76 ± 0.003
	Te–Te	0.8 ± 0.5	2.80 ± 0.010
1T′	Mo–Te	3	2.70
	Mo–Te	3	2.79
	Te–Mo	1.5	2.70
	Te–Mo	1.5	2.79
2H	Mo–Te	6	2.68
	Te–Mo	3	2.68

---

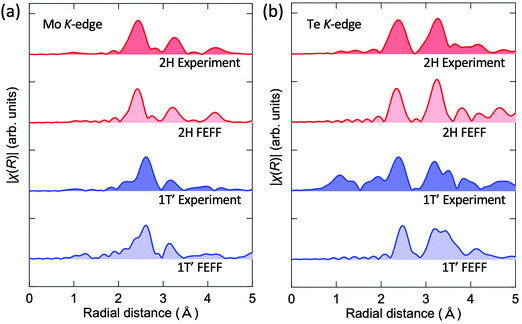
The experimental EXAFS spectra of the 1T′ (1 h) and 2H (15 h) films were compared with the simulated results as well. Fig. 5 shows the Fourier transformed experimental and simulated EXAFS chi spectra of the 1T′ and 2H phases for (a) the Mo and (b) Te K-edges measured at 10 K. As discussed in Fig. 3, the existence of defects in the vdW gaps is assumed to hinder the sliding motion of the sublayers parallel to the van der Waals gap required for the 1T′-Td transition. It is thus surmised that this situation allowed the measurement of the EXAFS spectrum of 1T′-MoTe₂ at a low temperature (10 K) where a reduced phonon population leads to a large decrease in Debye–Waller factors. For all spectra, the simulated results well reproduced the experimental EXAFS, supporting the XRD (Fig. 2) and Raman (Fig. 3) structural analysis of the local structure.

Fig. 5 Experimental Fourier transformed EXAFS spectra and the corresponding simulated spectra calculated using the FEFF for the 1T′ and 2H MoTe₂ phases at the Mo edge (a) and Te edge (b).

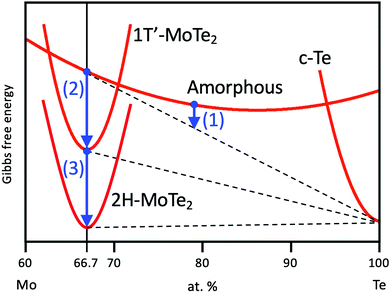
Based upon the obtained results, we propose a model for the phase-change process of Mo–Te films from the as-deposited amorphous to the crystalline phases. Fig. 6(a) shows the Mo–Te binary phase diagram.⁴¹ As mentioned in the Experimental section, the initial film composition is Te-rich, which is shown as step (i) in Fig. 6(a). The corresponding atomic arrangement is shown in Fig. 6(b). Te crystallizes first at 300 °C as shown in Fig. 1. Fig. 6(b) (ii) demonstrates the precipitation of Te crystal grains in the amorphous matrix. This situation is schematically depicted in Fig. 7 from the viewpoint of the Gibbs free energy vs. composition. In contrast to the crystalline phase appearing in the equilibrium phase diagram, the metastable amorphous phase can exist over a relatively wide compositional range, which is represented by a higher and broader Gibbs free energy curve as a function of composition. Since there is no stoichiometric compound for the given composition (Mo_21.1Te_78.9), the as-deposited Te-rich amorphous film is expected to undergo phase separation. This situation can be regarded as “primary crystallization” behavior.⁴² The arrow (1) in Fig. 7 represents the primary crystallization of the initial amorphous phase into Te. This reaction concomitantly leads to the Mo enrichment of the remaining amorphous phase, whose situation can be schematically shown as a common tangent between the crystalline Te (c-Te) and amorphous curves. Further heating at a higher temperature results in “polymorphic crystallization”⁴² shown as the arrow (2) in Fig. 7. This behavior characterizes the crystallization of the amorphous phase without a change in composition into the crystalline compound. The coexistence of two crystalline phases, MoTe₂ and Te, is realized as illustrated in Fig. 6(b)(iii). It should be noted that even though the crystallization process is complete, the obtained phase (1T′) is metastable in this temperature range, suggesting that the Gibbs free energy is not still at a minimum as shown in Fig. 7. Prior to the phase transition of MoTe₂, however, the annealing temperature exceeds the melting point of pure Te (∼450 °C) leading to the partial melting of Te (Fig. 6(b)(iv)). Since the liquid phase exhibits a diffusion rate orders of magnitude higher than that of the solid, the molten Te atoms can easily diffuse out of the crystalline MoTe₂ matrix toward grain boundaries and finally evaporate at a higher temperature (Fig. 6(b)(v)). According to the XRD results shown in Fig. 1(c), this temperature is estimated to be around 600 °C because the Te peak disappears under vacuum presumably via sublimation through cracks formed in the SiO₂ cap. By analogy, this process resembles the flux method where crystal growth is realized from a source dissolved in a flux. In general, a saturated solution is prepared and a decrease of the temperature results in the precipitation of the desired crystal from the solvent. In the present case, the nucleation of pure Te takes place in a saturated Mo–Te amorphous solid solution, and the remaining phase approaches a composition near that of stoichiometric MoTe₂. Subsequently, the preferential sublimation of Te during the vacuum anneal process leads to MoTe₂ polymorphic crystallization. After annealing at higher temperature for longer times, the 1T′-MoTe₂ phase eventually transforms into the stable 2H-MoTe₂ phase as shown in Fig. 6(b)(vi) and arrow (3) in Fig. 7. Consequently, the final film consists of a single phase of 2H-MoTe₂ with a stoichiometric composition even though the initial composition was strongly Te-rich.

Fig. 6 (a) A Mo–Te binary phase diagram with the proposed phase change process.⁴¹ Each number corresponds to (b). (b) A detailed schematic of the phase change process from the Te-rich amorphous Mo–Te phase to the 1T′ and 2H-MoTe₂ crystalline phases.

Fig. 7 Plot of the Gibbs free energy of all phases.

A cross-sectional TEM micrograph of the 2H-MoTe₂ film is shown in Fig. 8. The lateral grain size exceeds 200 nm, and moreover, a layered structure with lateral vdW gaps to the substrate is clearly visible, which is in good agreement with the XRD results showing 00l-oriented peaks. Such highly oriented features can be often observed in other layered tellurides.^43,44 A fast Fourier transformed (FFT) image shows spots along the out-of-plane direction, and the spot location was found to correspond to the (002) lattice spacing. These TEM results strongly support the potential of the large area growth of a MoTe₂ film by sputtering followed by optimized annealing.

Fig. 8 (a) High-resolution TEM image of the 2H-MoTe₂ film. (b) Zoomed in image of the dashed-square area in figure (a). (c) FFT image obtained from the entire area of figure (b).

4. Conclusions

The crystallization behavior of an off-stoichiometric amorphous Mo–Te thin film was systematically investigated. Depending on the annealing conditions, the as-deposited amorphous phase transformed to c-Te + amorphous MoTe₂, c-Te + 1T′-MoTe₂, 1T′-MoTe₂, and 2H-MoTe₂. The local structure of the amorphous phase was found to be similar to that of the 1T′-MoTe₂ phase and formed the initial crystalline phase although the phase is metastable and nominally a high temperature phase. Throughout the phase-change process, the preferential sublimation of Te was found to play a key role in obtaining the stoichiometric crystalline phase. In other words, this is a robust technique for fabrication of single phase MoTe₂ even from an off-stoichiometric amorphous phase, which has a great advantage over other thin film growth techniques.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the JSPS KAKENHI No. 19H02619, 21H05009, and 21K20509. M. K. acknowledges the Czech Science Foundation (19-17997S) and the Ministry of Education, Youth and Sports (LM2018103). EXAFS measurements were performed at beamline BL01B1 at SPring-8 with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal No. 2019B1324). The authors acknowledge Dr Toshiaki Ina for his technical help with the EXAFS measurements.

Notes and references

1. IEEE IRDS 2021 edition, https://irds.ieee.org/editions/2021.
2. A. V. Kolobov and J. Tominaga, Two-Dimensional Transition-Metal Dichalcogenides. 239, Springer International Publishing, 1st edn, 2016.
3. A. Zavabeti, A. Jannat, L. Zhong, A. A. Haidry, Z. Yao and J. Z. Ou, Nano-Micro Lett., 2020, 12, 66.
4. Z. Cai, B. Liu, X. Zou and H.-M. Cheng, Chem. Rev., 2018, 118, 6091–6133.
5. H. G. Kim and H.-B.-R. Lee, Chem. Mater., 2017, 29, 3809–3826.
6. B. J. Carey, J. Z. Ou, R. M. Clark, K. J. Berean, A. Zavabeti, A. S. R. Chesman, S. P. Russo, D. W. M. Lau, Z.-Q. Xu, Q. Bao, O. Kavehei, B. C. Gibson, M. D. Dickey, R. B. Kaner, T. Daeneke and K. Kalantar-Zadeh, Nat. Commun., 2017, 8, 14482.
7. A. Roy, H. C. P. Movva, B. Satpati, K. Kim, R. Dey, A. Rai, T. Pramanik, S. Guchhait, E. Tutuc and S. K. Banerjee, ACS Appl. Mater. Interfaces, 2016, 8, 7396–7402.
8. L. A. Walsh and C. L. Hinkle, Appl. Mater. Today, 2017, 9, 504–515.
9. Z. Yang and J. Hao, J. Mater. Chem. C, 2016, 4, 8859–8878.
10. S. Hussain, J. Singh, D. Vikraman, A. K. Singh, M. Z. Iqbal, M. F. Khan, P. Kumar, D.-C. Choi, W. Song, K.-S. An, J. Eom, W.-G. Lee and J. Jung, Sci. Rep., 2016, 6, 30791.
11. J.-H. Huang, K.-Y. Deng, P.-S. Liu, C.-T. Wu, C.-T. Chou, W.-H. Chang, Y.-J. Lee and T.-H. Hou, Adv. Mater. Interfaces, 2017, 4, 1700157.
12. J.-H. Huang, H.-H. Hsu, D. Wang, W.-T. Lin, C.-C. Cheng, Y.-J. Lee and T.-H. Hou, Sci. Rep., 2019, 9, 8810.
13. M. Krbal, V. Prokop, A. A. Kononov, J. R. Pereira, J. Mistrik, A. V. Kolobov, P. J. Fons, Y. Saito, S. Hatayama, Y. Shuang, Y. Sutou, S. A. Rozhkov, J. R. Stellhorn, S. Hayakawa, I. Pis and F. Bondino, ACS Appl. Nano Mater., 2021, 4, 8834–8844.
14. S. Ishihara, Y. Hibino, N. Sawamoto, K. Suda, T. Ohashi, K. Matsuura, H. Machida, M. Ishikawa, H. Sudoh, H. Wakabayashi and A. Ogura, Jpn. J. Appl. Phys., 2016, 55, 04EJ07.
15. A. V. Kolobov, P. Fons, A. I. Frenkel, A. L. Ankudinov, J. Tominaga and T. Uruga, Nat. Mater., 2004, 3, 703.
16. C. Ruppert, O. B. Aslan and T. F. Heinz, Nano Lett., 2014, 14, 6231–6236.
17. N. R. Pradhan, D. Rhodes, S. Feng, Y. Xin, S. Memaran, B.-H. Moon, H. Terrones, M. Terrones and L. Balicas, ACS Nano, 2014, 8, 5911–5920.
18. X. Liu, A. Islam, J. Guo and P. X.-L. Feng, ACS Nano, 2020, 14, 1457–1467.
19. Y. Wang, J. Xiao, H. Zhu, Y. Li, Y. Alsaid, K. Y. Fong, Y. Zhou, S. Wang, W. Shi, Y. Wang, A. Zettl, E. J. Reed and X. Zhang, Nature, 2017, 550, 487–491.
20. D. A. Rehn, Y. Li, E. Pop and E. J. Reed, npj Comput. Mater., 2018, 4, 2.
21. F. Zhang, H. Zhang, S. Krylyuk, C. A. Milligan, Y. Zhu, D. Y. Zemlyanov, L. A. Bendersky, B. P. Burton, A. V. Davydov and J. Appenzeller, Nat. Mater., 2019, 18, 55–61.
22. I. M. Datye, M. M. Rojo, E. Yalon, S. Deshmukh, M. J. Mleczko and E. Pop, Nano Lett., 2020, 20, 1461–1467.
23. W. Hou, A. Azizimanesh, A. Sewaket, T. Pen a, C. Watson, M. Liu, H. Askari and S. M. Wu, Nat. Nanotechnol., 2019, 14, 668–673.
24. Y.-Q. Bie, G. Grosso, M. Heuck, M. M. Furchi, Y. Cao, J. Zheng, D. Bunandar, E. Navarro-Moratalla, L. Zhou, D. K. Efetov, T. Taniguchi, K. Watanabe, J. Kong, D. Englund and P. Jarillo-Herrero, Nat. Nanotechnol., 2017, 12, 1124.
25. D. Kim, R. Lee, S. Kim and T. Kim, J. Alloys Compd., 2019, 789, 960–965.
26. Z. Wang, F. Wang, L. Yin, Y. Huang, K. Xu, F. Wang, X. Zhan and J. He, Nanoscale, 2016, 8, 13245–13250.
27. J. C. McGlynn, T. Dankwort, L. Kienle, N. A. G. Bandeira, J. P. Fraser, E. K. Gibson, I. Cascallana- Matías, K. Kamarás, M. D. Symes, H. N. Miras and A. Y. Ganin, Nat. Commun., 2019, 10, 4916.
28. D. H. Keum, S. Cho, J. H. Kim, D.-H. Choe, H.-J. Sung, M. Kan, H. Kang, J.-Y. Hwang, S. W. Kim, H. Yang, K. J. Chang and Y. H. Lee, Nat. Phys., 2015, 11, 482–486.
29. K. Deng, G. Wan, P. Deng, K. Zhang, S. Ding, E. Wang, M. Yan, H. Huang, H. Zhang, Z. Xu, J. Denlinger, A. Fedorov, H. Yang, W. Duan, H. Yao, Y. Wu, S. Fan, H. Zhang, X. Chen and S. Zhou, Nat. Phys., 2016, 12, 1105–1110.
30. A. Zhang, X. Ma, C. Liu, R. Lou, Y. Wang, Q. Yu, Y. Wang, T.-L. Xia, S. Wang, L. Zhang, X. Wang, C. Chen and Q. Zhang, Phys. Rev. B, 2019, 100, 201107.
31. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
32. S. Hatayama, Y. Shuang, P. Fons, Y. Saito, A. V. Kolobov, K. Kobayashi, S. Shindo, D. Ando and Y. Sutou, ACS Appl. Mater. Interfaces, 2019, 11, 43320–43329.
33. T. Siegrist, P. Jost, H. Volker, M. Woda, P. Merkelbach, C. Schlockermann and M. Wuttig, Nat. Mater., 2011, 10, 202.
34. K. Ueno and K. Fukushima, Appl. Phys. Express, 2015, 8, 095201.
35. D. C. Palmer, Crystalmaker, CrystalMaker Software Ltd, Begbroke, Oxfordshire, England, 2014.
36. J. C. Park, S. J. Yun, H. Kim, J.-H. Park, S. H. Chae, S.-J. An, J.-G. Kim, S. M. Kim, K. K. Kim and Y. H. Lee, ACS Nano, 2015, 9, 6548–6554.
37. S. Paul, S. Karak, M. Mandal, A. Ram, S. Marik, R. P. Singh and S. Saha, Phys. Rev. B, 2020, 102, 054103.
38. L. Zhou, K. Xu, A. Zubair, A. D. Liao, W. Fang, F. Ouyang, Y.-H. Lee, K. Ueno, R. Saito, T. Palacios, J. Kong and M. S. Dresselhaus, J. Am. Chem. Soc., 2015, 137, 11892–11895.
39. Y.-Y. Lv, L. Cao, X. Li, B.-B. Zhang, K. Wang, B. Pang, L. Ma, D. Lin, S.-H. Yao, J. Zhou, Y. B. Chen, S.-T. Dong, W. Liu, M.-H. Lu, Y. Chen and Y.-F. Chen, Sci. Rep., 2017, 7, 44587.
40. X.-J. Yan, Y.-Y. Lv, L. Li, X. Li, S.-H. Yao, Y.-B. Chen, X.-P. Liu, H. Lu, M.-H. Lu and Y.-F. Chen, npj Quantum Mater., 2017, 2, 31.
41. H. Okamoto, M. Schlesinger and E. Mueller, Mo (Molybdenum) Binary Alloy Phase Diagrams, Alloy Phase Diagrams, ASM International, 2016, vol. 3, pp. 489–498.
42. U. Köster and U. Herold, Crystallization of metallic glasses, in Glassy Metals I. Topics in Applied Physics, ed. H. J. Güntherodt and H. Beck, Springer Berlin Heidelberg, 1981, vol. 46, pp. 225–259.
43. Y. Saito, S. Hatayama, Y. Shuang, P. Fons, A. V. Kolobov and Y. Sutou, Sci. Rep., 2021, 11, 4782.
44. Y. Saito, M. Morota, K. Makino, J. Tominaga, A. V. Kolobov and P. Fons, Mater. Sci. Semicond. Process., 2021, 135, 106079.

---