Octahedral tilting in Prussian blue analogues

Abstract

Octahedral tilting is key to the structure and functionality of perovskites. We present a metastudy of published literature showing how these distortions manifest in the related Prussian blue analogues (PBAs): cyanide versions of double perovskites with formula AM[M′(CN)₆]_1−y□_y·nH₂O (A = alkali metal, M and M′ = transition metals, □ = vacancy/defect). Tilts are favoured by high values of x if A = Na or K, whereas the transition metals play a less important role. External hydrostatic pressure induces tilt transitions nearly irrespective of the stoichiometry, whereas thermal transitions are only reported for x > 1. Interstitial water can alter the transitions induced by a different stimulus, but (de)hydration per se does not lead to tilts. Finally, the implications for rational design of critical functionality—including improper ferroelectricity and electrochemical performance—are discussed. The results are integral for a fundamental understanding of phase transitions and for the development of functional materials based on PBAs.

---

Hanna L. B. Boström

Hanna Boström grew up in Uppsala (Sweden), but received her MChem from the University of St Andrews (UK). She then relocated to Oxford to carry out her DPhil in Inorganic Chemistry under the supervision of Prof. Andrew Goodwin. Following a short postdoctoral stint in Uppsala, she is currently a Humboldt research fellow at the Max Planck Institute for Solid State Research in Stuttgart (Germany), working in the group of Prof. Bettina Lotsch. Hanna's research interests revolve around the crystallography of metal–cyanide frameworks, often under nonambient conditions, and she has a particular soft spot for complexes containing the beautiful blue Cu^2+ ion.

1 Introduction

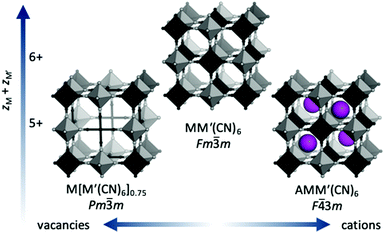
Prussian blue analogues (PBAs) are a versatile class of materials with a wide range of potential applications. The functional diversity partially arises from the large scope for compositional variation: the general formula is A_xM[M′(CN)₆]_1−y□_y·nH₂O, where A is an alkali metal, M and M′ are normally transition metals and □ denotes a vacancy. Porous, defective systems of formula M^II[M′^III(CN)₆]_0.67 can be used for catalysis and adsorption of gases and toxic metals,^1,2 whereas defect-free, alkali-containing PBAs, e.g. A₂M′^IIM′^II(CN)₆, are suitable electrode materials³ and/or may show interesting magnetic properties.⁴ The stoichiometry and associated functionality is stipulated by the charges of the transition metals, where lower charges increase the scope for inclusion of vacancies and/or A-site cations [Fig. 1]. The crystal structure of PBAs is reminiscent of that of double perovskites with two octahedrally coordinated metals: M(NC)₆ and M′(CN)₆. The parent structure (aristotype) adopts the space group Fm3̄m, although ordered A-site cations or vacancies may reduce the symmetry to F4̄3m or Pm3̄m [Fig. 1].

Fig. 1 The crystal structure of Prussian blue analogues. If the charges of the transition metals sum to 6, the ordered MM′(CN)₆ is formed. For lower charges, vacancies or A-site cations are included to give the formulae M[M′(CN)₆]_y<1 and A_x>0M[M′(CN)₆], respectively. M is shown in dark grey, M′ in light grey and A in purple.

A crucial feature of ABX₃ perovskite physics is octahedral tilting, which involves in-phase or out-of-phase rotation of BX₆ octahedra. In Glazer notation, this is denoted by superscripted ‘+’ and ‘−’ and lowercase letters indicate relative magnitudes around the three pseudo-cubic axes.⁵ The importance of tilts arises from their link to both the composition and to the properties. For example, the relative ionic radii of the constituent metals, as expressed by the tolerance factor,⁶ dictate whether tilts are favoured, which facilitates some degree of control. Compositional modification can be used to tune the tilt angle, which in turn affects e.g. the band gap and the Curie temperature.⁷ Moreover, the link between tilting and structure is well established via group-theoretical methods,^8,9 and knowledge of the tilts typically allows for the prediction of the space group symmetry. This was exploited in so-called tilt engineering of a multiferroic perovskite derivative, where careful activation of appropriate tilts led to polar symmetry with coexisting weak magnetism.¹⁰ Octahedral tilts therefore present an attractive route for the design of technologically relevant materials.

Given the structural similarities between perovskites and PBAs, it is natural that octahedral tilting also occurs in PBAs with functional implications. By way of example, the tilts in Na₂MnMn(CN)₆ nearly triple the magnetic transition temperature compared to the untilted Cs₂MnMn(CN)₆.¹¹ A less favourable situation is the drastic volume reduction of 17% in Mn[Mn(CN)₆]_0.93 upon Na intercalation, which is driven by a tilt transition from cubic symmetry (i.e. untilted) to a⁻a⁻a⁻.¹² This has a detrimental effect on the electrode stability and compromises the application of PBAs as energy storage materials. As a consequence, understanding and ultimately controlling the presence or absence of octahedral tilts in PBAs is key to their commercial development as functional materials.

In spite of its importance, octahedral tilting in PBAs is poorly understood and there is considerable confusion regarding the structural characterisation of these materials. To illustrate, cubic (no tilts) and monoclinic symmetries (a⁻a⁻b⁺ tilts) were postulated for the closely related Na_1.52Ni[Fe(CN)₆]_0.88 and Na_1.48Ni[Fe(CN)₆]_0.89, respectively,^13,14 while a third study claims Na_xNi[Fe(CN)₆]_0.83 to be rhombohedral (a⁻a⁻a⁻ tilts) at all x-values.¹⁵ A systematic understanding of the factors underlying octahedral tilting in PBAs would be beneficial to a wide range of fields and pave the way for tilt engineering approaches. Certain principles developed for inorganic perovskites are likely transferable to PBAs, which provides a starting point for such investigations. However, PBAs show features that are rare or unknown in perovskites, such as vacancies and porosity, and therefore their behaviour cannot be expected to exactly mirror that of perovskites.

Here, we perform a metastudy to investigate the octahedral tilting in Prussian blue analogues. Our manuscript identifies the possible driving forces for tilting—stoichiometry, composition, hydration, and nonambient conditions—and discusses their effect on the propensity for, and nature of, tilting. The results are compared and contrasted with the tilt behaviour of double perovskites throughout. Our results show that tilts are favoured by high A-site cation concentrations if A = Na or K, whereas the identity of the transition metals is considerably less relevant. The presence of interstitial water can direct the tilt transitions induced by a different stimulus, but (de)hydration does not appear to drive tilts in its own right. External hydrostatic pressure can induce tilt transitions almost regardless of the stoichiometry, whereas thermal transitions only occur for high A-site cation concentrations. We conclude by discussing strategies for tilt engineering, using energy storage, magnetism, and improper ferroelectricity as example functionalities.

2 Methods

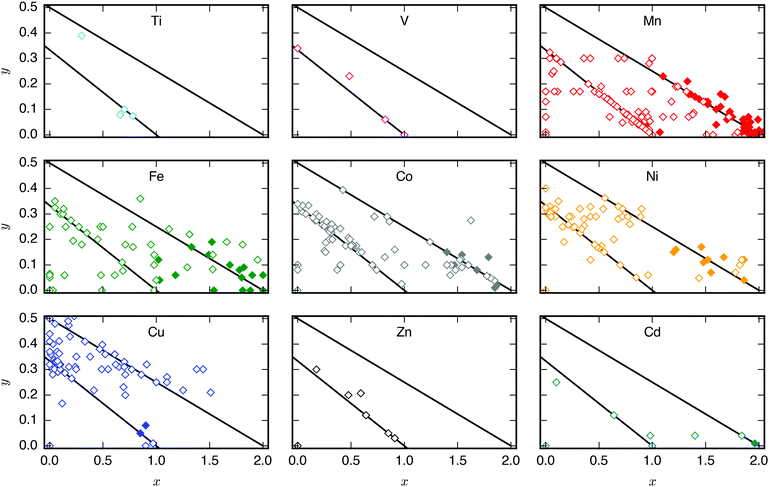
A database of PBA structures was created manually by retrieving a large number of research articles (170 articles, 564 compounds) [ESI†]. The identities of the A, M, and M′ sites, x- and y-values, and presence/absence of tilting were extracted. Only studies where the ambient structure was confirmed by diffraction and the composition characterised by either EDX or ICP were included. As Rietveld refinements are not routinely carried out, any deviation from cubic symmetry—manifested by reflection splitting—was considered to be due to tilting, except in cases where other symmetry-lowering distortion (i.e. Jahn–Teller distortions) are obviously present. As uncertainties from elemental analysis are rarely reported, no error bars were included in the figures and thus quantitative conclusions should be drawn with caution. Compounds with mixed cations on the A-site where the minority species exceeded 5% of the total x-value were excluded from Fig. 2, although it should be stressed that many PBAs contain a small amount of K⁺ from the synthesis. Likewise, systems with mixed M-site metals were not included in Fig. 4.

Fig. 2 Tilts in PBAs as a function of stoichiometry. Top panel: PBAs with composition A_xM[M′(CN)₆]_1−y□_y (□ = vacancy) for various A, where filled (empty) symbols denote tilted (untilted) structures. The diagonal lines show compositions with a constant sum of the transition metal charges (+5 and +4). Representative structures are shown for key stoichiometries, with the M and M′ ions in black and grey, respectively, and the A-site cation in purple. Cyanide ions are omitted for clarity. Lower panel: The above phase diagram plotted with a separate figure for each A-site cation.

3 Results

3.1 Stoichiometry

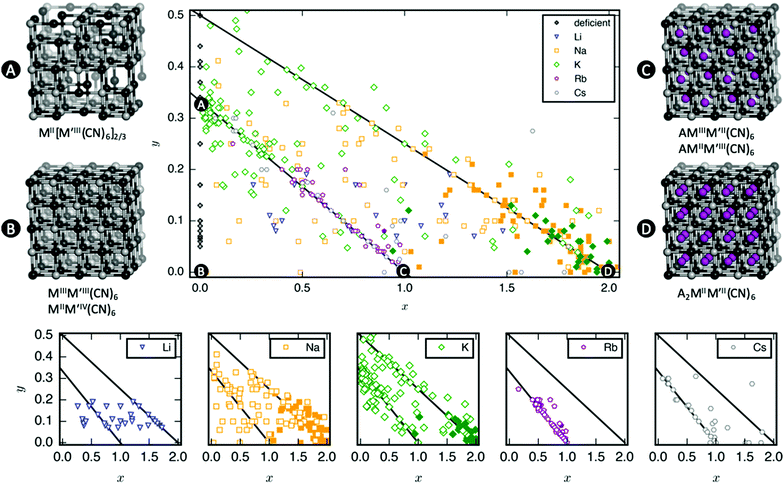
As mentioned, PBAs have a variable stoichiometry described by the general formula A_xM[M′(CN)₆] (□ = vacancy). As A-site cations (x) and vacancies (y) often coexist, a continuum of intermediate stoichiometries is accessible. Fig. 2 depicts the compositional space in terms of x and y, populated by structures reported in literature. Lines corresponding to compositions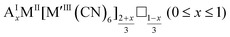 and 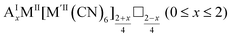are indicated and many structures fall close to these lines. In particular, PBAs with redox-inactive transition metals will be found here. Entries in other areas of the phase diagram represent PBAs with mixed oxidation states of M and/or M′, e.g. K_0.4Cu[Fe_0.6^IIFe_0.4^III(CN)₆]_2/3.¹⁶ This phase diagram highlights two common features of PBAs that rarely occur in double oxide perovskites: partially occupied A-sites, e.g. AMM′(CN)₆, and M′(CN)₆ vacancies, e.g. AM[M′(CN)₆]_y<1.

Fig. 2 demonstrates that a minimum concentration of alkali metals is required for tilting. As uncertainties from elemental analyses are rarely reported, no error bars are included in Fig. 2, and hence it is difficult to draw compelling quantitative conclusion. Still, nearly all tilted PBAs show x > 1, suggesting that this is a necessary condition for tilts. Yet, it is not a sufficient condition, as several reportedly cubic PBAs with higher A-site concentrations exist.^17,18 While such discrepancies may partially stem from suboptimal data quality of in-house diffractometers or incorrect compositions, differences in local structure due to deviating synthesis conditions may also play a role. The relatively empty region at x = 1.0–1.5 and y = 0–0.1 in Fig. 2 suggests a miscibility gap, which agrees with the phase separation sometimes reported in PBAs with large values of x.^12,19 A detailed understanding of the critical threshold concentration and potential miscibility gap is crucial for the application of PBAs in secondary ion batteries, as the tilt transition changes the transport properties and causes an unwanted strain.^12,14 Consequently, further studies are needed, though it is clear that the A-site concentration is central to the tilts.

In principle, vacancies could affect the propensity for tilting by reducing the tilt correlation length, thereby preventing global phase transitions. The disorder of the vacancies is complex and depends both on the metal ions and the synthesis conditions,²⁰ which complicates the study of the functional implications of missing M′(CN)₆ clusters. Moreover, as vacancies and A-site cations are interdependent, their respective roles are difficult to decouple. However, the absence of vacancies is not sufficient to induce tilting as PBAs with formula MM′(CN)₆ are invariably undistorted at ambient conditions.²¹ Likewise, certain PBAs exhibit tilts despite a high vacancy concentration, like Na_1.10Mn[Fe(CN)₆]_0.77.²² Thus, vacancies alone do not appear to play a major role in the tilting; however, this may be system-dependent and further studies are encouraged.

Finally, a few general comments can be made about Fig. 2. First, a considerable number of systems comprise transition metals ions with charges summing to less than 4 (area above the right diagonal line). This indicates a partially univalent transition metal or the presence of hydroxide ions in the framework.^23,24 Second, several structures feature an apparent vacancy content above 33% (top left corner). However, certain transition metal ions have been postulated to occupy both the A- and M-site, such as Cu[Fe(CN)₆]_0.5,²⁵ which means that the actual vacancy concentration of such structures is less than 50%. While the possibility of divalent A-site cations and their relation to the maximum vacancy concentration is interesting and merits further study, this will not be discussed further in this manuscript.

3.2 A-site composition

The tendency for tilting not only depends on the concentration of A-site cations, but also on the A-site ionic radius [Fig. 2]. PBAs based on Na or K feature the largest proportions of tilted structures, whereas systems with A = Li rarely tilt. Although relatively understudied, some Rb-containing tilted structures are known,^11,26,27e.g. Rb₂MnMn(CN)₆ (x ∼ 2). Due to the lack of elemental analysis, this compound is not included in Fig. 2.¹¹ To the best of our knowledge, distorted Cs-containing PBAs do not exist at ambient conditions. Experimental evidence additionally suggests that Cs⁺ may preferentially occupy the vacant sites in systems with M′-site vacancies,^28,29 which would further decrease the tendency for Cs to induce structural distortions. While some observational bias is present here—Na- and K-containing systems are the most intensely studied—intermediate alkali metal radii appear to favour tilting.

The correlation between A-site cation size and tilt propensity partially agrees with perovskites, where the driving force for tilts is considered to be the underbonding of small A-site cations, as quantified by the tolerance factor.^6,30,31 Although the tolerance factor has been extended to molecular perovskites,³² it is less applicable as it does not account for vacancies. Yet, the same argument underlies the prevalence of tilting in PBAs with A = Na/K relative to A = Rb/Cs, as smaller cations are more prone to underbonding. It is also consistent with the inverse relationship between tilt angles and A-site cation size in A₂MnMn(CN)₆.³³ It does not rationalise the lack of tilting in Li-based PBAs, but Li is believed to occupy the window sites of the PBA subcube, as opposed to the centre.³⁴ This mirrors the behaviour of Li-containing perovskites.^35,36 Thereby, the bonding environment can presumably be optimised even without tilts. Altogether, the radius of the A-site cation is a key factor to consider when evaluating the propensity for tilting of a given structure.

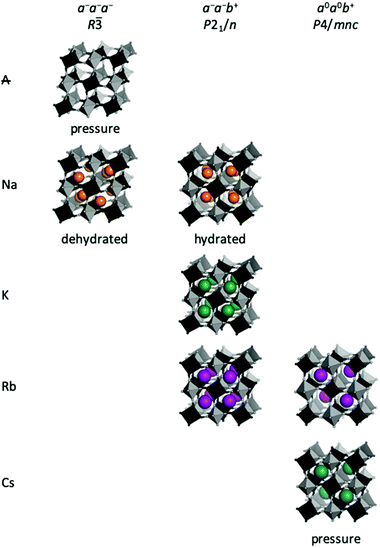
In general, the size of the A-site cation also stipulates the type of tilt [Fig. 3]. A-site deficient PBAs under compression preferentially adopt a⁻a⁻a⁻ tilts giving R3̄ symmetry,³⁷ which is also seen in the fluoride analogues MnNbF₆ and CaTiF₆.^38,39 This tilt pattern is also preferred by dehydrated Na-containing PBAs^11,40–42 and allows the Na ion to displace along the cubic [111] direction towards one of the transition metals. This displacement is sometimes considered the driving force for cubic–rhombohedral phase transitions, which would give rhombohedral R3̄m symmetry in the absence of tilts.^43–45 As the reflection conditions of R3̄m and R3̄ are identical, distinguishing between these space groups is difficult. Yet, as framework distortions and A-site displacements are likely to couple, we believe structures reported in R3̄m are possibly better described in R3̄ with a⁻a⁻a⁻ tilts in conjunction with A-site displacements. Similar situations have been noted for oxide perovskites.⁴⁶

Fig. 3 Tilt patterns in Prussian blue analogues. The distribution of tilt patterns across PBAs with various A-site cations, where ‘A’ denotes the absence of A-site cations. The space group refers to the symmetry that the tilt gives rise to in the absence of further distortions. Tilts that (so far) are only known under pressure are indicated.

The a⁻a⁻b⁺ tilt pattern is the most prevalent in oxide perovskites and it is known for PBAs with A = Na, K, or Rb and large x values.^11,46,47 This tilt pattern drives monoclinic P2₁/n symmetry⁹ and the A-site cation has three translational degrees of freedom, allowing a complete optimisation of the bonding environment.⁴⁸ In addition to PBAs with compositions close to the ideal A₂MM′(CN)₆, a⁻a⁻b⁺ tilts can also be induced by pressure in Rb_0.87Mn[Co(CN)₆]_0.91, which adopts cubic F4̄3m symmetry at ambient conditions.⁴⁹ For A = Na, the tilt pattern is also stipulated by the hydration state, which will be discussed in the subsequent section. It follows that a⁻a⁻b⁺ is the tilt system present for the widest range of A-site cations and can be observed both at ambient and non-ambient conditions.

Finally, PBAs with large cations (Rb/Cs) may exhibit the uniaxial a⁰a⁰b⁺ distortion. CsMnCo(CN)₆ develops a⁰a⁰b⁺ tilts upon compression to 2 GPa, leading to P4̄n2 symmetry, and this constitutes the only known tilted Cs-based PBA to date.⁴⁹ The relatively high transition pressure highlights how large A-site cations reduce the tendency for tilting. Pressure- and photo-induced a⁰a⁰b⁺ tilts are known in Rb-based PBAs,^49,50 but also feature at ambient conditions in the Jahn–Teller distorted RbCuM′(CN)₆ (M = Co^III or Fe^III).^26,27 Interestingly, the a⁰a⁰b⁺ distortion is exceedingly rare in double oxide perovskites,⁴⁶ albeit common in perovskite halides.⁵¹ This illustrates how trends observed in inorganic perovskites cannot always be directly applied to their molecular counterparts.

3.3 M/M′-site composition

The transition metal ions may impact the propensity for structural distortions in PBAs by modulating the bond strength and thereby the flexibility. For example, the M–N bond strength in MPt(CN)₆ depends on the identity of M according to the Irving–Williams series, with NiPt(CN)₆ (CdPt(CN)₆) as the most (least) rigid system.²¹ In general, smaller M-site cations are believed to decrease the flexibility, which also manifests in more positive thermal expansion.⁵² This agrees with the description of Na_xNiFe(CN)₆ as a zero-strain material with a low tendency for distortions upon Na intercalation.⁵³ To investigate this further, the data presented in Fig. 2 were replotted to highlight the effect of the different M-sites [Fig. 4].‡ While more tilted systems are reported for M = Mn, Fe, Co, and Ni, this probably results from observational bias and small sample sizes for some of the other M-site metals. There is not enough data to draw any conclusion regarding the the role of the M-sites on tilting. However, as several tilted PBAs with M = Ni are reported,^14,15 the idea of Ni-PBAs as zero-strain materials may require reevaluation.

Fig. 4 The effect of M-site transition metal ions on the propensity for tilting. PBAs with composition A_xM[M′(CN)₆]_1−y□_y (□ = vacancy) for various A, where filled (empty) symbols denote tilted (untilted) structures and the different panels refer to different M-site cations. The diagonal lines indicate compositions with a constant sum of the transition metal charges (+5 and +4).

Jahn–Teller active M-site cations can contribute to tilting in certain Rb-containing PBAs. Rb_0.85Cu[Fe(CN)₆]_0.95 and Rb_0.90Cu[Co(CN)₆]_0.92 exhibit tilts,^26,27 whereas related structures with M = Zn^II or Mn^II are undistorted at ambient conditions.^54,55 Group-theoretical analysis indicates that the observed a⁰a⁰b⁺ tilt mode arises from a combination of the Jahn–Teller distortion and the occupational (M-point) Rb arrangement.²⁶ Rb_0.58Mn[Fe(CN)₆]_0.86 shows a Jahn–Teller distortion, but remains untilted due to its different (R-point) Rb order.⁵⁶ As cubic symmetry is reported for KCuFe(CN)₆ and CsCuFe(CN)₆,^27,57 this phenomenon appears specific to Rb-containing systems. The interplay between tilts, Rb order and Jahn–Teller distortions is interesting and suggests that tilt engineering may be facilitated by introducing Cu^II ions in suitable systems.

There is less choice of metal ions for the M′-site, as they have to support octahedral low-spin coordination. Typical M′-site metals are Cr^III, Mn^II/III, Fe^II/III, Co^III, and Pt^IV, with the largest prevalence of Fe due to its stability, low toxicity, and low cost. As a result, it is difficult to evaluate the influence of the M′-site on the tilting propensity, but this effect is likely to be minor. As the M′–C interaction is largely covalent and features strong π-backbonding from the metal to the cyanide, linear M′–C–N bonding is favoured. Indeed, the N typically shows larger mobility than the C atom, highlighting how most flexibility stems from the N–M linkage, rather than from C–M′.²¹ A neutron diffraction study of the rhombohedrally tilted Na_1.89Mn[Fe(CN)₆]_0.97 also indicates a larger deviation from linearity at the N end of the cyanide relative to the C end.⁴¹ Hence, the tilt propensity is presumably relatively unchanged as a function of M′-site substitutions, athough experimental evidence is needed for confirmation.

3.4 Hydration

PBAs are nearly always synthesised from aqueous solution and the final products—if porous—thus contain water. It is generally accepted that defective PBAs contain two types of water: coordinated water completing the coordination sphere of the M-site cation, and interstitial water, which may hydrogen bond to the coordinated molecules.⁵⁸ Due to the porous nature of these compounds, over 10 water molecules per cell are possible.^58,59 A-site deficient PBAs of formula MM′(CN)₆ may also support ca. 4 water molecules per unit cell,⁶⁰ although these guest species are only weakly interacting with the framework. Regarding A-site-containing PBAs, systems with A = Li/Na are sufficiently porous to allow for interstitial H₂O, whereas increased A-site occupancy of larger alkali metals reduces the likelihood for solvent incorporation.⁶¹ Although interstitial in nature, water can have a profound effect on e.g. the electrochemical and mechanical properties of the system.^49,62

Unlike many other coordination polymers,⁶³ PBAs are not prone to major structural changes upon dehydration and typically remain cubic as the solvent is removed.^21,59,64 Nonetheless, a tilt transition was noted for Na_1.32Mn[Fe(CN)₆]_0.83·2.2H₂O upon further hydration.⁶⁵ To the best of our knowledge, this behaviour is a unique example of a solvent-induced phase transition in a Prussian blue analogue and further investigations will be valuable. While the role of water in PBAs is intriguing, it is associated with several challenges. Thermogravimetrical analysis (TGA) shows a considerable dependence on the experimental set-up,^16,66 and crystallographers are faced with the challenge of disordered solvent and the low scattering power of light elements. Studies into the role of water using local probes, perhaps using neutron radiation, would be beneficial.

While (de)hydration normally does not drive phase transitions, interstitial water sometimes dictates the tilt pattern. The distortion in Na₂MM′(CN)₆ switches from monoclinic a⁻a⁻b⁺ to rhombohedral a⁻a⁻a⁻ upon solvent removal accompanied by increased amplitude of the distortion.^11,41 Whether K-based PBAs also show hydration-switchable tilts is unknown: monoclinic symmetry is reported for several compounds with high concentration of K and low hydration states,^3,67 and the larger radius of K leaves less free space for water molecules. Furthermore, water alters the pressure-induced phase transition of MnPt(CN)₆, which—at least in the hydrated case—is driven by tilts.⁴⁹ Therefore, while (de)hydration per se does not drive tilting, it has an impact on the tilts pattern induced by a different stimulus (pressure or sodiation). Yet, many questions remain to be answered, regarding e.g. the mechanism and critical water content required for switching.

3.5 Nonambient conditions

Changes in temperature can induce a wealth of phase transitions in oxide perovskites,⁴⁶ and thermal tilts also occur in some PBAs with high A-site concentrations.^43,50,68 For instance, tilts appear in Rb_0.97Mn[Fe(CN)₆]_0.99 upon cooling to 91 K,⁵⁰ whereas a similar system with a lower Rb content, Rb_0.58Mn[Fe(CN)₆]_0.86, remains untilted to 30 K.⁵⁶ Phase diagrams as a function of temperature and A-site cation concentration have been created for certain PBAs, which highlight the possibility of thermal transitions between different tilt systems.⁶⁹ Further such efforts would be useful to understand the relationship between the A-site cation content and the structural instabilities. Conversely, A-site deficient PBAs typically remain cubic down to low temperatures^60,70,71 as the soft tilt modes do not condense. This is interesting in its own right, as transverse low-energy phonons—such as tilts—typically underlie negative thermal expansion.^72–74

Many PBAs undergo phase transitions when subjected to external hydrostatic pressure. For example, MnPt(CN)₆·nH₂O and Mn[Co(CN)₆]_2/3·nH₂O show a⁻a⁻a⁻ tilts when compressed to ∼1.5 GPa, which provides rare examples of tilted PBAs without A-site cations.³⁷ The latter system demonstrates that vacancies do not necessarily disrupt the correlations between individual metal octahedra. However, this transition relies on the presence of interstitial water, as the dehydrated analogue retains its Fm3̄m symmetry when compressed.⁴⁹ This is presumably a result of a hydrogen-bonded network of water molecules within the structure, which mediates correlations between individual metal sites separated by a vacancy. Likewise, FeCo(CN)₆ amorphises at 10 GPa without prior phase transitions,⁷⁵ and FePt(CN)₆ remains cubic to at least 3 GPa,⁷⁶ which shows that pressure does not universally induce tilts in A-site-deficient PBAs. Yet, as even Cs-based PBAs can be forced to tilt by the application of pressure,^49,77 compression is a useful method to obtain interesting phases and explore the tilting behaviour.

3.6 Tilt engineering

Tilt engineering—manipulating the octahedral tilting in order to achieve a desired property—is an appealing concept originally coined for oxide perovskites.¹⁰ Like for the inorganic counterparts, tilts in Prussian blue analogues have clear functional implications and there is potential to improve the performance of PBAs by judicious manipulation of the tilts. Some examples are provided below and more can be anticipated.

Ferroelectricity is a technologically revelant property, yet is only allowed in compounds with polar space groups, which is a subset of the non-centrosymmetric space groups. As tilts inevitably lower the symmetry of the parent structure, they can be exploited to construct polar symmetries via improper ferroelectricity.⁷⁸ Here, nonpolar structural distortions are combined to generate a polar space group and allow for polar secondary order parameters, e.g. a displacement of the A-site cation. Tilts alone cannot lift all the inversion centres of the Fm3̄m parent—as required for polar symmetry and ferroelectric properties; but this can be achieved by combining out-of-phase tilts (a⁻) with R-point occupational A-site cation order.⁷⁹ Such A-site arrangements are frequently found in AMM′(CN)₆, where A = Rb or Cs. For example, a⁻a⁻a⁻ tilts in A-site-cation-ordered PBAs yield the polar space group R3, whereas a⁻a⁻b⁺ drives Pn symmetry. The former symmetry may not be experimentally realisable as a⁻a⁻a⁻ tilts have not been observed for PBAs with ordered A-site cations, but the latter space group occurs in Rb_0.87Mn[Co(CN)₆]_0.91 under modest pressure.⁴⁹ As noted above, the tilting behaviour appears largely independent of the transition metals and transition metal combinations known to give ferromagnetic behaviour, e.g. Ni–Cr,⁸⁰ could be included. This may ultimately lead to the development of multiferroic PBAs.

PBAs are well known for their intriguing magnetic properties and this is also amenable to tilt engineering strategies. In a generic PBA, both antiferromagnetic—t_2g(M) and t_2g(M′)—and ferromagnetic—e_2g(M) and t_2g(M′)—interactions are present.⁴ Judicious manipulation of the relative strength of the coupling constants can give interesting phenomena, including pressure-induced magnetic pole reversal and high ordering temperatures.^4,81 The strength of the ferromagnetic coupling is a function of the M–N–C angle, i.e. the tilting angle, and as a result, the magnetic ordering temperature can be tuned by modifying the tilting.^11,33 This is feasible by manipulating the composition—as in A₂MnMn(CN)₆—or by applying external pressure to increase the amplitude of the distortion.^11,33 Consequently, tilting facilitates the rational design of intriguing magnetic phases of PBAs.

Electrode materials in secondary ion batteries must be able to reversibly insert and extract a high concentration of carrier ions, such as Na⁺. As demonstrated, A-site cations of a specific size and beyond a certain concentration induce tilting in PBAs, which can create a large volume strain leading to material degradation.^12,82 In general, a⁻a⁻a⁻ tilts in systems with A = Na lead to a larger tilt distortion relative to the a⁻a⁻b⁺ distortions observed in K-based systems.⁴¹ Furthermore, the magnitude of the tilt distortion in Na-based systems is reduced in the presence of water.⁴⁰ Taken together, a strategy to minimise the magnitude of the tilt transitions is to maximise the pore filling with species active in the electrochemical process—e.g. the larger K⁺ ion—or inactive species—e.g. water or acetonitrile.⁸³ As the inclusion of electrochemically inactive fillers may reduce the specific capacity through increased weight or occupancy of sites for mobile cations, this must be carefully weighed against improved stability. Any material adjustments must also be compatible with the electrochemical cell chemistry and operation conditions. For example, water excludes nonaqueous chemistries or operation at high voltages. Nonetheless, there are multiple possible approaches towards the same goal, opening up the possibility for engineering A-site cation-rich structures free of tilting.

4 Discussion and conclusion

To summarise, octahedral tilting in PBAs is a function of the stoichiometry, composition, and hydration state. A-site cations are key to the tilting behaviour: high concentrations of intermediately sized A-site cations favour tilting, whereas large ions on the A-site—or indeed no ions at all—lead to cubic, untilted structures. Tilts can condense upon compression in the two latter systems. Three tilt systems are known in PBAs, and again the A-site cation size dictates which one that is observed: small A-site ions drive a⁻a⁻a⁻ or a⁻a⁻b⁺ tilts, whereas larger ions favour a⁰a⁰b⁺ distortions. Moreover, Na-containing PBAs show peculiar hydration-switchable tilt patterns, although the underlying reasons are still unclear. In discussing the A-site cation, it must also be stressed that the A-site concentration interplays with the vacancy concentration and the role of the latter is still not well understood.

All tilt systems described here fall in the class of conventional tilts, i.e. the octahedra rotate in alternate directions parallel to the rotation axis. These are the only tilts allowed in inorganic perovskites. However, by virtue of the diatomic cyanide linker, PBAs theoretically also support so-called unconventional tilts and columnar shifts.^84,85 Yet, there are no confirmed cases of such distortions and a computational study found these modes, particularly the unconventional tilt, to be more energetically unfavourable compared to conventional tilts.⁷² This is presumably due to the strong preference for a linear M′–C–N arrangement, as discussed above, whereas the unconventional distortions require nonlinear binding at both ends of the linker.⁸⁶ While this simplifies the study of distortions in PBAs, as only conventional modes need to be considered, it also limits the diversity of possible distortions. Naturally, it cannot be excluded that even these higher-energy modes may condense under certain conditions.

Our results identify avenues for further research within the PBA community. Correct tilt assignment can be challenging: tilt patterns manifest in the position of the linkers and due to the low X-ray scattering power of light elements, locating cyanide ions using X-ray diffraction is difficult. Yet, accurate tilt determination is crucial and more structural studies using neutron diffraction are recommended. This is particularly important in light of the unconventional distortions mentioned above, as conventional and unconventional tilts cannot be distinguished solely based on the space group.²⁶ Furthermore, it is not known to what extent changes in local structures can affect the tilt modes, and PBAs are known for their diverse and complex vacancy-ordered states.²⁰ In addition to vacancies, this is also particularly relevant for the water arrangements and any local cation order. The field of PBAs would also benefit from computational studies, although the propensity for disorder and the presence of paramagnetic ions present challenges. Finally, the tilt distortions will certainly influence the electronic structure of PBAs; yet this is another field which is largely unexplored.

Octahedral tilting has a bearing on a wide range of properties, from ferroelectricity to magnetism to electrochemistry. As a result, there is clear scope for functional improvement by tilt engineering. In particular, Rb-based PBAs show a large diversity in tilt behaviour and are susceptible to many different external stimuli [Fig. 5], which may be exploited in responsive materials. It remains to be seen whether this is unique to Rb-containing systems. Likewise, there is room for further studies into Li-based PBAs, which has potential implications for energy storage, although the low scattering power of Li render these materials less suitable for studies using X-rays. In addition, since the A-site cation is crucial, tunability of the tilt transitions—whether desired or not—may be expected from A-site solid solutions, i.e.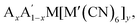 which have received relatively little attention to date. Consequently, advances within the understanding the fundamental tilt transition behaviour of PBAs will likely couple to improvements in functionality.

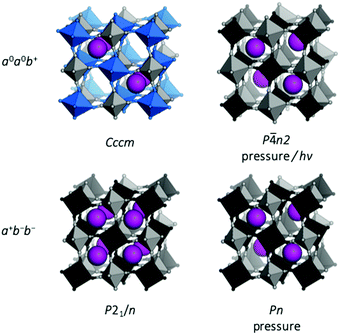Fig. 5 Tilted structures of Rb-based PBAs. (a) Rb_0.90Cu[Co(CN)₆]_0.92, where the tilting is driven by Jahn–Teller distorted Cu (blue) and the unusual Rb arrangement;²⁶ (b) Rb_0.97Mn[Fe(CN)₆]_0.99 under pressure;⁵⁰ (c) Rb₂MnMn(CN)₆ at ambient conditions;⁴⁷ and (d) Rb_0.87Mn[Co(CN)₆]_0.91 under pressure.⁴⁹

Author contributions

HLBB designed the study and collated the data. Both authors evaluated the data and contributed to the writing of the manuscript.

Conflicts of interest

WRB is a co-founder of the company ALTRIS AB which produces Prussian white powder for sodium ion battery applications.

Acknowledgements

We are grateful to A. E. Phillips (Queen Mary University London) for useful discussions. HLBB acknowledges financial support from the Alexander von Humboldt foundation. WRB is grateful to the strategic research area StandUp for Energy and Energimyndigheten project no. 45517-1 for financial support. Open Access funding provided by the Max Planck Society.

References

1. C. Marquez, F. G. Cirujano, S. Smolders, C. Van Goethem, I. Vankelecom, D. De Vos and T. De Baerdemaeker, Dalton Trans., 2019, 48, 3946–3954.
2. P. A. Haas, Sep. Sci. Technol., 1993, 28, 2479–2506.
3. V. Renman, D. O. Ojwang, C. Pay Gómez, T. Gustafsson, K. Edström, G. Svensson and M. Valvo, J. Phys. Chem. C, 2019, 123, 22040–22049.
4. M. Verdaguer, A. Bleuzen, V. Marvaud, J. Vaissermann, M. Seuleiman, C. Desplanches, A. Scuiller, C. Train, R. Garde, G. Gelly, C. Lomenech, I. Rosenman, P. Veillet, C. Cartier and F. Villain, Coord. Chem. Rev., 1999, 190–192, 1023–1047.
5. A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392.
6. V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485.
7. C. L. Bull and P. F. McMillan, J. Solid State Chem., 2004, 177, 2323–2328.
8. C. J. Howard and H. T. Stokes, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 782–789.
9. C. J. Howard, B. J. Kennedy and P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 463–471.
10. M. J. Pitcher, P. Mandal, M. S. Dyer, J. Alaria, P. Borisov, H. Niu, J. B. Claridge and M. J. Rosseinsky, Science, 2015, 347, 420–424.
11. C. M. Kareis, S. H. Lapidus, J.-H. Her, P. W. Stephens and J. S. Miller, J. Am. Chem. Soc., 2012, 134, 2246–2254.
12. D. Asakura, M. Okubo, Y. Mizuno, T. Kudo, H. Zhou, K. Ikedo, T. Mizokawa, A. Okazawa and N. Kojima, J. Phys. Chem. C, 2012, 116, 8364–8369.
13. H. Niwa, W. Kobayashi, T. Shibata, H. Nitani and Y. Moritomo, Sci. Rep., 2017, 7, 13225.
14. Y. Xu, J. Wan, L. Huang, M. Ou, C. Fan, P. Wei, J. Peng, Y. Liu, Y. Qiu, X. Sun, C. Fang, Q. Li, J. Han, Y. Huang, J. A. Alonso and Y. Zhao, Adv. Energy Mater., 2019, 9, 1803158.
15. Z. Ji, B. Han, H. Liang, C. Zhou, Q. Gao, K. Xia and J. Wu, Appl. Mater. Interfaces, 2016, 8, 33619–33625.
16. D. O. Ojwang, J. Grins, D. Wardecki, M. Valvo, V. Renman, L. Häggström, T. Ericsson, T. Gustafsson, A. Mahmoud, R. P. Hermann and G. Svensson, Inorg. Chem., 2016, 55, 5924–5934.
17. D. Yang, J. Xu, X.-Z. Liao, Y.-S. He, H. Liu and Z.-F. Ma, Chem. Commun., 2014, 50, 13377–13380.
18. P. Bhatt, S. S. Meena, M. D. Mukadam, B. P. Mandal, A. K. Chauhan and S. M. Yusuf, New J. Chem., 2018, 42, 4567–4578.
19. Y. Moritomo, K. Igarashi, T. Matsuda and J. Kim, J. Phys. Soc. Jpn., 2009, 78, 074602.
20. A. Simonov, T. De Baerdemaeker, H. L. B. Boström, M. L. Ríos Gómez, H. J. Gray, D. Chernyshov, A. Bosak, H.-B. Bürgi and A. L. Goodwin, Nature, 2020, 578, 256–260.
21. K. W. Chapman, P. J. Chupas and C. J. Kepert, J. Am. Chem. Soc., 2006, 128, 7009–7014.
22. Y. Xi and Y. Lu, Cryst. Growth Des., 2021, 21, 1086–1092.
23. L. Samain, F. Grandjean, G. J. Long, P. Martinetto, P. Bordet and D. Strivay, J. Phys. Chem. C, 2013, 117, 9693–9712.
24. P. R. Bueno, F. F. Ferreira, D. Giménez-Romero, G. O. Setti, R. C. Faria, C. Gabrielli, H. Perrot, J. J. Garcia-Jareño and F. Vicente, J. Phys. Chem. C, 2008, 112, 13264–13271.
25. S. Ayrault, C. Loos-Neskovic, M. Fedoroff, E. Garnier and D. J. Jones, Talanta, 1995, 42, 1581–1593.
26. H. L. B. Boström and R. I. Smith, Chem. Commun., 2019, 55, 10230–10233.
27. T. Matsuda, J. Kim and Y. Moritomo, Dalton Trans., 2012, 41, 7620–7623.
28. M. Ishizaki, S. Akiba, A. Ohtani, Y. Hoshi, K. Ono, M. Matsuba, T. Togashi, K. Kananizuka, M. Sakamoto, A. Takahashi, T. Kawamoto, H. Tanaka, M. Watanabe, M. Arisaka, T. Nankawa and M. Kurihara, Dalton Trans., 2013, 42, 16049–16055.
29. H. Hayashi, S. Aoki, M. Takaishi, Y. Sato and H. Abe, Phys. Chem. Chem. Phys., 2019, 21, 22553–22562.
30. P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 32–43.
31. P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 44–66.
32. G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2014, 5, 4712–4715.
33. M. Sugimoto, S. Yamashita, H. Akutsu, Y. Nakazawa, J. G. DaSilva, C. M. Kareis and J. S. Miller, Inorg. Chem., 2017, 56, 10452–10457.
34. Y. Moritomo and H. Tanaka, Adv. Condens. Matter Phys., 2013, 2013, 539620.
35. J. A. Alonso, J. Sanz, J. Santamaria, C. León, A. Várez and M. T. Fernández-Díaz, Angew. Chem., Int. Ed., 2000, 39, 619–621.
36. W. R. Brant, S. Schmid, A. Kuhn, J. Hester, M. Avdeev, M. Sale and Q. Gu, ChemPhysChem, 2012, 13, 2293–2296.
37. H. L. B. Boström, I. E. Collings, A. B. Cairns, C. P. Romao and A. L. Goodwin, Dalton Trans., 2019, 48, 1647–1655.
38. B. R. Hester and A. P. Wilkinson, J. Solid State Chem., 2019, 269, 428–433.
39. B. R. Hester and A. P. Wilkinson, Inorg. Chem., 2018, 57, 11275–11281.
40. A. Rudola, K. Du and P. Balaya, J. Electrochem. Soc., 2017, 164, A1098–A1109.
41. J. Song, L. Wang, Y. Lu, J. Liu, B. Guo, P. Xiao, J.-J. Lee, X.-Q. Yang, G. Henkelman and J. B. Goodenough, J. Am. Chem. Soc., 2015, 137, 2658–2664.
42. L. Wang, J. Song, R. Qiao, L. A. Wray, M. A. Hossain, Y.-D. Chuang, W. Yang, Y. Lu, D. Evans, J.-J. Lee, S. Vail, X. Zhao, M. Nishijima, S. Kakimoto and J. B. Goodenough, J. Am. Chem. Soc., 2015, 137, 2548–2554.
43. Y. Moritomo, T. Matsuda, Y. Kurihara and J. Kim, J. Phys. Soc. Jpn., 2011, 80, 074608.
44. L. Wang, Y. Lu, J. Liu, M. Xu, J. Cheng, D. Zhang and J. B. Goodenough, Angew. Chem., Int. Ed., 2013, 52, 1964–1967.
45. M. Pasta, R. Y. Wang, R. Ruffo, R. Qiao, H.-W. Lee, B. Shyam, M. Guo, Y. Wang, L. A. Wray, W. Yang, M. F. Toney and Y. Cui, J. Mater. Chem. A, 2016, 4, 4211–4223.
46. S. Vasala and M. Karppinen, Prog. Solid St. Chem., 2015, 43, 1–36.
47. J.-H. Her, P. W. Stephens, C. M. Kareis, J. G. Moore, K. S. Min, J.-W. Park, G. Ball, B. S. Kennon and J. S. Miller, Inorg. Chem., 2010, 49, 1524–1534.
48. J. Cattermull, M. Pasta and A. L. Goodwin, Mater. Horiz., 2021, 8, 3178–3186.
49. H. L. B. Boström, I. E. Collings, D. Daisenberger, C. J. Ridley, N. P. Funnell and A. B. Cairns, J. Am. Chem. Soc., 2021, 143, 3544–3554.
50. Y. Moritomo, M. Hanawa, Y. Ohishi, K. Kato, M. Takata, A. Kuriki, E. Nishibori, M. Sakata, S. Ohkoshi, H. Tokoro and K. Hashimoto, Phys. Rev. B, 2003, 68, 144106.
51. J. Young and J. M. Rondinelli, J. Phys. Chem. Lett., 2016, 7, 918–922.
52. T. Matsuda, J. E. Kim, K. Ohoyama and Y. Moritomo, Phys. Rev. B, 2009, 79, 172302.
53. Y. You, X.-L. Wu, Y.-X. Yin and Y.-G. Guo, J. Mater. Chem. A, 2013, 1, 14061–14065.
54. Y. Moritomo, T. Matsuda, R. Fuchikawa, Y. Abe and H. Kamioka, J. Phys. Soc. Jpn., 2011, 80, 024603.
55. S.-i. Ohkoshi, H. Tokoro and K. Hashimoto, Coord. Chem. Rev., 2005, 249, 1830–1840.
56. H. Tokoro, T. Matsuda, T. Nuida, Y. Moritomo, K. Ohoyama, E. D. Loutete-Dangui, K. Boukheddaden and S.-I. Ohkoshi, Chem. Mater., 2008, 20, 423–428.
57. A. Widmann, H. Kahlert, I. Petrovic-Prelevic, H. Wulff, J. V. Yakhmi, N. Bagkar and F. Scholz, Inorg. Chem., 2002, 41, 5706–5715.
58. F. Herren, P. Fischer, A. Ludi and W. Hälg, Inorg. Chem., 1980, 19, 956–959.
59. J. Roque, E. Reguera, J. Balmaseda, J. Rodríguez-Hernández, L. Reguera and L. F. del Castillo, Microporous Mesoporous Mater., 2007, 103, 57–71.
60. A. L. Goodwin, K. W. Chapman and C. J. Kepert, J. Am. Chem. Soc., 2005, 127, 17980–17981.
61. L. Deng, J. Qu, X. Niu, J. Liu, J. Zhang, Y. Hong, M. Feng, J. Wang, M. Hu, L. Zeng, Q. Zhang, L. Guo and Y. Zhu, Nat. Commun., 2021, 12, 2167.
62. X. Guo, Z. Wang, Z. Deng, X. Li, B. Wang, X. Chen and S. P. Ong, Chem. Mater., 2019, 31, 5933–5942.
63. F.-X. Coudert, Chem. Mater., 2015, 27, 1905–1916.
64. R. Martinez-Garcia, M. Knobel and E. Reguera, J. Phys.: Condens. Matter, 2006, 18, 11243–11254.
65. J. Sottmann, F. L. M. Bernal, K. V. Yusenko, M. Herrmann, H. Emerich, D. S. Wragg and S. Margadonna, Electrochim. Acta, 2016, 200, 305–313.
66. D. O. Ojwang, L. Häggström, T. Ericsson, J. Ångström and W. R. Brant, Dalton Trans., 2020, 49, 3570–3579.
67. G. He and L. F. Nazar, ACS Energy Lett., 2017, 2, 1122–1127.
68. Y. Moritomo, Y. Yoshida, H. Iwaizumi, D. Inoue, I. Nagai and T. Shibata, J. Phys. Soc. Jpn., 2021, 90, 013601.
69. Y. Moritomo, Y. Kurihara, T. Matsuda and J. Kim, J. Phys. Soc. Jpn., 2011, 80, 103601.
70. S. Margadonna, K. Prassides and A. N. Fitch, J. Am. Chem. Soc., 2004, 126, 15390–15391.
71. P. Bhatt, N. Thakur, M. D. Mukadam, S. S. Meena and S. M. Yusuf, J. Phys. Chem. C, 2013, 117, 2676–2687.
72. Y. Li, Q. Gao, D. Chang, P. Sun, J. Liu, Y. Jia, E. Liang and Q. Sun, J. Phys.: Condens. Matter, 2020, 32, 455703.
73. Q. Gao, N. Shi, Q. Sun, A. Sanson, R. Milazzo, A. Carnera, H. Zhu, S. H. Lapidus, Y. Ren, Q. Huang, J. Chen and X. Xing, Inorg. Chem., 2018, 57, 10918–10924.
74. N. Shi, Q. Gao, A. Sanson, Q. Li, L. Fan, Y. Ren, L. Olivi, J. Chen and X. Xing, Dalton Trans., 2019, 48, 3658–3663.
75. J. Catafesta, J. Haines, J. E. Zorzi, A. S. Pereira and C. A. Perottoni, Phys. Rev. B, 2008, 77, 064104.
76. H. L. B. Boström, A. B. Cairns, L. Liu, P. Lazor and I. E. Collings, Dalton Trans., 2020, 49, 12940–12944.
77. A. Bleuzen, J.-D. Cafun, A. Bachschmidt, M. Verdaguer, P. Münsch, F. Baudelet and J.-P. Itié, J. Phys. Chem. C, 2008, 112, 17709–17715.
78. N. A. Benedek and C. J. Fennie, Phys. Rev. Lett., 2011, 106, 107204.
79. M. S. Senn and N. C. Bristowe, Acta Crystallogr., Sect. A: Found. Adv., 2018, 74, 308–321.
80. D. M. Pajerowski, S. E. Conklin, J. Leão, L. W. Harriger and D. Phelan, Phys. Rev. B, 2015, 91, 094104.
81. L. Egan, K. Kamenev, D. Papanikolaou, Y. Tabayashi and S. Margadonna, J. Am. Chem. Soc., 2006, 128, 6034–6035.
82. D. O. Ojwang, M. Svensson, C. Njel, R. Mogensen, A. S. Menon, T. Ericsson, L. Häggström, J. Maibach and W. R. Brant, ACS Appl. Mater. Interfaces, 2021, 13, 10054–10063.
83. N. Tapia-Ruiz, A. R. Armstrong, H. Alptekin, M. A. Amores, H. Au, J. Barker, R. Boston, W. R. Brant, J. M. Brittain, Y. Chen, M. Chhowalla, Y.-S. Choi, S. I. R. Costa, M. Crespo Ribadeneyra, S. A. Cussen, E. J. Cussen, W. I. F. David, A. V. Desai, S. A. M. Dickson, E. I. Eweka, J. D. Forero-Saboya, C. P. Grey, J. M. Griffin, P. Gross, X. Hua, J. T. S. Irvine, P. Johansson, M. O. Jones, M. Karlsmo, E. Kendrick, E. Kim, O. V. Kolosov, Z. Li, S. F. L. Mertens, R. Mogensen, L. Monconduit, R. E. Morris, A. J. Naylor, S. Nikman, C. A. O’Keefe, D. M. C. Ould, R. G. Palgrave, P. Poizot, A. Ponrouch, S. Renault, E. M. Reynolds, A. Rudola, R. Sayers, D. O. Scanlon, S. Sen, V. R. Seymour, B. Silván, M. T. Sougrati, L. Stievano, G. S. Stone, C. I. Thomas, M.-M. Titirici, J. Tong, T. J. Wood, D. S. Wright and R. Younesi, J. Phys. Energy, 2021, 3, 031503.
84. H. L. B. Boström, J. A. Hill and A. L. Goodwin, Phys. Chem. Chem. Phys., 2016, 18, 31881–31894.
85. S. G. Duyker, J. A. Hill, C. J. Howard and A. L. Goodwin, J. Am. Chem. Soc., 2016, 138, 11121–11123.
86. H. L. B. Boström, CrystEngComm, 2020, 22, 961–968.

---

Footnotes

† Electronic supplementary information (ESI) available: The database of PBAs. See DOI: 10.1039/d2tc00848c

‡ Compounds with formula Cu[Fe(CN)₆]_<0.67 feature Cu on both the A- and M-site,²⁵ meaning that Fig. 4 is less appropriate for M = Cu.

---