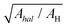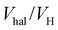Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the internal heavy-atom effect on thermally activated delayed fluorescence: application of Arrhenius and Marcus theories for spin–orbit coupling analysis†
Michał
Mońka
a,
Illia E.
Serdiuk
 *a,
Karol
Kozakiewicz
b,
Estera
Hoffman
a,
Jan
Szumilas
a,
Aleksander
Kubicki
a,
Soo Young
Park
*a,
Karol
Kozakiewicz
b,
Estera
Hoffman
a,
Jan
Szumilas
a,
Aleksander
Kubicki
a,
Soo Young
Park
 c and
Piotr
Bojarski
a
c and
Piotr
Bojarski
a
aFaculty of Mathematics, Physics and Informatics, University of Gdańsk, Wita Stwosza 57, 80-308 Gdańsk, Poland. E-mail: illia.serdiuk@ug.edu.pl; Tel: +48 58 523 22 44
bFaculty of Chemistry, University of Gdańsk, Wita Stwosza 63, 80-308 Gdańsk, Poland
cCenter for Supramolecular Optoelectronic Materials, Department of Materials Science and Engineering, Seoul National University, 1 Gwanak-ro, Gwanak-gu, Seoul 151-744, Republic of Korea
First published on 6th May 2022
Abstract
Hybrid organic emitters containing abundant heavy atoms (HAs) are of rapidly growing interest for organic light emitting diodes (OLEDs) based on thermally activated delayed fluorescence (TADF). As substitutes of expensive and toxic heavy-metals, HAs can accelerate reverse intersystem crossing (rISC), whose low rate is specifically troublesome in blue all-organic TADF materials. Unfortunately, due to complex photophysics even qualitative predictions of the HA effect on organic emitters and hence molecular design are currently very challenging. Here, we report a photoluminescence data analysis approach for investigations of the TADF mechanism based on empirical spin–orbit coupling constants. Using this approach, heavy-halogen derivatives of a popular blue TADF emitter are investigated to understand the mechanism of the HA effect and molecular design fundamentals of high-efficiency TADF materials bearing HAs. Different HA effects on direct and reverse ISC were revealed. We thus conclude that to improve TADF in organic emitters (i) HA should participate in low-energy molecular vibrations which activate rISC between the lowest excited triplet and singlet states of the charge-transfer (CT) character and (ii) ISC should be minimized through a large energy gap between the 1CT-state and HA-affected locally-excited (3LE) triplet state.
Introduction
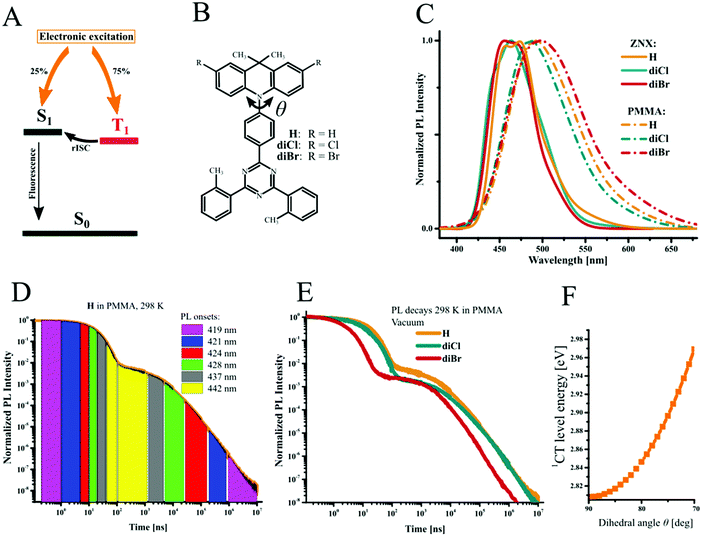
Pure organic materials with thermally activated delayed fluorescence (TADF) have been extensively investigated recently with an aim to replace heavy-metal complexes in organic light emitting diodes (OLEDs). The tempting prospect of minimization of the use of expensive and toxic rare-earth metals stimulates numerous efforts to develop highly efficient all-organic TADF materials which meet the specific demands of OLED technology. The most demanded here remains the efficient transformation of triplet excitons dominating under electric excitation to the light emission. Since the emission from the triplet state is conditioned by the change of spin, a spin-forbidden process, the rate and efficiency of such emission are usually low, which makes triplet harvesting a challenging task for organic materials.1,2 Thanks to stable emission color, TADF is regarded as one of the best triplet harvesting approaches. Triplet excitons are converted to the singlet ones via reverse intersystem crossing (rISC) and thus light emission always occurs from the S1 state of the emitter (Fig. 1A). Due to the spin-forbidden nature of the T1–S1 transition, the main limitation of TADF is the rISC rate, which depends on the strength of the spin–orbit coupling (SOC). After almost a decade of successful implementation of the first general molecular design strategy of TADF materials for OLEDs,3 achieving fast rISC in the nanosecond domain as demanded by the OLED technology remains the most challenging issue, especially for the deep-blue emitters. Obviously, our scarce knowledge about the origin, mechanisms and ways of manipulation of SOC in TADF emitters is a serious barrier for further progress in this field.In light-atom organic materials, SOC is too low to enable fast rISC.4 The introduction of cheap and abundant heavy atoms (HAs) into organic TADF emitters seems to be the most obvious and promising way to increase SOC,5–8 and accelerate rISC, generally referred to as a “heavy-atom effect”.9 Undoubtedly, modification of organic emitters with the heavy atoms of groups 14–17 opens new prospects in the engineering of heavy-metal-free materials for optoelectronics. Unfortunately, at the current state of knowledge, even qualitative prediction of the HA effect on organic TADF emitters is extremely challenging. The attachment of HA at different positions of the emitter can have a different effect on intersystem crossing (ISC), rISC, and other processes, intermolecular interactions and eventually TADF efficiency.
From the point of view of the molecular design of TADF emitters, the idea of introducing HA into organic emitters can be controversial. On the one hand, HA can accelerate rISC and thus help to convert triplet states into excited singlet ones, which is favorable for TADF emitters. On the other hand, HA can accelerate ISC thus leading to the conversion of the emissive S1 state to triplet ones. This is highly undesired for a TADF emitter, as it decreases the amount of singlet excitons in an OLED device which could be deactivated radiatively. The rapidly growing number of publications focusing on such hybrid organic emitters with nonmetallic HAs indicates their complex and non-intuitive effect on TADF.10–17 On the one hand, the reports on the increase in rISC rate constant (krISC)10 and even achievement of its record high value of 6 × 107 s−1,11 shortened lifetimes of delayed fluorescence (DF)12 and excellent OLED performance with suppressed efficiency roll-off13 indicate the beneficial role of the HA effect. Some other articles however, indicate its complex nature. For example, several articles report on a strong ISC enhancement and a weaker one for rISC14 or vice versa;15 some reports conclude negligible HA effect on rISC.16 Even more surprising is the observation that a TADF emitter with a silicon atom can show an rISC twice as fast as its germanium analogue.17 Such investigations indicate that HA presence itself does not necessarily warrant rISC acceleration, whilst the demanded selective enhancement of rISC instead of ISC is very challenging.18 Obviously, none of the literature reports confirm the HA effect in organic emitters to a quantum physical relation derived for atoms: V ∼ Z4, where V is a spin–orbit coupling constant and Z is the atomic number.
Taking the above mentioned into account, in this study we aimed to reveal the ways of selective rISC acceleration and define the main principles of molecular design to enable them. To shed light on the complex processes covered by the term “heavy-atom effect”, we performed thorough analysis of the electronic properties and spin–flip mechanisms in a series of (deep)-blue TADF emitters. Chlorine and bromine derivatives of a widely studied emitter 9,10-dihydro-9,9-dimethyl-10-(4-(4,6-diphenyl-1,3,5-triazin-2-yl)phenyl)-acridine (DMAC-TRZ, Fig. 1B) were selected after explanation of its photophysics.19 To focus on the internal HA effect and distinguish it from the external one, methyl groups were introduced to the side rings of an acceptor fragment which minimized the emitter-emitter intermolecular interactions.20 Temperature and polarity dependent photophysical investigations analyzed within Arrhenius and Marcus theories enabled estimation of SOC, energy gaps and reorganization energies using experimental data. It was found that due to different mechanisms of ISC and rISC, the HA effect manifests in different ways. Whilst ISC is accelerated up to 8 times due to the enhanced SOC between the states of different nature, rISC can be accelerated less than 3 times via vibronic activation of SOC between the states of the same nature. The presented results reveal that introduction of HA can improve TADF in the case of (i) effective activation of specific molecular vibrations involved in rISC and (ii) lack of ISC acceleration to localized triplet states.
Experimental section
Materials
Zeonex® (ZNX, Zeonex480R, density = 1.01 g cm−3) or poly-methyl methacrylate (PMMA, 120000 Mw, density = 1.18 g cm−3) were purchased from Zeon Europe GmbH and Sigma-Aldrich, respectively. Solvents for the synthesis and spectroscopic measurements were of corresponding grades and were used as supplied.Synthesis of emitters, isolated donor, and acceptor molecules
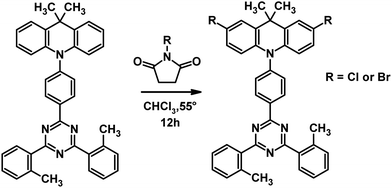
10-(4-(4,6-Bis(2-methylphenyl)-1,3,5-triazin-2-yl)phenyl)-9,9-dimethyl-9,10-dihydroacridine (H) was synthesized as described previously.20Typical halogenation procedure
0.1 mmol of H or 9,9-dimethyl-10-phenyl-9,10-dihydroacridine and 0.22 mmol N-chlorosuccinimide (for diCl and diCl-DMAC) or N-bromosuccinimide (for diBr and diBr-DMAC) were dissolved in 0.5 mL of chloroform and stirred at 55 °C for 12 h in the dark. ¾ of the solvent was evaporated and the residue was treated with methanol. The resulting precipitate was collected and purified using column chromatography on SiO2 with appropriate hexane-chloroform mixtures as eluents.10-(4-(4,6-Bis(2-methylphenyl)-1,3,5-triazin-2-yl)phenyl)-2,7-dichloro-9,9-dimethyl-9,10-dihydro-acridine (diCl)
Pale yellow powder, yield 87%. 1H NMR (500 MHz, CDCl3, δ): 1.67 (s, 6H) 2.87 (s, 6H), 6.28 (d, J = 8.80 Hz, 2H), 6.94 (d, J = 8.07 Hz, 2H), 7.34–7.64 (m, 10H), 8.31–8.34 (m, 2H), 8.94 (d, J = 7.70 Hz, 2H). 13C NMR (250 MHz, CDCl3, δ): 174.47, 170.01, 139.09, 139.05, 135.87, 131.98, 131.79, 131.38, 131.33, 131.26, 131.20, 126.49, 126.20, 126.18, 125.32, 115.45, 36.43, 30.86, 22.48. MALDI-TOF m/z: calcd for C38H30Cl2N4, 613.2 [M + H]+; found, 613.4. For 1H and 13C NMR spectra see the ESI† (Fig. S1 and S2).10-(4-(4,6-Bis(2-methylphenyl)-1,3,5-triazin-2-yl)phenyl)-2,7-dibromo-9,9-dimethyl-9,10-dihydro-acridine (diBr)
Pale yellow powder, yield 91%. 1H NMR (500 MHz, CDCl3, δ): 1.67 (s, 6H), 2.87 (s, 6H), 6.22 (d, J = 8.69 Hz, 2H), 7.08 (dd, J = 8.69, 2.27 Hz, 2H), 7.40 (t, J = 7.55 Hz, 4H), 7.44–7.51 (m, 4H), 7.53 (d, J = 2.27 Hz, 2H), 8.29–8.35 (m, 2H), 8.94 (d, J = 8.69 Hz, 2H). 13C NMR (250 MHz, CDCl3, δ): 174.47, 169.99, 144.35, 139.44, 139.09, 136.73, 135.86, 131.97, 131.85, 131.80, 131.33, 131.23, 131.20, 129.41, 128.19, 126.18, 115.91, 113.67, 36.35, 30.94, 22.47. MALDI-TOF m/z: calcd for C38H30Br2N4, 701.1 [M + H]+; found, 701.2. For 1H and 13C NMR spectra see the ESI† (Fig. S3 and S4).2,7-Dichloro-9,9-dimethyl-10-phenyl-9,10-dihydroacridine (diCl-DMAC)
White powder, yield 69%. 1H NMR (500 MHz, CDCl3, δ): 1.67 (s, 6H) 6.21 (d, J = 8.79 Hz, 2H) 6.94 (dd, J = 8.92, 2.06 Hz, 2H) 7.31 (d, J = 7.14 Hz, 2H) 7.40 (d, J = 2.20 Hz, 2H) 7.53–7.58 (m, 1H) 7.64–7.68 (m, 2H) MALDI-TOF m/z: calcd for C21H17Cl2N, 338.0 [M-CH3]+; found, 338.2.2,7-Dibromo-9,9-dimethyl-10-(4-methylphenyl)-9,10-dihydroacridine (diBr-DMAC)
White powder, yield 78%. 1H NMR (500 MHz, CDCl3, δ): 1.66 (s, 6H) 2.50 (s, 3H) 6.18 (d, J = 8.79 Hz, 2H) 7.07 (dd, J = 8.92, 2.33 Hz, 2H) 7.17 (d, J = 8.24 Hz, 2H) 7.44 (d, J = 7.96 Hz, 2H) 7.51 (d, J = 2.20 Hz, 2H) MALDI-TOF m/z: calcd for C22H19Br2N, 442.2 [M-CH3]+; found, 442.0.9,9-Dimethyl-10-phenyl-9,10-dihydroacridine
A mixture of 9,9-dimethyl-9,10-dihydroacridine (1 mmol, 209 mg), iodobenzene (1 mmol, 204 mg), tris(dibenzylideneacetone)dipalladium(0) (0.05 mmol, 46 mg) and tri-tert-butylphosphonium tetrafluoroborate (0.1 mmol, 29 mg) was dissolved in 15 ml of dry toluene under an argon atmosphere. Potassium tert-butoxide (1.5 mmol, 168 mg) was added and the mixture was stirred at 100 °C overnight. The solvent was removed under vacuum, and the dry residue was dissolved in dichloromethane and washed with water. Crude compound was purified by column chromatography using a mixture of dichloromethane and hexane (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9). White powder, yield 72%. 1H NMR (500 MHz, CDCl3, δ): 1.72 (s, 6H), 6.28 (d, J = 7.96 Hz, 2H), 6.93–7.01 (m, 4H), 7.36 (d, J = 7.41 Hz, 2H), 7.48 (d, J = 7.41 Hz, 2H), 7.51–7.55 (m, 1H), 7.62–7.67 (m, 2H). MALDI-TOF m/z: calcd for C21H19N, 270.3 [M-CH3]+; found, 270.1.
9). White powder, yield 72%. 1H NMR (500 MHz, CDCl3, δ): 1.72 (s, 6H), 6.28 (d, J = 7.96 Hz, 2H), 6.93–7.01 (m, 4H), 7.36 (d, J = 7.41 Hz, 2H), 7.48 (d, J = 7.41 Hz, 2H), 7.51–7.55 (m, 1H), 7.62–7.67 (m, 2H). MALDI-TOF m/z: calcd for C21H19N, 270.3 [M-CH3]+; found, 270.1.
9,9-Dimethyl-10-(4-methylphenyl)-9,10-dihydroacridine
Was synthesized using 4-iodotoluene using the same protocol as for 9,9-dimethyl-10-phenyl-9,10-dihydroacridine. White crystalline powder, yield 88%. 1H NMR (500 MHz, CDCl3, δ): 1.68 (s, 6H), 2.48 (s, 3H), 6.28 (d, J = 8.24 Hz, 2H), 6.87–6.93 (m, 2H), 6.95 (dt, J = 8.39, 1.45 Hz, 2H), 7.20 (dd, J = 8.09, 1.37 Hz, 2H), 7.39–7.46 (m, 4H). MALDI-TOF m/z: calcd for C22H21N, 300.4 [M + H]+; found, 300.2.2,4-Bis(2-methylphenyl)-6-phenyl-1,3,5-triazine
2-Methylbenzamidine hydrochloride (11 mmol) and potassium tert-butoxide (10.8 mmol) were mixed in DMSO and stirred at RT for 30 min. Benzaldehyde (5 mmol) was added and the mixture was stirred at 100 °C for 12h. After cooling to RT, 2,3-dichloro-5,6-dicyano-p-benzoquinone (5 mmol) was added and the mixture was stirred at 50 °C for another hour. 50% aqueous methanol was added and the precipitate was collected by filtration. Column chromatography using 50% CHCl3 in hexane afforded the pure title compound. White powder, yield 75%. 1H-NMR (300 MHz, CDCl3, δ): 2.84 (s, 6H), 7.35–7.41 (m, 4H), 7.42–7.47 (m, 2H), 7.53–7.57 (m, 2H), 7.58–7.61 (m, 1H), 8.28 (d, J = 7.63 Hz, 2H), 8.68 (s, 2H). MALDI-TOF m/z: calcd for C38H30Cl2N4, 338.2 [M + H]+; found, 338.2.Sample preparation for photophysical measurements
Stock solutions of H, diCl and diBr in dichloromethane were added to Zeonex or PMMA solutions in toluene and dichloromethane solutions to obtain homogeneous mixtures, which were used for film preparation. The films were prepared by drop cast deposition on warm quartz plates, and left in the dark for 5h to enable evaporation of solvents. The final mass fraction of emitters dispersed in polymers was ca. 1%.Photoluminescence measurements
UV-Vis absorption spectra were recorded using a Shimadzu UV-1900 spectrophotometer. Steady-state photoluminescence spectra were recorded using a Varian Cary Eclipse spectrofluorometer using front-face excitation geometry. The PL quantum yield (PLQY) was measured using an integrating sphere (Quantaurus C11347-11, Hamamatsu). Time-resolved measurements were performed at different temperatures using a customized system21 consisting of a pulsed YAG:Nd laser (PL2251A, EKSPLA) coupled with an optical parametric generator (PG 401/SH) as an excitation light source and 2501S grating spectrometer (Bruker Optics) combined with the streak camera system (C4334-01 Hamamatsu) as a detection unit. The system was equipped with a double-stage high vacuum pump (T-Station 85 Edwards) coupled with a closed-cycle helium cryostat (APD DE-202) and a temperature controller (LakeShore 336). To reduce scattering, reflections and secondary order artifacts, a set of various high performance optical bandpass (BP) and longpass (LP) filters were used: in the excitation path 325/50BP or 375/50BP (CWL/FWHM), depending on the selected excitation wavelength, together with LP filters: 375LP or 350LP (Edmund Optics). In order to build PL intensity decay profiles, streak camera images were integrated over a constant wavelength interval (460–490 nm for ZNX and 475–515 nm for PMMA samples).Quantum chemical calculations
Quantum chemical calculations were conducted at the DFT/TD-DFT level of theory using the Gaussian 16 program package.22 The B3LYP functional23 was used with the LAN2LDZ basis set. Firstly, for each compound, unconstrained geometry optimizations were performed for the ground (S0), excited singlet (S1) and excited triplet electronic states (T1, T2, T3). Convergance of all geometry optimizations was verified by the vibrational analysis: no negative frequencies were observed, therefore calculated minima correspond to the “true” stationary points. The nature of the electronic excited states was determined by the analysis of molecular orbitals. Spin–orbit coupling constants were computed using the ORCA 4.2 software24 package with the B3LYP functional, and the DEF2-TZVP basis set with included relativistic zero-order regular approximaion (ZORA).Results and discussion
Synthesis
diCl and diBr were synthesized via efficient and simple halogenation of H using N-chlorosuccinimide and N-bromosuccinimide, respectively, as shown in Scheme 1. The isolation yields were close to 90%.Photoluminescence and excited-state alignment
The investigations of the TADF mechanism start with the analysis of the spectral features of the compounds and alignment of their lowest excited-states. The absorption spectra of the investigated compounds measured in solutions are very similar (Fig. S5, ESI†). Minor changes can be noticed at the long-wavelength band corresponding to the CT transition. The blue shift of the absorption maximum from 379 nm (H) to 373 nm is observed for diCl and to 375 nm for diBr. All compounds show deep-blue and sky-blue photoluminescence (PL) in nonpolar Zeonex® (ZNX) and more polar PMMA films, respectively (Table 1, Fig. 1C and Fig. S6, ESI†). Positive solvatochromism evidences a large change in the dipole moment during the S1–S0 transition and charge-transfer (CT) character of the S1-state, like in DMAC-TRZ and other TADF emitters of D–A structure. The blue-shifted emission of diCl relative to H is the result of the negative inductive effect of chlorine atoms which decreases the donor strength and thus increases the 1CT energy. Interestingly, in diBr this effect is almost negligible. Taking into account a similar trend in the absorption spectra, one can conclude that in such large π-systems, the electronic effect of bromine on the S0–1CT transition is lower than that of chlorine. The PL quantum yields (PLQYs) are the highest for H (99%) and diCl (85%) in PMMA, whereas the respective value for diBr is lower (Table 1).| Cmpd | Medium | PLQYa [%] | PLbλmax [nm] | ΔE1CT–3LE(A)c [meV] | ΔE1CT–3CTc [meV] | ΔE1CT–3LE(D)c [meV] | τ PF [ns] | τ DF [μs] | k ISC [s−1 107] | k rISC [s−1 104] |
|---|---|---|---|---|---|---|---|---|---|---|
| a Values measured using integrating sphere and corrected for vacuum conditions (for the details see the ESI – Table S1). b Determined from steady-state photoluminescence measurement at 298 K (Fig. S6 and Table S1, ESI). c Determined from the difference of respective onsets of PL spectra, according to the general equation: ΔE1–2 = (1240/λonset1–1240/λonset2), onset values presented in Table S1 (ESI). d All of presented photophysical parameters (τPF, τDF, kISC and krISC) were calculated from the PL intensity decay profiles (Fig. S8A and S9A, ESI) measured at 298 K under a vacuum. A detailed procedure of the calculations of photophysical parameters is included in the ESI – Section S3). | ||||||||||
| H | ZNX | 60 | 465 | 94 | — | −230 | 15.3 | 171 | 5.1 | 1.03 |
| diCl | 75 | 462 | 133 | — | −55 | 13.1 | 333 | 6.1 | 0.87 | |
| diBr | 12 | 467 | 114 | — | −55 | 2.2 | 104 | 38.5 | 1.74 | |
| H | PMMA | 99 | 498 | 46 | 85 | −278 | 17.1 | 96 | 3.8 | 2.92 |
| diCl | 85 | 492 | 72 | 95 | −116 | 16.0 | 139 | 4.1 | 1.85 | |
| diBr | 21 | 499 | 60 | 86 | −109 | 2.8 | 38 | 30.8 | 8.23 | |
Time-resolved emission spectra (TRES) reveal that the “1CT-state” is a continuous energy band rather than a single-energy level (Fig. 1D and Fig. S7–S11, ESI†). In PMMA films, broadened steady-state emission spectra are the result of spectral shifts at different time delays due to coexistence of various rotameric species with different dihedral angles between donor and acceptor units (θ, Fig. 1B). Such rotamers play a key role in the TADF photophysics,19,25–28 as the 1CT-state energy and 3CT–1CT energy gap (ΔE1CT–3CT) are dependent on the θ value. Such θ-rotamers with high deviation from the optimal 90° value and high 1CT-energy emit in the blue region in the very early prompt fluorescence (PF) region and late DF, whereas θ-rotamers close to 90° correspond to low 1CT-energy, late-PF and early-DF emissions (Fig. 1E). The 1CT energy thus deviates from 2.96 to 2.81 eV (H) (Fig. 1F and Table S1, ESI†) and 2.98 to 2.82 eV (diCl, diBr). Similar, but less pronounced dependences are observed for ZNX films (discussed in the ESI† – Section S2).
Thorough analysis of TRES at low temperatures reveals that different triplet states are responsible for the phosphorescence in different media. In ZNX, the vibronic structure of the phosphorescence spectrum differs from that of fluorescence, but matches perfectly the phosphorescence of an isolated acceptor (Fig. S6G, ESI†).29 This suggests that the T1 state is localized on the acceptor fragment, the 3LE(A)-state. Its estimated energy is 2.84 eV, similar to that in DMAC-TRZ.27 In PMMA, the phosphorescence is different from the 3LE(A) one, but similar to fluorescence, and thus 3CT becomes the lowest triplet state (Fig. S6D–F, ESI†). In contrast to 1CT, the 3CT-emission onset is relatively constant, thus 3CT is a single-energy level of 2.80 eV (H) and 2.81 eV (diCl, diBr, see the phosphorescence spectra depicted in Fig. S6D–F and S11A–C, ESI†). The energy of the third triplet state localized on the donor fragment (3LE(D)) was estimated from the phosphorescence of free donor molecules (Fig. S6H, ESI†). Thus the estimated 3LE(D)-energy is affected by halogen atoms, decreasing from 3.16 eV (H) to 3.02 and 3.01 eV in diCl and diBr, respectively.
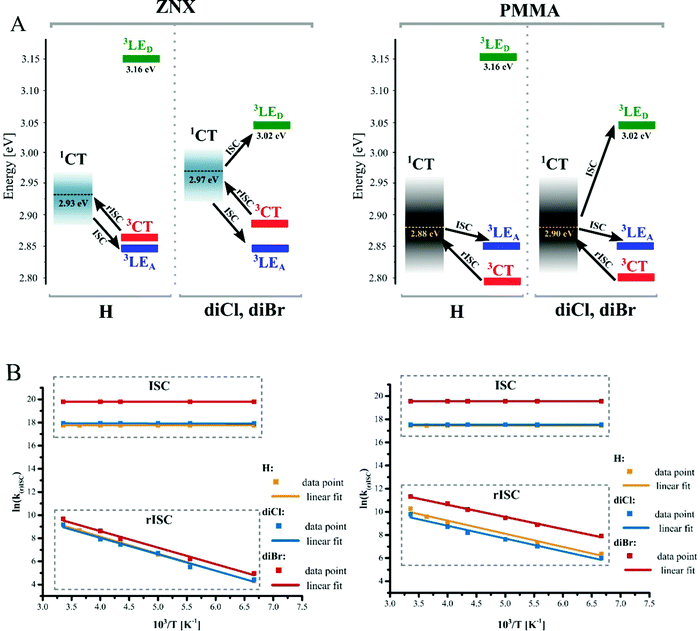
The alignment of the excited states presented in Fig. 2A summarizes the discussion of spectral properties. In view of the TADF mechanism and HA effect, singlet–triplet energy gaps (ΔE1CT–Ti) are discussed further. Minimal, maximal, and statistical mean energy gaps (Tables S2, S3 and Fig. S10, S11, ESI†) reveal the macroscopic diversity of molecular electronic systems due to the distribution of 1CT-state energies. As the 3LE(A)-state is negligibly affected by the halogens, ΔE1CT–3LE(A) varies similarly for all the emitters: in ZNX, from +0.06 to +0.15 eV with a mean value of ca. +0.10 eV; and in PMMA, from slightly negative to +0.14 eV with a mean value of ca. +0.05 eV (Table 1). The 1CT–3CT energy difference estimated for the PMMA medium is also very similar for H and diBr, varying from 6.3 meV to 0.16 eV with the mean value of 85 meV; in diCl bearing the weakest donor fragment, the CT states are slightly more distanced (Table 1 and Table S1, ESI†). Therefore, the alignment of S1, T1, and T2 states is generally similar for studied compounds. The distinguished electronic feature of halogenated emitters is the 3LE(D)-state being closer to 1CT. The lowest mean ΔE1CT–3LE(D) values are in the ZNX films: −0.23 eV (H) and −0.055 eV (diCl, diBr); in PMMA, they increase to −0.28 eV and −0.11, respectively.
Photoluminescence decays
The kinetics of emission decay and its strong temperature dependence unambiguously proves the TADF property of the investigated emitters, as discussed in detail in the ESI.† Well-distinguished time domains of PF and DF decays exhibit different sensitivity to the HA effect (Fig. 1D, and Fig. S8A, S9A, ESI†). Introduction of chlorine and especially bromine atoms leads to the shortening of PF lifetime, because the ISC rate constant (kISC) increases up to 1.2 and 8.1 times, respectively (Table 1). The situation is more complex in the case of the DF lifetime, as it is almost twice longer in diCl, but three times shorter in diBr compared to H. The rISC rate constant (krISC) thus decreases in diCl, but increases almost three times in diBr in the PMMA films. At this point one can notice that only bromine accelerates both types of intersystem crossing transitions, however it affects ISC more than rISC. This versatile effect of HA is analyzed further using experimental and computational approaches.Arrhenius and Marcus theories applied to the SOC analysis
Looking for the analysis approach which could help to reveal the TADF mechanism in emitters with complex photophysics, we found that the combination Arrhenius law30 (1) and Marcus–Hush eqn (2) can be a powerful tool for investigations of spin–flip processes.31 Transformation of (1) and (2) provides valuable relationships (3, 4):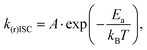 | (1) |
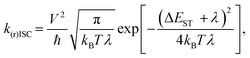 | (2) |
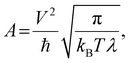 | (3) |
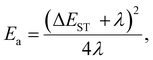 | (4) |
ISC
In the investigated compounds, ISC is a barrierless process (Ea = 0), which indicates that (i) according to eqn (4), the S1–T1 reorganization energy is equal to the energy gap and (ii) according to eqn (2), kISC is defined by the SOC constant. VISC increases from 0.29 (H) and 0.31 (diCl) to 0.76 cm−1 (diBr) (Table 2). Such an order of magnitude indicates that ISC occurs via a transition or a couple of transitions, so-called as “allowed by El-Sayed rules”.32 The ISC mechanism should thus involve excited states of different nature: 1CT and 3LE. In H, the key ISC channel is the 1CT → 3LE(A) transition due to the close energy of the respective states and well-matching computed V1CT→3LE(A) and experimental VISC values (Table 2 and Table S7, ESI†). In the halogenated derivatives, the rates of 1CT → 3LE(A) transition remain similar because of an identical ΔE1CT–3LE(A). In fact, the calculations indicate the absence of the HA effect on this transition as neither Cl nor Br increase its SOC (see the ESI† – Section 5, Table S7).| Cmpd | Process | Arrhenius eqn (1) | Marcus–Hush eqn (2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| A | E a | ΔEST | λ | E a | V | ||||
| [s−1 107] | [meV] | [meV] | [meV] | [meV] | [cm−1] | ||||
| ZNX | |||||||||
| H | ISC | 5.09 | 0 | −122 | 122 | 0 | 0.29 | ||
| diCl | 6.12 | 0 | 1.1 | −127 | 127 | 0 | 0.31 | 1.0 | |
| diBr | 38.43 | 0 | 2.9 | −125 | 125 | 0 | 0.76 | 2.6 | |
| H | rISC | 0.12 | 124 | 122 | 122 | 122 | 0.05 | ||
| diCl | 0.09 | 127 | 0.9 | 127 | 127 | 127 | 0.04 | 0.8 | |
| diBr | 0.16 | 126 | 1.2 | 125 | 125 | 125 | 0.05 | 1.1 | |
| PMMA | |||||||||
| H | ISC | 3.83 | 0 | −93 | 93 | 0 | 0.29 | ||
| diCl | 4.11 | 0 | 1.0 | −97 | 97 | 0 | 0.30 | 1.0 | |
| diBr | 30.85 | 0 | 2.8 | −94 | 94 | 0 | 0.76 | 2.5 | |
| H | rISC | 0.09 | 98 | 93 | 93 | 93 | 0.05 | ||
| diCl | 0.06 | 95 | 0.8 | 97 | 97 | 97 | 0.04 | 0.8 | |
| diBr | 0.26 | 92 | 1.7 | 94 | 94 | 94 | 0.07 | 1.5 | |
The observed strong HA effect on ISC correlates with the 1CT–3LE(D) energy gaps. As compared to PMMA, the decrease of |ΔE1CT–3LE(D)| in ZNX films leads to the increase of kISC. Theoretical calculations support this conclusion: the predicted SOC constants and rates of the 1CT → 3LE(D) transition evidence its sufficient role in diCl and diBr (Table S8, ESI†). For example, in PMMA films, the mean k1CT–3LE(D) increases drastically from 2.5 × 103 s−1 (H) to 1.8 × 106 s−1 (diCl) and 1.8 × 107 s−1 (diBr). Regarding the 1CT-energy distribution, in diBr species with minimal ΔE1CT–3LE(D), the maximal k1CT–3LE(D) value exceeds 1.5 × 108 s−1 (Table S8, ESI†). The HA effect on ISC is thus realized mainly via3LE(D)-state influenced directly by the heavy halogens (Table S9, ESI†). From the point of view of TADF efficiency, one can conclude the energetic closeness of the HA-affected 3LE state to the 1CT one and it is a negative factor, as it leads to strong acceleration of ISC.
rISC
A similar approach applied for rISC reveals that for all three compounds, thermal activation Ea is roughly constant (Table 2). According to eqn (4), this indicates that neither Cl nor Br change the energy gap or reorganization energy for rISC. As compared to ZNX, in PMMA films, Ea decreases by 30 meV from ca. 125 to 95 meV (Table 2). The SOC constant VrISC is significantly lower than that for ISC: in diBr, the HA effect is more than 2 times higher for ISC than for rISC (Vhal/VH, Table 2). Together with unexpected VrISC decrease in diCl, these observations indicate different mechanisms for ISC and rISC.In H, VrISC does not exceed 0.05 cm−1 evidencing a dominating role of the “forbidden” channel: the 3CT → 1CT transition. Similarly the low VrISC of the halogenated derivatives indicate that neither the 3LE(D) nor 3LE(A) state contribute significantly to rISC. Despite the strong HA effect on the calculated V3LE(D)–1CT, in ZNX, where 3LE(D) is closer to 1CT (Table 1 and Table S1, ESI†), diBr exhibits a lower experimental VrISC value than in PMMA. This indicates the insignificant role of the 3LE(D)-state in rISC due to its almost negligible population (Fig. 2A, Fig. S16 and Tables S10 and S11, ESI†). Neither the 3LE(A) → 1CT transition contributes noticeably, because the calculated rate constants and SOC of the 3LE(A) → 1CT transition decrease in the row diCl – H ≈ diBr (Table S11, ESI†), which is not the case for VrISC. Moreover, due to the large reorganization energies, k3LE(A)→1CT should exhibit much sharper temperature dependence than the experimental one (Fig. S14 and S15, ESI†).
The above-mentioned analysis indicates that rISC occurs mainly via the 3CT → 1CT transition. The analysis of molecular vibrations and inhomogeneity reveals why the effect of heavy halogens on the 3CT → 1CT spin–flip is so peculiar. Within our previously developed TADF model, in DMAC-TRZ,19 the 3CT → 1CT transition is efficient in rotamers with various θ-deviation due to non-zero SOC, low energy gap and reorganization energy. Surprisingly, in θ-rotamers, the increase in the atomic number of the substituent results in the decrease of SOC (Fig. 3C). As a consequence, the rotational model predicts that the statistical sum of the 3CT → 1CT transition rate constants (k3CT→1CT) for all θ-rotamers decreases in the row H–diCl–diBr (see the ESI† – Section S6, Fig. 3B, 4 and Fig. S17–S19, Tables S12–S14). Interestingly, this correlates with the observed rISC inhibition in diCl, but contradicts the rISC acceleration in diBr.
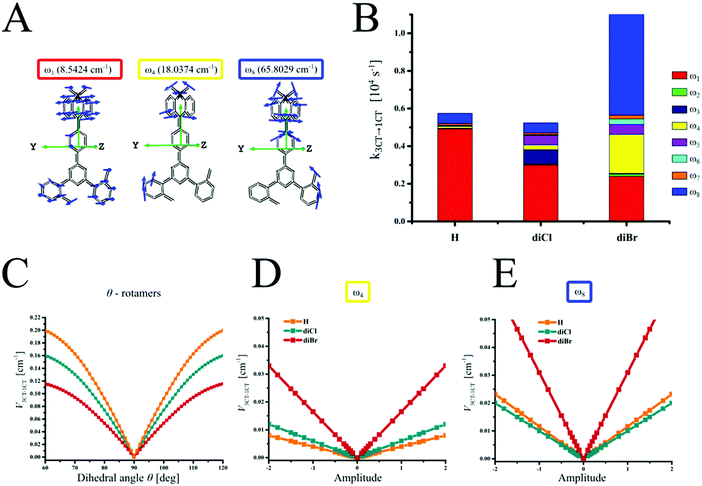 | ||
| Fig. 3 The most important vibrational modes for SOC enhancement (A), contributions of low-energy vibrational modes to rISC (B), and dependence of 3CT → 1CT SOC constants on their amplitudes (C–E). | ||
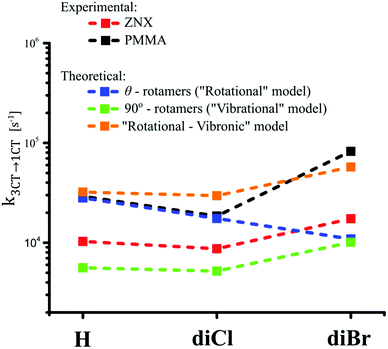 | ||
| Fig. 4 Comparison of the experimental and model rISC values (see Table S19, ESI†). | ||
The analysis of vibrational modes explains this discrepancy. In the case of the most stable 90°-rotamer, the k3CT–1CT values calculated taking into account eight lowest vibrational modes (ω1–ω8, see the ESI† – Section S7, Fig. 3A and Fig. S20–S25, Tables S15–S18, and the supporting animation file) follow the experimental trend of krISC (Fig. 4). Thus the calculated rISC rates are underestimated, because other rotamers are not taken into account. The complete TADF model should thus combine rotational and vibronic models via vibrational SOC analysis for all θ-rotamers, which unfortunately requires expensive and time-consuming computations. Assuming that vibrational SOC enhancement in all rotamers is similar to the 90°-rotamer, the rotational model was completed by the correction on vibrations (see the ESI† – Section S8). Thus the obtained corrected k3CT–1CT values better matched the experimental ones (Fig. 4 and Table S19).
Positive verification of such a rotational-vibronic model enables the analysis of key vibronic modes for rISC. In H, the ω1 mode leading to the θ-deviation is almost exclusive 3CT → 1CT channel (Fig. 3A). This supports our previous findings, that in the orthogonal TADF emitters without heavy atoms, rISC via3CT → 1CT transition is correctly predicted by the θ-rotamer model which takes into account only relative rotations of the D and A fragments.19 In diCl and diBr, however, k3CT→1CT realized via the ω1 mode decreases down to 1.6 and 2.0 times, respectively (Fig. 3B). In diBr, the enhanced rISC is due to the activated ω4 and ω8 channels of the 3CT → 1CT transition. The ω4 and ω8 modes distort the planarity of the donor, causing motions of bromine atoms and SOC enhancement up to three times (Fig. 3A–E). As a result, diBr gains a four-fold increase of k3CT→1CT initially activated by ω1. For diCl, the ω3–5 and ω8 modes also activate SOC but their contribution to k3CT→1CT is only 40%.
The activation of ω4 and ω8 vibronic rISC channels in diBr indicate the importance of the position of HA in the emitter. Obviously, HA should be involved in the low-energy vibrations to increase V3CT→1CT. On the other hand, diCl serves as an example of an unfortunate decrease of SOC via ω1 and weak compensation from other vibrations resulting in the rISC inhibition.
Conclusions
In summary, using heavy-halogen derivatives of the DMAC-TRZ emitter, we verified an approach for the photoluminescence data analysis within Arrhenius and Marcus theories to explain the heavy-atom effect on blue TADF materials. Such an approach provides experimental electronic data on spin–flip transitions, among which spin–orbit coupling constants are especially helpful for the analysis of the TADF mechanism.Triplet states of the LE character play an important role in the ISC process, especially in blue emitters like diCl and diBr. The introduction of such halogens into the donor fragment decreases the energy of the donor-localized T3-state in such a manner that it becomes close to the 1CT state of the blue emitters and thus decreases the S1–T3 energy gap. Together with the heavy atom effect which enhances SOC of the 1CT → 3LE(A) transition, this results in strong acceleration of ISC. From the point of view of potential application in OLED, the ISC rate should, however, be low to avoid competition with the radiative deactivation of singlet excitons. The first criterion of the molecular design of HA-containing emitters can thus be formulated as: avoid energetic closeness of singlet and triplet states of different nature directly affected by HA.
For the studied emitters, rISC is realized via the 3CT → 1CT transition, proving the appropriateness of the two-level model described in ref. 19 In the light-atom emitter H, the 3CT → 1CT SOC is enhanced by θ-rotations. For rISC modelling in heavy-atom emitters, the two-level model should take into account molecular vibrations involving HAs. In contrast to the commonly used three-level model, our results evidence the negligible role of local 3LE states in rISC.
Heavy atoms in the donor unit inhibit spin–orbit coupling of the 3CT → 1CT transition via the θ-rotational channel. However, SOC and rISC are activated by the low-energy vibrations which cause HA motions. Whilst in diCl, the former effect dominates causing rISC inhibition, in diBr, the latter effect is strong enough to accelerate rISC up to three times. Our second criterion of molecular design of TADF materials with HA is: the heavy atom should be involved in low-energy molecular vibrations to enhance the 3CT → 1CT transition.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
I. E. S. is grateful to the National Science Centre, Poland for financial support within the Sonata 16 project No. UMO-2020/39/D/ST5/03094 and the Polish Ministry of Science and Higher Education within the Mobility Plus project No. 1637/MOB/V/2017/0. M.M is grateful to the National Centre for Research and Development for financial support within the CHEMFIZ program (WND-POWR.03.02.00-00-I059/1). Quantum chemical calculations were performed on the computers of the Wroclaw Centre for Networking and Supercomputing (WCSS), Poland. The work at Seoul National University was partially supported by the research grant of Samsung Display Co., Ltd.References
- F. B. Dias, T. J. Penfold and A. P. Monkman, Methods Appl. Fluoresc., 2017, 5, 012001 CrossRef PubMed.
- P. K. Samanta, D. Kim, V. Coropceanu and J.-L. Bredas, J. Am. Chem. Soc., 2017, 139, 4042–4051 CrossRef CAS PubMed.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS PubMed.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed.
- Y.-F. Xiao, J.-X. Chen, W.-C. Chen, X. Zheng, C. Cao, J. Tan, X. Cui, Z. Yuan, S. Ji, G. Lu, W. Liu, P. Wang, S. Li and C.-S. Lee, Chem. Commun., 2021, 57, 4902–4905 RSC.
- D. R. Lee, K. H. Lee, W. Shao, C. L. Kim, J. Kim and J. Y. Lee, Chem. Mater., 2020, 32, 2583–2592 CrossRef CAS.
- C. E. Housecroft and E. C. Constable, J. Mater. Chem. C, 2022, 10, 4456–4482 RSC.
- C. Sun, L. Llanos, P. Arce, A. Oliver, R. Wannemacher, J. Cabanillas-Gonzalez, L. Lemus and D. Aravena, Chem. Mater., 2021, 33, 6383–6393 CrossRef CAS.
- IUPAC. Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997). Online version (2019-) created by S. J. Chalk. ISBN 0-9678550-9-8. 10.1351/goldbook.
- T. Huang, X. Song, M. Cai, D. Zhang and L. Duan, Mater. Today Energy., 2021, 21, 100705 CrossRef CAS.
- Y. Ren, Y. Wada, K. Suzuki, Y. Kusakabe, J. Geldsetzer and H. Kaji, Appl. Phys. Express, 2021, 14, 071003 CrossRef CAS.
- D. Song, Y. Yu, L. Yue, D. Zhong, Y. Zhang, X. Yang, Y. Sun, G. Zhou and Z. Wu, J. Mater. Chem. C, 2019, 7, 11953 RSC.
- T. Hua, L. Zhan, N. Li, Z. Huang, X. Cao, Z. Xiao, S. Gong, C. Zhou, C. Zhong and C. Yang, Chem. Eng. Sci., 2021, 426, 131169 CrossRef CAS.
- S. Gan, S. Hu, X.-L. Li, J. Zeng, D. Zhang, T. Huang, W. Luo, Z. Zhao, L. Duan, S.-J. Su and B. Z. Tang, ACS Appl. Mater. Interfaces, 2018, 10, 17327–17334 CrossRef CAS PubMed.
- Y. Xiang, Y. Zhao, N. Xu, S. Gong, F. Ni, K. Wu, J. Luo, G. Xie, Z.-H. Lu and C. Yang, J. Mater. Chem. C, 2017, 5, 12204–12210 RSC.
- D. Pereira, D. R. Lee, N. A. Kukhta, K. H. Lee, C. L. Kim, A. S. Batsanov, J. Y. Lee and A. P. Monkman, J. Mater. Chem. C, 2019, 7, 10481–10490 RSC.
- K. Matsuo and T. Yasuda, Chem. Sci., 2019, 10, 10687–10697 RSC.
- I. S. Park, K. Matsuo, N. Aizawa and T. Yasuda, Adv. Funct. Mater., 2018, 28, 1802031 CrossRef.
- I. E. Serdiuk, M. Mońka, K. Kozakiewicz, B. Liberek, P. Bojarski and S. Y. Park, J. Phys. Chem. B, 2021, 125, 2696–2706 CrossRef CAS PubMed.
- I. E. Serdiuk, C. H. Ryoo, K. Kozakiewicz, M. Mońka, B. Liberek and S. Y. Park, J. Mater. Chem. C, 2020, 8, 6052–6062 RSC.
- A. A. Kubicki, P. Bojarski, M. Grinberg, M. Sadownik and B. Kukliński, Opt. Commun., 2006, 269, 275–280 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Gaussian 16, Revision C.01 Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- S.-J. Woo, Y.-H. Kim and J.-J. Kim, Chem. Mater., 2021, 33, 5618–5630 CrossRef CAS.
- M. Hempe, N. A. Kukhta, A. Danos, M. A. Fox, A. S. Batsanov, A. P. Monkman and M. R. Bryce, Chem. Mater., 2021, 33, 3066–3080 CrossRef CAS PubMed.
- K. Stavrou, L. G. Franca and A. P. Monkman, ASC Appl. Electron. Mater., 2020, 2, 2868–2881 CrossRef CAS PubMed.
- L. G. Franca, A. Danos and A. Monkman, J. Mater. Chem. C, 2022, 10, 1313–1325 RSC.
- L.-S. Cui, H. Nomura, Y. Geng, J. U. Kim, H. Nakatomani and C. Adachi, Angew. Chem., 2016, 56, 1571–1575 CrossRef PubMed.
- F. B. Dias, K. N. Bourdakos, V. Jankus, K. C. Moss, K. T. Kametekar, V. Bhalla, J. Santos, M. R. Bryce and A. P. Monkman, Adv. Mater., 2013, 25, 3707–3714 CrossRef CAS PubMed.
- J. Gibson and T. J. Penfold, Phys. Chem. Chem. Phys., 2017, 19, 8428–8434 RSC.
- M. A. El Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic procedures and results of analyzes, description of methods used and procedure for the determination of photophysical parameters; detailed discussion on spectral properties; details of the analysis approach based on Arrhenius and Marcus theories; computational details and theoretical prediction of ISC and rISC rate constants within rotational, vibrational, and rotational-vibronic models; animation file for the key molecular vibrations. See DOI: https://doi.org/10.1039/d2tc00476c |
| This journal is © The Royal Society of Chemistry 2022 |