Open Access Article
Open Access ArticleThe paradigm of the filler's dielectric permittivity and aspect ratio in high-k polymer nanocomposites for energy storage applications†
Zouhair
Hanani
 *abc,
Daoud
Mezzane
ad,
M’barek
Amjoud
a,
Mohammed
Lahcini
a,
Matjaž
Spreitzer
*abc,
Daoud
Mezzane
ad,
M’barek
Amjoud
a,
Mohammed
Lahcini
a,
Matjaž
Spreitzer
 c,
Damjan
Vengust
c,
Arash
Jamali
e,
Mimoun
El Marssi
d,
Zdravko
Kutnjak
c and
Mohamed
Gouné
b
c,
Damjan
Vengust
c,
Arash
Jamali
e,
Mimoun
El Marssi
d,
Zdravko
Kutnjak
c and
Mohamed
Gouné
b
aIMED-Lab, Cadi Ayyad University, Marrakesh, 40000, Morocco
bICMCB, University of Bordeaux, Pessac, 33600, France
cJozef Stefan Institute, Ljubljana, 1000, Slovenia. E-mail: zouhair.hanani@ijs.si
dLPMC, University of Picardy Jules Verne, Amiens, 80039, France
ePME, University of Picardy Jules Verne, Amiens, 80039, France
First published on 16th June 2022
Abstract
Ceramic/polymer nanocomposites are promising materials for energy storage applications. The most common approach to optimize energy storage properties relies on combining a ceramic and a polymer having the highest possible dielectric permittivity and breakdown strength, respectively. It is also known that another significant factor is the aspect ratio of nanofillers where a higher aspect ratio gives rise to a higher effective dielectric permittivity of the composite. There is thus a duality between the dielectric permittivity of the ceramic and its aspect ratio that we propose to study in this paper. To achieve this, high-k nanocomposites were designed based on biodegradable polymer matrix polylactic acid (PLA) and different inorganic nanofillers having different shapes (spherical, rod and wire) and dielectric properties. The effects of the aspect ratio, core–shell structure, dielectric permittivity and volume fraction of the nanofillers on the dielectric and energy storage performances of PLA-based nanocomposites were assessed. An enhanced energy storage density and recovered energy density of 3.63 and 1.80 J cm−3, respectively, were obtained in nanocomposites based on rod-like fillers. We discussed, from a theoretical model, that, below the percolation threshold, the obtained properties resulted from a compromise between both the dielectric permittivity and the aspect ratio of the ceramic. This investigation provides an exciting opportunity to advance our knowledge of ceramic/polymer nanocomposites for energy storage applications.
1. Introduction
Ferroelectric ceramics have high dielectric permittivity (εr), however, their high dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ), low breakdown strength (BDS), poor processability and lack of flexibility significantly limit their integration in energy storage applications.1–6 However, polymers usually have a high BDS and ease of processing, but most have a low εr.7–9 An ideal high-k material will not only have a high εr but will also display low tan
δ), low breakdown strength (BDS), poor processability and lack of flexibility significantly limit their integration in energy storage applications.1–6 However, polymers usually have a high BDS and ease of processing, but most have a low εr.7–9 An ideal high-k material will not only have a high εr but will also display low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, high BDS, and good processability.10–13 Hence, it is reasonable to harness the advantages of both parts to design ceramic/polymer nanocomposites with enhanced energy storage performances.14–17 In recent years, many efforts have been made to improve both the dielectric properties and the energy density of the ceramic/polymer nanocomposites, for instance, (i) the use of polyvinylidene fluoride (PVDF) as a matrix because of its high εr and BDS, and (ii) the fabrication of advanced nanostructures and the improvement of their dispersion into the polymer matrix.11,18 Also, as these challenges include the need to understand the chemistry and the structure of the ceramic–polymer, the study of their interface become an attractive research topic.19,20 In this respect, the preparation of core–shell structured nanoparticles by surface-initiated in situ polymerisation has aroused significant interest because of its unique advantages: (i) the nanoparticles can be well encapsulated with controllable polymer layer thickness, resulting in a significant reduction in the surface energy of nanoparticles. (ii) The properties of the nanocomposites can be adjusted by adapting the physical properties of the polymeric shell and/or the interaction between the polymeric shell and the polymer matrix.21–26
δ, high BDS, and good processability.10–13 Hence, it is reasonable to harness the advantages of both parts to design ceramic/polymer nanocomposites with enhanced energy storage performances.14–17 In recent years, many efforts have been made to improve both the dielectric properties and the energy density of the ceramic/polymer nanocomposites, for instance, (i) the use of polyvinylidene fluoride (PVDF) as a matrix because of its high εr and BDS, and (ii) the fabrication of advanced nanostructures and the improvement of their dispersion into the polymer matrix.11,18 Also, as these challenges include the need to understand the chemistry and the structure of the ceramic–polymer, the study of their interface become an attractive research topic.19,20 In this respect, the preparation of core–shell structured nanoparticles by surface-initiated in situ polymerisation has aroused significant interest because of its unique advantages: (i) the nanoparticles can be well encapsulated with controllable polymer layer thickness, resulting in a significant reduction in the surface energy of nanoparticles. (ii) The properties of the nanocomposites can be adjusted by adapting the physical properties of the polymeric shell and/or the interaction between the polymeric shell and the polymer matrix.21–26
Indeed, the core–shell structure leads to improved dielectric, ferroelectric and energy storage properties.21,22,24,27 Usually, this improvement is ascribed to the interface compatibility enhancement between the embedded core–shell fillers and the polymer matrix.27 However, the dielectric properties depend also on the topological and morphological criteria.28 In fact, the arrangement and the alignment of the nanofillers inside the polymer matrix play a pivotal role in fostering the dielectric properties of the high-k nanocomposites.28,29 Likewise, high aspect ratio fillers like nanowires are beneficial for designing high-k nanocomposite films with enhanced performances for energy storage applications.30–34 For instance, Tang et al. demonstrated that the εr of the nanocomposite can be highly efficiently improved by the high aspect ratio of the fillers without additional fillers or defect incorporation into the nanocomposites.35 Furthermore, Tang et al. reported that embedding PbZr0.52Ti0.48O3 (PZT) nanowires in the PVDF matrix could enhance the energy storage density by 77.8% compared to that of PZT nanorods.36
In the background, studies on ceramic/polymer nanocomposites raise the question of the design of the nanocomposite. Indeed, the energy storage properties are expected to depend on the individual dielectric properties of the polymer and the ceramic, the volume fraction and the morphological and topological characteristics of the ceramic.31,36,37 From this perspective, an efficient design of the ceramic/polymer composite requires to define the optimal parameters that lead to the highest stored energy density. This is an important element to which there is no obvious answer at first glance. The reason for this is that (i) the storage properties result from complex interactions between the parameters listed above and (ii) some parameters may have antagonistic effects on the resulting storage properties. To better understand this, consider the first example, which will be studied in this paper, of the duality that exists between the εr and the aspect ratio of the ceramic. All things being the same, the choice of a high εr ceramic embedded in a polymer matrix results in a higher effective εr of the composite. This, at first glance, goes in the direction of an increase in the stored energy density. However, the negative impact of a large difference in the εr of the ceramic and the polymer that leads to local electric field intensification and interfacial polarization should also be taken into account, which induces a reduction of the effective BDS of the composite.38 Thus, lower stored energy density is obtained. As a consequence, the use of a high εr ceramic does not necessarily result in an increase of the stored energy density. Let us now consider the aspect ratio of the ceramic, a higher aspect ratio will inevitably improve the εr of the nanocomposites.8,39,40 There are two reasons behind this: first, the high aspect ratio fillers reach the percolation threshold (fc) more easily than the low aspect ratio fillers, which allows connectivity or a continuous path in the system and improves the dielectric properties of the composites.41 Second, the high aspect ratio fillers have lower surface area than low aspect ratio fillers, which helps to reduce the surface energy, thus preventing agglomeration, enhancing the overall performance of the composites.42
These are important aspects to which it is difficult to provide answers and an obvious correlation exists with the energy storage properties of the nanocomposite. Through experimental and theoretical approaches, this paper aims to study and to better understand the effects of the volume fraction, core–shell structure, dielectric permittivity and aspect ratio of the nanofillers on both the dielectric and energy storage properties of PLA-based nanocomposites. The polylactic acid (PLA) polymer was selected due to its biodegradability and biocompatibility, which could be encouraging to design eco-friendly high-k nanocomposites for biomedical applications.43,44 A comparison of the electrical properties of PLA, some biopolymers and petrol-based polymers are shown in Section S1.2 in the ESI.† Besides, the Ba0.85Ca0.15Zr0.10Ti0.90O3 (BCZT) lead-free ceramic known for its excellent dielectric, ferroelectric and energy storage performances was chosen.45–53
In the first step, near-spherical BZCT was embedded in the PLA matrix. Moreover, a core–shell structuration step was designed via polydopamine (PDA), which is an extensively used organic compound for this process,21,54,55 to enhance the compatibility between BCZT and PLA. In the second step, H2(Zr0.1Ti0.9)3O7 nanowires were usually used as an inorganic template to design architectured ferroelectric materials,56 and rod-like BCZT fillers57 were encapsulated in the PLA matrix. Both H2(Zr0.1Ti0.9)3O7 nanowires and rod-like BCZT fillers have different dielectric permittivities and aspect ratios compared to those of near-spherical BCZT particles.
2. Experimental
Ba0.85Ca0.15Zr0.10Ti0.90O3 near-spherical particles (B_NP), H2(Zr0.1Ti0.9)3O7 nanowires (HZTO_NW) and Ba0.85Ca0.15Zr0.10Ti0.90O3 rod-like (B_NR) nanopowders were synthesised using soft-chemistry routes.45,57–59 The elaborated nanofillers were shown to have different morphologies and/or permittivities (see Table 1 and Fig. 1). The core–shell structure of B_NP using a polydopamine (PDA) layer will be designed by B_NP@PDA. Using the solvent casting method, the elaborated nanofillers were then dispersed in the PLA matrix to form nanocomposites. In this study, the volume fraction of the fillers was set to less than or equal to 20 vol% because of the deterioration of the mechanical properties at high loading and the spherical packing limitations. The detailed experimental procedure, sample characterisations and structural properties of BCZT/PLA nanocomposites are provided in Sections S1 and S2 in the ESI.†| Ceramic | Shape | Aspect ratio | Dielectric permittivity |
|---|---|---|---|
| B_NP | Near-spherical | 1 | 12085 |
| HZTO_NW | Nanowire | 50 | 350 |
| B_NR | Nanorod | 10 | 11906 |
 | ||
| Fig. 1 (a) TEM micrograph of B_NP, and (b and c) FESEM micrographs of HZTO_NW and B_NR, respectively. | ||
3. Results and discussions
3.1. Morphological properties of the PLA-based nanocomposites
Fig. S5 (ESI†) shows the morphological characteristics of the PLA-based nanocomposites at the surface and the cross-section after embedding 3 vol% of B_NP, B_NP@PDA, HZTO_NW and B_NR fillers in the PLA matrix. The black region corresponds to the PLA matrix, while the white spots represent the fillers. It is observed that all nanofillers are correctly dispersed in the PLA matrix. To gain insight into the compatibility between the different nanofillers and PLA matrix, Fig. 2e–h provide an overview of the distribution of B_NP, B_NP@PDA, HZTO_NW and B_NR fillers inside the PLA matrix via cross-section views. The nanofillers show excellent dispersion in the PLA matrix and a large number of fillers are covered with the PLA matrix, especially in nanocomposites with high aspect ratio fillers. This suggests the excellent compatibility between the matrix and the loads. To study the effect of core–shell structure using PDA, 20 vol% of B_NP and B_NP@PDA were introduced in the PLA matrix, and the morphological characteristics of both films are presented in Fig. 2. Even though high filler content was embedded, a good dispersion of the fillers in PLA matrix is clearly observed. It is worth mentioning that several B_NP@PDA particles are bound together (see inset of Fig. 2b), which could be due to the high dopamine concentration used in the core–shell formation step. Remarkably, at a high filler concentration, B_NP@PDA particles form noticeable acicular paths in the PLA matrix (see the red eclipse in Fig. 2d), leading to the formation of well-connected ellipsoidal agglomerations of B_NP@PDA particles as illustrated in Fig. 2f. This further proves the chemical bounding of B_NP@PDA and PLA via the PDA shell.3.2. Dielectric properties of the PLA-based nanocomposites
The frequency-dependencies of the dielectric permittivity (εr) and the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of B_NP/PLA, B_NR@PDA/PLA, HZTO_NW/PLA and B_NR/PLA nanocomposite films with different volume fractions are provided in the S2.2 Section in the ESI.† Besides, Fig. 3 summarises the values of εr and tan
δ) of B_NP/PLA, B_NR@PDA/PLA, HZTO_NW/PLA and B_NR/PLA nanocomposite films with different volume fractions are provided in the S2.2 Section in the ESI.† Besides, Fig. 3 summarises the values of εr and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at different volume fractions as measured at 1 kHz for all nanocomposite films. From a global point of view, it appears that both εr and tan
δ at different volume fractions as measured at 1 kHz for all nanocomposite films. From a global point of view, it appears that both εr and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ gradually increase with the increase in the volume fraction. It can also be pointed out that for all filler concentrations, the dielectric properties of B_NP@PDA/PLA nanocomposites are systematically improved with respect to B_NP/PLA. Furthermore, the nanocomposites with high aspect ratio fillers (rods and nanowires) exhibit enhanced dielectric properties compared to those based on B_NP and B_NP@PDA although the dielectric permittivity of the fillers is lower than those of B_NP (see Table 1). For instance, at 20 vol%, the dielectric permittivity values of B_NP/PLA, B_NP@PDA/PLA, HZTO_NW/PLA and B_NR/PLA nanocomposite films are found to be 9.11, 11.24, 16.00 and 20.28, respectively. More interestingly, the dielectric loss is decreased in the nanocomposites based on fillers with a high aspect ratio, e.g., embedding PLA matrix with 20 vol% B_NR can enhance the dielectric permittivity more than two-fold compared to B_NP with the same loading, while keeping low dielectric loss.
δ gradually increase with the increase in the volume fraction. It can also be pointed out that for all filler concentrations, the dielectric properties of B_NP@PDA/PLA nanocomposites are systematically improved with respect to B_NP/PLA. Furthermore, the nanocomposites with high aspect ratio fillers (rods and nanowires) exhibit enhanced dielectric properties compared to those based on B_NP and B_NP@PDA although the dielectric permittivity of the fillers is lower than those of B_NP (see Table 1). For instance, at 20 vol%, the dielectric permittivity values of B_NP/PLA, B_NP@PDA/PLA, HZTO_NW/PLA and B_NR/PLA nanocomposite films are found to be 9.11, 11.24, 16.00 and 20.28, respectively. More interestingly, the dielectric loss is decreased in the nanocomposites based on fillers with a high aspect ratio, e.g., embedding PLA matrix with 20 vol% B_NR can enhance the dielectric permittivity more than two-fold compared to B_NP with the same loading, while keeping low dielectric loss.
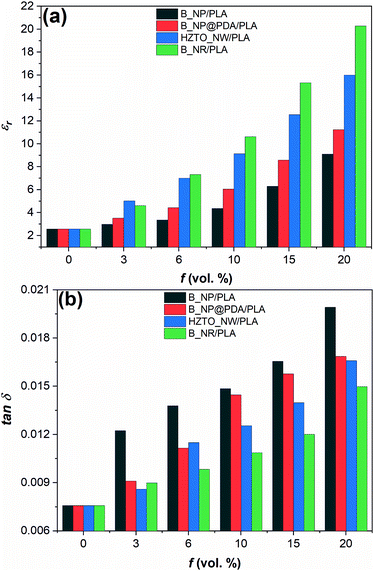 | ||
| Fig. 3 Effect of the volume fraction of B_NP, B_NP@PDA, HZTO_NW and B_NR fillers on the (a) dielectric permittivity and (b) dielectric loss of PLA-based nanocomposites. | ||
3.3. Energy storage properties of the PLA-based nanocomposites
To gain insights into the energy storage of PLA-based nanocomposite films, Fig. S7 in the ESI† displays the positive branch of the dielectric displacement–electric field (D–E) loops of the PLA-based nanocomposites measured at 100 Hz and under an electric field of 1 MV cm−1. The maximum electric displacement (Dmax) and the remnant electric displacement (Dr) of each nanocomposite increase with increasing filler concentration. Furthermore, Dmax and Dr of B_NR/PLA nanocomposites are higher than those of HZTO_NW/PLA, B_NP@PDA/PLA and B_NP/PLA. From the recorded D–E loops, the total energy density (Wtot) of the nanocomposites can be estimated using Eqn (1).60Wtot was calculated via numerical integration by adding the area around the closed area of the D–E hysteresis loops (energy loss density, Wloss) and the area between the polarisation axis and the upper branch curve of the unipolar D–E hysteresis loop (recovered energy density, Wrec). The calculated values of the energy density at 1 MV cm−1 are presented in Fig. 4a. The total stored energy density increases with increasing nanofiller concentration. It should be noted that the observed energy density values of B_NR/PLA nanocomposites are systematically higher than those of HZTO_NW/PLA, B_NP@PDA/PLA and B_NP/PLA due to the enhanced dielectric displacement in B_NR/PLA nanocomposites. At a nanofiller concentration of 20 vol%, the Wtot values are 3.63, 3.13, 2.47 and 1.43 J cm−3 for B_NR/PLA, HZTO_NW/PLA, B_NP@PDA/PLA and B_NP/PLA, respectively.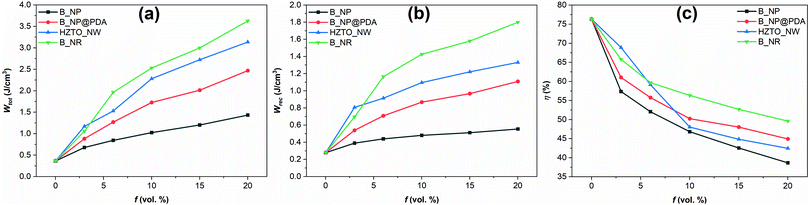 | ||
| Fig. 4 Energy storage performances of the PLA-based nanocomposites. (a) The total, (b) recovered energy densities and (c) energy storage efficiency. | ||
In order to evaluate the effective energy storage capability of our samples, the recovered energy density (Wrec) was determined. As shown in Fig. 4b, the recovered energy density values of B_NR/PLA nanocomposites are systematically higher than those of HZTO_NW/PLA, B_NP@PDA/PLA and B_NP/PLA, respectively. At 20 vol%, the Wrec values, determined from eqn (2), are 1.80, 1.31, 1.11 and 0.55 J cm−3 for B_NR/PLA, HZTO_NW/PLA, B_NP@PDA/PLA and B_NP/PLA, respectively. The energy storage efficiency (η) can be defined as the ratio of recovered energy density to the total stored energy density, as estimated in eqn (3).61 As shown in Fig. 4c, at a filler concentration of 20 vol%, the calculated values of η are 49.58, 41.85, 44.94 and 38.48% for B_NR/PLA, HZTO_NW/PLA, B_NP@PDA/PLA and B_NP/PLA, respectively.
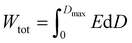 | (1) |
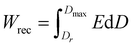 | (2) |
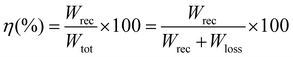 | (3) |
It is observed that the total stored energy density of the nanocomposite with 20 vol% of B_NR is ten times higher than that of the pure PLA polymer (0.365 J cm−3). Meanwhile, the recovered energy density of the nanocomposite with 20 vol% B_NR is more than six-fold that of PLA polymer (0.365 J cm−3). Surprisingly and although the permittivity of HZTO is much smaller than BCZT (approximately thirty times lower), the energy storage performances of HZTO_NW/PLA are much better than those of both B_NP/PLA and B_NP@PDA/PLA. In order to go further in this direction, it is interesting to note that Wtot, Wrec and η of HZTO_NW are higher than those of other PLA-nanocomposites at f = 3 vol% (Fig. 4). This can be related to a higher effective permittivity and lower dielectric loss of the HZTO_NW/PLA at 3 vol% (Fig. 3). As the matrix is identical in all the cases studied, this can be reasonably attributed to the large aspect ratio of HZTO which beneficially affects both the effective permittivity and dielectric loss of the nanocomposite. At a higher filler content, HZTO fillers tend to aggregate in the matrix because of their large specific surface energy. After the completion of the formation of a percolation network in the polymer matrix the dipoles of polymer are pinned by the surface charges or defects at the interface between the matrix and the filler. Accordingly, the electrical properties are degraded.28 Such behaviour was also observed by Wang et al. when comparing four kinds of nanowires (Na2Ti3O7, TiO2, BaTiO3 and SrTiO3).10
From the above results and as expected, the energy storage properties depend on both the effective dielectric permittivity and the dielectric loss of the nanocomposite. The two physical quantities are shown to result from a compromise between the dielectric permittivity and the aspect ratio of the filler. This point goes against the most common approach that consists in combining a ceramic and a polymer having the highest possible dielectric permittivity and breakdown strength, respectively. The alternative approach may be to focus more on the aspect ratio of the filler than its dielectric permittivity. However, this requires a better understanding of their relative contributions. This is an important point for the design of ceramic/polymer nanocomposites for high-efficiency energy storage applications. In the following section, we will discuss the results obtained via theoretical calculations.
3.4. Effect of the core–shell structure
Many works have demonstrated that polydopamine is very promising for utilization as a surface modifier to improve the inclusion of nanofillers inside polymer matrices, because of its powerful adhesion ability.18,62,63 It was found that the dielectric properties of the core–shell structured nanocomposites (B_NP@PDA/PLA), were higher compared to the non-core–shell structured ones (B_NP/PLA). This enhancement of the dielectric properties in B_NP@PDA/PLA films could be related to the improved interfacial compatibility between the nanoparticles and the PLA matrix, which suppresses the dipolar polarisation loss of the PLA matrix.64 Furthermore, the surface water layer and other impurities may be removed during the introduction of the PDA layer onto the B_NP nanoparticle's surface, resulting in reduced electrical conduction and/or interfacial polarisation loss.21 Moreover, the dielectric losses in B_NP@PDA/PLA are lower while it exhibits a higher permittivity than B_NP/PLA. Another important reason for the improvement of the dielectric properties of B_NP@PDA/PLA nanocomposite films could be the formation of well-connected ellipsoidal agglomeration of B_NP@PDA particles observed in Fig. 2d, which could affect both the 3D topology and the effective aspect ratio; the particles can no longer be considered spherical but rather ellipsoidal. This point will be discussed further. Nevertheless, it has been recognised that the functionalisation does not have a very pronounced effect on dielectric properties of the nanocomposites.3.5. Effect of the filler volume fraction on the iso-aspect ratio
Permittivity is a property that characterises the electrical polarisation of a material under an external electric field. In our composites, the PLA polymer shows a low permittivity (εr = 2.7), while the B_NP ceramic exhibits high permittivity as-sintered (εr = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 085). For the latter, the high dielectric permittivity reflects the spontaneous polarisation of ferroelectrics; a small electric field is enough to create large polarisation. In order to better understand the evolutions of the effective permittivity of the nanocomposites, the fundamental question that arises is how the inclusions of the B_NP ceramic into host PLA polymer influence the polarisation field. However, the answer depends on many factors such as morphology, 3D distribution and orientation of inclusions, the norm and the frequency of the external field applied, and the dielectric mismatch between the PLA polymer and the B_NP ceramic. From a general aspect, the problem that has arisen in determining the effective permittivity of heterostructures. It is a complex problem that has attracted attention beginning with the pioneering work of Maxwell.65 Section S2.3 in the ESI† provides step-by-step possible answers to the previous question. It was observed that the measured dielectric permittivities show a linear dependence on the volume fraction of BCZT (Fig. S8 in the ESI†). Moreover, below the percolation threshold (fc = 27% for spheres), the volume fraction effect is certainly present but much less than that beyond the percolation threshold. This can be explained by the fact that the domains are spatially separated, and electrostatic interactions between each inclusion and its neighbours are relatively weak when the volume fraction of fillers are below the percolation threshold.66
085). For the latter, the high dielectric permittivity reflects the spontaneous polarisation of ferroelectrics; a small electric field is enough to create large polarisation. In order to better understand the evolutions of the effective permittivity of the nanocomposites, the fundamental question that arises is how the inclusions of the B_NP ceramic into host PLA polymer influence the polarisation field. However, the answer depends on many factors such as morphology, 3D distribution and orientation of inclusions, the norm and the frequency of the external field applied, and the dielectric mismatch between the PLA polymer and the B_NP ceramic. From a general aspect, the problem that has arisen in determining the effective permittivity of heterostructures. It is a complex problem that has attracted attention beginning with the pioneering work of Maxwell.65 Section S2.3 in the ESI† provides step-by-step possible answers to the previous question. It was observed that the measured dielectric permittivities show a linear dependence on the volume fraction of BCZT (Fig. S8 in the ESI†). Moreover, below the percolation threshold (fc = 27% for spheres), the volume fraction effect is certainly present but much less than that beyond the percolation threshold. This can be explained by the fact that the domains are spatially separated, and electrostatic interactions between each inclusion and its neighbours are relatively weak when the volume fraction of fillers are below the percolation threshold.66
3.6. Effect of the dielectric permittivity on the iso-aspect ratio
As observed experimentally, below the percolation threshold the effective permittivity increases linearly with both increasing volume fraction and permittivity of B_NP. However, based on theoretical calculations, for a critical value of permittivity of around 100 (that corresponds to a dielectric mismatch of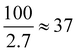 ), the effective permittivity no longer evolves. In other terms, when spherical inclusions do not touch each other, there is a critical permittivity of B_NP from which the effective permittivity does not increase even for giant permittivities of the B_NP ceramic (Fig. 5). As demonstrated in S2.3 Section in the ESI,† the polarisability α increases with increasing B_NP permittivity to reach a stagnant stage for a value of B_NP permittivity around 200 (Fig. S9, ESI†). Besides, the internal field inside inclusions decreases dramatically with increasing B_NP permittivity. This means that the penetration of the electrical field into B_NP inclusions is difficult when the electrical contrast between B_NP and PLA becomes high.67,68 There are reasons why the effective permittivity of the composite is no longer increased beyond a critical permittivity of B_NP (evaluated at around 200 in this work) for volume fractions of B_NP lower than the percolation threshold. This latter is thus the key parameter for controlling the resulting properties of the nanocomposites.
), the effective permittivity no longer evolves. In other terms, when spherical inclusions do not touch each other, there is a critical permittivity of B_NP from which the effective permittivity does not increase even for giant permittivities of the B_NP ceramic (Fig. 5). As demonstrated in S2.3 Section in the ESI,† the polarisability α increases with increasing B_NP permittivity to reach a stagnant stage for a value of B_NP permittivity around 200 (Fig. S9, ESI†). Besides, the internal field inside inclusions decreases dramatically with increasing B_NP permittivity. This means that the penetration of the electrical field into B_NP inclusions is difficult when the electrical contrast between B_NP and PLA becomes high.67,68 There are reasons why the effective permittivity of the composite is no longer increased beyond a critical permittivity of B_NP (evaluated at around 200 in this work) for volume fractions of B_NP lower than the percolation threshold. This latter is thus the key parameter for controlling the resulting properties of the nanocomposites.
 | ||
| Fig. 5 Evolution of the effective permittivity of the composite as a function of B_NP volume fraction for different values of B_NP permittivity. Comparison with the experimental data. | ||
In the case of non-spherical inclusions and/or the non-random distribution of inclusions, the percolation threshold is expected to decrease as it becomes more likely for the inclusions to touch each other. In our study, this is an interesting aspect since the morphology of dispersed B_NP is clearly not spherical in the B_NP@PDA/PLA composite and there is little chance that the distribution of B_NP into the composite is perfectly homogeneous. These are the probable reasons that would explain that the effective permittivities measured are located above the curves calculated (see Fig. 5).
3.7. Effect of the filler's aspect ratio on iso-permittivity
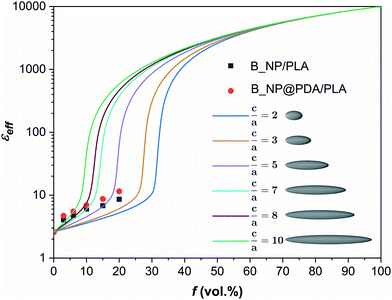
As explained before, the morphology of the dispersed B_NP ceramic can influence the effective permittivity of the composites. In order to study this effect, the model developed for a mixture of randomly oriented ellipsoids of the B_NP ceramic into the PLA matrix was adapted,69 as discussed in section S2.4 in the ESI.† For a given permittivity of B_NP of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, increasing the aspect ratio of B_NP ceramic leads to an increase of the effective permittivity of the composite because the induced polarisability is enhanced with the aspect ratio. Interestingly, From Fig. 6, it is observed that a prompt increase of the effective permittivity at a given volume fraction of B_NP depends on the aspect ratio. These occur as if the effective permittivity is highly improved at a volume fraction corresponding to the percolation threshold. In other words, this enhancement of the effective permittivity is attributed to the increase in the aspect ratio, which decreases the percolation threshold of the embedded fillers (Fig. S10, ESI†).70 These theoretical calculations corroborate those obtained experimentally, where an enhancement of the dielectric properties in the fillers with a high aspect ratio compared to near-spherical particles was noticed.
000, increasing the aspect ratio of B_NP ceramic leads to an increase of the effective permittivity of the composite because the induced polarisability is enhanced with the aspect ratio. Interestingly, From Fig. 6, it is observed that a prompt increase of the effective permittivity at a given volume fraction of B_NP depends on the aspect ratio. These occur as if the effective permittivity is highly improved at a volume fraction corresponding to the percolation threshold. In other words, this enhancement of the effective permittivity is attributed to the increase in the aspect ratio, which decreases the percolation threshold of the embedded fillers (Fig. S10, ESI†).70 These theoretical calculations corroborate those obtained experimentally, where an enhancement of the dielectric properties in the fillers with a high aspect ratio compared to near-spherical particles was noticed.
It was reported that the high aspect ratio fillers can improve the dielectric properties of the composites.35,71,72 Theoretically, the high aspect ratio fillers reach the percolation threshold more easily than the low aspect ratio fillers, which allows connectivity or continuous path in the system and improves the dielectric properties of the composites.41,73 Moreover, the high aspect ratio can improve the dielectric permittivity of the composites due to the large dipole moment.35 Besides, the high aspect ratio fillers have lower surface area than low aspect ratio fillers, which helps to reduce the surface energy, thus preventing agglomeration and enhancing the overall performance of the composites.42 Therefore, these results suggest that the use of high aspect ratio nanofiller could enhance the energy storage performance of PLA-based nanocomposites.8,31,74
3.8. Compromise between dielectric permittivity and the aspect ratio
Two main results were highlighted previously. For volume fractions of B_NP lower than the percolation threshold, the effective permittivity of the composite is no longer increased beyond a critical permittivity of B_NP (evaluated around 200 in this work). The development of ceramic/polymer composites is mainly motivated by the large difference in the dielectric properties of the ceramic as a filler and polymer as the matrix. It was observed that the composites based on ceramic fillers owning relatively low dielectric permittivity (B_NR and HZTO_NW) exhibit enhanced dielectric properties and energy storage performances compared to those with fillers with large dielectric permittivity (B_NP). As discussed before, according to the modelling results, there is a critical value of the ceramic fillers’ permittivity; beyond which, the effective permittivity of the composite is no longer increased. Besides, it was argued before that the percolation threshold is a crucial parameter to control the resulting properties of the composites. Below the percolation threshold, the effective permittivity increases linearly with increasing volume fraction and permittivity of B_NP. However, when tuning the shape and/or the distribution of the inclusions inside the polymer the percolation threshold is expected to decrease as it becomes more likely for the inclusions to touch each other. The composites based on ceramic fillers with a high aspect ratio percolate easily at a low filler content, hence enhanced electrical properties were observed at a low filler loading. Hence, there is a mutual effect of the dielectric permittivity and the aspect ratio of the ceramic filler on the dielectric properties and energy storage performances in the ceramic/polymer nanocomposite. A paradigm emerges, which can be summarised as follows: for improving the dielectric properties of the composite, it is not necessary to use ceramics with high permittivity, but we should instead control their geometry.The analyses performed in Section S2.4 in the ESI† show that both permittivity and aspect ratio of B_NP ceramic control the effective permittivity of the composite. Then, one might ask oneself what couples 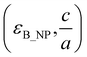 might fit the experimental data. The results of the calculations presented in Fig. 7 evidence that the solution is not unique; there exists an infinite. The most striking result that emerges is that the experimental data can be fitted with very different values of B_NP permittivity but relatively close values of aspect ratio (see for example the couples
might fit the experimental data. The results of the calculations presented in Fig. 7 evidence that the solution is not unique; there exists an infinite. The most striking result that emerges is that the experimental data can be fitted with very different values of B_NP permittivity but relatively close values of aspect ratio (see for example the couples 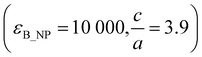 and
and 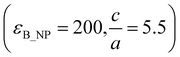 . We show here that a drastic decrease of the B_NP permittivity can be compensated by a relatively slight increase of the aspect ratio of B_NP. This is a key point for improving the energy storage properties of the composite since the large difference between the dielectric permittivity of the inclusions and the matrix can lead to local electric field intensification and interfacial polarization.23,42,75,76 Thus, there is a mutual interaction between the dielectric permittivity and the aspect ratio of the ceramic filler, and the resulting dielectric properties and energy storage performances are based on a compromise between the dielectric permittivity and the aspect ratio of the ceramic filler.
. We show here that a drastic decrease of the B_NP permittivity can be compensated by a relatively slight increase of the aspect ratio of B_NP. This is a key point for improving the energy storage properties of the composite since the large difference between the dielectric permittivity of the inclusions and the matrix can lead to local electric field intensification and interfacial polarization.23,42,75,76 Thus, there is a mutual interaction between the dielectric permittivity and the aspect ratio of the ceramic filler, and the resulting dielectric properties and energy storage performances are based on a compromise between the dielectric permittivity and the aspect ratio of the ceramic filler.
 | ||
Fig. 7 Calculation of the effective permittivity of the B_NP/PLA composite as a function of the B_NP volume fraction for different couples 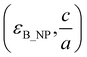 and comparison with the experimental data. and comparison with the experimental data. | ||
4. Summary and conclusions
High-k nanocomposites based on biodegradable polymer matrix polylactic acid (PLA) and different inorganic nanofillers with various shapes (spherical, rod and wire) and arrangements were successfully fabricated. The effects of nanofiller's permittivity, aspect ratio and the core–shell structure were explored by experimental and theoretical approaches. Very surprisingly, the core–shell structure does not have a very pronounced effect on the dielectric properties of the nanocomposites (effective permittivity and dielectric loss). Subsequently, the effect of the aspect ratio was studied after observing the ellipsoidal arrangement in the core–shell structured nanocomposites. It was concluded that a substantial decrease of the B_NP permittivity could be compensated by a relatively slight increase of the aspect ratio of B_NP. Consequently, a paradigm has emerged since the development of ceramic/polymer composites is mainly motivated by the significant differences in the dielectric properties of the ceramic as the filler and polymer as a matrix. To address this issue, two types of ceramic fillers possessing adverse properties, i.e., B_NR with high dielectric permittivity and high aspect ratio and HZTO_NW with low dielectric permittivity and very high aspect ratio, were embedded in the PLA matrix. The enhancement of the dielectric properties in fillers with a high aspect ratio compared to near-spherical particles was attributed to the low percolation threshold of such fillers with a high aspect ratio. Finally, the energy storage performances of PLA-based nanocomposites were evaluated by D–E loops using spherical, rod, and wire-shaped particles. The highest Wtot and Wrec of 3.63 and 1.80 J cm−3, respectively, were obtained in the nanocomposites based on rod-like fillers. Hence, the use of high-aspect-ratio nanofiller with high dielectric permittivity enhances the energy storage performance of PLA-based nanocomposites. Accordingly, this study reveals a paradigm between the dielectric permittivity and the aspect ratio of the ceramic filler. The resulting dielectric properties and energy storage performances in ceramic/polymer nanocomposite were based on a compromise between the dielectric permittivity and the aspect ratio of the ceramic filler.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the generous financial support from the European Union Horizon 2020 Research and Innovation actions MSCA-RISE-ENGIMA (No. 778072) and MSCA-RISE-MELON (No. 872631). Z. K. and M. S. acknowledge the Slovenian Research Agency program P1-0125 and P2-0091, respectively.References
- Y. Wang and Z. Peng, J. Ceram. Soc. Jpn., 2014, 122, 719–724 CrossRef.
- F. Wang, W. Li, H. Jiang, M. Xue, J. Lu and J. Yao, J. Appl. Phys., 2010, 107, 043528 CrossRef.
- Y. Lin, D. Li, M. Zhang, S. Zhan, Y. Yang, H. Yang and Q. Yuan, ACS Appl. Mater. Interfaces, 2019, 11, 36824–36830 CrossRef CAS PubMed.
- M. Zhang, H. Yang, Y. Yu and Y. Lin, Chem. Eng. J., 2021, 425, 131465 CrossRef CAS.
- M. Zhang, H. Yang, Y. Lin, Q. Yuan and H. Du, Energy Storage Mater., 2022, 45, 861–868 CrossRef.
- S. Merselmiz, Z. Hanani, S. Ben Moumen, A. Matavž, D. Mezzane, N. Novak, Z. Abkhar, L. Hajji, M. Amjoud, Y. Gagou, K. Hoummada, D. Črešnar, Z. Kutnjak and B. Rožič, J. Mater. Sci.: Mater. Electron., 2020, 31, 17018–17028 CrossRef CAS.
- S. Luo, J. Yu, S. Yu, R. Sun, L. Cao, W. H. Liao and C. P. Wong, Adv. Energy Mater., 2019, 9(5) DOI:10.1002/aenm.201803204.
- X. Huang, B. Sun, Y. Zhu, S. Li and P. Jiang, Prog. Mater. Sci., 2019, 100, 187–225 CrossRef CAS.
- Y. Qiao, X. Yin, T. Zhu, H. Li and C. Tang, Prog. Polym. Sci., 2018, 80, 153–162 CrossRef CAS.
- G. Wang, X. Huang and P. Jiang, ACS Appl. Mater. Interfaces, 2015, 7, 18017–18027 CrossRef CAS PubMed.
- Y. Huang and X. Huang, in Polymer Nanocomposites: Electrical and Thermal Properties, Springer International Publishing, Cham, 2016, pp. 29–50 Search PubMed.
- K. Yang, X. Huang, M. Zhu, L. Xie, T. Tanaka and P. Jiang, ACS Appl. Mater. Interfaces, 2014, 6, 1812–1822 CrossRef CAS PubMed.
- Q. Li, L. Q. L. Chen, M. R. Gadinski, S. Zhang, G. Zhang, H. Li, A. Haque, L. Q. L. Chen, T. Jackson and Q. Wang, Nature, 2015, 523, 576–579 CrossRef CAS PubMed.
- L. Zhu, J. Phys. Chem. Lett., 2014, 5, 3677–3687 CrossRef CAS PubMed.
- C. Wu, X. Huang, L. Lv, G. Chen, J. Yu, L. Xie and P. Jiang, in Proceedings of 2012 IEEE International Conference on Condition Monitoring and Diagnosis, CMD 2012, IEEE, 2012, pp. 347–349 Search PubMed.
- W. Ma, Y. Zhu, M. A. Marwat, P. Fan, B. Xie, D. Salamon, Z. G. Ye and H. Zhang, J. Mater. Chem. C, 2019, 7, 281–288 RSC.
- K. Liu, M. A. Marwat, W. Ma, T. Wei, M. Li, P. Fan, D. Lu, Y. Tian, C. Samart, B. Ye, J. He and H. Zhang, Ceram. Int., 2020, 46, 21149–21155 CrossRef CAS.
- H. Luo, X. Zhou, C. Ellingford, Y. Zhang, S. Chen, K. Zhou, D. Zhang, C. R. Bowen and C. Wan, Chem. Soc. Rev., 2019, 48, 4424–4465 RSC.
- M. Arbatti, X. Shan and Z. Cheng, Adv. Mater., 2007, 19, 1369–1372 CrossRef CAS.
- P. Barber, S. Balasubramanian, Y. Anguchamy, S. Gong, A. Wibowo, H. Gao, H. J. Ploehn and H. C. Zur Loye, Materials, 2009, 2, 1697–1733 CrossRef CAS.
- Y. Fan, X. Huang, G. Wang and P. Jiang, J. Phys. Chem. C, 2015, 119, 27330–27339 CrossRef CAS.
- L. Xie, X. Huang, Y. Huang, K. Yang and P. Jiang, J. Phys. Chem. C, 2013, 117, 22525–22537 CrossRef CAS.
- M. Ejaz, V. S. Puli, R. Elupula, S. Adireddy, B. C. Riggs, D. B. Chrisey and S. M. Grayson, J. Polym. Sci., Part A: Polym. Chem., 2015, 53, 719–728 CrossRef CAS.
- X. Huang and P. Jiang, Adv. Mater., 2015, 27, 546–554 CrossRef CAS PubMed.
- K. Bi, M. Bi, Y. Hao, W. Luo, Z. Cai, X. Wang and Y. Huang, Nano Energy, 2018, 51, 513–523 CrossRef CAS.
- Z. Pan, L. Yao, J. Liu, X. Liu, F. Pi, J. Chen, B. Shen and J. Zhai, J. Mater. Chem. C, 2019, 7, 405–413 RSC.
- H. Luo, C. Ma, X. Zhou, S. Chen and D. Zhang, Macromolecules, 2017, 50, 5132–5137 CrossRef CAS.
- M. H. Rahaman, U. Yaqoob and H. C. Kim, Adv. Manuf.: Polym. Compos. Sci., 2019, 5, 29–36 CAS.
- K. B. Nilagiri Balasubramanian and T. Ramesh, Polym. Adv. Technol., 2018, 29, 1568–1585 CrossRef CAS.
- X. S. Qian, H. J. Ye, Y. T. Zhang, H. Gu, X. Li, C. A. Randall and Q. M. Zhang, Adv. Funct. Mater., 2014, 24, 1300–1305 CrossRef CAS.
- H. Tang, Y. Lin and H. A. Sodano, Adv. Energy Mater., 2013, 3, 451–456 CrossRef CAS.
- Y. Huang, F. Li, H. Hao, F. Xia, H. Liu and S. Zhang, J. Materiomics, 2019, 5, 385–393 CrossRef.
- P. Zhu, L. Weng, X. Zhang, X. Wang, L. Guan and L. Liu, J. Mater. Sci., 2020, 55, 7665–7679 CrossRef CAS.
- B. Xie, Y. Zhu, M. A. Marwat, S. Zhang, L. Zhang and H. Zhang, J. Mater. Chem. A, 2018, 6, 20356–20364 RSC.
- H. Tang, Z. Zhou and H. A. Sodano, ACS Appl. Mater. Interfaces, 2014, 6, 5450–5455 CrossRef CAS PubMed.
- H. Tang, Y. Lin, C. Andrews and H. A. Sodano, Nanotechnology, 2011, 22, 015702 CrossRef PubMed.
- D. Zhang, X. Zhou, J. Roscow, K. Zhou, L. Wang, H. Luo and C. R. Bowen, Sci. Rep., 2017, 7, 45179 CrossRef CAS PubMed.
- Z. Pan, J. Zhai and B. Shen, J. Mater. Chem. A, 2017, 5, 15217–15226 RSC.
- H. Tang and H. A. Sodano, Nano Lett., 2013, 13, 1373–1379 CrossRef CAS PubMed.
- H. Zhang, M. A. Marwat, B. Xie, M. Ashtar, K. Liu, Y. Zhu, L. Zhang, P. Fan, C. Samart and Z. G. Ye, ACS Appl. Mater. Interfaces, 2020, 12, 1–37 CrossRef CAS PubMed.
- J. Kruželák, A. Kvasničáková, K. Hložeková and I. Hudec, Nanoscale Adv., 2021, 3, 123–172 RSC.
- Y. Feng, W. L. Li, Y. F. Hou, Y. Yu, W. P. Cao, T. D. Zhang and W. D. Fei, J. Mater. Chem. C, 2015, 3, 1250–1260 RSC.
- I. Navarro-Baena, V. Sessini, F. Dominici, L. Torre, J. M. Kenny and L. Peponi, Polym. Degrad. Stab., 2016, 132, 97–108 CrossRef CAS.
- S. Saravanamoorthy, M. Muneeswaran, N. V. Giridharan and S. Velmathi, RSC Adv., 2015, 5, 43897–43905 RSC.
- Z. Hanani, E. H. Ablouh, M. Amjoud, D. Mezzane, S. Fourcade and M. Gouné, Ceram. Int., 2018, 44, 10997–11000 CrossRef CAS.
- Z. Hanani, D. Mezzane, M. Amjoud, S. Fourcade, A. G. Razumnaya, I. A. Luk’yanchuk and M. Gouné, Superlattices Microstruct., 2019, 127, 109–117 CrossRef CAS.
- Z. Hanani, S. Merselmiz, D. Mezzane, M. Amjoud, A. Bradeško, B. Rožič, M. Lahcini, M. El Marssi, A. V. Ragulya, I. A. Luk’Yanchuk, Z. Kutnjak and M. Gouné, RSC Adv., 2020, 10, 30746–30755 RSC.
- K. K. Poon, M. C. Wurm, D. M. Evans, M. A. Einarsrud, R. Lutz and J. Glaum, J. Biomed. Mater. Res., Part B, 2019, 108, 1295–1303 CrossRef PubMed.
- Z. Hanani, D. Mezzane, M. Amjoud, Y. Gagou, K. Hoummada, C. Perrin, A. G. Razumnaya, Z. Kutnjak, A. Bouzina, M. El Marssi, M. Gouné and B. Rožič, J. Mater. Sci.: Mater. Electron., 2020, 31, 10096–10104 CrossRef CAS.
- S. Merselmiz, Z. Hanani, D. Mezzane, A. G. Razumnaya, M. Amjoud, L. Hajji, S. Terenchuk, B. Rožič, I. A. Luk’yanchuk and Z. Kutnjak, RSC Adv., 2021, 11, 9459–9468 RSC.
- Z. Hanani, D. Mezzane, M. Amjoud, A. G. Razumnaya, S. Fourcade, Y. Gagou, K. Hoummada, M. El Marssi and M. Gouné, J. Mater. Sci.: Mater. Electron., 2019, 30, 6430–6438 CrossRef CAS.
- Z. Hanani, S. Merselmiz, M. Amjoud, D. Mezzane, M. Lahcini, J. Ghanbaja, M. Spreitzer, D. Vengust, M. El Marssi, I. A. Luk’yanchuk, Z. Kutnjak, B. Rožič and M. Gouné, J. Materiomics, 2022 DOI:10.1016/j.jmat.2021.12.011.
- Z. Hanani, D. Mezzane, M. Amjoud, A. G. Razumnaya, S. Fourcade, Y. Gagou, K. Hoummada, M. El Marssi and M. Gouné, J. Mater. Sci.: Mater. Electron., 2019, 30, 6430–6438 CrossRef CAS.
- Z. Hanani, I. Izanzar, M. Amjoud, D. Mezzane, M. Lahcini, H. Uršič, U. Prah, I. Saadoune, M. El Marssi, I. A. Luk’yanchuk, Z. Kutnjak and M. Gouné, Nano Energy, 2021, 81, 105661 CrossRef CAS.
- A. Mayeen, M. S. Kala, M. S. Jayalakshmy, S. Thomas, D. Rouxel, J. Philip, R. N. Bhowmik and N. Kalarikkal, Dalton Trans., 2018, 47, 2039–2051 RSC.
- Z. Zhou, C. C. Bowland, M. H. Malakooti, H. Tang and H. A. Sodano, Nanoscale, 2016, 8, 5098–5105 RSC.
- Z. Hanani, S. Merselmiz, A. Danine, N. Stein, D. Mezzane, M. Amjoud, M. Lahcini, Y. Gagou, M. Spreitzer, D. Vengust, Z. Kutnjak, M. El Marssi, I. A. Luk’yanchuk and M. Gouné, J. Adv. Ceram., 2020, 9, 210–219 CrossRef CAS.
- Z. Hanani, E. H. Ablouh, S. Merselmiz, J. Ghanbaja, M. Amjoud, D. Mezzane, A. Alimoussa, M. Lahcini, M. Spreitzer, D. Vengust, M. El Marssi, I. A. Luk’yanchuk, Z. Kutnjak and M. Gouné, CrystEngComm, 2021, 23, 5249–5256 RSC.
- Z. Hanani, I. Izanzar, S. Merselmiz, T. El Assimi, D. Daoud Mezzane, M. Amjoud, H. Uršič, U. Prah, J. Ghanbaja, I. Saadoune, M. Lachini, M. Spreitzer, D. Vengust, M. El Marssi, Z. Kutnjak, I. A. Luk’yanchuk and M. Gouné, Sustainable Energy Fuels, 2022, 6(8), 1983–1991 RSC.
- M. A. Marwat, B. Xie, Y. Zhu, P. Fan, W. Ma, H. Liu, M. Ashtar, J. Xiao, D. Salamon, C. Samart and H. Zhang, Composites, Part A, 2019, 121, 115–122 CrossRef CAS.
- Y. Sun, Y. Zhou, Q. Lu and S. Zhao, Phys. Status Solidi RRL, 2018, 12, 1700364 CrossRef.
- Q. Chi, T. Ma, Y. Zhang, Y. Cui, C. Zhang, J. Lin, X. Wang and Q. Lei, J. Mater. Chem. A, 2017, 5, 16757–16766 RSC.
- Z. Pan, L. Yao, G. Ge, B. Shen and J. Zhai, J. Mater. Chem. A, 2018, 6, 14614–14622 RSC.
- W. Xia, Y. Yin, J. Xing and Z. Xu, Results Phys., 2018, 11, 877–884 CrossRef.
- J. C. Maxwell, A Treatise on Electricity and Magnetism, Cambridge University Press, Cambridge, 2010 Search PubMed.
- Y. Cheng, X. Chen, K. Wu, S. Wu, Y. Chen and Y. Meng, J. Appl. Phys., 2008, 103, 034111 CrossRef.
- V. A. Markel, J. Opt. Soc. Am. A, 2016, 33, 1244 CrossRef PubMed.
- H. Kang and G. W. Milton, Arch. Ration. Mech. Anal., 2008, 188, 93–116 CrossRef.
- L. Jylhä and A. Sihvola, J. Phys. D: Appl. Phys., 2007, 40, 4966–4973 CrossRef.
- A. B. Da Silva, M. Arjmand, U. Sundararaj and R. E. S. Bretas, Polymer, 2014, 55, 226–234 CrossRef.
- M. C. Araújo, C. M. Costa and S. Lanceros-Méndez, J. Non-Cryst. Solids, 2014, 387, 6–15 CrossRef.
- H. Tang, M. H. Malakooti and H. A. Sodano, Appl. Phys. Lett., 2013, 103, 222901 CrossRef.
- Z. Wang, J. K. Nelson, J. Miao, R. J. Linhardt, L. S. Schadler, H. Hillborg and S. Zhao, IEEE Trans. Dielectr. Electr. Insul., 2012, 19, 960–967 CAS.
- L. Shaohui, Z. Jiwei, W. Jinwen, X. Shuangxi and Z. Wenqin, ACS Appl. Mater. Interfaces, 2014, 6, 1533–1540 CrossRef PubMed.
- G. Chen, W. Yang, J. Lin, X. Wang, D. Li, Y. Wang, M. Liang, W. Ding, H. Li and Q. Lei, J. Mater. Chem. C, 2017, 5, 8135–8143 RSC.
- Q. Chi, G. Liu, C. Zhang, Y. Cui, X. Wang and Q. Lei, Results Phys., 2018, 8, 391–396 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2tc00251e |
| This journal is © The Royal Society of Chemistry 2022 |