Open Access Article
Open Access ArticleSpin to charge conversion in chemically deposited epitaxial La0.9MnO3 thin films capped with Pt†
Sergi
Martin-Rio
a,
Alberto
Pomar
 a,
Carlos
Frontera
a,
Hailin
Wang
a,
Ramón
Manzorro
bc,
César
Magén
bcd,
Lluis
Balcells
a,
Narcis
Mestres
a and
Benjamin
Martinez
a,
Carlos
Frontera
a,
Hailin
Wang
a,
Ramón
Manzorro
bc,
César
Magén
bcd,
Lluis
Balcells
a,
Narcis
Mestres
a and
Benjamin
Martinez
 *a
*a
aInstituto de Ciencia de Materiales de Barcelona (ICMAB), CSIC, Spain. E-mail: ben.martinez@icmab.es
bInstituto de Nanociencia y Materiales de Aragón (INMA), CSIC-U. de Zaragoza, 50009 Zaragoza, Spain
cLaboratorio de Microscopías Avanzadas, U. de Zaragoza, 50018 Zaragoza, Spain
dDepartamento de Física de la Materia Condensada, U. de Zaragoza, 50009 Zaragoza, Spain
First published on 15th March 2022
Abstract
Spin to charge conversion process in a broad range of temperatures is studied in La0.92MnO3/Pt bilayers prepared by polymer-assisted deposition (PAD). It is shown that an excellent LMO/Pt interface can be obtained in spite of using ex situ deposition of the Pt layer. The values obtained for the effective spin-mixing conductance, g↑↓eff = 0.76 × 1015 cm−2, suggest that significant spin transport across the LMO/Pt interface could be achieved. Spin pumping experiments generate a transversal voltage signal VISHE, due to spin to charge conversion via inverse spin Hall effect, that has been detected down to about 100 K with values of the spin-Hall angle, θSH, of about 2.5%, slightly decreasing on reducing temperature in the analyzed temperature range. These results indicate that LMO is a promising perovskite building block for all-oxide multifunctional high-frequency spintronics devices and that PAD technique provides oxide epitaxial thin films of good quality adequate for spintronic applications.
Introduction
Complex oxides are a class of materials of great relevance because they offer a broad range of functionalities of strong technological interest. Nowadays, most of these applications require the use of thin films and heterostructures, thus boosting a strong activity in the field of thin film growth. Physical deposition methods, such as molecular beam epitaxy, RF sputtering and pulsed laser deposition, offer unquestionable advantages for the growth of metal oxide thin films like high epitaxial crystal quality, and precise control of composition and thickness at atomic scale.1 However, these methods require high-vacuum and are expensive and difficult to scale up. In contrast, chemical deposition methods are easier to scale up and offer the possibility to grow over large areas at low cost while allowing an easy tuning of the stoichiometry.2 In particular, polymer assisted deposition (PAD) has appeared as a competitive route for environmentally friendly approaches as it is based on the deposition of cationic aqueous solutions.3 However, there exist some concerns regarding the suitability of films prepared by chemical methods for challenging applications requiring high microstructural quality and sharp interfaces, e.g. spintronics. Since the energy balance involved during the growth process is quite delicate, chemical growth methods may lead to a defect landscape different from that generated by using vacuum techniques, resulting in the modification of the physical properties of the films. Thus, relevant parameters for the development of spintronics devices, such as magnetic damping, α, magnetic anisotropy or spin-mixing conductance, g↑↓, may be substantially different from that observed in thin films and heterostructures prepared by physical deposition methods.4 On the other hand, the particular growth conditions of PAD, close to thermodynamic equilibrium conditions, have revealed to be very appropriate for the epitaxial growth of ternary and complex oxides thin films of a broad variety of materials.4–6 In our previous work,7 we showed that thin films of the ferromagnetic-metallic La0.92MnO3 (LMO) compound prepared by PAD exhibit magnetic damping values, αLMO, of the order of 1 × 10−2, similar to damping values reported for other perovskite oxide films prepared by physical methods.8–10 Additionally, it was also observed that magnetic damping substantially increased in LMO films caped with Pt, αLMO/Pt ≈ 2.5 × 10−2, thus suggesting a transfer of spin momentum from the LMO to the Pt layer by spin pumping (SP). These results allow envisaging that LMO films grown by PAD may potentially be an efficient spin source system in heterostructures for spintronic devices.The generation and transmission of spin currents necessary for the development of spintronics devices requires of low magnetic damping materials.11 Previous results show that the spin pumping efficiency is significantly influenced by the damping constant.10 Low magnetic damping constants may be achieved in transition metal oxide films, either in insulating materials as yttrium iron garnet or in half-metallic compounds, as the double exchange La2/3Sr1/3MnO3.12,13 However, in the latter case magnetic damping may be substantially increased due to extrinsic contribution associated with the scattering of conduction electrons by the two magnon scattering mechanism.14 Additionally, surface/interface roughness and/or magnetic inhomogeneities originated from the defect landscape of the film may also increase extrinsic damping. Previous results regarding the generation of pure spin currents by SP in complex oxides, such as SrIrO3, SrRuO3 and double exchange manganites,10,15–18 anticipate a major role of these materials in the development of the next generation of spin devices based on spin–orbit torques.19 Therefore, it is of strong interest to clarify if complex oxide thin films prepared by chemical deposition methods are good enough for the generation and manipulation of pure spin currents. To analyze this possibility, we have chosen the La0.92MnO3 (LMO) compound. Bulk stoichiometric LaMnO3 is a Mott insulator and an A-type antiferromagnet (AF), however it may become a ferromagnet (FM) in thin film form, due to structural strain,20 or by introducing cationic vacancies (in both La or Mn sites).21 La vacancies promotes de appearance of a Mn3+–Mn4+ mixed valence state to maintain charge neutrality and a double exchange mediated FM and metallic state is generated.21 With 8% of La vacancies LMO thin films prepared by PAD exhibit a robust ferromagnetic ordering with a FM transition temperature above room temperature (TC ≈ 320 K), slightly below that of ideally doped La1−xSrxMnO3 perovskites, but with a smaller cationic disorder and larger conductivity values, making it interesting for spintronic applications. In this work we have studied the spin injection and spin-charge conversion processes in LMO/Pt bilayers by using a broadband ferromagnetic resonance spectrometer for SP. Inverse spin Hall effect (ISHE) voltage signals were measured in a broad range of temperatures, in spite of larger values of magnetic damping, making evident that LMO films prepared by PAD are of high quality, overcoming the challenging difficulties of surface roughness and homogeneity control, even for properties highly dependent on defect structure as magnetic damping and spin currents generation and transmission.
Experimental
Epitaxial LMO thin films were grown on (001)-STO substrates via PAD.3,7 Individual solutions of La3+ and Mn2+ were prepared by dissolving La(NO3)3·6H2O and Mn(NO3)2·5H2O in water with ethylenediaminetetraacetic acid (EDTA) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio. Polyethylenimine (PEI), Sigma Aldrich Ref. 408727, with an average molecular weight of 25
1 molar ratio. Polyethylenimine (PEI), Sigma Aldrich Ref. 408727, with an average molecular weight of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 was then added to each solution in a 1
000 was then added to each solution in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mass ratio to EDTA. The cations bind to PEI through an electrostatic EDTA−PEI interaction.3 This feature not only ensures an even distribution of metal cations in the solution, but also serves to adjust the viscosity of the solution. The individual solutions were filtered using an Amicon filtration unit (10 kDa), and retained portions were analyzed by inductively couple plasma (ICP; Optima 4300 DV ICP.OES Perkin-Elmer). Finally, the solutions were mixed according to the desired final stoichiometry, La
1 mass ratio to EDTA. The cations bind to PEI through an electrostatic EDTA−PEI interaction.3 This feature not only ensures an even distribution of metal cations in the solution, but also serves to adjust the viscosity of the solution. The individual solutions were filtered using an Amicon filtration unit (10 kDa), and retained portions were analyzed by inductively couple plasma (ICP; Optima 4300 DV ICP.OES Perkin-Elmer). Finally, the solutions were mixed according to the desired final stoichiometry, La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn 0.92
Mn 0.92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Typical solution viscosity values were in the range η ≈ 3–4 mPa s (measured with a DMA 4100 M Anton Paar densimeter, with a micro-viscometer module Lovis 2000ME). The precursor solutions obtained in this way were spin-coated (4000 rpm, for 90 seconds) on 0.5 × 0.5 cm2 (001)-STO substrates from Crystec GmbH, Germany. Prior to deposition, the as-received STO substrates were chemically etched and thermally treated to generate TiO2-terminated surfaces with atomically flat terraces.22 Finally spin coated films were annealed for the elimination of the organic component at low temperatures (≈500 °C), and phase formation and crystallization at higher temperatures, under oxygen flow to avoid the formation of oxygen vacancies. Thermal annealing was performed using a horizontal tube furnace at 980 °C for 30 min, and oxygen flow above 0.2 L min−1. Consequently, mirror-like films that cover the whole surface of the substrate, and exhibit a low surface roughness (RMS values below ∼ 1 nm) were obtained (see Fig. 1). In this way LMO samples of thickness, t ≈ 17 nm, as determined by X-ray reflectometry, prepared using solutions with a total cation concentration of 240 mM were fabricated. Systematic θ–2θ scans in X-ray measurements showed that only the (00l) reflections of the film and substrate are present indicating the excellent purity of the phase and the optimum c-axis alignment of the grown films.7 The excess of material at the edges and corners of the sample have been removed by acid treatment (see ref. 7 for details). Previously to the acid treatment, a circular pattern, made by means of optical lithography, has been imprinted on the sample in order to control the total volume of the magnetic film. The overall result is a circular La0.92MnO3 thin film with a diameter of 4.4 mm and no excess of material at the corners nor the edges. Then, samples were capped with a Pt layer deposited at room temperature, in Ar–H2 atmosphere and working pressure of 5 mTorr, using a dc magnetron sputtering. Prior to Pt deposition, LMO film's surface was cleaned using a combination of acetone and ethanol and further anneal up to 500 °C for 1 min. The estimated thickness of Pt layer is about 6 nm. Additionally, the structural characterization of both the LMO surface and its interface with the STO substrate has been studied by a combination of atomic force microscopy (AFM), X-rays and scanning transmission electron microscopy (STEM) methods. Aberration corrected STEM characterization was carried out in a probe-corrected FEI Titan 60–300 operated at 300 kV, and equipped with a high-brightness field emission gun (X-FEG), a CETCOR aberration corrector for the probe from CEOS, and a Tridiem GIF spectrometer 866 ERS from Gatan. Atomically resolved images with Z contrast were acquired by high-angle annular dark field (HAADF); the convergence semiangle of the probe was 24 mrad to yield a probe size < 1 Å. STEM spectrum imaging was performed by combining HAADF imaging with Electron Energy Loss Spectroscopy (EELS) with a beam current of ∼180 pA, an energy dispersion of 0.1 eV, and a collection semiangle of about 45 mrad. EELS spectra were collected with an exposure time of 0.5 s, and afterwards noise-filtered by Principal Component Analysis (PCA).23
1. Typical solution viscosity values were in the range η ≈ 3–4 mPa s (measured with a DMA 4100 M Anton Paar densimeter, with a micro-viscometer module Lovis 2000ME). The precursor solutions obtained in this way were spin-coated (4000 rpm, for 90 seconds) on 0.5 × 0.5 cm2 (001)-STO substrates from Crystec GmbH, Germany. Prior to deposition, the as-received STO substrates were chemically etched and thermally treated to generate TiO2-terminated surfaces with atomically flat terraces.22 Finally spin coated films were annealed for the elimination of the organic component at low temperatures (≈500 °C), and phase formation and crystallization at higher temperatures, under oxygen flow to avoid the formation of oxygen vacancies. Thermal annealing was performed using a horizontal tube furnace at 980 °C for 30 min, and oxygen flow above 0.2 L min−1. Consequently, mirror-like films that cover the whole surface of the substrate, and exhibit a low surface roughness (RMS values below ∼ 1 nm) were obtained (see Fig. 1). In this way LMO samples of thickness, t ≈ 17 nm, as determined by X-ray reflectometry, prepared using solutions with a total cation concentration of 240 mM were fabricated. Systematic θ–2θ scans in X-ray measurements showed that only the (00l) reflections of the film and substrate are present indicating the excellent purity of the phase and the optimum c-axis alignment of the grown films.7 The excess of material at the edges and corners of the sample have been removed by acid treatment (see ref. 7 for details). Previously to the acid treatment, a circular pattern, made by means of optical lithography, has been imprinted on the sample in order to control the total volume of the magnetic film. The overall result is a circular La0.92MnO3 thin film with a diameter of 4.4 mm and no excess of material at the corners nor the edges. Then, samples were capped with a Pt layer deposited at room temperature, in Ar–H2 atmosphere and working pressure of 5 mTorr, using a dc magnetron sputtering. Prior to Pt deposition, LMO film's surface was cleaned using a combination of acetone and ethanol and further anneal up to 500 °C for 1 min. The estimated thickness of Pt layer is about 6 nm. Additionally, the structural characterization of both the LMO surface and its interface with the STO substrate has been studied by a combination of atomic force microscopy (AFM), X-rays and scanning transmission electron microscopy (STEM) methods. Aberration corrected STEM characterization was carried out in a probe-corrected FEI Titan 60–300 operated at 300 kV, and equipped with a high-brightness field emission gun (X-FEG), a CETCOR aberration corrector for the probe from CEOS, and a Tridiem GIF spectrometer 866 ERS from Gatan. Atomically resolved images with Z contrast were acquired by high-angle annular dark field (HAADF); the convergence semiangle of the probe was 24 mrad to yield a probe size < 1 Å. STEM spectrum imaging was performed by combining HAADF imaging with Electron Energy Loss Spectroscopy (EELS) with a beam current of ∼180 pA, an energy dispersion of 0.1 eV, and a collection semiangle of about 45 mrad. EELS spectra were collected with an exposure time of 0.5 s, and afterwards noise-filtered by Principal Component Analysis (PCA).23
Results and discussion
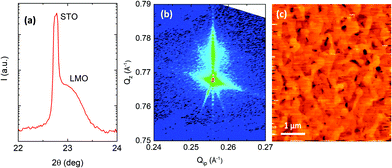
θ–2θ scan around the (001) diffraction peak is presented in Fig. 1a. Fitting of the (00l) peak positions leads to a pseudocubic out-of-plane parameter of a⊥≈3.87 Å. Moreover, the strain state of the LMO film was studied by using reciprocal space maps around (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 03)STO reflection, as shown in Fig. 1b. The fact that both peaks lie on the same Qip coordinate line indicates that the LMO film is fully strained. Therefore, the in-plane lattice parameter of the LMO film, a∣∣, matches that of the substrate one, i.e., a∣∣= 3.905 Å, resulting in a pseudocubic cell volume of Vpc ∼ 59.3 Å3.7 Surface topography of the as-grown LMO sample is shown in Fig. 1c. A relatively flat surface with an RMS roughness of about 1 nm is observed.
03)STO reflection, as shown in Fig. 1b. The fact that both peaks lie on the same Qip coordinate line indicates that the LMO film is fully strained. Therefore, the in-plane lattice parameter of the LMO film, a∣∣, matches that of the substrate one, i.e., a∣∣= 3.905 Å, resulting in a pseudocubic cell volume of Vpc ∼ 59.3 Å3.7 Surface topography of the as-grown LMO sample is shown in Fig. 1c. A relatively flat surface with an RMS roughness of about 1 nm is observed.
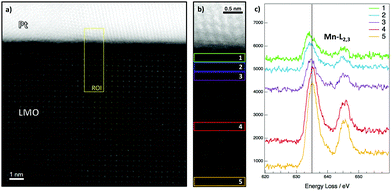
The quality of the LMO/Pt bilayers has been analyzed by using STEM. LMO film is epitaxial and shows and excellent crystalline quality without defects while Pt is of polycrystalline nature. No structural modifications are observed at the LMO/Pt interface (see Fig. 2a). A chemical analysis close to the LMO/Pt interface has been performed by Electron Energy Loss Spectroscopy (EELS) (see Fig. 2b and Fig. S1 and S2, ESI†). The Mn–L2,3 edge shows a uniform fine structure when monitored deep into the LMO film, while the L3 line experiences a gradual shift of ∼0.8 eV to lower energy at the interface, in the last 2–3 unit cells of LMO below Pt. This redshift indicates qualitatively a higher abundance of Mn3+, thus a Mn reduction at an interface with lower oxygen content than the inner part of the LMO film.24
The static magnetic properties of the LMO films were studied using a SQUID magnetometer by Quantum Design. The diamagnetic contribution of the substrate and other instrumental contributions for DC magnetization measurement were properly corrected.25 The possible relative error when determining the saturation magnetization (Ms) by SQUID measurements was estimated to be approximately 5% and is mainly ascribed to the error in the determination of the actual volume of the samples. The saturation magnetization value obtained at low temperatures for the LMO film is around 550 emu cm−3, in excellent agreement with the theoretical value for La0.92MnO3 (≈568 emu cm−3). The magnetization versus temperature, M(T), curves of the LMO film before and after the Pt deposition are depicted in Fig. 3a. As it can be observed, the Curie tem temperature in both cases is almost the same (around 320 K). However, the absolute value of the saturation magnetization after the Pt deposition is slightly reduced (∼9%) with respect to the saturation value of the LMO film alone. This small reduction may be attributed to minute changes of the oxygen content, as shown by EELS spectra (see Fig. 2 and Fig. S1, ESI†), during the deposition of the Pt capping layer in a slightly reducing atmosphere to prevent oxidation. On the other hand, in Fig. 3b, the hysteresis loops (M(H) curves) at different temperatures of the LMO/Pt bilayer show that the coercive field increases with decreasing temperature. An important feature of M(T) and M(H) curves is the lack of any signal of secondary magnetic phases or magnetic inhomogeneities in the samples.
The dynamic magnetic properties of the LMO and LMO/Pt thin films were studied by means of ferromagnetic resonance spectroscopy (FMR) using a commercial broadband coplanar waveguide (CPW) (by NanOsc) inserted into a Physical Properties Measurement System (PPMS by Quantum Design). The transversal voltage signal generated by ISHE in the LMO/Pt bilayer system has been measured by using a 2128A Keithley nanovoltmeter. This equipment has been programmed to act synchronously with the FMR spectrometer in order to measure both the FMR spectral curves and ISHE voltage signal simultaneously. A custom-made CPW specifically designed to measure voltage signals in FMR experiments has been employed. The electrical contact with the sample is enabled through two parallel Au ribbons on both sides of the CPW with bumps raised 20 μm above the sample holder surface. An image of the actual experimental setup is shown in the ESI† (see Fig. S3, ESI†). Each measurement was performed at a fixed temperature and sweeping the externally applied magnetic field, H, for several fixed microwave frequencies (from 2 GHz to 16 GHz). The external static magnetic field was applied in-plane and parallel to the [100] substrate direction. An example of the FMR absorption spectrum obtained at T = 200 K for the LMO film and LMO/Pt bilayer is shown in Fig. 4a. As evidenced by the figure the presence of a Pt capping layer promotes an enhancement of the resonant absorption line-width.
 | ||
| Fig. 4 (a) Example of the derivative of the resonant absorption line measured at T = 200 K and at a frequency of 6 GHz. The increase of the line-width after Pt capping is evidenced. (b) Kittel curves for the LMO and LMO/Pt systems showing the shift in the resonance field at high frequencies. The fitting curves (red lines) have been obtained using eqn (2). | ||
The derivative of the FMR spectra is described as the sum of symmetric and antisymmetric Lorentzian derivative contributions, i.e.,
 | (1) |
By fitting the FMR absorption spectrum at each microwave frequency using eqn (1) both the resonance field (Hres) and line width (ΔH) can be determined. The frequency dependence on the resonance field is conditioned by the existence of in-plane anisotropy in these films, as shown in our previous report.7 Therefore, for the [100] substrate direction, it may be written as:26
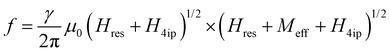 | (2) |
 | (3) |
On the other hand, the increase of the resonance linewidth, ΔH, in the LMO/Pt bilayer with respect to the LMO alone is also shown in Fig. 4a. As it has been stated previously, the resonance line width is related to magnetic relaxation processes in the system. Therefore, an increased line width would be related to additional dissipation channels in the LMO/Pt bilayer with respect to the LMO film. In fact, it could be indicative of the flow of spin angular momentum, i.e. SP effect, whereby the resonant precession of the LMO magnetization injects a pure spin current into the Pt film. As shown in our previous work,7 values of the Gilbert damping parameter at T = 150 K are around 1 × 10−2 for LMO, and increase appreciably, to ∼2.5 × 10−2, for LMO/Pt bilayers. These values are larger than these reported in similar high-quality complex oxide perovskites thin films grown by physical methods,27,28 therefore it is of strong interest to verify the actual capability of PAD prepared LMO films to act as spin injectors. The efficiency of the spin injection across the LMO/Pt interface is described by the effective spin-mixing conductance, g↑↓eff, which is the phenomenological parameter that quantifies the spin transparency of the magnetic/nonmagnetic (NM) layer systems interface. g↑↓eff of the LMO/Pt interface can be estimated from the change in the magnetic damping, i.e. Δα = αLMO/Pt − αLMO, through the relation Δα = (gμB/4πMstLMO)g↑↓eff, which results in an effective spin-mixing conductance g↑↓eff = 0.76 × 1015 cm−2, that is similar to values reported for other perovskite oxide films27,29 and slightly smaller than values reported for Py/Pt bilayers.30,31 Since a large value of g↑↓eff implies a large spin current, our results suggest that significant spin transport across the LMO/Pt interface could be achieved in spite of the ex situ deposition of Pt capping layer.
In order to assess the role of the chemical solution grown LMO films as effective spin injectors and verify that an actual injection of a pure spin current into the Pt layer takes place, the transversal voltage signal, due to spin to charge conversion through ISHE, across de Pt layer has been measured. In materials with large spin–orbit coupling, such as Pt, a pure spin current can be converted into a charge current, and vice versa, due to ISHE and spin Hall effect (SHE).32 The effective detection of SP-induced ISHE voltage signal allows to circumvent the problem of interfacial spin decoherence with important implications in the quantification of crucial spintronic parameters such as the spin Hall angle or the spin diffusion length.33–35
In SP experiments, the line shape of the measured voltage signals follows that of the FMR spectra, i.e., Lorentzian curve, therefore the measured voltage signal is given by the following expression:
 | (4) |
The experimental voltage signals at 200 K for the LMO/Pt bilayer are shown in Fig. 5. As it can be observed, the common trend of all the voltage curves is the dominance of the symmetric voltage amplitude, as expected for a voltage signal generated by ISHE (VISHE) free from parasitic SRE signals. The other important feature of the voltage curves is that they are all positive, in agreement with the expected polarity for an ISHE generated signal according to our experimental setup (see ESI†).
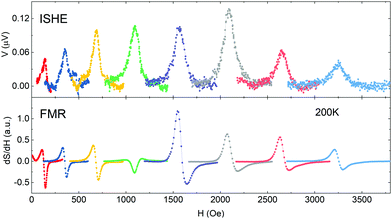 | ||
| Fig. 5 Transverse voltage measurements for the LMO/Pt bilayer at different microwave frequencies (upper panel). The corresponding derivative of the FMR absorption line is shown in the bottom panel. | ||
Fig. 5 also makes evident that the frequency dependence of voltage signal is not monotonic. In principle the spin current generated by SP is expected to be proportional to the precession frequency f,38 and so does the ISHE voltage signal (VISHE), however, it is observed that the spin current slightly decreases with increasing frequency.39 This behavior is generated due to the fact that even both, magnetization–precession and the spin current generated by a cycle of the precession of magnetization, depend on frequency they have different frequency dependencies giving place to a sort of compensation effect. VISHE is proportional to the elliptical area of the magnetization precession trajectory, S, increasing the excitation frequency generates a reduction of the cone angle leading to a reduction of S roughly dependent on f−2. Since VISHE is proportional to f·S a linear dependence on f−1 is roughly expected.39,40
From the values of the ISHE voltage signal, and assuming a λS ≈ 3 nm (according to the resistivities of the Pt layer, namely ρ ∼ 40 μΩ cm), a value of the Hall angle, θSH ∼ 0.025 ± 0.005, slightly decreasing on reducing temperature in the analyzed temperature range, is derived. This value, in the range of low values reported in the literature, agrees well with previous reports for systems with similar values of Pt conductivity.41
On the other hand, the temperature dependence of VISHE is shown in Fig. 6. As expected, the intensity of the voltage signal decreases on approaching TC since the magnetization of LMO layer decreases and so does the spin current injected into the Pt layer. However, it is also observed that the voltage signal decreases on cooling down the samples and becomes vanishing small below 100 K when the magnetization of the LMO layer is already saturated.
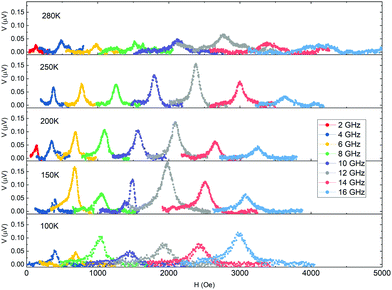 | ||
| Fig. 6 Temperature dependence of the transverse voltage signal for the LMO/Pt bilayer at different frequencies. | ||
Reports regarding the temperature dependence of VISHE are scarce and sometimes confusing. Temperature dependence of VISHE has been reported in La0.7Sr0.3MnO3/SrRuO3 (LSMO/SRO) bilayers showing the expected decrease on approaching TC of LSMO.42 However, the transition of SRO to the low temperature ferromagnetic phase at TC ∼155 K precludes the access to the low temperature behavior of VISHE. Temperature dependence of VISHE on LSMO/Pt bilayers has been reported by V. A. Atsarkin et al.43 In this case it is shown that VISHE follows approximately the temperature dependence of the square of the magnetization of LSMO, decreasing on approaching TC and showing a saturation effect below about 200 K. Unfortunately, experimental results are truncated at 100 K, so the behavior of VISHE at low temperature cannot be inferred. In order to clarify what the behavior at low temperatures should be, we have analyzed the expression of VISHE to try to derive the expected behavior of the different parameters appearing in the equation. According to the analysis in ref. 31 and after some algebra VISHE can be written as:43
 | (5) |
 | ||
| Fig. 7 (a) Simulation of the temperature dependence of the VISHE signal according to eqn (5) introducing the T-dependence of the different variables involved, i.e. λ, θSH, p, g↑↓eff, ΔH. (see Fig. S4 and S5 in ESI†). Data has been normalized by the value at maximum. Different scenarios have been considered for λ and θSH. Temperature-dependence, i.e. λ(T), θSH(T) or no dependence in temperature at all, i.e. λ, θSH. (b) Measured temperature dependence of the FMR linewidth ΔH. | ||
Taking into account the temperature dependence of the different variables involved in the eqn (5), i.e. λ, θSH, p, g↑↓eff, ΔH, it seems quite evident that the observed variation of VISHE is dominated by the temperature dependence of ΔH. Thus, we should conclude that the strong reduction of VISHE on lowering temperature is due to the increase of damping. In fact, a similar behavior has been observed in Pt/yttrium iron garnet bilayers in which a strong reduction of VISHE was detected on lowering temperature,49 which was also attributed to a strong increase of damping on lowering temperature. At this point it is also important to remember that on lowering temperature extrinsic contributions to damping, such as two-magnon scattering, defects, changes of magnetic anisotropy, presence of interfaces, etc., might substantially increase the damping, broadening resonance peaks, thus masking spin pumping effects and making it difficult to measure VISHE as the temperature drops below 100 K.50,51 Moreover, very recent results in La0.7 Sr0.3 MnO3 (LSMO),52 a double exchange ferromagnet thus, with magnetic behavior very similar to that of our LMO samples, clearly exhibits a strong increase of damping on reducing temperature. The observed temperature dependence of damping is interpreted considering two contributions, resistive-like and conductive-like, as in Kambersky's torque-correlation model53 and an additional term due to spin pumping. This latter term is attributed to the appearance of an insulating and magnetically active dead layer, caused by the lowering of the double exchange mechanism at surface and interfaces. Since LMO has a very similar magnetic behavior to that of LSMO, and in both cases magnetic interactions are mediated by the double exchange mechanism, this additional term may also contribute to the enhancement of damping in our case.
Conclusions
In conclusion, in this paper we have analyzed spin to charge conversion processes in LMO/Pt bilayers, were the LMO epitaxial layer has been prepared by using PAD method in a broad range of temperatures. It is shown that PAD allows obtaining LMO films of excellent crystalline and surface quality. Additionally, it is also shown that an excellent LMO/Pt interface can be obtained using ex situ deposition of the Pt layer. Values of the Gilbert damping parameter are α ≈ 1 × 10−2 for LMO, and increase appreciably for LMO/Pt bilayers. These values are larger than those reported in similar high-quality complex oxide perovskites thin films grown by physical methods. However, the values obtained for the effective spin-mixing conductance, g↑↓eff = 0.76 × 1015 cm−2, are similar to values reported for other perovskite oxide films. Thus, our results suggest that significant spin transport across the PAD deposited LMO/Pt interface could be achieved in spite of the ex situ deposition of the Pt capping layer. Spin pumping experiments have been performed in a broad temperature range and a transversal voltage signal VISHE, due to spin to charge conversion, has been measured down to about 100 K. The high resistance of the LMO layer, compared to that of Pt layer, precludes the appearance of parasitic spin rectification effects and therefore VISHE signal is fully symmetric. VISHE exhibits a non-monotonic temperature dependence and becomes vanishing small below about 100 K. The strong reduction of VISHE on decreasing temperature is attributed to the increase of the magnetic damping. These results indicate that chemical solution grown LMO is a promising perovskite building block for all-oxide multifunctional high-frequency spintronics devices.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from the Spanish Ministry of Science, Innovation and Universities through Severo Ochoa (CEX2019-000917-S), and SPINCURIOX (RTI2018-099960-BI00) and AMONANO (PID2020-112914RB-I00) projects co-financed by the European Regional Development Funds. AMONANO also received funding from the European Union's Horizon 2020 research and innovation program under grant agreement no. 823717-ESTEEM3. Hailin Wang acknowledges financial support from the China Scholarship Council (CSC).References
- See chapters 1-3 In Epitaxial growth of complex metal oxides, ed. G. Koster, M. Huijben and G.Rijnders, Woodhead Publishing Series in Electronic and Optical Materials, Woodhead Publishing, 2015, ch. 1–3, pp. 1–68, ISBN 9781782422457 Search PubMed
.
-
J. E. ten Elshof, In Chemical solution deposition techniques for epitaxial growth of complex oxides, ed. G. Koster, M. Huijben and G. Rijnders, Woodhead Publishing Series in Electronic and Optical Materials. Epitaxial Growth of Complex Metal Oxides, Woodhead Publishing, 2015, ch. 4, pp. 69–93. ISBN 9781782422457 Search PubMed
.
- Q. X. Jia, T. M. McCleskey, A. K. Burrell, Y. Lin, G. E. Collis, H. Wang, A. D. Li and S. R. Foltyn, Nat. Mater., 2004, 3, 529–532 CrossRef CAS PubMed
.
- J. M. Vila-Fungueiriño, C. T. Bui, B. Rivas-Murias, E. Winkler, J. Milano, J. Santiso and F. Rivadulla, J. Phys. D: Appl. Phys., 2016, 49, 315001 CrossRef
.
- J. M. Vila-Fungueiriño, B. Rivas-Murias, J. Rubio-Zuazo, A. Carretero-Genevrier, M. Lazzari and F. Rivadulla, J. Mater. Chem. C, 2018, 6, 3834 RSC
.
- H. Wang, J. Gazquez, C. Frontera, M. F. Chisholn, A. Pomar, B. Martinez and N. Mestres, NPG Asia Mater., 2019, 11, 41 CrossRef
.
- H. Wang, A. Pomar, S. Martin-Rio, C. Frontera, N. Mestres and B. Martinez, J. Mater. Chem. C, 2019, 7, 12633 RSC
.
- A. Monsen, J. E. Boschkerb, F. Macià, J. W. Wells, P. Nordblad, A. D. Kent, R. Mathieu, T. Tybell and E. Wahlström, J. Magn. Magn. Mater., 2014, 369, 197–204 CrossRef CAS
.
- A. Al Mamun, A. Haque, A. Pelton, B. Paul and K. Ghosh, J. Magn. Magn. Mater., 2019, 478, 132 CrossRef
.
- G. Y. Luo, C. R. Chang and J. G. Lin, J. Appl. Phys., 2014, 115, 17C508 CrossRef CAS PubMed
.
- A. Hoffmann and S. D. Bader, Phys. Rev. Appl., 2015, 4, 047001 CrossRef
.
- L. Soumah, N. Beaulieu, L. Qassym, C. Carrétéro, E. Jacquet, R. Lebourgeois, J. Ben Youssef, P. Bortolotti, V. Cros and A. Anane, Nat. Commun., 2018, 9, 3355 CrossRef PubMed
.
- Q. Qin, S. He, W. Song, P. Yang, Q. Wu, Y. P. Feng and J. Chen, Appl. Phys. Lett., 2017, 110, 112401 CrossRef
.
- M. A. Schoen, D. Thonig, M. L. Schneider, T. J. Silva, H. T. Nembach, O. Eriksson, O. Karis and J. M. Shaw, Nat. Phys., 2016, 12, 839–842 Search PubMed
.
- S. Crossley, A. G. Swartz, K. Nishio, Y. Hikita and H. Y. Hwang, Phys. Rev. B, 2019, 100, 115163 CrossRef CAS
.
- L. Liu, Q. Qin, W. Lin, C. Li, Q. Xie, S. He, X. Shu, C. Zhou, Z. Lim, J. Yu, W. Lu, M. Li, X. Yan, S. J. Pennycook and J. Chen, Nat. Nanotechnol., 2019, 14(10), 939–944 CrossRef CAS PubMed
.
- M. Wahler, N. Homonnay, T. Richter, A. Müller, C. Eisenschmidt, B. Fuhrmann and G. Schmidt, Sci. Rep., 2016, 6, 28727 CrossRef CAS PubMed
.
- S. Emori, U. S. Alaan, M. T. Gray, V. Sluka, Y. Chen, A. D. Kent and Y. Suzuki, Phys. Rev. B, 2016, 94, 224423 CrossRef
.
- D. Castro Vaz, A. Barthélémy and M. Bibes, Jpn. J. Appl. Phys., 2018, 57, 0902A4 CrossRef
.
- J. Roqueta, A. Pomar, L. Balcells, C. Frontera, S. Valencia, R. Abrudan, B. Bozzo, Z. Konstantinovic, J. Santiso and B. Martinez, Cryst. Growth Des., 2015, 15, 5332–5337 CrossRef CAS
.
- J. Töpfer and J. B. Goodenough, J. Solid State Chem., 1997, 130, 117–128 CrossRef
.
- M. Kareev, S. Prosandeev, J. Liu, C. Gan, A. Kareev, J. W. Freeland, M. Xiao and J. Chakhalian, Appl. Phys. Lett., 2008, 93, 061909 CrossRef
.
- M. Watanabe, E. Okunishi and K. Ishizuka, Microsc. Anal., 2009, 23, 5–7 Search PubMed
.
- H. K. Schmid and W. Mader, Micron, 2006, 37, 426 CrossRef CAS PubMed
.
- P. Stamenov and J. M. D. Coey, Rev. Sci. Instrum., 2006, 77, 15106 CrossRef
.
- M. Farle, Rep. Prog. Phys., 1998, 61(7)), 755 CrossRef CAS
.
- H. K. Lee, I. Barsukov, A. G. Swartz, B. Kim, L. Yang, H. Y. Hwang and I. N. Krivorotov, AIP Adv., 2016, 6, 055212 CrossRef
.
- Q. Qin, S. He, W. Song, P. Yang, Q. Wu, Y. P. Feng and J. Chen, Appl. Phys. Lett., 2017, 110, 112401 CrossRef
.
- C. Hauser, C. Ballani, P. Dürrenfeld, F. Heyroth, P. Trempler, S. G. Ebbinghaus, E. T. Papaioannou and G. Schmidt, Phys. Status Solidi B, 2020, 257, 1900606 CrossRef CAS
.
- R. A. Gallardo, A. Banholzer, K. Wagner, M. Körner, K. Lenz, M. Farle, J. Lindner, J. Fassbender and P. Landeros, New J. Phys., 2014, 16, 023015 CrossRef CAS
.
- O. Mosendz, J. E. Pearson, F. Y. Fradin, G. E. W. Bauer, S. D. Bader and A. Hoffmann, Phys. Rev. Lett., 2010, 104, 046601 CrossRef CAS PubMed
.
- H. Chen and D. Yi, APL Mater., 2021, 9, 060908 CrossRef CAS
.
- J.-C. Rojas-Sánchez,
et al.
, Phys. Rev. Lett., 2014, 112(10)), 106602 CrossRef PubMed
; J.-C. Rojas-Sánchez et al. , Spintronics VII, 2014. Vol. 9167, International Society for Optics and Photonics.
- Xinde Tao,
et al.
, Sci. Adv., 2018, 4(6)), eaat1670 CrossRef PubMed
.
- Weifeng Zhang,
et al.
, Nat. Phys., 2015, 11(6)), 496–502 Search PubMed
.
- M. Harder, G. Yongsheng and C.-M. Hu, Phys. Rep., 2016, 661, 1–59 CrossRef CAS
.
- R. Mahendiran,
et al.
, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 3348 CrossRef CAS PubMed
.
- Y. Tserkovnyak, A. Brataas and G. Bauer, Phys. Rev. Lett., 2002, 88, 117601 CrossRef PubMed
.
- K. Harii, T. An, Y. Kajiwara, K. Ando, H. Nakayama, T. Yoshino and E. Saitoh, J. Appl. Phys., 2011, 109, 116105 CrossRef
.
- V. Castel, N. Vlietstra, B. J. van Wees and J. Ben Youssef, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 134419 CrossRef
.
- Y. Wang, P. Deorani, X. Qiu, J. Hyun Kwon and H. Yang, Appl. Phys. Lett., 2014, 105, 152412 CrossRef
.
- M. Wahler, N. Homonnay and T. Richter,
et al.
, Sci. Rep., 2016, 6, 28727 CrossRef CAS PubMed
.
- V. A. Atsarkin, I. V. Borisenko, V. V. Demidov and T. A. Shaikhulov, J. Phys. D: Appl. Phys., 2018, 51, 245002 CrossRef CAS
; V. A. Atsarkin, V. V. Demidov and T. A. Shaikhulov, J. Exp. Theor. Phys., 2020, 130, 228 CrossRef
.
- L. Vila, T. Kimura and Y. Otani, Phys. Rev. Lett., 2007, 99, 226604 CrossRef PubMed
.
- S. Meyer, M. Althammer, S. Geprägs, M. Opel, R. Gross and S. T. B. Goennenwein, Appl. Phys. Lett., 2014, 104, 242411 CrossRef
.
- M. Isasa, E. Villamor, L. E. Hueso, M. Gradhand and F. Casanova, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 024402 CrossRef
.
- T. Kimura, T. Sato and Y. Otani, Phys. Rev. Lett., 2008, 100, 066602 CrossRef CAS PubMed
.
- S. R. Marmion, M. Ali, M. McLaren, D. A. Williams and B. J. Hickey, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 220404(R) CrossRef
.
- E. Shigematsu,
et al.
, Appl. Phys. Express, 2016, 9, 053002 CrossRef
.
- R. Arias and D. L. Mills, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 7395 CrossRef CAS
.
- S. Azzawi, A. T. Hindmarch and D. Atkinson, J. Phys. D: Appl. Phys., 2017, 50, 473001 CrossRef
.
- V. Haspot, P. Noël, J.-P. Attané, L. Vila, M. Bibes, A. Anane and A. Barthélémy, Phys. Rev. Mater., 2022, 6, 024406 CrossRef CAS
.
- V. Kambersky, Czechoslovak J. Phys. B, 1976, 26, 1366 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available: Compositional analysis of the LMO/Pt interface, details about the sample holder connections and analysis of the difrent factors contributing to the temperature dependence of VISHE. See DOI: 10.1039/d2tc00048b |
| This journal is © The Royal Society of Chemistry 2022 |