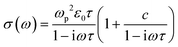Band structure modulation by methoxy-functionalization of graphene nanoribbons

Abstract

Graphene nanoribbons (GNRs) are considered as potential candidates for next-generation electronic materials, and chemical functionalization can be an efficient method to modulate their electronic properties. This work presents a solution synthesis of methoxy-substituted GNRs through the Diels–Alder polymerization of a tetraphenylcyclopentadienone-based monomer bearing four methoxy groups, followed by oxidative cyclodehydrogenation. The methoxy-functionalization of the GNRs was unambiguously validated by FTIR and solid-state NMR analyses. Moreover, theoretical studies by ab initio calculations predicted both charge redistribution and structural distortion induced by the methoxy substitution, revealing reduction of both the bandgap and of the effective mass of charge carriers. Employing THz spectroscopy, we found that methoxy-substitution at the edges enhanced the photoconductivity of GNRs by a factor of ∼25%, primarily due to the reduced charge effective mass.

---

Graphene nanoribbons (GNRs) are quasi one-dimensional cut-outs of graphene with the width typically between ∼1 and 100 nm and the length at least an order of magnitude larger than the width.^1,2 In contrast to graphene, GNRs have non-zero bandgaps due to the quantum confinement effect, which makes them highly promising as carbon-based semiconductors for nanoelectronics and optoelectronics.^3–8 The synthetic strategies to fabricate GNRs can be divided into “top-down” and “bottom-up” approaches.^9–12 While “top-down” methods such as cutting of graphene and unzipping of carbon nanotubes cannot avoid high structural disorder, the “bottom-up” chemical synthesis can afford GNRs with controllable widths and edge structures in atomic precision.^{3,5,6,9,11–18} To obtain GNRs with defined chemical structures, carefully chosen monomer precursors are polymerized and then subjected to cyclization in solution or on a metal surface.^9,11 The optical and electronic properties of GNRs, including bandgap and charge-carrier mobility, strongly depend on their structures. Thus, considerable efforts have been dedicated to the synthesis of various types of GNRs and elucidation of their structure–property relationships.^2,19

GNRs with different edge structures, including armchair, zigzag, cove, and fjord edges, have thus far been synthesized. The role of the GNR width on bandgaps of armchair GNRs and localized edge states of zigzag GNRs have been demonstrated.^9,10,12 While armchair and zigzag GNRs possess planar structures, cove and fjord edges induce non-planarity, which is advantageous to improve the solubility of the GNRs by suppressing the π–π interactions.^20–22 In addition, non-planarity is also predicted to affect the electronic properties of GNRs,^23–26 but its precise effects still remain unexplored.^{20,21,27–29}

For the investigation of non-planar GNRs, the solution synthesis protocols can be more advantageous than the on-surface methods.²⁰ The latter approach is optimal for studying planar GNRs under ultrahigh vacuum and elucidating the electronic properties of individual GNRs.^14,30–33 In general, the solution synthesis of GNRs can be categorized according to the methods of polymerization, e.g. Suzuki and Yamamoto polycondensation, and/or to the final cyclization steps, e.g. Scholl reaction and acid-catalyzed cycloaromatization.^11,12,15 We have explored the sequence of the AB-type Diels–Alder polymerization followed by the Scholl reaction to obtain long (>100 nm in average) GNRs with different widths (∼1–2 nm), which is very often difficult to achieve through transition-metal-catalyzed coupling reactions that are terminated due to loss of functional groups.³⁴

Another advantage of the solution synthesis is the capability of edge functionalization in a facile manner.^{11,12,35–38} Such modifications can be realized either by introducing functional groups on the appropriate positions of the monomer precursors or through the “post-functionalization” after the formation of the GNR structure, for example by the edge chlorination³⁹ or transition-metal-catalyzed coupling reactions using pre-installed halogen substituents.^40,41 Functionalization of GNRs with cyano, fluoro, and amino groups has been reported through the on-surface method, but pre-installed functional groups are often removed during the cyclodehydrogenation on metal substrates, prohibiting efficient synthesis of edge-functionalized GNRs.^42–45

Through edge functionalization with electron-donating or -withdrawing groups, it becomes possible to modulate the electronic properties of GNRs, including the position of energy levels and bandgap.^{42,43,46–49} Moreover, the planarity of GNRs can also be altered by inducing steric repulsion. To this end, we have recently synthesized planar and non-planar GNRs with the identical aromatic core structure by installing alkyl chains at different peripheral positions, causing steric congestion with neighboring aromatic protons.²¹ Theoretical studies revealed that the structural distortion also changes the band structure of these GNRs and a reduced bandgap was experimentally confirmed by UV-vis absorption. Nevertheless, there are thus far only a few experimental studies varying the planarity of one and the same GNR structure. Moreover, the combination of non-planarity effects with those of electron-donating or -withdrawing functional groups has rarely been considered.

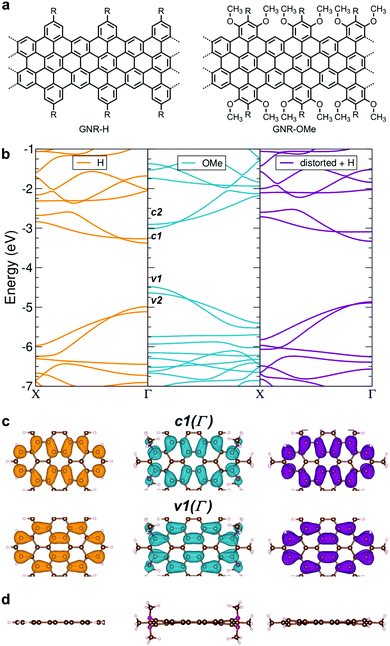
To this end, we have targeted a GNR with four electron-donating methoxy groups per repeating unit (GNR-OMe, Fig. 1a). Theoretical calculations based on Density-Functional Theory (DFT) and Many-Body Perturbation Theory (MBPT) elucidated that this methoxy-functionalization decreased the ionization potential and the bandgap, accompanied by a reduction of the effective mass of charge carriers, disentangling the effect of structural distortions and charge redistribution. The synthesis of GNR-OMe 9 (see Scheme 1 for the structure) was carried out through the AB-type Diels–Alder polymerization, followed by the oxidative cyclodehydrogenation, and the successful introduction of the methoxy groups was clearly evidenced by solid-state NMR analyses. UV-vis-NIR absorption spectroscopy revealed a more structured absorption profile for GNR-OMe 9 compared with GNR-H 10 without methoxy groups.¹³ An additional feature appeared at longer wavelength, in agreement with the theoretically predicted enhancement of the transition-dipole moment of the first excitonic state induced by distortions. Moreover, THz spectroscopy demonstrated the enhanced charge-carrier mobility of GNR-OMe 9 as compared with GNR-H 10. This is primarily due to the reduced effective mass of charge carriers, in line with the theoretical results.

Fig. 1 (a) Chemical structure of GNR-OMe (right) and GNR-H (left) (b) DFT band structures of GNR-OMe (R = Me; blue, center) and GNR-H (R = H; orange, left), as compared to the distorted GNR-H (R = Me; purple, right) with the same nonplanar geometry as GNR-OMe. The three band structures are aligned to the vacuum level, which is set to zero. (c) Plot of the frontier bands v1 and c1 (top view) at the Γ point and (d) optimized geometries (lateral view) of GNR-H, GNR-OMe and the distorted GNR-H.

Scheme 1 Synthetic route towards GNR-OMe 9.

Results and discussion

Theoretical studies of geometrical and electronic properties of GNR-OMe

We have initially carried out the DFT-based theoretical studies (see Methods for the details) on the structural and electronic properties of GNR-OMe in comparison with GNR-H (see Fig. 1a), i.e. a GNR with the same aromatic core structure, but without methoxy groups on the edges.^13,50Fig. 1b compares the calculated band structure of GNR-OMe (blue) and GNR-H (orange), which are aligned to the vacuum level. The comparison highlights upshifted frontier bands of GNR-OMe, which are ∼0.5 eV higher than those of GNR-H, due to the charge redistribution induced by the methoxy groups (see Fig. S1, ESI†), in agreement with prediction in previous studies.^17,51 We also find that the valence band top (v1) is more affected than the conduction band bottom (c1). The former shows a larger upshift, which leads to an overall reduction of the bandgap by about 150 meV, i.e. from 1.61 eV (GNR-H) down to 1.46 eV (GNR-OMe). A similar behavior, but with stronger effects on c1, has been reported for edge decoration with electron-withdrawing groups.^43,45,46

In addition to the modulation of the electronic properties, the DFT simulations indicate that the aromatic structure of GNR-OMe is slightly distorted by the introduction of multiple methoxy groups at the edges, due to the steric repulsion (Fig. 1d). DFT simulations of a non-planar GNR-H with the same distortion as GNR-OMe, but without the methoxy groups (Fig. 1b, violet) were then carried out to discern the effect of the electron-donating methoxy groups from that induced by the geometrical distortion. To this end, the methoxy groups were replaced by hydrogen atoms after the geometric optimization of GNR-OMe, while keeping the distorted aromatic core fixed. The results indicate that the geometric distortions are responsible for only one-half of the bandgap shrinkage, i.e. 75 meV, while the other half can be ascribed to the larger effective width of the π-conjugated system of GNR-OMe due to the delocalization of the frontier states over the oxygen of the methoxy groups (see Fig. 1c). Moreover, along with the bandgap shrinkage by the methoxyl substitution, the effective mass of charge carriers also decreases (see Table S1, ESI†), especially for the conduction bands. The reduced effective mass m* of charge carriers can be beneficial for charge transport through the GNRs, because the charge carrier mobility μ is proportional to the reciprocal of the effective mass of charge carriers. These theoretical insights encouraged us to experimentally study GNR-OMe, and investigate its charge transport properties.

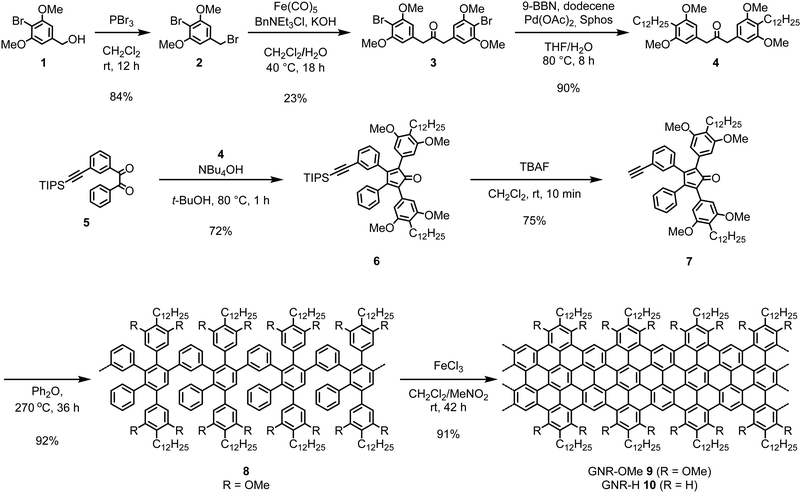
Bottom-up solution synthesis of GNR-OMe 9

The synthesis of GNR-OMe 9 was carried out through the AB-type Diels–Alder polymerization in a similar manner to our previous reports,^13,21,52 using a new monomer precursor 7 with four methoxy groups (Scheme 1). For the synthesis of monomer 7, 2-bromo-1,3-dimethoxybenzyl bromide (2) was initially prepared by bromination of benzyl alcohol 1 with phosphorus tribromide (PBr₃). Subsequently, a phase-transfer carbonylative dimerization of 2 with Iron pentacarbonyl (Fe(CO)₅) provided diarylacetone 3, which was alkylated by Suzuki coupling to yield diarylacetone 4. The Knoevenagel condensation of 4 with benzil 5 afforded tetraphenylcyclopentadienone 6 and the subsequent removal of triisopropylsilyl-protecting group gave monomer 7. The Diels–Alder polymerization of 7 was performed by refluxing in diphenyl ether at 260–270 °C. Size exclusion chromatography (SEC) analysis of the resulting crude mixture indicated the presence of small oligomers, which could be removed by fractionation with recycling preparative SEC to afford methoxy-substituted polyphenylene precursor 8 with the weight-average molecular weight (M_w) of 31 000–54 000 g mol⁻¹ and polydispersity index (PDI) of 1.5–1.7 based on the SEC analysis against poly(para-phenylene) (PPP) and polystyrene (PS) standards (Fig. S2, ESI†). The combination of PPP and PS standard calibrations is helpful for estimating the M_w of different polyphenylene samples as discussed in our previous reports.^13,52 Additionally, matrix-assisted laser desorption/ionization time-of-fight (MALDI-TOF) mass spectrometry (MS) analysis of the crude mixture of 8 displayed a pattern of peaks in agreement with the molecular weight of trimer to octamer, corroborating the successful installment of methoxy groups (Fig. S3, ESI†). Finally, the oxidative cyclodehydrogenation of 8 with iron(III) chloride provided GNR-OMe 9.

Structural characterizations of GNR-OMe 9

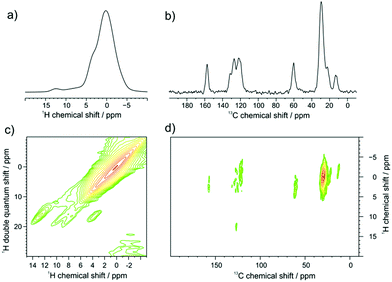
GNR-OMe 9 was initially characterized by FTIR, Raman, and UV-vis-NIR absorption spectroscopy (Fig. S4, S5, ESI† and Fig. 3a, respectively), which agreed well with the spectra previously reported for GNRs with similar structures.^13,21,40 Moreover, scanning tunnelling microscopy (STM) analysis of GNR-OMe 9 after deposition on Au(111) revealed multilayers of GNRs with the width of around 3.0 nm (Fig. S6, ESI†). This value is comparable to a width of ∼3.8 nm theoretically estimated for GNR-H 10 including the alkyl chains,¹³ which should have approximately the same width as GNR-OMe 9.

Solid-state ¹H- and ¹³C-NMR magic angle spinning (MAS) spectra of GNR-OMe 9 were measured at 16.4 T corresponding to 700 MHz ¹H Larmor frequency (Fig. 2). The ¹H MAS NMR spectrum of GNR-OMe 9 displayed a broad signal between 11–14 ppm from the aromatic protons as well as a small shoulder around 3.5 ppm that was assignable to the methoxy groups, along with the strong signal from the aliphatic side chains (Fig. 2a). Notably, the aromatic proton signal of GNR-OMe 9 was down-field shifted compared with that of the same proton in previously reported GNR-H 10 (see Scheme 1 for the structure),¹³ most likely due to the additional deshielding effect by the methoxy groups. Broad, featureless background signals observed between 6 and 10 ppm might be due to removal of some of the methoxy or dodecyl groups during the final synthetic step and/or incompleteness of the cyclodehydrogenation. In the 2D ¹H–¹H double-quantum single-quantum (DQ-SQ) correlation spectrum (Fig. 2c), these broad background signals appear as two parallel signal ridges close to the spectrum diagonal, indicating that the aromatic protons corresponding to these signals are heterogeneously distributed in the sample, which might be partly due to disordered aggregation. The aromatic signal at 12.5 ppm does not show any correlation to the background signals, but only correlates with the neighboring methoxy groups, fully consistent with its assignment to the aromatic proton of GNR-OMe 9. On the other hand, a weak correlation of the aromatic background signals to the methoxy protons can be seen, suggesting partial removal of the dodecyl chains.

Fig. 2 Solid-state NMR characterization of GNR-OMe 9 measured at 700 MHz. (a) ¹H MAS NMR at 60.0 kHz MAS; (b) ¹³C/¹H CP/MAS NMR at 25.0 kHz MAS, recorded with 3.0 ms CP contact time, and 100 kHz high-power swept-frequency two-pulse phase modulation (swfTPPM) decoupling; (c) 2D ¹H–¹H DQ-SQ NMR correlation spectrum, 60 kHz MAS, 2 rotor periods back-to-back (BABA); (d) 2D ¹³C–¹H CP-MAS HETCOR NMR spectrum recorded at 25 kHz MAS, 3.0 ms CP contact time, and 100 kHz high-power swfTPPM decoupling.

In the ¹³C/¹H cross polarization (CP)/MAS NMR spectrum (Fig. 2b), the ¹³C signal from the methoxy groups could be clearly observed at ∼60 ppm, along with aromatic signals from the edge of GNR-OMe 9 and the aliphatic signals from the dodecyl groups, which agreed with the previous studies.^21,52 From the 2D ¹H–¹³C CP/MAS heteronuclear correlation (HETCOR) NMR spectrum (Fig. 2d), strong correlation with the methoxy protons can be identified for the ¹³C signal of the methoxy and also for that of aromatic carbons at 158 ppm, which can thus be assigned to the ones covalently bound to the methoxy groups. The aromatic protons of GNR-OMe 9 observed at 12.5 ppm show a clear correlation to the aromatic ¹³C signals at 127 ppm. All these results corroborate the successful introduction of the methoxy groups on the GNR edges.

UV-vis-NIR absorption and photoluminescence spectroscopy of GNR-OMe 9

UV-vis-NIR absorption spectrum of GNR-OMe 9, recorded in tetrahydrofuran (THF), displays two maxima at 507 and 544 nm, which coincide with the absorption maxima of GNR-H 10 (Fig. 3a).¹³ GNR-OMe 9 shows a more structured absorption profile, which could be due to the suppression of aggregation by the geometrical distortion revealed by the theoretical studies (Fig. 1d). Moreover, an additional absorption peak is observed at 614 nm for GNR-OMe 9, which is absent in the spectrum of GNR-H 10.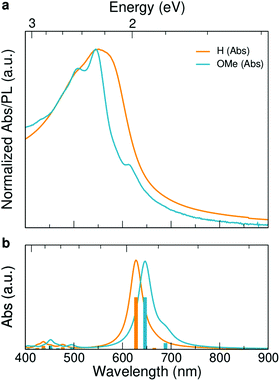

Fig. 3 Spectroscopic characterization: (a) UV-vis-NIR absorption spectrum of GNR-OMe 9 in THF (blue). UV-vis-NIR absorption spectrum of GNR-H 10 in N-methyl-2-pyrrolidone (orange) is plotted together for comparison.¹³ (b) GW–BS simulated absorption spectra (bottom) for ideal, gas-phase GNR-OMe (blue) and GNR-H (orange) in vacuum (see Fig. 1a for the structures). Vertical bars indicate the excitonic transitions with the same color code.

In order to understand the origin of this additional peak, we computed the first-principles optical spectra for the optimized DFT geometries of GNR-OMe and GNR-H (Fig. 1), according to the GW–BS approach that includes both quasi-particle corrections to the band structure and excitonic effects, as detailed in the Method section. The simulated absorption spectra (Fig. 3b) show a main peak at about ∼2 eV, which is mainly due to linear combination of transitions between the second valence band (v2) to the first conduction band (c1). This peak exhibits a ∼60 meV redshift for GNR-OMe 9, which is a fingerprint of the bandgap shrinkage discussed above, even though considerably reduced when compared to the absolute variation of the fundamental gap. GNR-OMe 9 also displays an additional peak about 130 meV lower than the main peak that can be attributed to a brightening of the first excitonic peak (linear combination of v1 → c2 transitions), which has negligible oscillator strength in the system without methoxy group, in agreement with the experimental observations. We note that the absorption spectra in THF (Fig. 3a) appear blue-shifted by ∼0.20 eV with respect to the GW–BS calculated optical spectra of ideal GNRs in vacuum (Fig. 3b), which is similar to previous reports for other GNRs.^21,53,54 Such a difference in the experimental and theoretical lowest energy excitations can be partly traced back to the 0.1–0.2 eV accuracy of our method,⁵⁵ and partly to other structural and environmental effects that are not taken into account in our gas-phase simulations. For example, aggregation, conformational disorder, or interaction with long side chains and with solvent molecules might be causing the blue-shift of the absorption peak. Nonetheless, the theoretical results successfully elucidate the appearance of a low-energy peak in the optical spectra of GNR-OMe 9, attributed to the influence of the methoxy group, in clear agreement with the experimental observations.

Accessing charge transport properties of GNR-OMe 9 by THz spectroscopy

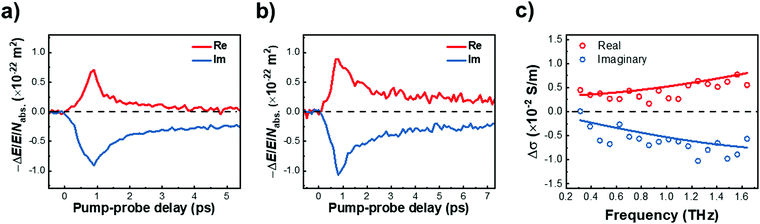
We further investigated the effect of methoxy side-group on the electrical properties of GNRs, employing ultrafast optical-pump THz-probe (OPTP) spectroscopy. As a purely optical technique, OPTP measurements have been demonstrated as a powerful method to investigate the photoconductivity dynamics of charge carriers in nanomaterials, in a contact-free and noninvasive manner.^{20,22,56–58}Fig. 4a and b compare the photoconductivity dynamics for GNR-H 10 and GNR-OMe 9, which were dispersed in 1,2,4-trichlorobenzene for measurements. In both cases, we observe a transient rise of the real photoconductivity due to the injection of free carriers into GNRs following beyond-bandgap optical excitations (by 2.25 eV laser pulses). Subsequently, a rapid decay is detected, which can be attributed to localization of charge carriers (by trapping and/or the formation of excitons).^20,59–61 Note that the photoconductivity Δσ is proportional to the number of charge carriers n and charge-carrier mobility μ, following: Δσ = enμ = e(N_absφ)μ, where e, N_abs and φ are elementary charge, absorbed photon density, and photon-to-charge conversion efficiency, respectively. Notably, for a given absorbed photon density N_abs, the photoconductivity Δσ of GNR-OMe 9 (i.e.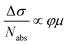) is ∼25% higher than that of GNR-H 10. We expect that φ is not changed substantially by the edge functionalization. Our results therefore indicate a higher charge-carrier mobility in GNR-OMe 9 than that in GNR-H 10.

Fig. 4 Time-resolved terahertz photoconductivity dynamics (proportional to the relative changes in the transmitted field, −ΔE/E), normalized by absorbed photon density N_abs, of (a) GNR-H 10 and (b) GNR-OMe 9. The samples are dispersed in 1,2,4-trichlorobenzene, and photoexcited by a 2.25 eV-energy laser pulse. (c) Frequency-resolved complex photoconductivity at the peak of 1D THz photoconductivity (following 3.1 eV excitations).

To provide further insight into the origin of the enhanced photoconductivity and charge-carrier mobility, we conducted frequency-resolved photoconductivity at the peak of the OPTP dynamics following 3.1 eV excitations, as shown in Fig. 4c (for GNR-OMe 9). The complex photoconductivity can be well-fitted by a phenomenological model, so called Drude–Smith (DS) model^56,62 following:

where τ, ω_p and ε₀ are the DS charge scattering time, the plasma frequency, and vacuum permittivity, respectively. In the DS model, free carriers are assumed to subject to preferential backscattering effect which is parameterized by the parameter c. The value of c ranges from 0 (for Drude-like isotropic momentum scattering process) and −1 (for the preferential 100% backscattering process). Note that the same measurements and fitting model have been applied previously to GNR-H 10, which gave nearly the same conductivity dispersion and the transport parameters (τ_DS = 30 ± 3 fs, and c = −0.92 ± 0.01).⁶³ Based on the DS fitting for GNR-OMe 9, we infer the DS scattering time and the c parameter to be 27 ± 7 fs and −0.92, respectively. At the dc limit, the charge-carrier mobility μ can be expressed as: . 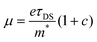As the scattering time remains nearly unchanged within the error bar, our results indicate that the enhancement of charge carrier mobility (and thus the photoconductivity) seems to originate from the decreased effectives mass due to the methoxy-functionalization. Indeed, by comparing the ratio of the reciprocals of the theoretically estimated effective mass (Table S1, ESI†), we expect a mobility enhancement by a factor of ∼11% following OMe functionalization, which is roughly in line with our experimental results here. Therefore, our result directly correlates the intrinsic electronic structure (tunable by the side group) to charge transport properties in GNRs.

Conclusion

A bottom-up synthesis of GNR-OMe 9 was achieved based on the AB-type Diels–Alder polymerization and the oxidative cyclodehydrogenation. The combination of FTIR, Raman, solid-state NMR, and UV-vis-NIR absorption spectroscopy analyses and STM visualization, complemented by ab initio simulations of structural, electronic and optical properties, corroborated the successful formation of GNR-OMe 9. THz spectroscopy revealed that the methoxy-substitution enhanced the photoconductivity of GNRs by a factor of ∼25%, primarily due to reduced charge effective mass following the edge functionalization, in agreement with DFT results. These results indicate the significant influence of edge functionalization on the electronic band structures of GNRs. Our results indicate that finer tuning of the optical and electronic properties of GNRs can be achieved by combining the charge redistribution effects of the substituents together with the steric effects to induce non-planarity. Moreover, the non-planarity can simultaneously suppress the aggregation of the GNRs while enhancing the conductivity, which can be advantageous for the fabrication of high-performance, single-GNR devices.

Methods

First-principles simulations

The structural, electronic and optical properties of GNR-OMe and GNR-H were simulated within an ab initio scheme based on density functional theory (DFT) and many-body perturbation theory (MBPT) approaches.⁵⁵ The ground state optimized geometries and electronic properties were computed by using a total-energy-and-forces DFT approach based on pseudopotentials and plane-waves, as implemented in the Quantum ESPRESSO package.^64,65 Norm-conserving pseudopotentials were employed, with a plane-wave cutoff energy of 80 Ry defining the basis set. A vacuum region of 15 Å in the nonperiodic directions was introduced to prevent interaction between periodic images. The atomic positions were fully optimized until forces within the cell were less than 0.01 eV Å⁻¹, using a 16 × 1 × 1 k-point grid for the sampling of the Brillouin zone. Note that, in order to simplify the modelling, the alkyl chains have been pruned and substituted with –H or –Me, having shown that this approximation does not affect significantly the characterization of the properties of interest.²¹ Quasiparticle energy corrections were computed within the G₀W₀ approximation to the electron self-energy in order to overcome the well-known underestimation of DFT bandgaps and dispersions. The optical absorption spectrum was then computed as the imaginary part of the macroscopic dielectric function by solving the Bethe–Salpeter (BS) equation for the GW-corrected quasi-electrons and quasi-holes, within the Tamm–Dancoff approximation. Both GW and BS calculations were performed with the Yambo code,⁶⁶ and further details can be found elsewhere.²¹

Solid-state NMR

¹H MAS NMR and ¹³C CP/MAS NMR measurements were performed with a Bruker Avance III console operating at 700.25 MHz ¹H Larmor frequency, using a double-resonance MAS probe supporting zirconia MAS rotors with 2.5 mm outer diameter spinning at 25 kHz MAS frequency. The rf nutation frequency was adjusted to 100 kHz corresponding to a 2.5 μs 90° pulse length for signal excitation as well as for heteronuclear dipolar decoupling during acquisition, using the swfTPPM scheme⁶⁷ for efficient ¹H decoupling. 1024 transients with a repetition delay of 10 s were recorded for the CP/MAS NMR spectra, using 1 ms CP contact pulse and a 90–100% amplitude ramp on the ¹H channel at ambient conditions. ¹H MAS NMR measurements at 60 kHz MAS have been performed using a commercial MAS probe supporting zirconia rotors of 1.3 mm outer diameter with a rf-nutation frequency of 140 kHz on the ¹H channel, corresponding to a 1.8 μs 90° pulse length. The xy16-Back-to-Back⁶⁸ sequence has been used to record the DQ-SQ correlation spectrum at 60 kHz MAS.

THz spectroscopy

We operate the optical pump–THz probe (OPTP) by the an amplified, mode-locked Ti:sapphire femtosecond laser system. The output laser pulse possesses a central wavelength of 800 nm, a pulse length of ∼50 fs, and a repeating frequency of 1 kHz. The THz pulse with ∼ a bandwidth of ∼2 THz is generated via optical rectification in ZnTe crystal, and probed via electro-optic sampling by a second ZnTe crystal. By controlling the pump–probe time delay, the photoinduced THz field attenuation (proportional to the real photoconductivity) and phase shift (related to the imaginary photoconductivity) can be tracked. The detailed working principle of OPTP spectroscopy and its applicability for studying the charge transporting properties in nanomaterials are widely reported previously.^20,56,63

Author contributions

X.-Y. W., K. M., and A. N. conceived the project. A. G. and X.-Y. W. synthesized all the materials and performed standard characterizations under the supervision by K. M. and A. N. A. R., E. M., and D. P. conceived and carried out all the theoretical studies. W. Z., P. S., and A. T. performed the THz spectroscopy measurements and analyses under the supervision by H. I. W., R. G. and M. R. H. conducted the solid-state NMR analyses. J. L. carried out the STM analyses under the supervision by C.-A. P. A. G., H. I. W., D. P., and A. N. co-wrote and finalized the manuscript with contributions and comments by other co-authors.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was financially supported by the Max Planck Society, the ANR-DFG NLE Grant GRANAO by DFG 431450789, and by the Italian Ministry of Research through the PRIN grant HARVEST. K. M. acknowledges a fellowship from Gutenberg Research College, Johannes Gutenberg University Mainz. We acknowledge Xinshun Qin and Shixuan Du for support with the STM measurements. C.-A. P. acknowledges the National Science Foundation of China (no. 11974403 and Sino-German Project no. 51761135130). Computational time on the Marconi100 machine at CINECA was provided by the Italian ISCRA program. Open Access funding provided by the Max Planck Society.

Notes and references

1. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
2. A. Bianco, H.-M. Cheng, T. Enoki, Y. Gogotsi, R. H. Hurt, N. Koratkar, T. Kyotani, M. Monthioux, C. R. Park, J. M. D. Tascon and J. Zhang, Carbon, 2013, 65, 1–6.
3. T. H. Vo, M. Shekhirev, D. A. Kunkel, M. D. Morton, E. Berglund, L. Kong, P. M. Wilson, P. A. Dowben, A. Enders and A. Sinitskii, Nat. Commun., 2014, 5, 3189.
4. Y.-C. Chen, T. Cao, C. Chen, Z. Pedramrazi, D. Haberer, D. G. de Oteyza, F. R. Fischer, S. G. Louie and M. F. Crommie, Nat. Nanotechnol., 2015, 10, 156–160.
5. S. Kawai, S. Saito, S. Osumi, S. Yamaguchi, A. S. Foster, P. Spijker and E. Meyer, Nat. Commun., 2015, 6, 8098.
6. L. Talirz, P. Ruffieux and R. Fasel, Adv. Mater., 2016, 28, 6222–6231.
7. Z. Chen, X.-M. Lin, M. J. Rooks and P. Avouris, Phys. E, 2007, 40, 228–232.
8. L. Chen, Y. Hernandez, X. Feng and K. Müllen, Angew. Chem., Int. Ed., 2012, 51, 7640–7654.
9. X. Zhou and G. Yu, Adv. Mater., 2020, 32, 1905957.
10. X.-Y. Wang, A. Narita and K. Müllen, Nat. Rev. Chem., 2017, 2, 0100.
11. X.-Y. Wang, X. Yao and K. Müllen, Sci. China: Chem., 2019, 62, 1099–1144.
12. K.-Y. Yoon and G. Dong, Mater. Chem. Front., 2020, 4, 29–45.
13. A. Narita, X. Feng, Y. Hernandez, S. A. Jensen, M. Bonn, H. Yang, I. A. Verzhbitskiy, C. Casiraghi, M. R. Hansen, A. H. R. Koch, G. Fytas, O. Ivasenko, B. Li, K. S. Mali, T. Balandina, S. Mahesh, S. De Feyter and K. Müllen, Nat. Chem., 2014, 6, 126–132.
14. Z. Chen, A. Narita and K. Müllen, Adv. Mater., 2020, 32, 2001893.
15. A. Jolly, D. Miao, M. Daigle and J.-F. Morin, Angew. Chem., Int. Ed., 2020, 59, 4624–4633.
16. J. Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. P. Seitsonen, M. Saleh, X. Feng, K. Müllen and R. Fasel, Nature, 2010, 466, 470–473.
17. W. Yang, A. Lucotti, M. Tommasini and W. A. Chalifoux, J. Am. Chem. Soc., 2016, 138, 9137–9144.
18. Y. Yano, N. Mitoma, H. Ito and K. Itami, J. Org. Chem., 2020, 85, 4–33.
19. Z. Hao, H. Zhang, Z. Ruan, C. Yan, J. Lu and J. Cai, ChemNanoMat, 2020, 6, 493–515.
20. X. Yao, W. Zheng, S. Osella, Z. Qiu, S. Fu, D. Schollmeyer, B. Müller, D. Beljonne, M. Bonn,H., I. Wang, K. Müllen and A. Narita, J. Am. Chem. Soc., 2021, 143, 5654–5658.
21. Y. Hu, P. Xie, M. De Corato, A. Ruini, S. Zhao, F. Meggendorfer, L. A. Straasø, L. Rondin, P. Simon, J. Li, J. J. Finley, M. R. Hansen, J.-S. Lauret, E. Molinari, X. Feng, J. V. Barth, C.-A. Palma, D. Prezzi, K. Müllen and A. Narita, J. Am. Chem. Soc., 2018, 140, 7803–7809.
22. W. Niu, J. Ma, P. Soltani, W. Zheng, F. Liu, A. A. Popov, J. J. Weigand, H. Komber, E. Poliani, C. Casiraghi, J. Droste, M. R. Hansen, S. Osella, D. Beljonne, M. Bonn, H. I. Wang, X. Feng, J. Liu and Y. Mai, J. Am. Chem. Soc., 2020, 142, 18293–18298.
23. C. Cocchi, D. Prezzi, A. Ruini, M. J. Caldas and E. Molinari, J. Phys. Chem. C, 2012, 116(33), 17328–17335.
24. P. Wagner, C. P. Ewels, V. V. Ivanovskaya, P. R. Briddon, A. Pateau and B. Humbert, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(13), 134110.
25. P. Koskinen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(20), 205429.
26. N. Rosenkranz, C. Till, C. Thomsen and J. Maultzsch, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(19), 195438.
27. X. Peng and S. Velasquez, Appl. Phys. Lett., 2011, 98, 023112.
28. Y. Li, X. Jiang, Z. Liu and Z. Liu, Nano Res., 2010, 3, 545–556.
29. G. Cocco, E. Cadelano and L. Colombo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 241412.
30. A. Narita, Z. Chen, Q. Chen and K. Müllen, Chem. Sci., 2019, 10, 964–975.
31. A. Narita, X.-Y. Wang, X. Feng and K. Müllen, New advances in nanographene chemistry, Chem. Soc. Rev., 2015, 44, 6616–6643.
32. P. Ruffieux, S. Wang, B. Yang, C. Sánchez-Sánchez, J. Liu, T. Dienel, L. Talirz, P. Shinde, C. A. Pignedoli, D. Passerone, T. Dumslaff, X. Feng, K. Müllen and R. Fasel, Nature, 2016, 531, 489–492.
33. L. Talirz, H. Söde, T. Dumslaff, S. Wang, J. R. Sanchez-Valencia, J. Liu, P. Shinde, C. A. Pignedoli, L. Liang, V. Meunier, N. C. Plumb, M. Shi, X. Feng, A. Narita, K. Müllen, R. Fasel and P. Ruffieux, ACS Nano, 2017, 11, 1380–1388.
34. I. C.-Y. Hou, Y. Hu, A. Narita and K. Müllen, Polym. J., 2018, 50, 3–20.
35. F. Xu, C. Yu, A. Tries, H. Zhang, M. Kläui, K. Basse, M. R. Hansen, N. Bilbao, M. Bonn, I. H. Wang and Y. Mai, J. Am. Chem. Soc., 2019, 141, 10972–10977.
36. D. Joshi, M. Hauser, G. Veber, A. Berl, K. Xu and F. R. Fischer, J. Am. Chem. Soc., 2018, 140, 9574–9580.
37. Y. Huang, W.-T. Dou, F. Xu, H.-B. Ru, Q. Gong, D. Wu, D. Yan, H. Tian, X.-P. He, Y. Mai and X. Feng, Angew. Chem., Int. Ed., 2018, 57, 3366–3371.
38. C. Rogers, W. S. Perkins, G. Veber, T. E. Williams, R. R. Cloke and F. R. Fischer, J. Am. Chem. Soc., 2017, 139, 4052–4061.
39. Y.-Z. Tan, B. Yang, K. Parvez, A. Narita, S. Osella, D. Beljonne, X. Feng and K. Müllen, Nat. Commun., 2013, 4, 2646.
40. A. Keerthi, B. Radha, D. Rizzo, H. Lu, V. Diez Cabanes, I. C.-Y. Hou, D. Beljonne, J. Cornil, C. Casiraghi, M. Baumgarten, K. Müllen and A. Narita, J. Am. Chem. Soc., 2017, 139, 16454–16457.
41. M. Slota, A. Keerthi, W. K. Myers, E. Tretyakov, M. Baumgarten, A. Ardavan, H. Sadeghi, C. J. Lambert, A. Narita, K. Müllen and L. Bogani, Nature, 2018, 557, 691–695.
42. J. Li, P. Brandimarte, M. Vilas-Varela, N. Merino-Díez, C. Moreno, A. Mugarza, J. S. Mollejo, D. Sánchez-Portal, D. Garcia de Oteyza, M. Corso, A. Garcia-Lekue, D. Peña and J. I. Pascual, ACS Nano, 2020, 14, 1895–1901.
43. E. Carbonell-Sanromà, J. Hieulle, M. Vilas-Varela, P. Brandimarte, M. Iraola, A. Barragán, J. Li, M. Abadia, M. Corso, D. Sánchez-Portal, D. Peña and J. I. Pascual, ACS Nano, 2017, 11, 7355–7361.
44. M. Ohtomo, H. Jippo, H. Hayashi, J. Yamaguchi, M. Ohfuchi, H. Yamada and S. Sato, ACS Appl. Mater. Interfaces, 2018, 10, 31623–31630.
45. M. Panighel, S. Quiroga, P. Brandimarte, C. Moreno, A. Garcia-Lekue, M. Vilas-Varela, D. Rey, G. Sauthier, G. Ceballos, D. Peña and A. Mugarza, ACS Nano, 2020, 14, 11120–11129.
46. J. Cai, C. A. Pignedoli, L. Talirz, P. Ruffieux, H. Söde, L. Liang, V. Meunier, R. Berger, R. Li, X. Feng, K. Müllen and R. Fasel, Nat. Nanotechnol., 2014, 9, 896–900.
47. X.-Y. Wang, J. I. Urgel, G. B. Barin, K. Eimre, M. Di Giovannantonio, A. Milani, M. Tommasini, C. A. Pignedoli, P. Ruffieux, X. Feng, R. Fasel, K. Müllen and A. Narita, J. Am. Chem. Soc., 2018, 140, 9104–9107.
48. Y. L. Li, C.-T. Zee, J. B. Lin, V. M. Basile, M. Muni, M. D. Flores, J. Munárriz, R. B. Kaner, A. N. Alexandrova, K. N. Houk, S. H. Tolbert and Y. Rubin, J. Am. Chem. Soc., 2020, 142, 18093–18102.
49. G. Li, K.-Y. Yoon, X. Zhong, J. Wang, R. Zhang, J. R. Guest, J. Wen, X. Y. Zhu and G. Dong, Nat. Commun., 2018, 9, 1687.
50. G. Soavi, S. Dal Conte, C. Manzoni, D. Viola, A. Narita, Y. Hu, X. Feng, U. Hohenester, E. Molinari, D. Prezzi, K. Müllen and G. Cerullo, Nat. Commun., 2016, 7, 11010.
51. C. Cocchi, A. Ruini, D. Prezzi, M. J. Caldas and E. Molinari, J. Phys. Chem. C, 2011, 115, 2969–2973.
52. A. Narita, I. A. Verzhbitskiy, W. Frederickx, K. S. Mali, S. A. Jensen, M. R. Hansen, M. Bonn, S. De Feyter, C. Casiraghi, X. Feng and K. Müllen, ACS Nano, 2014, 8, 11622–11630.
53. R. Denk, A. Lodi-Rizzini, S. Wang, M. Hohage, P. Zeppenfeld, J. Cai, R. Fasel, P. Ruffieux, R. F. J. Berger, Z. Chen, A. Narita, X. Feng, K. Müllen, R. Biagi, V. De Renzi, D. Prezzi, A. Ruini and A. Ferretti, Nanoscale, 2017, 9, 18326–18333.
54. R. Denk, M. Hohage, P. Zeppenfeld, J. Cai, C. A. Pignedoli, H. Söde, R. Fasel, X. Feng, K. Müllen, S. Wang, D. Prezzi, A. Ferretti, A. Ruini, E. Molinari and P. Ruffieux, Nat. Commun., 2014, 5, 4253.
55. G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601–659.
56. R. Ulbricht, E. Hendry, J. Shan, T. F. Heinz and M. Bonn, Rev. Mod. Phys., 2011, 83, 543–586.
57. W. Zheng, M. Bonn and H. I. Wang, Nano Lett., 2020, 20, 5807–5813.
58. R. Momper, H. Zhang, S. Chen, H. Halim, E. Johannes, S. Yordanov, D. Braga, B. Blülle, D. Doblas, T. Kraus, M. Bonn, H. I. Wang and A. Riedinger, Nano Lett., 2020, 20, 4102–4110.
59. E. Hendry, M. Koeberg, J. M. Schins, H. K. Nienhuys, V. Sundström, L. D. A. Siebbeles and M. Bonn, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 125201.
60. A. Tries, S. Osella, P. Zhang, F. Xu, C. Ramanan, M. Kläui, Y. Mai, D. Beljonne and H. I. Wang, Nano Lett., 2020, 20, 2993–3002.
61. I. Ivanov, Y. Hu, S. Osella, U. Beser, H. I. Wang, D. Beljonne, A. Narita, K. Müllen, D. Turchinovich and M. Bonn, J. Am. Chem. Soc., 2017, 139, 7982–7988.
62. T. L. Cocker, D. Baillie, M. Buruma, L. V. Titova, R. Sydora, F. Marsiglio and F. A. Hegmann, Phys. Rev. B, 2017, 96, 205439.
63. S. A. Jensen, R. Ulbricht, A. Narita, X. Feng, K. Müllen, T. Hertel, D. Turchinovich and M. Bonn, Nano Lett., 2013, 13, 5925–5930.
64. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
65. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
66. A. Marini, C. Hogan, M. Grüning and D. Varsano, Comput. Phys. Commun., 2009, 180, 1392–1403.
67. C. Vinod Chandran, P. K. Madhu, N. D. Kurur and T. Bräuniger, Magn. Reson. Chem., 2008, 46, 943–947.
68. K. Saalwächter, F. Lange, K. Matyjaszewski, C. F. Huang and R. Graf, J. Magn. Reson., 2011, 212, 204–215.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc05695f

‡ These authors contributed equally to this work.

---