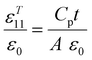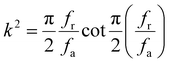Phase transition regulation and piezoelectric performance optimization of fresnoite crystals for high-temperature acceleration sensing

Abstract

Fresnoite (Ba₂TiSi₂O₈ or BTS) crystals can be potentially used for high-temperature piezoelectric sensing because of their high electrical resistivity and strong piezoelectric response at elevated temperatures. However, anomalies in the electro–elastic properties due to phase transition limit the application of BTS crystals over a broad temperature range. In this study, strontium substitution crystals Ba_2−xSr_xTiSi₂O₈ (x = 0, 0.2, 0.4, and 0.6) were designed and grown using the Czochralski (Cz) pulling method. Phase transition was analyzed by in situ high temperature transmission electron microscopy, single-crystal X-ray diffraction and Brillouin light-scattering spectroscopy, where the observed acoustic anomalies exhibited softening of the longitudinal acoustic phonon mode, accounting for the phase transition of the BTS crystal. The bond valence sum was analyzed and Sr substitution was demonstrated to significantly improve the underbonding of the interlayer Ba cations. Phase transition was regulated and piezoelectric activity was optimized by Sr substitution. The results confirmed that Sr substitution could significantly increase the phase transition temperature and weaken the effect of phase transition on macroscopic electrical properties. Finally, a shear-mode prototype acceleration sensor with a stable sensing performance of up to 600 °C was fabricated.

---

Introduction

High-temperature piezoelectric vibration sensors used for structural health monitoring have gained widespread attention in various industrial applications, such as turbine engines, automotive combustion systems, and aerospace propulsion systems.^1,2 Numerous types of piezoelectric materials have been explored for developing high-temperature piezoelectric vibration sensors, including langasite (La₃Ga₅SiO₁₄, LGS), bismuth layer-structure oxides, and yttrium calcium oxyborate (YCa₄O(BO₃)₃, YCOB) crystals. LGS has been considered as an attractive candidate for high-temperature applications owing to the advantage of having no phase transition before reaching its melting point (1470 °C) and achievable large crystal size.³ However, the raw materials (rare earth and Ga elements) of LGS entail high costs. Besides, the low electrical resistivity at elevated temperatures caused by oxygen vacancy diffusion can severely affect the stability of electro–elastic performances.⁴ Bismuth layer-structure oxides are recognized for the good temperature stability of their resonant frequency and piezoelectric activity at elevated temperatures.^2,5–7 However, the phase transition point (T_c) occurs at around ∼900 °C, and the upper limit of the effective usage temperature is considerably lower than the T_c point (normally T_c/3). YCOB crystals were reported to show no phase transition before their melting point of 1510 °C and good temperature stability of piezoelectric performance at high temperatures up to 1000 °C.^8,9 However, crosstalk between different vibration modes could affect the performance of sensors because of the low crystal symmetry (monoclinic).

Fresnoite (Ba₂TiSi₂O₈ or BTS) crystals have drawn significant interest since the 1970s when they were grown using the Czochralski (Cz) pulling method. The BTS crystal belongs to the intermediate category, and the crystal structure features tetragonal symmetry with the point group 4mm (space group P4bm).¹⁰ Owing to the crystal symmetry, BTS crystals possess piezoelectric,^11,12 pyroelectric,¹³ and nonlinear optical properties^14,15 and exhibit potential for numerous physical applications.^16,17 BTS crystals have high electric resistivity (>3.6 × 10⁹ Ω cm @700 °C for Z-cut), low dielectric loss (tan δ₃₃ < 1% @600 °C), and a strong piezoelectric coefficient (d₁₅ = 18 pC N⁻¹ @25 °C), allowing their use as piezoelectric elements at elevated temperatures.^12,18 Over the recent decade, many studies have been performed on the exploration of BTS piezoelectric crystals for high-temperature piezoelectric sensing.^12,18–20 However, it is reported that the BTS crystals undergo commensurate–incommensurate phase transition at approximately 160 °C.²¹ This process strongly affects multiple physical properties.¹⁹ To illustrate, the largest piezoelectric coefficient d₁₅ is particularly affected, and a distinct “jump” can be observed near the phase transition region (∼160 °C), limiting their application in shear mode piezoelectric sensing over a wide temperature range. To broaden the applicable temperature range and optimize the electro–elastic properties of BTS crystals, phase transition regulation is highly desirable.

The incommensurate phase transition of fresnoite crystals has been proven by various techniques, including X-ray diffraction,¹² thermal expansion,^18,19 and transmission electron microscopy, among others.²² However, in-depth studies need to be conducted because of a lack of knowledge concerning the mechanisms of phase transition. Comprehensive knowledge about the structural changes that occur during phase transition allows for an in-depth understanding of crystal structures and the prediction of the physical properties of compounds, which bears great significance for obtaining structures and exploring new crystals with optimized physical properties. Substitution is one of the important and effective strategies to change or modulate the phase transition of crystal materials and is expected to realize phase transition movements beyond the operating temperature range. Thus, in the current study, several experiments were conducted, involving Sr atom substitution modification experiments on the Ba site atoms of BTS crystals—Ba_2−xSr_xTS (x = 0, 0.2, 0.4, and 0.6) crystals; moreover, the structure of the substituted crystals were analyzed by single-crystal X-ray diffraction. Combined with Brillouin scattering data, the analysis established the relationship between incommensurate phase transition and macroscopic electro–elastic properties and showed an improvement in piezoelectric behavior. A high-performance acceleration sensor with an operational temperature reaching 600 °C is thus obtained.

Methodology

Crystal growth

High-purity (99.99%) powders—namely, BaCO₃, SrCO₃, TiO₂, and SiO₂—were used as starting materials for polycrystalline preparation. These raw materials were dried at 100 °C for 24 h before they were accurately weighed and mixed in the stoichiometric ratio. Specifically, an excess of 2 wt% TiO₂ was added into the initial oxide mixture to compensate for the nonuniformity during crystal growth. The oxide mixture was pressed into tablets and sintered at 1250 °C for at least 30 h to obtain the BTS and Sr-substituted BTS (Ba_2−xSr_xTS) compounds. This procedure was aimed at preventing the generation of excessive BaTiO₃ impurity phase as Ti ions tend to exist in a 6-coordination manner at high temperatures. Crystal growth experiments were then conducted using the Cz pulling method. The synthesized polycrystalline materials were charged into a platinum crucible and melted at temperatures exceeding 1400 °C. BTS and Ba_2−xSr_xTS crystals were grown under a pure-nitrogen atmosphere (>99.9%). The pulling and rotation rates were set to 0.3 mm h⁻¹ and 10 rpm, respectively. When the growth process was completed, the grown crystals were pulled out of the melt and cooled to room temperature at 20–30 °C h⁻¹. Crystal samples from the as-grown crystals were prepared to determine the weight percentages of SrO and BaO by X-ray fluorescence spectroscopy (PANalytical Axios).

Single-crystal X-ray diffraction

Rectangular parallelepiped specimens of Ba_2−xSr_xTS (x = 0, 0.2, 0.4 and 0.6) crystals were used for single-crystal X-ray data collection. Data on the structures were collected using a Bruker SMART APEX-II diffractometer equipped with a CCD area detector using graphite-monochromated MoKα radiation (λ = 0.71073 Å) at room temperature. The diffraction data were integrated using the software SAINT, with intensities corrected for Lorentz and polarization effects. The data were solved using a direct method via the program SHELXL and then refined with the full-matrix least-squares technique based on F². All atoms in the crystal structure were refined with anisotropic thermal parameters, and the refinements converged for I > 2σ(I). Related calculations were performed using the crystallographic software package SHELXTL.²³ Details related to crystal parameters, data collection, and structure refinement are summarized in Table 1. It is worth figuring out that crystal twining is observed for the Ba_2−xSr_xTS (x = 0.6) sample, which might be associated with the high Sr substitution concentration. The final refined atomic coordinates are listed in Table S1 (ESI†).

Table 1 Crystallographic data and structural refinements for Ba_2−xSr_xTS (x = 0, 0.2, 0.4, and 0.6) crystals

	x = 0	x = 0.2	x = 0.4	x = 0.6
Formula	Ba2TiSi2O8	Ba1.8Sr0.2TiSi2O8	Ba1.6Sr0.4TiSi2O8	Ba1.4Sr0.6TiSi2O8
Crystal system	Tetragonal	Tetragonal	Tetragonal	Tetragonal
Space group	P4bm	P4bm	P4bm	P4bm
Temperature (K)	293(2)	296(2)	293(2)	296(2)
Unit cell dimension	a = 8.5157(3)	a = 8.4984(3)	a = 8.4901(4)	a = 8.479(3)
(Å)	c = 5.2013(3)	c = 5.1902(2)	c = 5.1791(4)	c = 5.168(5)
Formula weight	506.76	496.82	486.87	476.93
Z	2	2	2	2
Unit cell vol	377.2(0)	374.85(3)	373.32(5)	371.55(19)
Limiting indices	−14 < h < 14	−14 < h < 14	−14 < h < 8	−8 < h < 11
	−14 < k < 14	−13 < k < 14,	−14 < k < 14,	−10 < k < 11,
	−6 < l < 8	−7 < l < 8	−8 < l < 8	−6 < l < 7
Reflections collected/unique	5402/775	5544/952	5511/969	1946/472
R(int)	0.0676	0.0335	0.0431	0.0453
GOF	1.067	1.109	1.056	1.132
wR2(reflections)	0.0814	0.0388	0.0496	0.1356

---

Brillouin scattering

Two high-quality and polished single-crystal samples—the (100) and (001) planes with thicknesses of less than 150 μm—were used for Brillouin scattering tests. The high-temperature Brillouin spectra were acquired using a custom-built Brillouin spectrometer with a 3+3 pass tandem Fabry–Perot interferometer. A solid-state single-mode laser (DIAMOND J-3, Coherent) at a wavelength of 532 nm was used as the excitation source. The scattered light generated from the crystal sample was collected via backscattering geometry. Temperature-dependence studies were performed using a resistance heater combined with a thermocouple. The samples were heated to 500 °C at a rate of 20 °C h⁻¹. A conventional photon-counting system and a multichannel analyzer were used to detect and determine the average of the backscattered signals. Brillouin spectra were recorded using 500 repetitions of accumulation. The Brillouin frequency shift (v_B) and full-width at half-maximum (Γ_B) were evaluated by fitting the experimental spectra to the convolution of the Gaussian instrumental function.

Property characterization

The thermal expansion behaviors of the Ba_2−xSr_xTS crystals were studied using the Diamond Thermomechanical Analyzer (PerkinElmer) within the 298–773 K temperature range. Crystal samples measuring 3 mm × 4 mm × 5 mm were prepared, and the heating rate was controlled at 10 K min⁻¹. The dielectric permittivities (ε^T₁₁ and ε^T₃₃) and the piezoelectric coefficient d₁₅ were determined in accordance with the IEEE Standard on Piezoelectricity.²⁴ The tested samples and correlation formulas are listed in Table 2.¹⁹ The dielectric permittivities were evaluated using a multifrequency LCR meter (HP4263B), and the resonance/antiresonance frequencies for the length extensional mode were measured using the Agilent 4194A impedance analyzer. The piezoelectric coefficient d₃₃ was measured with a quasistatic d₃₃ meter (Institute of Acoustics, Chinese Academy of Sciences, ZJ-3AN).

Table 2 Related material parameters and equations for different sample cuts

Crystal cuts	Material parameters	Equation
X-plate	k 15, d15
Z-plate

---

Acceleration sensor fabrication and sensing test

The acceleration sensor was fabricated using the shear-mode crystal cut. On the basis of crystal symmetry, the X-cut sample shows a shear vibration mode (d₁₅) and thus was adopted for the fabrication of the acceleration sensor. In this study, two pieces of X-cut samples were used for sensor assembly. Crystal samples measuring 8 × 8 × 1 mm³ were roughly polished using fine alumina powder. The large faces of the polished crystals cut were deposited with a 100 nm Pt electrode by radio-frequency magnetron sputtering. The assembling components were made of the Inconel 601 alloy. Pre-tightening torque with a value of 0.4 N m was applied for further experimental investigation using a torque control driver (Model 285-50, Wiha Quality Tools). The prototype of the acceleration sensor based on the Ba_2−xSr_xTS crystal is welded using a high-energy Nd:YAG laser welder. The sensing performance of the fabricated acceleration sensor was evaluated at elevated temperatures. The acceleration sensor was connected to a vibration exciter (CTG-5KG) via a stainless rod and placed into a vertical tube furnace. The vibration exciter, which could provide an acceleration reaching 16 g at the operational frequency, was controlled by a function generator (AFG1022). The sinusoidal signal from the function generator was amplified by a power amplifier (CT5701-100W) and then introduced into the vibration exciter to generate the desired vibration signal. The output charge signal produced by the acceleration sensor was further amplified by a preamplifier (CT5852) with a gain of 1000. The amplified signal was subsequently digitized with a data acquisition card (NI USB-6009) and displayed on a laptop via the LABVIEW interface. A commercial vibration sensor (PCB PE 352C22) was also used as a reference sensor to calibrate the acceleration at room temperature. For each temperature point, sensing tests were performed five times, and the mean was calculated.

Results and discussion

Crystal growth

Crystal growth for BTS and Sr-substituted BTS crystals was conducted using the Cz pulling method. The Sr-substituted BTS crystals were easier to crack than the pure BTS crystal: the higher the Sr substitution concentration, the easier the crystal cracked for the Ba_2−xSr_xTS crystals. This observation is attributed to two factors. One factor is that Sr₂TiSi₂O₈ is not an exactly congruent melting compound,^25,26 which can lead to component deviation in the melt when preparing the polycrystalline material in a stoichiometric ratio. The case is similar for the Sr-substituted BTS crystals. The other factor is the difference between the atomic radius of Sr and that of Ba, which tends to distort the original lattice and increase the internal strain,²⁷ thus promoting the generation of cracks. The principle of crystal growth states that the maximum internal strain ε_max allowed by crystal growth is as follows:²⁸where h is the height of the crystal, R is the radius of the crystal, and dT/dz is the temperature gradient within the crystal. The maximum strain ε_max in the crystal should be less than its breaking strain εc to eliminate crystal cracks, and the upper limit of the axial temperature gradient dT/dz that a non-cracked crystal can withstand could be estimated using the equation below:

From the earlier analysis, the conclusion may be drawn that the up-limit of the axial temperature gradient is nearly linearly related to the parameter R^−1.5. Therefore, reducing the axial temperature gradient should be an effective approach to growing crystals without cracking. In the current study, we increased the thickness of the radial thermal insulation layer to reduce the radial heat loss and decrease the axial temperature gradient. Consequently, Ba₂TiSi₂O₈, Ba_1.8Sr_0.2TiSi₂O₈ and Ba_1.6Sr_0.4TiSi₂O₈ crystals were successfully grown (Fig. 1). It needs to be highlighted that though Ba_1.4Sr_0.6TiSi₂O₈ can be crystallized, bulk crystals free of cracks are hard to achieve. To confirm the chemical ratio of the grown Sr-substituted BTS crystals, XRF tests were performed. The results are summarized in Table S2 (ESI†). The composition weight percentages of SrO in grown crystals were slightly lower than the theoretical values.

Fig. 1 As-grown Ba_2−xSr_xTS (x = 0, 0.2, 0.4, and 0.6) crystals.

Crystal structure analysis

The anisotropic displacement parameters (ADP) of BTS crystals are summarized in Table 3. The anisotropic thermal parameters U₁₁ and U₂₂ of O3 sites are considerably larger than U₃₃. Large anisotropic displacement ellipsoids are visualized in Fig. 2, where three atoms at the bottom of the Si–O tetrahedron are two O1 atoms and one O3 atoms, and the top atom is O2. For the Ti–O pentahedron, the top atom is O4, with four O1 atoms at the bottom. The thermal displacement of the central atom and oxygen atom (O2 and O4) distributed at the top of the polyhedron is nearly isotropic, whereas that of the oxygen atoms O1 and O3 is elliptical. This observation implies that the oxygen atoms at the bottom of the polyhedron statistically deviate within the xy plane. By contrast, the O2 and O4 atoms show small anisotropic displacements. These results suggest that the Ti–O pentahedron and Si–O tetrahedron are likely to rotate along the Z-axis (without distortion), exhibiting the feature of a distinctive phonon type of the “rigid unit mode.” This mode mostly exists in network materials, such as quartz and cristobalite, among others.²⁹ In addition to the Ti and Si atoms in the BTS crystal, the Ba atoms also show the same anisotropic displacement.

Table 3 Room temperature anisotropic displacement parameters (×10³, Ų) for BTS crystals

	U 11	U 22	U 33	U 23	U 13	U 12
Ba	13.08(18)	13.08(18)	10.8(2)	−0.73(12)	−0.73(12)	−5.53(8)
Ti	9.8(3)	9.8(3)	9.2(9)	0	0	0
Si	10.7(4)	10.7(4)	7.8(7)	−2.2(6)	−2.2(6)	0.8(4)
O1	44(3)	15.5(16)	16(2)	−3.8(16)	−6.5(18)	13.3(19)
O2	12.5(13)	12.5(13)	12(2)	0	0	−1.1(16)
O3	32(3)	32(3)	10(3)	0	0	−1.7(4)
O4	23.0(2)	23.0(2)	14.0(4)	0	0	0

---

Fig. 2 Thermal ellipsoid of BTS crystals, as determined from the anisotropic displacement parameters: (a) viewed along the Z-axis, (b) Ti–O pentahedron, and (c) Si–O tetrahedron.

Brillouin scattering

Brillouin scattering was used to study energy excitation processes with low energy, such as acoustic phonons or magnons near the center of the Brillouin zone.^30–32 Anomalies in the elastic constants can be characterized accurately using this technique; thus, Brillouin scattering is a valuable tool for revealing the nature of various phase transitions.^33,34

Phase transitions for the BTS crystal were examined by Brillouin scattering. Fig. 3(a) presents the Brillouin spectra for the BTS (100) plane at selected temperatures, where q⃑ is the wave vector of the incident light. Only one Brillouin peak in the vicinity of ±42.5 GHz was observed. This response is associated with a longitudinal acoustic (LA) phonon propagating in the [100] direction, corresponding to the elastic constant c₁₁. The LA mode noticeably shifted to a lower frequency range, and its linewidth increased from room temperature to the phase-transition temperature (∼190 °C). With further heating, the spectra remained qualitatively the same as the temperature rises. This phenomenon is related to the incommensurate-normal phase transition for BTS crystal, as proved by the in situ high temperature transmission electron microscope characterization (Fig. S1, ESI†). The temperature dependence of the Brillouin spectra for the (001) plane was also evaluated. The results are presented in Fig. 3(b). As shown in the figure, no clear anomaly is observed. The strong LA phonons near ±33.8 GHz correspond to the elastic constant c₃₃, whereas the weak peak appears near ±19.1 GHz relevant to the transverse acoustic (TA) phonons, corresponding to the elastic constant c₄₄.^33,35

Fig. 3 Brillouin spectra of BTS crystals at elevated temperatures (a: q⃑//[100] b:q⃑//[001]).

To elucidate the change in the location of peaks, a plot of the frequency shift v_B, together with the full-width at half-maximum value Γ_B for the LA mode of the (100) plane is presented in Fig. 4. As shown in the figure, the LA mode exhibits softening when heated to 160 °C, accompanied by a sharp increase in Γ_B. This behavior can be attributed to the incommensurate phase transition. In the Brillouin scattering spectra, the frequency shift ν_B is proportional to the longitudinal sound velocity.^36–38 Therefore, Γ_B is associated with the degree of acoustic damping represented by the acoustic attenuation coefficient, which is proportional to Γ_B divided by the sound velocity.

Fig. 4 Temperature dependence of (a) Γ_B and (b) v_B in the LA mode propagating in the [100] direction.

On the basis of the aforementioned phonon mode softening results combined with the thermal ellipsoid results presented in Fig. 2, the mechanisms of phase transitions for BTS crystals are thus described: according to lattice dynamics, the deviation of the crystal atoms from their equilibrium positions occurs as lattice waves. The frequency of a certain lattice wave reflects “resilience” to this mode offset. [SiO4]⁴⁻ and [TiO₅]⁶⁻ react as the “rigid unit”; when the temperature increases and reaches a certain value, the polyhedrons deviate from their original equilibrium positions by rotation around the top oxygen atom (O4/O2) because they are no longer subjected to the restoring force (i.e., phonon mode softening). Moreover, the freezing of the rotational thermal motion of the polyhedron affects the Ba atoms between the connected layers, causing them to freeze in a position that deviates from the equilibrium and leading to a mismatch between layers. The ions in the BTS crystals ultimately reach the condition for phase transition.

A strategy is presented to regulate the phase transition. The aforementioned analysis suggests that phase transition can be influenced by restricting phonon mode softening. Partial substitution of the Ba atoms with relatively light atoms such as Sr or Ca endows phonon vibrations with high energies. The phonon frequency is increased,^35,36 rendering it less susceptible to phonon mode softening and mitigating the degree of mismatch between layers. Consequently, the phase transition temperature is shifted to elevated temperatures.

Bond valence sum analysis

The bond valence sum (BVS) was analyzed to understand the distorted structure in the ferroelectric phase, particularly for the study of crystal chemistry in layered ferroelectrics.³⁹ The bond valence sum of the cation i and the coordinating anion j can be calculated from the following equation:where r_ij is the experimental bond length parameter of the cation i coordinated with the anion j; is an empirical parameter associated with the metal in a given oxidation state and the type of coordinating atom; and B is a constant value (the most reliable value for this parameter is 0.37 Å).^40,41

Table 4 presents the atomic distances determined from single-crystal structure analyses and the results of BVS calculations for Ba atoms in Ba_2−xSr_xTS (x = 0, 0.2, 0.4, and 0.6) crystals. Other selected bond distances (Å) and the bond valence sum are listed in Table S3 (ESI†). An increase in Sr²⁺ concentration leads to a gradual decrease in the bond length of Ba–O, whereas the bond valence sum of the Ba site continuously increases and shifts to its ideal value. In the BTS crystals, V_Ba in the parent P4bm fresnoite structure is 1.8469, rendering Ba slightly underbonded. The underbonding of the Ba atoms is proposed as the driving force provoking modulation in fresnoite framework structure compounds.^42,43 The modulation is caused by the Ba ions attempting to reach improved bonding conditions. The incorporation of Sr effectively improves the unsatisfactory bonding of the Ba site, particularly for the Ba_1.6 Sr_0.4TS crystal where the Ba site has a bond valence sum of 1.92773, very close to the ideal value of 2.0. This result proves that Sr substitution exerts a positive effect and can suppress the influence of phase transition in macrophysical properties, such as dielectric permittivity and the piezoelectric coefficient.

Table 4 Bond valence sum calculations for Ba_2−xSr_xTS crystals

	X = 0		X = 0.2		X = 0.4		X = 0.6
	Bond length	Bond valence	Bond length	Bond valence	Bond length	Bond valence	Bond length	Bond valence
Ba–O1	2.993	0.147561	2.838	0.22434	2.837	0.224947	2.833	0.227392
Ba–O1	2.993	0.147561	2.838	0.22434	2.837	0.224947	2.833	0.227392
Ba–O1	2.845	0.220135	2.99	0.148762	2.985	0.150786	2.979	0.153251
Ba–O1	2.845	0.220135	2.99	0.148762	2.985	0.150786	2.979	0.153251
Ba–O2	2.791	0.254726	2.637	0.386219	2.776	0.265265	2.773	0.267424
Ba–O2	2.791	0.254726	2.786	0.258191	2.776	0.265265	2.773	0.267424
Ba–O2	2.647	0.37592	2.786	0.258191	2.632	0.391473	2.623	0.401112
Ba–O3	2.835	0.226166	2.83	0.229243	2.825	0.232362	2.828	0.230485
BVS	1.84693		1.87805		1.90583		1.92773

---

Property characterization

Incommensurate phase transitions belong to second-order phase transitions. Although no thermal effect and entropy change are observed during these phase transitions, the thermal expansion coefficient, compressibility, and specific heat capacity change discontinuously.⁴⁴Fig. 5 depicts the temperature dependence of the thermal expansion coefficient for the Ba_2−xSr_xTS (x = 0, 0.2, 0.4, and 0.6) crystals. Notably, these figures share common characteristics. The corresponding thermal expansion coefficients are shown in Table S3 (ESI†). The thermal expansion coefficients α₁₁ and α₃₃ before the phase transition are considerably close, whereas the anisotropy becomes apparent when the temperature exceeds the phase transition. Notably, the phase transition temperatures for BTS crystals with different Sr substitution concentrations largely vary: the higher the Sr substitution concentration, the higher the phase transition temperature. The phase transition temperature for Ba_2−xSr_xTS crystals with x = 0, 0.2, 0.4, and 0.6 are determined to be 175 °C, 270 °C, 360 °C, and 420 °C, respectively.

Fig. 5 Thermal expansion as a function of temperature for Ba_2−xSr_xTS crystals. (a) x = 0; (b) x = 0.2; (c) x = 0.4; (d) x = 0.6.

Table 5 summarizes the main electro–elastic parameters for Ba_2−xSr_xTS (x = 0.2, 0.4, and 0.6) crystals at room temperature, including the relative dielectric permittivities ε^T₁₁/ε₀ and ε^T₃₃/ε₀, elastic compliances s^E₃₃ and s^E₅₅, and piezoelectric coefficients d₁₅ and d₃₃. For enhanced comparison, the properties of the Ba₂TiSi₂O₈ crystal are also listed. Notably, the relative dielectric permittivities slightly change before and after Sr substitution. However, the piezoelectric coefficients d₁₅ and d₃₃ substantially increase with increasing Sr substitution concentration. When the substitution concentration of Sr reaches 30%, the piezoelectric coefficients d₁₅ and d₃₃ reach 22.4 and 5.8 pC N⁻¹, respectively.

Table 5 Summary of the dielectric, mechanical, and piezoelectric parameters for Ba_2−xSr_xTS crystals at room temperature

	ε ^T ii /ε0 (100 kHz)		d ij (pC N^−1)		s ij (pm^2 N^−1)
	ε ^T11/ε0	ε ^T33/ε0	d 15	d 33	s ^E33	s ^E55
x = 0	16.3	10.8	17.8	4.0	13	25.5
x = 0.2	16.2	10.4	18.7	4.7	13.3	30.2
x = 0.4	16.5	11.4	20.7	5.3	13.5	31.2
x = 0.6	17.2	11.7	22.4	5.8	14.0	33.0

---

Two factors are believed to be associated with the increase of piezoelectric coefficient d₃₃. On the one hand, the piezoelectric property is associated with the lattice parameter ratio (c/a),^45–47 which is inversely proportional to the piezoelectric performance. For BSTS material, the lattice parameter ratio c/a is decreased with increasing molar fraction of Sr (Fig. S2, ESI†), thus the piezoelectric coefficient d₃₃ gets increased after Sr substitution. On the other hand, the high electronegativity of Sr ions as compared with the Ba ions is reported to have a positive and substantial contribution to the piezoelectric performance.^48,49 The Sr substitution in BTS is beneficial for the improvement of piezoelectric performance.

The abnormal structure distortion induced by the phase transition can alter the physical phenomenon; that is, not only the thermal expansion but also the electro–elastic properties. The abnormal structure distortion near the phase transition can directly induce a change in cell parameters and lead to the shift in thermal expansion in the special direction of the crystals, as shown in Fig. 5. Meanwhile, on the basis of the temperature dependence of the electrical properties, particularly the relative permittivity, the relationship between the phase transition temperature and substitution concentration can be reflected. The variation in the relative dielectric permittivity and dielectric loss as a function of temperature for Ba_2−xSr_xTS (x = 0, 0.2, 0.4, and 0.6) crystals are evaluated. The results are shown in Fig. 6. As observed, the relative dielectric permittivity for the Sr-substituted BTS crystals retains nearly the same value over the tested temperature range of 20–700 °C. The dielectric loss tan δ₁₁ maintains a low value (<10%) ranging from room temperature to 600 °C. By contrast, the relative dielectric permittivity ε^T₃₃/ε₀ exhibits a small dielectric anomaly during the temperature variation, associated with the incommensurate phase transition, and above which the dielectric permittivities remain steady. The shift of the abnormal dielectric permittivity to elevated temperatures with an increase in Sr substitution concentration bears research value. When x = 0.6, the incommensurate phase transition temperature for the Ba_1.4Sr_0.6TS crystal exceeds 400 °C, which verifies that Sr substitution can adjust the phase transition of BTS-type crystals.

Fig. 6 Variations in relative dielectric permittivity and dielectric loss as a function of temperature for Ba_2−xSr_xTS crystals. (a) x = 0; (b) x = 0.2; (c) x = 0.4; (d) x = 0.6.

Figure S3 (ESI) shows the impedance spectra and phase angles of the thickness shear mode d₁₅ for Ba_2−xSr_xTS crystals. The clear resonance/antiresonance peaks and 90° phase angle indicate the low dielectric loss of BTS crystals at room temperature; as the temperature increases, the phase angle gradually decreases from 90°, but the peak shape of resonance/antiresonance remains identified. Fig. 7 presents the variations in the piezoelectric coefficient d₁₅ (a) and elastic compliance s^E₅₅ (b) as a function of temperature for Ba_2−xSr_xTS (x = 0, 0.2, 0.4, and 0.6) crystals. For different substitution concentrations, the piezoelectric coefficient d₁₅ exhibits a similar variation trend—that is, slightly increasing prior to the phase transition, followed by a gradual decrease with increasing temperature. These results confirm that the stability of the piezoelectric coefficients for the Sr-substituted crystals is improved relative to the pure BTS crystal. When x equals 0.2, the variation in the piezoelectric coefficient d₁₅ is calculated to be 7.4%, nearly half that of the pure BTS crystals (17.5%), which is particularly useful for shear-mode vibration sensing over a broad temperature range. With regard to the elastic compliance s^E₅₅, only a slight anomaly related to the phase transition occurs at elevated temperatures, where variations <5.2% in s^E₅₅ for the Ba_2−xSr_xTS crystals.

Fig. 7 Temperature dependence of the piezoelectric coefficient d₁₅ (a) and elastic compliance S^E₅₅ (b) for Ba_2−xSr_xTS crystals.

With regard to the present experimental results, the shift trends of the piezoelectric coefficient d₁₅ and the phase transition temperature for crystals with higher Sr substitution concentration can be predicted, as shown in Fig. S4 (ESI†). We can reasonably speculate that when the Sr substitution concentration increased, a higher piezoelectric response can be achieved. Meanwhile, the phase transition temperature can be increased to ∼600 °C. To verify this prediction, in situ high-temperature X-ray powder diffraction (XRPD) tests for Ba_2−xSr_xTS (x = 0 and 0.9) polycrystalline were performed. The XRPD data were processed using Rietveld refinement (Fullprof). The Rietveld-refined profiles are presented in Fig. S5 (ESI†), which shows that the observed pattern is consistent with the calculated pattern, as determined by Rietveld analysis. The temperature dependence of the lattice parameters a and c and the ratio c/a for Ba_2−xSr_xTS (x = 0 and 0.9) samples is illustrated in Fig. 8. An apparent turning point related to phase transition both for the lattice parameters a and c and the lattice parameter ratio c/a around ∼180 °C is found in Fig. 8(a); meanwhile, c/a exhibits the opposite trend variations as that for d₁₅ (x = 0) presented in Fig. 7(a), which further proves the strong correlation between the c/a ratio and the piezoelectric coefficient. For the Ba_1.1Sr_0.9TS, the lattice parameters a and c increase slowly with no noticeable abnormal behavior as the temperature increases; only a discontinuous point for c/a occurring at ∼530 °C is observed (phase transition), which is in good agreement with the prediction. The variation in c/a as a function of temperature for the Ba_1.1Sr_0.9TS samples seems more stable than that for the BTS, which supports the finding that the influence of the phase transition on the macroscopic performance of the Ba_1.1Sr_0.9TS is further reduced. Predictably, a higher Sr substitution concentration can shift the phase transition temperature over 630 °C, which is currently the extreme working temperature of most high-temperature piezoelectric acceleration sensors. Overall, the benefits of Sr substitution regarding the regulation of the phase transition temperature and improvement of the piezoelectric performance are apparent. Therefore, Sr-substituted BTS crystals with attainable high-temperature piezoelectric performances are expected.

Fig. 8 Variation in lattice parameters for BTS (a) and Ba_1.1Sr_0.9TS (b) as a function of temperature.

Prototype acceleration sensor test

On the basis of the piezoelectric features of the Sr-substituted BTS crystals (Fig. 7), the Ba_1.8Sr_0.2TS crystal was selected for the design of the acceleration sensor prototype. For an improved comparison, a prototype of the acceleration sensor based on the BTS crystal with the same specification was fabricated and tested. Fig. 9 shows the variation in sensitivity of the two acceleration sensor prototypes as a function of temperature under 320 Hz. The charge sensitivity of the BTS-based sensor (inset of Fig. 9) significantly decreases after 100 °C. The average sensitivity is 1.484 pC g⁻¹ with a maximum temperature variation of ∼28.1% within the evaluated temperature range. By contrast, the sensitivity of the sensor fabricated based on Ba_1.8Sr_0.2TS crystals exhibits a negligible shift over the entire temperature range. The deviation is only ∼8.6%, indicating improved temperature stability. These results prove that Sr substitution can effectively alter the phase transition point and improve the temperature stability of BTS crystals, which is beneficial to promote the practical application of the larger shear mode (d₁₅) of BTS crystals.

Fig. 9 Temperature dependence of the sensitivity of the BTS (small inset) and Ba_1.8Sr_0.2TS-based shear-type sensors at 320 Hz.

Conclusions

In summary, Sr-substituted BTS crystals, Ba_2−xSr_xTiSi₂O₈ (x = 0, 0.2, 0.4, and 0.6), were designed and grown using the Cz pulling method. The phase transition of the BTS-type crystals was investigated by Brillouin scattering spectroscopy. The mechanisms of the phase transition were analyzed by single-crystal X-ray diffraction. The freezing of the rotational motion of the rigid polyhedron was found to cause the soft mode of the phonon, leading to ion displacement between the layers, hence the phase transition. The Sr substitution enhanced the piezoelectric performance of the BTS single crystal, and the piezoelectric coefficient d₁₅ of the Ba_1.4Sr_0.6TiSi₂O₈ crystal was markedly improved by 25.8%, reaching ∼22.4 pC N⁻¹. The effects of Sr substitution on the phase transition temperature and electrical properties were evaluated by bond valence sum analysis. Results verified that Sr substitution could significantly increase the phase transition temperature and weaken the effect of phase transition on macroscopic electrical properties, thereby enhancing the temperature stability of the piezoelectric performance. The shear-mode acceleration sensor based on the Sr-substituted BTS crystal was more suitable for practical application compared with the pure BTS-based sensor. The Sr substitution is an effective strategy for broadening the application field of BTS.

Author contributions

Chao Jiang and Fapeng Yu performed the research and wrote the manuscript. Caizi Zhang and Fangfei Li provided a Brillouin light-scattering spectroscopy test for the research. Fapeng Yu, Li Sun, Yanlu Li and Xian Zhao assisted with the experimental analysis. All authors discussed the results and reviewed the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The Primary Research and Development Plan of Shandong Province (Grant Number: 2019JZZY010313), the National Natural Science Foundation of China (Grant No. 51872165), and Shandong Provincial Natural Science Foundation (Grant No. ZR2020KA003) supported this study.

Notes and references

1. X. Jiang, K. Kim and S. Zhang, et al. , Sensors, 2014, 14, 144–169.
2. J. Wu, Y. Gao, J. Chen, C. Wang, S. Zhang and S. Dong, Acta Phys. Sin., 2018, 67, 1–30.
3. H. Fritze and H. L. Tuller, Appl. Phys. Lett., 2001, 78, 976.
4. H. Fritze, H. Seh, H. L. Tuller and G. Borchardt, J. Eur. Ceram. Soc., 2001, 21, 1473–1477.
5. C. Wang, J. Chen, H. Lu and Q. Wang, Chin. Sci. Bull., 2021, 66, 2061–2070.
6. Q. Wang, C. Wang, J. Wang and S. Zhang, Ceram. Int., 2016, 42, 6993–7000.
7. Q. Wang and C. Wang, J. Am. Ceram. Soc., 2020, 103, 2686–2693.
8. S. Zhang, E. Frantz, R. Xia, W. Everson, J. Randi and D. W. Snyder, J. Appl. Phys., 2008, 104, 084103.
9. F. Yu, S. Zhang, X. Zhao and D. Yuan, et al. , IEEE Trans. Sonics Ultrason., 2011, 58, 868–873.
10. M. Kimura, Y. Fujino and T. Kawamura, Appl. Phys. Lett., 1976, 29, 227–228.
11. M. Kimura, J. Appl. Phys., 1977, 48, 2850–2856.
12. C. Shen, H. Zhang, H. Cong, H. Yu, J. Wang and S. Zhang, J. Appl. Phys., 2014, 116, 044106.
13. A. Halliyal, A. Bhalla, S. Markgraf, L. Cross and R. Newnham, Ferroelectrics, 1985, 62, 27–38.
14. Y. Takahashi, Y. Benino, T. Fujiwara and T. Komatsu, J. Appl. Phys., 2004, 95, 3503–3508.
15. C. Shen, D. Wang, H. Zhang, J. Wang and R. I. Boughton, Appl. Phys. Express, 2016, 9, 122402.
16. H. Yamauchi, J. Appl. Phys., 1978, 49, 6162–6164.
17. J. Melngailis, J. Vetelino, A. Jhunjhunwala, T. Reed, R. Fahey and E. Stern, Appl. Phys. Lett., 1978, 32, 203–205.
18. S. Cao, B. Jiang, Y. Zheng, X. Tu, K. Xiong, P. Gao and E. Shi, J. Cryst. Growth, 2016, 451, 207–213.
19. C. Jiang, F. Chen, F. Yu, S. Tian, X. Cheng, S. Zhang and X. Zhao, Crystals, 2019, 9, 11.
20. C. Jiang, X. Liu, F.-P. Yu, S. Zhang, H. Fang, X. Cheng and X. Zhao, IEEE Trans. Ind. Electron., 2021, 68, 12850–12859.
21. Z. Chang and A. S. Bhalla, Mater. Lett., 1989, 8, 418–420.
22. R. Withers, Y. Tabira, Y. Liu and T. Höche, Phys. Chem. Miner., 2002, 29, 624–632.
23. G. Sheldrick, Inc., Madison, WI, 1997.
24. A. Meitzler, H. Tiersten, A. Warner, D. Berlincourt, G. Couqin and F. Welsh III, IEEE Trans. Sonics Ultrason., 1988.
25. T. Höche, M. Grodzicki, F. Heyroth, R. Uecker and P. Van Aken, Philos. Mag. Lett., 2007, 87, 431–439.
26. Y. Dai, B. Zhu, J. Qiu, H. Ma, B. Lu and B. Yu, Chem. Phys. Lett., 2007, 443, 253–257.
27. C. Zhang, L. Yi and X. M. Chen, Ceram. Int., 2014, 40, 6077–6082.
28. J. Brice, J. Cryst. Growth, 1977, 42, 427–430.
29. K. D. Hammonds, M. T. Dove, A. P. Giddy, V. Heine and B. Winkler, Am. Mineral., 1996, 81, 1057–1079.
30. J.-T. Hong, B. W. Lee, J.-H. Ko, I. Jankowska-Sumara, M. Podgórna and A. Majchrowski, Curr. Appl. Phys., 2018, 18, 642–647.
31. M. Mączka, T. H. Kim, M. Ptak, I. Jankowska-Sumara, A. Majchrowski and S. Kojima, J. Alloys Compd., 2014, 587, 273–277.
32. M. Mączka, T. H. Kim, A. Gągor, I. Jankowska-Sumara, A. Majchrowski and S. Kojima, J. Alloys Compd., 2015, 622, 935–941.
33. M. Mączka, J. Hanuza, A. Kaminskii and S. Kojima, J. Alloys Compd., 2015, 638, 34–37.
34. J. Wang, Q. Zhou, D. Chao, F. Li and T. Cui, RSC Adv., 2017, 7, 8670–8676.
35. J. Ding, T. Lanigan-Atkins and M. Calderón-Cueva, et al. , Sci. Adv., 2021, 7, eabg1449.
36. L. Arunachalam, Sintering of ceramics: new emerging techniques, BoD–Books on Demand, 2012.
37. R. Vacher and L. Boyer, Phys. Rev. B: Solid State, 1972, 6, 639–673.
38. J. Wang, X. Zhao, E. B. Berda, C. Chen, K. Wang, S. Chen, B. Zou, B. Liu, Q. Zhou and F. Li, Polymer, 2016, 90, 1–8.
39. Z.-G. Ye, Handbook of advanced dielectric, piezoelectric and ferroelectric materials: Synthesis, properties and applications, Elsevier, 2008.
40. I. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244–247.
41. I. Brown and K. Wu, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 1957–1959.
42. T. Höche, W. Neumann, S. Esmaeilzadeh, R. Uecker, M. Lentzen and C. Rüssel, J. Solid State Chem., 2002, 166, 15–23.
43. T. Höche, S. Esmaeilzadeh, R. L. Withers and H. Schirmer, Z. Kristallogr. – Cryst. Mater., 2003, 218, 788–794.
44. S. M. Stishov, Phase Transitions for Beginners, World Scientific, 2019.
45. H. Momida and T. Oguchi, Appl. Phys. Express, 2018, 11, 041201.
46. Y. Wei, C. Jin, P. Ye, P. Li, Y. Zeng and G. Xu, Appl. Phys. A: Mater. Sci. Process., 2017, 123, 218.
47. H. Liu, F. Zeng, G. Tang and F. Pan, Appl. Surf. Sci., 2013, 270, 225–230.
48. Y. Gao, J. Zhang and Y. Qing, et al. , J. Am. Ceram. Soc., 2011, 94, 2968–2973.
49. J. Wu, D. Xiao and J. Zhu, Chem. Rev., 2015, 115, 2559–2595.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2094165, 2094166, 2094167 and 2118488. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1tc03192a

---