Open Access Article
Open Access ArticleUnderstanding ion diffusion in anion exchange membranes; effects of morphology and mobility of pendant cationic groups†
Mohammad
Rezayani
a,
Farhad
Sharif
 *a and
Hesam
Makki
*a and
Hesam
Makki
 *ab
*ab
aDepartment of Polymer and Color Engineering, Amirkabir University of Technology, 424 Hafez Ave., Tehran, Iran. E-mail: sharif@aut.ac.ir
bDepartment of Chemistry and Materials Innovation Factory, University of Liverpool, Liverpool L69 7ZD, UK. E-mail: hmakki@liverpool.ac.uk
First published on 17th August 2022
Abstract
Anion exchange membranes (AEMs) are a promising low-cost alternative to cation exchange membranes (CEMs) in fuel cells. Among them, poly(2,6-dimethyl-1,4-phenylene oxide) with pendant quaternary ammonium (PPO-QA) is one of the most promising. PPO-QA membranes with flexible alkyl side-chains of varying lengths as a spacer (or extender) for QA have been studied and shown to have different performances; however, the exact underlying mechanisms have remained unclear. We study PPO-QA membranes with varying alkyl side-chains (n = 0, 6, 10, and 16 carbon atoms) with a constant QA position (near the backbone), and with the same side-chain length (n = 16) and varying QA positions on it: near the polymer backbone, in the middle, and at the end of the pendant side-chain, by molecular dynamics (MD) simulations. The calculated water diffusion coefficient in the membranes is in full agreement with experimental data. Our study on membranes with varying alkyl side-chain lengths and a constant QA position at different hydration levels shows a consistent and quantitative correlation between the anion diffusion coefficient (Da) and the hydrophilic pathway morphology. Also, at constant hydration, Da is considerably enhanced due to moving the QA position towards the end of the alkyl side-chain. However, we show that this enhancement is not due to morphological changes in the hydrophilic pathway or polymer phase. Still, the underlying mechanism is the enhanced mobility of QA, plus a lower residence time of anions close to QA. We show that the morphology of the membrane and the degree of phase separation between the hydrophobic/hydrophilic parts is almost constant, but the QA at the end of the alkyl side-chain is considerably easier to pull towards the water channels; therefore, its increased mobility and hydration result in the enhanced dynamics of the diffusing anion. Lastly, we introduce a new methodology to assess the correlation between membrane structure and ion transport rate for fuel cell membranes so that one can tune the permeation of ions (or other molecules) by two distinct mechanisms: (i) by controlling the hydrophilic pathway morphology by changing the polymer backbone structure, which determines the permeation according to the size of the diffusing moieties, and (ii) by side-chain modification, which enhances QA mobility and accordingly (selectively) increases the ion diffusion rate. We show that our methodology could successfully explain how the side-chain modification for PPO-QA membranes considerably increases the ion permeation while the methanol cross-over remains constant.
1 Introduction
Over the past few decades, we have witnessed tremendous growth in ion exchange membrane (IEM) applications in various industries, including water electrolysis,1 the automotive industry,2 redox flow batteries,3 and polyelectrolyte membrane fuel cells.4 Accordingly, fuel cell development has experienced considerable progress as a result of employing IEMs instead of traditional liquid electrolyte fuel cells.2,4,5 IEMs, as the heart of these energy conversion devices, control the ion conduction and ensure the long-term performance of fuel cells.Hydrophilic network management and the degree of phase separation between the hydrophilic and hydrophobic parts of the polymer are known to be the critical factors for water and ion transport through all types of IEMs.6,7 The term “hydrophilic network management” refers to developing a water network at a standard water level to hinder membrane dehydration and maintain fuel cell efficiency. Preparing an optimal phase-separated network with desirable ion transport capabilities while maintaining the minimum hydration level has been a fresh challenge for scientists.8–10 Thus, a clear correlation exists between the morphology and ion transport properties of IEMs. In a previous study,11 we investigated hydrophilic path formation and diffusivity of water/ions in a series of sulfonated polyether sulfone cation exchange membranes (CEMs). There, we established a quantitative relationship between the morphological parameters of the hydrophilic pathway in CEMs and their ion transport properties. We showed that the hydrophilic path, characterized by three measurable parameters, i.e., Pore Limiting Diameter (PLD), Largest Cavity Diameter (LCD), and Pore Size Distribution (PSD), plays a crucial role in controlling water and ion transport through the membranes. We established a quantitative relationship between these structural parameters and the diffusion coefficient of water and ions.
Using scarce and expensive platinum-based catalysts for CEMs hinders their widespread application in fuel cells.12 Therefore, Anion Exchange Membranes (AEMs) modified with cationic groups are attractive alternatives that function well without platinum catalysts.4,13 A variety of polymers, including poly(sulphone)s, poly(arylene ether)s, poly(styrene)s, poly(phenylene oxide)s, poly(ether ether ketone), and poly(olefin)s,4,14–19 modified with a broad range of cationic groups20–22 have been utilized for the production of AEMs. However, many AEMs show decreased performance over time and under different physical conditions. According to scientific reports,9,23 this issue can be attributed to the inability of AEMs to manage and maintain a uniform hydrophilic pathway inside the membranes during their service life. Among them, polyphenylene oxide (PPO) based polymers functionalized by trimethylammonium quaternary groups and their derivatives showed high alkaline stability and great ion transport properties, making them a promising candidate in fuel cell applications.24–27 Also, recent studies have shown that PPO backbones tethered with long flexible alkyl chains (more than four carbon units) as a spacer or extender bound to the cationic pendant group have better structural integrity and ion transport properties as compared to those without alkyl side-chains,28–35 while the underlying mechanisms remained unclear.
Experimental and computational approaches have been used to explore the relationship between membrane morphology and ion transport behavior in functionalized PPO. For instance, Dang et al.32 studied the effect of a flexible heptyl spacer on the hydroxide ion conductivity and hydrated membrane morphology of quaternary ammonium (QA) functionalized PPO (PPO-QA). Their SAXS results revealed that the heptyl spacer side-chain gives a more efficient phase separation between the ionomer and the backbone of the polymer as compared to conventional functionalized PPO without a spacer. They suggested that this could be attributed to the higher mobility of the QA group because of the flexible heptyl side-chain. In a related study,30 they investigated the effect of cationic alkyl side-chains of different lengths and configurations tethered as a spacer, extender, and spacer + extender on hydroxide ion conductivity and morphology of PPO-QA membranes. They concluded that membranes with no spacer and extender show very poor phase separation and ionic clustering.
Moreover, phase separation is mitigated as an alkyl chain is tethered to the cationic group as an extender. In contrast, alkyl spacer units (cationic head groups) facilitate ionic clustering as flexible alkyl fragments could provide appropriate local mobility for the cationic group to phase-separate from the polymer backbone. Along these lines, Lee9 studied the effect of hydrophobic (alkyl) and hydrophilic (ethylene oxide) long spacers attached to the cationic groups on the phase-segregated behavior of PPO and polystyrene-ethylene-butylene-styrene (SEBS). The results showed that adding hydrophobic spacers improves nano-separation, and the membranes have better conductivity while having a decreased ion exchange capacity and water content. Also, they found that the stretched hydrophilic side-chains in the presence of water induce steric hindrance and prevent water and hydroxide ions from being transported through the polymer network. In very recent work, Molinero et al.10,36 systematically explored the effect of alkyl spacer length (1–12 carbons) on ion diffusion in low water content (e.g., λ = 5) PPO-QA membranes. Their results showed that the alkyl side-chain length has a poor contribution to the width and clustering of the channels at a constant hydration level. At the same time, it enhances the anion diffusion coefficient. Their results suggest that the anion mobility increases while the width of the hydrophilic pathway remains constant.
Despite multiple computational and experimental observations of the side-chain architecture effect on anion transport through AEMs, the impact of water content, side-chain length, and position of the cationic group on the morphology of the hydrophilic pathway and its relationship with ion transport behavior in modified AEMs with alkyl side-chains is still not fully understood, and a comprehensive examination is yet to be performed. In the current study, we performed atomistic-level molecular dynamics simulations for a series of cationic quaternary ammonium poly(2,6-dimethyl-1,4-phenylene oxide) (PPO-QA) membrane models with similar ionic content and different spacer and extender units. In the first part of this study, we aim to outline how water content and extender length (n = 0, 6, 10, and 16) influence the morphology of the hydrophilic pathway and, accordingly, the water, anion (Br−) and methanol transport behavior. In the second part, we examine the effect of the cationic group position on a relatively long hydrophobic alkyl side-chain (16 carbon units) on the hydrophilic pathway morphology and water, anion and methanol diffusion coefficients at a constant hydration level. Also, we put forward a clear mechanism by which the position of QA on side-chains affects the anion transport. Our current study is focused on PPO-QA-based membranes; however, the resulting insight into the influence of structural parameters on transport properties and underlying mechanisms offers a rational molecular design strategy for new generations of polyelectrolyte membranes.
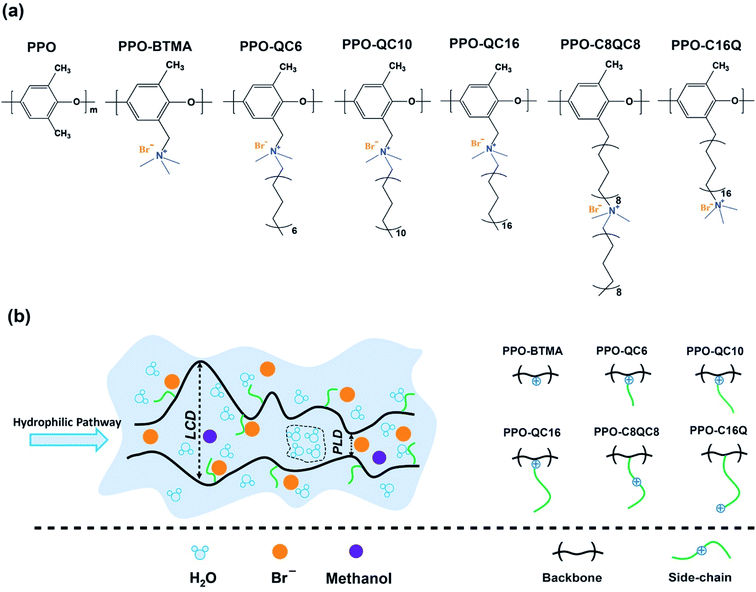
2 Methods
2.1 Molecular model approach
Model membranes consist of different types of cationic quaternary ammonium poly(2,6-dimethyl-1,4-phenylene oxide) (PPO-QA) random block-copolymers with a constant composition of 40% functionalized monomers and variable QA side-chain configurations in the presence of Br− ions. Monomers are functionalized by quaternary ammonium with and without an alkyl side-chain (0, 6, 10, and 16 carbon units) as extender, spacer, and spacer + extender attached to the cationic groups. Each polymer chain is constructed by 20 monomers, 8 of which are randomly functionalized by cationic quaternary ammonium. The chemical structure of different forms of functionalized and non-functionalized monomers of the PPO-QA chain is depicted in Scheme 1a. We named the membranes based on side-chain structure and position of cationic groups. For instance, PPO-BTMA stands for a polymer with cationic groups attached to the polymer backbone without an alkyl side-chain (n = 0), and PPO-C8QC8 refers to a polymer with a cationic group placed in the middle of the 16-carbon length alkyl side-chain.It is worth noting that our MD simulations utilize short polymer chains exhibiting enhanced end-group effects as compared to experimental systems with longer chains. However, all-atom MD simulations of polymer solutions with long chains are problematic since the chain structures do not equilibrate within the achievable duration of such simulations, which corresponds to a few hundreds of ns. Since we are not interested in the diffusive dynamics of the chains but rather in the diffusive dynamics of water and anions, and since the polymer solution structure does not depend much on chain length in the so-called semi-dilute solution regime,37 the chain length chosen by us should allow us to draw meaningful conclusions from our simulations. Also, an in-depth literature review of the recent works on similar systems shows that equal or even shorter polymer chain lengths are typically used in MD simulations.25,38–40 Simulations of hydrated membranes have been performed at different (intermediate) hydration levels in AEMs ranging from λ = 2 to 15, where λ is the number of water molecules per fixed ionic (quaternary ammonium) group. λ can be converted to water content (wt%) using eqn (1).
 | (1) |
2.2 Simulation details
Gromacs (version 2020-2)41 was employed for all MD simulations of AEMs using a leap-frog integration algorithm. We applied the OPLS-AA potential energy function,42 which has previously been effectively applied to polyelectrolytes,40,43–45 to define intermolecular bonded and non-bonded interaction parameters of AEMs. The individual partial charges of atoms in polyelectrolyte chains were assigned from DFT calculations using Gaussian 16 with the B3LYP method and 6-31++g(d,p) basis set, respectively.46,47 Partial charges of PPO-BTMA, as an example, are shown in Fig. S1 and Table S1 in the ESI.† The Particle Mesh Ewald (PME) method was employed in all runs to describe the long-range force of electrostatic interactions among partial charges with a cut-off distance of 1 nm. The van der Waals particle pair interactions are also described by the 12–6 Lennard-Jones potential, with the cut-off distance set at 0.9 nm. In addition, a TIP3P water model48 was selected owing to its fine reproduction of the diffusion coefficient. To accurately recover the density of the system, long-range dispersion and pressure corrections were applied. The LINCS algorithm was implemented to restrain covalent bonds of hydrogen atoms.49 Temperature and pressure are controlled using the V-rescale thermostat at 295 K and the Parrinello–Rahman barostat at 1 bar with a relaxation time of 0.1 ps and 2 ps, respectively. Finally, a time step of 2 fs was applied for the overall production run. The VMD software was used to create all simulation visualizations.50After the selection of appropriate methods and ensembles, the next critical stage is choosing the system size to avoid finite-size effects and inaccuracies of calculation. For this purpose, identical simulations were carried out for different box sizes with a varied number of polyelectrolyte chains, e.g., 20, 30, 40, 50, and 60 chains, and several structural and physical parameters were examined (see Fig. S2 in the ESI†). Analysis showed no specific discrepancy for the simulation boxes above 20 chains, so the system with 40 polymer chains was selected as an optimal system size to have a large enough system. The procedure of relaxation and simulation of the membranes is provided in the following section.
To construct the simulation box, 40 polyelectrolyte chains were added to a large enough cubic box with periodic boundary conditions in three dimensions to eliminate edge effects.51 Following that, 320 Br− ions and an appropriate number of water molecules depending on the defined hydration levels (λ) were dispersed randomly into the simulation box, so the system was totally uncharged. All system compositions are reported in Table S2 of the ESI.† The equilibration process is discussed in detail in the ESI† (Section 3). Equilibrated cell sizes were ∼6.2–8.2 nm with roughly 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 47
000 to 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms for different hydrated membranes. It should be noted that separate simulations, with 320 additional methanol molecules in each simulation box (for all AEMs), have been performed to assess methanol diffusion in comparison with water/ion diffusion. Each simulation was repeated three times, and an average of the results was reported with standard errors. Also, the last 5 ns of all production runs are ignored for all analyses.
000 atoms for different hydrated membranes. It should be noted that separate simulations, with 320 additional methanol molecules in each simulation box (for all AEMs), have been performed to assess methanol diffusion in comparison with water/ion diffusion. Each simulation was repeated three times, and an average of the results was reported with standard errors. Also, the last 5 ns of all production runs are ignored for all analyses.
Using the decay behavior of the time autocorrelation function of the squared radius of gyration, we characterized the relaxation properties of different polymer chains. The results are provided in the ESI in Fig. S3.† As shown in Fig. S3,† the squared radius of the gyration autocorrelation function dropped to zero in the early times of simulation, and all the samples show a relaxation time of less than 13 ns. These results indicate that the relaxation process was efficient. The 100 ns simulation time is long enough for the equilibration of the system and provides independent configurations for averaging the desired properties. All the samples followed a similar pattern at other hydration levels.
2.3 Analyses
A computational tool, Poreblazer (V4.0),52 has been used to characterize the porous membrane structure. Poreblazer provides several quantitative parameters of the porous polyelectrolyte matrix, including Largest Cavity Diameter (LCD), Pore Limiting Diameter (PLD), and Pore Size Distribution (PSD) that can be utilized for hydrophilic channel characterization. PLD and LCD are schematically depicted in Scheme 1b. For this purpose, first, we selected several frames of dried membrane for every 1 ns from 70 to 95 ns and reported an average of the calculated structural parameters with standard deviation.
| 〈(rj(t) − rj(0))2〉 = MSD(t) = 2dDt | (2) |
| 〈(rj(t) − rj(0))2〉 = MSD ∼ 2dDatn | (3) |
 | (4) |
3 Results and discussion
3.1 Validation of the simulations
To validate the selected force field and model membranes, we evaluated the dry mass density and water diffusion coefficient of hydrated membranes by reference experimental data.56 For instance, the dry mass density of PPO-BTMA obtained from the simulation was 1.25 g cm−3, which is in good agreement, i.e., less than 5% difference, with the experimentally reported value equal to 1.19 g cm−3. Also, the theoretical diffusion coefficients of water showed a similar trend in the range of the defined hydration levels. Density and diffusion data of experiments and simulations are provided in ESI Tables S3 and S4.† Therefore, the simulations are validated for further analysis based on the density and simulated diffusion results.3.2 Effect of the side-chain extender and hydration level
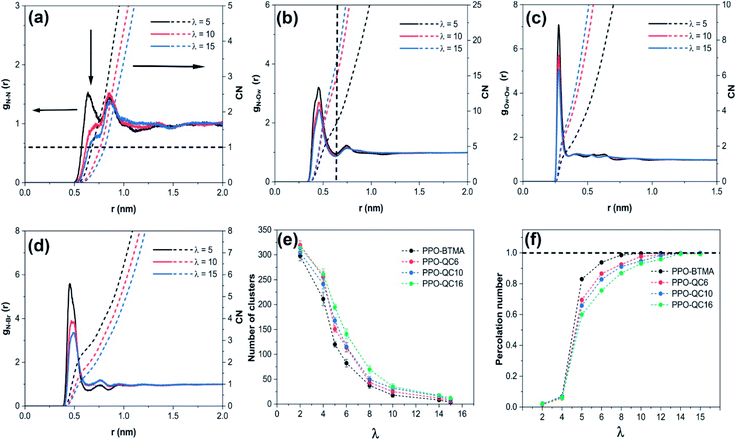
We investigated the radial distribution function of the N–Ow (water molecules), gN–Ow(r), and CN to study the structure of water channels and solvation of the N+ cationic groups in water (Fig. 1b). For all hydration levels, gN–Ow(r) for PPO-BTMA exhibits pronounced peaks commonly at ≈0.45 nm and ≈0.74 nm, which correspond to the first and second hydration shells surrounding the cationic group. Furthermore, when hydration increases, the peak height decreases owing to the solvation effect, as more water molecules seek to wet cationic groups. In addition, based on CN, the average number of water molecules around cationic groups increases from ≈8.5 to ≈18 as hydration increases from λ = 5 to λ = 15. A similar trend but with elevated peaks was observed for the other membrane with the increase in side-chain length, especially for PPO-QC16. The higher peaks at the same hydration levels are attributed to the stronger interaction between water molecules and QA. Steric hindrance exerted by the long side-chain extender holds water molecules near cationic groups for a more significant period and, on the other hand, fewer water molecules stand for longer times near cationic groups because of hydrophobic side-chain hindrance (Fig. S4 in the ESI†).
By using the radial distribution function of oxygen (water)–oxygen (water) (gOw–Ow(r)) and CN, we investigated the internal structure of water molecules at different hydration levels to study the water molecule's mutual tendency (Fig. 1c). As is evident, first, a distinct peak is observed at ≈0.27 nm for the PPO-BTMA membrane, which is ascribed to the first hydration shell of the water molecule around each water molecule. Second, CN increases with an increase in water content due to the solvation effect and overall packing of water molecules. Other membranes exhibited the same behavior but with a sharper peak height for membranes with longer side-chains (e.g., PPO-QC16) at constant hydration. This is attributed to more separated water molecules in the membrane network which shows that each water molecule holds fewer water molecules around itself (Fig. S4 of the ESI†).
Anion transport is another essential aspect controlling membrane efficiency. To further look into this, we analyzed gN–Br(r) and CN to study the correlation between cationic quaternary ammonium and Br− ions. As shown in Fig. 1d, at λ = 5 for the PPO-BTMA membrane, the first strong and second weak peaks emerged at ≈0.45 nm and ≈0.75 nm, respectively. An increase in hydration decreases peak height. It shifts it to a more distant position from ≈0.45 nm at λ = 5 to ≈0.50 nm at λ = 15, indicating that additional water molecules weaken electrostatic interactions between the cationic group and anions and move them to farther distances. This trend is comparable to that in other membranes; however, the first peak heights are stronger than those of other membranes in PPO-QC16 (see Fig. S4 in the ESI†), indicating that cationic groups and Br− ions have stronger electrostatic interaction again due to the presence of the alkyl side-chain extender that holds and hinders anions from moving from one cationic group to another.
We analyzed the number of clusters and cluster percolation thresholds to learn more about the hydrophilic channel nanostructure. Fig. 1e shows the number of clusters as a function of water content in different membranes. As shown, at e.g. λ = 5, small clusters of water molecules are entirely isolated. With the increase in hydration level in all membranes, water clusters grow and draw closer to each other, forming larger branches at high hydration levels. Accordingly, the number of clusters decreases. The PPO-BTMA membrane shows a smaller number of clusters at the same hydration level than other membranes. As discussed in Fig. 1c, fewer water molecules cover each other in the membrane with the largest side-chain extender resulting in smaller cluster size. Hence, to gain more insight into the formation of percolated water channels and the effect of quaternary ammonium position, we analyzed the normalized cluster size to study the percolation threshold of the water cluster:
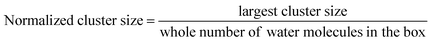 | (5) |
Here, the normalized cluster size is used to estimate the function of water molecules that form the largest hydrogen-bonded water network. A similar trend to the number of clusters is observed for other membranes. As shown in Fig. 1f, about 2% of water molecules in hydrated membranes belong to the largest cluster at very low hydration levels. All the membranes show substantial growth in cluster size at increasing hydration levels such that, at λ = 5, nearly 83% of water molecules belong to a single cluster in the PPO-BTMA membrane. In comparison, this number is less than 70% for the others. This trend continues up to λ = 10, where an almost complete hydrogen-bonded water cluster forms in PPO-BTMA and other membranes reach close to the percolation line at higher hydration levels. This means that forming a percolated water network depends on the water content and side-chain extender length.
To better visualize the water network morphology, typical simulation box snapshots of hydrated PPO-BTMA at different hydration levels are shown in Fig. 2a. These snapshots provide a nanoscale picture of water clustering inside the membrane, similar to the pictures that can be provided by cryogenic transmission electron microscopy (cryo-TEM)58 and X-ray computed tomography (CT)59 tools for hydrated membranes. It can be observed that small isolated clusters are distributed into the polymer matrix at the lowest water concentration, λ = 5. As the hydration increases up to λ = 15, small clusters grow, and the hydrophilic network is more interconnected, providing a fully developed hydrophilic domain for water and ion transport.
In what follows, we examine several geometrical factors contributing to water and anion diffusion, e.g., PLD, LCD, and PSD, as discussed in our recent work11 to further understand the water channel evolution in the polymer matrix function of water content and polymer architecture.
As previously stated, water molecules move from one pore to the next while passing through bottlenecks. The bottleneck size highly depends on water content and thermal fluctuations of polymer chains.60 PLD, the water channel bottleneck, is a critical diameter for water and ion diffusion. If PLD is larger than the water or Br− ion diameter, water and ions can pass from one pore to the next in cationic exchange membranes.11 Here, to trace the geometry of pores for water and anion diffusion, we defined PLD based on the selected water model and Br− ion diameter, i.e., ≈0.31 nm and ≈0.39 nm, respectively. As shown in Fig. 2b, the PLD of all membranes is far less than the critical diameter both for water and anions before λ = 8. But, PLD increases as hydration increases such that all membranes, except PPO-QC16, cross the PLD line of the water molecule at λ = 10, even though they are still smaller than the ion size. This means that Br− ions cannot freely move through all pores in the membrane.
Finally, all membranes pass the PLD line of the ion at λ = 15. Results for water are perfectly consistent with the number of clusters and normalized cluster size analyses, indicating that when PLD goes over the critical line, a noticeable shift in water channel structure occurs.
LCD is another critical parameter determining the maximum pore size in a heterogeneous polymer network. As shown in Fig. 2c, LCD increases in all membranes as water content rises so that all membranes have the largest LCD at λ = 15. This is attributed to the more extended polymer network because of higher water content. The similar trend of PLD and LCD as a function of hydration shows that the membrane's pore and bottleneck diameters grow with a more or less identical underlying process.
PSD is the final structural feature we wish to discuss to give a complete picture of the hydrophilic channel width distribution occupied by water and anions in a disordered polymer structure. Porous network transport properties are governed by the PSD and how pores are topologically structured, completing our diffusion picture in polymer membranes. The PSD variation of the PPO-BTMA membrane at different hydration levels is presented in Fig. 2d. A single narrow peak associated with the largest pore size exists in the heterogeneous structure, i.e., at 0.33 nm for λ = 5, which broadens in distribution and moves to farther distances with increasing water content, reflecting the presence of larger pores with different distribution forms in the structure. Similar trends are observed for other membranes (Fig. S5 in the ESI†). Increased hydration broadens the PSD and improves pore connectivity. It should be noted that in real applications, the chemistry and architecture of the polymer determine the amount of water taken up.61 Thus, the hydration level cannot be selectively adjusted under real conditions as is done in simulations. However, our selected range of hydration levels spans a typical range of hydration levels for this class of membranes.25,29,56,62 Thus, the morphological parameters of the hydrophilic pathway of membranes at their actual (and experimentally obtained) hydration level are accessible in the data shown in Fig. 2b–d.
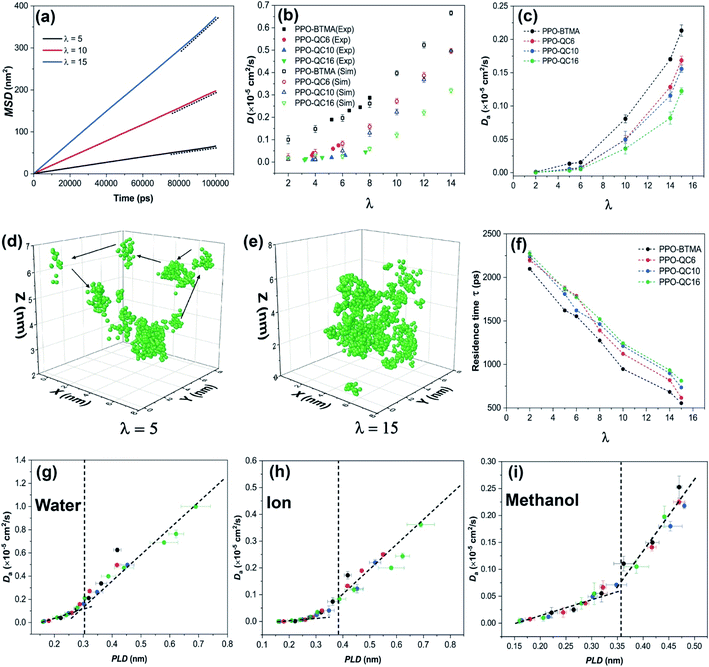 | ||
| Fig. 3 (a) MSD of water in PPO-QC16 at different hydration levels, (b) experimental diffusion coefficient56 and anomalous diffusion coefficient of water in hydrated membranes obtained from simulation, (c) anomalous diffusion coefficient of anions in hydrated membranes, (d and e) the trajectory of a single water molecule, respectively, at λ = 5 and λ = 15, (f) residence time of water near cationic groups at various hydration levels, and (g) anomalous diffusion coefficients of water, (h) the Br− ion and (i) methanol as a function of PLD. | ||
It has been proven that both water and ions show anomalous subdiffusion behavior in the polymer matrix.65,66 To gain a better insight into the transport behavior of water in PPO-QA membranes, we determined the anomalous diffusion exponent of water as a function of water content. Fig. S8a in the ESI† presents the anomalous diffusion exponent of water in the PPO-BTMA membrane at different hydration levels. As shown, anomalous diffusion exponents increase as time elapses. However, at λ = 5, the diffusion of water molecules in the membrane reveals anomalous subdiffusion characteristics with no apparent indicators of approaching the normal diffusion (n = 1). This behavior is attributed to the high tortuosity and isolated water clusters in polymer membranes preventing water molecules from being freely transported in water channels. At increasing hydration levels, the anomalous diffusion exponent comes closer to unity, where the water molecules may reach a diffusive limit (Fickian diffusion). However, the PPO-QC16 membrane follows a poor scenario, as shown in Fig. S8 of the ESI,† indicating that an anomalous diffusion exponent is more distant from the unity line even at long simulation times. It can be concluded that, as hydration increases and a well-developed water network forms, the transport behavior is less sensitive to the interaction of water and charged groups mediating normal diffusion. Another critical parameter is polymer proportion and chemical structure. Water diffusion in neutral polymers revealed that the strength of water molecule trapping in the polymer matrix could delay normal diffusion behavior to more extended periods, which are not usually accessible in MD simulations.67,68
To understand the origin of the non-Fickian behavior, a 10 ns single water trajectory at λ = 5 and λ = 15 in PPO-BTMA is shown in Fig. 3d and e. It can be seen that, at λ = 5, the trajectory of water molecules is more restricted at specific locations for a while and they jump to the next site, which is consistent with the reported jump-diffusion mechanism of water at low hydration levels.69 We hypothesize that these locations are isolated water clusters in which water molecules hop from one to the next due to temperature fluctuations. At λ = 15, on the other hand, the water molecules are more randomly distributed, and continuum mobility makes a significant contribution. Water molecules and ions have more freedom to traverse continuously along the polymer matrix.
To evaluate the influence of side-chain length on anomalous diffusion behavior, we measured the local residence time of water molecules near QA. Residence time relates to how long (on average) water molecules reside in the preset radial cut-off region around cationic groups. Using the radial distribution function, we set this cut-off to ≈0.61 nm, which corresponds to the first hydration shell radius around QA groups and is estimated by the first minimum of gN–Ow(r). The method of determining residence time is described in the ESI† (Section 10). According to Fig. 3f, all the membranes follow a decreasing trend as the hydration level increases. For instance, water molecules spend on average 1620 ps in the first hydration shell of the cationic groups in PPO-BTMA, while this time is 1866 ps for PPO-QC16 at λ = 5. This time decreases to 555 ps for PPO-BTMA and 812 ps for the PPO-QC16 membrane at λ = 15. Also, other membranes follow a moderate behavior.
Last, we summarize the discussion in this section by correlating water, ion, and methanol diffusion with PLD. PLD-Da data for all the membranes that have been studied so far are shown in Fig. 3g (Da of water molecules), Fig. 3h (Da of Br− ions), and Fig. 3i (Da of methanol molecules). The trends of both water and ion-related graphs are in full agreement with the hypothesis put forward for CEMs in a previous work:11 the critical role of PLD in controlling the diffusion coefficient of water and anions. This agreement shows that the morphology of the hydrophilic pathway plays a crucial role in maintaining ion transport for both CEMs and AEMs in a similar way.
As noted by other studies,70 methanol cross-over in AEMs has a detrimental effect on fuel cell performance; hence, one of the key roles of ion exchange membranes is to hinder the methanol cross-over. Thus, we studied methanol diffusion in similar systems but containing additional methanol molecules. As shown in Fig. 3i, a similar behavior was observed for the PLD-Da plot of methanol showing increased methanol diffusion coefficients as PLD crosses the critical value (an approximate methanol diameter is 0.36 nm (ref. 71)). According to this finding, methanol cross-over through the membrane increases as the hydrophilic channel width increases, in a manner that is comparable to that of water and ions.
We showed that increasing the hydration level significantly enhances the ion transport properties due to the formation of a more uniform and interconnected hydrophilic pathway. We also successfully examined the quantitative parameters in describing hydrophilic pathway morphology and correlated them to the water/ion diffusion coefficient for PPO-QA membranes. Moreover, we showed that alkyl side-chain extenders hinder water/ion transport through membranes, as evidenced by experiments.56 However, we proved that this is due to the morphological changes in the hydrophilic pathway so that alkyl side-chain extenders isolate QA groups from the water network, which results in isolated water clusters. On the other hand, when PLD rises, the methanol diffusion coefficient rises as well, which may restrict the performance of the membrane at very high hydration levels.
3.3 Effect of QA position on the alkyl side-chain
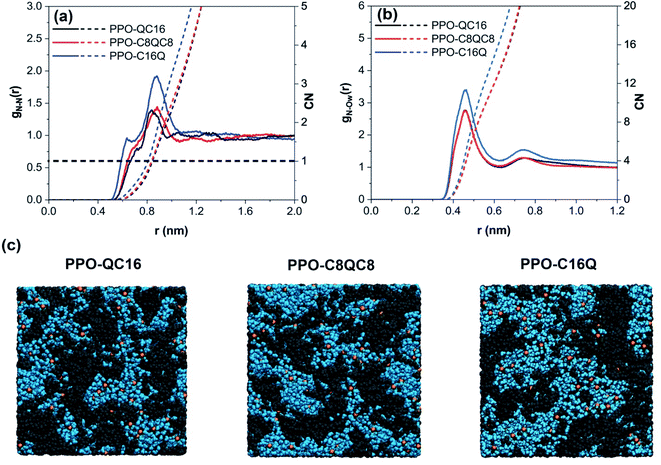
In this part, we aim to discuss the effect of the QA position, i.e., near the backbone, in the middle, and at the end of the alkyl side-chain, on the morphological and anion transport properties of the membranes. Note that PPO-QC16 represents a polymer with QA attached to the polymer backbone, PPO-C8QC8 represents a polymer with QA placed in the middle, and PPO-C16Q represents a polymer with QA at the end of the alkyl side-chain.First, we analyzed gN–N(r) and gN–Ow(r) to investigate the hydrophilic channel structure of various membranes. As shown in Fig. 4a and b, PPO-QC16 and PPO-C8QC8 show similar gN–N(r) and gN–Ow(r), while N+ in PPO-C16Q shows a much stronger interaction with other QA and water molecules. The position of N+ at the end of the alkyl side-chain results in pulling this group towards the water phase and placing more N+ groups at the polymer–water interface, as also discovered by SAXS analysis previously for similar membranes.30,32 Furthermore, the average number of water molecules around QA, the CN in PPO-QC16 and PPO-C8QC8 membranes (Fig. 4b), is less than λ (e.g., CN ≈ 13 at λ = 15), suggesting that some QA groups are located inside the polymer phase. However, in PPO-C16Q membranes, CN ≈ 16.8 and larger than λ = 15, implying that more QA is placed at the interface of the polymer and water. However, the typical simulation box snapshots shown in Fig. 4c suggest that the QA position has a negligible impact on the nano-phase separation between the polymer and water in the membranes.
We further analyzed the number of clusters of different membranes at λ = 15. As shown in Fig. 5a, the decrease in the number of clusters is also negligible as cationic groups move to the end of the alkyl side-chain. To quantify the hydrophilic pathway characteristics, we also looked at the PLD, LCD, and PSD of different membranes (Fig. 5b and c). As shown, they remain approximately constant with changing the position of the QA on the alkyl side-chain as well, which is in agreement with the qualitative perception of the hydrophilic membranes from Fig. 4c. We also analyzed the polymeric phase of the membrane by removing all polymer molecules and anions from the simulation box and calculating the PSD, this time for the polymeric phase. As depicted in Fig. 5d, the polymer region size distribution also shows no considerable change as the position of the QA is changed.
Therefore, these results confirm that the morphology of the membrane is more or less insensitive to the position of QA in a fixed side-chain length.
As shown in Fig. 5b, the hydrophilic channel width of the three membranes at λ = 15 is larger than that of all three diffusing species based on their previously mentioned sizes (i.e., water = 0.31 nm, Br− ion = 0.39 nm, and methanol = 0.36 nm). At the same time, the channel width is kept more or less constant by moving QA towards the end of the side-chain in similar membranes. As shown in Fig. 5e, the diffusion coefficients of the ion and water show a considerable enhancement as the QA group is moved towards the end of the side-chain. This is totally in line with a recent study,36 which reported enhanced ion mobility while the water channel width was found to be constant. Also, according to experimental studies,72 an increase in QA mobility inside the water channel could enhance the anion transport in the membrane. Therefore, we calculated the MSD of N+ in all membranes (Fig. 5f). Substantial growth is observed for MSD of N+ in the PPO-C16Q membrane as compared to the others, which is consistent with the suggestions from similar simulations and experimental results indicating that longer alkyl spacer chains are more flexible and enhance QA mobility.30,36 As the dynamics of N+ increase, more water molecules become available to N+, as also shown in Fig. 4b, enhancing water channel formation and increasing water and anion diffusion. Also, the anomalous diffusion exponent result (see Fig. 5g) suggests that PPO-OC16 and PPO-C8QC8 membranes show very similar behavior. In contrast, for PPO-C16Q, water diffusion showed a closer-to-normal diffusion behavior in shorter simulation times. In addition, the residence time of water and anions near QA groups (Fig. 5h) confirms our previous finding. An increase in the mobility of N+ decreases the residence time of the water/ion and facilitates their transport across the hydrophilic pathway. Thus, our study shows that moving the position of QA to the end of the alkyl side-chain enhances the anion transport but through a completely different mechanism. The hydrophilic pathway remains more or less similar, while the transport rate of the anion in the hydrophilic pathway is considerably enhanced as a result of the increased mobility of QA groups. In other words, our results suggest that while the morphologies of the membranes are similar, the longer spacer for QA groups results in a quicker hand-to-hand transport of anions due to the faster dynamics of QA and shorter residence time of anions close to QA groups in the hydrophilic pathway.
We also computed the diffusion coefficient of methanol for the three systems and our models show that it remains almost constant (Fig. 5e) despite the significant enhancement in the QA mobility (Fig. 5f). This is probably attributed to the less polar nature of methanol as compared to water and the Br− ion and accordingly weaker methanol–QA interaction so that the enhanced mobility of the pendant QA group does not affect the diffusion rate of methanol molecules in the channels. This is an interesting observation since it shows that one could enhance the ion conduction of these membranes by improving the QA group mobility while the methanol diffusion remains constant. This suggests that PPO membranes with pendant QA have a better ion/methanol selectivity as compared to PPO membranes without pendant QA.
4 Conclusion
In the current study, we conducted molecular dynamics simulations for hydrated PPO-QA-based AEMs to investigate the structure–diffusion relationship between them. The first aim of this work was to examine whether hydrophilic pathway morphology characteristics, i.e., PLD, LCD, and PSD, as described in ref. 11 for CEMs, are valid in describing the ion transport behavior of AEMs as well. We showed that the aforementioned characteristics are fairly able to describe the diffusion behavior of several PPO-QA membranes while the position of QA is fixed close to the polymer backbone. However, changing the position of QA on a long alkyl side-chain at constant hydration results in a significantly enhanced anion diffusion while the hydrophilic pathway morphological parameters remain almost constant. We showed that longer spacers for QA enhance the anion mobility in the water channels, thus affecting diffusion behavior by increasing the anion transport rate in the hydrophilic channels through enhanced QA dynamics but they have a negligible effect on the hydrophilic pathway morphology. Therefore, our findings suggest a two-stage strategy for designing polymer structures to be used as PPO-QA membranes: the polymer backbone in conjunction with the hydration level of the membranes determines the hydrophilic channel morphology while the QA spacers can tune the residence time and speed of anions in those channels. We also show that unlike polymer backbone modifications and increasing the hydration level (which increase ion and methanol diffusion more or less similarly), using a QA spacer does not increase the methanol diffusion rate despite the significant enhancement in ion mobility in the water channels. This is of great importance in the design of AEMs used for fuel cells in which the improvement in ion diffusion and controlling the methanol cross-over at the same time is a key requirement. It is worth emphasizing that our study puts forward a new methodology for assessing the effect of many material design strategies, like inclusion of nanoparticles, on the ion transport enhancement of IEMs to evaluate how they affect the hydrophilic channel morphology or ion transport rate in the channels.Conflicts of interest
We have no conflict of interest to declare.References
- Y. Leng, G. Chen, A. J. Mendoza, T. B. Tighe, M. A. Hickner and C.-Y. Wang, J. Am. Chem. Soc., 2012, 134, 9054–9057 CrossRef CAS PubMed.
- M. A. Abdelkareem, K. Elsaid, T. Wilberforce, M. Kamil, E. T. Sayed and A. Olabi, Sci. Total Environ., 2021, 752, 141803 CrossRef CAS PubMed.
- W. Wang, Q. Luo, B. Li, X. Wei, L. Li and Z. Yang, Adv. Funct. Mater., 2013, 23, 970–986 CrossRef CAS.
- T. B. Ferriday and P. H. Middleton, Int. J. Hydrogen Energy, 2021, 46, 18489–18510 CrossRef CAS.
- L. Li, J. Wang, L. Ma, L. Bai, A. Zhang, N. A. Qaisrani, X. Yan, F. Zhang and G. He, ACS Sustainable Chem. Eng., 2021, 46, 18489–18510 CrossRef.
- R. Zhang, Y. Chen, D. Troya and L. A. Madsen, Macromolecules, 2020, 53, 3296–3305 CrossRef CAS.
- J. Pan, S. Lu, Y. Li, A. Huang, L. Zhuang and J. Lu, Adv. Funct. Mater., 2010, 20, 312–319 CrossRef CAS.
- L. Hao, J. Liao, Y. Liu, H. Ruan, A. Sotto, B. Van der Bruggen and J. Shen, Sep. Purif. Technol., 2019, 211, 481–490 CrossRef CAS.
- M.-T. Lee, J. Phys. Chem. B, 2021, 125, 2729–2740 CrossRef CAS PubMed.
- A. Barnett, J. Lu and V. Molinero, J. Phys. Chem. C, 2021, 125, 27703–27713 CrossRef CAS.
- M. Rezayani, F. Sharif, R. R. Netz and H. Makki, J. Membr. Sci., 2022, 654, 120561 CrossRef CAS.
- L. Du, G. Zhang and S. Sun, Automotive Innovation, 2021, 4, 131–143 CrossRef PubMed.
- S. Lu, J. Pan, A. Huang, L. Zhuang and J. Lu, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20611–20614 CrossRef CAS.
- A. D. Mohanty, Y.-B. Lee, L. Zhu, M. A. Hickner and C. Bae, Macromolecules, 2014, 47, 1973–1980 CrossRef CAS.
- M. G. Marino, J. P. Melchior, A. Wohlfarth and K. D. Kreuer, J. Membr. Sci., 2014, 464, 61–71 CrossRef CAS.
- S. Chen, H. Wang, J. Zhang, S. Lu and Y. Xiang, J. Membr. Sci., 2020, 605, 118105 CrossRef CAS.
- C. Chen, Y.-L. S. Tse, G. E. Lindberg, C. Knight and G. A. Voth, J. Am. Chem. Soc., 2016, 138, 991–1000 CrossRef CAS PubMed.
- N. Chen and Y. M. Lee, Prog. Polym. Sci., 2021, 113, 101345 CrossRef CAS.
- M. Irfan, E. Bakangura, N. U. Afsar, M. M. Hossain, J. Ran and T. Xu, J. Power Sources, 2017, 355, 171–180 CrossRef CAS.
- H. Lim, B. Lee, D. Yun, A. Z. Al Munsur, J. E. Chae, S. Y. Lee, H.-J. Kim, S. Y. Nam, C. H. Park and T.-H. Kim, ACS Appl. Mater. Interfaces, 2018, 10, 41279–41292 CrossRef CAS PubMed.
- Z. Zhu, X. Luo and S. J. Paddison, Solid State Ionics, 2019, 340, 115011 CrossRef.
- J. Ran, L. Wu, Y. He, Z. Yang, Y. Wang, C. Jiang, L. Ge, E. Bakangura and T. Xu, J. Membr. Sci., 2017, 522, 267–291 CrossRef CAS.
- R. Gutru, Z. Turtayeva, F. Xu, G. Maranzana, B. Vigolo and A. Desforges, Int. J. Hydrogen Energy, 2020, 45, 19642–19663 CrossRef CAS.
- Q. Liu, Z. Wang, A. Yu, J. Li, H. Shen, H. Wang, K. Yang and H. Zhang, Int. J. Hydrogen Energy, 2021, 46, 24328–24338 CrossRef CAS.
- D. Dong, X. Wei, J. B. Hooper, H. Pan and D. Bedrov, Phys. Chem. Chem. Phys., 2018, 20, 19350–19362 RSC.
- A. Ding, J. Zhou, X. Cheng, C. Shen and S. Gao, J. Appl. Polym. Sci., 2021, 138, 50201 CrossRef CAS.
- J. Ran, L. Wu, Y. Ru, M. Hu, L. Din and T. Xu, Polym. Chem., 2015, 6, 5809–5826 RSC.
- S. A. Nunez, C. Capparelli and M. A. Hickner, Chem. Mater., 2016, 28, 2589–2598 CrossRef CAS.
- N. Li, Y. Leng, M. A. Hickner and C.-Y. Wang, J. Am. Chem. Soc., 2013, 135, 10124–10133 CrossRef CAS PubMed.
- H.-S. Dang and P. Jannasch, Macromolecules, 2015, 48, 5742–5751 CrossRef CAS.
- M.-T. Lee, J. Phys. Chem. C, 2020, 124, 4470–4482 CrossRef CAS.
- H.-S. Dang, E. A. Weiber and P. Jannasch, J. Mater. Chem. A, 2015, 3, 5280–5284 RSC.
- L. Li, J. Wang, M. Hussain, L. Ma, N. A. Qaisrani, S. Ma, L. Bai, X. Yan, X. Deng and G. He, J. Membr. Sci., 2021, 624, 119088 CrossRef CAS.
- X. Chu, J. Liu, S. Miao, L. Liu, Y. Huang, E. Tang, S. Liu, X. Xing and N. Li, J. Membr. Sci., 2021, 625, 119172 CrossRef CAS.
- H.-S. Dang and P. Jannasch, J. Mater. Chem. A, 2016, 4, 17138–17153 RSC.
- A. Barnett, J. Lu and V. Molinero, J. Phys. Chem. C, 2021, 125, 27693–27702 CrossRef CAS.
- P.-G. De Gennes and P.-G. Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, 1980 Search PubMed.
- W. Zhang, D. Dong, D. Bedrov and A. C. T. Van Duin, J. Mater. Chem. A, 2019, 7, 5442–5452 RSC.
- B. A. Paren, B. A. Thurston, A. Kanthawar, W. J. Neary, A. Kendrick, M. Maréchal, J. G. Kennemur, M. J. Stevens, A. L. Frischknecht and K. I. Winey, Chem. Mater., 2021, 33, 6041–6051 CrossRef CAS.
- A. L. Frischknecht, P. J. in’t Veld, I. V Kolesnichenko, D. J. Arnot and T. N. Lambert, ACS Appl. Polym. Mater., 2022, 4, 2470–2480 CrossRef CAS.
- E. Lindahl, B. Hess and D. Van Der Spoel, J. Mol. Model., 2001, 7, 306–317 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS PubMed.
- P. Batys, Y. Zhang, J. L. Lutkenhaus and M. Sammalkorpi, Macromolecules, 2018, 51, 8268–8277 CrossRef CAS PubMed.
- R. Zhang, X. Duan, M. Ding and T. Shi, J. Phys. Chem. B, 2018, 122, 6656–6665 CrossRef CAS PubMed.
- B. A. Paren, B. A. Thurston, W. J. Neary, A. Kendrick, J. G. Kennemur, M. J. Stevens, A. L. Frischknecht and K. I. Winey, Macromolecules, 2020, 53, 8960–8973 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- T. E. Gartner III and A. Jayaraman, Macromolecules, 2019, 52, 755–786 CrossRef.
- L. Sarkisov, R. Bueno-Perez, M. Sutharson and D. Fairen-Jimenez, Chem. Mater., 2020, 32, 9849–9867 CrossRef CAS.
- S. Das, Functional Fractional Calculus, Springer, 2011, vol. 1 Search PubMed.
- L. Masaro and X. X. Zhu, Prog. Polym. Sci., 1999, 24, 731–775 CrossRef CAS.
- R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Phys. Chem. Chem. Phys., 2014, 16, 24128–24164 RSC.
- L. M. Thieu, L. Zhu, A. G. Korovich, M. A. Hickner and L. A. Madsen, Macromolecules, 2018, 52, 24–35 CrossRef.
- L. Zhu, J. Pan, Y. Wang, J. Han, L. Zhuang and M. A. Hickner, Macromolecules, 2016, 49, 815–824 CrossRef CAS.
- F. I. Allen, L. R. Comolli, A. Kusoglu, M. A. Modestino, A. M. Minor and A. Z. Weber, ACS Macro Lett., 2015, 4, 1–5 CrossRef CAS PubMed.
- S. Kato, S. Yamaguchi, W. Yoshimune, Y. Matsuoka, A. Kato, Y. Nagai and T. Suzuki, Electrochem. Commun., 2020, 111, 106644 CrossRef CAS.
- F. Müller-Plathe, J. Membr. Sci., 1998, 141, 147–154 CrossRef.
- K. B. Daly, J. B. Benziger, P. G. Debenedetti and A. Z. Panagiotopoulos, J. Phys. Chem. B, 2013, 117, 12649–12660 CrossRef CAS PubMed.
- L. Zhu, T. J. Zimudzi, N. Li, J. Pan, B. Lin and M. A. Hickner, Polym. Chem., 2016, 7, 2464–2475 RSC.
- E. Lin, X. You, R. M. Kriegel, R. D. Moffitt and R. C. Batra, Comput. Mater. Sci., 2017, 138, 448–461 CrossRef CAS.
- P. Batys, S. Kivistö, S. M. Lalwani, J. L. Lutkenhaus and M. Sammalkorpi, Soft Matter, 2019, 15, 7823–7831 RSC.
- Q. Berrod, S. Hanot, A. Guillermo, S. Mossa and S. Lyonnard, Sci. Rep., 2017, 7, 8326 CrossRef PubMed.
- A. Sharifi-Viand, M. G. Mahjani and M. Jafarian, J. Electroanal. Chem., 2012, 671, 51–57 CrossRef CAS.
- F. Müller-Plathe, J. Chem. Phys., 1998, 108, 8252–8263 CrossRef.
- F. Müller-Plathe, Acta Polym., 1994, 45, 259–293 CrossRef.
- V. Molinero and W. A. Goddard III, Phys. Rev. Lett., 2005, 95, 45701 CrossRef PubMed.
- Y. Lu, X. Pan, N. Li, Z. Hu and S. Chen, Appl. Surf. Sci., 2020, 503, 144071 CrossRef CAS.
- Y. Tang, D. Dubbeldam and S. Tanase, ACS Appl. Mater. Interfaces, 2019, 11, 41383–41393 CrossRef CAS PubMed.
- M.-T. Lee, J. Phys. Chem. C, 2019, 123, 10802–10815 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ta04400e |
| This journal is © The Royal Society of Chemistry 2022 |