Li trapping in nanolayers of cation ‘disordered’ rock salt cathodes

Abstract

Disordered rock salt (DRS) cathodes have attracted considerable attention because of their high first charge capacities and relatively low cost. Here we investigate operando the structure and charge evolution of the Li_1.1Mn_0.7Ti_0.2O₂ Li-excess rock salt cathode with a first charge capacity of 270 mA h g⁻¹. We associate a certain extent of the capacity fade in DRS to the in situ formation of locally ordered layered nanodomains during the electrochemical cycling of the long-range cation disordered rock salt. We quantify the short-range ordering of cations during cycling and evaluate its effect on the lithium-ion diffusion and charge compensation using operando studies based on X-ray total scattering and advanced spectroscopic methods at the Mn K-edge, namely high energy resolution fluorescence detected XANES and emission spectroscopies including main and valence-to-core transitions.

---

Introduction

There is an intensifying demand for high-performance Li-ion batteries for their application in mobile devices, electric-powered vehicles, and energy storage systems to enable transformational carbon-neutral solutions.¹ Within the Li-ion cell, the cathode material currently limits the energy density and dominates the battery cost.² Improving the capacity and longevity performance of Li-ion cathode materials remains a significant challenge for the battery community. In recent years, there has been a surge of interest in Li-rich cathodes with a cation Disordered Rock Salt (DRS) structure which where once thought to be electrochemically inactive.³ DRS offers a tantalizing promise for high-energy-density Li-ion batteries with capacities beyond 300 mA h g⁻¹, low percolation energies of 3D Li-diffusion paths and absence of phase transformations during cycling.^4,5

In a recent study we identified an improved electrochemical performance of a nanostructured Li₂MnO₃ (nano- Li₂MnO₃) DRS cathode material displaying reversible capacities of 290 mA h g⁻¹ for over 10 cycles;⁶ whilst its crystalline counterpart, the well-researched Li₂MnO₃, displays a 50% capacity drop over the first five cycles.⁷ A joint neutron and X-ray total scattering approach evidenced a phase transformation during a high energy ball milling process, where Li₂MnO₃ synthesized at 900 °C with a layered structure (C2/m) transformed into a nanostructured and disordered cubic MnO-type rock salt (Fm3̄m). Interestingly, the well-known layered-to-spinel phase transformation of Li and Mn-rich layered cathodes⁸ could not explain the diffuse scattering reflections in nano-Li₂MnO₃ that were instead attributed to the formation of a short-range ordered superstructure due to the Li/Mn layering of ∼1 nm into alternating (111) planes in the rock salt structure, as previously reported in Li_xNi_2−xO_2.32.⁹

Other work identified short-range-ordering (SRO) in further DRS compositions which breaks the general assumption that all the cations are randomly distributed in these cathode materials. In Li_1.25Nb_0.25Mn_0.5O₂,¹⁰ the Li/(Nb, Mn) cations order in an ABAB sequence parallel to both [110] and [−110] of the rock salt sublattice resulting in a tetragonal I4₁/amd structure displayed by γ-LiFeO₂.¹¹ The correlation length of Li/(Nb, Mn) ordering was found to depend on the synthesis conditions, and had negative implications for the electrochemistry of these phases with a decrease of the first charge capacity by 5% and an increase of the capacity fade by 8% when the correlation length of SRO domains was increased from 1 to 13 nm.

DRS compositions containing several transition metal species including electrochemically inactive transition metals with a d⁰ electronic configuration have been extensively investigated. The presence of d⁰ transition metals can stabilize disordered structures,^12–14 and their ionic character can also stabilise the superoxide species formed during charge.^15–19 Within this group of DRS, Li_1.2Mn_0.4Ti_0.4O₂ displayed a superior electrochemical performance¹⁵ compared to the isoelectronic Zr⁴⁺-doped Li_1.2Mn_0.4Zr_0.4O₂. This result is counterintuitive as the performance of the Zr-doped rock salt is expected to be better based on its larger lattice parameters, which generally benefits Li diffusion. Here, the different electrochemical performance was reported to be due to different and more pronounced SRO of the Zr-doped rock salt.²⁰

In this work, we investigate operando the evolution of the average structure, SRO, and charge during the electrochemical cycling of a Li-excess Ti⁴⁺-doped DRS with composition Li_1.1Mn_0.7Ti_0.2O₂ (LMTO). Pristine LMTO did not show significant SRO, as the presence of the Ti⁴⁺-dopant aids to stabilize the disorder in the structure. However, during electrochemical cycling, we identify the appearance of diffuse peaks in the Bragg data which matched the SRO previously observed in nano-Li₂MnO₃.⁶ During the electrochemical cycling, the cation rearrangements in LMTO form in situ a SRO superstructure with nanodomains of Li:M layering, where M = Ti and Mn, that continue to grow over the first few cycles (up to 15 investigated in this work). Cation SRO, amid other subtle structural changes, has a profound effect on the population and connectivity of Li-migration channels and influence the electrochemical performance of DRS as a result. We have investigated the impact of these layered nanodomains on the material's electrochemical performance through a combination of total scattering and advanced X-ray spectroscopic techniques including High Energy Resolution Fluorescence Detected (HERFD-)XANES and emission spectroscopies including main, and valence-to-core (V2C) transitions performed operando. We identify the trapping of Li in the layered domains of DRS as a significant source of capacity fade alongside contributions from oxygen redox irreversibility. These results indicate the importance of SRO and provide another important handle to tailor the performance of DRS cathode materials. The results of this study provide insight into the relationship between the local chemistry and Li transport properties in DRS, enabling future design of better-performing cathode materials.

Results

Synthesis and electrochemical activity

We synthesized Li_1.1Mn_0.7Ti_0.2O₂ using the solid-state method proposed for Li_1.2Mn_0.4Ti_0.4O₂.²⁰ We identified TiO₂ impurities for Li_1+xMn_1−3xTi_2xO₂ with x > 0.1 and the x = 0.1 composition (hereafter referred to as LMTO) was used in the study (see Pawley fit in Fig. 1a). LMTO delivers a large first-cycle capacity of 270 mA h g⁻¹ (0.9 Li⁺ f.u.) as shown in the galvanostatic voltage profile in Fig. 1b. The sloped galvanostatic voltage profile is consistent with those of other cation DRS materials. LMTO displays an irreversible capacity of 30 mA h g⁻¹ (0.1 Li⁺ f.u.) after the first charge, after which the capacity is stable at around 240 mA h g⁻¹ (0.8 Li⁺ f.u.) with a further decrease at a slower rate of 17 mA h g⁻¹ (0.6 Li⁺ f.u.) for 15 cycles tested.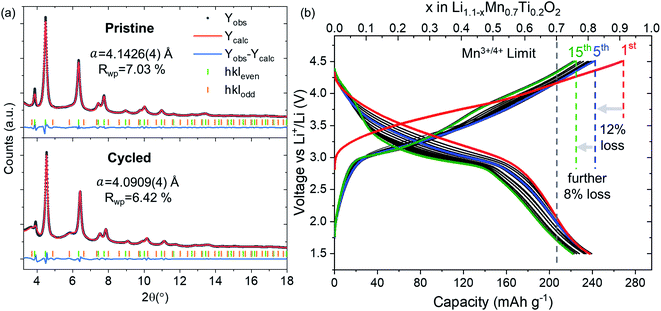

Fig. 1 Characterisation of LMTO. (a) Pawley fits of pristine (top) and cycled compositions (bottom) using an hkl-dependent model. These fits correspond to the first (t = 0 h, 2.8 V) and last (t = 37 h, 3.24 V) points of the operando Bragg data in Fig. 2. (b) Galvanostatic cycling at a rate of C/20.

Structural evolution during battery cycling

Previous work by Ji et al.²⁰ reports diffuse scattering patterns surrounding the Bragg reflection spots in electron diffraction patterns of a crystalline Li_1.2Mn_0.4Ti_0.4O₂ sample synthesized at high temperatures, suggesting the existence of SRO. In this work, we investigate the ball-milled LMTO electrode, and the extent of structural disorder after the milling is such that the structural characterization by electron diffraction is inhibited. Instead, we investigate the SRO in LMTO by total scattering analysis, combining Bragg and PDF data. The evolution of broad diffuse scattering features in the data could be successfully identified owing to the accurate background subtraction allowed by the DRIX electrochemical cells.²¹

While the Bragg data of pristine LMTO can be well explained with the average DRS model, broad diffuse scattering peaks appear during the first charge, which continued to increase in intensity during the subsequent (dis)charge cycles. Such diffuse scattering peaks have previously been attributed to the formation of a second phase in other work.²² However, these diffuse peaks could be explained by the formation of a SRO superstructure with nanodomains of Li/M layering into alternating (111) planes in the rock salt structure, as previously reported in materials such as Li_xNi_2−xO₂ (ref. 9) and nano-Li₂MnO₃.⁶ Both sets of broad and sharper reflections, corresponding to the layered (R3̄m) and DRS (Fm3̄m) sublattices, respectively, were fitted using the rhombohedral model. In the hexagonal unit cell description, reflections derived from the cubic structure have Miller indices with even values of l (hkl_even), whereas hexagonal reflections that are forbidden in the cubic unit cell, but arise due to Li and Mn layering, exhibit odd values of l (hkl_odd).⁹ The double-Voigt approach²³ was used to estimate the structural coherence of the layered and DRS components based on the peak broadening of hkl_odd and hkl_even reflections, respectively. This refinement approach allowed us to estimate the average crystallite size of the nanostructured material to be 4.6(2) nm, and the extent of Li/M layering to be 0.50(7) nm, which approximately equals four alternative layers of Li and M.

Operando Bragg data of LMTO cycled over the potential window of 1.5–4.5 V over the course of two charge–discharge cycles and a subsequent cycle discharged down to 3.2 V are shown in Fig. 2. The evolution of the lattice parameters (Fig. 2b) is in good agreement with the expected breathing behaviour of the cubic M framework of DRS with the lattice parameters contracting from 4.1426(4) Å in the lithiated compound to 4.0358(4) Å upon delithiation.

Fig. 2 LMTO structural evolution. (a) Electrochemical performance, (b) lattice parameters and (c) structural coherence of the layered sublattice from a sequential refinement. The fits for the first and last datasets are given in Fig. 1. (d and e) Operando Bragg data showing the increased intensity of the (101) and (107) SRO superstructure peaks with cycling.

Diffuse peaks in the pristine LMTO composition increase in intensity during battery cycling, as shown in Fig. 2d and e. We have performed a sequential refinement of the Bragg data to quantify the increase in the structural coherence of the layered nanodomains (see Fig. 2c). The Bragg refinement of operando data shows that during cycling, there is a steady increase of the layered nanodomain size of approximately 17% per half cycle over the course of the first two cycles.

The structural coherence of the layered domains was further investigated ex situ after 7 and 15 cycles (see Fig. S1†). The refined structural coherence of the layered domains of 1.0(2) and 2.25(9) nm after 7 and 15 cycles, respectively corresponds to a growth rate of 21(1)%, congruent with the growth rate observed operando. Thus, the SRO nanolayers at the initial stages of cycling evolve into long-range ordered domains after several cycles.

Li transport in LMTO. To investigate the effect of SRO on the diffusion of Li, we first need to produce physically sensible atomistic models of LMTO for the layered and DRS local environments. Supercells were produced by doubling the average structural models extracted from the refinement of Bragg data in every direction and were refined against the PDF data without any symmetry constraints. To force chemically sensible coordination environments, electrostatic potentials were used as penalty functions between Li, Mn, Ti and their neighbouring oxygen sites (more details about the refinements are provided in the Experimental section). Five different supercells with random substitutional disorder on the cation sites were produced for each layered and DRS models. Note the distribution of cations in our models is in good agreement with that of the probabilistic limit, as shown in Fig. S2.† Each refinement produced a good fit to the PDF data (see Fig. 3 and S3†). Therefore, the results from the five supercells for each layered and DRS models were averaged to improve the statistical quality of this study.

The refined atomistic models were analysed by the bond valence site energy (BVSE) approach,²⁴ where potentially accessible sites for lithium are identified by the calculation of the mismatch of the bond valence sum with respect to Li⁺ formal valence. The BVSE approach exploits the analogy between the squared bond valence mismatch and the Morse-type potential to transform valence into energy units.²⁵Fig. 3 shows graphical representations of isosurfaces in which Li⁺ could diffuse according to this method. The importance of basing BVSE calculations in atomistic models becomes clear when comparing the percolated volume fraction of average structural models of around 5%, which increases to 8.1(5) and 9(2)% for the layered and DRS models, respectively. The BVSE maps in Fig. 3 reveal the expected 3D Li diffusion for the DRS model, and 2D Li diffusion for the layered domains, where for both sublattices Li diffusion occurs along tetrahedral sites. To further analyse the Li transport environments in the two sublattices of the LMTO structure, we have quantified the variation of Li-diffusion energy barriers as a function of the number of M within the vicinity of the tetrahedral sites that participate in the Li diffusion.²⁶Fig. 4 summarizes the occurrence of tetrahedral cluster types as a function of M = Ti and Mn, and Li neighbours (M₄, LiM₃, Li₂M₂, Li₃M and Li₄) in layered and DRS domains. The tetrahedral cluster occurrence follows a standard distribution in the disordered model centred around the Li₂M₂ clusters. In the layered model, LiM₃ and Li₃M sites are favoured as expected since these are the only two sites present in stoichiometric LiMO₂ (see Fig. S4†). The different distribution of tetrahedral clusters in Fig. 4 indicates that the induced SRO during cycling of LMTO strongly modifies the population of local tetrahedral clusters. Despite the different cluster distribution, the calculated energies of each cluster type are similar in both models, as shown in Fig. 4a, which is indicative of the cluster energy strongly depending on the closest neighbours within the tetrahedra and not on the extended structure. Therefore, we consider occurrence of clusters and their distribution within a percolating network as the primary factors to sustain the migration of Li⁺ cations throughout LMTO.

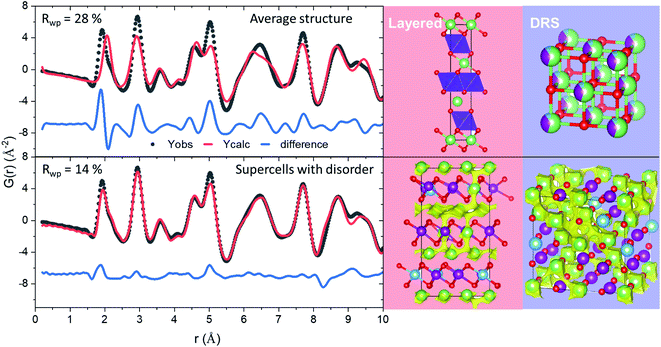Fig. 3 Local structure and Li diffusion of pristine LMTO based on structures derived from PDF refinement with electrostatic potential constraints. Left: Magnified view of the short r-range of the PDF refinements (to see the whole r-range used in the refinements the interested reader is referred to Fig. S5†) Right: Refined average structural models (top) and supercells of atomistic disorder (bottom). The compositions for the refined supercells are Li₁₈Mn₁₁Ti₃O₃₂ and Li₂₆Mn₁₇Ti₅O₄₈ for the disordered and layered models, respectively. Green, purple, blue and red spheres denote Li, Mn, Ti and O, respectively. The yellow isosurfaces represent the regions with a constant BVSE of −2.2 eV energy threshold.

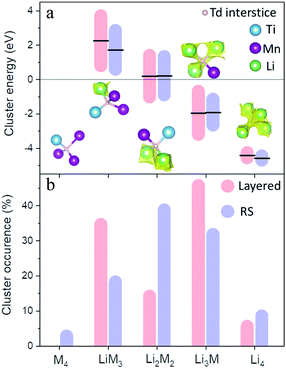Fig. 4 Cation clusters energy from the refined models in Fig. 3 (a) and probabilistic occurrence (b) in disordered (blue) and layered (red) LMTO.

We observe that the occurrence of Li₄ tetrahedra of 8.5%, which is the most important for good Li transport, is larger in the disordered model (against 5.5% in the layered model). In addition, the migration barrier through the Li₄ tetrahedra in the disordered model is on average 170 meV lower than that of the layered model, further aiding the Li₄-mediated Li diffusion in the disordered sublattice. On the other hand, the occurrence of Li₃M tetrahedra, whose range of energies partially lie below the energy threshold for Li-mobility of −2.2 eV, is higher in the layered (45.7%) than in the disordered model (31.8%). Therefore, to fully address the lithium migration in LMTO, we must also consider the distribution and evolution of the Li₄ and Li₃M tetrahedra with suitable Li migration barriers in both layered and DRS sublattices.

In other systems, the complete depletion of lithium from layered structures (R3̄m) is known to increase the repulsive interactions between adjacent layers of MO₂, which in turn results in oxygen loss and structural rearrangements where the layered structure tends to transform into a mixture of spinel and rock salt phases.^27,28 The decomposition of LMTO into other phases is not observed in this study, where changes in the structure with cycling entail an isotropic breathing of the cubic framework. This could indicate that the complete depletion of lithium between the MO₂ slabs in the layered nanodomains is not reached and the growth of these domains with the cycling is thereby acting as a Li trap (a structural feature that irreversibly immobilises Li⁺-ions), which correlates with the decay of the capacity with cycling. The formation of layered domains results in a higher occurrence of LiM₃ clusters where lithium becomes trapped away from the lithium percolation pathway where it was originally connected to.

Charge evolution during battery cycling

The charge evolution and coordination environment of electrochemically active Mn³⁺ were studied operando over the course of the first charge–discharge cycle.

Mn K-edge HERFD-XANES data provide information on the evolution of the local environment around MnO₆. The data in Fig. S6† show the expected evolution for Li–Mn–O rock salts in previous work,⁶ which are (1) fading of the shoulder in the white line transition due to change in composition and (2) increase of intensity of the e_g transition attributed to Mn³⁺ to Mn⁴⁺ oxidation. In this new experiment, the improved sensitivity of HERFD-XANES gave better resolved pre-edges, in which we clearly distinguish the quadrupole transitions toward the t_2g and e_g states, whereas conventional XANES shows a partial overlap of the e_g state with the white line.^29,30 HERFD-XANES data show an increase in the intensity of the e_g transition during the charge that could correspond to the emptying of electrons in the corresponding level because of the oxidation of Mn³⁺ (d⁴) to Mn⁴⁺ (d³). However, since the position and shape of the absorption edge are strongly influenced by structural effects due to the large overlap between the outer 4p orbitals of Mn and the oxygen ligands, the charge evolution of Mn was further investigated by the combined interpretation of main and V2C emission transitions (see Fig. S7†). Here, the main XES 3p-1s energy transition serves as a better probe of the number of unpaired 3d electrons in Mn, which are indirectly inferred from the magnitude of 3p–3d exchange interactions. In addition, the V2C energy transitions from hybridized Mn–O orbitals were recorded during the same experiment to further aid the identification of changes in the charge density and coordination environment of both Mn and the oxygen ligands.

Fig. 5 shows the comparison of the most intense kβ_1,3 and of kβ_2,5 of the main and V2C transitions respectively, as a gauge of the Mn oxidation state at different states of charge. The energy transitions of MnO₂ and Mn₂O₃ standards are given in the same figure for reference. In contrast with the high reversibility of HERFD-XANES transitions in the charge and discharge states, both kβ_1,3 and Kβ_2,5 transitions that were measured operando during the same experiment show some irreversibility on the reduction of Mn⁴⁺ to Mn³⁺ during the discharge. Based on the energy of the kβ_1,3 transition, and the linear response of this transition with the change in the oxidations state,³⁰ we estimate that 13% of manganese remains as Mn⁴⁺ in the cycled composition, which amounts to approximately 0.09 Mn per f.u.

Fig. 5 (a) kβ_1,3 and (b) kβ_2,5 XES transitions at t = 0, 16 and 28 h, corresponding to 2.4, 4.4 and 1.5 V respectively.

The irreversible charge evolution of Mn which is not appreciable by XAS, can be detected by XES and could be ascribed to the loss of accessible cation vacancy sites in the layered domains for the reincorporation Li⁺-ions during discharge.

Discussion

Capacity fade in DRS is generally associated to the lack of reversibility of oxygen redox. Here we use the results of our LMTO study in combination with other reported systems to explore the impact of the SRO evolution during cycling with a drop in capacity. We aim to compare the performance of LMTO to DRS with different extents of oxygen redox participation and SRO.

Fig. 6 summarises the theoretical, 1st charge capacity and capacity fade rate of cathode materials cycled in half cells at room temperature. We compare the reported performance of cathode materials with no extra capacities (LiFePO₄,³¹ LiCoO₂,³¹ NMC811 (ref. 32) and NMC311 (ref. 32)) to DRS cathodes with different extents of oxygen participation ranging from 25 to 100% of the extra capacities beyond the theoretical value given by the transition metal redox limit. As shown in Fig. 5, the higher 1st charge capacities of DRS are accompanied by a higher rate of capacity fade. While the capacity fade of cathode materials with no oxygen redox typically ranges from 0.2 up to 0.5%, the typical value of DRS is around one order of magnitude higher.

Fig. 6 Comparison of the theoretical capacities based on TM redox, experimental 1st charge capacities and capacity fade%. The experimental values were obtained in half cells cycled at room temperature,^{6,10,20,31,32} and the theoretical capacities were calculated using the transition metal redox activity.

We can further compare the performance of two DRS compositions in the LMTO system with different extent of O redox participation; Li_1.2Mn_0.4Ti_0.4O₂ (reported in this work) and Li_1.1Mn_0.7Ti_0.2O₂.²⁰ To calculate the expected capacity fade in Li_1.1Mn_0.7Ti_0.2O₂, we subtract the typical capacity fade value of 0.4% ascribed to other mechanisms than anion redox in Li_1.2Mn_0.4Ti_0.4O₂ and assume that the remaining capacity loss is due to oxygen redox. This calculated expected capacity fade has a value of 0.97% in Li_1.1Mn_0.7Ti_0.2O₂, which is significantly lower than the observed value of 1.9%. Such higher-than-expected capacity fade could be linked to the formation and growth of layered domains during the initial charge–discharge cycles. The results for the LMTO system agree with previous work on a DRS cathode material with composition Li_1.25Nb_0.25Mn_0.5O₂ (LNbMO), where the coherence length of the layered sublattice was successfully controlled by the change of the synthetic conditions. Slowly cooled LNbMO resulted in a DRS structure containing layered domains with a structural coherence of 12.5 nm, whereas the structural coherence of the layered domains in rapidly cooled LNbMO was only 1 nm. This work demonstrated a better capacity retention of LNbMO (−1.9%) vs. LNbMO with SRO (−2.9%). However, the study did not show the structural evolution of the ordered domains with battery cycling. As shown in this work, the structural changes during (de)lithiation can impact the structural coherence of these domains, and their correlation with the capacity should be also investigated during battery cycling. Future work in DRS should not only focus on the stabilization of oxygen redox to improve the capacity fade of DRS, but also to control the structural coherence of SRO domains both during the synthesis and their evolution with cycling.

We recently identified the presence of SRO in the nano-Li₂MnO₃ cathode material with an average DRS structure and a high first charge capacity of ca. 335 mA h g⁻¹. In nano-Li₂MnO₃, layered domains of 1 nm were already present in the pristine structure and their structural coherence remained constant during the first charge–discharge cycle.⁶ In pristine LMTO, cation SRO was inhibited by the presence of electrochemically inactive Ti⁴⁺ which stabilised the formation of a disordered structure.^12,14 However, during electrochemical cycling the SRO nanolayers were formed, which indicated that unfavourable cation rearrangements can still occur in spite of the presence of Ti⁴⁺ acting as a stabiliser of disorder in DRS.

While the growth of layered domains could be associated with a higher capacity fade in Li_1.1Mn_0.7Ti_0.2O₂vs. Li_1.2Mn_0.4Ti_0.4O₂, we believe there are qualities of the layered materials such as their inherently high capacity and rate capability that could benefit the performance of DRS cathode materials. As a matter of fact, the interplay between DRS and layered sublattices was recently exploited to enhance the performance of a Li_1.2Ni_0.4Ru_0.4O₂ cathode with a layered R3̄m structure and rock salt (Fm3̄m) domains.³³ Although containing only 30 mol% of the rock salt domains, Li_1.2Ni_0.4Ru_0.4O₂ displays isotropic structural changes resembling those of ‘pure’ DRS, as the interwoven rock salt structure prevents the anisotropic structural change that is typical for layered oxides. The Li_1.2Ni_0.4Ru_0.4O₂ cathode displays a preferred extraction of Li⁺ cations from the rock salt rather than layered phase, whilst the layered structure is believed to facilitate extraction of Li⁺ from the intergrown rock salt thanks to the 2D Li⁺ diffusion along the layers. Understanding the interplay between the layered and disordered sublattices, how they can be controlled during synthesis and their evolution with cycling is critical to harness the favoured figures of merit from each layered and disordered component and design better cathode materials that meet industrial demands for performance.

Strategies for improvement

We believe future work in DRS could be aimed at controlling the coherence length of layered domains during cycling either through the control of the particle size or the structural coherence of the layered domains. If the layered domains continue to grow during cycling, we will ultimately have a phase transition into a layered structure, which is not experimentally observed. Thus, there must be a limit value the layered domains will grow up to. Further work is needed to find the effect of particle size and the limit of growth of layered domains in each DRS system to inform future synthesis of DRS with optimal properties.

Alternatively, future efforts on DRS optimization could be aimed at tuning a favourable SRO through the choice of different co-dopants so that small, SRO- domains can be maintained through cycling. In Ni rich layered oxides, the introduction of electrochemically inactive Mg²⁺ (ref. 34 and 35) and Al³⁺ (ref. 36) cations acting as pillars can prevent the undesirable migration of atoms mitigating structural degradation. A similar doping strategy could potentially enhance the performance of DRS, although here the migration of transition metals into the vacancies generated from Li⁺ extraction is partly responsible for the high capacities observed (see Fig. S8†), and doping strategies aimed at preventing the transition metal diffusion should be exercised with care. An alternative doping strategy that seems not to interfere with the migration of transition metals into lithium vacancies has been demonstrated in a metastable LiMnO₂ nanostructured DRS integrating phosphorus ions located at a tetrahedral site.³⁷

Conclusion

The combined use of potential constraints, PDF data and BVS mismatch mapping revealed that Li trapping in LMTO originating from SRO can perturb the percolating Li-diffusion network in DRS. The lithium and cation vacancies in the layered domain formed during cycling become less accessible in the subsequent charge cycles, as evidenced by total scattering and XES. The comparison between LMTO and other DRS in the literature suggests that the trapping of Li in the layered domains could be associated with the capacity fade of DRS and could be a significant source of capacity fade alongside contributions from oxygen redox irreversibility.

The formation of SRO in DRS cathodes, either formed during the composite preparation by ball milling or the evolution of these domains with electrochemical cycling, should be further investigated in future materials. Preventing the formation of layered domains during cycling or controlling their size could be key to reduce capacity losses of DRS. This could be potentially achieved by nanostructuration or introducing electrochemically inactive dopants acting as pillars to mitigate the migration of the TM.

Although the growth of layered domains could effectively act as a trap for lithium, layered cathode materials have an inherently high capacity and rate capability. Thus, the interplay between the layered and DRS sublattices needs to be further investigated and the impact of SRO should be optimised. This work highlights the importance of local structures in cyclability of battery materials and provides insight into the design of better DRS cathodes. Successfully controlling the coexistence of layered and DRS sublattices exemplifies a new route to electrode design that opens a new path to develop high-performance cathode materials.

Experimental

Synthesis and sample preparation

We synthesized LMTO by a solid-state method from stoichiometric amounts of high purity Li₂CO₃, Mn₂O₃ and TiO₂. A small excess (∼5 wt%) of Li₂CO₃ was added to compensate for lithium evaporation at high temperatures. We obtained phase pure LMTO after annealing the sample at 1100 °C for several hours under Ar flow. The phase purity was confirmed by X-ray diffraction analyses.

The electrode material was prepared by combining LMTO with amorphous super P carbon in a 7 : 3 weight ratio. The homogeneity of the electrode mixture was aided by a short cycle of mechanical milling performed in a Fritsch Planetary Micro Mill PULVERISETTE 7 Premium Line. The electrode mixture was milled at 250 rpm for a set of two cycles of 30 min milling followed by a 20 min pause.

Electrochemistry

The electrochemical performance was tested with the as-prepared composite electrodes without the addition of binder. The composite electrode mixture was pressed to give a good electronic contact between the grains to minimize the cell polarization and tested in a Swagelok half-cell using lithium metal as a counter electrode and a cycling rate of C/10. The galvanostatic voltage profile of LMTO cycled in a voltage window of 1.5–4.5 V is consistent with previous reports by Yabuuchi et al.³⁸ and Ji et al.²⁰

Total scattering

In operando total scattering measurements were performed at the I15-1 XPDF beamline of the Diamond light source (UK) using high energy X-rays (76.6 keV) with a wavelength of 0.161669 Å. The measurements were performed in DRIX in situ electrochemical cells with a radial geometry and minimal background for optimal PDF extraction, where the only background contributions considered were the empty cell and acetylene black conductive additive present in the cathode mixture in 30 wt%. The real and reciprocal space data are given in Fig. S9.†

Samples for the pristine compositions and LMTO:C composite electrodes at cycles 7 and 15 were prepared in borosilicate glass capillaries of 1 mm internal diameter and measured ex situ.

The data collection was carried out using two PerkinElmer detectors at ∼20 cm from the sample for XPDF data collection and at 80 cm for Bragg data collection. ∼5 minute data collection gave excellent data quality for XPDF data analysis. In the operando study, four duplicates of these batteries were measured that gave identical results.

The relative geometry of the batteries and the detectors was calibrated with Si standards and the collected 2D data were processed into 1D diffraction patterns using the DAWN software. Total scattering data were background corrected and normalized with the GudrunX software using a Q_max of 25 Å⁻¹.

The Pawley fits were performed using the TOPAS software.³⁹ The scale factor, lattice parameters, and isotropic thermal parameters (B_iso) were refined. The backgrounds were fitted with Chebyshev polynomials and the peak profile shapes were described using a modified Thompson–Cox–Hastings pseudo-Voigt function,⁴⁰ where instrumental profiles were determined by the refinement of standards. The scale factors for the scattering signal from the carbon black and cell were included in the refinement as shown in Fig. S10 and S11.† Including these backgrounds in the refinement was key to improve the fit, given the large overlap of these signals with the diffuse scattering peaks of LMTO.

PDF refinements

The PDF data of pristine LMTO measured ex situ were fitted using electrostatic potentials implemented in TOPAS as the General Real Space (GRS) interaction⁴¹ with the Lennard-Jones potential as the repulsion term. The supercells for these refinements were produced from the averaged structural models refined by a Pawley fit. DRS supercells were built by doubling the unit cell in every direction, and layered supercells by doubling the unit cell in the ab plane.

Li⁺ diffusion in LMTO

BVSE pathways also known as energy-scaled bond-valence mismatch landscapes were derived from the proposed structural models by Pawley refinements, and the bond distances extracted from PDF refinements. BVSE maps were constructed by summing the BVSE contributions to a hypothetical Li⁺ ion at each point with a 7 × 10⁻⁴ ų volume up to 8 Å. SoftBV parameters⁴² were used to account for the influence of higher coordination shells and avoid cut-off effects at the boundaries of coordination shells.

The volume fraction of a percolating pathway with a 3 eV threshold, and the percolation threshold energy values along each axes were calculated from Monte-Carlo simulations using the BondStr software embedded in Fullprof-Suite.⁴³ The figures illustrating the local environments and diffusion pathways were produced with the VESTA software.⁴⁴

In operando absorption and emission spectroscopies

Commercial manganese oxide standards were diluted in BN (5 wt%), thoroughly mixed and uniaxially pressed into pellets that were mounted on a sample holder equipped with Kapton windows that allow the entry of X-rays. A C/LMTO cathode mixture was investigated operando and prepared in an in situ cell⁴⁵ equipped with a 200 μm thick window made of beryllium; more details on the preparation of the cell are given in ref. 30.

Operando HERFD-XANES and XES experiments were carried out at I20 beamline of the Diamond Light source⁴⁶ using angle dispersive analysis of the fluorescence X-ray signal emitted from the sample. The spectrometer was equipped with five spherically bent Si(440) crystal analysers focusing the diffracted beams onto a silicon drift detector for the recording of the Mn Kβ lines. The energy and experimental setup were calibrated by the recording a Mn foil spectrum. The energy resolution of the spectrometer, including contributions from both the monochromator and the CAS, was estimated from the recorded width of a pseudo-elastic peak.

For operando data acquisitions, the spectrometer was positioned at the maximum of the Mn Kβ emission line prior to the recording of the XANES spectra. HERFD-XANES spectra were then collected at the selected emission, which allowed discrimination of the detected photons with an energy resolution of 0.8 eV, smaller than the core-hole lifetime of the fluorescence line. This allows obtaining spectra with almost a core-hole lifetime-free broadening, that is, providing optimal energy resolution. XES and V2C data were averaged and background corrected using the PyMCA software.⁴⁷

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge Justine Jean at CRISMAT for technical assistance, Dr Matteo Aramini for support during beamtime at the I20 beamline of the Diamond Light Source and Diamond Light Source for beamtime under proposals CY24582 and SP2958.

References

1. The European Commission, A Clean Planet for All A European Strategic Long-Term Vision for a Prosperous, Modern, Competitive and Climate Neutral Economy, 2018.
2. S. G. Booth, N. N. Anthonisamy, R. Boston, H. Bronstein, S. J. Clarke, E. J. Cussen, N. A. Fleck, H. S. Geddes, N. Gollapally, J. M. Griffin, A. R. Haworth, M. A. Hayward, S. Hull, S. Price and D. O. Scanlon, APL Mater., 2021, 9, 109201.
3. M. N. Obrovac, O. Mao and J. R. Dahn, Solid State Ionics, 1998, 112, 9.
4. R. J. Clement, Z. Lun and G. Ceder, Energy Environ. Sci., 2020, 13, 345.
5. N. Yabuuchi, Curr. Opin. Electrochem., 2022, 34, 100978.
6. M. Diaz-lopez, P. A. Chater, Y. Joly, O. Proux, J. Hazemann and V. Pralong, J. Mater. Chem. A, 2020, 2, 10998.
7. M. Oishi, K. Yamanaka, I. Watanabe, K. Shimoda, T. Matsunaga, H. Arai, Y. Ukyo, Y. Uchimoto, Z. Ogumi and T. Ohta, J. Mater. Chem. A, 2016, 4, 9293.
8. K. Shimoda, M. Oishi, T. Matsunaga, M. Murakami, K. Yamanaka, H. Arai, Y. Ukyo, Y. Uchimoto, T. Ohta, E. Matsubara and Z. Ogumi, J. Mater. Chem. A, 2017, 5, 6695.
9. P. T. Barton, Y. D. Premchand, P. A. Chater, R. Seshadri and M. J. Rosseinsky, Chem.–Eur. J., 2013, 14521.
10. M. A. Jones, P. J. Reeves, I. D. Seymour, M. J. Cliffe, S. E. Dutton and C. P. Grey, Chem. Commun., 2019, 55, 9027.
11. G. C. Mather, C. Dussarrat, J. Etourneau and A. R. West, J. Mater. Chem., 2000, 10, 2219.
12. A. Urban, A. Abdellahi, S. Dacek, N. Artrith and G. Ceder, Phys. Rev. Lett., 2017, 176402, 1.
13. R. Chen, R. Witte, R. Heinzmann, S. Ren, S. Mangold, H. Hahn, R. Hempelmann and S. Indris, Phys. Chem. Chem. Phys., 2016, 7695.
14. L. Xu, W. Liu, X. Li, S. Rashid, C. Shen and Y. Wen, RSC Adv., 2015, 5, 12248.
15. D. Chen, J. Wu, J. K. Papp, B. D. Mccloskey, W. Yang and G. Chen, Small, 2020, 16, 2000656.
16. N. Yabuuchi, M. Takeuchi, M. Nakayama, H. Shiiba, M. Ogawa, K. Nakayama, T. Ohta, D. Endo, T. Ozaki, T. Inamasu, K. Sato and S. Komaba, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7650.
17. J. Lee, D.-H. Seo, M. Balasubramanian, N. Twu, X. Li and G. Ceder, Energy Environ. Sci., 2015, 3255.
18. Y. Li, X. Zhao, Q. Bao, M. Cui, W. Qiu and J. Liu, Energy Storage Mater., 2020, 32, 253.
19. Y. Kobayashi, M. Sawamura, S. Kondo, M. Harada, Y. Noda, M. Nakayama, S. Kobayakawa, W. Zhao, A. Nakao, A. Yasui, H. B. Rajendra, K. Yamanaka, T. Ohta and N. Yabuuchi, Mater. Today, 2020, 37, 43.
20. H. Ji, A. Urban, D. A. Kitchaev, D. Kwon, N. Artrith, C. Ophus, W. Huang, Z. Cai, T. Shi, J. C. Kim, H. Kim and G. Ceder, Nat. Commun., 2019, 10, 592.
21. M. Diaz-lopez, G. L. Cutts, P. K. Allan, D. S. Keeble, A. Ross, V. Pralong and P. A. Chater, J. Synchrotron Radiat., 2020, 27, 1.
22. K. Zhou, S. Zheng, H. Liu, C. Zhang, H. Gao, M. Luo, N. Xu, Y. Xiang, X. Liu, G. Zhong and Y. Yang, ACS Appl. Mater. Interfaces, 2019, 11, 45674.
23. D. Balzar, N. Audebrand, M. R. Daymond, A. Fitch, A. Hewat, J. I. Langford, A. Le Bail, D. Louer, O. Masson, C. N. McCowan, N. C. Popa, P. W. Stephens and B. H. Toby, J. Appl. Crystallogr., 2004, 37, 911.
24. S. Adams, Solid State Ionics, 2006, 177, 1625.
25. S. Adams and P. Rao, Struct. Bond., 2006, 119, 193.
26. A. Van der Ven and G. Ceder, J. Power Sources, 2001, 97–98, 529.
27. N. Tran, L. Croguennec, M. Ménétrier, F. Weill, P. Biensan, C. Jordy and C. Delmas, Chem. Mater., 2008, 20, 4815.
28. S. Jung, H. Gwon, J. Hong, K. Park and D. Seo, Adv. Energy Mater., 2014, 4, 1300787.
29. M. Diaz-lopez, P. Bordet, C. V Colin, M. Freire and V. Pralong, Chem. Mater., 2017, 30, 8598.
30. M. Diaz-lopez, Y. Joly, M. Freire, C. Colin, O. Proux, V. Pralong and P. Bordet, J. Phys. Chem. C, 2018, 122, 29586.
31. M. Diaz-lopez, P. A. Chater, P. Bordet, M. Freire, C. Jordy, O. I. Lebedev and V. Pralong, Adv. Energy Mater., 2020, 1902788, 1.
32. H. Noh, S. Youn, C. Seung and Y. Sun, J. Power Sources, 2013, 233, 2.
33. N. Li, M. Sun, W. H. Kan, Z. Zhuo, S. Hwang, S. E. Renfrew, M. Avdeev, B. D. Mccloskey, D. Su, W. Yang and W. Tong, Nat. Commun., 2021, 2348.
34. Q. Xie, W. Li and A. Manthiram, Chem. Mater., 2019, 31, 938–946.
35. H. Li, P. Zhou, F. Liu, H. Li, F. Cheng and J. Chen, Chem. Sci., 2019, 10, 1374.
36. M. Guilmard, L. Croguennec, D. Denux and C. Delmas, Chem. Mater., 2003, 2, 4476.
37. M. Sawamura, S. Kobayakawa, J. Kikkawa, N. Sharma, D. Goonetilleke, A. Rawal, N. Shimada, K. Yamamoto, R. Yamamoto, Y. Zhou, Y. Uchimoto, K. Nakanishi, K. Mitsuhara, K. Ohara, J. Park, H. R. Byon, H. Koga, M. Okoshi, T. Ohta and N. Yabuuchi, ACS Cent. Sci., 2020, 6, 2326.
38. N. Yabuuchi, M. Nakayama, M. Takeuchi, S. Komaba, Y. Hashimoto, T. Mukai, H. Shiiba, K. Sato, Y. Kobayashi, A. Nakao, M. Yonemura, K. Yamanaka, K. Mitsuhara and T. Ohta, Nat. Commun., 2016, 7, 13814.
39. A. A. Coelho, Topas-Academic, Version 6, 2016.
40. P. Thompson, D. E. Cox and J. B. Hastings, J. Appl. Crystallogr., 1987, 20, 79.
41. A. A. Coelho and R. W. Cheary, Comput. Phys. Commun., 1997, 4655, 15.
42. S. Adams, softBVS Web Page, 2003.
43. J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55.
44. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272.
45. J. B. Leriche, S. Hamelet, J. Shu, M. Morcrette, C. Masquelier, G. Ouvrard, M. Zerrouki, P. Soudan, S. Belin, E. Elkaïm and F. Baudelet, J. Electrochem. Soc., 2010, 157, A606.
46. S. Diaz-Moreno, S. Hayama, M. Amboage, A. Freeman, J. Sutter and G. Duller, J. Phys.: Conf. Ser., 2009, 190, 012038.
47. V. A. Solé, E. Papillon, M. Cotte, P. Walter and J. Susini, Spectrochim. Acta, Part B, 2007, 62, 63.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ta04262b

---