Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tracking the solid-state incorporation of Sn into the framework of dealuminated zeolite beta, and consequences for catalyst design†
Ricardo
Navar‡
b,
Giulia
Tarantino‡
 a,
Owain T.
Beynon
b,
Daniele
Padovan
b,
Luca
Botti
a,
Emma K.
Gibson
a,
Owain T.
Beynon
b,
Daniele
Padovan
b,
Luca
Botti
a,
Emma K.
Gibson
 cd,
Peter P.
Wells
cd,
Peter P.
Wells
 def,
Alun
Owens
b,
Simon A.
Kondrat
def,
Alun
Owens
b,
Simon A.
Kondrat
 g,
Andrew J.
Logsdail
g,
Andrew J.
Logsdail
 b and
Ceri
Hammond
b and
Ceri
Hammond
 *a
*a
aDepartment of Chemical Engineering, Imperial College London, London, SW7 2AZ, UK. E-mail: ceri.hammond@imperial.ac.uk
bCardiff Catalysis Institute, Cardiff University, Park Place, Cardiff, CF10 3AT, UK
cSchool of Chemistry, University of Glasgow, University Avenue, Glasgow, G12 8QQ, UK
dUK Catalysis Hub, Research Complex at Harwell, Rutherford Appleton Laboratories, Harwell Science and Innovation Campus, Oxon, OX11 0FA, UK
eSchool of Chemistry, University of Southampton, Southampton, SO17 1BJ, UK
fDiamond Light Source Ltd, Didcot, Oxon, OX11 0DE, UK
gDepartment of Chemistry, Loughborough University, Loughborough, LE11 3TU, UK
First published on 2nd September 2022
Abstract
Sn-Beta has emerged as a state-of-the-art catalyst for a range of sustainable chemical transformations. Conventionally prepared by bottom-up hydrothermal synthesis methods, recent research has demonstrated the efficiency of several top-down methods of preparation. One attractive top-down approach is Solid-State Incorporation, where a dealuminated Beta zeolite is physically mixed with a solid Sn precursor, in particular Sn(II) acetate, prior to heat treatment at 550 °C. This procedure is fast and benign, and metal incorporation requires no solvents and hence produces no aqueous Sn-containing waste streams. Although the performances of these catalysts have been well explored in recent years, the mechanism of heteroatom incorporation remains unknown, and hence, opportunities to improve the synthetic procedure via a molecular approach remain. Herein, we use a range of in situ spectroscopic techniques, alongside kinetic and computational methods, to elucidate the mechanisms that occur during preparation of the catalyst, and then improve the efficacy of the synthetic protocol. Specifically, we find that successful incorporation of Sn into the lattice occurs in several distinct steps, including (i) preliminary coordination of the metal ion to the vacant lattice sites of the zeolite during physical grinding; (ii) partial incorporation of the metal ion into the zeolite framework upon selective decomposition of the acetate ligands, which occurs upon heating the physical mixture in an inert gas flow from room temperature to 550 °C; and (iii) full isomorphous substitution of Sn into the lattice alongside its simultaneous oxidation to Lewis acidic Sn(IV), when the physically mixed material is exposed to air during a short (<1 h) isotherm period. Long isotherm steps are shown to be unnecessary, and fully oxidised Sn(IV) precursors are shown to be unsuitable for successful incorporation into the lattice. We also find that the formation of extra-framework Sn oxides is primarily dependent on the quantity of Sn present in the initial physical mixture. Based on these findings, we demonstrate a faster synthetic protocol for the preparation of Sn-Beta materials via Solid-State Incorporation, and benchmark their catalytic performance for the Meerwein-Ponndorf-Verley transfer hydrogenation reaction and the isomerisation of glucose to fructose.
Introduction
Microporous zeolites containing dilute amounts of isomorphously-substituted tri-, tetra- and penta-valent metal sites, such as TS-1, Sn-Beta and Fe-ZSM-5, have emerged in recent decades as state-of-the-art catalysts for a variety of sustainable chemical transformations.1–5 In contrast to classical aluminosilicate zeolites, which are widely employed as solid Brønsted acid catalysts, these metallosilicates exhibit high levels of performance as Lewis acid catalysts during liquid phase catalytic reactions. Of particular interest amongst these Lewis acidic metallosilicates is Sn-containing zeolite Beta (Sn-Beta). Sn-Beta is a medium pore BEA-topology zeolite, which contains small amounts of Sn(IV) isomorphously substituted into the otherwise siliceous framework.6 Over recent years, this catalyst has emerged as one of the most promising materials in the area of green chemistry, due to its ability to catalyse reactions including the Baeyer–Villiger oxidation of (renewable) ketones with H2O2, the isomerisation of glucose to fructose, the conversion of hexoses to α-hydroxyester compounds including methyl lactate and methyl vinyl glycolate, various C–C bond forming reactions, and the catalytic transfer hydrogenation of carbonyl compounds, amongst others.7–11Like many zeolite catalysts, Sn-Beta is classically prepared by hydrothermal synthesis, where an aqueous sol–gel containing the metal precursors and an appropriate Structure Directing Agent (SDA) is crystallised at elevated temperature and pressures.12–14 Despite resulting in the formation of highly active and selective catalysts, there are several drawbacks to this method of preparation, including the use of unfavourable mineralising agents (hydrofluoric acid), the need for long crystallisation times,14,15 inhibited crystallisation of the material at higher loadings of Sn, hence limiting catalyst productivity, and the production of materials possessing large crystallite sizes, which can possess less than ideal mass transfer properties.15–18
Given these disadvantages, the development of alternative preparation methodologies for Sn-Beta has received substantial attention.15,19–22 Of particular interest are “top-down” methods, in which readily prepared aluminosilicate zeolites are converted into a stannosilicate form by “demetallation–remetallation”. In such procedures, a commercially available aluminosilicate is first dealuminated in HNO3, resulting in the formation of silanol nests i.e. vacant “T” sites. Subsequently, the vacant T sites are “remetallated” with Sn by various approaches.22–27 For this reason, dealumination of the parental zeolite is an essential first step, so that vacant lattice sites are available for subsequent inclusion of a new heteroatom. Amongst top-down approaches, we have demonstrated that solid-state methods of incorporation are particularly suitable.15,17,28 In this approach, heat treatment of a physical mixture of dealuminated zeolite Beta with Sn(OAc)2, firstly in nitrogen (N2, 3 h) and subsequently in air (3 h), leads to the formation of active Sn-Beta catalysts. This approach, which we have termed Solid-State Incorporation (SSI), possesses several favourable features, including fast synthesis timescales, the absence of solvents and wet chemicals in the remetallation stage, and the ability to incorporate higher loadings of metal than conventional hydrothermal synthesis (>2 wt% Sn).15,17,28 The procedure has also been shown to be amenable for insertion of other metal centres, such as Al(III), Ti(IV) and Zr(IV), when desired.15,17,24,28,29
Given the broad applicability and success of this preparation method, Joshi et al. and Peeters et al. have recently studied the SSI synthesis procedure. In doing so, these groups have determined that the choice of mixing method, and the type of gas employed during the heating step, strongly influence the eventual speciation and activity of Sn in the final material.30,31 In particular, Joshi et al. observed that Sn can be directly oxidised to Sn(IV) during the grinding stage if a high energy ball mill is used for mixing.30 On the other hand, Peeters et al. discovered that performing the heat treatment in air flow as opposed to N2 flow resulted in the formation of both Sn(II) and Sn(IV) species, both of which exhibited different levels of performance for the Baeyer–Villiger oxidation reaction.31 However, although these studies further emphasise how the choice of preparation conditions influences successful synthesis of the catalyst, they do not directly study the process of heteroatom incorporation at real synthesis conditions, i.e. during the critical stages of the SSI procedure. Hence, limited knowledge is currently available as to what processes occur during conversion of the metal precursor into the final catalyst. However, such knowledge would make for a powerful tool, since elucidating the mechanism(s) of heteroatom incorporation during SSI could provide a blueprint towards improving the synthesis protocol from a molecular perspective.
By employing state-of-the-art spectroscopic methods, including 119Sn Carr–Purcell–Meiboom–Gill (CPMG) Magic Angle Spinning (MAS) Nuclear Magnetic Resonance (NMR), in situ X-ray Absorption Spectroscopy (XAS), in situ Diffuse Reflectance Infrared Fourier Transform Spectroscopy (DRIFTS), in situ Temperature Programmed Desorption-Mass Spectrometry (TPD-MS), Thermogravimetric analysis, UV-Raman, and Diffuse Reflectance UV-Vis (DRUV-Vis) spectroscopy, alongside complimentary kinetic studies and Density Functional Theory (DFT) simulations, we hereby present a detailed study focused upon the chemistry occurring during the synthesis of Sn-Beta catalysts by SSI. In addition to providing unique molecular level insight into the chemical processes occurring during the formation of the Sn-Beta catalyst, this study also reveals which parameters influence successful synthesis of the catalyst, and thereby reveals how the synthesis protocol can be improved to maximise its rapidity and minimise its energy requirements. The catalytic performances of the materials prepared by the improved synthesis protocol are evaluated by use of the Meerwein–Ponndorf–Verley transfer hydrogenation reaction, and the isomerisation of glucose to fructose at both batch and continuous processing conditions.
Results and discussion
Effect of physical grinding
SSI is a two-step procedure (Scheme 1), where dealuminated zeolite Beta and Sn(II) acetate (denoted deAl-Beta and Sn(OAc)2, respectively) are first grinded for 10 min with a pestle and mortar, prior to heat treatment of the solid mixture at elevated temperature (550 °C, 3 h in N2 flow and 3 h in air flow, ramp rate 10 °C min−1).15 Prior dealumination of the Beta zeolite is a prerequisite for the synthesis of Sn-Beta by SSI, since the removal of Al from the zeolite generates vacant lattice sites, denoted as silanol nests, the presence of which are required for Sn atoms to eventually be effectively incorporated into the material.15,22 Accordingly, we first focused on elucidating the changes that occurred to Sn(OAc)2 during the grinding stage. Although higher Sn content samples are known to possess a greater percentage of spectator sites i.e. extra-framework Sn species,28,32 a Sn(OAc)2/deAl-Beta mixture with a targeted Sn loading of 10 wt% was used for the initial spectroscopic studies, in order to maximise signal to noise ratio and aid spectroscopic definition of the Sn species potentially involved in the incorporation mechanism. Sn-Beta materials possessing higher loadings of Sn (e.g. 10 wt%, denoted 10Sn-Beta) have also been more thoroughly evaluated from a kinetic perspective.15,17,28,32Although the physical mixture of Sn(OAc)2/deAl-Beta was almost inactive when heat treatment was omitted (ESI Fig. S1†), changes to the Sn precursor following grinding of the physical mixture were nevertheless evident by 13C MAS NMR and DRIFT analysis. The 13C MAS NMR spectrum of untreated Sn(OAc)2 was composed of two symmetric doublets at −25.6 and −26.7 ppm, and −181.3 and −184.1 ppm (Fig. 1). These doublets correspond to [CH3–] and to [C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O], respectively, likely found in two separate crystal environments.33 Although no changes were observed following grinding of the acetate alone, the doublets disappeared when Sn(OAc)2 was physically mixed with deAl-Beta and only one intense peak for the methyl group, as well as a single, broader carbonyl resonance, were observed. These findings strongly indicate that grinding Sn(OAc)2 with the dealuminated zeolite causes its coordination to shift towards monodentate.
O], respectively, likely found in two separate crystal environments.33 Although no changes were observed following grinding of the acetate alone, the doublets disappeared when Sn(OAc)2 was physically mixed with deAl-Beta and only one intense peak for the methyl group, as well as a single, broader carbonyl resonance, were observed. These findings strongly indicate that grinding Sn(OAc)2 with the dealuminated zeolite causes its coordination to shift towards monodentate.
Alongside 13C MAS NMR analysis, DRUV-Vis and DRIFT analysis were also performed. FTIR analysis of the Sn(OAc)2/deAl-Beta mixture revealed the formation of a new vibration at 1297 cm−1 upon grinding, and that the difference between the asymmetric and the symmetric stretching modes of C–O, the so-called Δ value of Sn(OAc)2 [νCOasym − νCOsym],34,35 increased from 187 cm−1 (1600–1413 cm−1) in pure Sn(OAc)2 alone, to 310 cm−1 (1714–1404 cm−1) subsequent to grinding with the dealuminated zeolite (Fig. 2a). Physical grinding also modified the Ligand-to-Metal Charge Transfer (LMCT) bands of the Sn precursor, as observed by DRUV-Vis (Fig. 2b). The physically mixed sample Sn(OAc)2/deAl-Beta lost the lower energy signal at 245 nm associated with pure Sn(OAc)2. Notably, none of the changes to the Δ value or LMCT bands were observed when Sn(OAc)2 was grinded alone i.e. when the dealuminated zeolite material was absent (ESI Fig. S2–S3†), suggesting that the presence of the dealuminated zeolite is required for these changes to occur.
 | ||
| Fig. 2 (a) DRIFTS comparison of deAl-Beta, Sn(OAc)2 (grinded), and physical mixture Sn(OAc)2/deAl-Beta. (b) DRUV-vis spectra of deAl-Beta, Sn(OAc)2 (grinded), and physical mixture Sn(OAc)2/deAl-Beta. | ||
The loss of one LMCT band, coupled to the increase in the Δ value to ±310 cm−1, further suggests that the acetate ligands become more monodentate in nature during physical grinding, resulting in the formation of more inequivalent acetate oxygen atoms than those found in the original metal acetate complex.34–36 A shift towards monodentate coordination is further supported by detection of an additional vibrational feature at 1297 cm−1 for the Sn(OAc)2/deAl-Beta mixture, which has been attributed to monodentate acetate groups.34 Further support to this hypothesis was provided by computational analysis, which predicts that the Δ value of Sn(OAc)2 [νCOasym − νCOsym]35 increases from 102 cm−1 to 307 cm−1 when comparing pure Sn(OAc)2 and Sn(OAc)2/deAl-Beta, respectively (ESI Fig. S4†).
To investigate the role of the silanol nests produced during the dealumination process, and determine how these particular vacant sites are involved in the change of coordination of the acetate ligands, a control sample was prepared by grinding Sn(OAc)2 with Si-Beta, which is a purely siliceous sample of zeolite beta that has not undergone dealumination. Although Si-Beta possesses external silanol groups, it does not possess the internal T-atom vacancies surrounded by four Si–OH groups (i.e. silanol nests), as found in dealuminated zeolite Beta, which are formed by removal of the original aluminium centres. Grinding Sn(OAc)2 with a sample of Si-Beta also increases the Δ value, and generates the feature at 1297 cm−1, indicating that any silanol functionality can facilitate the change in acetate coordination. However, the spectral changes observed were somewhat more extensive for the deAl-Beta mixture, and the 1297 cm−1 feature was clearly of lower intensity when deAl-Beta was replaced by Si-Beta, both of which indicate that greater change occurs when internal silanol nests are present alongside the external silanol groups (ESI Fig. S5 and S6†).
To elucidate the impact of the grinding step on the Sn centres, preliminary XAS measurements were performed on the Sn(OAc)2/deAl-Beta grinded mixture and important reference samples (ESI Fig. S7†). Despite the changes exhibited by the acetate ligands during physical mixing, Sn was still found to be tetrahedral in geometry and in the +2 oxidation state in the grinded mixture, indicating that the overall speciation of the metal did not change during physical grinding. This suggests that, upon grinding, partial coordination of Sn to the zeolite occurred without change in oxidation state, with the lattice providing two of the bonds required to maintain tetrahedral geometry after the change in acetate coordination from bidentate to monodentate. The XAS data is more deeply discussed in the following section.
Further indications of metal–zeolite interactions after physical grinding were provided by UV-Raman analysis. Upon grinding, new bands in the region of 550–650 cm−1 were observed, the presence of which have previously been attributed to Sn–O vibrations (Fig. 3).37 Notably, the intensity of these bands was found to depend on the quantity of Sn mixed with the dealuminated zeolite, i.e. the intensity of the new bands increased going from 2 wt% of Sn to 10 wt%, whilst none of these vibrations was observed when grinding Sn(OAc)2 alone. Moreover, the bands observed between 550–650 cm−1 remained present even after heat treatment and removal of the acetate ligand (ESI Fig. S8†). Consequently, these bands can reasonably be assigned to Sn–O bonds in a range of different configurations as a result of interactions between Sn(OAc)2 and the zeolite.37
 | ||
| Fig. 3 UV-Raman spectra of (i) deAl-Beta (black line), (ii) pure Sn(OAc)2 (red line), and Sn(OAc)2/deAl-Beta mixture with (iii) 2 wt% of Sn (blue line), and iv) 10 wt% of Sn (green line). | ||
In summary, spectroscopic study of the first step of the SSI procedure revealed that, upon grinding the metal precursor with deAl-Beta, the acetate precursor switched from a bridged bidentate coordination to a more monodentate one. However, these changes were not accompanied by changes to the Sn centres, which remained in the oxidation state +2 and in a tetrahedral geometry, due to partial coordination to the zeolite. Comparison with control samples also showed different Sn(OAc)2–zeolite interactions occurred in the presence of silanol nests (i.e. substituting Si-Beta with deAl-Beta). These findings contrast to those recently reported by Joshi et al., which indicated formation of Sn(IV) via mechanochemical grinding using a high energy ball mill, as opposed to physical grinding.30 Nevertheless, samples of Sn(OAc)2/deAl-Beta, Sn(OAc)2/Si-Beta, and SnO2/deAl-Beta exhibited null or negligible levels of catalytic activity (ESI Fig. S1†),15,28 demonstrating that the heat treatment step typically employed during SSI is essential to generate catalytic properties.
Evolution of Sn during heat treatment of Sn(OAc)2/deAl-Beta
Despite the changes that occur to Sn(OAc)2 during the grinding stage, poor catalytic activity was observed for the Sn(OAc)2/deAl-Beta grinded mixture (ESI Fig. S1†). Thus, to obtain substantial catalytic activity by SSI, heat treatment of Sn(OAc)2/deAl-Beta is clearly required. During previous research, the heat treatment has been performed by heating the sample to 550 °C (10 °C min−1), first in a flow of N2 (ramp and 3 h isotherm), and subsequently in a flow of air (3 h), at gas flow rates of 60 mL min−1 throughout for 1.5 g of catalyst (WHSV = ∼2400 h−1).28 Accordingly, to understand how the physically grinded ‘pre-catalyst’ gains catalytic activity, the evolution of the metal precursor/deAl-Beta mixture during heat treatment was followed at real conditions with a variety of in situ techniques, including TPD-MS, DRIFTS and XAS. Control experiments were also performed on grinded samples of Sn(OAc)2 alone, deAl-Beta alone, and a physical mixture of Sn(OAc)2/Si-Beta, where required. Also in this case, spectroscopic studies were first focused using 10 wt% of Sn, to favour spectral definition, although specific experiments were later repeated for catalysts containing lower loadings of Sn to provide additional molecular insights (1 wt%, vide infra).To better understand the nature of the interactions between Sn(OAc)2 and the zeolite, the gaseous effluent generated during various heat treatments was monitored by Mass Spectrometry (TPD-MS) (Fig. 4). To maximise rigour, the MS system was connected directly to the calcination furnace employed for conventional catalyst synthesis, and identical conditions were used to our standard protocol. Furthermore, tracer experiments performed with CaCO3 were conducted to determine the delay between the evolution of the compound and the detection of the MS, and all reported spectra were offset accordingly (ESI Fig. S9†). To determine the relevance of the effluent evolutions with respect to formation of an active catalyst, control experiments were performed by measuring the gaseous effluent generated from Sn(OAc)2 alone, and a Sn(OAc)2/Si-Beta mixture, which did not result in the production of an active catalyst. For clarity, the ramping stage and the N2/air switch stage of the heat treatment are expanded in Fig. 4, as no changes were observed in the intermediate isotherms. However, the full TPD-MS profiles are presented for completion in SI Fig. S10–S12,† alongside the TPD-MS profile of deAl-Beta alone (ESI Fig. S13†).
In the absence of any zeolite material, pure Sn(OAc)2 decomposes at temperatures ≤280 °C, primarily releasing CO2, alongside smaller quantities of acetone and trace quantities of acetic acid. In contrast, TPD-MS of the Sn(OAc)2/Si-Beta mixture resulted first into evolution of acetic acid and CO2 at temperatures <250 °C, followed by the formation of acetone and additional CO2 in the temperature range 250–400 °C. The observations suggest that the co-presence of Si-Beta, and/or residual water molecules present in the siliceous zeolite, induces hydrolysis of the acetate precursor prior to its full decomposition. The observation is in line with the known hydrolysis and decomposition behaviour of acetate compounds.38,39
In contrast, mixing Sn(OAc)2 with deAl-Beta drastically modifies the decomposition process, shifting all product evolutions to a higher temperatures range (350–550 °C) compared to the temperatures found in the two former cases (<400 °C). Specifically, two intense peaks related to acetone and CO2 were observed at ca. 435 °C, while small amounts of acetic acid were gradually decomposed throughout the ramping period. The detection of volatile compounds at higher temperatures (≥350 °C) for the Sn(OAc)2/deAl-Beta mixture clearly indicates that stronger Sn(OAc)2–zeolite interactions occur when silanol nests are present. Interestingly, the TPD-MS profile of a deAl-Beta sample previously impregnated with acetic acid revealed similar product evolution to the Sn(OAc)2/deAl-Beta mixture (ESI Fig. S14†), suggesting that primary interconversion of the acetate ligands into acetic acid, prior to further decomposition into CO2, may be a key step towards the synthesis of an active catalyst. We note that no volatile products were detected during the initial isotherm period for any physical mixture, and that only small traces of CO2 were evolved when the inert gas was switched to air after the first 3 h isotherm period (Fig. 4b).
Complementing the TPD-MS data, the mass loss profiles of these samples were also measured by TGA during the initial ramping stage (Fig. 5). The mass loss profiles of both Sn(OAc)2 and Sn(OAc)2/Si-Beta are in excellent agreement to the TPD-MS data, exhibiting one major mass loss between 100–300 °C. Interestingly, the total mass lost during treatment of pure Sn(OAc)2 does not fully account for all the acetate present in the sample (mass loss of 40%, in contrast to approximately 50% mass of acetate in Sn(OAc)2). Since no further decomposition occurred during the isotherm (Fig. 4), the observation suggests that a solid product of higher mass than elemental Sn was formed, i.e. an oxide, carbonate, or oxycarbonate product. On the other hand, the mass loss profile of Sn(OAc)2/deAl-Beta exhibited mass losses up to 500 °C, in which the loss of mass observed at low temperatures (<200 °C) can be attributed to (partial) dehydration of deAl-Beta.
 | ||
| Fig. 5 TGA profiles and derivatives of (from top to bottom) (i) pure Sn(OAc)2, (ii) Sn(OAc)2/Si-Beta, and (iii) Sn(OAc)2/deAl-Beta. | ||
The findings from TPD-MS and TGA clearly indicate that the rate and mechanism of acetate decomposition is strongly influenced by the presence of a zeolite. Also, these changes were not solely due to additional hydrolysis processes caused by the presence of water present in the hydrated zeolite, since the pathway of acetate decomposition is different for Sn(OAc)2/Si-Beta and Sn(OAc)2/deAl-Beta. Hence, the mechanism is particularly modified when the zeolite also possesses silanol nests. These findings are in good agreement with the FTIR spectra reported in ESI Fig. S5 and S6,† which revealed different interactions occurring between Sn(OAc)2/deAl-Beta and Sn(OAc)2/Si-Beta.
To gain further insights into the various mechanisms occurring during heat treatment, in situ DRIFTS measurements were subsequently performed. DRIFT analysis of Sn(OAc)2/deAl-Beta (Fig. 6) revealed various changes to the 1755–1200 cm−1 region upon heating the sample to 325 °C, which may be related to changes in the acetate coordination and/or dehydration of the zeolite. Control experiments using Sn(OAc)2 alone (ESI Fig. S15†) and deAl-Beta alone (ESI Fig. S16†) confirmed that changes in intensity at 1751, 1714 (νCOasym), 1541 (νCOasym), 1413 (νCOsym) and 1280 cm−1 only occurred for the Sn(OAc)2/deAl-Beta physical mixture, suggesting these rearrangements to be related to changes in acetate coordination in the presence of the zeolite. As the temperature further increased from 325 °C to 550 °C, all the CO stretching bands disappeared, suggesting total decomposition of the acetate ligands. The result is in good agreement with the TPD-MS and TGA analysis. Due to the dehydration processes that occur throughout the heating step, a decrease in vOH bands located in the region 3750–3250 cm−1 was also observed. This finding is in agreement with 29Si MAS NMR analysis performed on samples of Sn(OAc)2/deAl-Beta removed from the furnace after different periods of time during the ramping stage. Specifically, 29Si MAS NMR analysis revealed that the signal at −98 ppm, assigned to isolated (Si(–OSi–)3OH) groups (Q3),40–42 decreased in the temperature range 300–550 °C (ESI Fig. S17†), suggesting a reduction in defect sites during heat treatment of the physical mixture. In situ DRIFT analysis of the following stages of the heat treatment was also performed, indicating that only minor changes occurred throughout the three hours isotherm in N2 and the three hours isotherm in air, whilst re-hydration of the material was clearly observed at the end of the calcination (ESI Fig. S18†).
To complement these findings and gain further insight into the changes occurring to the Sn species in the sample, the evolution of Sn during heat treatment was followed by in situ X-ray Absorption Spectroscopy (XAS). This experiment was performed using a Sn(OAc)2/deAl-Beta mixture with 10 wt% Sn, whose final form obtained after heat treatment is denoted as 10Sn-Beta. It is also worth noting that although the beamline could only provide helium (He) rather than N2 as inert gas, reference experiments (spectroscopic and catalytic) performed on 10Sn-Beta prepared in He/air demonstrated that precisely the same catalytic activity was observed for samples prepared in He/air and N2/air, for the Meerwein–Ponndorf–Verley (MPV) transfer hydrogenation of cyclohexanone to cyclohexanol (ESI Fig. S19–S21 and Table S1†).
Firstly, changes within the near edge structure by X-ray Absorption Near Edge Structure (XANES) were investigated by examining the maximum of the first derivative of the XANES data. Grinding Sn(OAc)2 with deAl-Beta led to a slight shift in edge position, although this was still consistent with Sn(II) being overwhelmingly present following physical grinding (ESI Fig. S7†). Heat treatment of the sample under the X-ray beam was subsequently performed at the precise conditions typically employed by SSI, albeit with He used instead of N2 as inert gas. To aid the understanding of the changes in the XANES spectra, the position of the 1st derivative maxima were plotted against time, allowing the oxidation state of Sn during the heat treatment to be monitored. Notably, the edge position was transformed to an oxidation state value by comparison to authentic standards of Sn(OAc)2 (+2) and SnO2 (+4), which were measured at 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 and 29
180 and 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185 eV, respectively (ESI Fig. S7† for the standards and ESI Fig. S22 and S23† for selected spectra measured throughout analysis).43–46 During the first stages of the heat treatment (ramp to 550 °C and 3 h isotherm in He flow), very little change was observed to the oxidation state of Sn, with Sn(II) clearly still present throughout the first isotherm in inert gas (Fig. 7a). However, significant changes to the XANES spectrum occurred upon switching the gas stream from the inert carrier to air (Fig. 7a). The introduction of air led to extremely rapid increases in the oxidation state of Sn. Indeed, within 60 min, the oxidation state of Sn increased from +2 to +4.
185 eV, respectively (ESI Fig. S7† for the standards and ESI Fig. S22 and S23† for selected spectra measured throughout analysis).43–46 During the first stages of the heat treatment (ramp to 550 °C and 3 h isotherm in He flow), very little change was observed to the oxidation state of Sn, with Sn(II) clearly still present throughout the first isotherm in inert gas (Fig. 7a). However, significant changes to the XANES spectrum occurred upon switching the gas stream from the inert carrier to air (Fig. 7a). The introduction of air led to extremely rapid increases in the oxidation state of Sn. Indeed, within 60 min, the oxidation state of Sn increased from +2 to +4.
 | ||
| Fig. 7 In situ XAS analysis of 10Sn-Beta synthesis. (a) Oxidation state of Sn as a function of time. (b) Coordination number of Sn and first-shell Sn–O bond distance obtained from XANES fitting data (further details are reported in ESI Table S2†). | ||
To gain further insight on how these changes correlate to the structure of the catalyst, and in particular the coordination environment of Sn, Extended X-ray Absorption Fine Structure (EXAFS) measurements were also performed (Fig. 7b, Tables 1 and ESI Table S2†). To simplify interpretation and the level of analysis required, focus was placed on the speciation of Sn (i) in the Sn(OAc)2/deAl-Beta mixture (i.e. prior heat treatment) and, (ii) just prior to, and following, the switch to air, where the major spectral changes were expected based on XANES. Firstly, Sn(OAc)2 was fitted to that expected from its crystal structure using two Sn–O paths at distances of 2.161 ± 0.013 Å (first-shell Sn–O) and 2.885 ± 0.024 Å (second-shell Sn–O) with coordination numbers of 4 and 3, respectively. Notably, the latter path arises from interactions between distinct [SnO4] centres, which is indicative of a crystalline material. Upon grinding Sn(OAc)2 with deAl-Beta, a reduction in the first-shell path length from 2.161 ± 0.013 Å to 2.087 ± 0.015 Å was observed (Table 1 entries 1 and 2), supporting the proposed changes in coordination of the acetate groups suggested by DRIFT and 13C MAS NMR analysis (Fig. 1 and 2). This change was also accompanied by the disappearance of the second-shell Sn–O path length at 2.885 ± 0.024 Å, indicating loss of the long-range order found in pure Sn(OAc)2, and confirming dispersion of the Sn centres on the zeolite (Table 1 entries 1 and 2). Moreover, a coordination number of 4.2 was measured, supporting the hypothesis that, upon grinding, the majority of the Sn atoms remain tetrahedrally coordinated. Upon heating the Sn(OAc)2/deAl-Beta to 550 °C under inert atmosphere, a stable coordination number of Sn equal to +3.3 ± 0.5 with a Sn–O distance of 2.04 ± 0.02 Å was observed (Fig. 7b), revealing a reduction in both coordination number of Sn and first-shell Sn–O path length, relative to the freshly ground sample. Upon changing the inert gas flow to air, significant changes to the material undergoing heat treatment were observed. Firstly, a notable reduction in 2σ2 was observed (from 0.0125 ± 0.0031 Å2 in He flow, to 0.0075 ± 0.0019 Å2 after 16 min in air flow), suggesting an increase in the order of the local environment. Furthermore, within 16 min after switching to air flow, the Sn coordination number increased from ca. 3.4 to 4, and the Sn–O path length was reduced to a value of 1.956 ± 0.012 Å. Notably, these values for the first-shell Sn–O bond distance are consistent with that of Sn atoms that are isomorphously substituted into the Beta framework,46 confirming that full isomorphous substitution occurs at the same time as the Sn atoms are oxidised from 2 to 4. Throughout this stage, the Sn atoms remain tetrahedrally coordinated, characterised by a Sn coordination number of 4 and an Sn–O bond distance of 1.956 Å, due to their dehydrated nature at high temperatures. Upon cooling the sample following the heat treatment, a higher coordination number (ca. 4.8) was observed. This is consistent with facile rehydration of the catalyst upon cooling, in line with our previous EXAFS studies of hydrated Sn-Beta catalysts.28
| Entry | Sample | Flow | Time/min | Coordination number (Sn) | R/Å (Sn–O) | 2σ2/Å2 | E t /eV | R-factor |
|---|---|---|---|---|---|---|---|---|
| a Fitting parameters: S02 = 1 as deduced by SnO2 and Sn(OAc)2 standard; Fit range 2.5 < k< 13, 1 < R < 4; Number of independent points = 19. Values in parenthesis give the experimental error. | ||||||||
| 1 | Sn(Oac)2 | — | 3.9 (0.4) | 2.161 (0.013) | 0.011 (0.0019) | 7 (1) | 0.0087 | |
| 3.3 (0.7) | 2.885 (0.024) | |||||||
| 2 | Sn(Oac)2/deAl-Beta (prior heat treatment) | — | 0 | 4.2 (0.6) | 2.087 (0.015) | 0.01 (0.0028) | 6 (1) | 0.0233 |
| 3 | Sn(Oac)2/deAl-Beta (during heat treatment) | He | 231 | 3.3 (0.5) | 2.045 (0.018) | 0.0125 (0.0031) | 6 (2) | 0.0126 |
| 4 | ′′ | He → air | 233 | 3.2 (0.5) | 2.038 (0.02) | 0.0117 (0.0032) | 6 (2) | 0.0158 |
| 5 | ′′ | Air | 249 | 4 (0.5) | 1.956 (0.012) | 0.0075 (0.0019) | 5 (1) | 0.0091 |
| 6 | 10Sn-Beta | — | 413 | 4.8 (0.3) | 1.959 (0.006) | 0.0074 (0.0008) | 2 (1) | 0.0026 |
As previously mentioned, Sn-Beta catalysts with high Sn loadings also possess unwanted spectator Sn species, which do not contribute to the catalytic activity of the material. To investigate the rate and extent of formation of these sites, focus was placed on both Sn–O and Sn–Sn scattering during the oxidation step (Fig. 8, presenting the magnitude of the k3-weighted Fourier transform of the EXAFS spectrum of the mixture in R-space). The first features present in the spectra (1–2 Å) in Fig. 8 can be assigned to Sn–O scattering interactions, whilst Sn–Sn scattering indicative of clustered/extra-lattice Sn species can be identified by features between 3.0 and 4 Å.45 Prior to the introduction of air, only one major feature is observed at approximately 1.8 Å, indicative of Sn–O bonding. Upon introduction of air into the system, a significant increase in the intensity of the first peak in the FT spectrum occurred, indicating either (i) an increase in the number of Sn–O bonds, (ii) an increase in the order and uniformity of the existing Sn–O bonds, or (iii) a combination of both.
Furthermore, upon switching to air, the feature at approximately 3.2 Å increases at a similar rate to that at 1.8 Å. The increase in the feature at ∼3.2 Å throughout the heat treatment protocol indicates some Sn–Sn formation occurs regardless of how long the heat treatment protocol is carried out for at these Sn loadings. Although preliminary, this observation suggests that both framework and extra-framework Sn species are formed at the same period of time, at this metal loading with this Sn precursor, albeit to different absolute quantities. This suggests that formation of Sn–Sn species may be related to the spatial proximity of Sn, and may not be possible to control by kinetic means.
Further elucidation of Sn incorporation into the zeolite lattice was achieved by 119Sn CPMG MAS NMR spectroscopy, performed in direct excitation (DE) mode.47 Technical limitations prohibited analysis of the samples at true operational conditions, and hence, the heat treatment was terminated at various stages prior to removal of the sample and measurement by ex situ119Sn MAS NMR. Consequently, all Sn resonances are characteristic of Sn samples in their hydrated state.48–53119Sn MAS NMR spectra of Sn(OAc)2/deAl-Beta obtained at different stages of the ramp only revealed minimal changes, showing −600 ppm species to still be the dominant resonance (Fig. 9). Moreover, no changes were observed throughout the first isotherm step (N2 flow), in excellent agreement with the XAS analysis. Upon switching the gas flow to air, changes in Sn speciation were evident, with a prominent increase in intensity at −689 ppm, which can be readily attributed to the active Sn species based on several previous reports (Fig. 9).32,42,54 Notably, only minor changes to the −689 ppm signal were detected over the final two hours in air, supporting the XAS analysis and indicating that isomorphous substitution occurs during the first stages of the air isotherm, when the oxidation state of Sn increases from +2 to +4. Due to the fact a variety of Sn–O compounds, including Sn(OAc)2, generate resonances at −600 ppm (ESI Fig. S24†),17 it is difficult to say from 119Sn MAS NMR analysis at which stage extra-framework Sn species form. Still, the final 119Sn MAS NMR spectrum strongly resembles those well benchmarked for active Sn-Beta samples prepared with higher loadings of Sn i.e. >5 wt%, which are known to contain a mixed active site population of isomorphously substituted Sn and extra-framework Sn compounds. Taken together, the XANES, EXAFS and 119Sn MAS DE CPMG NMR analyses all indicate that full isomorphous substitution of Sn into the framework of zeolite Beta, and its oxidation to Lewis acidic Sn(IV), only occurs upon introduction of air into the system. These findings are in line with those reported by Peeters et al.31 who, by means of 119Sn Mössbauer Spectroscopy, found that a Sn(IV)/Sn(II) ratio of 95/5 was obtained when Sn-Beta was heated first in a N2 flow followed by air flow, whilst only 18% of Sn(IV) was formed when heating Sn-Beta in N2 only, i.e. in the absence of air.
 | ||
| Fig. 9 119Sn MAS DE CPMG NMR spectra of 10Sn-Beta at different stages of the ramping period in N2, and at different stages of the isotherm periods. | ||
Increasing the relative proportion of active sites; spectroscopic analysis of 1Sn-Beta
As we have previously demonstrated,17,28 Sn-Beta catalysts possessing initial Sn loadings >5 wt% typically contain higher quantities of extra-framework SnOx species than Sn-Beta catalysts possessing Sn loadings of ≤2 wt%. Although these species do not contribute to the catalytic performance of the material, they can evidently influence the spectroscopic signals generated, which may complicate mechanistic understanding of this system. Accordingly, key experiments described above were repeated for samples of 1Sn-Beta, containing only 1 wt% Sn, which were also synthesised by SSI of a Sn(OAc)2/deAl-Beta mixture. Although samples with lower metal loadings are often more challenging to characterise due to their lower levels of signal to noise, studying samples with a higher fraction of active to inactive sites evidently allows better evaluation of which of the processes occurring during SSI are most relevant to catalysis and active site formation. We note that our recent studies of continuous glucose to fructose isomerisation have revealed that the turnover frequency of Sn is approximately 7-fold higher in 1Sn-Beta than for 10Sn-Beta.17,28,32Firstly, DRIFT measurements were performed on Sn(OAc)2/deAl-Beta (final Sn loading of 1 wt%) prior to heat treatment, revealing similar changes in the acetate coordination to the ones observed for the high loading sample (ESI Fig. S25†). However, in situ DRIFT analysis performed throughout the ramping stage (Fig. 10a, and ESI Fig. S26† for full spectra) indicated a greater level of clarity present in the 1% Sn mixture when compared to the high loading analogue. Specifically, upon heating the 1% Sn mixture, rapid decrease of the COasym stretching band at 1709 cm−1 was observed, accompanied by the formation of a band at 1751 cm−1 at 125 °C, which then disappeared at 375 °C. These findings clearly indicate changes of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O coordination throughout the ramp, prior to full decomposition of the acetate groups at temperatures >325 °C. The formation of a band at 1751 cm−1 because of a changing acetate ligand is supported by DFT vibrational analysis, which reveals a similar shift to a higher frequency (Δ = 40 cm−1) when a proton moves from the zeolite framework to the acetate ligand, yielding free acetic acid (ESI Fig. S27†). Moving to the following stages of the heat treatment, no change was observed throughout the isotherm in N2, whilst minor changes were observed in the isotherm in air in the –OH region (3750–3250 cm−1). Notably, fast rehydration of the catalyst was again observed upon cooling the sample to room temperature following synthesis, suggesting the formation of hydrated Sn sites (Fig. 10b). Summarising, DRIFT analysis of the 1 wt% Sn sample is in good agreement with that of the high loading analogue, confirming initial changes in acetate coordination in the temperature range 25–325 °C, likely related to the initial formation of acetic acid, which further decomposed at temperatures >325 °C.
O coordination throughout the ramp, prior to full decomposition of the acetate groups at temperatures >325 °C. The formation of a band at 1751 cm−1 because of a changing acetate ligand is supported by DFT vibrational analysis, which reveals a similar shift to a higher frequency (Δ = 40 cm−1) when a proton moves from the zeolite framework to the acetate ligand, yielding free acetic acid (ESI Fig. S27†). Moving to the following stages of the heat treatment, no change was observed throughout the isotherm in N2, whilst minor changes were observed in the isotherm in air in the –OH region (3750–3250 cm−1). Notably, fast rehydration of the catalyst was again observed upon cooling the sample to room temperature following synthesis, suggesting the formation of hydrated Sn sites (Fig. 10b). Summarising, DRIFT analysis of the 1 wt% Sn sample is in good agreement with that of the high loading analogue, confirming initial changes in acetate coordination in the temperature range 25–325 °C, likely related to the initial formation of acetic acid, which further decomposed at temperatures >325 °C.
Further key experiments repeated on 1Sn-Beta revealed that the major changes in both acetate evolution and Sn speciation previously observed for 10Sn-Beta were all comparable for 1Sn-Beta, suggesting that they were all broadly relevant to the synthesis of active Sn species. In particular, 29Si- and 119Sn-MAS NMR (ESI Fig. S28 and S29†), along with TPD-MS (ESI Fig. S30†), were shown to be consistent with the results obtained from 10Sn-Beta. However, a much smaller relative fraction of acetone was observed in the TPD-MS spectrum of 1Sn-Beta when compared to that of 10Sn-Beta. The negligible quantity of acetone in this case appears to correlate with the lower quantity of extra-framework Sn species formed at lower Sn loadings. DRIFT analysis of 1Sn-Beta presented minor differences due to the better resolution of 1Sn-Beta, showing clear formation of acetic acid and confirming the key role that it has during the synthesis of an active catalyst.
Proposed mechanism
Coupling both experimental and computational data, several observations on the mechanism that controls the incorporation of Sn into the zeolite lattice may be deduced. Focusing on the first step of SSI, i.e. physical mixing of Sn(OAc)2 with deAl-Beta, the following conclusions can be made: (i) Sn retains its oxidation state of +2 and a tetrahedral geometry (XAS and 119Sn MAS NMR), (ii) the acetate groups change their coordination to gain a more monodentate character (13C NMR and DRIFT), (iii) different acetate–zeolite interactions can be observed when silanol nests are present (DRIFT and TPD-MS), and (iv) direct interactions between Sn and the zeolite lattice are observed (DRIFT, EXAFS, Raman), and must occur in order to maintain tetracoordinated Sn species despite the monodentate nature of the acetates following grinding. Despite the complicated network of hydrogen bonds established between Sn(OAc)2 and molecules of water and/or silanol sites, a simplified scheme for the grinding step is proposed in Scheme 2. It should be noted that at this particular stage of preparation, the material exhibits very low levels of catalytic activity (ESI Fig. S1†).To gain substantial catalytic activity, heat treatment of the physical mixture Sn(OAc)2/deAl-Beta is required (550 °C, 3 h N2 and 3 h air). Based on the spectroscopic data obtained, the ramping stage and the first hour of isotherm in air are the key steps to achieve Sn incorporation. Throughout the ramping stage it was found that: (i) most of the acetate is released at temperatures higher than 325 °C (TPD-MS), (ii) CO2, acetone and acetic acid are the main products detected (TPD-MS), although acetic acid is clearly the primary product (TPD-MS, DRIFTS and DFT analysis), (iii) most of the Sn centres retain an oxidation state of +2 (XAS) and form tetracoordinated species (119Sn MAS DE CPMG NMR, XAS).
Focusing on the subsequent key step, i.e. moving from N2 to air, the following observations can be made: (i) Sn is rapidly oxidised from +2 to +4 (XANES), (ii) a large percentage of Sn centres are subjected to a change of coordination, and become consistent with Sn atoms that are isomorphously substituted into the Beta lattice (EXAFS and 119Sn MAS DE CPMG NMR), (iii) concurrently to the formation of framework Sn centres, some Sn–Sn interactions, indicative of extra-framework Sn species, are observed (EXAFS) and (iv) the final catalyst samples reveal a large percentage of the −689/−703 ppm species which are associated with hydrated active species (119Sn MAS DE CPMG NMR).28,29
These findings indicate that several chemical processes are clearly relevant during SSI. Throughout the ramping stage (Scheme 3), partial coordination of Sn in the zeolite, i.e. formation of the first Sn–O–Si bonds, may be achieved by donation of a proton from an adjacent silanol site to the acetate group, resulting in formation of free acetic acid (TPD-MS and DRIFT). Transition state calculations with DFT predict the formation of acetic acid from a monodentate acetate–Sn species, and its subsequent dissociation, are relatively low energy (≤0.72 eV), suggesting that the production of acetic acid would be facile from the initial physically mixed state of the catalyst (ESI Fig. S31†). Though the reaction is endothermic, entropic contributions can likely drive the process forward. Further decomposition of free acetic acid likely accounts for the generation of the majority of the products detected in the gas effluent of Sn(OAc)2/deAl-Beta (TPD-MS). This conclusion is supported by a TPD-MS experiment performed on a sample of deAl-Beta previously impregnated with acetic acid (ESI Fig. S14†), which results in the generation of a gaseous effluent comparable to the standard preparation procedure, with CO2 detected as main product alongside smaller amounts of acetic acid, acetone, and hydrogen. Based on the observations made for 10Sn-Beta, and especially the analogous experiments performed on 1Sn-Beta, we conclude this to be the preliminary step required to eventually form active, isomorphously-substituted Sn(IV) atoms.
Alongside this route, reaction pathways involving the release of acetone (TPD-MS) can also occur. Considering that higher percentages of acetone are observed at higher loadings of Sn, we propose that acetone could be formed from two neighbouring acetate groups. Based on steric reasons, we hypothesise that interactions between two proximal acetate groups may provide the opportunity for acetone to be released. Although interactions among proximal Sn acetate centres may be considered negligible in mixtures with low Sn loading (i.e. 1 wt%), such a mechanism may easily occur on materials with Sn loading ≥5 wt%, which are known to lead to Sn-Beta catalysts with higher percentages of extra-framework Sn, and, thus, more spectator Sn species.13,14 This effect is in excellent agreement with the much higher percentage of acetone detected during TPD-MS of Sn(OAc)2/deAl-Beta mixture with 10% Sn, compared to its low loading analogue (1 wt% Sn, ESI Fig. S30†), which exhibited only traces of acetone, and which is known to possess only small quantities of extra-framework Sn.17,32
Changing the calcination gas to the highly oxidising conditions, in addition to the presence of water vapour found in compressed air, leads to the genesis of Sn centres with the oxidation state +4, at the same time that XAS studies indicate full incorporation of Sn into the lattice occurs. To determine the full relationship between the oxidation state increase and full incorporation into the lattice, a series of experiments were performed using Sn(OAc)4 as precursor. Although use of this precursor resulted in a similar grinded complex being formed between Sn(OAc)4/deAl-Beta as found for Sn(OAc)2/deAl-Beta (ESI Fig. S32†), the Sn(OAc)4/deAl-Beta mixture was inactive when tested for the MPV reaction (SI Fig. S33†). The inactivity indicates that full isomorphous substitution of Sn into the zeolite lattice is essential for the synthesis of an active Sn-Beta catalyst, and not simply coordination of a Sn(IV) containing precursor. Furthermore, the Sn-Beta material prepared following heat treatment of Sn(OAc)4/deAl-Beta still exhibited poor activity for the MPV reaction when compared to the conventional Sn-Beta analogue prepared with Sn(OAc)2 (ESI Fig. S33†). This suggests full isomorphous substitution of Sn into the lattice cannot occur when a Sn(IV) precursor is used. Taken together, these results indicate that although Sn(OAc)4 and deAl-Beta interact in a similar manner to Sn(OAc)2 and deAl-Beta, Sn(II) is required to prepare a Sn-Beta material with substantial catalytic performances (ESI Fig. S33†). The finding also suggests that oxidation of Sn from +2 to +4 is undesirable during the grinding stage, and should preferentially occur throughout the heat treatment. This finding likely explains why poorer catalytic performance is achieved when a high energy ball mill is used for preparation, since such instruments have been shown to cause oxidation of Sn from +2 to +4 prior to heat treatment, potentially hindering isomorphous substitution.
On another level, however, these findings also suggest that full isomorphous substitution cannot be achieved if there is no oxidative driving force, strongly indicating that the oxidation and incorporation events are linked. Based on this, we propose that Sn oxidation occurs via hydrogen abstraction from Sn–O(H)–Si to Sn–O–Si bonds (Scheme 3), which leads to concurrent oxidation of Sn(II) to Sn(IV) whilst simultaneously achieving full incorporation of Sn(IV) species into the zeolite lattice. Transition state modelling indicates that direct release of H2 from geminal –SiOH bonds (Scheme 3) is characterised by a kinetic barrier of 3.26 eV, but a drastic reduction in the kinetic barrier to 1.38 eV occurs when transferring hydrogen via water (ESI Fig. S34†). The reduced barrier suggests that a network of water molecules, which may be present in the pore, but also in compressed air, would aid in the transfer of hydrogen during the oxidation step. Finally, hydration of Sn-Beta readily occurs throughout the cooling step, leading to the genesis of hydrated Sn sites, which are characterised by NMR signals at −689/−703 ppm. In regards to the formation of extra-framework Sn species, XAS studies indicate that their formation occurs at the same time as isomorphous substitution of Sn into the lattice, albeit to a lower absolute degree. This suggests that the ratio of active sites/spectator sites cannot be controlled by kinetic means, and instead depends on the spatial distribution of Sn, since the relative fraction of these undesirable species is much lower for samples with lower Sn loadings. Based on the TPD-MS experiments performed for 10Sn-Beta and 1Sn-Beta, we hypothesize that extra-framework Sn formation occurs due to the competing formation of acetone from two neighboring acetate groups, the probability of which increases markedly at higher loadings of Sn.
Application of mechanistic insight
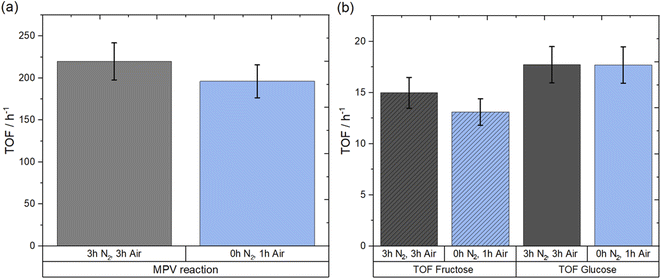
In addition to providing detailed mechanistic insight regarding the reactions occurring during the synthesis of Sn-Beta catalysts by SSI, the in situ spectroscopic data presented above suggests that long stages of the SSI synthesis procedure are superfluous to form active Sn-Beta catalysts. To clarify whether the extended stages of both isotherms were unnecessary with respect to forming active Sn-Beta catalysts, and with the objective of streamlining the synthesis procedure for future optimisation studies in mind, a final series of experiments aimed at clarifying the unnecessary nature of the isotherm periods was performed. Despite possessing higher distribution of spectator sites compared to 1Sn-Beta, 10Sn-Beta was used as the material for this study for two reasons. Firstly, its higher loading results in improved productivity per gram of catalyst, making it a more interesting material from an industrial perspective. Secondly, its higher ratio of spectator sites/active sites provides greater opportunity for improved catalyst performance, if extra-framework Sn species can be avoided simply by shortening the synthesis procedure. Based on spectroscopic data, two important key points were determined to be essential to synthesise an active catalyst: (i) the use of a N2 ramp, and (ii) subsequent change to air flow to oxidise the Sn(II) to Sn(IV). Therefore, to experimentally determine whether the long isotherm steps were superfluous, a new 10Sn-Beta material was prepared as follows: a physical mixture of Sn(OAc)2 and deAl-Beta was heated to 550 °C in a flow of N2 at a ramp rate of 10 °C min−1, before N2 flow was switched to a flow of air once a temperature of 550 °C was achieved. The furnace was subsequently held at 550 °C for one hour in air flow. The catalyst prepared with the rapid calcination is henceforth denoted as 10Sn-Beta (0 h, 1 h), whilst the conventional sample synthesised using three hours isotherm in N2 and three hours isotherm in air, is denoted as 10Sn-Beta (3 h, 3 h). The catalytic performances of both samples were then investigated for batch MPV reaction of cyclohexanone to cyclohexanol using 2-butanol as a secondary alcohol, and for the isomerisation of glucose to fructose, which are two reactions prevalent for the testing of Sn-Beta catalysts.8,9,54–57 Notably, glucose isomerisation has been receiving great attention from the scientific community due to the increasing demand for fructose as a building block for the synthesis of biobased chemicals and fuels in addition to its employment as a sweetener, and therefore, rapid synthesis of an active catalyst for glucose isomerisation to fructose is a challenge of fundamental societal relevance.58–61 To compare the intrinsic activity of the catalysts, turnover frequency (TOF) values were calculated during the early stage of batch reactions using eqn (4) in the Experimental Section, and reported in Fig. 11. When comparing the catalyst prepared with the shortened synthesis procedure to the conventional one, similar TOF values were observed for both MPV and glucose isomerisation reactions. Specifically, both catalysts exhibited TOFs of 200 ± 20 h−1 for MPV reaction of cyclohexanol to cyclohexanone, whilst TOFs of 17 h−1 and 14 h−1 were achieved on both catalysts for glucose conversion and fructose yield, respectively. The essentially identical values observed in Fig. 11 confirm identical catalytic performances between the conventional catalyst and the more rapidly prepared catalysts. This demonstrates that the successful synthesis of 10Sn-Beta can be achieved even with removal of the superfluous isotherm stages, confirming that isomorphous substitution of Sn by SSI remains successful even if the heat treatment protocol is shortened by 5 h.To verify whether the shortened synthesis procedure affected the stability of the isomorphously substituted Sn, additional glucose isomerisation experiments were performed at continuous processing conditions (Fig. 12). In line with the batch reactivity data, negligible differences to the TOF value of 10Sn-Beta were observed, despite the 5 h reduction of synthesis time. Moreover, at the conditions explored, the rate of deactivation (kd) of Sn-Beta catalyst was almost unaffected by the rapid preparation method, presenting a kd of 0.13 h−1 (0 h, 1 h) in contrast to 0.10 h−1 obtained from the original procedure (3 h, 3 h) (ESI Fig. S35†). Details on Levenspiel plots for rate of deactivation can be found in SI Fig. S35.† Thus, it is clear that omitting the isotherm step in N2 and reducing the time in air by 67% resulted in no loss in performance compared to the original material. Although the relationship between Sn species and TOF is non-trivial,18 with even different framework sites displaying different TOF values,32 we note that the fact the TOF values did not increase following the rapid synthesis procedure suggests that the formation of extra-framework Sn species is not avoided simply by shortening the synthesis procedure. This provides further confirmation that the formation of extra-framework Sn species is determined by the spatial distribution of Sn acetate, and not by the agglomeration of isomorphously substituted Sn(IV) atoms during the extended heat treatment protocol.
Conclusions
Using a broad range of in situ and ex situ techniques, along with computational simulations, this study investigated the key steps for the successful incorporation of Sn into the lattice of dealuminated Beta (deAl-Beta) zeolite by Solid State Incorporation. Spectroscopic analysis of the conventional synthetic protocol allowed us to gain insights into the key mechanistic steps, and then apply these findings to improve the synthesis procedure of Sn-Beta. We identified that although Sn does not fully incorporate into the lattice upon physical mixing alone, interactions between the Sn(OAc)2 precursor and the dealuminated zeolite occurred during this stage of the preparation, resulting in coordination of the acetate to the vacant lattice sites of the zeolite matrix. Subsequent heating of the Sn(OAc)2/deAl-Beta mixture to 550 °C under inert gas flow (N2 or He) is required to remove the acetates from Sn(OAc)2, and achieve the first stages of Sn incorporation. However, this step alone is insufficient to synthesise highly active Sn-Beta catalysts, and we find that replacing the inert gas flow with air flow at high temperatures is required to oxidise the Sn species from an oxidation state of +2 to +4, which occurs simultaneous to the full incorporation of Sn in the lattice. Formation of the active site, proposed to be a Sn(IV) species resonating at −689 ppm by 119Sn MAS NMR spectroscopy, and typically assigned to hydrated Sn centres, occurs during the first hour from the introduction of air in the calcination furnace, indicating completion of the synthesis during this time. Alongside Sn incorporation, XAS analysis revealed that spectator species such as SnO2 are formed at the same time that Sn is incorporated into the lattice, suggesting that the active species/spectator species ratios are driven by proximity of Sn centres, and are not controlled by kinetic means. Based on these mechanistic findings, we demonstrate that successful preparation of Sn-Beta can be achieved in a total of only two hours, by shortening the synthesis procedure so that it only includes the first ramp in N2, and the first hour of isotherm in air. Catalytic analysis of Sn-Beta materials prepared by this streamlined synthesis procedure, for the Meerwein–Pondorf–Verley transfer hydrogenation reaction of cyclohexanone to cyclohexanol and the isomerisation of glucose to fructose, reveal identical performance between the conventional Sn-Beta catalyst and that prepared by our shorter heat treatment method. Along with providing a more rapid procedure for future optimisation studies, this also demonstrates how the mechanistic information generated by in situ spectroscopic analysis can be used to make practical improvements to the Sn-Beta synthesis procedure.Experimental section
Catalyst synthesis
A commercial zeolite Al-β (Zeolyst, NH4+-form, Si/Al = 38) was dealuminated by treatment in HNO3 solution (13 M HNO3, 100 °C, 20 mL g−1 zeolite, 20 h). Solid-state stannation of dealuminated zeolite β was performed according to the procedure reported in ref. 17, by grinding the appropriate amount of Sn(OAc)2 with the necessary amount of dealuminated zeolite for 10 min in a pestle and mortar. Following this procedure, the samples were heated in a combustion furnace (Carbolite MTF12/38/400) to 550 °C with a ramp rate of 10 °C min−1, first in a flow of N2 and subsequently changed to air (60 mL min−1) after reaching set temperature and desired isotherm time.Kinetic studies
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 metal:glucose molar ratio. Once the oil had reached the desired temperature (110 °C), the reaction commenced with vigorous stirring with a magnetic stirrer bar (750 rpm). The reactor was stirred for an appropriate length of time, and time online samples were obtained by periodically quenching the reaction by rapidly cooling the reactor in an ice bath. Aliquots of solution were extracted with a syringe, centrifuged to remove solid particulates, and were subsequently analysed by 1260 Infinity HPLC coupled with a Hi-Plex Ca (6.5 × 300 mm, 8m particle size, Agilent) column, which was isothermally held at 80 °C, and an ELS detector where sorbitol was used as an external standard. HPLC grade water was used as the mobile phase, at a flow rate of 0.75 mL min−1.
50 metal:glucose molar ratio. Once the oil had reached the desired temperature (110 °C), the reaction commenced with vigorous stirring with a magnetic stirrer bar (750 rpm). The reactor was stirred for an appropriate length of time, and time online samples were obtained by periodically quenching the reaction by rapidly cooling the reactor in an ice bath. Aliquots of solution were extracted with a syringe, centrifuged to remove solid particulates, and were subsequently analysed by 1260 Infinity HPLC coupled with a Hi-Plex Ca (6.5 × 300 mm, 8m particle size, Agilent) column, which was isothermally held at 80 °C, and an ELS detector where sorbitol was used as an external standard. HPLC grade water was used as the mobile phase, at a flow rate of 0.75 mL min−1.
Continuous D-glucose isomerisation was performed in a plug flow, tubular (1/4′′, 4.1 mm ID) stainless-steel reactor using 1 wt% glucose in MeOH as feed. The reactor was connected to an HPLC pump to regulate the reactant flow and be able to operate in high pressures. Catalysts (100 mg) were placed between two plugs of quartz wool and packed in the reactor with a 0.5 μm frit in the reactor outlet. The reactor was then immersed in a thermostatic oil bath at 110 °C. Pressure in the system was controlled using a backpressure regulator, set at the desired pressure (typically 10 bar). Experiments were performed with a flow rate of 1 mL min−1. Periodic aliquots were taken from the reactor outlet and analysed by an Agilent 1260 Infinity HPLC coupled with a Hi-Plex Ca column and an ELS detector, where sorbitol was used as an external standard.
Formulas and mathematical expressions

| (1) |

| (2) |

| (3) |

| (4) |

| (5) |

| (6) |
Catalyst characterization
Specific surface area (SSA) was determined from N2 adsorption using the BET equation, and microporous volume was determined from N2 adsorption isotherms using the t-plot method. Porosimetry measurements were performed on a Quantachrome Quadrasorb, and samples were degassed prior to use (300 °C, 12 h). Adsorption isotherms were obtained at 77 K. TGA analysis was performed on a PerkinElmer system. Samples were held isothermally at 30 °C for 30 min before being heated to 550 °C (10 °C min−1 ramp rate) in N2.TPD-MS measurements were performed on a homemade system formed by a mass flow controllers (MFC) equipped with a horizontal tube furnace where the sample is placed, connected with a Hiden QGA Mass Spectrometer. A weighed amount of catalyst was placed inside a calcination boat and placed in the horizontal furnace and compound evolutions were monitored by the aforementioned spectrometer. The furnace was heated from 30 to 550 °C (ramp rate 10 °C min−1) and a constant flow of N2 was used throughout the experiment (20 mL min−1). N2 flow was switched to air after reaching set temperature and continued for 1 h.
Nuclear Magnetic Resonance (NMR) was carried out in a Bruker Avance III HD 400 MHz NMR spectrometer. 119Sn, 1H, 13C and 29Si NMR were carried out at operating frequencies of 149.23, 400.20, 188.41 and 79.508 MHz, respectively. All analyses were run with a 10 kHz spin rate, with samples packed into ZrO2 rotors. 119Sn MAS DE CPMG NMR experiments were performed with the CPMG echo-train acquisition as described in ref. 47 and 49. Spectra were measured by applying 100 echoes, using a 2.5 μs 90°-pulse with a 180° proton decoupling. The relaxation delay (t1) was set to 5 s, and 2048 scans were performed. Sn chemical shifts were calibrated using Sn(IV) oxide as reference. 29Si MAS NMR were obtained by one-pulse experiment with a 4 μs 45°-pulse with a 20 seconds recycle delay and 128 scans. Chemical shifts were calibrated using the Si(0Al) (4Q) chemical shift at −110 ppm of the commercial aluminium Beta zeolite.62,631H MAS NMR were obtained by a one-pulse experiment with a 2.5 μs pulse with a 3 seconds recycle delay. Adamantane was used for calibration of the 1H chemical shifts. 13C CP MAS were acquired with a relaxation delay of t1 = 5 s, using 2048 scans where glycine was used as the reference of 13C chemical shift.
DRIFT spectroscopy analyses were performed in a Harrick praying mantis cell, using a Bruker Tensor II spectrometer over a range of 4000–650 cm−1 at a resolution of 2 cm−1. In situ DRIFT spectroscopy was performed with the same conditions under flow. The samples were heated at a ramp rate of 10 °C min−1 to set temperature 550 °C under N2 flow, held at 550 °C under N2 flow for 3 h, then switched to air flow (20 mL min−1) for another 3 h. Raman spectra were obtained with a Renishaw inVia spectrometer equipped with a laser line at 266 nm. UV-Vis analysis was performed using a Cary 4000 UV-Vis spectrophotometer. The scan range was done between 200-800 at a scan rate of 200 nm min−1.
Computational simulation
Density functional theory (DFT) calculations were performed using the numeric atomic orbital (NAO) package, FHI-aims, which is an all-electron, full-potential electronic code structure, and is suitable for periodic and non-periodic systems.64 The generalised gradient approximation exchange–correlation functional of Perdew, Burke and Ernzerhof, reparameterised for solids (PBEsol), was used; several density functionals were tested, with PBEsol chosen due to its good comparative performance, and acceptance within the computational community.65 Dispersion interactions were accounted for using the Tkatchenko–Scheffler method, which is a pair-wise additive approach to include van der Waals interactions within the simulation.66 Calculations were performed using a ‘light’ basis set (version: 2010), with self-consistent field (SCF) convergence reached when the charge density was 10−6e/a03. Calculations were performed spin-restricted throughout, and the ZORA approximation was applied to provide relativistic treatments.67Structure optimisation, vibrational simulations and transition state sampling
An initial BEA unit cell structure was obtained from the International Zeolite Association (IZA) database.68 Models were built and manipulated using the Atomic Simulation Environment (ASE) python library.69 Full geometry and unit cell optimisations were performed on all structures using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm,70–73 with convergence reached when the residual forces on all atoms were less than 0.01 eV Å−1. Optimisations were performed with a converged Monkhorst-Pack74k-grid (2 × 2 × 2). Vibrational frequencies were also calculated on optimised structures using ASE, and scaled by a parameterised factor75 of 0.99 to correct for systematic over approximations, allowing direct comparison with experiment.Transition state structures and minimum energy pathways were identified using a machine learning nudged elastic band (ML-NEB) method approached, implemented in the CatLearn software.76 This machine learning approach uses a Gaussian process regression to evaluate uncertainty estimates of all images in a reaction pathway and sets this uncertainty to be a criterion for convergence. To improve computational efficiency without compromising accuracy, atoms beyond a distance from 2 nearest neighbours from the reaction site were frozen. Convergence was assumed when the force on individual atoms was below 0.05 eV Å−1 and the average uncertainty in the interpolated pathway was below 0.05 eV.
X-ray Absorption Spectroscopy analysis
Sn K-edge XAFS studies were performed on the B18 beamline at Diamond Light Source, Didcot, UK, using a Si(111) double crystal monochromator and were measured in transmission mode. The samples were placed into a Harrick X-ray transmission DRIFTS cell, details of which have been described previously.77,78 Spectra were recorded over 2 min intervals (kmax = 14, step size 0.5 eV), and on average three scans were acquired to improve the signal-to-noise level of the data for transmission measurements of each spectrum. All XAFS spectra were acquired concurrently with the appropriate foil placed between It and Iref. XAFS data processing was performed using IFEFFIT79 with the Horae package80 (Athena and Artemis). The amplitude reduction factor was derived from EXAFS data analysis of two reference compounds, SnO2, (with known coordination numbers which were fixed during analysis) to be 1.0, which was used as a fixed input parameter, and Sn(OAc)2.Author contributions
Conceptualisation: CH; experimental data generation: RN, GT, DP, LB, EKG, PPW, SAK, CH; theoretical data generation: OTB, AJL; formal analysis: RN, GT, OBJ, SAK, AJL, CH; funding acquisition: RN, AJL, CH; supervision: GT, AO, AJL, CH; writing: GT, AJL, CH. All authors have given final approval to the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
CH gratefully appreciates financial support from The Royal Society through provision of a University Research Fellowship (UF140207, URF\R\201003) and enhanced research grant funding (RGF/EA/180314). CH also gratefully acknowledges support from The Engineering and Physical Sciences Research Council, for research funding (EP/T024712/1). RN gratefully appreciates financial support from CONACYT (Fellowship 472256). AJL gratefully appreciates funding by the UKRI Future Leaders Fellowship program (MR/T018372/1). The Diamond Light Source and RCaH are thanked for the provision of beamtime (SP12597-1), and Dr Diego Gianolio is thanked for experimental support. OTB gratefully appreciates financial support from the Coleg Cymraeg Cenedlaethol scholarship programme. Computing resources for this work were provided by ARCCA at Cardiff University, Supercomputing Wales, the Isambard 2 UK National Tier-2 HPC Service as funded by EPSRC (EP/T022078/1), and through membership of the UK's HPC Materials Chemistry Consortium (MCC), which is funded by EPRSC (EP/R029431).References
- A. Corma, L. T. Nemeth, M. Renz and S. Valencia, Nature, 2001, 412, 423–425 CrossRef CAS PubMed.
- C. Hammond and G. Tarantino, Catalysts, 2015, 5, 2309–2323 CrossRef CAS.
- F. Cavani and J. H. Teles, ChemSusChem, 2009, 2, 508–534 CrossRef CAS PubMed.
- R. Joyner and M. Stockenhuber, J. Phys. Chem., 1999, 103, 5963–5976 CrossRef CAS.
- C. Hammond, M. M. Forde, M. H. Ab Rahim, A. Thetford, Q. He, R. L. Jenkins, N. Dimitratos, J. A. Lopez-Sanchez, N. F. Dummer, D. M. Murphy, A. F. Carley, S. H. Taylor, D. J. Willock, E. E. Stangland, J. Kang, H. Hagen, C. J. Kiely and G. J. Hutchings, Angew. Chem., Int. Ed., 2012, 51, 5129–5133 CrossRef CAS PubMed.
- M. Boronat, P. Concepcion, A. Corma, M. T. Navarro, M. Renz and S. Valencia, Phys. Chem. Chem. Phys., 2009, 11, 2876–2884 RSC.
- M. Renz, T. Blasco, A. Corma, V. Fornés, R. Jensen and L. Nemeth, Chem.–Eur. J., 2002, 8, 4708–4717 CrossRef CAS.
- A. Corma, M. E. Domine, L. Nemeth and S. Valencia, J. Am. Chem. Soc., 2002, 124, 3194–3195 CrossRef CAS PubMed.
- M. Moliner, Y. Román-Leshkov and M. E. Davis, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6164–6168 CrossRef CAS PubMed.
- M. S. Holm, S. Saravanamurugan and E. Taarning, Science, 2010, 328, 602–605 CrossRef CAS PubMed.
- S. Tolborg, S. Meier, I. Sádaba, S. G. Elliot, S. K. Kristensen, S. Saravanamurugan, A. Riisager, P. Fristrup, T. Skrydstrup and E. Taarning, Green Chem., 2016, 18(11), 3360–3369 RSC.
- H. Xu, X. Wang, P. Ji, H. Wu, Y. Guan and P. Wu, Inorg. Chem. Front., 2018, 5, 2763–2771 RSC.
- L. Nemeth, J. Moscoso, N. Erdman, S. R. Bare, A. Oroskar, S. D. Kelly, A. Corma, S. Valencia and M. Renz, Stud. Surf. Sci. Catal., 2004, 154, 2626–2631 CrossRef.
- S. Tolborg, A. Katerinopoulou, D. D. Falcone, I. Sádaba, C. M. Osmundsen, R. J. Davis, E. Taarning, P. Fristrup and M. S. Holm, J. Mater. Chem. A, 2014, 2(47), 20252–20262 RSC.
- C. Hammond, S. Conrad and I. Hermans, Angew. Chem., Int. Ed., 2012, 51(47), 11736–11739 CrossRef CAS PubMed.
- D. P. Serrano, R. Van Grieken, P. Sánchez, R. Sanz and L. Rodríguez, Microporous Mesoporous Mater., 2001, 46, 35–46 CrossRef CAS.
- L. Botti, R. Navar, S. Tolborg, J. S. Martinez-Espin, D. Padovan, E. Taarning and C. Hammond, Top. Catal., 2019, 62, 1178–1191 CrossRef CAS.
- P. Wolf, M. Valla, F. Núñez-Zarur, A. Comas-Vives, A. J. Rossini, C. Firth, H. Kallas, A. Lesage, L. Emsley, C. Copéret and I. Hermans, ACS Catal., 2016, 6, 4047–4063 CrossRef CAS.
- C. C. Chang, Z. Wang, P. Dornath, H. Je Cho and W. Fan, RSC Adv., 2012, 2, 10475–10477 RSC.
- W. N. P. Van Der Graaff, G. Li, B. Mezari, E. A. Pidko and E. J. M. Hensen, ChemCatChem, 2015, 7, 1152–1160 CrossRef CAS.
- D. Padovan, S. Tolborg, L. Botti, E. Taarning, I. Sádaba and C. Hammond, React. Chem. Eng., 2018, 3, 155–163 RSC.
- C. Hammond, D. Padovan and G. Tarantino, R. Soc. Open Sci., 2018, 5, 1–25 CrossRef PubMed.
- P. Li, G. Liu, H. Wu, Y. Liu, J. G. Jiang and P. Wu, J. Phys. Chem. C, 2011, 115, 3663–3670 CrossRef CAS.
- P. Wolf, C. Hammond, S. Conrad and I. Hermans, Dalton Trans., 2014, 43, 4514–4519 RSC.
- P. Y. Dapsens, C. Mondelli, J. Jagielski, R. Hauert and J. Pérez-Ramírez, Catal. Sci. Technol., 2014, 4, 2302–2311 RSC.
- Q. Guo, F. Fan, E. A. Pidko, W. N. P. Van Der Graaff, Z. Feng, C. Li and E. J. M. Hensen, ChemSusChem, 2013, 6, 1352–1356 CrossRef CAS PubMed.
- I. Y. Eom, S. Lee, S. Y. Hwang and M. Choi, Microporous Mesoporous Mater., 2020, 307, 110524 CrossRef CAS.
- C. Hammond, D. Padovan, A. Al-Nayili, P. P. Wells, E. K. Gibson and N. Dimitratos, ChemCatChem, 2015, 7, 3322–3331 CrossRef CAS PubMed.
- D. Padovan, A. Al-Nayili and C. Hammond, Green Chem., 2017, 19, 2846–2854 RSC.
- H. Joshi, C. Ochoa-Hernández, E. Nürenberg, L. Kang, F. R. Wang, C. Weidenthaler, W. Schmidt and F. Schüth, Microporous Mesoporous Mater., 2020, 309, 110566 CrossRef CAS.
- E. Peeters, G. Pomalaza, I. Khalil, A. Detaille, D. P. Debecker, A. P. Douvalis, M. Dusselier and B. F. Sels, ACS Catal., 2021, 11, 5984–5998 CrossRef CAS.
- L. Botti, D. Padovan, R. Navar, S. Tolborg, J. S. Martinez-Espin and C. Hammond, ACS Catal., 2020, 10, 11545–11555 CrossRef CAS.
- V. S. Stafeeva, A. S. Mitiaev, A. M. Abakumov, A. A. Tsirlin, A. M. Makarevich and E. V. Antipov, Polyhedron, 2007, 26, 5365–5369 CrossRef CAS.
- G. S. Groenewold, W. A. de Jong, J. Oomens and M. J. Van Stipdonk, J. Am. Soc. Mass Spectrom., 2010, 21, 719–727 CrossRef CAS PubMed.
- V. Zeleňák, Z. Vargová and K. Györyová, Spectrochim. Acta, Part A, 2007, 66, 262–272 CrossRef.
- E. G. Palacios, G. Juárez-López and A. J. Monhemius, Hydrometallurgy, 2004, 72, 139–148 CrossRef CAS.
- A. Kuzume, M. Ozawa, Y. Tang, Y. Yamada, N. Haruta and K. Yamamoto, Sci. Adv., 2019, 5, 1–8 Search PubMed.
- T. Arii and A. Kishi, Thermochim. Acta, 2003, 400, 175–185 CrossRef CAS.
- J. D. Donaldson, W. Moser and W. B. Simpson, J. Chem. Soc., 1964, 5942–5947 RSC.
- W. Hao, W. Zhang, Z. Guo, J. Ma and R. Li, Catalysts, 2018, 8, 504 CrossRef.
- J. Dijkmans, M. Dusselier, W. Janssens, M. Trekels, A. Vantomme, E. Breynaert, C. Kirschhock and B. F. Sels, ACS Catal., 2016, 6, 31–46 CrossRef CAS.
- D. Padovan, L. Botti and C. Hammond, ACS Catal., 2018, 8, 7131–7140 CrossRef CAS.
- F. Farges, R. L. Linnen and G. E. Brown, Can. Mineral., 2006, 44, 795–810 CrossRef CAS.
- J.-W. Park and C.-M. Park, J. Electrochem. Soc., 2015, 162, A2811–A2816 CrossRef CAS.
- N. Murata, T. Suzuki, M. Kobayashi, F. Togoh and K. Asakura, Phys. Chem. Chem. Phys., 2013, 15, 17938–17946 RSC.
- S. R. Bare, S. D. Kelly, W. Sinkler, J. J. Low, F. S. Modica, S. Valencia, A. Corma and L. T. Nemeth, J. Am. Chem. Soc., 2005, 127, 12924–12932 CrossRef CAS PubMed.
- Y. G. Kolyagin, A. V. Yakimov, S. Tolborg, P. N. R. Vennestrøm and I. I. Ivanova, J. Phys. Chem. Lett., 2016, 7, 1249–1253 CrossRef CAS PubMed.
- S. J. Hwang, R. Gounder, Y. Bhawe, M. Orazov, R. Bermejo-Deval and M. E. Davis, Top. Catal., 2015, 58, 435–440 CrossRef CAS.
- W. Dai, Q. Lei, G. Wu, N. Guan, M. Hunger and L. Li, ACS Catal., 2020, 10, 14135–14146 CrossRef CAS.
- A. V. Yakimov, Y. G. Kolyagin, S. Tolborg, P. N. R. Vennestrøm and I. I. Ivanova, J. Phys. Chem. C, 2016, 120, 28083–28092 CrossRef CAS.
- P. Wolf, M. Valla, A. J. Rossini, A. Comas-Vives, F. Núñez- Zarur, B. Malaman, A. Lesage, L. Emsley, C. Copéret and I. Hermans, Angew. Chem., Int. Ed., 2014, 53, 10179–10183 CrossRef CAS PubMed.
- P. Wolf, W. C. Liao, T. C. Ong, M. Valla, J. W. Harris, R. Gounder, W. N. P. van der Graaff, E. A. Pidko, E. J. M. Hensen, P. Ferrini, J. Dijkmans, B. Sels, I. Hermans and C. Coperet, Helv. Chim. Acta, 2016, 99, 916–927 CrossRef CAS.
- G. Qi, Q. Wang, J. Xu, Q. Wu, C. Wang, X. Zhao, X. Meng, F. Xiao and F. Deng, Commun. Chem., 2018, 1, 1–7 CrossRef CAS.
- R. Bermejo-Deval, R. S. Assary, E. Nikolla, M. Moliner, Y. Roman-Leshkov, S.-J. Hwang, A. Palsdottir, D. Silverman, R. F. Lobo, L. A. Curtiss and M. E. Davis, Proc. Natl. Acad. Sci., 2012, 109, 9727–9732 CrossRef CAS PubMed.
- R. Gounder and M. E. Davis, J. Catal., 2013, 308, 176–188 CrossRef CAS.
- G. Yang, E. A. Pidko and E. J. M. Hensen, ChemSusChem, 2013, 6, 1688–1696 CrossRef CAS PubMed.
- M. Boronat, A. Corma and M. Renz, J. Phys. Chem. B, 2006, 110, 21168–21174 CrossRef CAS PubMed.
- A. A. Marianou, C. M. Michailof, D. K. Ipsakis, S. A. Karakoulia, K. G. Kalogiannis, H. Yiannoulakis, K. S. Triantafyllidis and A. A. Lappas, ACS Sustainable Chem. Eng., 2018, 6, 16459–16470 CrossRef CAS.
- H. Li, S. Yang, S. Saravanamurugan and A. Riisager, ACS Catal., 2017, 7, 3010–3029 CrossRef CAS.
- R. Bermejo-Deval, M. Orazov, R. Gounder, S. J. Hwang and M. E. Davis, ACS Catal., 2014, 4, 2288–2297 CrossRef CAS.
- L. Botti, S. A. Kondrat, R. Navar, D. Padovan, J. S. Martinez-Espin, S. Meier and C. Hammond, Angew. Chem., Int. Ed., 2020, 59, 20017–22002 CrossRef CAS PubMed.
- K. Chalupka, R. Sadek, L. Valentin, Y. Millot, C. Calers, M. Nowosielska, J. Rynkowski and S. Dzwigaj, J. Chem., 2018, 2018, 1–11 CrossRef.
- P. Shestakova, C. Martineau, V. Mavrodinova and M. Popova, RSC Adv., 2015, 5, 81957–81964 RSC.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- E. Van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- J. M. Newsam, M. M. J. Treacy, W. T. Koetsier and C. B. De Gruyter, Proc. R. Soc. A, 1988, 420, 375–405 CAS.
- A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- C. G. Broyden, J. Inst. Math. Its Appl., 1970, 6, 76–90 CrossRef.
- R. A. Fletcher, Comput. J., 1970, 13, 317–322 CrossRef.
- D. Goldfarb, Math. Comp., 1970, 24, 23 CrossRef.
- D. F. Shanno, Math. Comp., 1970, 24, 647 CrossRef.
- M. Alcolea Palafox, Phys. Sci., 2018, 3, 1–30 Search PubMed.
- J. A. Garrido Torres, P. C. Jennings, M. H. Hansen, J. R. Boes and T. Bligaard, Phys. Rev. Lett., 2019, 122, 156001 CrossRef CAS PubMed.
- E. K. Gibson, A. M. Beale, R. A. Catlow, A. Chutia, D. Gianolio, A. Gould, A. Kroner, K. M. H. Mohammed, M. Perdjon, S. M. Rogers and P. P. Wells, Chem. Mater., 2015, 27, 3714–3720 CrossRef CAS.
- E. K. Dann, E. K. Gibson, R. A. Catlow, P. Collier, T. E. Erden, D. Gianolio, C. Hardacre, A. Kroner, A. Raj, A. Goguet and P. P. Wells, Chem. Mater., 2017, 29, 7515–7523 CrossRef CAS.
- M. Newville, J. Synchrotron Radiat., 2001, 8, 322–324 CrossRef CAS PubMed.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional kinetic, spectroscopic and theoretical data, is available. See https://doi.org/10.1039/d2ta03837d. All structures calculated in this work have been uploaded to the NOMAD repository (DOI: 10.17172/NOMAD/2022.09.02-2). |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |