Effect of structure on oxygen diffusivity in layered oxides: a combined theoretical and experimental study

Abstract

Electrochemical systems based on oxide ion conduction such as solid oxide fuel cells (SOFCs) and solid oxide electrolysis cells (SOECs) provide efficient means of converting energy between chemical and electrical forms, integral to a hydrogen-based energy society. Fundamental understanding of oxygen diffusivity in solids – which can depend on defect type, concentration, as well as migration barrier – is critical in developing their key components: electrolytes and mixed ionic-electronic conducting electrodes. It has been speculated that crystal structure affects the key three factors impacting oxygen diffusion, but no such experiments have been done, without changing cation chemistries, to the best of the authors' knowledge. In this work, oxygen diffusivities in two different but related structures of lanthanum cuprate (La₂CuO_4+δ) thin films were measured through oxygen isotope exchange experiments and secondary ion mass spectrometry (SIMS) at multiple temperatures. We find that while oxygen diffusion is faster in a T-structured layered cuprate, it nevertheless exhibits a higher activation energy as compared to a T′-structured layered cuprate of the same cation chemistry. This seemingly contradictory phenomenon is explained by a lower oxygen defect formation energy (thus higher oxygen defect concentration) but higher defect migration barrier in the T-structure as calculated by density functional theory, offering insight towards structural design of SOFC and SOEC electrolyte and electrode materials for different target temperatures.

---

1. Introduction

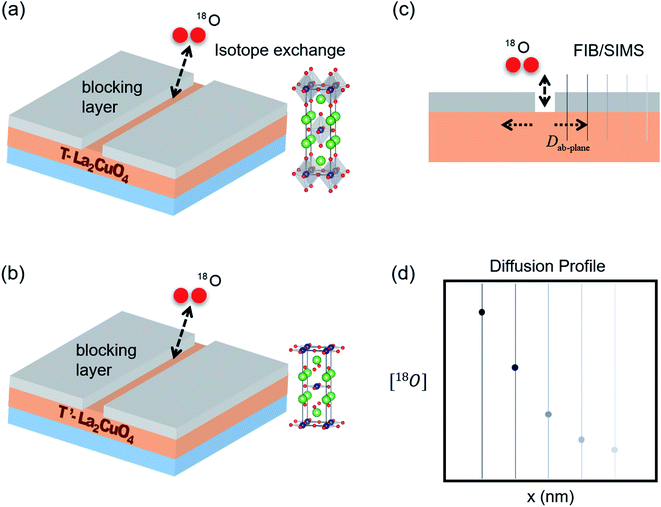
Atomic and ionic diffusion in solids has received growing interest over the past few decades as solid state electrochemical systems such as batteries and fuel cells have become efficient and effective means of generating and storing electrical energy derived from chemical energy.^1–6 Diffusion in solids is of particular interest in solid state batteries (lithium ions)^7,8 and solid oxide fuel cells (oxygen ions),^9–11 as higher diffusivity correlates with higher electrolyte and electrode performances. In the case of oxygen diffusion, there exist two types of oxygen defects – oxygen vacancies and interstitials – that can support oxygen diffusivity. Oxygen ions adjacent to vacant sites enable oxygen ions to hop from normally occupied to adjacent unoccupied sites in the lattice, while interstitials can diffuse via two different mechanisms, viz., via interstitial (from normally occupied to a nearby empty interstitial site), and interstitialcy (interstitial ion displacing a normally occupied ion into an adjacent empty interstitial site) mechanisims.¹² Unlike fluorite and perovskite oxides, which can normally only accommodate oxygen vacancies (UO_2+x is an exception¹³), layered oxides can accommodate both types of defects,^14–17 thus offering an advantage in their ability to operate at high oxygen partial pressures via oxygen interstitial/interstitialcy diffusion, and at low oxygen partial pressures via oxygen vacancy diffusion.

A common form of layered oxide is A₂B₁O₄ – also known as the 214 phase (term n = 1 of the Ruddlesden–Popper series A_n+1B_nO_3n+1) – including nickelates, cobaltates, and cuprates in which Ni, Co, and Cu occupy the B-site, respectively. Nickelate and cobaltate 214 phases exhibit the K₂NiF₄, or T structure, with alternating stacks of rock-salt AO- and perovskite ABO₃-layers. Because copper can accommodate three different oxygen coordinations, as shown in Fig. S1,† three different crystal structures exist for the 214 cuprates. For layered cuprates with large A-site cations, such as lanthanum or strontium, copper is octahedrally coordinated by six oxygen atoms (T-A₂CuO₄). With small A-site cations, such as praseodymium or cerium, copper forms square-planar coordination (T′-A₂CuO₄), and in between the two phases there is the T* structure, a hybrid of T and T′, in which copper forms pyramidal coordination blocks with oxygen.¹⁸ These three structures may share similar chemistries, but show very distinct characteristics. For example, T′-structured Pr₂CuO₄ has an extremely low oxygen diffusivity of 7.2 × 10⁻¹³ cm² s⁻¹ at 700 °C.¹⁹ The incorporation of the larger Sr²⁺ cations on the A-site leads to the T* structure, as in Pr_1.6Sr_0.4CuO₄, which exhibits a significantly higher oxygen diffusivity of 6.7 × 10⁻¹⁰ cm² s⁻¹ at 700 °C.²⁰ T-structured La₂CuO₄ exhibits an even higher oxygen diffusion coefficient D* of around 1 × 10⁻⁸ cm² s⁻¹.²¹ However, it is unclear whether the difference in diffusivity comes from the crystal structure, since both the cation chemistry and size are changing. Increasing acceptor/donor concentrations will likely lead to larger numbers of oxygen vacancies/interstitials. Different diffusion mechanisms also affect how fast oxygen can migrate. Oxygen diffusion in Pr₂CuO₄ or T-La₂CuO₄ is believed to be through oxygen interstitialcy mechanism, while in acceptor-doped Pr_1.6Sr_0.4CuO₄, diffusion is via the oxygen vacancy mechanism. Different cation sizes can affect local charge distribution, lattice parameter and lattice strain, thereby affecting diffusivity. There is no direct comparison of oxygen diffusivities among these structures as each cation chemistry is stable in only one structure. This study aims to answer the question of how different structures of identical cation chemistry affect diffusion and investigate underlying mechanisms by combining experimental (structural control and oxygen isotope exchange) and theoretical (density functional theory) methods.

2. Experimental methods

2.1 Thin film preparation

T and T′-structured La₂CuO₄, thin films of ∼30 nm thickness were grown by pulsed laser deposition (PLD). After loading single crystal LaAlO₃ (LAO) substrates (MTI Corporation) and a bulk target of desired composition (refer to Experimental section in Kim, et al.¹⁷), the PLD chamber was pumped down to a base pressure of 3 × 10⁻⁶ Torr, and then the substrate was heated to 600 °C. A Coherent COMPex Pro 205 KrF eximer laser of 248 nm wavelength with 260 mJ per pulse at 1 Hz was used to ablate the bulk targets. The surface of each target was pre-ablated with 300–3000 pulses before every deposition. The chamber was maintained at 10 mTorr oxygen pressure during deposition.

2.2 Structural characterization

2.2.1 X-ray diffraction. X-ray diffraction (XRD) measurements for thin films were performed using Rigaku Smartlab with high resolution PB-Ge(220)×2 package. Alignment to the symmetric substrate (single crystal LAO with (001) orientation) peak was performed prior to each scan.

2.2.2 TEM analysis. TEM samples from layered cuprate thin films were prepared by using FEI Nova NanoLab focused ion beam. To eliminate any charge effect and protect the sample surface from Ga⁺ ion beam damage, 90 nm of Au and 30 nm of Pt/Pd (80/20) were deposited on the sample by DC sputtering. Additional protective layers of polymer resin and 5 nm of Pt/Pd (80/20) were subsequently deposited, and finally 1.7 μm of Pt was deposited by gas injection system (GIS). The sample was Ga⁺ ion milled at 30 kV, at various currents. A tungsten (W) omniprobe was used to pick up the milled plate and attach it on a Mo TEM grid. After the sample attachment on the grid, fine milling was conducted at low currents by reducing the milling current gradually. The atomic structures of the La₂CuO₄ thin films were investigated using HAADF (High-Angle Annular Dark Field) and BF (Bright Field) images obtained by FEI Titan scanning/transmission electron microscope (S/TEM) at accelerating voltage of 300 kV. Here, a 300 kV electron beam is focused down to a spot with probe size of <0.1 nm, and scanned across the thinned sample.

2.3 Oxygen diffusivity measurement

2.3.1 Oxygen isotope exchange experiment. Schematic illustrations of the experiment is shown in Fig. 1(a) and (b). A 90 nm thick gold blocking layer was deposited on top of a PLD-deposited T- or T′-La₂CuO₄ thin film except for a narrow area masked by a thin kapton tape. After removing the tape, the film was annealed at 673 K for five hours in air to stabilize the gold layer. A custom-built oxygen isotope exchange setup as shown in Fig. S2† was used. The sample is placed inside a quartz tube, then a high vacuum pump system consisting of Edwards EXT70 turbomolecular pump, RV3 rotary vane pump, and EXC120 turbomolecular pump controller is used to pump down to 5.0 × 10⁻⁶ Torr range. The tube is then filled with ultra high purity oxygen to 0.5 atm = 506.625 hPa and the furnace is slid on tracks so that the sample is located at the center of the furnace and annealed for at least 10 times longer than the isotope exchange exposure period at 500, 550, and 600 °C. The sample is then quenched to room temperature by sliding the furnace away from the sample chamber and exposing the sample tube to a fan to further cool the specimen. The tube is then pumped down again to 5.0 × 10⁻⁶ Torr, then filled with ¹⁸O₂ gas (99%, Sigma Aldrich) to the same pressure of 0.5 atm = 506.625 hPa. The process is then repeated for each exchange experiment. The diffusion profiles of the oxygen isotope are subsequently analyzed by secondary ion mass spectrometry (SIMS).

Fig. 1 Schematic figures of ¹⁸O isotope exchange of (a) T and (b) T′ structures of LCO thin films. (c) The oxygen isotope in the gas becomes incorporated into the thin film at the break in the blocking layer, shown schematically at the center of the specimen, and subsequently diffuses along the film's ab-plane. Diffusion profiles of the isotope, shown schematically in (d) are obtained by focused ion beam (FIB) secondary ion mass spectroscopy (SIMS).

2.3.2 Secondary ion mass spectrometry. Oxygen isotope diffusion profile in T- and T′-structured La₂CuO₄ thin films were analyzed by IONTOF TOF. SIMS 5 (Münster, Germany) Time-of-Flight Secondary Ion Mass Spectrometry (ToF-SIMS) as illustrated in Fig. 1(c) and (d). First, a 30 nA beam of 3 keV Cs⁺ ions was rastered to etch the gold layer. Then, secondary ion images were obtained with a 0.2 pA beam of 30 keV Bi₁⁺ ions.

3. Computational methods

3.1 Bulk T- and T′-structures

We modeled bulk T- and T′-structured La₂CuO₄ (space group = I4/mmm) using a 2 × 2 × 2 supercell composed of 112 atoms with DFT calculations. DFT calculations were performed using VASP^22,23 with projected augmented wave (PAW) pseudopotentials from the VASP database and generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE).²⁴ An energy cutoff of 700 eV and a 3 × 3 × 1 Monkhorst–Pack k-point mesh were used after convergence tests. Atom positions were relaxed until all forces were less than 0.005 eV Å⁻¹. Lattice constants of La₂CuO₄ used in this study are a = b = 3.803 Å and c = 13.15 Å for the T-structure and a = b = 4.005 Å and c = 12.55 Å for the T′-structure.^18,25 The probable strain and its effect on defect formation energies by the lattice mismatch between T- and T′-structured La₂CuO₄ thin films and LaAlO₃ substrates are so small that they were not taken into account in this study (explained in more detail in the ESI Fig. S3 and S4†).

3.2 Oxygen defect formation energies

To calculate the change in enthalpy when oxygen vacancies or interstitials are generated in La₂CuO₄, O atoms were removed from or added to the perfect La₂CuO₄ supercells, and then relaxed as done for the perfect La₂CuO₄ supercell. The defect formation or generation energy in the field of computational chemistry – when an oxygen defect of charge q is inserted in bulk La₂CuO₄ is defined as:where E^defect:q_tot is the total energy of a relaxed supercell containing oxygen defect with charge q, and E^perfect_tot is the total energy for the perfect crystal using an equivalent supercell. The integer n_O indicates the number of O atoms that have been removed from (or added to) the supercell to form the defect, and μ_O is the oxygen chemical potential. The electrochemical potential for electrons is the Fermi energy, E_F, which is measured from the valence band edge maximum (VBM). To calculate the E_F relative to VBM, we employed the DFT + Hubbard U (DFT+U) approach within spin-polarized density functional theory by applying U_eff (U − J) = 3 eV for ferromagnetic (FM) spin ordered La²⁶ and 8 eV for type-II antiferromagnetic (AFM-II) spin ordered Cu.²⁷ As shown in Fig. S5,† we found that the value of E_F relative to VBM does not change with respect to the U_eff value applied on Cu, even though band gaps similar to experimental values (1–2 eV (ref. 28)) could be obtained in a range of 4 eV < U_eff for Cu < 8 eV. Therefore, we conclude that U_eff value is not a critical factor for calculating the oxygen defect formation energy of La₂CuO₄. E^perfect_VBM is the VBM of the perfect supercell, which is obtained by E^perfect_tot − E^perfect,+1_tot, where E^perfect,+1_tot is the total energy of the +1 charged perfect supercell. ΔV_avg is the difference in average potentials (V_avg) far from the defect relative to the perfect supercell, i.e., ΔV_avg = V^defect:q_avg − V^perfect_avg, where V^defect:q_avg and V^perfect_avg are the average potentials of the defective and perfect supercells, respectively. The last two terms in eqn (1), q(E^perfect_VBM + ΔV_avg), are the same as E_corr, a correction term that accounts for finite k-point sampling in the case of shallow impurities, or for elastic and/or electrostatic interactions between supercells, introduced in ref. 29 and 30. The calculation of the correction term is explained in Fig. S6 in ESI.†

To describe the defects in experimentally prepared T- and T′-La₂CuO₄,^31,32 we chose single and paired oxygen defects in eight unit cells of T- and T′-La₂CuO_4±δ (i.e., δ = 1/64 and 1/32). Oxygen defects in T- and T′-La₂CuO_4±δ were created by removing/adding an oxygen atom in the perfect T- and T′-La₂CuO₄ structures. The formation energy of each oxygen defect was calculated relative to the perfect LCO crystal, using eqn (1). For examination of defect pairs in T- and T′-La₂CuO_4±δ, an additional oxygen atom was removed/added from the previous LCO structures with a single oxygen defect. We named the oxygen defect pairs ‘V_O²⁺–V_O²⁺ pairs’ and ‘I_O²⁻–I_O²⁻ pairs’. Their defect formation energies were calculated relative to the previous states with single defects using eqn (1), reflecting how much energy is required to create additional oxygen defects from the LCO structures with a single defect in eight unit cells.

3.3 Activation energy for diffusion

The nudged elastic band (NEB) routine^33–35 along with the climbing image method³⁴ implemented in VASP, was used with DFT calculations to predict the lowest energy pathway for oxygen diffusion in T- and T′-LCO. The initial and final configurations of diffusion pathways were optimized as done for the relaxation of the structures containing doubly charged defects. Eight images of intermediate atomic configurations were generated with constant spacing between the initial and final configurations. A spring constant of 5.0 eV Å⁻² and energy cutoff of 700 eV were used. The ionic relaxations were conducted until all forces were less than 0.005 eV Å⁻¹, and the electronic convergence was terminated at an energy difference of 10⁻⁴ eV.

4. Results and discussion

4.1 Structural characterization

XRD spectra of La₂CuO₄ (LCO) thin films grown by PLD on single crystal LaAlO₃ (100) substrates with and without seed layer (deposited between substrate and desired film) are shown in Fig. 2. LCO grows as a single-phase T-structure on LaAlO₃ without seed layer, but forms a T′-structure when deposited on top of a thin seed layer of La_1.85Ce_0.15CuO₄ (LCCO15). Both films are grown c-axis oriented perpendicular to the substrates.

Fig. 2 Symmetric 2θ–ω HRXRD scans of La₂CuO₄ thin films on LaAlO₃ single crystal substrates with (bottom/blue) and without (top/red) a La_1.85Ce_0.15CuO₄ (LCCO15) seed layer (2–3 nm thick). Both films have c-axis perpendicular to the substrates.

T- and T′-structured LCO thin films without and with the LCCO15 seed layer on LaAlO₃ substrates were further investigated by STEM-HAADF and -BF images, as shown in Fig. 3. As can be seen in Fig. 3(a) and S3,† the T-structured LCO thin film grows epitaxially on the LaAlO₃(001) substrate and perpendicular to the substrate (parallel to c-axis of the LCO film), which agrees with the results from HRXRD analyses in Fig. 2. The T′-structured LCO film grown on the LCCO15 seed layer/LaAlO₃ substrate (Fig. 3(b)) is not as epitaxial compared to the T-LCO film without seed layer, presumably due to lattice mismatch (refer to ‘strain in LCO thin film’ section in ESI†). However, the film is highly crystalline with near-uniform structure and with preferred orientation (c-axis perpendicular to the substrate as analyzed with respect to the locations of La, Cu and O atoms), agreeing with the results from HRXRD in Fig. 2.

Fig. 3 Scanning transmission electron microscopy (STEM) – high angle annular dark field (HAADF) and – bright field (BF) images of (a) T-La₂CuO₄ (LCO) thin film on LaAlO₃ (LAO) substrate and (b) T′-La₂CuO₄ thin film on LCCO15 seed layer/LAO substrate. Green, blue, and red circles in each image are inserted in order to identify the atomic positions of La, Cu, O atoms in T- or T′-structured LCO, respectively.

The difference in the positions of some oxygen atoms between T- and T′-LCO are clearly observed in the STEM-BF images of Fig. 3; the STEM-BF image of oxygen atoms in apical sites in T-LCO shows brighter line contrast along a- or b-axis of the thin film (denoted with blue dotted lines in Fig. 3(a)) than that of oxygen atoms in equatorial sites, while T′-LCO shows little difference in the STEM-BF contrast of oxygen atoms between O-and CuO₂-planes as can be seen in Fig. 3(b). This contrast difference in T- and T′-LCO confirms that T- and T′-LCO thin films form on LAO(001) substrates without and with LCCO15 seed layer.

4.2 Oxygen diffusivities of T- and T′-La₂CuO₄

The oxygen diffusivities of both T- and T′-LCO thin films are studied to examine the effect of structure on diffusivity with films of the same cation chemistry but different structures. The two structures of LCO are prepared on insulating LAO substrates with and without a LCCO15 seed layer as described in Section 4.1. Cation diffusion is so slow for heavy atoms such as La and Ce that studies have been conducted at 900 °C and above .^36–39 By extrapolating the diffusivity temperature dependence down to 600 °C, D of La and Ce comes out to be less than 10⁻²⁴ cm² s⁻¹. The highest temperature our samples experienced was at 600 °C for less than two hours (including deposition and isotope exchange experiments), and total diffusion length, comes out to be less than 1 Å. Therefore, it is valid to assume that there is not sufficient Ce diffusion from the seed layer (∼1.5 nm thick) to LCO (∼30 nm thick) to affect oxygen diffusion behavior.

Oxygen diffusion in the ab-plane is faster than along the c-axis as evidenced in the isostructural nickelates,^40,41 and will dominate the performance in polycrystalline bulk materials used for practical purposes. Therefore, diffusion in the ab-plane for the two structures is compared with films oriented c-axis perpendicular to the substrate. After the ¹⁸O isotope exchange is completed, the isotope profiles are obtained by SIMS as described in experimental methods and Fig. 1. Oxygen isotope concentration–distance profiles for T- and T′-LCO are plotted in Fig. 4(a) and (b). The ¹⁸O isotope density in both thin films decreases along the direction of in-plane diffusion. The distribution of the ¹⁸O isotope in the T-LCO thin film extends further from the origin than in the T′-LCO thin film over the same period of time, indicating that the ¹⁸O isotope exhibited a higher diffusivity in T-LCO than in T′-LCO.

Fig. 4 ¹⁸O isotope concentration profiles measured by ToF-SIMS after oxygen isotope exchange for one hour at aO₂ = 0.5 atm and 600 °C for (a) T- and (b) T′-La₂CuO₄ thin films.

Fig. 5 Oxygen tracer diffusion coefficients along the ab-plane for T- and T′-LCO thin films at aO₂ = 0.5 atm as a function of inverse temperature (1/T).

Values for (oxygen diffusion coefficient along ab-plane) are extracted by fitting the data with the aid of Crank's solution⁴² for diffusion in a semi-infinite medium. The fits to the data in Fig. 4 resulted in = 1.06 × 10⁻⁸ cm² s⁻¹ for T-LCO and = 1.30 × 10⁻⁹ cm² s⁻¹ for T′-LCO at 600 °C showing that the oxygen diffusivity for the T-structure is approximately ten times higher than that in the T′-structure.

Oxygen tracer diffusion experiments were performed at two additional temperatures, 500 and 550 °C, with the derived diffusion coefficients plotted in Fig. 4. The temperature dependence of diffusivity can be expressed as

where [def] is the migrating defect concentration, Z the number of potential defect migration sites, d the jump distance, and ν₀ the attempt frequency. The extracted pre-exponential terms and activation energies for diffusion (i.e., migration enthalpy E_m) for T- and T′-LCO are 2.21 × 10² cm² s⁻¹ and 1.07 × 10⁻³ cm² s⁻¹, and 1.79 ± 0.03 eV and 1.03 ± 0.24 eV, respectively. Because Z, d, and ν₀ cannot differ by more than few factors between T- and T′-LCO, we can deduce that T-LCO has several orders of magnitude more oxygen defects than T′-LCO. It is notable that while the magnitude of oxygen tracer diffusion is larger for T-LCO in this temperature range due to the large number of defects, it nevertheless exhibits a higher activation than that of T′-LCO. Extrapolating the diffusivity fits, T-LCO will have smaller diffusion coefficients below 415 °C. This represents the first direct comparison of oxygen diffusivity between T- and T′-structures with the same cation chemistry. Previous comparisons of oxygen diffusivities obtained for the T- and T′-structured layered cuprates were derived from studies on cuprates with different chemical compositions.¹⁹

4.3 Oxygen defect formation energies

In oxygen-diffusion mediated materials, a higher oxygen diffusion coefficient is generally correlated with a lower activation energy for diffusion (E_a).⁴³ However, we observe that while the T-structured LCO shows faster oxygen diffusion, it nevertheless exhibits a higher activation barrier compared to T′-structured LCO. In an attempt to explain this unexpected relationship, we examine the respective defect chemistries of T- and T′-structured LCO, utilizing DFT calculations (described in Computational methods section) to identify the dominant type(s) of oxygen defects contributing to diffusion and their relative concentrations in the two structures.

4.3.1 Case of single defects. Fig. 6 shows atomic configurations in T- and T′-LCO, and the positions of different oxygen defects in the structures. In both structures, two distinct oxygen vacancy sites exist, the so-called apical and equatorial oxygen sites for the T-structure, and the O- and CuO₂-plane sites for the T′-structure. Out of two interstitial sites in T-LCO, only one – shown in Fig. 6(a) – is thermodynamically feasible,⁴⁴ which is also confirmed by our calculations. There is only one interstitial site in T′-LCO. The defect formation energy of each defect type was examined with different defect charges, i.e., neutral, singly- and doubly-charged. As summarized in the tables in Fig. 6, oxygen interstitials are highly likely to be formed in T-LCO regardless of their charge. Among oxygen interstitials with different charges, doubly-charged interstitials show the lowest formation energy, suggesting that doubly-charged oxygen interstitials predominantly form in T-LCO. Likewise, oxygen interstitials prefer to be generated in T′-structured LCO (Fig. 6(b)), while oxygen vacancy formation is also highly feasible in the O-plane. Two types of oxygen defects are therefore predicted to exist in the T′-structured LCO. Considering that the formation energy of oxygen interstitials in T-LCO is much lower than in T′-LCO (nearly twice lower), the oxygen interstitial concentration naturally formed in T-LCO is predicted to be much higher than in T′-LCO. For example, at 600 °C, is 7.95 × 10¹⁵ and 2.01 × 10⁷ for doubly-charged oxygen interstitials in T- and T′-LCO, respectively.

Fig. 6 Images: atomic configurations of (a) T-La₂CuO₄ and (b) T′-La₂CuO₄ used for the calculation of defect formation energies in this study. Green, blue, red circles denote La, Cu, O atoms, respectively. Apical and equatorial oxygen sites in T-LCO are denoted with ‘A’ and ‘E’, oxygen sites in O and CuO₂-planes in T′-LCO are denoted with ‘O’ and ‘C’. The oxygen interstitial site most stable in T- or T′-LCO considered in this study is indicated by ‘I’. Tables: defect formation energies of neutral, singly- and doubly-charged (a) V^A_O, V^E_O, and I_O in T-LCO and (b) V^O_O, V^C_O, and I_O in T′-LCO, where A, E, O, C denote different oxygen sites. The unit used for the defect formation energy is eV per defect.

4.3.2 Case of defect pairs. In order to examine whether oxygen defect pairs can be formed in local regions, defect pair formation energies for V_O²⁺–V_O²⁺ and I_O²⁻–I_O²⁻ in T- and T′-LCO were calculated and are shown in Fig. 7 and 8. Since interactions between closely-located defect pairs predominate in their impact on formation and defect migration energies, we only consider defect pairs at 1^st and 2^nd nearest neighbor distances. Furthermore, the formation of oxygen vacancy pairs is considered only around equatorial oxygen sites in T-LCO, or oxygen sites in O-plane in T′-LCO because oxygen vacancy formation is more stable at these sites as summarized in the tables in Fig. 6.

Fig. 7 Images: atomic configurations of T-LCO showing the locations of (a) V_O²⁺–V_O²⁺ pairs and (b) I_O²⁻–I_O²⁻ pairs in T-LCO. Green, blue, red circles denote La, Cu, O atoms, respectively. ‘E’ and ‘I’ in gray and yellow circles denote the first oxygen vacancy existing on equatorial oxygen site (1^st V_O²⁺) and first oxygen interstitial existing in the most possible/stable sites (1^st I_O²⁻) in T-LCO according to Fig. 6(a), respectively. ‘I’ and ‘II’ in pink circles indicate the 2^nd defect position at the 1^st and 2^nd nearest neighbors from the 1^st defect. Yellow and pink circles on the right side of (b) denote 1^st I_O²⁻ and 2^nd I_O²⁻, respectively. Tables: defect formation energy (E_f) of (a) V_O²⁺–V_O²⁺ pairs and (b) I_O²⁻–I_O²⁻ pairs in T-LCO, with respect to the 2^nd defect location. Unit is eV per defect. When the 2^nd I_O²⁻ exists in the 2^nd nearest neighbor (position II in (b)), the T-LCO structure becomes unstable and the 2^nd I_O²⁻ moves to position I. Therefore, the formation energy of the 2^nd I_O²⁻ at position II could not be calculated.

Fig. 8 Images: atomic configurations of T′-LCO showing the locations of (a) V_O²⁺–V_O²⁺ pairs and (b) I_O²⁻–I_O²⁻ pairs in T′-LCO. Green, blue, red circles denote La, Cu, O atoms, respectively. ‘O’ and ‘I’ in gray and yellow circles denote oxygen vacancy in O-plane and oxygen interstitial in the most stable interstitial site in T′-LCO (according to Fig. 6(b)), respectively. Numbers ‘1’ through ‘4’ in pink circles indicate the 2^nd defect position relative to the 1^st defect. Yellow and pink circles on the right side of (b) denote 1^st I_O²⁻ and 2^nd I_O²⁻, respectively. Tables: defect formation energy (E_f) of (a) V_O²⁺–V_O²⁺ pairs and (b) I_O²⁻–I_O²⁻ pairs in T′-LCO, with respect to the 2^nd defect location. Unit is eV per defect.

As summarized in the tables in Fig. 7, T-LCO strongly favors a second oxygen interstitial in the 1^st nearest neighbor position (position I in Fig. 7(b)) to form a pair, given the highly negative formation energy of I_O²⁻–I_O²⁻ pair. Oxygen vacancy pairs, on the other hand, hardly form in T-LCO, regardless of the locations of the defect pairs. This result is in accordance with the formation energy of a single oxygen defect shown in Fig. 6(a); T-LCO thermodynamically prefers to form a high concentration of interstitials while incapable of accommodating oxygen vacancies.

For T′-LCO, both V_O²⁺–V_O²⁺ (Fig. 8(a)) and I_O²⁻–I_O²⁻ pairs (Fig. 8(b)) have negative formation energies, and therefore local regions with both oxygen vacancy and interstitial pairs can exist. Among several configurations with different neighbors, the 2^nd nearest neighbor (position 1 in Fig. 8) is the most energetically favorable for vacancy defects. For interstitial defects, the 1^st nearest neighbor pair is the most energetically favorable. Note that this is only considering oxygen interstitials; oxygen atoms on O- and CuO₂-planes as well as lanthanum and copper atoms are closer than the first nearest interstitial.

4.4 Oxygen diffusion path

To find the minimum energy path (MEP) for oxygen diffusion along the ab-plane in T- and T′-structured La₂CuO₄, diffusion energy barriers were calculated using NEB methods as explained in Computational methods for every possible migration pathway taken by oxygen vacancies or interstitials in the structures. For the NEB calculations, only doubly charged oxygen interstitials and vacancies were considered given that they are thermodynamically favored to be generated, according to the defect deformation energies reported in Section 4.3. The diffusion pathways along the ab-plane were considered only when oxygen point defects migrate via first- or second-nearest neighbor sites, as indicated in Fig. 9–12. Some examples of energy landscapes calculated along diffusion coordinates of defects in T- and T′-structured La₂CuO₄ were shown in Fig. S7.†

Fig. 9 (a) Three (A, B and C) diffusion pathways of doubly charged oxygen interstitials (I_O²⁻) along the ab-plane in T-La₂CuO_4+δ. Paths A and B represent interstitialcy migrations, and path C is a direct interstitial migration pathway. (b) Atomic configurations of T-LCO perpendicular to ab-plane (oxygen diffusion plane) showing A, B and C paths. Yellow and cyan circles denote oxygen interstitial and lattice oxygen atom participating in the interstitialcy migration, respectively. Green, blue, red circles are La, Cu, O atoms, respectively, that do not directly participate in the migration. Table: diffusion energy barriers of doubly charged oxygen interstitials along paths A, B and C, shown in figures (a) and (b).

Fig. 10 (a) Two (A and B) diffusion pathways of doubly charged oxygen interstitials (marked with “I” indicated by yellow circle) along ab-plane in T-LCO, when an additional oxygen interstitial (2^nd I_O²⁻) exists in the nearest neighbor (marked with “I” in pink circle). Paths A and B are interstitialcy migration pathways. (b) Atomic configurations of T-LCO perpendicular to ab-plane (oxygen diffusion plane) showing the paths A and B, when 2^nd I_O²⁻ is present in position I (refer to Fig. 7). Yellow, pink and cyan circles denote 1^st I_O²⁻, 2^nd I_O²⁻, and a lattice oxygen atom participating in the migration. Green, blue, red circles are La, Cu, O atoms, respectively, that do not directly participate in the migration. Table: diffusion energy barriers of doubly charged oxygen interstitials along paths A and B shown in figures (a) and (b).

Fig. 11 (a) Left: five (1′ to 5′) diffusion pathways of doubly charged oxygen vacancy (V_O²⁺) along ab-plane or c-axis in T′-La₂CuO_4−δ. Paths 1′ and 2′ are migration on O-plane along ab-plane, paths 3′ is along c-axis between O- and CuO₂-planes, and paths 4′ and 5′ are on CuO₂-plane along ab-plane. Right: table of energy barriers of oxygen vacancy-mediated diffusion via 1′ to 5′ pathways. (b) Left: three (A′, B′ and C′) pathways of doubly charged oxygen interstitials (I_O²⁻) along ab-plane in T′-La₂CuO_4+δ. A′ and B′ paths are interstitialcy migration, C′ path is direct interstitial migration. B′ and C′ paths are purely related to ab-plane migration. Right: diffusion energy barriers of doubly charged oxygen interstitial along A′ to C′ pathways. Bottom: atomic configurations of T′-LCO showing A′, B′ and C′ paths. Yellow and cyan circles denote oxygen interstitials and lattice oxygen atoms participating in the interstitialcy migration, respectively. Green, blue, red circles are La, Cu, O atoms, respectively, that do not directly participate in the migration.

Fig. 12 (a) Left: diffusion pathway 2′ of doubly charged oxygen vacancy (marked with “O” in yellow circle, 1^st V_O²⁺) on O-plane in T′-LCO, when an additional oxygen vacancy (2^nd V_O²⁺) exists in close distances (positions 1 to 4 in pink circles). Table: diffusion energy barriers of oxygen via 1^st V_O²⁺ movement along path 2′, when there are 2^nd V_O²⁺ in positions 1–4 (refer to Fig. 8(a)). (b) Left: diffusion pathway C′ of doubly charged oxygen interstitials (marked with “I” in yellow circle, 1^st I_O²⁻) in T′-LCO, when an additional oxygen interstitial (2^nd I_O²⁻) exists in the first and second nearest neighbors (positions 1 and 2 in pink circles). Table: diffusion energy barriers of oxygen via 1^st I_O²⁻ movement along path C′, when 2^nd I_O²⁻ exists in position 2 (refer to Fig. 8(b)). Bottom right: atomic configurations of T′-LCO perpendicular to ab-plane (oxygen diffusion plane) showing the path C′, when 2^nd I_O²⁻ is present in position 2 (refer to Fig. 8(b)). Yellow, and pink circles denote 1^st I_O²⁻ and 2^nd I_O²⁻, respectively. Green, blue, red circles are La, Cu, O atoms, respectively, that do not directly participate in the migration.

4.4.1 T-structured La₂CuO₄. Fig. 9 shows energy barriers for the migration of a doubly charged oxygen interstitial in the ab-plane via interstitialcy (paths A and B) and the direct interstitial (path C) migration mechanisms in T-structured La₂CuO_4+δ. Among paths A, B and C, paths A and B show lower energy barriers for migration (1.81 and 1.87 eV), which agree closely with the experimentally estimated value of 1.79 eV in Fig. 5. The energy barrier is also comparable to that of I_O²⁻–I_O²⁻ pairs via interstitialcy mechanism via path A, as summarized in Fig. 10. This suggests that in T-structured LCO, oxygen diffusion dominantly occurs via interstitialcy migration of doubly charged oxygens; A and B pathways are available for unpaired interstitials while only path A dominates when two interstitials are paired.

4.4.2 T′-structured La₂CuO₄. Fig. 11(a) shows energy pathways for doubly charged oxygen vacancy migration along five possible pathways (1′ to 5′) for a single oxygen vacancy created in T′-structured La₂CuO_4−δ. Paths 1′, 2′, 4′, 5′ except 3′, contribute to ab-plane diffusion; among them, path 2′ appears to be most confined to ab-plane diffusion, not only because oxygen vacancies are created and move on the O-plane (most favorable sites for vacancies) (refer to Fig. 6(b)), but also because it exhibits the lowest energy barrier for migration (2.09 eV). However, the calculated value is much higher compared to the experimentally estimated energy barrier for diffusion (1.03 eV in Fig. 4).

In the case of interstitial atoms (Fig. 11(b)), the direct interstitial mechanism along the ab-plane (path C′) shows a minimum energy barrier for diffusion (1.94 eV), unlike the interstitialcy mechanism in T-La₂CuO₄ (path A in Fig. 9). However, this value is also much higher than the experimental value.

For oxygen vacancy pairs (Fig. 12(a)), the energy barrier for oxygen movement via path 2′ does not show a discernible change in comparison with that of a single vacancy (Fig. 11(a)), regardless of the relative position of V_O²⁺–V_O²⁺ pairs (position 1 to 4 in Fig. 12(a)). Whereas, oxygen interstitial pairs (position 2 in Fig. 12(b)) show a decrease in migration barrier for diffusion from a single, unpaired interstitial (1.94 → 1.06 eV) along the direct interstitial diffusion pathway (path C′). This reduced value agrees well with the experimentally derived one of 1.03 eV (Fig. 4). Therefore, we conclude that the oxygen diffusion in T′-LCO is via direct interstitial mechanism with the help of neighboring oxygen interstitials resulting in a lower activation energy for diffusion as observed in the experiment.

4.5. Summary

The defect formation energies (E_f) and migration energies (E_m) calculated by DFT, as well as pre-exponential terms (D₀) and activation energies (E_a,D) of diffusion from oxygen isotope exchange experiments for T and T′ structures of LCO are summarized in Table 1. Oxygen vacancy formation energies for T-La₂CuO₄ are positive (see Fig. 6), and therefore are excluded from the table. The oxygen interstitial formation energy for the T-structure is found to be highly negative (−2.83 eV). This implies the ready formation of a high concentration of oxygen interstitials already at reduced temperatures, and thus oxygen diffusion is predicted to be limited only by the migration barrier. This is confirmed by the agreement between the activation energy of diffusion 1.79 ± 0.03 eV from the isotope exchange experiment and the calculated migration energy of 1.81 eV. It should be noted that this is unlike the case of traditional mixed ionic and electronic conducting (MIEC) oxides in which the overall diffusion activation energy includes a contribution from thermally activated defect formation, given a low initial defect concentration at reduced temperatures and increase in oxygen vacancies at higher temperatures.

Table 1 Summary of defect formation and migration energies, and extracted diffusion parameters for T and T′-structured La₂CuO₄ for isolated and paired cases

Structure	T	T′
Defect type	I O ^2−	VO^2+	I O ^2−
E f (eV), DFT	−2.83	−1.2	−1.3
Pair Ef (eV), DFT	−2.07	−0.53	−0.9
exp(−Ef/kBT), T = 897 K	7.95 × 10^15	5.52 × 10^6	2.01 × 10^7
D 0 (cm^2 s^−1), experiment	2.21 × 10^2		1.07 × 10^−3
Diffusion mechanism	Interstitialcy	Vacancy	Direct interstitial
E m (eV), DFT	1.81	2.09	1.94
Pair Em (eV), DFT	1.96	1.92	1.06
E a,D (eV), experiment	1.79 ± 0.03		1.03 ± 0.24

---

Oxygen vacancy formation energies for T′-La₂CuO₄ are negative and comparable to that of oxygen interstitials. However, since the vacancy migration energies are significantly higher than that of the pair-wise interstitial diffusion, the net diffusion is dominated by oxygen interstitials. This, again, is confirmed by comparing the migration energy of interstitial pairs (1.06 eV) as calculated by DFT and the activation energy of diffusion 1.03 ± 0.24 eV as obtained from the experiment. Because of much lower interstitial formation energy for T-LCO, the amount of oxygen interstitials is likely much greater in T-LCO compared to T′-LCO, thus much larger pre-exponential term in diffusivity.

In summary, oxygen diffusion in T-LCO is dominated by large concentration of oxygen interstitials migrating via interstitialcy mechanism, while T′-LCO has several orders of magnitude lower concentrations of oxygen defects and oxygen diffusion is via direct interstitial mechanism as interstitial pairs with significantly lower migration barrier compared to T-LCO. For both structures, thermal activation is determined solely by the corresponding migration energies. This is consistent with our earlier findings of surprisingly low reduction/oxidation enthalpies that result in defect concentrations being insensitive to temperature excursions at a given aO₂.^17,32

5. Conclusions

The effect of structure on oxygen diffusion was successfully separated from those induced by variations in cation chemistry by successfully growing two different structures of La₂CuO₄ in thin film form with the aid of buffer layers. Oxygen diffusivity as derived from isotope exchange studies with the aid of SIMS profiling is faster in T-than in T′-structured La₂CuO₄, while the activation energy of diffusion is surprisingly lower for the T′-structure. Oxygen defect formation energies and migration energies were calculated by DFT for both types of oxygen defects in the T and T′ structures. Oxygen interstitials are the dominant defect species for both structures. Oxygen diffusion is through interstitialcy mechanism in T-LCO, but is through direct interstitial mechanism in pairs in T′-LCO. The magnitude of diffusivity is dominated by the density of available mobile defects, and is therefore higher in the T-structure which exhibits considerably lower defect formation energies. The activation energies for diffusion as derived from oxygen isotope exchange experiments are directly correlated with the activation energies of migration calculated by DFT, explaining the lower activation energy for diffusion in the T′-structure. This provides an insight into creating models for diffusion mechanisms in layered structures with multiple defect species by combining experimental and computational approaches.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This publication is based on work funded by the Skolkovo Institute of Science and Technology (Skoltech), with program name “Center for Research, Education and Innovation for Electrochemical Energy Storage” under contract number 186-MRA. The computational research was supported by the International Research & Development Program of the National Research Foundation (NRF) of Korea funded by the Ministry of Science and ICT (2019K1A4A7A02102530), and the National Supercomputing Center with supercomputing resources including technical support (KSC-2020-CRE-0246). X-ray diffraction scans of the samples were conducted in the MRSEC Shared Experimental Facilities at MIT, supported by the National Science Foundation under award number DMR-1419807. STEM imaging was performed by the Advanced Analysis Center at the Korea Institute of Science and Technology.

References

1. M. Winter and R. J. Brodd, What Are Batteries, Fuel Cells, and Supercapacitors?, Chem. Rev., 2004, 104, 4245–4270.
2. E. Kendrick and P. Slater, Battery and solid oxide fuel cell materials, Annu. Rep. Prog. Chem., Sect. A: Inorg. Chem., 2012, 108, 424.
3. L. Bi, E. Fabbri, Z. Sun and E. Traversa, A novel ionic diffusion strategy to fabricate high-performance anode-supported solid oxidefuel cells (SOFCs) with proton-conducting Y-doped BaZrO₃ films, Energy Environ. Sci., 2011, 4, 409–412.
4. W. Li, Y. Yang, G. Zhang and Y.-W. Zhang, Ultrafast and Directional Diffusion of Lithium in Phosphorene for High-Performance Lithium-Ion Battery, Nano Lett., 2015, 15, 1691–1697.
5. H. Li, N. L. Okamoto, T. Hatakeyama, Y. Kumagai, F. Oba and T. Ichitsubo, Fast Diffusion of Multivalent Ions Facilitated by Concerted Interactions in Dual-Ion Battery Systems, Adv. Energy Mater., 2018, 8, 1801475.
6. Y. Xia, Z. Jin, H. Wang, Z. Gong, H. Lv, R. Peng, W. Liu and L. Bi, A novel cobalt-free cathode with triple-conduction for proton-conducting solid oxide fuel cells with unprecedented performance, J. Mater. Chem. B, 2019, 7, 16136–16148.
7. A. Bates, S. Mukherjee, N. Schuppert, B. Son, J. G. Kim and S. Park, Modeling and simulation of 2D lithium-ion solid state battery: Effects of materials and geometry on the performance of SSB, Int. J. Energy Res., 2015, 39, 1505–1518.
8. Y. Nomura, K. Yamamoto, T. Hirayama, E. Igaki and K. Saitoh, Visualization of Lithium Transfer Resistance in Secondary Particle Cathodes of Bulk-Type Solid-State Batteries, ACS Energy Lett., 2020, 5, 2098–2105.
9. A. Chroneos, R. V. Vovk, I. L. Goulatis and L. I. Goulatis, Oxygen transport in perovskite and related oxides: A brief review, J. Alloys Compd., 2010, 494, 190–195.
10. A. B. Muñoz-García, A. M. Ritzmann, M. Pavone, J. A. Keith and E. A. Carter, Oxygen Transport in Perovskite-Type Solid Oxide Fuel Cell Materials: Insights from Quantum Mechanics, Acc. Chem. Res., 2014, 47, 3340–3348.
11. F. H. Taylor, J. Buckeridge and C. R. A. Catlow, Defects and Oxide Ion Migration in the Solid Oxide Fuel Cell Cathode Material LaFeO ₃, Chem. Mater., 2016, 28, 8210–8220.
12. A. Chroneos, B. Yildiz, A. Tarancón, D. Parfitt and J. A. Kilner, Oxygen diffusion in solid oxide fuel cell cathode and electrolyte materials: mechanistic insights from atomistic simulations, Energy Environ. Sci., 2011, 4, 2774.
13. T. G. Stratton and H. L. Tuller, Thermodynamic and transport studies of mixed oxides. The CeO2–UO2 system, J. Chem. Soc., Faraday Trans. 2, 1987, 83, 1143–1156.
14. D. Lee and H. Lee, Controlling Oxygen Mobility in Ruddlesden–Popper Oxides, Materials, 2017, 10, 368.
15. K. Mukherjee, Y. Hayamizu, C. S. Kim, L. M. Kolchina, G. N. Mazo, S. Ya. Istomin, S. R. Bishop and H. L. Tuller, Praseodymium Cuprate Thin Film Cathodes for Intermediate Temperature Solid Oxide Fuel Cells: Roles of Doping, Orientation, and Crystal Structure, ACS Appl. Mater. Interfaces, 2016, 8, 34295–34302.
16. C. S. Kim and H. L. Tuller, Fine-tuning of oxygen vacancy and interstitial concentrations in La_1.85Ce_0.15CuO_4+δ by electrical bias, Solid State Ionics, 2018, 320, 233–238.
17. C. S. Kim, K.-W. Park and H. L. Tuller, Electrochemically controlled defect chemistry: From oxygen excess to deficiency, Acta Mater., 2021, 211, 116866.
18. M. Naito, A. Tsukada, T. Greibe and H. Sato, Phase control in La-214 epitaxial thin films, Proc. SPIE Superconducting and Related Oxides: Physics and Nanoengineering V, 2002, vol. 4811, pp. 140–154.
19. M. S. Kaluzhskikh, S. M. Kazakov, G. N. Mazo, S. Ya. Istomin, E. V. Antipov, A. A. Gippius, Yu. Fedotov, S. I. Bredikhin, Y. Liu, G. Svensson and Z. Shen, High-temperature crystal structure and transport properties of the layered cuprates Ln₂CuO₄, Ln=Pr, Nd and Sm, J. Solid State Chem., 2011, 184, 698–704.
20. G. N. Mazo, S. M. Kazakov, L. M. Kolchina, S. Ya. Istomin, E. V. Antipov, N. V. Lyskov, M. Z. Galin, L. S. Leonova, Yu. S. Fedotov, S. I. Bredikhin, Y. Liu, G. Svensson and Z. Shen, Influence of structural arrangement of R₂O₂ slabs of layered cuprates on high-temperature properties important for application in IT-SOFC, Solid State Ionics, 2014, 257, 67–74.
21. E. Boehm, J.-M. Bassat, M. C. Steil, P. Dordor, F. Mauvy and J.-C. Grenier, Oxygen transport properties of La₂Ni_1−xCu_xO_4+δ mixed conducting oxides, Solid State Sci., 2003, 5, 973–981.
22. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B, 1993, 47, 558–561.
23. G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B, 1994, 49, 14251–14269.
24. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
25. A. Tsukada, M. Naito and H. Yamamoto, Valence of Ce in T- and T′-La_2−xCe_xCuO₄, Phys. C, 2007, 463–465, 64–67.
26. J. Meng, L. Zhang, F. Yao, X. Liu, J. Meng and H. Zhang, Density Functional Characterization of the 4f-Relevant Electronic Transitions of Lanthanide-Doped Lu₂O ₃ Luminescence Materials, ChemPhysChem, 2018, 19, 2947–2953.
27. S. Pesant and M. Côté, DFT + U study of magnetic order in doped La₂CuO₄ crystals, Phys. Rev. B, 2011, 84, 085104.
28. M. Enhessari, M. Shaterian, M. J. Esfahani and M. N. Motaharian, Synthesis, characterization and optical band gap of La₂CuO₄ nanoparticles, Mater. Sci. Semicond. Process., 2013, 16, 1517–1520.
29. S. Zhang and J. Northrup, Chemical potential dependence of defect formation energies in GaAs: Application to Ga self-diffusion, Phys. Rev. Lett., 1991, 67, 2339–2342.
30. C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, First-principles calculations for point defects in solids, Rev. Mod. Phys., 2014, 86, 253–305.
31. H. Kanai, J. Mizusaki, H. Tagawa, S. Hoshiyama, K. Hirano, K. Fujita, M. Tezuka and T. Hashimoto, Defect Chemistry of La_2−xSr_xCuO_4-δ: Oxygen Nonstoichiometry and Thermodynamic Stability, J. Solid State Chem., 1997, 131, 150–159.
32. E. J. Opila and H. L. Tuller, Thermogravimetric Analysis and Defect Models of the Oxygen Nonstoichiometry in La_2−xSr_xCuO_4-y, J. Am. Ceram. Soc., 1994, 77, 2727–2737.
33. G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113, 9978–9985.
34. G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904.
35. D. Sheppard and G. Henkelman, Paths to which the nudged elastic band converges, J. Comput. Chem., 2011, 32, 1769–1771.
36. M. Izuki, M. E. Brito, K. Yamaji, H. Kishimoto, D.-H. Cho, T. Shimonosono, T. Horita and H. Yokokawa, Interfacial stability and cation diffusion across the LSCF/GDC interface, J. Power Sources, 2011, 196, 7232–7236.
37. V. M. Bekale, A. M. Huntz, C. Legros, G. Sattonnay and F. Jomard, Impurity diffusion of cerium and gadolinium in single- and polycrystalline yttria-stabilized zirconia, Philos. Mag., 2008, 88, 1–19.
38. T. Akashi, M. Nanko, T. Maruyama, Y. Shiraishi and J. Tanabe, Solid-State Reaction Kinetics of LaCrO₃ from the Oxides and Determination of La³⁺ Diffusion Coefficient, J. Electrochem. Soc., 1998, 145, 2090–2094.
39. S. Beschnitt, T. Zacherle and R. A. De Souza, Computational Study of Cation Diffusion in Ceria, J. Phys. Chem. C, 2015, 119, 27307–27315.
40. J. Bassat, Anisotropic ionic transport properties in La₂NiO_4+δ single crystals, Solid State Ionics, 2004, 167, 341–347.
41. M. Burriel, G. Garcia, J. Santiso, J. A. Kilner, R. J. Chater and S. J. Skinner, Anisotropic oxygen diffusion properties in epitaxial thin films of La₂NiO_4+δ, J. Mater. Chem., 2008, 18, 416–422.
42. J. Crank, The Mathematics of Diffusion, Oxford University Press, 2nd edn., 1980.
43. H. Tuller, in Springer Handbook of Electronic and Photonic Materials, ed. S. Kasap and P. Capper, Springer International Publishing, Cham, 2017, pp. 247–266.
44. W. Xie, Y.-L. Lee, Y. Shao-Horn and D. Morgan, Oxygen Point Defect Chemistry in Ruddlesden–Popper Oxides (La_1−xSr_x)₂MO_4±δ (M = Co, Ni, Cu), J. Phys. Chem. Lett., 2016, 7, 1939–1944.

---

Footnotes

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ta02580a

‡ Equally contributed.

---