Defects and disorder in apatite-type silicate oxide ion conductors: implications for conductivity

Abstract

The structure and composition of La-silicate apatite oxide ion conductor, La₁₀Si₆O₂₇, in which the types of defects it contains are controversial, has been thoroughly investigated. Large crystals were grown using the floating zone method, and their structure was characterised by X-ray and neutron single crystal diffraction and second harmonic generation measurements. Structure refinements reveal extensive positional disorder on the oxygen substructure, the presence of La vacancies and no evidence of sites occupied by excess oxide ions. The actual composition of the crystal was determined through SEM-EDX and density measurements and was found to be La_9.64Si_5.77O₂₆, differing significantly from the nominal composition but in agreement with the structure refinements. Structural models considering the actual composition, the disorder on the O sublattice, and local relaxations around these defects were able to reproduce the key features of the diffuse scattering observed in single crystal neutron diffraction patterns.

---

Introduction

The development of solid oxide ion conductors for use as electrolytes in solid oxide fuel cells relies on improving the conductivity of the materials by design, to make them suitable for lower operating temperatures. Tetrahedrally coordinated cations have been identified as structural motifs that can contribute to the oxide ion conductivity mechanisms in materials belonging to different structural families, including brownmillerites,^1–3 melilites,^4,5 δ-Bi₂O₃ derivatives,^6–8 A₃OhTd₂O_7.5 compounds,^9,10 apatites,^11–13 scheelites^14–16 and hexagonal perovskites.^17,18

La-containing apatite-type silicate materials, La_9.33+x(SiO₄)₆O_26+1.5x (0 ≤ x ≤ 0.67), are particularly interesting owing to their high thermal and chemical stability, low toxicity and low cost. They comprise a network of corner-linked La1O₆ and SiO₄ polyhedra with the La2 and remaining O atoms (O4) residing in 1D channels along the c-axis (Fig. 1). The structure has been reported to accommodate both La-site vacancies and oxygen interstitials, and the presence of the latter has been thought to underpin the high ionic conductivity.^19–24

Fig. 1 Structure of a La₁₀Si₆O₂₆ apatite. Green and blue polyhedra show La1 and Si sites, respectively. Green and red spheres indicate La2 and O sites, respectively. The O4 site at the centre of the O4 channels is labelled and highlighted in cyan.

There are, however, certain inconsistencies which preclude full understanding of these materials. Firstly, reported conductivity values for polycrystalline samples of the La_9.33+xSi₆O_26+1.5x (0 ≤ x ≤ 0.67) series vary significantly for materials of the same nominal compositions, even when measured on pellets of similar densities in the same temperature ranges. For example, the reported conductivity of La₁₀Si₆O₂₇ varies by around an order of magnitude, between 1.8 × 10⁻³ and 3.2 × 10⁻² S cm⁻¹ at 800 °C^{22,23,25–29} whereas La_9.33Si₆O₂₆ has a reported conductivity range of 6.0 × 10⁻⁴–5.0 × 10⁻³ S cm⁻¹ at the same temperature.^{21–23,25,30,31} Unit cell parameters also show significant differences between different reports in the literature.

A second factor is the uncertainty in reported oxygen-excess compositions, stemming mainly from the formation of La-rich impurities such as La₂SiO₅ during synthesis. This is commonly observed when attempting to synthesise compounds with a large number of excess oxide ions.^20,27,32 These findings suggest that the upper solubility limit is around La_9.67Si₆O_26.5, above which, La₂SiO₅ forms.^33–35 Formation of this impurity phase reduces the La : Si ratio in the target apatite, resulting in more La-site vacancies and the incorporation of fewer interstitial oxygens.

Finally, there is no agreement over the position of the excess oxygens in the structure (see Fig. S1† for illustration). Multiple powder diffraction studies put the interstitial site at the O4 channel periphery,^22,23,34,36 consistent with low energy sites found by computational prediction of the oxide ion migration pathway.^37–41 However, these lie close to the SiO₄ and recent NMR results indicate that interstitial oxygens do not have bonding interactions with SiO₄.³³ Others suggested positions in the centre of the channel,⁴² or failed to identify distinct sites altogether.^43,44

Interestingly, there have recently been a few reports of Si-deficient apatites.^45–47 In these compounds, vacancies on La and Si sites form at the expense of interstitial oxide ions, resulting in oxygen-stoichiometric compounds with 26 oxygen atoms per formula unit. Of the several reports of the phase with composition La₁₀Si₆O₂₇,^{22,24–27,29,48} few provide compositional analysis,^28,49,50 and those relied mainly on elemental analysis from EDX or ICP, resulting in only a La : Si ratio and not an absolute chemical composition.

To further develop apatite-type silicate oxide ion conductors into useful solid electrolytes, it is important to establish the type of defects present and which one(s)/combinations lead to high conductivities. This work moves towards this goal by reporting a detailed study into the nominal oxygen excess compound La₁₀Si₆O₂₇ (hereinafter referred to as LSO). Large single crystals have been grown, their average and local structures investigated using neutron diffraction and their compositions determined by measurement of density and SEM-EDX characterization. All the experimental evidence points towards there being no significant oxygen beyond the O₂₆ composition.

Experimental

Synthesis

A 20 g polycrystalline sample of nominal composition La₁₀Si₆O₂₇ (LSO) was prepared using a sol–gel method.²⁵ A stoichiometric amount of Si(OC₂H₅)₄ (Sigma Aldrich, >99.0%, ∼14 g) was dissolved in the minimum amount of H₂O/ethanol (1 : 1, ∼10 mL) to form a cloudy solution. Acetic acid was added dropwise until the solution appeared clear (pH 1). La₂O₃ (Alfa Aesar, >99.9%, ∼17 g), dried at 1000 °C for 12 h, was dissolved in 10 mL dil. HNO₃. The two solutions were mixed, heated to 80 °C and stirred for 6 h to form a gel. The gel was dried in an oven at 90 °C for 12 h yielding a sticky white powder which was ground then sintered at 600 °C for 7 h, 800 °C for 6 h and finally 1400 °C for 20 h with intermittent grinding.

The 20 g of LSO was pressed hydrostatically at 30 MPa into two rods of ∼5 mm diameter and sintered for 10 h at 1600 °C. A large single crystal was grown from these rods using the floating zone method. The rods were melted using four 500 W halogen lamps at 84% power, rotated at 30 rpm throughout the growth and translated through the lamp focus at 1–3 mm h⁻¹. The growth atmosphere was a 4 : 1 mixture of Ar and O₂ to simulate dry air.

Single crystal X-ray diffraction

The resulting crystal rod was broken into pieces and screened under a polarising microscope to assess crystal quality. Some small crystal pieces were selected for lab single crystal X-ray diffraction to confirm the unit cell. A complete data collection was also performed on a piece of the large crystal used for neutron diffraction (see below). All measurements were done using an Oxford Gemini S Ultra diffractometer with a charge-coupled detector (CCD) using Mo Kα radiation (0.71073 Å). An Oxford Cryostream Plus Controller was employed to keep the sample temperature at 120 K. Raw datasets were indexed, integrated and reduced in the CrysAlisPro program (Agilent Technologies), and structure refinements were performed in the Jana2006 software.⁵¹ Visualisation of the structure was done in VESTA.⁵²

Powder X-ray diffraction

Some small crystals were crushed, and the powder sprinkled on a vaseline coated Si disc. PXRD patterns were recorded on a Bruker D8 Advance in Bragg–Brentano geometry with a Lynx-eye detector and Cu Kα radiation. A 2θ-range of 5°≤ 2θ ≤ 140° was measured in steps of 0.02° for 5.5 h. Analysis of powder patterns was done by Rietveld refinement⁵³ implemented in Topas Academic.⁵⁴

Second harmonic generation measurements

SHG measurements were performed on 200 mg of the crushed crystal. The sample was placed in fused silica tubes with a diameter of 4 mm. A 1064 nm pulsed Nd:YAG laser (Quantel Laser, Ultra 50) was used to generate the fundamental light and the SHG intensity was recorded at room temperature by a digital phosphor oscilloscope (Tektronix, TDS3032). Intensity comparisons were made with the known SHG material α-SiO₂ under the same conditions.

SEM-EDX

A large crystal was polished smooth and set in resin. A strip of gold paste was applied around the resin to connect both sides of the crystal, and the whole assembly was coated in a conductive carbon layer to prevent charge build-up. The elemental composition and morphology were analysed using a Hitachi SU-70 field emission gun scanning electron microscope optimised to an energy of 12 keV and calibrated with a standard cobalt chip. 15 area spectra at 5 sites on the crystal were used for quantification at three different magnifications to confirm homogeneity across different scales for a total of 225 spectra. Oxygen content was calculated based on charge balancing the measured La and Si content.

Specific gravity measurements

The mass of several crystals (>0.05 g) were measured, in air and in ethanol, and the density was derived from the difference following eqn S1.†⁵⁵ Further information can be found in the ESI.†

Single crystal neutron diffraction

A large piece of the crystal (∼4 mm diameter) was selected for neutron diffraction experiments on the SXD beamline⁵⁶ at ISIS neutron and muon facility, Didcot, UK. The crystal was attached to a goniometer head using adhesive Al foil and placed in a rotating bottom-loading CCR. The sample environment was evacuated, and data were collected on 10 crystal orientations for 3 h each at 40 K. This was followed by a further 4 orientations (3 h each) at 295 K. Initial data integration and reduction was performed in SXD2001⁵⁷ within the IDL virtual machine, then refinement of the structural model was carried out against F in Jana2006. For both 295 and 40 K datasets, reflections were counted as unobserved if I < 3σ(I) and outliers if |F_obs–F_calc| > 10σ and were omitted from the refinements.

Diffuse scattering modelling

Single crystal neutron diffuse scattering was modelled qualitatively using a direct Monte Carlo (MC) approach. An atomistic model was constructed by expanding the refined average structure to a 32 × 32 × 32 supercell. Thermal diffuse scattering was modelled using a nearest-neighbour ball and spring model, following the procedure from Welberry et al.⁵⁸ MC moves were accepted based on the spring energies, with the average bond distance defined as the ideal and the starting force constant ratios taken from ref [⁵⁸]. Force constants were adjusted at the end of every MC cycle (one cycle corresponds to the number of moves required to displace each atom in the model once on average) until the simulated isotropic atomic displacement parameters (ADPs) remained constant, and consistent with the experimental ones.

Occupational disorder was added into the model using random number generators following the balls-and-springs model. Correlations between neighbouring defects were implemented using the MC algorithm and an Ising spin-like energy function. Defects were assigned ‘spins’ of ±1 depending on the sites they occupy. The interaction energy between them was then defined as

where E_i is the energy of atom i, k_ij is the exchange interaction between atom i and its neighbour j, σ_i is the assigned spin of atom i and n is the number of neighbours of atom i. Ordering of the spins is achieved by specifying the correlation coefficient
and accepting the MC moves which decrease the difference between the current and desired correlation. A positive correlation results in clustering of like defects, while negative correlations favour the opposite.

Diffuse scattering sections from the models were calculated using the method laid out by Butler and Wellberry.⁵⁹ In all calculations, average scattering was subtracted and the noise from the finite Fourier summation was mitigated by summing the scattering from 200 smaller sections of the model crystal, each containing 10 × 10 × 10 units cells.

Results and discussion

The diffraction studies described below showed that the synthesis of the precursor powder and subsequent crystal growth were successful. The crystal rod was broken into multiple crystal pieces: one large for neutron diffraction, various smaller crystals for laboratory analysis and smaller-still pieces that were crushed into powder. Preliminary single crystal X-ray diffraction measurements using a laboratory (Mo Kα) instrument confirmed that all crystals had the expected ∼9.7 × 9.7 × 7.2 Å hexagonal unit cell. A powdered sample was found to be SHG-active, indicating a non-centrosymmetric structure. The centrosymmetric P6₃/m model reported for La_9.33Si₆O₂₆ by Okudera et al.,⁶⁰ was therefore transformed into space group P6₃. This model gave satisfactory fits to both the powder (Fig. S2†) and single crystal X-ray diffraction. However, refinement of the La occupancies indicated that the composition differed from the nominal La₁₀Si₆O₂₇, with the La site occupancies refining to 0.845(4), 0.904(4), and 0.999(4) for sites La1_1, La1_2 and La2, respectively in the single crystal refinement. Assuming full Si and O occupancies, this corresponds to a composition of La_9.50(2)Si₆O₂₆.

Compositional analysis

This deviation from the nominal composition prompted further compositional analysis. SEM micrographs were taken of the polished surface of a piece of the large crystal, and EDX analysis was performed. An SEM micrograph is shown in Fig. S3.† A total of 225 EDX spectra were measured across the surface, with the ratio of La : Si determined for each one. Fig. S4a† shows a histogram of the measured ratios fitted with a Gaussian distribution with a mean of 1.684(2) and a standard deviation of 0.026. The measured La : Si ratio is slightly higher than its nominal ratio 1.667 : 1. A mean ratio of 1.684 gives a composition of La_9.67Si_5.74O₂₆ when normalised to O₂₆. If normalised to full La occupancy, it corresponds to La₁₀Si_5.94O_26.88.

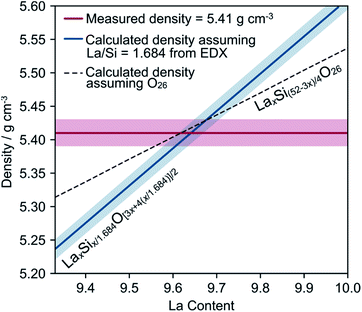
The densities of different pieces of crystal, including a piece of the same crystal that had been used for neutron diffraction and SEM, were measured using a purpose-built specific gravity apparatus. The overall average density was 5.41 g cm⁻³ with a standard deviation of 0.02 g cm⁻³, with no significant differences between the different crystals. This density is significantly lower than the theoretical density (5.62 g cm⁻³) of La₁₀Si₆O₂₇ using cell parameters from powder diffraction (a = 9.71786(2) Å, c = 7.18543(2) Å, γ = 120°), suggesting that the crystal contains significant vacancies. We can calculate a theoretical density based on the fixed La : Si ratio from EDX, a particular La content and an oxygen content from charge balance according to La_xSi_x/1.684O_{[3x+4(x/1.684)]/2}.

By combining this with the measured density, we produce the graph in Fig. 2. The intersection of the blue and red lines gives the region of the true composition of our crystal, consistent with the density and EDX analysis. The dotted line makes a different assumption and shows the calculated density assuming a fixed oxygen content of O₂₆ and a Si content sufficient to charge balance it (La_xSi_(52−3x)/4O₂₆). Compositions below the dotted line would have fewer than 26 oxygens in the unit cell; examples of this are not known in the literature. The best estimate for the actual composition of this crystal is therefore likely to lie on this dotted line, with a La content of 9.64 and a density of 5.42 g cm⁻³. This would correspond to the charge-balanced formula La_9.64(3)Si_5.77(3)O₂₆ (see ESI† for further information).

Fig. 2 A graph summarising the elemental analysis. Shaded regions represent one standard deviation away from the mean. For the blue calculated density, this corresponds to using La : Si ratio limits of 1.684 ± 0.026. The blue composition ranges from La_9.33Si_5.54O_25.1 to La₁₀Si₆O₂₇. The red line shows the measured density and uncertainty of our crystal; the area of intercept with the dashed and blue lines gives an indication of the uncertainty in the final composition.

Average structure from single crystal neutron diffraction

Example reciprocal space sections from single crystal neutron diffraction experiments are given in Fig. S6b.† The P6₃ X-ray model was used to fit the neutron single crystal diffraction data at 40 and 295 K. Atomic positions and anisotropic ADPs were refined for all atoms as well as the occupancies of the La sites, the resulting structure is shown in Fig. 3.

Fig. 3 (a) Initial refined structure of LSO at 295 K. ADPs are represented as ellipsoids drawn at 50% probability. Oxygen atoms of interest are highlighted in orange (O3_2) and cyan (O4) and other important atoms are labelled. (b) A section of the Fourier difference map calculated at 295 K with O4 atoms removed. The isosurface is drawn at 2.7 fm Å⁻³ and the cross sections are coloured by scattering density with red being the highest. The scattering density along 0,0,z is also plotted on the right.

At room temperature, the La occupancies refined to 0.78(1), 0.988(10) and 0.997(8) for sites La1_1, La1_2 and La2, respectively, showing a preference for vacancies solely on the La1 site in the polyhedral network and full La2 occupancy, similar to that found from X-ray diffraction. Therefore, the occupancy of La2 was fixed at 1 in further refinement cycles. The Si site occupancy was initially fixed as it refined to 1.008(9). The large elongated thermal ellipsoids of two oxygen sites (O3_2, in orange, and O4, in blue) indicate substantial positional disorder. Interestingly, the behaviours of O3_1 and O3_2 are quite different. The O3_2 site can be modelled slightly better by splitting it into two and refining occupancies and isotropic ADPs, but this is not the case for O4. La1_1, and La1_2 sites also have slightly anisotropic ADPS, likely owing to the displacement of La atoms near vacancies.

Fourier difference maps, F(obs)–F(calc), calculated using this model showed the only significant residual density peaks were very close to existing atoms, and indicated no obvious additional sites. The residuals were largest near the O4 sites, suggesting that the ADPs were insufficient to accurately model the scattering density in that part of the structure. This was investigated further by removing all O4 oxygens in the channel and re-calculating the difference map (Fig. 3b). The nuclear density is centred at (0,0,0.25), and the spread along the z-axis is extensive. Shoulders on either side of the central peak at (0,0,0.21) and (0,0,0.30) at 40 K, and slightly further apart at (0,0,0.15) and (0,0,0.33) at 295 K, suggest that three oxygen sites could be contributing to this density. Similar conclusions were drawn in other single crystal studies^19,45,60 where the disorder was represented as three distinct sites.

Accordingly, the O4 site was split into three (O4, O4′ and O4′′) sites, the z-coordinates of all three were refined freely, U_iso values were constrained to be equal, and occupancies were constrained to sum to one. At 40 K, this resulted in one of the sites having a negligible occupancy. There was no R-factor improvement over the model just using anisotropic ADPs, probably because at this low temperature, the three sites are too close together to distinguish in the fit. However, at room temperature, using three sites did improve the fit to the diffraction data slightly, bringing wR down from 6.34% to 6.16%, and the refined positions and occupancies were stable. The refined occupancies suggest that around half of the O4 atoms are displaced away from the ideal (0, 0, 0.25) position. These O4 sites cannot be simultaneously occupied without significant local distortion as they are only approximately 1.3 Å apart. A Fourier difference map calculated using this model gave no significant residual density. As such, no other possible sites were detected that would result in an O content of >26. This suggests that there are no, or only a very small number, of interstitial oxygen atoms present, consistent with the compositional analysis.

The consistency of the neutron model with the experimentally measured composition (Fig. 2) was checked by introducing additional composition constraints. The previous best models at 40 K and 295 K were altered so that the La1_1 and La1_2 site occupancies were constrained to give an overall La content of La_9.64 and the Si site occupancy was fixed at 0.9617 to give a Si content of Si_5.77. Split O site occupancies were constrained to keep the overall sum at 1, and their isotropic ADPs were equated. R factors did not change significantly under these new constraints, and the final structures and refinement parameters are given in Tables S2 and S3,† and the room temperature refined structure is displayed in Fig. S7.†

Diffuse scattering modelling

Significant diffuse scattering was observed in the single crystal neutron diffraction patterns of LSO at both 40 K and 295 K. The most intense features were diffuse planes normal to c* in the hxl sections, and hexagonal patterns in h k 0.5n sections. The former is incommensurate with the Bragg positions and so does not indicate the presence of simple supercell ordering. It would be consistent with rod-like local ordering along c in direct space. Similarly, the hexagonal patterns have complex intensity modulations and are different at each value of n, making them hard to interpret directly. To try and relate this scattering to the defect model suggested by the average structure, an atomistic ball and spring model, based on the refined average structure at 40 K, was constructed. The split O4 and O3_2 sites were initially modelled as just one site each (see below), and an appropriate number of vacancies were distributed randomly across the La1_1, La1_2 and Si sites.

Firstly, the thermal diffuse scattering was simulated by adjusting the spring constant until the atomic displacements were consistent with the size of the experimental U_iso. This resulted in the expected spherical distribution of atoms around their equilibrium positions, as shown by the grey clouds in Fig. S8a.† The simulated diffuse scattering patterns produced by this model are shown in Fig. S8b,† alongside corresponding experimental patterns. The deviation of atoms from their average position causes the intensity of the diffuse scattering to increase with Q² according to the Debye-Waller factor, resulting in high intensities at the edges of the simulations. Some additional intensity patterns can be seen on top of this due to the correlated motion between neighbouring atoms. The presence of vacancies does not give rise to any structured diffuse scattering in these simulations as they are randomly distributed, and so cause isotropic scattering. Comparing the experimental and simulated patterns in Fig. S8b,† it is clear that thermal motion alone cannot account for the most intense features observed experimentally, indicating that some other local correlations exist in LSO. Thermal motion was not simulated in the following models to allow clearer distinction between different models.

A second potential source of diffuse scatter is local relaxation around the La and Si vacancies. This was modelled by displacing neighbouring atoms along the bond vector either towards or away from the vacant site and produced more defined diffuse scattering patterns (Fig. S9†). However, the scattering was again not entirely consistent with the experimental patterns.

Disorder on the O4 site is another likely source of diffuse scattering, based on the large ADPs in the average structure and the regions of reciprocal space where it was observed. Building from the previous model, O4 atoms were distributed across the three sites identified from the room temperature average structure, as shown in Fig. 4a. 50% of the central O4 sites were occupied and the remaining 50% of atoms were distributed over the upper and lower sites equally. An Ising-like energy function was used to create different correlations in the O4 positions, both within and between individual columns. Example configurations are given in Fig. S10b and S10c.† In the model, these correlations correspond to O4 atoms with the same vertical displacement being clustered together along c, i.e. if one O4 is displaced downwards, its neighbour will likely be displaced downwards as well. This approximates the correlated displacements that would result from electrostatics in a real material. The corresponding anti-correlation, where adjacent O4s prefer to be displaced in opposite directions, would model the effects of elastic strain. Further information on the production of these models can be found in the ESI,† and the calculated diffuse scattering from the various models is shown in Fig. S11.†

Fig. 4 (a) The average structure highlighting areas where disorder has been introduced and corresponding schematics of the disorder included in the final model. (b) Selected experimental and corresponding simulated diffuse scattering h k l sections. Calculated patterns are indicated with a black circle and the dividing line between calculated and experimental patterns is shown by a red dashed line. Intensities of the calculated patterns are arbitrary and are coloured to match the experimental patterns.

From these models, we can deduce that LSO has O4 displacements that are positively correlated in columns along the c-axis, but there is no relationship to correlated displacements in neighbouring columns. This is the only one of the models tested which produced the diffuse planes normal to c* in the experimentally observed positions. However, none of the above models produce diffuse scattering patterns which match the experimental ones for the h k 0.5n sections. Coupling the O4 displacements with the displacements of the O₃ atoms, which also show significant disorder in the average model, did not significantly change the scattering patterns relative to the previous model. Various other models, including the ordering of La and Si vacancies, were tested, but each model either resulted in no additional features, or features that were not observed experimentally.

Another option is to couple the O4 displacements to a contraction of the coordination triangle made by neighbouring La2 atoms as was suggested by Fujii et al.⁴⁵ A schematic of this distortion is shown in Fig. 4b, and was added to the model where the O4s were positively correlated along the c-axis. If an O4 atom was displaced away from the central position, each neighbouring La atom was set to move towards the O4 by 10% of the La–O4 distance, resulting in displacements of around 0.25 Å. At a local level, this distortion helps O4 retain a close-to-ideal bond valence sum. The simulated diffuse scattering patterns are given in Fig. 4b. This model is significantly better at reproducing the hexagonal patterns in the h k 0.5n sections than any of the previous models, with both the shape and relative intensity of the experimental scattering patterns being reproduced reasonably well. Similarly, in the h 0.5n l sections, the diffuse scattering in planes perpendicular to c* is predicted due to the correlations in the O4 chains, but the La2 triangle contractions modulate the intensity in a similar way to the experimental patterns.

While the general diffuse features are well reproduced, there are some discrepancies between the predicted and experimental patterns. The hexagonal patterns in the experimental h k 0.5n sections are tilted at an angle relative to the vertical axis, and this angle is not exactly matched in the simulated patterns. The models also predict diffuse scattering in the h k 0.5 plane, which is not observed experimentally, suggesting that the crystal has some more complex local correlations. Despite this, the overall good agreement between the calculated and experimental patterns shows that just three types of local distortion can explain the most striking diffuse features: breathing distortions around randomly distributed La and Si vacancies, positively correlated O4 displacements in individual chains along the c-axis and the contraction of La2 triangles as O4 atoms displace. Because the magnitudes of each distortion and other parameters are not being refined against the data, this only gives a qualitative picture. It is, however, fully consistent with the average model from the Bragg data and the composition from elemental analysis. We can therefore conclude that both average and short-range structural features of LSO are consistent with there being no excess interstitial oxide ions.

Implications for properties

With regard to the ionic conductivity properties, there are two important structural findings from this work: Si and La vacancies are more favourable than oxygen interstitials beyond O₂₆; and, while there is significant local disorder in the structure, this is mainly static with simple correlations and local distortions able to explain most of the diffuse scattering we observe. Assuming these findings hold for other reported La₁₀Si₆O₂₇ samples, they have implications for the sinusoidal interstitial conductivity mechanism down the O4 channel, and the hypothesis that higher conductivities can be achieved by adding more interstitial oxide ions. A lack of additional oxide ions in the structure implies that the proposed mechanism would be less likely as the mobile oxide ions would have to diffuse from their equilibrium sites to an interstitial site before travelling down the channel, likely increasing the activation energy of migration. Our findings are more consistent with the alternative suggestions by Béchade³⁸ and León-Reina³¹ where migration relies on the formation of O4 vacancies. This would agree with the observed disorder on the O4 site, where only one of three possible sites are occupied at any one time, and a high level of local distortion can be accommodated.

Both our diffuse scattering model and previous work by Fujii et al.⁴⁵ suggest that O4 displacements are connected to the distortions around the cations, hinting that (assuming the real conductivity mechanism does involve the O4 site) cation vacancies will have a significant impact on conductivity. Interestingly, there are some reports that oxygen stoichiometric compounds with A-site vacancies outperformed those without vacancies,^61,62 or those with interstitials.^31,34 More recently, compositions with Si vacancies have also been shown to have high conductivities.^45,46 Again, these suggest that the important factor in determining conductivity is the presence of cation vacancies rather than excess oxide ions. Our work demonstrates that the previously reported high conductivity La₁₀Si₆O₂₇ compounds, are likely to have been La- and Si-deficient, strengthening this hypothesis. Because of the uncertainty in these compositions, a systematic study with careful elemental analysis is needed to properly correlate defects to conductivity, but an emphasis on cation vacancies might lead to new doping studies not previously considered.

Conclusions

In conclusion, a combination of powder and single crystal neutron and X-ray diffraction experiments, coupled with elemental analysis and physical property measurements, have shown that a nominal La₁₀Si₆O₂₇ oxygen excess apatite contains significant cation vacancies leading to a composition close to La_9.64Si_5.77O₂₆. A P6₃ model of this composition explains all features of the X-ray and neutron diffraction patterns, and difference Fourier maps show no evidence for oxygen atoms beyond O₂₆. The average structure from single crystal diffraction data suggests La vacancies are predominantly on the La1 sites and that several O sites show significant positional disorder. This is particularly true for the O4 species thought to be important for transport parallel to the c-axis. Neutron diffraction data also shows significant diffuse scattering even at 40 K. The essential features of this scattering can be explained through a combination of three correlated local structural distortions. A breathing distortion of oxygens around vacant cation sites and a contraction of the La2₃ triangle coordinating O4 produce the hexagonal patterns in the a*b* plane, while correlated O displacements of around 0.7 Å from their ideal site along the O4 channels, with no correlation between adjacent channels, lead to diffuse rods normal to c*. A simple structural model then explains both the average and local structure.

The work shows the importance of careful consideration of the true defect structure of apatite silicate oxide ion conductors, and suggests that cation vacancies may be more important in optimising O²⁻ migration than interstitial oxygens beyond O₂₆. In this regard, the silicates differ significantly from related germanates, and the mechanism of migration must also differ.

Author contributions

CAF performed the bulk of the sample synthesis and data analysis. CW, CDL helped with single crystal growth experiments. WZ and PSH performed SHG measurements. MJG was involved in neutron diffraction experiments and data analysis. IRE and JSOE devised the project and were involved in all aspects.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

IRE and CDL thank the Royal Society for the International Exchanges grant IE150409. CDL and CW thank the Australian Research Council for grants LE0668302 and DP150102863. PSH and WZ thank the Welch Foundation (Grant E-1457) and the National Science Foundation (DMR-2002319) for support.

Notes and references

1. W. Paulus, H. Schober, S. Eibl, M. Johnson, T. Berthier, O. Hernandez, M. Ceretti, M. Plazanet, K. Conder and C. Lamberti, J. Am. Chem. Soc., 2008, 130, 16080–16085.
2. C. A. Fuller, Q. Berrod, B. Frick, M. R. Johnson, S. J. Clark, J. S. O. Evans and I. R. Evans, Chem. Mater., 2019, 31, 7395–7404.
3. C. A. Fuller, Q. Berrod, B. Frick, M. R. Johnson, M. Avdeev, J. S. O. Evans and I. R. Evans, Chem. Mater., 2020, 32, 4347–4357.
4. X. Kuang, M. A. Green, H. Niu, P. Zajdel, C. Dickinson, J. B. Claridge, L. Jantsky and M. J. Rosseinsky, Nat. Mater., 2008, 7, 498–504.
5. L. Zhou, J. Xu, M. Allix and X. Kuang, Chem. Rec., 2020, 20, 1117–1128.
6. X. Kuang, J. L. Payne, M. R. Johnson and I. R. Evans, Angew. Chem., Int. Ed., 2012, 51, 690–694.
7. J. R. Peet, C. A. Fuller, B. Frick, M. Koza, M. R. Johnson, A. Piovano and I. R. Evans, J. Am. Chem. Soc., 2019, 141, 9989–9997.
8. C. D. Ling, W. Miiller, M. R. Johnson, D. Richard, S. Rols, J. Madge and I. R. Evans, Chem. Mater., 2012, 24, 4607–4614.
9. C. A. Fuller, D. A. Blom, T. Vogt, I. R. Evans and J. S. O. Evans, J. Am. Chem. Soc., 2022, 144, 615–624.
10. C. A. Fuller, J. I. Murrell, D. A. Blom, T. Vogt, W. Zhang, P. S. Halasyamani, I.R. Evans and J. S. O. Evans, Chem. Mater., 2022, 34, 3185–3196.
11. E. Kendrick, M. S. Islam and P. R. Slater, J. Mater. Chem., 2007, 17, 3104–3111.
12. P. M. Panchmatia, A. Orera, G. J. Rees, M. E. Smith, J. V. Hanna, P. R. Slater and M. S. Islam, Angew. Chem., Int. Ed., 2011, 50, 9328–9333.
13. M. S. Chambers, P. A. Chater, I. R. Evans and J. S. O. Evans, Inorg. Chem., 2019, 58, 14853–14862.
14. S. S. Pramana, T. Baikie, T. An, M. G. Tucker, J. Wu, M. K. Schreyer, F. Wei, R. D. Bayliss, C. L. Kloc, T. J. White, A. P. Horsfield and S. J. Skinner, J. Am. Chem. Soc., 2016, 138, 1273–1279.
15. C. Ferrara, A. Mancini, C. Ritter, L. Malavasi and C. Tealdi, J. Mater. Chem. A, 2015, 3, 22258–22265.
16. J. E. Auckett, L. Lopez-Odriozola, S. J. Clark and I. R. Evans, J. Mater. Chem. A, 2021, 9, 4091–4102.
17. S. Fop, J. M. S. Skakle, A. C. McLaughlin, P. A. Connor, J. T. S. Irvine, R. I. Smith and E. J. Wildman, J. Am. Chem. Soc., 2016, 138, 16764–16769.
18. M. S. Chambers, K. S. Mccombie, J. E. Auckett, A. C. Mclaughlin, J. T. S. Irvine, P. A. Chater, J. S. O. Evans and I. R. Evans, J. Mater. Chem. A, 2019, 7, 25503–25510.
19. K. Fukuda, T. Asaka, M. Oyabu, D. Urushihara, A. Berghout, E. Béchade, O. Masson, I. Julien and P. Thomas, Chem. Mater., 2012, 24, 4623–4631.
20. E. Kendrick, J. E. H. Sansom, J. R. Tolchard, M. S. Islam and P. R. Slater, Faraday Discuss., 2007, 134, 181–194.
21. A. Pons, J. Jouin, E. Béchade, I. Julien, O. Masson, P. M. Geffroy, R. Mayet, P. Thomas, K. Fukuda and I. Kagomiya, Solid State Sci., 2014, 38, 150–155.
22. H. Yoshioka, J. Am. Ceram. Soc., 2007, 90, 3099–3105.
23. H. Yoshioka, J. Alloys Compd., 2006, 408412, 649–652.
24. G. Ou, X. Ren, L. Yao, H. Nishijima and W. Pan, J. Mater. Chem. A, 2014, 2, 13817–13821.
25. S. Tao and J. T. S. Irvine, Mater. Res. Bull., 2001, 36, 1245–1258.
26. S. Nakayama and M. Sakamotob, J. Eur. Ceram. Soc., 1998, 18, 1413–1418.
27. S. Nakayama, T. Kageyama, H. Aono and Y. Sadaoka, J. Mater. Chem., 1995, 5, 1801–1805.
28. S. P. Jiang, L. Zhang, H. Q. He, R. K. Yap and Y. Xiang, J. Power Sources, 2009, 189, 972–981.
29. H. Yoshioka, Chem. Lett., 2004, 33, 392–393.
30. S. Beaudet-Savignat, A. Vincent, S. Lambert and F. Gervais, J. Mater. Chem., 2007, 17, 2078–2087.
31. L. León-Reina, E. R. Losilla, M. Martínez-Lara, S. Bruque, A. Llobet, D. V Sheptyakov and M. A. G. Aranda, J. Mater. Chem., 2005, 15, 2489.
32. A. Orera and P. R. Slater, Chem. Mater., 2010, 22, 675–690.
33. W. Liu, S. Geng, W. Zhang, F. Liao, M. Tang, H. Fu and X. Kuang, Inorg. Chem., 2021, 60, 16817–16825.
34. L. Leon-Reina, E. R. Losilla, M. Martinez-Lara, S. Bruque and M. a. G. Aranda, J. Mater. Chem., 2004, 14, 1142–1149.
35. Y. Kim, D. K. Shin, E. C. Shin, H. H. Seo and J. S. Lee, J. Mater. Chem., 2011, 21, 2940–2949.
36. J. R. Tolchard and P. R. Slater, J. Phys. Chem. Solids, 2008, 69, 2433–2439.
37. M. S. Islam, J. R. Tolchard and P. R. Slater, Chem. Commun., 2003, 1486.
38. E. Béchade, O. Masson, T. Iwata, I. Julien, K. Fukuda, P. Thomas and E. Champion, Chem. Mater., 2009, 21, 2508–2517.
39. K. Matsunaga and K. Toyoura, J. Mater. Chem., 2012, 22, 7265.
40. T. Liao, T. Sasaki, S. Suehara and Z. Sun, J. Mater. Chem., 2011, 21, 3234.
41. A. Jones, P. R. Slater and M. S. Islam, Chem. Mater., 2008, 20, 5055–5060.
42. Y. Zhang, Z. Su, A. K. Azad, W. Zhou and J. T. S. Irvine, Adv. Energy Mater., 2012, 2, 316–321.
43. Y. Matsushita, F. Izumi, K. Kobayashi, N. Igawa, H. Kitazawa, Y. Oyama, S. Miyoshi and S. Yamaguchi, Nucl. Instrum. Methods Phys. Res. A, 2009, 600, 319–321.
44. O. Masson, A. Berghout, E. Béchade, J. Jouin, P. Thomas, T. Asaka and K. Fukuda, Sci. Technol. Adv. Mater., 2017, 18, 644–653.
45. K. Fujii, M. Yashima, K. Hibino, M. Shiraiwa, K. Fukuda, S. Nakayama, N. Ishizawa, T. Hanashima and T. Ohhara, J. Mater. Chem. A, 2018, 6, 10835–10846.
46. K. Fukuda, T. Asaka, S. Hara, M. Oyabu, A. Berghout, E. Béchade, O. Masson, I. Julien and P. Thomas, Chem. Mater., 2013, 25, 2154–2162.
47. K. Fukuda, R. Hasegawa, T. Kitagawa, H. Nakamori, T. Asaka, A. Berghout, E. Béchade, O. Masson, J. Jouin and P. Thomas, J. Solid State Chem., 2016, 235, 1–6.
48. Y. Ma, N. Fenineche, O. Elkedim, M. Moliere, H. Liao and P. Briois, Int. J. Hydrogen Energy, 2016, 41, 9993–10000.
49. B. Li, W. Liu and W. Pan, J. Power Sources, 2010, 195, 2196–2201.
50. Y. Ma, M. Moliere, Z. Yu, N. Fenineche and O. Elkedim, J. Alloys Compd., 2017, 723, 418–424.
51. V. Petricek, M. Dusek and L. Palatinus, Z. Kristallogr. Krist., 2014, 229, 345–352.
52. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
53. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
54. A. A. Coelho, J. S. O. Evans, I. R. Evans, A. Kern and S. Parsons, Powder Diffr., 2011, 26, 22–25.
55. M. E. Brandriss, J. Geosci. Educ., 2010, 58, 155–165.
56. D. A. Keen, M. J. Gutmann and C. C. Wilson, J. Appl. Crystallogr., 2006, 39, 714–722.
57. M. Gutmann, Acta Crystallogr. A, 2005, 61, C164.
58. T. R. Welberry, M. J. Gutmann, H. Woo, D. J. Goossens, G. Xu, C. Stock, W. Chen and Z. G. Ye, J. Appl. Crystallogr., 2005, 38, 639–647.
59. B. D. Butler and T. R. Welberry, J. Appl. Crystallogr., 1992, 25, 391–399.
60. H. Okudera, Y. Masubuchi, S. Kikkawa and A. Yoshiasa, Solid State Ionics, 2005, 176, 1473–1478.
61. J. E. H. Sansom, D. Richings and P. R. Slater, Solid State Ionics, 2001, 139, 205–210.
62. S. Nakayama, M. Sakamoto, M. Highchi and K. Kodaira, J. Mater. Sci. Lett., 2000, 19, 91–93.

---

Footnote

† Electronic supplementary information (ESI) available: Single crystal neutron diffraction data. See https://doi.org/10.1039/d2ta02328h

---