Unfolding the terahertz spectrum of soft porous crystals: rigid unit modes and their impact on phase transitions

Abstract

Phase transitions in flexible metal–organic frameworks or soft porous crystals are mediated by low-frequency phonons or rigid-unit modes. The alteration of specific building blocks may change the lattice dynamics of these frameworks, which can influence the phase transition mechanism. In this work, the impact of building block substitution on the rigid-unit modes in flexible MIL-53 analogs with a winerack topology will be investigated via ab initio lattice dynamics calculations. First, the accuracy of the theoretical simulations is verified via experimental Raman measurements, which provide unique fingerprint vibrations in the terahertz range to characterize the phase transition. Following analysis of the low-frequency vibrations shows that there exists a set of universal rigid-unit modes inducing translations and/or rotations of the building blocks. The theoretical results demonstrate that linker substitutions have a large effect on the rigid-unit mode frequencies, whereas this is less so for inorganic chain substitutions. These findings may help to rationally tune the phonon frequencies in soft porous crystals.

---

1 Introduction

Phonons are the quanta of vibrations in solids. They play a crucial role in a variety of physical processes such as thermal conductivity^1,2 and expansion,^3,4 charge transport,⁵ diffusion,⁶ phase transitions,⁷etc. With an eye toward development of functional materials it is valuable to be able to control these phonon modes.

In this regard, metal–organic frameworks (MOFs) are an interesting class of micro- and/or nanoporous crystalline materials.^8–10 They consist of inorganic polynuclear clusters, also called secondary building units, connected by organic ligands or linkers. The concept of reticular chemistry^11,12 allows these building blocks to be easily adapted, which enables the phonons in MOFs to be tuned and, consequently, the related properties.¹³

A first phonon property that is of importance in MOFs is the vibrational entropy, which mostly depends on the vibrations with the lowest frequencies. Its contribution to the free energy increases with increasing temperature.^14–17 As such, it influences the thermal stability of a structure. Another interesting phenomenon, largely affected by phonons, is thermal expansion. A vast number of MOFs exhibit large negative thermal expansion (NTE),^18,19 whereas most materials experience positive thermal expansion (PTE). The specific framework topology of these MOFs provides a large number of low-frequency vibrations that contract the structure, such as trampoline motions of the linkers.^20,21 A last example in which phonons influence the MOF behavior is the occurrence of phase transitions.^22,23 When a phonon mode becomes unstable, i.e. its frequency approaches zero, its energy is sufficiently low to induce static displacements and, in the end, trigger a structural transition. Such a mode is referred to as a soft mode.²³

From the above examples, it is clear that vibrations with a low frequency in the terahertz range, i.e. terahertz vibrations, affect the stability and dynamic behavior of MOFs. In the case of high-frequency vibrations, which induce displacements within a single building block, the phonon modes can often be easily interpreted based on chemical insight. For terahertz vibrations a straightforward identification of the normal modes is no longer possible, as they involve displacements of the whole structure and they heavily depend on long-range interactions between the different building blocks. Consequently, the characterization of these terahertz vibrations requires theoretical input.^23,24

A simple approach to predict the vibrations with the lowest frequencies is by considering the structure to be made up of rigid units. This rigid unit mode (RUM) approach was successfully applied by Hammonds et al. to a wide-range of aluminosilicates, supposed to consist of rigid tetrahedral units, in order to explain the occurrence of phase transitions and anomalous thermal expansion.²⁵ For that purpose, the Crush program was adopted, which could predict the RUMs and frequencies for any wave vector.²⁶ The program makes use of the split-atom method, which assumes that atoms shared between neighboring building blocks are split in two halves and are connected with each other by a harmonic spring.²⁷ In this way, the RUMs can be identified as those modes with zero frequency. A non-zero frequency corresponds to a mode that would generate a distortion of the rigid units. The RUM approach has proven to be successful in various framework materials²⁸ and several alternative methods have been developed.^29–32

The RUM model has also been used to investigate low-frequency phonons in MOFs, the first time on Zn(CN)₂ by Goodwin et al.³³ Zn(CN)₂ exhibits an anomalously large and negative thermal expansion coefficient. Their analysis showed that the NTE behavior results from a large set of RUMs, which dominate the dynamic behavior due to their very low frequencies. The diatomic ligand allows more flexibility compared to the oxide-bridged analogs of Zn(CN)₂ giving rise to significantly more RUMs.

The application of the RUM model on more complex MOFs with extensive linkers is not trivial, as the latter have the possibility to flex e.g. by trampoline-like motions. This should also be taken into account to analyze the flexibility of the material correctly.²⁸ Rimmer et al. applied different RUM models with increasing complexity on MOF-5 to investigate the low-frequency vibrations.³⁴ The models that allowed flexing of the benzenedicarboxylate (BDC) linkers performed well to accurately predict the RUMs.

A disadvantage of the RUM approach is the inability to provide correct vibrational frequencies. The model delivers RUMs with zero frequency, whereas in reality the terahertz vibrations with RUM character do have a small non-zero frequency. To predict these terahertz frequencies, one can resort to ab initio lattice dynamics calculations, which provides the normal modes in the harmonic approximation via electronic structure calculations. Frequently, the density functional theory (DFT) formalism is applied due to its suitable trade-off between the required computational resources and accuracy.³⁵

One of the first phenomena in MOFs, for which DFT calculations of the vibrational modes proved to be useful, is NTE in MOF-5.^20,34,36 Another research topic that has greatly benefited from ab initio lattice dynamics calculations is gate-opening in ZIF-8.^37–39 However, it has also been used to investigate, among other aspects, rotational dynamics in MIL-140A,⁴⁰ the phase transition in ZIF-4,⁴¹ and the link between soft modes and anomalous elastic behavior such as a negative Poisson ratio, NTE, and low shear moduli in HKUST-1.⁴²

The accurate prediction of terahertz vibrations via DFT is challenging, because they originate from weak interactions which need high computational settings to be described properly.^17,43–45 To verify whether the proposed computational model is suitable to gain insight in the desired physical phenomena, one can compare theoretical spectra with a range of experimental spectroscopic techniques such as infrared spectroscopy,^{37–40,42,46} Raman spectroscopy,^40,42,46 and inelastic neutron scattering (INS).^37,40,41

A combined experimental/theoretical approach was followed by some of the presenting authors to investigate the breathing phenomenon in MIL-53(Al).⁴⁶ MIL-53(Al)⁴⁷ is the prototype of a flexible breathing MOF or soft porous crystal.⁴⁸ It has a winerack topology consisting of 1D aluminum-oxide chains connected by BDC linkers and exhibits a phase transition between a contracted pore (cp) and large pore (lp) phase that induces a large change in unit cell volume. Based on subtle differences in the IR spectrum above 300 cm⁻¹, we could distinguish the cp and lp phases. Furthermore, the good agreement with experiment enabled the theoretical prediction of normal modes that could induce breathing.⁴⁶

A follow-up study analyzed the frequencies of all terahertz vibrations as a function of the volume.⁴⁹ This allowed to pinpoint the modes with a large frequency difference between the cp and lp phase, which can serve as a fingerprint for the phase transition. As could be expected, the most interesting modes induced translations and rotations of the different building blocks. Due to the lack of IR active terahertz vibrations in MIL-53(Al), the theoretical prediction of the RUMs could not be experimentally verified. Raman spectroscopy proved to be a better tool to characterize the low-frequency spectrum of flexible porous framework materials based on reports of DUT-8(Ni).^50,51 The terahertz region showed a characteristic Raman peak in both the closed pore and open pore phase, although it was shifted significantly.

In this work, it will be evidenced, both experimentally and theoretically, that Raman spectroscopy provides clear fingerprints in the terahertz region of MIL-53 analogs, i.e. soft porous crystals with a winerack topology consisting of a 1D inorganic chain connected by ditopic organic linkers (see Table 1). Consequently, it is the ideal tool to characterize the phase transition in these soft porous crystals. However, not all terahertz vibrations are Raman active. Therefore, the characterization of all RUMs in these MOFs required a thorough analysis via ab initio lattice dynamics calculations (see Fig. 1). By means of static DFT calculations, the RUMs typical for the winerack topology in MIL-53 were identified, including the Raman active phonon modes inducing rotations of the organic linker. Furthermore, a reduced Hessian approach was applied,⁵⁹ which allowed to subdivide the RUM displacements into translations and rotations of the building blocks yielding, for the first time, a quantification of the RUM character of terahertz vibrations in MOFs. Additionally, the influence of building block substitution on the terahertz frequencies was investigated illustrating the impact on the vibrational entropy and, hence, the thermal stability of the structures. As such, this study provides a microscopic picture of the mechanism behind the phase transition in MIL-53 analogs complementing our earlier macroscopic investigation.⁶⁰

Table 1 Overview of the structures included in this study with their corresponding inorganic octahedra (blue figure) and linkers (red figure) (BDC = 1,4-benzenedicarboxylate, FA = fumarate, NDC = 2,6-naphthalenedicarboxylate, BPDC = 4,4′-biphenyldicarboxylate)

Structure
MIL-53(Al)^47	Al^3+ + OH^−	BDC
MIL-53(Ga)^52	Ga^3+ + OH^−	BDC
MIL-53(Cr)^53	Cr^3+ + OH^−	BDC
MIL-53(V)^54	V^3+ + OH^−	BDC
MIL-53(Al)-F^55	Al^3+ + F^−	BDC
MIL-47(V)^54	V^4+ + O^2−	BDC
A520(Al)^56	Al^3+ + OH^−	FA
DUT-4(Al)^57,58	Al^3+ + OH^−	NDC
DUT-5(Al)^58	Al^3+ + OH^−	BPDC

---

Fig. 1 Schematic overview of the scope of this research. Different linkers are combined with aluminium-oxide octahedra and different inorganic octahedra are combined with BDC linkers to form a winerack framework. These frameworks exhibit general rigid-unit modes (RUMs) i.e. terahertz vibrations with translations and/or rotations of the building blocks. Two of these RUMs are visualized and their theoretically predicted frequencies for the different structures are plotted with Lorentzian lineshapes with the same amplitude. The color of the curve matches the color of the linker or inorganic octahedron that is substituted in the reference structure of MIL-53(Al).

2 Methods

2.1 Theory

2.1.1 General procedure to compare RUMs between structures with winerack topology. First, geometry optimizations were performed to obtain the equilibrium structures of the cp and lp phases of the different materials. For that purpose, several fixed volume optimizations were executed, in which the cell vectors and ions were allowed to relax. The resulting energies were used to construct an energy–volume equation of state for which a Rose–Vinet fit was derived to determine the equilibrium volume.⁴³ Subsequently, a final fixed volume optimization was performed for a structure at this optimal volume. For all materials listed in Table 1, it was possible to determine (meta-)stable cp and lp phases, except for the lp phase of DUT-4(Al). At the current level of theory (see Section 2.1.3), DUT-4(Al) does not exhibit a local minimum in the energy–volume equation of state for the lp phase.¹⁷ Therefore, a single fixed volume geometry optimization was performed at the experimentally measured unit cell volume of the lp phase.⁵⁸

Once equilibrium structures were obtained, the Hessian was calculated via a finite difference approach. The second-order derivatives of the energy with respect to the atom displacements were determined via numerical differentiation of the forces in distorted structures. Each distortion was created by displacing one of the atoms by 0.015 Å in the positive or negative sense of one of the Cartesian directions. The normal modes were derived from the Hessian after a normal mode analysis and mass-weighted.

These mass-weighted normal modes could now be compared between the materials of interest. For structures consisting of the same building blocks it is possible to directly determine the similarity of different mass-weighted normal modes by calculating the dot product between them. As the mass-weighted Hessian of a structure is real symmetric, its eigenmodes are orthonormal. Therefore, a dot product of 1 indicates that the compared eigenmodes are completely equivalent, whereas a dot product of 0 means that there is no overlap between the two eigenmodes. However, in case of different building blocks the matter is more complicated as the normal modes no longer have the same dimension, preventing a direct comparison. Luckily, in this study we are only interested in terahertz modes that affect the phase transition, which are collective in nature, meaning that they induce displacements of entire building blocks i.e. RUMs. Therefore, we can reduce the coordinate space to include only translations and rotations of the building blocks. In literature, this is referred to as a reduced Hessian technique.⁵⁹ The reduced Hessian, H^re, can be derived from the full Hessian by multiplication with the projection matrix P:

H^re = P^TH^fullP (1)

Here, the columns of P are formed by the translation and rotation vectors of the building blocks expressed in the original basis (see also Section S1.1 in the ESI†). As all structures have the same topology consisting of the same type of building blocks, the dimension of their reduced Hessian is the same and enables identification of normal modes of equal type. The reduced Hessian can also be mass-weighted by defining the reduced mass-matrix, M^re:

M^re = P^TM^fullP (2)

As the mass-weighted reduced Hessian is also real symmetric, the corresponding mass-weighted reduced normal modes are again orthonormal. Therefore, the dot product between two mass-weighted normal modes of reduced Hessians is a good measure to identify similar normal modes. Furthermore, it is possible to express the reduced normal modes in the original basis. Comparing the reduced normal modes in this form with the original terahertz vibrations shows that the modes exhibiting mainly rigid-unit vibrations are indeed included in the reduced Hessian. However, the vibrational frequencies of the reduced normal modes differ substantially from those obtained from the full Hessian. Therefore, the vibrational frequencies of the full Hessian will still be compared with each other, which is possible due to the one-to-one correspondence between the terahertz vibrations and the reduced normal modes of interest (see Section S1.2 in the ESI†).

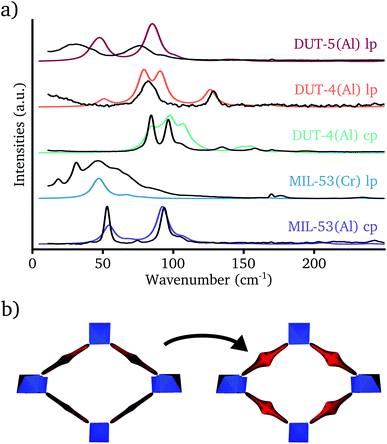
An important aspect in the methodology is the definition of the different rigid building blocks. This is not trivial as there is no unique choice. Firstly, there are the compensating anions in the inorganic chain that are shared between two inorganic octahedra. To maintain the symmetry of the octahedra each anion was attributed for one half to both inorganic groups. Secondly, each organic linker shares a carboxylate group with two inorganic octahedra. Each oxygen atom of a carboxylate group inherently belongs to a single inorganic octahedron, whereas the carbon atom acts as a hinge atom between the linker and the two neighboring inorganic octahedra. The carbon atom should not be fully assigned to the inorganic octahedra, because the carboxylate group can coordinate to the metal atom in various ways. However, it can also not fully be assigned to the linker, because the carbon atom does not completely follow the translational motion of the other linker atoms, hence it cannot be considered as a rigid group. Therefore, in correspondence with the rigid unit model proposed for MOF-5 by Rimmer et al.,³⁴ the carbon atom was partially assigned to the two inorganic groups and the linker with a weight of 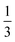. This is illustrated for MIL-53(Al) in Fig. 2.

Fig. 2 Visualization of the subdivision in building blocks for the case of MIL-53(Al). The carbon atom of the carboxyl group is shared between three blocks and has weight . The hydroxyl group is shared between two blocks and has weight .

2.1.2 Raman spectroscopy. Raman intensities of specific normal modes can be computed after obtaining the third-order derivatives of the energy with respect to the external electric field (twice) and with respect to the atom displacements (once). These derivatives can first be used to calculate the Raman tensor:⁶¹

Here χ represents the susceptibility tensor, which is the macroscopic equivalent of the polarizability tensor and corresponds to the second-order derivative of the energy with respect to the external electric field. Furthermore, N stands for the number of atoms in the unit cell of the structure and ṽ^κ is the mass-weighted eigenvector of normal mode κ.

represents the derivative of an element of the susceptibility tensor with respect to an atom displacement. This can be determined via a finite difference approach i.e. through numerical differentiation of the susceptibility tensors in distorted structures. Each distortion was created by displacing one of the atoms by 0.01 Å in the positive or negative sense of one of the Cartesian directions. Instead of the susceptibility tensor, the static dielectric tensor was calculated. They are directly related to each other via the addition of the identity matrix. The Raman intensity of mode κ follows from its Raman tensor via:

I_κ ∼ 45a_κ² + 7b_κ² (4)

with

2.1.3 Computational settings. All static DFT calculations have been performed with the Vienna Ab initio Simulation Package (VASP).^62–64 The projector-augmented wave (PAW) method⁶⁵ was used at the PBE level of theory⁶⁶ employing plane waves with a cutoff energy of 600 eV. Grimme's D3 corrections with Becke–Johnson damping were used in order to describe the long-range dispersion interactions.^67,68 Generally, a Monkhorst–Pack k-mesh⁶⁹ of 6 × 6 × 2 k-points for the cp phase and 6 × 2 × 2 k-points for the lp phase was applied. However, for the larger DUT-4(Al) and DUT-5(Al) materials only 1 k-point was taken into account along the longest cell vector to limit the computational cost.

Some structures consist of magnetic metal ions (those including Cr or V) for which the spin state needs to be defined. The choice of the spin direction is not trivial, as it has been shown that the relative orientation of neighboring spins can impact the structure.⁷⁰ In this work, we choose a ferromagnetic spin configuration meaning that all spins point in the same direction, as this is computationally less expensive than any other spin configuration.⁷⁰

The electronic structure calculations were considered to be converged when the change in the total energy between subsequent self consistent field (SCF) steps decreased below 10⁻⁸ eV. The Hessian calculations of the cp and lp phases of MIL-47 formed exceptions, because an SCF convergence of 10⁻¹⁰ eV was required to obtain a positive definite Hessian. For the geometry optimizations, the conjugate-gradient algorithm was employed to obtain structures that were converged up to 10⁻⁷ eV.

2.2 Experiment

Commercially available chemicals and solvents were used as received without further purification. 2,6-Naphthalenedicarboxylic acid (2,6-H₂NDC) from Aldrich (99%), 1,4-biphenyldicarboxylic acid (1,4-H₂BPDC) from Sigma Aldrich (97%), and 1,4-benzenedicarboxylic acid (1,4-H₂BDC) from Acros Organics (99+%) were used. N,N-Dimethylformamide (DMF) was purchased from Fisher Scientific (99.5%).

2.2.1 Synthesis.
2.2.1.1 MIL-53(Al) ([Al(OH)(1,4-BDC)]_n). A mixture containing Al(NO₃)₃·9H₂O (14.1 g, 37.6 mmol), 1,4-H₂BDC (31.3 g, 18.7 mmol) and 55 mL H₂O was put into a 250 cm³ Teflon liner, placed in an autoclave and heated to 220 °C and annealed for 72 h. The product was separated, washed with H₂O and dried at 150 °C for 2 h in an oven. The dry powder was mixed with fresh DMF and the mixture was tempered at 150 °C for 16 h. MIL-53(Al) powder was separated by centrifugation and washed with DMF and water. After drying at 150 °C in an oven, the powder was calcined at 330 °C for 52 h.
2.2.1.2 MIL-53(Cr) ([Cr(OH)(1,4-BDC)]_n). MIL-53(Cr) was synthesized according to the procedure reported in ref. 71. Cr(NO₃)₃·9H₂O ((2.0 g, 5.0 mmol), 1,4-H₂BDC (0.67 g, 4.0 mmol) and hydrofluoric acid (0.53 g, 2.65 mmol) were added to 22.5 mL water. The mixture was ultrasonicated for 30 minutes and transferred to a Teflon liner, placed into an autoclave, and heated in an oven to 220 °C and annealed for 72 h. The solid was washed with EtOH, dried at 300 °C in vacuum drying cabinet, and calcined by 330 °C for 22 h.
2.2.1.3 DUT-4(Al) cp (MIL-69) ([Al(OH)(2,6-NDC)]_n). A mixture, containing Al(NO₃)₃·9H₂O (1.310 g, 3.5 mmol), 2,6-H₂NDC (0.378 g, 1.75 mmol), KOH (0.244 g, 0.44 mmol) and 5 mL H₂O was placed into a 50 cm³ Teflon liner, placed in an autoclave and heated at 210 °C for 16 h. The product was separated, washed with H₂O and dried at 150 °C for 2 h in an oven.
2.2.1.4 DUT-4(Al) lp ([Al(OH)(2,6-NDC)]_n) and DUT-5 ([Al(OH)(1,4-BPDC)]_n). The synthesis was conducted according to the synthetic procedures reported in ref. 58. Instead of an autoclave, the Schott DURAN borosilicate glass bottle was used as reaction vessel. The products were separated by centrifugation and thoroughly washed with ethanol (Soxhlet extraction, 16 h).

2.2.2 Characterization. To ensure the phase purity the samples were subjected to powder X-ray diffraction analysis (PXRD). The samples for PXRD measurements were prepared in air. The measurements were performed on a Stoe Stadi P diffractometer in transmission geometry using monochromatic CuKα1 radiation (λ = 0.154056 nm) and MYTHEN detector (DECTRIS).

The PXRD pattern of MIL-53(Al) (see Fig. S3†) contains reflections of the cp and lp phases (due to the partial adsorption of moisture from air). The calcination of MIL-53(Cr) was obviously not successful. The PXRD pattern of the material correspond to the calculated PXRD of the as made form (see Fig. S4†). Therefore, the sample may contain terephthalic acid in the pores. DUT-4(Al) was prepared in the cp and lp phase (PXRD patterns are presented in Fig. S5 and S6,† respectively). The PXRD pattern of DUT-5(Al) indicates the formation of lp phase (see Fig. S7†).

2.2.3 Raman spectroscopy. The spectra in the backscattering geometry were collected in air (23 °C, 25% relative humidity) with a triple grating spectrometer (Horiba Jobin Yvon T64000) equipped with a liquid nitrogen-cooled charge-coupled device detection system. The Spectra-Physics diode-pumped solid-state laser Excelsior-532-300-CDRH with wavelength 532 nm and power 1 mW on a sample was used for spectra excitation. The incident laser beam was focused on the sample by a 50× Olympus MPlan objective lens with a numerical aperture of 0.75. The same objective lens collected the scattered light. Spectroscopic measurements were performed in the subtractive dispersion mode to investigate the low-wavenumber spectra, which attained a low-wavenumber limit of 10 cm⁻¹ in the present setup. The rigorous optical alignment allowed eliminating deformation of the low-wavenumber spectral edge by an optical slit, which sometimes smears the genuine features of low-wavenumber spectra.

3 Results and discussion

3.1 Raman spectra in the terahertz range

Before analyzing the theoretically predicted terahertz vibrations in the different MIL-53 materials, it should be verified that the calculated frequencies correspond to the experimentally measured ones. For that purpose, theoretical Raman spectra of five structures have been compared with their experimental counterparts in the range 0–250 cm⁻¹ (see Fig. 3a). As terahertz frequencies might exhibit a strong dependence on the unit cell volume⁴⁹ and to increase the overlap between experiment and theory, the normal modes have been determined for structures at the experimentally measured unit cell volume.

Fig. 3 (a) Raman spectra of different MIL-53 analogs in the range 0–250 cm⁻¹. The colored lines represent the static DFT spectra with a Lorentzian broadening of 10 cm⁻¹, whereas the underlying black lines are the corresponding experimental spectra. (b) Visualization of the Raman active terahertz vibration inducing rotations of the linkers.

In contrast to the IR spectrum in the terahertz range,⁴⁶ a set of modes with high Raman activity could be observed in experiment, which were well reproduced by the DFT simulations. Based on this correspondence, the Raman active modes could all be identified as vibrations inducing rotations of the aromatic groups (see Fig. 3b). The Raman spectrum of the cp phase of MIL-53(Al) shows two strong Raman peaks. The one with the lowest frequency around 50 cm⁻¹ is assigned to vibrations inducing linker rotations around their principal axis in which opposite linkers rotate in the opposite direction, whereas the Raman band around 90 cm⁻¹ originates from linker rotation modes in which opposite linkers rotate in the same direction. The higher frequency of the latter mode is due to the constrained movement in the dense cp phase structure.⁴⁹

The lp phase of MIL-53(Cr) has only a single strong Raman band in the theoretical spectrum. The two types of linker rotation vibrations that could be distinguished in the cp phase spectrum of MIL-53(Al) are also present here, but due to the increased unit cell volume in the lp phase there is no constrained movement anymore and their vibrational frequencies coincide. The experimental Raman spectrum of the lp phase of MIL-53(Cr) shows a very broad Raman peak centered around the theoretically predicted frequency of the linker rotation vibrations, which is probably caused by residual linker molecules in the pore. These residual linker molecules can imply constraints on the framework linkers broadening the Raman peak.

For DUT-4(Al), the Raman spectra have been measured in both the cp and the lp phase. The former structure can also be referred to as MIL-69.⁵⁷ Both phases exhibit a couple of strong Raman bands around 100 cm⁻¹ which can be assigned to vibrations inducing linker rotations around their principal axis. In contrast to the structures with a BDC linker, the two different types of these modes have similar frequencies in both the lp and the cp phase. This can be explained by the fact that these modes already have a higher frequency in the lp phase due to the disalignment of the carboxyl groups of the NDC linker (see Section S3 in the ESI† for a visualization). The reduced movement range of the linkers in the cp phase is in this case a secondary effect and will now only slightly increase the vibrational frequencies of these modes. DUT-4(Al) exhibits also some weak Raman bands due to vibrations inducing linker rotations around an axis parallel with the 1D chain. They are located around 50 cm⁻¹ and 130 cm⁻¹ in the lp phase and around 150 cm⁻¹ in the cp phase. The increased Raman activity compared with the other MIL-53 analogs originates from the larger polarizability of the disaligned NDC linker due to delocalized electrons.

The last structure, for which the experimental Raman spectrum was determined, is the lp phase of DUT-5(Al). It is characterized by two intense Raman bands around 30 cm⁻¹ and 75 cm⁻¹. The theoretical calculation also predicts these two bands, although slightly shifted to higher wavenumbers. The former originates from the vibrations inducing linker rotations around their principal axis, already discussed for the other structures. The latter Raman band can be assigned to rotations in the opposite direction of the two phenyl rings on the same BPDC linker.

As a final note, it has to be mentioned that the experimental Raman spectra were recorded in ambient conditions. Under these circumstances, adsorbed water molecules are supposed to be present in the 1D channel. Conversely, theoretical Raman spectra were determined without any water molecules, because this requires a dynamic approach to account for the mobility of the guest molecules.⁷² However, by means of ab initio molecular dynamics simulations it was verified that the presence of water had negligible impact on the predicted Raman spectra in the terahertz range. This is because water has only Raman active vibrations outside the terahertz spectrum and it leaves framework vibrations unaffected (see Section S4 in the ESI†).

In summary, the validity of our theoretical model could be verified via comparison with experimental Raman spectra in the terahertz range. The latter showed unique fingerprints in both the lp and cp phase spectra and, therefore, it is also the ideal tool to identify the phase transition in breathing MOFs.

3.2 Rigid unit modes in MIL-53(Al)

The good correspondence between the experimental and simulated Raman spectra in the terahertz range allows for a thorough characterization of the RUMs at the gamma point in the MIL-53 analogs. To quantify the character of these terahertz vibrations, we can differentiate between translations and rotations of the different building blocks induced by the mode. A similar approach has already been pursued in the case of molecular crystals^73,74 in which the building blocks, i.e. the molecules, were clearly separated. For MOFs, however, this has never been done to the best of our knowledge. The quantification depends on the definition of the building blocks, which may differ based on the assignment of hinge atoms. A description of the characterization procedure can be found in Section S5 of the ESI.†

In this section, we will investigate the RUMs present in the unit cell of MIL-53(Al), which will serve as the reference material. In our earlier study, a detailed description of the terahertz modes within this flexible MOF has been provided.⁴⁹ However, it lacked a quantification of the RUM character of each mode with subsequent division in specific building block movements. Nevertheless, this analysis is very useful to identify universal terahertz vibrations in MIL-53 analogs that are independent of the building block structure. In Fig. 4, the phonon modes with the 15 lowest vibrational frequencies (except from the translational modes) in the lp phase of MIL-53(Al) are characterized. To reduce the number of graphical representations of the modes, only the lowest frequency mode of each mode type has been presented in Fig. 4d. The schematic visualization of the other terahertz vibrations can be found in Section S6 of the ESI.†

Fig. 4 Characterization of the different rigid-unit modes in MIL-53(Al) grouped according to mode type: (A) metal-oxide rotation and linker translation, (B) metal-oxide translation and linker rotation, (C) linker rotation, (D) linker translation, (E) metal-oxide rotation, and (F) metal-oxide translation. (a) Vibrational frequencies of the rigid-unit modes in the lp phase. (b) Frequency difference of the rigid-unit modes between the cp and the lp phase. (c) Quantification of the displacements of the building blocks induced by the rigid-unit mode. Possible building block displacements are rotations and translations of the metal-oxide (MO) and the linker. (d) Schematic visualization of the different types of rigid-unit modes characterized in (a–c). For clarity, only the lowest frequency mode of every mode type is illustrated. Visualization of mode types A to E show the view on the pores, whereas mode type F provides a view on the 1D inorganic chain.

A first observation is that the displacements in all these terahertz vibrations can almost strictly be described by translations and rotations of the building blocks. In that sense, the 15 identified modes can be considered RUMs. The softest mode in the lp phase of MIL-53(Al) at 19 cm⁻¹ consists of rotations of the metal-oxide octahedra and translations of the linkers (mode A in Fig. 4). Its vibrational frequency decreases slightly in the cp phase. Nevertheless, it is significant given the very low frequency of this mode. The softness of this mode does induce a transition to a very closed pore phase in the Sc analog,^75,76 however such a transition is not observed in any of the structures studied here. The complementary mode, i.e. translations of the metal-oxide octahedra and rotations of the linkers (mode B in Fig. 4), has a much higher vibrational frequency in the lp phase (98 cm⁻¹) because it creates a strained configuration. In the cp phase, the increased dispersion enforces the collective behavior of this mode.

Modes A and B are the only phonon modes exhibiting a substantial relative decrease in vibrational frequency going from the lp phase to the cp phase. Mode E4 has also a negative frequency difference between the lp and cp phase structure, but this is small compared to the absolute vibrational frequency. The other modes exhibit an increase in frequency, such as the vibrations inducing rotations of the linkers (modes C in Fig. 4). As mentioned in the previous section (Section 3.1), two types can be distinguished: vibrations in which opposite linkers rotate in the opposite direction (C1 and C2) and vibrations in which opposite linkers rotate in the same direction (C3 and C4) (see Fig. S33 in the ESI†). In the lp phase of MIL-53(Al), the former are mixed up with either rotations of the metal-oxide units or translations of the building blocks, whereas the latter induce pure rotations of the linkers. They all have a vibrational frequency around 50 cm⁻¹. After transition to the cp phase, the first type of linker rotation modes can be found around the same frequency. In contrast, the dense cp phase induces an increase in the vibrational frequency of the second type of linker rotation modes as became clear already from Raman spectroscopy (see Section 3.1).

Modes D in Fig. 4 can mainly be characterized by translations of the linkers in the direction of the pore. They are often referred to as trampoline-like motions and have both a frequency in the lp phase of 58 cm⁻¹, which increases significantly when going to the cp phase again due to the hindered movement. This strong increase in vibrational frequency from the lp to the cp phase does also show up for three RUMs inducing rotations of the metal-oxide units (modes E in Fig. 4). Mode E1 at 63 cm⁻¹ in the lp phase consists of rotations of all metal-oxide units in the same direction combined with a rotation of the linker around an axis parallel with the 1D metal-oxide chain. Modes E2 and E3 induce rotations of neighboring metal-oxide units in the opposite direction combined with small linker translations (E2, at 75 cm⁻¹ in the lp phase) or linker rotations (E3, at 80 cm⁻¹ in the lp phase). Mode E4 with mainly metal-oxide rotations at 104 cm⁻¹ in the lp phase exhibits rotations of metal-oxide units on a single chain in the opposite direction as those on a neighboring chain. This rotation is combined with a translation of the linker, similar to mode A, although the translation is now in the opposite direction. This might explain why the frequency of this mode slightly decreases when going to the cp phase, which was the case for mode A.

A last set of RUMs that are discussed in Fig. 4 consist of shearing type vibrations (modes F). Their frequencies vary with the kind of displacements involved. A very low frequency mode, F1, located at 41 cm⁻¹ in the lp phase is characterized by a translation of neighboring 1D chains in the direction of the chain in the opposite sense, which goes hand in hand with a rotation of the linkers enabling this translation. At a slightly higher frequency (67 cm⁻¹ in the lp phase), RUM F2 is found consisting of translations of the 1D chain in the direction of the short pore diagonal combined with translations of the linkers in the opposite sense. Finally, mode F3 is present at 106 cm⁻¹ involving translations of the linkers in the direction of the 1D chain, in which opposite linkers move in opposite sense. This translation is facilitated by a translation of the metal-oxide units. These shearing modes have similar frequencies in the lp and cp phase and are, consequently, less relevant to understand the breathing mechanism.

The abovementioned modes all have more than 85% RUM character and can thus be considered as true RUMs. Within MIL-53(Al) there are four other modes with higher frequency that achieve the same target (see ESI†). Around 130 cm⁻¹, there are two modes inducing shearing of the linkers in the direction of the 1D chain and at 173 cm⁻¹ and 186 cm⁻¹, two modes involving in-plane rotation of the linker and rotation of the metal-oxide units can be found. These modes have relatively high frequencies because they create distortions of the metal-oxide units. The relatively high RUM character is an artefact of the partial occupation of hinge atoms in our model. Therefore, these modes will not be considered in the remainder.

3.3 Terahertz vibrations in winerack frameworks

Since the RUMs identified in MIL-53(Al) can be characterized independently from the building blocks, they are also present in topologically identical structures. Changing the building blocks has an impact on the vibrational frequencies of the RUMs due to altered interactions, which may affect the free energy and, hence, the stability of the MOF.¹⁷ However, the free energy consists mainly of an energetic contribution. Therefore, to analyze the effect of phonons on the flexibility, one should evaluate to what extend the entropic contribution, greatly influenced by the low-frequency RUMs, is able to counteract the internal energy. In the following, we will first estimate the effect of building block substitutions on the RUM frequencies and, consequently, the entropy. Afterwards, we will assess the impact on the flexibility.

3.3.1 Inorganic chain substitution. First, the influence of inorganic chain substitution on the RUM frequencies will be discussed (see Fig. 5). Looking at the frequency differences of the lp phase structures with the lp phase of MIL-53(Al) (Fig. 5a), no significant changes in vibrational frequencies can be observed. This is not surprising as inorganic chain substitution will yield only small volume differences (see Table 2), slightly affecting the dispersion interactions and, consequently, the normal mode frequencies. The most noteworthy frequency differences are found for the vibrations inducing linker rotations (modes C in Fig. 5). The presence of vanadium instead of aluminum gives rise to a frequency decrease of about 20 cm⁻¹, which is substantial for modes with a vibrational frequency of 50 cm⁻¹ in the original MIL-53(Al) structure. This can be explained by an increase in unit cell volume for the structures with vanadium. Although the increase is modest, it results in an equilibrium structure in which the phenyl units are planar with the carboxylate units, whereas these were tilted in the other MIL-53 analogs. This increases the symmetry of the lp phase (see Section S8 in the ESI† for a visualization). Therefore, the vibrational frequency of linker rotations will be reduced.

Fig. 5 Effect of inorganic chain substitution on the terahertz frequencies of the RUMs. (a) Frequency difference between the structure with substituted inorganic chain and MIL-53(Al), both in the lp phase. (b) Frequency difference between the cp and lp phase structures.

Table 2 Electronic energy difference, entropy difference at 300 K (TΔS term), and entropy difference at 300 K only due to the RUMs (TΔS term) (in kJ mol⁻¹ (in terms of the unit cell)) between the lp and cp phase. Also the theoretical unit cell volume (in ų) of both phases for the different MIL-53 analogs are presented

	MIL-53(Al)	MIL-53(Ga)	MIL-53(Cr)	MIL-53(V)	MIL-53(Al)-F	MIL-47(V)	A520(Al)	DUT-4(Al)^a	DUT-5(Al)
a There is no theoretically predicted metastable lp phase in DUT-4(Al). The volume of the simulated lp phase corresponds to the experimentally measured value in ref. 58.
Δlp–cpEel	26.7	34.1	27.5	39.0	0.6	−3.0	−15.2	113.1	138.1
TΔlp–cpS	9.5	12.1	13.1	25.7	9.4	14.0	10.3	2.9	24.2
TΔlp–cpSRUM	9.8	10.5	12.5	20.3	8.5	11.2	13.6	4.8	16.1
V cp	843	831	836	840	882	921	604	1097	1209
V lp	1426	1510	1510	1534	1430	1549	946	2159^a	2779

---

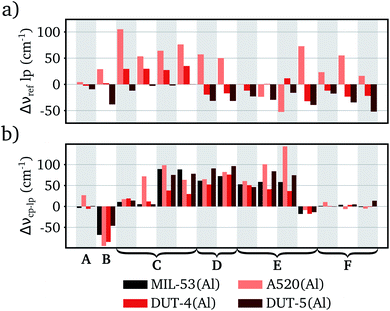
This decrease in frequency adds to the frequency difference between the cp and lp phase of this RUM, which will stimulate the entropic trigger to transform to the lp phase. Although also other factors will impact the frequency difference of linker rotation vibrations and other RUMs (see Fig. 5b). Adapting the type of metal, for example, increases the frequency difference for the RUMs inducing rotations and translations of the linkers (modes C and D in Fig. 5). Evidently, the larger ionic radii hinder the rotations of the phenyl unit and the trampoline motion of the linker in the cp phase. In contrast, replacing the anionic hydroxyl group by F⁻ (MIL-53(Al)-F) or O²⁻ (MIL-47(V)) reduces the frequency difference in these two RUM types. This decrease originates from the reduced dispersion interactions after removal of the hydrogen atoms. Consequently, the equilibrium volume of the cp phases of MIL-53(Al)-F and MIL-47 are substantially higher than for the other structures (see Table 2) and these type of vibrations become less hindered yielding lower frequencies. Therefore, this decrease in frequency difference is merely a function of the unit cell volume and not of other factors, as is demonstrated by volume–frequency relations of MIL-53(Al) and MIL-47(V) (see Section S9 in the ESI†). Nevertheless, it reduces the entropic trigger to transition from the cp to the lp phase, making the structures more rigid.

The frequency differences between the cp and lp phase of the other RUMs remain more or less the same upon inorganic chain substitution, except for one RUM exhibiting rotations of the inorganic octahedra (modes E in Fig. 5). Substitution of Al³⁺ with Cr³⁺ or V³⁺ significantly increases the frequency difference, whereas substitution of Al³⁺ with Ga³⁺ decreases the frequency difference. It is not clear what causes this deviating trend, however it is not expected to have a large impact on the breathing behavior given the almost unaltered frequency of this RUM in the lp phase and the relatively high frequency in the cp phase.

In conclusion, inorganic chain substitutions yield only small vibrational frequency differences in the lp phase structures. The changes in frequency differences between the cp and lp phases are more pronounced for two types of RUMs, i.e. those inducing linker rotations and translations. Substitution of metal atoms with larger ionic radii increases the frequency difference, whereas replacing the hydroxyl group reduces the frequency difference. This will increase, respectively decrease, the probability of an entropy driven phase transition between the cp and the lp phase.

3.3.2 Linker substitution. Besides substitution of the inorganic octahedra, also the linker can be exchanged. In the case of inorganic chain replacement, it was clear that small structural changes such as an increased unit cell volume could already lead to noticeable frequency differences. By changing the linkers, it can be expected that these frequency differences will be even more pronounced, because the type of linker directly determines the size of the framework and the strength of the intermolecular interactions. This becomes clear when looking at Fig. 6 comparing, on the one hand, the RUM frequencies in the lp phase of A520(Al) (fumarate linker), DUT-4(Al) (NDC linker), and DUT-5(Al) (BPDC linker) with the lp phase of MIL-53(Al) (BDC linker) (panel a). On the other hand, the RUM frequency differences between the cp and lp phase of all these structures are compared (panel b).

Fig. 6 Effect of linker substitution on the terahertz frequencies of the RUMs. (a) Frequency difference between the structure with substituted linker and MIL-53(Al), both in the lp phase. (b) Frequency difference between the cp and lp phase structures.

Observation of the frequency differences between the lp phases learns that the incorporation of the small fumarate linker generally increases the terahertz frequencies. The only exceptions are the RUMs inducing rotations of the inorganic octahedra (modes E in Fig. 6) for which also a decrease can be noted in some cases. Conversely, the use of the extended BPDC linker tends to decrease the lp phase frequencies of the RUMs, except for those inducing linker rotations (modes C in Fig. 6) which have frequencies comparable to MIL-53(Al). Clearly, the size of the linker has a direct impact on the vibrational frequencies of the RUMs in the lp phase. Short and light linkers yield higher frequencies, whereas long and heavy linkers give rise to lower frequencies. Based on these findings and their influence on the entropic contribution, we can expect structures with short linkers to be less flexible, while the opposite is true for structures with long linkers. The increased vibrational frequency of the modes exhibiting linker rotations (modes C) within DUT-4(Al) with long NDC linkers, seems contradictory. However, as was pointed out in Section 3.1 already, the disalignment of the carboxyl groups of the NDC linker (see Section S3 in the ESI† for a visualization) hinders the rotation in the lp phase increasing the mode frequency.

Interpreting the frequency differences between the cp and the lp phases of structures with substituted linkers is less straightforward. On the one hand, it appears that the disaligned NDC linker yields smaller frequency differences, because the RUMs are more hindered in the lp phase and/or less hindered in the cp phase. Long BPDC linkers, on the other hand, give rise to larger frequency differences, mainly due to the lower RUM frequencies in the lp phase. The RUM frequency differences in A520(Al) with the fumarate linker show no clear trends. We refer to Section S7 in the ESI† for a more detailed analysis of the specific RUM frequency differences.

We can conclude that short linkers such as fumarate yield higher absolute RUM frequencies making the structure more rigid. Conversely, long linkers such as BPDC yield lower absolute RUM frequencies enhancing the flexibility. Structures with an NDC linker, although it is more extended than BDC, did not always follow this rational due to disalignment of the carboxyl groups, which reduces the ability to undergo an entropically driven phase transition. Therefore, DUT-4(Al) can be considered more rigid than structures with well-aligned linkers.

3.3.3 Impact on flexibility. Up to this point, only the direct effect of building block substitution on the separate RUM frequencies has been treated. However, studying the impact of building block substitution on the flexibility requires an analysis of all phonon modes at once, because the effect on one mode can be counteracted by the effect on another. A property that contains information of all phonons is the entropy, which, together with the internal energy, determines the free energy (see Section S10 in the ESI†). To assess the possibility of a phase transition, the entropy difference and the internal energy difference between the lp and cp phase should be balanced against each other. The latter does primarily depend on the electronic energy difference between both phases. The calculated electronic energy difference and the entropy difference at 300 K between the lp and cp phases are given in Table 2. The theoretical values can vary depending on the level-of-theory that is applied.¹⁷ Furthermore, the actual equilibrium volume will depend on several factors, such as the zero-point energy and the temperature, which affects the vibrational frequencies.⁴⁹ Therefore, we will restrict ourselves to a qualitative discussion in the following.

First, it can be observed that at 300 K the lp phase is entropically favored over the cp phase for all MIL-53 analogs, which indicates that low-frequency vibrations are more abundant in the lp phase compared to the cp phase. Substitution of the inorganic octahedra has, in most cases, a limited effect on the entropy difference. Only for MIL-53(V) a substantial increase of the entropy difference between the lp and cp phase is observed. This stems from the very low frequency of the RUMs inducing linker rotations (modes C) in the lp phase of MIL-53(V), which was already discussed in Section 3.3.1. However, this does not necessarily make the structure more prone to a phase transition, because also the electronic energy difference is larger than with other inorganic octahedra.

In general, MIL-53 analogs with BDC linkers in combination with inorganic octahedra containing a hydroxyl group exhibit a moderate positive electronic energy difference between the lp and the cp phase. The entropy difference at 300 K calculated at the current level of theory is slightly smaller, but still of the same order of magnitude. Therefore, the entropy difference is able to outweigh the internal energy difference at some point, driving the transition from a cp phase to a lp phase. This is in agreement with experimental studies, evidencing breathing in MIL-53 with aluminum,⁴⁷ gallium,⁷⁷ chromium,⁵³ or vanadium⁷⁸ as the metal ion under certain thermodynamic conditions. When the hydroxyl group is replaced by fluor or oxygen, but the BDC linker is maintained, the electronic energy difference between both phases vanishes. Therefore, the entropy is the leading term in the free energy and only a stable lp phase is expected. This is also what is seen in experiments where both MIL-53(Al)_F (ref. 79) and MIL-47(V)⁷⁸ are found to remain in a rigid lp phase under atmospheric conditions.

In contrast to inorganic chain substitution, changing the linker can affect the entropy difference between both phases greatly. Substitution of BDC with BPDC linkers significantly increases the entropy difference, whereas to opposite is true when NDC linkers are considered. Replacing BDC with fumarate linkers keeps the entropy difference almost unchanged. Based on the large differences in RUM frequencies the latter finding is rather unexpected, but of low importance for the flexibility. The lack of dispersion interactions between neighboring fumarate linkers gives rise to a lp phase which is energetically more stable than the cp phase. Therefore, A520(Al) is expected to exist only in the lp phase under atmospheric conditions, which is also observed in experiments.⁸⁰

The introduction of NDC linkers reduces the entropy difference between both phases. The disalignment of the carboxyl groups increases the RUM frequencies mainly in the lp phase, which results in an entropy contribution of almost the same size in the lp and cp phase. Consequently, there is no entropic trigger towards one of both phases and the structure will remain in its energetically most stable phase, being the cp phase in the case of DUT-4(Al). Actually, our simulations show that no metastable lp phase exists. Experimentally, DUT-4(Al) can be synthesized in a cp⁵⁷ and a lp⁵⁸ phase, which are both rigid and cannot transition to the other phase. Apparently, synthesis with dimethylformamide (DMF) gives rise to a rigid metastable lp phase of DUT-4(Al).⁵⁸

Finally, the BPDC linkers yield a large entropy difference between the phases. This is due to a decrease in RUM frequencies and an increase in the frequency differences. Hence, there is a substantial entropic push towards the lp phase. Nevertheless, the strong dispersion interactions between neighboring BPDC linkers energetically favor the cp phase. In fact, the electronic energy difference is so large that a transition to the lp phase should only be possible at high temperature. This is not seen in experiments in which DUT-5(Al) is only present in the lp phase at atmospheric conditions and, on top of that, remains rigid.⁵⁸ This discrepancy between theory and experiment can, similarly to the occurrence of a lp phase of DUT-4(Al), be explained by the applied synthesis technique.

To end this discussion, it has to be noted that the vibrational entropies depend on all phonon frequencies and not merely the RUM frequencies. However, calculation of the entropy by only taking into account the RUM frequencies does yield entropy differences between the lp and cp phase which are close to the actual differences reported in Table 2 (see Section S10). Accordingly, the RUMs supply all relevant contributions to the entropy to interpret the flexibility. Another important consideration is that the current microscopic picture of flexibility in MOFs starts from an idealized situation without taking into account the presence of defects and explicit temperature effects. Defects may change the mode character and can lead to frequency shifts of the RUMs, which can be observed via broadening of the Raman peaks (see Section S11 in the ESI†). The RUM frequencies are also affected by temperature. Increasing the temperature may lead to frequency shifts, which can impact the entropy differences between phases of soft porous crystals (see Section S12 in the ESI†). Besides temperature effects and defects, the presence of guest molecules and multiple other factors can have an impact on the behavior of the framework. A detailed analysis of breathing transitions under experimental conditions should bear these in mind.

4 Conclusions

Reticular chemistry has provided a way to synthesize a vast number of MOFs with varying properties. Many properties depend on the characteristic phonons such as thermal conductivity, thermal expansion, and the occurrence of phase transitions. Carefully selecting the building blocks allows to tune the phonon properties of the MOF. In this work, the effect of inorganic chain and linker substitutions on the terahertz vibrations in MIL-53 analogs were investigated via ab initio lattice dynamics calculations.

A new theoretical framework was developed that enabled the characterization of the RUMs, involving translations and rotations of the building blocks, that allowed to identify these modes within the different MOFs, and that could analyze their impact on different properties. The accuracy of the simulations was verified by comparing theoretical Raman spectra with the experimentally measured ones. This resulted in a very good correspondence between theory and experiment. Moreover, the observed Raman bands in the terahertz range, mainly due to rotations of the linkers, proved to be unique fingerprints for the structures in their respective phases. As such, they can be used to pinpoint phase transitions in soft porous crystals.

Most of the RUMs showed no Raman activity and required a theoretical analysis. Taking MIL-53(Al) as the reference structure, this led to the identification of 15 RUMs, which could be classified into 6 types according to the induced translations and/or rotations of the inorganic octahedra and/or linker units. The first two types are phonon modes that become very soft in the cp phase. They involve rotations of the inorganic chains and translations of the linkers or vice versa. The next three mode types induce either rotations of the linkers, translation of the linkers, or rotations of the inorganic octahedra. The corresponding phonon modes are characterized by a low vibrational frequency in the lp phase and a high frequency in the cp phase. A last set of modes gives rise to translations of the inorganic octahedra and/or the linkers yielding shearing type of motions. Their frequency is similar in both phases and, therefore, they will not contribute to the breathing mechanism.

The RUMs identified in MIL-53(Al) appeared in all topologically identical structures. Consequently, their entropic contribution could be tuned by building block substitution. Linker substitution had the largest impact on the RUM frequencies. It was shown that short linkers yielded higher absolute RUM frequencies, whereas long linkers yielded lower absolute RUM frequencies. Therefore, longer linkers increase the intrinsic flexibility of the structure. Furthermore, the frequency difference between the cp and lp phase of several RUMs, such as the one inducing trampoline motion of the linker, increased when including the long BPDC linker, again enlarging the entropic trigger for the phase transitions. The introduction of the NDC linker resulted in the opposite effect because the disalignment of the carboxylate groups gave rise to hindrance of specific RUMs, such as those inducing linker rotations, increasing the frequency difference. The substitution of inorganic octahedra had a more subtle effect on the RUM frequencies. Including metal atoms with larger ionic radii slightly increased the frequency difference between the cp and lp phase, whereas replacing the hydroxyl group reduced it. This could increase, respectively decrease, the probability of the entropy driven phase transition.

Our theoretical study illustrated the influence of building block substitution on the phonon properties of flexible MOFs. It could pinpoint the effect of specific changes to the RUM frequencies and relate it with the impact on the flexibility by analyzing the entropy. This provided mechanical insight in the breathing phenomenon. However, the entropic contribution cannot be detached from the electronic contribution, which should also be taken into account to obtain a complete picture of flexibility in MOFs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Fund for Scientific Research Flanders (FWO), the Research Board of the Ghent University (BOF), the Deutsche Forschungsgemeinschaft (DFG, project number 448809307), and the Russian Foundation for Basic Research (RFBR, project number 21-52-12018). The authors thank Kerstin Zechel for sample synthesis. The computational resources and services used in this work were provided by the Flemish Supercomputer Center (VSC), funded by FWO and the Flemish Government.

References

1. A. J. H. McGaughey, A. Jain, H.-Y. Kim and B. Fu, J. Appl. Phys., 2019, 125, 011101.
2. X. Qian, J. Zhou and G. Chen, Nat. Mater., 2021, 20, 1–15.
3. G. Ernst, C. Broholm, G. R. Kowach and A. P. Ramirez, Nature, 1998, 396, 147–149.
4. R. Mittal, M. K. Gupta and S. L. Chaplot, Prog. Mater. Sci., 2018, 92, 360–445.
5. H. Oberhofer, K. Reuter and J. Blumberger, Chem. Rev., 2017, 117, 10319–10357.
6. H. Jin and Y. Li, Curr. Opin. Chem. Eng., 2018, 20, 107–113.
7. M. T. Dove, Am. Mineral., 1997, 82, 213–244.
8. S. Yuan, L. Feng, K. Wang, J. Pang, M. Bosch, C. Lollar, Y. Sun, J. Qin, X. Yang, P. Zhang, Q. Wang, L. Zou, Y. Zhang, L. Zhang, Y. Fang, J. Li and Z. Hong-Cai, Adv. Mater., 2018, 30, 1704303.
9. X. Zhang, Z. Chen, X. Liu, S. L. Hanna, X. Wang, R. Taheri-Ledari, A. Maleki, P. Li and O. K. Farha, Chem. Soc. Rev., 2020, 49, 7406–7427.
10. Z. Ji, H. Wang, S. Canossa, S. Wuttke and O. M. Yaghi, Adv. Funct. Mater., 2020, 30, 2000238.
11. M. J. Kalmutzki, N. Hanikel and O. M. Yaghi, Sci. Adv., 2018, 4, eaat9180.
12. O. M. Yaghi, Mol. Front. J., 2019, 3, 66–83.
13. T. Kamencek, N. Bedoya-Martínez and E. Zojer, Phys. Rev. Mater., 2019, 3, 116003.
14. A. M. Walker, B. Civalleri, B. Slater, C. Mellot-Draznieks, F. Corà, C. M. Zicovich-Wilson, G. Román-Pérez, J. M. Soler and J. D. Gale, Angew. Chem., Int. Ed., 2010, 122, 7663–7665.
15. K. T. Butler, A. Walsh, A. K. Cheetham and G. Kieslich, Chem. Sci., 2016, 7, 6316–6324.
16. T. D. Bennett, A. K. Cheetham, A. H. Fuchs and F.-X. Coudert, Nat. Chem., 2017, 9, 11–16.
17. J. Wieme, K. Lejaeghere, G. Kresse and V. Van Speybroeck, Nat. Commun., 2018, 9, 1–10.
18. D. Dubbeldam, K. S. Walton, D. E. Ellis and R. Q. Snurr, Angew. Chem., 2007, 119, 4580–4583.
19. N. C. Burtch, S. J. Baxter, J. Heinen, A. Bird, A. Schneemann, D. Dubbeldam and A. P. Wilkinson, Adv. Funct. Mater., 2019, 29, 1904669.
20. W. Zhou, H. Wu, T. Yildirim, J. R. Simpson and A. R. H. Walker, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 054114.
21. M. T. Dove and H. Fang, Rep. Prog. Phys., 2016, 79, 066503.
22. A. Ghoufi, G. Maurin and G. Férey, J. Phys. Chem. Lett., 2010, 1, 2810–2815.
23. B. Kuchta, F. Formalik, J. Rogacka, A. V. Neimark and L. Firlej, Z. für Kristallogr. - Cryst. Mater., 2019, 234, 513–527.
24. M. T. Ruggiero, J. Infrared, Millim. Terahertz Waves, 2020, 41, 491–528.
25. K. D. Hammonds, M. T. Dove, A. P. Giddy, V. Heine and B. Winkler, Am. Mineral., 1996, 81, 1057–1079.
26. K. D. Hammonds, M. T. Dove, A. P. Giddy and V. Heine, Am. Mineral., 1994, 79, 1207–1209.
27. A. P. Giddy, M. T. Dove, G. S. Pawley and V. Heine, Acta Crystallogr., Sect. A: Found. Crystallogr., 1993, 49, 697–703.
28. M. T. Dove, Philos. Trans. R. Soc. London, Ser. A, 2019, 377, 20180222.
29. A. E. Phillips, Acta Crystallogr., 2018, 74, 406–407.
30. A. L. Goodwin, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 134302.
31. S. A. Wells and A. Sartbaeva, Mol. Simul., 2015, 41, 1409–1421.
32. B. Campbell, C. J. Howard, T. B. Averett, T. A. Whittle, S. Schmid, S. Machlus, C. Yost and H. T. Stokes, Acta Crystallogr., 2018, 74, 408–424.
33. A. L. Goodwin and C. J. Kepert, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 140301.
34. L. H. N. Rimmer, M. T. Dove, A. L. Goodwin and D. C. Palmer, Phys. Chem. Chem. Phys., 2014, 16, 21144–21152.
35. J. L. Mancuso, A. M. Mroz, K. N. Le and C. H. Hendon, Chem. Rev., 2020, 120, 8641–8715.
36. L. Wang, C. Wang, Y. Sun, K. Shi, S. Deng and H. Lu, Mater. Chem. Phys., 2016, 175, 138–145.
37. M. R. Ryder, B. Civalleri, T. D. Bennett, S. Henke, S. Rudić, G. Cinque, F. Fernandez-Alonso and J.-C. Tan, Phys. Rev. Lett., 2014, 113, 215502.
38. N. Y. Tan, M. T. Ruggiero, C. Orellana-Tavra, T. Tian, A. D. Bond, T. M. Korter, D. Fairen-Jimenez and J. A. Zeitler, Chem. Commun., 2015, 51, 16037–16040.
39. F. Formalik, M. Fischer, J. Rogacka, L. Firlej and B. Kuchta, Microporous Mesoporous Mater., 2020, 304, 109132.
40. M. R. Ryder, B. Van de Voorde, B. Civalleri, T. D. Bennett, S. Mukhopadhyay, G. Cinque, F. Fernandez-Alonso, D. De Vos, S. Rudić and J.-C. Tan, Phys. Rev. Lett., 2017, 118, 255502.
41. K. T. Butler, P. Vervoorts, M. G. Ehrenreich, J. Armstrong, J. M. Skelton and G. Kieslich, Chem. Mater., 2019, 31, 8366–8372.
42. M. R. Ryder, B. Civalleri, G. Cinque and J.-C. Tan, CrystEngComm, 2016, 18, 4303–4312.
43. D. E. P. Vanpoucke, K. Lejaeghere, V. Van Speybroeck, M. Waroquier and A. Ghysels, J. Phys. Chem. C, 2015, 119, 23752–23766.
44. N. Bedoya-Martínez, A. Giunchi, T. Salzillo, E. Venuti, R. G. Della Valle and E. Zojer, J. Chem. Theory Comput., 2018, 14, 4380–4390.
45. P. A. Banks, Z. Song and M. T. Ruggiero, J. Infrared, Millim. Terahertz Waves, 2020, 41, 1411–1429.
46. A. E. J. Hoffman, L. Vanduyfhuys, I. Nevjestić, J. Wieme, S. M. J. Rogge, H. Depauw, P. Van Der Voort, H. Vrielinck and V. Van Speybroeck, J. Phys. Chem. C, 2018, 122, 2734–2746.
47. T. Loiseau, C. Serre, C. Huguenard, G. Fink, F. Taulelle, M. Henry, T. Bataille and G. Férey, Chem.–Eur. J., 2004, 10, 1373–1382.
48. S. Horike, S. Shimomura and S. Kitagawa, Nat. Chem., 2009, 1, 695–704.
49. A. E. J. Hoffman, J. Wieme, S. M. J. Rogge, L. Vanduyfhuys and V. Van Speybroeck, Z. für Kristallogr. - Cryst. Mater., 2019, 234, 529–545.
50. A. Krylov, A. Vtyurin, P. Petkov, I. Senkovska, M. Maliuta, V. Bon, T. Heine, S. Kaskel and E. Slyusareva, Phys. Chem. Chem. Phys., 2017, 19, 32099–32104.
51. A. S. Krylov, I. D. Yushina, E. A. Slyusareva, S. Krylova, A. Vtyurin, S. Kaskel and I. Senkovska, Phys. Chem. Chem. Phys., 2022, 24, 3788–3798.
52. M. Vougo-Zanda, J. Huang, E. Anokhina, X. Wang and A. J. Jacobson, Inorg. Chem., 2008, 47, 11535–11542.
53. C. Serre, F. Millange, C. Thouvenot, M. Nogues, G. Marsolier, D. Louër and G. Férey, J. Am. Chem. Soc., 2002, 124, 13519–13526.
54. K. Barthelet, J. Marrot, D. Riou and G. Férey, Angew. Chem., Int. Ed., 2002, 41, 281–284.
55. L. Liu, X. Wang and A. J. Jacobson, Dalton Trans., 2010, 39, 1722–1725.
56. M. Gaab, N. Trukhan, S. Maurer, R. Gummaraju and U. Müller, Microporous Mesoporous Mater., 2012, 157, 131–136.
57. T. Loiseau, C. Mellot-Draznieks, H. Muguerra, G. Férey, M. Haouas and F. Taulelle, C. R. Chim., 2005, 8, 765–772.
58. I. Senkovska, F. Hoffmann, M. Fröba, J. Getzschmann, W. Böhlmann and S. Kaskel, Microporous Mesoporous Mater., 2009, 122, 93–98.
59. A. Ghysels, B. T. Miller, F. C. Pickard IV and B. R. Brooks, J. Comput. Chem., 2012, 33, 2250–2275.
60. L. Vanduyfhuys, S. M. J. Rogge, J. Wieme, S. Vandenbrande, G. Maurin, M. Waroquier and V. Van Speybroeck, Nat. Commun., 2018, 9, 1–9.
61. M. Ceriotti, F. Pietrucci and M. Bernasconi, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104304.
62. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
63. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
64. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
65. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
66. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
67. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
68. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
69. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
70. T. Bogaerts, L. Vanduyfhuys, D. E. P. Vanpoucke, J. Wieme, M. Waroquier, P. Van Der Voort and V. Van Speybroeck, CrystEngComm, 2015, 17, 8612–8622.
71. X. Li, J. Zhang, W. Shen and S. Xu, Mater. Lett., 2019, 255, 126519.
72. I. Lezcano-Gonzalez, E. Campbell, A. E. J. Hoffman, M. Bocus, I. V. Sazanovich, M. Towrie, M. Agote-Aran, E. K. Gibson, A. Greenaway, K. De Wispelaere, V. Van Speybroeck and A. M. Beale, Nat. Mater., 2020, 19, 1081–1087.
73. A. D. Burnett, J. Kendrick, J. E. Cunningham, M. D. Hargreaves, T. Munshi, H. G. M. Edwards, E. H. Linfield and A. G. Davies, ChemPhysChem, 2010, 11, 368–378.
74. M. R. C. Williams, A. B. True, A. F. Izmaylov, T. A. French, K. Schroeck and C. A. Schmuttenmaer, Phys. Chem. Chem. Phys., 2011, 13, 11719–11730.
75. J. P. S. Mowat, V. R. Seymour, J. M. Griffin, S. P. Thompson, A. M. Z. Slawin, D. Fairen-Jimenez, T. Düren, S. E. Ashbrook and P. A. Wright, Dalton Trans., 2012, 41, 3937–3941.
76. L. Chen, J. P. S. Mowat, D. Fairen-Jimenez, C. A. Morrison, S. P. Thompson, P. A. Wright and T. Düren, J. Am. Chem. Soc., 2013, 135, 15763–15773.
77. C. Volkringer, T. Loiseau, N. Guillou, G. Férey, E. Elkaïm and A. Vimont, Dalton Trans., 2009, 2241–2249.
78. H. Leclerc, T. Devic, S. Devautour-Vinot, P. Bazin, N. Audebrand, G. Férey, M. Daturi, A. Vimont and G. Clet, J. Phys. Chem. C, 2011, 115, 19828–19840.
79. C. Nanthamathee, S. Ling, B. Slater and M. P. Attfield, Chem. Mater., 2015, 27, 85–95.
80. E. Alvarez, N. Guillou, C. Martineau, B. Bueken, B. Van de Voorde, C. Le Guillouzer, P. Fabry, F. Nouar, F. Taulelle, D. De Vos, J.-S. Chang, K. H. Cho, N. Ramsahye, T. Devic, M. Daturi, G. Maurin and C. Serre, Angew. Chem., 2015, 127, 3735–3739.

---

Footnote

† Electronic supplementary information (ESI) available: Reduced Hessian approach, PXRD patterns, alignment of linker, effect of water on theoretical Raman spectra, mode characterization, RUM visualization, effect of linker substitution on RUMs, linker orientation in MIL-53(V), volume–frequency relations, free energy and entropy, impact of defects on RUMs, and effect of temperature on RUMs. See https://doi.org/10.1039/d2ta01678h

---