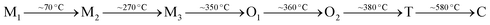Silver niobate perovskites: structure, properties and multifunctional applications

Abstract

AgNbO₃ exhibits “peculiar” anti-/ferroelectricity and narrow bandgap semi-conductivity that lead to active responses to different types of external stimuli, including electric fields, light and mechanical forces. Some of these unique properties are also mutually coupled and could be suited for the development of multifunctional devices for a broad range of applications, including dielectric, piezoelectric, high-power energy storage/conversion, photocatalytic and photovoltaic devices. In this review, recent studies of AgNbO₃ and AgNbO₃-based materials are summarized. The main scope is to establish the correlations between chemical composition, synthesis conditions, structure, and properties, with an improved understanding of the phase transformations taking place in the three so called “M” phases, to ultimately provide guidance on the materials development in two key sectors: high-power energy storage and photocatalysis. Finally, current challenges in multifunctional applications and future research directions are summarized.

---

The present review is organized into six main sections. The first section contains a broad introduction to the generalities of AgNbO₃-based ceramics and their importance within the lead-free perovskite family. Particular attention is given to the peculiar shapes of the polarization–electric field hysteresis loops, which represent one of the most fascinating aspects of these materials. The second section is dedicated to the synthesis, structure and relevant properties of AgNbO₃. In particular, the initial part of this section is focused on the procedures used to fabricate bulk ceramics, single crystals and thin films and the main issues encountered in obtaining high quality products. This part is followed by an extensive discussion on the ongoing debate concerning the actual nature of the crystal structure of AgNbO₃ at room temperature, during which ferroelectric, ferrielectric and antiferroelectric structures are compared and contrasted against each other. After that, a detailed survey on the polymorphic nature of AgNbO₃ is presented, by summarizing the current understanding of the temperature-induced structural modifications, in relation to the anomalies found in the temperature dependence of the dielectric properties. The following part is dedicated to the shapes of the current–polarization–electric field hysteresis loops and their relationships with the electric field-induced structural transformations that take place during the application of an external electric field. The second section is concluded with a survey on the photocatalytic and photovoltaic behavior of AgNbO₃. The third section is focused on the variations of crystal structure, and dielectric, ferroelectric and hysteresis loop characteristics, induced by chemical modifications using iso- and aliovalent elements. This helps outline general compositional design criteria aimed at obtaining desired properties. Sections four and five are respectively dedicated to two main applications, namely high-power energy storage and photocatalysis. The comparison of key properties obtained in different AgNbO₃-based systems provides additional information on composition and processing optimization to achieve maximized properties. The review is concluded with a broad summary and outlook presented in section six, in which the main findings are concisely described to increase the focus. At the same time, open questions, outstanding issues, and future research directions that could possibly fill the current knowledge gap are discussed.

1. Introduction

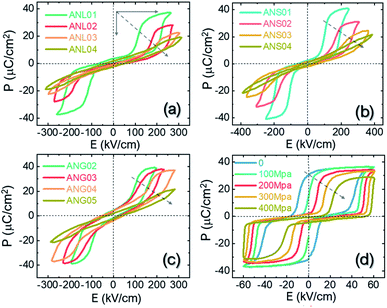
Pb-containing antiferroelectric compounds such as lead zirconate can transform into ferroelectrics when they are subjected to an electric field beyond a certain threshold. During these electric-field-driven phase transitions, various properties (such as polarization and strain) exhibit significant changes.^1–3 Chemically-modified Pb-based antiferroelectric materials mainly display two types of field-induced transition process.^1,2 The first type is characterized by reversible double polarization–electric field hysteresis loops (Fig. 1a), while the second is distinguished by “ferroelectric-like” hysteresis loops, which are observed after an irreversible transition has taken place during the first electrical loading cycle, as shown in Fig. 1b.

Fig. 1 Polarization vs. electric field loops for an antiferroelectric: (a) double polarization hysteresis loop for a reversible antiferroelectric–ferroelectric (AFE–FE) transition, (b) first-poling of an antiferroelectric displaying an irreversible AFE–FE transition, and (c) P–E loop evolution under increasing in situ pressure (indicated by arrow), showing a pressured-induced transition from metastable FE to AFE.

Double hysteresis loops are characterized by high charge storage density, which can be released over very short times, even in nanoseconds.⁴ Ferroelectric-like hysteresis loops can become “double” or even “linear” under pressure or shock pressure waves (Fig. 1c),³ and the charge stored in the electric-field-induced metastable ferroelectric state can be instantly released. These properties have allowed for the widespread application of Pb-containing antiferroelectric functional oxides in energy storage technologies, such as pulse power electronic devices,⁵ and in energy conversion systems, such as explosive power exchange.^3,6 Moreover, the electric-field-induced anti-/ferroelectric phase transition determines the on–off properties and can provide tunable dielectric, piezoelectric, pyroelectric, and electrocaloric properties by varying the magnitude of the applied electric-field. These multifunctional properties make Pb-based antiferroelectrics useful materials for applications in intelligent sensors, actuators, infrared detectors, and solid-state refrigeration systems.^7–9 However, Pb-containing electronic products are being progressively eliminated from these applications, due to increasingly stricter environmental legislation.¹⁰ Thus, in recent years, research has focused on the search for alternative Pb-free materials.

Amongst Pb-free perovskites, silver niobate (AgNbO₃) shows a “peculiar” response to the application of an electric field, that is different to that shown by antiferroelectric lead-based materials, such as PbZrO₃.^11–14 It was reported that AgNbO₃ shows “ferroelectric-like” hysteresis loops under weak electric-fields, as shown in Fig. 2a;^14,15 meanwhile, it displays classic “double” hysteresis (similar to PbZrO₃) at larger electric fields, as shown in Fig. 2b.^13,16

Fig. 2 Schematic polarization–electric field hysteresis loops for AgNbO₃ ceramic under (a) weak-field (≤20 kV cm⁻¹) and (b) strong-field (≥170 kV cm⁻¹).^15,16

The discovery of “double” polarization hysteresis under strong electric fields indicated that AgNbO₃ could potentially replace Pb-based antiferroelectrics in energy storage applications. Based on chemical composition adjustments, the field-induced phase transitions and the associated physical properties can be optimized. Thus, chemically-modified AgNbO₃-based materials could not only meet the stringent property requirements for energy storage and energy exchange devices, but also overcome the environmental drawbacks of lead-based materials. In 2016, our research team reported that AgNbO₃ ceramics show great potential in energy storage applications due to the high recoverable energy density,¹⁵ triggering increased research interest in this material. The energy storage capability in chemically-modified AgNbO₃ ceramics has been subsequently improved;¹⁷ it is now triple the value first reported for the unmodified composition, and even outperforms many Pb-based antiferroelectrics.

Although a large number of research studies on AgNbO₃ have been reported since its discovery in 1958, comprehensive reviews on this system are still rare. Early publications dating back about 20 years ago proposed that AgNbO₃ could be useful for piezoelectric and microwave applications.^18,19 Additionally, following the seminal work on semiconductor-based photocatalytic technology in 1972,²⁰ studies have also reported that AgNbO₃ exhibits attractive visible-light photocatalytic activity related to its narrow band gap (∼2.8 eV) that could be suitable for producing hydrogen and for degrading water pollutants.²¹ More recently, the photovoltaic properties of AgNbO₃ have also been explored for potential solar cell applications.²² Therefore, it is timely to comprehensively review the past and present understanding of AgNbO₃ and AgNbO₃-based materials to guide future development. The scope of this article is to review the synthesis, crystalline structure, microstructure and properties of these systems. In particular, the structure–property relationships of AgNbO₃-based perovskites are described and recent progress on AgNbO₃-based materials for high-power energy storage and photocatalysis is extensively discussed. The review is concluded with the proposal of future research, which could further improve the understanding and boost the applications of silver niobate-based materials.

2. Silver niobate (AgNbO₃)

2.1 Synthesis

In the binary phase diagram of Ag₂O–Nb₂O₅, there are five confirmed compounds with different Ag₂O : Nb₂O₅ stoichiometric ratios. Besides the perovskite-structured AgNbO₃ (1 : 1),²² the other confirmed phases are the layer-structured natrotantite Ag₂Nb₄O₁₁ (1 : 2),²³ the tungsten bronze-structured AgNb₃O₈ (1 : 3),²⁴ and the AgNb₇O₁₈ (1 : 7)²⁵ and AgNb₁₃O₃₃ (1 : 13)^26,27 compounds. It has been reported that these other compounds have similar properties to AgNbO₃, also exhibiting anti-/ferroelectricity and photocatalytic activity.^23,25 Although these compounds can be synthesized via conventional solid-state reaction routes, it has been widely experienced that synthesizing single phase AgNbO₃ in air by solid-state reaction is very difficult, due to the thermodynamic instability of Ag⁺ ions at elevated temperatures. To overcome this problem, the synthesis process is often carried out in an atmosphere of pure oxygen.¹³ The successful synthesis of AgNbO₃ in pure O₂ atmosphere using Ag₂O and Nb₂O₅ as raw materials has been reported in several publications.^15–20 During heating up to 200 °C, there is a slow reduction of Ag₂O:²⁸

Ag₂O → 2Ag + ½O₂(↑)

The thermogravimetric curves of metallic Ag, Ag₂O and Ag₂CO₃ as different silver sources in the formation of AgNbO₃ indicate that all these Ag precursors can react with Nb₂O₅, to finally form AgNbO₃, as shown in Fig. 3.

Fig. 3 Thermogravimetric curves of mixtures of Nb₂O₅ with different silver sources: metallic Ag powder, Ag₂O, and Ag₂CO₃.²⁸ [Reprinted by permission from Springer Nature: Journal of Materials Research, copyright (2007)].

By analyzing the three curves, it can be found that Ag₂O and Ag₂CO₃ go through a rather fast decomposition, leading to the formation of metallic Ag and O₂ at ca. 450 °C. On further heating, the metallic Ag is re-oxidized and reacts with Nb₂O₅ to form AgNbO₃ at ca. 800 °C, which melts and decomposes at ca. 1140 °C. The kinetics of the chemical reaction using metallic Ag are much slower than that using Ag₂O/Ag₂CO₃ precursors. The temperature for the complete formation of AgNbO₃ using metallic Ag is ca. 1060 °C. From Fig. 3, it is evident that only part of the Ag content is reduced in the initial stages of the reactions involving Ag₂O and Ag₂CO₃ and that the subsequent re-oxidation stage is completed more rapidly than in the case of the reaction with pure Ag, where the oxidation of the entire Ag content is required. An alternative strategy to synthesize pure AgNbO₃ without O₂ atmosphere is represented by wet chemical methods. It was reported that pure AgNbO₃ powders can be synthesized via hydrothermal processing at 160–240 °C using analytical grade NH₄HF₂, Nb₂O₅, and Ag₂O as raw materials in an acid solution (pH = 3).^29,30

Other chemical methods, such as sol–gel and co-precipitation have also been developed, using Ag and Nb alkoxides or citrates as precursors, with a firing step performed at 650 or 800 °C that burns off the organic ligands and leads to the formation of AgNbO₃.³¹ The color of the AgNbO₃ synthesized powders is usually milk-like or faint yellow, but it becomes darker, from red to gray, under visible-light.

AgNbO₃ single crystals can be grown via the molten-salt method using NaCl or V₂O₅ as flux agents.^32,33 Using flux methods, recently, Zhao et al. have successfully grown AgNbO₃ single crystals using Ag₂O (99.9%), Nb₂O₅ (99.99%), and V₂O₅ (99.2%) with a molar ratio of 7.4 : 1 : 4 in the starting mixture.³⁴ Polycrystalline bulk ceramics can be obtained by sintering synthesized AgNbO₃ powders at high temperature (usually from 1060 to 1120 °C) in O₂ atmosphere.^28,35 The prepared AgNbO₃ ceramics are generally yellowish in color. It should be noted that the decomposition temperature of AgNbO₃ is ca. 1120 °C, which is very close to the densification temperature of the ceramics, making the sintering of high density AgNbO₃ ceramics rather challenging. Therefore, precise temperature control is essential to prepare high-quality AgNbO₃ bulk ceramics. Generally, the melting or decomposition of AgNbO₃ ceramics begins at the surface when the sintering temperature is too high, and leads to the appearance of impurity phases, such as Ag₂Nb₄O₁₁ and AgNb₃O₈, amongst others. These impurities are usually confined within the surface layers and can be removed via a fine grinding process. By contrast, rough grinding would lead to the modification of the original lattice and to a number of artificial defects originating from the unstable chemical structure. Recently, it has been reported that Ag quantum-dots/nanoparticles are formed on AgNbO₃ after irradiation with a Xe lamp.³⁶ Theoretical modelling and simulations have shown that due to Ag deficiency, Schottky defect clusters consisting of two Ag vacancies and an O vacancy (i.e.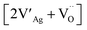 defect complex using the Kroger–Vink notation) can be formed in AgNbO₃ perovskites.³⁷ Kania et al. investigated the influence of Ag deficiency on microstructure and found that a few percent excess of Ag₂O in the starting composition can significantly increase the homogeneity of the perovskite structure and can thus improve the quality of AgNbO₃ ceramics.³⁸ On the other hand, a large excess of Ag₂O in the starting composition leads to the presence of metallic Ag. To avoid Ag deficiency at high temperature, Kitanaka et al. attempted to grow AgNbO₃ single crystals using slow cooling and Czochralski methods in a high-pressure O₂ atmosphere. They found that a high oxygen pressure can significantly prevent Ag deficiency, especially in the Czochralski method.³⁹ The materials used in high-power energy storage systems require high electrical insulation under strong field conditions and large electrical breakdown strength (E_b). The E_b of unmodified AgNbO₃ ceramics prepared by the solid-state method in pure O₂ atmosphere is 200 ± 20 kV cm⁻¹.^13,15,16 The effects of Ag deficiency on electrical properties were also reported in our recent publication, where small amounts of Ag deficiency favor increased stability of the AFE state.⁴⁰

Due to the demand for miniaturized electronic devices, the preparation of AgNbO₃ thin films has also been explored over the past ten years, particularly for microwave applications. The two primary deposition techniques used to prepare AgNbO₃ films include chemical solution deposition (CSD) and pulsed laser deposition (PLD). Telli et al. showed that AgNbO₃ thin films can be grown on (001) SrRuO₃/(001) LaAlO₃ substrates by CSD.⁴¹ Nevertheless, thin films prepared using this method showed significantly distinct dielectric properties compared to bulk ceramics. Kim et al. reported that AgNbO₃ films can be grown on LaAlO₃ (001) and sapphire (Al₂O₃-0112, r-cut) single crystals substrates by PLD, from stoichiometric AgNbO₃ ceramic targets.⁴² Using PLD technology,⁴³ thin films grown on SrTiO₃ (STO) single crystal substrates with different orientation can exhibit ultrahigh E_b values (∼400 kV cm⁻¹). Furthermore, it is interesting to note that AgNbO₃ films grown on (001) STO exhibited “double” polarization hysteresis, while AgNbO₃ films deposited on (110) and (111) STO substrates showed a “ferroelectric-like” polarization hysteresis under strong-field cycling. However, the authors did not perform a structure investigation to clarify the reasons for this difference. More recently, Zhang et al. grew AgNbO₃ epitaxial films on (001) STO substrates using the PLD method.⁴⁴ The film showed double polarization hysteresis with a higher AFE–FE phase transition field and a higher E_b value (624 kV cm⁻¹), indicating that such methodology may be viable for the fabrication of AgNbO₃ with high breakdown strength.

2.2 Crystal structure

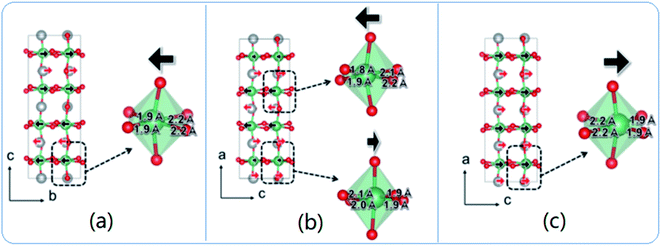
The exact crystallographic structure of AgNbO₃ is still under debate. Initially, it was suggested that AgNbO₃ is ferroelectric at room temperature with a tiny “ferroelectric-like” polarization observed under a weak electric field of 17 kV cm⁻¹ (remnant polarization P_r ≈ 0.04 μC cm⁻²) and a low piezoelectric response (piezoelectric coefficient d₃₃ ≈ 0.24 pC N⁻¹).^14,45 Subsequent investigations using powder diffraction techniques, including X-ray diffraction (XRD) and neutron diffraction (ND), demonstrated that AgNbO₃ displays an antipolar ordering with antiparallel displacements of Ag⁺ and Nb⁵⁺ in the centrosymmetric space group, Pbcm,^46–48 which is inconsistent with its electrical response. To resolve this ambiguity, in 2011, Yashima et al. carried out a comprehensive investigation by analyzing data generated by convergent beam electron diffraction (CBED), ND and synchrotron XRD, and suggested a weak polar or ferrielectric (FIE) structure, modelled with the non-centrosymmetric space group, Pmc2₁, where both Nb⁵⁺ and Ag⁺ cations show antipolar behavior. Since the unit-cell showed a weak net polarization, AgNbO₃ was categorized as a “non-compensated AFE”, which is distinct from typical AFEs.⁴⁹ In 2012, based on theoretical calculations, Niranjan et al.⁵⁰ revealed the possibility that Pmc2₁ and Pbcm phases may coexist, as supported by the small difference between their free energies (only 0.1 meV f.u.⁻¹).

Fig. 4 shows that the refined structure models of Pmc2₁ and Pbcm space groups are very similar. Both structures show a structural distortion with a (a⁻b⁻c⁺)/(a⁻b⁻c⁺) tilting using Glazer's notation. Actually, distinguishing the two structures based on average structural analysis methods such as XRD and ND is very difficult, since both structural models can fit the experimental data very accurately and give satisfactory refinement results. The Pbcm space group is a super-group of Pb2₁m, with some classes of diffraction peaks theoretically present in the latter but systematically absent in the former.¹⁶ For Pbcm, the full Hermann–Maugin symbol is P 2/b 2₁/c 2₁/m generating systematic absences of the type k = odd for 0kl, l = odd for h0l and hence k = odd for 0k0, and l = odd for 00l reflections. For Pb2₁m (transformed from Pmc2₁ to ensure that the axial assignments are consistent with Pbcm), the center of symmetry is lost as is much of the translational symmetry leaving only the b-glide perpendicular to the a-axis and a 2₁ screw axis parallel to the b-axis, to generate systematic absences of the type k = odd for 0kl and k = odd for 0k0. Thus, the Pb2₁m structure can be distinguished by the presence of 00l or h0l reflections where l is odd. Indeed in our previous work,¹⁶ 00l diffraction spots with l = odd were found in selected area electron diffraction (SAED) patterns, while further tilting experiments confirmed that these were not due to double diffraction (Fig. 5).

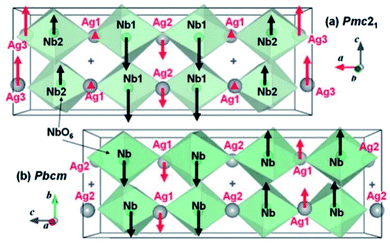Fig. 4 Refined structure models of non-centrosymmetric Pmc2₁ and centrosymmetric Pbcm phases. Red and black arrows indicate the displacements of Ag⁺ and Nb⁵⁺ ions, respectively, from the center of the bonded oxygen positions. The “cross” symbol indicates the center of symmetry in the Pbcm structure.⁴⁹ [Reproduced with permission from ref. 49 copyright 2011 American Chemical Society].

Fig. 5 (a) HREM and (b) observed SAED pattern at the [−1−10] zone axis; (c) and (d) calculated SAED patterns of Pb2₁m and Pbcm space groups, respectively.¹⁶

The simulated electron diffraction (ED) patterns clearly indicate that the space group is Pb2₁m rather than Pbcm, consistent with the early structure investigation reported by Yashima et al.⁴⁹ Using spherical aberration correction methods, Li et al. obtained high-angle annular dark-field (HAADF) images of AgNbO₃, where the fast Fourier transform pattern, as well as the ED patterns, indicated that the structure tends to the non-polar Pbcm space group.⁵¹ However, more recently, using a combination of high-resolution neutron and synchrotron X-ray powder diffraction, Farid et al. reported the structure as being polar in space group P2₁am (related to Pb2₁m by axial transformation).⁵²

Second harmonic generation (SHG) experiments can be used to identify whether or not a structure has inversion symmetry. A very weak SHG signal was found in AgNbO₃ powder and ceramic samples, which disappeared on heating at around 170 °C, indicating that at least part of the structure has inversion symmetry below this temperature.¹⁶ Recently, Lu et al. systematically demonstrated the difference between the Pbcm and Pmc2₁ structures in terms of crystallographic symmetry.⁵³ Each of the two distorted structures can be constructed via the coupling/competition between specific “softening” symmetry-modes within the first Brillouin-zone of the non-distorted parent structure. The scheme in Fig. 6 shows the structure distortion induced from the undistorted parent structure (Ammm) by specific symmetry-modes. The T4+ and H2 modes, located at the zone-boundary, can induce an R(〈110〉_p)-type octahedral rotation (i.e., (a⁻a⁻c⁰) tilting) and an R(〈001〉_p)-type octahedral rotation (i.e., (a⁰a⁰c⁻)/(a⁰a⁰c⁺) tilting), respectively. The Λ3 mode is mainly associated with the off-centering displacement of cations, which can result in an anti-parallel alignment of dipoles. The Γ4− mode, located at the zone-center, is an FE mode, which can induce all ions to move along a specific direction but with different magnitudes. The coupling of T4+ and H2 modes could induce a secondary Λ3 mode and finally construct the Pmca (axial transformation from Pbcm) distorted structure, while an additional “softening” of the primary mode Γ4− could lower the symmetry from Pmca to Pmc2₁. The global amplitude of the Γ4− mode is far from the amplitude of the Λ3 mode, which is responsible for the observed weak-ferroelectricity in AgNbO₃.

Fig. 6 (a) and (b) Distorted AgNbO₃ (AN) structure induced by the T4+ mode only, viewed along (a) the c-axis and (b) the a-axis. (c) and (d) Distorted AN structure induced by the H2 mode only, viewed along (c) the a-axis and (d) the b-axis. The +/− signs on the right in panel (d) show clockwise/anticlockwise rotations, respectively, of the right-hand column of octahedra around the a-axis. (e) The distorted structure induced by the Λ3 mode only, and (f) that of the Γ4− mode only. The black arrows in panel (e) show the off-center displacements of Nb⁵⁺ and Ag⁺ cations, while the red arrows in panels (e) and (f) indicate the local spontaneous polarization. The horizontal dashed red lines represent antiphase boundaries for octahedral rotation around the a-axis in panel (d), and cation displacements along the c-axis in panel (e).⁵³

2.3 Dielectric properties and temperature-driven transitions

Besides the controversy regarding its crystallographic structure at room temperature, AgNbO₃ has also been reported to display a series of temperature-induced phase transitions between different polymorphs, the details of which are still under debate. Generally, the structural transitions for non-linear dielectric materials (such as anti-/ferroelectrics) can be detected by measuring the temperature-dependence of dielectric properties and identifying the presence of dielectric anomalies that could originate from phase transitions. In 1958, Francombe et al. synthesized AgNbO₃ and studied its structure and dielectric properties; the relevant results of their study are reported in Fig. 7a and b.³⁵ In the plots, three dielectric anomalies at ca. 60, 260 and 340 °C can be observed; however, the structure analysis indicated that only the dielectric anomaly around ca. 340 °C relates to a phase transition (from orthorhombic to tetragonal structures). Furthermore, the structure analysis indicated that when the temperature approaches ca. 580 °C, a phase transition from the tetragonal to the cubic phase occurs, although no obvious dielectric anomaly can be found around this temperature (Fig. 7a).

Fig. 7 Thermal dependence of (a) permittivity and (b) lattice parameters of AgNbO₃ reported by Francombe et al.;³⁵ (c) temperature dependence of dielectric permittivity and loss of AgNbO₃ reported by Kania et al.;⁵⁴ [reproduced from ref. 54https://doi.org/10.1088/0953-8984/11/45/316 with permission from copyright IOP Publishing]. (d) Schematic showing the axial relationship between orthorhombic symmetry in rhombic (a_R, b_R, c_R) and parallel orientations (a_p, b_p, c_p), respectively (a_c, b_c, c_c represent the axes of the pseudo-cubic unit cell).

With the improvement of characterization equipment, Kania et al. re-investigated the relationship between polymorphic structure and dielectric properties and proposed the following polymorphic phase transition sequence during heating⁵⁴ (Fig. 7c):

M₁, M₂ and M₃ denote phases with orthorhombic (O) symmetry in rhombic orientation. The T and C phases have tetragonal and cubic symmetries, respectively. O₁ and O₂ represent phases with orthorhombic symmetry in parallel orientation. A schematic diagram of the O symmetry with different orientations is shown in Fig. 7d. The transitions between the high-temperature M₃, O (O₁ and O₂), T and C phases are related to the thermal evolution of octahedral tilting,^55,56 as observed by XRD^35,55,57 and TEM⁵⁶ experiments. However, no evidence of structural change can be observed in XRD or TEM for the O₁ ↔ O₂ transition. It should be noted that the M-type phase transitions were only ascertained via analyzing in situ diffraction data based on the primitive perovskite pseudo-cubic unit-cell using monoclinic parameters (hence their designation as “M” phases). The changes in structural parameters that distinguish the three M phases are mostly consistent with the dielectric anomalies around ca. 70 °C and ca. 270 °C. Additionally, dielectric spectroscopy also revealed a peculiar sharp anomaly at ca. 170 °C which appeared only in the cooling cycle and was hardly detected during heating, as shown in Fig. 7c. This was attributed to the dipole freezing temperature, T_f. During the 1980s, it was believed that the M₁ phase was ferroelectric, while the M₂ and M₃ phases were antiferroelectric, and the O₁, O₂, T and C phases were paraelectric. With the help of neutron diffraction, the symmetries of the high-temperature phases O, T and C have been better understood and their space groups have been identified as Cmcm, P4/mbm and Pm3̄m, respectively.⁴⁷ However, the exact symmetry of the M phases, the dielectric anomalies related to M-type phase transitions, as well as the so-called freezing temperature (T_f) are still under debate. Based on dielectric studies combined with infrared and Raman spectroscopy results reported in early publications,^58–60 the dielectric anomalies have been related to the different evolutionary stages of displacive Nb⁵⁺ ion dynamics, evidenced by the presence of submillimeter relaxation modes in the dielectric spectra shown in Fig. 8a and b, and the center component (P₁ peak) in Raman spectra shown in Fig. 8c.

Fig. 8 (a) Real (ε') and (b) imaginary (ε′′) parts of the dielectric permittivity as functions of temperature for AgNbO₃ in the 1–100 cm⁻¹ frequency range (data as reported by Fortin et al.)⁶⁰ reproduced from ref. 60https://doi.org/10.1063/1.361796 with the permission of AIP Publishing; (c) temperature dependence of the low-frequency Raman spectra of AgNbO₃ (data as reported by Kania et al.)⁶¹ reproduced from ref. 61https://doi.org/10.1088/0022-3719/19/1/007 with permission from copyright IOP Publishing (note: only Stokes Raman scattering is re-plotted in (c)). The spectra show an intense low-frequency phonon peak (P₂) and a strong central component (P₁), the intensity of which clearly rises with temperature and reaches a maximum at around 240 °C (corresponding to the M₂–M₃ transition). The phonon peak (P₂) shifts to lower frequency with increasing temperature and abruptly disappears around 378 °C (corresponding to the O–T transition). The diffuse peak, P₁, above 320 °C, is caused by the scattering of the initial phonon peak; (d) schematic of the octahedral framework within the non-polar Pbcm symmetry of AgNbO₃, in which octahedral rotations about the c-axis are indicated using arrows, while Ag1 and Ag2 specify c-planes occupied by the symmetrically non-equivalent Ag cations; (e) (left) schematic of the chain-like correlations for the local Nb displacements directed along [111]_c and [11–1]_c directions; (e) (right) a random mixture of chains 1 and 2 equivalent to average Nb displacements along the [110]_c direction (i.e., b-axis of orthorhombic crystal); (f) schematic for the Nb⁵⁺ displacive order–disorder behavior as a function of temperature.⁴⁸ [Reprinted with permission from ref. 48https://doi.org/10.1103/PhysRevB.79.104113 copyright 2003 by the American Physical Society].

These connections have been further explored in a systematic structure investigation reported by Levin et al. in 2009.⁴⁸ Based on various techniques that allow for probing of the local structure, such as neutron pair distribution functions (PDFs) and extended X-ray absorption fine structure (EXAFS), local structural distortions upon heating were detected and correlated to the order–disorder behavior of displacive Nb⁵⁺ cations in the octahedral framework of the non-polar Pbcm matrix. The octahedral framework in the Pbcm symmetry of AgNbO₃ observed from the c–b and c–a planes is shown in Fig. 8d, in which a sequence of two in-phase and two antiphase octahedral rotations about the c-axis yields a 4a_c periodicity with two crystallographically distinct Ag sites. The chain-like correlation for the local off-centering Nb displacements within two adjacent octahedral columns directed along [111]_c and [11–1]_c can give rise to the average Nb displacements along the [110]_c direction (i.e., the b-axis of the orthorhombic Pbcm structure) as shown in Fig. 8e. At high temperature, the Nb⁵⁺ cations are randomly displaced among eight sites along the 〈111〉_c directions, which give the ideal positions on average in the O phase. Upon cooling, the off-centered ordered arrays of Nb⁵⁺ cations displacement along the [111]_c and [11–1]_c directions in two adjacent octahedral layers gives an average displacement component along the [110]_c direction (i.e., along the b-axis of the orthorhombic Pbcm structure). In the two next adjacent layers, these average displacement components point in opposite directions, leading to AFE structural order. Locally, Nb⁵⁺ cations still occupy these eight positions, but two of these locations are preferred. Upon further cooling, the occupancy probabilities for the remaining six sites decrease and vanish below T_f, leading to a partial long-range ordered antipolar-like array of Nb⁵⁺ cations and to the observed sharp dielectric response at T_f. Miga et al.⁶² suggested that further freezing of the displacive Nb⁵⁺ and Ag⁺ sites on sub-lattice scales could lead to a weakly-polar relaxor ferroelectric or dipolar glass transition corresponding to the M₁ ↔ M₂ transition. Such disorder–order behavior of displacive cations has been used to successfully explain the polymorphic ferroelectric transitions in KNbO₃ and BaTiO₃, as reported in early studies.^63–65 In these cases, due to the absence of octahedral tilting, the partial ordering of off-center Nb⁵⁺/Ti⁴⁺ displacements, on cooling, triggers a sequence of well-defined thermodynamic phase transitions accompanied by changes in symmetry (i.e., tetragonal → orthorhombic → rhombohedral).

It should be noted that the local structural distortions that induce the dielectric anomalies separating the M-type polymorphs of AgNbO₃ suggested by Levin et al.⁴⁸ are based on the lattice matrix with Pbcm symmetry. However, in 1983, Kania et al. reported that the weak ferroelectricity in AgNbO₃ disappeared during heating at ca. 70 °C.¹⁴ After discovering this weak ferroelectricity, researchers preferred to link the M₁↔ M₂ phase transition to a structural change between the Pmc2₁ and Pbcm symmetries. This phase transition should be accompanied by a soft mode at the first Brillouin zone center, but Raman scattering does not offer any evidence for such an effect near ∼70 °C (see Fig. 8c). Instead, the central component corresponding to P₁ in Fig. 8c presents more obvious changes as a function of temperature and it progressively disappears approaching ca. 300 °C (in the M₃ region). This feature is closely related to the Nb⁵⁺-ion dynamics. In other words, the M₁ ↔ M₂ phase transition is possibly related to local structural variations or to an improper ferroelectric transition as defined by Dvorak (i.e., the primary driving force inducing this transition is not the polarization order parameter).⁶⁶ Based on in situ high-energy X-ray diffraction studies, Yoneda et al. provided additional insights into the temperature-driven polymorphic nature of the so-called M-phases.⁶⁷ In this study, the authors found that the Ag⁺ ion shows displacive disorder behavior. This discovery indicated the existence of an intricate coupling between octahedral tilting and local displacements of Ag⁺ ions since the octahedral tilting can usually lead to the off-centering of A-site cations within the AO₁₂ cage of the perovskite structure. The authors suggested that these interactions trigger a series of changes in the cation displacements across the so-called M phases, being similar to the situation in Pb-based solid-solutions near the morphotropic phase boundary (MPB). In Pb-based perovskites, three kinds of monoclinic phases (M_A, M_B, and M_C) can be formed due to the displacive ordering of cations shifting along specific directions (i.e., polarization rotation) from the parent tetragonal phase, as shown in Fig. 9.⁶⁸ Considering PbZr_0.48Ti_0.52O₃ as an example, the monoclinic structure can be derived from the tetragonal structure by shifting the Pb and Zr/Ti cations along the tetragonal [101] axis. The monoclinic phase in Pb-based solid-solutions provides a bridge between the ground states of rhombohedral and tetragonal structures.

Fig. 9 Direction of the spontaneous polarization in the three types of monoclinic phases with the usual nomenclature M_A, M_B (Cm) and M_C (Pm) redrawn, according to ref. 68.

However, early ND studies on AgNbO₃ provided no evidence for a ground state with rhombohedral symmetry, even at low temperatures down to 1.5 K.⁴⁷ Nevertheless, a ground state rhombohedral phase can be found in (Ag_0.94Li_0.06)NbO₃, which suggests that a rhombohedral-like structure may be buried in the local disorder of Ag atoms of the undoped AgNbO₃.⁶⁹ In 2014, Zhang et al.⁷⁰ reported the occurrence of an additional dielectric anomaly in the low-frequency range around 250 K in AgNbO₃ ceramics related to a first-order phase transition (denoted as M₀ ↔ M₁), as also supported by the presence of sharp anomalies in the differential scanning calorimetry (DSC) thermogram (see ref. 70, and Fig. 4 and 5). It should be noted that this ceramic was prepared using an AgNbO₃ powder synthesized by a hydrothermal method.⁷¹ Kania et al. carefully re-measured the DSC and dielectric properties of AgNbO₃ ceramics and single crystals, and found results to be consistent with previous investigations with no additional events found around 250 K in the dielectric and thermal data.⁷² Kania et al.⁷² argued that the extra dielectric anomaly reported by Zhang et al.⁷⁰ is more likely to originate from the increasing electrical conductivity around 250 K rather than an intrinsic dielectric process of AgNbO₃, indicating that water contamination is not negligible and that its prevention is necessary during experiments to avoid misinterpretation. Recently, our research team compared the variation of the temperature-dependent properties of unpoled samples including dielectric, DSC, dynamic mechanical analysis (DMA), as well as SHG data as shown in Fig. 10.¹⁶ It was found that the dielectric anomaly at the freezing temperature T_f (see Fig. 7c),⁵² also appeared in the dielectric data on heating, suggesting that this dielectric anomaly might be related to a temperature-driven reversible transition.

Fig. 10 Thermal dependencies of (a) relative dielectric permittivity (ε_r) and dielectric loss tangent (tan δ) at selected frequencies, (b) dε_r/dT, (c) DSC thermogram, (d) storage modulus (SM); (e) SHG for ceramic powders and (f) SHG for bulk ceramics (note: q = I_2w/I_2w (SiO₂)) of AgNbO₃. All plots were generated during heating.¹⁶

The comprehensive analysis of the properties shown in Fig. 10 indicated that the dielectric anomaly at “T_f” might not be associated with the freezing of Nb-ion dynamics, but could rather be ascribed to a second-order structural transition related to the breaking of inversion symmetry (i.e., Pmc2₁ ↔ Pbcm). It is possible that the primary driving force of this transition is the spontaneous strain rather than the spontaneous polarization (i.e., an improper ferroelectric transition),^66,73 since a significant change in the storage modulus can be found at T_f (see Fig. 10d). Additionally, the dielectric behavior under a DC bias field is very similar to that of typical relaxor-ferroelectrics, such as PbMg_1/3Nb_2/3O₃ (see ref. 16, Fig. 7). It could be reasonably deduced that the M₁ ↔ M₂ and M₂ ↔ M₃ transitions are related to local structural distortion in the polar (Pmc2₁) and non-polar (Pbcm) phases, respectively. In particular, the diffuse dielectric anomaly associated with the M₂ ↔ M₃ transition can be intimately related to disorder–order behavior of displacive Nb⁵⁺ dynamics on the sub-lattice scale in the non-polar Pbcm structure matrix. Recently, by studying Ag_1−3xBi_xNb_0.8Ta_0.2O₃ ceramics, Yan et al. found that within the M₂ phase stability region, two structural characteristics can be identified, and were denoted as the M_2a phase (at T < T_f) and the M_2b phase (at T > T_f). The M_2a phase is polar non-centrosymmetric, while M_2b is centrosymmetric. Moreover, they also proposed that even in the M₃ region, a few polar regions still persist, as evidenced by the observed weak satellite spot assigned to the (003) reflection of the Pb2₁m structure.⁷⁴ Additionally, Gao et al. investigated the local structural features, including interatomic distance distributions and atomic displacements, using neutron small-box pair distribution function (PDF) refinement in conjunction with large-box reverse Monte Carlo modelling, and found that at room temperature (300 K), with increasing the sizes of small-box PDF refinement, the structure tends to be non-polar, while at high temperature (T > T_f, e.g. 500 K), the non-polar structure provides a better description, regardless of the size of the PDF refinement. The results of this study further support the difference between the structure below and above T_f, and indicate that the dielectric anomaly assigned as T_f, originates from a phase transition.⁷⁵ Most recently, after analyzing the local structure data obtained from spherical aberration-corrected STEM, Li et al. suggested that at room temperature, besides the off-centering of Nb⁵⁺ ions along ±[110]_c forming AFE Pbcm or FIE Pmc2₁ structures, the deviation of Nb⁵⁺ ions along ±[001]_c directions was also found in local regions. They further point out that these local off-centering cations form polar nanoregions (PNRs), which are responsible for the observed relaxor dielectric response assigned to the M₁ ↔ M₂ phase transition. Their results further support the idea that the so-called M₁ ↔ M₂ transition is more likely related to a local structural evolution.⁷⁶

2.4 Ferroelectric properties and field-induced transitions

The earliest proofs of ferroelectricity in AgNbO₃ were based on the observation of non-linear and hysteretic P–E loops under a weak-field (<20 kV cm⁻¹)^14,45 that displayed a very small remnant polarization. In 2007, based on high quality AgNbO₃ ceramic samples, Fu et al.¹³ observed a “double” polarization hysteresis under high electric fields (see Fig. 11). The different polarization behavior under weak-field and strong-field conditions suggested that the virgin structure undergoes at least two types of field-induced processes, involving FE domain switching and a field-induced phase transition. In other words, the virgin structure should contain either FE or AFE states. To explain the peculiar polarization hysteresis observed in the experiments, Yashima et al.⁴⁹ suggested an FIE (i.e. “non-compensated AFE”) Pmc2₁ structure after studying diffraction data including CBED, ND and synchrotron XRD data. Furthermore, Moriwake et al. carried out molecular dynamics simulations on monocrystalline AgNbO₃, and proposed that polarization switching or a field-induced transition occurs at temperatures around −73 °C and above. Regardless of whether the simulations commenced from the AFE Pbcm or FE Pmc2₁ structures, above −73 °C the crystal fluctuates between the two forms.⁷⁷

Fig. 11 Electric displacement vs. electric field loops measured under (a) a maximum applied field of 220 kV cm⁻¹, and (b) a maximum applied field of 80 kV cm⁻¹.¹³ [Reproduced from ref. 13https://doi.org/10.1063/1.2751136 with the permission of AIP Publishing].

However, detailed studies of polarization–current–electric field hysteresis loops reported by Tian et al.^15,16 revealed more complicated electric-field-induced polarization events taking place in AgNbO₃ ceramics, providing further insights into the virgin structure and electric field-induced transformations, as well as on the temperature dependence of the polymorphic nature of AgNbO₃ perovskites. At room temperature, a ferroelectric-like polarization hysteresis with weak remnant polarization can be observed upon applying an alternating electric field of 60 kV cm⁻¹ (Fig. 12a), being similar to that reported in early studies. The I–E loops revealed two current peaks (denoted as P₁ and P₂) located at 6 and 30 kV cm⁻¹, respectively, which represent two kinds of field-induced polarization events.

Fig. 12 (a) P–E and I–E loops for AgNbO₃ with successive cycles under a maximum applied field of ±60 kV cm⁻¹ and a frequency of 10 Hz; (b) I–E data generated in the initial 1^st and 2^nd semi-cycles; thermal dependence of the current peaks on (c) heating and (d) cooling.^15,16

The data recorded in the first-poling cycle shown in Fig. 12b clearly reveal a sharp current peak, +P₁, around 6 kV cm⁻¹. The peak +P₂ located at higher electric field is not clearly visible in the first poling cycle, but careful observation reveals a small step around 30 kV cm⁻¹. Further insights into the origin of these current peaks were obtained by their temperature-dependence shown in Fig. 12c and d, which confirmed that the current peaks P₁ and P₂ disappeared around the temperatures associated with the M₁ ↔ M₂ transition and T_f, respectively. Similar features have been observed in the I–E curves of Ag(Nb_0.8Ta_0.2)O₃ ceramics shown in Fig. 13a.⁷⁸ In the same study, a sharp dielectric anomaly, assigned to T_f, was clearly observed during heating, in contrast to the case of pure AgNbO₃. Linear fitting of the reciprocal of permittivity using the Curie–Weiss law gave T₀ = 80 °C, which is very close to the value of T_f (∼75 °C) (see Fig. 13b).

Fig. 13 (a) Detail of the I–E curves for Ag(Nb_0.8Ta_0.2)O₃ ceramics at 10 Hz under an applied field of 8 MV m⁻¹ at different temperatures; (b) temperature-dependence of reciprocal relative permittivity (1/ε_r) for unpoled Ag(Nb_0.8Ta_0.2)O₃ ceramics measured at 1 MHz.⁷⁸

Based on these observations and the data discussed in Section 2.3, the following possible phase scenario can be derived. The phase M₁ would include the presence of polar and weakly-polar domains, both belonging to the Pmc2₁ symmetry. In other words, the virgin microstructure would include two kinds of polar domains with different electric dipole arrangement types in the same Pmc2₁ symmetry, which can be regarded as polar ferroelectric and polar ferrielectric (i.e., a non-compensated antiferroelectric). This suggestion is also supported by the simulations carried out by Moriwake et al.,⁷⁷ which indicated that the polar ferrielectric phase has the same space group, Pmc2₁, as the polar phase, but it is characterized by a slightly different ion arrangement that makes its distinction difficult in microscopy and diffraction techniques. Fig. 14(a)–(c) further illustrate the ordering of electric dipole arrangements resulting in AFE Pbcm, FIE Pmc2₁ and FE Pmc2₁ structures, respectively.⁷⁷ Most recently, domain structure observation on AgNbO₃ single crystals, has also revealed the existence of polar domains, which would further support the deduction.⁷⁹

Fig. 14 Comparison of crystal structures of (a) Pbcm (antiferroelectric), (b) Pmc2₁ (ferrielectric/weakly-polar), and (c) Pmc2₁ (ferroelectric) phases of AgNbO₃. The arrows indicate the relative magnitude and direction of atom displacement contributing to the ferroelectricity (or lack thereof) in each structure.⁷⁷ [Reprinted with permission from ref. 77https://doi.org/10.1103/PhysRevB.97.224104 copyright 2003 by the American Physical Society].

In this structural context, the current peak P₁ corresponds to the switching of the polar domains in non-centrosymmetric Pmc2₁ symmetry. This switching event is no longer present above the M₁ ↔ M₂ transition temperature, suggesting that these polar domains are not switchable in the M₂ phase region. It is noted that the size of polar domains should be nanometric and only emerge on local scales as supported by recent results based on STEM investigation.⁷⁶ The current peak P₂ could be related to the presence of weakly-polar domains, which are further stabilized by the applied field, as suggested by the sharpening of the peak P₂ after the first cycle. This peak disappears above T_f, suggesting that these domains do not switch in the M_2b centrosymmetric phase, in agreement with the loss of inversion symmetry and the closeness of T_f and the Curie–Weiss temperature. The absence of the peak P₂ in the M_2b phase offers further support to the idea that the T_f might be identified with the Curie point (T_C) of the weakly-polar phase.

Under strong-field conditions, a “double” polarization hysteresis loop is generated (Fig. 15a), which is consistent with the results reported by Fu et al.¹³ In the I–E loops, six current peaks can be observed; these are different from those observed in Pb-based AFEs like PbZrO₃, which only show four current peaks representing reversible phase transitions.¹ The peaks denoted as E_F and E_B correspond to the forward field-induced transition during loading and the backward transition during unloading, respectively. The polarization induced during loading achieves a value of about 40 μC cm⁻², while the remnant polarization is about 4 μC cm⁻², which is much higher than the P_r in the low-field loops. This means that the sample is left with a sizable remnant polarization, which is only recovered by reversing the applied field, in correspondence to the extra current peaks ±P near ±50 kV cm⁻¹ (denoted as key fields ±E_U). It is interesting to observe that the peak P at key field E_U is absent during the first poling cycle (see Fig. 15b), confirming that these additional current peaks ±P should originate from the polarization reversal of the residual strong-field-induced FE state. Interestingly, after strong-field poling of virgin sample, the authors found that the current peak P₂ in the I–E loop under weak field conditions becomes stronger.^15,16 This indicates that the weakly-polar phase leading to the sharp dielectric response (T_f) is metastable, and can be modified by the strong electric field. At the moment, the mechanisms of the field-induced transitions at E_F are still unclear and the nature of the high field-induced structure is unknown. Based on the structural model discussed above, the transition at E_F might involve the weakly-polar ferrielectric phase, as well as the non-polar antiferroelectric phase that would both transform to a polar FE phase, the former irreversibly, leading to a larger P_r and the latter reversibly, recovering at E_B. However, the first-principles calculations reported by Moriwake et al.,⁸⁰ indicated that a complete transition from an antiparallel alignment of electric dipoles in the non-polar Pbcm structure to the parallel alignment in the FE Pmc2₁ phase would require an ultrahigh electric field of 9 MV cm⁻¹ (see Fig. 14c). Thus, the double polarization hysteresis observed in pure AgNbO₃ is unlikely to originate from a typical AFE ↔ FE transition, but from a metastable weakly-polar FIE ↔ FE transition, which is not fully reversible, as suggested by the increased remnant polarization after high field cycling. The metastable FIE structure represents an intermediate state arising from the competition between the AFE Pbcm and FE Pmc2₁ phases. Additionally, the simulations by Moriwake et al. indicated that the field-induced FE phase and the weakly-polar/FIE phase have the same space group, Pmc2₁ (see Fig. 14). However, this deduction is only based on known data reported in the literature. To date, there are no experimental studies on the structure of the strong-field-induced FE phase.

Fig. 15 (a) Polarization–current–field hysteresis loops for AgNbO₃ with successive cycles under a maximum applied field of ±180 kV cm⁻¹ at a frequency of 10 Hz; (b) current–field loops generated in the initial 1st and 2nd cycles;¹⁶ (c) calculated P–E hysteresis loop for AgNbO₃ induced by an irreversible phase transition from AFE Pbcm to FE Pmc2₁ phases.⁸⁰ [Reproduced from ref. 80https://doi.org/10.1063/1.4941319 with the permission of AIP Publishing].

2.5 Photocatalytic, photoelectrochemical and photovoltaic properties

Besides showing anti-/ferroelectric behavior, AgNbO₃ perovskites are semiconductors possessing a narrow band gap, which ranges from 2.08 to 2.93 eV (determined from UV-vis diffuse reflectance spectra).⁸¹ Initially, AgNbO₃ was reported to be a visible-light-driven photocatalyst possessing the ability to obtain H₂ or O₂ from water in the presence of sacrificial reagents. Table 1 lists the photocatalytic activity of AgNbO₃ reported by Kato et al. under various conditions.²¹ In particular, the photocatalytic activity of AgNbO₃ was found to increase on the addition of an excess amount of Ag during preparation (i.e., Ag/Nb > 1) as shown in Table 1. Recently, a series of AgNbO₃-based photocatalysts, including solid-solutions, composites and heterojunctions, have been developed for water purification and will be discussed in Section 5.3.

Table 1 Photocatalytic activity of AgNbO₃ (ref. 21)

Catalyst	Ag/Nb ratio^a	Incident light/nm	Reaction conditions	Activity/μmol h^−1
				H2	O2
a In the starting materials. b Pressures of H2O and CH3OH were 20 and 70 torr, respectively. Catalyst: 0.3 g for liquid-phase reactions and 1.0 g for gas-phase reactions; reactant solution: 150 mL, 300 W Xe lamp, top window cell made of Pyrex.
AgNbO3	1.00	>420	0.05 M AgNO3(aq)	—	14
AgNbO3	1.00	>300	0.05 M AgNO3(aq)	—	119
AgNbO3	1.05	>420	0.05 M AgNO3(aq)	—	37.0
AgNbO3	1.05	>300	0.05 M AgNO3(aq)	—	240
AgNbO3	1.05	>420	H2O, CH3OH vapor^b	1.7

---

Electronic structure studies based on the plane-wave-based density functional method have revealed that the narrow band gap is due to the fact that the top of the valence band mainly consists of a hybrid orbital of Ag 4d and O 2p. To further understand the photocatalytic activity of AgNbO₃, Li et al. investigated the surface photoelectric properties of Ag/AgNbO₃ photocatalysts and suggested that the two peaks at ∼375 nm and ∼420 nm in the surface photovoltage spectrum (SPS) (see Fig. 16) are associated with two electronic transitions.⁸² One could correspond to the transition from O 2p to Nb 4d, being related to the UV light absorption property, and the other (∼420 nm, located at a shorter wavelength than the light absorption edge) related to visible-light absorption property was proposed to correspond to an electronic transition from Ag 4d to Nb 4d. In particular, the electric field-induced surface photovoltage spectrum (EFISPS) suggested that the second SPS peak (at∼ 420 nm related to the transition from Ag 4d to Nb 4d), determining the visible light absorption, could be enhanced or completely restrained under positive and negative external voltages, respectively, indicating tunable visible-light photocatalytic activity.

Fig. 16 (a) SPS of Ag/AgNbO₃ with different Ag contents without an external bias. The inset shows the variations in photovoltage and wavelength of the peak in the visible light region with Ag content. (b) EFISPS of Ag/AgNbO₃ (10%) at different external voltages. (c) SPS of Ag/AgNbO₃ (10%) at different external voltages. (d) Schematic band structure under different biases.⁸² [Reproduced from ref. 82https://doi.org/10.1088/0022-3727/42/23/235503 with permission from copyright IOP Publishing].

In 2014, Zhou et al.⁸³ revealed that AgNbO₃ exhibits surface plasmon resonance (SPR) under visible light. Surface plasmons (SPs) can exist on the surface of noble metals or narrow band gap semiconductors with abundant active current carriers.⁸⁴ This indicates that AgNbO₃ can absorb extra visible light with wavelengths ranging from 450 to 700 nm giving it huge potential in light-harvesting technologies. The SPR was suggested to originate from weakly bound Ag atoms in the perovskite structure, favoring a metal-like state of silver ions and self-assembled microstructures of AgNbO₃. The different absorptions were divided into two parts as shown in the inset of Fig. 17.⁸³ The electron-density map and the partial density of states of AgNbO₃ reported in earlier studies by Yashima et al.⁸¹ reveal a large valence band width (∼6 eV). The latter is due to the existence of Ag atoms and Ag–O and Nb–O covalent bonds, which lead to a narrower band gap (∼1.83 eV) compared to the experimental values reported in early studies, and a visible-light response. The metal-like characteristics and these transmission paths play a key role in promoting hot-electron generation and transmission.

Fig. 17 Ultraviolet-visible diffuse reflectance spectrum of AgNbO₃ samples. The red dashed line is the tangential line of the eigen-absorption band side, showing the location of the band gap. Inset: schematic showing two kinds of absorption mechanism.⁸³ [Reproduced from ref. 83https://doi.org/10.1063/1.4903912 with the permission of AIP Publishing].

Recently, Lu et al.³⁶ discovered that Ag nanoparticles with a size of 10 nm can be grown in situ on AgNbO₃ using illumination by Xe lamps, yielding a color change from yellow to brown, as shown in Fig. 18a. A change in color under light illumination was also found in our AgNbO₃ fresh powders. Fig. 18c shows SEM images taken after different irradiation times. Increasing numbers of nanoparticles can be observed on the surface of grains with increasing irradiation time. These Ag nanoparticles appearing on the surface of AgNbO₃ grains bring an extra absorption in the visible-light range as shown in Fig. 18b, which can be attributed to the SPR effect of Ag metal, as proposed by Zhou et al.⁸³ Thus, the SPR effect is responsible for the enhanced photocatalytic activity at increased ratios of Ag to Nb, as shown in Table 1. The appearance of such Ag nanoparticles would lead to the creation of Ag⁺ vacancies in the AgNbO₃ surface layers and be consistent with the theoretical prediction of Schottky defects in AgNbO₃.³⁷

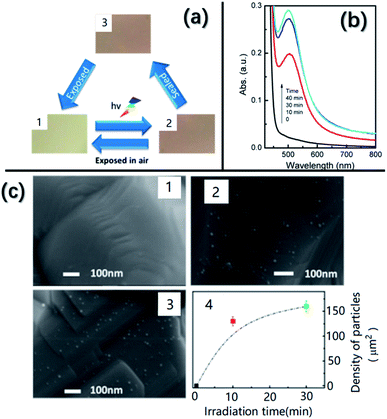Fig. 18 (a) Color of AgNbO₃ samples in different states: (1) initial, (2) after irradiation, and (3) isolated from air and kept in the dark for 48 h. (b) UV-vis spectra of AgNbO₃ irradiated with a Xe lamp for different times. (c) SEM images obtained from the samples in different states: (1) initial, (2) after 10 min of irradiation, and (3) after 30 min of irradiation. (4) Plot of density of nanoparticles versus irradiation time.³⁶ Reprinted with permission from ref. 36https://doi.org/10.1021/acs.jpcc.6b10961 copyright 2016 by the American Chemical Society.

Bulk samples of AgNbO₃ have recently been reported to exhibit linear and symmetric current–voltage (I–V) curves under dark and illuminated conditions.²² In particular, the extremely weak dark conductivity (in absence of illumination) can be significantly improved by illumination. Further analysis shows that the photocurrent under a certain bias voltage increases linearly with increasing light intensity (see Fig. 19a). The UV-vis absorption spectrum shown in Fig. 19b reveals obvious absorption in the visible-light wavelength range up to 800 nm, where a weak photoelectric response (compared to the UV-light region) can be noticed up to 550 nm. The authors of the study linked the photoelectric response in the visible-light region to the presence of defects rather than to the SPR behavior mentioned above.²² The time evolution of the photocurrent response under intermittent on/off illumination shown in Fig. 19c reveals very stable photocurrent values over 1.7 nA under 10 V bias, and a large on/off ratio of 1250. The transient photocurrent curves obtained under the illumination of a nanosecond pulse laser with an emission wavelength of 355 nm (see Fig. 19d) show an instantaneous photoresponse speed of 4.7 ns and highlight the great potential for quick-response optical sensing and detection applications.

Fig. 19 (a) Light intensity dependence of photocurrent under a 10 V bias on illumination with a 405 nm laser. (b) UV-vis absorption spectrum and photocurrent as a function of wavelength with a 10 V bias and light intensity of 150 mW cm⁻². (c) Variation of photocurrent with time on intermittent on/off illumination (405 nm laser and white light) under a 10 V bias and a constant light intensity of 150 mW cm⁻². (d) Transient photocurrent curves under the illumination of a nanosecond pulse laser with an emission wavelength of 355 nm, on tripling the frequency and a pulse duration of 3–4 ns.²² [Reproduced with permission from ref. 22 copyright 2019 by John Wiley and Sons].

AgNbO₃ ceramics have been also reported to exhibit a sizeable photovoltaic (PV) effect after electrical poling or mechanical polishing,²² evidenced by a non-zero short-circuit current, I_sc, and open-circuit voltage, V_oc, as shown in Fig. 20. However, the poling-induced PV response disappeared when the annealing temperature approached 200 °C, where no polarization switching phenomenon is observed in the I–E loop, as discussed in Section 2.4. This suggests that the PV response upon poling should be intimately related to the ferrielectric polarization. In contrast to the poling-induced PV effect, the mechanical polishing-induced PV response still persists after annealing the sample at 400 °C, which suggests that ferroelastic domains still exist at 400 °C, as reported in early studies on the domain structure.^56,57 The authors suggested that the flexoelectricity induced by strain gradients could be responsible for the polishing-induced PV effects, which lead to complex spatial strain gradients distributed along the scratches.

Fig. 20 I–V curves of AgNbO₃ ceramic samples prepared using different (a) poling and (b) polishing conditions. I–V curves collected under dark and illuminated (405 nm laser, 200 mW cm⁻²) conditions at room temperature after annealing the (c) positively poled and (d) positively polished AgNbO₃ ceramic at different temperatures for 1 h.²² [Reproduced with permission from ref. 22 copyright 2019 by John Wiley and Sons].

3. AgNbO₃-based solid-solutions

3.1 Anti-/ferroelectricity in perovskite oxides

Chemical modification represents a widely applied strategy to obtain specific physical properties for different applications. Based on the physical properties discovered in AgNbO₃ perovskites, a number of AgNbO₃-based materials have been explored; in particular, some AgNbO₃-based solid-solutions were found to hold great potential for microwave applications, as well as for dielectric capacitors and piezoelectric, pyroelectric and high-power energy storage devices.

The structure of the ideal ABO₃ cubic perovskite can be described as being based on a cubic close packed array of oxide ions with ¼ of these replaced by A cations. The B cations are located in ¼ of the octahedral interstices. Generally, the occurrence of anti-/ferroelectricity in perovskite structures is caused by the slight distortion from the high-temperature cubic phase. There is an important question to be clarified: why does a distorted structure form in some perovskite-structured compounds during cooling? Especially for AgNbO₃, the structural distortion is highly complex. It is well known that the stability of the perovskite structure (see Fig. 21) can be linked to its geometry by the tolerance factor (t) as discussed by Bartel et al.,⁸⁵

where r_O, r_A, and r_B are the ionic radii of the O, A, and B ions, respectively. In some publications, an alternative expression has been proposed:^86,87where r_A–O and r_B–O are the bond lengths of A–O and B–O bonds, respectively. In some crystals, the interaction between A-/B-site cations and the O anion is not only based on ionic bonds, but also on covalent ones, which play an essential role in the origin of ferroelectricity. The evolution of the perovskite structure and its dependence on the tolerance factor, t, in various metal oxides is summarized in Fig. 22.

Fig. 21 The parent cubic perovskite structure of ABO₃. The A-site cation is located at the interstice within the BO₆ octahedral framework.

Fig. 22 Perovskite structure evolution with reference to the tolerance factor. The data are from ref. 87 and 88.

From the structural geometry point of view, the following three situations can be identified (see Fig. 23): (1) in general, when t > 1, the B-site cation can spontaneously move off-center within the oxygen octahedron and generate ferroelectric distortion as in the cases of KNbO₃ and BaTiO₃ (see Fig. 22). Since the –A–O–A– atomic links are close packed (i.e., the close packed atomic link is along the 〈011〉 crystallographic directions of the cubic perovskite), this leads to greater space between the B-site cation and its surrounding O anions (see Fig. 23); (2) when t = 1, no A-/B-site cations can move off-center from their ideal positions in the parent cubic phase, as occurs in the cases of BaZrO₃ and SrTiO₃ (see Fig. 23). In this case both the atomic stacking along the directions of –A–O–A– (i.e., 〈011〉) and –B–O–B– (i.e., 〈001〉) are ideally packed. (3) When t < 1, the A-site cation is able to spontaneously move off-center in the AO₁₂ cage to generate ferroelectric distortion since the –B–O–B– bonding linkages are shorter, hindering the spontaneous off-center movement of the B-site cation in its oxygen octahedron, leading to a large space between the A-site cation and its surrounding O anions. However, in practical situations, the large stereochemical space results in the A-site cation only partially bonding with the adjacent O anions. Consequently, tilting of two adjacent BO₆ octahedra (i.e., antiferrodistortion, AFD) occurs with the formation of a superlattice. For example, in the case of BiFeO₃, two adjacent BO₆ octahedra undergo an antiphase rotation around the [111]_p direction, resulting in an A-site driven FE phase with R3c symmetry (see Fig. 23). In some cases, the AFD behavior is also accompanied by the antiparallel displacement of A-site cations in two adjacent perovskite cubic units from their ideal positions, without breaking the inversion symmetry. Thus, many perovskite compounds with t < 1 cannot display anti-/ferroelectricity, and show only antipolar behavior within supercells (i.e., antipolar phases or commonly, non-polar phases), as in the cases of CaTiO₃,⁸⁹ LnFeO₃ (Ln: rare-earth element)⁹⁰ and SrSnO₃ (see Fig. 24a).⁹¹ The difference between antiferroelectric (AFE) and antipolar (AP) lattices is shown in Fig. 24b.⁹²

Fig. 23 Schematic showing packing directions of atoms in a perovskite: the –A–O–A– close packed atom linkage is along the equivalent [011] direction, while the –B–O–B– atoms link along the equivalent [001] direction. The atomic arrangements in each A–O and B–O layers of (pseudo) cubic perovskite when t > 1, t = 1 and t < 1 are also drawn.

Fig. 24 (a) Schematic layer-resolved polarization of non-polar Pnma SrSnO₃. The polarizations induced in the Sr–O layers in SrSnO₃ are exactly equal and opposite and hence cancel each other out so that the macroscopic polarization is zero.⁹¹ [Reproduced with permission from ref. 91 copyright 2013 by John Wiley and Sons]. (b) A schematic representation of the differences between antipolar (AP) and antiferroelectric (AFE) structures.⁹²

The partial covalent character of compounds such as PbZrO₃ and BiFeO₃ is due to the hybridization between the A-site cation and O anion caused by the unique electron configuration (i.e., the 6s² lone-pair of electrons) and is responsible for the observed anti-/ferroelectricity in compounds with t < 1.⁹³ The t-factor of AgNbO₃ calculated using eqn (2) is 0.98. In theory, it should not display anti-/ferroelectricity; however, more detailed calculations reveal a hybridization between Ag and O,⁸¹ although unlike Pb and Bi, the Ag⁺ ion does not have a lone-pair of electrons. Additionally, experimental studies based on X-ray photoelectron spectroscopy,⁹⁴ have suggested the presence of partial covalent character in the chemical bonds between Ag and O, as well as in those between Nb and O, is responsible for the observed anti-/ferroelectricity in AgNbO₃.

Analysis based on structural geometry can be used to guide the development of novel AgNbO₃-based materials with specific polar states. Increasing the t-factor via suitable elemental substitution could favor the off-centering of B-site cations and induce B-site driven ferroelectricity, while reducing the t-factor could promote the stability of A-site driven anti-/ferroelectricity. Both anti- and ferroelectric structures of AgNbO₃ perovskites display off-centering of Ag⁺ and Nb⁵⁺ cations. This feature is very rare in anti-/ferroelectric perovskites and should provide wider possibilities to design new solid-solution materials with excellent performance. In Sections 3.2 and 3.3, we will give more detailed comments on these aspects in relation to recently developed AgNbO₃-based materials.

3.2 AgNbO₃-based ferroelectric solid-solutions

Two main types of AgNbO₃-based ferroelectric solid-solution with remarkable piezoelectric properties have been developed by A-site isovalent substitution. One type is represented by Li-doped AgNbO₃ compounds, such as (Ag,Li)NbO₃, (ALN), and (Ag,Li)(Nb,Ta)O₃, (ANLT) systems, and the other includes K-doped AgNbO₃ systems, such as (Ag_1−xK_x)NbO₃ (AKN).

3.2.1 Li-modified AgNbO₃. The ionic radius of the Li⁺ ion is much smaller than that of the Ag⁺ ion (r = 0.92 Å and 1.28 Å, respectively for the ions in 8 coordinate geometry).⁹⁵ Thus, the t-factor is gradually reduced in the ALN system with increasing level of Li substitution. This should enhance the stability of an antiferroelectric structure rather than a ferroelectric structure, as demonstrated in Section 3.1. However, it was found that Li-doping destabilizes the antiferroelectricity of AgNbO₃ at low Li content, and induces ferroelectric order at high Li doping levels.^52,69,96,97 A theoretical study based on density functional calculations focused on (K_0.5Li_0.5)NbO₃ (t < 1) revealed a frustration of tilt instabilities by A-site disorder, leading to a large off-centering of Li⁺ ions and a strong A-site driven ferroelectricity.⁹⁸ These results might explain the occurrence of strong ferroelectricity in ALN solid-solutions. Apart from the remarkable piezoelectricity, a composition-driven AFE/FE phase boundary can be found in ALN solid-solutions,^52,69,96,97 which could be suited to various applications, such as energy conversion, infrared detection and electrocaloric refrigeration, owing to irreversible electric field-induced phase transitions occurring near this phase boundary. However, the composition–structure–property relationships reported in previous studies are inconsistent, giving us the motivation to systematically survey and analyze the main factors responsible for these differences.

From the analysis of the strain-electric field simulated curves, it was reported that the piezoelectric property of Li-modified AgNbO₃ single crystals can reach 390 pm V⁻¹,⁶⁹ indicating that these compounds are promising lead-free materials for piezoelectric applications. Table 2 lists the piezoelectric properties of Li-modified AgNbO₃ single crystals and ceramics.

Table 2 Partial piezoelectric properties of Li-modified AgNbO₃ ferroelectric materials

Materials	d 33/d31 (pC N^−1)	k 33/k31 (%)	g ^33 (10^−3 V m N^−1)	T C (°C)
a Single crystal. b Ceramic.
Ag0.949Li0.051NbO3 (ref. 69)	65/—	—	11.3	173
Ag0.938Li0.062NbO3 (ref. 69)	180/—	—	38.4	199
Ag0.935Li0.065NbO3 (ref. 69)	190/—	—	53.8	204
Ag0.914Li0.086NbO3 (ref. 69)	210/—	—	53.9	275
Ag0.9Li0.1NbO3 [010]o (ref. 99)	—/−39.2	—/15.5	—	470
Ag0.9Li0.1NbO3 [110]o (ref. 99)	—/−80.0	—/30.4	—	470
Ag0.9Li0.1NbO3 (ref. 99)	—/−130.0	—/70.5	—	470
Ag0.9Li0.1NbO3 (ref. 100)	52/—	44/—	—	—

---

3.2.1.1 Solid-solution synthesis. It was reported that ALN ceramics can be synthesized via the conventional solid-state method in O₂ atmosphere using Ag₂O, Li₂CO₃ and Nb₂O₅ as raw materials. However, the preparation conditions significantly affect the structure and properties as reported in various studies. In the papers by Niewiadomski et al.,⁹⁷ and Kania et al.,¹⁰¹ the authors synthesized (Ag_1−xLi_x)NbO₃ ceramics using a two-step synthesis strategy as summarized in Fig. 25a. Using this synthesis strategy, a bi-phasic ceramic consisting of ALN solid-solution and LiNbO₃ was obtained for x > 0.03. At higher Li concentrations, higher amounts of the LiNbO₃ phase were found in the X-ray diffraction patterns, as evidenced by the increasing intensity of the peaks belonging to this phase.⁹⁷ Based on the compositional dependence of dielectric properties, it could be deduced that at higher Li concentrations, while the amount of LiNbO₃ increased, more Li⁺ ions also diffused into the AgNbO₃ lattice.⁹⁷ In the papers reported by Fu et al. and Khan et al.,^102,103 stoichiometric mixtures of Ag₂O, Nb₂O₅ and Li₂CO₃ were calcined and subsequently sintered, as summarized in Fig. 25b, and appeared to eliminate the problem with the secondary LiNbO₃ phase. The differences between these syntheses are mainly represented by the processing parameters, such as calcination and sintering temperatures. In particular, the ALN solid-solution ceramics reported by Fu et al., exhibited a very high solid solubility of Li⁺ ions (ca. 10 mol%), which should reflect the real solid-solution limit.

Fig. 25 Schematic synthesis procedures for (Ag,Li)NbO₃ ceramics reported by (a) Niewiadomski et al.,⁹⁷ and A. Kania et al.,¹⁰¹ and (b) Fu et al. and Khan et al.;^102,103 schematic synthesis procedures for (Ag,Li)NbO₃ single crystals reported by (c) Wada et al.⁹⁹ and (d) Fu et al.⁶⁹

The synthesis of ALN single crystals using the procedures shown in Fig. 25c and d also results in different structure and properties. It was reported that ALN thin films can be fabricated on (001), (110) and (111) SrTiO₃ (STO) substrates by pulsed laser deposition (PLD),¹⁰⁴ while the ALN ceramic targets for fabricating thin films were prepared by a solid-state reaction method, being similar to the processing reported by Fu et al.¹⁰²

3.2.1.2 Composition–structure–property relationships. The composition–structure–property relationships in ALN solid-solutions reported in previous publications^{50,67,90,91,99–101} differ with respect to the different processing conditions used. As demonstrated above, using the synthesis approach described in Fig. 24a, bi-phasic ceramics (i.e., ALN solid-solution and LiNbO₃) are obtained when x > 0.03 mol. Diffraction analysis of samples prepared using the synthesis method reported by Fu et al.¹⁰² (see Fig. 26b), shows that the solubility limit of Li is near x = 0.1 and a composition-driven transition from orthorhombic to rhombohedral (O–R) phases was found in the range x = 0.05 to 0.06, above which, the ALN solid-solution exhibits a single rhombohedral ferroelectric phase, as shown in Fig. 26a. Significant property variation was also revealed in ALN ceramics, giving additional evidence to support a composition-driven phase transition. With increasing x-value, a significant change in the dielectric behavior is observed (Fig. 26b), with a sharp maximum peak found at x ≥ 0.06.¹⁰² This peak shifts to higher temperature with further increase of the x-value. The temperature corresponding to the dielectric peak is believed to be the Curie point (T_C) of the FE R phase. Fu et al.¹⁰² proposed that as the x-value increases, the FE R phase develops from the FE structure originally found in the M₁ region. However, further examination of the dielectric pattern reveals that the dielectric anomaly T_I (assigned to the M₁ ↔ M₂ transition) gradually shifts to lower temperature and disappears for x > 0.06. Thus, the M₁ ↔ M₂ transition could correspond to a local structural evolution rather than to a symmetry change, as proposed in our previous study on AgNbO₃.¹⁶ The double P–E hysteresis loops evolve into a ferroelectric-type loop when the composition approaches the AFE_O/FE_R phase boundary, consistent with the structure characterization. The ALN single crystals prepared using the procedure described in Fig. 25d reported by Fu et al.⁶⁹ also show similar results to the ceramic samples. Interestingly, the investigation on ALN single crystals, prepared using the procedure shown in Fig. 25c reported by Wada et al.,⁹⁶ highlights a structural change from the AFE orthorhombic (Pbcm) phase to an FE orthorhombic (Pc2₁b) phase at x = 0.07. On further increasing the x-value, an extra composition-driven FE orthorhombic (Pc2₁b) to FE rhombohedral (R3c) phase transition occurred at x = 0.1 (see Fig. 26d). For x > 0.1, this phase transition shifts to higher temperature, indicating the possible presence of an intermediate structure connecting the AFE_O and FE_R phases. It is possible that the range of this intermediate structure is dependent on the quality of samples.

Fig. 26 (a) XRD patterns of synthesized powder, (b) temperature-dependent dielectric permittivity and (c) P–E loops of Ag_1−xLi_xNbO₃ ceramic solid-solutions reported by Fu et al. in 2011.¹⁰² [Reproduced from ref. 102https://doi.org/10.1088/0953-8984/23/7/075901 with permission from copyright IOP Publishing]. (d) Schematic phase diagram of ALN system (using the preparation procedure shown in Fig. 25c) and (e) schematic configuration of [010]_o and [110]_o directions for Pc2₁b orthorhombic symmetry reported by Wada et al. in 2006;⁹⁶ [reproduced from ref. 96https://doi.org/10.1143/JJAP.45.7389 with permission from copyright IOP Publishing]. (f) Schematic phase diagram of ALN system reported by Farid et al. in 2020 (using the preparation procedure shown in Fig. 25b).⁵² [Reproduced with permission from ref. 52 copyright 2020 American Chemical Society].

It should be noted that the FE_OPc2₁b structure exhibits the same unit-cell dimensions as the AFE_OPbcm structure (see Fig. 26d). After the FIE structure of AgNbO₃ was identified in 2011,⁴⁹ Farid et al.⁵² re-investigated the structural evolution of ALN powders synthesized by the method described in Fig. 25b, using high-resolution ND and synchrotron XRD. They suggested a new phase diagram for the ALN system, where the coexistence of FIE P2₁am (axial transformation of Pmc2₁) and FE R3c phases was found for x > 0.05. In addition, for x > 0.05, a distinct polymorphic phase behavior compared to that of pure AgNbO₃ on heating was proposed: both P2₁am and R3c polar structures evolved into a non-polar Pbnm phase and caused the maximum dielectric peak (T_C) shown in Fig. 26b. By means of electron diffraction (ED), additional structural details for the x > 0.05 compositions were revealed. The ED study by Khan et al.¹⁰³ reported a new complex modulated oxygen octahedral tilt system with a unit-cell, which could be considered as an intermediate structure bridging the AFE_O phase and the FE_R phase. Such intermediate modulated structures are not unusual in anti-/ferroelectric perovskites and have been found near the MPB in many solid solutions, such as BNT-based and BFO-based perovskites, due to the complex interaction between off-centering cation displacements and oxygen octahedral tilting.^105–109 Thus, it is hard to describe the exact structural nature of the so-called MPB region based on the coexistence of two or more well-defined crystallographic phases. Therefore, more structural investigations are needed to deepen the understanding of the MPB region in ALN solid solutions.

3.2.2. (Ag,Li)(Nb,Ta)O₃ ferroelectric solid-solutions. Recently, our research team prepared (1 − x)AgNbO₃–xLiTaO₃ (ANLT100x) perovskite solid-solution ceramics,⁵³ using the same preparation procedure as Fu et al.¹⁰² shown in Fig. 25b. Using ND data on the ceramic samples, the simultaneous presence of O and R phases (using FIE Pmc2₁ and FE R3c models) was detected when x ≥ 0.05. The composition-driven structural evolution of the ANLT system is very similar to that found in the ALN system by Farid et al.⁵² The ED study also revealed the presence of inhomogeneous local structures including disordered in-/antiphase octahedral tilting and off-centering cation displacements in the O–R phase transition regions.¹¹⁰ More importantly, in order to understand the origin of the structural evolution from the lattice dynamics view point, our structural refinement used the symmetry-mode-decomposition approach and revealed that the destabilizing AFE mode and the a⁰a⁰c⁺/a⁰a⁰c⁻ AFD mode with increasing Li⁺ ion concentration constitute the driving force to induce the composition-driven Pmc2₁ ↔ R3c phase transition, as shown in Fig. 27a.⁵³ In particular, a sudden change in the lattice parameters of the FIE_OPmc2₁ phase can be found for x ≥ 0.05 (see Fig. 27b), indicating that the structure is highly distorted or that an additional unknown intermediate structure is present. The dielectric spectrum of the ANLT system also shows a similar behavior to that of ALN. An additional dielectric peak (denoted as T_U) could be found when x > 0.05 (see Fig. 27c). The dielectric peak T_U is related to a temperature-driven FE_R phase transition. Moreover, through a detailed analysis of the dielectric loss, it can be found that the dielectric anomaly (T_I) assigned to the M₁ ↔ M₂ transition is still present at x = 0.06 (ANLT6). This feature demonstrated that the composition ANLT6 still possesses the AgNbO₃-based O symmetry and that the M₁ ↔ M₂ transition is linked to a local structural evolution, being consistent with our previous studies on pure AgNbO₃.¹⁶ It is well known that electric field-induced irreversible AFE–FE transitions generally occur near the composition-driven AFE–FE phase boundary once the applied electric-field is larger than the characteristic field indicated by E_F (see Fig. 1b). In this case, the FE state can persist even after removing the applied electric field. In the ANLT system, our research group has recently discovered an interesting phenomenon considered as a type of ferroelectric “wake-up” effect.¹¹⁰ In x = 0.045 and 0.06 ceramics near the phase transition regions, ferroelectric loops can be triggered by increasing the number of electric field bipolar cycles, even when the maximum applied field is much smaller than the characteristic field, E_F (see Fig. 27d and e). The “woken-up” state means that the ferroelectric loops remain almost unchanged on further increase of the number of bipolar cycles. Due to the “wake-up” effect, the dielectric peak T_I in Fig. 27f is gradually suppressed and the dielectric peak T_U appears, indicating that the electric field bipolar cycles induce a transition from the FIE Pmc2₁ phase to the FE R3c phase, as confirmed by the ND data analysis (see Fig. 27g).¹¹⁰ Moreover, the structure refinements also reveal that the off-center cation displacements of the Ag⁺ and Nb⁵⁺ ions gradually increase, indicating enhanced ferroelectricity of the FE R3c lattice (see Fig. 27h). As discussed in Section 2.4, the field-induced FE structure of pure AgNbO₃ should be iso-symmetric with the initial FIE structure. However, this prediction was not verified in the case of the ALN and ANLT systems. The explanation is that near the phase coexistence region, the FIE (P2₁am or Pmc2₁) lattice is highly distorted, and the disordered octahedral tilting and off-centering cation displacements (originating from destabilized AFE and a⁰a⁰c⁺/a⁰a⁰c⁻ AFD modes⁵³) provide a favorable energy path to the R3c phase. Once the external electric field (smaller than E_F) is applied, the phase transition from FIE Pmc2₁ to FE R3c is induced. The discovered intrinsic FE “wake-up” effect in AN-based perovskite ceramics may represent a potential solution for the long-standing fatigue problem in FE materials. This is evident in Fig. 28b, which shows that after 10⁴ bipolar cycles, the remnant polarization P_r of a (Bi_0.5Na_0.5)_0.94Ba_0.06TiO₃ (BNBT6) capacitor drops by 60%. When connecting the ANLT6 ceramic in parallel with the BNTBT ceramic to form a BNBT6–ANLT6 dual capacitor, the reduction of P_r can be controlled within 10% after 10⁴ cycles.¹¹⁰

Fig. 27 (a) A schematic drawing reflecting the structure–property relationships present in the ANLT100x system in the form of symmetry modes, phases and electrical properties; (b) composition-driven variation of lattice parameters of orthorhombic Pmc2₁ and rhombohedral R3c phases, as well as the phase fraction of the R3c phase; (c) temperature-dependent dielectric spectrum of ANLT100x reported by Lu et al.⁵³ Evolution of P_r (d) and P–E hysteresis loops during bipolar cycling measured on ANLT4.5 (50 kV cm⁻¹ and 10 Hz) and ANLT6 (30 kV cm⁻¹ and 10 Hz). (f) Temperature-dependent dielectric permittivity and loss tangent (at 10 kHz) of pristine, intermediate (IM), and “woken-up” (three conditions) ANLT4.5 ceramics; (g) neutron diffraction pattern of selected peaks collected under the three conditions. (h) R3c phase fraction, with cation displacements along the c-axis for the pristine, IM, and “woken-up” conditions of ANLT4.5 and ANLT6 ceramic reported by Lu et al.¹¹⁰ [(d–h) are reproduced with permission from ref. 110 copyright 2020 American Chemical Society].

Fig. 28 (a) Schematic diagram of the measurement circuit for BNBT6–ANLT6 dual capacitors and (b) evolution of normalized P_r during bipolar cycling measured on a BNBT6 capacitor and a BNBT6–ANLT6 dual capacitor reported by Lu et al.¹¹⁰ [Reproduced with permission from ref. 110 copyright 2020 American Chemical Society]. (c) Temperature-dependent pyroelectric coefficient (p) for poled ANLT100x ceramics; (d) Olsen cycle diagram of pyroelectric energy harvesting for the ANLT5 ceramic reported by Li et al.¹¹¹

Li et al.¹¹¹ recently reported that the ANLT solid-solution also exhibits excellent pyroelectric properties during the depolarization process of the electric field-induced FE state (see Fig. 28c). ANLT compositions with x ≥ 0.04 exhibit a high pyroelectric coefficient p ≈ 3–3.7 × 10⁻⁸ C cm⁻² K⁻¹ at room temperature and an ultrahigh peak value (p = 120–160 × 10⁻⁸ C cm⁻² K⁻¹) at the depolarization temperature (T_d). If T_d could be adjusted to room temperature, these materials could have important applications as pyroelectric detectors. It is well-known that field-induced transitions can cause an enhancement of dielectric response via the creation of an MPB, providing an extra contribution to the total pyroelectric coefficient. Li et al.¹¹¹ also studied the pyroelectric energy harvesting performance of ANLT5 ceramics. The energy harvesting process can be achieved using an Olsen cycle,¹¹² as schematically shown in Fig. 28d, while the harvested pyroelectric energy density (W) can be estimated from the area of the blue region shown in the figure. The harvested energy between 30 °C and 190 °C was estimated to be about 1.4 J cm⁻³, which holds promise for energy harvesting.

3.2.3. (Ag,K)NbO₃ ferroelectric solid-solutions. KNbO₃ (t = 1.06) is a classic ferroelectric without AFD instability, where three well-defined ferroelectric transitions separating tetragonal, orthorhombic and rhombohedral phases are found during cooling.¹¹³ These polymorphic transitions are related to the sudden change of the spontaneous polarization direction due to the B-site Nb⁵⁺ ions. Hence, in the Ag_1−xK_xNbO₃ (AKN) solid-solution, by increasing the concentration of K⁺ ions, the t–factor should gradually increase, favoring B-site driven ferroelectricity and reducing the AFD instability. Studies on the AKN system are still rare to date. Fu et al. successfully synthesized AKN compositions by solid-state reaction and sintering in an O₂ atmosphere.¹¹⁴ The structural analysis suggested a perovskite structure with a solubility limit of K⁺ ions approaching x = 0.2. At higher K⁺ ion concentrations (0.2 < x < 0.8), the perovskite solid-solution does not readily form under these conditions. However, it is possible that the perovskite solid-solution could be formed using high-pressure synthesis.¹¹⁵ Structural analysis based on the perovskite primitive unit-cell reveals a change in the structural parameters at x = 0.07, indicating a phase transition (see Fig. 29a), with the new phase stable up to x ≈ 0.2. An orthorhombic structure is formed when x > 0.8. In 2016, Xu et al. suggested that an AFE_O–FE_O transition occurs in the range 0.04 < x < 0.06, evidenced by the vanishing of AFE superlattice satellite reflections in the XRD patterns and by the presence of a ferroelectric-type hysteresis loop.¹¹⁶ Recently, Liu et al.¹¹⁷ investigated the new phase using ND, revealing a FE structure in space group Pmc2₁, consisting of four perovskite primitive pseudo-cubic unit-cells.

Fig. 29 (a) Composition-driven variation of pseudo-cubic parameters and (b) temperature-dependent dielectric pattern of (Ag_1−xK_x)NbO₃ solid-solution reported by Fu et al.¹¹⁴ [Reproduced from ref. 114https://doi.org/10.1063/1.3259410 with the permission of AIP Publishing]. The temperature T^FE_C was assigned by Fu et al.¹³ to the Curie point, due to the discovered weak-FE/FIE Pmc2₁ structure reported by Yashima et al. in 2011.⁴⁹ The temperature T^AFE_C indicates the Curie temperature of the AFE phase; the other dielectric anomalies were assigned to the M₁ ↔ M₂ transition, T_f and the M₂ ↔ M₃ transition by Kania et al. in 1983.¹⁴

The dielectric behavior of the AKN system also exhibits significant changes upon composition modification, as shown in Fig. 29b. Observing the variation of the temperature-dependent dielectric behavior with composition, it can be noticed that the dielectric anomalies assigned to the M₁ ↔ M₂ and M₂ ↔ M₃ phase transitions are gradually suppressed, and a sharp peak denoted as T_c1 can be found at x = 0.07. Furthermore, another anomaly denoted as T_c2 can be noticed near 150 °C, the origin of which is still unclear. Below T_c2, the structure could be FE Pmc2₁ as reported in a recent paper.¹¹⁷ Therefore, the dielectric anomaly denoted as T_c2 could correspond to the T_f transition or to the T_C of the FIE phase, as reported for the case of AgNbO₃.^16,74 This would indicate that the FIE phase was gradually replaced by an FE phase. There are no studies clarifying the structural nature in the range between T_c2 and T_c1; hence, the question whether this phase is AFE is still unsettled. Most recently, Liu et al.¹¹⁷ investigated the pressure-induced variations of structure and properties in the AKN system. A composition–pressure phase diagram is outlined in Fig. 30a. The FE–AFE (note: the authors refined the structure using the AFE Pbcm model and not the FIE Pmc2₁ model) transition can occur when the loading pressure reaches 350 MPa for x = 0.065 (Fig. 30a and b). Meanwhile, this material shows a very high charge release density (∼37 μC cm⁻²) under a shock pressure of 6.9 GPa (Fig. 30c). The simulated energy density of this material is about 5.401 J g⁻¹, which is significantly higher than in other FE ceramics (Fig. 30d). The high discharge energy density after shock pressure gives a potential application for explosive energy conversion. It is noticed that after shock-pressure loading, a “double” hysteresis with non-zero remnant polarization can be observed in Fig. 30b. This feature may indicate that the pressure-induced structure is not AFE, but FIE.

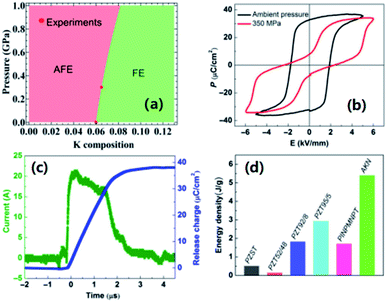Fig. 30 (a) Pressure–composition phase diagram of the (Ag_0.935K_0.065)NbO₃ (AKN065) system; (b) pressure-dependent polarization–electric field (P–E) loops of AKN065 ceramics measured at room temperature; (c) dynamic discharging response of assembled AKN065 ceramic devices collected under a shock pressure of 6.9 GPa; and (d) comparison of the energy storage densities per unit weight of the AKN065 ceramics and other FE materials, reported by Liu et al.¹¹⁷

3.3 AgNbO₃-based antiferroelectric solid-solutions

In the early studies of AgNbO₃, various solid-solutions, such as AgNb_1−xTa_xO₃, were intensively studied due to their excellent dielectric properties.¹⁹ Measurements performed in the 1 GHz region showed ε_r ≈ 400, Q × f ≥ 700 GHz, and Δf/f = 0–0.22 in the temperature range −40 to 60 °C for a composition close to AgNb_0.5Ta_0.5O₃,¹⁹ which represents an attractive material for high-frequency applications. In recent years, due to the development of new types of energy storage technologies, various research teams have started devoting their attention to AgNbO₃-based antiferroelectric materials, due to their double P–E loops. The field-induced phase transition can be significantly influenced by the concentration of doping elements, giving rise to enhanced energy storage performance compared to non-doped AgNbO₃. In this section, a detailed survey of the previous fundamental studies on AgNbO₃-based antiferroelectric materials is provided with the aim of identifying a general principle to optimize the related performance, as well as providing guidelines for future studies.

3.3.1 Ag_1−xNa_xNbO₃ solid-solution. The t-factor of NaNbO₃ (t = 0.967) is slightly smaller than that of AgNbO₃, but like AgNbO₃ (t = 0.98), NaNbO₃ also displays complex polymorphism on heating (see Fig. 31a), some of which are accompanied by the presence of dielectric anomalies.^54,118 However, the exact crystalline structures of these polymorphs, as well as their temperature stability ranges are still controversial.¹¹⁹ A concise structural evolution of NaNbO₃ upon cooling is shown in Fig. 31b. The intricate structural evolution indicates that NaNbO₃ should exhibit more complicated interactions between AFD instabilities and off-centering of cations compared to AgNbO₃.

Fig. 31 (a) Temperature-dependence of dielectric permittivity and loss tangent for NaNbO₃ as reported by Kania et al.;⁵⁴ [reproduced from ref. 54https://doi.org/10.1088/0953-8984/11/45/316 with permission from copyright IOP Publishing]. (b) The reported phase transitions of NaNbO₃ studied using X-ray diffraction. Note: the structural nature of the P phase, as well as its temperature stability range are still controversial (see ref. 119, Fig. 1).

The high temperature phases (cubic, tetragonal and orthorhombic) have been carefully studied and have been found to be isostructural with the three paraelectric phases of AgNbO₃.^47,120 At room temperature, the structure of ceramic samples prepared by conventional solid-state reaction is orthorhombic AFE, which is isostructural with AgNbO₃, although some publications have also reported the existence of a metastable FE_O phase in local regions.^121,122 At low temperature, the structure of ceramic samples displays a FE R3c phase, which is isostructural with the FE phase reported in ALN or ANLT systems, as discussed in Section 3.2.1.2. Previous studies on the Ag_1−xNa_xNbO₃ (ANN) solid-solution are rare. It has been reported that ANN compositions can be obtained via conventional solid-state reaction and sintering in O₂ atmosphere.⁵⁴ AgNbO₃ and NaNbO₃ should form a continuous solid-solution due to their similar crystalline structures.⁴⁶ However, the temperature–composition diagram proposed by Fu et al.¹²³ indicates that a phase boundary exists when the concentration of Na⁺ ions exceeds 0.8, as shown in Fig. 32a. It is not clear whether in the composition range 0.8 < x < 0.9, a solid-solution can be formed; therefore, further studies on these compositions are needed. Kania et al.⁵⁴ investigated the dielectric spectroscopy of the ANN system (see Fig. 32b and c) to understand the microscopic mechanisms that contribute to the appearance of a diffuse dielectric peak at around 270 °C (denoted as the M₂ ↔ M₃ transition in AgNbO₃).

Fig. 32 (a) Variation of transition temperatures in the Ag_1−xNa_xNbO₃ system derived from the dielectric measurements reported by Fu et al.¹²³ [Reproduced from ref. 123https://doi.org/10.1063/1.3609234 with the permission of AIP Publishing]. Temperature-dependence of dielectric permittivity in Ag_1−xNa_xNbO₃ (b) on heating and (c) on cooling, reported by Kania et al.⁵⁴ [Reproduced from ref. 54https://doi.org/10.1088/0953-8984/11/45/316 with permission from copyright IOP Publishing].

The diffuse dielectric response in the Ag_1−xNa_xNbO₃ system has attracted great research interest for high-frequency applications. The temperature dependence of the dielectric permittivity (see Fig. 32b) shows that the high-temperature anomaly gradually shifts to higher temperature with increasing Na concentration, up to x = 0.6, and starts shifting to lower temperature at higher Na content, with an increase in the value of the dielectric permittivity near the transition point. The low temperature anomaly monotonously shifts to higher temperature with increasing Na concentration, while the dielectric permittivity decreases near the transition point. The gradual suppression of the diffuse dielectric anomaly with increasing Na⁺ ion concentration can be more clearly observed in the dielectric pattern obtained during cooling (see Fig. 32c). In particular, upon cooling, the dielectric peak corresponding to the AFE–PE transition presents a negligible shift with composition. Kania et al.⁵⁴ proposed that Na substitution causes a decrease of the oxygen octahedron size, diminishing the freedom of Nb⁵⁺ ions, resulting in a gradual decrease of the diffuse dielectric anomaly. This viewpoint is consistent with the gradual decrease of the t-factor due to the occupation of the A-site by Na⁺, which makes it harder for the Nb⁵⁺ ions to move off-center in their oxygen octahedra. Furthermore, it was reported that this solid-solution exhibits a large electric field-induced strain response of about 0.2% over the wide compositional range 0.4 < x < 0.8 (see Fig. 33), which might be interesting for the development of lead-free actuators.

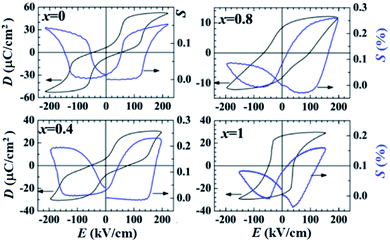Fig. 33 P–E and S–E hysteresis loops of ANN solid-solution reported by Fu et al.¹²³ [Reproduced from ref. 123https://doi.org/10.1063/1.3609234 with the permission of AIP Publishing].

3.3.2 Ag(Nb,Ta)O₃ solid-solutions. Among AgNbO₃-based materials, the system Ag(Nb,Ta)O₃ (ANT) has been extensively investigated for its excellent dielectric properties in the microwave range, as mentioned above.^19,124–126 Recent studies have demonstrated that this solid-solution also exhibits excellent energy storage performance.¹⁷ At 0.64 Å, the radius of the Ta⁵⁺ ion is identical to that of the Nb⁵⁺ ion. However, various Ta-containing perovskites, such as KTaO₃ and AgTaO₃, do not exhibit anti-/ferroelectricity.^127,128 The reason can be attributed to weak/non-existent off-centering of the Ta⁵⁺ cation in the oxygen octahedron due to the nature of the Ta–O bond. Valant et al. reported a survey on these systems in 2007, with discussions focused on the synthesis methods, crystal chemistry and dielectric properties.¹²⁶ Similarly to AgNbO₃, the ANT solid-solution can be synthesized by solid-state reaction and conventional sintering in O₂ atmosphere. In order to obtain a homogenous distribution of Nb⁵⁺ and Ta⁵⁺ and avoid the formation of undesired phases, it has been frequently proposed that Nb₂O₅ and Ta₂O₅ should be initially mixed and heated above 1200 °C to form a chemically homogenous (Nb,Ta)₂O₅ powder, which could be used as a precursor and subsequently mixed with Ag₂O. Wet chemical methods have also been used to synthesize ANT solid-solutions, to reduce the sintering temperature or to prepare thin films using spin-coating techniques.³¹ In early studies, the temperature–composition phase diagram of ANT were proposed by Pawełczyk et al.⁵⁵ as shown in Fig. 34a. It can be observed that with increasing Ta⁵⁺ ion concentration, the dielectric peak related to the M₃ ↔ O₁ or AFE–PE transition shows a slight shift toward high temperature, while the dielectric anomalies assigned to the M-type phase transitions, significantly shift toward lower temperature. In particular, the broad dielectric response (ε ≈ 400), corresponding to the M₂ ↔ M₃ transition, shifts to around room temperature in compositions with 0.4 ≤ x ≤ 0.6 (see Fig. 34b).^126,129 Furthermore, the high-frequency dielectric spectrum reveals that the dielectric permittivity is very stable up to the submillimeter wave region (see Fig. 34c), and a dielectric dispersion is present when the temperature approaches the broad dielectric anomaly related to the M₂ ↔ M₃ transition. Further Raman spectroscopic studies have suggested that the presence of a dielectric dispersion in the submillimeter range is intimately related to the disordered off-centering motion of Nb⁵⁺ ions, which could be the origin of the broad dielectric response. This deduction was further confirmed by a structure investigation carried out on ANT50 samples by Levin et al.,¹³⁰ who proposed the presence of partial ordering of local B-cation displacements, when the temperature approaches the broad maximum of dielectric permittivity corresponding to the M₂ ↔ M₃ transition. Tantalum substitution suppresses this ordering because of the dissimilar off-centering trends for Ta⁵⁺ and Nb⁵⁺, as revealed by EXAFS results.¹³⁰ Therefore, the dielectric anomalies assigned to the M-type transitions shift to lower temperature with increasing Ta⁵⁺ ion concentration. Additionally, it was suggested that Ag⁺ cations also exhibit displacive disorder, and on cooling, undergo ordering coupled to that of the B-cations, which could explain the enhanced dielectric response assigned to the M₁ ↔ M₂ transition. Although in an early study it was suggested that all of the three M phases show the same structure with the non-polar Pbcm space group,⁴⁷ the dielectric response under DC electric field reported by Li et al.¹³¹ (shown in Fig. 34d) reveals that a composition-driven FIE–AFE transition occurs with increasing Ta⁵⁺ ion concentration. For pure AgNbO₃, the dielectric permittivity gradually decreases until the DC bias field reaches 50 kV cm⁻¹, above which it gradually increases with increasing DC bias. The P–E loop exhibits a large hysteresis, consistent with the recently-discovered ferrielectric structure in space group Pmc2₁.⁴⁹ The unique dielectric tunability might be of interest for dielectric tunable devices. For ANT50, the dielectric permittivity hardly changes under weak DC electric fields, but significantly increases under higher DC fields, indicating that the virgin structure does not present ferroelectricity, but antiferroelectricity. The ferrielectric nature has also been evidenced in our recent work.^16,74 Based on high-quality ANT samples, Zhao et al. characterized the P–E loops of the ANT100x system with x ≤ 0.20,¹³² extrapolating the key parameters listed in Table 3. One can notice that with increasing Ta concentration, the characteristic fields E_B and E_F are enhanced, the remnant polarization gradually decreases and the field-induced FE polarization presents negligible changes, indicating a more stable antiferroelectric state. Most recently, Luo et al. synthesized ANT100x ceramic samples with ultrahigh quality, and systematically characterized their ferroelectric properties under high electric fields.¹⁷ As shown in Fig. 35a, the field-induced double P–E loops of ANT100x gradually evolve into linear-like loops accompanied by reduced polarization with increasing Ta concentration, indicating the gradual decrease or even the suppression of the field-induced ferroelectric state under strong-field conditions. For ANT55 ceramics, the P–E loop exhibits an almost linear trend, while the unipolar I–E loop of ANT55 ceramic reveals a couple of weak current peaks, indicating that there are still a few AFE regions in the Pbcm non-polar lattice.

Fig. 34 (a) Temperature–composition phase diagram of the AgNb_1−xTa_xO₃ reported by Pawełczyk et al.⁵⁵; [reproduced from ref. 55https://doi.org/10.1080/01411598708220073 with permission from Taylor & Francis Informa Ltd]. (b) Temperature-dependent dielectric pattern of the AgNb_1−xTa_xO₃ system original reported by Kania et al.;¹²⁹ [reproduced with permission from ref. 129https://doi.org/10.1080/01411598308244116 with permission from Taylor & Francis Informa Ltd]. (c) The dielectric dispersion in the millimeter and submillimeter wave region of AgNb_0.6Ta_0.4O₃ as calculated from the oscillator and relaxor additive model (solid lines) at different temperatures; points are experimental values reported by Volkov et al.;⁵⁸ [reproduced from ref. 58https://doi.org/10.1088/0953-8984/7/4/009 with permission from copyright IOP Publishing]. (d) Variation of dielectric permittivity of AgNb_1−xTa_xO₃ ceramics at 100 kHz with a maximum electric field bias of 125 kV cm⁻¹ as reported by Li et al.¹³¹ [Reproduced from Ref. 131https://doi.org/10.1063/1.4875581 with the permission of AIP Publishing].

Table 3 List of the key parameters of field-induced transitions in ANT100x systems reported by Zhao et al.¹³²

Samples	P max [μC cm^−2]	P r [μC cm^−2]	E F [kV cm^−1]	E B [kV cm^−1]	ΔE [kV cm^−1]
AN	35.9	3.6	110	52	58
ANT5	37.2	2.0	153	95	58
ANT10	35.5	1.9	166	110	56
ANT15	36.8	1.7	189	130	59
ANT20	31.5	1.2	222	163	59

---

Fig. 35 (a) P–E loops of ANT100x ceramics and (b) I–E loops of ANT55 ceramics reported by Luo et al.¹⁷

3.3.3 A-site deficient AgNbO₃-based solid-solutions. As discussed above, reducing the t-factor can favor AFD instabilities, promoting antiferroelectricity. Hetero-valent (3+ or 2+) elements have been considered for A-site dopants as an alternative strategy to develop AgNbO₃-based antiferroelectric solid-solutions. In these systems, A-site vacancies are created to maintain charge neutrality, such as in BiNb₃O₉ (i.e., Bi_1/3NbO₃) and LaNb₃O₉ (i.e., La_1/3NbO₃).^133,134 Structural investigations revealed that these materials exhibit ordering of A-site cations and vacancies. Table 4 lists various M_1/3NbO₃ compounds and their crystalline structures.¹³⁵

Table 4 List of various A-site deficient niobates¹³⁵

Chemical formula	Mineral	Crystal system	Space group
Bi1/3NbO3 (Bi3NbO9)	Perovskite	Tetragonal	P4/mmm
La1/3NbO3	Perovskite	Orthorhombic	Pmmm or Cmmm
Ce1/3NbO3	Perovskite	Monoclinic	P2/m
Pr1/3NbO3	Perovskite	Orthorhombic	Cmmm
Nd1/3NbO3	Perovskite	Orthorhombic	Cmmm

---

In 2006, Hu et al. successfully prepared a bismuth-modified AgNbO₃ solid-solution (Ag_1−xBi_x/3NbO₃).¹³⁶ The structure analysis suggested that about 20 mol% of Bi³⁺ ions can be incorporated into the lattice of AgNbO₃ to form a perovskite structured solid-solution without impurity phases, implying that 40% of the A-sites are vacant. A dielectric study on this solid-solution indicated that all dielectric anomalies shift to lower temperature and the diffuse dielectric peak corresponding to the M₂ ↔ M₃ transition becomes broader with increasing Bi concentration (see Fig. 36). In particular, the dielectric permittivity is almost independent on temperature in the range from −50 °C to 50 °C for some compositions, making them of interest for capacitor applications. When x ≥ 0.4, the sharp maximum corresponding to the AFE–PE phase transition disappeared and the response of a typical relaxor was observed. Our research team has also successfully prepared Ag_1−3xBi_xNbO₃ solid-solutions with high-quality.¹³⁷ The dielectric response under DC field reveals that the ferrielectric/weak-ferroelectric behavior progressively disappears when x reaches 0.04 (corresponding to x = 0.12 according to the chemical formula reported by Hu et al.¹³⁶), as shown in Fig. 37a. Above x = 0.04, the ceramic samples exhibit a single AFE phase. The enhanced antiferroelectric stability is evidenced by the D–E loops under strong-field cycling as shown in Fig. 37b. By increasing the Bi³⁺ ion concentration, the characteristic fields of the AFE–FE field-induced transition increase, indicating a higher energy barrier between AFE and FE phases.

Fig. 36 Temperature-dependent dielectric spectra of Ag_1−xBi_x/3NbO₃ ceramics reported by Hu et al.¹³⁶ [Reproduced from ref. 136https://doi.org/10.1063/1.2209552 with the permission of AIP Publishing].

Fig. 37 (a) Percentage variation in relative permittivity (ε_r) at low DC field in (Ag_1−3xBi_x)NbO₃ (ABNx) ceramics, and (b) high-field ferroelectric D–E loops of ABNx ceramics reported by Tian et al.¹³⁷

Based on the design and the successful preparation of the A-site deficient Ag_1−3xBi_xNbO₃ solid-solution, a series of other A-site deficient Ag_1−3xLn_xNbO₃ (Ln: rare-earth elements, x < 0.05) ceramics have been subsequently reported,^138–141 in the search for new materials with improved energy storage performance.

The temperature dependence of the dielectric permittivity of various A-site deficient compounds is reported in Fig. 38. It can be noticed that La³⁺ doping induces similar trends to those produced by Bi³⁺ doping, while Sm³⁺ and Gd³⁺ doping shifts the maximum dielectric peak related to the AFE–PE transition with a decrease of the dielectric permittivity. The transition almost disappears for 4 mol% Sm³⁺ and Gd³⁺ doping. This might suggest that the dopant elements are also present on the B-site of the AgNbO₃ lattice, resulting in composition fluctuation and breaking of the AFE distortion. These features also suggest that the solubility limit of Sm³⁺/Gd³⁺ in AgNbO₃ is around 4 mol%. As with Bi-doped AgNbO₃, the characteristic field E_F increases with increasing Ln³⁺ concentration, while the field-induced polarization visibly reduces as shown in Fig. 39a–c. The composition-driven property variation is very similar to the changes observed in the ferroelectric loops of AKN6 ceramics with increasing pressure shown in Fig. 39d.¹¹⁷ Similar phenomena have also been observed in rare-earth substituted BiFeO₃, in which the field-induced FE polarization is significantly suppressed at high concentrations of rare-earth dopants.^108,109 It can be inferred that the reduced t-factor weakens the AFE distortion and reduces the freedom of cation displacement. In addition to Ln³⁺-doped AgNbO₃, alkaline earth elements such as Ca²⁺ have been also used as dopants for AgNbO₃ and showed similar effects to La³⁺ doping.¹⁴³

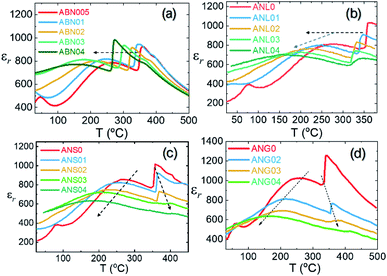Fig. 38 Temperature-dependent dielectric spectra of (a) Ag_1−3xBi_xNbO₃ (reported by Tian et al.¹³⁷); (b) Ag_1−3xLa_xNbO₃ (reported by Gao et al.¹⁴²); (c) Ag_1−3xSm_xNbO₃ (reported by Gao et al.¹³⁸) [reproduced with permission from ref. 138 copyright 2020 American Chemical Society] and (d) Ag_1−3xGd_xNbO₃ (reported by Li et al.¹⁴⁰).

Fig. 39 P–E hysteresis loops of (a) Ag_1−3xLa_xNbO₃,¹³⁹ (b) Ag_1−3xSm_xNbO₃,¹³⁸ [reproduced with permission from ref. 138 copyright 2020 American Chemical Society] (c) Ag_1−3xGd_xNbO₃ (ref. 140) and (d) Ag_0.94K_0.06NbO₃ (ref. 117) under different pressures.

3.3.4 Other AgNbO₃-based antiferroelectric solid-solutions. Besides the chemical modification of AgNbO₃via A- or B-site doping, co-doping of A- and B- sites through formation of solid-solutions between AgNbO₃ and A²⁺B⁴⁺O₃ or A³⁺B³⁺O₃ perovskites with smaller t-factors (such as CaTiO₃, Bi_0.5Na_0.5TiO_3, and BiMnO₃) represents an alternative strategy to achieve enhanced stability of the AFE state and develop new materials with improved energy storage performance.^144–146 These materials also show enhanced antiferroelectric stability with increasing concentration of the second perovskite compound added, as shown in Fig. 40a and b. These perovskite dopants can severely interrupt the ordered arrangement of antipolar A-site and B-site cations and reduce the domain size, giving rise to relaxor-like antiferroelectric behavior accompanied by a gradual decrease of the field-induced FE polarization. Recently, Yan et al. reported on the (1 − x)AgNbO₃–xBi(Zn_2/3Nb_1/3)O₃ system, highlighting that the changes in relative permittivity before and after DC poling can be also used to study the polarization behavior in AgNbO₃-based ceramics, as shown in Fig. 40c.¹⁴⁷ For x = 0.000 and x = 0.005 compositions, the relative permittivity shows a small decrease after DC poling, which can be attributed to decreased domain wall density. In contrast, for x = 0.030, the relative permittivity increased on successive polarization under low and high electric fields due to the contribution of the field-induced polar structure. In the case of the x = 0.010 composition, intermediate behavior is observed, with a decrease in relative permittivity on the initial polarization at low field, followed by an increase at high field. The initial decrease in permittivity is attributed to the decrease in FE domain wall density, while the increase in permittivity at higher field arises from the metastable FIE structure.

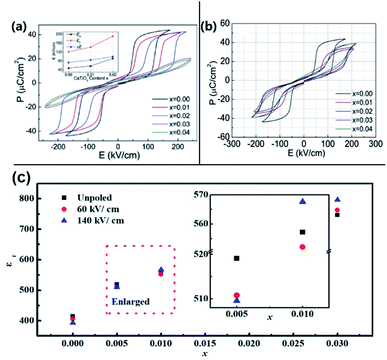Fig. 40 P–E loops of (a) (1 − x)AgNbO₃–xCaTiO₃ (ref. 144) [reproduced with permission from ref. 144 copyright 2020 by Elsevier]; (b) (1 − x)AgNbO₃–x(Bi_0.5Na_0.5)TiO₃,¹⁴⁵ [reproduced with permission from ref. 145 copyright 2020 by Elsevier] and (c) Bi(Zn_2/3Nb_1/3)O₃ (BZN) concentration dependence of relative permittivity of (1 − x)AN–xBZN ceramics before and after poling.¹⁴⁷

4. AgNbO₃-based materials for high-power energy storage

The direct way to calculate the total stored energy density (W) of a dielectric material is through integration of the D–E curve:where E is the electric field and D is the electric displacement. In dielectrics, D = ε₀E + P; however, since the polarization of ferroelectrics is very high, D ≈ P. Thus, the recoverable energy storage density (W_rec) for anti-/ferroelectrics can be obtained by a modified expression as:where P_max is the polarization under the maximum external applied electric field, while P_r is the remnant polarization under zero electric field. Due to the difference between W and W_rec, a parameter to simulate the energy efficiency (η) can be expressed as:where W is the total stored energy density. A schematic showing the electrical energy storage of dielectrics is shown in Fig. 41, in which the colored area represents the recoverable energy density W_rec of the dielectric material.

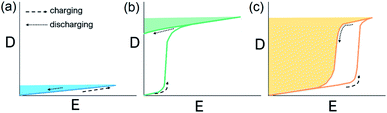Fig. 41 Schematic energy storage density (colored area) of (a) linear dielectrics, (b) ferroelectrics, and (c) antiferroelectrics under the same applied electric field.

From Fig. 41, it is clear that under the same applied field, antiferroelectrics should display higher energy density compared to the other types of dielectrics. A summary of the energy storage performances of AgNbO₃-based antiferroelectric materials is reported in Table 5. It can be noticed that the value of W_rec in chemically-modified AgNbO₃ ceramics can reach 6 J cm⁻³, which is three times that of unmodified AgNbO₃ ceramics. Besides the composition modification, the W_rec of AgNbO₃-based ceramic capacitors can be greatly improved through multilayer chip ceramic technology, as reported by Zhu et al. in a recent study.¹⁴⁸ In particular, an AgNbO₃ epitaxial film grown on a (001) STO substrate reported by Zhang et al. showed an ultrahigh characteristic field E_F (∼250 kV cm⁻¹) while the E_B remained unchanged compared to an AgNbO₃ ceramic sample. Nevertheless, the film showed a higher W_rec than the ceramic sample of AgNbO₃.⁴⁴

Table 5 Key parameters and energy storage performance of currently reported AgNbO₃-based ceramics^a

Materials compositions	D max (μC cm^−2)	E F (kV cm^−1)	ΔE (kV cm^−1)	E b (kV cm^−1)	W rec (J cm^−3)	η (%)	Ref.
a BZN: Bi(Zn1/3Nb2/3)O3; BNT: Bi0.5Na0.5TiO3; CT: CaTiO3; CTH: Ca(Ti,Hf)O3; ANT15: Ag(Nb0.85Ta0.15)O3.
AgNbO3 (AN)	41	125	75	175	2.1	39	15
AN epitaxial film	∼40	∼250	∼200	624	5.8	55.8	44
AN–0.1 wt% WO3	∼42	∼165	75	200	3.3	50	149
AN–0.1 wt% MnO2	37	117	54	150	2.5	57	150
Ag0.97Bi0.03NbO3	26	—	—	205	2.6	86	137
Ag0.94La0.02NbO3	∼28	∼250	∼75	273	4.4	73	139
Ag0.94La0.02NbO3	∼30	∼175	∼75	230	3.12	63	151
Ag0.94Sm0.02NbO3	∼30	∼270	∼80	∼300	4.5	63	138
Ag0.91Sm0.03NbO3	∼38	∼225	∼75	∼290	5.2	68	141
Ag0.97Sm0.01NbO3	∼40	∼125	∼40	∼175	3.8	73	152
Ag0.88Gd0.04NbO3	∼34	∼250	80	290	4.5	63	140
Ag0.97Nd0.01NbO3	∼40	∼150	∼70	210	3.2	52	153
Ag0.92Ca0.04NbO3	39	179	80	220	3.5	56	143
Ag(Nb0.85Ta0.15)O3	∼37	189	59	240	4.2	69	132
Ag(Nb0.8Ta0.2)O3	37	175	55	270	3.7	58	78
Ag(Nb0.45Ta0.55)O3	∼28	∼300	∼60	470	6.3	90	17
ANT15 multilayer ceramic	∼44	∼190	∼90	1020	7.9	71	148
Sm0.02Ag0.94Nb0.9Ta0.1O3	38.5	∼220	∼80	280	4.87	63.5	154
Nd0.01Ag0.97Ta0.2Nb0.8O3	∼40	∼275	∼75	370	6.5	71	155
Ag0.94La0.02Nb0.8Ta0.2O3	∼50	∼300	∼100	∼400	6.9	71	156
Ag0.9Ca0.05Nb0.95Ta0.05O3	∼30	∼190	∼120	210	3.36	58.3	157
0.99AN–0.01BZN	54	198	80	220	4.6	57	147
0.97AN–0.03BNT	35	180	80	220	3.4	62	145
0.98AN–0.02CT	40	190	90	220	3.7	52	144
0.94AN–0.06CTH	40	266	98	300	5.4	66	158

---

The energy storage efficiency in these materials is usually less than 70%. The main advantage of antiferroelectric capacitors compared to linear dielectrics is the possibility of a large field-induced polarization under certain applied electric fields. An increase of the characteristic field E_F can give rise to an enhancement of W_rec for an antiferroelectric material. Another key parameter to impact the energy storage performance is the degree of hysteresis. Nano-structured domains or polar nanoregions (PNRs) generally found in relaxor-ferroelectrics lead to slim D–E loops accompanied by a large FE polarization, as observed in PbMg_1/3Nb_2/3O₃ and BaTiO₃-based compounds. Therefore, further efforts should be directed to develop AgNbO₃-based relaxors/anti-/ferroelectrics as proposed in Fig. 42 to improve the energy efficiency η.

Fig. 42 Schematic strategy to develop AgNbO₃-based antiferroelectrics for practical applications¹⁵⁹ [reproduced with permission from ref. 159 copyright 2019 by Elsevier].

Considering practical applications of dielectric capacitors, the energy storage capability per unit volume of a linear dielectric material can generally be estimated using the following expression:¹⁶⁰

where C is the capacitance, V is the voltage, ε is the dielectric permittivity of the material, ε₀ is the dielectric permittivity of a vacuum, and E_b is the breakdown field. The dielectric is susceptible to breakdown under the application of high external fields. To avoid any premature breakdown of the capacitor, it is advised that the maximum applied external field should be about half of the value of E_b (i.e., V = ηV_b (0 < η < 1)).¹⁶¹ This means that the value of E_b should be at least two times higher than the characteristic field E_F of the antiferroelectric capacitor. For dielectrics, E_b is affected by several factors including intrinsic factors such as the band gap, and extrinsic factors such as grain size, porosity and sample geometry. Here, we briefly summarize these factors to provide guidance for obtaining larger E_b values. Widening the band gap will result in a higher E_b, because the narrower the band gap, the easier is the jump of the electrons from the valence band to the conduction band, increasing the possibility of intrinsic breakdown.¹⁶² Research has shown that increasing the sample density, i.e. decreasing the cavities existing in the ceramic body, is beneficial to obtaining high E_b values.^163,164 In addition, lowering grain size is also particularly useful in increasing E_b. Tunkasiri and Rujijanagul proposed an empirical relationship between breakdown strength and grain size, i.e., E_b ∝ (grain size)^−0.5, in the micron range for BaTiO₃ ceramics.¹⁶⁵ Similar results were also reported for MgO ceramics with grains in the sub-micron size range.¹⁶⁶ Recently, Yang et al. systematically fitted the dependence of E_b on the grain size in various ceramic systems, including MgO, Al₂O₃ and BaTiO₃-based systems, and proposed a relationship of the type E_b ∝ (grain size)^−a, where a is in the range of 0.2–0.4.¹⁶⁷ From these two relationships, it can be concluded that reducing grain size leads to an improved E_b. This is mainly due to the fact that smaller grains can lead to higher grain boundary density and provide more depletion regions, which could hinder charge carrier transport, increasing the resistivity of the material.^165–169 The trend described above has also been observed in AgNbO₃-based ceramics, as shown in Fig. 43. The E_b values can be evaluated using the Weibull distribution, which has been widely used in ceramics and polymer-based systems.^{132,139–141,144,147,149,153,154}

Fig. 43 Electrical breakdown strength (E_b, BDS) of AgNbO₃-based ceramics as a function of grain size: (a) small grain sizes and (b) large grain sizes.

Additionally, it is generally believed that the sample thickness has a significant effect on the E_b, because fewer defects exist in thinner layers.^170–172 More interestingly, E_b can be significantly improved through microstructural design, such as introducing core–shell features, with a ferroelectric core and a non-ferroelectric (e.g. paraelectric) shell.^173,174

5. AgNbO₃-based materials for photocatalysis

Semiconductor-based photocatalytic technologies have been extensively investigated since 1972,²⁰ for the production of renewable hydrogen from water and for the degradation of organic pollutants by photo-generation of electricity and photoelectrochemical reactions.^175–177 AgNbO₃-based perovskites were reported to exhibit visible-light-driven photocatalysis activity due to their narrow band gap (2.08–2.93 eV),⁸¹ which has attracted increased research interest over the past decade. The following sections will give a detailed review of photocatalysis associated with AgNbO₃-based materials.

5.1 Fundamental principles of semiconductor photocatalysis

The underlying mechanisms of the photocatalysis process have been extensively discussed in textbooks and in primary literature.^178–180 Here, a brief introduction to the fundamental principles of semiconductor photocatalysis is provided. The principle of photocatalytic degradation of water pollutants is schematically shown in Fig. 44a. Upon light-illumination, with photons of larger energy (E = hν) than the band gap (E_g) of the semiconductor, electrons will be excited from the valence band to the conduction band, generating an equal number of free electrons and holes. The excited electrons and holes will be separated and will migrate to the surface of the semiconductor. The photo-generated electrons could reduce a dye or react with electron acceptors, such as the O₂ molecules adsorbed on the surfaces of the semiconductor, generating superoxide radical anions (˙O₂⁻). The photo-generated holes can oxidize organic substances or react with electron donors, such as OH⁻, resulting in hydroxyl radicals (˙OH). The hydroxyl radicals can oxidize most dyes into mineral end-products due to their strong tendency to oxidation (standard redox potential +2.8 V).

Fig. 44 (a) A schematic of the photocatalytic mechanism in semiconductors for degrading an organic pollutant; (b) a schematic illustration of the fundamental principles of a semiconducting photocatalytic water-splitting process; (c) energy diagrams for photocatalytic water-splitting, and (d) a schematic illustration of the fundamental principles for a semiconducting photoelectrochemical water-splitting process.¹⁸⁴ [Reproduced with permission from ref. 184 copyright 2018 by John Wiley and Sons].

The processes of generating hydrogen from water under light irradiation can be mainly classified into two reaction categories: (1) photocatalytic; and (2) photoelectrochemical.¹⁸⁰ The photocatalytic reaction process for hydrogen production is very similar to the process of water pollutant degradation, but usually involves a heterogeneous co-catalyst (such as TiO₂–Pt powder).¹⁸¹ The photocatalytic reaction of water splitting is schematically shown in Fig. 44b. During light-illumination, the semiconductor photocatalyst is first excited by absorbing photons, generating an equal number of electrons and holes; then, water molecules are reduced by the photo-generated electrons to form H₂ and are oxidized by the photo-generated holes to form O₂. To ensure the occurrence of these photocatalytic reactions and achieve water-splitting, the energy band of a semiconductor-based photocatalyst should straddle the redox potentials of water. In particular, the bottom of the conduction band has to be more negative than the redox potential of H⁺/H₂ (0 V versus standard hydrogen electrode (SHE)), while the top of the valence band has to be more positive than the redox potential of O₂/H₂O (1.23 V), as shown in Fig. 44c.

The generation of hydrogen by photoelectrochemical reaction is usually achieved in a photoelectrochemical cell (PEC), which consists of a photoelectrode (i.e., a semiconductor-based photocatalyst such as TiO₂), a counter electrode (typically Pt or graphite) and an electrolyte solution.^182,183 The fundamental photoelectrochemical reaction is schematically shown in Fig. 44d for a TiO₂–Pt PEC as an example. TiO₂ is a well-known n-type semiconductor, and can work as a photoanode in the PEC, while Pt serves as a counter electrode. Upon light-illumination, photo-excited electrons and holes are generated in the conduction band and valence band of TiO₂, respectively, and then, the photo-generated electrons are transferred and transported onto the surface of the counter electrode, Pt, through an external circuit with ohmic contacts, where H⁺ is reduced to H₂. Concurrently, the photo-generated holes can favor the oxygen evolution reaction at the surface of the TiO₂ photoanode, generating O₂. It is noted that if a p-type semiconductor is used as the photocatalyst, it would usually act as a photocathode for hydrogen evolution. When comparing the PEC to powdered photocatalytic processes using a co-catalyst, the powdered co-catalyst system can be considered as a short-circuit version of a PEC since the photocatalytic reactions are spatially separated on the powdered catalyst and occur on a much shorter length scale than that for the PEC. The advantage of the PEC is that it can be more effective in separating photo-generated electrons and holes on the macroscale using different electrodes and in decreasing recombination, but the cost for industrial production of long-life and efficient PECs is high. The powdered catalyst, instead, shows an easier process and holds great potential due to its much lower costs, although its catalytic efficiency is lower than that of a PEC.

5.2 Fundamentals of ferroelectric photocatalysis

Currently, great efforts have been devoted to improve the photocatalytic activity of powdered catalysts, mainly including: (1) the search for semiconductors with a narrow band gap (for providing a maximum utilization of solar energy especially in the visible light range);^185–187 (2) microstructure optimization by controlling the particle size, and by establishing a balance between large specific surface areas (providing a high density of available reaction sites) and transport pathways for photo-generated charge carriers (affecting recombination rates and back reaction);^176,188 (3) decoration of the surface with a metallic co-catalyst; (4) introduction of heterogeneous interfaces such as hetero-junctions, to create an internal electric field for enhancing the separation rate of photo-generated charge carriers.^{180,189–191}

Additionally, the internal electric field induced by the spontaneous polarization (P_s) of a ferroelectric has been considered an important factor in photocatalytic performance.^192,193 AgNbO₃ is a weak-ferroelectric/ferrielectric compound possessing a narrow band gap ((2.08–2.93 eV)).^21,81 Ambient ferroelectricity with large P_s can be obtained in doped compounds, such as ALN and AKN solid-solutions,^69,117 which could represent potential candidates for ferroelectric photocatalysts.

In ferroelectrics, the intrinsic P_s can generate bound charges on the ferroelectric surfaces/interfaces. These bound charges are not energetically stable and can be compensated in two ways: internal screening and/or external screening,¹⁹⁴ as schematically shown in Fig. 45a. The internal screening can be realized by the flow of free charge carriers within the ferroelectric crystal, whereas external screening is achieved by the adsorption of charged ions and molecules on the surface of the crystal from the surrounding media. Internal screening by the flow of free charge carriers redistributes the charge carriers near the surface, leading to band bending and a space charge region (SCR),¹⁹⁵ as schematically shown in Fig. 45b. If the ferroelectric surface with negative polarity is exposed, electrons would be depleted from the surface, giving rise to a SCR called the depletion layer and to an upward bending of the band. The depletion means that the transfer of photo-generated electrons toward the surface is blocked, but the movement of photo-generated holes toward the surface is promoted. Conversely, if the surface with positive polarity is exposed, electrons would be accumulated for screening the surface-bound positive charges, resulting in a SCR called the accumulation layer and a downward bending of the band.

Fig. 45 Schematic diagrams of (a) external/internal screening by adsorbing charges or free carriers/defects in ferroelectric crystals,¹⁹⁴ [reproduced from ref. 194https://doi.org/10.1088/0953-8984/17/16/012 with permission from copyright IOP Publishing], and band bending in the exposed surface of ferroelectrics with (b) negative or (c) positive polarity.¹⁹⁵ SCR: space charge region. [Reproduced from ref. 195https://doi.org/10.1088/0957-4484/18/18/185702 with permission from copyright IOP Publishing].

The charged surface due to the spontaneous polarization deforms the movements of photo-generated electron–hole pairs, and thus determines the unique photochemical properties of the ferroelectric. The length of the SCR (note: L_d is the length of the depletion layer and L_a is that of the accumulation layer) can be written as a function of the surface potential V_s and the Debye length (L_D).^196,197 The voltage V_s depends not only on P_s, but also on the conduction band edge and the medium surrounding the surface. The Debye length L_D depends on the dielectric permittivity of the material and the donor concentration according to the following equation:^184,185

where ε₀ is the permittivity of free space, ε_r is the relative permittivity of the material, and N_D is the donor density. The widths of the space charge layers are then:andfor the depletion and accumulation layers, respectively. The term e is the electronic charge, k_B is Boltzmann's constant, and T is the absolute temperature. From the above three equations, it can be deduced that a wider SCR requires a longer L_D. Thus, a ferroelectric material possessing high dielectric permittivity and low density of free charge carriers could enhance the separation of photo-generated carriers, benefiting the photochemical properties. If the charged surfaces cannot be fully neutralized by the internal screening mechanism, external screening by adsorption of charged molecules or ions from the environment would occur. The above discussions are based on theoretical aspects. Indeed, to minimize the depolarization field for neutralizing the charges on the surface, the ferroelectric crystal splits into domains separated by domain walls.¹⁹⁸ Thereby, the motion of domain walls could have a significant influence on the separation of charge carriers. Previous studies have suggested that domain walls affect the local surface potential and surface free energy, and may influence the surface chemistry.^199,200 Recent experimental evidence implies that the enhanced photoactivity arises from the inherent P_s of domains rather than from domain walls.²⁰¹ In particular, an experimental investigation conducted on PbTiO₃ nanoplates exhibiting single domains further supports the contribution of domains as mentioned above.²⁰² Moreover, the authors found that increasing the thickness along the direction of P_s can enhance the charge separation ability. The P_s decreases with decreasing grain size as found in PbTiO₃ and BaTiO₃.^203,204 Thus, for the design of powdered ferroelectric photocatalysts, the particle size is a crucial parameter to be considered. Appropriate control of the particle size would allow for more efficient conduction of the photo-generated charge carriers to the sites where redox reactions take place.

5.3 Progress on AgNbO₃-based photocatalysts

Since Kato et al.²¹ reported the photocatalytic activity of AgNbO₃ in 2006, many strategies have been applied to improve its photocatalytic performance. These strategies include surface morphological control, metal coating, design of solid-solutions or composites, and doping, among others. Indeed, these strategies do not differ from the four strategies for improving the photocatalytic performance of a given semiconductor, as mentioned in Section 5.2.

5.3.1 Surface morphology control. Arney et al.²⁰⁵ investigated flux synthetic routes to obtain smaller particle sizes of AgNbO₃, and compared the resultant surface areas and photocatalytic activities with those obtained from traditional solid-state methods. The results showed that controlling the surface morphology via flux synthesis methods can significantly enhance the visible-light photocatalytic rates of H₂ formation. The enhanced photocatalytic performance via morphology control was further evidenced by Li et al.,²⁰⁶ who synthesized polyhedron-shaped AgNbO₃ and Cu-doped AgNbO₃ particles with a “nano-ladder” surface microstructure via a solvothermal (ST) method (see Fig. 46b and c), achieving enhanced visible-light absorption capability and photocatalytic rates of O₂ evolution. The structural analysis revealed that the powdered photocatalyst consists of AgNbO₃/Ag₂Nb₄O₁₁ composites. Furthermore, XPS results implied the existence of Nb⁴⁺, suggesting the presence of defects. This defect structure might be intimately related to the formation of the “nano-ladder” surface morphology during the solvothermal reaction. Upon Cu²⁺-doping, a highly asymmetric peak in the XPS spectrum was observed (see Fig. 46e), indicating a higher concentration of defect structures/clusters associated with Nb⁴⁺ leading to higher visible-light photocatalytic activity. A similar behavior was also observed in La³⁺-doped AgNbO₃.²⁰⁷ Wang et al.²⁰⁸ synthesized AgNbO₃/Ag₂Nb₄O₁₁ and AgNbO₃/Ag₂Nb₄O₁₁/Nb₂O₅ composites via a solvothermal process and further investigated the temperature impact on the photochemical reaction. These composite particles showed similar surface morphology to those reported by Li et al.²⁰⁶ However, the UV-vis absorption spectra revealed an enhanced absorption tail, consisting of two absorption peaks (one near 500 nm and the other near 600 nm), which cover the visible-light range. This suggests that there are two different mechanisms to generate extra absorption in the visible-light range.

Fig. 46 (a) SEM images of AgNbO₃ prepared by solid-state reaction, AN (SSR); (b) AgNbO₃ prepared by a solvothermal method, AN (ST); and (c) Cu-doped AgNbO₃ prepared by a solvothermal method, Cu : AN (ST); (d) UV-vis diffuse reflection spectra of AN (SSR), Ag₂Nb₄O₁₁, AN (ST) and Cu : AN (ST); (e) Nb 3d_5/2 XPS line obtained from AN (SSR) (black line), AN (ST) (red line) and Cu : AN (ST) (blue line); (f) photocatalytic O₂ evolution rates over AN (SSR), AN (ST) and Cu : AN (ST) under visible light irradiation (λ ≥ 420 nm) reported by Li et al.²⁰⁶

Recently, Cao et al.²⁰⁹ synthesized one-dimensional AgNbO₃ nanostructures via a topochemical transition process using K₂Nb₂O₆·nH₂O filiform crystals as precursors (see Fig. 47a and b). These nanostructured samples also showed a broadened absorption peak in the visible-light range (see Fig. 47c). As mentioned in Section 2.5, in the UV-vis diffuse reflection spectrum of pure AgNbO₃, Zhou et al. found an absorption peak in the same wavelength range, which was proposed to originate from the SPR effect (see Fig. 17).⁸³ This effect could be responsible for the enhanced photocatalytic activity under visible-light irradiation.

Fig. 47 (a) FE-SEM and (b) TEM images of AgNbO₃; (c) UV-visible diffuse reflectance spectra, (d) photographic image of AgNbO₃ powder and (e) photocatalytic degradation of methylene bule (MB) by AgNbO₃ nanostructures reported by Cao et al.²⁰⁹ [Reproduced with permission from ref. 209 copyright 2014 by Elsevier].

Lu et al.²¹⁰ synthesized one-dimensional AgNbO₃ using Ag nanowires as the raw material template. In contrast to the results reported by Cao et al., the final product was a one-dimensional nanostructured composite of Ag₂Nb₄O₁₁ and AgNbO₃, which showed an enhanced activity to degradation of 2,4-dichlorophene and rhodamine B (RhB). Most recently, Gao et al.²¹¹ synthesized submicron cubes of AgNbO₃via hydrothermal treatment (HT) of Ag₂O–Nb₂O₅–NH₄HF₂ aqueous suspensions, which exhibited excellent photocatalytic activity under visible-light irradiation (λ ≥ 400 nm) (see Fig. 48g). The microstructure analysis indicated that a (001) facet with high surface energy was exposed (see Fig. 48c and d). Further photoelectrochemical and photocatalytic performance analysis suggested that the cubes with an exposed (001) facet exhibit higher charge carrier separation efficiency with the greater redox ability of photogenerated electrons and holes being responsible for the superior photocatalytic activity.

Fig. 48 Field-emission scanning electron microscopy images of AgNbO₃ (AN) prepared by (a) hydrothermal (HT) and (b) solid state (SSR) methods; (c) transmission electron microscopy image and (d) selected-area electron diffraction pattern of AN (HT); the insets in (b) and (c) show high-resolution transmission electron microscopy images of AN (SSR) and AN (HT), respectively; the inset in (d) shows the angle between the (020) and (110) facets in the AN (HT) cube; (e) UV-vis diffuse reflectance spectra of AN (HT) and AN (SSR); (f) transient photocurrent of AN (HT) and AN (SSR) irradiated with visible light (λ ≥ 400 nm); (g) specific photocatalytic activity of the catalysts. The inset in (g) shows repeated photocatalytic degradation of tetracycline in the presence of AN (HT) and nitrogen-doped TiO₂, reported by Gao et al.²¹¹ [Reproduced with permission from ref. 211 copyright 2019 by Elsevier].

5.3.2 Solid-solution semiconductors with modulated band structure. It is expected that solid-solutions of AgNbO₃ with another perovskite semiconductor could exhibit improved photocatalytic properties compared to each of the end members as a result of the electronic structure that would arise. Based on this idea, two solid-solution systems have been explored so far, namely AgNbO₃–SrTiO₃ and AgNbO₃–NaNbO₃. In the AgNbO₃–SrTiO₃ solid-solution, the hybridization between the Ag 4d and O 2p orbitals and between the Nb 4d and Ti 3d orbitals plays a crucial role in tuning the band structure (see Fig. 49a reported by Wang et al.) and in tailoring the photocatalytic properties.²¹² As a result of the competition between the reduction/oxidation abilities and the absorption activity, the enhanced visible-light activities for the evolution of O₂ and the decomposition of organic compounds can be realized in specific compositions. In the AgNbO₃–NaNbO₃ solid-solution, an increased content of NaNbO₃ decreases the hybridization ratio of Ag 4d and O 2p and the top of the valence band shifts upwards, leading to a blue shift in the optical absorption edge and to an enhancement of oxidizing power (see Fig. 49b).²¹³ In this solid-solution, Li et al.²¹⁴ reported an enhancement of visible-light photocatalytic activity for the decomposition of isopropanol (IPA) into acetone at an intermediate composition. This was considered to be related to the competition between oxidizing power, enhanced surface area and visible-light absorption. In particular, the authors fabricated AgNbO₃–NaNbO₃ solid-solution films on fluorine-doped tin oxide (FTO) conducting glass substrates and investigated their band structure and photoelectrochemical behavior. The schematic band structure is shown in Fig. 49b, which highlights that the bottom of the conduction band potential in the intermediate composition is significantly more positive than that of the two end compounds.²¹³

Fig. 49 (a) Schematic band structure (a1) and experimental photocatalytic performance (a2 and a3) of (AgNbO₃)_1−x(SrTiO₃)_x (ANST) solid-solution.²¹² [Reproduced with permission from ref. 212 copyright 2009 American Chemical Society]. The hybridization of the Ag 4d with O 2p lifts the top of the valence band. In the sample x = 0.25, both the conduction band and valence band are continuous. In the case of x = 0.95, discontinuous inter-bands (or doping levels) are formed by the small number of dopants. (b) Schematic band structure (b1)²¹³ [reproduced with permission from ref. 213 copyright 2010 by Elsevier] and experimental photocatalytic performance (b2 and b3) [reproduced with permission from ref. 215 copyright 2007 by Elsevier] of (AgNbO₃)_1−x(NaNbO₃)_x (ANN) solid-solution.^213,215

5.4 Composites possessing hetero-junction interfaces

The presence of interfaces in composite materials may bring an enhancement of photocatalytic activity. To date, several AgNbO₃-based composites that show an enhancement of photocatalytic performance compared to the pristine bulk have been reported. Table 6 summarizes the photocatalytic properties of various AgNbO₃-based composites. In AgBr/AgNbO₃ composites, Wang et al.²¹⁶ suggested that the enhancement of photocatalytic activity can be attributed to the AgBr/AgNbO₃ heterostructure (formed at the interface), which creates an internal electric field, modulates the band structure, and favors an efficient separation of electrons and holes. Similar mechanisms have contributed to the enhanced photocatalytic activity of Ag₂O/AgNbO₃ p–n junctions as reported by Yang et al.²¹⁷ Recently, Yu et al.²¹⁸ synthesized an Ag/AgNbO₃ plasmonic photocatalyst via a facile combustion method, obtaining a special porous nano-structure where high energy {001} and {220} facets were exposed (see Fig. 50). The authors believed that the enhanced photocatalytic efficiency is related to the synergy between surface plasmonic resonance (SPR), ferroelectric polarization, specific exposed crystal-facets and interfacial crystallinity.

Table 6 Photocatalytic performance of AgNbO₃-based composites for degrading organic pollutants^a

Catalysts	Organics	UV/vis	Degrad./time (h)	k	Ref.
a RhB: rhodamine B; TC: tetracycline; MB: methylene blue.
AgNbO3/AgSbO3	RhB (2.5 mg L^−1)	Vis	—	0.02667	219
Ag@AgCl/AgNbO3	MB (10 mg L^−1)	Vis	∼65%/2 h	0.007	220
NiO/AgNbO3	MB (10 mg L^−1)	UV	∼84%/3 h	—	221
AgBr/AgNbO3	MB (10 mg L^−1)	Vis	74.62%/3 h	0.0083	216
Ag2O/AgNbO3	RhB (10 mg L^−1)	Vis	95.4%/1.5 h	—	217
Ag/AgNbO3	RhB (5 mg L^−1)	—	—	0.0447	218
	TC (10 mg L^−1)	—	70.2%/1 h	0.0293

---

Fig. 50 (a) SEM image of Ag/AgNbO₃ porous nano-structure, (b) enlargement of (a) with the structure model (the inset illustration) of the as-prepared particle; (c) typical HRTEM image of Ag/AgNbO₃ porous nano-structure and the corresponding SAED pattern in (d); (e) HRTEM image of the prepared Ag/AgNbO₃. (f) Schematic drawing illustrating the possible photocatalytic mechanism of the Ag/AgNbO₃ plasmonic photocatalysts: (1) spatial separation of photo-generated carriers along the direction of potentials originating from ferroelectric polarization; (2) orientation transfer of photo-generated carriers onto {001} and {220} facets; (3) photo-generated electrons transfer from the {220} facets to Ag nanoparticles to reduce O₂; (4) formation of free ˙OH via the reaction of ˙O₂⁻ with H₂O; (5) formation of free ˙OH via the reaction of photo-generated holes with OH⁻ in the solution; (6) rapid oxidation of RhB or (tetracycline)TC by free ˙OH.²¹⁸ [Reproduced with permission from ref. 218 copyright 2019 by Elsevier].

6. Summary and outlook

In this review, progress in research on AgNbO₃ and AgNbO₃-based perovskites since their discovery in 1958 has been summarized. The review covers various aspects, from fundamental science to emerging applications, and allows us to draw some important conclusions in the following areas.

6.1 Structures, polymorphic phases, and electric field-induced transitions

AgNbO₃ is polymorphic and shows complex phase behavior, with intricate transformations induced by temperature variations and the application of an electric field. The M₁ phase, stable up to ca. 70 °C, consists of an antiferroelectric-like matrix, in which ferroelectric clusters are locally present, which can successfully explain the non-linear polarization under weak and strong electric fields. Both structure and analysis of properties suggest that the dielectric anomaly denoted as (T_f) could originate from a phase transition associated with inversion symmetry. Electrical loading under high electric fields produces double polarization hysteresis loops, but the structure induced under high electric fields is still experimentally unknown. Future studies should be aimed at revealing the nature of the electric field-induced structure, by in situ diffraction techniques which have still not been carried out in this important material. Above the temperature T_f (∼170 °C in pure AgNbO₃), the microstructures of both M₂ (stable in the range of ∼70–270 °C) and M₃ (stable in the range of ∼270–350 °C) phases still show the presence of polar clusters, but field-induced transformations are significantly suppressed and are difficult to drive, even at high electric fields. The frequency-independent diffuse dielectric anomaly near 270 °C is intimately related to the local disorder–order behavior of off-center cation displacements (especially Nb⁵⁺ ions) in the sub-lattice of its average AFE matrix. This emphasizes the importance of local structural heterogeneity at the sub-lattice scale to improve the dielectric response of a given material, especially at high frequency, and will guide the property optimization for specific applications, such as microwave capacitors.

6.2 Effects of compositional modification

Chemical modifications by suitable elements can be guided by the perovskite tolerance factor and may result in the suppression of the local displacive behavior, as well as in an increased local structural disorder down to very low temperatures.

Isovalent substitutions on the A-site, using Li, restrains antiferroelectricity and leads to the promotion of a ferroelectric-type order with rhombohedral structure possessing high piezoelectric, pyroelectric and fatigue performances. Gradual substitution of Ag⁺ with isovalent Na⁺ ions with a smaller radius than Ag⁺ allows for the formation of a perovskite solid solution and induces the crossover from double polarization hysteresis to ferroelectric-like loops. The presence of Na restricts the displacement of Nb⁵⁺ ions and suppresses the diffuse dielectric dispersion of AgNbO₃. Additionally, the replacement of Ag⁺ by isovalent K⁺ has the effect of reducing antiferrodistortive instabilities and promotes ferroelectricity, characterized by orthorhombic symmetry and an emerging potential for explosive energy conversion due to the possibility of driving pressure-induced FE → AFE transitions.

A possible strategy to develop AgNbO₃-based antiferroelectric solid-solutions is to substitute Ag⁺ with cations of different radius and valence, including bi- and tri-valent elements, such as Ca²⁺, Bi³⁺ and various rare-earth cations, which can provide chemical pressure to suppress ferroelectricity and increase the energy barrier between AFE and FE phases. Besides, the doping also creates defects and enhances local structural heterogeneity that can have negative impacts on the field-induced polar ordering. Similar effects can be obtained by the isovalent substitution of Nb⁵⁺ by Ta⁵⁺ on the B-site producing an increase in the characteristic fields E_B and E_F, and a decrease of the remnant polarization, with P–E loops tending to a linear shape with increasing Ta content, evidencing the stabilization of an antiferroelectric state.

6.3 Applications in dielectric energy storage

AgNbO₃-based materials are promising lead-free candidates for energy storage capacitors, due to their large energy density values. These range from 2.1 J cm⁻³ in AgNbO₃ to 6.3 J cm⁻³ in Ag(Nb_0.45Ta_0.55)O₃ ceramics obtained at room temperature, attributed to the enhanced stability of antiferroelectricity and improved breakdown strength. Two methods can be used to further enhance E_b and are based on either intrinsic or extrinsic effects. One method consists of modulating the band structure and increasing the band gap to prevent the excitation of electrons from the valence band to the conduction band (intrinsic). The other method is based on reducing the grain size to increase the resistivity by increasing the amount of grain boundaries (extrinsic).

One of the main issues that should be overcome in future research is to increase the energy storage efficiency, which is often lower than 70%. This can be achieved by reducing the hysteresis area of the polarization–electric field loop. Previous investigations on relaxor-ferroelectrics such as Pb(Mg_1/3Nb_2/3)O₃ may provide guidance for designing the AgNbO₃-based materials displaying field-induced reversible polar ordering with low hysteresis (i.e. ergodic relaxor-antiferroelectrics). Systematic studies combining experimental techniques and modelling should be able to provide improved compositional design criteria to obtain increased energy storage efficiency.

A better synergy between research groups in academia and companies engaged in the energy storage capacitor sector should be promoted to overcome additional technical issues that are currently preventing AgNbO₃-based devices entering the energy storage market. These issues include the difficulties related to the processing of AgNbO₃ in oxygen-rich environments with accurate temperature control and specific heat treatment schedules. Metallic Ag can easily form near the AgNbO₃ surface when the oxygen content in the processing environment is not sufficient, inducing an n-type semiconductor state. Additionally, the cost of the Ag precursors and the compatibility with electrode materials are also important factors to consider in future development.

6.4 Applications in photocatalysis and photovoltaics

As a functional semiconductor, AgNbO₃ is emerging not only as a potential photocatalyst for splitting water and degrading organic pollutants, but also as a photovoltaic material for solar-cells due to its narrow E_g, which can extend the absorption edge of the solar spectrum to the visible-light range, providing enhanced photocatalytic and photovoltaic performances. Theoretical calculations also suggest a narrower band gap (E_g ≈ 1.83 eV) compared to the reported experimental values (E_g ≈ 2.08–2.93 eV). This is attributed to the existence of unbonded Ag atoms and the Ag–O/Nb–O covalent bonds formed in the AgNbO₃ lattice. The presence of metallic Ag is believed to be responsible for the surface plasmon resonance effect and for the observed extra visible-light absorption event and thus for ultimately enhancing the photocatalytic and photovoltaic performances. Furthermore, the visible-light photocatalytic activity can be tuned by the external voltage bias, which can modify the width of surface space charge regions (SCRs) in AgNbO₃, allowing for the regulation of photocatalytic activity.

To further improve the photocatalytic performance for specific applications, chemically-modified AgNbO₃-based materials have been explored since 2006 according to the following three materials design strategies: (1) control of the nanostructured surface morphology by wet chemical methods to provide more reaction-sites; (2) change of the surface chemical potential by modulating the band structure to enhance redox reactions; and (3) introduction of heterogeneous interfaces to create an internal electric-field to promote the separation of photo-generated electron–hole pairs.

To date, rare studies have been carried out integrating two or three of these approaches to further improve the photocatalytic performance. In particular, AgNbO₃-based ferroelectric materials would attract interest for photocatalytic application due to the large P_s coupled with the narrow E_g and SPR response. Besides AgNbO₃-based ferroelectric photocatalysts, AgNbO₃-based piezo- and pyro-electric semiconducting nanomaterials could also emerge as potential candidates for converting mechanical and thermal energy into chemical energy. Additionally, research focused on ferroelectric photocatalysis of AgNbO₃ is still rare. However, previous studies reported intriguing photovoltaic properties found in electrically poled and mechanically polished AgNbO₃ ceramics, which were proposed to originate from intrinsic FE polarization and strain gradient-induced flexoelectricity, respectively. At the same time, electrical poling and/or mechanical polishing can also cause the precipitation of metallic Ag from the lattice of AgNbO₃ and change the surface electronic structure, such as the width of SCRs, influencing the photovoltaic properties. Therefore, more fundamental studies should be carried out in future to further understand the photovoltaic mechanism.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 52072227), the Opening Project of the State Key Laboratory of High Performance Ceramics and Superfine Microstructures (Grant No. SKL202111SIC), the Postdoctoral Science Foundation of China (Grant No. 2019M653604), the Natural Science Pre-research Funding of Shaanxi University of Science & Technology (Grant No. 2020QNBJ-03), and The Royal Society (Newton Advanced Fellowship, Grant No. NAF\R1\201126).

References

1. X. H. Hao, J. W. Zhai, L. B. Kong and Z. K. Xu, Prog. Mater. Sci., 2014, 63, 1–57.
2. L. Jin, F. Li and S. J. Zhang, J. Am. Ceram. Soc., 2014, 97, 1–27.
3. H. R. Jo and C. S. Lynch, J. Appl. Phys., 2014, 116, 074107.
4. Z. Liu, T. Lu, J. Ye, G. Wang, X. Dong, R. Withers and Y. Liu, Adv. Mater. Technol., 2018, 3, 1800111.
5. H. Wang, Y. Liu, T. Yang and S. Zhang, Adv. Funct. Mater., 2019, 29, 1807321.
6. Z. P. Gao, W. Peng, B. Chen, S. A. T. Redfern, K. Wang, B. J. Chu, Q. He, Y. Sun, X. F. Chen, H. C. Nie, W. Deng, L. K. Zhang, H. L. He, G. S. Wang and X. L. Dong, Phys. Rev. Mater., 2019, 3, 035401.
7. Y. J. Ji, Q. Li, F. P. Zhuo, Q. F. Yan, Y. L. Zhang and X. C. Chu, ACS Appl. Mater. Interfaces, 2019, 11, 32135–32143.
8. X. H. Hao and J. W. Zhai, Appl. Phys. Lett., 2014, 104, 022902.
9. Q. F. Zhang, S. C. Chen, M. Y. Fan, S. L. Jiang, T. Q. Yang, J. F. Wang, G. Li and X. Yao, Mater. Res. Bull., 2012, 47, 4503–4509.
10. EU-Directive 2002/95/EC: Restriction of the Use of Certain Hazardous Substances in Electrical and Electronic Equipment (RoHS), Off. J. Eur. Union., 2003, 46, (L37), 19–23.
11. K. M. Rabe, in Functional Metal Oxides, 2013, pp. 221–244,  DOI:10.1002/9783527654864.ch7.
12. Y. T. G. Viola, C. Yu, Y. Tan, V. Koval, X. Wei, K. Choy and H. Yan, Prog. Mater. Sci., 2021, 122, 10083.
13. D. Fu, M. Endo, H. Taniguchi, T. Taniyama and M. Itoh, Appl. Phys. Lett., 2007, 90, 252907.
14. A. Kania, K. Roleder and M. Łukaszewski, Ferroelectrics, 1983, 52, 265–269.
15. Y. Tian, L. Jin, H. F. Zhang, Z. Xu, X. Y. Wei, E. D. Politova, S. Y. Stefanovich, N. V. Tarakina, I. Abrahams and H. X. Yan, J. Mater. Chem. A, 2016, 4, 17279–17287.
16. Y. Tian, J. Li, Q. Y. Hu, L. Jin, K. Yu, J. L. Li, E. D. Politova, S. Y. Stefanovich, Z. Xu and X. Y. Wei, J. Mater. Chem. C, 2019, 7, 1028–1034.
17. N. N. Luo, K. Han, M. J. Cabral, X. Z. Liao, S. J. Zhang, C. Z. Liao, G. Z. Zhang, X. Y. Chen, Q. Feng, J. F. Li and Y. Z. Wei, Nat. Commun., 2020, 11, 4824.
18. T. Takeda, Y. Takahashi, N. Wada and Y. Sakabe, Jpn. J. Appl. Phys., 2003, 42, 6023.
19. M. Valant and D. Suvorov, J. Am. Ceram. Soc., 1999, 82, 88–93.
20. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
21. H. Kato, H. Kobayashi and A. Kudo, J. Phys. Chem. B, 2002, 106, 12441–12447.
22. X. He, C. Chen, C. Li, H. Zeng and Z. Yi, Adv. Funct. Mater., 2019, 29, 1900918.
23. N. Maso, D. I. Woodward, P. A. Thomas, A. Varez and A. R. West, J. Mater. Chem., 2011, 21, 2715–2722.
24. P. Rozier and O. Szajwaj, J. Solid State Chem., 2008, 181, 228–234.
25. D. I. Woodward and R. Beanland, Inorg. Chem., 2014, 53, 8941–8948.
26. X. Liu, C. Qin, Y. Huang, L. Qin and H. J. Seo, J. Taiwan Inst. Chem. Eng., 2017, 78, 530–538.
27. Z. Chen, X. Cheng, W. Ye, R. Zheng, H. Zhu, H. Yu, N. Long, M. Shui and J. Shu, Chem. Eng. J., 2019, 366, 246–253.
28. M. Valant, A. K. Axelsson, B. Zou and N. Alford, J. Mater. Res., 2007, 22, 1650–1655.
29. H. B. Chang, M. Y. Shang, C. Y. Zhang, H. M. Yuan and S. H. Feng, J. Am. Ceram. Soc., 2012, 95, 3673–3677.
30. J. Wang, X. Wan, Y. Rao, L. Zhao and K. Zhu, J. Eur. Ceram. Soc., 2020, 40, 5589–5596.
31. M. B. Telli, Chemical solution deposition of silver tantalate niobate Ag(Ta_xNb_1–x)O₃ thin films, Doctoral Thesis, The Pennsylvania State University, 2005..
32. A. Kania, J. Cryst. Growth, 1989, 96, 703–704.
33. M. Łukaszewski, A. Kania and A. Ratuszna, J. Cryst. Growth, 1980, 48, 493–495.
34. W. Zhao, Z. Fu, J. Deng, S. Li, Y. Han, M.-R. Li, X. Wang and J. Hong, Chin. Phys. Lett., 2021, 38, 037701.
35. M. Francombe and B. Lewis, Acta Crystallogr., 1958, 11, 175–178.
36. Y. Lu, Q. Y. Shen, Q. N. Yu, F. Zhang, G. Q. Li and W. F. Zhang, J. Phys. Chem. C, 2016, 120, 28712–28716.
37. H. Moriwake, C. A. J. Fisher, A. Kuwabara and D. S. Fu, Jpn. J. Appl. Phys., 2013, 52, 09KF08.
38. A. Kania, A. Niewiadomski, S. Miga, I. Jankowska-Sumara, M. Pawlik, Z. Ujma, J. Koperski and J. Suchanicz, J. Eur. Ceram. Soc., 2014, 34, 1761–1770.
39. Y. K. T. Egawa, Y. Noguchi and M. Miyayama, Jpn. J. Appl. Phys., 2016, 55, 10TB03.
40. J. Li, Y. Tian, Y. Lan, L. Jin, C. Chen and X. Wei, Ceram. Int., 2021, 47, 26178–26184.
41. M. B. Telli, S. S. N. Bharadwaja, M. D. Biegalski, J. G. Cheng and S. Trolier-McKinstry, J. Appl. Phys., 2007, 101, 014111.
42. J.-Y. Kim and A. M. Grishin, Thin Solid Films, 2006, 515, 615–618.
43. H. Sakurai, S. Yamazoe and T. Wada, Appl. Phys. Lett., 2010, 97, 042901.
44. Y. Zhang, X. Li, J. Song, S. Zhang, J. Wang, X. Dai, B. Liu, G. Dong and L. Zhao, J. Materiomics, 2021, 7, 1294–1300.
45. A. Kania and K. Roleder, Ferroelectr. Lett. Sect., 1984, 2, 51–54.
46. J. Fabry, Z. Zikmund, A. Kania and V. Petříček, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2000, 56, 916–918.
47. P. Sciau, A. Kania, B. Dkhil, E. Suard and A. Ratuszna, J. Phys.: Condens. Matter, 2004, 16, 2795.
48. I. Levin, V. Krayzman, J. C. Woicik, J. Karapetrova, T. Proffen, M. G. Tucker and I. M. Reaney, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 104113.
49. M. Yashima, S. Matsuyama, R. Sano, M. Itoh, K. Tsuda and D. S. Fu, Chem. Mater., 2011, 23, 1643–1645.
50. M. K. Niranjan and S. Asthana, Solid State Commun., 2012, 152, 1707–1710.
51. G. Li, H. Liu, L. Zhao, J. Gao, J. F. Li, R. Yu and J. Zhu, Appl. Phys. Lett., 2018, 113, 242901.
52. U. Farid, A. S. Gibbs and B. J. Kennedy, Inorg. Chem., 2020, 59, 12595–12607.
53. T. Lu, Y. Tian, A. Studer, N. Narayanan, Q. Li, R. Withers, L. Jin, Y. Mendez-González, A. Peláiz-Barranco and D. Yu, IUCrJ, 2019, 6, 740–750.
54. A. Kania and J. Kwapulinski, J. Phys.: Condens. Matter, 1999, 11, 8933.
55. M. Pawełczyk, Phase Transitions, 1987, 8, 273–292.
56. M. Verwerft, D. Van Dyck, V. Brabers, J. Van Landuyt and S. Amelinckx, Phys. Status Solidi A, 1989, 112, 451–466.
57. S. Miga and J. Dec, J. Appl. Phys., 1999, 85, 1756–1759.
58. A. Volkov, B. Gorshunov, G. Komandin, W. Fortin, G. Kugel, A. Kania and J. Grigas, J. Phys.: Condens. Matter, 1995, 7, 785.
59. W. Fortin, G. Kugel, J. Grigas and A. Kania, Ferroelectrics, 1996, 184, 273–276.
60. W. Fortin, G. Kugel, J. Grigas and A. Kania, J. Appl. Phys., 1996, 79, 4273–4282.
61. A. Kania, K. Roleder, G. Kugel and M. Fontana, J. Phys. C: Solid State Phys., 1986, 19, 9.
62. S. Miga, A. Kania and J. Dec, J. Phys.: Condens. Matter, 2011, 23, 155901.
63. M. Ivliev, S. Raevskaya, I. Raevskiĭ, V. Shuvaeva and I. Pirog, Phys. Solid State, 2007, 49, 769–779.
64. B. Zalar, A. Lebar, J. Seliger, R. Blinc, V. V. Laguta and M. Itoh, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 064107.
65. R. Blinc, Ferro-and Antiferroelectricity, 2007, pp. 51–67.
66. A. Levanyuk and D. G. Sannikov, Sov. Phys., Usp., 1974, 17, 199.
67. Y. Yoneda, K. Yoshii and S. Kohara, Trans. Mater. Res. Soc. Jpn., 2012, 37, 73–76.
68. F. Cordero, Materials, 2015, 8, 8195–8245.
69. D. Fu, M. Endo, H. Taniguchi, T. Taniyama, S.-y. Koshihara and M. Itoh, Appl. Phys. Lett., 2008, 92, 172905.
70. T. Zhang, C. Zhang, L. Wang, Y. Chai, S. Shen, Y. Sun, H. Yuan and S. Feng, J. Am. Ceram. Soc., 2014, 97, 1895–1898.
71. H. Chang, M. Shang, C. Zhang, H. Yuan and S. Feng, J. Am. Ceram. Soc., 2012, 95, 3673–3677.
72. A. Kania and S. Miga, J. Am. Ceram. Soc., 2015, 98, 1040–1041.
73. V. Dvořák, Ferroelectrics, 1974, 7, 1–9.
74. Z. Yan, D. Zhang, X. Zhou, M. Zhang, L. Zhang, H. Zhang, G. Xue, I. Abrahams and H. Yan, J. Mater. Chem. A, 2021, 9, 3520–3529.
75. J. Gao, W. Li, J. Liu, Q. Li and J.-F. Li, Research, 2022, 2022, 9782343.
76. G. Li, H. Liu, L. Zhao, J. Gao, J.-F. Li and J. Zhu, J. Appl. Phys., 2022, 131, 124107.
77. H. Moriwake, A. Konishi, T. Ogawa, C. A. Fisher, A. Kuwabara, K. Shitara and D. Fu, Phys. Rev. B, 2018, 97, 224104.
78. Y. Tian, L. Jin, Q. Hu, K. Yu, Y. Zhuang, G. Viola, I. Abrahams, Z. Xu, X. Wei and H. Yan, J. Mater. Chem. A, 2019, 7, 834–842.
79. W. Zhao, Z. Fu, J. Deng, S. Li, Y. Han, M.-R. Li, X. Wang and J. Hong, Chin. Phys. Lett., 2021, 38, 037701.
80. H. Moriwake, A. Konishi, T. Ogawa, C. A. Fisher, A. Kuwabara and D. Fu, J. Appl. Phys., 2016, 119, 064102.
81. M. Yashima and S. Matsuyama, J. Phys. Chem. C, 2012, 116, 24902–24906.
82. G. Li, Y. Bai, X. Liu and W. Zhang, J. Phys. D: Appl. Phys., 2009, 42, 235503.
83. F. Zhou, J. Zhu, Z. Lai, Y. Liu and X. Zhao, Appl. Phys. Lett., 2014, 105, 231121.
84. S. Linic, P. Christopher and D. B. Ingram, Nat. Mater., 2011, 10, 911–921.
85. C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5, eaav0693.
86. S. G. Kang, Int. J. Quantum Chem., 2017, 117, e25420.
87. N. A. Benedek and C. J. Fennie, J. Phys. Chem. C, 2013, 117, 13339–13349.
88. J. Zhao, Etude théorique d'oxydes nano-structurés multifonctionnels, Université Sciences et Technologies – Bordeaux I, 2013, NT : 2013BOR14866.
89. M. Yashima and R. Ali, Solid State Ionics, 2009, 180, 120–126.
90. C. Shivakumara, Solid State Commun., 2006, 139, 165–169.
91. A. T. Mulder, N. A. Benedek, J. M. Rondinelli and C. J. Fennie, Adv. Funct. Mater., 2013, 23, 4810–4820.
92. M. E. Lines and A. M. Glass, Principles and Applications of Ferroelectrics and Related Materials, Oxford University Press, New York, 1977.
93. N. A. Benedek, J. M. Rondinelli, H. Djani, P. Ghosez and P. Lightfoot, Dalton Trans., 2015, 44, 10543–10558.
94. M. Kruczek, E. Talik and A. Kania, Solid State Commun., 2006, 137, 469–473.
95. R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
96. S. Wada, A. Saito, T. Hoshina, H. Kakemoto, T. Tsurumi, C. Moriyoshi and Y. Kuroiwa, Jpn. J. Appl. Phys., 2006, 45, 7389.
97. A. Niewiadomski, D. Kajewski, A. Kania, K. Balin, S. Miga, M. Pawlik and J. Koperski, Ceram. Int., 2016, 42, 4445–4451.
98. D. I. Bilc and D. J. Singh, Phys. Rev. Lett., 2006, 96, 147602.
99. S. Wada, A. Saito, T. Hoshina, H. Kakemoto, T. Tsurumi, C. Moriyoshi and Y. Kuroiwa, Ferroelectrics, 2007, 346, 64–71.
100. A. Saito, S. Uraki, H. Kakemoto, T. Tsurumi and S. Wada, Mater. Sci. Eng., B, 2005, 120, 166–169.
101. A. Kania and S. Miga, Mater. Sci. Eng., B, 2001, 86, 128–133.
102. D. Fu, M. Endo, H. Taniguchi, T. Taniyama, M. Itoh and S.-y. Koshihara, J. Phys.: Condens. Matter, 2011, 23, 075901.
103. H. Khan, I. Sterianou, S. Miao, J. Pokorny and I. Reaney, J. Appl. Phys., 2012, 111, 024107.
104. Y. Yamamoto, I. Fujii and T. Wada, (Ag,Li)NbO3 thin films fabricated on (001), (110), and (111) SrTiO3 substrates by pulsed laser deposition, Joint IEEE International Symposium on Applications of Ferroelectric and Workshop on Piezoresponse Force Microscopy (ISAF/PFM), 2013, pp. 127–129,  DOI:10.1109/ISAF.2013.6748673.
105. Y. Guo, Y. Liu, R. L. Withers, F. Brink and H. Chen, Chem. Mater., 2011, 23, 219–228.
106. I. Levin and I. M. Reaney, Adv. Funct. Mater., 2012, 22, 3445–3452.
107. R. Garg, B. N. Rao, A. Senyshyn, P. Krishna and R. Ranjan, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 014103.
108. D. Kan, L. Pálová, V. Anbusathaiah, C. J. Cheng, S. Fujino, V. Nagarajan, K. M. Rabe and I. Takeuchi, Adv. Funct. Mater., 2010, 20, 1108–1115.
109. D. Kan, C. J. Long, C. Steinmetz, S. E. Lofland and I. Takeuchi, J. Mater. Res., 2012, 27, 2691.
110. T. Lu, Y. Tian, A. Studer, Q. Li, R. L. Withers, L. Jin, D. Yu, Z. Xu, X. Wei and Y. Liu, Chem. Mater., 2020, 32, 6456–6463.
111. S. Li, H. Nie, G. Wang, N. Liu, M. Zhou, F. Cao and X. Dong, J. Mater. Chem. C, 2019, 7, 4403–4414.
112. Y. Kim, J. Kim, S. Yamanaka, A. Nakajima, T. Ogawa, T. Serizawa, H. Tanaka, M. Baba, T. Fukuda, K. Yoshii, M. Takeda, N. Yamada, T. Nakayama and K. Niihara, Adv. Energy Mater., 2015, 5, 1401942.
113. M. E. Lines and A. M. Glass, Principles and Applications of Ferroelectrics and Related Materials, Oxford University Press, 2001.
114. D. Fu, M. Itoh and S.-y. Koshihara, J. Appl. Phys., 2009, 106, 104104.
115. R. A. Klein, A. B. Altman, R. J. Saballos, J. P. S. Walsh, A. D. Tamerius, Y. Meng, D. Puggioni, S. D. Jacobsen, J. M. Rondinelli and D. E. Freedman, Phys. Rev. Mater., 2019, 3, 064411.
116. Y. Xu, G. Wang, Y. Tian, Y. Yan, X. Liu and Y. Feng, Ceram. Int., 2016, 42, 18791–18797.
117. Z. Liu, T. Lu, F. Xue, H. Nie, R. Withers, A. Studer, F. Kremer, N. Narayanan, X. Dong and D. Yu, Sci. Adv., 2020, 6, eaba0367.
118. H. D. Megaw, Ferroelectrics, 1974, 7, 87–89.
119. S. K. Mishra, N. Choudhury, S. L. Chaplot, P. S. R. Krishna and R. Mittal, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024110.
120. A. Glazer and H. D. Megaw, Philos. Mag., 1972, 25, 1119–1135.
121. H. Z. Guo, H. Shimizu, Y. Mizuno and C. A. Randall, J. Appl. Phys., 2015, 117, 214103.
122. H. Guo, H. Shimizu and C. A. Randall, J. Appl. Phys., 2015, 118, 174107.
123. D. Fu, T. Arioka, H. Taniguchi, T. Taniyama and M. Itoh, Appl. Phys. Lett., 2011, 99, 012904.
124. D. Klement, M. Spreitzer and D. Suvorov, J. Eur. Ceram. Soc., 2014, 34, 1537–1545.
125. M. Valant, D. Suvorov, C. Hoffmann and H. Sommariva, J. Eur. Ceram. Soc., 2001, 21, 2647–2651.
126. M. Valant, A.-K. Axelsson and N. Alford, J. Eur. Ceram. Soc., 2007, 27, 2549–2560.
127. H. P. Soon, H. Taniguchi and M. Itoh, Appl. Phys. Lett., 2009, 95, 242904.
128. D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 176.
129. A. Kania, Phase Transit., 1983, 3, 131–139.
130. I. Levin, J. Woicik, A. Llobet, M. Tucker, V. Krayzman, J. Pokorny and I. Reaney, Chem. Mater., 2010, 22, 4987–4995.
131. L. Li, M. Spreitzer and D. Suvorov, Appl. Phys. Lett., 2014, 104, 182902.
132. L. Zhao, Q. Liu, J. Gao, S. Zhang and J. F. Li, Adv. Mater., 2017, 29, 1701824.
133. P. Iyer and A. Smith, Acta Crystallogr., 1967, 23, 740–746.
134. W. G. Mumme, I. E. Grey, B. Edwards, C. Turner, J. Nino and T. A. Vanderah, J. Solid State Chem., 2013, 200, 323–327.
135. Z. Zhang, C. J. Howard, B. J. Kennedy, K. S. Knight and Q. Zhou, J. Solid State Chem., 2007, 180, 1846–1851.
136. X. Hu, M. Valant and D. Suvorov, J. Appl. Phys., 2006, 99, 124109.
137. Y. Tian, L. Jin, H. Zhang, Z. Xu, X. Wei, G. Viola, I. Abrahams and H. Yan, J. Mater. Chem. A, 2017, 5, 17525–17531.
138. J. Gao, Q. Liu, J. Dong, X. Wang, S. Zhang and J.-F. Li, ACS Appl. Mater. Interfaces, 2020, 12, 6097–6104.
139. J. Gao, Y. Zhang, L. Zhao, K.-Y. Lee, Q. Liu, A. Studer, M. Hinterstein, S. Zhang and J.-F. Li, J. Mater. Chem. A, 2019, 7, 2225–2232.
140. S. Li, H. Nie, G. Wang, C. Xu, N. Liu, M. Zhou, F. Cao and X. Dong, J. Mater. Chem. C, 2019, 7, 1551–1560.
141. N. Luo, K. Han, F. Zhuo, C. Xu, G. Zhang, L. Liu, X. Chen, C. Hu, H. Zhou and Y. Wei, J. Mater. Chem. A, 2019, 7, 14118–14128.
142. J. Gao, Y. C. Zhang, L. Zhao, K. Y. Lee, Q. Liu, A. Studer, M. Hinterstein, S. J. Zhang and J. F. Li, J. Mater. Chem. A, 2019, 7, 2225–2232.
143. N. Luo, K. Han, F. Zhuo, L. Liu, X. Chen, B. Peng, X. Wang, Q. Feng and Y. Wei, J. Mater. Chem. C, 2019, 7, 4999–5008.
144. Y. H. Xu, Y. Guo, Q. Liu, Y. H. Yin, J. L. Bai, L. Lin, J. J. Tian and Y. Tian, J. Alloys Compd., 2020, 821, 153260.
145. Y. H. Xu, Y. Guo, Q. Liu, G. D. Wang, J. L. Bai, J. J. Tian, L. Lin and Y. Tian, J. Eur. Ceram. Soc., 2020, 40, 56–62.
146. A. Song, J. Song, Y. Lv, L. Liang, J. Wang and L. Zhao, Mater. Lett., 2019, 237, 278–281.
147. Z. N. Yan, D. Zhang, X. F. Zhou, H. Qi, H. Luo, K. C. Zhou, I. Abrahams and H. X. Yan, J. Mater. Chem. A, 2019, 7, 10702–10711.
148. L.-F. Zhu, L. Zhao, Y. Yan, H. Leng, X. Li, L.-Q. Cheng, X. Xiong and S. Priya, J. Mater. Chem. A, 2021, 9, 9655–9664.
149. L. Zhao, J. Gao, Q. Liu, S. Zhang and J.-F. Li, ACS Appl. Mater. Interfaces, 2018, 10, 819–826.
150. L. Zhao, Q. Liu, S. J. Zhang and J. F. Li, J. Mater. Chem. C, 2016, 4, 8380–8384.
151. N. Luo, K. Han, L. Liu, B. Peng, X. Wang, C. Hu, H. Zhou, Q. Feng, X. Chen and Y. Wei, J. Am. Ceram. Soc., 2019, 102, 4640–4647.
152. J. Li, L. Jin, Y. Tian, C. Chen, Y. Lan, Q. Hu, C. Li, X. Wei and H. Yan, J. Materiomics, 2022, 8, 266–273.
153. P. Ren, D. Ren, L. Sun, F. Yan, S. Yang and G. Zhao, J. Eur. Ceram. Soc., 2020, 40, 4495–4502.
154. K. Han, N. Luo, S. Mao, F. Zhuo, L. Liu, B. Peng, X. Chen, C. Hu, H. Zhou and Y. Wei, J. Mater. Chem. A, 2019, 7, 26293–26301.
155. Z. Lu, W. Bao, G. Wang, S.-K. Sun, L. Li, J. Li, H. Yang, H. Ji, A. Feteira, D. Li, F. Xu, A. K. Kleppe, D. Wang, S.-Y. Liu and I. M. Reaney, Nano Energy, 2021, 79, 105423.
156. W. Chao, J. Gao, T. Yang and Y. Li, J. Eur. Ceram. Soc., 2021, 41, 7670–7677.
157. W. Chao, T. Yang, Y. Li and Z. Liu, J. Am. Ceram. Soc., 2020, 103, 7283–7290.
158. Y. Xu, Z. Yang, K. Xu, Y. Cao, Y. Tian, L. Guo, J. Tian, H. Tian, X. Liu, L. Lin and G. Wang, Chem. Eng. J., 2021, 426, 131047.
159. L. Jin, J. Pang, R. Jing, Y. Lan, L. Wang, F. Li, Q. Hu, H. Du, D. Guo and X. Wei, J. Alloys Compd., 2019, 788, 1182–1192.
160. H. Borkar, V. Singh, B. Singh, M. Tomar, V. Gupta and A. Kumar, RSC Adv., 2014, 4, 22840–22847.
161. J. Li, L. Zhang and S. Ducharme, Appl. Phys. Lett., 2007, 90, 132901.
162. L. M. Wang, Relationship between Intrinsic Breakdown Field and Bandgap of Materials, 25th International Conference on Microelectronics, 2006, pp. 576–579,  DOI:10.1109/ICMEL.2006.1651032.
163. R. Gerson and T. C. Marshall, J. Appl. Phys., 1959, 30, 1650–1653.
164. A. Kishimoto, K. Koumoto, H. Yanagida and M. Nameki, Eng. Fract. Mech., 1991, 40, 927–930.
165. T. Tunkasiri and G. Rujijanagul, J. Mater. Sci. Lett., 1996, 15, 1767–1769.
166. E. Beauchamp, J. Am. Ceram. Soc., 1971, 54, 484–487.
167. L. T. Yang, X. Kong, F. Li, H. Hao, Z. X. Cheng, H. X. Liu, J. F. Li and S. J. Zhang, Prog. Mater. Sci., 2019, 102, 72–108.
168. H. Y. Lee, K. H. Cho and H.-D. Nam, Ferroelectrics, 2006, 334, 165–169.
169. Z. Song, H. X. Liu, S. J. Zhang, Z. J. Wang, Y. T. Shi, H. Hao, M. H. Cao, Z. H. Yao and Z. Y. Yu, J. Eur. Ceram. Soc., 2014, 34, 1209–1217.
170. C. Neusel, H. Jelitto, D. Schmidt, R. Janssen, F. Felten and G. A. Schneider, J. Eur. Ceram. Soc., 2015, 35, 113–123.
171. G. Mazzanti, G.C. Montanari, F. Peruzzotti and A. Zaopo, Some remarks regarding the test cells used for electric strength measurements, IEEE International Symposium on Electrical Insulation, 1996, vol. 2, pp. 474–477,  DOI:10.1109/ELINSL.1996.549385.
172. H. Kim and F. Shi, IEEE Trans. Dielectr. Electr. Insul., 2001, 8, 248–252.
173. F. Bian, S. G. Yan, C. H. Xu, Z. Liu, X. F. Chen, C. L. Mao, F. Cao, J. J. Bian, G. S. Wang and X. L. Dong, J. Eur. Ceram. Soc., 2018, 38, 3170–3176.
174. K. Bi, M. H. Bi, Y. N. Hao, W. Luo, Z. M. Cai, X. H. Wang and Y. H. Huang, Nano Energy, 2018, 51, 513–523.
175. M. R. Hoffmann, S. T. Martin, W. Choi and D. W. Bahnemann, Chem. Rev., 1995, 95, 69–96.
176. A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278.
177. M. Grätzel, in Materials for Sustainable Energy: A Collection of Peer-Reviewed Research and Review Articles from Nature Publishing Group, World Scientific, 2011, pp. 26–32.
178. I. K. Konstantinou and T. A. Albanis, Appl. Catal., B, 2004, 49, 1–14.
179. D. Chatterjee and S. Dasgupta, J. Photochem. Photobiol., C, 2005, 6, 186–205.
180. L. Li, P. A. Salvador and G. S. Rohrer, Nanoscale, 2014, 6, 24–42.
181. J. F. Reber and K. Meier, J. Phys. Chem., 1984, 88, 5903–5913.
182. O. Khaselev and J. A. Turner, Science, 1998, 280, 425–427.
183. J. Luo, J.-H. Im, M. T. Mayer, M. Schreier, M. K. Nazeeruddin, N.-G. Park, S. D. Tilley, H. J. Fan and M. Grätzel, Science, 2014, 345, 1593–1596.
184. L. Fang, L. You and J.-M. Liu, in Ferroelectric Materials for Energy Applications, 2018, pp. 265–309,  DOI:10.1002/9783527807505.ch9.
185. Z. Zhang, W. Wang, L. Wang and S. Sun, ACS Appl. Mater. Interfaces, 2012, 4, 593–597.
186. H. Razavi-Khosroshahi, K. Edalati, J. Wu, Y. Nakashima, M. Arita, Y. Ikoma, M. Sadakiyo, Y. Inagaki, A. Staykov and M. Yamauchi, J. Mater. Chem. A, 2017, 5, 20298–20303.
187. R. B. Marcelino and C. C. Amorim, Environ. Sci. Pollut. Res., 2019, 26, 4155–4170.
188. M. Kaneko and I. Okura, Photocatalysis: Science and Technology, Springer Berlin Heidelberg, 2002.
189. H. Wang, L. Zhang, Z. Chen, J. Hu, S. Li, Z. Wang, J. Liu and X. Wang, Chem. Soc. Rev., 2014, 43, 5234–5244.
190. S. J. Moniz, S. A. Shevlin, D. J. Martin, Z.-X. Guo and J. Tang, Energy Environ. Sci., 2015, 8, 731–759.
191. X. Wang and C. Li, J. Phys. Chem. C, 2018, 122, 21083–21096.
192. Y. Cui, J. Briscoe and S. Dunn, Chem. Mater., 2013, 25, 4215–4223.
193. M. Khan, M. Nadeem and H. Idriss, Surf. Sci. Rep., 2016, 71, 1–31.
194. W. Yang, B. Rodriguez, A. Gruverman and R. Nemanich, J. Phys.: Condens. Matter, 2005, 17, S1415.
195. P. M. Jones and S. Dunn, Nanotechnology, 2007, 18, 185702.
196. W. Mönch, Electronic Properties of Semiconductor Interfaces, Springer Science & Business Media, 2013.
197. A. Bhardwaj, N. V. Burbure, A. Gamalski and G. S. Rohrer, Chem. Mater., 2010, 22, 3527–3534.
198. D. Tiwari and S. Dunn, J. Mater. Sci., 2009, 44, 5063–5079.
199. S. V. Kalinin, D. A. Bonnell, T. Alvarez, X. Lei, Z. Hu, J. Ferris, Q. Zhang and S. Dunn, Nano Lett., 2002, 2, 589–593.
200. G. Nataf, M. Guennou, J. Kreisel, P. Hicher, R. Haumont, O. Aktas, E. Salje, L. Tortech, C. Mathieu and D. Martinotti, Phys. Rev. Mater., 2017, 1, 074410.
201. Y. Wang, M. Zhang, J. Liu, H. Zhang, F. Li, C. W. Tseng, B. Yang, G. Smith, J. Zhai and Z. Zhang, Adv. Energy Mater., 2020, 10, 2001802.
202. Y. Liu, S. Ye, H. Xie, J. Zhu, Q. Shi, N. Ta, R. Chen, Y. Gao, H. An and W. Nie, Adv. Mater., 2020, 32, 1906513.
203. E. K. Akdogan, C. J. Rawn, W. D. Porter, E. A. Payzant and A. Safari, J. Appl. Phys., 2005, 97, 084305.
204. M. Yashima, T. Hoshina, D. Ishimura, S. Kobayashi, W. Nakamura, T. Tsurumi and S. Wada, J. Appl. Phys., 2005, 98, 014313.
205. D. Arney, C. Hardy, B. Greve and P. A. Maggard, J. Photochem. Photobiol., A, 2010, 214, 54–60.
206. G. Li, S. Yan, Z. Wang, X. Wang, Z. Li, J. Ye and Z. Zou, Dalton Trans., 2009, 8519–8524.
207. G. Li, T. Kako, D. Wang, Z. Zou and J. Ye, Dalton Trans., 2009, 2423–2427.
208. W. Wang, J. Phys. Chem. Solids, 2011, 72, 1457–1461.
209. L. Cao, Z. Guo, J. Huang, C. Li, J. Fei, Q. Feng, P. Wen, Y. Sun and X. Kong, Mater. Lett., 2014, 137, 110–112.
210. Y. Lu, Q. Yu, F. Zhang, G. Li and W. Zhang, Appl. Phys. A, 2016, 122, 1–5.
211. B. Gao, D. Hu, C. Xiao, D. Li, B. Lin, Y. Chen and Y. Zheng, J. Phys. Chem. Solids, 2019, 135, 109083.
212. D. Wang, T. Kako and J. Ye, J. Phys. Chem. C, 2009, 113, 3785–3792.
213. G. Li, N. Yang, W. Wang and W. Zhang, Electrochim. Acta, 2010, 55, 7235–7239.
214. G. Li, Mater. Chem. Phys., 2010, 121, 42–46.
215. G. Li, T. Kako, D. Wang, Z. Zou and J. Ye, J. Solid State Chem., 2007, 180, 2845–2850.
216. C. Wang, J. Yan, X. Wu, Y. Song, G. Cai, H. Xu, J. Zhu and H. Li, Appl. Surf. Sci., 2013, 273, 159–166.
217. M. Yang, Y. Pu, W. Wang, J. Li, X. Guo, R. Shi and Y. Shi, J. Alloys Compd., 2019, 811, 151831.
218. Z. Yu, B. Zhan, B. Ge, Y. Zhu, Y. Dai, G. Zhou, F. Yu, P. Wang, B. Huang and J. Zhan, Appl. Surf. Sci., 2019, 488, 485–493.
219. G. Li, Y. Bai, W. Zhang and H. Zhang, Mater. Chem. Phys., 2013, 139, 1009–1013.
220. L. Yang, J. Liu, H. Chang and S. Tang, RSC Adv., 2015, 5, 59970–59975.
221. H. Shu, J. Xie, H. Xu, H. Li, Z. Gu, G. Sun and Y. Xu, J. Alloys Compd., 2010, 496, 633–637.

---