Atomistic insight into the dopant impacts at the garnet Li₇La₃Zr₂O₁₂ solid electrolyte grain boundaries

Abstract

The garnet-type Li₇La₃Zr₂O₁₂ (LLZO) as one of the most promising solid electrolytes (SEs) has attracted great research attention owing to its high compatibility with Li metal anodes. Doping with a supervalent cation is an effective strategy to stabilize cubic LLZO with desired high ion conductivity. The behaviour of dopants at the grain boundary (GB) (e.g. segregation) is expected to have a great influence on the properties of LLZO but is far from understood. Here we have performed first-principles calculations to reveal the atomic-scale impact of dopants at the GB of the LLZO SE. The results show that Al and Ga dopants at the GB are preferentially segregated at the 24d site of Li with three neighbouring Li-ions, and Nb and Ta dopants prefer to locate at the 5-coordinated and partially distorted 6-coordinated Zr sites at the GB. The segregation of a Nb-like dopant at the GB will improve Li-ion conductivity, while the GB with an Al-like dopant shows conductivity comparable to that of the undoped one and fragmentation of the Li-ion diffusion network. Moreover, the electronic state calculations indicate electron accumulation at the doped GBs, in contrast to the mitigation effect of the dopants on dendrite formation along LLZO GBs revealed by the calculation of Li interstitial formation energy. We also explored the potentially existing phases at the doped coarse GBs, and a series of products have been proposed. These comprehensive calculations provide valuable atomistic insights into the dopants at the GB in the LLZO SE and substantial knowledge of optimization of this material.

---

1. Introduction

Nowadays, energy storage devices are of great interest owing to their high demand in the utilization of renewable and environmentally friendly energy resources.¹ The Li-ion battery as one of the most important energy storage devices has been commercialized and extensively applied in portable devices and electric vehicles.^2,3 However, due to the flammability of organic liquid electrolytes, the safety issue of conventional Li-ion batteries is always a critical concern and has to be resolved urgently in the further development of batteries with higher energy density. To this end, all-solid-state batteries (ASSBs) have been developed as the next-generation batteries in terms of their improved safety and energy density.^4–6

In ASSBs, non-flammable solid electrolytes (SEs) are used to replace liquid electrolytes. Since the development over several decades, a number of SEs with superior ion conductivity comparable to that of liquid electrolytes have been synthesized.^7–10 Among them, garnet-type Li₇La₃Zr₂O₁₂ (LLZO) has attracted tremendous attention because of its high conductivity (10⁻³ to 10⁻⁴ S cm⁻¹), wide electrochemical stability window (∼6 eV), and compatibility with Li metal anodes.^9,11–15

There are two phases, tetragonal and cubic phases, existing in garnet-type LLZO. Especially, the tetragonal LLZO (t-LLZO) is an ordered phase with low ion conductivity (10⁻⁵ S cm⁻¹) and is stable at the ambient temperature.¹⁶ The cubic LLZO (c-LLZO) is a Li-disordered structure with desired high conductivity but stable under elevated temperature.⁹ The doping strategy with supervalent cations has been a mainstream method to reduce Li concentration thereby stabilizing the c-LLZO at the ambient temperature.^17–22 Moreover, it has been proved that doping with appropriate content is helpful for enhancing the ion conductivity.^23–25 For example, doping of Ga or La can increase the conductivity of LLZO to the magnitude of 10⁻³ S cm⁻¹.^26,27 Meanwhile, the elementary steps of Li-ion hopping have been revealed in Mo-doped LLZO using NMR.²⁸

Nowadays, a variety of metal elements are adopted as dopants.²⁹ Among them, four important dopants, Al, Ga, Nb and Ta, have been widely selected in the synthesis of LLZO.^18,20–22 Particularly for the Al dopant, there is a debate about its stable location site in LLZO. Part of studies based on ²⁷Al magic angle spinning (MAS) NMR measurement and density functional theory (DFT) calculation reported that Al occupies the 24d site of Li,^19,30 while some other studies utilizing similar approaches observed that Al can stay at another site (e.g. 96h site of Li).^18,31–33 Recently, Karasulu et al. have performed a comprehensive investigation and confirmed that the Al dopant only locates at the 24d site.³⁴ Similar to the Al dopant, Ga also prefers to locate at the 24d site of Li.^20,34–36 For Nb and Ta dopants, they usually occupy the Zr site coordinated with 6 O ions.^21,22

As most of the synthesized LLZO materials are polycrystalline phases, the grain boundary (GB) naturally plays an important role in determining the material's performance. It has been widely reported that the GB has a great impact on ion and electron conductivities and dendrite formation.^37–42 Meanwhile, the behaviour of a dopant (e.g. segregation) is usually affected by the GB. There are several studies finding the formation of Al-rich amorphous phases at the GB in Al-doped LLZO.^21,43–46 Moreover, Brugge et al. have observed abundance of Al and Ga in the GB regions, indicating the segregation of these dopants.⁴⁷ Regarding the segregation preferences of Nb and Ta dopants at the GB, to the best of our knowledge, there is no report related to them. Nevertheless, a recent study has reported a strong tendency of the Nb dopant to diffuse toward the LLZO/Li metal interface.²² This implies that Nb can show segregation behaviour at the LLZO/Li interface, and may be segregated at the GB. Overall, until now, there is still a lack of studies related to dopants at the GB, limiting the understanding of their further influence on the performance of the LLZO SE.

In this work, we have performed comprehensive investigations on four representative dopants, Al, Ga, Nb and Ta, at the GB of LLZO based on first-principles DFT simulations. The energetically stable sites for dopants at the GB have been determined from calculated segregation energies. Molecular dynamics (MD) simulation has been carried out to reveal the influences of dopants on the ion conductivity at the GB. The dopant effects on dendrite formation along the GB have also been discussed based on the calculated Li interstitial formation energies and electronic properties. We have also investigated the potentially existing phase at the doped coarse GB by conducting thermodynamics calculation. The current work provides a valuable atomistic insight into the dopants at the GB and their further impact on the LLZO SE.

2. Method

The c-LLZO bulk structure has been used in this study, and the previously proposed favourable structure with the lattice parameter a = 13.03 Å, obtained from a number of candidates, has been selected.⁴⁸ For the undoped GBs of LLZO, two energetically stable GB models, Σ1(110) and Σ3(112) GBs (Fig. 1) searched from a systematically high-throughput calculation in our recent work,⁴¹ have been selected. More details about the calculation scheme can be found in ref. ⁴¹. Here the Σ1(110) and Σ3(112) GB models contain 384 atoms with the atom composition of Li₁₁₂La₄₈Zr₃₂O₁₉₂, and 576 atoms with the atom composition of Li₁₆₈La₇₂Zr₄₈O₂₈₈, respectively. In order to maintain charge neutrality, three and one Li-ions are removed simultaneously in the doping of one Al (Ga) and Nb (Ta) atoms, respectively. In the geometrical optimization of the doped bulk and GB models, the lattice parameters are fixed.

Fig. 1 Atomistic structures of (a) LLZO bulk, and (b) Σ1(110) and (c) Σ3(112) GBs. The green, red, blue and orange spheres represent the Li, O, Zr and La ions, respectively. The dark blue polyhedra represent the ZrO₆ units. Particularly in (c), the light blue polyhedra indicate the ZrO₅ units. In (b) and (c), the grey areas indicate the regions of the GB. In each figure, selected Li doping sites are marked and the enlarged local configurations are shown in the panels with black borders, in which the pink spheres represent the selected sites and the nearest neighbouring Li ions are connected with dashed lines.

In order to examine the stability of the dopant site, the segregation energy (E_seg) is defined as

E_seg = (E^doped_GB − E^undoped_GB) − (E^doped_bulk − E^undoped_bulk), (1)

where E^doped_GB and E^undoped_GB are the calculated total energies of the doped and undoped GB models, respectively. E^doped_bulk and E^undoped_bulk represent the total energies of the unit cells of the doped and undoped bulks, respectively.

The defect formation energies (E_f) for Li vacancies and interstitial were calculated using

where E_total(X) and E_pristine are the total energies of the simulation models with and without defect X, respectively. n_i is the number of removed (n_i < 0) or added (n_i > 0) Li in the model. μ_Li(metal) is the chemical potential of Li in the BCC-type metal phase.

The reaction energy (E_r) is calculated in the investigation of phase segregation at the doped GB. The E_r is defined as

E_r = ∑E_product − ∑E_reactant, (3)

where E_product and E_reactant represent the total energies of the product and reactant. Here all of the crystal structures of ternary oxides were obtained from the Material Project database.⁴⁹

The DFT method was employed within the generalized gradient approximation of the Perdew, Burke, and Ernzernhof functional as implemented in the Vienna ab initio simulation package (VASP).⁵⁰ Electron–ion interactions were described using projector-augmented wave pseudopotentials.⁵¹ A plane-wave kinetic-energy cutoff of 520 eV and a k-spacing of 0.25 Å⁻¹ in reciprocal space were used to achieve converged results. The partial (band decomposed) charge density was calculated by analysing the total charge density using VASP software. First-principles molecular dynamics (FPMD) simulations were performed in the canonical ensemble (NVT) using the Nosé-Hoover thermostat⁵² at 700, 1000 and 1200 K with a timestep of 1 fs. In the MD simulations, in order to trade off the computational cost and accuracy, the kinetic-energy cutoff was set to 450 eV, and the only Γ point is used in the k-point sampling scheme. For each MD simulation, the total duration is set to 55 ps. Based on the energy history profiles depicted in Fig. S1,† all of the simulations reach the equilibrium states after 20 ps. Therefore, the data of the last 35 ps are considered in the subsequent analysis of ion diffusion. The detailed methods for calculating time averaged mean squared displacement (MSD), diffusion coefficient, conductivity, activation energy and the van Hove space–time correlation function are described in the ESI.† All of the structures are visualized using VESTA software.⁵³

3. Results and discussion

3.1 Site preferences for dopants in LLZO bulk and at the GBs

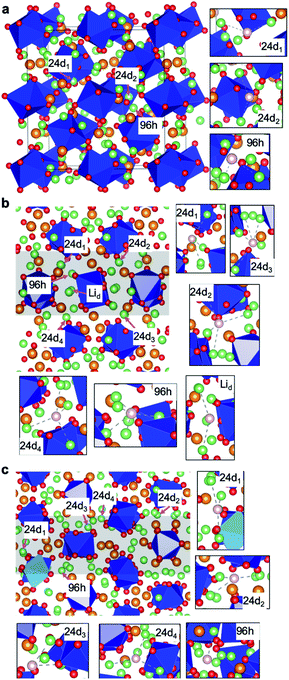
Four typical dopants, Al, Ga, Nb and Ta, were considered in this work. Note that the Al and Ga dopants locate at the Li site, and the Nb and Ta dopants stay at the Zr site. First, we investigated the site preference of the Al dopant in bulk. Fig. 1a shows the atomistic structure of LLZO bulk, which contains two types of Wyckoff positions for Li-ions: 24d and 96h sites. The Li(24d) and Li(96h) sites are coordinated with 4 and 6 neighbouring O, forming the LiO₄ tetrahedron and LiO₆ octahedron, respectively. Particularly for the Li(24d) site, we also considered its deviation in the polyhedral coordination, which has a non-negligible effect on the NMR spectra.³⁴ There are two typical Li(24d) sites with, respectively, 3 and 4 nearest neighbouring Li(96h), which are denoted as 3-NN and 4-NN Li(24d), respectively. These sites are the candidates for the Al dopant. Note that a rare Li(24d) site without the nearest neighbouring Li(96h) (only one in the cell) has been found in the cell as well. This site can be regarded as a special case and was not considered as the general site in the current study.

It is noteworthy that two surrounding Li-ions (in total three) are needed to be removed when one Al dopant is introduced to maintain charge neutrality. Therefore, for each dopant site, we sampled a series of structures with different removed surrounding Li sites. The calculated results show that removing the nearest neighbouring Li-ions (solid points in Fig. 2a) is energetically preferable. Furthermore, the calculated energies indicate that the Al dopant prefers to locate at the Li(24d) site with energies remarkably lower than that at the Li(96h) site. This result is in good agreement with the former NMR measurement.^19,30,34 We have drawn the local configurations of 24d₁ and 96h sites in Fig. S2† to understand this result. We found that the nearest distances between 24d₁ and Zr, and between 96h and Zr are 3.44 and 2.87 Å, respectively. The 96h is closer to the Zr site, resulting in higher electrostatic repulsion interaction, which may contribute to the unfavourable doping stability compared to that of the 24d site. Besides, we found that the lowest-energy structure with the Al dopant at the 3-NN Li(24d) site (24d₁ in Fig. 2a) is slightly more stable by 25.3 meV per cell than that at the 4-NN Li(24d) site (24d₂ in Fig. 2a), which may be attributed to the weaker electrostatic repulsion interaction between neighbouring Li-ions and the Al dopant at the 3-NN Li(24d) site.

Fig. 2 (a) Energy distributions of bulk structures with Al dopants at the different sites shown in Fig. 1 and various surrounding Li sites. (b and c) Calculated segregation energies for Al located at the different sites with various surrounding Li sites at the (b) Σ1(110) and (c) Σ3(112) GBs. (d) Energy distributions of bulk structures with Ga dopants at the different sites and various surrounding Li sites. (e and f) Calculated segregation energies for Ga located at the different sites with various surrounding Li sites at the (e) Σ1(110) and (f) Σ3(112) GBs. In each figure, the blue and black points refer to the 3-NN and 4-NN Li(24d) sites, respectively. Particularly in (a) and (d), the solid points show that the nearest neighbouring Li-ions are removed, and the open circles indicate that the removed Li-ions are relatively far from the dopant.

Taking the stable Al-doped LLZO bulk as the reference, we have calculated the segregation energies (E_seg) of the Al dopant at the Σ1(110) and Σ3(112) GBs, whose structures are depicted in Fig. 1b and c, respectively. The calculated E_seg values are plotted in Fig. 2b and c, respectively. Similar to bulk, the 3-NN and 4-NN Li(24d), and Li(96h) are adopted as the dopant sites. The calculated E_seg values show a similar result to that of bulk, where the Al dopant preferentially occupied at the Li(24d) site rather than at the Li(96h) site. Here we also considered a representative distorted site at the Σ1(110) GB, which is formed due to structure deformation. The calculated E_seg for the Al dopant located at this site is significantly high, proving to be unfavourable for dopant occupation. Interestingly, we found that all of the energetically stable structures with the Al dopant at the 3-NN Li(24d) sites (blue points) in the Σ3(112) GBs show obviously negative E_seg values (Fig. 2c). The lowest E_seg is −0.31 eV. Although the Al at the 4-NN Li(24d) sites (black points) shows remarkably higher E_seg, one structure at the Σ1(110) GB (24d₁ in Fig. 2b) has a slightly negative E_seg value. These results clearly indicate that the Al dopant can be segregated at the 3-NN 24d site at the LLZO GB.

For the Ga dopant, the calculated site preferences in the bulk and at the GBs (Fig. 2d–f) are quite analogous with those of the Al dopant. Nevertheless, the E_seg values at both GBs (Fig. 2e and f) are totally decreased compared to that of the Al dopant. The lowest E_seg for the Ga dopant at the Σ3(112) GB is further decreased to −0.37 eV. To understand this decrease in the E_seg of the Ga dopant, we have compared the ionic radii among Li, Al and Ga. The crystal ionic radius of 4-coordinated Ga³⁺ is 0.61 Å, which is closer to the ionic radius of 4-coordinated Li⁺ (0.73 Å) than to that of 4-coordinated Al³⁺ (0.53 Å).⁵⁴ This smaller deviation in ionic radius between Ga and Li ions may result in the slightly lower E_seg at the GB.

We then investigated the preferential site for the Nb dopant. In the doping of one Nb, one Li-ion is simultaneously removed to maintain charge neutrality. Fig. 3a depicts the calculated energies of Nb-doped LLZO bulks with different removed surrounding Li sites. Generally, the structure with the removed Li(96h) site shows a lower energy that that with the Li(24d) vacancy. Besides, although the doped structure with a nearest neighbouring Li(96h) vacancy has the lowest energy, the deviation in energy for the structures with different removed Li(96h) sites is not significant. The calculated E_seg values for the Nb dopant in different sites at the Σ1(110) and Σ3(112) GBs are shown in Fig. 3b and c. We can see that all of the selected dopant sites give rise to positive E_seg values at the Σ1(110) GB, indicating no preference of segregation of Nb at this GB. Instead, we observed negative E_seg for the dopant at the 5-coordinated Zr (Zr_5c in Fig. 3c) (the lowest value is −0.32 eV) and some 6-coordinated Zr sites (Zr_6c(2) in Fig. 3c) (the lowest value is −0.17 eV) at the Σ3(112) GB, indicating the segregation behaviour at this GB.

Fig. 3 (a) Energy distribution of the Nb-doped bulk structure with different removed Li sites. (b and c) Calculated segregation energies for Nb located at the different sites at the (b) Σ1(110) and (c) Σ3(112) GBs. (d) Energy distribution of the Ta-doped bulk structure with different removed Li sites. (e and f) Calculated segregation energies for Ta located at the different sites at the (e) Σ1(110) and (f) Σ3(112) GBs. Particularly in (a) and (d), the black and red points indicate the removed Li(24d) and Li(96h) sites, respectively. The solid points show that the nearest neighbouring Li-ions are removed, and the open circles indicate that the removed ions are relatively far from the dopant.

To understand why Nb-doped Σ3(112) GB structures with dopants at the Zr_5c and Zr_6c(2) have lower E_seg, we calculated the related vacancy formation energy [E_f(V_Li)] at this GB, as shown in Fig. S3† together with the corresponding E_seg. We found that the site with a small E_f(V_Li) value also shows a low E_seg. As is known that one Li (Li vacancy) is removed (created) when doping one Nb in LLZO, the schematic reaction for this process can be written as

Nb + LLZO → Nb-doped LLZO + V_Li.

If E_f(V_Li) at the GB is lower than that of the bulk, the total energy in the right side of this reaction is decreased. In this sense, the feasibility of doping at the GB becomes easier than that in the bulk, indicating the negative E_seg value, as shown in Fig. S3.† These results indeed demonstrate that the lower E_f(V_Li) is one of the main reasons for the segregation of the Nb dopant at the Σ3(112) GB.

For the Ta dopant, the calculated energy distribution for bulk structures and the E_seg at both GBs are shown in Fig. 3d–f, respectively, which are evidently similar to the results for the Nb dopant. Particularly, we found that the E_seg of the Ta dopant at the Zr_5c is slightly higher than that of the Nb dopant. The lowest E_seg value is from −0.32 eV for the Nb dopant to −0.11 eV for the Ta dopant. Here we have checked the ionic radii for these two dopants and found that the 6-coordinated Nb⁵⁺ and Ta⁵⁺ possess the same value (0.78 Å), which is less than that of 6-coordinated Zr⁴⁺ (0.86 Å).⁵⁴ This increase in E_seg of the Ta dopant should be attributed to other reasons. For example, the lower electronegativity of Ta (1.5 on the Pauling scale) than that of Nb (1.6 on the Pauling scale) may induce weaker electrostatic interaction between Ta and O, leading to the higher E_seg value.

The partial densities of states (PDOSs) of undoped and energetically most stable doped bulks and GB models have been calculated and depicted in Fig. S4.† Note that compared to the Σ1(110) GB, the dopants at the Σ3(112) GB show an obvious nature of segregation. Therefore, we focused on the Σ3(112) GB here. For the Al, Ga-doped LLZO bulks (Fig. S4b and c†), their valence band maxima (VBMs) and conduction band minima (CBMs) do not show an apparent difference from those of the undoped bulk (Fig. S4a†). However, in the Nb-doped bulk, the states of Nb are located in the region below the VBM, evidently narrowing the band gap (Fig. S4d†). This indicates the potential preferential reduction of the Nb dopant, as already observed in our previous investigation on the Nb-doped LLZO/Li metal interface.⁴⁸ Unlike the Nb-doped bulk, the states of the Ta dopant stay in the conduction band and contribute to the CBM (Fig. S4e†). Compared to the bulk, the undoped Σ3(112) GB model has a slightly reduced band gap (Fig. S4f†).⁴¹ For the doped GB models, the calculated PDOSs (Fig. S4g–j†) show similar results except for the Ta dopant, whose states are marginally downshifted from the valence band (Fig. S4j†).

3.2 Ion diffusions at the doped GBs

Extensive previous studies have reported that doping with appropriate concentration can effectively improve Li-ion conductivity in LLZO.^43,55–57 Therefore, we have explored the dopant effect on Li-ion diffusion at the GB of LLZO using FPMD simulations. Here we selected the Al and Nb-doped Σ3(112) GB models as the representative GBs with Li and Zr-site substitutions, respectively. Considering the site preference of dopants, 6 energetically stable Li(24d) sites and 4 Zr sites around the Σ3(112) GB were selected as the doping sites of Al and Nb, respectively, and the corresponding chemical compositions of the models are Li_6.25Al_0.25La₃Zr₂O₁₂ and Li_6.833La₃Zr_1.833Nb_0.167O₁₂, respectively. The diffusion coefficients calculated from the mean squared displacements (Fig. S5†) of undoped and doped Σ3(112) GB models are plotted in Fig. 4a. The calculated activation energies (E_a) and extrapolated Li-ion conductivities at 300 K [σ(300 K)] are tabulated in Table 1. Note that the obtained E_a for the undoped Σ3(112) GB model (0.28 eV) is higher than the calculated value in our previous work (0.20 eV).⁴¹ Consequently, the extrapolated Li-ion conductivity at 300 K [σ(300 K)] of the undoped GB model (4.30 × 10⁻⁴ S cm⁻¹) is reduced compared to the previously calculated σ at 298.15 K (4.73 × 10⁻³ S cm⁻¹).⁴¹ This is because of the different adopted densities of the k-grid in the calculations. As mentioned in the Method section, the Γ point is used in the current simulation in order to reasonably reduce the computational cost. Note that compared to the experimental observations, the previous calculation more or less underestimated the E_a and overestimated σ. Therefore, the current results decrease the discrepancies between these theoretical and experimental values.

Fig. 4 (a) Arrhenius plots of diffusion coefficients in undoped, and Al and Nb doped Σ3(112) GB models of LLZO. (b–d) Partial Li-ion trajectory densities accumulated from 20 to 55 ps in the FPMD simulations at 1000 K in (b) undoped, (c) Al-doped and (d) Nb-doped Σ3(112) GB models. The dashed circle indicates the disconnection of the trajectory density. The colour scheme for Li, La, Zr and O is the same as in Fig. 1. The light blue spheres in (c) and (d) represent the Al and Nb dopants, respectively, which are marked by the arrows as well.

Table 1 Calculated activation energies (E_a) and extrapolated Li-ion conductivities at 300 K [σ(300 K)] for undoped, and Al and Nb-doped Σ3(112) GB models of LLZO

	E a (eV)	σ(300 K) (S cm^−1)
Undoped	0.28	4.30 × 10^−4
Al-doped	0.27	3.85 × 10^−4
Nb-doped	0.23	2.66 × 10^−3

---

Fig. 4a shows that the Nb-doped GB model exhibits pronouncedly faster Li-ion diffusion, and the diffusivities in undoped and Al-doped GB models are close to each other. Accordingly, the achieved E_a and σ(300 K) of the Al-doped GB model are comparable to those of the undoped one, while the Nb-doped GB model shows evidently smaller E_a and increased σ(300 K). These results indicate that the Nb dopant can improve Li-ion conductivity around the GB, while the Al dopant has no obvious contribution to the improvement of conductivity at the GB. For an in-depth understanding of this finding, we have plotted the Li diffusion trajectories in the MD simulations in Fig. 4b–d. Comparing the trajectories in the undoped (Fig. 4b) and Nb-doped (Fig. 4d) GB models, we observed more disconnections in the diffusion network in the undoped GB models, which may imply relatively slow diffusion. We speculated that introducing the Nb dopant can decrease Li concentration, thereby creating more available Li vacancies, which is beneficial for Li diffusion. However, in the Al-doped GB model, we found that the Al located at the Li(24d) site shows immobile behaviour and Li transport in the vicinity of Al is blocked (Fig. 4c), leading to a lower diffusivity than that of the Nb-doped GB model. This fragmentation of the Li-ion diffusion network has been seen in Ga-doped LLZO bulk in previous classical MD simulation as well.¹⁷

Besides, we have calculated the distinct part of the van Hove space–time correlation function [G_d(t,r)] shown in Fig. S6† to understand the diffusion correlation of Li-ions in the investigated GB models, which has been widely discussed in previous studies on SE bulks.^17,58G_d(t,r) accounts for the average probability of finding one Li-ion (i) at a distance r from a site that was formerly occupied by another Li-ion (j) at time t. The build-up of G_d(t,r) around r = 0 with the increase of t indicates that more and more Li-ions occupy the other Li-ion sites, showing highly concerted diffusion behaviour in the investigated GB models.

It should be noteworthy that the total ion conductivity of the LLZO polycrystalline material is contributed to by both the bulk and GB. Therefore, the obtained GB conductivities should have an effect on the total conductivity instead of governing it. In reality, a series of experiments^26,33,45,56 have observed quite high conductivities in the Al and Ga-doped LLZO. We found that the conductivities in those doped LLZO are strongly dependent on the concentrations of Li and the dopant. The optimal Li and dopant compositions are about 6.04–6.55, and 0.15–0.32, respectively, from previous reports.^26,33,45,56 The conductivity will decrease when the Li (dopant) composition is lower (higher) than the optimal value. In the currently adopted Al-doped GB model, although the Li and dopant compositions (6.25 and 0.25, respectively) are in the ranges of optimal compositions, the Al dopants are segregated in the GB regions in the model, resulting in a much higher dopant concentration at the GB than the optimal value. This serves as a possible reason for the low Li-ion conductivity in the Al-doped GB model. To further understand this issue, some other approaches will be needed to be considered in future. For example, a recently proposed approach⁵⁹ which combines the methods of CAVD and band valence site energy is a promising way by analysing the specific ion transport path using much less computational cost than that for FPMD simulation.

Moreover, the Li diffusion behaviour at the GB should be influenced by many factors. For example, the reported conductivity of Ga-doped LLZO is usually higher than that of Al-doped LLZO.^{26,33,45,56,60} This may have led to the better densification and smaller grains in Ga-doped LLZO.³³ The current results provide the knowledge about the LLZO GB from a microscopic viewpoint. We expect that the obtained calculations combined with other simulations and observations can provide a comprehensive understanding of ion conductivity in doped LLZO.

3.3 Li interstitial stabilities at the doped GBs

To understand the dopant effect on Li dendrite formation at the LLZO GB during cycling, we have calculated the formation energy of Li interstitial [E_f(Li_i)] at the doped GB. According to the results of segregation energy, we found that Ga (Ta) dopants show almost the same nature as Al (Nb) dopants. Therefore, Al and Nb are selected as the typical dopants in this part. Here the energetically most stable Al and Nb-doped Σ3(112) GB models are adopted.

The calculated results depicted in Fig. 5a show that compared to the undoped GB, the E_f(Li_i) at the Al and Nb-doped GBs is slightly increased, implying that the dendrite formation is relatively suppressed at the doped GBs. On the other hand, electronic conductivity is also thought to have a significant contribution to dendrite formation.^40,42,61 Therefore, we calculated the partial densities of states (PDOSs) of doped GBs with one low-energy Li_i (Fig. 5b and c). Our previous work has found that the undoped Σ3(112) GB shows the capability of capturing the excess electron from Li_i.⁴¹ For the Al-doped GB (Fig. 5b), the dopant states have a negligible contribution to the mid-gap states as reflected from its almost identical PDOS at the VBM to that of the undoped GB (Fig. S7†). However, in the Nb-doped GB model, we observed that the interstitial electron is localized around the dopant at the Zr_5c site, leading to the reduction of Nb, which is similar to that at the undoped GB, where the excess electron prefers to locate at the same Zr site.⁴¹ As discussed in our recent study⁴¹ and other experimental work⁴² on the undoped LLZO GB, this preferential accumulation of electrons can lead to the reduction of the GB and possibly high electronic conductivity, which has been proved as one of the key factors of dendrite growth.⁶¹ Therefore, based on these calculations, we concluded that doping can increase the formation energy of Li interstitial, which may be helpful for suppressing dendrite formation, but is still not able to prevent electron transport at the GB, which also contributes to dendrite growth along the GB.

Fig. 5 (a) Calculated E_f(Li_i) at the undoped and Al and Nb-doped Σ3(112) GBs. (b and c) Calculated PDOSs of (b) Al and (c) Nb-doped Σ3(112) GB models with one Li_i site. Here the dashed lines indicate the Fermi levels. The right panels are the enlarged figures around the Fermi level.

3.4 Phase segregations at the doped coarse GBs

It is noteworthy that, besides the well-contacted GBs, there is a large proportion of coarse GBs within poor-contacted areas and pores existing in the synthesized LLZO polycrystalline materials. A number of experimental studies have reported the presence of the Li–Al–O phase at the GB in Al-doped LLZO.^27,45,62 Therefore, examination of the secondary phases at the doped coarse GB is quite necessary. Here we have calculated the E_r for all of the possible reactions for doped LLZO decomposing into pristine LLZO and the corresponding ternary oxides. The reactions with relatively low and high E_r are tabulated in Tables 2 and S1,† respectively.

Table 2 Calculated reaction energies (E_r) for doped LLZO decomposing into pristine LLZO and the corresponding ternary oxides

		E react (eV)
Al-doped	Li53AlLa24Zr16O96 + 4Li2O → Li56La24Zr16O96 + Li5AlO4	−1.12
	Li53AlLa24Zr16O96 + 2Li2O → Li56La24Zr16O96 + LiAlO2	−0.86
Ga-doped	Li53GaLa24Zr16O96 + 4Li2O → Li56La24Zr16O96 + Li5GaO4	−1.21
	Li53GaLa24Zr16O96 + 2Li2O → Li56La24Zr16O96 + LiGaO2	−0.93
Nb-doped	Li55La24Zr15NbO96 + 2.5Li2O + ZrO2 → Li56La24Zr16O96 + 0.5Li8Nb2O9	−1.08
	Li55La24Zr15NbO96 + 2Li2O + ZrO2 → Li56La24Zr16O96 + Li3NbO4	−0.92
Ta-doped	Li55La24Zr15TaO96 + 3Li2O + ZrO2 → Li56La24Zr16O96 + Li5TaO5	−1.05
	Li55La24Zr15TaO96 + 2Li2O + ZrO2 → Li56La24Zr16O96 + Li3TaO4	−0.81

---

From the calculated results, we found that, for Al-doped LLZO, the decomposition reaction from this phase to pristine LLZO and Li₅AlO₄ has the lowest E_r. This result is consistent with the previous calculation on the decomposition of this material.⁶³ It is highly possible for this decomposed product to be segregated at the coarse GB, acting as the secondary phase. Meanwhile, some other phases, such as LiAlO₂ and La₄Al₂O₉, may exist at the GB due to their relatively low E_r. In Ga-doped LLZO, the potentially existing products at the GB are similar to those in Al-doped LLZO. Li₅GaO₄ is the main candidate and other phases (LiGaO₂, La₄Ga₂O₉, etc.) possibly emerge. Moreover, we found that the lowest E_r for the decomposition reaction of Ga-doped LLZO is slightly lower than that of Al-doped LLZO, indicating a higher tendency of segregation at the GB in Ga-doped LLZO, which is consistent with the obtained results of E_seg at the well-contacted GB.

In Nb-doped LLZO, the calculated E_r shows that the secondary phases (Li₈Nb₂O₉, Li₃NbO₄, etc.) can be presented at the GB. Similarly, Li₅TaO₅, Li₃TaO₄ and La₃TaO₇ may emerge at the GB in Ta-doped LLZO. Note that Ta-doped LLZO shows slightly higher E_r than Nb-doped LLZO, which is in good agreement with the results achieved from E_seg at the well-contacted GB. These results demonstrate that all of the investigated doped LLZO can exhibit segregations of ternary oxides at the coarse GBs.

4. Conclusions

We have performed systematic investigations on the dopants around the GBs in the LLZO SE by means of a first principles method. The results of site preferences of dopants show that Al and Ga are preferentially segregated at the Li(24d) site with three nearest neighbouring Li at the GB, and Nb and Ta can be segregated at the 5-coordinated and partially distorted 6-coordinated Zr sites at the GB. The FPMD simulations indicate that the segregation of the Nb-like dopant at the GB shows improved Li-ion conductivity, while doping Al-like atoms at the GB results in a conductivity comparable to that of the undoped one and the fragmentation of the Li-ion diffusion network. We also explored the dopant influence on Li dendrite formation at the GB by calculating the Li interstitial formation energy and found that introducing the dopants can suppress Li accumulation at the GB, but can't mitigate the potentially high electron conductivity at the GB which plays an important role in dendrite growth. Furthermore, we investigated the possible existing secondary phases at the doped coarse GBs, and a series of segregation products have been proposed for each dopant by calculating the decomposition reaction energy. The current results provide substantial knowledge about the dopant at the LLZO GB and pave the way towards a high-performance LLZO SE by eliminating the adverse effects originating from the GB.

Author contributions

B. G. and Y. T. conceived the study with the help of R. J. Calculations were performed by B. G. Contributions were made by Y. T. and R. J. in relation to the analysis and discussion of the results. The manuscript was written by B. G. with input/comments/feedback from other authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported in part by JSPS KAKENHI grant numbers JP19H05815 and JP21K14729, and by MEXT as “Program for Promoting Research on the Supercomputer Fugaku” grant number JPMXP1020200301, Elements Strategy Initiative grant number JPMXP0112101003, and Data Creation and Utilization Type Material Research and Development Project grant number JPMXP1121467561 and Materials Processing Science project (“Materealize”) grant number JPMXP0219207397, as well as by JST ALCA-SPRING grant number JPMJAL1301 and COI-NEXT grant number JPMJPF2016. The calculations were performed on the supercomputers at NIMS (Numerical Materials Simulator), Hokkaido University, and the supercomputer Fugaku at the RIKEN through the HPCI System Research Project (project ID: hp210173).

References

1. T. M. Gür, Energy Environ. Sci., 2018, 11, 2696–2767.
2. M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657.
3. J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176.
4. T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Nat. Mater., 2019, 18, 1278–1291.
5. Y. Tian, T. Shi, W. D. Richards, J. Li, J. Chul Kim, S.-H. Bo and G. Ceder, Energy Environ. Sci., 2017, 10, 1150–1166.
6. B. Gao, R. Jalem, Y. Ma and Y. Tateyama, Chem. Mater., 2020, 32, 85–96.
7. N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686.
8. Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030.
9. R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778–7781.
10. Z. Liu, W. Fu, E. A. Payzant, X. Yu, Z. Wu, N. J. Dudney, J. Kiggans, K. Hong, A. J. Rondinone and C. Liang, J. Am. Chem. Soc., 2013, 135, 975–978.
11. L. Xu, J. Li, W. Deng, H. Shuai, S. Li, Z. Xu, J. Li, H. Hou, H. Peng, G. Zou and X. Ji, Adv. Energy Mater., 2021, 11, 2000648.
12. T. Thompson, S. Yu, L. Williams, R. D. Schmidt, R. Garcia-Mendez, J. Wolfenstine, J. L. Allen, E. Kioupakis, D. J. Siegel and J. Sakamoto, ACS Energy Lett., 2017, 2, 462–468.
13. T. Krauskopf, H. Hartmann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2019, 11, 14463–14477.
14. F. Han, Y. Zhu, X. He, Y. Mo and C. Wang, Adv. Energy Mater., 2016, 6, 1501590.
15. X. Han, Y. Gong, K. Fu, X. He, G. T. Hitz, J. Dai, A. Pearse, B. Liu, H. Wang, G. Rubloff, Y. Mo, V. Thangadurai, E. D. Wachsman and L. Hu, Nat. Mater., 2017, 16, 572–579.
16. J. Wolfenstine, E. Rangasamy, J. L. Allen and J. Sakamoto, J. Power Sources, 2012, 208, 193–196.
17. R. Jalem, M. J. D. Rushton, W. Manalastas, M. Nakayama, T. Kasuga, J. A. Kilner and R. W. Grimes, Chem. Mater., 2015, 27, 2821–2831.
18. C. A. Geiger, E. Alekseev, B. Lazic, M. Fisch, T. Armbruster, R. Langner, M. Fechtelkord, N. Kim, T. Pettke and W. Weppner, Inorg. Chem., 2011, 50, 1089–1097.
19. H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg, A. Lotnyk, V. Duppel, L. Kienle and J. Janek, Phys. Chem. Chem. Phys., 2011, 13, 19378.
20. M. A. Howard, O. Clemens, E. Kendrick, K. S. Knight, D. C. Apperley, P. A. Anderson and P. R. Slater, Dalton Trans., 2012, 41, 12048–12053.
21. Y. Ren, Y. Shen, Y. Lin and C.-W. Nan, Electrochem. Commun., 2015, 57, 27–30.
22. Y. Zhu, J. G. Connell, S. Tepavcevic, P. Zapol, R. Garcia-Mendez, N. J. Taylor, J. Sakamoto, B. J. Ingram, L. A. Curtiss, J. W. Freeland, D. D. Fong and N. M. Markovic, Adv. Energy Mater., 2019, 9, 1803440.
23. L. J. Miara, S. P. Ong, Y. Mo, W. D. Richards, Y. Park, J.-M. Lee, H. S. Lee and G. Ceder, Chem. Mater., 2013, 25, 3048–3055.
24. Z. Hu, H. Liu, H. Ruan, R. Hu, Y. Su and L. Zhang, Ceram. Int., 2016, 42, 12156–12160.
25. N. Janani, S. Ramakumar, S. Kannan and R. Murugan, J. Am. Ceram. Soc., 2015, 98, 2039–2046.
26. S. Qin, X. Zhu, Y. Jiang, M. Ling, Z. Hu and J. Zhu, Appl. Phys. Lett., 2018, 112, 113901.
27. H. Xie, J. A. Alonso, Y. Li, M. T. Fernández-Díaz and J. B. Goodenough, Chem. Mater., 2011, 23, 3587–3589.
28. P. Bottke, D. Rettenwander, W. Schmidt, G. Amthauer and M. Wilkening, Chem. Mater., 2015, 27, 6571–6582.
29. A. J. Samson, K. Hofstetter, S. Bag and V. Thangadurai, Energy Environ. Sci., 2019, 12, 2957–2975.
30. A. Moradabadi and P. Kaghazchi, Solid State Ionics, 2019, 338, 74–79.
31. A. Düvel, A. Kuhn, L. Robben, M. Wilkening and P. Heitjans, J. Phys. Chem. C, 2012, 116, 15192–15202.
32. A. A. Hubaud, D. J. Schroeder, B. Key, B. J. Ingram, F. Dogan and J. T. Vaughey, J. Mater. Chem. A, 2013, 1, 8813–8818.
33. D. Rettenwander, P. Blaha, R. Laskowski, K. Schwarz, P. Bottke, M. Wilkening, C. A. Geiger and G. Amthauer, Chem. Mater., 2014, 26, 2617–2623.
34. B. Karasulu, S. P. Emge, M. F. Groh, C. P. Grey and A. J. Morris, J. Am. Chem. Soc., 2020, 142, 3132–3148.
35. C. Bernuy-Lopez, W. Manalastas, J. M. Lopez del Amo, A. Aguadero, F. Aguesse and J. A. Kilner, Chem. Mater., 2014, 26, 3610–3617.
36. L. Buannic, B. Orayech, J.-M. López Del Amo, J. Carrasco, N. A. Katcho, F. Aguesse, W. Manalastas, W. Zhang, J. Kilner and A. Llordés, Chem. Mater., 2017, 29, 1769–1778.
37. I. N. David, T. Thompson, J. Wolfenstine, J. L. Allen and J. Sakamoto, J. Am. Ceram. Soc., 2015, 98, 1209–1214.
38. T. Thompson, A. Sharafi, M. D. Johannes, A. Huq, J. L. Allen, J. Wolfenstine and J. Sakamoto, Adv. Energy Mater., 2015, 5, 1500096.
39. H.-K. Tian, Z. Liu, Y. Ji, L.-Q. Chen and Y. Qi, Chem. Mater., 2019, 31, 7351–7359.
40. Y. Song, L. Yang, W. Zhao, Z. Wang, Y. Zhao, Z. Wang, Q. Zhao, H. Liu and F. Pan, Adv. Energy Mater., 2019, 9, 1900671.
41. B. Gao, R. Jalem, H.-K. Tian and Y. Tateyama, Adv. Energy Mater., 2021, 12, 2102151.
42. X. Liu, R. Garcia-Mendez, A. R. Lupini, Y. Cheng, Z. D. Hood, F. Han, A. Sharafi, J. C. Idrobo, N. J. Dudney, C. Wang, C. Ma, J. Sakamoto and M. Chi, Nat. Mater., 2021, 20, 1485–1490.
43. Y. Li, J.-T. Han, C.-A. Wang, H. Xie and J. B. Goodenough, J. Mater. Chem., 2012, 22, 15357.
44. Y. Ren, H. Deng, R. Chen, Y. Shen, Y. Lin and C.-W. Nan, J. Eur. Ceram. Soc., 2015, 35, 561–572.
45. L. Zhuang, X. Huang, Y. Lu, J. Tang, Y. Zhou, X. Ao, Y. Yang and B. Tian, Ceram. Int., 2021, 47, 22768–22775.
46. Y. Wang, P. Yan, J. Xiao, X. Lu, J.-G. Zhang and V. L. Sprenkle, Solid State Ionics, 2016, 294, 108–115.
47. R. H. Brugge, F. M. Pesci, A. Cavallaro, C. Sole, M. A. Isaacs, G. Kerherve, R. S. Weatherup and A. Aguadero, J. Mater. Chem. A, 2020, 8, 14265–14276.
48. B. Gao, R. Jalem and Y. Tateyama, ACS Appl. Mater. Interfaces, 2020, 12, 16350–16358.
49. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
50. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
51. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
52. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
53. K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658.
54. R. D. Shannon, Acta Crystallogr., Sect. A: Found. Adv., 1976, 32, 751–767.
55. S. Ohta, T. Kobayashi and T. Asaoka, J. Power Sources, 2011, 196, 3342–3345.
56. J.-F. Wu, E.-Y. Chen, Y. Yu, L. Liu, Y. Wu, W. K. Pang, V. K. Peterson and X. Guo, ACS Appl. Mater. Interfaces, 2017, 9, 1542–1552.
57. J. Sakamoto, E. Rangasamy, H. Kim, Y. Kim and J. Wolfenstine, Nanotechnology, 2013, 24, 424005.
58. Z. Zou, N. Ma, A. Wang, Y. Ran, T. Song, B. He, A. Ye, P. Mi, L. Zhang, H. Zhou, Y. Jiao, J. Liu, D. Wang, Y. Li, M. Avdeev and S. Shi, Adv. Funct. Mater., 2021, 31, 2107747.
59. B. He, P. Mi, A. Ye, S. Chi, Y. Jiao, L. Zhang, B. Pu, Z. Zou, W. Zhang, M. Avdeev, S. Adams, J. Zhao and S. Shi, Acta Mater., 2021, 203, 116490.
60. E. Rangasamy, J. Wolfenstine and J. Sakamoto, Solid State Ionics, 2012, 206, 28–32.
61. F. Han, A. S. Westover, J. Yue, X. Fan, F. Wang, M. Chi, D. N. Leonard, N. J. Dudney, H. Wang and C. Wang, Nat. Energy, 2019, 4, 187–196.
62. Y. Li, Z. Wang, C. Li, Y. Cao and X. Guo, J. Power Sources, 2014, 248, 642–646.
63. L. J. Miara, W. D. Richards, Y. E. Wang and G. Ceder, Chem. Mater., 2015, 27, 4040–4047.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d2ta00545j

---