Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pore and grain chemistry during sintering of garnet-type Li6.4La3Zr1.4Ta0.6O12 solid-state electrolytes†
Joshua A.
Hammons
 *a,
J. Ali
Espitia
*a,
J. Ali
Espitia
 b,
Erika
Ramos
a,
Rongpei
Shi
a,
Frederick
Meisenkothen
b,
Erika
Ramos
a,
Rongpei
Shi
a,
Frederick
Meisenkothen
 c,
Marissa
Wood
a,
Maira R.
Cerón
c,
Marissa
Wood
a,
Maira R.
Cerón
 a and
Jianchao
Ye
*a
a and
Jianchao
Ye
*a
aPhysical and Life Sciences Directorate, Lawrence Livermore National Laboratory, 7000 East Avenue, Livermore, CA 94550, USA. E-mail: hammons3@llnl.gov
bDepartment of Physics, University of Texas El Paso, 500 W University Ave, El Paso, TX 79968, USA
cMaterials Measurement Science Division, National Institute of Standards and Technology, Gaithersburg, Maryland, USA
First published on 11th March 2022
Abstract
Garnet-type solid-state electrolytes have significant advantages over liquid organic electrolytes but require energy-intensive sintering to achieve high density and ionic conductivity. The aim of this study is to understand the chemical and microstructural evolution towards optimizing sintering conditions to achieve good conductivity at low sintering temperatures. To this end, the pore surface chemistry, morphology, and elemental enrichment along grain boundaries are investigated using scanning electron microscopy, X-ray scattering, and thermo-gravimetric analysis at temperatures below and above 1000 °C where the conductivity is significantly affected. Combined with theoretical simulations, three transition regions during the temperature ramp to 900 °C were identified: (1) 200 °C to 350 °C where the air-exposed protonated Li6.4La3Zr1.4Ta0.6O12 (H-LLZTO) releases H+ and the lattice constant decreases, (2) 550 °C to 700 °C where the LLZTO surface structure becomes unstable, which leads to the formation of a La2Zr2O7 (LZO) phase, and (3) 700 °C to 870 °C, where the surface Li2CO3 layer starts to decompose and react with the intermediate LZO phase to reform the LLZTO cubic phase. While gradual densification is observed between 750 °C and 900 °C, higher temperatures (1000 °C and above) significantly reduce the pore volume and increase the conductivity. Backscattered electron (BSE) imaging and energy dispersive spectroscopy (EDS) under cryo conditions reveals Ta enrichment and Zr depletion at grain boundaries after sintering at 1100 °C for 6 hours.
Introduction
The increasing market of rechargeable Li-ion batteries for various applications has raised safety concerns due to the use of highly flammable liquid electrolytes.1,2 There are also strong demands for high energy density batteries to increase the mileage range of electric vehicles. To achieve the gravimetric energy density goal of 500 W h kg−1 set by the U.S. Department of Energy, it is almost inevitable that metallic lithium must be used as the anode, paired with a high-capacity sulfur or high-voltage cathode. This further limits the use of organic liquid electrolytes due to their narrow voltage stability window and difficulty preventing Li dendrite growth and polysulfide shuttling.3 By replacing organic liquid electrolytes with non-flammable, highly conductive and electrochemically stable solid-state electrolytes (SSEs), these safety and energy density issues can be resolved.4 Among the promising SSEs developed in the past few decades,4–6 garnet-type SSEs such as doped cubic phase Li7La3Zr2O12 (LLZO) are extremely interesting due to their high ionic conductivity (10−4 to 10−3 S cm−1) and wide voltage stability window.5 LLZO's high Young's modulus (≈150 GPa (ref. 7)) is also beneficial in blocking Li dendrite penetration, though Li dendrites are still observed, particularly along grain boundaries and in microcrack/void defects.8,9Sintering is critically important to controlling the LLZO microstructure (impurities, density, pore size, grain size, chemical inhomogeneity, etc.), which can greatly affect its electrochemical performance. Importantly, the cubic phase LLZO (rather than the tetragonal phase) must be obtained to achieve higher ionic conductivity.10,11 Stabilization of the cubic phase at low synthesis temperatures has been achieved by doping with various elements such as Al3+,11 Ga3+,12 Fe3+ (ref. 13) at Li+ sites, Ta5+,14 Nb5+,15 Sb5+,16 Bi5+,17 Mo6+,18 W6+,19 Y3+ (ref. 20) at Zr4+ sites, and Rb+,21 Ca2+,22 Ba2+ (ref. 23) at La3+ sites. Among these various doping options, Ta doping is very attractive due to the resulting higher ionic conductivity (>10−3 S cm−1 at room temperature).24,25 Although the synthesis temperature of the garnet phase can be reduced to 900 °C,26 the densification temperature is still too high and leads to Li loss. For example, typical furnace sintering of LLZO materials requires temperatures over 1100 °C for several hours.27 A recent approach aims to reduce Li loss by applying pressure to allow a lower sintering temperature and a shorter time (i.e., hot pressing, flash sintering, spark plasma sintering),28–30 or by rapid Joule heating to high temperatures to dramatically reduce sintering time to seconds.31 However, the reaction/sintering kinetics are unclear and lead to open questions, such as whether the solid-state sintering conditions result in homogeneous chemical distribution. Furthermore, the condition of the starting powders (particle size, degree of Li+/H+ exchange) is also important in reducing sintering temperature and in achieving high density and ionic conductivity.27,32,33 The sintering environment also plays a key role in controlling Li loss and overall density. Using a graphite crucible with inert gas flow helps reduce Li loss without using mother powder,33,34 and an O2 environment promotes the annihilation of pores via easier O2 diffusion through the oxides.35,36
In situ measurements are necessary to observe changes in the microstructure during heating without taking the sample in and out of the furnace for measurements at room temperature and provide information about kinetics in one experiment, rather than multiple experiments at different times and temperatures.37Ex situ characterization has provided information to correlate sintering conditions with final microstructure and electrochemical properties. For example, as the sintering temperature is increased, the sample density also increases and grains grow, which leads to generally improved ionic conductivity.33 Rapid sintering methods tend to generate finer grains, which could help to increase critical current density.38,39 However, much of the critical transient information during sintering has been overlooked in ex situ characterization. Understanding the temperature and time dependent pore evolution/annihilation, possible reaction intermediates, and the related kinetics problems is essential to optimizing the sintering process.
In this work, in situ ultra-small-angle X-ray scattering and wide-angle X-ray scattering (USAXS/WAXS) techniques are used to reveal the physical and chemical processes involved in sintering LLZTO solid-state electrolyte. Changes in pore morphology, density, and surface contrast are evaluated as a function of sintering temperature and time by in situ USAXS and comparison with computational models. In situ WAXS provides the X-ray diffraction (XRD) patterns that reveal lattice constant changes (caused by Li+/H+ exchange, intermediate phase formation, and thermal expansion), as well as peak width changes (caused by grain and microstress evolution). The final, sintered product was also analyzed by cryo-SEM to further reveal the chemical discrepancy in the grain boundary regions.
Materials and methods
Ball milling and pellet preparation
Li6.4La3Zr1.4Ta0.6O12 (LLZTO) powder (volume-median diameter = 7 μm) was purchased from MTI Corporation and stored in an argon glove box (O2 and H2O < 10−4%). A SPEX 8000D mixer mill with 50 mL zirconia jars was used for high-energy ball milling with a procedure of 30 minute mill, 30 minute rest, and another 30 minute mill. Each milling sample contained 10 g of LLZTO, 60 g of yttria-stabilized zirconia (YSZ) beads (0.5 mm diameter, Inframat Advanced Materials), and 10 g of acetonitrile (anhydrous 99.8%, Sigma Aldrich) mixed with 20 μL of Triton X-100. After the milling process, the beads were filtered out by repeated washing using 30 g of acetonitrile through a 100 μm mesh to collect the powder. The filtered powder was then centrifuged (VWR Laboratory Centrifuge) at 50 Hz (3000 rpm) for 4 minutes to separate the solvent, dried in a vacuum oven at 70 °C overnight, and finally sieved through a 75 μm mesh.The sieved powder was pressed into a pellet using a 15 T compact hydraulic press (MTI Corporation). Approximately 0.2 g of LLZTO powder was used for each pellet. The powder was poured into a 10 mm diameter die (MTI Corporation), then pressed at a displayed pressure of 3000 psi (890 MPa for a 10 mm diameter pellet) for 2 minutes. Typical densities of 3.11 g cm−3 (56.6% relative density) and pellet thicknesses between 0.4 mm and 0.5 mm were obtained after pressing. Sintered pellets for ex situ experiments were prepared by wrapping the green pellets in graphite foil and placing them inside a ceramic furnace tube for heat treatment under argon flow at different furnace temperatures (900 °C, 1000 °C, and 1100 °C) with a heating rate of 10 °C per minute for various times (2 hours, 4 hours, and 6 hours) before cooling to room temperature. These samples were removed from the oven, encapsulated in Kapton tape, and stored in Ar for shipment to the Advanced Photon Source. Lastly, the density of each pellet was calculated using Archimedes' method by dividing its mass by the volume measured by comparing its weight in air and in Fluorinert FC-40 (Sigma Aldrich).
Scanning electron microscope (SEM) and X-ray microanalysis
Scanning electron microscope (SEM) images of the powders were acquired using a JEOL JSM-7401F field emission scanning electron microscope. Samples sintered for 6 hours at each temperature were fractured and imaged to reveal the bulk morphology after sintering. To amplify the growth of the Li2CO3 layer by air exposure, a portion of the as-received powder was aged in air for one day before SEM imaging.In order to observe possible chemical inhomogeneity in the well-sintered LLZTO pellets (sintered at 1100 °C in Ar) one pellet was fractured (approximately through its diameter) to expose the cross-section. Half of the fractured pellet was mounted on a 45° pre-tilted SEM stub to permit access to the cross-section for imaging and analysis. The entire mounted sample was then coated with a thin film of Au–Pd alloy in a Cressington sputter coater. Using an FEI Helios 660 NanoLab FIB-SEM instrument, a 69Ga+ ion beam was directed nominally parallel to the fracture surface. A region roughly 100 μm by 100 μm in area and several micrometers deep, was ion milled at room temperature to remove fracture topography and to provide a fresh surface for analysis, free from reaction products and surface films. The sample was subsequently coated with a conductive carbon thin film in another Cressington coater via a carbon arc process. Room temperature imaging of the sample at incident beam energies above 2 keV and probe currents conducive to X-ray microanalysis resulted in rapid surface modification, making it impossible to get images and analyses truly representative of the material. Active specimen cooling was required for proper X-ray microanalysis and BSE imaging. The sample was cooled to −170 °C using a Quorum Technologies Polar Prep 2000 liquid nitrogen cryo-transfer station and cold stage. Electron beam imaging and X-ray microanalysis were then carried out at incident beam energies between 5 keV and 10 keV and probe currents between 100 pA and 3200 pA. An EDAX Octane plus (30 mm2) SEM-EDS detector, with the APEX acquisition and analysis software, was used to collect X-ray spectral images. A custom analysis script, written in the R-programming language for statistical computing,40 was used to read the spectral image data and to segment different specimen regions of interest for analysis – e.g., grain boundary regions vs. grain interiors. Image processing was carried out using Fiji41 (Image J v 1.53f).
Ultra small/wide angle X-ray scattering
Three of the as-pressed pellets, as well as the ex situ sintered pellets, were characterized using the USAXS/SAXS/WAXS beamline,42 9IDC, at the Advanced Photon Source using a monochromatic X-ray beam of 21 keV. The scattering intensity, I(q), is reported as a function of the absolute value of the scattering vector, or momentum transfer q, defined as q = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ, where λ is the wavelength of the X-rays and 2θ is the scattering angle. In this approach, large structures scatter at small angles and small structures scatter at large angles. Each of the as-pressed pellets was loaded into a Linkam 1500 stage that was immediately placed under Ar flow; typically, the sample was exposed to air for less than 1 minute. Once loaded, the hutch was closed and the X-ray scattering, in the q-range: 10−4 Å−1 < q < 6 Å−1, was collected from the room temperature pellet. The sample was then heated to temperature (900 °C, 1000 °C, 1100 °C measured near the sample) at 10 °C min−1 and held for four hours whilst collecting the USAXS, SAXS and WAXS sequentially.42 Measurements had an effective temporal resolution of ≈5 minutes, with USAXS scan times of 90 s and 30 s exposure times for the SAXS and WAXS detectors; dead time arises from configuration changes and tuning. The USAXS data, collected with the Bonse-Hart instrument (0.8 mm × 0.8 mm beam) was reduced and desmeared using the Irena package for Igor Pro.43 The SAXS and WAXS data was collected using a beam size of 0.2 mm × 0.8 mm and reduced using the Nika package for Igor Pro.44
θ/λ, where λ is the wavelength of the X-rays and 2θ is the scattering angle. In this approach, large structures scatter at small angles and small structures scatter at large angles. Each of the as-pressed pellets was loaded into a Linkam 1500 stage that was immediately placed under Ar flow; typically, the sample was exposed to air for less than 1 minute. Once loaded, the hutch was closed and the X-ray scattering, in the q-range: 10−4 Å−1 < q < 6 Å−1, was collected from the room temperature pellet. The sample was then heated to temperature (900 °C, 1000 °C, 1100 °C measured near the sample) at 10 °C min−1 and held for four hours whilst collecting the USAXS, SAXS and WAXS sequentially.42 Measurements had an effective temporal resolution of ≈5 minutes, with USAXS scan times of 90 s and 30 s exposure times for the SAXS and WAXS detectors; dead time arises from configuration changes and tuning. The USAXS data, collected with the Bonse-Hart instrument (0.8 mm × 0.8 mm beam) was reduced and desmeared using the Irena package for Igor Pro.43 The SAXS and WAXS data was collected using a beam size of 0.2 mm × 0.8 mm and reduced using the Nika package for Igor Pro.44
In order to present the general trends in the time-resolved USAXS data, a heuristic model was fit to extract the temporal evolution of discernible features in the data. Using well-known scattering approximations, the simple unified equation makes it possible to extract the temporal evolution of the size, scale and surface scattering from phases within the pellet during sintering. Only two unified levels were necessary to fit all of the data:
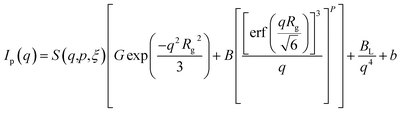 | (1) |
 | (2) |
 | (3) |
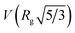 is the volume of a sphere of radius,
is the volume of a sphere of radius,  and ΔρLLZTO is the scattering contrast between LLZTO and void (1673 × 1020 cm−4), where the theoretical density of 5.5 g cm−3 is used for LLZTO. In the case where eqn (1) represents the scattering from only pores surrounded by the maximum density of LLZTO, Ĝ is approximately equal to the volume fraction of pores observable by USAXS. The general trend in the key fit parameters Rg, P and G are used in combination with the TGA and SEM imaging to interpret the data and formulate a more specific model that is presented in the Discussion section of the manuscript.
and ΔρLLZTO is the scattering contrast between LLZTO and void (1673 × 1020 cm−4), where the theoretical density of 5.5 g cm−3 is used for LLZTO. In the case where eqn (1) represents the scattering from only pores surrounded by the maximum density of LLZTO, Ĝ is approximately equal to the volume fraction of pores observable by USAXS. The general trend in the key fit parameters Rg, P and G are used in combination with the TGA and SEM imaging to interpret the data and formulate a more specific model that is presented in the Discussion section of the manuscript.
The WAXS data contains information about phases present during sintering, as well as their relative size evolution and lattice parameters. The evolution in lattice spacing was analyzed by selecting the XRD reflections (400) and (321), which were fitted to Gaussian curves using the data analysis HighScore Plus software. These specific reflections were selected as they did not overlap with nearby peaks, were spread across the spectra, and represented a mix of indices. Unit cell parameters were obtained from the average of these specific reflections.
Simulated sintering
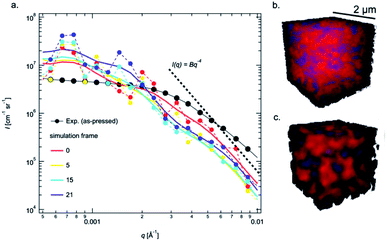
To gain a better understanding of the pore evolution and densification kinetics during sintering, a multi-phase field model was also employed to study the microstructure (including solid grains and pore) evolution from a green-body with the same particle size distribution as the realistic pellets informed by experimental SEM characterization. The phase-field model, developed by the present authors,33,46 accounts for multiple transport mechanisms operating during sintering, including surface transport (such as surface diffusion, lattice diffusion from the particle surface to the sintering neck, vapor transport through evaporation and condensation) and bulk transport (such as grain boundary (GB) diffusion and lattice diffusion from the GB to the pore). The latter transport mechanism leads to densification (i.e., reduction in particle spacing) while the former does not. As such, the model allows for consideration of the dynamic interplay between microstructure evolution and mass transport during sintering. Model formulation and model parameters have been described in detail in prior work.33 The simulation was performed using a system with a volume of 96Δx by 96Δy by 96Δz with the spatial grid size Δx(yz) = 25 nm. Zero flux boundary conditions were used along all three dimensions. It is worth pointing out that in the phase-field simulation, the driving force for sintering has been increased by increasing the surface energy and lowering the grain boundary energy to speed up the simulation and reduce computational cost. Thus, a dimensionless time in the simulation is used here since it may not correspond to the realistic experimental sintering time.In order to compare the simulation results with in situ experimental data, the USAXS from the sintered body at each simulation step was calculated using a Monte Carlo approach.47 With this approach, the simulated scattering from pores and particles within the simulation box can only be calculated up to a maximum q value of 0.02 Å−1, due to the inherent resolution of the simulation box (25 nm). Scattering from the simulation box itself ultimately limits the interpretable q-range of the simulated USAXS, as the whole box will scatter as a single object. Because the simulation box shrinks during sintering, only the innermost 60% of the box was used, resulting in box dimensions of ≈(1.4 μm × 1.4 μm × 1.4 μm). Therefore, some scattering from the box is expected at q < 10−3 Å−1 in the form of an intensity decay with overlaying Bessel-function oscillations due to the monodisperse nature of the box itself.48 Therefore, the q-range 10−4 Å−1 < q < 10−2 Å−1 was simulated to identify contributions of the box and disregard the resolution of the simulation. Such a broad range in q requires a large number of points and therefore USAXS was simulated using first principles and assuming only a center of symmetry by the equation:
 | (4) |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) , was calculated and used to compute the contrast. The square of the amplitude was calculated over an average of 20 different scattering vectors to obtain the average USAXS curve, which was scaled by the mean volume-squared occupied by a point
, was calculated and used to compute the contrast. The square of the amplitude was calculated over an average of 20 different scattering vectors to obtain the average USAXS curve, which was scaled by the mean volume-squared occupied by a point ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) 2, and an arbitrary scaling factor K = 4 for comparison to the experimental data. Each Isim(q) curve was subsequently smoothed on a log-scale for comparison using Igor pro. Unsmoothed curves and contributions from the overall simulation box size and voxel size can be found in the ESI (Fig. S3†).
2, and an arbitrary scaling factor K = 4 for comparison to the experimental data. Each Isim(q) curve was subsequently smoothed on a log-scale for comparison using Igor pro. Unsmoothed curves and contributions from the overall simulation box size and voxel size can be found in the ESI (Fig. S3†).
Thermogravimetric analysis (TGA)
Thermogravimetric analysis was performed on a pressed LLZTO pellet to evaluate mass loss as a function of temperature and time using a Mettler Toledo TGA/DSC 3+ instrument. The pressed LLZTO pellet (71.9954 mg) was placed in a Pt crucible, capped and immediately transferred to the TGA/DSC furnace. The furnace and sample were purged with N2 (flow rate = 100 mL min−1) for 30 min at ≈25 °C, then heated to 1050 °C at 2 °C min and held at 1050 °C for 2 hours. Finally, the sample was cooled down to room temperature at a rate of 20 °C min. Reported temperatures were measured at the sample holder. A total of 12.80% mass loss was observed, with the final mass of 62.7808 mg measured.Electrochemical characterization
Electrochemical characterization was carried out on the sintered pellets to demonstrate the link between conductivity and sintering temperature. In order to remove any Li2CO3 from the surface of the LLZTO pellets, each pellet was treated with a solution of phosphoric acid (H3PO4) and ethanol (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol ratio) for 3 min to form a lithiophilic Li3PO4 layer, which effectively improves the interfacial contact between Li metal and the LLZTO surface as demonstrated by Ruan et al.49 Each pellet was then washed with two different ethanol solutions for 1 min each and dried under vacuum for at least 20 min before cell assembly. Each pellet was placed between two lithium foils, which were then annealed at 280 °C for 20 min on a heating plate to improve the contact between Li and LLZTO. Temperature dependent conductivity measurements were carried out in a temperature chamber (Espec) in the temperature range from 25 °C to 60 °C. The SP-300 from Biologic Science Instruments was used for electrochemical characterization. The software package EC-Lab V10.02 was used for data acquisition and impedance data fitting. Impedance spectroscopy was obtained in the frequency range from 100 mHZ to 1 MHZ. Impedance data were fitted with an equivalent circuit with either 1 or 2 RC components depending on whether the respective sample showed one or two semicircles by the equations:
1 vol ratio) for 3 min to form a lithiophilic Li3PO4 layer, which effectively improves the interfacial contact between Li metal and the LLZTO surface as demonstrated by Ruan et al.49 Each pellet was then washed with two different ethanol solutions for 1 min each and dried under vacuum for at least 20 min before cell assembly. Each pellet was placed between two lithium foils, which were then annealed at 280 °C for 20 min on a heating plate to improve the contact between Li and LLZTO. Temperature dependent conductivity measurements were carried out in a temperature chamber (Espec) in the temperature range from 25 °C to 60 °C. The SP-300 from Biologic Science Instruments was used for electrochemical characterization. The software package EC-Lab V10.02 was used for data acquisition and impedance data fitting. Impedance spectroscopy was obtained in the frequency range from 100 mHZ to 1 MHZ. Impedance data were fitted with an equivalent circuit with either 1 or 2 RC components depending on whether the respective sample showed one or two semicircles by the equations: | (5) |
 | (6) |
 | (7) |
Results and discussion
The experimental results are discussed in light of three different features of the LLZTO: (1) pore morphology evolution, (2) pore-wall chemistry, and (3) grain boundary chemistry. The evolution in pore morphology is described in light of the ex situ SEM and density measurements and in situ USAXS measurements. At the same time, the WAXS and TGA provide valuable information that is necessary to understand the in situ USAXS data at lower temperatures where chemical reactions are involved. Finally, the grain structure such as grain size and grain boundary chemistry is presented from SEM and SEM-EDS analysis.Pore evolution with sintering temperature and time
Building on previous work,33 high energy ball milling is used here to reduce the particle size from several microns to 190 nm (Fig. S5a and S5c†), to facilitate sintering at lower temperatures. The as-pressed pellet has randomly packed particles (Fig. 1a) with a relative density of 56.6% ± 0.5% (Table 1). After sintering at 900 °C in Ar for 6 hours, a porous structure is observed (Fig. 1b). The size of open pores and interconnected LLZTO ligaments is on the order of 1 μm, which is significantly larger than the as-pressed pellet, and the sintered pellet also shows a relative density increase to 85.1% ± 3.8%. When the temperature is increased to 1000 °C, the pores are closed and the fracture surface shows an intergranular fracture pattern (Fig. 1c). The relative density increases to 94.0% ± 0.4% and correlates well with the low area fraction of pores observed. Further increasing the sintering temperature to 1100 °C leads to a trans-granular fracture indicating stronger grain boundaries and a higher density of 96.3% ± 0.4% (Fig. 1d). It is noteworthy that the sample-to-sample variation in the 900 °C sintered samples is larger than in the 1000/1100 °C samples, which suggests 900 °C is a critical temperature for accelerated densification.33 Above 900 °C, the conductivity increases dramatically due in part to the removal of a larger fraction of pores (Table 1 and Fig. S8†). | ||
| Fig. 1 Secondary electron images of fractured surfaces of LLZTO pellets in the as-pressed state (a), after sintering at 900 °C (b), 1000 °C (c) and 1100 °C for 6 hours (d). | ||
| Sample | Density [g cm−3] | Relative density [%] | ν pore [%] | Ionic conductivity (mS cm−1) |
|---|---|---|---|---|
| LLZTO as-pressed | 3.11 ± 0.03 | 56.6 ± 0.5 | 43.4 ± 0.5 | N/A |
| LLZTO 900 °C | 4.68 ± 0.21 | 85.1 ± 3.8 | 14.9 ± 3.8 | 0.002 ± 0.018 |
| LLZTO 1000 °C | 5.17 ± 0.02 | 94.0 ± 0.4 | 6.0 ± 0.4 | 0.20 ± 0.02 |
| LLZTO 1100 °C | 5.29 ± 0.02 | 96.3 ± 0.4 | 3.7 ± 0.4 | 0.53 ± 0.30 |
To understand the detailed structural evolution with time and temperature, time-resolved USAXS is used to resolve the meso-scale heterogeneities (nm to a few mm). Selected USAXS data shown in Fig. 2a and b reveal clear shifts in the Guinier “knee” region, a change in scale and a slight change in the power-law slope at high q as the temperature is increased. Importantly, the general shape of the USAXS data is the same between sequential scans up to ≈950 °C and beyond ≈1000 °C; in between these temperatures, the USAXS changes significantly (Fig. 2b). Therefore, the model fits of eqn (1) are able to describe the scattering from within the pellets reliably well during sintering and are not smeared by temporal changes during the measurement time (≈5 minutes).
 | ||
| Fig. 2 Time-resolved USAXS plots of LLZTO pellets sintered at 900 °C (a) and 1000 °C (b), along with the temporal evolution of the relevant parameters obtained from the least-squared fitting of eqn (1) to all of the data collected from pellets sintered at 900 °C (black), 1000 °C (blue), and 1100 °C (red) (c). The evolution in Rg (circles) is shown with the evolution in P (triangles) in the bottom plot, along with Ĝ (circles) in the middle plot and measured temperature in the top plot. Guinier knee and power-law features in the final USAXS curve are shown in (a). Error bars associated with the parameter uncertainty were obtained from the curve-fitting routine in Igor Pro. | ||
Agreement between the USAXS data and the model fits (Fig. 2a and b) allow for the key fit parameters to be extracted and used to interpret the data. Between 200 °C and 350 °C, Ĝ increases, while Rg slightly decreases by 30%. As the sources of the scattering can be either the LLZTO particles or pores, it is not immediately clear to what the reduction in size is attributed. The value of P is almost constant at ≈3.6. For a simple two-phase system with smooth interfaces, P would equal 4 (Porod condition), while values between 3 and 4 may be attributed to roughened surfaces50 or polydisperse surfaces phases.51 This first transition region (region I) is referred to as the contrast region because Ĝ is expected to be dominated by the phase contrast, as no increase in either the pore or particle volume or their relative volume fractions is observed or expected.52 The contrast change has to be explained from the chemical composition within the pore or bulk LLZTO instead of morphological aspects and thus will be further discussed in the next portion of this manuscript. After this first transition, all three key parameters (Ĝ, Rg, P) remain constant, indicating little to no morphological changes. Above 550 °C, P increases to values slightly above 4 and Ĝ increases again. While a P value of 3.6 can have multiple interpretations involving surface heterogeneities, a value above 4 for P is unique to a surface gradient in density at the pore-particle interface.53 Therefore, the second region (region II) is referred to as the surface region (550 °C to 700 °C). In the final region (region III), Ĝ decreases and Rg increases monotonically from 700 °C to the target temperature and continues for the remainder of the sintering experiment (∼4 h). In this region, the USAXS is dominated by pores that increase from ≈0.5 μm to ≈2 μm. With most of the water and Li2CO3 removed, the value of Ĝ is very close to what is expected from the pore volume from a sample sintered at 900 °C (Table 1). Therefore, this region is referred to as the growth region, as only the pores grow in size towards a steady state value.
The final values of the three parameters are temperature dependent and offer insights into the temperature dependent conductivity. First, the value of P remains above 4 in the sample sintered at 900 °C, indicating that the electron density gradient is still present at the pore wall. This gradient manifests as a gradual transition from the bulk LLZTO electron density to the void (zero), rather than a sharp transition.53 The samples sintered at 1000 °C and 1100 °C both have P values of 4, indicating no electron density gradient at the pore wall. Rather, a sharp, well-defined surface of the pore wall is present at these two higher temperatures. While separate pore-wall phases in the 900 °C sample are not detected by X-ray diffraction, they are likely decomposition products such as Li2O from pre-existing Li2CO3, which is not a good Li+ conductor.54 Furthermore, these phases likely also reduce the connectivity of partially sintered LLZTO phases, as they necessarily reside on the surface. While Rg increases at all three temperatures, the magnitude of increase is three times higher at 1000 °C and 1100 °C, indicating that higher temperatures are required to collapse larger pores, thereby increasing the LLZTO volume available for ion transport. Finally, Ĝ approaches 0.07, 0.015 and 0.007 for the pellets sintered at 900 °C, 1000 °C and 1100 °C, respectively, which are close to the pore volume fractions estimated by density measurements (Table 1). The reason the Ĝ values are lower than the respective porosities in Table 1 is likely due to the presence of large (>5 μm) pores outside of the range that USAXS can detect, as evidenced by the intensity decay present at 10−4 Å−1 from larger phases. Based on the observations of region III, the meso-scale pore volume (accessible with USAXS) reduces when the sintering temperature increases from 900 °C to 1000 °C, while the conductivity increases 100-fold.33 However, according to typical linear law or percolation law for the relationship of conductivity with porosity,55 such a large drop of conductivity cannot be solely explained by porosity. Additional phases at the pore-wall interface and pore volume observed in our USAXS are expected to adversely affect the conductivity. The higher temperature sintering may also increase the Li+ and O2− vacancies by mild Li loss, which may facilitate Li+ transport and thus further increase the conductivity.56–58
While the temperature dependent observations in region III offer clear insight into the change in pore morphology, the USAXS data in regions I and II contain important information about morphological changes that occur at lower temperatures that are desired for sintering. However, these regions are ambiguous because scattering from pores, particles and other pore wall phases may contribute in varying amounts.48 The USAXS from phase-field simulations of the pellets offer key insight into interpreting the data during these times, as only particles and pores are present. Using the same size distribution of powder to construct a green body to represent the realistic as-pressed pellet, the Guinier knee in the simulated USAXS is observed at slightly lower q compared to the measured data (Fig. 3a). Quantitatively, a shift in q of ≈30% higher results in good overlap and is shown in Fig. S4.† The apparent discrepancy suggests that the pores in the pellets measured by USAXS are smaller, which is likely attributed to Li2CO3 on the pore wall, but also could be attributed to the packing efficiency, relatively small simulation size, or errors in the size distribution; the simulated density is higher (65%) than that obtained experimentally (57%), which indicates some discrepancy in the packing, likely due to the irregular particle morphology in experiments compared to the spheres used in simulations. However, once the sintering is initiated, the simulated intensity decay at high q immediately steepens and the Guinier region shifts to lower q values (Fig. 3a) as the simulated pellet rapidly densifies (Fig. S1b†). While the intensity decay (Fig. 2) captured by parameter, P, may be attributed to both smaller pores and/or surface fractal scattering,50 the intensity decay at q > 0.003 Å−1 in the simulations is unambiguously associated with the presence of smaller pores between particles that disappear first (Fig. S2†) and follows the Porod relationship (P = 4) in Fig. 3a. Therefore, the increase in P in region II from 3.6 to 4 cannot be associated with sintering/fusing of very small particles because the Guinier region does not simultaneously shift to lower q (increase Rg) to the degree that it increases in the simulations shown in Fig. 3a. Furthermore, the transitions in region I and II must be associated with phenomena at the pore wall interface (Li2CO3), since this would change both P and the real contrast in Ĝ. Importantly, these surface phases remain at low temperatures and may even be present to some extent at 900 °C, as evidenced by the gradient scattering (P > 4) in Fig. 2c.
Chemical evolution
Although SEM shows the surface of the LLZTO powder is relatively clean compared with the powder intentionally exposed to air for 24 hours (Fig. S5a and S5b†), the Raman spectrum (Fig. S7†) is able to capture the existence of Li2CO3 in the fresh powder due to inevitable air exposure during synthesis, transportation, and storage. Li2CO3 is formed by H+/Li+ exchange and the following reaction with CO2:59,60| Li7La3Zr2O12 + xH2O → Li7−xHxLa3Zr2O12 + xLiOH | (8) |
| 2LiOH + CO2 → Li2CO3 + H2O | (9) |
Since the ball milling, filtering, and pellet preparation were all carried out in ambient conditions, it is reasonable to believe a significant amount of Li2CO3 and LiOH exist in the as-pressed LLZTO pellets. It reduces the contrast between the pore and bulk, and therefore Ĝ in Fig. 2c in regions I and II.
In situ wide angle X-ray scattering (WAXS) collected in between USAXS measurements, provides information about crystalline phases within the pellet, as well as changes in the degree of crystallinity and lattice parameter of the bulk LLZTO. Before heating, LLZTO shows a single cubic phase with little detectable crystalline impurities (Fig. 4a and b). However, the lattice constant is 12.99 Å, larger than that of the raw LLZTO powders protected from air exposure (12.92 Å).33 The expanded lattice observed in Fig. 4c is attributed to H+/Li+ exchange.61,62 Above 150 °C, the LLZTO peaks shift to higher 2q (Fig. 4c and d), and the lattice parameter decreases until 300 °C. This abnormal negative thermal expansion is attributed to the reverse reaction of the H+/Li+ exchange. In this mechanism, H+ is released as H2O, which spontaneously leads to the mass loss as revealed from TGA analysis (Fig. 5). The densification of the LLZTO phase by lattice shrinkage and release of H2O from the pores correlates well with the slight increase in Ĝ in region I observed in the USAXS plot in Fig. 2c. With little change in the scattering size, and assuming no change in number density of scatterers, the ratio of Ĝ at 350 °C and 200 °C is very close to that expected from release of water from the pores by the relationship:
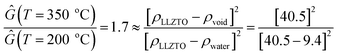 | (10) |
 | ||
| Fig. 4 Stacked plots showing the reference LLZTO63 and LZO64 XRD positions with the time evolution of select XRD data collected in the relevant q-range (solid circles) during sintering of the LLZTO pellets at 900 °C (a) and 1000 °C (b) along with the evolution in peak position observed in the intensity vs. 2θ plot (c) and the temporal evolution of the lattice parameter (d). Error bars associated with the lattice parameter were obtained from the curve fitting routine in the HighScore Plus software. | ||
 | ||
| Fig. 5 TGA plot showing the mass loss of the as-pressed pellet as a function of time and temperature. The black dashed line is the temperature profile. The red line is the mass loss. | ||
As most of the H+ is released by 300 °C, the lattice parameter reaches a minimum and starts to increase again above 350 °C due to thermal vibration-induced expansion. Between 350 °C and 550 °C, WAXS shows no new phase formation except thermal expansion, which is consistent with no change in Ĝ, Rg and P (Fig. 2c) and the mass loss in TGA (Fig. 5). When the temperature rises to between 600 °C and 700 °C, two new diffraction peaks are observed at q = 1.99 Å−1 and q = 2.29 Å−1 in all three experiments (Fig. 4a and b), which correspond to the formation of La2Zr2O7 (LZO). The formation of the LZO phase is accompanied by the structural collapse of dehydrated LLZO materials (indicated by the slowing down of lattice expansion) and is consistent with the literature,65 although the starting temperature could be affected by composition. The appearance of LZO is preceded by the beginning of the surface region II (Fig. 2c), and strongly suggests that the LZO is forming on the pore wall. In this case, the dense LZO layer is formed at the same time as the rough Li2CO3 surface layer is melting (melting point: 723 °C), which explains the observation of surface gradient scattering in region II (Fig. 2c). Furthermore, the LZO phase can only be observed ex situ in samples rapidly cooled after sintering at 650 °C (Fig. S10†), suggesting that it is transitory in nature during sintering.
The increase in Ĝ that follows is then expected as the Li2CO3 decomposes at the pore wall and is released (Fig. 5), thereby increasing the contrast of the pore. From the TGA, the Li2CO3 content can be estimated from the release of CO2 gas above ≈600 °C. Given a CO2 mass loss of ≈2.7%, a total of ≈4.5 wt% Li2CO3 is calculated in the as-pressed LLZTO pellet. Although the formation of the LZO phase is not desirable for real applications due to its non-conductive nature, it reacts with Li2CO3 and other previously formed stoichiometrically balanced species (e.g., Li–La–Ta–O oxides) to recreate the LLZTO phase above 700 °C; and at 870 °C, the LZO phase is no longer detectable from WAXS (Fig. 4a and b), which shows only the cubic LLZTO phase. This LLZTO reformation conclusion is also consistent with an in situ TEM study, where LZO to Ga-LLZO transformation was directly observed via incorporating surrounding Li2CO3 and Ga2O3 at 750 °C.66 Therefore, from the USAXS, TGA, SEM and phase-field simulations, the chemistry at the pore wall undergoes a transition beginning at ≈550 °C whereby Li2CO3 begins to melt at the same time that LZO forms. By 900 °C, the LZO phase is no longer observed, but the electron density gradient at the pore wall remains until 1000 °C (Fig. 2c), which indicates that a small amount of mass with a lower density than the bulk LLZTO is present at the pore-wall surface.
Grain structures
The evolution in grain size and grain boundary composition are key features of the sintering process. SEM shows the average particle/grain size increases from 0.19 mm for as milled particles, to 0.8 mm ± 0.2 mm, 1.1 mm ± 0.4 mm, and 1.2 mm ± 0.5 mm for samples sintered for 6 hours at 900 °C, 1000 °C, and 1100 °C, respectively; errors in the grain size were obtained as the standard deviation from the average grain size values among tens of grains in the SEM images. These results are qualitatively consistent with the evolution in peak widths observed in Fig. 4c; due to the low (3–5) number of points in each peak, precise grain sizes are not reported here, as the grains are too large for the 2θ resolution of the detector. The mechanical fracture behaviour changes from intergranular fracture to trans-granular fracture (Fig. 1c and d), indicating the strengthening of the grain boundaries with sintering temperature. To understand the strengthening mechanism, the chemical distribution among grains and grain boundaries were examined with backscattered electron (BSE) imaging and energy dispersive spectroscopy (SEM-EDS). The atomic number contrast (Z-contrast) present in the BSE images (Fig. 6a) revealed a clear contrast difference between the grain interiors and the grain boundary regions. The lighter contrast associated with the grain boundaries suggests a higher average atomic number relative to the grain interiors. By constructing a pixel mask on the BSE image, the SEM-EDS spectral image could be segmented into two average signals – one for the grain boundary regions and one for the grain interiors. A mask with a width of about 200 nm was chosen, as this is approximately the width of the light contrast regions associated with the grain boundary regions in the BSE image. The spectra (Fig. 6c) indicate the grain boundary regions are slightly enriched in Ta, and slightly depleted in Zr, relative to the grain interiors. This result is consistent with the observed Z-contrast in the BSE image. This is the first empirical evidence for such Ta enrichment and Zr depletion at the grain boundaries in sintered LLZTO, and as such, this information can be of benefit to modelling and simulation efforts. Although it is unclear if this chemical inhomogeneity is the primary reason for strengthening of the grain boundaries, it may explain the slightly decreased ionic conductivity observed in 1100C sintered LLZTO sample.33 The inhomogeneity may also affect the Li dendritic growth behaviour, which inspires further investigation in future studies. Ta enrichment (and Zr depletion) at the grain boundaries appears to occur at high sintering temperatures. As indicated by the additional SEM BSE/EDS images pairs provided in Fig. S6,† whereby no Ta enrichment can be observed in a sample sintered at 1000 °C.Conclusions
Combined with simulation and TGA, the time-resolved in situ X-ray scattering measurements reveal changes in the pore-wall chemistry within the LLZTO pellets as the temperature increases. Three distinct regions were identified during the temperature ramp to 900 °C: (1) 200 °C to 350 °C that is associated with water escape and de-protonation of the LLZTO, (2) 550 °C to 700 °C whereby the LZO forms followed by Li2CO3 melting on the pore-wall and (3) 700 °C to 870 °C, where the LZO phase disappears, and a surface gradient at the pore-wall surface at 900 °C is observed and remains until 1000 °C. While coarsening is observed from 600 °C and 900 °C, higher temperatures are required to collapse larger pores and improved conductivity of the pellet. Faster kinetics were observed over 1000 °C in the USAXS. Chemical inhomogeneity was also observed in the sintered LLZTO at 1100 °C, whereby an increase in Ta and reduction in Zr were observed at the grain boundaries. Together, these results are consistent with the USAXS results (Fig. 2c) that suggest the chemistry at the pore-wall interface changes significantly and may significantly affect pore collapse and grain growth at temperatures below 1000 °C. Moreover, observable chemical heterogeneities in the sintered materials may also play a role in the mechanical properties and ionic conductivity of the LLZTO pellet.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Disclaimer
This document was prepared as an account of work sponsored by an agency of the United States government. Neither the United States government nor Lawrence Livermore National Security, LLC, nor any of their employees makes any warranty, expressed or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States government or Lawrence Livermore National Security, LLC or the National Institute of Standards and Technology. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States government or Lawrence Livermore National Security, LLC, and shall not be used for advertising or product endorsement purposes.Certain commercial equipment, instruments, or materials are identified in this paper in order to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the Lawrence Livermore National Laboratory, the University of Texas, or the National Institute of Standards and Technology, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This manuscript (LLNL-JRNL-827446) was prepared at the Lawrence Livermore National Laboratory under the auspices of the U.S. Department of Energy under Contract DE-AC52-07NA27344. This research used resources of the Advanced Photon Source (9-IDC), a U.S. Department of Energy (DOE) Office of Science User Facility, operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. The authors acknowledge financial support from the U.S. Department of Energy (DOE), Office of Energy Efficiency and Renewable Energy (EERE), Vehicle Technologies Office (VTO) through the Advanced Battery Materials Research (BMR), in addition to the Laboratory Directed Research and Development Program at LLNL (project 20-ERD-018).Notes and references
- C. Arbizzani, G. Gabrielli and M. Mastragostino, J. Power Sources, 2011, 196, 4801–4805 CrossRef CAS.
- K. Liu, Y. Liu, D. Lin, A. Pei and Y. Cui, Sci. Adv., 2018, 4, eaas9820 CrossRef PubMed.
- Q. Li, J. Chen, L. Fan, X. Kong and Y. Lu, Green Energy Environ., 2016, 1, 18–42 CrossRef.
- Z. Gao, H. Sun, L. Fu, F. Ye, Y. Zhang, W. Luo and Y. Huang, Adv. Mater., 2018, 30, 1705702 CrossRef PubMed.
- C. Wang, K. Fu, S. P. Kammampata, D. W. McOwen, A. J. Samson, L. Zhang, G. T. Hitz, A. M. Nolan, E. D. Wachsman and Y. Mo, Chem. Rev., 2020, 120, 4257–4300 CrossRef CAS PubMed.
- F. Zheng, M. Kotobuki, S. Song, M. O. Lai and L. Lu, J. Power Sources, 2018, 389, 198–213 CrossRef CAS.
- J. E. Ni, E. D. Case, J. S. Sakamoto, E. Rangasamy and J. B. Wolfenstine, J. Mater. Sci., 2012, 47, 7978–7985 CrossRef CAS.
- E. Kazyak, R. Garcia-Mendez, W. S. LePage, A. Sharafi, A. L. Davis, A. J. Sanchez, K.-H. Chen, C. Haslam, J. Sakamoto and N. P. Dasgupta, Matter, 2020, 2, 1025–1048 CrossRef.
- E. J. Cheng, A. Sharafi and J. Sakamoto, Electrochim. Acta, 2017, 223, 85–91 CrossRef CAS.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778–7781 CrossRef CAS PubMed.
- H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg and A. Lotnyk, Phys. Chem. Chem. Phys., 2011, 13, 19378–19392 RSC.
- C. Bernuy-Lopez, W. Manalastas Jr, J. M. Lopez del Amo, A. Aguadero, F. Aguesse and J. A. Kilner, Chem. Mater., 2014, 26, 3610–3617 CrossRef CAS.
- D. Rettenwander, C. A. Geiger and G. Amthauer, Inorg. Chem., 2013, 52, 8005–8009 CrossRef CAS PubMed.
- H. Buschmann, S. Berendts, B. Mogwitz and J. Janek, J. Power Sources, 2012, 206, 236–244 CrossRef CAS.
- S. Ohta, T. Kobayashi and T. Asaoka, J. Power Sources, 2011, 196, 3342–3345 CrossRef CAS.
- S. Ramakumar, L. Satyanarayana, S. V. Manorama and R. Murugan, Phys. Chem. Chem. Phys., 2013, 15, 11327–11338 RSC.
- R. Wagner, D. Rettenwander, G. n. J. Redhammer, G. Tippelt, G. Sabathi, M. E. Musso, B. Stanje, M. Wilkening, E. Suard and G. Amthauer, Inorg. Chem., 2016, 55, 12211–12219 CrossRef CAS PubMed.
- X. Liu, Y. Li, T. Yang, Z. Cao, W. He, Y. Gao, J. Liu, G. Li and Z. Li, J. Am. Ceram. Soc., 2017, 100, 1527–1533 CrossRef CAS.
- Y. Li, Z. Wang, Y. Cao, F. Du, C. Chen, Z. Cui and X. Guo, Electrochim. Acta, 2015, 180, 37–42 CrossRef CAS.
- J. Gai, E. Zhao, F. Ma, D. Sun, X. Ma, Y. Jin, Q. Wu and Y. Cui, J. Eur. Ceram. Soc., 2018, 38, 1673–1678 CrossRef CAS.
- L. J. Miara, S. P. Ong, Y. Mo, W. D. Richards, Y. Park, J.-M. Lee, H. S. Lee and G. Ceder, Chem. Mater., 2013, 25, 3048–3055 CrossRef CAS.
- X. Chen, T. Wang, W. Lu, T. Cao, M. Xue, B. Li and C. Zhang, J. Alloys Compd., 2018, 744, 386–394 CrossRef CAS.
- A. Ramzy and V. Thangadurai, ACS Appl. Mater. Interfaces, 2010, 2, 385–390 CrossRef CAS PubMed.
- F. M. Du, N. Zhao, Y. Q. Li, C. Chen, Z. W. Liu and X. X. Guo, J. Power Sources, 2015, 300, 24–28 CrossRef CAS.
- K. Liu and C. A. Wang, Electrochem. Commun., 2014, 48, 147–150 CrossRef CAS.
- J. Li, Z. Liu, W. Ma, H. Dong, K. Zhang and R. Wang, J. Power Sources, 2019, 412, 189–196 CrossRef CAS.
- E. Yi, W. Wang, J. Kieffer and R. M. Laine, J. Power Sources, 2017, 352, 156–164 CrossRef CAS.
- J. Sakamoto, E. Rangasamy, H. Kim, Y. Kim and J. Wolfenstine, Nanotechnology, 2013, 24, 424005 CrossRef PubMed.
- V. Avila and R. Raj, J. Am. Ceram. Soc., 2019, 102, 6443–6448 CrossRef CAS.
- S.-W. Baek, J.-M. Lee, T. Y. Kim, M.-S. Song and Y. Park, J. Power Sources, 2014, 249, 197–206 CrossRef CAS.
- C. Wang, W. Ping, Q. Bai, H. Cui, R. Hensleigh, R. Wang, A. H. Brozena, Z. Xu, J. Dai and Y. Pei, Science, 2020, 368, 521–526 CrossRef CAS PubMed.
- M. Rosen, R. Ye, M. Mann, S. Lobe, M. Finsterbusch, O. Guillon and D. Fattakhova-Rohlfing, J. Mater. Chem. A, 2021, 4831–4840 RSC.
- M. Wood, X. Gao, R. Shi, T. W. Heo, J. A. Espitia, E. B. Duoss, B. C. Wood and J. Ye, J. Power Sources, 2021, 484, 229252 CrossRef CAS.
- E. Y. Yi, W. M. Wang, J. Kieffer and R. M. Laine, J. Mater. Chem. A, 2016, 4, 12947–12954 RSC.
- Y. Li, Z. Wang, C. Li, Y. Cao and X. Guo, J. Power Sources, 2014, 248, 642–646 CrossRef CAS.
- F. Shen, W. Guo, D. Zeng, Z. Sun, J. Gao, J. Li, B. Zhao, B. He and X. Han, ACS Appl. Mater. Interfaces, 2020, 12, 30313–30319 CrossRef CAS PubMed.
- T. Konegger, C. Drechsel and H. Peterlik, Microporous Mesoporous Mater., 2021, 324, 111268 CrossRef CAS.
- M. Hong, Q. Dong, H. Xie, X. Wang, A. H. Brozena, J. Gao, C. Wang, C. Chen, J. Rao and J. Luo, Mater. Today, 2021, 42, 41–48 CrossRef CAS.
- X. Huang, T. P. Xiu, M. E. Badding and Z. Y. Wen, Ceram. Int., 2018, 44, 5660–5667 CrossRef CAS.
- R. c. Team, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, 2020, https://www.R-project.org Search PubMed.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682 CrossRef CAS PubMed.
- J. Ilavsky, F. Zhang, R. N. Andrews, I. Kuzmenko, P. R. Jemian, L. E. Levine and A. J. Allen, J. Appl. Crystallogr., 2018, 51, 867–882 CrossRef CAS PubMed.
- J. Ilavsky and P. R. Jemian, J. Appl. Crystallogr., 2009, 42, 347–353 CrossRef CAS.
- J. Ilavsky, J. Appl. Crystallogr., 2012, 45, 324–328 CrossRef CAS.
- A. Guinier and G. Fournet, Small-angle Scattering of X-Rays, Wiley, New York, 1955 Search PubMed.
- R. Shi, Y. Gao, D. Li, W. Zhao and Y. Zheng, Adv. Eng. Mater., 2021, 2100152 CrossRef CAS.
- B. C. McAlister and B. P. Grady, Macromol. Symp., 2002, 190, 117–129 CrossRef CAS.
- O. Glatter and O. Kratky, Small Angle X-Ray Scattering, Academic Press, New York, New York, U.S.A, 1982 Search PubMed.
- Y. Ruan, Y. Lu, X. Huang, J. Su, C. Sun, J. Jin and Z. Wen, J. Mater. Chem. A, 2019, 7, 14565–14574 RSC.
- H. D. Bale and P. W. Schmidt, Phys. Rev. Lett., 1984, 53, 596–599 CrossRef CAS.
- K. Larson-Smith, A. Jackson and D. C. Pozzo, J. Colloid Interface Sci., 2010, 343, 36–41 CrossRef CAS PubMed.
- G. Beaucage, J. Appl. Crystallogr., 1995, 28, 717–728 CrossRef CAS.
- W. Ruland, J. Appl. Crystallogr., 1971, 4, 70–73 CrossRef.
- Y. Ren, H. Deng, R. Chen, Y. Shen, Y. Lin and C.-W. Nan, J. Eur. Ceram. Soc., 2015, 35, 561–572 CrossRef CAS.
- F. Ternero, L. G. Rosa, P. Urban, J. M. Montes and F. G. Cuevas, Metals, 2021, 11, 730 CrossRef.
- M. Kubicek, A. Wachter-Welzl, D. Rettenwander, R. Wagner, S. Berendts, R. Uecker, G. Amthauer, H. Hutter and J. Fleig, Chem. Mater., 2017, 29, 7189–7196 CrossRef CAS.
- C. Chen, Z. Lu and F. Ciucci, Sci. Rep., 2017, 7, 40769 CrossRef CAS PubMed.
- Y. Chen, E. Rangasamy, C. Liang and K. An, Chem. Mater., 2015, 27, 5491–5494 CrossRef CAS.
- L. Qiu, J. Z. Liu, S. L. Y. Chang, Y. Wu and D. Li, Nat. Commun., 2012, 3, 1241 CrossRef PubMed.
- C. Galven, J.-L. Fourquet, M.-P. Crosnier-Lopez and F. Le Berre, Chem. Mater., 2011, 23, 1892–1900 CrossRef CAS.
- Y. Li, J.-T. Han, S. C. Vogel and C.-A. Wang, Solid State Ionics, 2015, 269, 57–61 CrossRef CAS.
- Z. F. Yow, Y. L. Oh, W. Gu, R. P. Rao and S. Adams, Solid State Ionics, 2016, 292, 122–129 CrossRef CAS.
- A. Logéat, T. Köhler, U. Eisele, B. Stiaszny, A. Harzer, M. Tovar, A. Senyshyn, H. Ehrenberg and B. Kozinsky, Solid State Ionics, 2012, 206, 33–38 CrossRef.
- Y. Tabira, R. L. Withers, T. Yamada and N. Ishizawa, Z. für Kristallogr. - Cryst. Mater., 2001, 216, 92–98 CrossRef CAS.
- A. Orera, G. Larraz, J. A. Rodriguez-Velamazan, J. Campo and M. L. Sanjuan, Inorg. Chem., 2016, 55, 1324–1332 CrossRef CAS PubMed.
- C.-Y. Huang, Y.-T. Tseng, H.-Y. Lo, J.-K. Chang and W.-W. Wu, Nano Energy, 2020, 71, 104625 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta10338e |
| This journal is © The Royal Society of Chemistry 2022 |