 Open Access Article
Open Access ArticleRelevance of Ge incorporation to control the physical behaviour of point defects in kesterite†
Thomas
Ratz
 *ab,
Ngoc Duy
Nguyen
*ab,
Ngoc Duy
Nguyen
 a,
Guy
Brammertz
a,
Guy
Brammertz
 c,
Bart
Vermang
c,
Bart
Vermang
 bcd and
Jean-Yves
Raty
a
bcd and
Jean-Yves
Raty
a
aCESAM | Q-MAT | Solid State Physics, Interfaces and Nanostructures, University of Liège, Allée du Six Août 19, B-4000 Liège, Belgium
bInstitute for Material Research (IMO), Hasselt University, Agoralaan gebouw H, B-3590 Diepenbeek, Belgium
cIMEC Division IMOMEC | Partner in Solliance, Wetenschapspark 1, B-3590 Diepenbeek, Belgium
dEnergyville, Thor Park 8320, B-3600 Genk, Belgium
First published on 28th January 2022
Abstract
To reduce the prominent VOC-deficit that limits kesterite-based solar cell efficiencies, Ge has been proposed over the recent years with encouraging results as the reduction of the non-radiative recombination rate is considered as an approach to improve the well-known Sn-kesterite world record efficiency. To gain further insight into this mechanism, we investigate the physical behaviour of intrinsic point defects upon both Ge doping and alloying of Cu2ZnSnS4 kesterite. Using a first-principles approach, we confirm the p-type conductivity of both Cu2ZnSnS4 and Cu2ZnGeS4, attributed to the low formation energies of the VCu and CuZn acceptor defects within the whole stable phase diagram range. By doping of the Sn-kesterite matrix, we report the lowest formation energy for the substitutional defect GeSn. We also confirm the detrimental role of the substitutional defects XZn (X = Sn, Ge) acting as recombination centres within the Sn-based, the Ge-doped and the Ge-based kesterite. Upon Ge incorporation, we highlight, along with the increase of the XZn (X = Sn, Ge) neutral defect formation energy, the reduction of the lattice distortion resulting in the reduction of the carrier capture cross section. Both of these elements lead to a decrease of the non-radiative recombination rate within the bulk material following Sn substitution by Ge.
1 Introduction
Emerging solar cell technologies often struggle with a minority carrier lifetime, leading to large open circuit voltage deficit (VOC-deficit) and consequently low solar cell efficiency. With no exception, in opposition to their well-established CuInGa(S,Se)2 chalcogenide parent showing high cell efficiency,1,2 kesterite materials are faced with efficiency issues.3–5 As -possible culprits of the actual limitation, electronic defects acting as recombination centres have been pointed out6–11 together with other obstacles such as band alignments,9,12,13 secondary phases10,11 and/or band tailing caused by electrostatic potential fluctuations due to the presence of charged electronic defects.8,9,14Focusing on defects, as a result of the complex structure of kesterite materials, a wide range of intrinsic and cluster defects can form within the crystal, leading to various impacts on the kesterite absorber layer opto-electronic properties. Using first-principles calculations, Chen et al. were able to predict the p-type conductivity of Cu2ZnSn(S,Se)4via the high population of the CuZn and VCu defects while identifying the [2 CuZn + SnZn] cluster defect as a recombination centre leading to charge carrier losses.6 Experimentally, Dimitrievska et al. reported the possible tuning of the VOC value according to the Cu concentration and consequently the amount of [VCu + ZnCu] defect clusters.10 More recently, Kim et al. identified the intrinsic defect SnZn as the origin of the electron capture and emission in the Cu2ZnSnS4 compound resulting of the Sn multivalence.7,15 The same authors also highlighted the large lattice distortion attributed to the Sn in its oxidation state +2 with respect to its +4 state leading to a large carrier capture cross section associated with this so-called “lone-pair effect”.16 Furthermore, Gong et al. established a link between the Sn oxidation states Sn2+ and Sn4+ and the kesterite growth conditions.17 Consequently, gaining further knowledge on point defects and cluster defects in kesterite materials could allow the control of the absorber layer physical properties in view of increasing kesterite-based cell efficiencies.
Over the recent years, attempts have been made to circumvent these actual limitations using alloying and doping of kesterite materials with other elements.3,18–23 Both theoretical and experimental approaches have been used. A wide range of cationic substitutions have been investigated: Cu by Ag,24,25 Zn by Cd,24,26–28 Sn by Ge,28–32 S by Se4 and doping of both Cu2ZnSnS4 and Cu2ZnSnSe4 by Na, Li, Ga33 and Ge18,34–36 or even using more exotic elements as in ref. 20. Some of these substitutions resulted in cell efficiencies as large as 12.3% as in the case of Ga or Ge doping.33,34 Double cation incorporation like Ge and Ag37 or Ge and Cd28,38 was also realised simultaneously combining the benefits of both substitutional elements. Nevertheless, the reported efficiencies are still below the world-record of pure Sn-kesterite compounds.39
From these investigations, Ge emerged as an interesting doping/alloying element as several studies reported high solar cell efficiencies through the improvement of the VOC values following the incorporation of small amounts of Ge35 or via the complete substitution of Sn by Ge.31 In a recent study, Deng et al. demonstrated experimentally that Ge4+ can be introduced in Cu2ZnSnS4 to suppress the detrimental deep SnZn defects.36 In addition, compared to Cu2ZnSnS4, pure Ge-kesterite absorber layers present a larger band gap value which limits the maximal single solar cell efficiency.40 Nevertheless, Ge alloying could be used for the synthesis of wide band gap kesterite which is of high interest for top cells in a tandem approach.29,30 Gaining further insight into the physical behaviour of intrinsic defects in Ge-kesterite and into the mechanisms of Ge doping within the Sn-kesterite is therefore strongly desirable.
Moreover, although several material modelling studies have focused on the physical behaviour of defects in kesterite compounds,6,7,20,33 only a few studies have been dedicated so far to Ge compounds.28,41,42 To fill this void, in this work, we report the investigation of point defects in both Cu2ZnSnS4 and Cu2ZnGeS4. We first study the physical behaviour of intrinsic point defects in both kesterite materials to highlight the impact of Ge alloying and secondly, we investigate Ge-related point defects in the Sn-kesterite compound to illustrate the Ge doping mechanism. Focusing on the physical behaviour of point defects in these materials, our aim is to establish a link between the growth conditions of the kesterite thin films, the formation of point defects and the resulting kesterite solar cell performances by identifying the defect physical behaviour (dopant or recombination centre). In addition, based on the empirical rule proposed by Li et al. we derive meaningful trends concerning the defect carrier capture cross sections. Indeed, it was reported that this quantity can be related to lattice distortion caused by the defect incorporation in its various charge states.43
The paper is organised as follows. The phase diagrams of the two kesterites are first presented. Once appropriate chemical potential ranges are set, avoiding secondary phases and obtaining the desired kesterite phase, the defect formation energies are obtained according to the Fermi level position. Then, we present the defect charged states and their possible ionisation levels in order to evaluate their physical behaviour in their various electronic configurations. This approach allows us to identify their roles as a dopant or as a recombination centre. Finally, in the last part of this paper, we present a study of the lattice distortions around the different incorporated defects. This information allows us to provide a guide for the extraction of general trends concerning the capture cross sections of the various point defects at play. As a result, we are able to predict which point defects are the most abundant in the kesterite materials and eventually characterise the defect levels (acceptor, donor or recombination centre) and their relative impact on the capture of charge carriers. Considering various locations in the phase diagram, we also consider different growth conditions of the kesterite materials. This study allows us to highlight (i) the impact of Ge-alloying of kesterite on the intrinsic point defect physical behaviour and (ii) the physical behaviour of Ge dopants in Cu2ZnSnS4.
2 Computational methodology
2.1 Theoretical framework
Beyond materials properties predictions, the first-principles approach is a powerful tool to understand the behaviour of defects in semiconductor compounds.44–47 In this work, the supercell approach is considered and the calculations are performed with a 64-atom supercell corresponding to an expansion of 2 × 2 × 2 of the kesterite conventional cell as presented in Fig. 1.Using this approach, the formation energy of a defect α in a charge state q can be calculated as follows,
 | (1) |
 44 To obtain the chemical potential values μi leading to the formation of a stable kesterite phase without secondary phases, the kesterite phase diagrams have first to be computed. To do so, a set of thermodynamic conditions must be fulfilled as presented in the ESI.† Then, assuming a defect with a charge state q, a fourth term is added to eqn (1). In this term, εVBM,host refers to the valence band maximum (VBM) of the host supercell and EF is the Fermi level acting as a parameter of the defect formation energy function and ranging from the VBM to the band gap energy EG of the kesterite material. Furthermore, based on the formation energy of a given defect, the position of its ionisation levels in the materials band gap can be obtained using the following relationship:
44 To obtain the chemical potential values μi leading to the formation of a stable kesterite phase without secondary phases, the kesterite phase diagrams have first to be computed. To do so, a set of thermodynamic conditions must be fulfilled as presented in the ESI.† Then, assuming a defect with a charge state q, a fourth term is added to eqn (1). In this term, εVBM,host refers to the valence band maximum (VBM) of the host supercell and EF is the Fermi level acting as a parameter of the defect formation energy function and ranging from the VBM to the band gap energy EG of the kesterite material. Furthermore, based on the formation energy of a given defect, the position of its ionisation levels in the materials band gap can be obtained using the following relationship: | (2) |
2.2 Methodology
To compute the total energies of the defected and host supercells (as required in eqn (1)) and of the secondary phases and pure elemental phases (see ESI†), first-principles calculations have been performed using the Vienna Ab initio Simulation Package (VASP) code48 with the Projector-Augmented Wave (PAW) potential method.49 Perdew–Burke–Ernzerhof (PBE) GGA pseudo-potentials50 were used with the following valence electrons considered for each element: Cu: 3d104s1, Zn: 3d104s2, Sn: 4d105s25p2, Ge: 3d104s24p2 and S: 3s23p4. Based on the previously presented supercell approach, within a 64-atom supercell, ionic and electronic relaxations were achieved using a cut-off energy of 520 eV and a Γ-centered uniform k-points mesh of 2 × 2 × 2 k-points. Applying the strongly constrained and appropriately normed semilocal density functional (SCAN),51,52 the structures were relaxed until the numerical convergence regarding the self-consistent cycles reached forces between ions less than 10−3 eV Å−1. Starting from the relaxed structures, a single-shot calculation using the Heyd–Scuseria–Ernzerhof exchange-correlation functional (HSE06)53 is performed using an energy convergence criterion upon 10−3 eV. The combination of SCAN ionic relaxations followed by a single HSE06 electronic relaxation was reported as an efficient method to obtain accurate results by Fritsch et al. in ref. 54. Concerning Ge-containing compounds, a correction was applied to the Ge-chalcogenide formation energies to tackle the systematic underestimation as reported by Wexler et al.42 (see the ESI†).3 Results and discussion
3.1 Kesterite growth: chemical environment
Let us first determine the chemical environment in which the kesterite materials can be synthesised without secondary phases. In Fig. 2, the phase diagrams of Sn-based and Ge-based kesterites are presented for three different Cu concentrations: μCu = −0.27 (Cu-rich) eV, μCu = −0.55 eV (Cu-moderate) and μCu = −0.82 eV (Cu-poor). | ||
| Fig. 2 Phase diagrams of Cu2ZnSnS4 (a–c) and Cu2ZnGeS4 (d–f) for three different Cu chemical potentials. Each line corresponds to a secondary phase as listed in the legends (see the ESI† for secondary phases calculations). The grey-shaded areas correspond to chemical potential values for which the kesterite can be thermodynamically synthesised (stable phase). Upon taking into account the possible presence of the secondary phases, the green shading indicates the chemical potential ranges for which a kesterite stable phase is encountered without any secondary phase. | ||
A first general observation is the narrow chemical potential range in which the kesterite phase can be found without any secondary phase (green shading) in comparison to the possible chemical potential combinations that could lead to the formation of the kesterite (grey shading). For lower Cu concentrations, corresponding to a μCu value lower than −0.82 eV (resp. −0.85 eV for Cu2ZnGeS4), no pure kesterite phase is available within stable combinations of chemical potentials values. This means that below such a critical μCu value, the kesterite phase cannot be formed without the presence of secondary phases. In addition, from Fig. 2a–c, we observe a reduction of the stable kesterite phase area (grey shading). This reduction occurs as we move towards lower Cu concentrations (see the ESI†). If one chemical potential absolute value increases for a constant kesterite formation energy, the available chemical potential combination range is reduced (i.e. the edge of the stable kesterite phase corresponding to μS = 0 is shrunk). Physically, it means that for a lower chemical potential value corresponding to a lower concentration, another element concentration has to increase to keep obtaining a stable kesterite phase.
The reduction of the stable kesterite areas (grey shading) to pure kesterite areas (green shading) is the result of the multiple secondary phases that can be formed using the 4 chemical elements present in the kesterite compounds. As shown in Fig. 2a, around the green area, the dominant secondary phases are ZnS, Cu7S4, Cu2SnS3 and SnS. The phases predicted by our calculations are in good agreement with those reported by Chen et al. in ref. 6. In addition, in the recent review of Schorr et al., the authors reported the presence of ZnS in each thin film where the composition Zn/Sn exceeded the value of 1. It was also reported that the concentrations of both ZnS and SnS secondary phases increase upon deviation from the stoichiometry.10,11,55 Similarly, for the Ge-compound in Fig. 2d, the secondary phases located next to the pure kesterite phase are ZnS, Cu7S4 and Cu2GeS3. Experimentally, using XRD and HAADF-STEM imaging, Khelifi et al. reported that the ZnSe secondary phase at the top of the absorber layer and a thick Cu2GeSe3 secondary phase (120–160 nm) at the bottom of the kesterite thin film were responsible for the main efficiency loss.29 In the case of the Ge-based compound and in comparison with the SnS phase in the Sn-kesterite, the GeS secondary phase appears to be shifted towards positive Ge chemical potential values. As a result, the Ge-kesterite pure phase area (green shading) is slightly larger compared to the Sn-kesterite one. Following the phase diagram evolution from Fig. 2a–c, we observe that, as the absolute value of the Cu chemical potential increases, the SnS2 and SnS secondary phase limits shift towards lower Sn concentrations while the ZnS secondary edge shifts towards lower Zn concentrations until both SnS2 and ZnS secondary phase edges cross each other for a Cu chemical potential value of μCu = −0.82 eV, leading to the vanishing of the pure kesterite area. The same behaviour can be observed for Cu2ZnGeS4 with an extreme copper chemical potential value of −0.85 eV involving the following secondary phases: GeS, GeS2 and ZnS. Recently, Choubrac et al. reported the effectiveness of a set of different surface treatments to get rid off all detrimental secondary phases for Cu2ZnGeS4.31
Then, to compute Ge-doping point defects in the Sn-based kesterite, one has to obtain a chemical potential value for the Ge (μGe). To do so, as presented in the ESI,† several additional secondary phases were computed.
In the next section, we will focus on the formation energy of the point defects using chemical potential combinations providing a pure kesterite phase. As explained with additional details in the ESI,† using eqn (1) to compute the defect formation energies, one has to ensure that the chemical reservoirs used (i.e. chemical potentials) contribute only to the formation of the kesterite phase and not to the synthesis of secondary phases.
3.2 Intrinsic point defect formation energies
In Fig. 3, we present the formation energies of kesterite point defects for the chemical potentials μi corresponding to point E in Fig. 2b and e (see eqn (1)). The choice for this particular composition point was motivated by the perspective of selecting a chemical potential combination corresponding to a pure kesterite phase and as close as possible to the Cu-poor and Zn-rich conditions usually used to synthetise kesterite thin films.6,11,56 One has to keep in mind that Fig. 3 shows a glimpse of the defect formation energy function for one material growth condition. According to eqn (1), the defect formation energy ΔHF(EF) is represented as a function of the Fermi energy level within the kesterite band gaps as predicted by the HOMO–LUMO Kohn–Sham eigenvalues extracted from the first-principles calculations which are equal to 1.32 eV and 1.89 eV respectively for Cu2ZnSnS4 and Cu2ZnGeS4.40 | ||
| Fig. 3 Formation energies of point defects in (a) Cu2ZnSnS4 and (b) Cu2ZnGeS4 for three different kinds of defects using a particular marker: vacancy VX (circle), substitution XY (square) and interstitial XI (diamond) calculated at the chemical potential point E corresponding to μCu = −0.55 eV, μZn = −1.56 eV, μSn = −0.56 eV and μGe = −0.79 eV for the Sn-kesterite and μCu = −0.55 eV, μZn = −1.506 eV and μGe = −0.675 eV for the Ge-compound. The Fermi level under thermodynamic equilibrium conditions is represented by the maroon dashed lines (see the ESI†). Extrinsic defects corresponding to Ge doping in the Sn-based kesterite matrix are represented using a star marker. A specific color is attributed to each defect and each marker corresponds to a possible transition level between two different charge states of the same defect. | ||
Let us first focus on the intrinsic point defect formation energies in the Sn-compound as it is used as our reference material. As shown in Fig. 3a, independent of the Fermi energy value, a first general trend is the lower formation energies of the vacancies (except VZn) and the substitutional defects in comparison to the interstitial ones. This observation can be explained by the lattice distortion cost induced by the interstitial incorporation. As can be observed, the lowest formations energies (below 1.5 eV) are reported for the copper vacancy VCu, and for CuZn, SnZn and ZnCu substitutional defects. In Fig. 3b we report the same trend concerning the behaviour of the intrinsic point defect formation energies in the Ge-based compound, highlighting the similarity of intrinsic defects in both kesterites.
In addition, as presented in Fig. 3 and described in the ESI,† the Fermi level under thermodynamic equilibrium conditions can be extracted. As shown, in both kesterites, under equilibrium conditions the Fermi energy is pinned mainly by the charged defects VCu and CuZn, both being in a charge state of −1 thus providing holes for the electrical conductivity while the substitutional defect ZnCu is in a charge state of +1, supplying electrons. Under equilibrium, the extracted Fermi energy level value is located at 0.468 eV and 0.409 eV above the VBM, respectively for Cu2ZnSnS4 and Cu2ZnGeS4. Through this observation, we consequently highlight the p-type conductivity of Cu2ZnSnS4, a well-established experimental fact, also confirmed theoretically by Chen et al.6 More interestingly, we highlight the same behaviour for the Ge-based kesterite. To complete these observations, we also report the substitutional defect SnZn (resp. GeZn) which would be in a charge state +2. However as will be described later on, SnZn (resp. GeZn) would more likely behave as a recombination centre.
Then, we present Ge-doping of extrinsic point defects in the Sn-kesterite matrix such as GeCu, GeZn, and GeSn substitutional defects and the GeI interstitial defect. As shown in Fig. 3a, both GeCu and GeI have high formation energies with values above 2 eV. This result highlights the low probability for the Ge element to be incorporated in the Sn-kesterite via Cu substitution or as an interstitial defect. In contrast, the substitutional defect GeZn presents a formation energy below 2 eV, whereas GeSn has a formation energy below 0.5 eV, meaning that this defect could form quite spontaneously in the presence of Ge. It is also interesting to note that in Fig. 3a, if one compares GeCu and SnCu (resp. GeZn and SnZn), both extrinsic doping substitutional defects present higher formation energies than the intrinsic ones. It is also worth noting that the Ge chemical potential μGe used to compute the Ge-doping defects corresponds to the richest composition value leading consequently to the lowest formation energies. As a result, for a Ge chemical potential value lower than μGe = −0.79 eV (poorer composition), the Ge-related defect formation energies will increase (see the ESI†).
However, depending on the growth conditions of the materials, the defect formation energies will vary. Indeed, for a lower concentration of copper during the materials growth, Cu vacancies will form with a greater ease and will consequently be present in a higher concentration. This behaviour is captured by the lowering of the formation energy following the change of the Cu chemical potential value in eqn (1). To visualise these trends, as shown in Fig. 4, the defect formation energies were represented for different hypothetical growth conditions. To do so, we represent the evolution of the formation energies following a specific path in the phase diagrams presented in Fig. 2 and for a Fermi energy value under thermodynamic equilibrium conditions (see the ESI†). As presented in the phase diagrams of the Sn- and the Ge-kesterite, the chemical potential path studied here is labelled as A–I. The chemical potential coordinates A–D correspond to Cu-rich conditions, E–H to Cu-moderate conditions and finally the I label corresponds to a Cu-poor condition. This path was selected to study the behaviour of the formation energies at the edges of the kesterite pure phases (as represented via the green shading in Fig. 2) and following a Cu concentration from high values to lower ones. The relevant message here is consequently focused on the trends of the defect formation energies for different growth conditions and not specifically on the selected path.
 | ||
| Fig. 4 Evolution of the point defect formation energies in (a) Cu2ZnSnS4 and (b) Cu2ZnGeS4 for different hypothetical growth conditions. The calculations were performed at various chemical potential combinations corresponding to the label points presented in Fig. 2 (see the ESI† for specific values) and for the Fermi energy levels under thermodynamic equilibrium conditions located at 0.468 eV and 0.409 eV above the VBM respectively for Cu2ZnSnS4 and Cu2ZnGeS4. Each defect is represented using a specific color and using the following markers: circles for intrinsic vacancies, squares for intrinsic substitutional defects, diamonds for intrinsic interstitials and stars for Ge extrinsic doping defects in the Sn-based kesterite. | ||
In Fig. 4, we identify CuZn1−, ZnCu1+, SnZn2+ (resp. GeZn2+) and VCu1− as the intrinsic point defects showing the lowest formation energies over the different chemical potential combinations. Following these results, the usually observed Cu/Zn disorder in Sn-kesterite can also be expected in the Ge-kesterite as the two substitutional defects CuZn1− and ZnCu1+ present formation energies below 1 eV for any chemical potential combination. This result is in good agreement with those described by Chen et al. where CuZn1− is the dominant point defect.6 In addition, we report a lower formation energy concerning the ZnCu1+ antisite with a formation energy between 0.03 eV and 0.63 eV while this previous work predicted a formation energy between 0.6 and 0.9 eV. As a result, our calculations predict a substitutional defect ZnCu1+ concentration within the same range as the CuZn1− defect. This observation is in good agreement with the work of Du et al. reporting a similar ZnCu1+ behaviour.33 The facilitated formation of these defects could be explained by the similar atomic radii of Zn (rZn = 1.35 Å) and Cu (rZn = 1.35 Å) while their electronic configurations differ only by one electron.57 Several studies report that the related Cu/Zn disorder defects are responsible for potential fluctuations detrimental to solar cell performances58,59 which could however be suppressed via Ag incorporation.38
As shown in Fig. 4a, focusing on the Ge extrinsic doping defects, the substitutional defect GeSn presents formation energy values below 0.5 eV for every chemical potential combination. The smaller atomic radius of Ge (rGe = 1.25 Å in comparison to the Sn element (rSn = 1.45 Å) and their similar electronic behaviours could explain the high occurrence of this defect. Then, a general trend observed, moving from the Sn-based kesterite to the Ge-doped kesterite, is the increase of the formation energy from the intrinsic defect SnZn2+ with ΔHF = 1.24 eV to GeZn2+ with ΔHF = 1.34 eV (one should also note that for some chemical potentials, those quantities can be equal). As reported in Fig. 3, an increase of the formation energy is also observed as we move from the neutral defect SnZn in the Sn-based kesterite to the Ge-doped and then Ge-alloyed kesterite defect GeZn with values of 1.45, 1.79 and 1.85 eV respectively. This implies that if Ge is available, the ease of formation of the Zn substitutional defect would be further reduced, first in the Sn-kesterite following Ge doping and then in the Ge-kesterite upon complete substitution of Sn. In their study, Wexler et al. reported an increase of the 2CuZn + XZn defect cluster formation energy following the complete Sn substitution.28 This observation was attributed to the multivalence of Sn which can reduce from a 4+ to a 2+ oxidation state. This change of oxidation allows Sn to exist in a +2 state on the Zn2+ site. In contrast, Ge only exists in a 4+ state explaining the formation energy increase between the GeZn and the SnZn substitutional defects.15,16,28
Here, we have reported CuZn1−,.ZnCu1+., SnZn2+ (resp. GeZn2+) and VCu1− as the most abundant point defects in Cu2ZnSnS4 (resp. Cu2ZnGeS4). In the next section, we focus on their physical behaviour: acceptors, donors or recombination centres.
3.3 Defect identification: ionisation levels
In Fig. 5, we show the ionisation levels for each defect according to eqn (2). It is important to note that these levels within the kesterite band gap are, in contrast to the formation energies, independent of the chemical potential values. The relevant information here is (i) the position of the ionisation level in the material band gap, which determines the behaviour of the defect, and (ii) as a guide for the eye, the “formation energy value” of the ionisation energy level β for a Fermi level located at the transition level within the kesterite band gap (see also markers in Fig. 3). | ||
| Fig. 5 Ionisation energy levels of intrinsic point defects in (a) Cu2ZnSnS4 and (b) Cu2ZnGeS4 calculated for a chemical potential combination corresponding to point E in Fig. 2b and e. Their locations within the kesterite band gaps are reported here on the y-axis while the β value corresponds to the formation energy value at which the transition occurs in Fig. 3. This β value is provided as a guide for the eye to highlight the most dominant transition levels. | ||
For both Cu2ZnSnS4 and Cu2ZnGeS4, as shown Fig. 5, we highlight the (0/−1) transition levels of CuZn and VCu located at a few kBT over the VBM. From the calculation of the Fermi energy under thermodynamic equilibrium conditions, these transition levels are ionised and consequently, these defects act as acceptors both providing holes to the kesterite conductivity. Combined with their low formation energies, these levels are particularly suited to account for the p-type intrinsic conductivity of these compounds. Then, as donor defects, we report the (+1/0) transition level of the substitutional defect ZnCu located close to the conduction band minimum (CBM). With its previously reported low formation energy, this defect is the most abundant donor in both kesterites. We can also note that in the case of the Ge-compound, in opposition to the Sn-kesterite, the (+1/0) transition level of ZnCu is below the CBM. This is a direct consequence of the band gap increase associated with the Ge alloying. The pinning of the Fermi level under thermodynamic equilibrium conditions is a result of these two observations, which explain the p-type conductivity of kesterite materials generally reported in the literature.6 We also note that the VZn defect provides energy levels close to the VBM; however, assuming a p-type material, the Fermi level would be close to the valence band leading to an unionised defect with a high formation energy as presented in Fig. 3a. Concerning the substitutional defect SnCu (resp. GeCu), it presents ionisation states not suited for intrinsic doping (i.e. “donor states” close to the valence band). A similar behaviour is observed for the substitutional defect CuSn. As a consequence, these defects should not contribute significantly to conductivity in either of the kesterites.
One can identify SnZn (resp. GeZn), ZnSn (resp. ZnGe) and to a lesser extent CuSn (resp. CuGe) and SnCu (resp. GeCu) as deep defects. Indeed, all these substitutional defects offer transition levels located close to the middle of the kesterite band gap. In addition, as presented in Fig. 4, the substitution of Zn by Sn (resp. Ge) is the only defect presenting also a low formation energy. The latter has several transition levels within the kesterite band gap corresponding to the various transitions between its various charge states: (+2/0) at 0.584 eV (resp. 0.736 eV), (+2/+1) at 0.735 eV (resp. 0.585 eV) and (+1/0) at 0.43 eV (resp. 0.890 eV) above the VBM (below the CBM). These values are comparable to those reported by Li et al. with SnZn (+1/0) at 0.86 eV and (+2/0) at 0.67 eV below the CBM.43 Moreover, as a result of the p-type conductivity, the SnZn (resp. GeZn) defect should be ionised into a charge state +2, with the most probable transition energy level being the two-electron transition (+2/0) (see Fig. 3). Using deep-level transient spectroscopy, Deng et al. reported a defect activation energy of 0.581 eV for the Sn-based kesterite, and identified this defect as a recombination centre.36 As shown in Fig. 5a and in agreement with this experimental observation, this defect could be reported as the substitutional defect SnZn with its two-electron transition level (+2/0) at 0.584 eV above the VBM. Furthermore, the same authors reported a decrease of the transition level position to 0.542 eV following Ge incorporation, while in this work, upon Ge incorporation we report the spreading of the ionisation levels located between 0.42 eV and 0.73 eV for SnZn, between 0.46 eV and 0.91 eV for GeZn (in Sn-based kesterite) and between 0.44 eV and 1.9 eV for GeZn (in Ge-based kesterite). It should also be noted that in all three situations, the transition level (+2/0) is the closest to the middle of the gap.
Beyond formation energies, other physical parameters can also act as indicators for the evaluation of the impact of point defects on solar cell properties. In the following section, we consider recombination centre capture cross sections, which can be related to the kesterite lattice distortion upon introduction of defects.
3.4 Atomic distortions
In Fig. 6, we present the evolution of the interatomic distances between the defect position and the surrounding S atoms with respect to the charge states q of the defect, both in the Sn-based and the Ge-based compounds. As reported by Li et al.43 an empirical approach to evaluate the carrier capture cross section of defects consists in studying the local structural relaxation undergone by the lattice when the defect captures/emits electron(s).43 They suggested that strong bonds and large structural relaxations imply large defect capture cross sections. Such a qualitative approach can be more firmly grounded using a quantitative study of the defect carrier capture cross section via the computation of the phonon-electron Hamiltonian.16,43,60 As expressed in eqn (3), the emission/capture rate of a defect does not depend solely on the capture cross section. Indeed, the electron emission rate en (resp. ep for holes) is related to its ionisation level in the kesterite band gap with respect to the CBM: EC − Et (resp. to the VBM: Et − EV for holes) and to the capture cross section of the defect σn (resp. σp) following this relation: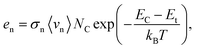 | (3) |
A first general trend that can be observed for each defect is that as the charge state of the defect gets closer to the electronic configuration of the pristine system, the lattice distortion tends to get closer to the reference distance. For example, in the case of a substitutional defect, if both elements have similar atomic radii and if their electronic configurations are close, one could expect the lattice to undergo a small distortion upon defect incorporation.
A similar behaviour is observed in both Cu2ZnSnS4 and Cu2ZnGeS4 concerning defects providing transition levels close to the band gap edges and showing low formation energies (CuZn, ZnCu and VCu). The introduction of the copper vacancy leads only to a small distortion of the lattice as the interatomic distance variation is less than 0.1 Å. In addition, assuming the capture of an electron by such a defect, the value of the interatomic distance remains quite constant in comparison to the one in the pristine lattice. This result supports the readiness of these defects to provide charge carriers in kesterite materials. We report the same behaviour for the substitutional defects CuZn and ZnCu. The results also support that the Cu/Zn disorder commonly observed in Sn-based kesterites should be present in the Ge-based compound as well. In addition, for the GeSn substitutional defect in the Ge-based kesterite, we report a reduction of the X–S (X = Sn,Ge) interatomic distance from 2.46 Å in the Sn-based compound to 2.30 Å in the Ge-based material. This can be interpreted as a direct consequence of the smaller atomic radius of Ge (rGe = 1.25 Å compared to the Sn element: rSn = 1.45 Å (ref. 57)).
Moreover, we observe the largest lattice distortions for both substitutional defects SnCu (resp. GeCu) and SnZn (resp. GeZn) which were identified as possible recombination centres in the previous section. In good agreement with our calculations, Li et al. reported similar values concerning the Sn–S distances for various charged states of the SnZn defect, i.e. 2.71 Å (q = 0), 2.57 Å (q = 1) and 2.43 Å (q = 2) while the values obtained in this work are 2.73 Å, 2.59 Å and 2.49 Å respectively for q = 0, 1 and 2. In addition, the distortion inside the Sn-kesterite is stronger than that found in the Ge-based kesterite. Following the empirical rule proposed by Li et al. in ref. 43, this would lead to a smaller carrier capture cross section in the Ge-compound, partially explaining the smaller VOC deficit reported in the Ge-based kesterite with respect to the Sn-based material.
To summarise, following the Ge incorporation in the Sn-kesterite, from Ge-doping to pure Ge-alloyed materials, we report an increase of the neutral XZn (X = Sn, Ge) substitutional defect formation energies which consequently results in a decrease of the defect concentrations. Secondly, along with this observation, the ionisation levels associated with the XZn (X = Sn, Ge) defect tend to spread within the material band gap as we move from Ge doping to Ge alloying with the (+2/0) transition level still located in the middle of the gap. Finally, from the lattice distortion investigation, we report a reduction of the XZn–S (X = Sn, Ge) interatomic distance, which results in a decrease of the associated carrier capture cross section. In addition to these observations, we previously reported an increase of the VOC value as well as a decrease of the JSC value as a result of the increase of the material band gap from 1.32 eV (Cu2ZnSnS4) to 1.89 eV (Cu2ZnGeS4).40 Combining the results from both investigations, we thus conclude that the improvement of the solar cell efficiency associated with the Ge doping of Sn-based kesterites is ascribed to the improvement of the VOC value while maintaining the JSC value of the Sn-based kesterite cell. In comparison to the Sn counterpart, this enhancement is the result of both the increase of the GeZn substitutional defect formation energy and the reduction of its associated carrier capture cross section. As reported in several studies, both of these observations can be related to the ability of Sn to reduce its oxidation state from 4+ to 2+ known as the “lone-pair” effect while, in contrast, Ge possess only one oxidation state which is 4+.15,16,42
4 Conclusion
This work was devoted to first-principles investigations of Ge-related defects in kesterite. First, we highlight the slightly wider pure phase range of chemical potential values of the Ge-based kesterite compared to the Sn-based kesterite. In both cases, the pure phase remains limited in terms of possible chemical potential ranges due to the numerous secondary phases, which are a direct consequence of all four elements present in these kesterites. Near the stable phase region, the secondary phases are ZnS, CuS and Cu2SnS3 (resp. Cu2GeS3) in the Sn-kesterite (resp. Ge-kesterite). We found a similar physical behaviour of the intrinsic point defects for the Sn-kesterite and the Ge-kesterite. In both compounds, we identified VCu1−, CuZn1− and ZnCu1+ as low formation energy defects acting as acceptors and as donor defects for the latter. By calculating the Fermi level under equilibrium conditions, we confirmed the p-type conductivity reported in the literature for both the Sn-based and the Ge-based compounds. We also shed light on the commonly observed Cu/Zn disorder encountered in kesterite compounds. In addition, via the study of Ge doping in the Sn-kesterite compound, we identified the GeSn neutral defect as a quite spontaneous defect, an indication that the Ge doping within the kesterite matrix occurs via a Sn substitution. Finally, we identified SnZn and GeZn as recombination centres. We reported an increase of the substitutional defect formation energy following Ge-doping and alloying which would result in a decrease of the defect concentration. Moreover, it appeared that the lattice distortion induced by the formation of these defects is reduced for the GeZn substitutional defect in comparison to its Sn counterpart. This result hints at a reduced carrier capture cross section and consequently a less detrimental defect behaviour ascribed to GeZn with respect to SnZn. As a consequence, we point out the reduction of the non-radiative recombination rate induced by both the decrease of the concentration and the reduction of the carrier capture cross section of the detrimental defect XZn (X = Sn, Ge) as one of the sources of the VOC improvement reported in the literature upon Ge incorporation.The objective of this work was to strengthen the understanding of the effects of Ge doping and Ge alloying in kesterite materials for photovoltaic applications. We believe that our results clarified the fundamental mechanisms that operate at the atomic scale via the formation of a wide range of point defects and linked them to photovoltaic property enhancement of Ge-based kesterite reported in previous studies.
Author contributions
All authors contributed to the elaboration of the study and the main conceptual ideas. The data production and analysis, the figure elaboration and the interpretations as well as the writing, editing and review of the manuscript were realised by TR. JY and NDN contributed to the result interpretations, the final discussions and the review of the manuscripts. GB and BV contributed to the result discussion and the final manuscript review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Computational resources have been provided by the Consortium des Équipements de Calcul Intensif (CÉCI), funded by the Fonds de la Recherche Scientifique de Belgique (F. R. S.-FNRS) under Grant No. 2.5020.11 and by the Walloon Region. J. Y. R. thanks the F. R. S.-FNRS for the ABIGLO grant J.0154.21. N. D. N. acknowledges the financial support by the F. R. S.-FNRS of Belgium (project J.0124.19). We would also like to acknowledge Robert B. Wexler and the research group of Prof. Emily Carter for the fruitful discussions shared concerning Ge-related defects in kesterite materials.Notes and references
- M. Green, E. Dunlop, J. Hohl-Ebinger, M. Yoshita, N. Kopidakis and X. Hao, Prog. Photovoltaics Res. Appl., 2021, 29, 3–15 CrossRef.
- M. Nakamura, K. Yamaguchi, Y. Kimoto, Y. Yasaki, T. Kato and H. Sugimoto, IEEE J. Photovolt., 2019, 9, 1863–1867 Search PubMed.
- S. Giraldo, Z. Jehl, M. Placidi, V. Izquierdo-Roca, A. Pérez-Rodríguez and E. Saucedo, Adv. Mater., 2019, 31, 1806692 CrossRef PubMed.
- T. Ratz, G. Brammertz, R. Caballero, M. León, S. Canulescu, J. Schou, L. Gütay, D. Pareek, T. Taskesen, D.-H. Kim, J. K. Kang, C. Malerba, A. Redinger, E. Saucedo, B. Shin, H. Tampo, K. Timmo, N. D. Nguyen and B. Vermang, J. Phys.: Energy, 2019, 1, 042003–042024 CAS.
- T. Todorov, H. Hillhouse, S. Aazou, Z. Sekkat, O. Vigil-Galán, S. Deshmukh, R. Agrawal, S. Bourdais, M. Valdés and P. Arnou, et al. , J. Phys.: Energy, 2020, 2, 012003 CAS.
- S. Chen, A. Walsh, X.-G. Gong and S.-H. Wei, Adv. Mater., 2013, 25, 1522–1539 CrossRef CAS PubMed.
- S. Kim, J.-S. Park and A. Walsh, ACS Energy Lett., 2018, 3, 496–500 CrossRef CAS.
- M. Grossberg, J. Krustok, C. J. Hages, D. M. Bishop, O. Gunawan, R. Scheer, S. M. Lyam, H. Hempel, S. Levcenco and T. Unold, J. Phys.: Energy, 2019, 1, 044002 CAS.
- K. Pal, P. Singh, A. Bhaduri and K. B. Thapa, Sol. Energy Mater. Sol. Cells, 2019, 196, 138–156 CrossRef CAS.
- M. Dimitrievska, A. Fairbrother, E. Saucedo, A. Pérez-Rodríguez and V. Izquierdo-Roca, Sol. Energy Mater. Sol. Cells, 2016, 149, 304–309 CrossRef CAS.
- S. Schorr, G. Gurieva, M. Guc, M. Dimitrievska, A. Pérez-Rodríguez, V. Izquierdo-Roca, C. S. Schnohr, J. Kim, W. Jo and J. M. Merino, J. Phys.: Energy, 2019, 2, 012002 Search PubMed.
- C. Platzer-Björkman, N. Barreau, M. Bär, L. Choubrac, L. Grenet, J. Heo, T. Kubart, A. Mittiga, Y. Sánchez, J. Scragg, S. Sinha and M. Valentini, J. Phys.: Energy, 2019, 1, 044005–044022 Search PubMed.
- A. Crovetto and O. Hansen, Sol. Energy Mater. Sol. Cells, 2017, 169, 177–194 CrossRef CAS.
- T. Gokmen, O. Gunawan, T. K. Todorov and D. B. Mitzi, Appl. Phys. Lett., 2013, 103, 103506 CrossRef.
- K. Biswas, S. Lany and A. Zunger, Appl. Phys. Lett., 2010, 96, 201902 CrossRef.
- S. Kim, J.-S. Park, S. N. Hood and A. Walsh, J. Mater. Chem. A, 2019, 7, 2686–2693 RSC.
- Y. Gong, Y. Zhang, Q. Zhu, Y. Zhou, R. Qiu, C. Niu, W. Yan, W. Huang and H. Xin, Energy Environ. Sci., 2021, 14, 2369–2380 RSC.
- Y. E. Romanyuk, S. G. Haass, S. Giraldo, M. Placidi, D. Tiwari, D. J. Fermin, X. Hao, H. Xin, T. Schnabel, M. Kauk-Kuusik, P. Pistor, S. Lie and L. H. Wong, J. Phys.: Energy, 2019, 1, 044004–044023 CAS.
- A. Crovetto, S. Kim, M. Fischer, N. Stenger, A. Walsh, I. Chorkendorff and P. C. Vesborg, Energy Environ. Sci., 2020, 13, 3489–3503 RSC.
- M. V. Jyothirmai, H. Saini, N. Park and R. Thapa, Sci. Rep., 2019, 9, 1–12 CAS.
- J. Li, D. Wang, X. Li, Y. Zeng and Y. Zhang, Adv. Sci., 2018, 5, 1700744 CrossRef PubMed.
- M. Neuschitzer, M. E. Rodriguez, M. Guc, J. A. Marquez, S. Giraldo, I. Forbes, A. Perez-Rodriguez and E. Saucedo, J. Mater. Chem. A, 2018, 6, 11759–11772 RSC.
- Q. Tian and S. F. Liu, J. Mater. Chem. A, 2020, 8, 24920–24942 RSC.
- Z.-K. Yuan, S. Chen, H. Xiang, X.-G. Gong, A. Walsh, J.-S. Park, I. Repins and S.-H. Wei, Adv. Funct. Mater., 2015, 25, 6733–6743 CrossRef CAS.
- W.-C. Huang, S.-Y. Wei, C.-H. Cai, W.-H. Ho and C.-H. Lai, J. Mater. Chem. A, 2018, 6, 15170–15181 RSC.
- M. H. Sharif, T. Enkhbat, E. Enkhbayar and J. Kim, ACS Appl. Energy Mater., 2020, 3, 8500–8508 CrossRef CAS.
- S. Hadke, W. Chen, J. M. R. Tan, M. Guc, V. Izquierdo-Roca, G.-M. Rignanese, G. Hautier and L. H. Wong, J. Mater. Chem. A, 2019, 7, 26927–26933 RSC.
- R. B. Wexler, G. S. Gautam and E. A. Carter, J. Mater. Chem. A, 2021, 9, 9882–9897 RSC.
- S. Khelifi, G. Brammertz, L. Choubrac, M. Batuk, S. Yang, M. Meuris, N. Barreau, J. Hadermann, H. Vrielinck and D. Poelman, et al. , Sol. Energy Mater. Sol. Cells, 2021, 219, 110824 CrossRef CAS.
- B. Vermang, G. Brammertz, M. Meuris, T. Schnabel, E. Ahlswede, L. Choubrac, S. Harel, C. Cardinaud, L. Arzel and N. Barreau, et al. , Sustainable Energy Fuels, 2019, 3, 2246–2259 RSC.
- L. Choubrac, M. Bär, X. Kozina, R. Felix, R. G. Wilks, G. Brammertz, S. Levcenko, L. Arzel, N. Barreau and S. Harel, et al. , ACS Appl. Energy Mater., 2020, 3, 5830–5839 CrossRef CAS.
- S. Giraldo, M. Neuschitzer, T. Thersleff, S. López-Marino, Y. Sánchez, H. Xie, M. Colina, M. Placidi, P. Pistor and V. Izquierdo-Roca, et al. , Adv. Energy Mater., 2015, 5, 1501070 CrossRef.
- Y. Du, S. Wang, Q. Tian, Y. Zhao, X. Chang, H. Xiao, Y. Deng, S. Chen, S. Wu and S. Liu, Adv. Funct. Mater., 2021, 31, 2010325 CrossRef CAS.
- S. Kim, K. M. Kim, H. Tampo, H. Shibata and S. Niki, Appl. Phys. Express, 2016, 9, 102301 CrossRef.
- S. Giraldo, E. Saucedo, M. Neuschitzer, F. Oliva, M. Placidi, X. Alcobé, V. Izquierdo-Roca, S. Kim, H. Tampo and H. Shibata, et al. , Energy Environ. Sci., 2018, 11, 582–593 RSC.
- Y. Deng, Z. Zhou, X. Zhang, L. Cao, W. Zhou, D. Kou, Y. Qi, S. Yuan, Z. Zheng and S. Wu, J. Energy Chem., 2021, 61, 1–7 CrossRef.
- J. Fu, D. Kou, W. Zhou, Z. Zhou, S. Yuan, Y. Qi and S. Wu, J. Mater. Chem. A, 2020, 8, 22292–22301 RSC.
- M. He, J. Huang, J. Li, J. S. Jang, U. P. Suryawanshi, C. Yan, K. Sun, J. Cong, Y. Zhang and H. Kampwerth, et al. , Adv. Funct. Mater., 2021, 2104528 CrossRef CAS.
- W. Wang, M. T. Winkler, O. Gunawan, T. Gokmen, T. K. Todorov, Y. Zhu and D. B. Mitzi, Adv. Energy Mater., 2014, 4, 1301465 CrossRef.
- T. Ratz, J.-Y. Raty, G. Brammertz, B. Vermang and N. D. Nguyen, J. Phys.: Energy, 2021, 3, 035005 CAS.
- H. Nishihara, T. Maeda, A. Shigemi and T. Wada, Jpn. J. Appl. Phys., 2017, 56, 04CS08 CrossRef.
- R. B. Wexler, G. S. Gautam and E. A. Carter, Phys. Rev. B, 2020, 102, 054101 CrossRef CAS.
- J. Li, Z.-K. Yuan, S. Chen, X.-G. Gong and S.-H. Wei, Chem. Mater., 2019, 31, 826–833 CrossRef CAS.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253 CrossRef.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235104 CrossRef.
- C. Persson, Y.-J. Zhao, S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035211 CrossRef.
- J. S. Park, S. Kim, Z. Xie and A. Walsh, Nat. Rev. Mater., 2018, 3, 194–210 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- J. Sun, R. C. Remsing, Y. Zhang, Z. Sun, A. Ruzsinszky, H. Peng, Z. Yang, A. Paul, U. Waghmare and X. Wu, et al. , Nat. Chem., 2016, 8, 831 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- D. Fritsch and S. Schorr, J. Phys.: Energy, 2020, 3, 015002 Search PubMed.
- J. Just, C. M. Sutter-Fella, D. Lützenkirchen-Hecht, R. Frahm, S. Schorr and T. Unold, Phys. Chem. Chem. Phys., 2016, 18, 15988–15994 RSC.
- W. Wang, M. T. Winkler, O. Gunawan, T. Gokmen, T. K. Todorov, Y. Zhu and D. B. Mitzi, Adv. Energy Mater., 2013, 4, 1301465 CrossRef.
- J. C. Slater, J. Chem. Phys., 1964, 41, 3199–3204 CrossRef CAS.
- S. Ma, H. Li, J. Hong, H. Wang, X. Lu, Y. Chen, L. Sun, F. Yue, J. W. Tomm and J. Chu, et al. , J. Phys. Chem. Lett., 2019, 10, 7929–7936 CrossRef CAS PubMed.
- G. Rey, G. Larramona, S. Bourdais, C. Choné, B. Delatouche, A. Jacob, G. Dennler and S. Siebentritt, Sol. Energy Mater. Sol. Cells, 2018, 179, 142–151 CrossRef CAS.
- A. Alkauskas, Q. Yan and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 075202 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Further details about the theoretical framework used to compute the formation energy of point defects, the phase diagrams, the Fermi energy level under thermodynamic equilibrium conditions and the formation energy correction terms are provided. In addition, the specific formation energy values of the kesterite materials, secondary phases and the chemical potential values of the points labelled in the phase diagrams are provided as well as the kesterite lattice parameters. Relaxed structures (CONTCAR) and raw calculation outputs (WAVECAR, CHGCAR,etc.) as well as the resulting calculation total energies are available upon reasonable request to the corresponding author. See DOI: 10.1039/d1ta09620f |
| This journal is © The Royal Society of Chemistry 2022 |


