Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interface effects from moisture in nanocomposites of 2D graphene oxide in cellulose nanofiber (CNF) matrix – A molecular dynamics study†
Hanieh
Mianehrow
 ,
Lars A.
Berglund
,
Lars A.
Berglund
 and
Jakob
Wohlert
and
Jakob
Wohlert
 *
*
Department of Fibre and Polymer Technology, Wallenberg Wood Science Center, KTH Royal Institute of Technology, Teknikringen 56, 100 44 Stockholm, Sweden. E-mail: jacke@kth.se
First published on 4th January 2022
Abstract
Molecular dynamics (MD) simulation is used to study effects from moisture at cellulose nanofibril (CNF)–graphene oxide (GO) interfaces adhering in the wet state. Two CNF models with different surface chemistry are used: native cellulose nanofibrils (NCNF) and TEMPO-oxidized cellulose nanofibrils (TOCNF). Work of adhesion and interfacial shear strength at the CNF–GO interface is compared with CNF–graphene interfaces to interpret interaction mechanisms. Any trapped interfacial water reduces adhesion strongly. Results show, however, that there is a meta-stable state where water is initially present at the CNF–GO interface but disappears with time to form a dry interface. Once a solvent-excluded interface is formed between CNF and GO, the surface oxidation has little effect on molecular adhesion. We propose that the main adhesion mechanism is entropy gain from release of water molecules as CNF and GO jump into contact when brought close together. Hydrogen bonding does not govern the work of adhesion between CNF and GO, but plays an important role for interfacial shear strength.
Introduction
Polymers are strongly reinforced by well-dispersed 2D nanoplatelets oriented in-plane. Young's modulus and tensile strength can reach high values for such nanocomposites, especially for strong, high aspect ratio nanoplatelets.1 Graphene,2,3 graphene oxide,4 clay,5 molybdenum disulfide6 and boron nitride7 are examples of 2D reinforcements which, besides mechanical properties, also can provide good gas barrier properties, fire retardancy, electrical properties and thermal conductivity.Many nanoplatelets have a thickness of only approx. 1 nm, so the specific surface area and the cross-sectional interface density (number of interfaces per unit thickness) in nanocomposites can be very high. The nanoplatelet/matrix interfacial interactions are thus critical during formation of the nanostructure, but they also offer tremendous opportunities for unique nanocomposite properties if molecular adhesion mechanisms8 can be controlled. Here, we are using molecular dynamics (MD) to simulate interfacial interactions (work of adhesion, interfacial shear strength) in cellulose–graphene oxide and graphene nanocomposites and investigate mechanisms for moisture effects. Results can guide processing efforts for high volume fraction nanocomposites9 and may inspire new drying procedures but also ideas for chemical surface modification of the nanoparticles. The interface is critical for the strength/toughness balance in 2D nanocomposites,10 and simply needs to be better understood.
Cellulose nanofibrils (CNF)5,11 constitute the matrix phase in the present nanocomposite models. Experimentally, after vacuum filtration and drying, CNF hydrocolloids can form almost non-porous high-strength films with flexible CNF fibrils (approx. 4 nm by 1 μm) in swirled, densely packed structures.12 Most likely, large capillary forces13 are responsible for film formation during drying, and fibrils are plastically deformed14 so that nanoscale porosity is reduced. The first 2D nanoplatelet composites with CNF matrix were prepared in our lab15,16 simply by mixing two hydrocolloids (one with CNF and one with nanoplatelets) followed by vacuum filtration. CNF offers considerable advantages in the development of more sustainable nanomaterials. In addition, polymer matrix nanocomposites based only on physically interacting nano-objects can be readily functionalized and possibly recycled.
Graphene oxide, the oxidized derivative of graphene, can have a Young's modulus of around 250 GPa.17 The oxidation introduces different functionalities such as hydroxyl, epoxy and carboxyl groups,18,19 which facilitates GO dispersion in water and reduces the aggregation problems observed for graphene.
The properties of both CNF-based20–23 and GO-based24–26 nanomaterials are influenced by moisture. Barthelat and colleagues showed that GO membranes can be given complex shapes in the wet state by the use of 25% of cellulosic slurries of fibres 50–2600 μm in length.27 3D printing of CNF inks is a real possibility,28 where it should be possible to include 2D nanosheets. For CNF–GO nanocomposites, there are not so many previous studies,29–32 whereas graphene or reduced GO have been used more frequently30,33–36 when high electrical conductivity is desirable. (A table comparing mechanical properties reported in the literature is presented in ref. 29). We have recently investigated the mechanical behaviour of CNF–GO nanocomposites,29 and carefully characterized the nanostructure using wide angle X-ray scattering (WAXS) and small angle X-ray scattering (SAXS) techniques. The gas barrier properties were influenced by moisturizing–drying cycles, where interfacial interactions seemed to improve by moisture cycling, although in general, aspects of molecular adhesion effects are poorly understood.
There are some interesting previous molecular scale investigations of the cellulose-GO interface. As a background, one may note that moisture at cellulose–cellulose interfaces increases ductility in films from nanocellulose rods37 and that also GO–GO interaction is influenced by moisture.38 The cellulose–GO interfaces are, however, specific and need careful investigation. Rahman et al.39 investigated a model graphene–amorphous cellulose composite and identified basic parameters of importance for mechanical behaviour. Mao et al.40 simulated XRD spectra in GO–cellulose nanocrystal composites, and interpreted mechanisms for changes in the (200) lattice parameters from interactions with GO. Alqus et al.41 performed MD simulations of native cellulose and graphene in water. They found a stable, “solvent-excluded” (no water) interface between graphene and the “hydrophobic” cellulose face in water. Zhu et al.42 investigated GO–TEMPO (2,2,6,6-tetramethylpiperidine-1-oxyl radical)-mediated oxidized CNF systems with small GO sheets and large CNF “fibres”, with focus on the material system rather than on interfacial adhesion details. The most relevant previous study to the present work was by Tsukruk and colleagues,43 who combined experiments and MD simulations to investigate the assembly of GO and oxidized TEMPO-CNF in water. Focus was on effects from GO oxidation degree and formation of the nanoobjects, although the role of water was not analysed in detail. Simulations showed the importance of, in particular, the van der Waals interactions across the interface.
Here, molecular adhesion is investigated at CNF/GO, TEMPO-CNF/GO and graphene interfaces in the presence of water. The objectives are to quantify work of adhesion and interfacial shear strength, describe interaction mechanisms and clarify the role of water for materials design purposes. In the lowest energy state (equilibrium), there is no water present at the interfaces, but if water becomes kinetically trapped (e.g., during drying) it substantially reduces adhesion. In either case, the net effect from hydrogen bonding is negligible. The potential of interface tailoring of nanocomposites at molecular scale is apparent from the present results.
Methods
Model development and molecular dynamics simulations
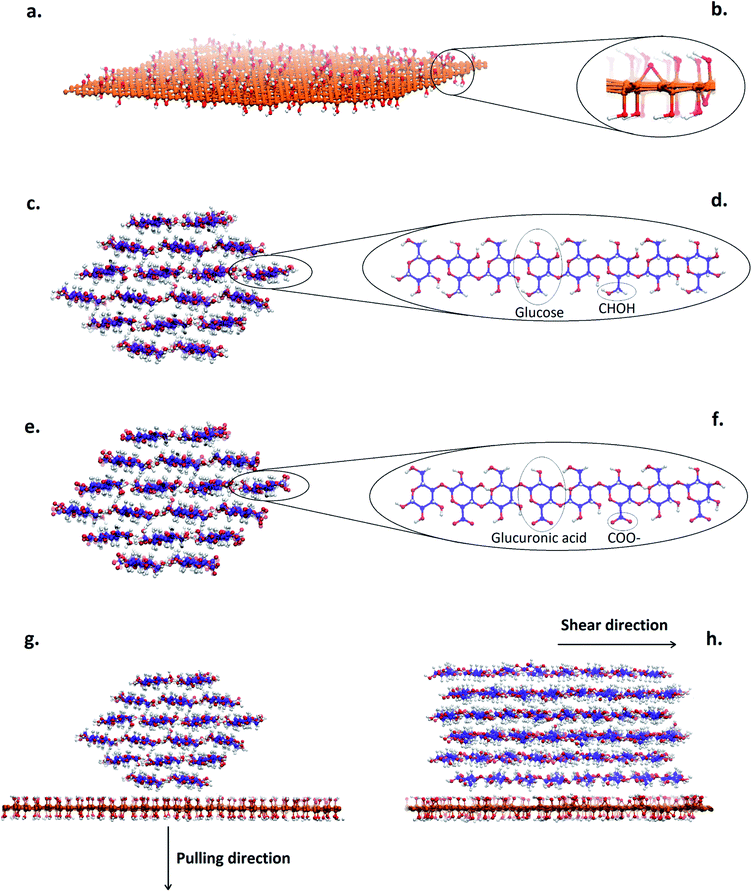
A graphene model was constructed from 1472 carbon atoms in a hexagonal lattice with lateral size 7 nm × 6 nm. Carbon atoms on the edges of the sheet were covalently bonded to the opposite side of the sheet over the periodic box boundary, which makes the graphene sheet infinitely large. The graphene was further randomly functionalized on both sides by adding hydroxyl and epoxy groups to make GO. The total epoxy to hydroxyl ratio was 25% to resemble common GO made by Hummer's method.44The native cellulose nanofibril (NCNF) model was constructed from 18 glucan chains, each with 8 glucose units, arranged in a hexagonal cross-section, which currently is the most accepted model45–48 (Fig. 1c and d). This NCNF model is a result of cellulose biosynthesis arguments,49,50 with support from SAXS data.51. In the TEMPO-oxidized cellulose nanofibril (TOCNF), every other glucose unit in the surface chains was substituted for a glucuronic acid unit to represent highly oxidized TOCNF. Carboxyl groups were arranged such that they were all exposed to the outside of the crystal. Chains in the centre of the TOCNF crystal remained chemically identical to NCNF (Fig. 1e and f).
Two “nanocomposite” systems of NCNF–GO and TOCNF–GO were built by placing the CNFs in close proximity of the GO, with the crystallographic (2 0 0) plane of the CNFs exposed to the GO (Fig. 1g). Simulations in which the (1 1 0) plane was exposed to the GO were also performed. However, during equilibration the CNF spontaneously rotated to expose its (2 0 0) plane to the GO, indicating that this is the most stable configuration in line with what was reported by Alqus et al.41 Finally, Na+ counter ions were added to the TOCNF–GO system to neutralize the negative charge. Systems with graphene were built in a similar manner.
MD simulations were performed using GROMACS 2019.4 (ref. 52) with a basic time step of 1 fs. The non-bonded interactions used a cut-off distance of 1.2 nm and long-range electrostatic interactions were employed using PME.53,54 Bonds were kept rigid at their equilibrium lengths using P-LINCS.55 The pressure was maintained at 1 atm using Parrinello–Rahman barostat56 with semi-isotropic coupling and temperature was maintained at 298 K using a Nosé–Hoover thermostat.57,58 GLYCAM06 (ref. 59) parameters were used for the carbohydrates, combined with GAFF60 for graphene/GO, and the TIP3P61 water model. Parameters for the Na+ ions were taken from ref. 62.
Since the purpose of the study is to investigate the effect of moisture at the CNF–GO interface, MD simulations of the CNF–GO systems were performed both in a box filled with water, and in vacuum. For the CNF–GO nanocomposites immersed in water, the CNF and GO were positioned close to each other, see Fig. 1g, but each particle was completely surrounded by liquid water. Each system was equilibrated for 10 ns. To study the effect of drying history, the dry nanocomposites in vacuum were equilibrated, wetted in water and equilibrated for an additional period of 10 ns. This condition is termed “dry-wetted”. The VMD package was used to visualize simulated nanocomposite systems.63 All systems were energy-minimized using steepest descents prior to simulations.
Potential of mean force calculations for work of adhesion
The potential of mean force (PMF) between the CNF and the GO in different environments was calculated to investigate molecular adhesion and estimate work of adhesion WA. Umbrella sampling was used, where the umbrella simulations used the centre-of-mass distance between the CNF and the GO as reaction coordinate. 101 intermediate states in 0.5 Å intervals were used for umbrella simulations in the CNF–GO systems. These states were prepared by starting from each equilibrated structure and then pull the CNF–GO complex apart by varying the reference centre-of-mass distance continuously during 50 ns of MD. Here, positional restraints were applied on the CNF and a spring constant of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−1 was used. For the umbrella sampling, each state was simulated for 1 ns and a harmonic restraining potential acting on the centre-of-mass distance between the CNF and the GO was employed with a force constant of 50
000 kJ mol−1 nm−1 was used. For the umbrella sampling, each state was simulated for 1 ns and a harmonic restraining potential acting on the centre-of-mass distance between the CNF and the GO was employed with a force constant of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−1. No additional positional restraints were applied during the umbrella sampling simulations. Weighted histogram analysis (WHAM)64 was used to construct the full PMF for each system. This gives the free energy of separation between the CNF and the GO and can be converted into work of adhesion by normalizing the results over the initial contact area. The contact area was calculated based on the projected area of the CNF on the GO/graphene (see Fig. S1†), which may be conservative, since the real area of molecular contact may be smaller than this. The error bar for each point in PMF was estimated using bootstrapping.65
000 kJ mol−1 nm−1. No additional positional restraints were applied during the umbrella sampling simulations. Weighted histogram analysis (WHAM)64 was used to construct the full PMF for each system. This gives the free energy of separation between the CNF and the GO and can be converted into work of adhesion by normalizing the results over the initial contact area. The contact area was calculated based on the projected area of the CNF on the GO/graphene (see Fig. S1†), which may be conservative, since the real area of molecular contact may be smaller than this. The error bar for each point in PMF was estimated using bootstrapping.65
Interfacial shear strength calculations for shear slippage between CNF and GO
Interfacial shear strength between reinforcement and surrounding matrix is a key property for composites and is critical for reinforcement pull-out mechanisms during failure, which influence tensile strength and fracture toughness.66 Shear slippage between the GO or graphene platelet and the CNF matrix was induced using constant force loading. The force was applied to the CNF centre-of-mass in the longitudinal CNF direction (Fig. 1h), so that shear is induced at the interface. Depending on the system, the force was varied in steps of 10–100 kJ mol−1 nm−1 until slippage occurred within a 10 ns simulation. Positional restraints were applied on the GO/graphene. Interfacial shear strength was determined as the minimum force required to slide the CNF on the GO or graphene, divided by the initial contact area.Results and discussion
CNF and GO interface interactions were investigated in different environments to support interpretation of moisture effects on global mechanical behaviour of CNF/GO nanocomposites. Native NCNF–GO and oxidized TOCNF–GO were simulated immersed in water, in the dry vacuum state and also in dry-wetted state where the dry nanocomposites in vacuum were subsequently exposed to water (see Methods).The CNF–GO interface
Fig. 2a and b show the final configurations after 10 ns unconstrained simulation in water. Spontaneous adsorption of both types of CNF to the GO is observed, where they jumped into contact. In both cases, however, water is present at the CNF–GO interface. Note that there is more water at the TOCNF–GO interface due to the Na+ ions surrounding TOCNF in water. Zonghui et al.67 reported that the presence of monovalent counter-ions physically increases the distance between two adjacent cellulose crystals and hence decreases the molecular adhesion between them. Here we observe a similar effect from Na+ counter-ions in TOCNF–GO system, but the question is whether the water layer at the interface would disappear after longer simulation times?Fig. 2c and d show the configurations after 100 ns simulation in water. Now the water layer has disappeared for NCNF–GO, while it remains at the TOCNF–GO interface even after 100 ns. In Fig. 2e and f, both systems are simulated in vacuum for 10 ns, with no water present. The CNF quickly adheres to the GO, and since there is no water, the CNF and GO can immediately form a tight interface with molecular/atomic contact (Fig. 2e and f). Note from the images that the CNF deforms strongly as it adheres to GO due to the strong adhesion forces. Finally, the dry nanocomposites in vacuum were wetted (Fig. 2g and h). These dry–wetted nanocomposites largely retain the tight interfaces formed in the dry state, even after longer (100 ns) times, and only a few water molecules are observed at the interface between the CNF and the GO.
These simulations show that water may become kinetically trapped at the interface between CNF and GO. This is expected to influence mechanical properties. For native NCNF immersed in water, water leaves spontaneously, forming a dry NCNF/GO interface. This case of “solvent-excluded contact” then represents the global equilibrium and the kinetically trapped water condition is temporary. For TOCNF however, simulation results are not conclusive about which state is lower in energy: with or without water at the interface. Therefore, the work of adhesion between CNF and GO is further investigated in the following section. As expected, there is no water inside the CNFs and moisture effects are dominated by interparticle interface effects.
Interfacial adhesion
Fig. 3 shows potential of mean force (PMF) versus separation distance between CNF and GO, measured perpendicular to the interface. The reference level is selected as the fully separated state, where there is no interaction between the CNF and GO, since this state is the same across the different simulations. Here, the value of the PMF is zero. In this representation, the PMF is the free energy per unit contact area gained by moving the CNF and GO to a separation distance z, relative to the non-interacting state. The work of adhesion, WA thus is the lowest PMF value, which is obtained at contact but with the opposite sign (Fig. 3a). The use of umbrella sampling presupposes (local) equilibrium conditions. This facilitates the thermodynamic analysis and is actually necessary to estimate WA, since it is an equilibrium property by definition. CNF–GO trajectories at different separation distances are shown in Fig. 3b.Fig. 3 also shows the effect of water at the CNF–GO interface. The WA for NCNF–GO after 10 ns in water is much lower than for NCNF–GO after 100 ns in water (Fig. 3c). After 10 ns, there is still water at the interface, but this has disappeared after 100 ns. Interestingly, the dry–wetted interface gives similar WA as for the 100 ns NCNF–GO case for simulation in water. This supports the previous observation that water does not penetrate into the interface during soaking of a dry interface in water. We can now draw conclusions about water in the TOCNF–GO nanocomposite interfaces: a similar WA trend is observed for TOCNF–GO in Fig. 3d as for the previous NCNF–GO. The WA is higher for TOCNF–GO after 100 ns in water than after 10 ns in water, since water is leaving the interface after a longer equilibration time, compare Fig. 2b and d. The dry–wetted interface even gives the highest WA in this case. The reason is that for TOCNF–GO, some water remains at the interface even after 100 ns (Fig. 2d). WA data for each system is reported in Table 1. A similar behaviour was recently shown in MD simulations of interacting NCNFs in water.68
| System | State | Number of CNF–GO hydrogen bonds | Potential of mean force (kJ mol−1) | Work of adhesion (mJ m−2) | Interfacial adhesion strength (MPa) | Interfacial shear strength (MPa) |
|---|---|---|---|---|---|---|
| NCNF–GO | 10 ns in water | 6 ± 2.0 | 114.0 ± 0.5 | 10.5 ± 1.8 | 36.04 ± 1.5 | 55.3 ± 1.8 |
| 100 ns in water | 11 ± 4.0 | 235.5 ± 3.0 | 28.3 ± 1.8 | 186.3 ± 4.5 | — | |
| 10 ns dry/vacuum | 31 ± 5.0 | ≥1650.0 | ≥120 | — | — | |
| Dry/vacuum + 10 ns wetted | 17 ± 3.0 | 249.1 ± 4.4 | 27.6 ± 2.5 | 97.9 ± 4.7 | — | |
| TOCNF–GO | 10 ns in water | 1 ± 1.0 | 65.3 ± 0.4 | 7.7 ± 0.5 | 21.8 ± 1.1 | 41.5 ± 1.3 |
| 100 ns in water | 6 ± 2.0 | 129.2 ± 3.5 | 12.0 ± 1.2 | 31.7 ± 2.3 | 53.4 ± 1.8 | |
| 10 ns dry/vacuum | 36 ± 4.0 | ≥1650.0 | ≥120 | — | — | |
| Dry/vacuum + 10 ns wetted | 31 ± 2.0 | 242.7 ± 7.3 | 28.8 ± 3.2 | 93.3 ± 4.6 | — | |
| NCNF–graphene | 10 ns in water | 0 | 307.8 ± 5.2 | 29.2 ± 1.7 | 126.6 ± 6.3 | 4.8 ± 0.2 |
| TOCNF–graphene | 10 ns in water | 0 | 184.5 ± 0.5 | 17.0 ± 1.0 | 71.6 ± 3.6 | 3.7 ± 0.1 |
The difference between the WA of dry–wetted TOCNF–GO and TOCNF–GO after 100 ns in water, suggests an influence of the drying history. It indicates that the hydrated interface is a meta-stable state and that the hydration/dehydration process is kinetically controlled and the stable state is essentially a dry TOCNF–GO interface. In essence, this is analogous to the concept of cellulose fibril co-crystallization (hornification), which is the term used for the strong aggregation of native cellulose fibrils when dried from wet state.69–71
In an attempt to quantify interfacial interactions in dry/vacuum state, we observed very high adhesion forces between CNF and GO. For this case, the CNF does not detach completely from GO during the separation simulations and the PMF graph does not level off (Fig. S3†). The interfacial adhesion forces are so strong that if no positional constraints are used for CNF, the CNF itself is failing during separation simulations. This is visualized in Fig. S4† and the WA in dry/vacuum state is therefore reported as ≥120 in Table 1.
To investigate the significance of GO surface oxidation for CNF–GO, simulations of NCNF–graphene and TOCNF–graphene were performed in water and the corresponding WA were calculated. Fig. 3e compares the PMF curves for NCNF–graphene and TOCNF–graphene. Here, 10 ns of simulation was enough to achieve a completely solvent-excluded, dry interface between the CNF and the graphene (no interfacial water, Fig. S2†). Interestingly, the meta-stable state (hydrated interface) is observed as a small dent at around 1.7 nm separation, which corresponds to one hydration layer between CNF and graphene. For the case of graphene, this state is relatively short-lived. Both NCNF–graphene and TOCNF–graphene exhibit similar behaviour, although TOCNF–graphene has lower WA, again possibly due to the presence of Na+ counter ions.
In the Fig. 3f–h, the same data is replotted as stress vs. displacement for pedagogical purpose. The slope of the PMF curve is simply translated into “stress”, although this is most often a macroscopic parameter. The specific procedure (see Methods) may influence the shape of the curve and is introducing uncertainties in this respect. The area under the stress–displacement curve is, however, of high accuracy. Here, the displacement is measured from the point where the stress changes sign, which is the equilibrium separation distance. The maximum value in these curves is the interfacial adhesion strength. This data is also reported in Table 1 for each case. Note that these stress levels for molecular adhesion are expected to be higher than stresses measured in micromechanical experiments involving cellulosic fibres, due to factors such as contaminants or non-ideal molecular scale contact. Fig. 3f shows that for NCNF–GO the strength is the lowest when there is water present at the interface. Once the interface becomes solvent-excluded (dry) the interfacial strength increases drastically. It is interesting that the strength is much higher for 100 ns adsorption in water than the dry–wetted structure, although WA is the same for both. The reason for similar WA is that lower strength interfaces carry higher stress at larger displacements. A similar trend for moisture effects is observed for TOCNF–GO where the wet interfaces both show lower adhesion strength than the solvent-excluded interface (Fig. 3g). This is consistent with results from a MD study on acetylated CNF which shows that the lack of solvent-excluded interface between acetylated CNFs reduces WA significantly.72 Importantly, with no water at the interface, both NCNF–GO and TOCNF–GO exhibit similar work of adhesion (Table 1). In the case of graphene, the strength is higher for NCNF–graphene than TOCNF–graphene (Fig. 3h), possibly due to the presence of counter ions in the latter case.
A general observation from Fig. 3c–h is that water is apparently the main factor influencing curves of PMF versus separation distance and WA, despite the substantial interface differences between these four systems, (NCNF–GO, TOCNF–GO, NCNF–graphene, TOCNF–graphene). When there is no water at the interface, the WA is similar in all cases, and for NCNF–GO, TOCNF–GO and NCNF–graphene, they are the same. Thus, in the following sections, various interaction mechanisms are analysed.
Interaction mechanisms for work of adhesion
To analyse the adhesion, it is important to study the work of adhesion between CNF and GO as calculated in the previous section. It is defined by the difference in total excess Helmholtz’ free energy, ΔAex, between the adsorbed and desorbed states. Since ΔAex is an excess property, it is independent of concentration effects from CNF or GO. Using the familiar relation ΔA = ΔE − TΔS (where the superscript is dropped for convenience) it is possible to analyse energetic (ΔE) and entropic (ΔS) contributions to WA separately, and also to further decompose these parts into contributions from specific interactions.The typical explanation for interfacial adhesion in cellulose materials is strong ability of cellulose surfaces to form hydrogen bonds. It has indeed been suggested that hydrogen bonds between CNF and GO are responsible for interfacial adhesion.40 Considering that a typical bond energy for a hydrogen bond is 20 kJ mol−1,73 the WA's obtained here for the dry–wetted systems correspond to breaking one hydrogen bond per nm2, which is quite reasonable. The summary in Table 1 shows correlation between hydrogen bonds and work of adhesion, which seems enough to conclude a strong effect from hydrogen bonds. However, this conclusion is actually wrong. First of all, interfacial hydrogen bonds in wet systems can be readily replaced by hydrogen bonds to water molecules, e.g., when CNF and GO are separated. Indeed, the total number of hydrogen bonds in the NCNF–GO system before and after separation shows no significant difference (Table 2). Since work of adhesion is calculated by comparing energy states before and after separation, this means that the total contribution to work of adhesion from forming and breaking hydrogen bonds is close to zero. Another argument against hydrogen bond effects is that the WA between CNF and graphene was quite substantial (29 mJ m−2, similar to dry–wetted NCNF–GO), although graphene lacks surface functionalization and cannot form any hydrogen bonds to the CNF. Thus, it is apparent that hydrogen bonding cannot be the main adhesion mechanism between NCNF and GO. This is consistent with previous simulation studies that found that hydrogen bonding is not the dominant interaction mechanism in polymer–GO interfaces.74,75
| System | Total H-bonds before separation | Total H-bonds after separation |
|---|---|---|
| NCNF–GO | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 954 ± 13 954 ± 13 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 964 ± 7 964 ± 7 |
| TOCNF–GO | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 458 ± 8 458 ± 8 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 515 ± 10 515 ± 10 |
| NCNF–graphene | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 748 ± 6 748 ± 6 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 745 ± 7 745 ± 7 |
| TOCNF–graphene | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 ± 6 730 ± 6 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 690 ± 6 690 ± 6 |
The data for TOCNF-based systems are not conclusive, since the presence of counter-ions affects hydrogen bond formation.
Let us then return to the free energy analysis based on ΔAex. To better understand the molecular mechanisms for strong adhesion between CNF and GO, the internal energy contribution to WA was calculated from the difference in total potential energy before and after separation. For NCNF it was ΔE = −10 mJ m−2, and for TOCNF it was ΔE = −390 mJ m−2. Since these contributions are negative in both cases, these effects are working against adhesion. The largest contribution to the potential energy difference originates in the structural deformation of the CNF as it becomes adsorbed to GO, see Fig. 2 (and in-depth discussion in ESI†).
Since ΔE < 0, the dominating mechanism for the adhesion must be of entropic origin. A water molecule close to a solid attractive interface will have lower entropy than a water molecule in the liquid bulk, since its translational and rotational mobility is restricted. MD simulations of hydrated cellulose surfaces show a free energy penalty of 2–4 kJ mol−1 per water molecule.76,77 From the liquid water number density one can estimate the number of interfacial water molecules in the first hydration layer to approx. 10 nm−2, which gives a contribution of 66–133 mJ m−2. In reality it is higher since the water density close to a hydrophilic surface typically is larger than in the pure liquid.76,77 This conservative estimate is large enough to dominate WA for the case of NCNF–GO, but it becomes too small to explain adhesion for TOCNF–GO alone.
We propose that the adhesion of CNF to GO in the wet state is dominated by a gain in free energy from the reduction of interfacial water molecules upon CNF adsorption, which thus explains why a partially hydrated interface becomes weaker (Fig. 2 and Table 1).
Such water-mediated entropic force is akin to the driving force of hydrophobic assembly. The free energy of the system ΔAex is decreased if water is removed from the interface, even for hydrophilic substrates such as cellulose. This was previously shown to be the dominating contribution to adhesion of hydrophilic xyloglucan to cellulose.76
Interfacial shear strength
Interfacial shear strength between reinforcement and surrounding matrix is a key property for composites and is critical for reinforcement pull-out mechanisms during failure, which influence tensile strength and fracture toughness.66 Interfacial shear strength between the CNF and the GO was calculated from the minimum force required to initiate sliding of CNF on the GO in longitudinal direction, τmax = Fmin/A, where A is the contact area. Thus, Fmin is the static friction force. A typical value for interfacial shear strength between plant fibers and polymeric matrices from micromechanics tests is 2–13 MPa.78–82 Interfacial shear strength values for GO–GO interface is investigated theoretically in the literature38,83 and is reported to be 17–132 MPa depending on the surface chemistry of GO and the relative humidity of the environment. Just as experimental values can depend strongly on the loading rate, the τmax calculated from MD simulations can depend on the simulation time. Assuming that plastic shear deformation is an activated process, the value obtained from MD simulations represents an upper limit. For activated rate processes, slippage would occur at a lower shear force if the material system is loaded during longer time.The simulated interfacial shear strength τmax at onset of sliding is higher for NCNF–GO than for TOCNF–GO (55.3 MPa and 41.5 MPa respectively, Table 1). Fig. 4a and b shows profiles of the sliding distance as a function of time for NCNF–GO and TOCNF–GO. Note that the applied force is constant and higher for NCNF–GO in Fig. 4b, since the interfacial strength is higher. The NCNF–GO nanocomposite shows so-called stick–slip behaviour during sliding,84 which is related to breakage and formation of intermolecular bonds under shear forces (Fig. 4a). This effect is very weak for TOCNF–GO, since there is more water at this interface which facilitates sliding by lowering interfacial friction (Fig. 4b). It is not easy to quantify the amount of water at interface, since we deal with complex interfaces. However, it is evident from Fig. 2a and b that after 10 ns simulation in water, there is more water at TOCNF–GO interface than in NCNF–GO. This screening effect from water at the interface is also discussed by Zhang et al.85 In contrast to the PMF and work of adhesion simulations discussed in the previous section, the present interfacial shear simulations are non-equilibrium processes so that energy is dissipated in the sliding process.
In vacuum, the interfacial interactions are so strong that both NCNF and TOCNF deform under shear forces rather than sliding on the GO (Fig. 4c and d). This indicates that the CNF–GO interaction energy is higher than the cohesive energy of the CNF itself, and no shear strength can be estimated for this case. Even after wetting of the dry structures in Fig. 4c and d, this deformation behaviour of cellulose nanofibers is repeated for both NCNF and TOCNF (Fig. 4e and f). The reason is that the tight, strong interface formed between CNF and GO stays mostly intact and only a few water molecules can penetrate into the interface. This shows that the lubricating effect of water is necessary for the CNF to slide on the GO, similar to what has been reported for CNF–CNF interfaces.37,85,86
One interesting observation is that CNF–graphene interfaces show one order of magnitude lower shear strength than CNF–GO, although they show similar work of adhesion WA, see Table 1. Both these graphene nanocomposites show very low values for interfacial shear strength: NCNF–graphene (4.8 MPa), TOCNF–graphene (3.7 MPa). One reason is the lack of hydrogen-bonding across these interfaces. Hydrogen bonds are highly directional and the OH groups are relatively free to change their orientation. This means they can have a significant in-plane component in contrast to dispersion forces. They can moreover break and reform on sub-nanosecond timescales. The lack of directional hydrogen bonds thus results in much lower static friction between CNF and graphene and lower τmax. One may note that Zhang et al.87 also reported that higher work of adhesion at the interface does not necessarily lead to higher static friction between two surfaces and the present results for the role of water clarify why this can be the case. Other contributions than hydrogen bonds to increased energy barriers for shear sliding may include increased nano-scale surface roughness.87,88
Moisture effects in real CNF–GO nanocomposites
In real nanocomposites, one would expect moisture to be trapped at the CNF–GO interface after drying. For instance, vacuum-assisted filtration, which is widely used for making CNF–GO nanopaper,29,34,36,42,89 is a relatively fast production method with insufficient time for complete drying. If real material interfaces showed as high microscale interfacial strength properties as we observed for molecular adhesion in the present study, stress–strain curves and fracture surfaces would possibly show more brittle behaviour than observed in experiments.29 This suggests that real interfaces are likely contaminated by trapped moisture, which decreases the total work of adhesion, in line with what has been shown in the present study. It has also been suggested that moisture sorption can decrease stress transfer efficiency between cellulose nanocrystals (CNC) and graphene.90Yet, another possible effect from water in experiments is that the ductility of the material is increased.37,38,86 Global mechanical properties of CNF–GO or CNF/graphene nanocomposites are highly sensitive to the use of NCNF or oxidized TOCNF and GO or graphene, although the present study shows that the specific nanocellulose or GO/graphene used does not strongly influence molecular adhesion properties at the interface.
There are many other 2D materials having largely hydrophilic interfaces, including layered silicates, MXenes, etc., which are used as the reinforcing phase in polymer nanocomposites. Due to advantages of water-based processing these are often combined with hydrophilic or even water-soluble polymers such as poly (vinyl alcohol), a variety of polyelectrolytes or polysaccharides including cellulose derivatives. The results presented here show that both adhesion and shear strength in such systems are likely to be highly influenced by the presence and location of residual moisture. This suggests that factors such as dispersion state, drying methods and defects dominate macroscale mechanical behaviour of this class of 2D nanocomposites.
Conclusions
Nanocomposites based on CNF nanocellulose matrix and 2D GO nanoplatelets have very large CNF/GO interface area. Since mechanical properties from experiments are sensitive to moisture, molecular adhesion effects are investigated for the CNF/GO and CNF/graphene interfaces, using two different CNFs. Somewhat surprising, the work of adhesion WA is similar for all 4 combinations when the interface is dry. Water molecules at the interface gives a strong reduction in WA, with water acting as a contaminant affecting the molecular adhesion. Water can be kinetically trapped from the initial water-soaked condition, and therefore there is an effect of drying history on WA. Interestingly, hydrogen bonding has no effect on the WA. In fact, the energetic (enthalpic) balance is working against adhesion where the largest contribution originates in elastic deformation of the CNF. Instead, the WA is controlled by the entropy gain in the material system when water molecules are released from entrapment in the interface region.The interfacial shear strength τmax is also controlled by the presence of moisture, and failure is by a stick–slip mechanism. For dry interfaces, the strong molecular adhesion results in excessively large CNF deformation without interface failure. In contrast to the WA simulations in dry state, hydrogen bonding is of critical importance in shear simulations due to their favourable directional nature and their ability to break and re-form on short timescales.
Mechanical properties from experiments on CNF nanocellulose reinforced by GO or graphene, are highly sensitive to the specific CNF and GO reinforcement used. In contrast, the present investigation shows no effect on WA from the type of nanocellulose or GO or graphene. This suggests that factors such as dispersion state, drying methods (entrapped water at interface) and imperfect interface contact may dominate macroscale mechanical behaviour in CNF–GO and similar 2D nanomaterials. Improved preparation methods for nanocomposites should therefore be investigated further. We also note that “real” nanocomposites will have less water close to the interface than in the present simulations. An important aspect of this investigation though, using soaked conditions, is that the critical importance of interfacial water and related mechanisms has been clarified.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding from the Knut and Alice Wallenberg Foundation (KAW) through the Wallenberg Wood Science Center. Computational resources were provided by the Swedish National Infrastructure for Computing (SNIC) at the PDC Center for High Performance Computing, KTH, partially funded by the Swedish Research Council through grant agreement no. 2016-07213.References
- M. Ahmadi, O. Zabihi, S. Jeon, M. Yoonessi, A. Dasari, S. Ramakrishna and M. Naebe, J. Mater. Chem. A, 2020, 8, 845–883 RSC.
- S. Stankovich, D. A. Dikin, G. H. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Nature, 2006, 442, 282–286 CrossRef CAS PubMed.
- M. A. Rafiee, J. Rafiee, Z. Wang, H. Song, Z.-Z. Yu and N. Koratkar, ACS Nano, 2009, 3, 3884–3890 CrossRef CAS PubMed.
- J. W. Suk, R. D. Piner, J. An and R. S. Ruoff, ACS Nano, 2010, 4, 6557–6564 CrossRef CAS PubMed.
- D. Klemm, F. Kramer, S. Moritz, T. Lindström, M. Ankerfors, D. Gray and A. Dorris, Angew. Chem., Int. Ed., 2011, 50, 5438–5466 CrossRef CAS PubMed.
- X. Wang, W. Xing, X. Feng, L. Song and Y. Hu, Polym. Rev., 2017, 57, 440–466 CrossRef CAS.
- W. L. Song, P. Wang, L. Cao, A. Anderson, M. J. Meziani, A. J. Farr and Y. P. Sun, Angew. Chem., Int. Ed., 2012, 51, 6498–6501 CrossRef CAS PubMed.
- K. Kendall, Molecular adhesion and its applications: the sticky universe, Springer Science & Business Media, 2007 Search PubMed.
- J. George and H. Ishida, Prog. Polym. Sci., 2018, 86, 1–39 CrossRef CAS.
- R. O. Ritchie, Nat. Mater., 2011, 10, 817–822 CrossRef CAS PubMed.
- K. Li, C. M. Clarkson, L. Wang, Y. Liu, M. Lamm, Z. Pang, Y. Zhou, J. Qian, M. Tajvidi and D. Gardner, ACS Nano, 2021, 15, 3646–3673 CrossRef CAS PubMed.
- X. Yang, E. Jungstedt, M. S. Reid and L. A. Berglund, Macromolecules, 2021, 54, 4443–4452 CrossRef CAS.
- Z. Zhou, Q. Li and X. Zhao, Langmuir, 2006, 22, 3692–3697 CrossRef CAS PubMed.
- Y. Ogawa, Y. Nishiyama and K. Mazeau, Cellulose, 2020, 27, 9779–9786 CrossRef CAS.
- H. Sehaqui, A. Liu, Q. Zhou and L. A. Berglund, Biomacromolecules, 2010, 11, 2195–2198 CrossRef CAS PubMed.
- A. Liu, A. Walther, O. Ikkala, L. Belova and L. A. Berglund, Biomacromolecules, 2011, 12, 633–641 CrossRef CAS PubMed.
- C. Gómez-Navarro, M. Burghard and K. Kern, Nano Lett., 2008, 8, 2045–2049 CrossRef PubMed.
- D. R. Dreyer, S. Park, C. W. Bielawski and R. S. Ruoff, Chem. Soc. Rev., 2010, 39, 228–240 RSC.
- S. H. Dave, C. Gong, A. W. Robertson, J. H. Warner and J. C. Grossman, ACS Nano, 2016, 10, 7515–7522 CrossRef CAS PubMed.
- L. A. Berglund and T. Peijs, MRS Bull., 2010, 201–207 CrossRef CAS.
- R. J. Moon, A. Martini, J. Nairn, J. Simonsen and J. Youngblood, Chem. Soc. Rev., 2011, 40, 3941–3994 RSC.
- A. Walther, F. Lossada, T. Benselfelt, K. Kriechbaum, L. Berglund, O. Ikkala, T. Saito, L. Wågberg and L. Bergström, Biomacromolecules, 2020, 21, 2536–2540 CrossRef CAS PubMed.
- A. Benítez and A. Walther, J. Mater. Chem. A, 2017, 5, 16003–16024 RSC.
- X. Gao, P. Ju, X. Liu, L. Chen, L. Ji, H. Li, H. Zhou and J. Chen, Ind. Eng. Chem. Res., 2019, 58, 5464–5471 CrossRef CAS.
- L. Zhang, Y. Zhang, F. Li, S. Yan, Z. Wang, L. Fan, G. Zhang and H. Li, ACS Appl. Mater. Interfaces, 2019, 11, 12890–12897 CrossRef CAS PubMed.
- N. V. Medhekar, A. Ramasubramaniam, R. S. Ruoff and V. B. Shenoy, ACS Nano, 2010, 4, 2300–2306 CrossRef CAS PubMed.
- S. Liu, M. Cerruti and F. Barthelat, ACS Nano, 2020, 14, 15936–15943 CrossRef PubMed.
- Y. Chen, Z. Yu, Y. Ye, Y. Zhang, G. Li and F. Jiang, ACS Nano, 2021, 15, 1869–1879 CrossRef CAS PubMed.
- H. Mianehrow, G. L. Re, F. Carosio, A. Fina, P. T. Larsson, P. Chen and L. A. Berglund, J. Mater. Chem. A, 2020, 8, 17608–17620 RSC.
- L. N. Dang and J. Seppälä, Cellulose, 2015, 22, 1799–1812 CrossRef CAS.
- F. Ren, W. Tan, Q. Duan, Y. Jin, L. Pei, P. Ren and D. Yan, Carbohydr. Polym., 2019, 209, 310–319 CrossRef CAS PubMed.
- C. Xu, G. Wang, C. Xing, L. M. Matuana and H. Zhou, BioResources, 2015, 10, 2809–2822 CAS.
- N. D. Luong, N. Pahimanolis, U. Hippi, J. T. Korhonen, J. Ruokolainen, L.-S. Johansson, J.-D. Nam and J. Seppälä, J. Mater. Chem., 2011, 21, 13991–13998 RSC.
- J.-M. Malho, P. i. Laaksonen, A. Walther, O. Ikkala and M. B. Linder, Biomacromolecules, 2012, 13, 1093–1099 CrossRef CAS PubMed.
- J. Duan, S. Gong, Y. Gao, X. Xie, L. Jiang and Q. Cheng, ACS Appl. Mater. Interfaces, 2016, 8, 10545–10550 CrossRef CAS PubMed.
- W. Yang, Z. Zhao, K. Wu, R. Huang, T. Liu, H. Jiang, F. Chen and Q. Fu, J. Mater. Chem. C, 2017, 5, 3748–3756 RSC.
- Y. Hou, Q.-F. Guan, J. Xia, Z.-C. Ling, Z. He, Z.-M. Han, H.-B. Yang, P. Gu, Y. Zhu and S.-H. Yu, ACS Nano, 2020, 15, 1310–1320 CrossRef PubMed.
- R. A. Soler-Crespo, W. Gao, L. Mao, H. T. Nguyen, M. R. Roenbeck, J. T. Paci, J. Huang, S. T. Nguyen and H. D. Espinosa, ACS Nano, 2018, 12, 6089–6099 CrossRef CAS PubMed.
- R. Rahman, J. Foster and A. Haque, J. Phys. Chem. A, 2013, 117, 5344–5353 CrossRef CAS PubMed.
- Q. Mao, L. Yang, X. Geng, L. Chen, B. Sapkota, H. Zhao and H. Zhu, Adv. Mater. Interfaces, 2017, 4, 1700995 CrossRef.
- R. Alqus, S. J. Eichhorn and R. A. Bryce, Biomacromolecules, 2015, 16, 1771–1783 CrossRef CAS PubMed.
- C. Zhu, S. Monti and A. P. Mathew, ACS Nano, 2018, 12, 7028–7038 CrossRef CAS PubMed.
- R. Xiong, H. S. Kim, L. Zhang, V. F. Korolovych, S. Zhang, Y. G. Yingling and V. V. Tsukruk, Angew. Chem., Int. Ed., 2018, 57, 8508–8513 CrossRef CAS PubMed.
- A. Hunt, D. A. Dikin, E. Z. Kurmaev, T. D. Boyko, P. Bazylewski, G. S. Chang and A. Moewes, Adv. Funct. Mater., 2012, 22, 3950–3957 CrossRef CAS.
- A. N. Fernandes, L. H. Thomas, C. M. Altaner, P. Callow, V. T. Forsyth, D. C. Apperley, C. J. Kennedy and M. C. Jarvis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, E1195–E1203 CrossRef PubMed.
- D. J. Cosgrove, Curr. Opin. Plant Biol., 2014, 22, 122–131 CrossRef CAS PubMed.
- K. Daicho, T. Saito, S. Fujisawa and A. Isogai, ACS Appl. Nano Mater., 2018, 1, 5774–5785 CrossRef CAS.
- S. Djerbi, M. Lindskog, L. Arvestad, F. Sterky and T. T. Teeri, Planta, 2005, 221, 739–746 CrossRef CAS PubMed.
- J. L. Morgan, J. Strumillo and J. Zimmer, Nature, 2013, 493, 181–186 CrossRef CAS PubMed.
- G. Guerriero, J. Fugelstad and V. Bulone, J. Integr. Plant Biol., 2010, 52, 161–175 CrossRef CAS PubMed.
- L. H. Thomas, V. T. Forsyth, A. Šturcová, C. J. Kennedy, R. P. May, C. M. Altaner, D. C. Apperley, T. J. Wess and M. C. Jarvis, Plant Physiol., 2013, 161, 465–476 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122 CrossRef CAS PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef PubMed.
- K. N. Kirschner, A. B. Yongye, S. M. Tschampel, J. González-Outeiriño, C. R. Daniels, B. L. Foley and R. J. Woods, J. Comput. Chem., 2008, 29, 622–655 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- D. E. Smith and L. X. Dang, J. Chem. Phys., 1994, 100, 3757–3766 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- J. S. Hub, B. L. De Groot and D. Van Der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720 CrossRef CAS.
- A. Kelly and P. Sciences, Proc. R. Soc. London, Ser. A, 1970, 319, 95–116 Search PubMed.
- Z. Wei, R. Sinko, S. Keten and E. Luijten, ACS Appl. Mater. Interfaces, 2018, 10, 8349–8358 CrossRef CAS PubMed.
- M. Garg, M. Linares and I. Zozoulenko, Biomacromolecules, 2020, 21, 3069–3080 CrossRef CAS PubMed.
- C. Moser, G. Henriksson and M. Lindström, Nord. Pulp Pap. Res. J., 2018, 33, 647–650 CrossRef CAS.
- H. Nilsson, S. Galland, P. T. Larsson, E. K. Gamstedt, T. Nishino, L. A. Berglund and T. Iversen, Compos. Sci. Technol., 2010, 70, 1704–1712 CrossRef CAS.
- R. H. Newman, Cellulose, 2004, 11, 45–52 CrossRef CAS.
- P. Chen, G. L. Re, L. A. Berglund and J. Wohlert, J. Mater. Chem. A, 2020, 8, 23617–23627 RSC.
- E. Peris, J. C. Lee, J. R. Rambo, O. Eisenstein and R. H. Crabtree, J. Am. Chem. Soc., 1995, 117, 3485–3491 CrossRef CAS.
- X. Zhang, H. Nguyen, M. Daly, S. T. Nguyen and H. D. Espinosa, Nanoscale, 2019, 11, 12305–12316 RSC.
- J. Y. Choi, X. Zhang, H. T. Nguyen, M. R. Roenbeck, L. Mao, R. Soler-Crespo, S. T. Nguyen and H. D. Espinosa, J. Mech. Phys. Solids, 2021, 156, 104578 CrossRef CAS.
- S. Kishani, T. Benselfelt, L. Wågberg and J. Wohlert, J. Colloid Interface Sci., 2020, 588, 485–493 CrossRef PubMed.
- S.-T. Lin, M. Blanco and W. A. Goddard III, J. Chem. Phys., 2003, 119, 11792–11805 CrossRef CAS.
- R. B. Adusumali, M. Reifferscheid, H. Weber, T. Roeder, H. Sixta and W. Gindl, 2006.
- H. A. Khalil, H. Ismail, H. Rozman and M. Ahmad, Eur. Polym. J., 2001, 37, 1037–1045 CrossRef CAS.
- D. Cho, S. B. Yoon and T. Drzal, Compos. Interfaces, 2009, 16, 769–779 CrossRef CAS.
- J. Trejo-O'Reilly, J. Cavaille, M. Paillet, A. Gandini, P. Herrera-Franco and J. Cauich, Polym. Compos., 2000, 21, 65–71 CrossRef.
- J. Karlsson, P. Gatenholm, J. F. Blachot and A. Peguy, Polym. Compos., 1996, 17, 300–304 CrossRef CAS.
- M. Daly, C. Cao, H. Sun, Y. Sun, T. Filleter and C. V. Singh, ACS Nano, 2016, 10, 1939–1947 CrossRef CAS PubMed.
- J. Keckes, I. Burgert, K. Frühmann, M. Müller, K. Kölln, M. Hamilton, M. Burghammer, S. V. Roth, S. Stanzl-Tschegg and P. Fratzl, Nat. Mater., 2003, 2, 810–813 CrossRef CAS PubMed.
- C. Zhang, S. Keten, D. Derome and J. Carmeliet, Carbohydr. Polym., 2021, 117682 CrossRef CAS PubMed.
- R. Sinko and S. Keten, Appl. Phys. Lett., 2014, 105, 243702 CrossRef.
- Q. Zhang, Y. Qi, L. G. Hector Jr, T. Cagin and W. A. Goddard III, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 144114 CrossRef.
- I.-S. Byun, D. Yoon, J. S. Choi, I. Hwang, D. H. Lee, M. J. Lee, T. Kawai, Y.-W. Son, Q. Jia and H. Cheong, ACS Nano, 2011, 5, 6417–6424 CrossRef CAS PubMed.
- P. Laaksonen, A. Walther, J. M. Malho, M. Kainlauri, O. Ikkala and M. B. Linder, Angew. Chem., Int. Ed., 2011, 50, 8688–8691 CrossRef CAS PubMed.
- J. Morgan, M. Craciun and S. Eichhorn, Compos. Sci. Technol., 2019, 177, 34–40 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta09286c |
| This journal is © The Royal Society of Chemistry 2022 |