Correction: The structural, vibrational, and mechanical properties of jammed packings of deformable particles in three dimensions

Dong Wang; John D. Treado; Arman Boromand; Blake Norwick; Michael P. Murrell; Mark D. Shattuck; Corey S. O'Hern

doi:10.1039/D2SM90054H

View PDF VersionPrevious ArticleNext Article

Open Access Article

This Open Access Article is licensed under a
Creative Commons Attribution 3.0 Unported Licence

DOI: 10.1039/D2SM90054H (Correction) Soft Matter, 2022, 18, 3815-3815

Correction: The structural, vibrational, and mechanical properties of jammed packings of deformable particles in three dimensions

Dong Wang ^a, John D. Treado ^ab, Arman Boromand ^a, Blake Norwick ^c, Michael P. Murrell ^bcde, Mark D. Shattuck ^f and Corey S. O'Hern *^abcg
^aDepartment of Mechanical Engineering & Materials Science, Yale University, New Haven, Connecticut 06520, USA. E-mail: corey.ohern@yale.edu
^bIntegrated Graduate Program in Physical and Engineering Biology, Yale University, New Haven, Connecticut 06520, USA
^cDepartment of Physics, Yale University, New Haven, Connecticut 06520, USA
^dDepartment of Biomedical Engineering, Yale University, New Haven, Connecticut 06520, USA
^eSystems Biology Institute, Yale University, West Haven, Connecticut, 06516, USA
^fBenjamin Levich Institute and Physics Department, The City College of New York, New York, New York 10031, USA
^gDepartment of Applied Physics, Yale University, New Haven, Connecticut 06520, USA

Received 14th April 2022 , Accepted 14th April 2022

First published on 4th May 2022

Abstract

Correction for ‘The structural, vibrational, and mechanical properties of jammed packings of deformable particles in three dimensions’ by Dong Wang et al., Soft Matter, 2021, 17, 9901–9915, DOI: 10.1039/D1SM01228B.

The authors regret the error in eqn (3) and the subsequent errors in the surrounding paragraph. The correct text for eqn (3) and the surrounding paragraph is given below.

We calculate the Love stress tensor under periodic boundary condition¹ using


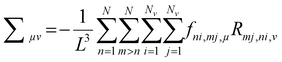	(3)

where μ,ν = x,y,z, f_ni,mj,μ is the μth component of the force on vertex i belonging to particle n from vertex j belonging to particle m, R_mj,ni,ν is νth component of the separation vector from the center of mass of particle n to the contact point between vertex i on particle n and vertex j on particle m. The pressure is defined as

. We have verified that eqn (3) gives the same value for the pressure and shear stress compared to those obtained by calculating the change in the total potential energy with respect to changes in area and shear strain.

The Royal Society of Chemistry apologises for these errors and any consequent inconvenience to authors and readers.

References

S. Edwards and D. Grinev, Phys. A, 2001, 302, 162–186 CrossRef.

Click here to see how this site uses Cookies. View our privacy policy here.