Open Access Article
Open Access ArticleProbing foams from the nanometer to the millimeter scale by coupling small-angle neutron scattering, imaging, and electrical conductivity measurements†
Julien
Lamolinairie
 a,
Benjamin
Dollet
b,
Jean-Luc
Bridot
c,
Pierre
Bauduin
a,
Benjamin
Dollet
b,
Jean-Luc
Bridot
c,
Pierre
Bauduin
 d,
Olivier
Diat
d and
Leonardo
Chiappisi
d,
Olivier
Diat
d and
Leonardo
Chiappisi
 *a
*a
aInstitut Max von Laue – Paul Langevin (ILL), 71 Avenue des Martyrs, 38042 Grenoble, France. E-mail: chiappisil@ill.fr
bUniversité Grenoble Alpes, CNRS, LIPhy, 38000 Grenoble, France
cTeclis Scientific, 69380 Civrieux-d'Azergues, France
dICSM, Univ Montpellier, CEA, CNRS, ENSCM, Marcoule, France
First published on 2nd November 2022
Abstract
Liquid foams are multi-scale structures whose structural characterization requires the combination of very different techniques. This inherently complex task is made more difficult by the fact that foams are also intrinsically unstable systems and that their properties are highly dependent on the production protocol and sample container. To tackle these issues, a new device has been developed that enables the simultaneous time-resolved investigation of foams by small-angle neutron scattering (SANS), electrical conductivity, and bubbles imaging. This device allows the characterization of the foam and its aging from nanometer up to centimeter scale in a single experiment. A specific SANS model was developed to quantitatively adjust the scattering intensity from the dry foam. Structural features such as the liquid fraction, specific surface area of the Plateau borders and inter-bubble films, and thin film thickness were deduced from this analysis, and some of these values were compared with values extracted from the other applied techniques. This approach has been applied to a surfactant-stabilized liquid foam under free drainage and the underlying foam destabilization mechanisms were discussed with unprecedented detail. For example, the information extracted from the image analysis and SANS data allows for the first time to determine the disjoining pressure vs. thickness isotherm in a real, draining foam.
1 Introduction
Liquid foam structure and aging are influenced by several physical and chemical parameters, such as the type of gas,1,2 the surfactant used,3,4 the liquid fraction,5–7 the size of bubbles,8,9 the thickness of the inter-bubble film,10–12 the surface tension13,14 and the interfacial elastic modulus.15,16 Predicting the dominant factors to control the resulting foam properties is therefore a challenging task. For example, how the texture and taste of beer depend on the foam structure – notably on size and number of bubbles – has only recently been understood.17,18 Even the surface state of the container plays a role and can contribute to a rapid breakdown of the foam. To further develop on the example of beverages, superamphiphobic surface coatings are used to prevent the formation of unwanted foam during the filling of bottles.19 Foams are not limited to beverages, and can be found in many other applications: detergency, food, cosmetics, and also for industrial processes such as froth or foam flotation applied for materials or waste recycling, oil recovery from the ground, firefighting, mitigation of blast waves from explosions with very active research in each of these fields nowadays.20–25 Depending on the application, the desired foam properties might vary considerably. Sometimes, an expanded and stable foam is required, for example in firefighting applications, to create a dense blanket acting as an insulating barrier between the fuel and the air and preventing the development of combustion.26 Sometimes, as for cleaning, a rather unstable foam shows better performance.27However, the importance of each of the parameters listed above and more especially their coupled influences on the structural evolution of foams remain difficult to quantify because foams are multi-scale structures. The different structural scales of the foam are depicted in Fig. 1 and can be probed using suitable techniques. At the centimetre scale, optical studies provide general information on the foamability, i.e. the amount of gas that can be trapped in foam. It is also possible to measure the size distribution of gas bubbles28,29 that create in close contact, when the foam dries, a continuous network of liquid channels (Plateau borders) connected by nodes and thin films. At the bubble scale (>100 μm), this 3D network evolution and connectivity can be understood through foam rheology analysis.30,31 Foam drainage is primarily governed by the vertical flow of the liquid due to gravity through these channels and nodes and strongly depends on the viscosity of the fluid.32,33 Then, inter-bubble films, stabilized at both interfaces by surfactants or other colloidal particles, start to thin which initiates or accelerates phenomena of bubble ripening and/or coalescence. Depending on the cohesive interactions between surfactant molecules at water/air interfaces and their dynamic exchange between interfaces and the bulk solution, foam aging can be slowed down or accelerated. Repulsive interactions between facing surfactant monolayers, of electrostatic or steric origin, can also be tuned to counterbalance the capillary pressure that increases as the Plateau borders become thinner and more curved.34 It is through the succession of film ruptures that the foam collapses. Accordingly, information on the film thickness (<100 nm), correlated to that at other scales, is crucial for a deep understanding of the stability of the foam. The stability of the foam might further be impacted by the presence of colloidal aggregates (1–10 nm), such as surfactant micelles or proteins.35,36
Commercial foam analyzers are recurrently used to study foams. They allow liquid foams to be generated by mechanical means – beating or whipping the solution – or by bubbling gases through porous plates. Once generated, various structural foam parameters, such as water volume fraction, foam height, and bubble size distribution are followed over time by image processing and electrical techniques. This information, although crucial to probe the foam destabilization mechanism, lacks an essential piece of information: the inter-bubble film thickness. A common method to measure it is the thin film pressure balance. A surfactant film is subjected to external gas pressure and the difference with the capillary pressure causes the film to drain until the pressures are balanced.37,38 The film thickness is then measured by interferometry as a function of the applied pressure to build a pressure isotherm allowing the experimentalist to quantify the interactions between facing interfaces. However, these experiments are carried out on isolated films, and the extrapolation of these observations to the evolution of the 3D structures such as liquid foams where other effects impact the drainage is far from trivial.
In situ foam film thickness measurement is possible performing small-angle neutron scattering (SANS).39–48 SANS data also provide information on the internal structure of the foam solution over a large length scale. The relatively large diameter of the beam (a few tens of millimetres) allows the probing of several hundred bubbles and films. This method, therefore, provides acceptable statistics on data collected during time scales of a few minutes, a sufficient temporal resolution if the foam does not collapse too quickly. The first cell was manufactured in the early 2000 s and consisted of a Plexiglas cell with a quartz window allowing the study of foam at a single given height.49 Since then, interest in this technique has continued to grow with new cells recently developed.50 The technique has been employed to investigate stimuli responsive foams,42,43 foams stabilized by polymeric surfactants,44 proteins,45 or, more recently, nano-ions.47
While SANS enables us to determine with precision the thickness of films in real foams, it is essential to characterize the foam in its entirety and on all its scales simultaneously: from the bubble to the film, in order to optimize the different parameters involved in the aging of the foam. To address this challenge, we have developed a new device that enables to simultaneously collect microscopic information on the foam via SANS experiments and macroscopic information, with the acquisition of 2D images using an optical camera, as well as conductivity data measured through the foam. Moreover, we have developed an analysis framework to combine the results obtained simultaneously from the different techniques.
In this article, we present the features of this new device as well as the methodology for data analysis. The possibilities offered by the combined analysis are demonstrated using a foam stabilized by a commercial non-ionic polyoxyethylene (10) oleyl ether surfactant (BrijO10) with a very low CMC51 and good foaming capacity,52 and with the anionic sodium dodecyl sulfate (SDS) to induce an electrostatic stabilization of the foam.
2 Materials and methods
2.1 Materials
The non-ionic surfactant polyoxyethylene (10) oleyl ether surfactant BrijO10 (C18:1E10) and the ionic surfactant sodium dodecyl sulfate (SDS, NaC12H25SO4, ≥99.0%) were purchased from Sigma Aldrich and were used without further purification. The data presented in this article were conducted with a foam stabilized with 0.5 mM BrijO10 which is well above the critical micelle concentration of 40 μM molar51 and upon addition of 0.2 mM SDS. Samples were prepared in Millipore water for Foam-analyser experiments and in D2O purchased from Eurisotop (99.9% isotopic purity) for small-angle neutron scattering (SANS) experiments.2.2 Quartz column
The main part of the new device is a column – entirely made of quartz, a material transparent for neutrons – and designed on the model of the FOAMSCAN from Teclis Scientific (France) in which the foam is formed. This cell, shown in Fig. 2a and b, is cylindrical (30 cm high with an internal diameter of 3.5 cm and a wall thickness of 2 mm) and is always opened at the top. A flat face was machined to glue four prisms at different fixed heights, allowing image capture of the bubbles in contact with the wall. Five pairs of electrodes were also integrated to measure the conductance through the foam at different heights. This cell is therefore compatible with the FOAMSCAN and can be used both in a laboratory and on a neutron diffractometer dedicated to small-angle scattering technique.The quartz cell is clipped onto a base via an O-ring to get a set “column and rigid support” tight but easy to dismount for efficient cleaning. The base is composed of a silica frit (pore size 10–16 μm, porosity P16 (ISO 4793)) and can be exchanged depending on the required bubbling size. The flux of injected gas is controlled by a digital Mass Flow Controller (MFC) from MKS Instruments (Andover, Massachusetts, U.S.) with a flow range 0–100 mL min−1 for model GE50 series. When the foaming solution is injected into the bottom of the column, a slight overpressure is maintained to avoid filling the pores of the frit with the solution (with a gas flow rate of 2 mL min−1). The foams are then produced with a gas flow rate of 50 mL min−1 using nitrogen. On the diffractometer, the cell was fixed on a set of X–Z stages (as shown in Fig. 2c) to first center the cylinder in the neutron beam path and second to vary its Y-position so that the neutron beam passes through the cell at heights predefined by the position of the prisms and to be able to simultaneously capture photographs of the foam probed by neutrons.
2.3 Image capture
The photographs of the foam were taken with the acA780-75gm camera from BASLER (Germany). It consists of a Sony ICX415AL CCD sensor with a diagonal of 8 mm and a resolution of 782 × 582 pixels. A Computar TEC-M55 55 mm Telecentric Lens (C Mount) with a focal length of 55 mm and an F11 aperture is added to provide a sharp image at a minimum distance of 14 cm. The telecentric lens also allows only light rays parallel to the optical axis to be selected. The light source and camera are located on either side of the prism, at an angle of 45° to the column wall. This experimental method allows us to visualize only the layer of bubbles located against the inner wall of the column. In the images, the bubbles appear white and the dark part corresponds to the Plateau borders.53 The scaling calibration is done with a calibrated steel ball, 2 mm, fixed in mobile support that can be placed in front of the prism before starting the photographic captures.2.4 Conductance measurements
Electronic conductivity measurements were performed using an EPU 452 Quad Multi-Function isoPod developed by eDAQ (Colorado Springs, CO, US) and configured to measure ionic conductance G = kσ. The cell-constant k in cm only depends on the distance between the electrodes and the surface area of the electrodes, which are equivalent for each position of the pair of electrodes. The cell constants of the different electrodes were calibrated using dilute NaCl solutions.2.5 Small-angle neutron scattering (SANS)
Small-angle neutron scattering (SANS) experiments were performed at room temperature on the D33 diffractometer54 at Laue-Langevin Institute (ILL) in Grenoble. We opted for the monochromatic mode with a wavelength λ = 6 Å. The detector consists of a central panel set at 10 m and 4 side panels set at 1.7 m. The collimation length was set to 12.8 m and the beam size at the sample position was fixed at 15 mm in diameter. Under these conditions, the accessible scattering vector q range, with q defined as q = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2)/λ, varies from 0.002–0.25 Å. The neutron beam was set at the same height as the camera to correlate the various collected data. Acquisition time was fixed at 60 s for scattering data and 30 s for transmission data. Normalization and azimuthal averaging of the 2D data were applied using the GRASP software package.55 The empty cell signal was subtracted for each scattering curve. The absolute scale was obtained by normalizing the neutron beam flux. The experiments described in this article were performed at the height of the second prism, at 8 cm above the level of the solution at rest. SANS experiments were also conducted on foaming solutions in a quartz cuvette of 2 mm thick on the D22 diffractometer to obtain structural information of micellar solution. In this configuration, neutron wavelength was also set at 6 Å and with two detector distances at 1.4 and 17.6 m and with a 17.6 m collimation, resulting in a q-vector range from 0.003 to 0.64 Å−1.
sin(θ/2)/λ, varies from 0.002–0.25 Å. The neutron beam was set at the same height as the camera to correlate the various collected data. Acquisition time was fixed at 60 s for scattering data and 30 s for transmission data. Normalization and azimuthal averaging of the 2D data were applied using the GRASP software package.55 The empty cell signal was subtracted for each scattering curve. The absolute scale was obtained by normalizing the neutron beam flux. The experiments described in this article were performed at the height of the second prism, at 8 cm above the level of the solution at rest. SANS experiments were also conducted on foaming solutions in a quartz cuvette of 2 mm thick on the D22 diffractometer to obtain structural information of micellar solution. In this configuration, neutron wavelength was also set at 6 Å and with two detector distances at 1.4 and 17.6 m and with a 17.6 m collimation, resulting in a q-vector range from 0.003 to 0.64 Å−1.
The SANS data analysis was performed in absolute units, considering the scattering length densities and molecular volumes given in Table S1 in the ESI.† The models are described later in the text. The best-fitting parameters and their uncertainty were estimated by least-square minimization.
2.6 Foam generation and aging procedure
Before SANS measurements, foams were studied using the FOAMSCAN apparatus by injecting 40 mL of the foaming solution into the column in 10 mL steps through the inlet at the bottom of the column, just above the frit. After each injection step, the conductance was measured, resulting in a linear calibration curve (conductance versus liquid volume). Then, N2 flowed at 50 mL min−1 through the porous frit. Once the column was filled by the foam, the N2 flow was stopped leaving the foam under free drainage conditions for 2 to 3 hours. The foam structure was captured using one camera when using the FOAMSCAN. The sample was analyzed 3 times from a fresh foaming solution. The quartz column was rinsed generously with Millipore water and dried after each test. The SANS experiments were performed using the same procedure: after stopping the gas flux, the evolution of the foam was followed using simultaneously conductivity, imaging, and SANS techniques for 75 minutes (see Fig. 2c).2.7 Surface tension measurement
The surface tension of the surfactants at the air–water interface was measured at room temperature using a Tracker developed by Teclis Scientific. The measurement of surface tension was performed on bubbles of 5 μL for 10 min. This measurement was repeated 3 times and the surface tension obtained is γ = (32 ± 1) mN m−1.3 Data analysis procedure
3.1 Data collection
The foam is generated in the quartz cell from the foaming solution containing the nonionic surfactant Polyoxyethylene (10) oleyl ether (Brij O10) at 0.5 mM doped with 0.2 mM sodium dodecyl sulfate. The molar ratio of anionic to nonionic surfactant is 1/2.5. The gas flow is stopped once the column is filled, defining the starting point t = 0 of the time-resolved experiments. The structure of the foam is then investigated as a function of time at the level of prism 2 for this study, at approx. 8 cm above the liquid surface, as shown in Fig. 2c. The measurement of the conductance was performed simultaneously through the foaming solution and the foam at three different heights. Fig. 3 presents a typical set of kinetics data recorded simultaneously during the free drainage of a foam: 2D SANS scattering data (Fig. 3a and c) with the corresponding radially averaged scattering curves (Fig. 3f), 2D optical images of the foam (Fig. 3b and d), and conductance values recorded on electrode pairs below and above the prism 2 (Fig. 3e).3.2 Image processing
The collected optical images were binarised to extract the relevant information: bubble size, liquid volume fraction, specific surface area of the foam, and radius of the Plateau borders. This binarisation process was automated using the “Adaptive Threshold” command from OpenCV package,56 for which the binarisation threshold value varies for each pixel depending on the gray level of its neighborhood. Once the image is binarised, “findContours” and “drawContours” commands from OpenCV package56 are applied to remove artefacts from impurities within the bubbles. The source code used for the image treatment is provided in Section S2 of the ESI.† An updated version of the software is freely available at https://github.com/leonardo-chiappisi/pyFoam_analysis.From the binarised images, the surface area of each bubble in contact with the wall of the column Sbubble was measured as well as their surface radius expressed as  . The distribution of the radii can be characterized by the Polydispersity Index (PI) expressed as
. The distribution of the radii can be characterized by the Polydispersity Index (PI) expressed as
 | (1) |
From the foam images, the liquid fraction ϕ is also determined as a function of time. Its estimation is based on the calculation of the surface fraction ϕs, expressed as the ratio between the area of the pseudo Plateau borders APB – that corresponds to the number of black pixels after binarization – and the total area of the foam Afoam: ϕs = APB/Afoam. By considering the foam as a network of liquid channels with a characteristic length close to the bubble radius, a relationship exists between ϕs and ϕ using the following equation:58
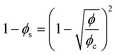 | (2) |
The specific surface area of the foam, i.e. the ratio of the total surface area of the water/air interfaces over the total volume of foam, can also be estimated by image analysis. The model holds for dry polydispersed foams, where the surface size distribution obtained from the images represents the true bulk polydispersity of the foam. In this case, the specific surface area of the foam can be approximated by:
 | (3) |
It is also possible to extract the radius of the Plateau borders rPB from the binarised and skeletonized images. The analysis method is detailed in Section S2 of the ESI.†
3.3 Conductance data
The liquid fraction ϕ is also determined using electrical conductance values. This measurements is possible for the investigated system thanks to the presence of a charged surfactant. The following empirical relation is valid for both wet and dry foams:59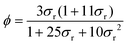 | (4) |
3.4 SANS data analysis
A third approach was followed to study the liquid volume fraction evolution by applying the Beer–Lambert law from the neutron transmission values and using 1.549 cm as adsorption length for D2O.60 The uncertainty on the transmission ΔT related to the counting statistic of the 2D detector is propagated to obtain the uncertainty on the liquid fraction. The transmission value measured at 6 min is equal to 0.85 and is higher than 0.99 after 17 min. The values are high enough to safely neglect multiple scattering.In addition to the determination of the liquid fraction of the foam, small-angle scattering is mainly employed for the microstructural characterization of the foam. In particular, given the large size of the neutron beam (15 mm diameter), the large sample thickness (3.5 cm), and the relatively small size of the bubbles (∼1 mm), isotropic scattering patterns are obtained throughout the drainage, except at the end of the sequence when the foam is very dry. Given the fact that the characteristic sizes associated with the different contributions strongly differ – a few nm for the micelles, a few tens of nanometers for the films, several μm for the Plateau borders – the azimuthal averaged SANS intensities can be analyzed as the coherent sum of different contributions.
| Imicelle(q) = 1N·ϕ·PCS(q)ScHS(q) | (5) |
 | (6) |
In the first approach, the contribution of the foam films is calculated considering scattering from flat discs of radius r and thickness h, i.e., with h ≪ r:63
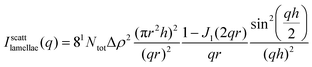 | (7) |
 | (8) |
 | ||
| Fig. 5 (a) Foam scattering data collected at 65 min of aging to which are superimposed either scattering intensity from randomly-oriented discs (eqn (7), blue line) or reflectivity signal with (eqn (16), purple line) or without (eqn (15), orange line) the Born approximation from the same set of discs without taking into account a surface roughness. (b) Same data adjusted with a model at three contributions: IPB from Plateau borders, Imicelle from micelles present within the foam and Irefleclamellae from discs considering the reflectivity assumption according to eqn (15) with a film roughness /polydispersity Σ = 1.5 nm. Ibkg is the incoherent scattering background. | ||
Thus, in a second approach, we assume that the disks are large and flat, compared to the neutron coherence length, and so a specular reflection of the air/D2O/air interface takes place. From the definition of the scattering intensity which relates the scattering cross section to the illuminated volume A0T and solid angle ΔΩ, it follows that:66
 | (9) |
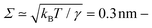 , off-specular reflection can be safely neglected. The solid angle is given by:
, off-specular reflection can be safely neglected. The solid angle is given by:ΔΩ = 2π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θΔθ θΔθ | (10) |
A(θ) = Nspecπr2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2) sin(θ/2) | (11) |
 | (12) |
 | (13) |
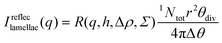 | (14) |
 | (15) |
To confirm that the difference between the calculated “scattered” (eqn (7)) vs. “reflected” (eqn (15)) wave comes from the different formalism used to derive the two calculated curves, the reflectivity signal was also calculated within the Born approximation. For a thin film of thickness h of D2O in air, the reflected intensity calculated within the Born approximation is given by:68
 | (16) |
Fig. 5b shows the different contributions and the resulting intensity for a dry, 65 min-old foam, taking into account the Porod scattering from the Plateau borders, the reflection at the foam-film interface without Born approximation, and the scattering of the micellar aggregates presents in the foam channels. While several examples dealing with the analysis of SANS data from liquid foams can be found in the literature,39–45,47,48 this is the first example of quantitative analysis, in absolute scale, of the scattering data recorded from liquid foams. The analysis was performed using a value for the film roughness Σ of 1.5 nm, which is much larger than the roughness due to thermal fluctuation of around 0.3 nm. A higher value for Σ was chosen since the films in the scattering volume are not fully monodisperse and it is, therefore, necessary to take into account the thickness polydispersity to analyze the scattering curves. The value of Σ is thus used to describe both the roughness and the polydispersity between the films and was arbitrarily set to 1.5 nm. However, the value represents a higher estimate for the film roughness, since the choice of smaller values down to 0.1 nm, has no impact on the fit quality and the obtained fit parameters, as demonstrated in Fig. S5 in the ESI.† There are only 4 parameters that are adjusted during the fit procedure: the liquid fraction ϕ, the film thickness h, and the specific surface area of the films S/V|film and of the Plateau borders S/V|PB. The values obtained for the foam shown in Fig. 5b, at 65 min, are ϕ = (2.5 ± 0.5)%, h = (40 ± 3) nm, S/V|PB = (6.1 ± 0.1) cm−1 and S/V|film = (14.3 ± 0.5) cm−1. Such information is not available by any other technique.
4 Results and discussion
Hereafter, the stability of a nonionic/anionic surfactant stabilized foam is investigated by following foam volume using the foam analyzer, and by measuring bubble size distribution, specific surface areas, liquid fraction, and thickness of the film as a function of time using the multi-scale setup. The goal of this case study is to provide the reader with an overview of the information that can be extracted from this multi-method approach coupled with suitable data analysis.4.1 Macrostructural characterization
The evolution of the foam volume is shown as a function of time in Fig. 6. Time zero is defined as the moment where the gas flow is stopped. Accordingly, at negative times the foam is created, and fills the column for approximately 4 min. In parallel, the volume of the sub-phase solution is decreasing (dotted red curve in Fig. 6). Once the gas flow is stopped, the foam then evolves through a free drainage process. During the first 10 min after foaming, the kinetic of drainage is fast and water trapped within the foam drains through the Plateau borders with a drainage front which shifts downwards at constant velocity.34 The volume of the foam decreases and reaches an inflection point. The second stage of drainage then begins, characterized by a slower regime. It has to be noted here that the decrease in foam volume, associated with the drainage of the liquid solution, takes place at the bottom of the foam, and that the total volume of the system, {foam + liquid solution}, remains relatively constant in this phase. Once the excess solution has drained within the foam after 10 minutes, the second regime of drainage, much slower, begins. In this phase, the interlamellar interactions and capillary forces act against gravity. This stage is characterized by a pseudo-plateau in the foam volume variation, which ends, in the investigated system, at approx. 30 minutes. At this stage, the foam at the top of the column is very dry; the bubbles start to break and the foam gradually collapses.While the foam volume evolution provides a general overview of the foam stability, the simultaneous recording of foam photographs, electrical conductivity, and small-angle neutron scattering patterns allows us to get a deeper structural understanding of the foam aging mechanisms.
The mean radius 〈r〉 increases from 0.04–0.43 mm with a slight inflection in its evolution around 40 min. The PI of the distribution increases quickly from 0.37–0.58 in the first 10 min to be then almost constant, whereas the number of bubbles N decreases continuously as a function of time. The radius of the Plateau borders decreases until reaching a plateau around 20 min. The increase in the radius of the bubbles over time as well as the decrease of N mean that coalescence and coarsening play a role in the decay of the foam as expected, but with kinetics that remain slow.
The SANS data give an overestimated value of ϕ compared to the other techniques which will be discussed in the Section 4.2. For the three other methods, although slight differences are visible, they are consistent and provide a clear trend for the evolution of the liquid volume fraction in the foam as a function of time. These three methods have different strengths and weaknesses to estimate the liquid volume fraction within the foam at a given height: electrical conductivity is a reliable and robust method when the system is rich in charge, but it can be applied to conductive solutions only; ϕ obtained from the image analysis suffers from the choice of the threshold during the binarisation procedure and is limited by the camera resolution. However, it can be applied to any foam, even non-ionic ones. Neutron transmission suffers from a low signal-to-noise ratio and although the measurements are taken primarily to obtain absolute units of the SANS data they are also used in this context to corroborate the correctness of the solution volume fraction at a given height in the foam and as a function of time. In our experiments, and in particular at high times (after 20 min), the measured conductance is low and close to the sensitivity limit of the conductivity meter (see Fig. 3e) which explains the large uncertainty of the liquid fraction. Despite different strengths and weaknesses, all three methods give similar results and make it possible to determine the time evolution type of the foam quality: wet foam (ϕ > 10%), dry foam (ϕ < 5%) or very dry foam (ϕ < 1%). The evolution of the liquid fraction determined by these three methods shows a bi-exponential decay:
ϕ(t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) exp(−t/τ1) + B exp(−t/τ1) + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) exp(−t/τ2) exp(−t/τ2) | (17) |
| τ 1 (min) | τ 2 (min) | |
|---|---|---|
| Conductance | 5 ± 1 | 77 ± 1 |
| Neutron transmission | 4 ± 2 | 40 ± 20 |
| Image analysis | 7 ± 1 | 51 ± 2 |
4.2 Microstructural characterization of the foam
As detailed previously, SANS experiments were performed during foam aging to obtain microstructural information about the foam as a function of time. The SANS analysis model was applied to all the recorded scattering curves as shown in Fig. S7 in the ESI.† However, the SANS patterns of the young, wet foam (before 10 minutes), could not be fitted assuming specular reflection at the air/D2O/air interface. At this stage, owing to the high liquid fraction (around 5%), the surfaces are too curved to provide a reflectivity signal. Between 10 and 20 min, the total reflectivity signal is visible in the experimental data. However, no Kiessig fringes, arising from the interference between the two interfaces of the film, are observed presumably due to the large film thickness or thickness polydispersity. Accordingly, the data between 10 and 20 min were fitted assuming a “thick” film of 60 nm. This dimension has, however, no real physical meaning. While the thickness of the foam films cannot be determined, this approach allows us to calculate the specific surface of the films from the intensity of the reflected signal below the total reflection angle q around 0.15 Å−1. From 20 min onward, all structural parameters – the liquid fraction ϕ, the inter-bubble film thickness h, the specific surface areas from the Plateau borders S/V|PB and from the films S/V|film – can be obtained from the fit of the SANS data, and are shown in Fig. 9. | ||
| Fig. 9 Time evolution of the liquid fraction ϕ obtained from the small-angle scattering of the micelles (eqn (5)), the inter-bubble film thickness h and the specific surface S/V obtained from the reflectivity contribution from the thin films (eqn (15)). The total specific surface area of the foam S/V|foam is obtained by summing the surface area from the Plateau borders S/V|PB and from the films S/V|film. Error bars are represented as shaded regions and are obtained by minimizing the residual error using the least squares method. The specific surface area obtained from image analysis S/V|img is also plotted for the sake of comparison. | ||
The liquid fraction obtained from the SANS analysis varies from 4 down to 2% in this time range. It appears to be overestimated compared to the values determined using conductance, neutron transmission, and image analysis. We recall that the liquid fraction from SANS was estimated assuming that concentration and shape of the surfactant micelles in the foam is equal to that in solution. The mismatch indicates that either the concentration of micelles in the foam is higher than in the bulk solution, or that the micellar aggregates are larger in the foam than in the solution. We refrain from further investigating the variation of the shape/size/concentration of the micellar aggregates in the foam since, despite being a fundamentally interesting observation, it exceeds the scope of this work. We only hint that performing contrast variation experiments would allow probing the structure of colloidal assemblies within the foam with high accuracy. However, this overestimation of the liquid fraction is not prejudicial to the estimation of specific surface areas and film thickness. Indeed, the specific surface areas S/V are obtained from the q−4 decay for the PB and from the inflection point at the critical angle for the films. They are both well-defined, which explains the small errors on these parameters, and located in regions of the scattering pattern where the contribution of the micelles is negligible. For what concerns the foam film thickness h, it is determined from the position of the oscillations, which are found in the q range from 0.003 to 0.05 Å−1. In this region, the contribution of the micelles is constant, despite being non-negligible. In other words, if an error is made in the contribution of the micelle scattering to the overall scattering intensity, this does not impact the reliability of the other values determined by the analysis of the SANS data. This is confirmed by the correlation coefficients between the four fit parameters which are very low and given in Table S3 of the ESI.† Besides, the specific surface area of the foam (represented in red in Fig. 9) obtained with SANS perfectly agrees with the one obtained from image analysis (represented in grey), ruling out systematic errors in the absolute scale of the SANS experiments.
As soon as the Kiessig fringes are observable, the foam film thickness decreases from about 55 nm down to 40 nm a value which remains constant over the last 30 min of the experiment. These values are in the range of what has been determined using a thin film pressure balance technique on a single film submitted to an external pressure before rupture, but still much thicker than Newton black films.69 Finally, the last microscopic features are the specific areas from Plateau borders and foam films. Their sum agrees very well with the results from the image analysis, at least in the last 30 minutes, supporting the use of the absolute scale in the scattering experiment. In particular, the analysis of the SANS data allows us to discern directly between the two specific surface areas, S/V|PB and S/V|film. While the surface area of the foam film decreases only moderately with time, the Plateau border area decreases significantly within the investigated time range, from 100 to less than 10 cm−1. The Plateau borders specific surface area decreases with a bi-exponential law (see Fig. S8 in the ESI†), with characteristic times of (7 ± 1) and (42 ± 2) minutes. In contrast, the specific surface area of the films decreases slowly, mostly linearly in time. Thus, the sum is dominated by the Plateau borders contribution at the beginning of drainage and then by the foam film when the foam is aged and dried.
4.3 Calculation of the disjoining pressure
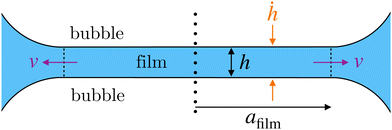
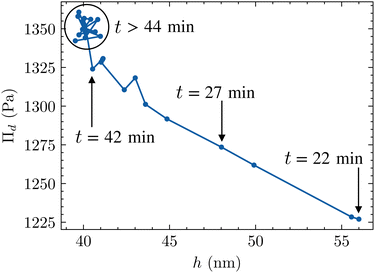
As soon as the foam is formed, in the example presented here, the liquid structure is immediately subjected to free drainage which will contribute to its destabilization. During the first drainage stage, water drains rapidly through the foam with a drainage front that moves down to reach the foam/solution interface within a characteristic time of approximately 5–10 min in this geometry and formulation. For times larger than this characteristic time, the entire foam structure relaxes into an aging phase in which gravity is not the only force acting on the liquid. This time phase corresponds to the pseudo plateau observed around 10 min in Fig. 6. The foam becomes dry with a liquid fraction ϕ < 5%. It is interesting to note that during the first 10 minutes, the PI of the radius of the bubble increases significantly to achieve a quasi-constant and large value of about 0.57. This second phase in the foam aging observed after 10 min, corresponds to a much slower process characterized by a set of bubbles that become faceted. The signature of this evolution can be followed by the fluctuations of the scattering intensity, which increase in number and amplitude, and start to be detectable on the 2D-detector (see Fig. S9 and S10 in the ESI†).70 The bubble size variation first follows a quasi-proportional time law (proportional to tβ with β < 1) and then a trend close to t1/2 at long time (see Fig. S11 in the ESI†), an evolution characteristic of a coarsening process.71 The specific surface area of the foam decreases, mainly due to the decrease in the specific surface area of the Plateau borders contribution, until the one of the films becomes predominant. The film thickness decreases until a quasi-constant value. This value is tuned by a balance between the capillary pressure Pc and the sum of the disjoining pressure Πd, that prevents further thinning of the film and ensures mechanical resistance to coalescence and to coarsening, and the hydrodynamic pressure ΔP due to capillary suction: Pc = Πd + ΔP.72 Determining roughly the Plateau borders radius from image analysis, of about rPB = 24 μm at the end of the experiment and with the measurement of the surface tension in this system, equal to γ = 32 mN m−1, it is possible to estimate the capillary pressure – defined for a dry foam34 as Pc = γ/rPB – of about 1350 Pa. At that time, the film thickness is constant and the foam reaches an equilibrium state, thus the capillary pressure is equal to the disjoining pressure Πd. For the younger foam, it is necessary to estimate the hydrodynamic pressure loss between the centre of a soap film and the neighbouring Plateau borders during capillary suction. Let v be the typical velocity of the liquid within the film, driven by capillary suction, and afilm the typical radius of the film, as represented in Fig. 10.Then by Poiseuille law, the typical pressure drop across the film73 is ΔP ≈ ηafilmv/h2. It is possible to estimate the velocity v from the film thinning rate ḣ considering the following mass balance:
| ρafilmvh ≈ ρafilm2ḣ | (18) |
| ΔP ≈ ηafilm2ḣ/h3. | (19) |
Two trends can be observed in Fig. 11. Between 22 and 42 min, the foam film thins while the disjoining pressure – approximated by the capillary pressure as the hydrodynamic contribution is negligible as discussed above – increases. The liquid fraction estimated by image analysis changes from (0.7 ± 0.2)% to (0.3 ± 0.1)%. Thus, the two interfaces of the film get closer to each other until the film reaches an equilibrium thickness h = 40 nm from 44 min onward. The films do not drain anymore and the equilibrium pressure is reached. It is interesting to notice that the thinning velocity is close to zero (slope of the thickness variation versus time, see Fig. 9) when the contribution of the films to the foam specific surface area becomes larger than that of the Plateau borders. Both the liquid content of the foam and the Plateau border specific area show a similar bi-exponential decay supporting the idea that the drainage of the solution takes place mainly through the Plateau borders.75,76 After this transient period ending around 40 min, the foam aging enters a self-similar growth regime where the mean radius of bubble 〈r〉 evolves in t1/2 (see Fig. S11 in the ESI†).
5 Conclusion
In summary, the analysis of foam stability requires the collection of a wide range of information from the nano- to the centimetre scale that has to be correlated for a better understanding of the underlying processes. While such a multi-scale analysis is mostly performed using different techniques separately in the literature,34,77 herein the evolution of foam has been followed simultaneously using macro-photography, electrical conductivity, and small-angle neutron scattering. The combination of these three techniques allows us to perform this multi-scale analysis in real-time on a given sample. In particular, the analysis in absolute scale of the SANS data allows quantifying of the specific surface areas from Plateau borders and from inter-bubble thin films as well for which time their evolution can be correlated to the film thickness variation, while the analysis of the SANS data in arbitrary units only provided reliable values for the foam film thickness.47,48To demonstrate the relevance of the method and the setup, the aging of a liquid foam stabilized by a non-ionic BrijO10 and anionic SDS surfactant mixture was studied. With this new device, we have been able to follow the evolution of the number of bubbles, and liquid fraction using three different methods, but also the thickness of the inter-bubble film as well as the specific surface of the foam. To the best of our knowledge, it is the first report of the structural characterization of a liquid foam which simultaneously covers six orders of magnitude in size, from the nanometer scale of the micelles to the millimeter scale of the foam bubbles. From the evolution of the parameters, it was found that the aging of the foam follows a bi-exponential decay. The initial fast drying of the foam is due to the free drainage of the liquid through the Plateau borders. This process takes approximately 5–7 minutes to be completed. The free drainage is followed by further drying of the foam, where the liquid drainage is slowed down by capillary forces and repulsion between the foam films. This second drainage phase takes one hour approximately to be completed and to observe a self-similar regime of bubble growth. A rapid collapse of the foam follows its full drying once a critical disjoining pressure is achieved, about 1350 Pa for the studied system. This is the first time that a relationship between the disjoining pressure Πd in foams under free drainage (so in out-of-equilibrium conditions) and the foam film thickness h has been measured. These experiments are generally done on single films in a thin-film pressure balance. Moreover, the final disjoining pressure values obtained are relatively low compared to the maximum value of disjoining pressure measured at rupture for the film alone74 suggesting that the destabilization of the foam does not depend directly on disjoining pressure.
Getting such a detailed overview of the evolution of foam is a fundamental step to tailor the foam for specific needs. For instance, one of the strategies to obtain wet foams is to reduce drainage by adding thickeners.78 The present approach allows us to relate the characteristic times of drainage with the thickener concentration, which enables to refine the properties of the foam. In more general terms, having access to the details of the destabilization mechanisms of liquid foams is the prerequisite for designing novel foams with the desired properties.
Author contributions
L. C., O. D. and J.-L. B. conceived the project. L. C. and O. D. supervised the project, J. L., L. C., O. D. and P. B. conducted the experiments. J. L. participated in the development of the device. J. L., B. D., and L. C. performed data analysis. J. L., L. C. and O. D. discussed the results. All authors commented on the work and reviewed the manuscript.Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
The Institut Laue-Langevin is acknowledged for providing beamtime on the small-angle scattering machines D22 and D33 (data available at: https://doi.ill.fr/10.5291/ILL-DATA.9-10-1730); the PSCM for providing the laboratory infrastructure where all off/line experiments were performed. Fruitful discussions with Sylvain Prevost, Charles Dewhurst, Frédéric Nallet, and Oleg Konovalov are heartily acknowledged. We thank Michel Bonnaud, Benoit Laurent and Abdelali Elaazzouzi for their help in the instrumental development. O. D. and P. B. acknowledge fundings from Agence Nationale de la recherche for FOAMEX project, grant number ANR17-CE008-0016.Notes and references
- C. Wang and H. A. Li, Stability and mobility of foam generated by gas-solvent/surfactant mixtures under reservoir conditions, J. Nat. Gas Sci. Eng., 2016, 34, 366–375 CrossRef CAS.
- M. H. Alooghareh, A. Kabipour, M. Ghazavi, S. Mohammad Mousavi Sisakht and M. Razavifar, Effects of different gases on the performance of foams stabilized by Cocamidopropyl betaine surfactant and silica nanoparticles: A comparative experimental study, Petroleum, 2021 DOI:10.1016/j.petlm.2021.09.002.
- S. N. Tan, D. Fornasiero, R. Sedev and J. Ralston, The role of surfactant structure on foam behaviour, Colloids Surf., A, 2005, 263, 233–238 CrossRef CAS.
- Z. Briceño-Ahumada and D. Langevin, On the influence of surfactant on the coarsening of aqueous foams, Adv. Colloid Interface Sci., 2017, 244, 124–131 CrossRef PubMed.
- A.-L. Biance, A. Delbos and O. Pitois, How Topological Rearrangements and Liquid Fraction Control Liquid Foam Stability, Phys. Rev. Lett., 2011, 106, 068301 CrossRef PubMed.
- A. Salonen, R. Lhermerout, E. Rio, D. Langevin and A. Saint-Jalmes, Dual gas and oil dispersions in water: production and stability of foamulsion, Soft Matter, 2012, 8, 699–706 RSC.
- E. Yoshida, R. Farajzadeh, S. Vincent-Bonnieu and N. Bourada Bourada, Effect of Gas Permeability and Solubility on Foam, Soft Matter, 2014, 2014, 145352 Search PubMed.
- A. Saint-Jalmes, Physical chemistry in foam drainage and coarsening, Soft Matter, 2006, 2, 836–849 RSC.
- J. Boos, W. Drenckhan and C. Stubenrauch, Protocol for Studying Aqueous Foams Stabilized by Surfactant Mixtures, J. Surfactants Deterg., 2013, 16, 1–12 CrossRef CAS.
- V. V. Yaminsky, S. Ohnishi, E. A. Vogler and R. G. Horn, Stability of Aqueous Films between Bubbles. Part 1. The Effect of Speed on Bubble Coalescence in Purified Water and Simple Electrolyte Solutions, Langmuir, 2010, 26, 8061–8074 CrossRef CAS PubMed.
- C. T. Nguyen, H. M. Gonnermann, Y. Chen, C. Huber, A. A. Maiorano, A. Gouldstone and J. Dufek, Film drainage and the lifetime of bubbles, Geochem., Geophys., Geosyst., 2013, 14, 3616–3631 CrossRef.
- J. Miguet, F. Rouyer and E. Rio, The Life of a Surface Bubble, Molecules, 2021, 26(5), 1317 CrossRef CAS PubMed.
- O. Arciniega Saavedra and J. Gracia Fadrique, Surface Tension and Foam Stability Prediction of Polydimethylsiloxane-Polyol Systems, Open J. Phys. Chem., 2012, 2, 189–194 CrossRef.
- K. G. Marinova, E. S. Basheva, B. Nenova, M. Temelska, A. Y. Mirarefi, B. Campbell and I. B. Ivanov, Physico-chemical factors controlling the foamability and foam stability of milk proteins: Sodium caseinate and whey protein concentrates, Food Hydrocolloids, 2009, 23, 1864–1876 CrossRef CAS.
- D. Georgieva, A. Cagna and D. Langevin, Link between surface elasticity and foam stability, Soft Matter, 2009, 5, 2063–2071 RSC.
- K. Małysa, R. Miller and K. Lunkenheimer, Relationship between foam stability and surface elasticity forces: Fatty acid solutions, Colloids Surf., 1991, 53, 47–62 CrossRef.
- E. S. Benilov, C. P. Cummins and W. T. Lee, Why do bubbles in Guinness sink?, Am. J. Phys., 2013, 81, 88–91 CrossRef.
- G. Liger-Belair and C. Cilindre, How Many CO2 Bubbles in a Glass of Beer?, ACS Omega, 2021, 6, 9672–9679 CrossRef CAS PubMed.
- W. S. Y. Wong, A. Naga, L. Hauer, P. Baumli, H. Bauer, K. I. Hegner, M. D'Acunzi, A. Kaltbeitzel, H.-J. Butt and D. Vollmer, Super liquid repellent surfaces for anti-foaming and froth management, Nat. Commun., 2021, 12, 5358 CrossRef CAS PubMed.
- C. Hill and J. Eastoe, Foams: From nature to industry, Adv. Colloid Interface Sci., 2017, 247, 496–513 CrossRef CAS PubMed.
- C. Micheau, D. Dedovets, P. Bauduin, O. Diat and L. Girard, Nanoparticle foam flotation for caesium decontamination using a pH-sensitive surfactant, Environ. Sci.: Nano, 2019, 6, 1576–1584 RSC.
- B. S. Murray, Recent developments in food foams, Curr. Opin. Colloid Interface Sci., 2020, 50, 101394 CrossRef CAS.
- F. Elias, J. Crassous, C. Derec, B. Dollet, W. Drenckhan, C. Gay, V. Leroy, C. Noûs, J. Pierre and A. Saint-Jalmes, The Acoustics of Liquid Foams, Curr. Opin. Colloid Interface Sci., 2020, 50, 101391 CrossRef CAS.
- T. Majeed, M. S. Kamal, X. Zhou and T. Solling, A Review on Foam Stabilizers for Enhanced Oil Recovery, Energy Fuels, 2021, 35, 101391 CrossRef.
- P. Trinh, A. Mikhailovskaya, M. Zhang, P. Perrin, N. Pantoustier, G. Lefèvre and C. Monteux, Leaching Foams for Copper and Silver Dissolution: A Proof of Concept of a More Environmentally Friendly Process for the Recovery of Critical Metals, ACS Sustainable Chem. Eng., 2021, 9, 14022–14028 CrossRef CAS.
- J. Rakowska, Best practices for selection and application of firefighting foam, MATEC Web Conf., 2018, 247, 00014 CrossRef CAS.
- T. Schad, N. Preisig, D. Blunk, H. Piening, W. Drenckhan and C. Stubenrauch, Less is more: Unstable foams clean better than stable foams, J. Colloid Interface Sci., 2021, 590, 311–320 CrossRef CAS PubMed.
- C. Stubenrauch, M. Hamann, N. Preisig, V. Chauhan and R. Bordes, On how hydrogen bonds affect foam stability, Adv. Colloid Interface Sci., 2017, 247, 435–443 CrossRef CAS PubMed.
- R. Höhler, S. Cohen-Addad and D. J. Durian, Multiple light scattering as a probe of foams and emulsions, Curr. Opin. Colloid Interface Sci., 2014, 19, 242–252 CrossRef.
- B. Dollet and C. Raufaste, Rheology of aqueous foams, C. R. Phys., 2014, 15, 731–747 CrossRef CAS.
- D. Langevin, Influence of interfacial rheology on foam and emulsion properties, Adv. Colloid Interface Sci., 2000, 88, 209–222 CrossRef CAS PubMed.
- S. A. Koehler, S. Hilgenfeldt and H. A. Stone, A Generalized View of Foam Drainage: Experiment and Theory, Langmuir, 2000, 16, 6327–6341 CrossRef CAS.
- A. Saint-Jalmes, Physical chemistry in foam drainage and coarsening, Soft Matter, 2006, 2, 836–849 RSC.
- I. Cantat, C.-A. Sylvie, E. Florence, G. François, H. Reinhard, O. Pitois, R. Florence and A. Saint-Jalmes, Foams: Structure and Dynamics, Oxford University Press, 2013 Search PubMed.
- A.-L. Fameau, A. Saint-Jalmes, F. Cousin, B. Houinsou Houssou, B. Novales, L. Navailles, F. Nallet, C. Gaillard, F. Boué and J.-P. Douliez, Smart Foams: Switching Reversibly between Ultrastable and Unstable Foams, Angew. Chem., Int. Ed., 2011, 50, 8264–8269 CrossRef CAS PubMed.
- K. G. Marinova, E. S. Basheva, B. Nenova, M. Temelska, A. Y. Mirarefi, B. Campbell and I. B. Ivanov, Physico-chemical factors controlling the foamability and foam stability of milk proteins: Sodium caseinate and whey protein concentrates, Food Hydrocolloids, 2009, 23, 1864–1876 CrossRef CAS.
- A. Sheludko, Thin liquid films, Adv. Colloid Interface Sci., 1967, 1, 391–464 CrossRef CAS.
- O. Velev, G. Constantinides, D. Avraam, A. Payatakes and R. Borwankar, Investigation of Thin Liquid Films of Small Diameters and High Capillary Pressures by a Miniaturized Cell, J. Colloid Interface Sci., 1995, 175, 68–76 CrossRef CAS.
- O. T. Mansour, B. Cattoz, M. Beaube, M. Montagnon, R. K. Heenan, R. Schweins, M.-S. Appavou and P. C. Griffiths, Assembly of small molecule surfactants at highly dynamic air–water interfaces, Soft Matter, 2017, 13, 8807–8815 RSC.
- S. Yada, H. Shimosegawa, H. Fujita, M. Yamada, Y. Matsue and T. Yoshimura, Microstructural Characterization of Foam Formed by a Hydroxy Group-Containing Amino Acid Surfactant Using Small-Angle Neutron Scattering, Langmuir, 2020, 36, 7808–7813 CrossRef CAS PubMed.
- R. Poryles, T. Chevalier, N. Gland, E. Rosenberg and L. Barré, Characterization of foam flowing in a granular medium in the presence of oil by small angle neutron scattering, Soft Matter, 2020, 16, 1771–1778 RSC.
- C. Micheau, P. Bauduin, O. Diat and S. Faure, Specific Salt and pH Effects on Foam Film of a pH Sensitive Surfactant, Langmuir, 2013, 29, 8472–8481 CrossRef CAS PubMed.
- L. Zhang, A. Mikhailovskaya, P. Yazhgur, F. Muller, F. Cousin, D. Langevin, N. Wang and A. Salonen, Precipitating Sodium Dodecyl Sulfate to Create Ultrastable and Stimulable Foams, Angew. Chem., Int. Ed., 2015, 54, 9533–9536 CrossRef CAS PubMed.
- J. Hurcom, A. Paul, R. K. Heenan, A. Davies, N. Woodman, R. Schweins and P. C. Griffiths, The interfacial structure of polymeric surfactant stabilised air-in-water foams, Soft Matter, 2014, 10, 3003–3008 RSC.
- I. Schmidt, B. Novales, F. Boué and M. Axelos, Foaming properties of protein/pectin electrostatic complexes and foam structure at nanoscale, J. Colloid Interface Sci., 2010, 345, 316–324 CrossRef CAS PubMed.
- S. Perticaroli, J. Herzberger, Y. Sun, J. D. Nickels, R. P. Murphy, K. Weigandt and P. J. Ray, Multiscale Microstructure, Composition, and Stability of Surfactant/Polymer Foams, Langmuir, 2020, 36, 14763–14771 CrossRef CAS PubMed.
- M. Hohenschutz, I. Grillo, C. Dewhurst, P. Schmid, L. Girard, A. Jonchère, O. Diat and P. Bauduin, Superchaotropic nano-ions as foam stabilizers, J. Colloid Interface Sci., 2021, 603, 141–147 CrossRef CAS PubMed.
- M. Kühnhammer, L. Braun, M. Ludwig, O. Soltwedel, L. Chiappisi and R. von Klitzing, A new model to describe small-angle neutron scattering from foams, J. Appl. Crystallogr., 2022, 55, 758–768 CrossRef PubMed.
- M. A. V. Axelos and F. Boué, Foams As Viewed by Small-Angle Neutron Scattering, Langmuir, 2003, 19, 6598–6604 CrossRef CAS.
- T. Widmann, L. P. Kreuzer, M. Kühnhammer, A. J. Schmid, L. Wiehemeier, S. Jaksch, H. Frielinghaus, O. Löhmann, H. Schneider, A. Hiess, R. von Klitzing, T. Hellweg and P. Müller-Buschbaum, Flexible Sample Environment for the Investigation of Soft Matter at the European Spallation Source: Part II—The GISANS Setup, Appl. Sci., 2021, 11(9), 4036 CrossRef CAS.
- F. Liu, Z. Wang, D. Sun, X. Wei, W. Zhou, G. Li and G. Zhang, Adsorption Kinetics of Brij 97 at the Air/Solution Interface, J. Dispersion Sci. Technol., 2006, 27, 657–663 CrossRef CAS.
- B. Petkova, S. Tcholakova, M. Chenkova, K. Golemanov, N. Denkov, D. Thorley and S. Stoyanov, Foamability of aqueous solutions: Role of surfactant type and concentration, Adv. Colloid Interface Sci., 2020, 276, 102084 CrossRef CAS PubMed.
- S. Mukherjee and H. Wiedersich, Morphological and viscoelastic properties of dense foams generated from skin cleansing bars, Colloids Surf., A, 1995, 95, 159–172 CrossRef CAS.
- C. D. Dewhurst, I. Grillo, D. Honecker, M. Bonnaud, M. Jacques, C. Amrouni, A. Perillo-Marcone, G. Manzin and R. Cubitt, The small-angle neutron scattering instrument D33 at the Institut Laue-Langevin, J. Appl. Crystallogr., 2016, 49, 1–14 CrossRef CAS.
- ILL, GRASP, https://www.ill.eu/users/support-labs-infrastructure/software-scientific-tools/grasp, [Online; accessed 22-July-2022].
- G. Bradski, The OpenCV Library, Dr Dobb's Journal of Software Tools, 2000.
- Y. Wang and S. J. Neethling, The relationship between the surface and internal structure of dry foam, Colloids Surf., A, 2009, 339, 73–81 CrossRef CAS.
- E. Forel, E. Rio, M. Schneider, S. Beguin, D. Weaire, S. Hutzler and W. Drenckhan, The surface tells it all: relationship between volume and surface fraction of liquid dispersions, Soft Matter, 2016, 12, 8025–8029 RSC.
- K. Feitosa, S. Marze, A. Saint-Jalmes and D. J. Durian, Electrical conductivity of dispersions: from dry foams to dilute suspensions, J. Phys.: Condens. Matter, 2005, 17, 6301–6305 CrossRef CAS.
- NIST, Neutron Activation and Scattering Calculator, https://www.ncnr.nist.gov/resources/activation, [Online; accessed 22-July-2022].
- G. Porod, Small angle X-ray scattering, Academic Press, New York, 1982, pp. 17–51 Search PubMed.
- W. Drenckhan and S. Hutzler, Structure and energy of liquid foams, Adv. Colloid Interface Sci., 2015, 224, 1–16 CrossRef CAS PubMed.
- J. S. Pedersen, Neutrons, X-rays and Light: Scattering Methods Applied to Soft Condensed Matter, Elsevier Science BV, 2002, pp. 391–420 Search PubMed.
- M. Born, Quantenmechanik der Stoßvorgänge, Z. Phys., 1926, 38, 803–827 CrossRef CAS.
- A. Mikhailovskaya, L. Zhang, F. Cousin, F. Boué, P. Yazhgur, F. Muller, C. Gay and A. Salonen, Probing foam with neutrons, Adv. Colloid Interface Sci., 2017, 247, 444–453 CrossRef CAS PubMed.
- Neutrons, X-rays and Light: Scattering Methods Applied to Soft Condensed Matter, ed. P. Lindner and T. Zemb, Elsevier Science Bv, Amsterdam, 2002, p. 444 Search PubMed.
- L. G. Parratt, Surface Studies of Solids by Total Reflection of X-Rays, Phys. Rev., 1954, 95, 359–369 CrossRef.
- J. Penfold and R. K. Thomas, Neutron reflectivity and small angle neutron scattering: An introduction and perspective on recent progress, Curr. Opin. Colloid Interface Sci., 2014, 19, 198–206 CrossRef CAS.
- A. Mikhailovskaya, E. Chatzigiannakis, D. Renggli, J. Vermant and C. Monteux, From Individual Liquid Films to Macroscopic Foam Dynamics: A Comparison between Polymers and a Nonionic Surfactant, Langmuir, 2022, 38, 10768–10780 CrossRef CAS PubMed.
- J. Etrillard, M. A. V. Axelos, I. Cantat, F. Artzner, A. Renault, T. Weiss, R. Delannay and F. Boué, In Situ Investigations on Organic Foam Films Using Neutron and Synchrotron Radiation, Langmuir, 2005, 21, 2229–2234 CrossRef CAS PubMed.
- B. S. Gardiner, B. Z. Dlugogorski and G. J. Jameson, Coarsening of two- and three-dimensional wet polydisperse foams, Philos. Mag. A, 2000, 80, 981–1000 CAS.
- R. G. Horn, M. Asadullah and J. N. Connor, Thin Film Drainage: Hydrodynamic and Disjoining Pressures Determined from Experimental Measurements of the Shape of a Fluid Drop Approaching a Solid Wall, Langmuir, 2006, 22, 2610–2619 CrossRef CAS PubMed.
- E. Chatzigiannakis, N. Jaensson and J. Vermant, Thin liquid films: Where hydrodynamics, capillarity, surface stresses and intermolecular forces meet, Curr. Opin. Colloid Interface Sci., 2021, 53, 101441 CrossRef CAS.
- N. Schelero, G. Hedicke, P. Linse and R. von Klitzing, Effects of Counterions and Co-ions on Foam Films Stabilized by Anionic Dodecyl Sulfate, J. Phys. Chem. B, 2010, 114, 15523–15529 CrossRef CAS PubMed.
- R. A. Leonard and R. Lemlich, A study of interstitial liquid flow in foam. Part I. Theoretical model and application to foam fractionation, AIChE J., 1965, 11, 18–25 CrossRef CAS.
- O. Pitois, E. Lorenceau, N. Louvet and F. Rouyer, Specific Surface Area Model for Foam Permeability, Langmuir, 2009, 25, 97–100 CrossRef CAS PubMed.
- C. Ochoa, S. Gao, S. Srivastava and V. Sharma, Foam film stratification studies probe intermicellar interactions, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, 8915–8924 CrossRef PubMed.
- H. Wang, X. Wei, Y. Du and D. Wang, Effect of water-soluble polymers on the performance of dust-suppression foams: Wettability, surface viscosity and stability, Colloids Surf., A, 2019, 568, 92–98 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01252a |
| This journal is © The Royal Society of Chemistry 2022 |