 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of blockage ratio on flow of a viscoelastic wormlike micellar solution past a cylinder in a microchannel†
Cameron C.
Hopkins
 *,
Amy Q.
Shen
*,
Amy Q.
Shen
 and
Simon J.
Haward
and
Simon J.
Haward
 *
*
Okinawa Institute of Science and Technology Graduate Univerisity, Onna-son, Okinawa 904-0495, Japan. E-mail: c.c.hopkins91@gmail.com; simon.haward@oist.jp
First published on 14th November 2022
Abstract
We present experiments on the flow of a viscoelastic wormlike micellar solution around cylinders (radius R) confined in straight microchannels (width W). Thirteen flow geometries are tested where the blockage ratio is varied over a wide range 0.055 ≤ BR = 2R/W ≤ 0.63. Experiments are performed at negligible Reynolds number, and for Weissenberg numbers Wi = λU/R up to 1000, where U is the average flow speed and λ is the relaxation time of the fluid. Micro-particle image velocimetry is used to characterise the flow state at each BR and Wi. In all of the geometries, a first critical Weissenberg number marks a transition from symmetric flow to an asymmetric but time-steady flow state, while a second higher critical Weissenberg number marks the onset of time-dependent flows. However, we report a clear shift in behaviour over a narrow intermediate range of 0.33 ≲ BR ≲ 0.41. Channels with BR ≤ 0.33 fall in a ‘low’ BR regime, with instabilities that originate from the downstream stagnation point, while those with BR ≥ 0.44 fall in a ‘high’ BR regime, with instabilities developing at the upstream stagnation point. Behaviour within the newly-identified intermediate BR regime is complex due to the competing influence of the two stagnation points. We summarise all our results in a flow state diagram covering Wi–BR parameter space, clearly defining the different regimes of blockage ratio for the first time. Our results contribute to the understanding of the complexities of viscoelastic flow in this benchmark geometry.
1 Introduction
Developing an accurate prediction of the viscoelastic flow around a cylinder in a channel is a fundamental problem in non-Newtonian fluid mechanics. The specific case of a cylinder of radius R located in the centre of a straight channel of width W = 4R, such that the ‘blockage ratio’ BR = 2R/W = 0.5 (Fig. 1), has been considered as one of the ‘benchmark’ non-Newtonian flows for testing the predictions of constitutive equations against experimental results.1 However, it has long been recognised that the choice of BR = 0.5 is somewhat arbitrary, and that varying BR around this value can result in substantially different behaviour of the fluid.2,3Flow past a cylinder confined in a channel (Fig. 1) presents a complex mix of shearing and extensional flow kinematics. Shear rates increase and then decrease as fluid squeezes through the gaps between the cylinder and the channel walls. This squeezing also amounts to a transient extensional (contraction/expansion) flow. In addition, axial stagnation points exist at the leading and trailing edges of the cylinder, which result in shear-free and persistent extensional kinematics with high residence times.
For microstructured viscoelastic fluids such as polymeric or wormlike micellar solutions, with a rheology that depends on the imposed shear and/or extensional deformation rate, the combination of kinematics encountered in flow past a cylinder can lead to unexpected and complex dynamical behaviour and instabilities. Comprehensive recent reviews on the topic are available in ref. 4 and 5. We focus here only on microfluidic experiments on flows around cylinders that conveniently allow the effects of inertia on the flow dynamics to be neglected due to the small characteristic length scales involved.6 In this case, at low average flow velocities around the cylinder, U, a viscoelastic fluid will largely behave in a ‘Newtonian-like’ way, exhibiting streamlines that are symmetric with respect to both the x and y-axes (as indicated in Fig. 1). However, as U is increased beyond a critical value, non-Newtonian effects may be observed. For higher blockage ratios (BR ≳ 0.5), the most dominant effects are manifested upstream of the cylinder, for example with the occurrence of large recirculating regions fixed at the upstream stagnation point.7–10 However, at lower blockage ratios the deviation from Newtonian-like behaviour is most obvious downstream of the cylinder, for example with regions of low flow velocity forming a trailing wake that may extend for many cylinder radii.11–15 In both cases, the critical flow velocity for the onset of non-Newtonian behaviour typically scales with the dimensionless Weissenberg number Wi = λ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . Here, λ represents a characteristic relaxation time of the fluid, and
. Here, λ represents a characteristic relaxation time of the fluid, and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) represents a characteristic deformation rate (shear or extensional) in the flow field. For Wi ≳ 0.5, the microstructure can be deformed by the flow, giving rise to rheological effects such as shear thinning in regions of shearing kinematics and extension thickening (or elasticity) in regions of extensional kinematics.16 Varying BR modifies the relative importance of the various kinematic features in the flow field around the cylinder, and thus modifies the way in which a given viscoelastic fluid will respond for Wi ≳ 0.5.
represents a characteristic deformation rate (shear or extensional) in the flow field. For Wi ≳ 0.5, the microstructure can be deformed by the flow, giving rise to rheological effects such as shear thinning in regions of shearing kinematics and extension thickening (or elasticity) in regions of extensional kinematics.16 Varying BR modifies the relative importance of the various kinematic features in the flow field around the cylinder, and thus modifies the way in which a given viscoelastic fluid will respond for Wi ≳ 0.5.
Other non-Newtonian flow features may also be observed depending on the fluid rheology, the blockage ratio and/or the magnitude of the imposed Weissenberg number. For instance, the buckling of streamlines upstream of the cylinder has been observed in fluids of various rheology and BR.12,17,18 However, the development of strong lateral flow asymmetry around, and downstream of, the cylinder has so far been exclusively reported at low BR ≤ 0.1 and with fluids exhibiting both strong shear thinning and elasticity.13–15,19 Recently, with a shear thinning and elastic wormlike micellar solution, the occurrence of wall-attached vortices upstream of a cylinder at BR = 0.5 has also been reported.18
In the present work, we employ a single viscoelastic fluid (a shear thinning and elastic wormlike micellar solution) with model Maxwellian relaxation dynamics, and we study its flow behaviour for Weissenberg numbers up to 1000 around cylinders presenting a wide range of blockage ratios 0.055 ≤ BR ≤ 0.63. Such a wide ranges of BR and Wi in combination have not previously been examined for viscoelastic flows around cylinders. A total of thirteen different blockage ratio cylinders are contained in microchannels of high aspect ratio (AR = H/W = 5), such that the flow can be assumed to be inertialess and two-dimensional (2D), greatly facilitating the possibility of comparison with numerical modelling. In each channel, several distinct flow states are observed as Wi is increased. The large number of channels with incrementally varying blockage also allows trends of behaviour to be followed with BR. A flow state diagram in Wi–BR parameter space, reveals an abrupt transition in behaviour for 0.33 ≲ BR ≲ 0.41, defining a clear boundary between the ‘low’ and ‘high’ BR regimes. This ‘phase diagram’ will be a valuable aid for predicting the nature of viscoelastic flows around cylinders as a function of fluid rheology, imposed flow rate, and channel geometry. Furthermore, it provides a comprehensive benchmarking target for reproduction in future numerical simulations.
2 Experimental methods
2.1 Test fluid rheology
The test fluid is a strongly shear thinning (in fact, shear banding)20 and viscoelastic semidilute and entangled aqueous wormlike micellar solution composed of 100 mM cetylpyridinium chloride and 60 mM sodium salicylate (100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 CPyCl
60 CPyCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NaSal).21,22 The fluid is identical to that used in a recent study of the flow past a microfluidic cylinder of BR = 0.5,18 and similar to that used in an earlier related study in which BR = 0.1.13 At the ambient laboratory temperature (24 °C), the fluid has a zero shear viscosity η0 ≈ 27.5 Pa s. With increasing shear rate
NaSal).21,22 The fluid is identical to that used in a recent study of the flow past a microfluidic cylinder of BR = 0.5,18 and similar to that used in an earlier related study in which BR = 0.1.13 At the ambient laboratory temperature (24 °C), the fluid has a zero shear viscosity η0 ≈ 27.5 Pa s. With increasing shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , the viscosity η(
, the viscosity η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) thins dramatically with a power law index n ≈ 0 towards a high-shear-rate plateau value of η∞ = 2 mPa s. The linear viscoelastic response of the fluid is well-described by a single mode Maxwell model that provides a terminal relaxation time of λ = 1.54 s. Full details of the rheological characterization of the fluid, also including measurements of the first normal stress difference, are available in ref. 18.
) thins dramatically with a power law index n ≈ 0 towards a high-shear-rate plateau value of η∞ = 2 mPa s. The linear viscoelastic response of the fluid is well-described by a single mode Maxwell model that provides a terminal relaxation time of λ = 1.54 s. Full details of the rheological characterization of the fluid, also including measurements of the first normal stress difference, are available in ref. 18.
2.2 Microchannel design and experimental setup
Microchannels are fabricated in fused silica glass by the technique of selective laser-induced etching using a LightFab instrument (LightFab GmbH).23–25 Each channel has height H = 2000 μm and width W = 400 μm, and thus aspect ratio AR = H/W = 5 (see Fig. 1). Cylinders have radii R = 11, 20, 30, 40, 58, 66, 76, 80, 88, 96, 100, 116, and 126 μm, thus providing respective blockage ratios of BR = 2R/W = 0.055, 0.1, 0.15, 0.2, 0.29, 0.33, 0.38, 0.4, 0.44, 0.48, 0.5, 0.58, and 0.63. Flow through the microchannels is imposed using two Nemesys low pressure syringe pumps, one of which infuses fluid at the upstream inlet to the channel, and the other of which withdraws fluid from the downstream outlet (both at the same volumetric flow rate Q). Each channel is configured with a distance of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 μm (= 31.25W) between the inlet and the cylinder, in order to allow the flow to become fully developed upstream of the cylinder, and an equal distance between the cylinder and the outlet to allow redevelopment of the flow in the downstream.
500 μm (= 31.25W) between the inlet and the cylinder, in order to allow the flow to become fully developed upstream of the cylinder, and an equal distance between the cylinder and the outlet to allow redevelopment of the flow in the downstream.
The average flow velocity in the channel is U = Q/WH, providing a nominal wall shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w = 6U/W. The reduction in cross-sectional area due to the cylinder causes the flow velocity to increase in the gaps between the cylinder and the channel walls. At the location x = 0, the average flow velocity in the gaps is given by Ugap = U/(1 − BR), and the nominal wall shear rate in the gap is given by
w = 6U/W. The reduction in cross-sectional area due to the cylinder causes the flow velocity to increase in the gaps between the cylinder and the channel walls. At the location x = 0, the average flow velocity in the gaps is given by Ugap = U/(1 − BR), and the nominal wall shear rate in the gap is given by ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap = 6Ugap/0.5W(1 − BR) = 12U/W(1 − BR)2 = 2
w,gap = 6Ugap/0.5W(1 − BR) = 12U/W(1 − BR)2 = 2![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w/(1 −BR)2.
w/(1 −BR)2.
As mentioned in the Introduction (Section 1), the Weissenberg number can be defined based on either a shear or an extensional deformation rate. Here, consistent with our prior work (e.g., ref. 13, 18), we consider the deformation rate based on the nominal velocity gradient along the channel centreline near the upstream and downstream stagnation points of the cylinder, i.e., the nominal extensional rate in those locations. Hence we consider an extensional Weissenberg number defined as Wi = λU/R. Note that this definition of Wi is numerically equivalent to the Deborah number of the flow De = λ/Tflow, where Tflow = R/U is the characteristic time for the flow to pass the cylinder. Based on this definition, at the maximum values of Weissenberg number tested (Wimax = 1000), the average flow velocities are U ≈ 7 mm s−1 (for the lowest BR = 0.055) and U ≈ 82 mm s−1 (for the highest BR = 0.63). Corresponding shear rate values for BR = 0.055 are ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w ≈ 106 s−1 and
w ≈ 106 s−1 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap ≈ 240 s−1, while those for BR = 0.63 are
w,gap ≈ 240 s−1, while those for BR = 0.63 are ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w ≈ 1230 s−1 and
w ≈ 1230 s−1 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap ≈ 17970 s−1. An alternative definition of the Weissenberg number, based on the wall shear rate in the gap, can be written Wigap = λ
w,gap ≈ 17970 s−1. An alternative definition of the Weissenberg number, based on the wall shear rate in the gap, can be written Wigap = λ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap = 12λU/W(1 − BR)2. For each blockage ratio considered, Wigap ∝ Wi, however the constant of proportionality depends on BR. For instance, at the lowest blockage ratio of BR = 0.055, we find that Wigap ≈ 0.37Wi, while for the highest blockage ratio of BR = 0.63, we find that Wigap ≈ 28Wi.
w,gap = 12λU/W(1 − BR)2. For each blockage ratio considered, Wigap ∝ Wi, however the constant of proportionality depends on BR. For instance, at the lowest blockage ratio of BR = 0.055, we find that Wigap ≈ 0.37Wi, while for the highest blockage ratio of BR = 0.63, we find that Wigap ≈ 28Wi.
As discussed in ref. 18, we consider the most appropriate definition of the Reynolds number (describing the ratio of inertial to viscous forces in the flow), to be Re0 = ρUR/η0, where ρ = 1000 kg m−3 is the fluid density. By this definition, based on the zero shear rate viscosity of the fluid, for the largest cylinder at the highest flow rate imposed in our experiments, we obtain the maximum value Re0,max ≈ 4 × 10−4. If instead we consider a Reynolds number based on the infinite shear rate viscosity, Re∞ = ρUR/η∞, we obtain Re∞,max ≈ 5. However, for all but the largest cylinders at the highest flow rates tested, Re∞ < 1. Furthermore, the elasticity number (comparing elastic to inertial forces in the flow) can be defined as El = Wi/Re. Even for the case of the largest cylinder (i.e., highest Re), we find El0 = Wi/Re0 ≈ 2.7 × 106, while El∞ = Wi/Re∞ ≈ 200. Since the Reynolds number is small and El∞ ≫ 1, we consider that inertia plays a negligible role in determining the flow dynamics.
2.3 Flow velocimetry
Quantitative and spatially-resolved 2D velocity fields are acquired using micro-particle image velocimetry (μ-PIV, TSI Inc.).26,27 For these measurements, the fluid is seeded with fluorescent tracer particles (2 μm-diameter, Fluoromax red, Thermo Scientific Inc.) at a low concentration (≈0.02 wt%) that does not affect the fluid rheology. Measurements are made by focussing on the mid-plane of the channel (z = 0) using an inverted microscope (Nikon Ti) with a 5× magnification, NA = 0.15 numerical aperture Nikon Plan Fluor objective lens. The fluid volume is illuminated by an Nd:YLF dual-pulsed laser (wavelength 527 nm), which is synchronized with a high speed camera (Phantom Miro) working in frame-straddling mode. With this camera and microscope objective, the field of view is 2.05 × 1.28 mm, and with the 2 μm seeding particles the measurement depth is 124 μm, (≈0.06H). At each imposed flow rate, the flow is held constant for at least 60 seconds, (≈40λ) before initiating the recording of image pairs for analysis. For time-steady flows, 250 μ-PIV frame pairs are recorded at 25 pairs-per-second. For time-dependent flows, 1500 frame pairs are recorded at 50 pairs-per-second. In both cases, frame pairs are cross-correlated both individually and by an ensemble average processing algorithm, providing two-component velocity vectors u = [u,v], where u and v are the x and y components of the velocity, respectively. The cross-correlation is performed using OpenPIV, an open-source Python package.283 Results
3.1 Steady flow instabilities around the cylinders
We commence the presentation of our experimental results by describing the flow patterns observed around the cylinders over a lower range of Weissenberg numbers at which the flow remains steady in time. For all blockage ratios examined, for Weissenberg numbers below a first critical value 10 ≲ Wic1 ≲ 100 (depending on BR), the flow field around the cylinder appears approximately symmetric about the x and y axes. For Wi > Wic1, the flow destabilizes but continues to remain steady. The nature of this initial instability and the resulting flow patterns also depend on BR, as will be described in detail in the following. | ||
| Fig. 2 Flow patterns observed for flow of the WLM solution at Wi = 40 around cylinders with ‘low’ blockage ratios: (a) BR = 0.055, (b) BR = 0.15, (c) BR = 0.2, (d) BR = 0.33. | ||
Fig. 2 shows that by increasing the blockage ratio in the range 0.055 ≤ BR ≤ 0.33, the system transitions from a steady symmetric state into a state of increasingly intense lateral asymmetry. For a fixed value of BR, and increasing the Weissenberg number, the flow also transitions from symmetric to asymmetric (as shown in a prior publication with BR = 0.1).13 Both Wi and BR can be used as control parameters to vary the degree of lateral asymmetry.
For each value of BR examined, we quantify the degree of flow asymmetry via the rate of flow around either side of the cylinder using the following asymmetry parameter:
| I = |u+ −u−|/(u+ + u−), | (1) |
Fig. 3(a–d) shows examples of the asymmetry parameter I plotted as a function of the imposed Weissenberg number for the same four blockage ratio cases illustrated in Fig. 2. For BR = 0.055 (Fig. 3(a)), as the Weissenberg number is increased the flow becomes laterally asymmetric at Wic1 ≈ 70, and subsequently stays strongly asymmetric (with I ≈ 1) over the remaining range of Wi probed (Wi up to ≈1000). As BR is progressively increased through Fig. 3(b–d), the value of Wic1 progressively decreases, and the rate of growth of the asymmetry decreases. In each case, for Wi > Wic1 the flow becomes strongly asymmetric, but the range of Wi over which the asymmetry is maintained is progressively reduced as BR increases. At higher Wi, the flow transitions back towards a laterally symmetric state (I → 0).
 | ||
| Fig. 3 Characterization of the lateral flow asymmetry observed around cylinders presenting low blockage ratios BR ≤ 0.33. Asymmetry parameter I (eqn (1)) as a function of Wi for the same four BR cases shown in Fig. 2: (a) BR = 0.055, (b) BR = 0.15, (c) BR = 0.2, (d) BR = 0.33. Data points are experimental measurements, solid lines are the best fits of the Landau model (eqn (2)). (e) Fitting parameters extracted from the Landau model for all tested blockage ratios in the range 0.055≤ BR ≤0.33. Solid lines are fits to the experimental data points of the form Wic1 ∼ 1/BR (black), and g ∼ 1/(a − BR), where a = 0.41 (red), see main text. | ||
Consistent with prior work at BR = 0.1,13 the transition to asymmetry is well described using a minimized quartic Landau potential:
| Wi = Wic1(gI2 + hI−1 + 1), | (2) |
The values of Wic1 and g obtained for each value of BR are plotted as a function of BR in Fig. 3(e). Here, the error bars represent a one standard deviation confidence interval determined from the least-squares curve fitting of eqn (2) to the experimental data. The critical Weissenberg number is well described by Wic1 = 3.3/BR, in agreement with the 1/BR scaling predicted by McKinley and coworkers,31,32 and also recently shown for this instability by numerical simulations with the linear Phan–Thien–Tanner model.15 This is a further experimental confirmation that the instability is induced by the growth of elastic tensile stress along the curved streamlines near the downstream stagnation point.5 The instability growth rate parameter is well described by g = 0.5/(0.41 − BR). Interestingly, this suggests that g → ∞ as BR → 0.41, indicating that the instability should disappear (infinitely slow growth).
 | ||
| Fig. 4 Flow patterns observed for flow of the WLM solution at Wi = 30 around cylinders with ‘high’ blockage ratios: (a) BR = 0.44, (b) BR = 0.48, (c) BR = 0.58, (d) BR = 0.63. | ||
We quantify the bending streamline instability observed at higher blockage ratios by extracting a probe velocity vp, which is the y-component of the flow velocity at a probe location (x = −1.4R) upstream of the cylinder. The data points in Fig. 5(a–d), show |vp/U| measured as a function of Wi for the same four blockage ratio cases presented in Fig. 4.
 | ||
| Fig. 5 Characterization of the bending streamlines instability observed for flow around cylinders presenting high blockage ratios BR ≥ 0.44. Normalized magnitude of the transverse component of the velocity at an upstream probe location |vp/U| (see text for full description) as a function of Wi for the same four BR cases shown in Fig. 4: (a) BR = 0.44, (b) BR = 0.48, (c) BR = 0.58, (d) BR = 0.63. Data points are experimental measurements, solid lines are the best fits of the Landau model (eqn (3)). (e) Fitting parameters extracted from the Landau model for all tested blockage ratios in the range 0.44 ≤ BR ≤ 0.63. Solid lines are fits to the experimental data points of the form Wic1∼ 1/BR (black), and g ∼ 1/(a − BR), where a = 0.64 (red), see main text. | ||
The solid lines in Fig. 5(a–d) are fits of the following Landau equation:
| Wi = Wic1[g(|vp/U|)2 + h(|vp/U|)−1 + 1], | (3) |
At BR = 0.44 (Fig. 5(a)), the onset of streamline bending is extremely abrupt at Wic1 ≈ 30, at which |vp/U| increases rapidly to a maximum, before gradually decreasing with further increasing Wi. Increasing the blockage through BR = 0.48 (Fig. 5(b)), BR = 0.58 (Fig. 5(c)), and BR = 0.63 (Fig. 5(d)), the transition occurs at progressively lower Wic1 and becomes more gradual (i.e., g increases).
Fig. 5(e) shows Wic1 and g plotted as a function of BR for all channels tested with BR ≥ 0.44. As before for the lower BR cases, we find a 1/BR dependence for both Wic1 and g with Wic1 = 3.5/(BR − 0.33) and g = 0.1/(0.64 − BR). The scaling Wic1 ∼ 1/BR is again consistent with the prediction of an elastic instability driven by a combination of elastic tensile stress and streamline curvature,31,32 in this case the location of importance clearly being the upstream stagnation point. The asymptote in Wic1 at BR = 0.33 suggests that bending streamlines upstream of the cylinder should not be observed for lower blockage ratios than this. The asymptote in g at BR = 0.64 further suggests that the bending streamline instability should vanish at even higher blockage ratios. Unfortunately, we were unable to test this due to difficulty in fabricating devices with BR > 0.63.
Comparing the asymptotes found for ‘low’ BR and ‘high’ BR behaviour (Fig. 3(e) and 5(e), respectively) indicates the presence of an ‘intermediate’ blockage ratio regime for 0.33 ≲ BR ≲ 0.41, where the lateral asymmetry and the upstream bending streamline instabilities could coexist.
In general, for this example intermediate BR case, we observe that the transition between flow states with increasing Wi is more complex than at either low or high BR. Although we see both flow behaviours that could be classified as ‘lateral asymmetry’ or ‘upstream bending streamlines’, neither progresses with increasing Wi in the same way as seen when the blockage ratio is clearly either ‘low’ or ‘high’. For this intermediate BR = 0.4 case, there appears to be a competition between the instabilities that arise at low and high BR.
For low BR, the lateral flow asymmetry is initiated due to the accumulation of elastic tensile stress on the streamlines that curve near the downstream stagnation point of the cylinder, in accordance with the prediction of McKinley and coworkers.5,15,32 For high BR, it appears that elastic tensile stress on the streamlines curving near the upstream stagnation point drive the onset of instability there, too. Within the intermediate regime it seems that neither stagnation point clearly dominates and that both stagnation points actively contribute to the observed dynamics, competing for dominance in a complex interplay.
4 Time-dependent fluctuations
As the Weissenberg number is increased well beyond Wic1, the flow eventually exhibits time-dependent features. In this section, we provide a brief discussion of the time-dependence observed above a second critical Weissenberg number Wic2 at various blockage ratios. A thorough analysis of the time-dependence is beyond the scope of this work, but two prior works provide detailed studies, including spectral analysis, performed at low BR = 0.1,13 and high BR = 0.5.18 Here we mostly seek to find the approximate value of Wic2 for each blockage ratio and to broadly categorise the observed flow states. Although the flow likely fluctuates in all three spatial directions,18 we assume that this occurs simultaneously in each direction at a coincident Weissenberg number. Therefore we may find Wic2 with reasonable accuracy based on our 2D flow velocimetry. To this end, we use time-resolved 2D velocity fields to approximately quantify the turbulence intensity T as a function of the imposed Wi. The turbulence intensity is defined as: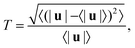 | (4) |
In Fig. 7, we present time-averaged velocity magnitude fields along with their corresponding turbulence intensity fields obtained at Wi ≈ 400 in devices of various blockage ratio. At the three lowest values of BR = 0.055, 0.1, and 0.15 (Fig. 7(a)–(c), respectively), we observe a time-dependent lateral asymmetry, where the flow mostly fluctuates within the low-velocity wedge of fluid located at positive y. At this Wi, with increasing BR, that fluctuating wedge of fluid becomes compressed as the streamlines push further past the cylinder into the downstream region before doubling back. For BR = 0.15 (Fig. 7(c)), the low-velocity region has become completely pinched resulting in a thin layer of sheared fluid that curves from the rear stagnation point of the cylinder towards the top wall of the channel at y = 0.2 mm. All of the flow fluctuations occur in this strongly sheared region. Increasing the blockage further to BR = 0.2 (or alternatively if Wi is increased further at BR = 0.15), the flow is able to push past the cylinder on both sides of the channel (although unequally) resulting in ‘asymmetric jets’ of high flow velocity extending downstream near the walls of the channel (Fig. 7(d)). All of the flow fluctuations are concentrated in the wake behind the cylinder where the flow velocity is generally low, but frequent pulses of high velocity occur. Further increasing the blockage ratio to BR = 0.33, 0.44, and 0.63 (Fig. 7(e)–(g), respectively), progressively larger wall vortices form upstream of the cylinder and the flow fluctuations in the wake decrease progressively in intensity. A vortex forms at the upstream stagnation point of the cylinder and there are flow fluctuations in both the wall-attached and cylinder-attached vortices. As reported in a prior publication at BR = 0.5,18 when there is an upstream cylinder-attached vortex, it competes with the wall-attached vortices for time and space in the channel. In some of the present experiments only a cylinder vortex is observed over the entire 20 s duration of the data acquisition. However, in repeated test runs, both cylinder and wall vortices could be observed at various times. In subsequent discussion, we will refer to flow states such as ‘upstream cylinder vortex’ or ‘upstream wall vortex’, however these are not necessarily exclusive. It is possible for multiple flow ‘states’ to be observable for a given pair of Wi and BR.
In order to unambiguously determine a value for Wic2, at which a flow state becomes time dependent, we spatially average the turbulence intensity over the field of view to obtain a quantity ΣT. Fig. 8 shows plots of ΣT as a function of Wi for three blockage ratios: BR = 0.055 (Fig. 8(a), illustrating low BR behaviour), BR = 0.4 (Fig. 8(b), illustrating intermediate BR behaviour), and BR = 0.58 (Fig. 8(c), illustrating high BR behaviour). For each blockage ratio there is a clear increase in ΣT as the flow becomes time dependent. For the low and high BR cases, the increase is step-like, but at intermediate BR the increase is more gradual. The experimental data is fitted with a hyperbolic tangent function given by:
 | (5) |
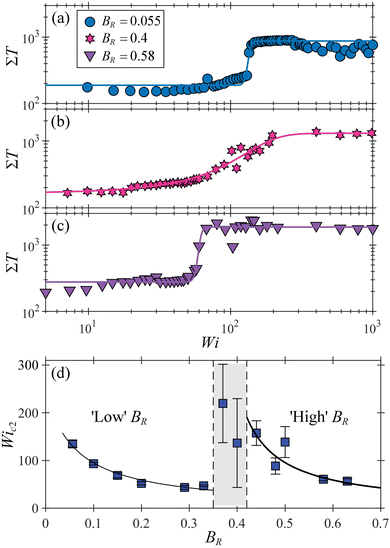 | ||
| Fig. 8 Transition to time dependent flow. Spatially-averaged turbulence intensity ΣT as a function of Wi for (a) low BR, (b) intermediate BR, and (c) high BR cylinders. Experimental data (points) are fitted with a hyperbolic tangent function (eqn (5), lines) in order to extract values for Wic2 marking the onset of time-dependent flow at each value of BR. (d) Wic2 as a function of BR for all blockage ratios tested in the experiments. Data are fitted as Wic2 = 15.5/BR (low BR regime) and Wic2 = 15/(0.3 − BR) (high BR regime). The intermediate BR regime is shaded gray. | ||
5 Flow state diagram
Finally, we summarise our experimental results by constructing a flow state diagram in Wi–BR parameter space, as shown in Fig. 9(a). Here the different symbols refer to different observed steady and time-dependent flow states illustrated alongside in Fig. 9(b–i), and identified by corresponding symbols. The stability boundaries marked by dashed lines at Wic1 and Wic2 are the fits to the experimental data shown in Fig. 3(e), 5(e) and 8(d). The intermediate BR regime is shaded gray in Fig. 9(a), and marks a striking change in behaviour between the low and high BR regimes. For instance, increasing BR across the intermediate range at a fixed Weissenberg number (say Wi = 20), the flow state switches from ‘laterally asymmetric’ (Fig. 9(c)) to ‘symmetric’ (Fig. 9(b)). Similarly, at a higher Weissenberg number (say Wi = 100), increasing BR across the intermediate range causes the flow to switch from a ‘time-dependent laterally asymmetric’ state (Fig. 9(f)) into a time-steady state characterized by ‘upstream bending streamlines’ (Fig. 9(d)). Note that for increasing Wi at a fixed BR, changes in the flow state, e.g., from ‘time-dependent upstream wall vortices’ (Fig. 9(h)) to ‘upstream cylinder vortex’ (Fig. 9(i)) are not necessarily abrupt or exclusive. For instance, as discussed above, an upstream cylinder vortex can appear at a given Wi and coexist with upstream wall vortices over a certain range of Wi. Similarly, the ‘asymmetric jetting’ state Fig. 9(g) may coexist with upstream wall vortices. The flow state indicated by a given symbol in Fig. 9(a) represents the ultimate state to be observed as Wi is increased to the given value at the given BR. For the interested reader, the ESI† includes an alternative flow state diagram presented in Wigap–BR parameter space (Fig. S1, ESI†), where Wigap is computed based on the shear rate between the cylinder and the channel wall (as described in Section 2.2). While, compared to Fig. 9(a), this results in a BR-dependent shift in the boundaries between flow transitions, the low and high BR regimes remain clearly demarcated.6 Discussion and conclusions
We have presented microfluidic experiments on the flow of a viscoelastic wormlike micellar solution around cylinders presenting a wide range of blockage ratios 0.055 ≤ BR ≤ 0.63. The experiments have been performed at negligible Reynolds numbers (i.e., vanishing inertia) and over a wide range of the Weissenberg number (Wi up to 1000). Experiments on flows around cylinders in channels (a benchmark geometry for studying non-Newtonian flows) have never before been carried out over such a wide range of Wi–BR parameter space. Our experiments reveal a rich variety of steady and time-dependent flow states that can be observed depending on both Wi and BR. For BR ≲ 0.33 (i.e., ‘low’ BR), flow instabilities originate from the downstream stagnation point. An initial instability at Wic1 ∼ 1/BR marks a transition from a symmetric to a laterally asymmetric, but time-steady flow state. Above a higher critical value Wic2 (also ∼1/BR), the flow becomes time dependent, exhibiting strong fluctuations downstream of the cylinder. For BR ≳ 0.44 (i.e., ‘high’ BR), the observed steady flow instabilities above Wic1 ∼ 1/BR originate from the upstream stagnation point, initially manifesting as bending streamlines, and subsequently developing into wall-attached vortices upstream of the cylinder. Above Wic2, time-dependence in the flow around the high-BR cylinders manifests as strong fluctuations in the upstream wall-attached vortices and subsequently in an upstream cylinder-attached vortex that forms as Wi is further increased.It has long been recognised that changing the blockage ratio of the cylinder in the channel can shift the influence of the different features in the flow field, leading to different dynamical flow phenomena.2,3 By varying BR incrementally over a wide range, we have been able to clearly distinguish the ranges of BR that can be considered to be in either the ‘low’ or the ‘high’ BR regimes. We also identify a narrow ‘intermediate’ BR regime spanning 0.33 ≲ BR ≲ 0.41, across which there is a clear shift in behaviour. Within the intermediate BR regime, the flow transitions are more complex and less well defined than in either the low- or the high-BR regime. This is presumably due to the competing influence between instabilities arising from each stagnation point. In future work, it will be interesting to perform a more detailed study focussing specifically within this intermediate range of BR in order to understand this complex behaviour more thoroughly. We suspect there may be some analogies to be made to phase transitions in thermodynamic36 or active matter37 systems. The distinct boundaries between flow states delineated by the Wic1 curves within the low and high BR regimes may be similar to spinodal curves. The apparent observation of competing, or merging, flow states within the intermediate BR regime may indicate a coexistence regime (analogous to the ‘miscibility gap’) and hence suggests the possible presence of a binodal curve in this region of the flow state diagram. As such, the observed instabilities in the intermediate BR regime may be prone to hysteresis or ‘priming’-like behaviour, where the system can become stuck in a given state while the control parameter is varied. Similar behaviour has been observed for the flow of wormlike micellar solutions past side-by-side microcylinders.38 Since it is practically impossible to hold Wi constant while varying BR in an experiment, a numerical study of this system with dynamically varying Wi and/or BR (such as that performed for viscoelastic flow past low BR cylinders i.e., ref. 15) may prove invaluable for the calculation of theoretical boundaries in the phase diagram. Note that the high aspect ratio of our experimental devices, AR = 5 greatly facilitates a comparable numerical study since the flow can be reasonably approximated as being two-dimensional.
The present work has revealed that viscoelastic flow in a simple geometry comprised of a single obstacle in a channel is rich in time-steady and time-dependent flow behavior. Like high-Reynolds number inertial flows in geometrically simple systems such as between co- or counter-rotating cylinders,39 pipe flow,40 and flow past a cylinder,41 geometric simplicity does not preclude rich and dynamic flow behaviour as the geometric and flow conditions are varied. The study of inertia-less viscoelastic flow instabilities in microfluidic geometries is growing rapidly with the recent advancement in microfluidic channel fabrication25 and promises to yield similarly rich flow behaviour. We believe that the flow state diagram we have constructed can serve as a foundation for future studies on viscoelastic flow past obstacles in microchannels, and aid in the design of microfluidic systems where viscoelastic fluids will be used. In recent prior works on flows past cylinders (e.g., ref. 13–15, 38), we have observed broadly analogous behaviour for both wormlike micellar solutions and for shear thinning viscoelastic polymer solutions (especially in the time-steady regime). However, it would be interesting to employ polymeric fluids to examine how the flow state diagram becomes modified as the degrees of shear thinning and elasticity are fine-tuned by variation of e.g., the polymer concentration or molecular weight, or the solvent quality or viscosity.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the support of the Okinawa Institute of Science and Technology Graduate University (OIST) with subsidy funding from the Cabinet Office, Government of Japan. We also acknowledge funding from the Japan Society for the Promotion of Science (JSPS, Grant No. 20K14656 and 21K03884) and the Joint Research Projects (JRPs) supported by the JSPS and the Swiss National Science Foundation (SNSF). We are grateful for the help and support provided by the Engineering Section of the Research Support Division at OIST.Notes and references
- O. Hassager, J. Non-Newtonian Fluid Mech., 1988, 29, 2–5 CrossRef.
- K. Walters and R. I. Tanner, Transport Processes in Bubbles, Drops and Particles, Hemisphere, New York, 1992, pp. 73–86 Search PubMed.
- G. H. McKinley, R. C. Armstrong and R. A. Brown, Philos. Trans. R. Soc., A, 1993, 344, 265–304 CrossRef.
- J. P. Rothstein and H. Mohammadigoushki, J. Non-Newtonian Fluid Mech., 2020, 285, 104382 CrossRef CAS.
- S. J. Haward, C. C. Hopkins, S. Varchanis and A. Q. Shen, Lab Chip, 2021, 21, 4041–4059 RSC.
- T. M. Squires and S. R. Quake, Rev. Mod. Phys., 2005, 77, 977–1026 CrossRef CAS.
- S. Kenney, K. Poper, G. Chapagain and G. F. Christopher, Rheol. Acta, 2013, 52, 485–497 CrossRef CAS.
- X. Shi, S. Kenney, G. Chapagain and G. F. Christopher, Rheol. Acta, 2015, 54, 805–815 CrossRef CAS.
- Y. Zhao, A. Q. Shen and S. J. Haward, Soft Matter, 2016, 12, 8666–8681 RSC.
- B. Qin, P. F. Salipante, S. D. Hudson and P. E. Arratia, J. Fluid Mech., 2019, 864, R2 CrossRef CAS PubMed.
- K. P. Nolan, A. Agarwal, S. Lei and R. Shields, Microfluid. Nanofluid., 2016, 20, 101 CrossRef.
- S. J. Haward, K. Toda-Peters and A. Q. Shen, J. Non-Newtonian Fluid Mech., 2018, 254, 23–35 CrossRef CAS.
- S. J. Haward, N. Kitajima, K. Toda-Peters, T. Takahashi and A. Q. Shen, Soft Matter, 2019, 15, 1927–1941 RSC.
- S. J. Haward, C. C. Hopkins and A. Q. Shen, J. Non-Newtonian Fluid Mech., 2020, 278, 104250 CrossRef CAS.
- S. Varchanis, C. C. Hopkins, A. Q. Shen, J. Tsamopoulos and S. J. Haward, Phys. Fluids, 2020, 32, 053103 CrossRef CAS.
- R. G. Larson, The Structure and Rheology of Complex Fluids, Oxford University Press, New York, 1999 Search PubMed.
- F. J. Galindo-Rosales, L. Campo-Deaño, P. C. Sousa, V. M. Ribeiro, M. S. N. Oliveira, M. A. Alves and F. T. Pinho, Exp. Them. Fluid Sci., 2014, 59, 128–139 CrossRef.
- C. C. Hopkins, S. J. Haward and A. Q. Shen, Soft Matter, 2022, 18, 4868–4880 RSC.
- A. A. Dey, Y. Modarres-Sadeghi and J. P. Rothstein, Phys. Rev. Fluids, 2018, 3, 063301 CrossRef.
- S. M. Fielding, J. Rheol., 2016, 60, 821–834 CrossRef CAS.
- H. Rehage and H. Hoffmann, J. Phys. Chem., 1988, 92, 4712–4719 CrossRef CAS.
- H. Rehage and H. Hoffmann, Mol. Phys., 1991, 74, 933–973 CrossRef CAS.
- J. Gottmann, M. Hermans and J. Ortmann, Physics Procedia, 2012, 39, 534–541 CrossRef.
- G. Meineke, M. Hermans, J. Klos, A. Lenenbach and R. Noll, Lab Chip, 2016, 16, 820–828 RSC.
- N. Burshtein, S. T. Chan, K. Toda-Peters, A. Q. Shen and S. J. Haward, Curr. Opin. Colloid Int., 2019, 43, 1–14 CrossRef CAS.
- S. T. Wereley and C. D. Meinhart, Microscale Diagnostic Techniques, Springer-Verlag, Heidelberg, 2005, pp. 51–112 Search PubMed.
- S. T. Wereley and C. D. Meinhart, Annu. Rev. Fluid Mech., 2010, 42, 557–576 CrossRef.
- A. Liberzon, T. Käufer, A. Bauer, P. Vennemann and E. Zimmer, OpenPIV/openpiv-python: OpenPIV-Python v0.23.4 (0.23.4), 2021 DOI:10.5281/zenodo.4409178.
- M. B. Khan and C. Sasmal, Phys. Fluids, 2021, 33, 033109 CrossRef CAS.
- M. Kumar and A. M. Ardekani, Phys. Fluids, 2021, 33, 074107 CrossRef CAS.
- P. Pakdel and G. H. McKinley, Phys. Rev. Lett., 1996, 77, 2459–2462 CrossRef CAS PubMed.
- G. H. McKinley, P. Pakdel and A. Öztekin, J. Non-Newtonian Fluid Mech., 1996, 67, 19–47 CrossRef CAS.
- V. Steinberg, Annu. Rev. Fluid Mech., 2021, 53, 27–58 CrossRef.
- S. S. Datta, A. M. Ardekani, P. E. Arratia, A. N. Beris, I. Bischofberger, G. H. McKinley, J. G. Eggers, J. E. López-Aguilar, S. M. Fielding, A. Frishman, M. D. Graham, J. S. Guasto, S. J. Haward, A. Q. Shen, S. Hormozi, R. J. Poole, A. Morozov, V. Shankar, E. S. G. Shaqfeh, H. Stark, V. Steinberg, G. Subramanian and H. A. Stone, Phys. Rev. Fluids, 2022, 7, 080701 CrossRef.
- A. Bhardwaj, E. Miller and J. P. Rothstein, J. Rheol., 2007, 51, 693–719 CrossRef CAS.
- P. Gallo, K. Amann-Winkel, C. A. Angell, M. A. Anisimov, F. Caupin, C. Chakravarty, E. Lascaris, T. Loerting, A. Z. Panagiotopoulos, J. Russo, J. A. Sellberg, H. E. Stanley, H. Tanaka, C. Vega, L. Xu and L. G. M. Pettersson, Chem. Rev., 2016, 116, 7463–7500 CrossRef CAS PubMed.
- T. Bertrand and C. F. Lee, Phys. Rev. Research, 2022, 4, L022046 CrossRef CAS.
- C. C. Hopkins, S. J. Haward and A. Q. Shen, Phys. Rev. Lett., 2021, 126, 054501 CrossRef CAS PubMed.
- S. Grossmann, D. Lohse and C. Sun, Annu. Rev. Fluid Mech., 2016, 48, 53–80 CrossRef.
- T. Mullin, Annu. Rev. Fluid Mech., 2011, 43, 1–24 CrossRef.
- C. H. K. Williamson, Annu. Rev. Fluid Mech., 1996, 28, 477–539 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Alternative flow state diagram presented in Wigap–BR parameter space. See DOI: https://doi.org/10.1039/d2sm01162j |
| This journal is © The Royal Society of Chemistry 2022 |




