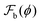Thermodynamics predicts a stable microdroplet phase in polymer–gel mixtures undergoing elastic phase separation

Abstract

We study the thermodynamics of binary mixtures with the volume fraction of the minority component less than the amount required to form a flat interface and show that the surface tension dominated equilibrium phase of the mixture forms a single macroscopic droplet. Elastic interactions in gel–polymer mixtures stabilize a phase with multiple droplets. Using a mean-field free energy we compute the droplet size as a function of the interfacial tension, Flory parameter, and elastic moduli of the gel. Our results illustrate the role of elastic interactions in dictating the phase behavior of biopolymers undergoing liquid-liquid phase separation.

---

1 Introduction

Membraneless compartmentalisation in cells that are driven by phase-separation processes due to changes in temperature or pH, and maintained by a non-vanishing interfacial tension, is one of the most exciting recent biological discoveries.^1–4 These membraneless compartments composed bio-molecular condensates have been implicated in important biological processes such as transcriptional regulation,⁵ chromosome organisation⁶ and in several human pathologies e.g. Huntington's, ALS etc.⁷ Self-assembly processes that lead to organelle formation however need to be tightly regulated such that the phase separated droplets do not grow without bound and remain small compared to the cell size. Understanding the regulatory processes that control droplet size in cellular environments is therefore a crucial interdisciplinary question. The two candidate mechanisms proposed for arresting droplet growth are (i) incorporation of active forces that break detailed balance,^8,9 and (ii) non-equilibrium reaction mechanisms which couple to the local density field.⁴ Although biological systems are inherently out of equilibrium, an estimation of diffusion constant of bio-molecules indicates that non-equilibrium effects are negligible on length-scales beyond microns and timescales beyond microseconds. Hence, the framework of equilibrium thermodynamics can be readily applied to analyse biological phase separation in cells.¹⁰

For synthetic polymer mixtures, in the absence of active processes, droplet growth is limited by the elastic interactions of the background matrix that alters the thermodynamics of phase separation.^11–13 Recent experiments on mixtures of liquid PDMS and fluorinated oil in a matrix of cross-linked PDMS show the dependence of the droplet size on the nucleation temperature and the network stiffness.^14,15 Despite theoretical attempts^16,17 a complete understanding of elasticity mediated arrested droplet growth is still lacking.

The connection between coarsening phenomena and network elasticity is an important, and exciting area of research across several disciplines, biological regulation of cellular function,^1–4 tailoring mechanical properties of materials,^18–20 controlling morphology,^21–23 size of precipitates in food products,^24,25 and even growth of methane bubbles in aquatic sediments.^26–28

In this paper, we develop a consistent thermodynamic formalism to compute the equilibrium radius of the droplet of the minority phase in (a) binary polymer, and (b) a polymer–gel mixture, using mean-field theories utilising the Flory–Huggins²⁹ and the Flory–Rehner³⁰ free energies, respectively. A parallel tangent construction for droplets, used to obtain the densities of coexisting phases is presented. This procedure is a generalisation of the common tangent construction for flat interfaces and in the thermodynamic limit allows us to compute the equilibrium radius of a single droplet. For phase separation processes in mixtures with a gel component, elastic interactions limit droplet growth stabilising a phase with multiple droplets, in the correct parameter regime.³¹

2 Model

Consider a binary mixture of a gel and a solvent, close to but below the gelation temperature, where the gel-formation and the phase-separation are competing processes. The physical system considered is different from the recent experimental^14,15 and theoretical studies.^16,17 The experiments have been performed on mixtures of liquid PDMS (uncrosslinked PDMS polymers) and fluorinated oil in a matrix of cross-linked PDMS, thus it is a ternary system. The two previous theoretical attempts^16,17 however approach this by describing the thermodynamics of a binary mixture (oil and uncrosslinked PDMS) in the background of the elastic matrix (crosslinked PDMS), where the volume-fraction of the matrix does not enter the calculation. The matrix only provides an elastic background in which the phase separation of the binary mixture occurs. On the other hand, the elastic matrix is considered in reference,^14,15 but the translational entropy of the gel has been explicitly put to zero. However, this is a contentious issue, as we discuss later in the manuscript, and it leads to unstable solutions for a binary mixture of a gel and a solvent. References^14,15 does not encounter this issue as they do not perform the parallel tangent construction, which is a condition that arises from the minimisation of the free-energy, and they bypass this by assuming that the dispersed microdroplets of the solvents can be described as an ideal gas.

The thermodynamic formalism to understand phase separation is as follows: an unstable mixture of composition ϕ₀ splits into two coexisting phases in a slab-like geometry respecting volume and mass conservation, with the equilibrium configuration being a minimum of the free energy (Fig. 1(a)). The volume fraction of the two coexisting phases are ϕ_in, and ϕ_out respectively, with V_d denoting the volume occupied by phase with density ϕ_in, and is the Helmholtz free-energy per unit volume (in units of 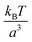). The solvent fraction is 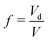, and the free-energy density of the planar configuration (Fig. 1(a)) is given by,

where = 2γV^−1/3, corresponds to the surface energy with γ being the surface tension, V the volume of the system considered, and λ a Lagrange multiplier that enforces the mass conservation constraint.

Fig. 1 A (i) common tangent (solid pink line) and a (ii) parallel tangent (dashed green line) construction for planar interfaces (a) and droplets (b) (with volume V_d) for a binary polymer mixture. A Flory–Huggins functional with χ = 1.2χ_c, N_A = 100, N_B = 200 is used. Coexistence volume fractions inside ϕ_in and outside ϕ_out droplet approach the values obtained for a flat interface ϕ_α, and ϕ_β in the thermodynamic limit V → ∞.

A calculation of the equilibrium thermodynamics proceeds via minimising the free energy in eqn (1) w.r.t to the independent quantities ϕ_in, ϕ_out, f, and λ. The constrained minimization of the free-energy function in eqn (1) w.r.t. ϕ_in, ϕ_out and f leads to the common tangent construction

μ(ϕ_in) = μ(ϕ_out), and Π(ϕ_in) = Π(ϕ_out), (2)

where μ(ϕ), and Π(ϕ) refers to the exchange chemical potential and the osmotic pressure of the phases respectively. Eqn (2) ensures chemical, and mechanical equilibrium (see ESI†). Thermal equilibrium is ensured as calculations are carried out in a constant temperature ensemble. We obtain coexistence volume fractions ϕ_in and ϕ_out from eqn (2). The solvent fraction f is obtained by minimising the functional w.r.t λ, i.e (ϕ_in, ϕ_out, f, λ)/∂λ = 0, which yields, 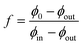. For a planar interface, the surface energy term does not explicitly depend on the solvent volume fraction f. Consequently, the minimisation conditions lead to four uncoupled equations (ESI†) and a knowledge of the coexistence volume fractions ϕ_in and ϕ_out is enough to determine f. As evident from eqn (1), the effect of the surface energy term vanishes in the thermodynamic limit, i.e., as volume V → ∞. In contrast, a spherical droplet geometry introduces a non-trivial coupling among the minimisation conditions and a knowledge of the volume, V, of the system is required to obtain the equilibrium configuration.

A spherical droplet

Spherical droplets of the minority phase arise in finite systems when the volume fraction is less than a critical value.^32,33 The thermodynamics in such situations differ from the common tangent construction and leads to the classical Gibbs-Thomson relations.⁴Fig. 1(b) shows an unstable system of volume fraction ϕ₀, that phase separates into a background matrix of volume fraction ϕ_out and a single droplet of radius R of volume fraction ϕ_in in a finite box of volume V. Assuming an ansatz of a phase separated mixture comprising of N spherical droplets of identical radius R, (referred to as the micro-droplet phase henceforth), the solvent fraction is given by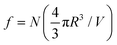 . The free energy of the micro-droplet phase is therefore [scr F, script letter F] = f [scr F, script letter F]_b (ϕ_in) + (1 − f) [scr F, script letter F]_b (ϕ_out) + [scr F, script letter F]_s(f), where , accounts for the interfacial energy between the droplet and the background phase. By imposing the mass conservation constraint and expressing the surface energy in terms of the solvent fraction f, the free energy per unit volume is given by

The surface energy of the droplet depends on the solvent fraction f on account of the its spherical shape. The equilibrium conditions therefore lead to four coupled equations, involving the yet unknown system volume V. The chemical and mechanical equilibrium conditions for the micro-droplet phase involving the coexisting densities translates to, μ(ϕ_in) = μ(ϕ_out) and , where the extra term in the pressure equation accounts for the Laplace pressure acting across the interface. We carry out a minimisation procedure akin to the planar interface to obtain the solvent volume fraction f, and the coexistence volume fractions inside and outside the droplet, ϕ_in and ϕ_out respectively for a given box volume V. In the absence of elastic interactions the equilibrium phase corresponds to a single droplet of the minority phase, i.e. N = 1 in eqn (3). The radius of the drop is determined in terms of the coexistence densities and is given by

R = νL. (4)

where , and L = V^1/3 is the length of the cubic box. We apply the framework to compute the radius of the minority phase droplet of a binary polymer mixture described by a Flory–Huggins free energy in the thermodynamic limit i.e. V → ∞, performing our calculation for different box volumes V. The surface tension γ for the micro-droplet phase is taken to be the same as that of a planar interface.

The thermodynamics of binary polymer mixtures is well described by the Flory–Huggins free-energy 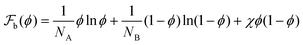, where N_A, and N_B are the lengths of A and B polymers respectively, and χ is the mixing parameter. For χ > χ_c, where χ_c is the value of the mixing parameter at criticality, the mixture is unstable and spontaneously phase separates into low and high volume fraction phases determined by the minimisation conditions. We consider an unstable polymer mixture with N_A = 100, N_B = 200, and an initial composition ϕ₀ = 0.35, and χ = 1.2χ_c. Fig. 1(a) shows the common tangent construction which yields the coexistence volume fractions ϕ_α = 0.235 and ϕ_β = 0.885 for a flat interface. If the amount of material is not enough, the minority phase forms a droplet whose coexistence volume fractions outside ϕ_out and inside ϕ_in are determined by the parallel tangent construction (Fig. 1(b)) as a function of the box volume V. A combination of the parameters ϕ₀, ϕ_α and ϕ_β determines that the fraction of the solvent-rich phase f ≈ 0.17. The equilibrium phase is a single drop. To obtain the coexistence volume fractions and the droplet radius in the thermodynamic limit, we perform parallel tangent constructions for cubic boxes of lengths L = 160, … 10⁴ using eqn (4).

Fig. 2 shows a finite size scaling analysis of the droplet radius R in units of the box-size L, (R/L) as a function of 1/L. The thermodynamic limit 1/L→0 corresponds to the y-intercept R/L ≈ 0.34 for the Flory parameters listed above. The numerical derivative of R/L w.r.t. L approaches zero in this limit (Fig. 2 inset). The solvent fraction f, is also a function of the systems size (f ∼ (R/L)³). The coexistence densities calculated from eqn (4) are functions of L and can be quantified in terms of their deviation from the coexistence volume fractions for a planar interface, i.e., [small phi, Greek, tilde]_in = (ϕ_in−ϕ_β)/ϕ_β and [small phi, Greek, tilde]_out = (ϕ_out−ϕ_α)/ϕ_α. As shown in Fig. 2ϕ_out → ϕ_α, and ϕ_in → ϕ_β in the thermodynamic limit.

Fig. 2 Finite size scaling of equilibrium drop radius R(L)/L, of a phase separated binary polymer mixture using a Flory–Huggins free energy functional with parameters described in Fig. 1. Coexistence volume fractions inside and outside the droplet ϕ_in and ϕ_out approaches the coexistence values obtained from a common tangent construction as L → ∞. Inset shows the rate of change of the radius approaches zero as L → ∞.

A microdroplet phase

The Helmholtz free-energy per unit volume of the micro-droplet configuration of a gel–solvent mixture, with N droplets (see Fig. 4(d) inset), is given by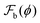where is the Flory–Huggins free energy given by 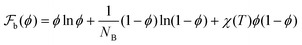. We consider a situation where the strand length of the gel, N_B, is considered to be finite in these calculations (N_B = 25 and N_A = 1). The reason for this, and not letting N_B → ∞, is based on stability arguments and is discussed in the ESI† and we set χ(T) = 1.38χ_c in our calculations. The surface-energy per unit volume in eqn (5), is expressed in terms of the solvent fraction f using the relation between the drop radius and the number density, i.e., . The elastic part of the free-energy density in eqn (5) can be expressed as a function of the solvent fraction, f, (see ESI†) and is given by

To incorporate the effects of the finite stretch-ability of the gel, we adopt the Gent model.^34,35 The elastic free energy density has the form, 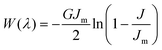, where J = λ_r² + λ_θ² + λ_ϕ²− 3, with λ's corresponding to the strains in the radial, azimuthal, and polar directions, J_m ∼ 10⁶ is the stretching limit of the network, and G is the shear modulus. The shear modulus is related to the microscopic parameters via the relation, , where n_dry and R₀ are the average cross-link density and the mesh size of the dry gel respectively³⁶ (see ESI†). Due to the volume-preserving nature of the deformation, λ_r = 1/λ² and λ_ϕ = λ_θ = λ and its magnitude is bounded, i.e., 0 < J/J_m < 1.³⁴ The energy minimisation conditions w.r.t the independent variables as outlined earlier, leads to a modified equilibrium conditions: μ(ϕ_in) = μ(ϕ_out) and 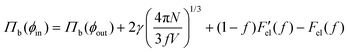. These conditions lead to a set of coupled equations that we solve numerically to yield the four unknown variables, ϕ_in, ϕ_out, f, and λ, associated with each droplet number, N. A geometrical interpretation of these equations lead to the construction of parallel tangents.

We substitute the equilibrium values of the coexistence volume fractions and solvent fraction into the original free-energy expression in eqn (5), to obtain a free energy F̃(N), as a function of the number of droplets N. The minimisation of F̃(N) w.r.t N yields N_m, the optimal number of droplets of the micro-droplet phase.

Fig. 3(a) shows the free-energy F̃(N) = (N) −(1) (eqn (5)) as a function of the number of droplets, once the coexistence volume fractions have been obtained for a cubic box of side L = 200 and the surface tension γ = 1.67 × 10⁻³ (in units of k_BT/a²). It is evident that this is a convex function, with a well defined minimum occurs around N_m ≈ 23. The inset shows the contrasting behaviour of F̃(N) for a binary polymer mixture. In the absence of elastic interactions, surface tension dominates the thermodynamics and a phase with a single droplet is the equilibrium state corresponding to the free energy minimum. The convex nature of the free energy F̃(N) arises from a balance between the surface, elastic, and bulk free energies of the micro-droplet phase. As the number of droplets N increases, the surface energy monotonically increases on account of the increase of the total interfacial area. In contrast, the elastic energy monotonically decreases as a function of N, since an increase in the number of droplets translates to smaller sized drops and less deformation of the gel matrix. The elastic free energy has a lower bound corresponding to a minimum droplet of size R/L ∼ a, length of a monomer. The combined effect of these two contributions to the free energy therefore stabilizes the micro-droplet phase. The bulk free energy is nearly independent of N. Fig. 3(b) shows the variation of the different components of the total free energy as a function of the number of droplets N, while Fig. 3(c) shows the variation of number density n = N_m/V, and droplet radius R as a function of the shear modulus G. The shear modulus G is tuned by varying the mesh size, R₀, of the gel. We compute the number density by minimizing F̃(N) w.r.t. N and determine the drop radius using R(N_m) = (ν/N_m^1/3)L for a given shear modulus G. As shown, the radii of the droplets decrease (and hence the number density n increases commensurately) as the gel becomes stiffer.

Fig. 3 Total free energy, (a), as a function of the number of droplets N showing a minimum at N_m ≈ 23 for L = 200. Surface energy F_s, increases, the elastic energy F_el, decreases, whereas, the bulk free energy is almost independent of N as shown in (b). Panel (c) shows the dependence of the droplet radius R and the number density of the droplets n and the shear modulus of the gel G. The inset of panel (a) shows the free-energy as a function of the number of droplets for a system with no elastic interaction. Thus a single macro-droplet is the stable phase.

The convex nature of F̃(N) as a function of N is independent of the system size L as shown in Fig. 4(a). Fig. 4(b) shows the dependence of F̃(N) as a function of the surface tension, γ = 0.0025, … 0.004, while keeping the shear modulus of the gel–solvent mixture fixed at G = 1.9 × 10⁻⁴ (in units of k_BT/a³). The free energy minimum shifts to smaller values of N_m with increasing surface tension as shown in Fig. 4(b). The inset of Fig. 4(b) shows that for γ < γ_c ≈ 4.0 × 10⁻³, a micro-droplet phase is the equilibrium configuration, with N_m, monotonically increasing with decreasing γ. Fig. 4(c) shows that the equilibrium number density of droplets n = N_m/V, and the droplet radius R(N_m) have reached a thermodynamic limit and are independent of the system size L. Fig. 4(d) shows the phase boundary demarcating regions of a stable macro-droplet and dispersed micro-droplet phases in the γ−G plane. The mean field phase-boundary (symbols) qualitatively agrees with the scaling results³¹ (red dashed line) for softer gels while significant deviations are observed for stiffer ones. The mean-field phase boundary (symbols) is now a function of the gel-strand length N_B, a variable that is associated with the network heterogeneity of the system. Such quenched disorder dramatically modifies the equilibrium thermodynamics of gel networks.

Fig. 4 Free energy of the micro-droplet phase F̃(N) vs. number of droplets, N for different system sizes L = 100, 200, … 500 is shown in panel (a). Panel (b) shows F̃(N) vs. number of droplets, N, when the surface tension is varied between γ = 0.0025, … 0.004. Inset of (b), shows a stable micro-droplet phase for γ < γ_c ≈ 4.0 × 10⁻³ for G = 1.9 × 10⁻⁴k_BT/a³ and box size L = 200. The number density and droplet radii n, and R as a function of system size L is shown in (c), and a phase boundary demarcating regions of stable macrodroplet and multiple micro-droplet phase is shown in panel (d). The symbols denote the phase boundary computed via mean-field theory (N_B = 25) and the dashed line is that via scaling arguments.

Fig. 5 (a), which is similar to Fig. 4(d), shows the contour-plot of the dimensionless ratio between the surface energy and the elastic energy, h/α, has been shown in the γ–G plane, where α is equal to 2.5 (see ESI† for a discussion on this). Also shown is the phase boundary from the mean field theory calculations (inverted triangles, the inverted triangle and the dashed line are similar to that presented in Fig. 4(d)). Simple scaling arguments would suggest that the phase boundary would occur at h/α equal to unity (see the dashed line in Fig. 5(a)) and we observe that for small values of the shear modulus, G, this is indeed the case. However, as the value of G increases deviations between the mean-field phase boundary (inverted triangles) and the h/α equal to unity increase. In order to facilitate comparison with present and future experiments, we have studied how the equilibrium number of droplets evolve as a function of a tuning parameters (shear modulus or surface tension in this case) as one crosses the phase boundary along the principal directions in the phase plane. Panel (b) shows the transition from a dispersed micro-droplet to a single macro-droplet as one crosses the phase boundary while keeping G fixed and increasing γ. For γ < γ_c, the dependence of the number of droplets on the surface tension follows the linear relationship, 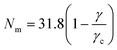. Similarly, panel (c) shows the transition from a single macro-droplet to a dispersed micro-droplet state when one keeps γ constant and increases G and here the dependence of the number of droplets on the elastic modulus again follows a linear dependence . The linear dependence of the number of droplets on the elastic modulus of the matrix is a result of the mean-field theory calculations (and not an assumptions as in¹⁶) and has been observed in the experiments.¹⁴

Fig. 5 Panel (a) shows the contour plot of the dimensionless ratio h/α in the γ–G plane, where α is equal to 2.5. The inverted triangles denotes the phase-boundary between the macro-droplet and the dispersed micro-droplet phases computed from our mean-field theory. Panel (b) and (c) shows the macro-droplet to dispersed micro-droplet transition as one crosses the phase boundary along the two principal directions.

In summary, we consider phase separation in an elastic medium, where the background matrix influences the equilibrium thermodynamics of the. Previous studies consider the background matrix as an inert phase.^16,17 For composition regimes where the solvent is a minority phase and there is a dearth of material to form a flat interface, solvent-rich droplets coexist with the majority phase. We demonstrate, via a mean-field theory that the dispersed micro-droplet phase is indeed a thermodynamic minimum for a binary gel–solvent mixture. A competition between surface tension and network elasticity stabilizes this phase. When the surface-tension exceeds a critical value, a single macroscopic droplet is the stable thermodynamic phase. Though the Flory–Huggins functional has been used to describe polymer mixtures, our results are generic and valid for any bistable potential.³⁷

3 Discussion

A macroscopic gel would possess intrinsic heterogeneities in the mesh size resulting in different values of N_B in different that leads to a micro-droplet phase with different sized droplets.³⁸ Thus our mean-field theory needs to be extended to incorporate a distribution of mesh sizes, i.e. P(N_B). Assuming that the disorder correlation length is ψ, our mean-field theory is applicable for length scales [small script l] ≤ ψ from which the coexistence densities ϕ_in and ϕ_out can be obtained. The coexistence densities are functions of N_B, a parameter in the FH free-energy. Thus a distribution of mesh sizes, P(N_B), leads to a distribution of coexistence volume fractions (akin to “mosaic state” in spin-glass models³⁹) within the sample, which can be computed using the formalism presented here. The differing coexistence volume fractions in different parts of the sample corresponding to different local values of N_B would result in additional surface energy cost between domains that has not been considered in the present calculation. However, this would have effect on the thermodynamics of the mixture gel–solvent mixture.¹³ Upon investigating the slope of the common-tangent for the bulk free-energy, , for different values of N_B, we infer that at a constant temperature (and hence constant χ(T)) the effect of increasing N_B leads to the lowering of the slope of the common tangent. Thus, a heterogeneous mesh-size would result in random slopes of the common tangent to . The situation is analogous to the behaviour of random-field Ising models, where the relative depth of the bistable free-energy is set by the value of the field h(x).⁴⁰

The effect of network disorder and its relation to the thermodynamics of random field Ising models would be studied in a future work. Elastically mediated phase transitions admit a third thermodynamic phase, where the gel network partially wets and intrudes the solvent rich droplets.³¹ A variational calculation allowing for polydisperse droplets and their associated wetting behaviour is currently underway and will be reported elsewhere.

We place our work in context of previous work in this exciting area. The importance of elastic interactions in modifying the equilibrium state of phase separating system was first discussed in context of a ternary system with the elastic network and a polymer interacting with a solvent.^14,15 The stability of a droplet phase is argued along the lines of classical nucleation theory, using the Gibbs free energy (eqn (1) of¹⁵) to relate the work done by an expanding drop against the pressure exerted by the bounding polymer network. The droplet is identified as a dilute solvent and the ideal gas equation is used to determine the chemical potential difference 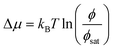. Based on this formalism (and the eqn (1)–(9) of the ESI†) the authors argue that when ϕ < ϕ_sat, the mixture is stable, independent of elasticity. When ϕ > ϕ_cond, the mixture is unstable. While in the interim region ϕ_sat < ϕ < ϕ_cond a microdroplet phase is stabilised. This experimental situation is closely modelled by Kothari et al.¹⁷ who focus on the kinetics of a three-component system written in terms of the volume fractions of liquids A (uncrosslinked part of the background gel) ϕ_A, part of liquid B ϕ_B that resides within the gel, and ϕ_D, the part of liquid B which exists in droplet form. Our model bears resemblance with the model free energy proposed by Wei et al.,¹⁶ though differing significantly in detail. Perhaps the work that is most relevant to the present study is the beautiful scaling theory backed by simulation data by Ronceray et al.³¹ We believe that our work is the first calculation against which these results can be compared. In fact, the schematic phase diagram (Fig. 2 of³¹) can be derived from the thermodynamic treatment presented in the present manuscript. In addition, deviations from the scaling theory can also be captured within our model. We hope that our work will prompt careful experimental and theoretical studies in this area. Lastly, we note that our thermodynamic formalism does not capture the exciting non-equilibrium effects.³⁸ A time-dependent Ginzburg-Landau formalism based on the free energy form explored in this article that incorporates network inhomogeneity, and adhesion of droplets to gel matrices will be explored in a future study. We hope that our theoretical work will instigate experimental work on binary gel–polymer mixtures towards a complete understanding of this fascinating problem.

Author contributions

B. M., and B. C. designed the research. B. M. and S. B. contributed equally to this work. B. C. obtained funding for the research. All authors contributed to the paper.

Conflicts of interest

The authors declare that no competing interests exist.

Acknowledgements

S. B., and B. C. thank University of Sheffield, IMAGINE: Imaging Life grant for financial support. S. B., B. M., and B. C. acknowledge funding support from EPSRC via grant EP/P07864/1, and P & G, Akzo-Nobel, and Mondelez Intl. Plc. The authors thank Dr S. Kundu for a critical reading of the manuscript.

References

1. C. P. Brangwynne, C. R. Eckmann, D. S. Courson, A. Rybarska, C. Hoege, J. Gharakhani, F. Jülicher and A. A. Hyman, Science, 2009, 324, 1729–1732.
2. A. A. Hyman, C. A. Weber and F. Jülicher, Annu. Rev. Cell Dev. Biol., 2014, 30, 39–58.
3. J. Berry, C. P. Brangwynne and M. Haataja, Rep. Prog. Phys., 2018, 81, 046601.
4. C. A. Weber, D. Zwicker, F. Jülicher and C. F. Lee, Rep. Prog. Phys., 2019, 82, 064601.
5. D. Hnisz, K. Shrinivas, R. A. Young, A. K. Chakraborty and P. A. Sharp, Cell, 2017, 169, 13–23.
6. S. Sanulli, M. Trnka, V. Dharmarajan, R. Tibble, B. Pascal, A. Burlingame, P. Griffin, J. Gross and G. Narlikar, Nature, 2019, 575, 390–394.
7. Y. Shin and C. P. Brangwynne, Science, 2017, 357, eaaf4382.
8. E. Tjhung, C. Nardini and M. E. Cates, Phys. Rev. X, 2018, 8, 031080.
9. R. Singh and M. Cates, Phys. Rev. Lett., 2019, 123, 148005.
10. A. W. Fritsch, A. F. Diaz-Delgadillo, O. Adame-Arana, C. Hoege, M. Mittasch, M. Kreysing, M. Leaver, A. A. Hyman, F. Jülicher and C. A. Weber, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2102772118.
11. J. Krawczyk, S. Croce, T. McLeish and B. Chakrabarti, Phys. Rev. Lett., 2016, 116, 208301.
12. B. Mukherjee and B. Chakrabarti, Polymers, 2020, 12, 1576.
13. M. S. Dimitriyev, Y.-W. Chang, P. M. Goldbart and A. Fernández-Nieves, Nano Futures, 2019, 3, 042001.
14. R. W. Style, T. Sai, N. Fanelli, M. Ijavi, K. Smith-Mannschott, Q. Xu, L. A. Wilen and E. R. Dufresne, Phys. Rev. X, 2018, 8, 011028.
15. K. A. Rosowski, T. Sai, E. Vidal-Henriquez, D. Zwicker, R. W. Style and E. R. Dufresne, Nat. Phys., 2020, 16, 422–425.
16. X. Wei, J. Zhou, Y. Wang and F. Meng, Phys. Rev. Lett., 2020, 125, 268001.
17. M. Kothari and T. Cohen, J. Mech. Phys. Solids, 2020, 145, 104153.
18. F. Tancret, J. Laigo, F. Christien, R. Le Gall and J. Furtado, Mater. Sci. Technol., 2018, 34, 1333–1343.
19. T. Smith, B. Esser, N. Antolin, A. Carlsson, R. Williams, A. Wessman, T. Hanlon, H. Fraser, W. Windl and D. McComb, et al. , Nat. Commun., 2016, 7, 1–7.
20. F. R. N. Nabarro, Proc. R. Soc. London, Ser. A, 1940, 175, 519–538.
21. M. Doi, T. Miyazaki and T. Wakatsuki, Mater. Sci. Eng., 1985, 74, 139–145.
22. P. Fratzl, O. Penrose and J. L. Lebowitz, J. Stat. Phys., 1999, 95, 1429–1503.
23. S. Y. Karpov, Research, 1998, 3, 16.
24. P. Lonchampt and R. W. Hartel, Eur. J. Lipid Sci. Technol., 2004, 106, 241–274.
25. Y. H. Roos, in Handbook of food engineering, CRC Press, 2006, pp. 299–364.
26. B. D. Johnson, B. P. Boudreau, B. S. Gardiner and R. Maass, Mar. Geol., 2002, 187, 347–363.
27. C. K. Algar and B. P. Boudreau, J. Geophys. Res.: Earth Surf., 2010, 115(F3), 1–12.
28. L. Liu, Environ. Sci. Technol., 2018, 52, 2007–2015.
29. M. Rubinstein and R. H. Colbyet al., Polymer physics, Oxford university press; New York, 2003, vol. 23.
30. L. G. Treloar, The physics of rubber elasticity, OUP Oxford, 1975.
31. P. Ronceray, S. Mao, A. Košmrlj and M. P. Haataja, Europhys. Lett., 2022, 137, 67001.
32. M. Schrader, P. Virnau and K. Binder, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 061104.
33. K. Binder, B. J. Block, P. Virnau and A. Tröster, Am. J. Phys., 2012, 80, 1099–1109.
34. S. Raayai-Ardakani, Z. Chen, D. R. Earl and T. Cohen, Soft Matter, 2019, 15, 381–392.
35. J. Zhu, T. Li, S. Cai and Z. Suo, J. Adhes., 2011, 87, 466–481.
36. T. Tanaka, Phys. Rev. Lett., 1978, 40, 820.
37. P. M. Chaikin, T. C. Lubensky and T. A. Witten, Principles of condensed matter physics, Cambridge university press; Cambridge, 1995, vol. 10.
38. E. Vidal-Henriquez and D. Zwicker, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2102014118.
39. G. Parisi, Phys. A, 2007, 386, 611–624.
40. T. Nattermann, Spin Glasses and Random Fields, World Scientific, 1997.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01101h

---