 Open Access Article
Open Access ArticleFlow-driven synthesis of calcium phosphate–calcium alginate hybrid chemical gardens†
Réka
Zahorán
a,
Pawan
Kumar
 a,
Ádám
Juhász
b,
Dezső
Horváth
a,
Ádám
Juhász
b,
Dezső
Horváth
 c and
Ágota
Tóth
c and
Ágota
Tóth
 *a
*a
aDepartment of Physical Chemistry and Materials Science, University of Szeged, Rerrich Béla tér 1., Szeged, H-6720, Hungary. E-mail: atoth@chem.u-szeged.hu
bMTA-SZTE Lendület “Momentum” Noble Metal Nanostructures Research Group, Interdisciplinary Excellence Center, Department of Physical Chemistry and Materials Science, University of Szeged, Rerrich Béla tér 1, Szeged, H-6720, Hungary
cDepartment of Applied and Environmental Chemistry, University of Szeged, Rerrich Béla tér 1., Szeged, H-6720, Hungary
First published on 5th October 2022
Abstract
Systems far-from-equilibrium self-assemble into spatiotemporal structures. Here, we report on the formation of calcium alginate gardens along with their inorganic hybrids when a sodium alginate solution containing sodium phosphate in various compositions is injected into a calcium chloride reservoir. The viscoelastic properties of the membranes developed are controlled by the injection rate, while their thickness by the amount of sodium phosphate besides diffusion. Inorganic hybrid membranes with constant thickness are synthesized in the presence of a sufficient amount of sodium phosphate. The electrochemical characterization of the membranes suggests that the driving force is the pH-gradient developing along the two sides; hence, the cell potential can be controlled by the addition of alkaline sodium phosphate into the sodium alginate solution.
1 Introduction
The interplay between transport processes and chemical reactions develops self-organized patterns ranging from the nano- to macro-scale.1,2 In a classic example, a “chemical garden” grows by seeding a salt pellet into a sodium silicate solution.3,4 The dissolution of the salt instantaneously creates a semipermeable membrane along the interface of the reacting species. The transfer of water molecules by osmosis from the outer alkaline region to the inner electrolyte builds up higher internal pressure, under which the membrane ruptures and ejects a salt jet. Buoyancy then aids in the upward growth of tubular, bulbous, or budding precipitates up to several centimeters.5–7 Flow-injection systems provide convenient control of the various growth types and dynamical activities.8–13 Most of the underlying self-assembled architectures have been explored by utilizing a wide range of inorganic materials, including even alkali14 or light-sensitive metal ions.15 However, the self-organization of pure organic garden architectures is not much explored; it is limited to a few investigations, e.g., the formation of iron(III) oleate in organic solvents,16 instabilities of tubular chitosan hydrogels,17,18 and alginate coiling.19Here we have employed sodium alginate due to its favorable environmental properties, such as biocompatibility20 and biodegradability.21 Alginate is an anionic linear block copolymer of α-L-guluronate and (1,4)-linked β-D-mannuronate residues typically obtained from brown seaweed.22 Ionic crosslinking of alginate with divalent metal cations creates a hydrogel which has been used for biomedical applications, such as drug delivery23 or tissue engineering.24 Nowadays, organic and inorganic composites are of great interest in an effort to control the fabrication of functional materials. Researchers have developed complex architectures,25,26 hierarchical patterns27,28 and synthesized inorganic micro- and nanomaterials, in particular calcium carbonate29 and calcium phosphate.30–32 The organic component provides adhesivity and flexibility, while the inorganic component enhances the mechanical strength of the materials. Thus, inorganic–organic hybrid materials fulfill the gap between pure inorganic precipitates and organic forms by ensuring the required synergy.
To develop technological applications for energy production, the scientific community also focuses on understanding the electrical properties of membranes. In the field of chemobrionics, the compartmentalization of distinct environments by semipermeable membranes creates constant chemical gradients. The different ionic species on both sides of the membrane act as precursors to generate electrochemical energy; in addition, transport processes provide the dynamic characteristics of the redox gradients. The self-organized precipitated membranes of geological resources containing various inorganic and organic complex species, such as black smoker chimneys33 or hydrothermal vents,34,35 can produce electric energy. These natural formations have rich ecosystems and contribute significantly to prebiotic chemistry.36 In the last few years, there were several reports on the electrochemical activities of various minerals, e.g., iron-sulfide and iron-hydroxide,37 calcium-carbonate,38 silica-based chemical gardens,7,39 or even chitosan membranes.28 Nonetheless, the complexity and the fragility of the structures impede the systematic characterization of electrochemical measurements. A simple approach has been developed to enhance the membrane properties by aggregating the precipitation on a porous dialysis membrane37 or creating an organic membrane28 at the interface of aqueous solutions like in a fuel-cell setup.
In this work, we study the change in the morphology of organic chemical gardens arising from the addition of an inorganic salt via a flow-injection technique. Furthermore, we characterize the evolving membranes with a special focus on their rheological and electrochemical properties.
2 Experimental
Analytical grade chemical reagents from VWR International, including sodium alginate (Na–Alg, technical), calcium chloride dihydrate (99–105% ACS), and trisodium phosphate dodecahydrate (technical) were used in all experiments. Aqueous solutions with concentrations of 0.07–2.04 M CaCl2, 0.3% w/v Na–Alg, and 2.63–263 mM of Na3PO4 in 0.3% w/v Na–Alg were prepared with deionized water (Purite RO100). Methylene blue (Reanal) with 0.001% w/v concentration was added in the Na–Alg solution to visualize the otherwise transparent organic structures. All experiments were carried out at 23 ± 2 °C.To perform the flow-driven experiments (see Fig. 1), a plexiglass cuvette of 3.5 × 3.5 × 10 cm3 was filled with 25 mL CaCl2 aqueous solution. Organic (O: Na–Alg) or organic–inorganic (OI: Na3PO4 mixed with Na–Alg) solutions were injected from the bottom of the cuvette through a Tygon tube (i.d. = 0.76 mm) and needle (i.d. = 0.4 mm) with a peristaltic pump (Ismatic Reglo). Sideview images of the evolving patterns were recorded using a digital camera (Unibrain Fire-i 630c) with a Vivitar lens in color mode controlled by in-house imaging software. An LED light source was placed near the reactor to illuminate the structures. All experiments were repeated 3–5 times to provide appropriate reproducibility. The saved images were analyzed by ImageJ software in order to determine various characteristics of the tubes and their growth.
To measure the membrane thickness, separate experiments using a smaller (1 × 1 × 10 cm3) cuvette were performed. Only 5 mL of 2.04 M CaCl2 solution was used to fill the container. A green laser beam (Roithner LaserTechnik, λ = 532 nm, P = 100 mW) with the help of a thin convex cylindrical lens (TechSpec) was positioned along the y-axis to illuminate the center vertical slice (x–z plane) of the growing structure. Only the membrane wall scattered the light, which allowed visualization of the wall against the dark background.
For rheology experiments, an alginate membrane sample was prepared by injecting the 0.3% w/v alginate reagent into 0.07 M CaCl2 solution with Q = 0.83 mL min−1 flow rate. For the inorganic–organic hybrid, 0.3% w/v alginate with 2.63 mM phosphate concentration was pumped with an injection rate of Q = 0.33 mL min−1 into 2.04 M CaCl2 electrolyte. The samples were then transferred into a Petri dish, filled with 10 mL deionized water. A circular cutter (diameter of 9 mm) was used to cut the membrane. Amplitude sweep measurements were carried out with an Anton Paar Physica MCR 301 Rheometer (Anton Paar, GmbH, Germany). The plate gap was set to 0.5 mm with a constant sweep frequency of 10 Hz and changing of the rheological behavior was followed at 25 ± 0.1 °C (P-PTD200) in the range of strain 0.01–100%. The overfilled samples were carefully trimmed with a sharp cutter to cover the gap between the parallel plates completely.
For the electrochemical measurements, a cuboid plexiglass cuvette of dimension 20 × 40 × 30 mm3 was separated into two compartments with a thin polyvinyl sheet (thickness ≈ 0.2 mm). As we removed the sheet, a thin membrane formed at the interface of the electrolytes. Electric potential was measured by placing platinum (Pt) wires (diameter = 0.5 mm and exposed height = 8 mm), connected to a Thermo Orion 420 pH/mV meter, into the electrolytes. The pH of both solutions was measured separately using a pH electrode.
3 Results and discussion
3.1 Self-organized patterns
Chemo-mechanical forces can lead to various types of organized structures, where density differences, material compositions, and injection rates have a vital role in controlling the evolving shapes. The development of calcium alginate organic structures is monitored first by injecting 0.3% w/v sodium alginate solution into a calcium salt solution with concentrations varying in the range of 0.1–2.04 M. Upon contact, a calcium alginate gel immediately forms via cross-linking. Under all the conditions used, the calcium solution has a greater density compared to the sodium alginate; therefore, buoyancy aids the upward growth of the developing gel. At low concentrations of Ca2+ (triangular markers in Fig. 2a), however, buoyancy is weak and it is not able to force the hydrogel upwards, and the alginate membrane aggregates horizontally, at the bottom of the reactor. During the time scale of our experiments, the height of the structure typically reaches only 0.8–0.9 cm. Increasing Ca2+ concentration not only increases the density difference between the two solutions (ΔρO = ρCa2+ − ρO) but also increases the extent of cross-linking and, hence, the rate of gelation. At a lower flow rate, the vertically growing calcium alginate forms spherical buds near the top of the structure, as shown by diamond markers in Fig. 2a. Upon increasing the flow rate, the budding structures transform into gelling tubes of constant diameters (asterisk markers in Fig. 2a). The hollow tubule with a closed tip continuously lengthens upward without popping or rupturing and coils at the top of the salt solution.To check the feasibility of the formation of hybrid spatial structures, sodium phosphate solution is added to the sodium alginate solution which is then injected into the pool of 2.04 M CaCl2 solution. In the range of ΔρO ≈ 0.154 g cm−3 density gradients, pure organic gardens develop budding and – on increasing the injection rate of the sodium alginate solution – straightly growing tubes as shown in Fig. 2a. However, for the same density difference, which corresponds to the case with ca. 0.01 M Na3PO4 solution, phosphate–alginate based membranes aggregate at the bottom of the reactor (triangular markers in Fig. 2b). The increase in phosphate concentration decreases the density difference between the electrolytes, i.e., Δρ = ρCa2+ − ρOI, where ρOI represents the density of phosphate containing alginate solution. In the region of intermediate phosphate concentrations, depicted with square markers in Fig. 2b, a balloon appears, which ruptures and elongates the parachute-like shape. Interestingly, at greater phosphate concentrations a balloon structure without fracture evolves (see the circular markers in Fig. 2b), which shrinks on a longer timescale because of osmosis.
3.2 Characterization of the membrane
In the parameter space for pure calcium alginate where straight tubes form, we have measured the tube diameter. We have found that, on average, it is constant within the experimental error (0.90 ± 0.06 mm) independent of the flow rate and calcium ion concentration (see Table S2 in the ESI†). We have then selected the wall width of the tube (w), as a descriptor, for the characterization of phosphate hybrid structures. Under the non-equilibrium conditions, the sol–gel transition thickens the hybrid membrane (2.63 mM PO43−) due to the diffusion of Ca2+, as illustrated by the image sequence in Fig. 3a–d. Notice that the wall grows inward as the inward diffusion of calcium ions is faster compared to the outward diffusion of the bulkier polysaccharide. The increase in the phosphate content affects the gelation process, since more calcium phosphate precipitate forms, hindering the diffusion of calcium ions through the membrane. The membrane wall becomes constant on a hundredfold increase in the phosphate concentration as presented in Fig. 3e–h. For silicate40 and chitosan tubes17 the temporal evolution of wall width scales with time as| w = (kt)α. | (1) |
 | ||
| Fig. 3 Image sequence of the hybrid membrane wall width growth in the x–z plane with Q = 1.68 mL min−1, (a–d) [Na3PO4] = 2.63 mM in 0.3% w/v alginate with Δt = 10 s and (e–h) [Na3PO4] = 263 mM in 0.3% w/v alginate with Δt = 5 s. Field of view: 4.04 × 3.37 mm2, the bar corresponds to 1 mm. (i) Temporal evolution of the membrane wall width and (j) the log–log presentation of the temporal growth for 2.63 mM (black), 26.3 mM (red), and 263 mM (blue) sodium phosphate in 0.3% w/v alginate. The solid lines correspond to the fitting of eqn (1), the dashed line to that of a straight line. | ||
| [Na3PO4] (mM) | α | k/(10−2 × mm1/α s−1) |
|---|---|---|
| 2.63 | 0.50 ± 0.01 | 1.59 ± 0.22 |
| 26.3 | 0.44 ± 0.03 | 1.12 ± 0.20 |
The structural properties of the pure organic and the hybrid membranes have been determined by rheology measurements. Fig. 4a shows the elastic (storage modulus G′, square markers) and the viscous (loss modulus G′′, circular markers) behavior of the pure organic (blue color) and the inorganic–organic hybrid (red color) membranes. The storage modulus at lower shear strain is greater for the pure organic membrane. At 7.7% strain percentage (so called flow point) the situation is reversed, hence, at lower shear strain the elastic, while at higher the viscous properties dominate, typical of hydrogels. Furthermore, at shear strain <1%, the gels are linearly viscoelastic, as both the storage and the loss moduli are constant. The viscoelasticity of the alginate membrane decreases upon the addition of a small amount of phosphate, i.e., [Na3PO4] = 2.63 mM, because both the storage and the loss moduli are lowered by a factor of two in the linear viscoelastic region. The position of the flow point is shifted slightly to 8.6% shear strain percentage upon adding phosphate into the alginate solution (see the inset in Fig. 4a), which implies no variation in the flow behavior at lower phosphate concentrations. The presence of inorganic material slightly decreases the damping factor of the hybrid membrane (γ < 1%), depicted by red markers in Fig. 4b. Therefore, hampering the molecular motion of polymer chains enhances the elastic nature of alginate–phosphate based membranes at low shear strain. At higher strain, however, the addition of phosphate and the appearance of calcium phosphate precipitate will not influence the viscous behavior of the sol state.
3.3 Electrochemical characterization
The synthesized self-organized organic or inorganic–organic hybrid membranes separate the two reactant electrolytes generating a gradient of chemical composition between the two sides. In order to elucidate the temporal evolution of the electrochemical activities of the membrane, a special cuboid reactor (Fig. 5a) is divided into two compartments using a polyvinyl sheet. Equal amounts of sodium alginate solution with or without sodium phosphate and calcium chloride solution are filled into the two chambers. After the quick removal of the sheet, a thin membrane immediately forms at the interface. The potential difference related to hydrogen ion concentration is measured between the platinum wires immersed in the solutions. Under these conditions, the setup comprises a concentration cell with electrode reaction 2H+ + 2e− ⇌ H2. The electrode in the sodium alginate solution serves initially as the anode and in the calcium chloride solution as the cathode.In the case of polyanionic alginate, the potential difference with respect to the alginate compartment (ΔE = ECa2+ − EO) changes in two steps, as shown in Fig. 5b. Initially the potential is 54 mV, which decays sharply to a saturation potential of −20 mV, during which time both electrodes are in the solution. A visual inspection of the recorded images shows that during the second stage, when the potential difference changes from −20 mV to −50 mV, the gelation process takes place at the Pt wire in the alginate compartment. The gel gradually engulfs the entire wire surface by the end of the second stage. A greater concentration of calcium chloride generates a greater concentration gradient as the mobility of calcium is greater. This causes faster transportation of Ca2+ and gelation in the alginate side which induces a sharper potential decay. The overall change in the pH of the solutions, measured independently, is negligible during the entire process, as shown in the inset of Fig. 5b. The sodium alginate solution is less acidic than the calcium chloride solution with |ΔpH| = 1.00.
In the hybrid phosphate–alginate system with a sodium phosphate concentration of 26.3 mM, the alginate solution has an initial pH ≈ 12. The greater pH gradient in the system generates a higher initial electric potential of ΔE = ECa2+ − EOI = 260 ± 15 mV. The potential drops sharply (see Fig. 5c) following a two-stage process similarly to the pure alginate gel. At about 1 h, when the potential difference is 75 ± 10 mV, the gelation accompanied by precipitate formation begins to cover the wire surface. With full coverage, ΔE saturates to −120 ± 27 mV in the time scale of our experiments. At the same time, the pH of OI decreases because Ca2+ ions diffuse in and the calcium hydrogen phosphate precipitate formation depletes the solution of phosphate ions around the electrode. The pH of the Ca2+ side, however, increases, since hydroxide ions from the basic OI solution diffuse out on a shorter time scale, as shown in the inset.
At greater phosphate concentrations (263 mM), where a thin hybrid membrane develops between the electrodes, the potential change follows a single-stage process. From the initial value of 276 ± 40 mV, the potential decays to 60 ± 15 mV (see Fig. 5d), leaving the electrode surface in the OI side entirely in the solution. The accompanying pH change shows the same trend in the Ca2+ solution. There is no significant variation in the pH of the phosphate–alginate compartment because the formation of calcium phosphate precipitate is spatially restricted to the thin hydrogel membrane with a constant width. In this case, the precipitate deposited in the membrane wall hinders diffusion, and hence, the time scale lengthens as the rate of potential change and that of the pH gradient change drop significantly.
Using the Nernst equation, the pH-dependent potential difference across the membrane can be expressed as
 | (2) |
| [Na3PO4]/mM | ΔEH/mV | ΔE/mV |
|---|---|---|
| 0 | 44 | 54 |
| 26.3 | 340 | 260 ± 15 |
| 263 | 330 | 276 ± 40 |
4 Equilibrium distribution
The concentration evolution of possible species in the pH range 1–14 is examined using the known solubility products and equilibrium constants for protonation and complex formation. Calcium ions are likely to form tricalcium phosphate (TCP), calcium hydrogen phosphate (ACP), and calcium hydroxide precipitates, shown underlined, according to | (3) |
 | (4) |
 | (5) |
 | (6) |
 | (7) |
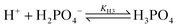 | (8) |
 | (9) |
The total concentrations of reactants are set as cT,Ca = 2.0 M and cT,PO4 = 0.263 M to mimic the experiments. Equilibrium constant values are included in Table S3 in the ESI.† The component balance equations for calcium and phosphate ions are solved at constant pH with a preset accuracy of 10−2–10−4 using Wolfram Mathematica.
Fig. 6 shows that in the range of 1.55 ≤ pH ≤ 9.35, ACP precipitate is produced from PO43− and Ca2+ ions, with the latter remaining in excess in the aqueous phase. Upon increasing the pH above 9.35, TCP is formed instead of ACP, while 80% of the total calcium ion still remains as Ca2+ in the solution. Only for pH > 11.4, Ca(OH)2 precipitate appears, removing all Ca2+ from the solution, while phosphate remains in the form of TCP.
 | ||
| Fig. 6 Percentage distribution of (a) Ca2+ and (b) PO43− containing species using cT,Ca = 2.0 M and cT,PO4 = 0.263 M concentrations. | ||
In short, the calculations predict that for the experimental conditions calcium hydrogen phosphate is the major form of precipitate when pH < 9.35, above that tricalcium phosphate is expected with Ca(OH)2 dominating for pH > 11.4. A similar distribution is observed for lower cT,PO4 concentrations, irrespective of the production percentage (see Fig. S3, ESI†).
5 Conclusions
In summary, we have produced tubular, budding calcium alginate hydrogels and their inorganic phosphate composites. We have also generated hybrid balloons and parachute-like complex patterns. The increase of the phosphate content in the alginate results in the inward growth of tube walls. There exists an upper phosphate concentration limit, above which the wall stops growing. Its thickness becomes constant because the precipitation of calcium hydrogen phosphate occurring hinders the diffusion of calcium ions across the membrane. The presence of precipitates in the inorganic–organic gel increases its elasticity. Characteristics of the in situ potential difference across the membrane, driven by the pH gradient, exhibit a two-step evolution for the pure polysaccharide tubes due to the thickening wall. The inorganic–organic hybrid materials produce a larger electric potential difference, and at a greater phosphate concentration, the potential gradient decays steeply in a one-step process observed at constant wall thickness. The ratio of inorganic and organic contents greatly influences the material properties of the synthesized tubular hydrogel structures. Designing and controlling new hybrid materials with ionic compartmentalization may be a significant leap toward understanding the formation of chemical gardens that may also contribute to the syntheses of materials of industrial interest.Author contributions
Conceptualization D. H., Á. T.; data curation and investigation R. Z.; formal analysis R. Z.; visualization R. Z.; resources D. H., Á. T.; software P. K., D. H.; supervision P. K., D. H., Á. T.; validation P. K., Á. T.; funding acquisition Á. T.; writing – original draft R. Z.; and rheology measurements Á. J. All authors are involved in reviewing and editing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research, Development and Innovation Office (K138844) and by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund (TKP2021-NVA-19). We gratefully acknowledge the Raman microscopy measurements by Dr. Ádám Balog. The authors would like to acknowledge the contribution of the COST Action CA17120. We also thank the University of Szeged Open Access Fund (5923) for support.Notes and references
- G. M. Whitesides and B. Grzybowski, Self-assembly at all scales, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- L. Cera and C. A. Schalley, Under diffusion control: From structuring matter to directional motion, Adv. Mater., 2018, 30, 1707029 CrossRef PubMed.
- L. M. Barge, S. S. S. Cardoso, J. H. E. Cartwright, G. J. T. Cooper, L. Cronin, A. D. Wit, I. J. Doloboff, B. Escribano, R. E. Goldstein, F. Haudin, D. E. H. Jones, A. L. Mackay, J. Maselko, J. J. Pagano, J. Pantaleone, M. J. Russell, C. I. Sainz-Diaz, O. Steinbock, D. A. Stone, Y. Tanimoto and N. L. Thomas, From chemical gardens to chemobrionics, Chem. Rev., 2015, 115, 8652–8703 CrossRef CAS.
- S. S. S. Cardoso, J. H. E. Cartwright, J. Čejková, L. Cronin, A. De Wit, S. Giannerini, D. Horváth, A. Rodrigues, M. J. Russell, C. I. Sainz-Daz and A. Tóth, Chemobrionics: From self-assembled material architectures to the origin of life, Artif. Life, 2020, 26, 315–326 CrossRef.
- J. H. E. Cartwright, B. Escribano and C. I. Sainz-Daz, Chemical-garden formation, morphology, and composition. I. Effect of the nature of the cations, Langmuir, 2011, 27, 3286–3293 CrossRef CAS.
- A. Tóth, D. Horváth, R. Smith, J. McMahan and J. Maselko, Phase diagram of precipitation morphologies in the Cu2+–PO43− system, J. Phys. Chem. C, 2007, 111, 14762–14767 CrossRef.
- F. Glaab, M. Kellermeier, W. Kunz, E. Morallon and J. M. Garca-Ruiz, Formation and evolution of chemical gradients and potential differences across self-assembling inorganic membranes, Angew. Chem., Int. Ed., 2012, 51, 4317–4321 CrossRef CAS PubMed.
- S. Thouvenel-Romans and O. Steinbock, Oscillatory growth of silica tubes in chemical gardens, J. Am. Chem. Soc., 2003, 125, 4338–4341 CrossRef CAS PubMed.
- S. Thouvenel-Romans, W. Van Saarloos and O. Steinbock, Silica tubes in chemical gardens: Radius selection and its hydrodynamic origin, Europhys. Lett., 2004, 67, 42 CrossRef CAS.
- B. C. Batista and O. Steinbock, Chemical gardens without silica: The formation of pure metal hydroxide tubes, Chem. Commun., 2015, 51, 12962–12965 RSC.
- E. Rauscher, G. Schuszter, B. Bohner, Á. Tóth and D. Horváth, Osmotic contribution to the flow-driven tube formation of copper-phosphate and copper-silicate chemical gardens, Phys. Chem. Chem. Phys., 2018, 20, 5766–5770 RSC.
- F. Haudin, J. H. Cartwright, F. Brau and A. De Wit, Spiral precipitation patterns in confined chemical gardens, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17363–17367 CrossRef CAS PubMed.
- B. C. Batista, P. Cruz and O. Steinbock, From hydrodynamic plumes to chemical gardens: The concentration-dependent onset of tube formation, Langmuir, 2014, 30, 9123–9129 CrossRef CAS PubMed.
- M. Emmanuel, E. Lantos, D. Horváth and A. Tóth, Formation and growth of lithium phosphate chemical gardens, Soft Matter, 2022, 18, 1731–1736 RSC.
- B. Busupalli and V. K. Patel, Dark-induced vertical growth of chemobrionic architectures in silver based precipitating chemical gardens, Chem. Commun., 2022, 58, 4172–4175 RSC.
- G. Pampalakis, The generation of an organic inverted chemical garden, Chem. – Eur. J., 2016, 22, 6779–6782 CrossRef CAS PubMed.
- P. Kumar, D. Horváth and Á. Tóth, Bio-inspired flow-driven chitosan chemical gardens, Soft Matter, 2020, 16, 8325–8329 RSC.
- P. Kumar, C. Hajdu, Á. Tóth and D. Horváth, Flow-driven surface instabilities of tubular chitosan hydrogel, ChemPhysChem, 2021, 22, 488 CrossRef CAS PubMed.
- A. Chakrabarti, S. Al-Mosleh and L. Mahadevan, Instabilities and patterns in a submerged jelling jet, Soft Matter, 2021, 17, 9745–9754 RSC.
- G. Orive, S. K. Tam, J. L. Pedraz and J.-P. Hallé, Biocompatibility of alginate-poly-l-lysine microcapsules for cell therapy, Biomaterials, 2006, 27, 3691–3700 CrossRef CAS PubMed.
- K. Norajit, K. M. Kim and G. H. Ryu, Comparative studies on the characterization and antioxidant properties of biodegradable alginate films containing ginseng extract, J. Food Eng., 2010, 98, 377–384 CrossRef CAS.
- J.-S. Yang, Y.-J. Xie and W. He, Research progress on chemical modification of alginate: A review, Carbohydr. Polym., 2011, 84, 33–39 CrossRef CAS.
- H. H. Tønnesen and J. Karlsen, Alginate in drug delivery systems, Drug Dev. Ind. Pharm., 2002, 28, 621–630 CrossRef.
- J. Venkatesan, I. Bhatnagar, P. Manivasagan, K.-H. Kang and S.-K. Kim, Alginate composites for bone tissue engineering: A review, Int. J. Biol. Macromol., 2015, 72, 269–281 CrossRef CAS PubMed.
- S. Deville, E. Saiz, R. K. Nalla and A. P. Tomsia, Freezing as a path to build complex composites, Science, 2006, 311, 515–518 CrossRef CAS PubMed.
- A. Fogde, S. Qudsia, T.-A. Le, T. Sandberg and T.-P. Huynh, (Calcium-phosphate)/carrageenan gardens grown from the gel/liquid interface, ChemSystemsChem, 2021, 3, e2000064 CrossRef CAS.
- E. Pouget, E. Dujardin, A. Cavalier, A. Moreac, C. Valéry, V. Marchi-Artzner, T. Weiss, A. Renault, M. Paternostre and F. Artzner, Hierarchical architectures by synergy between dynamical template self-assembly and biomineralization, Nat. Mater., 2007, 6, 434–439 CrossRef CAS.
- P. Kumar, D. Sebök, A. Kukovecz, D. Horváth and Á. Tóth, Hierarchical self-assembly of metal-ion-modulated chitosan tubules, Langmuir, 2021, 37, 12690–12696 CrossRef CAS PubMed.
- I. Lee, S. W. Han, H. J. Choi and K. Kim, Nanoparticle-directed crystallization of calcium carbonate, Adv. Mater., 2001, 13, 1617–1620 CrossRef CAS.
- H. Wang, M. Bongio, K. Farbod, A. W. G. Nijhuis, J. Van Den Beucken, O. C. Boerman, J. C. M. Van Hest, Y. Li, J. A. Jansen and S. C. G. Leeuwenburgh, Development of injectable organic/inorganic colloidal composite gels made of self-assembling gelatin nanospheres and calcium phosphate nanocrystals, Acta Biomater., 2014, 10, 508–519 CrossRef CAS PubMed.
- E. A. B. Hughes, M. Chipara, T. J. Hall, R. L. Williams and L. M. Grover, Chemobrionic structures in tissue engineering: self-assembling calcium phosphate tubes as cellular scaffolds, Biomater. Sci., 2020, 8, 812–822 RSC.
- E. A. B. Hughes, T. E. Robinson, R. J. A. Moakes, M. Chipara and L. M. Grover, Controlled self-assembly of chemical gardens enables fabrication of heterogeneous chemobrionic materials, Commun. Chem., 2021, 4, 145 CrossRef CAS.
- R. Nakamura, T. Takashima, S. Kato, K. Takai, M. Yamamoto and K. Hashimoto, Electrical current generation across a black smoker chimney, Angew. Chem., 2010, 122, 7858–7860 CrossRef.
- M. Yamamoto, R. Nakamura, K. Oguri, S. Kawagucci, K. Suzuki, K. Hashimoto and K. Takai, Generation of electricity and illumination by an environmental fuel cell in Deep-Sea hydrothermal vents, Angew. Chem., Int. Ed., 2013, 52, 10758–10761 CrossRef CAS PubMed.
- M. Yamamoto, R. Nakamura, T. Kasaya, H. Kumagai, K. Suzuki and K. Takai, Spontaneous and widespread electricity generation in natural Deep-Sea hydrothermal fields, Angew. Chem., 2017, 129, 5819–5822 CrossRef.
- K. Ruiz-Mirazo, C. Briones and A. de la Escosura, Prebiotic systems chemistry: New perspectives for the origins of life, Chem. Rev., 2014, 114, 285–366 CrossRef CAS PubMed.
- L. M. Barge, Y. Abedian, M. J. Russell, I. J. Doloboff, J. H. E. Cartwright, R. D. Kidd and I. Kanik, From chemical gardens to fuel cells: Generation of electrical potential and current across self-assembling iron mineral membranes, Angew. Chem., Int. Ed., 2015, 54, 8184–8187 CrossRef CAS PubMed.
- M. Getenet, J. Rieder, M. Kellermeier, W. Kunz and J. Manuel Garca-Ruiz, Tubular Structures of calcium carbonate: Formation, characterization, and implications in natural mineral environments, Chem. – Eur. J., 2021, 27, 16135–16144 CrossRef CAS PubMed.
- L. M. Barge, I. J. Doloboff, L. M. White, G. D. Stucky, M. J. Russell and I. Kanik, Characterization of iron-phosphate-silicate chemical garden structures, Langmuir, 2012, 28, 3714–3721 CrossRef CAS PubMed.
- L. Roszol and O. Steinbock, Controlling the wall thickness and composition of hollow precipitation tubes, Phys. Chem. Chem. Phys., 2011, 13, 20100–20103 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01063a |
| This journal is © The Royal Society of Chemistry 2022 |




