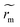Open Access Article
Open Access ArticleThermal Marangoni trapping driven by laser absorption in evaporating droplets for particle deposition†
N.-A.
Goy
,
N.
Bruni
,
A.
Girot
,
J.-P.
Delville
 and
U.
Delabre
and
U.
Delabre
 *
*
Univ. Bordeaux, CNRS, LOMA, UMR 5798, F-33405 Talence, France. E-mail: ulysse.delabre@u-bordeaux.fr
First published on 4th October 2022
Abstract
Controlling the deposition of particles is of great importance in many applications. In this work, we study particle deposition driven by Marangoni flows, triggered by laser absorption inside an evaporating droplet. When the laser is turned on, thermal gradients are generated and produce a toroidal Marangoni flow that concentrates the particles around the laser beam and ultimately controls the final deposition. We experimentally characterize the radius of the Marangoni flows as a function of the laser parameters. Counter-intuitively, the radius of the Marangoni region appears to remain constant and is not proportional to the thickness of the drop which decreases due to evaporation. We develop a model to predict the size of the Marangoni region that combines evaporative flows and laser-induced Marangoni flows. The experimental data are in good agreement with the predictions, allowing us to estimate the particle overconcentration factor resulting from the laser heating effects. The addition of surfactants to the solution allows the coupling of solutal Marangoni flows with thermal ones to achieve a final micron-scale deposit located at the laser spot. These results pave the way for new methods with high tunability provided by spatio-temporal light control for surface patterning applications.
Controlling the microscopic organization of large particle assemblies on surfaces is of great importance to design dedicated functional patterns in surface material processing for biosensing, particle chromatography, 2D-photonics, or printing applications for example.1–5 Complementary to top-down techniques such as lithography, bottom-up approaches represent a very appealing and low cost alternative strategy6,7 that have attracted intensive studies in the past decades. Among them, evaporation-driven self-assembly is now recognized as a smart process to organize particles at the micron and submicron scales.8,9 The underlying mechanism was firstly demonstrated with the so-called coffee ring effect7,10 where the evaporation of the solvent of sessile droplets triggers particle deposition at the contact line due to internal outwards flows induced by the evaporation gradient. To go beyond simple organizations of deposits and to control the size of the final deposit which is essential for surface functionnalizations, additional strategies have been proposed based on either the use of external fields or the control of internal flows during the evaporation process. For instance, evaporation masks to control locally the evaporation rate at the droplet interface or to modify the flow field inside the droplets have been successfully proposed.11 External fields, such as electric,12 light,13 electroosmotic14 or acoustic3,15 fields, were also devised to increase versatility and functionalization but they often require specific substrate properties. Another interesting and very general strategy is based on the Marangoni effect as proposed initially by Hu and Larson.16 The Marangoni effect is based on the variation of surface tension due to either a thermal gradient (Thermal Marangoni Effect (TME)) or a solutal chemical gradient (Solutal Marangoni Effect (SME)). The Marangoni effects generate surface flows which trigger a reorganization of the deposit after the evaporation of the solvent. Marangoni flows can then oppose to the evaporative flows and offer another degree of freedom to assemble and organize 2D materials. In this context, solutal (using surfactants or vapour chemical)17–20 and thermal (using heating sources)21 Marangoni effects have been exploited to reverse the coffee ring effect. Recently, laser actuation has been proposed to induce SME using UV laser photoactivation of specific surfactants22 or to induce TME from laser absorption or plasmonic resonance.23–25 Lasers are indeed appealing to drive Marangoni flows since a huge thermal gradient with weak overheating can be obtained depending on the laser focusing, and offer a simple route to texture and tune dynamically the flows with dedicated optics. Such laser-induced Marangoni flows offer control of the particle deposition around the laser focus24,26 instead of the droplet periphery and enable new types of patterns22 for dedicated applications. However, up to now the typical size of the final deposit is still large, typically around a few tenths of millimeters.21–23,25,26 So the optimization of the final deposit size remains an open question although it is essential for future miniaturized applications. A detailed study depending on the laser and temperature parameters is still lacking and a quantitative model is required to understand the resulting laser-induced flows in non-equilibrium conditions during the evaporation process. The present investigation proposes such a detailed experimental investigation of the laser-induced Marangoni flows inside an evaporating droplet as a function of laser and thermal parameters. To do this, we use a near infrared focused laser to locally heat an aqueous suspension and induce a localized thermal gradient inside an evaporating droplet deposited on a glass substrate. When the laser is turned on, the temperature inside the droplet increases rapidly and a thermal gradient at the interface triggers hydrodynamic flows. We show that a Marangoni recirculating zone rapidly appears around the laser spot at the drop center and maintains all along the evaporation process as presented in Fig. 1a (see Movie in ESI†). Interestingly, this Marangoni recirculating zone concentrates particles in a specific and localized region around the heating laser beam, which sets the final deposit size. We finally show that the addition of surfactants could be an important issue to reduce the final deposit size beyond standard limitations.
In the following, we first introduce the experimental setup and present the experimental results depending on laser properties. We then develop a model to account for the amplitude of the Marangoni flow and the size of the recirculating region depending on the heating laser characteristics and on the thermal properties of the suspension. This model is quantitatively confronted to experiments in order to show that the size of the recirculation region controls the evolution of the particle concentration. We anticipate that the size of this recirculation region is crucial to control the size and the particle density of the final deposit as well as the particle organization within this deposit, which are all essential aspects for further patterning and surface functionnalization applications.
1 Materials and methods
1.1 Solutions
Aqueous solutions containing 0.1 wt% of fluorescent particles (Fluoresbrite, YG, Polysciences, diameter = 1 μm) are prepared with deionized (DI) water. Solutions are sonicated during 20 min before use to avoid possible aggregates. Drops of volume ranging from 0.1 μL up to 1.0 μL of solutions are deposited using a SGE glass syringe on a microscope slide. Microscope slides (Menzel Glazer) are first cleaned with acetone, then with DI water and with ethanol. Finally slides are dried with dry air and argon gas. Experiments are performed at room temperature (T = 20 °C) and at a relative humidity (RH) varying between 40% and 70% depending on room humidity conditions.1.2 Optical and imaging setup
A sketch of the experimental setup is given in Fig. 1b. A continuous near infrared (NIR) laser beam (LUMICS, LuOcean Mini) operating at λ = 1470 nm is used. The absorption coefficient of water at this wavelength is β = 2354 m−1. The laser beam is first collimated and then focused inside the sample using a microscope NIR objective (OL ×2.5 (Zeiss, NA = 0.075) or ×8 (Nachet Vision, NA = 0.25)). The laser intensity profile has been characterized with a beam profiler (DataRay, Beam R2) along the beam path and the resulting laser waist at the focus is w0 ≈ 320 μm for the ×2.5 objective and w0 ≈ 110 μm for the ×8 objective, respectively. To adjust accurately the laser focus inside the sample, we use a temperature sensitive fluorescent dye (Rhodamine B at 50 mg mL−1 in HEPES solution (buffer pH = 7)) that enables the characterization of the overheating due to the laser absorption:27,28 the higher the temperature, the lower the fluorescent intensity is. The focus of the laser is then obtained when the width of the dark region in the Rhodamine B sample is the smallest. The Rayleigh range of the laser beam, which defines the region where the beam can be assumed as almost cylindrical, is around zR ≈ 12 mm for the ×2.5 objective and zR ≈ 1.6 mm for the ×8 objective, respectively (see ESI†). For the drop volumes investigated here, the height of the droplet varies between 100–300 μm <2 zR which means that the laser beam can be assumed as cylindrical during its propagation inside the drop. The microscope slide on which the drop is deposited, is mounted on a translating stage (Markzhauzer Wetzlar) to align the center of the drop on the laser axis. Finally, the drop is illuminated by an HBO lamp mounted on an inverted microscope (Olympus, IX71) in epifluorescence configuration. The drop is imaged from below with a CDD video camera (C5405 Hamamatsu, fps between 5 Hz and 25 Hz) attached to the microscope.1.3 Laser heating characterization
Two different methods are used to map the temperature field resulting from the laser absorption of the drop suspension. First, we used the standard fluorescence thermometry technique considering the decrease of fluorescence intensity of Rhodamine B (RhB) with temperature;27,29 the procedure is explained in Riviere et al.29 They show that fluorescence can be used to measure accurately the temperature field induced by the laser in a contactless approach. However, the RhB concentration may increase drastically during the water evaporation and may become inhomogeneous due to the Marangoni flows, preventing its use during the late stage of the evaporation dynamics. Indeed, as shown in ESI† after few seconds the local concentration of RhB becomes dependent on the hydrodynamics flows (Peclet number Pe > 1) inside the drop. As an alternative method, we used an infrared camera (FLIR SC7000, spectral range 1.5–5 μm, IR Objective FLIR ATS L0905) to characterize accurately the temperature field inside the drop.25,30 Due to geometrical constraints in the optical setup, the infrared camera was tilted (ϕ = 55°) relatively to the vertical axis of the laser. We checked that this inclination angle has no effect on the temperature measurements (see ESI†). A correction taking into account both the thickness and emissivity of the water and glass layers is also applied on the measured signal to get the real temperature distribution within the droplet. Note that results from both methods (RhB and IR camera measurements) are equivalent in the first stages of the evaporation dynamics as discussed later and shown in ESI.†2 Results
2.1 Laser induced Marangoni recirculating flows
Once the droplet is deposited on the substrate, it first spreads rapidly until it reaches its equilibrium contact angle θ0 ≈ 15–20°. The initial drop radius and drop apex height at the beginning of the evaporation process are denoted R and h0 respectively (see Fig. 1c). In the absence of laser heating, particles are transported toward the contact line and the standard coffee ring effect occurs at the pinned contact line (R = constant). The drop evaporates completely after an evaporation time called with V the initial volume and j0 the evaporation rate (j0 ≈ 10−6 mm2 s−1 for water).9 For V ≈ 0.1 μL, and R ≈ 1 mm, the evaporation time is typically tf ≈ 100 s at a relative humidity rate RH = 50%. For a laser-heating experiment, once the spreading phase is over and the droplet has reached its final radius R (at most in one second), the center of the droplet is rapidly aligned with the laser axis.
with V the initial volume and j0 the evaporation rate (j0 ≈ 10−6 mm2 s−1 for water).9 For V ≈ 0.1 μL, and R ≈ 1 mm, the evaporation time is typically tf ≈ 100 s at a relative humidity rate RH = 50%. For a laser-heating experiment, once the spreading phase is over and the droplet has reached its final radius R (at most in one second), the center of the droplet is rapidly aligned with the laser axis.
The laser is then turned on, which defines the starting time to our experiment t = 0 s. Very rapidly, fluorescent particles are transported by the recirculation flows towards the laser spot as shown in Fig. 1a. By shifting the focus plane of the imaging objective (OM in Fig. 1b), it appears that close to the substrate, particles are convected towards the center of the drop whereas they are expelled from the center at the drop interface. Since the temperature is the highest at the laser location, the induced thermal gradient at the surface and in the bulk results in a gradient of surface tension and a variation of the bulk density. The surface tension gradient triggers Marangoni flows whereas density gradient generates thermogravitational flows.29 Their relative importance is quantified by the dynamical Bond number which compares thermogravitational with Marangoni velocity:31 . As in our case the variations of surface tension and density are negative with respect to temperature (for classical fluids dγ/dT < 0 and dρ/dT < 0 respectively) both contributions generate convection rolls with outward surface radial flows as sketched in Fig. 1c. However, for drops of small volume and thickness h considered in this study, thermogravitational flows are negligible compared to Marangoni ones since the dynamical Bond number Bo,D ≪ 1. The recirculating flow inside small droplets is then triggered solely by intrinsic evaporation and Marangoni stresses. Particles are then concentrated in a recirculating region as shown by the increase in collected fluorescent intensity of the beads in the center region in Fig. 1a (see also movie in ESI†). Note that particles are still transported towards the contact line, but in a much less ratio, because the evaporative flows dominate Marangoni ones in this region as it will be discussed below. Due to this competition between recirculation around the center and evaporation flows close to the contact line, we experimentally observe a stagnation point for r = rS ≈ 0.8 R. Importantly, almost all along the evaporation process, the contact line is pinned and the drop radius R is constant. However, at the final stages of the evaporation (for t ≥ 0.8tf), as already noticed by several studies,32–34 the contact line starts to recede due to the final drying (see C.L.R. region in Fig. 2). Here, we only focus on the main regime where the contact line is pinned and the drop radius is constant.
. As in our case the variations of surface tension and density are negative with respect to temperature (for classical fluids dγ/dT < 0 and dρ/dT < 0 respectively) both contributions generate convection rolls with outward surface radial flows as sketched in Fig. 1c. However, for drops of small volume and thickness h considered in this study, thermogravitational flows are negligible compared to Marangoni ones since the dynamical Bond number Bo,D ≪ 1. The recirculating flow inside small droplets is then triggered solely by intrinsic evaporation and Marangoni stresses. Particles are then concentrated in a recirculating region as shown by the increase in collected fluorescent intensity of the beads in the center region in Fig. 1a (see also movie in ESI†). Note that particles are still transported towards the contact line, but in a much less ratio, because the evaporative flows dominate Marangoni ones in this region as it will be discussed below. Due to this competition between recirculation around the center and evaporation flows close to the contact line, we experimentally observe a stagnation point for r = rS ≈ 0.8 R. Importantly, almost all along the evaporation process, the contact line is pinned and the drop radius R is constant. However, at the final stages of the evaporation (for t ≥ 0.8tf), as already noticed by several studies,32–34 the contact line starts to recede due to the final drying (see C.L.R. region in Fig. 2). Here, we only focus on the main regime where the contact line is pinned and the drop radius is constant.
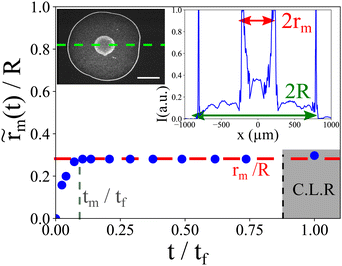
We define  the Marangoni radius of the recirculating region; it is measured from the fluorescence intensity as presented in the insets of Fig. 2. Here, notation indicates a time dependent variation. Fig. 2 shows the evolution of
the Marangoni radius of the recirculating region; it is measured from the fluorescence intensity as presented in the insets of Fig. 2. Here, notation indicates a time dependent variation. Fig. 2 shows the evolution of 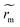 (t) renormalized by the radius R as the function of the renormalized time t/tf. At the onset of the laser exposure (t/tf = 0), the Marangoni radius increases and rapidly reaches a stationary value denoted rm as illustrated in Fig. 1a and 2. The transient time called tm to reach this stationary value rm corresponds to a characteristic time for the Marangoni flows to settle in the drop. Hence, tm ∼ R/Um where Um is a characteristic Marangoni velocity. With a typical Marangoni velocity at the drop interface around Um ≈ 100–300 μm s−1 for Pin = 250 mW and R ≈ 750 μm, we get tm ≈ 2.5–7.5 s which is of the order of the experimental transient time tm ≈ (0.1). tf ≈ 4 s observed in Fig. 2. Here, the Marangoni radius rm remains constant while the drop height h decreases continuously due to the evaporation of the solvent. This is rather counter intuitive as in many examples such as Marangoni-Bénard instabilities,35 the size of the recirculation cells is set by the thickness of the liquid layer. Interestingly, our Marangoni recirculation acts as a trapping region for particles where the concentration in particles increases due to laser absorption and Marangoni stresses at the drop interface. Indeed, for particles before the stagnation point (r < rS), they are attracted towards the drop center where the Marangoni coupling is the largest, whereas for r > rS ≈ 0.8 R, particles are transported towards the contact line. Thus, particles with a position r < rS in the initial state are concentrated in the Marangoni region. The increase in particle concentration inside the Marangoni recirculation zone is roughly multiplied by a factor
(t) renormalized by the radius R as the function of the renormalized time t/tf. At the onset of the laser exposure (t/tf = 0), the Marangoni radius increases and rapidly reaches a stationary value denoted rm as illustrated in Fig. 1a and 2. The transient time called tm to reach this stationary value rm corresponds to a characteristic time for the Marangoni flows to settle in the drop. Hence, tm ∼ R/Um where Um is a characteristic Marangoni velocity. With a typical Marangoni velocity at the drop interface around Um ≈ 100–300 μm s−1 for Pin = 250 mW and R ≈ 750 μm, we get tm ≈ 2.5–7.5 s which is of the order of the experimental transient time tm ≈ (0.1). tf ≈ 4 s observed in Fig. 2. Here, the Marangoni radius rm remains constant while the drop height h decreases continuously due to the evaporation of the solvent. This is rather counter intuitive as in many examples such as Marangoni-Bénard instabilities,35 the size of the recirculation cells is set by the thickness of the liquid layer. Interestingly, our Marangoni recirculation acts as a trapping region for particles where the concentration in particles increases due to laser absorption and Marangoni stresses at the drop interface. Indeed, for particles before the stagnation point (r < rS), they are attracted towards the drop center where the Marangoni coupling is the largest, whereas for r > rS ≈ 0.8 R, particles are transported towards the contact line. Thus, particles with a position r < rS in the initial state are concentrated in the Marangoni region. The increase in particle concentration inside the Marangoni recirculation zone is roughly multiplied by a factor  compared to the initial concentration c0 with data taken from Fig. 2. In the next section, we show how the Marangoni radius rm of the recirculation zone is affected by laser and thermal parameters.
compared to the initial concentration c0 with data taken from Fig. 2. In the next section, we show how the Marangoni radius rm of the recirculation zone is affected by laser and thermal parameters.
2.2 Dependence of the Marangoni radius with laser parameters
The Marangoni radius for various absorbed laser powers is shown in Fig. 3. Fig. 3a shows how the renormalized Marangoni radius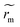 (t)/R varies as a function of renormalized time t/tf for several initial absorbed powers Pabs, defined as Pabs = Pabs(h0) = Pin(1 − e−βh0) where h0 is the initial thickness of the drop. This confirms our first observation: after a transient regime,
(t)/R varies as a function of renormalized time t/tf for several initial absorbed powers Pabs, defined as Pabs = Pabs(h0) = Pin(1 − e−βh0) where h0 is the initial thickness of the drop. This confirms our first observation: after a transient regime,  (t) saturates to a stationary value rm that depends on the absorbed power Pabs. We plot the stationary value of the Marangoni radius rm/R as function of the absorbed power in Fig. 3b for various volumes. Despite some data dispersion, the general trend clearly indicates a close correlation between rm and the absorbed power Pabs. This dispersion results mainly from the dispersion in drop radii (see ESI†) and the laser centering process, which both affects the absorbed power. We checked that the relative humidity does not have a significant impact on these results as expected (see Fig. 3c). In addition, it is important to investigate how the Marangoni radius rm/R is affected by the laser waist w(z). Results are shown in Fig. 3d, which shows that the beam size w(z) significantly affects the Marangoni radius rm. All together, these results indicate that laser beam parameters strongly affect the size of the Marangoni recirculation region. In the next section, we characterize the temperature field inside the drop when varying the power and the waist of the heating laser.
(t) saturates to a stationary value rm that depends on the absorbed power Pabs. We plot the stationary value of the Marangoni radius rm/R as function of the absorbed power in Fig. 3b for various volumes. Despite some data dispersion, the general trend clearly indicates a close correlation between rm and the absorbed power Pabs. This dispersion results mainly from the dispersion in drop radii (see ESI†) and the laser centering process, which both affects the absorbed power. We checked that the relative humidity does not have a significant impact on these results as expected (see Fig. 3c). In addition, it is important to investigate how the Marangoni radius rm/R is affected by the laser waist w(z). Results are shown in Fig. 3d, which shows that the beam size w(z) significantly affects the Marangoni radius rm. All together, these results indicate that laser beam parameters strongly affect the size of the Marangoni recirculation region. In the next section, we characterize the temperature field inside the drop when varying the power and the waist of the heating laser.
2.3 Temperature profile inside the drop induced by laser absorption
A typical example of the experimental spatial distribution of the temperature rise ΔT = T − Tamb induced by the laser absorption in a evaporating drop is plotted in Fig. 4a. As suggested by previous studies,29,36 we fit our data with a Lorentzian function in Fig. 4a, defined by ΔT =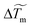 /(1 + (r/
/(1 + (r/![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) )2) where
)2) where 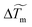 is the maximum temperature rise and
is the maximum temperature rise and ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) the width distribution. The fit (see Fig. 4a) shows a very good agreement with the experimental data. We then use this Lorentzian function and its parameters to characterize the absorption of the laser inside the drop. The instantaneous absorbed laser power, defined as Pin(1 − e−βh(t)) based on a Beer–Lambert formulation, decreases during the evaporation since h decreases as well. It is then expected that
the width distribution. The fit (see Fig. 4a) shows a very good agreement with the experimental data. We then use this Lorentzian function and its parameters to characterize the absorption of the laser inside the drop. The instantaneous absorbed laser power, defined as Pin(1 − e−βh(t)) based on a Beer–Lambert formulation, decreases during the evaporation since h decreases as well. It is then expected that  and
and ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) evolve with time during the evaporation process. Fig. 4b shows the variation of
evolve with time during the evaporation process. Fig. 4b shows the variation of  (t) and
(t) and  during an evaporation process as a function of time. Interestingly, the maximum temperature rise decreases almost linearly with time whereas the temperature width
during an evaporation process as a function of time. Interestingly, the maximum temperature rise decreases almost linearly with time whereas the temperature width  reaches a constant value (denoted σ for simplicity) except at the end of the evaporation process. We plot in Fig. 4c and d the maximum temperature amplitude of
reaches a constant value (denoted σ for simplicity) except at the end of the evaporation process. We plot in Fig. 4c and d the maximum temperature amplitude of 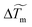 , denoted ΔTm, taken at the beginning of the evaporation process and σ as a function of the initial absorbed power. Whereas ΔTm increases almost linearly with the initial absorbed power, the temperature width σ remains almost constant for given laser waist w0 and drop volume V. This tends to show that ΔTm ∼ a·Pabs in the laser power range investigated here and that σ = constant at given V and w0. Considering that the beam waist affects significantly rm (see Fig. 3d), we then performed experiments with various laser waists by translating the focusing objective OL in the optical setup; such a way to vary the beam size makes sense because the height h of the drop is always very small compared to the Rayleigh range (zR) of the laser. This allows us to control the initial absorbed power Pabs almost independently to the laser waist in the sample. The resulting maximum temperature rise ΔTm and width σ are shown in Fig. 4e and f. Even if a full modelling of the temperature field induced by the laser in a evaporating droplet is far beyond the objectives of the present study, in the thin film approximation (h ≪ w0), a scaling analysis of the heat diffusion equation gives
, denoted ΔTm, taken at the beginning of the evaporation process and σ as a function of the initial absorbed power. Whereas ΔTm increases almost linearly with the initial absorbed power, the temperature width σ remains almost constant for given laser waist w0 and drop volume V. This tends to show that ΔTm ∼ a·Pabs in the laser power range investigated here and that σ = constant at given V and w0. Considering that the beam waist affects significantly rm (see Fig. 3d), we then performed experiments with various laser waists by translating the focusing objective OL in the optical setup; such a way to vary the beam size makes sense because the height h of the drop is always very small compared to the Rayleigh range (zR) of the laser. This allows us to control the initial absorbed power Pabs almost independently to the laser waist in the sample. The resulting maximum temperature rise ΔTm and width σ are shown in Fig. 4e and f. Even if a full modelling of the temperature field induced by the laser in a evaporating droplet is far beyond the objectives of the present study, in the thin film approximation (h ≪ w0), a scaling analysis of the heat diffusion equation gives  which shows that ΔTm tends to decrease when the waist of the laser increases as shown in Fig. 4e. Yet, such scaling requires to be confirmed by further studies.
which shows that ΔTm tends to decrease when the waist of the laser increases as shown in Fig. 4e. Yet, such scaling requires to be confirmed by further studies.
3 Model
In this section, our goal is to propose a simple model to account for the hydrodynamic flows and the Marangoni radius as a function of the thermal parameters based on our previous experimental observations.In the absence of laser heating, the hydrodynamics flows result from the inhomogeneous evaporation rate. As characterized by Deegan et al.,37 the evaporation of the solvent is controlled by the diffusion of the solvent in the atmosphere. Since the drop is deposited on a substrate with a low contact angle, the evaporation rate is inhomogeneous and is maximum at the contact line. In our case, the laser induces a localized heating and a thermal gradient inside the drop which generates Marangoni flows. Then, the whole velocity field results then from the addition of two main mechanisms: the first one results from the inhomogeneous evaporation rate, and the second one from the thermal Marangoni effect.
Our goal, here is to propose a simple model in the case of small absorbed laser powers Pabs ≪ 150 mW. In that case, the evaporation is still governs by diffusion and the evaporation rate is still maximum at the contact line. Indeed as shown by Yen et al.,38 to induce non negligible differential evaporation by laser absorption, higher absorbed powers are required and contact angle have to be close to θ ∼ 90° which is not the case here. In first approximation, at small absorbed powers, it is then reasonable to use the standard evaporation flows and to superimpose the Marangoni flows induced by laser absorption.
3.1 Evaporative driven flows
We first focus on the evaporative flows. As already mentioned, the evaporation is controlled by diffusion in the atmosphere, so the evaporation rate is given, at small contact angles, by:39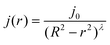 | (1) |
 | (2) |
Since the drop radius is smaller than the capillary length 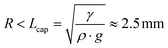 , the droplet shape can be well approximated by a spherical cap which gives:
, the droplet shape can be well approximated by a spherical cap which gives: 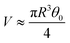 and h0 ≈ Rθ0/2 with θ0 the initial contact angle.
and h0 ≈ Rθ0/2 with θ0 the initial contact angle.
Based on the mass conservation equation, the analytical profile of the flows driven by evaporation in the isothermal case for a diffusion regime has been proposed by Hu and Larson.39 The height averaged radial velocity is given by:
 | (3) |
 , which determines the whole velocity profile induced by evaporation. The streamlines are shown in Fig. 5a. Evaporative flows show a weak downward axial flow in the drop centre while, near the drop's edge an outward radial flow is induced. As shown by eqn (3), the typical evaporation velocity scales as
, which determines the whole velocity profile induced by evaporation. The streamlines are shown in Fig. 5a. Evaporative flows show a weak downward axial flow in the drop centre while, near the drop's edge an outward radial flow is induced. As shown by eqn (3), the typical evaporation velocity scales as  where tf is the evaporation time. In our experiment, the evaporation time under laser irradiation is typically tf ≈ 40 s with V = 0.1 μL, R = 800 μm, h0 = 80 μm, RH = 50% and an absorbing power Pabs ≈ 50 mW. Then the typical evaporation velocity is Ue ∼ 20 μm s−1 which is confirmed experimentally by tracking particles near the contact line.
where tf is the evaporation time. In our experiment, the evaporation time under laser irradiation is typically tf ≈ 40 s with V = 0.1 μL, R = 800 μm, h0 = 80 μm, RH = 50% and an absorbing power Pabs ≈ 50 mW. Then the typical evaporation velocity is Ue ∼ 20 μm s−1 which is confirmed experimentally by tracking particles near the contact line.
 | ||
| Fig. 5 Numerical streamlines of the evaporative (a) and of the Marangoni (b) flows for ΔTm = 20 K, σ = 350 μm, R = 1 mm, tf = 40 s and h0 = 176 μm. | ||
3.2 Thermal Marangoni flows induced by laser absorption
We focus now on the Marangoni flows. The analytical profile of the thermal Marangoni effect can be derived under specific conditions. First of all, it is possible to neglect the convection term in the Navier–Stokes equation as the Reynolds number is smaller than unity ( as Uexpm ∼ 100 μm s−1 experimentally) where the m index stands for Marangoni. Moreover, despite laser heating, the Boussinesq approximation |∂ρ/∂TΔT| ≪ ρ0 is verified for thin droplets so that stationary flow can be described by Stokes and incompressibility equations (Boussinesq approximation29):
as Uexpm ∼ 100 μm s−1 experimentally) where the m index stands for Marangoni. Moreover, despite laser heating, the Boussinesq approximation |∂ρ/∂TΔT| ≪ ρ0 is verified for thin droplets so that stationary flow can be described by Stokes and incompressibility equations (Boussinesq approximation29): | (4) |
Since the droplet is relatively flat (h0 ≪ R), we can also work in the lubrication regime. Then the Stokes equation can be solved by only considering the axial dependence of the radial velocity in axisymmetric coordinates:
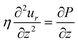 | (5) |
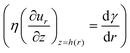 , and mass conservation
, and mass conservation  . The Marangoni velocity40 is finally given by:
. The Marangoni velocity40 is finally given by: | (6) |
In first approximation, the drop's profile can be written as a parabolic profile (spherical cap approximation):  , and the temperature gradient is given by the derivative of the Lorentzian profile:
, and the temperature gradient is given by the derivative of the Lorentzian profile:  . The streamlines of this Marangoni flows are shown in Fig. 5b and give rise to recirculation rolls inside the droplet. The resulting Marangoni flows scale typically as:
. The streamlines of this Marangoni flows are shown in Fig. 5b and give rise to recirculation rolls inside the droplet. The resulting Marangoni flows scale typically as: 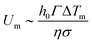 where
where  . With the experimental values (σ ≈ 0.35 R and ΔTm ≈ 20 K) we can get a predicted Marangoni velocity: Um ∼ 0.5 m s−1 which means that Marangoni flows are orders of magnitude stronger than evaporative ones. It can be useful to define the Marangoni number Ma = Um/Ue which defines the ratio between Marangoni and evaporation velocity. In perfect clean conditions, we get Ma ≈ 30
. With the experimental values (σ ≈ 0.35 R and ΔTm ≈ 20 K) we can get a predicted Marangoni velocity: Um ∼ 0.5 m s−1 which means that Marangoni flows are orders of magnitude stronger than evaporative ones. It can be useful to define the Marangoni number Ma = Um/Ue which defines the ratio between Marangoni and evaporation velocity. In perfect clean conditions, we get Ma ≈ 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for water. However, the predicted Marangoni velocity is much higher than the experimental one: Uexp ∼ 100–300 μm s−1 in the central part of the drop. Nonetheless, as pointed out by Hu and Larson,16,41 water interface is easily polluted by impurities which deeply modifies the amplitude of the Marangoni flows; this is even accentuated for heated interfaces. Following Hu and Larson's idea, impurities can be taken into account by rescaling the Marangoni velocity through an impurity surface concentration ν such as Ueffm = Um/(1 + aν) where a is a numerical coefficient depending on the fluid/impurities properties. For clarity, full expressions of the Marangoni velocity are given in ESI.† Typically, it has been estimated41 that impurity concentrations as small as 300 molecules per μm2 could reduce the Marangoni velocity by a factor of 100 at least. In our case, it is then equivalent to define an effective Marangoni number Maeff = Ueffm/Uevap where Ueffm is the effective Marangoni velocity which takes into account pollution. The Marangoni term is thus simply rescaled.
000 for water. However, the predicted Marangoni velocity is much higher than the experimental one: Uexp ∼ 100–300 μm s−1 in the central part of the drop. Nonetheless, as pointed out by Hu and Larson,16,41 water interface is easily polluted by impurities which deeply modifies the amplitude of the Marangoni flows; this is even accentuated for heated interfaces. Following Hu and Larson's idea, impurities can be taken into account by rescaling the Marangoni velocity through an impurity surface concentration ν such as Ueffm = Um/(1 + aν) where a is a numerical coefficient depending on the fluid/impurities properties. For clarity, full expressions of the Marangoni velocity are given in ESI.† Typically, it has been estimated41 that impurity concentrations as small as 300 molecules per μm2 could reduce the Marangoni velocity by a factor of 100 at least. In our case, it is then equivalent to define an effective Marangoni number Maeff = Ueffm/Uevap where Ueffm is the effective Marangoni velocity which takes into account pollution. The Marangoni term is thus simply rescaled.
We then superimpose the evaporation and the Marangoni flows. We find that a good agreement with the experimental velocity values for an effective Marangoni number Maeff ≈ 30 can be achieved, compatible with an impurity surface concentration as detailed in ESI.† The typical streamlines of the combined Marangoni-evaporative flows are plotted in Fig. 6a. First, the resulting flows exhibit a recirculating region in the drop center as in the experiments. Interestingly, for such effective Marangoni flows, close to the contact line, a competition between Marangoni recirculation and outwards evaporative flows is observed numerically, as in experiments. This competition enables to define a stagnation point rS ≈ 0.8R (see Fig. 6a and b) as observed in our experiments. In Fig. 6b, a comparison between radial Marangoni flows and evaporative flows is shown. The hydrodynamical flows in the central part are thus mainly governed by the Marangoni contribution since evaporative flows are only strong enough close to the contact line.
3.3 Size of the recirculating region: the Marangoni radius
As illustrated in Fig. 6a, the definition of the size of the recirculating region is complex as the field velocity depends on z. Here, the position of rm results from both the Marangoni flows and the parabolic drop shape. To match with the experimental observation, we define the size of the recirculating region as the location where the flows becomes essentially vertical. If we consider a toroidal Marangoni convection roll, a simple model consists in identifying the position r* at the maximum of ur,m(r*) given by eqn (6). The Marangoni radius is then given by twice the distance between the center of the drop and the maximum of the radial velocity: rm ≈ 2r*. As it can been seen in Fig. 6c, the velocity profile um(r) and r* depend on the vertical position z/h(r), so the full analytical resolution requires to solve it for each z/h(r). To give an insight, we first propose a toy model in the case where σ ≪ R which means that h ≈ h0 for r ≤ σ. Then r* is roughly given by the maximum of the height averaged radial velocity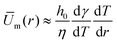 which is obtained for d2T(r)/dr2 = 0. Using the Lorentzian profile, we get r* = σ/2 which allows us to conclude a simple and important result: rm ≈ σ, in the case σ ≪ R. So the size of the Marangoni region is directly given by the width of the temperature profile in agreement with experiments.
which is obtained for d2T(r)/dr2 = 0. Using the Lorentzian profile, we get r* = σ/2 which allows us to conclude a simple and important result: rm ≈ σ, in the case σ ≪ R. So the size of the Marangoni region is directly given by the width of the temperature profile in agreement with experiments.
When σ is close to R, it is necessary to take into account the parabolic drop profile h(r) and to solve numerically 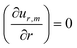 for each z/h(r) altitude. The numerical resolution of this equation which allows the calculation rm = 2r* is shown in Fig. 6. Interestingly, the position r* is exactly the same for each z/h(r) and all the solutions collapse on a single curve (referred as model “rm= 2r*”, see Fig. 7). When σ ≪ R, the numerical solution also confirms the simple scaling model rm ≈ σ. However, despite the good agreement between this model and experimental data, it can be surprising to observe a dispersion in the experimental data whereas there is only one single theoretical curve. One possible reason is that experimentally, we can only observe the 2D image of the Marangoni flows (top view).
for each z/h(r) altitude. The numerical resolution of this equation which allows the calculation rm = 2r* is shown in Fig. 6. Interestingly, the position r* is exactly the same for each z/h(r) and all the solutions collapse on a single curve (referred as model “rm= 2r*”, see Fig. 7). When σ ≪ R, the numerical solution also confirms the simple scaling model rm ≈ σ. However, despite the good agreement between this model and experimental data, it can be surprising to observe a dispersion in the experimental data whereas there is only one single theoretical curve. One possible reason is that experimentally, we can only observe the 2D image of the Marangoni flows (top view).
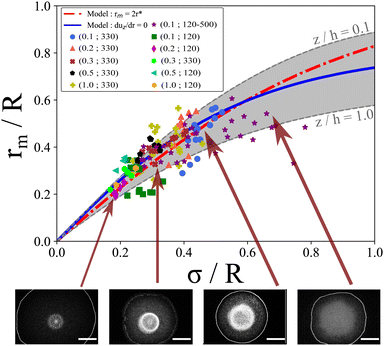 | ||
| Fig. 7 Normalized stationary Marangoni radius rm/R as a function of the normalized temperature width σ/R for various drop volumes V and laser waist w0 indicated as (V in μL; w0 in μm). Red dashed line corresponds to the rm = 2r* model (eqn (5)), whereas the blue line corresponds to the average solution ∂uz/∂r = 0. Grey region indicates the boundary solution of this equation for z/h = 0.1 and z/h = 1. | ||
To test this idea, we identify rm by the position where uz(r,z) is maximum (and negative) which is more appropriate and in better agreement with the experimental observations. We find numerically the position of rm which defines the maximum of uz(r,z) for each z/h(r). As shown in Fig. 6d, the position of this maximum depends significantly on the altitude z/h(r). Numerical results are shown in Fig. 7. From z/h(r) = 0.1 to z/h(r) = 1, it is possible to find two limit curves shown in grey in Fig. 7. This means that the positions where uz(r,z) is maximum are inside this grey region. We also plot the mean behaviour of these specific positions (referred as “duz/dr = 0” in Fig. 7) which is in good agreement with our experiment data. These results shows that depending on the altitude in the drop, the location rm is slightly changed which could explain the dispersion of the experimental data since experimentally we only observe a projection of the flows. If for σ ≪ R all the models are very similar and give rm ≈ σ, we observe a strong deviation to this simple rule of thumb when σ ≈ R. It then seems essential to take into account the full numerical solution for large σ to calculate rm. This limit has not been tested in our experiments as it requires very large waists and higher laser powers; the dynamics of the contact line may change as well due to entanglement of length scales.
4 Addition of surfactants
The use of infrared laser allows the coupling of the thermal Marangoni flows with additional surfactant flows (solutal Marangoni effects). Surfactants have been proven to change the evaporation dynamics as they may affect flows inside the droplets.17 To test the effects of surfactants in our case, we add Triton X-100 (Sigma-Aldrich), a non-ionic surfactant to the initial solution at various concentrations relative its critical micellar concentration (csurfactant from 0.1 to 5 cmc, with cmc = 0.23 10−3 M). As shown in Fig. 8a, a Marangoni region is still observed around the laser spot. However, the Marangoni radius is not constant along the evaporation contrary to the pure thermally-driven case presented in Fig. 1 and 2. A transient regime is observed where the Marangoni radius decreases versus time. No specific dependence has been observed in Fig. 8b, when the concentration of surfactants is changed from 0.5 cmc to 5 cmc. In the presence of surfactants, Marangoni flows are due to both thermal Marangoni flows and solutal Marangoni flows which can lead to an inhomogeneous surfactant concentration along the evaporation process. Furthermore, it is observed that the contact line is not pinned anymore and starts to recede from the first stages of the evaporation. The resulting final deposit is then much more centred and less scattered with surfactant than without surfactant as illustrated in Fig. 8a and c and compared with Fig. 1a. In Fig. 8d, we show a magnification of a final deposit in the presence of surfactants. Particles are highly concentrated and exhibit a hexagonal pattern with multiple layers. Thus, the presence of surfactants can have two major effects: firstly, a transient effect on the dynamics of the Marangoni radius, which allows more particles to be trapped in the central region; secondly, surfactants help to slow down the recession dynamics of the contact line, especially at the end of evaporation, generating better final deposits.5 Discussions
The results presented in this work indicate that it is possible to control the size of the Marangoni region with laser and thermal parameters. They also show that laser absorption can be confidently applied to increase the concentration of particles in a specific region, which is highly relevant for several applications such as biosensing applications, or DNA replication42 for instance where a small temperature rise is required but a high temperature gradient induced by the laser could be applied. It is then possible to calculate the size of this overconcentrated region. The model is based on the superimposition of evaporative and Marangoni flows. Interestingly, even if the magnitude of the Marangoni flows does depend on the contaminants and the pollution through the surface concentration ν, the position of the Marangoni radius rm is independent of it. The results presented in Fig. 7 are then very general. It is important to note that our analysis does not take into account the variation of the evaporation rate j0(ΔT(r)) with temperature due to laser heating. Indeed, the local laser heating at the center of the drop increases the local evaporation rate, and then can induce an inward surface flow due to a difference in evaporation rate. However, for small absorbed power, it is expected that evaporative rate is not strongly modified by the laser heating.Our results also propose a simple strategy to control the final size of the deposit. If a uniform deposit is required, the temperature field should be as wide as possible whereas for high resolution deposits, very small laser waists and so very small temperature width σ should be considered. The proposed model could be also extended towards other Marangoni actuations to control the size of the deposit with photoactive surfactants or solutal Marangoni flows for instance since the temperature field can be replaced in the eqn (6) by other fields. As suggested by the deposit shown in Fig. 1a, the final deposit size seems to be highly correlated with the Marangoni recirculation size. However, at the end of the evaporation process, the evaporation becomes stronger and stronger whereas the Marangoni flows vanish as the thickness of the drop is thinner and thinner. Hence, we do not expect that a simple theoretical relation exist between the Marangoni radius rm and the final deposit size even if experiments seem to suggest a correlation between these two quantities. Furthermore, the contact line starts to recede which means that the proposed model becomes by definition inadequate. In addition, experiments with surfactants tend to show that the recession of the contact line is an important aspect to reduce the final deposit size. A further analysis would require to consider a competition between the fast evaporation and Marangoni flows during the last stage of the evaporation process which would be addressed in a future work.
6 Conclusions
In this study, we have investigated Marangoni flows induced by the local absorption of a laser inside an evaporating droplet. We have shown that Marangoni flows allow to concentrate the particles in a region centered around the laser beam. The size of the recirculation region can be experimentally controlled by laser and thermal parameters such as absorbed power, laser size and temperature width. We have proposed a model to understand the Marangoni flows driven by laser heating inside the evaporating droplet and to predict the size of the Marangoni recirculation as a function of temperature width. Data are obtained for a variety of experimental conditions in good agreement with predictions highlighting a universal behavior. Interestingly, the proposed model can be extended to other actuation strategies such as solute Marangoni effects. The addition of surfactants was found to induce transient effects and smooth contact line recession that are important for reducing the final deposit size. This study paves the way for fine control of the final deposit size and density which are crucial parameters for future applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Antoine Aubret, Hamid Kellay, Jean-Christophe Delagnes, Marie Adier, David Babonneau, Sophie Camelio for very helpful discussions. N.-A. Goy thanks the EUR Light S&T Graduate Program of the University of Bordeaux. The authors thank the Region Nouvelle Aquitaine (project 2018-1R10221) for financial funding and the LOMA machine and electronic shop for their technical contributions in this work.Notes and references
- R. G. Larson, Angew. Chem., Int. Ed., 2012, 51, 2546–2548 CrossRef CAS PubMed.
- K. Sefiane, Adv. Colloid Interface Sci., 2014, 206, 372–381 CrossRef CAS PubMed.
- D. Mampallil and H. B. Eral, Adv. Colloid Interface Sci., 2018, 252, 38–54 CrossRef CAS PubMed.
- T.-S. Wong, T.-H. Chen, X. Shen and C.-M. Ho, Anal. Chem., 2011, 83, 1871–1873 CrossRef CAS PubMed.
- D. Brutin and V. Starov, Chem. Soc. Rev., 2018, 47, 558–585 RSC.
- J.-M. Meijer, F. Hagemans, L. Rossi, D. V. Byelov, S. I. Castillo, A. Snigirev, I. Snigireva, A. P. Philipse and A. V. Petukhov, Langmuir, 2012, 28, 7631–7638 CrossRef CAS PubMed.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827–829 CrossRef CAS.
- C. J. Brinker, Y. Lu, A. Sellinger and H. Fan, Adv. Mater., 1999, 11, 579–585 CrossRef CAS.
- R. G. Larson, AIChE J., 2014, 60, 1538–1571 CrossRef CAS.
- H. Hu and R. G. Larson, J. Phys. Chem. B, 2002, 106, 1334–1344 CrossRef CAS.
- D. J. Harris, H. Hu, J. C. Conrad and J. A. Lewis, Phys. Rev. Lett., 2007, 98, 148301 CrossRef PubMed.
- H. B. Eral, D. M. Augustine, M. H. Duits and F. Mugele, Soft Matter, 2011, 7, 4954–4958 RSC.
- M. R. Bittermann, D. Bonn, S. Woutersen and A. Deblais, Soft Matter, 2021, 17, 6536–6541 RSC.
- S. J. Kim, K. H. Kang, J.-G. Lee, I. S. Kang and B. J. Yoon, Anal. Chem., 2006, 78, 5192–5197 CrossRef CAS PubMed.
- D. Mampallil, J. Reboud, R. Wilson, D. Wylie, D. R. Klug and J. M. Cooper, Soft Matter, 2015, 11, 7207–7213 RSC.
- H. Hu and R. G. Larson, J. Phys. Chem. B, 2006, 110, 7090–7094 CrossRef CAS PubMed.
- T. Still, P. J. Yunker and A. G. Yodh, Langmuir, 2012, 28, 4984–4988 CrossRef CAS PubMed.
- T. H. Kim, E. Kommer, S. Dessiatoun and J. Kim, Int. J. Multiphase Flow, 2012, 40, 56–67 CrossRef CAS.
- R. Malinowski, G. Volpe, I. P. Parkin and G. Volpe, J. Phys. Chem. Lett., 2018, 9, 659–664 CrossRef CAS PubMed.
- J. Pyeon and H. Kim, Soft Matter, 2021, 17, 3578–3585 RSC.
- Y. Li, C. Lv, Z. Li, D. Quéré and Q. Zheng, Soft Matter, 2015, 11, 4669–4673 RSC.
- S. N. Varanakkottu, M. Anyfantakis, M. Morel, S. Rudiuk and D. Baigl, Nano Lett., 2015, 16, 644–650 CrossRef PubMed.
- J. A. Vieyra Salas, J. M. van der Veen, J. J. Michels and A. A. Darhuber, J. Phys. Chem. C, 2012, 116, 12038–12047 CrossRef CAS.
- V. Ta, R. Carter, E. Esenturk, C. Connaughton, T. Wasley, J. Li, R. Kay, J. Stringer, P. Smith and J. Shephard, Soft Matter, 2016, 12, 4530–4536 RSC.
- C. Farzeena and S. N. Varanakkottu, Langmuir, 2022, 38, 2003–2013 CrossRef CAS PubMed.
- M. Anyfantakis, S. N. Varanakkottu, S. Rudiuk, M. Morel and D. Baigl, ACS Appl. Mater. Interfaces, 2017, 9, 37435–37445 CrossRef CAS PubMed.
- D. Ross, M. Gaitan and L. E. Locascio, Anal. Chem., 2001, 73, 4117–4123 CrossRef CAS PubMed.
- J. Sakakibara and R. J. Adrian, Exp. Fluids, 1999, 26, 7–15 CrossRef CAS.
- D. Rivière, B. Selva, H. Chraibi, U. Delabre and J.-P. Delville, Phys. Rev. E, 2016, 93, 023112 CrossRef PubMed.
- D. Brutin, B. Sobac, F. Rigollet and C. Le Niliot, Exp. Therm. Fluid Sci., 2011, 35, 521–530 CrossRef CAS.
- X. Zhong and F. Duan, Sci. Rep., 2017, 7, 1–9 CrossRef PubMed.
- E. Y. Gatapova, A. M. Shonina, A. I. Safonov, V. S. Sulyaeva and O. A. Kabov, Soft Matter, 2018, 14, 1811–1821 RSC.
- X. Man and M. Doi, Phys. Rev. Lett., 2016, 116, 066101 CrossRef PubMed.
- J. Freed-Brown, Soft Matter, 2014, 10, 9506–9510 RSC.
- M. F. Schatz, S. J. VanHook, W. D. McCormick, J. Swift and H. L. Swinney, Phys. Rev. Lett., 1995, 75, 1938 CrossRef CAS PubMed.
- M. L. Cordero, E. Verneuil, F. Gallaire and C. N. Baroud, Phys. Rev. E, 2009, 79, 011201 CrossRef PubMed.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Phys. Rev. E, 2000, 62, 756 CrossRef CAS PubMed.
- T. M. Yen, X. Fu, T. Wei, R. U. Nayak, Y. Shi and Y.-H. Lo, Sci. Rep., 2018, 8, 3157 CrossRef PubMed.
- H. Hu and R. G. Larson, Langmuir, 2005, 21, 3963–3971 CrossRef CAS PubMed.
- E. Guyon, J.-P. Hulin, L. Petit, C. D. Mitescuet al., Physical hydrodynamics, Oxford University Press, 2001 Search PubMed.
- H. Hu and R. G. Larson, Langmuir, 2005, 21, 3972–3980 CrossRef CAS PubMed.
- C. B. Mast and D. Braun, Phys. Rev. Lett., 2010, 104, 188102 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01019d |
| This journal is © The Royal Society of Chemistry 2022 |