Open Access Article
Open Access ArticleControlling the anisotropic self-assembly of polybutadiene-grafted silica nanoparticles by tuning three-body interaction forces†
Barbara
Di Credico
 *a,
Gerardo
Odriozola
*a,
Gerardo
Odriozola
 b,
Simone
Mascotto
b,
Simone
Mascotto
 c,
Andreas
Meyer
d,
Laura
Tripaldi
a and
Arturo
Moncho-Jordá
c,
Andreas
Meyer
d,
Laura
Tripaldi
a and
Arturo
Moncho-Jordá
 *ef
*ef
aDepartment of Materials Science, INSTM, University of Milano-Bicocca, Via R. Cozzi, 55, 20125 Milano, Italy. E-mail: barbara.dicredico@unimib.it; Tel: +39-02-64485189
bÁrea de Física de Procesos Irreversibles, División de Ciencias Básicas e Ingeniería, Universidad Autónoma Metropolitana-Azcapotzalco, Av. San Pablo 180, 02200 Ciudad de México, Mexico
cInstitut für Anorganische und Angewandte Chemie, Universität Hamburg, Martin-Luther-King-Platz 6, 20146 Hamburg, Germany
dInstitut für Physikalische Chemie, Universität Hamburg, Grindelallee 117, 20146 Hamburg, Germany
eInstitute Carlos I for Theoretical and Computational Physics, Facultad de Ciencias, Universidad de Granada, Campus Fuentenueva S/N, 18071, Granada, Spain. E-mail: moncho@ugr.es
fDepartamento de Física Aplicada, Universidad de Granada, Campus Fuentenueva S/N, 18071 Granada, Spain
First published on 4th October 2022
Abstract
Recently, the significant improvements in polymer composites properties have been mainly attributed to the ability of filler nanoparticles (NPs) to self-assemble into highly anisotropic self-assembled structures. In this work, we investigate the self-assembly of core–shell NPs composed of a silica core grafted with polybutadiene (PB) chains, generating the so-called “hairy” NPs (HNPs), immersed in tetrahydrofuran solvent. While uncoated silica beads aggregate forming uniform compact structures, the presence of a PB shell affects the silica NPs organization to the point that by increasing the polymer density at the corona, they tend to self-assemble into linear chain-like structures. To reproduce the experimental observations, we propose a theoretical model for the two-body that considers the van der Waals attractive energy together with the polymer-induced repulsive steric contribution and includes an additional three-body interaction term. This term arises due to the anisotropic distribution of PB, which increases their concentration near the NPs contact region. The resulting steric repulsion experienced by a third NP approaching the dimer prevents its binding close to the dimer bond and favors the growth of chain-like structures. We find good agreement between the simulated and experimental self-assembled superstructures, confirming that this three-body steric repulsion plays a key role in determining the cluster morphology of these core–shell NPs. The model also shows that further increasing the grafting density leads to low-density gel-like open structures.
1 Introduction
Self-assembly is the process by which disordered building blocks, such as atoms, molecules, or nanoparticles (NPs), spontaneously organize into a macroscopic structure with a higher level of structural complexity,1 giving rise to novel morphological organizations with collective new properties which can differentiate completely from that of a single NP. In recent years, many different synthetic and functionalization methods have been developed for the preparation of a variety of building blocks, engineering their structure and symmetry for the desired organization. NPs of different dimensions, shapes (rods, wires, rings, ellipsoids, cubes, triangular prisms), composition (core–shell), and surface chemistry have been prepared,2–4 creating the foundations for different studies on their respective.5–8In principle, by controlling the NPs interactions, it could be possible to obtain different assemblies.9,10 Indeed, different studies have focused on mapping the force fields around them and predict the self-assembled structures by computer simulation.11–13 In all these cases, an important requirement for the self-assembly is the NPs mobility: colloidal NPs can organize spontaneously in a colloidal suspension,14 at interfaces,15 on smooth surfaces,16 or on a substrate during the evaporation of the solvent.17 A possibility to control self-assembly of inorganic NPs is to graft polymers onto their surfaces, generating the so-called “hairy” NPs (HNPs), which naturally combine the unique features of both inorganic NP cores and tethered polymers. It is well demonstrated that HNPs can assemble in a variety of higher-order structures, like sheets, vesicles and percolating clusters, as either one-component systems, namely matrix-free HNPs,18,19 and in macromolecular matrices producing polymer nanocomposites.20,21 Since NPs spatial dispersion and organization affect the macroscale materials properties (e.g. mechanical reinforcement, thermal conduction, and selective permeation of gases), HNPs can be considered promising building blocks for the synthesis of advanced materials for several technological applications, such as tire and rubber industry, catalysis, nanomedicine, coatings, and water treatment.22–25
The HNPs organization on shaped-controlled superstructures depends on several parameters such as particle dimension, morphology, surface chemistry, polymer type, grafting density, molecular weight (Mw),11 and even on the grafting mechanism employees to create the polymer-grafted NP.26 The theoretical and simulation methods offer an effective way to study the self-assembly behavior of HNPs at the molecular level and investigate how the HNPs morphologies depend on the ligand grafting density, chain length, etc.1–6,11,27–32
Recently, the preparation and characterization of SiO2 HNPs were reported, having polybutadiene (PB) chains as polymeric brushes, which are rarely used with respect to polymer brushes with higher glass transition temperatures, such as polystyrene or polymethacrylate. These PB-silica core–shell particles are able to organize in anisotropic superstructures in a matrix-free system,33 which suggests that the PB coating, having a mushroom regime, induces a modification of NP–NP interactions. The self-assembly capability of these SiO2-HNPs was also studied by introducing HNPs in a homopolymer PB matrix. The resulting nanocomposite films exhibited the packing of particles, which self-organize in “string-like” superstructures, confirming the tendency of SiO2-HNPs to create complex arrangements, driven by a delicate balance of non-covalent attractive and repulsive intermolecular interactions.
In this scenario, the present work aims to more-in depth investigate the PB-grafted SiO2-HNPs spatial organization when dispersed in tetrahydrofuran solvent (THF) thanks to a combination of experiments, theoretical calculations, and coarse-grained computer simulations. To our knowledge, no theoretical study has been performed so far considering effective three-body contributions to the self-assembly of PB-grafted SiO2 HNPs. Here, we introduce a model for particle–particle interactions based on the superposition of three contributions (van der Waals attraction, mixing, and elastic repulsion), and discuss the necessity of including an orientation-dependent three-body repulsive interaction in order to account for the increase of PB polymer density when approaching three SiO2-HNPs together, as suggested in previous theoretical and simulation studies.11,31 Simulation results confirm that the self-assembled structures observed in the experiments are indeed caused by the existence of a repulsive three-body interaction that promotes the formation of nonisotropic structures. The present study is relevant in highlighting how the attractive and repulsive intermolecular interactions affect the self-assembly of HNPs and determining the formation of isotropic or anisotropic superstructures on the bases of specific core–shell particle parameters.
This article is organized as follows. Section 2 reports the experimental procedures to synthesize the PB-grafted SiO2 HNPs, and describes the morphological and structural characterization performed by thermogravimetric analysis (TGA), small-angle X-ray scattering (SAXS) analysis and transmission electron microscopy (TEM) images of bare SiO2 NPs and PB-functionalized SiO2 HNPs. The theoretical model for the two-body and three-body interparticle interaction potential between hairy silica spheres is described in Section 3. The replica-exchange Monte Carlo computer simulation method used to investigate the particle self-assembly is described in Section 4. Finally, in Sections 5 and 6, we compare the experimental and simulated self-assembled structures, discuss the results and summarize the key findings.
2 Experimental section
2.1 Materials
Tetraethyl orthosilicate (TEOS, ≥99%), 25% aqueous ammonia solution, and 3-aminopropyltriethoxysilane (APTES, ≥98%) were purchased from Sigma-Aldrich. Ethanol (EtOH) (≥99.8%) was purchased from Honeywell, and toluene (99%) from Alfa-Aesar. Liquid maleated polybutadiene (Polyvest MA75, Mw ∼ 3000 g mol−1, PB) was purchased from Evonik. Tetrahydrofuran (anhydrous, ≥99.9%, with 250 ppm butylated hydroxytoluene as inhibitor) was purchased from Sigma-Aldrich and used without further purification.2.2 Samples preparation
Bare SiO2 NPs and PB-grafted SiO2 HNPs were prepared according to the procedure reported elsewhere.33 Briefly, 31 mL of an aqueous solution of ammonium hydroxide (25 wt%) and 625 mL of EtOH were added to a 1000 mL two-necked flask equipped with a reflux condenser. The mixture was stirred at 300 rounds per minute (rpm) and heated at 60 °C. A mixture of 15 mL of TEOS and 17 mL of EtOH was then transferred to a dropping funnel and added dropwise in ∼30 min. The mixture was then left to react under magnetic stirring for 20 h. Afterward, the NPs were centrifuged, washed twice with 240 mL of EtOH, and redispersed in 60 mL of EtOH by ultrasonication. The bare NPs, obtained by a modified Stöber synthesis, were labeled SiO2-ST.The suspension of SiO2-ST in EtOH was heated at reflux under stirring at 300 rpm. Then, 25 μL of 25 wt% of ammonia solution and 0.4 mL of APTES were added and the mixture was stirred at 80 °C for 24 h. The particles were then recovered by centrifugation at 9000 rpm and washed three times with 240 ml of toluene. The product was centrifuged and washed twice with 180 mL of toluene and redispersed in 60 mL of toluene. The SiO2-ST functionalized with APTES were labelled SiO2-APTES.
Finally, PB polymer (three different amounts: 0.234, 0.468, or 0.936 g), was dissolved in 5–10 mL of toluene. The SiO2-APTES dispersion in toluene and the PB mixture were refluxed under stirring at 300 rpm for 24 h. The SiO2 HNPs were obtained after drying at 85 °C under vacuum overnight. The HNPs were labeled SiO2-HNP_X, where X = 5, 8, 11 is the weight percentage of PB polymer coating. SiO2-HNP_X samples were dispersed in THF due to the high solubility of PB and good dispersion of both bare and functionalized SiO2.
2.3 Morphological, structural, and spectroscopic characterization
The polymer density and thickness of the external shell are mainly responsible for the stability and self-assembly behavior.20,33,34 Using TGA (details on method are reported in ESI†), we determined the surface density of grafted PB chains (σPB) of SiO2-ST, SiO2-APTES and SiO2-HNP_X. TGA curves of SiO2-HNP_X (Fig. S1 in ESI†) clearly show the effective functionalization of SiO2-ST NPs with increasing amounts of PB coating. To determine σPB, the weight loss obtained from TGA needs to be divided into different contributions, as shown in eqn (1). This calculation considers the loss of three surface silanols for each APTES molecule, assuming that APTES is anchored onto the SiO2 surface with all its three ethoxysilane groups. | (1) |
 is the TGA weight loss between 150 and 1000 °C, wt%OH-OEt is the weight percentage of silanol and ethoxy groups obtained from the TGA weight loss of bare SiO2-ST, wt%APTES is the APTES weight percentage, MwAPTES is the molecular weight of APTES after functionalization, MwH2O is the molecular weight of water, and wt%PB is the weight percentage of PB.
is the TGA weight loss between 150 and 1000 °C, wt%OH-OEt is the weight percentage of silanol and ethoxy groups obtained from the TGA weight loss of bare SiO2-ST, wt%APTES is the APTES weight percentage, MwAPTES is the molecular weight of APTES after functionalization, MwH2O is the molecular weight of water, and wt%PB is the weight percentage of PB.
Once the wt% of PB was determined, the grafting density for HNPs was obtained by considering the SiO2 NPs specific surface area (SSA) (273 m2 g−1) obtained from BET analysis,33 as shown in eqn (2).
 | (2) |
The degree of APTES functionalization obtained by TGA is 1.58 wt%. The resulting values of functionalization percentage and grafting density for SiO2-HNP_X are reported in Table 1.
| Sample | PB shell (wt%) | σ PB (chains per nm−2) | a (nm) | δ (nm) | St. dev. (%) |
|---|---|---|---|---|---|
| SiO2-ST | 0 | 0 | 13.5 | 0 | 11.3 |
| SiO2-HNP_5 | 4.54 | 0.03 | 16.1 | 2.6 | 12.8 |
| SiO2-HNP_8 | 7.57 | 0.05 | 16.6 | 3.1 | 14.0 |
| SiO2-HNP_11 | 11.0 | 0.08 | 16.7 | 3.2 | 14.1 |
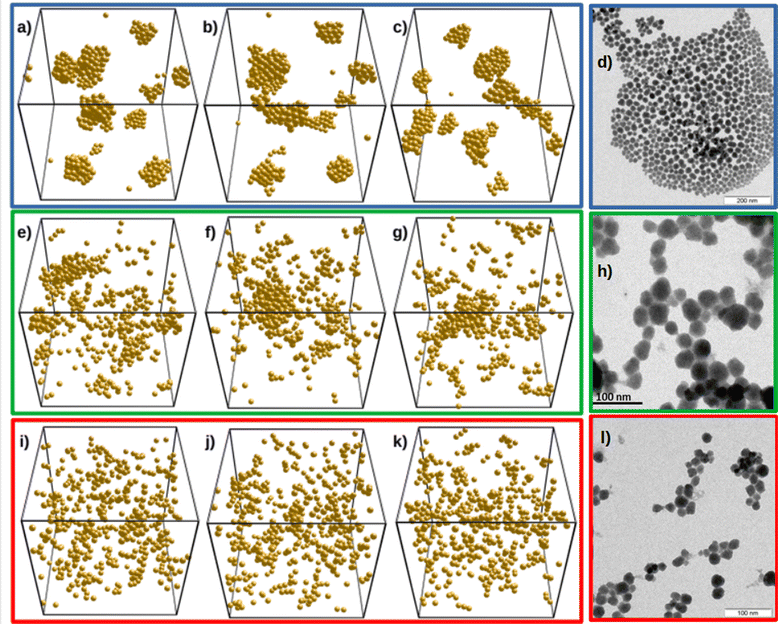
The morphology of NPs samples and the resulting self-assembled structures were investigated by TEM analysis. Regarding the sample preparation, the material was ground into a fine powder and suspended in toluene by sonication. Finally, the suspension was dropped onto a carbon-coated 400-mesh TEM grid and the solvent in excess removed by drying under air. The reported TEM images are explicative and representative examples of at least six different analyses. Representative TEM micrographs are depicted in Fig. 1. SiO2-ST (Fig. 1(a)) and SiO2-APTES (Fig. S4 in ESI†) present uniform spherical shapes and diameter of about 20–25 nm. They aggregate forming compact close-packing structures NPs.
Conversely, the packing of SiO2-HNP_X system is remarkably different. Fig. 1(b), (c) and (d) show representative TEM images of the resulting structures formed by the systems SiO2-HNP_5, SiO2-HNP_8, and SiO2-HNP_11, respectively. As observed, the shape of the polymer-coated NPs is not perfectly spherical, and instead, they resemble a slighltly ellipsoidal inhomogeneous morphology as a result of the polymer grafting. The NPs tend to spontaneously self-organize in nonisotropic structures by increasing the concentration of grafted polymer. Indeed, TEM micrographs of SiO2-HNP_5 and SiO2-HNP_8 show a lesser tendency to form linear arrangements. For the case of SiO2-HNP_11, string-like aggregates are observed. In addition, we observed that aggregation rates decrease with increasing σPB. The inhomogeneous nanoparticles arrange independently from their aspect ratio, showing that their light anisotropy is likely not affecting the assembly mechanism. Therefore, this suggest the existence of a different interaction between NPs when the particle surfaces are functionalized with PB polymer chains. Anisotropic self-organization, originally observed in homopolymer matrices,11,20 depends on polymer PB grafting density and has been predicted to take place also in solvent-free and matrix-free conditions.18,19,35 Additional TEM snapshots of the NPs samples may be found in the ESI† (Fig. S3–S7).
Finally, SAXS measurements provide structural and morphological information about the HNPs in solution, such as core size and polymer shell thickness. For SAXS, the functionalized NPs present a three-phase system made of a silica core, organic shell, and the surrounding voids. As in general, the SAXS analysis proceeds with the assumption of a two-phase system with uniform electron density, the functionalized material could not be precisely analyzed.36,37 However, as the scattering difference between SiO2 and the polymer is minimal with respect to the contrast with the voids (ρC = 15.31 × 10−6 Å−2, ρSiO2 = 18.89 × 10−6 Å−2),38 we considered for the following analysis the functionalized NPs as a single-phase body, the two-phase system formed by hybrid NPs and surroundings voids. The analysis and fitting of the SAXS data were performed by using the software Scatter (ver. 2.5).39,40 The curves were modeled by combining a spherical form factor with a fcc structure factor component, originated by the NPs aggregation. More details about the SAXS measurements provided in the ESI.†
SAXS curves of SiO2-ST and SiO2-HNP_X suspensions in THF are reported in Fig. S2 in the ESI.† All samples show the typical form factor oscillation of spherical NPs. SiO2-ST sample presents the sharpest pattern, which indicates the higher size and shape homogeneity. Upon functionalization (SiO2-HNP_5 to SiO2-HNP_11), we observe a shift of the first minimum of the curve towards lower q values along with a sensitive decrease in the number of oscillations. As expected, this indicates an increase in the particle size and a higher shape inhomogeneity, respectively. More precise information on the NPs morphology variation is obtained by fitting the SAXS curves (Table 1).
The particle radius (a) as well as the standard deviation increase by approx. 20% as the surface coverage is increased, because of the BP polymer shell on the functionalized materials. The values confirm the experimental data from the TEM analysis. Interestingly, the radius of the SiO2-HNPs increases more rapidly and looks independent from the grafting degree, suggesting that the surface rapidly saturates.
The thickness δ of the polymer shell in THF, required for the theoretical calculations, was obtained by subtracting the radius of bare SiO2-ST from the radius of SiO2-HNP_X. From these data, the value of δ goes from 2.6 nm for the SiO2-HNP_5 sample to 3.2 nm for the SiO2-HNP_11 one, which implies an enlargement of 23% of the PB polymer shell induced by the increase of its surface coverage.
3 Theoretical approach
The theoretical description of the observed self-assembled structures must start considering the following features of the real experimental system. First, pristine SiO2-ST aggregate forming compact clusters of particles. Second, SiO2-HNPs are uncharged in THF solvent. Finally, when the particles are covered with PB chains, SiO2-HNP_X tend to self-assemble to form anisotropic (more elongated) structures by increasing the concentration of grafted PB polymer.Based on the state of the art, the possible explanations for the self-assembly behavior of HNPs, shown by TEM and SAXS analyses, could be multiple: (i) the grafted chains are not uniformly distributed. That is, the grafted chains are concentrated in spots or patches. This kind of non-uniform distribution of polymer coils will lead to the formation of asymmetric structures due to directional interactions. However, in our case, the experimental results show that the particle coverage is uniform in all cases, so chain-like superstructuring cannot be justified in this way. (ii) The particles possess anisotropic shapes. However, we just showed in the experimental section that the NPs self-assemble independently from their aspect ratio, so their small anisotropy does not have any significant effect on the assembly mechanism. (iii) The existence of flow or other non-equilibrium effects. However, HNPs assemblies are formed in equilibrium conditions (static self-assembly). (iv) The surface coverage is uniform, but the particle interactions are affected by three-body contributions. This is the case of SiO2 HNPs.
Indeed, previous computer simulations and experiments of spherical NPs uniformly grafted with polymer chains have recently been shown to assemble into anisotropic phases like strings and sheets.11,20,29,31,32 The resulting three-body contribution is found to be highly repulsive and anisotropic, with the degree of repulsion rising with increasing angular deviation from the dimer axis, which can be explained in terms of free energy. Indeed, the free energy is determined by a competition between a favorable enthalpic energy gained by forming contacts between HNPs and an entropic cost associated with compressing the polymer grafts to create such contacts. When two particles covered by long polymer brushes bind, the polymer chains redistribute, resulting in an increase of polymer concentration close to the contact region. This density increase makes a dimer more hindered against binding with another particle than a monomer, being more likely to aggregate with another particle at the points diametrically opposite to its bond.
We can visualize the three-body anisotropic contribution with the help of the illustration shown in Fig. 2. It depicts a dimer formed by the binding of two HNPs. When the dimer is created, the enthalpic (attractive) energy must overcome the entropic and elastic repulsion exerted by the compressed polymer shells in the region between the particles, where both polymer shells overlap. The resulting dimer has a region where polymer concentration is larger (dark gray area). If a third particle approaches the dimer following path A, it will experience an enhanced steric repulsion induced by the already compressed polymer layers of the dimer. This repulsion goes beyond the pairwise additive interaction picture, as it involves a three-body contribution. However, if the third HNP tries to bind through path B, the three-body repulsion will be negligible. Therefore, this mechanism favors the assembly of HNPs into linear structures, such as chains.
3.1 Two and three-body interaction potentials
We now discuss a simplified coarse-grained model for particle interactions between HNPs. If the system has N particles, the total interaction potential up to third order contribution is given by eqn (3): | (3) |
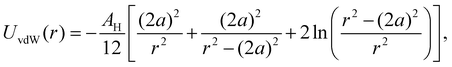 | (4) |
 , where A22 is the Hamaker constant of silica in vacuum, given by A22 = 8.53 × 10−20 J.41A11 can be determined from42A11 = γLW24πl02, where γLW is the surface tension of THF, given by γLW = 27.4 mJ m−2, and l0 = 1.57 × 10−10 m, which leads to A11 = 5.095 × 10−20 J.42 Therefore, the value of the Hamaker constant of SiO2 in THF is AH = 4.41 × 10−21 J. Normalizing by the thermal energy (kBT, with T = 298 K), we find AH/(kBT) = 1.07.
, where A22 is the Hamaker constant of silica in vacuum, given by A22 = 8.53 × 10−20 J.41A11 can be determined from42A11 = γLW24πl02, where γLW is the surface tension of THF, given by γLW = 27.4 mJ m−2, and l0 = 1.57 × 10−10 m, which leads to A11 = 5.095 × 10−20 J.42 Therefore, the value of the Hamaker constant of SiO2 in THF is AH = 4.41 × 10−21 J. Normalizing by the thermal energy (kBT, with T = 298 K), we find AH/(kBT) = 1.07.
The van der Waals force is attractive and reaches the minimum value AvdW = −10.34 times the thermal energy. In order to quantify the total amount of attraction, we calculate the normalized second virial coefficient of this pair potential, defined as
 | (5) |
 , the attraction is strong enough to phase separate the system in stable aggregates. In our particular case, the van der Waals attraction leads to
, the attraction is strong enough to phase separate the system in stable aggregates. In our particular case, the van der Waals attraction leads to  , which implies a large amount of attraction that is able to join together particles into clusters by an irreversible aggregation process. It is important to remark that the van der Waals attraction is a very short-ranged interaction. Indeed, the SiO2-ST NPs will only feel mutual attraction when they are very close to contact.
, which implies a large amount of attraction that is able to join together particles into clusters by an irreversible aggregation process. It is important to remark that the van der Waals attraction is a very short-ranged interaction. Indeed, the SiO2-ST NPs will only feel mutual attraction when they are very close to contact.
At the initial stage, individual particles aggregate to form dimers. When a third particle gets close to the dimer, it will naturally tend to aggregate in the region nearby both particles because the total attraction is larger due to the addition of the pairwise additive interaction of the third particle with the particles of the dimer. Consequently, the particles tend to form a compact and isotropic trimer. With the subsequent binding of more colloids, this effect is expected to lead to the formation of compact isotropic aggregates, very similar to the ones observed in Fig. 1(a) for ungrafted SiO2-ST and SiO2-APTES NPs.
Hence, the total particle–particle interaction potential is given by the sum of three contributions, that is
| U2(r) = UvdW(r) + Umix(r) + Uelas(r). | (6) |
 | (7) |
 | (8) |
 | (9) |
 | (10) |
Fig. 3(a) shows the total interaction pair potential between two SiO2-HNPs together with the three contributions (mixing, elastic, and van der Waals), calculated for a surface coverage of polymer of σPB = 0.05 chains per nm2. As observed, the steric repulsion exerted by the polymer shell reduces the range and strength of the particle–particle attraction. In particular, the normalized second virial coefficient for these cases is given by  . Even though this attraction is weaker than the one obtained for uncoated SiO2-ST NPs, it is still strong enough to induce the formation of stable clusters. The total pair interaction potentials, U2, for different values of the surface coverage, are shown in Fig. 3(b). The corresponding
. Even though this attraction is weaker than the one obtained for uncoated SiO2-ST NPs, it is still strong enough to induce the formation of stable clusters. The total pair interaction potentials, U2, for different values of the surface coverage, are shown in Fig. 3(b). The corresponding  values for each sample are shown in Table 2. Increasing the σPB, the enhanced repulsion induced by the elastic and mixing term leads to a reduction of the net attraction. We emphasize again that, in all cases, the total pair potential has a very short interaction range compared to the particle size. For the largest studied surface coverage (system SiO2-HNP_11, σPB = 0.08 chains per nm2), the resulting pair potential is still attractive, but with less attraction strength (
values for each sample are shown in Table 2. Increasing the σPB, the enhanced repulsion induced by the elastic and mixing term leads to a reduction of the net attraction. We emphasize again that, in all cases, the total pair potential has a very short interaction range compared to the particle size. For the largest studied surface coverage (system SiO2-HNP_11, σPB = 0.08 chains per nm2), the resulting pair potential is still attractive, but with less attraction strength (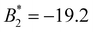 ).
).
 (see Section 3). Forth and fifth columns depict the values of ε and Δ used in the Monte Carlo simulations, obtained from the theoretical predicted pair potential using eqn (15) and (16), assuming rc = 2.2a
(see Section 3). Forth and fifth columns depict the values of ε and Δ used in the Monte Carlo simulations, obtained from the theoretical predicted pair potential using eqn (15) and (16), assuming rc = 2.2a
Once the pairwise interaction has been described, we need to introduce the additional three-body steric repulsion of HNPs. As mentioned before, this three-body term represents the extra repulsion exerted by the anisotropic distribution of polymer grafted chains that occurs when two HNPs come into close contact due to the increase in polymer concentration near the contact region of both particles. This effect, already suggested by Tang and Arya,31 causes an anisotropic steric repulsive interaction experienced by a third approaching NP, so that it has a larger binding probability at the two poles on the longitudinal axis of the dimer, thus enhancing the formation of string-like structures. Therefore, this three-body term depends on the trajectory direction of the third particle with respect to the axis of the dimer. We define θ as the angle subtended by the line connecting the centers of two SiO2-HNPs forming a dimer with the line connecting the position of the third particle, as shown in Fig. 4.
 | ||
| Fig. 4 Top: Three different positions of the third particle forming the trimer. Bottom: Angular dependence of the three-body interaction term as a function of exponent n (see eqn (11)). | ||
In order to include the three-body repulsive interaction, we propose the following simplified expression:
 | (11) |
In the next section, we describe the computer simulation method and present the results, comparing them with the experimental data reported in Section 2. The experiments were performed at a mass fraction of silica particles of 5%. Knowing that the density of amorphous silica is 2.2 g cm−3 and the density of THF is 0.889 g cm−3, we found that the corresponding volume fraction of silica particles is ϕpart = 0.0208.
4 Simulations
The replica-exchange Monte Carlo (REMC) method45–47 was employed to obtain equilibrium configurations of our system as a function of the reduced temperature, T* = kBT/|ε|. It is custom within computer simulations to fix ε and vary T* instead, but it must be noted that it produces the same results. A single run considers M = 12 cubic simulation cells containing N = 500 particles, with a fixed volume V so that the volume fraction of particles correspond to the experimental one, i.e. ϕpart = (4/3)πa3N/V = 0.0208. The method sets different temperatures for each replica while considering swap trial moves. In other words, we perform 12 computer simulations at 12 different temperatures. In order to achieve the equilibrium between the 12 system copies at different temperatures, the simulation procedure swaps replicas among them. These trials allow the replicas to sample from an expanded ensemble defined by: | (12) |
| Pacc = min{1,e−(βi−βj)(Ui−Uj)}, | (13) |
We start all simulation cells from randomly dispersed configurations and apply periodic boundary conditions for all directions. Verlet lists are used to improve performance. In addition, we implemented a CUDA code where these neighbor lists are calculated by the GPUs, while the standard cores make the remaining calculations. Once the energy reaches a steady state, we proceed to capture some system snapshots. In this stage, we have only focused on this feature to try matching qualitatively the TEM images from the experimental system.
In order to simplify the simulations, we take advantage of the fact that the pair interactions (U2) have all a very short-range compared to the particle size since the attractive range does not extend more than 1 nm (see Fig. 3). Since in our particular case the assembly process do not depend on the specific details of the particle interaction, U2 can be represented by a simple square-well potential:
 | (14) |
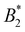 of the real U2 and the one obtained from the square-well approximation must be the same. The resulting value of ε is given by:
of the real U2 and the one obtained from the square-well approximation must be the same. The resulting value of ε is given by: | (15) |
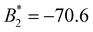 ) we find ε = −5.4. For PB-grafted SiO2-HNPs we obtain ε= − 5.2, − 4.7, and − 4.1 for σPB = 0.03 chains per nm2, 0.05 chains per nm2, and 0.08 chains per nm2, respectively (see Table 2).
) we find ε = −5.4. For PB-grafted SiO2-HNPs we obtain ε= − 5.2, − 4.7, and − 4.1 for σPB = 0.03 chains per nm2, 0.05 chains per nm2, and 0.08 chains per nm2, respectively (see Table 2).
To estimate Δ for each polymer surface coverage, it should be reminded that it represents a three-body repulsive energy term accounting for the enhanced polymer concentration near the contact region of the particles forming the dimer. The repulsive part of the pair potential, Umix(h) + Uelas(h) = Urep(h), depends on the polymer volume fraction of each particle, which we will denote by ϕ1 for particle 1 and ϕ2 for particle 2, i.e. Urep(h;ϕ1,ϕ2). The mixing term is proportional to ϕ1ϕ2, whereas the elastic one scales us (ϕ1ϕ2)1/2. For two isolated interacting NPs, we find ϕ1 = ϕ2 = ϕ. However, if we consider the interaction between a third NP (with polymer volume fraction ϕ1 = ϕ) and an already formed dimer, then the polymer volume fraction that the third particle experiences is ϕ2 = 2ϕ close to the contact region of the dimer due to the overlap of the hairy shells. The value of Δ corresponds to the additional energy required to approach the third particle to the contact region of the dimer, that is
| Δ = 2(Urep(h = 0;ϕ,2ϕ) − Urep(h = 0;ϕ,ϕ)). | (16) |
5 Simulation snapshots vs. TEM images
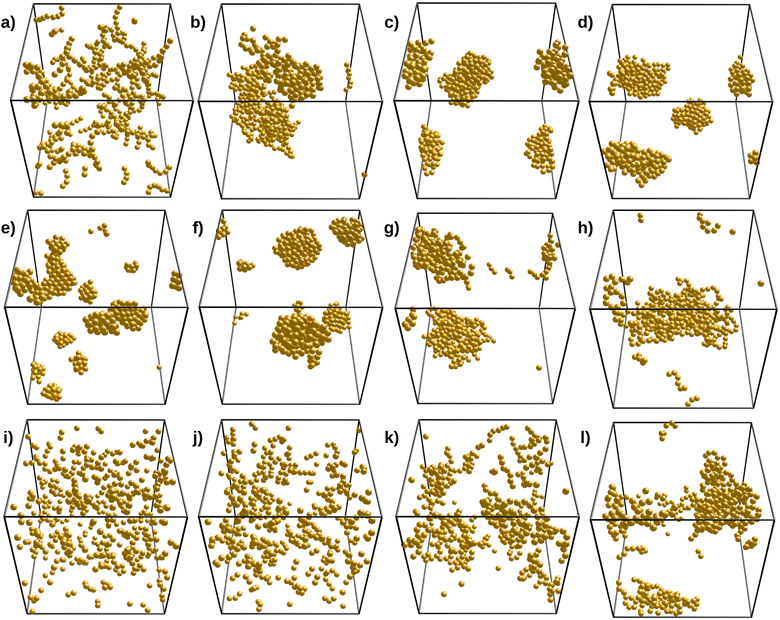
To explore the system behavior, the ε (or T*) values were first varied in the range −3 to −10 and the cutoff distance was set to rc = 2.2a. We define Δ/|ε| in the range 0 to 2.0 and n in the range 2 to 8. Δ/|ε| represents the strength of the three-body energy repulsion compared to the van der Waals attraction for grafted silica particles at θ = 60°. In addition, n controls the angular decay of the three-body repulsion.Fig. 5 explores the effect of Δ, n, and ε on the structure of the final simulated clusters. The influence of n is shown in panels (a)–(d) for Δ/|ε| = 1.2 and ε = −10. As shown, values of n above 4 lead to compact structures, whereas n below 4 yields open and fractal-like structures. Indeed, for n = 2, the three-body repulsion extends over angles of about 120°, promoting the formation of linear chains with a few brunches that make the system percolate. On the other hand, structures for n = 8 are more compact. However, these organized structures do not form fcc or hcp-like crystallites (as they do in the absence of three-body interactions) since the three-body repulsion Δ/|ε| is above 1, thus preventing the formation of closed packed trimer arrangements. For Δ/|ε|<1, the three-body repulsion still makes the closed packed trimer arrangements energetically expensive, but this is compensated at some point by the fact that compact structures allow for higher coordination numbers. The Δ/|ε| value at which crystallites appear/disappear is expected to increase with n (by shortening the angular range of the three-body potential).
The effect of Δ/|ε| is depicted by the second row of Fig. 5 (panels (e)–(h)), for fixed values of ε and n. We have chosen n = 4 since we expect the three-body repulsion to contribute only for angles below 120° while having some relevant influence at 90°. In addition, we have not observed string-like chains with n above 4, with Δ/|ε|≤2, and thus, n > 4 cannot explain the string-like structures for a reasonable value of Δ/|ε|. As expected, the Δ = 0 case produces compact and crystallite-like assemblies as the three-body interaction is simply turned off. Note that hcp or fcc crystals are only possible in the absence of polydispersity and for perfectly spherical particles. Thus, we do not observe these structures in the TEM micrographs of naked SiO2-ST particles. In fact, with n = 4, Δ/|ε| = 0.2 is large enough to hinder the formation of crystal-like aggregates, as shown in panel (f), but aggregates are still compact. Large but reasonable values of Δ/|ε|, such as 1.4, yield chain-like structures like the ones observed in the experiments, as shown in panel (g) (see also panel (b) for n = 4 and = 1.2). We expect these 3D chains to further align into strings when confined to a quasi-2d space, as observed in the TEM micrographs. Further increasing Δ/|ε| yields more open structures, as shown in panel (h).
Finally, the third row of panels in Fig. 5 depicts the effect of ε by setting n = 4 and Δ/|ε| = 1.2. From the theoretical analysis, we found that these are reasonable values, capable of producing chain-like aggregates. A low ε value such as −3.3 leads to little aggregation for the volume fraction we are setting (ϕpart = 0.0208), as shown by panel (k). By decreasing ε to more negative values, we observe the growth of branched clusters, some of them having chain-like resemblance, but they turn a little more compact for lower ε values. We observed that ε values in the range from −7 to −5 produce the desired structures (panels (j) and (k)). Note that panel (c) of Fig. 5 shows the obtained structure for the same n = 4 and Δ/|ε| = 1.2 values, but for ε = −10. As compared to naked particles, Δ = 0, we need larger ε values to grow structures since they are now based on single bonds contrasting with the multiple bond-forming bare systems. Note that a central particle inside a crystallite can have up to 12 bonds when achieving an fcc or hcp structure, which strongly lowers the energy. Conversely, open clusters can have much fewer bonds. Hence, ε = −3.3 is not low enough to grow structures, and the system keeps outside the vapor–liquid (or solid) binodal. It is worth mentioning that increasing Δ has a smaller effect than decreasing n on the system structure because the assemblies already grow by avoiding the formation of bond angles lower than 90°.
With the guidance of the structures shown in Fig. 5 and the Δ and ε estimates found in the previous section, we build Fig. 6. This figure compares the experimental TEM images (right panels) with the structures from simulations (left panels). Here, the first row corresponds to bare SiO2-ST system. In this case Δ = 0 (i.e. no three-body repulsion) and ε = −5.4. The three different snapshots correspond to equilibrium. The value ε = −5.4 theoretically found produces the desired behavior. As already explained, differences between experiments and simulations arise because we considered a perfectly monodisperse system for simulations. It is well-known that attractive monodisperse systems crystallize at low temperatures, explaining the simulated crystal-like arrangements that contrast with the less ordered structures shown in panel (d).
The second and third rows of panels in Fig. 6 compare systems SiO2-HNP_5 and SiO2-HNP_11 with our simulations for Δ = 1.3 and ε = −4.8, and Δ = 3.1 and ε = −4.1 (estimated from the theoretical predictions), respectively. Again, all snapshots within a row correspond to equilibrium. In the second row of Fig. 6, panels (e)–(g) of the simulations should behave as SiO2-HNP_8, and in the third row, panels (i)–(k), as HNP_11. We observe a good resemblance between the TEM micrographs and the computer simulation snapshots, which supports our theoretical analysis. In particular, for the second row, we reproduce thick linear structures, in which the cross section of the chain is formed by more than one particle, in good agreement with the experimental results. Conversely, we find thinner linear chains in the third row of snapshots due to the strong three-body repulsion. These chain-like structures are very similar to the experimentally obtained linear assemblies formed for the largest polymer surface coverage. The simulation snapshots also show the existence of individual isolated HNPs that coexist with linear clusters, in accordance with the experimental observations (see Fig. 1(d)).
The experiments performed with SiO2-HNP_11 system indicate that the aggregation kinetics is slower than in the other cases, confirming that the two and three-body repulsion exerted by the polymer corona is most effective in reducing the net attraction between particles. Although we do not provide experiments for denser surface coverages, we expect to reach out full stabilization of the system for large enough σPB, in which the steric repulsion dominates over the van der Waals attraction.
Our simulations and experiments findings are consistent with previous coarse-grained computer simulation studies that explicitly consider the grafted polymers at the monomer level. In particular, Akcora et al.11 report the formation of compact spherical clusters for σ < 0.03 chains per nm2, sheets and chains for σ between 0.03 and 0.1 chains per nm2, and dispersed (non-aggregating) systems for σ > 0.1 chains per nm2, in accordance to our results. In addition, Tang and Arya31 show that the three-body contribution becomes highly repulsive and anisotropic, with the degree of repulsion rising with increasing angular deviation from the dimer axis.
Finally, it should be emphasized that TEM micrographs are two-dimensional systems obtained after solvent evaporation, whereas simulation snapshots depict the full three-dimensional structures. Therefore, the comparison between experiments and simulations is performed at the qualitative level. Despite this, the comparison clearly shows that increasing the surface coverage of grafted polymer leads to asymmetric chain-like structures that can only be explained in terms of the enhanced three-body interparticle repulsion.
6 Conclusions
In this work, we investigated the self-assembly of PB-grafted SiO2-HNPs dispersed in THF solvent for different surface coverages, from σPB = 0 to 0.08 chains per nm2. For this purpose, we combined experiments, theory, and replica-exchange computer simulations. We found that the systems are unstable for all surface coverages, and the morphology of the final structures depends on σPB. For uncoated silica beads, particles assemble into compact uniform aggregates. By increasing the surface coverage, the obtained structures adopt anisotropic chain-like morphologies in agreement with previous observations of similar core–shell systems. We link the anisotropy to the existence of a repulsive three-body contribution to the interaction potential, which arises from the exclusion of PB chains close to the contact region of binding HNPs. This effect gives rise to an anisotropic distribution of grafted polymer near the surface of binding HNPs, leading to an additional three-body repulsion that reaches the maximum intensity when the third particle touches the surfaces of both already linked HNPs.In order to reproduce these experimental self-assembled structures, we proposed a simple theoretical model that includes two and three-body interaction terms. For the former, we considered the interplay between the van der Waals attractive contribution and the polymer-induced repulsive steric interaction. For the second, we used a phenomenological potential that depends on the orientation θ as  , where Δ is the three-body repulsion strength (in kBT units) and n is an exponent that controls the decay of the repulsion with θ. In fact, Δ increases with the concentration of grafted polymers, whereas n decreases with the polymer length. We found good agreement between the simulated and the experimental self-assembled structures, thus confirming that this orientation-dependent three-body steric repulsion is the main responsible for the formation of chain-like assemblies of polymer-grafted silica NPs.
, where Δ is the three-body repulsion strength (in kBT units) and n is an exponent that controls the decay of the repulsion with θ. In fact, Δ increases with the concentration of grafted polymers, whereas n decreases with the polymer length. We found good agreement between the simulated and the experimental self-assembled structures, thus confirming that this orientation-dependent three-body steric repulsion is the main responsible for the formation of chain-like assemblies of polymer-grafted silica NPs.
Finally, it is worth mentioning that although particle anisotropy can indeed modify the 2 and 3-body interaction potentials between the polymer-coated SiO2 NPs, this effect in itself does not justify the existence of anisotropic self-assembled structures.
In future work, we would like to explore the role that the parameters involved in the three-body steric repulsion play on the vapor–liquid phase diagram. In particular, we believe it is possible to achieve reversible gels and empty liquids as occurs when dealing with low-valence colloids (patchy particles),48,49 anisotropic particles,50–52 anisotropic particles,53 and clays,54–56 which should arise for dense and thick polymer shells. Also, potential future studies will deal with the execution of in situ light or X-ray scattering methods in solution to thoroughly address the assembly mechanism of the hybrid NPs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was in the frame of the European Institute of Innovation and Technology – EIT Raw Materials Doctoral Programme. L. T. thanks CORIMAV (“Consortium for the Research of Advanced Materials between Pirelli and Milano Bicocca University) for its support within the PCAM European Doctoral Program. A. M.-J. acknowledge the financial support provided by the Junta de Andalucía and European Regional Development Fund – Consejería de Conocimiento, Investigación y Universidad, Junta de Andalucía (Projects PY20-00241, A-FQM-90-UGR20). G. O. and A. M.-J. acknowledge CONACyT (proyect A1-S-9197).Notes and references
- G. A. Ozin, K. Hou, B. V. Lotsch, L. Cademartiri, D. P. Puzzo, F. Scotognella, A. Ghadimi and J. Thomson, Mater. Today, 2009, 12, 12–23 CrossRef CAS.
- L. Tadiello, M. D’Arienzo, B. Di Credico, T. Hanel, L. Matejka, M. Mauri, F. Morazzoni, R. Simonutti, M. Spirkova and R. Scotti, Soft Matter, 2015, 11, 4022–4033 RSC.
- B. Di Credico, E. Cobani, E. Callone, L. Conzatti, D. Cristofori, M. DArienzo, S. Dirè, L. Giannini, T. Hanel, R. Scotti, P. Stagnaro, L. Tadiello and F. Morazzoni, Appl. Clay Sci., 2018, 152, 51–64 CrossRef CAS.
- R. Scotti, L. Conzatti, M. D’Arienzo, B. Di Credico, L. Giannini, T. Hanel, P. Stagnaro, A. Susanna, L. Tadiello and F. Morazzoni, Polymer, 2014, 55, 1497–1506 CrossRef CAS.
- I. Tagliaro, E. Cobani, E. Carignani, L. Conzatti, M. D’Arienzo, L. Giannini, F. Martini, F. Nardelli, R. Scotti, P. Stagnaro, L. Tadiello and B. Di Credico, Appl. Clay Sci., 2022, 218, 106383 CrossRef CAS.
- M. S. Lee, D. W. Yee, M. Ye and R. J. Macfarlane, J. Am. Chem. Soc., 2022, 144, 3330–3346 CrossRef CAS PubMed.
- Z. Xue, C. Yan and T. Wang, Adv. Funct. Mater., 2019, 29, 1807658 Search PubMed.
- N. R. Jana, Angew. Chem., Int. Ed., 2004, 43, 1536–1540 CrossRef CAS.
- K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600–1630 CrossRef CAS PubMed.
- D. Luo, C. Yan and T. Wang, Small, 2015, 11, 5984–6008 CrossRef CAS PubMed.
- P. Akcora, H. Liu, S. K. Kumar, J. Moll, Y. Li, B. C. Benicewicz, L. S. Schadler, D. Acehan, A. Z. Panagiotopoulos, V. Pryamitsyn, V. Ganesan, J. Ilavsky, P. Thiyagarajan, R. H. Colby and J. F. Douglas, Nat. Mater., 2009, 8, 354–359 CrossRef CAS PubMed.
- S. C. Glotzer, M. J. Solomon and N. A. Kotov, AIChE J., 2004, 50, 2978–2985 CrossRef CAS.
- Z. L. Zhang, Z. Y. Tang, N. A. Kotov and S. C. Glotzer, Nano Lett., 2007, 7, 1670–1675 CrossRef CAS.
- K. Zhao and T. G. Mason, Rep. Prog. Phys., 2018, 81, 126601 CrossRef CAS.
- A. Böker, J. He, T. Emrick and T. P. Russell, Soft Matter, 2007, 3, 1231–1248 RSC.
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- T. Ming, X. Kou, H. Chen, T. Wang, H.-L. Tam, K.-W. Cheah, J.-Y. Chen and J. Wang, Angew. Chem., Int. Ed., 2008, 47, 9685–9690 CrossRef CAS PubMed.
- N. J. Fernandes, H. Koerner, E. P. Giannelis and R. A. Vaia, MRS Commun., 2013, 3, 13–29 CrossRef CAS.
- A. Chremos and J. F. Douglas, Soft Matter, 2016, 12, 9527–9537 RSC.
- S. K. Kumar, N. Jouault, B. Benicewicz and T. Neely, Macromolecules, 2013, 46, 3199–3214 CrossRef CAS.
- C. Chevigny, F. Dalmas, E. Di Cola, D. Gigmes, D. Bertin, F. Boué and J. Jestin, Macromolecules, 2011, 44, 122–133 CrossRef CAS.
- X. Wang, V. J. Foltz, M. Rackaitis and G. G. Böhm, Polymer, 2008, 49, 5683–5691 CrossRef CAS.
- M. Elimelech and W. A. Phillip, Science, 2011, 333, 712–717 CAS.
- C. Yi, S. Zhang, K. T. Webb and Z. Nie, Acc. Chem. Res., 2017, 50, 12–21 CrossRef CAS.
- X. Chen, L. Zhang, B. Xu, T. Chen, L. Hu, W. Yao, M. Zhou and H. Xu, Nanoscale Adv., 2021, 3, 2879–2886 RSC.
- M. Asai, D. Zhao and S. K. Kumar, ACS Nano, 2017, 11, 7028–7035 CrossRef CAS PubMed.
- G. Malescio and G. Pellicane, Nat. Mater., 2003, 2, 97–100 CrossRef CAS PubMed.
- V. Pryamtisyn, V. Ganesan, A. Z. Panagiotopoulos, H. Liu and S. K. Kumar, J. Chem. Phys., 2009, 131, 221102 CrossRef.
- H. Koerner, L. F. Drummy, B. Benicewicz, Y. Li and R. A. Vaia, ACS Macro Lett., 2013, 2, 670–676 CrossRef CAS PubMed.
- J. A. Luiken and P. G. Bolhuis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012303 CrossRef.
- T.-Y. Tang and G. Arya, Macromolecules, 2017, 50, 1167–1183 CrossRef CAS.
- V. V. Ginzburg, Macromolecules, 2017, 50, 9445–9455 CrossRef CAS.
- L. Tripaldi, E. Callone, M. DArienzo, S. Dirè, L. Giannini, S. Mascotto, A. Meyer, R. Scotti, L. Tadiello and B. Di Credico, Soft Matter, 2021, 17, 9434–9446 RSC.
- A. Chancellor, B. T. Seymour and B. Zhao, Anal. Chem., 2019, 91, 6391–6402 CrossRef CAS PubMed.
- V. Goel, J. Pietrasik, R. Poling-Skutvik, A. Jackson, K. Matyjaszewski and R. Krishnamoorti, Polymer, 2018, 159, 138–145 CrossRef CAS.
- J. Scholz, B. Kayaalp, A. C. Juhl, D. Clemens, M. Fröba and S. Mascotto, ACS Energy Lett., 2018, 3, 387–392 CrossRef CAS.
- E. Gericke, D. Wallacher, R. Wendt, G. Greco, M. Krumrey, S. Raoux, A. Hoell and S. Mascotto, J. Phys. Chem. Lett., 2021, 12, 4018–4023 CrossRef CAS PubMed.
- S. Mascotto, D. Wallacher, A. Kuschel, S. Polarz, G. A. Zickler, A. Timmann and B. M. Smarsly, Langmuir, 2010, 26, 6583–6592 CrossRef CAS.
- S. Förster, L. Apostol and W. Bras, J. Appl. Crystallogr., 2010, 43, 639–646 CrossRef.
- S. Förster, A. Timmann, M. Konrad, C. Schellbach, A. Meyer, S. S. Funari, P. Mulvaney and R. Knott, J. Phys. Chem. B, 2005, 109, 1347–1360 CrossRef PubMed.
- B. Dahneke, J. Colloid Interface Sci., 1972, 40, 1–13 CrossRef CAS.
- C. J. van Oss, Interfacial Forces in Aqueous Media, CRC Press, 2nd edn, 2006 Search PubMed.
- B. Vincent, J. Edwards, S. Emmett and A. Jones, Colloids Surf., 1986, 18, 261–281 CrossRef CAS.
- J. E. Mark, Physical Properties of Polymers Handbook, Springer, 2007 Search PubMed.
- A. P. Lyubartsev, A. A. Martsinovski, S. V. Shevkunov and P. N. Vorontsov-Velyaminov, J. Chem. Phys., 1992, 96, 1776–1783 CrossRef CAS.
- E. Marinari and G. Parisi, EPL, 1992, 19, 451–458 CrossRef CAS.
- K. Hukushima and Y. Sakai, J. Phys.: Conf. Ser., 2013, 473, 012012 CrossRef.
- E. Bianchi, J. Largo, P. Tartaglia, E. Zaccarelli and F. Sciortino, Phys. Rev. Lett., 2006, 97, 168301 CrossRef.
- F. Sciortino and E. Zaccarelli, Curr. Opin. Solid State Mater. Sci., 2011, 15, 246 CrossRef CAS.
- E. Meneses-Júarez, S. Varga, P. Orea and G. Odriozola, Soft Matter, 2014, 9, 5277–5284 RSC.
- E. Meneses-Júarez, S. Varga, P. Orea and G. Odriozola, Soft Matter, 2013, 9, 11178–11182 RSC.
- S. Varga, E. Meneses-Júarez and G. Odriozola, J. Chem. Phys., 2014, 140, 134905 CrossRef PubMed.
- T. N. Carpency, J. D. Gunton and J. M. Rickman, J. Chem. Phys., 2016, 145, 214904 CrossRef CAS PubMed.
- B. Ruzicka, E. Zaccarelli, L. Zulian, R. Angelini, M. Sztucki, A. Moussaïd, T. Narayanan and F. Sciortino, Nat. Mater., 2011, 10, 56–60 CrossRef CAS PubMed.
- M. Delhorme, B. Jönsson and C. Labbez, RSC Adv., 2014, 4, 34793–34800 RSC.
- R. K. Pujala, N. Joshi and H. B. Bohidar, Colloid Polym. Sci., 2015, 293, 2883–2890 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00943a |
| This journal is © The Royal Society of Chemistry 2022 |