Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evaporation-driven liquid flow in sessile droplets
Hanneke
Gelderblom
 ac,
Christian
Diddens
ac,
Christian
Diddens
 bc and
Alvaro
Marin
bc and
Alvaro
Marin
 bc
bc
aDepartment of Applied Physics and Institute for Complex Molecular Systems, Eindhoven University of Technology, The Netherlands. E-mail: h.gelderblom@tue.nl
bPhysics of Fluids, University of Twente, The Netherlands. E-mail: c.diddens@utwente.nl; a.marin@utwente.nl
cJ.M. Burgers Center for Fluid Dynamics, The Netherlands
First published on 31st October 2022
Abstract
The evaporation of a sessile droplet spontaneously induces an internal capillary liquid flow. The surface-tension driven minimisation of surface area and/or surface-tension differences at the liquid–gas interface caused by evaporation-induced temperature or chemical gradients set the liquid into motion. This flow drags along suspended material and is one of the keys to control the material deposition in the stain that is left behind by a drying droplet. Applications of this principle range from the control of stain formation in the printing and coating industry, to the analysis of DNA, to forensic and medical research on blood stains, and to the use of evaporation-driven self-assembly for nanotechnology. Therefore, the evaporation of sessile droplets attracts an enormous interest from not only the fluid dynamics, but also the soft matter, chemistry, biology, engineering, nanotechnology and mathematics communities. As a consequence of this broad interest, knowledge on evaporation-driven flows in drying droplets has remained scattered among the different fields, leading to various misconceptions and misinterpretations. In this review we aim to unify these views, and reflect on the current understanding of evaporation-driven liquid flows in sessile droplets in the light of the most recent experimental and theoretical advances. In addition, we outline open questions and indicate promising directions for future research.
1 Introduction
A droplet is a liquid fragment that may adopt a spherical shape when its size is below the liquid's capillary length (a few millimeters for water), and a spherical-cap shape when it enters in contact with a solid surface. In the latter situation, we will refer to them as sessile droplets. The evaporation of a sessile droplet spontaneously induces an internal liquid flow. This flow is the result of several complex phenomena, as illustrated in Fig. 1: first, the surface-tension driven minimization of the interfacial area generates a capillary flow to compensate for the evaporative loss from the droplet surface.1 If the contact line is not pinned, evaporation-induced contact-line motion can couple with the internal flow.2 Third, the non-uniform evaporative flux could induce temperature and/or solute concentration gradients that in turn give rise to a Marangoni flow.3 Fourth, in liquid mixtures natural convection triggered by evaporation could drive internal flow.4,5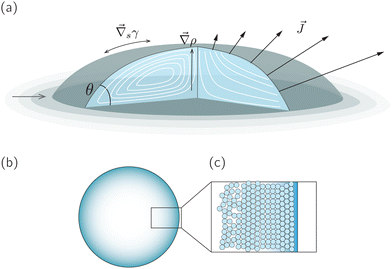 | ||
Fig. 1 (a) Sketch of a generic evaporating sessile droplet with a contact angle θ, and inhomogeneous evaporative flux ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) from its surface. The droplet might experience contact line motion with a velocity from its surface. The droplet might experience contact line motion with a velocity ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) cl or/and surface tension gradients along its liquid–air interface cl or/and surface tension gradients along its liquid–air interface 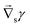 . In this review we will cover how all these different phenomena influence the velocity field . In this review we will cover how all these different phenomena influence the velocity field ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) inside the droplet. (b) Top view of the droplet showing its circular perimeter. (c) Close-up of the contact line. When the droplet contains a diluted suspension of monodisperse colloids and a capillary flow1 dominates their transport, particles self-organize in a well-defined way.6 inside the droplet. (b) Top view of the droplet showing its circular perimeter. (c) Close-up of the contact line. When the droplet contains a diluted suspension of monodisperse colloids and a capillary flow1 dominates their transport, particles self-organize in a well-defined way.6 | ||
The most ubiquitous of these evaporation-driven flows gives rise to the so-called coffee-stain effect, which appears when the capillary flow drags suspended particles towards the droplet's contact line. This effect was first demonstrated by Deegan et al.1 and opened up an entirely new field of research. Since the pioneering work of the Chicago group1,7,8 many studies focused on the evaporation process itself (see reviews9–13). Other related works concentrated on wetting and spreading14 or on contact-line motion,2 with little attention on evaporation. A number of studies addressed specifically the evaporation-driven flow inside sessile droplets.6,15–23 In his review from 2014, Larson24 showed a selection of the most important contributions to the field from a chemical engineering perspective. Indeed, the major boom in the studies on evaporating droplets has occurred in the field of material science and chemical engineering, motivated by the desire to control the shape and structure of the deposits, see e.g. review articles25–28 for an overview. The key aspiration in these works is that by controlling the evaporation-driven flow, one could in principle predict and eventually manipulate the distribution of suspended non-volatile material at will. However, due to this practical motivation and the diversity of communities involved, the influence of internal flows in evaporating droplets is often overlooked or misinterpreted, and detailed knowledge remains dispersed among the different fields.
In this review, we discuss the current theoretical, numerical and experimental insights on the flow inside evaporating droplets. We aim to present a unified view and identify key open questions from a fluid-dynamic perspective and discuss its consequences to systems constituted by soft matter. We restrict ourselves to the paradigmatic case of droplets evaporating in ambient conditions, where free-convective transport of humid air29 and evaporative cooling30 are of negligible influence such that the evaporation is diffusion-limited,9,13 and the droplet shape evolves in a quasi-steady fashion.31 We start from the simplest case of a freely suspended droplet, and then show how the interaction with different types of substrates gives rise to an evaporation-driven capillary flow, and how this flow is influenced by the contact angle and contact-line dynamics. Second, we discuss the influence of the liquid–gas interface on the internal flow, via solutal and thermal Marangoni stress. Third, we address the internal flow due to natural convection in evaporating liquid mixtures. Fourth, we discuss how evaporation-driven flows influence the transport and deposition of a dilute concentration of suspended non-volatile material, e.g. colloidal particles. We close by laying out the main open fluid-dynamical questions and promising directions for future work.
2 Capillary flow and the role of the substrate
Evaporative mass loss from the surface of a drying drop can induce an internal flow, as was first demonstrated in the seminal work by Deegan et al.1 This flow has its origin in capillarity: evaporative mass loss causes the droplet to change its shape, while at the same time it has to maintain its spherical-cap shape dictated by surface tension. As a consequence of the mismatch between these two effects, a capillary flow arises.1 However, the presence and nature of such capillary flow depends in a highly non-trivial way on the evaporative flux profile19,32 and the interaction of the droplet with a substrate, i.e. on the contact angle18,19,22 and the motion of the contact line.18,19,33 In the literature, this complexity often leads to confusion when addressing the flow direction (inward, outward, or circulatory) inside an evaporating droplet.In this section we will discuss the influence of the liquid-substrate interaction on the capillary flow step by step, always assuming thermal equilibrium among all phases involved. We start from the simplest situation: a freely suspended evaporating droplet. Then, we move to the situation where the droplet is in contact with a substrate. We separately discuss the influence of the contact angle, pinning and motion of the contact line on the capillary flow, and argue that -perhaps counter-intuitively- neither contact-line pinning nor a diverging evaporative flux at the contact line are essential for the existence of a radially outward capillary flow. On partially wetting substrates, two situations will be analyzed in detail: the freely moving contact line, in which the contact angle remains constant (CCA or constant contact-angle mode), and the pinned contact line, in which the wetted area remains constant (CCR or constant contact-radius mode).34,35 Finally, we discuss the influence of complete wetting and hydrophobic substrates on the capillary flow.
2.1 Freely suspended droplet
The simplest geometry to consider is a droplet that is freely suspended in quiescent air, as illustrated in Fig. 2. This configuration, which has first been studied by Maxwell36 and Langmuir,37 is found in e.g. spray drying applications, aerosols, airborne disease transmission, combustion and atmospheric science (see e.g. ref. 9 and 38, 39 and references therein). In absence of a substrate, the evaporative flux from the droplet surface is uniform and directed radially outwards. In the diffusion-limited regime the evaporative mass flux (in kg m−2 s−1) is given by9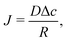 | (1) |
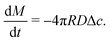 | (2) |
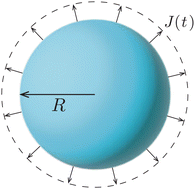 | ||
| Fig. 2 Uniform evaporation from the surface of a freely suspended spherical droplet causes the inward motion of the liquid–air interface. | ||
Upon combining (2) with the expression for the shape change dM/dt = 4πρR2dR/dt, where ρ the density of the liquid, we find that dR/dt = −J/ρ. Upon integration we arrive at the famous R2 – law
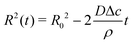 | (3) |
Importantly, the evaporative flux from the surface of a freely suspended drop does not induce any flow inside the droplet. As the evaporation proceeds, the interface of the droplet recedes inwards to accommodate for the mass loss. One could think about this situation as if the evaporation were just “peeling off a layer of liquid” from the droplet. Hence, the particle agglomeration at the interface of a colloidal suspension droplet in spray drying conditions (see e.g. ref. 38 and 40, 41) is purely due to the inward apparent motion of the liquid–air interface that collects the particles and not to an evaporation-induced internal flow, as is sometimes suggested in the literature. Indeed, it is not the particles that get advected to the interface, but vice versa: the interface recedes inwards, dragging particles along.
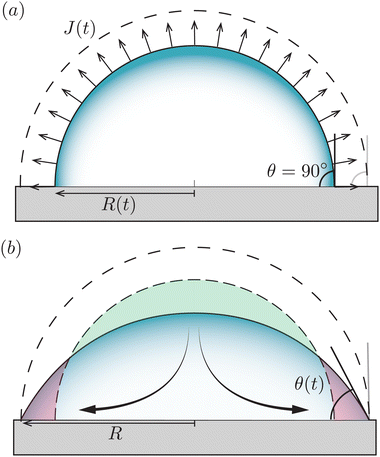
2.2 Sessile droplet with a contact angle θ = 90°
We now turn to the situation where the droplet is in contact with a substrate: a sessile droplet. For illustrative purposes, the configuration of a sessile droplet with a contact angle θ = 90° is described first. In that case, the evaporative flux from the surface is still uniform and given by (1), as mathematically, the impermeable substrate can be considered as a mirroring surface.1 The velocity field inside an evaporating droplet in CCA and CCR mode subject to a uniform evaporative flux has been studied both under the assumption of a potential flow19,42–44 and in Stokes flow.18 In these studies the general evaporation problem is simplified dramatically by assuming a uniform evaporative flux, however, in case θ = 90° the Stokes flow solution18 becomes exact.Fig. 3 illustrates that, in contrast to what is often believed, a divergence of the evaporative flux at the contact line is not required for the generation of a capillary flow. Indeed, outward flows are also found when the evaporative flux is uniform.18,42–44 Whenever there is a mismatch between the local evaporation rate and the constraints posed by the droplet's spherical-cap shape and contact-line motion, a capillary flow arises. Clearly, as soon as the droplet starts to loose mass the contact angle will decrease below 90°, which is the situation that will be considered next.
2.3 Sessile droplet on a partially wetting substrate (0 < θ < 90°)
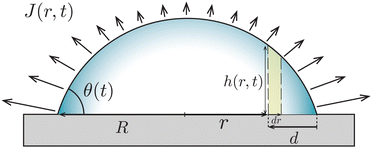
In the classical example of a pinned droplet on a partially wetting substrate (finite contact angle θ < 90°, Fig. 4), the singular corner geometry of the droplet leads to a divergence of the evaporative flux at the contact line1,45 and the expression (1) does not hold anymore.We will consider here the case where θ ≪ 90°, such that the drop shape is relatively shallow (i.e. its height is much smaller than its base radius, h ≪ R). In this situation, the capillary flow inside the droplet can be calculated analytically.6,15 For this exemplary case, we will summarize the calculation here, considering both the CCR and the CCA modes.
Consider the axisymmetric, shallow droplet sketched in Fig. 4. Following6,7 we define an infinitesimally small control volume of width dr at a distance r from the droplet center. Mass conservation requires that the rate of change of the amount of liquid inside this control volume is equal to the net inflow of liquid minus the amount of liquid that evaporates from the droplet surface:
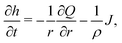 | (4) |
In the following, we will consider the situation where the droplet shape is not affected by the flow inside the droplet or by gravity, which means that both the capillary number μU/γ and the Bond number ρgR2/γ are small,24 where γ is the surface tension, μ the dynamic viscosity, U the typical velocity scale and g the gravitation acceleration. Hence, the droplet shape is restricted to a spherical cap as dictated by surface tension, with either a pinned or a moving contact line (i.e. evaporation in CCA or CCR mode). Consequently, the local change in droplet height (left-hand side of (4)) is also restricted. Whenever this local height change does not match the evaporative flux a capillary flow arises, as illustrated in Fig. 5.
In the limit of small contact angles (θ ≪ 90°) simplified expressions for h and J are available, which allows for an explicit analytical solution to (4). For θ ≪ 90° the evaporative flux is given by6,7
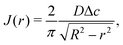 | (5) |
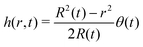 | (6) |
To obtain an expression for the capillary flow Q using (4)–(6), we now discriminate again between the case of a pinned and a moving contact line.
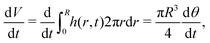 | (7) |
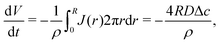 | (8) |
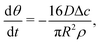 | (9) |
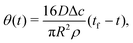 | (10) |
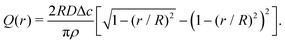 | (11) |
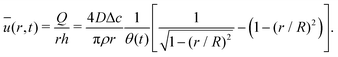 | (12) |
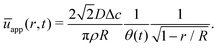 | (13) |
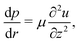 | (14) |
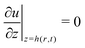 (no shear stress at the liquid–air interface). Upon integration of (14) we then find
(no shear stress at the liquid–air interface). Upon integration of (14) we then find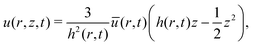 | (15) |
The velocity field (15) and (12) displays two singularities:6 a spatial singularity arises as one approaches the contact line, which originates from the divergence of the evaporative flux (5), as is clearly seen in (13). On top of that, there is a temporal singularity that originates from the vanishing droplet height towards the end of the droplet lifetime, as θ → 0 in (12) and (13), or h → 0 in (15). This temporal singularity, which is completely decoupled from the spatial one, has dramatic consequences for the particle deposition in the ring stain that forms,6 as will be discussed in Section 5.
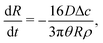 | (16) |
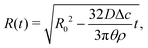 | (17) |
 | (18) |
The velocity field can again be obtained in the lubrication approximation and is given by (15), but now with the height-averaged velocity expressed as
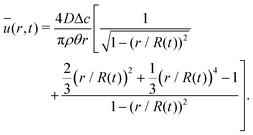 | (19) |
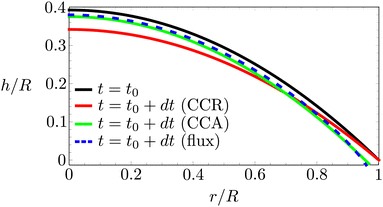
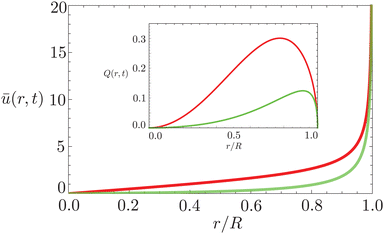
In Fig. 6 we compare the height-averaged velocities for a droplet in CCR mode (12) and CCA mode (19). In the inset, the same is done for the flows in CCR (11) and CCA mode (18). In both modes, the flow increases from the center of the droplet, where it must be zero for symmetry reasons, reaches a maximum and then decreases back to zero at the contact line, as there can be no net flow out of the droplet. Clearly, in both cases (CCR and CCA) the flow and velocity are directed radially outward, as was already expected from the sketch in Fig. 5. Hence, even though in CCA mode the contact-line itself is receding, the internal flow is directed radially outward. However, the magnitude of the flow and radial velocity are much larger in CCR mode, as a result of the larger mismatch between the evaporative flux profile and the constrained motion of the liquid–air interface (compare the blue dashed with the green and red solid lines in Fig. 5).
First of all, the contact-line motion is often not completely free, but restricted by properties of the substrate (i.e. the substrate's receding angle)35,48 and potential self-pinning due to the deposition of solutes.8 Pinning forces could therefore induce a stick-slide/stick-slip motion of the contact line.33,35 During the sliding phase there will be an inward flow away from the contact line, as described by Huh & Scriven.49 At the same time, the evaporation flux from the droplet surface causes an outward flow, as discussed above. Since both flows are governed by the Stokes equations, the two solutions can be superimposed,22 and one would expect a cross-over length scale where the two velocity fields cancel each other.2,33 Using the previously derived expression for the capillary flow close to the contact line (13), we find for this cross-over length scale33
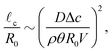 | (20) |
Second, for droplets evaporating in CCA mode, a deformation of the interface will occur close to the contact line: the no-slip boundary condition at the solid substrate conflicts with the moving contact-line condition, causing a divergence of the internal pressure49 and hence a local deformation of the interface. This interface deformation occurs only close to the contact line, while the remainder of the droplet is still described by a spherical cap receding with a macroscopic or apparent contact angle close to its equilibrium value.14 However, when the equilibrium contact angle is small (θ < 5°),33 the interfacial deformation becomes more prominent and the macroscopic contact angle changes, such that expressions (18) and (19) no longer apply.
Third, also the incompatibility of the diverging evaporative flux with the no-slip condition at the boundary causes a diverging internal pressure field.22 This condition applies to droplets in both CCA and CCR mode, and may again cause interface deformations. However, again the effect is only prominent for small contact angles (θ < 5°)33 and at small distances (≪R) from the contact line.22 We note that, importantly, the introduction of a slip length will not cure this pressure divergence as it is even stronger than the one found in the moving contact line problem.22
Finally, for droplets larger than the capillary length, the spherical-cap assumption is no longer valid and gravity modifies the droplet shape to become puddle-like. This different shape will alter the evaporative-flux profile. Moreover, for large droplets natural convective transport of vapor comes into play, which further alters the evaporative flux.29 These changes in droplet shape and evaporative flux will of course also alter the internal flow, which will then depend on the specific shape adopted by the liquid phase on the substrate and it is therefore not universal.
2.4 Complete wetting
When a droplet is deposited onto completely wetting substrate, it will want to spread out in accordance to Tanner's law while its macroscopic contact angle is decreasing to zero. However, if the droplet is also evaporating, and the evaporative mass loss takes place on the timescale of the spreading, a very delicate problem arises. In this case, the droplet will not reach a zero contact angle: while the droplet tries to spread out, evaporation causes the droplet's apparent contact angle to remain finite.50–53 Moreover, the droplet shape is no longer constrained to a spherical cap, but evolves over time as a function of both the evaporative flux and internal flow. Indeed, for small contact angles the influence of evaporation-induced interface deformations increases dramatically.33 In turn, the change in drop shape affects the evaporative-flux profile and internal flow.52,53 In addition, as the droplet spreads out to a thin film, disjoining pressure will start to play a role.9 As a result the shape of the droplet is not known a priori,14 which poses a challenging problem: the droplet shape, internal flow and evaporative flux are coupled, and local solutions close to the contact line54,55 depend on the global evaporation characteristics.52 An approximate description of the spreading dynamics based on a pre-described evaporative-flux profile combined with a phenomenological description of the time-dependent droplet radius has been derived by ref. 55–58. A self-consistent theoretical description of the complex coupling that arises between the droplet shape, internal flow and evaporative flux in complete wetting is provided by ref. 52 and 53. However, in complete wetting, the shape of the droplet, its apparent contact angle, the spreading dynamics and the width of the contact line region still remain subject of debate.52–552.5 Sessile droplet on a (super)hydrophobic substrate (θ > 90°)
For arbitrary contact angles, the evaporative flux in the wedge-shaped region close to the contact line ((1 − r/R) ≪ 1) can be approximated as1,22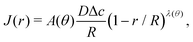 | (21) |
For large contact angles, the calculation of the internal flow becomes extremely complicated. First of all, the description of the evaporative flux and droplet shape are difficult and require the use of toroidal coordinates. An analytical solution for the evaporative flux along the entire spherical-cap surface has been derived by Popov59 based on the solution for the electro-static potential of a lens-shaped, charged conductor provided by Lebedev.60 Second, the mass conservation eqn (4), in which one implicitly assumes h ≪ R, is no longer applicable. As a consequence, the description of the internal flow becomes challenging and exact explicit solutions are not available.
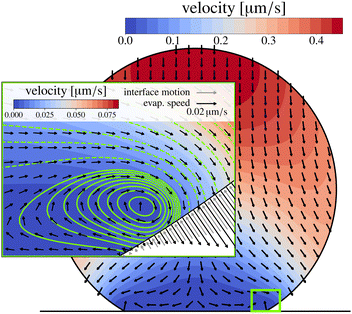
The velocity fields inside an evaporating droplet19 or liquid line44 of arbitrary contact angle have been derived under the simplifying assumption of inviscid flow and hence free slippage over the solid substrate. Stokes flow solutions have been obtained for either a uniform18 or a regularized20 evaporative flux. Similarity solutions to the Stokes flow subject to the evaporative flux (21) in the wedge-shaped region close to the contact line have been derived by Gelderblom et al.22 This analysis showed that, surprisingly, for large contact angles (θ > 127°) reversing flow structures appear. Moreover, for θ > 133.4° Moffatt eddies61 dominate the flow near the contact line. To investigate how these corner flows relate to the flow in the entire droplet, numerical simulations are required. Up to now, however, numerical studies15,32 focused on smaller contact angles. In Fig. 7 we show, for the first time, numerical results for the velocity field inside a water droplet with a contact angle of 150°. The inset indeed confirms the presence of the analytically predicted22 reversing corner flow. The extend of this region grows for higher contact angles and indeed vanishes at a critical contact angle of θ ≈ 133.4°, however, the size of the region and the reversed velocity is small compared to the size and typical velocity of the entire droplet.
Experimentally, too, assessment of the flow inside a droplet on a hydrophobic or superhydrophobic substrate is challenging, as the shape of the droplet obscures the view in the contact-line area. Up to now, there is no reliable experimental method available to fully resolve the predicted flows in the whole volume18–20,22,44 for evaporating droplets with contact angles above 90°.
3 Evaporation-driven Marangoni flow: the role of the liquid–gas interface
Until now, the liquid–gas interface has been considered shear-free. However, in practice, the free surface is often subject to an interfacial shear stress that gives rise to an additional internal flow. In this section, we will discuss how gradients in the interfacial temperature and in the concentration of surface-active material can give rise to interfacial shear, and, as a consequence, induce a Marangoni flow inside the evaporating droplet.Such a flow can be quantified by the Marangoni number Ma. In its most generic version, the Ma number can be defined as the ratio between Marangoni-driven advective flow and the diffusive transport of the property generating the surface tension gradient (temperature or interfacial concentration of solute): Ma = UL/DX, where L is the length scale of the concentration gradient and DX is a diffusion constant of the variable X (with units of area per unit time). The order of magnitude of the Marangoni flow U can be approximated by Δγ/μ, where μ is the liquid's dynamic viscosity. The change of surface tension Δγ can be expressed as a function of the variable X, which refers to either the temperature or the concentration of solute along the interface, resulting in the following generic expression of the Marangoni number:
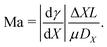 | (22) |
3.1 Thermal Marangoni flow
Up to now, we described the evaporation process as thermodynamically out-of-equilibrium, but thermally in equilibrium. However, the loss of enthalpy in evaporating droplets unavoidably leads to a loss of thermal energy, manifested by a temperature decrease. Surface tension, as all thermodynamic variables, is temperature dependent and it will typically increase for decreasing temperatures. Therefore, any interfacial temperature gradient will lead to a surface tension gradient and consequently to a so-called thermal Marangoni flow.We start our reasoning as in Section 2.1 with a freely suspended droplet in air. In this simpler case, the evaporation flux is homogeneous along the liquid–air interface, and the loss of enthalpy leads to a homogeneous temperature drop that diffuses inwards. Therefore, the symmetry of the system prevents the onset of any liquid flow in a spherical evaporating droplet.
Such a symmetry is broken when the droplet becomes sessile by entering in contact with a solid substrate. In that case, as we analyzed in Section 2.3, the evaporative flux at the liquid–gas interface becomes non-uniform, which could give rise to interfacial temperature gradients. In addition, the liquid phase is now in contact with a solid phase, and heat can also be exchanged through the liquid–solid interface. The solid surface would become a source or a sink of heat depending on the thermal conductivity ratio of the liquid and the solid phase.30 In summary, the interfacial temperature field at every instant in an evaporating sessile drop needs to be carefully computed and can easily change substantially during the droplet's lifetime.
The direction of the interfacial shear and hence the Marangoni flow is given by the direction of the temperature gradient along the liquid–gas interface.62 The strength of the Marangoni flow depends on several factors, and can be quantified by the Marangoni number (22), which in the case of thermal gradients can be easily derived from (22), leading to:
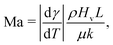 | (23) |
For example, in the classical case of a sessile water droplet on a glass substrate, the solid phase is 1.6 times more conductive than the liquid phase. For droplets with a contact angle <90°, the heat loss is largest at the contact line. However, since glass is more thermally conductive than water, the heat is supplied from the solid substrate. The contact-line region is in direct contact with the substrate and therefore this will be the warmest region in the droplet. As a result, a thermal gradient is established from the apex to the droplet base.62 This effect was analyzed numerically by Diddens et al.,64 who noticed that not only thermal conductivity of the solid and liquid is important, but also the substrate thickness, as suggested earlier by experiments and theoretical models.30,65,66
Interestingly, theoretical modelling predicts that interfacial temperature gradients can change directions (towards contact line or away from it) depending in a very subtle way on the liquid properties, droplet contact angle, substrate conductivity and evaporative cooling rate.62,67 Such an inversion of the surface temperature gradient should result in an inversion of the Marangoni flow circulation. Unfortunately, up to now, no direct experimental evidence of such a flow inversions has been shown. Some of the reasons for such mismatch will be discussed in the following sections.
A case that deserves an extended discussion is that of water under atmospheric conditions. For a millimetric water droplet at room temperature (where |dγ/dT| = 0.166 × 10−3 N m−1 K−1, Hv = 2.26 × 106 J kg−1 and k = 0.59 J m−1 s−1 K−1),71 the Marangoni number reaches values of the order of 105 (see Hu & Larson16 and Gelderblom et al.22). Quantitative theoretical and numerical solutions for the Marangoni flow were first computed for sessile water droplets in atmospheric conditions in the limit of small contact angles by Hu & Larson.16 All numerical models following in the literature64,72,73 predict that thermal Marangoni flow should overcome the capillary flow driving the coffee-stain effect by orders of magnitude. Only close to the contact line and on partially wetting substrates, where the evaporative flux diverges (see Section 2), the capillary flow dominates the Marangoni flow. Hence, a cross-over length scale should exist beyond which the Marangoni flow dominates.22 For most practical cases, this length-scale is sub-micron, which implies that the Marangoni flow should significantly alter the flow inside evaporating droplets.
Experimental observations, however, dramatically diverge from these theoretical and numerical findings. The disagreement between experimental and numerical values for the flow velocity reaches up to three orders of magnitude:23,74–76 from typical values of 1 μm s−1 experimentally measured at room temperature conditions,23,76 up to 1 mm s−1 in numerical simulations.16 Similar conclusions were reached in early works on droplet evaporation by analyzing the heat transport within the evaporating droplet by laser interferometry77 and by temperature measurements.3 In these studies it was found that thermal advection was negligible, despite the large Marangoni numbers computed.
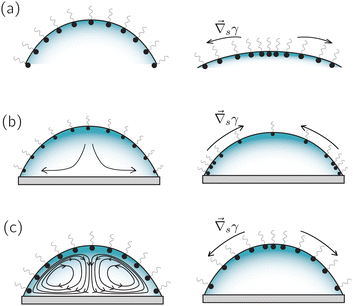
Such disagreement between experiments and theory resembles the one found in classical thermocapillary convection studies.78 In these systems, the discrepancy has been explained by the accidental presence of monolayers of surfactants (i.e. contaminants). Surfactants can have a significant effect on the convective flow when they form a loose monolayer and can completely neutralize the flow when they form a compact monolayer (see the sketch in Fig. 8c), with surface concentrations of approximately 108 and 1010 molecules per μm2 respectively.79 Cammenga et al.3 and Hu & Larson16 also ascribed the discrepancy observed in evaporating droplets to certain amount of unknown contamination.
Although the identity of these impurities is not yet known, their presence at the water–air interface has been clearly detected in the past. For example, making use of oscillating liquid bridges, Ponce-Torres, Vega & Montanero80 monitored the surface tension of different liquids as the liquid interface “ages”. They obtained a minor decrease of surface tension for alcanes, and a substantial decrease for deionized water, from 40% to 30% depending on the atmosphere (open, saturated air or argon). In a more recent example, Molaei et al.81 studied the flow field generated by colloidal particles trapped at a quiescent water–air interface while experiencing Brownian motion. They obtained a surface-divergence free flow field, which is a clear signature of an interfacial incompressibility caused by contamination. The authors estimated an interfacial contaminant concentration of 103 molecules per μm2 and Marangoni numbers up to Ma ≈ 400. Such estimates are compatible with the calculations by Hu & Larson.16
A recent numerical study confirms that surfactants or contaminants that reduce the surface tension of pure water by ∼0.1% are sufficient to suppress the thermal Marangoni flow.82 To our knowledge, no study has attempted yet to identify which contaminant(s) can be so generally present at water–air interfaces and induce practically the same disturbances in hundreds of different experiments for decades around the globe.
We cannot close this section without mentioning that water droplets far from atmospheric conditions can develop strong Marangoni flows, as evidenced in the extensive work of Ward et al.83–85 By carefully designing a closed setup to reduce the contamination of the liquid phase and manipulating the chamber's temperature and pressure, the authors reported interfacial velocities reaching up to 1 mm s−1. Unfortunately, no comparison with numerical or analytical models was reported by the authors or by any posterior work.
3.2 Solutal Marangoni flow due to surface active material
In the previous section we have discussed how surfactants can suppress evaporation-driven flows in water droplets and other liquids. However, surfactants can also have the opposite effect and induce a surface flow when their dynamics couples with another destabilizing process such as evaporation or dissolution.79,86 The simplest scenario that can be considered is an initially homogeneous distribution of insoluble surface active material at the liquid–gas interface of an evaporating droplet with a pinned contact line, as illustrated in Fig. 8a. If the surface shrinks with a negligible surface velocity (tangential to the surface), surfactants will accumulate at the apex of the droplet due to the surface area reduction.87 As a consequence, a surface concentration gradient will be created that points towards the apex, where the surface tension is then reduced. The resulting surface-tension gradient then drives a Marangoni flow towards the contact line.This simple (but unrealistic) case shows how easily the surfactant and the evaporation dynamics can be coupled to set a quiescent interface into motion. The situation becomes more complex in the case of soluble surfactants, which are found more often in practical situations. They can lead to a wide range of possible scenarios, from very dynamic and compressible interfaces (Fig. 8b and c) to surfactant-saturated and incompressible interfaces, depending on the cohesive/repulsive surfactant interaction, the time scales of the surfactant adsorption/desorption,88 combined with the time scale of the evaporation process and the time scale of the surface flow.86
In the following section, we discuss a number of experimental studies on flow measurements performed in surfactant-laden droplets. However, since different physical processes are taking place in the droplet simultaneously and in competition (capillary flow, thermal Marangoni flow, solutal Marangoni flow, etc.), fluid flow measurements are essentially incomplete and cannot give a complete picture on the role of surfactants.89 Therefore, such studies should combine experiments with numerical simulations to gain a deeper understanding of the dynamics of such complex systems.
These results were confirmed and directly measured by Marin et al.23 using three-dimensional particle tracking. A characteristic Marangoni eddy was found systematically in SDS for concentrations ranging from the critical micellar concentration (CMC) up to 50× CMC (as sketched in Fig. 8b). At extremely high concentrations, even an additional (but weaker) counter-rotating eddy could be identified and quantified. Marin et al.23 also studied the effect of the non-ionic surfactant Polysorbate 80 (P-80), which is much larger and slower than SDS or Triton X-100. While SDS and Triton X-100 generated certain motion at the surface, P-80 causes the opposite effect: decreasing interfacial flow for increasing P-80 concentrations and an almost stagnant interface for bulk concentrations above the CMC.
3.3 Solutal Marangoni flow due to compositional gradients in mixtures
In mixtures where the components have different vapor pressures, the preferential evaporation of one component induces a compositional gradient: on a partially wetting substrate the concentration of the most volatile component is lowest at the contact line (where the evaporation rate is largest). If the components also have a different surface tension, this preferential evaporation leads to a surface tension gradient, and hence, a Marangoni flow.The corresponding solutal Marangoni number can be estimated according to (22) by using a compositional quantity, e.g. the mass fraction w of one component at the interface, for the surface property X. However, the estimation of the compositional difference ΔX = Δw in (22) involves the calculation of the evaporation rates of all constituents. Since these strongly depend on the local composition of the mixture due to Raoult's law, the vapor diffusivity of each component and the contact angle of the droplet, the interested reader is referred to Diddens et al.95 for a detailed derivation of the solutal Marangoni number for mixtures.
Perhaps the best-known example of such a coupling between evaporation dynamics and solutal composition is the case of water and ethanol, featured in the tears of wine phenomenon, in which the faster evaporation of ethanol at the triple line of a glass of wine drives a solutal Marangoni flow of liquid creeping up the glass.96
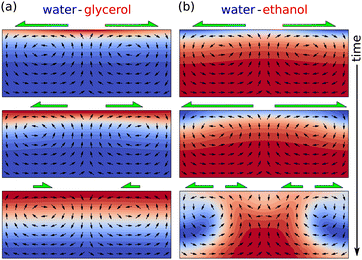
Evaporating sessile droplets of water and ethanol exhibit an erratic flow with larger fluctuations in the early stages, when the ethanol concentration is high, which relaxes to a classical capillary flow profile after certain amount of time, when the concentration of ethanol in the droplet is minimal.97,98 This sequence of flow patterns have been reproduced using fully three-dimensional numerical simulations by Diddens et al.,64 since the Marangoni instability unavoidably breaks the axial symmetry of the system.
The same sequence of flow patterns are observed in popular alcoholic drinks such as ouzo64,99 or whisky.100 Evaporating droplets of ouzo, a ternary system compound of water, ethanol and anise oil, also show such fluctuating flow in the first stage, until most of the ethanol is evaporated and the ternary system turns unstable, manifested in the nucleation of oil droplets.64,99
The resulting flow when two or more components are left to evaporate in a sessile droplet can be quite different from the case of ethanol and water. A factor to observe is whether the most volatile liquid decreases the total surface tension of the solution. If this is the case, as in the ethanol-water mixture, the resulting flow is typically largely dominated by a violent Marangoni surface flow that eventually breaks the axial symmetry of the system.64,97,98 If the most volatile liquid increases the surface tension of the solution, as in a glycerol–water solution, the resulting Marangoni flow is a much weaker, gentle and axisymmetric flow. The reason for these entirely different flow scenarios can be found in the Marangoni instability,78,101 which is explained in Fig. 9. As we will see in the next section, in glycerol–water mixtures the density difference can have a more important influence on the internal flow than the stable Marangoni flow.
Ethanol or glycerol are polar molecules which can be considered as lyophobic solutes that decrease the surface tension of water-based solutions. On the other hand, lyophilic solutes such as ionic salts or sucrose remain in the bulk and tend to increase surface tension, as is explained in ref. 102. Consequently, even at small concentrations they can have a tremendous impact on evaporation-driven flows. Marin et al.103 showed that small amounts of sodium chloride can lead to a radical change of the flow structure inside the droplet. The evaporation-induced enrichment of such a solute at the droplet's contact line leads to a surface Marangoni flow towards the contact line. This Marangoni flow is the dominant source of motion within the droplet, over both the capillary and the thermal Marangoni flow.103
4 Gravitational effects in evaporating sessile droplets
Typically, the size of the droplets considered in this review are comparable or below the capillary length. As a consequence, their shape is dominated by surface tension and not by gravity (i.e. the Bond number is much smaller than unity, see Section 2.3). However, gravitational effects can still have a significant influence on the fluid flow in an evaporating drop. Such influence might occur, e.g., when the liquid is a mixture of two components with different densities and different vapor pressures. In that case evaporation will lead to density differences that might induce an internal flow (Section 4.1). Additionally, density differences might also appear due to the temperature differences naturally occurring during evaporation. These two scenarios will be discussed in the following sections.Strong density gradients can be induced thermally by actively heating the substrate. Substrate heating introduces a new control parameter, the substrate temperature, and a plethora of instabilities which will not be covered in this review. We direct the interested reader to the review by Brutin & Starov104 and references therein.
4.1 Internal natural convection in mixtures
Density gradients can occur naturally when the evaporating liquid phase consists of a mixture of two components with different densities. If the density difference is large enough, natural convection comes into play and contributes to the internal flow. The most paradigmatic example of natural convection in an evaporating droplet is the case of glycerol–water solutions,5 due to the large density difference involved (glycerol is 25% heavier than water). A similar flow has been observed in water/butanol and water/ethanol solutions by Edwards et al.,4 although in the latter case solutal Marangoni flows enter in competition with natural convection.In principle, both Marangoni instabilities and natural convection might be present in any arbitrary binary solution. Assuming that thermal effects can be neglected and that the base capillary flow is much weaker than such instabilities, Diddens et al.95 could reduce the problem using two dimensionless numbers, namely the Marangoni number (eqn (22)) and the Rayleigh number (the ratio between transport via natural convection and diffusion). For a more elaborated discussion on the different regimes that can be found, we refer the interested reader to Diddens et al.95
4.2 Gravitational effects generated by evaporation-driven temperature differences
Depending on the thermal properties of the liquid phase and the solid holding the sessile droplet, the liquid's vapor pressure, the droplet's contact angle and its size, different thermal gradients can build up during the evaporation of a sessile droplet.Under standard room conditions and in the absence of active heating, the temperature gradients will mostly lead to large surface-tension gradients rather than large density gradients, and therefore stronger Marangoni flows than natural convection. We can reach this conclusion by comparing the magnitude of the Marangoni number (23) to the Rayleigh number, i.e. the ratio between the diffusive time scale and the convective time scale, defined as
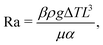 | (24) |
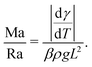 | (25) |
5 Particle transport and deposition by evaporation-driven flows
When an evaporating droplet contains tiny particles, these will get transported by the internal flow and deposit onto the substrate, leaving a stain. The patterns formed by these drying stains can be a signature of the evaporation dynamics.25 However, in many occasions the same evaporation dynamics can yield similar or identical stains. For example, both capillary flows1,8 and salt-induced solutal Marangoni flows103,105 lead to ring-shaped stains. Therefore, inferring on the evaporation dynamics based solely on the dried deposition patterns can often lead to wrong conclusions. In this section we will describe step by step how the capillary and Marangoni flows discussed in Sections 2 and 3 affect the particle deposition. We will restrict ourselves to the hydrodynamic transport of neutrally buoyant colloidal particles only, and to dilute suspensions, in which particle–particle interaction and changes in the suspension rheology during evaporation are negligible. There are very few situations in which only hydrodynamics can determine the final fate of the dispersed particles. In general, the final position of a dispersed particle in an evaporating droplet involves complex physico-chemical processes that will not be discussed in depth in this review.In evaporating drops two modes of particle transport exist: transport via Brownian motion of the particles and transport by convection in the evaporation-driven flow.106 The ratio of importance of these two modes is expressed by the Peclet number
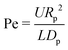 | (26) |
When Pe ≪ 1 the particle diffusive timescale is much shorter than the convective timescale, and particles will cross streamlines instead of following them. By contrast, when Pe ≫ 1 particles will get transported by the flow and follow the streamlines because of their hydrodynamic drag.106 If that is the case, and the particle interacts weakly with the liquid–gas and liquid–solid interfaces, the internal flow will have a crucial impact on the particle deposition.
We will discuss the influence the internal flow on particle deposition patterns for droplets with a pinned contact line where capillary flow dominates in Section 5.1 and for a dominant Marangoni flow in Section 5.2. The deposition pattern for droplets where the contact line moves continuously or shows stick-slip behavior is described in Section 5.3.
5.1 Pinned contact lines and capillary flow
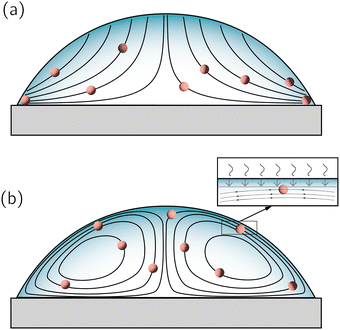
In a droplet evaporating with a pinned contact line, the capillary flow causes the deposition of particles into a ring-shaped stain: the well-known coffee-stain effect.1,8 This particle deposition by capillary flows is so robust and reproducible that it has generated an immense interest and led to many applications.26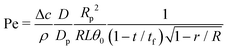 | (27) |
First of all, particles could get adsorbed at the solid substrate before they reach the contact line, due to a combination of hydrodynamic and physico-chemical effects: Particles will not remain on a single stationary streamline for the entire droplet lifetime but follow the instantaneous streamlines that change in time as the droplet shrinks. When a particle ends up on a streamline passing close to the solid substrate, it can eventually get adsorbed either by simple mechanical friction, electrostatic107 or chemical (e.g. van der Waals) forces.108 Hence, non-hydrodynamic forces, i.e. the physico-chemistry of the solvent, particle surface and boundary material, eventually determine whether the particle can continue its path or will be adsorbed at the boundary. Clearly, adsorption becomes even more important if the Peclet number (eqn (27)) is much smaller than unity and the particle motion is dominated by Brownian motion. In that case particles can spontaneously change streamline, and eventually attach irreversibly to the solid substrate before reaching the contact line.
Second, particles could get adsorbed at the receding liquid–gas interface. Any particle moving on a streamline parallel to a receding liquid–gas interface (for example when there are closed streamlines, as in Fig. 10b), will eventually come close to the interface. Note that this is again a purely hydrodynamic (and geometric) fact, in which the physico-chemistry has not yet been invoked. Similarly to the particle-solid interaction described above, as soon as the radius of the particle becomes smaller than the distance to the interface, non-hydrodynamic forces come into play, i.e. van der Waals forces, electrostatics and wetting.109 In principle, such hydrodynamic particle trapping could also occur for open streamlines110 (see Fig. 10a), i.e. in thermal equilibrium and for a force-free interface. Hence, regardless of the streamline configuration, hydrodynamics tells us that particles dispersed in an evaporating drop will approach the liquid–gas interface at a rate proportional to its receding pace. However, their final destination ultimately depends on the physico-chemistry of both the particle and the boundary.
Third, the particles may not have enough time to reach the contact line before the droplet has completely dried.111 To estimate the ratio between the particle transport time and the droplet drying time we will use the results of Section 2.3.1 for droplets with a small initial contact angle θ0 ≪ 90°. The total drying time of the droplet scales as (see eqn (10)) tf ∼ θ0ρR2/DΔc, with θ0 the initial contact angle of the droplet. For the convective timescale we take the time required for a particle to move from a position r to the contact line tc ∼ (R − r)/U with U the characteristic height-averaged velocity (13). Hence
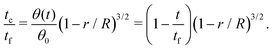 | (28) |
Experimentally, the ring-shaped stain pattern found in droplets with pinned contact lines is remarkably robust and reproducible,1,112–115 in the sense that other factors as particle size or substrate material are subdominant to the capillary flow transporting the particles. Importantly, the accumulation of particles at the contact line due to the capillary flow reinforces the pinning of the contact line (a phenomenon termed self-pinning8,116), thereby increasing the robustness of the ring stain. With the droplet's contact line pinned and therefore static, contact-line dynamics has no influence on the deposition pattern, which results in a reproducible ring stain.
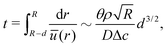 | (29) |
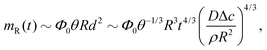 | (30) |
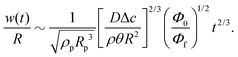 | (31) |
The scaling analysis above is restricted to the case where θ ≪ 90°, due to the simplified expressions used for e.g. the internal velocity field. On hydrophobic substrates, however, similar effects will occur in the later stages of the droplet life: when the contact line remains pinned, the droplet will always pass through a regime where θ ≪ 90° and the majority of the ring stain forms.
5.2 Pinned contact lines and Marangoni flow
Whenever the capillary flow encounters a competing source of flow, most of the streamlines – that previously ended at the static contact line – will now be closed, typically forming eddies distributed radially along the droplet volume (see Fig. 10b). These eddies can occur both due to the presence of forces (Marangoni stresses) at the liquid–gas interface or by volumetric forces (natural convection), as discussed in previous sections. Particles following closed streamlines will be simply circulating within the droplet volume until something stops them. As the droplet volume shrinks, the chances that a particle gets intercepted by the liquid–gas interface, or gets attached to the substrate increase. Nonetheless, from a purely hydrodynamic perspective, one cannot immediately tell where the particles will end up. In the lines below, we will discuss the conditions under which one can make a valid prediction on the particles’ fate.The simplest situation would occur if the particles are lyophilic (i.e. have no tendency to breach the liquid–gas interface) and have low affinity for the solid substrate. In that case, the particles will be simply circulating all over the volume until the solvent is gone. The expected result should be an homogeneous distribution of particles along the droplet's contact area. Note that the nature of the competing flow is not important: thermal,17 solutal118 Marangoni flows or natural convective flows should give similar results. Clearly, in the absence of a hydrodynamic deposition mechanism, non-hydrodynamic forces become more important to determine the final position of the particles. For example, the addition of surface-adsorbed macromolecules to enhance the particle adhesion to the substrate has been shown to promote homogeneous deposition of particles in an evaporating droplet with a dominant Marangoni flow.100 In any case, a homogeneous particle deposition is in general the combined result of the evaporation dynamics and particle-boundary properties.
Another situation in which the particles destination can be predicted, even when the streamlines are closed, occurs when particles are adsorbed at the liquid–air interface. The fate of the particles depends then on the direction of the interfacial flow, and the final pattern depends on the particle concentration. For example, in droplets where a solutal Marangoni flow is directed from the apex to the contact line, particles can get adsorbed at the liquid–air interface and transported towards the contact line, forming a ring-shaped stain. In contrast to the classical 3D ring-shaped stains formed by the capillary flow,1,6 this ring would actually be formed at the liquid–gas interface and is therefore two-dimensional.103,105 When particles adsorb at the interface and the interfacial flow is directed towards the droplet apex, particles would instead accumulate around the apex, either forming a “Marangoni ring” or a cap, depending on the strength of the flow. This is typically observed with thermal Marangoni flows,1,76,119,120 but the final fate of the particles agglomerated at the droplet apex depends on the particle affinity to the liquid interface, the interfacial/bulk flow and the receding interface. Nevertheless, when particle concentration is high enough and/or particles have a strong affinity for the interface,121,122 particles form a dense network that immobilises the interface and leading to an homogeneous deposition of particles. The presence of interfacial Marangoni flows increases the time particles spend in the vicinity of the interface and therefore increases the chances of adsorption. Nevertheless, note that hydrodynamics play a secondary role in this scenario, and the colloidal physico-chemistry is dominant. While there is some degree of understanding on the dominating forces attaching colloids to solid surfaces,123 interfacial adsorption is a complex issue under debate and strongly dependent on the particle surface chemistry and on the solvent's properties.109,124,125 Consequently, homogeneous distributions of particles cannot be achieved by exploiting hydrodynamics only.
We would like to stress that in none of the described situations in this subsection the capillary flow completely disappears. Depending on the strength of the dominant recirculating flow, a region of variable size will always remain in the vicinity of the contact line in which the capillary flow still dominates.22 This capillary flow will transport a certain amount of particles transported towards the contact line, which is manifested by a thin line that denotes the contact line position.17,62,90,126
5.3 Moving contact lines and stick-slip behavior
In pure liquids, the contact-line dynamics is governed by capillary forces (i.e. the unbalanced Young's force) and the interaction with the substrate.127 In suspensions however, the presence of particles induces a self-pinning behaviour:8,116 the particles deposited at the contact line due to the capillary flow provide an additional force128 that keeps the contact line pinned. When the contact angle becomes small enough, the contact line is pulled away from the deposit by the unbalanced Young's force and recedes.8 Often, local depinning occurs and the contact line switches between pinned and depinned states (termed stick-slip129 or stick-slide35 behaviour), leaving behind a trace of heterogeneous deposits.8,129 The strength of these self-pinning events depends on the time the contact line can remain pinned and deposit can accumulate. The pinning time depends on the substrate wettability, manifested in large contact angles (i.e. more space in the wedge-shaped geometry that needs to be filled with particles in order to pin) and larger roughness or contact-angle hysteresis130 (i.e. a large difference between advancing and receding angle, which makes it easier to pin the contact line, and hence increases the pinning time).In the presence of stick-slip motion of the contact line, when the radially outward capillary flow dominates the flow, a pattern of concentric rings is typically left behind. Such a pattern depends on properties such as the evaporation rate, particle concentration and intrinsic viscosity.131 However, if the capillary flow is sub-dominant, the self-pinning effect is typically weaker. Additionally, if the particles do not have a strong affinity for the substrate, the final result is a smooth contact line motion (no stick-slip visible). In that case, most particles will remain in suspension until the droplet evaporates completely, leaving a compact stain at the center of the droplet, much smaller than the initial droplet contact diameter.132
In evaporating droplets with large contact angles, i.e. on hydrophobic and superhydrophobic substrates, the contact line typically recedes smoothly. In these cases, the patterns left by evaporating suspension droplets depend on the contact-line dynamics and the amount of particles in the droplet, rather than on the hydrodynamics of the internal flow. Such systems can yield either flat particle agglomerates, when the particle number is small,133 or three-dimensional spheroids, when the particle number is large.117,133,134
6 Open questions and future directions
In this review we presented our current understanding on evaporation-driven flows in sessile droplets. As we have seen, these tiny and seemingly mundane systems present complicated and surprising physical challenges and have, and will continue having, a great impact on many fields. We hope that our work will help a wide community of scientists to discover (or to relearn) the beautiful science contained in tiny vanishing liquid volumes. Twenty-five years after the appearance of its foundational paper,1 many open questions in the field still remain. Moreover, new challenges appeared over the years, for example through the discovery of active colloids. To conclude our review, we now summarize the most prominent outstanding questions.• Evaporation-driven flows outside the partial wetting regime. Very soon after one leaves the classical configuration of a sessile droplet with pinned contact line and small contact angle, internal flows become hard to determine, both in experiment and in theory. On the one hand, on wetting surfaces with vanishing contact angles a coupling arises between the evaporative flux, internal flow, droplet shape and contact-line dynamics that complicates theoretical progress. On the other hand, on hydrophobic surfaces the droplet geometry poses challenges to both experimental measurements as well as theoretical calculations of the internal flow. Previous asymptotic analyses and the numerical results of the present paper have revealed intriguing reversing flow structures arise at large contact angle that certainly deserve more attention, but would require the development of new experimental techniques to overcome the optical hurdles involved. The impact of these flow structures (if any) on particle deposition patterns also remains to be explored.
• Contact-line singularities. In the contact-line region of an evaporating droplet extremely complicated phenomena are at play, and one quickly encounters the limitations of a continuum description. Even for the classical situation of a pinned droplet on a partial wetting substrate, the physical mechanisms that regularize contact-line singularities in both the evaporative flux and the internal flow field are still far from understood. Progress in this direction is unavoidably linked with the debate on contact-line dynamics.2 Accurate modelling of what happens at the contact line requires a coupling between the macroscopic and the – yet to be clearly defined – microscopic phenomena happening at the contact line in an evaporating droplet.
• Surfactants and contaminants. As we have seen, interfacial-driven flows in water-based droplets are typically two or three orders of magnitude smaller than those obtained by numerical simulations or theoretical predictions. Moreover, while this issue has been first identified in the context of thermal Marangoni flows, it also extends to solutal Marangoni flows. For this reason, Marangoni numbers are not a good indicator for the flow strength in such systems. The most accepted explanation for these observations is the presence of contamination at water–air interfaces. However, the physical chemistry and origin of such ubiquitous contaminants still remain unknown and require further experimental investigation. To our knowledge, none of the surfactants used in the experimental literature23,90,91 share properties with the presumed contaminants. The confirmation of such a contamination effect might lead to a better understanding of surfactant dynamics. The development of accurate surfactant-dynamics models is also essential for further numerical progress on (solutal) Marangoni flows.
• Particle physical-chemistry & deposition patterns. The majority of the literature one can find nowadays on evaporation-driven flows in droplets is motivated by the dream of controlling the patterns that emerge from the non-volatile material within the droplets. This control is often claimed to be achieved by manipulating the hydrodynamic flow. In this context, the only hydrodynamic mechanism capable of achieving a reproducible and general (independent on the type of particle and solvent employed) control on particle deposition is the pure radially outward capillary flow described by Deegan et al.1 As discussed in Section 5, this is the only evaporation-driven flow in which all streamlines end at the contact line, dragging particles towards the contact line in an universal way, independent of their nature. The presence of any additional source of flow unavoidably leads to a closure of the streamlines, and, consequently, the fate of the dispersed particles cannot be determined solely by hydrodynamics. Instead, the particle deposition pattern becomes strongly dependent on the particle physical chemistry, i.e. their adsorption to the solid substrate and to the liquid–air interface, and will be highly specific for the particular system (particles, solvent, substrate) under study.
Many applications require homogeneous deposition patterns.28 An obvious way to obtain such a pattern occurs when evaporation occurs purely in the CCA mode with weak interaction of the particles with the boundaries. The milder capillary flow and the lack of attraction of the particles to the surfaces lead them to end up accumulated at the center of the droplet. How to obtain a pure CCA mode and weak attraction to the surface is of course not trivial, but there are strategies that can be implemented.132,135,136
Evaporation in CCR with a pinned contact line mostly leads to ring-shaped stains. Probably the most effective way of obtaining an homogeneous distribution of particles with pinned contact lines is to have particles adsorb strongly to the liquid–air interface as it recedes, such that an interfacial monolayer of particles is formed.121,122 A few recipes are known to obtain such strong interfacial adhesion, but a proper understanding of the phenomenon and broader exploration of means to achieve it is still lacking.
• Evaporation-driven rheological changes. In Section 5 we have discussed particle deposition in evaporation-driven flow. In our discussion, we always considered the case where the suspension remains dilute up to the moment that the particles get deposited and leave the suspension. In doing so, we have not discussed the complications arising when the non-volatile material that remains in suspension reaches high concentrations during droplet evaporation.
For large particle concentrations, the suspension rheology gets altered. These changes in the suspension's rheological response can be highly localized e.g. at the contact line, where the evaporation is strongest and the particle transport largest.129 The altered rheology can affect both the internal flow and the motion of the contact line and thereby give rise to peculiar deposition patterns,137 such as regularly spaced concentric rings,131,138 striped, fingered or branched structures.139,140
Moreover, a dense contact-line deposit can alter the local flow, which now encounters a porous medium141 with a porosity dependent on the particle size, which in turn affects the deposition pattern. Such models do not consider solutes of different nature, and a modification to take these differences into account would be desirable. How close such models can reproduce the experimentally observed patterns for solid particles, and whether their packing can be predicted, is yet a problem to tackle. A detailed exploration of how both rheological changes and the porous structure of large particles inside a deposit modify the internal flow, contact line motion and thereby give rise to a plethora of different deposition patterns is still lacking. Moreover, a detailed description of the dynamic particle ordering inside the deposit requires a coupling between the macroscopic dense-suspension flow and the microscopic deposition dynamics.141
• Self-propelled colloids. The discovery of active colloidal particles has opened a myriad of possibilities,142,143 not only from the engineering point of view, but for the study of natural systems.144 The presence of synthetic or biological self-propelled particles inside an evaporating-driven flow involves two competing time scales, the particle's own self-propelling time-scale and the droplet's flow time-scale, which lead to a rich and novel scenario. On top of that, hydrodynamic interactions between the active swimmers could give rise to an active stress that locally alters the flow inside an evaporating droplet.145 However, the unavoidable presence of surfactants, salts or other solvent mixtures in such solutions induce solutal Marangoni flows that interfere with the flows under study. Therefore, to understand the interaction between the convective flow and the particle's own propulsion the droplet's evaporation-driven flow needs to be well characterized.91,146
A specially interesting subclass of systems yet to be explored is that of active particles at interfaces147–149 of evaporating droplets. If the interfacial flow is weak enough, such particles would explore the droplet interface at their own time scale, independent of the bulk flow.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Stephen Wilson, Jacco Snoeijer and Detlef Lohse for stimulating discussions. HG acknowledges financial support from the Netherlands Organisation for Scientific Research (NWO) through Veni Grant No. 680-47-451. AM acknowledges financial support from the European Research Council Starting Grant No. 678573.Notes and references
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827–828 CrossRef CAS.
- J. H. Snoeijer and B. Andreotti, Annu. Rev. Fluid Mech., 2013, 45, 269–292 CrossRef.
- H. Cammenga, D. Schreiber, G. Barnes and D. Hunter, J. Colloid Interface Sci., 1984, 98, 585–586 CrossRef CAS.
- A. M. J. Edwards, P. S. Atkinson, C. S. Cheung, H. Liang, D. J. Fairhurst and F. F. Ouali, Phys. Rev. Lett., 2018, 121, 184501 CrossRef CAS PubMed.
- Y. Li, C. Diddens, P. Lv, H. Wijshoff, M. Versluis and D. Lohse, Phys. Rev. Lett., 2019, 122, 114501 CrossRef CAS PubMed.
- A. Marin, H. Gelderblom, D. Lohse and J. H. Snoeijer, Phys. Rev. Lett., 2011, 107, 085502 CrossRef PubMed.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 756 CrossRef CAS PubMed.
- R. D. Deegan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 475 CrossRef CAS PubMed.
- A. M. Cazabat and G. Guéna, Soft Matter, 2010, 6, 2591–2612 RSC.
- H. Erbil, Adv. Colloid Interface Sci., 2012, 170, 67–86 CrossRef CAS PubMed.
- N. Kovalchuk, A. Trybala and V. Starov, Curr. Opin. Colloid Interface Sci., 2014, 19, 336–342 CrossRef CAS.
- S. K. Wilson and B. R. Duffy, Drying of Complex Fluid Drops: Fundamentals and Applications, 2022, vol. 14, p. 47 Search PubMed.
- H.-M. D’Ambrosio and S. Wilson, Annu. Rev. Fluid Mech., 2023, 55, 481–509 Search PubMed.
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739–805 CrossRef CAS.
- H. Hu and R. G. Larson, Langmuir, 2005, 21, 3963–3971 CrossRef CAS PubMed.
- H. Hu and R. Larson, Langmuir, 2005, 21, 3972–3980 CrossRef CAS PubMed.
- H. Hu and R. Larson, J. Phys. Chem. B, 2006, 110, 7090–7094 CrossRef CAS PubMed.
- A. J. Petsi and V. N. Burganos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 036324 CrossRef CAS PubMed.
- H. Masoud and J. D. Felske, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 042102 CrossRef PubMed.
- H. Masoud and J. Felske, Phys. Fluids, 2009, 21, 042102 CrossRef.
- A. Marin, H. Gelderblom, J. Snoeijer and D. Lohse, Phys. Fluids, 2011, 23, 091111 CrossRef.
- H. Gelderblom, O. Bloemen and J. H. Snoeijer, J. Fluid Mech., 2012, 709, 69–84 CrossRef CAS.
- A. Marin, R. Liepelt, M. Rossi and C. J. Kähler, Soft Matter, 2016, 12, 1593–1600 RSC.
- R. Larson, AlChE J., 2014, 60, 1538–1571 CrossRef CAS.
- K. Sefiane, J. Bionic Eng., 2010, 7, S82–S93 CrossRef.
- W. Han and Z. Lin, Angew. Chem., Int. Ed., 2012, 51, 1534–1546 CrossRef CAS PubMed.
- K. Sefiane, Adv. Colloid Interface Sci., 2014, 206, 372–381 CrossRef CAS PubMed.
- D. Mampallil and H. Eral, Adv. Colloid Interface Sci., 2018, 252, 38–54 CrossRef CAS PubMed.
- O. Carrier, N. Shahidzadeh-Bonn, R. Zargar, M. Aytouna, M. Habibi, J. Eggers and D. Bonn, J. Fluid Mech., 2016, 798, 774–786 CrossRef.
- G. J. Dunn, S. K. Wilson, B. R. Duffy, S. David and K. Sefiane, J. Fluid Mech., 2009, 623, 329–351 CrossRef CAS.
- H. Gelderblom, A. G. Marín, H. Nair, A. van Housselt, L. Lefferts, J. H. Snoeijer and D. Lohse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 026306 CrossRef PubMed.
- B. Fischer, Langmuir, 2002, 18, 60–67 CrossRef CAS.
- G. Berteloot, C. T. Pham, A. Daerr, F. Lequeux and L. Limat, Europhys. Lett., 2008, 83, 14003 CrossRef.
- R. G. Picknett and R. Bexon, J. Colloid Interface Sci., 1977, 61, 336–350 CrossRef CAS.
- J. M. Stauber, S. K. Wilson, B. R. Duffy and K. Sefiane, Phys. Fluids, 2015, 27, 122101 CrossRef.
- J. Maxwell, Encyclopedia Britannica, Cambridge, 1877 Search PubMed.
- I. Langmuir, Phys. Rev., 1918, 12, 368–370 CrossRef CAS.
- D. Sen, S. Mazumder, J. Melo, A. Khan, S. Bhattyacharya and S. D’Souza, Langmuir, 2007, 25, 6690–6695 CrossRef PubMed.
- L. Bourouiba, Annu. Rev. Fluid Mech., 2021, 53, 473–508 CrossRef.
- L. Pauchard and Y. Couder, Europhys. Lett., 2004, 66, 667 CrossRef CAS.
- C. Loussert, A. Bouchaudy and J.-B. Salmon, Phys. Rev. Fluids, 2016, 1, 084201 CrossRef.
- A. Petsi and V. Burganos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 047301 CrossRef CAS PubMed.
- Y. Y. Tarasevich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 027301 CrossRef PubMed.
- A. Petsi and V. Burganos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041201 CrossRef CAS PubMed.
- L. Bocquet, Am. J. Phys., 2007, 75, 148 CrossRef.
- A. Oron, S. Davis and S. Bankoff, Rev. Mod. Phys., 1997, 69, 931–980 CrossRef CAS.
- H. Bodiguel and J. Leng, Chem. Eng. Process.: Process Intensification, 2013, 68, 60–63 CrossRef CAS.
- P.-G. De Gennes, Rev. Mod. Phys., 1985, 57, 827 CrossRef CAS.
- C. Huh and L. E. Scriven, J. Colloid Interface Sci., 1971, 35, 85–101 CrossRef CAS.
- M. Cachile, O. Benichou and A. M. Cazabat, Langmuir, 2002, 18, 7985–7990 CrossRef CAS.
- G. Guena, P. Allancon and A.-M. Cazabat, Colloids Surf., A, 2007, 300, 307–314 CrossRef CAS.
- J. Eggers and L. M. Pismen, Phys. Fluids, 2010, 22, 112101 CrossRef.
- S. Morris, J. Fluid Mech., 2014, 793, 308–337 CrossRef.
- C. T. Pham, G. Berteloot, F. Lequeux and L. Limat, Europhys. Lett., 2010, 92, 54005 CrossRef.
- G. Guéna, C. Poulard and A. M. Cazabat, J. Colloid Interface Sci., 2007, 312, 164–171 CrossRef PubMed.
- C. Poulard, O. Benichou and A. M. Cazabat, Langmuir, 2003, 19, 8828–8834 CrossRef CAS.
- C. Poulard, G. Guéna, A. M. Cazabat, A. Boudaoud and M. Ben Amar, Langmuir, 2005, 21, 8226–8233 CrossRef CAS PubMed.
- C. Poulard, G. Guena and A. Cazabat, J. Phys.: Condens. Matter, 2005, 17, S4213–S4227 CrossRef CAS.
- Y. O. Popov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 036313 CrossRef PubMed.
- N. Ledebev, Special functions and their applications, Prentice-Hall, 1965 Search PubMed.
- H. K. Moffatt, J. Fluid Mech., 1964, 18, 1–18 CrossRef.
- W. D. Ristenpart, P. G. Kim, C. Domingues, J. Wan and H. A. Stone, Phys. Rev. Lett., 2007, 99, 234502 CrossRef CAS PubMed.
- G. Navascues, Rep. Prog. Phys., 1979, 42, 1131–1186 CrossRef.
- C. Diddens, H. Tan, P. Lv, M. Versluis, J. G. M. Kuerten, X. Zhang and D. Lohse, J. Fluid Mech., 2017, 823, 470–497 CrossRef CAS.
- G. J. Dunn, S. K. Wilson, B. R. Duffy, S. David and K. Sefiane, Colloids Surf., A, 2008, 323, 50–55 CrossRef CAS.
- F. Schofield, S. Wilson, D. Pritchard and K. Sefiane, J. Fluid Mech., 2018, 851, 231–244 CrossRef CAS.
- T. Nguyen, S. Biggs and A. Nguyen, Langmuir, 2018, 34, 6955–6962 CrossRef CAS PubMed.
- D. Brutin, B. Sobac, F. Rigollet and C. Le Niliot, Exp. Therm. Fluid Sci., 2011, 35, 521–530 CrossRef CAS.
- G. Karapetsas, O. K. Matar, P. Valluri and K. Sefiane, Langmuir, 2012, 28, 11433–11439 CrossRef CAS PubMed.
- F. Carle, B. Sobac and D. Brutin, J. Fluid Mech., 2012, 712, 614–623 CrossRef CAS.
- D. R. Lide, CRC handbook of chemistry and physics, CRC Press, 2004, vol. 85 Search PubMed.
- P. J. Sáenz, K. Sefiane, J. Kim, O. K. Matar and P. Valluri, J. Fluid Mech., 2015, 772, 705–739 CrossRef.
- C. Diddens, J. G. M. Kuerten, C. W. M. Van der Geld and H. M. A. Wijshoff, J. Colloid Interface Sci., 2017, 487, 426–436 CrossRef CAS PubMed.
- X. Xu and J. Luo, Appl. Phys. Lett., 2007, 91, 124102 CrossRef.
- J. R. Trantum, Z. E. Eagleton, C. A. Patil, J. M. Tucker-Schwartz, M. L. Baglia, M. C. Skala and F. R. Haselton, Langmuir, 2013, 29, 6221–6231 CrossRef CAS PubMed.
- M. Rossi, A. Marin and C. J. Kähler, Phys. Rev. E, 2019, 100, 033103 CrossRef CAS PubMed.
- G. Barnes and D. Hunter, J. Colloid Interface Sci., 1982, 88, 437–443 CrossRef CAS.
- J. Pearson, J. Fluid Mech., 1958, 4, 489–500 CrossRef.
- J. Berg and A. Acrivos, Chem. Eng. Sci., 1965, 20, 737–745 CrossRef CAS.
- A. Ponce-Torres, E. Vega and J. Montanero, Exp. Fluids, 2016, 57, 1–12 CrossRef.
- M. Molaei, N. G. Chisholm, J. Deng, J. C. Crocker and K. J. Stebe, Phys. Rev. Lett., 2021, 126, 228003 CrossRef CAS PubMed.
- R. van Gaalen, H. Wijshoff, J. Kuerten and C. Diddens, J. Colloid Interface Sci., 2022, 622, 892–903 CrossRef CAS PubMed.
- C. A. Ward and F. Duan, Phys. Rev. E, 2004, 69, 056308 CrossRef CAS PubMed.
- K. Sefiane and C. A. Ward, Adv. Colloid Interface Sci., 2007, 134–135, 201–223 CrossRef CAS PubMed.
- H. Ghasemi and C. Ward, Phys. Rev. Lett., 2010, 105, 136102 CrossRef CAS PubMed.
- V. Nguyen and K. Stebe, Phys. Rev. Lett., 2002, 88, 164501 CrossRef PubMed.
- H. Stone, Phys. Fluids A, 1990, 2, 111–112 CrossRef CAS.
- J. Chen and K. J. Stebe, J. Colloid Interface Sci., 1996, 178, 144–155 CrossRef CAS.
- H. Manikantan and T. M. Squires, J. Fluid Mech., 2020, 892, P1 CrossRef CAS PubMed.
- T. Still, P. J. Yunker and A. G. Yodh, Langmuir, 2012, 28, 4984–4988 CrossRef CAS PubMed.
- W. Sempels, R. De Dier, H. Mizuno, J. Hofkens and J. Vermant, Nat. Commun., 2013, 4, 1757–1758 CrossRef PubMed.
- G. Karapetsas, K. C. Sahu and O. K. Matar, Langmuir, 2016, 32, 6871–6881 CrossRef CAS PubMed.
- R. van Gaalen, C. Diddens, H. Wijshoff and J. Kuerten, J. Colloid Interface Sci., 2020, 579, 888–897 CrossRef CAS PubMed.
- R. van Gaalen, C. Diddens, H. Wijshoff and J. Kuerten, J. Colloid Interface Sci., 2021, 584, 622–633 CrossRef CAS PubMed.
- C. Diddens, Y. Li and D. Lohse, J. Fluid Mech., 2021, 914, A23 CrossRef CAS.
- J. Thomson, Lond. Edinb. Dublin Philos. Mag. J. Sci., 1855, 10, 330–333 CrossRef.
- J. R. Christy, Y. Hamamoto and K. Sefiane, Phys. Rev. Lett., 2011, 106, 205701 CrossRef PubMed.
- R. Bennacer and K. Sefiane, J. Fluid Mech., 2014, 749, 649–665 CrossRef CAS.
- H. Tan, C. Diddens, P. Lv, J. G. M. Kuerten, X. Zhang and D. Lohse, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8642–8647 CrossRef CAS PubMed.
- H. Kim, F. Boulogne, E. Um, I. Jacobi, E. Button and H. A. Stone, Phys. Rev. Lett., 2016, 116, 124501 CrossRef PubMed.
- C. V. Sternling and L. E. Scriven, AIChE J., 1959, 5, 514–523 CrossRef CAS.
- R. J. Hunter, Foundations of colloid science, Oxford University Press, 2001 Search PubMed.
- A. Marin, S. Karpitschka, D. Noguera-Marín, M. A. Cabrerizo-Vílchez, M. Rossi, C. J. Kähler and M. A. Rodríguez-Valverde, Phys. Rev. Fluids, 2019, 4, 041601 CrossRef.
- D. Brutin and V. Starov, Chem. Soc. Rev., 2018, 47, 558–585 RSC.
- M. A. Bruning, L. Loeffen and A. Marin, Phys. Rev. Fluids, 2020, 5(8), 083603 CrossRef.
- A. Petsi, A. Kalarakis and V. Burganos, Chem. Eng. Sci., 2010, 65, 2978–2989 CrossRef CAS.
- D. Noguera-Marín, C. L. Moraila-Martínez, M. A. Cabrerizo-Vílchez and M. A. Rodríguez-Valverde, Soft Matter, 2015, 11, 987–993 RSC.
- H.-J. Butt, Biophys. J., 1991, 60, 1438–1444 CrossRef CAS PubMed.
- D. M. Kaz, R. McGorty, M. Mani, M. P. Brenner and V. N. Manoharan, Nat. Mater., 2012, 11, 138–142 CrossRef CAS PubMed.
- S. Jafari Kang, V. Vandadi, J. D. Felske and H. Masoud, Phys. Rev. E, 2016, 94, 063104 CrossRef PubMed.
- C. N. Kaplan and L. Mahadevan, J. Fluid Mech., 2015, 781, R2–R13 CrossRef.
- J. Conway, H. Korns and M. R. Fisch, Langmuir, 1997, 1–6 Search PubMed.
- T. Kajiya, D. Kaneko and M. Doi, Langmuir, 2008, 24, 12369–12374 CrossRef CAS PubMed.
- G. Berteloot, A. Hoang, A. Daerr, H. P. Kavehpour, F. Lequeux and L. Limat, J. Colloid Interface Sci., 2012, 370, 155–161 CrossRef CAS PubMed.
- F. Boulogne, F. Ingremeau and H. A. Stone, J. Phys.: Condens. Matter, 2016, 29, 074001 CrossRef PubMed.
- B. M. Weon and J. Je, Phys. Rev. Lett., 2013, 110, 028303 CrossRef PubMed.
- A. Marin, H. Gelderblom, A. Susarrey-Arce, A. van Houselt, H. Gardeniers, D. Lohse and J. H. Snoeijer, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16455–16458 CrossRef CAS PubMed.
- M. Majumder, C. S. Rendall, J. A. Eukel, J. Y. Wang, N. Behabtu, C. L. Pint, T.-Y. Liu, A. W. Orbaek, F. Mirri and J. Nam, et al. , J. Phys. Chem. B, 2012, 116, 6536–6542 CrossRef CAS PubMed.
- M. Parsa, S. Harmand, K. Sefiane, M. Bigerelle and R. Deltombe, Langmuir, 2015, 31, 3354–3367 CrossRef CAS PubMed.
- L. Thayyil Raju, C. Diddens, Y. Li, A. Marin, M. van der Linden, X. Zhang and D. Lohse, Langmuir, 2022, 38, 12082–12094 CrossRef CAS PubMed.
- T. P. Bigioni, X.-M. Lin, T. T. Nguyen, E. I. Corwin, T. A. Witten and H. M. Jaeger, Nat. Mater., 2006, 5, 265–270 CrossRef CAS PubMed.
- P. J. Yunker, T. Still, M. A. Lohr and A. G. Yodh, Nature, 2011, 476, 308–311 CrossRef CAS PubMed.
- Q. Xie and J. Harting, Langmuir, 2018, 34, 5303–5311 CrossRef CAS PubMed.
- N. Ballard, A. D. Law and S. A. F. Bon, Soft Matter, 2019, 15, 1186–1199 RSC.
- J. Vialetto, M. Zanini and L. Isa, Curr. Opin. Colloid Interface Sci., 2021, 101560 Search PubMed.
- R. Malinowski, G. Volpe, I. P. Parkin and G. Volpe, J. Phys. Chem. Lett., 2018, 9, 659–664 CrossRef CAS PubMed.
- D. Orejon, K. Sefiane and M. Shanahan, Langmuir, 2011, 27, 12834–12843 CrossRef CAS PubMed.
- L. Zhang, Y. Nguyen and W. Chen, Colloids Surf., A, 2014, 449, 42–50 CrossRef CAS.
- E. Rio, A. Daerr, F. Lequeux and L. Limat, Langmuir, 2006, 22, 3186–3191 CrossRef CAS PubMed.
- D. Noguera-Marín, C. L. Moraila-Martínez, M. A. Cabrerizo-Vílchez and M. A. Rodríguez-Valverde, Langmuir, 2014, 30, 7609–7614 CrossRef PubMed.
- L. Frastia, A. Archer and U. Thiele, Soft Matter, 2012, 8, 11363 RSC.
- D. Mampallil, H. Eral, D. Van Den Ende and F. Mugele, Soft Matter, 2012, 8, 10614–10617 RSC.
- C. Seyfert, E. J. Berenschot, N. R. Tas, A. Susarrey-Arce and A. Marin, Soft Matter, 2021, 17, 506–515 RSC.
- V. Rastogi, S. Melle, O. G. Calderón, A. A. García, M. Márquez and O. D. Velev, Adv. Mater., 2008, 20, 4263–4268 CrossRef CAS.
- C. L. Moraila-Martínez, M. A. Cabrerizo-Vílchez and M. A. Rodríguez-Valverde, Soft Matter, 2013, 9, 1664 RSC.
- C. L. Moraila-Martínez, M. A. Cabrerizo-Vílchez and M. A. Rodríguez-Valverde, Interfacial Phenom. Heat Transf., 2013, 1, 195–205 CrossRef.
- U. Thiele, Adv. Colloid Interface Sci., 2014, 206, 399–413 CrossRef CAS PubMed.
- A. Dede Eren, D. Eren, T. Wilting, J. de Boer, H. Gelderblom and J. Foolen, Sci. Rep., 2021, 11, 1516 CrossRef CAS PubMed.
- G. Berteloot, A. Hoang, A. Daerr, H. P. Kavehpour, F. Lequeux and L. Limat, J. Colloid Interface Sci., 2012, 370, 155–161 CrossRef CAS PubMed.
- B. Weon and J. Je, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 013003 CrossRef PubMed.
- C. N. Kaplan and L. Mahadevan, J. Fluid Mech., 2015, 781, R2 CrossRef.
- M. Das, C. F. Schmidt and M. Murrell, Soft Matter, 2020, 16, 7185–7190 RSC.
- W. Wang, X. Lv, J. L. Moran, S. Duan and C. Zhou, Soft Matter, 2020, 16, 3846–3868 RSC.
- W. C. K. Poon, Proc. Int. Sch. Phys. Enrico Fermi, 2013, 184, 317–386 CAS.
- T. Kasyap, D. Koch and M. Wu, Phys. Fluids, 2014, 26, 111703 CrossRef.
- T. Andac, P. Weigmann, S. K. P. Velu, E. Pinçe, G. Volpe, G. Volpe and A. Callegari, Soft Matter, 2019, 15, 1488–1496 RSC.
- P. Malgaretti, M. N. Popescu and S. Dietrich, Soft Matter, 2016, 12, 4007–4023 RSC.
- K. Dietrich, D. Renggli, M. Zanini, G. Volpe, I. Buttinoni and L. Isa, New J. Phys., 2017, 19, 065008 CrossRef.
- M. Jalaal, B. T. Hagen, H. L. The, C. Diddens, D. Lohse and A. Marin, arXiv, 2022, preprint, arXiv:2210.03228, pp. 1–10 Search PubMed.
| This journal is © The Royal Society of Chemistry 2022 |