Adsorption of sterically-stabilized diblock copolymer nanoparticles at the oil–water interface: effect of charged end-groups on interfacial rheology

Abstract

The RAFT aqueous emulsion polymerization of either methyl methacrylate (MMA) or benzyl methacrylate (BzMA) is conducted at 70 °C using poly(glycerol monomethacrylate) (PGMA) as a water-soluble precursor to produce sterically-stabilized diblock copolymer nanoparticles of approximately 30 nm diameter. Carboxylic acid- or morpholine-functional RAFT agents are employed to confer anionic or cationic functionality at the ends of the PGMA stabilizer chains, with a neutral RAFT agent being used as a control. Thus the electrophoretic footprint of such minimally-charged model nanoparticles can be adjusted simply by varying the solution pH. Giant (mm-sized) aqueous droplets containing such nanoparticles are then grown within a continuous phase of n-dodecane and a series of interfacial rheology measurements are conducted. The interfacial tension between the aqueous phase and n-dodecane is strongly dependent on the charge of the terminal group on the stabilizer chains. More specifically, neutral nanoparticles produce a significantly lower interfacial tension than either cationic or anionic nanoparticles. Moreover, adsorption of neutral nanoparticles at the n-dodecane–water interface produces higher interfacial elastic moduli than that observed for charged nanoparticles. This is because neutral nanoparticles can adsorb at much higher surface packing densities owing to the absence of electrostatic repulsive forces in this case.

---

Introduction

Pickering emulsions typically comprise oil or water droplets coated with particles dispersed within water or oil respectively.^1,2 The adsorbed particles minimize the interfacial area and provide a physical barrier to prevent droplet coalescence.^3,4 Compared to small molecule surfactants, the particles are strongly adsorbed at the oil–water interface, which leads to relatively stable emulsions.³ The surface wettability of the particles is much more important than their bulk composition: many types of particles have been employed as Pickering emulsifiers, including silica,^5–9 barium sulfate,¹⁰ magnetite,^11,12 clays,^13,14 carbon black,^15,16 latexes,^17,18 microgels^19,20 and sterically-stabilized block copolymer nanoparticles.^21–24 Pickering emulsions offer important advantages over surfactant-stabilized emulsions in terms of long-term stability, reduced foamability, enhanced reproducibility and lower toxicity.^25,26 As such, they are preferred for certain applications, including food manufacture,^27–29 agrochemicals^30–32 and cosmetics formulations.^33–35

A useful model system for understanding Pickering emulsions involves the study of individual mm-sized oil droplets.^36–38 For example, Wanless and co-workers used high-speed video imaging to examine the stability and dynamics of pairs of such oil droplets coated with polystyrene latexes,³⁶ pH-responsive microgels^39,40 or diblock copolymer nanoparticles³⁸ on close approach.^41,42 These studies demonstrate that (i) isolated particle-coated oil droplets exhibit good long-term stability and (ii) complex coalescence dynamics are observed on short time scales when two such giant droplets are brought into close proximity.

The interfacial properties of adsorbed species play a role in determining their efficacy as emulsion stabilizers.^43–48 The interfacial and surface viscoelastic properties of surfactants,^49–53 polymers^51–62 or nanoparticles at the air–water or oil–water interface^49,63–69 have been studied using interfacial dilatational rheology.^70,71 In this technique, an equilibrated interface is subjected to a sinusoidal or step change deformation^72–74 and the resulting change in interfacial tension is used to determine the dilatational moduli, ε. This parameter describes how the interfacial tension, γ, varies with surface area during deformation (ΔA/A₀).

Adsorbed polymers or particles generally form viscoelastic interfaces in which the overall modulus can be separated into an elastic storage modulus (ε′) and a viscous loss modulus (ε′′).

Although most research has focused on the interfacial rheology of adsorbed polymers,⁵⁶ a significant body of work has examined the effect of adsorbed nanoparticles.^{63–69,75–79} Indeed, the effect of adsorbed nanoparticles on the interfacial properties has been the subject of some debate.⁶³ In at least some cases, nanoparticle adsorption appears to have minimal effect on either the interfacial tension or the corresponding interfacial rheology.⁶³

Recently, the adsorption of ‘hairy’ or sterically-stabilized nanoparticles has been shown to reduce the interfacial tension.^63,69 Similarly, both Saigal et al.⁶⁸ and Huang et al.⁶¹ showed that star copolymers comprising crosslinked divinylbenzene cores and poly(ethylene oxide) arms adsorbed strongly at the oil–water interface, reduced the interfacial tension and formed an elastic layer. Such copolymers formed stable Pickering-type emulsions and foams even when used at relatively low copolymer concentrations. In contrast, adsorbed linear poly(ethylene oxide) had little effect on the interfacial tension and led to essentially zero elasticity. Alvarez et al.⁶⁹ reported that the adsorption of hydrophilic silica particles coated with a dense layer of grafted (poly(2-dimethylamino)ethyl methacrylate) (PDMA) chains at pH 7.5 reduced the interfacial tension and afforded elastic interfacial layers for the m-xylene–water system. Moreover, silica particles with lower grafting densities had little effect on the interfacial tension. Similarly, Manga et al.⁶³ demonstrated that the adsorption of pH-responsive polystyrene nanoparticles coated with a PDMA-based diblock copolymer was critically dependent on the degree of protonation of the PDMA stabilizer chains, which behaved as a weak cationic polyelectrolyte. At high pH, the neutral (uncharged) PDMA chains promoted strong adsorption at the hexadecane–water interface. In contrast, the PDMA chains became highly protonated at low pH and the resulting cationic nanoparticles had no effect on the interfacial properties. Remarkably, stable o/w Pickering emulsions could be obtained at both high and low pH, suggesting that interfacial tension and rheology alone are not reliable predictors of emulsion stability. It has been reported that interfacial dilatational elasticity is a key parameter for preventing emulsion coalescence^{44,45,48,49,61} and Ostwald ripening.⁴⁶ Nevertheless, the precise relationship between elasticity and coalescence is not well understood – indeed, there is at least one literature example where a high elasticity alone does not discriminate between good and poor emulsifying agents.⁶⁰ Droplet coalescence is essentially a dilatational process in which the interface becomes stretched during its rupture: Bergeron⁸⁰ suggested that differences in foam or emulsion stability can be explained by taking into account the dilatational viscoelastic effects with respect to prevention of thin film thinning. For w/o emulsions stabilized by Span 80, Carvalho and co-workers⁴⁸ found that the resistance to coalescence was related to the interfacial dilatational properties for systems with the same interfacial tension. Saigal et al.⁶⁸ suggested that the stability of emulsions formed by star copolymers was a result of the elastic nature of the adsorbed layer and their high adsorption energy compared to the analogous linear copolymers.

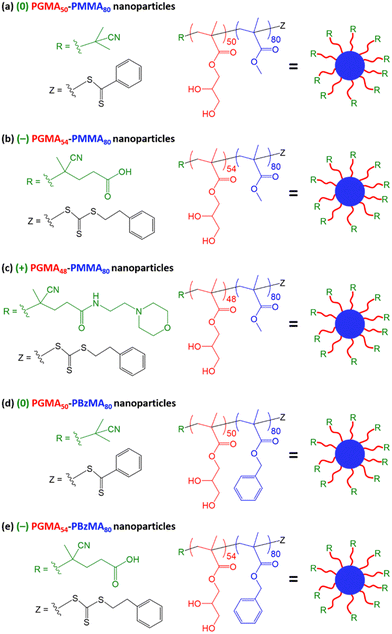
Herein we exploit recent advances in polymerization-induced self-assembly (PISA)^81,82 to design a series of model organic nanoparticles for a fundamental study of the effect of surface charge on the extent of nanoparticle adsorption at the oil–water interface and the influence of such layers on the interfacial rheology. More specifically, reversible addition–fragmentation chain transfer (RAFT) polymerization^83–87 is used to prepare sterically-stabilized diblock copolymer spheres of comparable size in which the steric stabilizer chain-ends comprise neutral/non-ionic, anionic or cationic groups (see Scheme 1). In each case, RAFT aqueous emulsion polymerization is utilized to prepare these nanoparticle dispersions. The solution pH is adjusted to modulate the nanoparticle surface charge and then giant (mm-sized) aqueous droplets containing such nanoparticles are grown within an oil continuous phase (n-dodecane). It is demonstrated that minimal nanoparticle surface charge has a significant effect on the interfacial rheology exhibited by such model systems.

Scheme 1 Schematic representation of the synthesis of (a) dithiobenzoate-capped (0) PGMA₅₀–PMMA₈₀ nanoparticles, (b) carboxylic acid-functionalized trithiocarbonate-based (−) PGMA₅₄–PMMA₈₀ nanoparticles, (c) morpholine-functionalized trithiocarbonate-based (+) PGMA₄₈–PMMA₈₀ nanoparticles, (d) dithiobenzoate-capped (0) PGMA₅₀–PBzMA₈₀ nanoparticles and (e) carboxylic acid-functionalized trithiocarbonate-based (−) PGMA₅₄–PBzMA₈₀ nanoparticles via RAFT aqueous emulsion polymerization. Conditions: ACVA initiator, macro-CTA/ACVA molar ratio = 5.0, and 10% w/w solids was targeted in each case.

Experimental

Materials

Glycerol monomethacrylate (GMA) was donated by GEO Specialty Chemicals (Hythe, UK). Methyl methacrylate (MMA; 99%), benzyl methacrylate (BzMA; 96%), 4,4′-azobis(4-cyanopentanoic acid) (ACVA; 98%), 2,2′-azobisisobutyramide dihydrochloride (AIBA; 99%) and 2-cyano-2-propyl benzodithioate (CPDB; 97%) were purchased from Sigma-Aldrich (UK) and used as received. 4-Cyano-4-(2-phenylethanesulfanylthiocarbonyl)-sulfanylpentanoic acid (PETTC) was prepared according to a literature protocol.⁸⁸ Morpholine-functionalized, trithiocarbonate-based RAFT agent (MPETTC) was prepared according to a literature protocol.⁸⁹

Synthesis of neutral (0) PGMA₅₀ precursor by RAFT solution polymerization in ethanol

GMA monomer (30.0 g, 187 mmol), CPDB RAFT agent (0.589 g, 2.66 mmol; target PGMA DP = 70), ACVA initiator (0.149 g, 0.53 mmol; CPBD/ACVA molar ratio = 5.0) and ethanol (46.5 g, 60% w/w) were weighed into a 250 mL round-bottom flask. The flask was immersed in an ice bath and degassed with N₂ gas for 30 min. Then it was placed in an oil bath set at 70 °C and the ensuing polymerization was quenched after 165 min by exposing the reaction mixture to air while cooling to 20 °C. A final GMA monomer conversion of 71% was determined by ¹H NMR spectroscopy. The reaction solution was diluted with methanol (30 mL) and then the crude polymer was precipitated into a ten-fold excess of dichloromethane (three times). A mean degree of polymerization (DP) of 50 was determined by end-group analysis via¹H NMR spectroscopy (integrated aromatic proton signals at 7.4–7.8 ppm were compared to the methacrylic backbone protons at 0.7–2.5 ppm). A similar protocol was employed for the synthesis of the anionic (−) PGMA₅₄ precursor and the cationic (+) PGMA₄₈ precursor by RAFT solution polymerization in ethanol (see ESI† for further details).

Synthesis of PGMA–PMMA nanoparticles by RAFT aqueous emulsion polymerization of MMA

A typical protocol for the synthesis of (0) PGMA₅₀–PMMA₈₀ diblock copolymer nanoparticles was as follows. The (0) PGMA₅₀ precursor (0.150 g, 18.2 μmol), MMA monomer (0.146 g, 1.46 mmol, target DP = 80), ACVA initiator (1.00 mg, 3.65 μmol, PGMA₅₀/ACVA molar ratio = 5.0) and deionized water (2.675 g, 10% w/w solution) were added to a 20 mL round-bottom flask and the solution was adjusted to pH 7 using 1 M NaOH. The flask was cooled by immersion in an ice bath and the reaction mixture was degassed with N₂ gas for 30 min. Then the flask was placed in an oil bath set at 70 °C. After 3 h, it was removed from the oil bath and the reaction mixture was quenched by exposure to air while cooling to 20 °C. A similar protocol was employed for the synthesis of anionic (−) PGMA₅₄–PMMA₈₀ nanoparticles. A (−) PGMA₅₄ precursor (0.15 g, 16.7 μmol), MMA monomer (0.134 g, 1.33 mmol, target DP = 80), ACVA (0.94 mg, 3.34 μmol, PGMA₅₄/ACVA molar ratio = 5.0) and deionized water (2.561 g, 10% w/w solution) were added to a 20 mL round-bottom flask and the solution was adjusted to pH 7 using 1 M NaOH. A similar protocol was employed for the synthesis of cationic (+) PGMA₄₈–PMMA₈₀ nanoparticles. A (+) PGMA₄₈ precursor (0.15 g, 18.4 μmol), MMA monomer (0.148 g, 1.47 mmol, target DP = 80), ACVA (1.03 mg, 3.69 μmol, PGMA₄₈/ACVA molar ratio = 5.0) and deionized water (2.688 g, 10% w/w solution) were added to a 20 mL round-bottom flask and the solution was adjusted to pH 3 using 1 M HCl. In each case, ¹H NMR spectroscopy studies indicated a final MMA conversion of more than 99% and the nanoparticles were purified by dialysis to remove trace small molecule impurities using dialysis tubing with a molecular weight cut-off of 3500. However, a few interfacial rheology experiments were also performed without further purification (see Results and discussion for further details).

Synthesis of PGMA₅₀–PBzMA₈₀ nanoparticles by RAFT aqueous emulsion polymerization of BzMA

A typical protocol for the synthesis of neutral (0) PGMA₅₀–PBzMA₈₀ diblock copolymer nanoparticles was as follows. The (0) PGMA₅₀ precursor (0.150 g, 18.2 μmol), BzMA monomer (0.257 g, 1.46 mmol, target DP = 80), ACVA initiator (1.00 mg, 3.65 μmol, PGMA₅₀/ACVA molar ratio = 5.0) and deionized water (3.674 g, 10% w/w solution) were added to a 20 mL round-bottom flask and the solution was adjusted to pH 7 using 1 M NaOH. The flask was cooled by immersion in an ice bath and the reaction mixture was degassed with N₂ gas for 30 min. Then the flask was placed in an oil bath set at 70 °C. After 6 h, it was removed from the oil bath and the reaction mixture was quenched by exposure to air while cooling to 20 °C. ¹H NMR spectroscopy studies indicated a final BzMA conversion of 99% and the nanoparticles were used without further purification. A similar protocol was employed for the synthesis of anionic (−) PGMA₅₄–PBzMA₈₀ nanoparticles. The (−) PGMA₅₄ precursor (0.15 g, 16.7 μmol), BzMA monomer (0.235 g, 1.33 mmol, target DP = 80), ACVA (0.94 mg, 3.34 μmol, PGMA₅₄/ACVA molar ratio = 5.0) and deionized water (3.475 g, 10% w/w solution) were added to a 20 mL round-bottom flask and the solution was adjusted to pH 7 using 1 M NaOH.

Dynamic light scattering

Hydrodynamic z-average diameters for 0.1% w/w aqueous dispersions were determined by dynamic light scattering (DLS) at 20 °C using a Malvern Zetasizer NanoZS instrument. Scattered light was detected at a fixed scattering angle of 173° and data were averaged over three consecutive measurements.

Aqueous electrophoresis

Aqueous electrophoresis studies were performed using the same Malvern Zetasizer NanoZS instrument. In this case, 0.1% w/w aqueous dispersions were analyzed at 20 °C in the presence of 1 mM KCl as background electrolyte, with the solution pH being adjusted as required using either NaOH or HCl. Zeta potentials were calculated via the Henry equation using the Smoluchowski approximation. Data were averaged over three consecutive measurements.

Gel permeation chromatography (GPC)

Molecular weight distributions for the three PGMA precursors and the various corresponding diblock copolymers were analyzed at 60 °C using a GPC set-up comprising two Polymer Laboratories PL gel 5 μm Mixed-C columns connected in series with a Varian 290-LC pump injection module and a refractive index detector at a flow rate of 1.0 mL min⁻¹. The eluent was HPLC-grade DMF containing 10 mM LiBr and a series of near-monodisperse PMMA standards (M_p values ranging from 645 g mol⁻¹ to 618 000 g mol⁻¹) were used to calibrate the instrument.

Transmission electron microscopy

Copper/palladium TEM grids (Agar Scientific, UK) were surface-coated with a thin film of amorphous carbon. Each grid was exposed to a plasma glow discharge for 30 s to produce a hydrophilic surface. One 10 μL droplet of a 0.10% w/w aqueous dispersion was carefully placed onto a grid using a micropipet and left for 1 min before blotting to remove excess liquid. The adsorbed nanoparticles were then stained using a 0.75% w/w aqueous solution of uranyl formate (9.0 μL) for 20 s before blotting to remove excess stain. Each grid was dried under vacuum and images were recorded at 100 kV using a Philips CM100 instrument equipped with a Gatan 1 k CCD camera.

Small-angle X-ray scattering (SAXS)

SAXS patterns were recorded for 1.0% w/w aqueous dispersions within 2.0 mm diameter glass capillary cells over a scattering vector q range of 0.04–0.4 Å⁻¹ using a Xeuss 2.0 (Xenocs) SAXS instrument equipped with a Dectris Pilatus 1 M detector and an Excillum liquid gallium MetalJet X-ray source (λ = 1.34 Å). The X-ray scattering of deionized water was used for absolute intensity calibration. Igor Pro software with the appropriate Irena SAS macros were used for background subtraction, normalization and further data analysis.⁹⁰

Interfacial tension measurements

The interfacial tension between 0.1% w/w aqueous dispersions of various diblock copolymer nanoparticles and n-dodecane was determined using a DataPhysics ODG20 tensiometer by optical profilometry. The pH-sensitive nanoparticles were analyzed at pH 3 and pH 7, while the non-ionic nanoparticles were examined at pH 7 alone. Droplets of the aqueous copolymer dispersions were formed in n-dodecane with the aid of an Agla micrometer screw gauge using a 1.0 mL syringe equipped with a 1.65 mm o.d. needle. The droplet volume was approximately 20 mm³ and the droplets were formed on a timescale of 1–2 s. Once the aqueous droplet had been formed, its shape was analyzed at 1 s intervals using software provided by the instrument manufacturer to determine the change in interfacial tension over time. The interfacial tension of the bare n-dodecane–water interface was 52 mN m⁻¹, which is in satisfactory agreement with literature data.⁹¹ All measurements were performed at 21.0 ± 0.5 °C.

Interfacial rheology measurements

Interfacial dilatational moduli for the adsorbed nanoparticles at the n-dodecane/water interface were determined for the same aqueous droplets that were used for the initial interfacial tension measurements. These droplets were allowed to reach equilibrium overnight (ca. 17 h), with the interfacial tension showing no significant further time dependence. Equilibrated droplets were then dilated using the micrometer syringe such that the interfacial area was increased by 5–12% within 0.50 seconds. The interfacial tension increased during droplet expansion and subsequently decayed over time as the interface was allowed to regain its equilibrium state. The droplet shape was recorded as a video both before and for 20 000 seconds after the expansion. The video frame rate was reduced exponentially from an initial rate of 12.5 frames per second to 0.125 frames per second. The resulting videos were analyzed using the instrument software for both droplet area and interfacial tension, which allowed both the fractional increase in interfacial area, ΔA/A₀, and the temporal decay in interfacial tension, Δγ(t), to be determined. The full decay function β(t) (= A₀Δγ(t)/ΔA) versus time was fitted to either a triple exponential decay function or to two separate triple exponential decay functions using the data analysis package Origin (version 6). This approach enabled the data to be reproduced at 200 ms intervals over the entire decay period of 20 000 seconds, with this constant time interval being required for the data analysis. For the two-part fitting, the decay was split into two parts spanning 0 to 200 seconds and 200 to 20 000 seconds. This protocol was implemented in cases where the initial decay curve was too steep for the whole curve to be satisfactorily fitted. This approach was required for the two non-ionic nanoparticles and also for the three pH-sensitive nanoparticles in their uncharged form. The fitted curves were converted to frequency-dependent elastic and viscous moduli in the frequency range of 4 × 10⁻⁵ to 1.0 rad s⁻¹ by calculating the Fourier transform of the decay curve via numerical integration within Excel (further details are provided in the ESI†).

Results and discussion

Synthesis and characterization of spherical diblock copolymer nanoparticles

Three PGMA precursors were prepared via RAFT solution polymerization of GMA in ethanol using the following RAFT agents in turn: neutral CPDB,²¹ carboxylic acid-functionalized PETTC⁹² and morpholine-functionalized MPETTC.⁸⁹ End-group analysis by ¹H NMR spectroscopy indicated mean PGMA DPs of 50, 54 and 48, respectively. Each PGMA precursor was then subsequently chain-extended via RAFT aqueous emulsion polymerization of either methyl methacrylate (MMA) or benzyl methacrylate (BzMA) at 70 °C using an ACVA initiator and a core-forming block DP of 80 was targeted in each case. The corresponding chemical structures and schematic cartoons for the resulting sterically-stabilized diblock copolymer nanoparticles are summarized in Scheme 1.

A shorthand notation is used to denote each type of nanoparticle: ‘(0)’ refers to permanently neutral nanoparticles prepared using CPDB, ‘(−)’ refers to nanoparticles prepared using PETTC and ‘(+)’ refers nanoparticles prepared using MPETTC. Thus the ‘(−)’ and ‘(+)’ is a reminder that such nanoparticles may acquire either anionic or cationic surface charge with appropriate adjustment of the solution pH, rather than indicating the actual surface charge for a given set of conditions. In this context, it is worth bearing in mind that the pK_a values for the terminal carboxylic acid and protonated morpholine groups are 4.7 and 6.3 respectively, as previously reported.^89,92

TEM studies confirmed that spherical nanoparticles were obtained for each PISA synthesis (Table 1 and Fig. 1). Furthermore, dynamic light scattering (DLS) analysis indicated that these sterically-stabilized nanoparticles had hydrodynamic z-average diameters ranging between 28 and 33 nm and relatively low DLS polydispersities (Table 1 and Fig. 1). SAXS patterns (Fig. 2) were fitted using a well-known spherical micelle model⁹³ to determine the mean core diameter and an associated standard deviation for each type of nanoparticle (Table 1). As expected, the core diameters determined for the three types of PGMA–PMMA nanoparticles and (−) PGMA₅₄–PBzMA₈₀ nanoparticles were comparable at 14.5 nm to 15.9 nm. However, the (0) PGMA₅₀–PBzMA₈₀ nanoparticles had an unexpectedly larger mean core diameter of 20.5 nm.

Table 1 Summary of mean hydrodynamic z-average diameters determined by DLS and core diameters calculated from SAXS analysis of (0) PGMA₅₀–PMMA₈₀, (−) PGMA₅₄–PMMA₈₀, (+) PGMA₄₈–PMMA₈₀, (0) PGMA₅₀–PBzMA₈₀ and (−) PGMA₅₄–PBzMA₈₀ nanoparticles

Diblock copolymer composition	RAFT agent	DLS z-average diameter/nm	DLS polydispersity	TEM morphology	SAXS core diameter/nm
(0) PGMA50–PMMA80	CPDB	29	0.04	Spheres	15.7 ± 1.9
(−) PGMA54–PMMA80	PETTC	28	0.06	Spheres	15.9 ± 2.8
(+) PGMA48–PMMA80	MPETTC	33	0.09	Spheres	14.5 ± 3.3
(0) PGMA50–PBzMA80	CPDB	33	0.04	Spheres	20.5 ± 2.0
(−) PGMA54–PBzMA80	PETTC	30	0.06	Spheres	15.2 ± 2.8

---

Fig. 1 (a) DLS intensity-average size distributions and (b–f) representative TEM images obtained for (0) PGMA₅₀–PMMA₈₀ (black), (−) PGMA₅₄–PMMA₈₀ (blue), (+) PGMA₄₈–PMMA₈₀ (red), (0) PGMA₅₀–PBzMA₈₀ (purple) nanoparticles and (−) PGMA₅₄–PBzMA₈₀ (orange).

Fig. 2 SAXS patterns recorded for 1.0% w/w aqueous dispersions of (0) PGMA₅₀–PMMA₈₀, (−) PGMA₅₄–PMMA₈₀, (0) PGMA₅₀–PBzMA₈₀ and (−) PGMA₅₄–PBzMA₈₀ nanoparticles at pH 7. In contrast, the SAXS pattern for the (+) PGMA₄₈–PMMA₈₀ nanoparticles (red curve) was recorded at pH 5.

Aqueous electrophoresis studies were undertaken on the PGMA–PMMA nanoparticles prepared using three different RAFT agents (Fig. 3). As expected, the (0) PGMA₅₀–PMMA₈₀ diblock copolymers exhibited zeta potentials close to zero (i.e., −2 to −3 mV) across the entire pH range owing to the non-ionic nature of the end-groups on the steric stabilizer chains. In contrast, the terminal morpholine groups confer cationic character on the (+) PGMA₄₈–PMMA₈₀ nanoparticles, which had zeta potentials of around +12 to +15 mV below pH 5. The (−) PGMA₅₄–PMMA₈₀ nanoparticles exhibited complementary behavior: ionization leads to the formation of an anionic carboxylate end-group, which confers a negative zeta potential (approximately −15 mV). In a related recent study, we reported that a similar series of three sterically-stabilized PGMA–PTFEMA nanoparticles exhibited strongly pH-dependent behavior when employed as emulsifiers for the preparation of n-dodecane-in-water Pickering nanoemulsions.⁹⁴ More specifically, charged nanoparticles adsorbed less efficiently at the oil–water interface than neutral nanoparticles. Moreover, nanoemulsion droplets prepared using the former nanoparticles exhibited significantly poorer long-term stability as judged by analytical centrifugation. These observations informed our current study, which is focused on interfacial rheology studies of mm-sized aqueous droplets grown in n-dodecane.

Fig. 3 Zeta potential vs pH curves constructed for dilute aqueous dispersions of: (a) (+) PGMA₄₈–PMMA₈₀ nanoparticles prepared using the morpholine-functionalized PGMA₄₈ precursor; (b) (0) PGMA₅₀–PMMA₈₀ nanoparticles prepared using the non-ionic PGMA₅₀ precursor; (c) (−) PGMA₅₄–PMMA₈₀ nanoparticles prepared using the carboxylic acid-functionalized PGMA₅₄ precursor.

Interfacial tension measurements

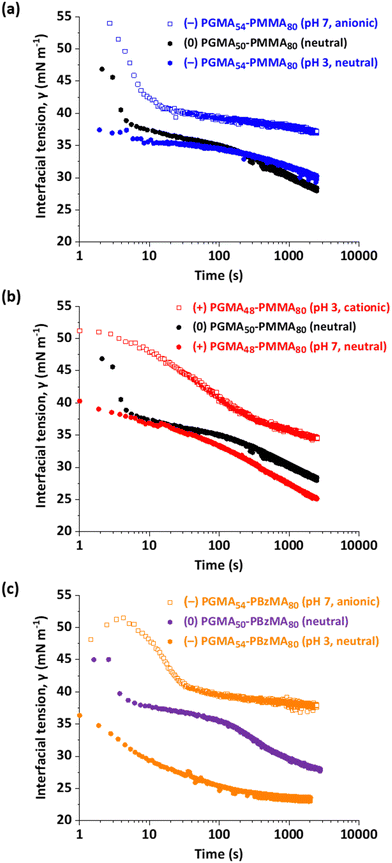
Interfacial adsorption of surfactants, polymers or nanoparticles at a surface necessarily depletes their concentration in the bulk solution. This is potentially problematic when the surface-active species is contained within a 20 mm³ droplet of relatively large surface area, as is the case herein for the interfacial tension experiments on diblock copolymer nanoparticles. This effect becomes increasingly important at low nanoparticle concentrations. However, the copolymer concentration is 0.1% w/w, which is sufficiently high for this issue to be negligible. More specifically, if the adsorbed amount is of the order of 5 mg m⁻² (which is a realistic value for adsorbed nanoparticles) and the actual droplet volume and surface area are 20 mm³ and 30 mm² respectively, then we calculate that the adsorbed amount is of the order of 1% of the total number of nanoparticles within the aqueous droplet. Thus, interfacial adsorption leads to a minimal change in the concentration of non-adsorbed nanoparticles.

Fig. 4 shows the time-dependent dynamic surface tension curves obtained for a series of 20 mm³ aqueous droplets containing 0.1% nanoparticles formed in n-dodecane. Clearly, nanoparticle adsorption at the water/n-dodecane significantly reduces the interfacial tension compared to that for the bare n-dodecane–water interface (52 mN m⁻¹). Similar observations have been reported for polymer-grafted silica or polystyrene particles by Alvarez et al.⁶⁹ and Manga et al.⁶³ In the present study, both the magnitude and the initial rate of reduction in the dynamic interfacial tension depend markedly on whether the steric stabilizer chains contain a neutral or a charged end-group. For the non-ionic (0) PGMA₅₀–PMMA₈₀ and (0) PGMA₅₀–PBzMA₈₀ nanoparticles, a rapid initial reduction in dynamic interfacial tension to below 40 mN m⁻¹ was achieved within approximately 5 s. It is perhaps worth emphasizing that droplet formation took ca. 1–2 s. Within this short time frame, sufficient neutral nanoparticles had adsorbed at the n-dodecane–water interface to reduce the dynamic interfacial tension to well below that of pure n-dodecane. Similar behavior was observed with nanoparticles bearing terminal carboxylic acid or morpholine groups, provided that each of these groups was present in their uncharged form. However, we cannot rule out specific end-group effects on the interfacial tension because the morpholine- and the carboxylic acid-functionalized nanoparticles each exhibited a faster initial reduction in dynamic interfacial tension in their uncharged form compared to the permanently non-ionic nanoparticles bearing isobutyrylnitrile end-groups. On the other hand, minor differences in the nanoparticle core diameter and/or PGMA chain length may also influence both the magnitude and the rate of reduction of the dynamic interfacial tension. In this context, nanoparticles bearing either neutral or carboxylic acid end-groups exhibited almost identical PMMA–core diameters of 15.9 and 15.7 nm respectively, whereas the PBzMA–core nanoparticles bearing neutral end-groups had a somewhat larger mean core diameter of 20.5 nm.

Fig. 4 Initial interfacial tension vs. time curves recorded for 20 mm³ droplets immersed in n-dodecane, where the droplet phase comprises the following 0.1% w/w aqueous copolymer dispersions. (a) (0) PGMA₅₀–PMMA₈₀ nanoparticles prepared using the non-ionic PGMA₅₀ precursor and (−) PGMA₅₄–PMMA₈₀ (pH 7, anionic) nanoparticles and (−) PGMA₅₄–PMMA₈₀ (pH 3, neutral) nanoparticles prepared using the carboxylic acid-functionalized PGMA₅₄ precursor. (b) (0) PGMA₅₀–PMMA₈₀ nanoparticles prepared using the non-ionic PGMA₅₀ precursor and (+) PGMA₄₈–PMMA₈₀ (pH 3, cationic) nanoparticles and (+) PGMA₄₈–PMMA₈₀ (pH 7, neutral) nanoparticles prepared using the morpholine-functionalized PGMA₄₈ precursor. (c) (0) PGMA₅₀–PBzMA₈₀ nanoparticles prepared using the non-ionic PGMA₅₀ precursor, (−) PGMA₅₄–PBzMA₈₀ (pH 7, anionic) nanoparticles and (−) PGMA₅₄–PBzMA₈₀ (pH 3, neutral) nanoparticles prepared using the carboxylic acid-functionalized PGMA₅₄ precursor.

When allowed to equilibrate overnight (approximately 17 h), each nanoparticle dispersion exhibited a further modest reduction in interfacial tension of 1–3 mN m⁻¹ compared to that observed after 2500 s. Saigal et al. reported a similarly slow reduction in interfacial tension when allowing star copolymers comprising divinylbenzene cores and poly(ethylene oxide) arms to equilibrate overnight at the water/m-xylene interface.⁶⁸ For all three pH-sensitive nanoparticles, the charged nanoparticles exhibited a higher interfacial tension relative to the corresponding neutral nanoparticles. The lowest interfacial tension was obtained for the neutral PBzMA–core nanoparticles and all of the neutral nanoparticles had interfacial tensions in the 20.9–25.0 mN m⁻¹ range. Moreover, the morpholine-bearing PMMA–core nanoparticles exhibited lower interfacial tensions at both pH 3 and pH 7 compared to the corresponding carboxylic acid-bearing PMMA–core nanoparticles. More specifically, the former nanoparticles had an interfacial tension of 20.9 mN m⁻¹ while the latter nanoparticles had an interfacial tension of 25 mN m⁻¹ in their respective neutral forms. Similarly, the cationic morpholine-capped and anionic carboxylate-capped PMMA–core nanoparticles exhibited interfacial tensions of 29.5 mN m⁻¹ and 35.6 mN m⁻¹ respectively. Clearly, the introduction of terminal ionic groups significantly reduces the propensity for such sterically-stabilized nanoparticles to adsorb at the n-dodecane–water interface.

Furthermore, the carboxylic acid-capped PBzMA–core nanoparticles exhibited comparable equilibrium dynamic interfacial tension data at pH 3 and pH 7 to that observed for the corresponding carboxylic acid-capped PMMA–core nanoparticles. This suggests that the nature of the core-forming block has little or no influence on the interfacial adsorption behavior. Finally, the slightly lower dynamic interfacial tension data obtained for the morpholine-capped nanoparticles suggests that this terminal group is marginally more hydrophobic in its neutral form than the corresponding carboxylic acid end-group.

Clearly, there are subtle differences between the five examples of uncharged nanoparticles, which reduce the equilibrium n-dodecane/water interfacial tension to approximately 20–26 mN m⁻¹ (see Table 2). This is attributed to a combination of end-group effects, and differing degrees of polymerization of the steric stabilizer and core-forming chains (with the latter two parameters affecting both the mean core radius and the number concentration of the nanoparticles). More importantly, neutral nanoparticles exhibit faster initial adsorption kinetics and significantly lower equilibrium interfacial tension (by approximately 8–11 mN m⁻¹) than either cationic or anionic nanoparticles. Recently, we reported that the adsorbed amount of closely related sterically-stabilized diblock copolymer nanoparticles at the surface of n-dodecane droplets was sensitive to whether the morpholine or carboxylic acid end-groups had acquired charge, with the neutral form of such nanoparticles exhibiting approximately twice the surface coverage compared to the analogous charged nanoparticles.⁹⁴ The same pH-dependent adsorption behavior at an oil/water interface is expected for the morpholine- and carboxylic acid-functionalized nanoparticles described herein, which accounts for the striking differences in the equilibrium interfacial tension. Similarly, the differing initial rates of lowering the interfacial tension are attributed to mutual electrostatic repulsion between charged nanoparticles adsorbed at the oil–water interface. Thus, initial adsorption is diffusion-controlled since the adsorbed charged nanoparticles are effectively isolated from each other at very low surface coverage. However, the gradual accumulation of charged nanoparticles at the oil–water interface eventually leads to the electrostatic repulsion of incoming nanoparticles, leading to an effective activation energy for adsorption and a significantly lower final surface coverage compared to that achieved when using the corresponding neutral nanoparticles.

Table 2 Summary of the equilibrium interfacial tension data and high frequency moduli, β(0), determined for nanoparticles adsorbed at the surface of a 20 mm³ aqueous droplet immersed in n-dodecane for the following systems: neutral (i.e. (0) PGMA₅₀–PMMA₈₀ and (0) PGMA₅₀–PBzMA₈₀), carboxylic acid-functionalized (−) PGMA₅₄–PMMA₈₀ and (−) PGMA₅₄–PBzMA₈₀ or morpholine-functionalized (+) PGMA₄₈–PMMA₈₀ nanoparticles at either pH 3 or pH 7. Data in bold refer to charged (anionic or cationic) nanoparticles

Diblock copolymer composition	Equilibrium interfacial tension/mN m^−1		High frequency elastic modulus, β(0)/mN m^−1
	pH 3	pH 7	pH 3	pH 7
(0) PGMA50–PMMA80	—	22.6 ± 1.1	—	41 ± 7
(−) PGMA54–PMMA80	25.0 ± 1.1	35.6 ± 1.6	26 ± 3	12 ± 2
(+) PGMA48–PMMA80	29.5 ± 1.5	21.5 ± 0.8	15 ± 2	62 ± 13
(0) PGMA50–PBzMA80	—	20.9 ± 0.1	—	127 ± 72
(−) PGMA54–PBzMA80	23.1 ± 1.2	34.6 ± 0.9	44 ± 8	8.5 ± 2.0

---

Interfacial rheology measurements

Fig. 5 shows a representative plot of interfacial tension before and after volumetric expansion of an aqueous 20 mm³ droplet of a 0.1% w/w copolymer dispersion immersed in n-dodecane, with a 5–10% change in surface area occurring within a timescale of 500 ms. This expansion causes the interfacial tension to increase by an amount that depends on both the interfacial modulus and the fractional increase in surface area.

Fig. 5 Initial response of interfacial tension with time to the applied step change in droplet surface area at zero time for a 20 mm³ droplet containing a 0.1% w/w aqueous dispersion of (0) PGMA₅₀–PMMA₈₀ nanoparticles at pH 7 immersed in n-dodecane.

Fig. 6 shows the decay function, β(t) over time observed for a 20 mm³ droplet containing a 0.1% w/w aqueous dispersion of (−) PGMA₅₄–PMMA₈₀ nanoparticles immersed in n-dodecane. Clearly, the decay timescale is pH-dependent: the interfacial tension returns close to its equilibrium value within 18 000 s (5.0 h) for the anionic nanoparticles at pH 7, whereas full relaxation had not occurred within 21 000 s (5.8 h) for the neutral nanoparticles at pH 3. The pH 7 data set has greater scatter owing to the smaller change in interfacial tension compared to that at pH 3 and the experimental error in the interfacial tension is magnified when normalized to the fractional change in droplet surface area.

Fig. 6 Variation in the decay function β(t) over time for a 20 mm³ droplet containing a 0.1% w/w aqueous dispersion of (−) PGMA₅₄–PMMA₈₀ nanoparticles at either pH 3 or pH 7 immersed in n-dodecane.

For all systems studied herein, an initial rapid decay was followed by a more gradual reduction. The initial value of the decay function, β(0), is essentially the high frequency modulus of the adsorbed layer of nanoparticles at the oil/water interface and these data are summarized in Table 2. This parameter is pH-sensitive: significantly larger values are observed for neutral nanoparticles compared to charged nanoparticles. Such moduli are subject to relatively large experimental uncertainty owing to the steep initial decay plus variation in the step change for the droplet surface area. The widest range of β(0) values was observed for the (0) PGMA₅₀–PBzMA₈₀ nanoparticles but the reason for the relatively poor reproducibility in this particular case is not clear. Given these caveats, the high frequency moduli are best viewed as indicators of relative differences between various types of nanoparticles, rather than absolute parameters. To better understand the interfacial behavior of the nanoparticles, the β(t) decay curves were subjected to Fourier transform analysis to determine their elastic and viscous components; these two parameters are obtained over much longer timescales and are hence more consistent.^72–74 The magnitude of the initial rise in β(t) on droplet expansion reflects the high frequency elastic response of the adsorbed layer of nanoparticles as the interfacial excess is reduced. The decay back to the equilibrium interfacial tension represents the viscous response and depends on relaxation processes: over short time scales, this is likely to be dominated by rearrangement of the adsorbed steric stabilizer chains.⁵⁶ Alvarez et al.⁶⁹ partly ascribed the frequency-independent elastic modulus (i.e. no viscous relaxation) of adsorbed silica nanoparticles bearing grafted PDMA chains to the lack of exchange between the adsorbed nanoparticles and the bulk solution on the timescale of their measurements (1.9–25 rad s⁻¹). Facile transfer of nanoparticles to and from the interface during oscillation reduces the variation in interfacial tension during oscillation, leading to increasingly viscoelastic (rather than purely elastic) behavior. However, over the longer time scales employed for the relaxation measurements reported herein, nanoparticle adsorption from the bulk solution is expected to restore the original nanoparticle surface coverage, thus facilitating relaxation back to equilibrium.

The magnitudes of the interfacial elastic moduli obtained for the various adsorbed nanoparticle layers – both as a function of angular frequency (Fig. 7) and at a fixed arbitrary frequency (see Table 3 overleaf) – are strongly dependent on the solution pH for the morpholine- or carboxylic acid-functionalized PMMA–core nanoparticles. Similar behavior was observed for the carboxylic acid-functionalized PBzMA–core nanoparticles, although the moduli were somewhat lower in this case. However, adsorption of the neutral (0) PGMA₅₀–PBzMA₈₀ nanoparticles resulted in a significantly higher modulus (58.9 mN m⁻¹; see Table 3) than that for the corresponding neutral (0) PMMA–core nanoparticles (27.9 mN m⁻¹), although the differing nanoparticle core diameters (15.7 vs. 20.5 nm) complicates this comparison. The neutral PMMA–core nanoparticles exhibited broadly similar behavior to that of the carboxylic acid- or morpholine-functionalized nanoparticles in their uncharged form, with moduli ranging from 10 to 60 mN m⁻¹. In contrast, the moduli for the corresponding charged form of the latter two types of nanoparticles varied from 0 to 10 mN m⁻¹ over the same frequency range.

Fig. 7 Interfacial elastic modulus vs. angular frequency curves obtained for 20 mm³ droplets immersed in n-dodecane, where the droplet phase comprises the following 0.1% w/w aqueous copolymer dispersions. (a) (0) PGMA₅₀–PMMA₈₀ nanoparticles, (−) PGMA₅₄–PMMA₈₀ (pH 7, anionic) nanoparticles and (−) PGMA₅₄–PMMA₈₀ (pH 3, neutral) nanoparticles. (b) (0) PGMA₅₀–PMMA₈₀ nanoparticles, (+) PGMA₄₈–PMMA₈₀ (pH 3, cationic) nanoparticles and (+) PGMA₄₈–PMMA₈₀ (pH 7, neutral) nanoparticles. (c) (0) PGMA₅₀–PBzMA₈₀ nanoparticles, (−) PGMA₅₄–PBzMA₈₀ (pH 7, anionic) nanoparticles and (−) PGMA₅₄–PBzMA₈₀ (pH 3, neutral) nanoparticles.

Table 3 Summary of interfacial elastic moduli (ε′), viscous moduli (ε′′) and phase angle (ϕ) obtained at an arbitrary angular frequency of 0.125 rad s⁻¹ for 20 mm³ droplets immersed in n-dodecane, where the droplet phase comprises the following 0.1% w/w aqueous copolymer dispersions in turn: (0) PGMA₅₀–PMMA₈₀, (−) PGMA₅₄–PMMA₈₀, (+) PGMA₄₈–PMMA₈₀, (0) PGMA₅₀–PBzMA₈₀ and (−) PGMA₅₄–PBzMA₈₀ nanoparticles at pH 3 and pH 7. Data shown in bold refer to charged (i.e., anionic or cationic) nanoparticles

Diblock copolymer composition	ε′/mN m^−1		ε′′/mN m^−1		Phase angle ϕ/°
	pH 3	pH 7	pH 3	pH 7	pH 3	pH 7
(0) PGMA50–PMMA80	—	27.9	—	3.6	—	7.3
(−) PGMA54–PMMA80	21.4	10.2	0.17	0.74	0.46	4.1
(+) PGMA48–PMMA80	13.8	40.3	0.18	7.50	0.80	10.5
(0) PGMA50–PBzMA80	—	58.9	—	13.8	—	13.1
(−) PGMA54–PBzMA80	14.0	6.8	2.50	0.12	10.3	1.00

---

Interestingly, the adsorbed non-ionic (0) PGMA₅₀–PBzMA₈₀ nanoparticles exhibited much higher interfacial elastic moduli than the other types of nanoparticles but there was significantly greater data scatter between runs for the former system. Moreover, the adsorbed (−) PGMA₅₄–PBzMA₈₀ nanoparticles exhibited much lower interfacial elastic moduli than the corresponding permanently neutral (0) PGMA₅₀–PBzMA₈₀ nanoparticles, regardless of the solution pH (see Fig. 7c). The reason(s) for this difference are not clear but such comparisons are complicated by differences in the nanoparticle core diameter, as noted above.

The frequency dependence for the elastic modulus of the adsorbed layer suggests that different processes are relevant at differing relaxation timescales for the adsorbed nanoparticles. At low frequencies (i.e. long relaxation times), nanoparticle adsorption from the bulk solution restores the nanoparticle surface coverage to its original equilibrium value.

At higher frequencies, the timescale becomes too short for nanoparticle adsorption to occur. In this case, the interface becomes almost entirely elastic in its response. Instead, relaxation must be attributed to changes in conformation for the steric stabilizer chains at the surface of the adsorbed nanoparticles. The high elasticity of the nanoparticle–laden interface is indicated by the phase angle (ϕ), which is given by tan ϕ = ε′′/ε′. Phase angle vs. frequency plots are shown in Fig. 8. A purely elastic interfacial layer should exhibit a phase angle of zero. The neutral (0) PGMA₅₀–PMMA₈₀ nanoparticles approached this limiting value at high frequency. More specifically, phase angles were less than 10° at frequencies above 10⁻² rad s⁻¹ (see Table 3 for typical values determined at an arbitrary frequency of 0.125 rad s⁻¹), suggesting that no significant additional adsorption occurs on this timescale. In contrast, higher phase angles (ca. 20°) are observed at lower frequencies (10⁻⁴ rad s⁻¹). The morpholine- and carboxylic acid-functionalized nanoparticles exhibited broadly similar behavior in their neutral form to that observed for the permanently non-ionic nanoparticles. In contrast, a rapid increase in phase angle up to 70° was observed for the corresponding cationic or anionic nanoparticles in the low-frequency regime, which indicates a greater viscous component for the rheological response (a purely viscous response has a phase angle of 90°). This suggests that interfacial adsorption of additional charged nanoparticles to restore the surface coverage to its former equilibrium value occurs over longer timescales (or lower frequencies). This important point is discussed in more detail below.

Fig. 8 Phase angle, ϕ, vs. angular frequency curves obtained for 0.1% w/w aqueous dispersions of the following nanoparticles adsorbed at the n-dodecane–water interface. (a) (0) PGMA₅₀–PMMA₈₀ nanoparticles, (−) PGMA₅₄–PMMA₈₀ (pH 7, anionic) nanoparticles and (−) PGMA₅₄–PMMA₈₀ (pH 3, neutral) nanoparticles. (b) (0) PGMA₅₀–PMMA₈₀ nanoparticles, (+) PGMA₄₈–PMMA₈₀ (pH 3, cationic) nanoparticles and (+) PGMA₄₈–PMMA₈₀ (pH 7, neutral) nanoparticles.

The relaxation measurements on aqueous droplets after equilibration overnight were supplemented by oscillatory dilatation studies (see Fig. S4 and S5, ESI†). Owing to instrumental limitations, such measurements could not be equilibrated overnight but were instead performed on systems that had been allowed to partially equilibrate for 2 h. The effect of varying the solution pH on the interfacial moduli and interfacial tension was consistent with the relaxation data, despite the slightly higher interfacial tensions (+1–3 mN m⁻¹) and 10–20% lower moduli compared to fully equilibrated systems. The same approach was used to compare the effect of dialysis on a 0.1% w/w aqueous dispersion of (−) PGMA₅₄–PMMA₈₀ nanoparticles in their anionic form at pH 7. Interestingly, no significant difference was observed for the moduli obtained for dialyzed and undialyzed nanoparticles (see ESI†).

Although such changes in interfacial tension and moduli are comparable to those reported by Manga et al.,⁶³ the differences observed herein are more subtle. This is because each PDMA steric stabilizer chain grafted to the silica particles employed by Manga et al. contains many tertiary amine repeat units, which leads to a relatively high charge density at low pH. In contrast, the sterically-stabilized nanoparticles used in the present study possess a single pH-sensitive end-group on each steric stabilizer chain. Thus this represents a model system comprising minimally-charged nanoparticles. Manga et al.⁶³ reported an electrophoretic mobility for their charged PDMA-grafted silica particles of 3.5–4.0 μm cm V⁻¹ s⁻¹ at low pH, which corresponds to a zeta potential of around +44 to +50 mV according to the Smoluchowski approximation.⁹⁵ In contrast, the maximum zeta potential observed for the cationic (or anionic) nanoparticles used in the present study is either +15 mV or −15 mV owing to protonation of the morpholine end-group or ionization of the carboxylic acid end-group, respectively. Nevertheless, such minimal surface charge is sufficient to cause a significant reduction in the surface coverage of the aqueous droplets, which results in discernible differences in the interfacial tension and interfacial modulus compared to data obtained for the corresponding neutral nanoparticles.

Manga et al.⁶³ attributed the differences in elasticity observed for their cationic and neutral nanoparticles to entanglements between the steric stabilizer chains. They determined interfacial moduli using the oscillating drop method and suggested that the neutral steric stabilizer chains became entangled and disentangled during the change in surface area induced by the sinusoidal oscillation. This led to a strong elastic response, whereas the corresponding cationic chains had no tendency to become entangled owing to electrostatic repulsion, thus producing a relatively low elasticity. However, an alternative explanation is that the elastic response simply arises from a change in the surface excess of the adsorbed nanoparticles and the accompanying change in interfacial tension, either during oscillation or a step change in the surface area.

The interfacial elastic modulus of the adsorbed layer of nanoparticles depends on the change in interfacial tension with surface coverage. Lateral interactions between adsorbed nanoparticles contribute to the interfacial tension and these may be either attractive or repulsive in nature. Such lateral interactions contribute to the interfacial pressure, π, where π = γ₀ − γ and γ₀ is the interfacial tension for the bare interface. For example, octadecylamine adsorbed in its neutral form has virtually zero surface pressure at interfacial areas greater than 24 Ų per molecule. For smaller interfacial areas, the close proximity of neighbouring adsorbed molecules leads to strong lateral steric interactions and a very steep increase in surface pressure.⁹⁶ In contrast, charged molecules (or nanoparticles) exhibit long-range effects. For example, long-range repulsive interactions and high surface pressures at large interfacial areas are observed for polyethylene nanocrystals comprising one carboxylic acid per 45 carbon atoms once this substituent undergoes ionization on raising the solution pH.⁹⁷ However, such long-range interactions are much softer than the steric interactions reported for octadecylamine. In the case of the sterically-stabilized nanoparticles reported herein, the attractive van der Waals interactions between the hydrophobic PMMA (or PBzMA) cores should be offset by the steric or electrosteric repulsive interactions between the solvated neutral or charged stabilizer chains. For close-packed neutral nanoparticles adsorbed at an oil–water interface, a purely steric interaction should produce a relatively steep potential that is strongly dependent on the interparticle distance. Thus, even a modest expansion of the droplet surface area should lead to a significant reduction in the magnitude of this steric repulsive term and a lower interfacial pressure (in the absence of any nanoparticle adsorption from the bulk solution). In the case of adsorbed charged nanoparticles, the interparticle separation distance is greater owing to the lower adsorbed amount. Hence the electrosteric interaction is expected to be a much softer potential that is less sensitive to small changes in the interparticle separation distance. This results in the interfacial pressure being less sensitive to a modest change in the droplet surface area. Thus lower interfacial moduli are expected for adsorbed layers of charged nanoparticles compared to neutral nanoparticles. Moreover, systems comprising charged nanoparticles can relax more rapidly than their neutral nanoparticle counterparts. This suggests that the nanoparticles adsorb from the bulk solution to restore the surface coverage to its original equilibrium value, which results in the interfacial moduli exhibiting a stronger frequency dependence. In the initial interfacial tension vs. time plots, charged nanoparticles adsorb more slowly and reduce the interfacial tension to a lesser extent than when present in their neutral form. This difference is attributed to electrostatic repulsion between adsorbed nanoparticles and incoming nanoparticles. In contrast, the initial adsorption of neutral nanoparticles is significantly faster owing to the absence of this repulsive interaction. However, when such systems are at (or close to) equilibrium, the packing and interfacial mobility of the adsorbed nanoparticles become important. When the interfacial area is expanded by 5–10%, the increase in interparticle separation is small compared to the nanoparticle radius. Thus, if an incoming nanoparticle is to adsorb at the interface to return the (lower) surface coverage to its former value, the adsorbed nanoparticles must undergo co-operative lateral movement to create an adsorption site. For charged nanoparticles, the relatively low surface coverage (typically only 50% of that for neutral nanoparticles⁹⁴) and the soft interaction potential should allow a relatively high degree of interfacial mobility for the adsorbed nanoparticles, which are therefore able to rearrange themselves more readily to accommodate an incoming nanoparticle. The higher surface coverage for the neutral nanoparticles means that co-operative lateral relaxation is hindered to a much greater extent, leading to significantly slower adsorption. Such differences are manifest in the phase angle data: the low phase angles observed for the neutral nanoparticles indicates that their adsorption is slow relative to the experimental time scale of 20 000 s (or 5.6 h). In contrast, the much higher phase angles observed at low frequency for the charged nanoparticles indicate their facile adsorption within 1000 to 20 000 s (0.28 to 5.6 h). These effects are analogous to the apparent activation energy reported for surfactant adsorption close to equilibrium by Eastoe and Dalton.⁹⁸ Surfactant adsorption is diffusion-controlled at very low surface coverage so incoming surfactant molecules adsorb immediately on reaching the interface. On approaching equilibrium, the rate of surfactant adsorption is often reduced because there is insufficient space for adsorption to occur at any given time, which leads to an activation energy.

Conclusions

RAFT aqueous emulsion polymerization of either methyl methacrylate or benzyl methacrylate using a water-soluble poly(glycerol monomethacrylate) precursor enables the rational synthesis of a series of model sterically-stabilized diblock copolymer nanoparticles. Varying the chemical nature of the RAFT agent in such syntheses enables an isobutyryl group, a morpholine group or a carboxylic acid group to be placed at the end of each non-ionic steric stabilizer chain. Thus, judicious variation of the solution pH allows the introduction of either cationic or anionic charge via protonation of the morpholine group or ionization of the carboxylic acid group, respectively. Such minimal surface charge has a profound effect on the adsorption of such nanoparticles at the oil–water interface. More specifically, such minimally-charged nanoparticles adsorb at significantly lower surface coverages and reduce the dynamic interfacial tension much less than the corresponding neutral nanoparticles.

Interfacial tension relaxation after rapid expansion of an aqueous droplet enables determination of the interfacial rheology of such nanoparticles adsorbed at the n-dodecane–water interface. Moreover, the introduction of minimal surface charge by varying the solution pH leads to a significant reduction in the interfacial elastic modulus. On the other hand, the neutral form of such morpholine- or carboxylic acid-functionalized nanoparticles exhibit broadly similar behavior to that of permanently neutral particles. In such cases, neutral particles can pack much more efficiently at the oil–water interface and hence reduce the interfacial tension to a greater extent, resulting in a significantly more elastic interface. The relaxation data also suggest that loosely-packed, minimally-charged nanoparticles exhibit greater surface mobility than well-packed neutral nanoparticles, leading to a faster relaxation rate. Relaxation studies of systems after equilibration overnight were consistent with oscillation measurements performed on systems equilibrated for just 2 h.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. P. A. acknowledges a four-year EPSRC Established Career Particle Technology Fellowship (EP/R003009). Syngenta is thanked for an EPSRC Industrial CASE studentship for D. H. H. C. and for permission to publish this work.

References

1. S. U. Pickering, J. Chem. Soc. Trans., 1907, 91, 2001–2021.
2. W. Ramsden, Proc. R. Soc. London, 1904, 72, 156–164.
3. R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100–102, 503–546.
4. T. N. Hunter, R. J. Pugh, G. V. Franks and G. J. Jameson, Adv. Colloid Interface Sci., 2008, 137, 57–81.
5. B. P. Binks and S. O. Lumsdon, Phys. Chem. Chem. Phys., 1999, 1, 3007–3016.
6. B. P. Binks and S. O. Lumsdon, Langmuir, 2000, 16, 2539–2547.
7. Y. Zhu, T. Fu, K. Liu, Q. Lin, X. Pei, J. Jiang, Z. Cui and B. P. Binks, Langmuir, 2017, 33, 5724–5733.
8. D. J. French, P. Taylor, J. Fowler and P. S. Clegg, J. Colloid Interface Sci., 2015, 441, 30–38.
9. D. J. French, A. T. Brown, A. B. Schofield, J. Fowler, P. Taylor and P. S. Clegg, Sci. Rep., 2016, 6, 31401.
10. J. H. Schulman and J. Leja, Trans. Faraday Soc., 1954, 50, 598–605.
11. X. Qiao, J. Zhou, B. P. Binks, X. Gong and K. Sun, Colloids Surf., A, 2012, 412, 20–28.
12. A. Vílchez, C. Rodríguez-Abreu, A. Menner, A. Bismarck and J. Esquena, Langmuir, 2014, 30, 5064–5074.
13. Y. Cui, M. Threlfall and J. S. Van Duijneveldt, J. Colloid Interface Sci., 2011, 356, 665–671.
14. Y. Cui and J. S. Van Duijneveldt, Langmuir, 2012, 28, 1753–1757.
15. R. Van Hooghten, L. Imperiali, V. Boeckx, R. Sharma and J. Vermant, Soft Matter, 2013, 9, 10791–10798.
16. K. C. Powell and A. Chauhan, Langmuir, 2014, 30, 12287–12296.
17. B. P. Binks and S. O. Lumsdon, Langmuir, 2001, 17, 4540–4547.
18. A. J. Morse, D. Dupin, K. L. Thompson, S. P. Armes, K. Ouzineb, P. Mills and R. Swart, Langmuir, 2012, 28, 11733–11744.
19. S. Fujii, E. S. Read, B. P. Binks and S. P. Armes, Adv. Mater., 2005, 17, 1014–1018.
20. B. P. Binks, R. Murakami, S. P. Armes and S. Fujii, Langmuir, 2006, 22, 2050–2057.
21. V. J. Cunningham, A. M. Alswieleh, K. L. Thompson, M. Williams, G. J. Leggett, S. P. Armes and O. M. Musa, Macromolecules, 2014, 47, 5613–5623.
22. K. L. Thompson, C. J. Mable, A. Cockram, N. J. Warren, V. J. Cunningham, E. R. Jones, R. Verber and S. P. Armes, Soft Matter, 2014, 10, 8615–8626.
23. S. J. Hunter and S. P. Armes, Langmuir, 2020, 36, 15463–15484.
24. F. Wang, J. Tang, H. Liu, G. Yu and Y. Zou, Mater. Chem. Front., 2019, 3, 356–364.
25. B. P. Binks, Curr. Opin. Colloid Interface Sci., 2002, 7, 21–41.
26. J. Wu and G. H. Ma, Small, 2016, 12, 4633–4648.
27. C. C. Berton-Carabin and K. Schroën, Annu. Rev. Food Sci. Technol., 2015, 6, 263–297.
28. F. Liu and C. H. Tang, J. Agric. Food Chem., 2013, 61, 8888–8898.
29. J. Xiao, Y. Li and Q. Huang, Trends Food Sci. Technol., 2016, 55, 48–60.
30. R. D. Malaquin and P. Taylor, Pickering emulsion formulations, Int. Pat., WO2009112836A2, 2009.
31. J. Fowler, Pickering emulsion formulations, US Pat., US10925279B2, 2007.
32. C. Tang, Y. Li, J. Pun, A. S. Mohamed Osman and K. C. Tam, Colloids Surf., A, 2019, 570, 403–413.
33. S. Simovic, N. Ghouchi-Eskandar and C. A. Prestidge, J. Drug Delivery Sci. Technol., 2011, 21, 123–133.
34. D. Marku, M. Wahlgren, M. Rayner, M. Sjöö and A. Timgren, Int. J. Pharm., 2012, 428, 1–7.
35. F. G. Hougeir and L. Kircik, Dermatol. Ther., 2012, 25, 234–237.
36. K. L. Thompson, E. C. Giakoumatos, S. Ata, G. B. Webber, S. P. Armes and E. J. Wanless, Langmuir, 2012, 28, 16501–16511.
37. C. J. Mable, K. L. Thompson, M. J. Derry, O. O. Mykhaylyk, B. P. Binks and S. P. Armes, Macromolecules, 2016, 49, 7897–7907.
38. V. J. Cunningham, E. C. Giakoumatos, P. M. Ireland, C. J. Mable, S. P. Armes and E. J. Wanless, Langmuir, 2017, 33, 7669–7679.
39. A. J. Morse, S. Y. Tan, E. C. Giakoumatos, G. B. Webber, S. P. Armes, S. Ata and E. J. Wanless, Soft Matter, 2014, 10, 5669–5681.
40. A. J. Morse, E. C. Giakoumatos, S. Y. Tan, G. B. Webber, S. P. Armes, S. Ata and E. J. Wanless, Soft Matter, 2016, 12, 1477–1486.
41. S. Ata, Langmuir, 2008, 24, 6085–6091.
42. S. Ata, J. Colloid Interface Sci., 2009, 338, 558–565.
43. D. Langevin, Adv. Colloid Interface Sci., 2000, 88, 209–222.
44. H. W. Yarranton, D. M. Sztukowski and P. Urrutia, J. Colloid Interface Sci., 2007, 310, 246–252.
45. H. W. Yarranton, P. Urrutia and D. M. Sztukowski, J. Colloid Interface Sci., 2007, 310, 253–259.
46. D. Georgieva, V. Schmitt, F. Leal-Calderon and D. Langevin, Langmuir, 2009, 25, 5565–5573.
47. E. H. Lucassen-Reynders and D. T. Wasan, Food Struct., 1993, 12, 1–12.
48. T. C. Botti, A. Hutin, E. Quintella and M. S. Carvalho, Soft Matter, 2022, 18, 1423–1434.
49. H. Zhou, C. Dai, Q. Zhang, Y. Li, W. Lv, R. Cheng, Y. Wu and M. Zhao, J. Mol. Liq., 2019, 293, 111500.
50. V. B. Fainerman, E. V. Aksenenko, S. V. Lylyk, A. V. Makievski, F. Ravera, J. T. Petkov, J. Yorke and R. Miller, Colloids Surf., A, 2009, 334, 16–21.
51. V. I. Kovalchuk, E. V. Aksenenko, A. V. Makievski, V. B. Fainerman and R. Miller, J. Colloid Interface Sci., 2019, 539, 30–37.
52. P. Ramírez, L. M. Pérez, L. A. Trujillo, M. Ruiz, J. Muñoz and R. Miller, Colloids Surf., A, 2011, 375, 130–135.
53. R. Miller, V. B. Fainerman, J. Krägel and G. Loglio, Curr. Opin. Colloid Interface Sci., 1997, 2, 578–583.
54. M. Liu, Y. Zheng, Y. Liu, Z. Zhang, Y. Wang, J. Li, Q. Chen, J. Li, Y. Huang and Q. Yin, Int. J. Hydrogen Energy, 2020, 45, 2925–2935.
55. P. Ramírez, A. Stocco, J. Muñoz and R. Miller, J. Colloid Interface Sci., 2012, 378, 135–143.
56. B. A. Noskov, A. V. Akentiev, A. Y. Bilibin, I. M. Zorin and R. Miller, Adv. Colloid Interface Sci., 2003, 104, 245–271.
57. D. Langevin and F. Monroy, Curr. Opin. Colloid Interface Sci., 2010, 15, 283–293.
58. M. A. Bos and T. Van Vliet, Adv. Colloid Interface Sci., 2001, 91, 437–471.
59. E. M. Freer, K. S. Yim, G. G. Fuller and C. J. Radke, J. Phys. Chem. B, 2004, 108, 3835–3844.
60. T. L. Hsieh, M. R. Martinez, S. Garoff, K. Matyjaszewski and R. D. Tilton, J. Colloid Interface Sci., 2021, 581, 135–147.
61. Y. R. Huang, M. Lamson, K. Matyjaszewski and R. D. Tilton, Phys. Chem. Chem. Phys., 2017, 19, 23854–23868.
62. L. I. Atanase, S. Bistac and G. Riess, Soft Matter, 2015, 11, 2665–2672.
63. M. S. Manga, T. N. Hunter, O. J. Cayre, D. W. York, M. D. Reichert, S. L. Anna, L. M. Walker, R. A. Williams and S. R. Biggs, Langmuir, 2016, 32, 4125–4133.
64. B. A. Noskov and A. G. Bykov, Curr. Opin. Colloid Interface Sci., 2018, 37, 1–12.
65. A. Maestro, E. Santini, D. Zabiegaj, S. Llamas, F. Ravera, L. Liggieri, F. Ortega, R. G. Rubio and E. Guzman, Adv. Condens. Matter Phys., 2015, 1–17.
66. A. J. Mendoza, E. Guzmán, F. Martínez-Pedrero, H. Ritacco, R. G. Rubio, F. Ortega, V. M. Starov and R. Miller, Adv. Colloid Interface Sci., 2014, 206, 303–319.
67. A. Stocco, W. Drenckhan, E. Rio, D. Langevin and B. P. Binks, Soft Matter, 2009, 5, 2215–2222.
68. T. Saigal, A. Yoshikawa, D. Kloss, M. Kato, P. L. Golas, K. Matyjaszewski and R. D. Tilton, J. Colloid Interface Sci., 2013, 394, 284–292.
69. N. J. Alvarez, S. L. Anna, T. Saigal, R. D. Tilton and L. M. Walker, Langmuir, 2012, 28, 8052–8063.
70. R. Miller, J. K. Ferri, A. Javadi, J. Krägel, N. Mucic and R. Wüstneck, Colloid Polym. Sci., 2010, 288, 937–950.
71. M. Karbaschi, M. Lotfi, J. Krägel, A. Javadi, D. Bastani and R. Miller, Curr. Opin. Colloid Interface Sci., 2014, 19, 514–519.
72. G. Loglio, U. Tesei and R. Cini, J. Colloid Interface Sci., 1979, 71, 316–320.
73. G. Loglio, E. Rillaerts and P. Joos, Colloid Polym. Sci., 1981, 259, 1221–1227.
74. S. Kitching, G. D. W. Johnson, B. R. Midmore and T. M. Herrington, J. Colloid Interface Sci., 1996, 177, 58–69.
75. B. Madivala, S. Vandebril, J. Fransaer and J. Vermant, Soft Matter, 2009, 5, 1717–1727.
76. J. R. Samaniuk and J. Vermant, Soft Matter, 2014, 10, 7023–7033.
77. M. Kamkar, P. Bazazi, A. Kannan, V. C. Suja, S. H. Hejazi, G. G. Fuller and U. Sundararaj, J. Colloid Interface Sci., 2020, 576, 252–263.
78. R. Van Hooghten, V. E. Blair, A. Vananroye, A. B. Schofield, J. Vermant and J. H. J. Thijssen, Langmuir, 2017, 33, 4107–4118.
79. G. G. Fuller and J. Vermant, Annu. Rev. Chem. Biomol. Eng., 2012, 3, 519–543.
80. V. Bergeron, Langmuir, 1997, 13, 3474–3482.
81. B. Charleux, G. Delaittre, J. Rieger and F. D’Agosto, Macromolecules, 2012, 45, 6753–6765.
82. S. L. Canning, G. N. Smith and S. P. Armes, Macromolecules, 2016, 49, 1985–2001.
83. J. Chiefari, Y. K. B. Chong, F. Ercole, J. Krstina, J. Jeffery, T. P. T. Le, R. T. A. Mayadunne, G. F. Meijs, C. L. Moad, G. Moad, E. Rizzardo and S. H. Thang, Macromolecules, 1998, 31, 5559–5562.
84. G. Moad, E. Rizzardo and S. H. Thang, Aust. J. Chem., 2006, 59, 669–692.
85. G. Moad, E. Rizzardo and S. H. Thang, Aust. J. Chem., 2009, 62, 1402–1472.
86. G. Moad, E. Rizzardo and S. H. Thang, Aust. J. Chem., 2012, 65, 985–1076.
87. G. Moad, E. Rizzardo and S. H. Thang, Aust. J. Chem., 2005, 58, 379–410.
88. M. Semsarilar, V. Ladmiral, A. Blanazs and S. P. Armes, Langmuir, 2013, 29, 7416–7424.
89. N. J. W. Penfold, J. R. Lovett, N. J. Warren, P. Verstraete, J. Smets and S. P. Armes, Polym. Chem., 2016, 7, 79–88.
90. J. Ilavsky and P. R. Jemian, J. Appl. Crystallogr., 2009, 42, 347–353.
91. R. Aveyard and D. A. Haydon, Trans. Faraday Soc., 1965, 61, 2255–2261.
92. J. R. Lovett, N. J. Warren, L. P. D. Ratcliffe, M. K. Kocik and S. P. Armes, Angew. Chem., Int. Ed., 2015, 54, 1279–1283.
93. J. S. Pedersen and M. C. Gerstenberg, Macromolecules, 1996, 29, 1363–1365.
94. S. J. Hunter, N. J. W. Penfold, D. H. Chan, O. O. Mykhaylyk and S. P. Armes, Langmuir, 2020, 36, 769–780.
95. R. J. Hunter, Zeta Potential in Colloid Science, Academic Press, Cambridge, 1981.
96. Z. Avazbaeva, W. Sung, J. Lee, M. D. Phan, K. Shin, D. Vaknin and D. Kim, Langmuir, 2015, 31, 13753–13758.
97. R. Machatschek, P. Ortmann, R. Reiter, S. Mecking and G. Reiter, Beilstein J. Nanotechnol., 2016, 7, 784–798.
98. J. Eastoe and J. S. Dalton, Adv. Colloid Interface Sci., 2000, 85, 103–144.

---

Footnote

† Electronic supplementary information (ESI) available: Additional experimental details for the synthesis of the anionic and cationic PGMA precursors. Background information for the interfacial tension relaxation method and corresponding data analysis; summary of the oscillatory measurements. See DOI: https://doi.org/10.1039/d2sm00835a

---