Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The effects of surfactant and oil chemical structures on self-assembly in apolar media
Adhip
Rahman
 and
Julian
Eastoe
*
and
Julian
Eastoe
*
School of Chemistry, University of Bristol, Cantock's Close, Bristol BS8 1TS, UK. E-mail: Julian.Eastoe@bristol.ac.uk
First published on 29th November 2022
Abstract
The thermodynamic and chemical structural aspects of surfactant self-assembly in aqueous systems have been much studied. On the other hand, for oil–water interfaces the effects of chemical structures of surfactants and solvents have received less attention. This review focuses on the surfactant chemical effects in low dielectric solvents, in particular formation and properties of surfactant films at oil–water interfaces. For this purpose, reversed micelles (RMs) and water-in-oil (W/O) microemulsions (μEs) serve as model systems, since electrostatic effects are minimized, allowing a focus on chain architecture of the surfactants and oil solvents themselves. It is noted that chemical structure can have profound effects on stability and self-assembly, suggesting a possibility of identifying unified chemical principles for designing and formulating systems across various thermodynamic conditions.
1. Introduction
Most colloidal systems of interest comprise charged particles in aqueous media; theoretical understanding of colloidal stability of such systems is well established and pertains to systems using high dielectric solvents. The celebrated DLVO theory provides basis for understanding stability in such common systems.1a,b The principal parameter attributed to solvent in DLVO theory is the dielectric constant ε, and, of course, the solvent of interest is nearly always water. Hence, it can be argued that in the DLVO framework the solvent merely serves as a benign medium, the purpose of which is to support charge (i.e. accommodating ions). Hence, the effect of solvent chemical structure on stability of aqueous colloidal systems are not explicitly considered.Consider now an alternative class of colloidal systems utilizing low dielectric oily solvents. These systems are stabilized predominantly by steric interactions, rather than electrostatics as for charged aqueous colloids exhibiting different physical properties. It is true that electrostatic interactions are found in such non-aqueous colloidal systems,1c but these are generally longer range and with weaker interactions compared to aqueous systems. There is a wide variety of different oily solvents with diverse chemical structures, which can be mixed to compose solvent mixtures exhibiting wide ranges of physical properties and molecular interactions. Such mixtures offer a landscape wider than usually available in aqueous colloids. Hence, for non-aqueous low dielectric colloidal systems variations in solvent chemical structure are expected to be significant considerations. Water-in-oil (W/O) dispersions (emulsions) or microemulsions (μEs) (thermodynamically stable systems comprising water-immiscible oils) are common classes of non-aqueous colloidal systems. For these systems there must be intimate molecular contact between the stabilizing surfactant (films) and the “continuous phase” external solvents. Therefore, it can be expected that solvent-specific effects may become significant for system phase-stability, structure, and properties. In this review, a fresh perspective on solvent–surfactant specific effects is offered – with a view to improving the understanding of such systems and facilitating their formulation.
Typical surfactants comprise hydrophilic (polar) heads and hydrophobic (non-polar) tail group(s) – such chemical factors lead to their dissolution in aqueous or non-aqueous solvents. Another consequence of the surfactant molecular structure is that surfactants self-assemble in aqueous and non-aqueous media forming micelles, swollen micelles/reverse micelles (RMs) (i.e. microemulsions, μEs) or emulsions. These self-assembly structures are in the size range of between a few tens or hundreds of angstroms (Å) and have well-defined morphologies (spherical, ellipsoid, cylindrical, disk shaped and so on). In water (or polar media) the hydrophilic heads orient towards the solvent bulk, whereas hydrophobic tails tend to point inwardly, away from the solvent. On the other hand, in oily solvent media reverse micelles (RMs) may form – in which the surfactant tails point outwards towards the solvent and the heads are buried in the reverse micellar core.1a,b,2 An important aspect of such self-assembly structures is that they can accommodate substances of opposite polarity relative to the dispersion media inside the RM cores – for example, solubilizing a polar liquid, water. Such ternary systems may be called μEs if they form spontaneously, are optically transparent and thermodynamically stable dispersions; in such systems, nano domains (or droplets) containing one fluid dispersed in the other – with the two liquids being separated by surfactant monolayers.2–5 To be specific, μEs can be understood as surfactant monolayers thermodynamically stabilizing an otherwise unstable oil–water (O–W) interface where the oil is immiscible with water.2,4 As such, surfactants straddle the oil–water interface, and there is necessarily intimate contact between surfactant tail groups and the continuous-phase oil, so that solvent-specific effects can be expected. They show interesting variation in interfacial as well as bulk properties and have been recognized for their applicability in controlling morphology of nanomaterials in the fields of catalysis, personal care, drug delivery, enhanced oil recovery, lubrication, and cleaning technology.6–9
The effect of physical variables such as temperature, pressure, concentration, and composition on surfactant self-assembly in polar or non-polar media has been studied in much detail.10,11 While effects of surfactant and solvent chemical structure have been studied for some decades, the vast majority of these are scattered efforts. Early theoretical models interpreted surfactant self-assembly (micelles and μEs) entirely from the context of thermodynamics.11,12 However, whether surfactant and solvent-chemical architecture exert any significant control over μE thermodynamic stability and morphology of self-assembled structures has not been considered in exhaustive detail.
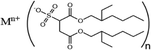
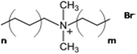
This review aims to compile, summarize, and compare the most important results and interpretations related to the chemical effects on surfactant self-assembly in low dielectric solvents. μEs, water-in-oil μEs (W/O-μEs) in particular, are chosen instead of normal emulsions as model colloidal systems for discussion. There are two reasons – (i) the former systems are thermodynamically stable, which is not the case for emulsions, and (ii) W/O systems make it possible to focus entirely on the chemical structure effects of surfactant hydrophobic chains and solvents owing to their intimate contact.12a Surface films of surfactants, wherein the head groups are oriented in intimate contact with diverse solid phases,12b with and without water associated with such head groups are also important but are not discussed in this review. Systems primarily stabilized by the dichain anionic surfactant, Aerosol-OT (AOT) and its analogues, are extensively discussed here; in addition, cationic dialkyldimethylammonium (CnCmDAB) and nonionic polyoxyethylene glycol alkyl ether (CiEj) surfactants are also considered. Table 1 lists the types of surfactants and nonpolar solvents covered here.
2. Understanding surfactant–solvent thermodynamic stability: phase behaviour, curvature, and interfacial tension
The macroscopic phase-stability of three-component μEs containing a surfactant, water and an oil is accounted for in terms of ternary phase diagrams. A typical ternary phase diagram encompasses the whole composition range. For more than three components (hydrotrope or cosurfactant as an additional component) a pseudoternary phase diagram is often used.4,13,14 The phase diagram covers all possible phases including non-transparent, non-μE phases – since not all combinations result in single-phase μEs. An example of a typical phase diagram of an AOT-based μEs is given in Fig. 1. The location of different boundaries in a phase diagram depends on the chemical nature of the μE-components and thermodynamic conditions (temperature and pressure).15–18 A phase diagram of a typical three component system may comprise single-phase L1-μE (oil-in-water (O/W)), L2-μE (water-in-oil (W/O)), W/O-μE phase separated from excess water (Winsor II), O/W-μE phase-separated from excess oil (Winsor I), and a μE in equilibrium with excess oil and water (Winsor III).3,4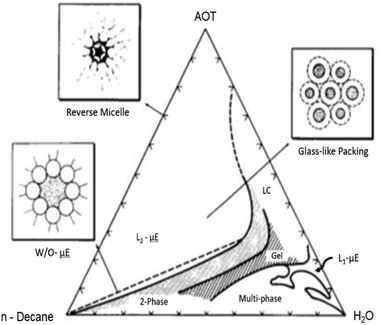 | ||
| Fig. 1 Ternary phase diagram of AOT/H2O/n-decane μE along the entire composition range for each of the three components (at room temperature and pressure); the phases are described in the text. Insets show various nanostructural ensembles in the single-phase L2-μE region. The units of the axes are represented as wt%. The figure was reprinted from ref. 20. Copyright 1986, with permission from Elsevier. | ||
Normally, surfactant-coated droplets (containing water in W/O-μEs or oil in O/W-μEs inside droplets) in these systems are spherical in nature, but under certain circumstances, the μEs may be viscoelastic – surfactant curvature in such systems is often complex (ellipsoidal, cylindrical or polymerlike).15 In addition, non-μE phases (such as gels, liquid crystalline (LC) lamellar, cubic or hexagonal phases) and bicontinuous (L3) μEs may also appear.19–21
2.1. Water solubilization and Wmax
Before proceeding to the discussion, the difference between RMs and W/O-μEs should be clarified; RMs form when surfactants self-assemble in nonpolar organic solvents; the core may be “dry”, i.e. no water (Section 3.1 will discuss dry RMs in detail) or may have small-quantity of water in which case the water molecules interact strongly with the hydrophilic head-groups.22b,e W/O-μEs, as pointed out in the introduction, are swollen with water so the water solubilization by the RM cores is much higher; in addition, the core-water resembles regular bulk-water evidenced by spectroscopic studies.22A simple and convenient way to understand W/O-μE macroscopic phase-stability is in terms of water solubilization capacity W (where W = [water]/[surfactant]). W/O-μEs droplets can be swollen by water up to a limit; physical variables such as temperature, salinity and cosurfactant affect the extent of W (maximum water solubilization, Wmax).23a Shah et al.23b,c attempted to understand W/O-μE phase transitions in terms of the correlation between Wmax and O–W interfacial curvature (details can be found in Section 2.2). According to these publications, the balance between the interfacial contribution towards a limiting curvature and droplet–droplet attractive interactions leads to bending of a flat film – leading to μE-formation. For rigid interfaces (see Section 2.3), the droplet radius in W/O-μEs does not exceed a threshold “radius of spontaneous curvature, ρ0” (for details, see the later), as exceeding ρ0 results in phase separation of water from the μE-droplets (i.e. WII-systems).23 The interface, nevertheless, becomes more flexible if ρ0 increases (i.e. water-solubilization increases in L2-μEs).23c Moreover, on increasing the water content, droplets in L2-μEs tend to achieve a “critical radius” – above which macroscopic phase separation occurs. Attempts were made to link solvent chemical-structure with ρ0 and the critical radius23b,c (Fig. 2). The inference was that ρ0 (linked to Wmax) would be correlated to solvent molecular volume – given no surfactant structural variation has been considered.23,24 Some early works assumed that the ability of hydrocarbon solvents, due to variation in their molecular volumes, to penetrate surfactant monolayers would govern Wmax by controlling surfactant film-curvature (more on this later) and, thus, droplet–droplet interactions.17,25,26 Any correlation of Wmax directly to the solvent chemical architecture was, however, unclear.
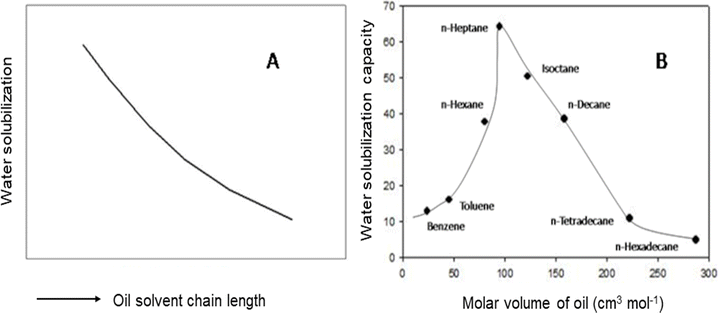 | ||
| Fig. 2 (A) A schematic illustration showing the relationship between water solubilization limit of L2-μEs and oil solvent chain length, the arrow along the X-axis indicates increasing (oil chain length); the region below the curve represents L2-μEs, and above the curve indicates μE-phase separation; (B) maximum water-solubilization (Wmax) in AOT-based W/O-μEs as a function of the solvent molar volumes at room temperature and pressure. The scheme in (A) was based on Fig. 2 of ref. 23c. Copyright (1987), with permission from Elsevier. Data for (B) were reprinted (adapted) from ref. 23b. Copyright 1987. Reproduced with permission from American Chemical Society. | ||
A more convenient approach to probe Wmax as a function of surfactant–solvent chemical variation is through temperature-composition phase-diagrams. This will be covered in Section 2.3 and onwards.
2.2. Packing and surfactant film-bending
The effect of surfactant chemical structure on interfacial film topology was discussed by Israelachvili.27 According to these arguments, surfactant chemical structure was understood in terms of the following parameters:– Surfactant head-group area (ah) owing to repulsive (steric and/or electrostatic) interactions between headgroups
– Effective hydrophobic tail volume (υ) and extended tail length (lc) attributed to a balance between attractive hydrophobic interactions and steric interactions between the tails
Overall, the quantity υ/a0lc, known as the packing parameter (p) is consistent with W/O-μE formation for p > 1. This predicts that for a given surfactant chain length, a small a0 and high υ favours reversed curvature W/O-μEs. High υ can be achieved by means of introducing branching, unsaturation, or double chains into surfactant hydrophobic tail regions.4,27 The role of solvent was discussed mostly in the context of the penetration capacity – the greater the solvent penetration the more favoured would be the W/O-μE formation. However, extensive contrast variation small-angle neutron scattering (SANS) studies, designed specifically to assess penetration of oil molecules into the hydrocarbon regions of surfactant films, suggested that solvent penetration is likely to be a subtle effect; moreover, not all types of solvent molecules penetrate through the surfactant tip-regions, and solvent penetration shows a two-way solvent–surfactant chemical-dependency.28,29 This aspect will be enlarged on in Section 3.4.
The first realistic model for interpreting properties of surfactant-films at O–W interfaces from the context of film-mechanical properties was developed based on the early theoretical concepts for film-bending and rigidity in liquid crystals by Frank, and later Helfrich for amphiphilic systems.30–32 The model considers conformational degrees of freedom of surfactant hydrophobic tails dispersed in a “seemingly” gas-phase, i.e. solvent molecules were considered unimportant. Conformational free energy of total film bending can be expressed as
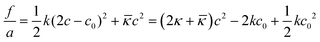 | (1) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) is the so-called saddle-splay constant (or Gaussian modulus) and c is the mean curvature – which is related to principal radii of curvature ρ1 and ρ2 at any given point on the surfactant film (ρ1 = 1/c1 and ρ2 = 1/c2) by
is the so-called saddle-splay constant (or Gaussian modulus) and c is the mean curvature – which is related to principal radii of curvature ρ1 and ρ2 at any given point on the surfactant film (ρ1 = 1/c1 and ρ2 = 1/c2) by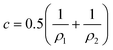 | (2) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) is close to zero. This means that the lateral pressure among the longer chains lessens due to shorter chains acting as “spacers”.
is close to zero. This means that the lateral pressure among the longer chains lessens due to shorter chains acting as “spacers”.
The theoretical phase-diagram arising from these considerations, Fig. 3, shows regions of various structural forms in W/O-μEs as a function of ρ/ρ0 and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) /κ, where ρ0 is spontaneous radius of curvature and ρ is radius of curvature. This is related to c0 as ρ0 = 1/c0. ρ has an inverse relationship with mean curvature c and can be expressed by eqn (2) above.4 More importantly, ρ may related to the surfactant chemical architecture by
/κ, where ρ0 is spontaneous radius of curvature and ρ is radius of curvature. This is related to c0 as ρ0 = 1/c0. ρ has an inverse relationship with mean curvature c and can be expressed by eqn (2) above.4 More importantly, ρ may related to the surfactant chemical architecture by
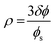 | (3) |
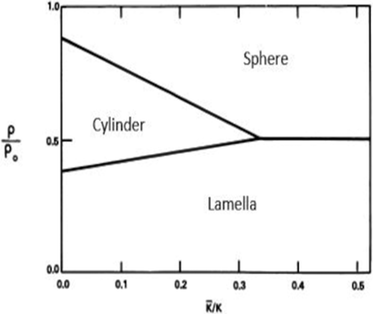 | ||
Fig. 3 Theoretical stability regions of lamellar, cylindrical, and spherical phases of μEs as a function of bending constant ratios (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) /κ); all the parameters are described in the text. The figure was reproduced from ref. 33 (S. A. Safran et al., J. Phys. Lett., 1984, 45, 69) with permission. /κ); all the parameters are described in the text. The figure was reproduced from ref. 33 (S. A. Safran et al., J. Phys. Lett., 1984, 45, 69) with permission. | ||
This model explains a range of cylinder-to-sphere transitions which have been observed in diverse W/O-μE systems – for example cationic CnCmDAB W/O-μEs in cyclohexane (cylindrical aggregates until W = 7 and spherical aggregates at W = 10, [surfactant] ≈ 0.050 M), AOT containing divalent cations such as Mg2+, Co2+ and Ni2+ (for the effect of counterions see Section 4) and mixtures of AOT and hydrotropes.38–40 The interpretations and models discussed above suggest that there indeed are intimate links between chemical structure of the components (oils21 and surfactants26–30) and phase stability, O–W interfacial curvature and structure of typical W/O-μEs.
2.3. Chemical-control over phase behaviour: AOT-based μEs
As it was suggested by earlier theoretical models, solvent penetration capacity into the surfactant hydrophobic tips (di-chain surfactants in particular) could influence μE-phase stability and structures. However, as mentioned above and below, direct observation of surfactant shells by contrast variation SANS indicated this effect to be of limited significance.28,29 Nevertheless, here it is worth revisiting how the solvent chemical architecture affects phase-transitions.Before discussing anionic AOT-based μEs, it should be noted that each of the AOT-hydrophobic chains contains eight carbon-atoms and the longer of the two chain fragments contains six carbon-atoms. It was pointed out that the single-phase L2-μEs are more ubiquitous in linear alkane solvents having lower alkane carbon number (ACN).41 An extensive phase-mapping of AOT/H2O/n-hexane μEs showed that in n-hexane, the amount of solubilized water in L2-μE domains can be as high as 40 wt% (at 293 K); on increasing temperature, the L2-phase, however, narrowed.42,43 Meanwhile, comparison between the L2-μEs in cyclohexane and the aromatic solvent p-xylene showed that the L2-domain in cyclohexane was wider than that of in p-xylene.44–47 Comparative phase-mapping between isooctane and p-xylene (both having eight carbon-atoms) showed that the L2-phase is more extensive in isooctane.47–49 Such an apparent disparity in the macroscopic phase-stability due to solvent chemical structure was also demonstrated by Hall et al.50 in flow birefringence studies. AOT-μEs in n-decane showed interesting phase behaviour; Wmax is not significantly high and bicontinuous μEs occupy a significant portion of the ternary phase diagram; the multiphase regions are narrow, and transitions from L2- to LC-phases end in a gel-like phase.51,52a The L2-phase further narrowed by replacing n-decane (C10) for n-dodecane (C12).52b
Consideration of temperature with a ternary composition phase diagram leads to a three-dimensional phase-prism, which can become rather difficult to interpret.4,23a A more simplified approach is to reduce the degrees of the 3-D phase prism into a two-dimensional composition-temperature phase diagram.4 In this representation, μE-composition may be represented by W, and an example phase diagram of AOT W/O-μEs in n-octane is shown in Fig. 4(A).
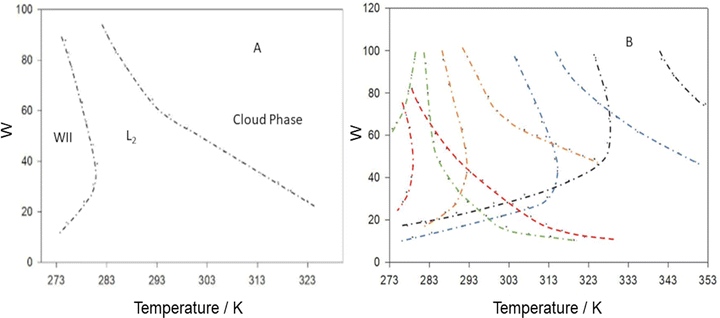 | ||
| Fig. 4 (A) AOT-based W/O-μE temperature-composition phase-diagram in n-octane; WII, L2 and cloudy phases are described in the text, (B) effect of structural variation at the AOT hydrophobic tails – colours indicate AOT analogues:(green) AOT3, (red) AOT5, (orange) AOT1 (i.e. normal AOT), (blue) AOT2 and (black) AOT4. Chemical structures of AOT1–AOT5 are shown in Fig. 7. The left-side boundary for each of the phase-funnels represents a WII-to-L2 transition, whereas right-most boundary represents L2-to-cloudy phase (defined below) transition. Pressure: 1 bar, [surfactant] = 0.100 M. Data in (A) were reproduced (adapted) from ref. 23a. Copyright (1991), with permission from Elsevier. Data in (B) were reprinted (adapted) from ref. 55. Copyright 2000. Reproduced with permission from American Chemical Society. | ||
It should be noted that throughout this review, the phase-transitions discussed are macroscopic phase-transitions, i.e. the phase-changes can be seen by naked eye. In this sense, the macroscopic phase-transitions account for the phase-diagrams shown in Fig. 4. The phase-transitions occur in such systems involve Winsor-type phase transitions4 (it is true that beyond the macroscopic phase-realms, μEs show microscopic phase-transitions – the so-called “second-order phase transition” – as well; this has been quantified by Texter53a,b and Antalek et al.53c by droplet-apparent diffusion coefficient measurements in AOT-based W/O-μEs. It was shown that W/O-droplet to a fractal-like bicontinuous phase transition could be quantified by the order parameter). The funnel-like region covered between the lower and upper temperature phase-boundaries (TL and TU, respectively) is of interest as this represents the stability extent (i.e. the region in temperature-composition phase diagrams covered by single-phase transparent L2-systems) of the single-phase L2-μEs – otherwise termed as the “L2-μE domain size” for convenience. The lower temperature boundary, TL, accounts for Winsor II to transparent L2-μE phase transition, whereas the upper-temperature boundary, TU, accounts for the so-called “cloud-point” phase separation, i.e. L2-to-cloudy phases. The use of “cloud point” in W/O-μEs may have different meanings based on appearance of the systems; often when the cloud-point has been reached, the systems turn bluish and more viscous, and over the time, a surfactant-rich phase-separates from the L2-μEs.37 For other systems, close to cloud points the L2-μEs can separate into two coexisting μE-phases20 (i.e. a critical-type separation, this will be discussed in detail in Section 3.6). In general, the volcano-like L2-region normally shifts towards lower temperature on increasing the ACN of linear n-alkane solvents.54
The L2-μE domain size and its relationship to chemical variation of hydrophobic tail architecture (with AOT analogue surfactants) was studied by Nave et al.55–57 In this work, a class of straight chain and branched chain AOT-analogues were custom synthesized (example structures see Fig. 7). For un-branched linear hydrophobic chains, μEs did not form with the surfactants alone, but rather required short-chain alcohol-cosolvents (i.e. four component systems) to stabilize transparent L2-phases. This is consistent with the work of Safran et al.33 who outlined the need for sufficient entropic freedom of the hydrophobic chains.44 A clear chemical structural effect on temperature-guided phase stability (i.e. the L2-μE domain sizes in the temperature-composition phase diagrams) was seen, in general, shortening the surfactant alkyl chains shifted the L2-funnel towards higher temperature, and vice versa. On the other hand, introduction of chain-branching brought the surfactants into line with normal AOT, and three component μEs could be stabilized. Interestingly, larger L2-μE domains at higher temperatures were especially noted for surfactants bearing brush-like trimethyl hedgehog chain-tips. (Fig. 4B).55
A striking and, un-subtle, manifestation of a highly specific surfactant–solvent chemical structural effect was observed. Upon introducing aromatic fragments onto the AOT chain-tips, μEs only formed in aromatic solvents, such as toluene, but did not form in linear alkane solvents. These “phenyl-tipped” AOT-stabilized W/O-μEs in toluene were rather less sensitive to temperature – compared to the normal AOT-based μEs in toluene.56 It is notable that the temperature-dependent L2-μEs domain sizes could be correlated to the aqueous phase solubility of each of the surfactants.55 These experimental observations show the importance of chemical structure for μE-stability, supporting and amplifying the earlier literature discussed above.21,26–30
2.4. Cationic surfactants
Surfactants based on quaternary dialkyldimethylammonium (CnCmDAB) cations (Table 1) having double-chain architecture, like the anionic AOT, have been much studied.58–68 The two-tailed structure of these cationics indicate a preference for stabilizing W/O-μEs – despite them being only very weakly soluble in water as well as hydrocarbon solvents (<1 wt%).58,59 Like the AOT-analogues, phase behaviour of CnCmDAB-μEs was observed to be highly oil and surfactant-chain specific;58–62 for the common symmetric di-chain surfactant di-C12DAB (DDAB), μE-formation shows a systematic “oil-specificity”.58,61 The onset water content at which μEs form was ∼6 wt% for n-hexane, rising to 26 wt% for n-tetradecane; however, W/O-μEs in n-tetradecane could not be formed at low surfactant concentration. Another study compared n-alkanes and alkenes with the same carbon numbers (C6 to C14); for each of the pairs, the onset volume fraction of water to form L2-phases was lower for the alkene than the corresponding n-alkane.63 A comparison between cyclic and linear n-alkanes showed that the cycloalkane narrows the single-phase region compared to the linear alkane; for cyclohexane, the onset water content for W/O-μE formation (2 wt%) was found to be much lower compared to its linear chain homologue n-hexane.59 In addition, microstructure topology in di-C12DAB-based μEs was found to be correlated with oil-solvent chemical nature – surfactant films were more rigid in short chain n-alkanes.64 The case of aromatic solvents is interesting – since di-C12DAB is highly soluble in toluene (>30 wt%). Unlike n-alkanes or cycloalkanes, in which detectable W/O-spherical droplets could be formed, pulse-field gradient NMR experiments carried out by Olla et al.65,66 showed no evidence for droplet formation in aromatic solvents such as toluene or fluorinated toluene. Rather, in oil-continuous systems, μE phase-transitions followed from discrete hydrated molecular clusters to connected bilayers on increasing droplet volume fraction (surfactant + water).66 Fluorinated alkanes, on the other hand, induced formation of kinetically stable emulsions, but not thermodynamically stable μEs.66Surfactant–solvent structure-property relationships for asymmetric chain CnCmDAB (n ≠ m) surfactants were studied in aromatic solvents; uneven chain-lengths (m > n)67a,b and incorporation of phenyl-groups in one of the chains67b resulted in W/O-μEs of W as high as 80 in aromatic hydrocarbons. Moreover, light-scattering and interdroplet exchange kinetics results67c revealed a two-fold effect; for a given surfactant chain-length, inclusion of polar fragments into the aromatic solvent resulted in reduced interdroplet collision-rate constants, for example, in chlorobenzene (on the order of 108 M−1 s−1) compared to non-halogenated benzene (≈109 M−1 s−1). This was found to be equivalent to shortening the hydrophobic chains by around three carbon-atoms, since shortened hydrophobic tails induced high collision rate and enhanced aggregation in a solvent and experimental condition.
Surfactant chemical-effects with the CnCmDAB class was further explored by Warr et al.68 They observed that the chain-melting temperature of CnCmDAB determined whether the surfactant formed μEs between a given temperature window or not. Chain-melting temperature is related to hydrophobic-chain fluidity and on increasing the chain carbon-number chain-melting temperature increases. For di-C12DAB it was 289 K, whereas for di-C14DAB it was 304 K. Indeed, μEs formed beyond 304 K in a range of linear hydrocarbons for the latter surfactant, whereas for the former μEs were found at around 298 K and beyond. The oil specificity with di-C12DAB was also evident, the minimum water content required to form μEs increases on increasing solvent ACN. The oil-specificity was clearly observed for surfactants with chain-length asymmetry such as C8C16DAB. For instance, while for C8C16DAB oil-continuous W/O-μEs formed in n-hexane, in n-decane the μEs were bicontinuous with zero mean curvature at O–W interfaces. Nevertheless, literature on cationic μEs suggests that the surfactant film properties and water solubilization mutually depend on solvent as well as surfactant hydrophobic tail chemical nature – similar to the W/O-μEs containing anionic AOT and its analogues.
Hence, for two of the common classes of surfactants discussed above, solvent structural specific effects are major features related to μE-phase stability.
2.5. Nonionics
For historical reasons,15,69–73 the phase-behaviour for nonionic CiEj (Table 1 for chemical structures) μEs is presented in a manner different from the ionic μEs; temperature effects are often studied in terms of Winsor I (O/W-μE) to surfactant-rich bicontinuous state through to Winsor II (W/O-μE) transitions. The macroscopic phase-transitions are commonly presented in terms of the so-called “fish-cut like phase-diagram”.15 A schematic representation can be found in Fig. 1 of ref. 15 – the region covered by the upper-temperature and lower-temperature boundaries corresponds to a three-phase bicontinuous Winsor III-μE through which transitions from O/W to W/O-μEs take place. For short chain CiEjs (such as C6E5), the temperature-boundaries shift towards lower temperature on reducing ACN of linear alkane solvents.69 Moreover, on increasing Cj, the three-phase “fish-cut” region requires a lower amount of surfactant. An important factor in these temperature-composition phase diagrams is the phase-inversion temperature (PIT). At a given surfactant concentration, this is the temperature at which a transition from O/W-μEs to W/O-μEs takes place.70,71 Shinoda et al. extensively studied PITs in nonionic systems; in general, the PIT depends on the solubility of a CiEi in any given hydrocarbon solvent, and increased solubility of CiEj leads to lower PIT.71–73 Interestingly, surfactant–solvent chemical effects are seen, for instance if CiEj surfactants contain a phenyl group, then the PIT for O/W to W/O transition is lower in aromatic solvents as compared to linear hydrocarbon solvents.71,72These CiEj surfactants are of interest because both the hydrophilic and hydrophobic fragments can be simultaneously and sequentially varied. According to a molecular model proposed by Paunov et al.,74 a CiEj surfactant can be treated as a diblock copolymer containing a hydrophilic (EO) and a hydrophobic block (Ci); the curvature and bending constants of surfactant films arise due to total contributions from both blocks. Therefore, in a CiEj-μE phase (W/O or O/W), interfacial properties of CiEj, surfactant-films vary in a regular fashion as a function of both Ci and Ej.75,76 Extensive oil–water (O–W) interfacial tension (IFT) measurements by Sottmann et al.75 revealed that the limiting surfactant molecular area at the O–W interface depends strongly on the length of EO fragment (Ej) and is essentially independent of the solvent ACN as well as surfactant chain-length Ci. Despite this, contrast-variation SANS and O–W interfacial tension γo/w measurements by Gradzielski et al.76 revealed that the bending constant (2κ + ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ) and γo/w increases with surfactant chain-length Ci, so that longer chain CiEj-films are more “rigid”. This trend was echoed in studies28,29 with cationic CnCmDAB W/O-μEs, as will be discussed in more detail in Section 3.4.
) and γo/w increases with surfactant chain-length Ci, so that longer chain CiEj-films are more “rigid”. This trend was echoed in studies28,29 with cationic CnCmDAB W/O-μEs, as will be discussed in more detail in Section 3.4.
2.6. Very-low oil–water interfacial tension
A widely known application of μEs is in enhanced recovery (EOR) of crude oils, which is because the thermodynamically stable surfactant monolayers at O–W interfaces reduce O–W interfacial tension (γo/w) to very low values – on the order of 10−2 to 10−4 mN m−1.4,77 The history of exploring surfactants at brine-oil interfaces for EOR is extensively covered in the review of Taber.77 In fact, in the early years of EOR in the 1970's, the importance of very-low γo/w was recognized to be an important factor and accelerated the development of spinning drop tensiometry (SDT) for experimentally accessing very-low γo/w values.A standard method for investigating γo/w involves SDT studies with an electrolyte scan using a surfactant aqueous solution > CMC and oil droplet injected into the tensiometer (see Aveyard et al.).78Fig. 5 shows a typical IFT dependence of AOT at brine-n-heptane interfaces, consistent with Winsor I → Winsor III → Winsor II-μEs macroscopic phase transitions.57 Since the surfactant is at a concentration ≫ CMC, addition of electrolyte changes aqueous-phase surfactant solubility; the minimum γo/w corresponds to the salt concentration (optimal salinity, OS) at which surfactant solubility in both the oil and water is balanced.79
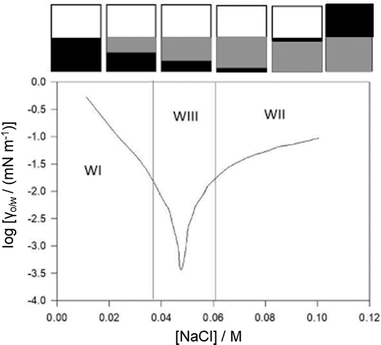 | ||
| Fig. 5 (top) Cartoon representation of WI → WIII → WII transitions (white: excess oil, black: μE-phase and grey: excess water), (bottom) water–n-heptane interfacial tension progression as a function of [NaCl], the surfactant is AOT. [AOT] is much higher than the CMC. Temperature: 298 K. Data for (bottom) were reprinted (adapted) from ref. 57. Copyright 2002. Reproduced with permission from American Chemical Society. | ||
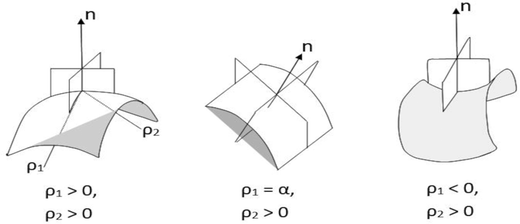
In a benchmark series of studies, Binks et al. showed the effects of linear solvent ACN;78,80,81 on increasing ACN the OS shifts towards higher concentration – meaning equal O–W partitioning needs enhanced “salting out” of AOT. In addition, the minimum in γo/w at the OS tends to increase upon increasing the solvent ACN. Whether this has anything to do with the surfactant hydrophobic chain-length cannot be inferred because only the 2-ethylhexyl chain of AOT has been considered in these works. This observation was correlated to the saddle-splay energy (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ) of AOT films: in Winsor III systems, this energy is positive (ρ1 and ρ2 are of opposite signs, see Scheme 1 – suggesting presence of saddle-like bicontinuous structures) in n-dodecane, close to zero but negative in n-decane and negative in n-octane (ρ1 and ρ2 are of same signs suggesting spheres).82 A similar trend was seen for nonionic C12E5 on increasing solvent ACN.83
) of AOT films: in Winsor III systems, this energy is positive (ρ1 and ρ2 are of opposite signs, see Scheme 1 – suggesting presence of saddle-like bicontinuous structures) in n-dodecane, close to zero but negative in n-decane and negative in n-octane (ρ1 and ρ2 are of same signs suggesting spheres).82 A similar trend was seen for nonionic C12E5 on increasing solvent ACN.83
The surfactant chemical effect on γo/w has also been explored with cationic CnCmDABs,35 zwitterionic dichain phosphocholine84 and anionic AOT structural analogues.57 Two aspects of the AOT hydrophobic architecture were seen to be potentially important in promoting surfactant efficiency at O–W interfaces – (i) brushlike branching at the chain-tips, (ii) absence of branching at the carbon atom immediate to the C–O–C oxygen atom.
Table 2 lists the optimum salinity (OS) and minimum γo/w for various branched AOTs taken from ref. 57 – depicting the chemical effect.55,57 For CnCmDAB surfactants in W/cyclohexane Winsor II μEs, γo/w was seen to increase on increasing surfactant hydrophobic chain-length.35 Therefore, for a range of different nonionic, cationic, and anionic surfactants the O–W interfacial properties are notably affected by chemical variation both at the surfactants and solvents.
| Surfactants | OS/M | γ o/w × 104/(mN m−1) |
|---|---|---|
| AOT1 | 0.047 | 4 |
| AOT2 | 0.037 | 6 |
| AOT3 | 0.062 | 8 |
| AOT4 | 0.012 | 2 |
| AOT5 | 0.12 | 10 |
3. Surfactant–solvent chemical effects on self-assembly
3.1. Dry reverse micelles
As pointed out in Section 2.1, dry reverse micelles (RMs) are surfactant solutions in a non-polar hydrocarbon solvent – without water or with small-quantity of water bound to the surfactant head-groups. Not all surfactants are highly soluble in hydrocarbon solvents – as it was mentioned in Section 2.3. AOT and many of its derivatives are highly soluble and hence these are good model systems to consider. However, for normal AOT, the CMC and aggregation number (nagg) are harder to determine in non-polar media as compared to in aqueous systems.85–87 Work of Peri indicated that nagg increases with solvent ACN;88nagg for AOT in n-nonane and n-dodecane were between 26 and 29 respectively, whereas a separate SANS study suggested nagg to be 22 in n-decane.89 Pulse-field gradient NMR studies supported the idea that at zero water content, nagg of AOT is of the order of only few molecules.53a In cyclic hydrocarbon solvents such as benzene, p-xylene or cyclohexane nagg was found between 20-30.47,89,90 Studies of dry-RMs of CiEj or DDAB surfactants in nonpolar solvents are few and far between. An infra-red spectroscopic study by Pacynko et al.91 indicated that intermolecular hydrogen bonding among the EO units is unimportant for CiEj aggregation in non-polar solvents. In addition, CiEj aggregation in linear and cyclic hydrocarbon solvents was observed, but not in solvents such as benzene and CCl4.92,93 For instance, SANS measurements of Ravey et al.93 suggested that based on nagg, solvents for C12E4 could be categorized into three classes (i) long-chain hydrocarbons (n-decane and n-hexadecane) in giving nagg ≈ 13, (ii) medium-chain hydrocarbons (n-heptane) in which nagg ≈ 5–8, (iii) polar organics (methanol, CCl4etc.) in which no significant aggregation was observed. Some hypotheses suggest that the key factor in switching aggregation on/off (i.e. aggregation or no aggregation) might be the solvent polarity/dielectric properties.94 Hollamby et al.95 showed that aggregation of AOT and C12E5 can be correlated with “solvent quality” – characterized by solvent Hildebrand and Snyder polarity parameters.Early SANS measurements indicated lack of micellization of AOT in cyclohexane until the concentration exceeded 0.225 mM; the dry-RM radius (i.e. radius covered by surfactant tails and head-groups) in cyclohexane was 12 Å, which was a little smaller compared n-decane (15 Å).89 Smith et al.96 applied contrast variation-SANS to investigate aggregation and CMCs of AOT in deuterated cyclohexane, benzene and n-dodecane: it was found that the CMCs (≈0.09–0.13 mmol kg−1) were very similar in these solvents. At [AOT] ≫ CMCs, the dry-RMs in these solvents were spherical (Fig. 6), with radii between 15–16 Å. The aggregation number nagg was essentially constant at ∼28 between ∼0.1 mmol kg−1 (just above CMC) and ∼10 mmol kg−1 (≫CMC) in both n-dodecane-d26 and cyclohexane-d12; however, in benzene-d6, nagg ≈ 20 when the AOT concentration was just above the CMC (0.09 ± 0.06 mmol kg−1 in benzene-d6), and gradually increased to ∼28 upon increasing the AOT concentration to ∼10 mmol kg−1. These results indicated that the solvent chemical nature (aromatic solvents especially) might have a subtle effect on AOT-aggregation. Nevertheless, for linear n-alkanes it can be said that the solvent ACN has no notable influence on the dry AOT RMs.89,93,95–97
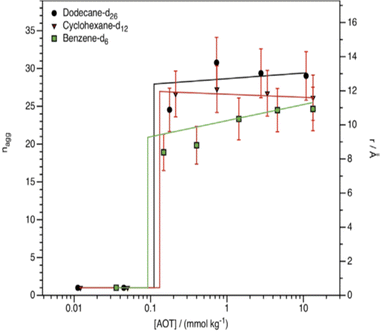 | ||
| Fig. 6 Aggregation number (nagg) and radii of h-AOT dry-RMs in various organic solvents. Temperature: 298 K. The sudden increase of nagg is consistent with a free molecule to aggregated transition, i.e. a CMC. (Reprinted from ref. 96, Copyright (2016), with permission from Elsevier.) | ||
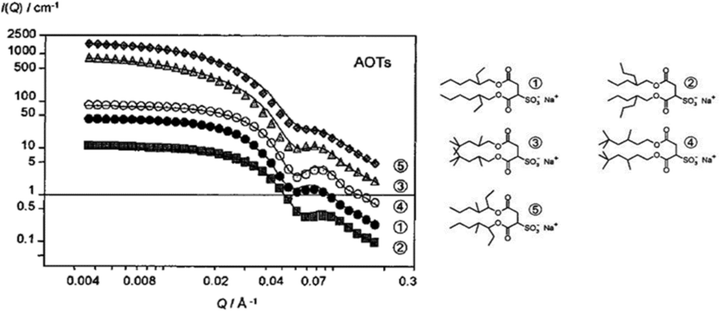 | ||
| Fig. 7 Surfactant shell-contrast (D2O/h-surf/d-alkane: D/H/D; D: deuterated, H: proteated) SANS profiles for W/O-μEs of normal AOT (AOT1) and AOT-analogues ([surfactant]: 0.050 M, n-heptane-d16 as the solvent). Experimental temperatures are listed in Table 3, W = 30. Lines are fits to the Schultz core–shell model. Data and fits were multiplied by various factors for better resolution. The figure was reprinted (adapted) with permission from ref. 55. Copyright 2000 American Chemical Society. | ||
A comparison of AOT aggregation in deuterated n-decane-d22 and toluene-d8 solvents by Spehr et al.98 found the internal RM polar core radii (surfactant heads) to be 3 Å and 2 Å respectively and surfactant shell-thickness ≈13 Å. The scattering length density (ρs) of solvent-free AOT-shells is ideally ρshell = −0.38 × 10−6 Å−2; analyses gave ρshell in toluene-d8 +1.1 × 10−6 Å−2 compared to −0.1 × 10−6 Å−2 in n-decane-d22 – suggesting higher penetration of toluene into the surfactant chain-tips compared to n-decane. Nevertheless, the general finding based on all the results mentioned above is that solvent chemical identity appears not to have much significant effect on dry-RM aggregation. It is worth noting the differences between these findings and the high degree of sensitivity to phase behaviour for AOT-based μEs nevertheless (see Section 2.3).
3.2. W/O-μEs: surfactant chemical structural effects on interfacial films
The packing parameter model would predict that efficient surfactant packing is a function of surfactant hydrophobic chain length as well as chain-volume – pointing to the importance of sufficiently long hydrophobic chains with branching.4,27 This was discussed in Sections 2.2 and 2.3. Theoretical calculations of Nagarajan99 emphasized the idea that hydrophobic tails have important effects – adding that the effects can be either “explicit” (modification of hydrophobic tail molecular area) or “implicit” (by satellite-control over surfactant head-group area, ah). Values listed in Table 3 derived from SANS and surface tension analysis by Nave et al.55,102 suggest that the surfactant hydrophobic architecture might not influence the surfactant–shell thickness (ts) and headgroup area (ah) significantly.55 There might be a structure-aggregation correlation in terms of interdroplet attractions, however (Fig. 7);55 alkyl-branching at the carbon atom next to the C–O–C group, as it is in AOT3 and AOT5, led to structure factor S(Q) > 1 – reminiscent of an Ornstein–Zernike S(Q).100 Looking back at Fig. 4(B), these two surfactants form single-phase L2-μEs only at low temperatures – and so attractive interactions might become evident at higher temperatures.| AOTs | Aqueous CMC ± 0.03/mM | W/O-μEs (W = 30) | |||
|---|---|---|---|---|---|
| Temperature/K | Water-core radius, Rc ± 1/Å | Surfactant film thickness, ts ± 1/Å | Headgroup area, ah (swelling law)a ± 2/Å2 | ||
a Swelling law: 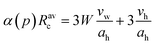 where vw is volume of a water molecule, vh is surfactant head-group volume and α(p) = 1 + 2p2, p is droplet polydispersity. where vw is volume of a water molecule, vh is surfactant head-group volume and α(p) = 1 + 2p2, p is droplet polydispersity.
|
|||||
| 1 | 2.56 | 295 | 46 | 9.1 | 74 |
| 2 | 3.18 | 318 | 41 | 8.7 | 79 |
| 3 | 4.36 | 282 | 43 | 8.6 | 76 |
| 4 | 1.10 | 323 | 45 | 9.4 | 74 |
| 5 | 7.15 | 282 | 41 | 8.4 | 86 |
In non-polar solvents, the effect of the total carbon number at both cationic and anionic surfactant-tails is believed to be inversely linked to nagg.92 Additionally, introducing branching in these hydrophobic fragments reduces nagg.90 This pattern is in accordance with the measurements of Frank et al., and CMCs of various linear-chain AOT measured in hydrocarbon solutions as well as aqueous media respectively.101,102
On introducing aromatic phenyl tips into the AOT-hydrophobic tails, the effective hydrophobic-tail area at the CMC (ACMC) increases.56 The limiting aqueous surface tensions (γCMC) of these surfactants were also higher compared to normal AOT – which was attributed to the polarizable phenyl groups. Adding branching into the phenyl-tipped AOTs reduced γCMC but increased ACMC. As mentioned before, and importantly, it was observed that these phenyl-tipped AOTs could only form W/O-μEs in an aromatic solvent such as toluene – effectively mimicking the aromatic nature of the surfactant chain-tips – but not in linear hydrocarbon such as n-heptane. Moreover, inclusion of branched groups in these phenyl-tipped AOTs results in weaker packing at water-toluene interfaces – hence less water uptake inside the droplets. Nevertheless, similar to the linear and branched AOTs mentioned in ref. 55, the phenyl-tipped AOTs also did not notably affect the ah – showing that the droplet core properties may be dominated by water-headgroup interactions.55–57
Cationic CnCmDAB surfactant films at the O–W interfaces were introduced previously in Sections 2.2 and 2.4. in the light of the cylinder → spheroid → sphere structural evolution on increasing water content.28,38,39 Contrast variation SANS results showed that increasing the Cn-chain length leads to an increase of the cylinder radius, although no clear correlation in terms of cylinder length could be found.28 It was mentioned previously that cyclohexane weakly penetrates the surfactant chains on increasing asymmetry of the two alkyl-tails Cn and Cm.29 (Note, nonionic-film properties have been discussed in Section 2.5.)
3.3. Surfactant-film rigidity
In W/O-μEs, surfactant monolayers bend towards water – generating negative curvature; on the other hand, in O/W-μEs the curvature is towards the oil and is said to be positive.4 In this context, surfactant film-bending rigidity is synonymous with film-curvature. The loose term “film rigidity”, which is a measure of the energy required for a surfactant monolayer to bend towards a continuous solvent (either oil or water), is a key aspect in understanding μE-film stability.31 Part of the model was discussed in Section 2.3., which relates surfactant monolayer free-energy of bending to curvature c.For low volume fractions of spherical droplets (ϕ), the free energy of bending of surfactant film per unit area of μEs (F/A) can be expressed as35,76
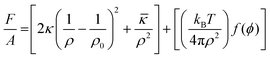 | (4) |
| f(ϕ) = {ln(ϕ) − 1}3 | (5) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ), by the following
), by the following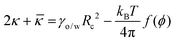 | (6) |
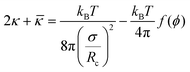 | (7) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ) constant was observed, i.e., surfactant “film rigidity” increased with surfactant chain length (Fig. 8).35 As pointed out in Section 2.5., similar observations were made for the nonionics. The variation of film-bending parameters was attributed to surfactant hydrophobic chain-length; however, the solvent chain-length effect, contrary to the model proposed by Shah et al.,23b,c was interpreted to be secondary.76,103–105
) constant was observed, i.e., surfactant “film rigidity” increased with surfactant chain length (Fig. 8).35 As pointed out in Section 2.5., similar observations were made for the nonionics. The variation of film-bending parameters was attributed to surfactant hydrophobic chain-length; however, the solvent chain-length effect, contrary to the model proposed by Shah et al.,23b,c was interpreted to be secondary.76,103–105
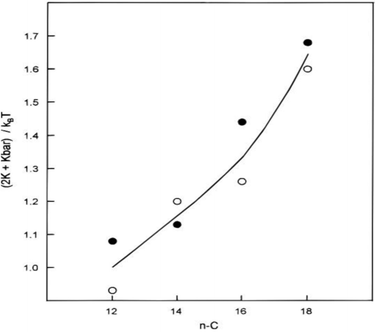 | ||
Fig. 8 Variation of surfactant film-bending constant (in units of kBT) as a function of CnC12DAB W/O-μEs (solvent: cyclohexane, temperature: 298 K), the line is a guide to the eye. Circles represent calculation of (2κ + ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ) using eqn (6) (white circles) and eqn (7) (black circles); γo/w was estimated using surface light scattering (SLS), Rc and σ/Rc were obtained by SANS measurements. The figure was reprinted with permission from ref. 35. Copyright 1997 American Chemical Society. ) using eqn (6) (white circles) and eqn (7) (black circles); γo/w was estimated using surface light scattering (SLS), Rc and σ/Rc were obtained by SANS measurements. The figure was reprinted with permission from ref. 35. Copyright 1997 American Chemical Society. | ||
Rather, Sottmann et al.105 claimed that for the nonionics, ah at O–W interface is only dependent on the length of EO fragment and independent of the solvent as well as surfactant hydrophobic chain-length; nevertheless, the film-bending constants increase upon increasing surfactant hydrophobic chain-length. In this respect, data for AOT-based μEs are scarce, for example, ellipsometry experiments by Binks et al.80,82 (Section 2.6). To recap, for the AOT, on increasing solvent ACN the tendency to develop saddle-like or bicontinuous structures increases. Surprisingly, fluorescence quenching studies by Almgren et al.106 could not find any such variation – suggesting the film-bending estimation might be exclusively responsive to the experimental technique being employed.
3.4. Solvent chemical-effect on μE droplet morphology
The ellipsometry data of Binks et al.80 indicate that solvent chemical nature (i.e. the effect of n-alkane ACN variation, presence of aromaticity etc.) might have a subtle role in controlling the surfactant-film properties. Regarding solvent molecular penetration into the surfactant monolayers, the key point is that it is subtle – although some solvents might be able to slightly penetrate the surfactant chain-tips, most show only limited effects.8,28,29,36 In AOT-based W/O-μEs, solvent penetration was mostly studied by indirect techniques such as nuclear magnetic resonance (NMR), fluorescence correlation or imaging.46,107–110 These results suggest that cyclic molecules (cycloalkanes or aromatic hydrocarbons) are more efficiently incorporated into AOT-monolayers compared to branched or linear alkanes. In addition, IFT measurements by Aveyard et al.111 suggested that solvent penetration into planar AOT-monolayers at the brine (0.100 M NaCl) solution/oil interface increases with reduction of solvent ACN.All these methods discussed above were indirect, however, direct and quantitative information on solvent penetration can be obtained from carefully designed and executed contrast-variation SANS measurements.17,28,29 Analysis of the SANS data reveals that solvent penetration with symmetric dichain surfactants is not significant – regardless solvent chemical structure. On the other hand, solvent penetration could be detected into monolayers of di-chain surfactants having asymmetric tails: for example, using CnC12DAB-based W/O-μEs, on increasing n (n = 12, 14, 16 and 18) the measured volume fraction of cyclohexane penetrating into the chain region increases from 0 (no penetration) to no greater than 0.12. This maximum value observed corresponds to approximately one cyclohexane molecule penetrating for every two surfactant molecules.29 Interestingly, these SANS analyses (Table 4) suggested that the ah can be influenced by changing the solvent chemical nature.
| Surfactants (CnC12DAB) | Solvents | Maximum water solubilization, Wmax | Headgroup area,aah/Å2 | Surfactant film thickness,ats ± 1/Å | Oil volume fractionaϕoil |
|---|---|---|---|---|---|
| a Uncertainties: ts ± 1 Å, ah (swelling law) ± 2 Å2, ϕoil ± 10%. | |||||
| C12–C12 | n-Heptane | 25 | 65.8 | 10.8 | 0.01 |
| Cyclohexane | 12 | 54.8 | 11.0 | 0 | |
| C14–C12 | n-Heptane | 23 | 66.3 | 10.6 | 0.01 |
| Cyclohexane | 12 | 59.7 | 11.7 | 0.05 | |
| C16–C12 | n-Heptane | 21 | 66.8 | 11.5 | 0.02 |
| Cyclohexane | 11 | 55.6 | 12.8 | 0.07 | |
| C18–C12 | n-Heptane | 19 | 66.3 | 11.8 | 0.02 |
| Cyclohexane | 11 | 58.9 | 13.5 | 0.08 | |
Coming to the second aspect of droplet size and morphology, SANS-results reveal that the effect of n-alkane ACN on water-core radius (Rc) in W/O-μEs is minimal.113–116 The solvent, however, affects droplet polydispersity and the extent of interdroplet attractive interactions (see next section) quite significantly. For instance, neutron spin-echo (NSE) experiments117 suggested that for W/O-μEs, water-core droplets were less rigid and more polydisperse in linear n-alkanes such as n-hexane compared to cyclohexane (p = 0.24 vs. 0.39 and bending constant K = 0.19 kBT vs. 0.24 kBT, W = 10). In particular, droplet attractive interactions are minimal in n-hexane to n-decane, but significant for linear n-alkanes with ACN > 10.118,119 Interdroplet interactions can be understood in terms of material exchange through the channels formed due to droplet attraction – time-resolved fluorescence results suggested that nagg as well as interdroplet exchange rate increases on increasing solvent ACN.120 Solvent chemical effects on droplet size distribution and surfactant-film geometry were observed by Balakrishnan et al.;121 the size probability distribution tended to be more uneven (less Gaussian-like) as the solvents were progressively changed from n-hexane to n-dodecane.
To summarize Sections 3.2–3.4, the chemical effects on droplet morphology and surfactant-films should be discussed more holistically, i.e. the effects may not be due to solely the surfactant or solely the solvent – rather a surfactant–solvent chemical combination might be governing the interfacial and structural properties. For a given set of surfactants, understanding surfactant chemical variation might be relevant considering the solvent identity and vice versa. It is seen that the solvent chemical-structure effects are notably manifest in terms of interdroplet attraction parameters, as discussed below.
3.5. Attractive interaction in W/O-μEs: square-well potential
Shifts in μE phase-transition boundaries are correlated with the interfacial film bending and droplet–droplet attractive interactions. When droplets in W/O-μEs start swelling on increasing W and they get closer to one another, interdroplet attractive interactions caused by the overlapping of surfactant hydrophobic tails drive the L2-to-cloud point/critical-type phase separation.37,112 The attractive interaction between two hard sphere-like surfactant-coated droplets can be interpreted in terms of an attractive square well potential function, expressed as97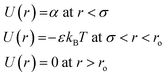 | (8) |
| A = 8(λ3 − 1)(eε′ − 1) | (9) |
| ε′ = log(ε + 1) | (10) |
3.6. Attractive interactions and critical behaviour
To further extend discussions from the previous sections, the attractive interactions between μE-droplets is theorized as mutual penetration of surfactant chain-tips. The upper temperature (i.e. L2-to-cloud point) phase separation can be accounted for by considering interdroplet attractive potential – when ϕ is sufficiently high (10 vol% and onwards for instance);97 in W/O-μEs, at this range the droplets are close enough to one-another due to the surfactant–shell overlapping. Lemaire et al.112 interpreted the surfactant–shell interaction (U) as a sum of hard-sphere (Uhs) and attractive potential (UA) as| U = Uhs + UA | (11) |
| Eij = 2εijrij6/r6 | (12) |
In terms of experimental observations,55,56,112,126 on increasing temperature the attractive potential reaches to a threshold, initiating phase separation; close to the upper temperature phase-boundary, μEs show enhanced turbidity suggesting strong attraction among droplets. In AOT-based W/O-μEs, an interesting phenomenon has been of much attention; here near the phase-boundary, the L2-μE is split to two nearly equal volume μEs of different μE-densities.97,112,122,125 This is interpreted analogous to liquid-liquid critical separation due to two different types of local structures resulting in a density gradience126 within the single-component liquid (such as water). In AOT-in-n-decane W/O-μEs, this separation takes place around 316 K (droplet volume fraction, ϕ = 0.075).20,125 Near the critical temperature (Tc), droplet-hydrodynamic correlation-length increased from 100 Å to several thousand angstroms.125 A simplified expression of SANS scattering intensity I(Q) near Tc includes a structure-factor S(Q)4,97
| I(Q) = nP(Q)S(Q) | (13) |
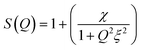 | (14) |
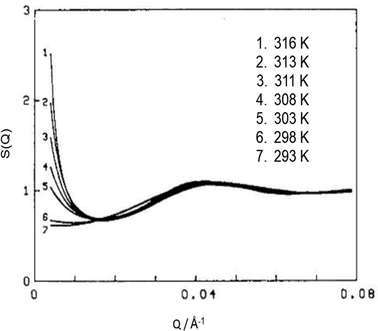 | ||
| Fig. 9 Mean droplet–droplet structure factor S(Q) depicting interdroplet attractive interactions – the μE is AOT/D2O/n-decane (3/5/92 wt%), ϕ = 0.075, and it is approaching critical temperature (∼316 K). S(Q) were calculated using a mean-spherical approximation procedure described in ref. 20. The figure was adapted from ref. 20. Copyright (1986), with permission from Elsevier. | ||
The extent of attractive interactions near the L2-to-cloud point phase-boundary location is governed by temperature as well as solvent.128 Earlier (Section 2.3) it was discussed that in AOT-based W/O-μEs, this boundary shifts to lower-temperature.54 The effect of n-alkane solvent ACN near this phase-boundary was studied by Toprakcioglu et al.;128 for W = 20 at [AOT] = 0.100 M, the critical-behaviour in n-decane could be seen around 313 K, whereas in n-undecane and n-dodecane the critical behaviour is observed at much lower temperatures (295 K and 278 K respectively).
The SANS results explain electrical percolation of droplets in AOT-based W/O-μEs in various n-alkanes.129–131 Percolation is interpreted as material exchange (i.e. surfactant counterions or dispersed medium) due to droplet clustering owing to the attractive interactions – which results in a sudden rise in electrical conductivity by several orders of magnitude on increasing temperature or ϕ.13,129,130 On increasing n-alkane ACN, the onset of percolation shifts to lower ϕ and lower temperature in AOT-based W/O-μEs.16,130
It should be noted that the critical-type OZ behaviour is not exclusive to dichain anionics but was observed in CiEj-based μEs (n-octane as solvent) as well.131 This indicates that regardless of the surfactant chemical identity, the critical behaviour might be a universal phenomenon in W/O-μEs, but more studies are necessary – especially on dichain cationics. Lemaire et al.112 argued about a potential role of solvent molecular volume and their model hinted at a possible effect of surfactant–solvent mutual interaction energies, which are functions of the chemical nature of the constituents.
3.7. W/O μEs: aromatic hydrocarbons
Aromatic solvents are chemically versatile, differing from their aliphatic counterparts not only in terms of chemical structures, but smaller effective molecular volumes and presence of delocalized electrons. In Section 3.2, it was shown that solvent–surfactant chemical matching is important, as observed in phenyl-tipped AOT-based W/toluene μEs.56 Literature on ionic W/O-μEs hints that auxiliary aliphatic chains might be important for governing μE-phase behaviour and surfactant film properties.96,132–135 Appel et al. studied the effect of aromatic solvents on droplet percolation; the temperature corresponding to an onset of percolation in AOT-based μEs decreased on increasing the substituted aliphatic chain-length in aromatic hydrocarbons, this parallels observations of Alexandridis et al. for n-alkane solvents on increasing ACN.25,132NSE and SANS investigations by Spehr et al.98 found film bending constants in AOT/water/toluene μEs to be higher than in the μEs containing linear- or cycloalkanes. In terms of the water-droplet size and surfactant film-geometry, nevertheless, droplet-exchange kinetics, light scattering and SANS studies pointed out that aromatic solvent-chemical structure, except halogenated aromatics, seldom affects μE-droplet characteristics.67c,133–135 The hydrodynamic size of water-droplets in medium-chain aliphatic and aromatic hydrocarbons was compared but no significant variation was found.135 The case was similar for dry-RMs, which was noted by Smith et al.96 (discussed in Section 3.1), as the morphology and radii of these aggregates were insensitive to solvent chemical nature (n-alkanes, cycloalkanes or the aromatics).
3.8. Solvent blends
An interesting approach to tune hydrocarbon solvents, in particular physical properties such as density, is using controlled blends, as shown by Salabat et al.136 This allows different intermediate solvent properties to be accessed, and the results show clear links between phase behaviour and mixed solvent identity. With blends of n-heptane and toluene, L2-μEs domains could be tuned between the two pure-solvent extremes and shifted to higher or lower temperatures by varying solvent composition mole fraction (Fig. 10). The same study showed that the aggregation and colloidal stability in such μEs could also be controlled; translational diffusion coefficients of droplets decreased (i.e. “switching off” of interdroplet interactions) on increasing toluene mole fraction. The opposite effect dominates when n-dodecane is used in place of toluene. To characterize the solvent mixtures the effective molar volume of the mixed solvent (Veffmol) can be defined as –| Veffmol = X1Vmol1 + X2Vmol2 | (15) |
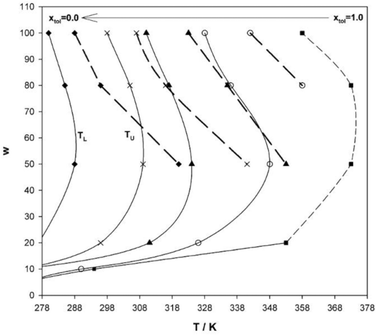 | ||
| Fig. 10 Phase-behaviour of AOT-based W/O-μEs in pure n-heptane and toluene and their solvent blends at toluene mole-fractions xtol = 0.25, 0.50 and 0.75 (from left to right). xtol = 0 (far left) represents pure n-heptane, xtol = 1 (far right) is pure toluene. [AOT] = 0.100 M, solid lines indicate WII-to-L2 transition boundary and dashed lines represent L2-to-cloud point boundary. Lines are guides to the eye. The figure was reprinted from ref. 136. Copyright (2007), with permission from Elsevier. | ||
3.9. Supercritical alkanes: oil-density guided self-assembly?
Above the critical pressure (Pc) and temperature (Tc), the gas–liquid boundary for a fluid disappears and a supercritical fluid will form. Supercritical fluids generally have much lower density and higher diffusivity than normal liquids. Due to being supercritical fluids at room temperature and more compressible than normal liquids, low-density n-alkanes (n-ethane, n-propane and n-butane for instance) expand the horizon of stable μEs. In such low-density supercritical n-alkanes, μE stability is expected to be a strong function of temperature and pressure. It has been observed that on increasing pressure (i.e. increasing fluid density) of short-chain supercritical n-alkanes the phase transition in AOT-based W/O-μEs involves a gradual shift from a three-phase system to L2-μEs.138–140 At high pressures, water solubilization in n-propane showed similarity to that of medium-chain n-alkanes at ambient conditions.139,140 Density is an important factor here: the effect of solvent ACN and pressure on Wmax of AOT-based W/O-μEs can be understood from Table 5 based on studies by Tingey et al.;124 lowering Wmax in isooctane on increasing pressure is worth noting. At 300 bar and 298 K, isooctane has a density of 0.716 g cm−3 which is very close to n-nonane density at room temperature and pressure.141,142 This observation correlates to the L2-phase shift of AOT W/O-μEs towards low temperatures on increasing linear hydrocarbon ACN (discussed in Section 2.3). It is clear, that the solvent-density change due to application of pressure is an important parameter, as it enables stabilization of μEs under different thermodynamic conditions which are not accessible with normal liquid-like solvents at atmospheric pressure.| Solvents | Pressure/bar | W max |
|---|---|---|
| Xenon | 200 | 1 |
| 520 | 5.6 | |
| Ethane | 200 | 1 |
| 350 | 5 | |
| 620 | 10 | |
| 840 | 35 | |
| n-Butane | 100 | 45 |
| 300 | 45 | |
| n-Pentane | 1 | 43 |
| 100 | 43 | |
| 300 | 43 | |
| n-Hexane | 100 | 116 |
| 100 | 105 | |
| 300 | 87 | |
| Isooctane | 1 | 74 |
| 100 | 69 | |
| 300 | 59 | |
Fulton et al.139 reported that the pressure-dependent electrical conductivity of AOT/water/isooctane μEs at 298 K at a specific AOT concentration (0.036 M) could nearly be mimicked by AOT/water/n-propane μEs at 376 K (103 °C); while the increase of pressure did not affect electrical conductivity of AOT/water/isooctane μEs, the conductivity of AOT/water/n-propane μEs lowered and appeared to reach closer to the former as pressure was gradually increased. Meanwhile, phase behaviour and scattering investigations116,140 of AOT-μEs in low density n-propane and n-butane, as a function of pressure and temperature, found that lowering the pressure from 400 bar to 70 bar pushed L2-μEs towards unstable systems. This transition pressure, and the nature of phase-separation, depend on temperature and the surfactant chemical nature. The pressure (and hence solvent density) was used to control interdroplet attraction: lowering pressure, and hence fluid density, promoted growth of droplet clusters, whereas increasing pressure/density led to split the droplets from those clusters. This demonstrated that even in low density n-alkanes, it is possible to emulate the phase-boundaries that are often observed in long-chain linear n-alkanes The observations also support SANS results by Kaler et al.123 indicating that μE-droplets formed in supercritical n-propane were of similar size to μE-droplets in regular solvents, for example, n-hexane. Nonionic CiEjs in near-critical ethane and n-propane solvent blends were studied by Beckman et al.143 by dynamic light scattering; on increasing pressure they found droplet diffusion increased, which was attributed to lowering interdroplet attraction. This is also consistent with the system locating away from the cloud-point phase boundary.
4. The effect of surfactant counterions
So far, the focus on ionic surfactant-chemical architecture was exclusively on the chemical nature of the surfactant-ion (i.e. hydrophobic moieties). This section considers the effects of variation in head group counterion in anionic surfactants. Sodium (Na+) is the natural counterion for the anionic AOT and its analogues (i.e., Na-AOT), but this counterion can be readily varied by ion exchange techniques. In addition, the “inorganic” nature of the counterion can be changed by substitution with different “organic” quaternary ammonium ions.151 The counterion provides screening of Coulombic repulsion between the like charged head-groups,39 and this effect is important for surfactant self-assembly. In the study by Oshitani et al.,144 electrostatic screening was found to follow the order: K+ ≈ Rb+ > Cs+ > Na+ > Li+. Substituting Na+ by monovalent Cs+ led to a change of AOT-reverse micellar morphology in n-decane from slightly oblate spheroids to disks.145 The effect of substituting monovalent counterions with divalent ones, such as Mg2+, Ca2+, Co2+, Cu2+, Ni2+ and Zn2+, yields a class of surfactant salts conveniently labeled M2+(AOT)2 – in which now one counterion associates with two-anionic surfactant-ions. The effects of this variation on droplet morphology, surfactant-film geometry and overall μE-phases are significant.Temperature-composition phase-diagrams39 showed that while Na-AOT μEs in cyclohexane exhibit two-phase boundaries (Winsor II-to-L2 and L2-to-cloudy phase), substitution of Na+ with Mg2+, Ca2+, Co2+, Cu2+ and Zn2+ made the W/O-μEs less temperature-sensitive, and only one phase boundary (L2 to Winsor II) could be observed.146 The SANS profiles for Mn+(AOT)n W/O-μEs at a high dilution region has been represented by a log–log plot.148 In this representation, at Q < 0.10 Å−1, the I(Q) profile can be expressed in terms of a dimensionality (fractal) parameter characterizing the aggregate structure, D, as
| I(Q) ∼ npQ−D | (16) |
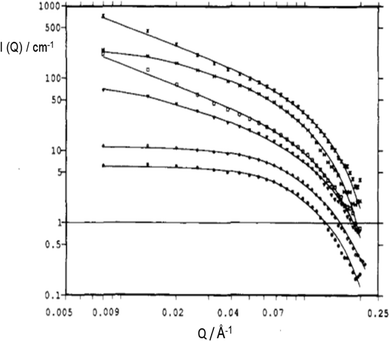 | ||
Fig. 11 SANS profiles of Mn+(AOT)n W/O-μEs in cyclohexane-d12 (W = 5, [surfactant] = 0.075 M); ( ) Mg2+, ( ) Mg2+, ( ) Co2+, ( ) Co2+, ( ) Ni2+, ( ) Ni2+, ( ) Cu2+, ( ) Cu2+, ( ) Zn2+, ( ) Zn2+, ( ) Cd2+. Solid lines are fits for rigid rod; data were multiplied by arbitrary numbers for better visual. The figure was reprinted (adapted) with permission from ref. 149. Copyright 1993 American Chemical Society. ) Cd2+. Solid lines are fits for rigid rod; data were multiplied by arbitrary numbers for better visual. The figure was reprinted (adapted) with permission from ref. 149. Copyright 1993 American Chemical Society. | ||
Another related class of AOT surfactants includes symmetrical cations such as quaternary ammoniums [R4N]+ (e.g. tetra-n-ethylammonium).151 In W/O-μEs, it was observed that the NH4+ ion induced spherical droplets, similarly as seen for the Na+ ion.152a On the other hand, substituting the hydrogen atoms of the NH4+ with bulky alkyl groups (tetra-n-ethylammonium) induced cylindrical micelles at low W and gave a cylinder-to-sphere transition on increasing W – reminiscent of the transition-metal AOTs.152a,b Interestingly, the counterion can be exchanged by even more exotic chemical moieties; for instance, when the Na+ ion of AOT is exchanged with polymerizable units such as [2-methacryloyloxy]ethyl trimethylammonium cations and the surfactant has been dispersed to polar oils such as methyl methacrylate (MMA), L2 W/O-μEs could be formed.152c Similar ion exchange could be carried out for cationic C12DAB surfactants by exchanging the Br− ion with a more bulky MMA− ion – albeit the L2-μE region is not as broad compared to the former systems.152c,d
Here, the discussions imply that while the surfactant tails as well as solvents significantly affect the phase-behaviour, structural properties, and O–W IFT of W/O-μEs (Sections 2 and 3), surfactant counterions also have profound control over the phase appearance and droplet morphology. In particular, the cylinder → sphere transition, as it was observed for cationic CnCmDAB – μEs (Section 2.2),28,29,38 is a phenomenon associated with counterion variation for dichain anionics as well. The landscape for exploring this aspect is still wide-open, especially for AOT analogues – since the hydrophobic tails in this class of surfactants can be manipulated to a larger degree due to its flexible synthetic routes,37 for example by incorporating silicon atoms into the tails.153
5. General discussion and conclusion
As examples of model thermodynamically stable colloidal systems, it is clear that stability and phase behaviour of W/O-μEs are clearly linked to surfactant and solvent chemical structures. In terms of phase stability alone, these chemical effects are manifested by the relative position of single-phase μEs within temperature-composition phase diagrams. Chemical effects can be seen more obviously at the macroscopic level (i.e. visual means), whereas, on a microscopic local structural level chemical effects are more subtle. It is observed that – (i) enhanced hydrophobicity in the surfactant chains (i.e. longer hydrophobic tails and/or presence of branching – including branching at the chain-tip), may result in better surfactant partitioning at an O–W interface – evidenced by lowering the minimum γo/w values compared to surfactants with less branching or shorter hydrophobic chain-length, (ii) the role of solvent is subtle but significant – solvent chemical structure dictates the L2 W/O-μEs phase domains on the temperature-composition landscape (phase diagrams); in addition, depending on the surfactant chemical nature, the solvent might control droplet–droplet attractive interactions, (iii) furthermore, chemical variation in the surfactant-ions and counterions (for ionic surfactants) or in the hydrophobic and hydrophilic moieties (both ionic and nonionic surfactants) renders notable changes in μE-phase stability. Of particular note, especially for double tail anionic surfactants, chain branching seems to be important, since it allows sufficient surfactant conformational chain freedom, which is needed for efficient μE-formation. The degree of importance of chain branching is, however, not completely understood, and synthesis of surfactants with different chain-branching motifs might shine light on this matter. On the other hand, using linear, more ordered, hydrophobic chains tends to limit conformational degrees of freedom and this is detrimental to μE-formation.An important question remains: what are the actual chemical structural factors required for efficient μE-formation? Is there a universal feature, such as matching of solvent and surfactant-hydrophobic tail density/molecular volume that can be correlated to chemical matching/mismatching? Although these remain open-ended issues, it should be possible to develop a universal surfactant–solvent framework. Clearly, these all go back to thermodynamic and geometric aspects of surfactant films at O–W interfaces, and a recent review154 is very instructive in this respect. This missing link may be considered as the “holy grail”, accounting for μE-formation, stability, and structure from a chemical viewpoint. Furthermore, since W/O-μEs represent ideal systems for probing surfactant–solvent effects, this would have widespread general applications in colloid science, especially for dispersion in non-aqueous and low dielectric solvents. Molecular dynamics (MD) simulations have potential for unraveling these local rules at surfactant–solvent interfaces, especially, since surfactant tip–solvent interactions can be probed which are dominated by van der Waals interactions. A likely advance might be the quantification of surfactant tail–solvent mixing entropies by MD simulations. Attempts for surfactant and solvent chemical unification have been made before, by Peck et al.,155 based on classical thermodynamics. In that model, surfactant tail–solvent mixing energy was modelled based on the Flory interaction parameter (χ),156 which can then be related to corresponding solubility parameters (δ). In the end however, the interactions were interpreted based on solvent penetration into the surfactant shell, for which careful SANS experiments (see discussions in Sections 2.4 and 3.4) have shown to be only limited.
It is important to remember that these are “fluid” systems; therefore, in W/O-μEs the boundaries between the surfactant hydrophobic tips and solvent molecules experience local fluctuations over time.157 It might be possible by MD simulations to “see” these ever-evolving boundaries (i.e. chemical configurations) or “feel” (i.e. electronic properties, charge and polarizability distribution) to shed light on chemical structural effects. Examples of all-atom as well as coarse-grained modelling of W/O-μEs, have been emerging recently.158–161 Clearly a close link up between experiments and computational modelling is desired, and this might be the ultimate tool for conclusive understanding of the mutual surfactant–solvent chemical effects at fluid interfaces.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. R. thanks Commonwealth Scholarship Commission (CSC) of the Foreign, Commonwealth and Development Office (FCDO), UK for a PhD scholarship. A. R. thanks the Commonwealth Scholarship Commission (CSC) – which is funded by the Foreign, Commonwealth and Development Office (FCDO), UK – for a PhD scholarship.References
- (a) J. N. Israelachvili, Intermolecular and surface forces, Academic Press (Elsevier), Massachusetts, 2011 Search PubMed; (b) Y. Moroi, Micelles (Theoretical and Applied Aspects), Springer Science + Business Media, New York, 1992 Search PubMed; (c) G. N. Smith and J. Eastoe, Phys. Chem. Chem. Phys., 2013, 15, 424 RSC.
- J. Eastoe, in Colloid science principles, methods and applications, ed. T. Cosgrove, Wiley, New York, 2nd edn, 2010, ch. 4, pp. 61–90 Search PubMed.
- I. Danielsson and B. Lindman, Colloids Surf., 1981, 3, 391 CrossRef.
- J. Eastoe, Surfactant chemistry, Wuhan University Press, China, 2005 Search PubMed.
- D. Langevin, Acc. Chem. Res., 1988, 21, 255 CrossRef.
- E. Acosta, J. H. Harwell, J. F. Scamehorn and D. A. Sabatini, in Handbook for cleaning/decontamination of surfaces, ed. I. Johansson and P. Somasundaran, Elsevier B. V., Amsterdam, 1st edn, 2007, ch. 7, vol. 1, pp. 831–884 Search PubMed.
- (a) A. K. Ganguli, A. Ganguly and S. Vaidya, Chem. Soc. Rev., 2010, 39, 474 RSC; (b) S. Eriksson, U. Nylen, S. Rojas and M. Boutonnet, Appl. Catal., A, 2004, 265, 207 CrossRef; (c) M. Boutonnet, S. Lodgberg and E. Svensson, Curr. Opin. Colloid Interface Sci., 2008, 13, 270 CrossRef.
- V. C. Santana, F. D. Curbelo, T. N. Castro Dantas, A. A. Dantas Neto, H. S. Albuquerque and A. C. Garnica, J. Pet. Sci. Eng., 2009, 66, 117 CrossRef.
- C. W. Pouton, Adv. Drug Delivery Rev., 1997, 25, 47 CrossRef.
- R. G. Laughlin, The aqueous phase behavior of surfactants, Academic Press, San Diego, 1994 Search PubMed.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans., 1976, 72, 1525 RSC.
- (a) E. Ruckenstein and J. C. Chi, J. Chem. Soc., Faraday Trans., 1975, 71, 1690 RSC; (b) G. N. Smith, S. Alexander, P. Brown, D. A. Gillespie, I. Grillo, R. K. Heenan, C. James, R. Kemp, S. E. Rogers and J. Eastoe, Langmuir, 2014, 30, 3422 CrossRef PubMed.
- S. P. Moulik and B. K. Paul, Adv. Colloid Interface Sci., 1998, 78, 99 CrossRef.
- P. A. Winsor, Trans. Faraday Soc., 1948, 44, 376 RSC.
- T. Hellweg, Curr. Opin. Colloid Interface Sci., 2002, 7, 50 CrossRef.
- M. Kahlweit, R. Strey and G. Busse, J. Phys. Chem., 1990, 94, 3881 CrossRef.
- G. J. McFann and K. P. Johnston, J. Phys. Chem., 1991, 95, 4889 CrossRef.
- A. Skauge and P. Fotland, SPE Res. Eng., 1990, 5, 601 CrossRef.
- L. E. Scriven, Nature, 1976, 263, 123 CrossRef.
- S. H. Chen, Phys. B, 1986, 137, 183 CrossRef.
- W. Meier, Langmuir, 1996, 12, 6341 CrossRef.
- (a) B. Bagchi, Water in Biological and Chemical Processes, Cambridge University Press, Cambridge (UK), 2013 CrossRef; (b) H. MacDonald, B. Bedwell and E. Gulari, Langmuir, 1986, 2, 704 CrossRef; (c) M. Valero, F. Sanchez, C. Gomez-Herrera and P. Lopez-Cornezo, Chem. Phys., 2008, 345, 65 CrossRef; (d) K. P. Johnston, K. L. Harrison, M. J. Clarke, S. M. Howdle, M. P. Heitz, F. V. Bright, C. Carlier and T. W. Randolph, Science, 1996, 271, 624 CrossRef; (e) N. Zhou, Q. Li, J. Wu, J. Chen, S. Weng and G. Xu, Langmuir, 2001, 17, 4505 CrossRef.
- (a) J. Eastoe, B. H. Robinson, D. C. Steytler and D. Thorn-Leeson, Adv. Colloid Interface Sci., 1991, 36, 1 CrossRef; (b) M. J. Hou and D. O. Shah, Langmuir, 1987, 3, 1086 CrossRef; (c) R. Leung and D. O. Shah, J. Colloid Interface Sci., 1987, 120, 320 CrossRef.
- D. Liu, J. Ma, H. Cheng and Z. Zhao, Colloids Surf., A, 1998, 143, 59 CrossRef.
- P. Alexandridis, J. F. Holzwarth and T. A. Hatton, J. Phys. Chem., 1995, 99, 8222 CrossRef.
- R. P. Bagwe and K. C. Khilar, Langmuir, 2000, 16, 905 CrossRef.
- J. N. Israelachvili, Colloids Surf., A, 1994, 91, 1 CrossRef.
- (a) J. Eastoe, J. Dong, K. J. Hetherington, D. Steytler and R. K. Heenan, J. Chem. Soc., Faraday Trans., 1996, 92, 65 RSC; (b) J. Eastoe, K. J. Hetherington, D. Sharpe, J. Dong, R. K. Heenan and D. C. Steytler, Langmuir, 1996, 12, 3876 CrossRef.
- A. Bumajdad, J. Eastoe, R. K. Heenan, J. R. Lu, D. Steytler and S. Egelhaaf, J. Chem. Soc., Faraday Trans., 1998, 94, 2143 RSC.
- F. C. Frank, Discuss. Faraday Soc., 1958, 25, 19 RSC.
- W. Helfrich, Z. Naturforsch., C: J. Biosci., 1973, 28, 693 CrossRef PubMed.
- I. Szleifer, D. Kramer, A. Ben-Shaul, W. M. Gelbart and S. A. Safran, J. Chem. Phys., 1990, 92, 6800 CrossRef.
- S. A. Safran, L. A. Turkevich and P. Pincus, J. Phys. Lett., 1984, 45, 69 CrossRef.
- M. E. Cates, D. Andelman, S. A. Safran and D. Roux, Langmuir, 1988, 4, 802 CrossRef.
- J. Eastoe, D. Sharpe, R. K. Heenan and S. Egelhaaf, J. Phys. Chem. B, 1997, 101, 944 CrossRef.
- J. Eastoe, K. J. Hetherington, D. Sharpe, D. C. Steytler, S. Egelhaaf and R. K. Heenan, Langmuir, 1997, 13, 2490 CrossRef CAS.
- S. Nave, PhD doctoral thesis, University of Bristol, 2001.
- J. Eastoe, Langmuir, 1992, 8, 1503 CrossRef CAS.
- J. Eastoe, G. Fragneto, B. H. Robinson, T. F. Towey, R. K. Heenan and F. Leng, J. Chem. Soc., Faraday Trans., 1992, 88, 461 RSC.
- M. H. Hatzopoulos, J. Eastoe, P. J. Dowding and I. Grillo, J. Colloid Interface Sci., 2013, 392, 304 CrossRef.
- O. Ghosh and C. A. Miller, J. Phys. Chem., 1987, 91, 4528 CrossRef CAS.
- C. La Messa, L. Coppola, G. A. Ranieri, M. Terenzi and G. Chidichimo, Langmuir, 1992, 8, 2616 CrossRef.
- W. Sager, W. Sun and H. F. Eicke, Prog. Colloid Polym. Sci., 1992, 89, 284 Search PubMed.
- H. Kunieda and K. Shinoda, J. Colloid Interface Sci., 1979, 70, 577 CrossRef.
- K. Sato, Y. Hotta, T. Nagaoka, M. Yasuoka and K. Watari, J. Mater. Sci., 2006, 41, 5424 CrossRef.
- C. A. Martin and L. J. Magid, J. Phys. Chem., 1981, 85, 3938 CrossRef.
- P. Ekwall, L. Mandell and K. Fontell, J. Colloid Interface Sci., 1970, 33, 215 CrossRef.
- B. Tamamushi and N. Watanabe, Colloid Polym. Sci., 1980, 258, 174 CrossRef.
- A. M. Bellocq, Langmuir, 1998, 14, 3730 CrossRef.
- A. C. Hall, E. Tekle and Z. A. Schelly, Langmuir, 1989, 5, 1263 CrossRef.
- S. H. Chen, S. L. Chang and R. Strey, J. Chem. Phys., 1990, 93, 1907 CrossRef.
- (a) J. Rouviere, J. M. Couret, M. Lindheimer, J. L. Dejardin and R. Mammy, J. Chim. Phys., 1979, 76, 289 CrossRef; (b) J. Peyrelasse and C. Boned, J. Phys. Chem., 1985, 89, 370 CrossRef.
- (a) J. Texter, B. Antalek and A. J. Williams, J. Chem. Phys., 1997, 106, 7869 CrossRef; (b) J. Texter, Colloids Surf., A, 2000, 167, 115 CrossRef; (c) B. Antalek, A. J. Williams, J. Texter, Y. Feldman and N. Garti, Colloids Surf., A, 1997, 128, 1 CrossRef.
- P. D. Fletcher, A. M. Howe and B. H. Robinson, J. Chem. Soc., Faraday Trans., 1987, 83, 985 RSC.
- S. Nave, J. Eastoe, R. K. Heenan, D. C. Steytler and I. Grillo, Langmuir, 2000, 16, 8741 CrossRef.
- S. Nave, A. Paul, J. Eastoe, A. R. Pitt and R. K. Heenan, Langmuir, 2005, 21, 10021 CrossRef PubMed.
- S. Nave, J. Eastoe, R. K. Heenan, D. C. Steytler and I. Grillo, Langmuir, 2002, 18, 1505 CrossRef.
- F. D. Blum, S. Pickup, B. W. Ninham, S. J. Chen and D. F. Evans, J. Phys. Chem., 1985, 89, 711 CrossRef.
- S. J. Chen, D. F. Evans, B. J. Ninham, D. J. Mitchell, F. D. Blum and S. Pickup, J. Phys. Chem., 1986, 90, 842 CrossRef.
- K. Fontell, A. Ceglie, B. Lindman and B. J. Ninham, Acta Chem. Scand., 1986, 40, 247 CrossRef.
- D. F. Evans, D. J. Mitchell and B. W. Ninham, J. Phys. Chem., 1986, 90, 2817 CrossRef.
- M. Monduzzi, F. Caboi, F. Larche and U. Olsson, Langmuir, 1997, 13, 2184 CrossRef.
- B. W. Ninham, S. J. Chen and D. F. Evans, J. Phys. Chem., 1984, 88, 5855 CrossRef.
- I. S. Barnes, S. T. Hyde, B. W. Ninham, P. J. Derian, M. Drifford and T. N. Zemb, J. Phys. Chem., 1988, 92, 2286 CrossRef.
- M. Olla and M. Monduzzi, Langmuir, 2000, 16, 6141 CrossRef.
- M. Olla, M. Monduzzi and L. Ambrosone, Colloids Surf., A, 1999, 160, 23 CrossRef.
- (a) R. E. Verrall, S. Milioto and R. Zana, J. Phys. Chem., 1988, 92, 3939 CrossRef; (b) A. Jada, J. Lang and R. Zana, J. Phys. Chem., 1990, 94, 381 CrossRef; (c) A. Jada, J. Lang, R. Zana, R. Makhloufi, E. Hirsch and S. J. Candau, J. Phys. Chem., 1990, 94, 387 CrossRef.
- G. G. Warr, R. Sen, D. F. Evans and J. E. Trend, J. Phys. Chem., 1988, 92, 774 CrossRef.
- M. Kahlweit, R. Strey, P. Firman and D. Haase, Langmuir, 1985, 1, 281 CrossRef.
- S. Friberg, I. Lapczynska and G. Gillberg, J. Colloid Interface Sci., 1976, 56, 19 CrossRef.
- K. Shinoda and H. Arai, J. Phys. Chem., 1964, 68, 3485 CrossRef.
- K. Shinoda and H. Arai, J. Colloid Interface Sci., 1967, 25, 429 CrossRef.
- K. Shinoda, J. Colloid Interface Sci., 1967, 24, 4 CrossRef.
- V. N. Paunov, S. I. Sandler and E. W. Kaler, Langmuir, 2000, 16, 8917 CrossRef.
- T. Sottmann and R. Strey, J. Chem. Phys., 1997, 106, 8606 CrossRef.
- M. Gradzielski, D. Langevin and B. Farago, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1996, 53, 3900 CrossRef CAS.
- J. J. Taber, Pure Appl. Chem., 1980, 52, 1323 CAS.
- R. Aveyard, B. P. Binks, S. Clark and J. Mead, J. Chem. Soc., Faraday Trans., 1986, 82, 125 RSC.
- K. S. Chan and D. O. Shah, J. Dispersion Sci. Technol., 1980, 1, 55 CrossRef.
- B. P. Binks, H. Kellay and J. Meunier, Europhys. Lett., 1991, 16, 53 CrossRef.
- H. Kellay, B. P. Binks, Y. Hendrikx, L. T. Lee and J. Meunier, Adv. Colloid Interface Sci., 1994, 49, 85 CrossRef.
- H. Kellay, J. Meunier and B. P. Binks, Phys. Rev. Lett., 1993, 70, 1485 CrossRef.
- R. Aveyard, B. P. Binks, T. Lawless and J. Mead, J. Chem. Soc., Faraday Trans., 1985, 81, 2155 RSC.
- J. Eastoe and D. Sharpe, Langmuir, 1997, 13, 3289 CrossRef.
- A. Kitahara, T. Kobayashi and T. Tachibana, J. Phys. Chem., 1962, 66, 363 CrossRef.
- C. J. O’Connor, T. D. Lomax and R. E. Ramage, Adv. Colloid Interface Sci., 1984, 20, 21 CrossRef.
- H. F. Eicke, Top. Curr. Chem., 1980, 87, 85 CrossRef PubMed.
- J. B. Peri, J. Colloid Interface Sci., 1969, 29, 6 CrossRef.
- M. Kotlarchyk, J. S. Huang and S. H. Chen, J. Phys. Chem., 1985, 89, 4382 CrossRef CAS.
- K. Kon-no and A. Kitahara, J. Colloid Interface Sci., 1971, 35, 636 CrossRef CAS.
- W. F. Pacynko, J. Yarwood and G. J. Tiddy, J. Chem. Soc., Faraday Trans., 1989, 85, 1397 RSC.
- R. Zana, Colloids Surf., A, 1997, 123–124, 27 CrossRef CAS.
- J. C. Ravey, M. Buzier and C. Picot, J. Colloid Interface Sci., 1984, 97, 9 CrossRef CAS.
- E. Ruckenstein and R. Nagarajan, J. Phys. Chem., 1980, 84, 1349 CrossRef CAS.
- M. J. Hollamby, R. Tabor, K. J. Mutch, K. Trickett, J. Eastoe, R. K. Heenan and I. Grillo, Langmuir, 2008, 24, 12235 CrossRef CAS.
- G. N. Smith, P. Brown, C. James, S. E. Rogers and J. Eastoe, Colloids Surf., A, 2016, 494, 194 CrossRef CAS.
- J. S. Huang, S. A. Safran, M. W. Kim, G. S. Grest, M. Kotlarchyk and N. Quirke, Phys. Rev. Lett., 1984, 53, 592 CrossRef CAS.
- T. Spehr, B. Frick, I. Grillo, P. Falus, M. Muller and B. Stuhn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 031404 CrossRef.
- R. Nagarajan, Langmuir, 2002, 18, 31 CrossRef CAS.
- L. S. Ornstein and F. Zernike, Proct. Sect. Sci. K. Med. Akad. Wet., 1914, 17, 793 Search PubMed.
- S. G. Frank and G. Zografi, J. Pharm. Sci., 1969, 58, 993 CrossRef CAS PubMed.
- S. Nave, J. Eastoe and J. Penfold, Langmuir, 2000, 16, 8733 CrossRef CAS.
- M. Gradzielski, D. Langevin, T. Sottmann and R. Strey, J. Chem. Phys., 1997, 106, 8232 CrossRef CAS.
- F. Sicoli, D. Langevin and L. T. Lee, J. Chem. Phys., 1993, 99, 4759 CrossRef CAS.
- T. Sottmann, R. Strey and S. H. Chen, J. Chem. Phys., 1997, 106, 6483 CrossRef CAS.
- M. Almgren, R. Johannsson and J. C. Eriksson, J. Phys. Chem., 1993, 97, 8590 CrossRef CAS.
- J. P. Cason, M. E. Miller, J. B. Thompson and C. B. Roberts, J. Phys. Chem. B, 2001, 105, 2297 CrossRef CAS.
- F. M. Menger and G. Saito, J. Am. Chem. Soc., 1978, 100, 4376 CrossRef CAS.
- A. Maitra, J. Phys. Chem., 1984, 88, 5122 CrossRef CAS.
- E. Keh and B. Valeur, J. Colloid Interface Sci., 1981, 79, 465 CrossRef CAS.
- R. Aveyard, B. P. Binks, P. Cooper and P. D. Fletcher, Adv. Colloid Interface Sci., 1990, 33, 59 CrossRef CAS.
- B. Lemaire, P. Bothorel and D. Roux, J. Phys. Chem., 1983, 87, 1023 CrossRef CAS.
- L. Arleth and J. S. Pedersen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 061406 CrossRef CAS PubMed.
- B. H. Robinson, C. Toprakcioglu, J. C. Dore and P. Chieux, J. Chem. Soc., Faraday Trans., 1984, 80, 13 RSC.
- M. Hirai, R. K. Hirai, M. Sanada, H. Iwase and S. Mitsuya, J. Phys. Chem. B, 1999, 103, 9658 CrossRef.
- J. Eastoe, W. K. Young, B. H. Robinson and D. C. Steytler, J. Chem. Soc., Faraday Trans., 1990, 86, 2883 RSC.
- C. L. Kitchens, D. P. Bossev and C. B. Roberts, J. Phys. Chem. B, 2006, 110, 20392 CrossRef PubMed.
- H. Kellay and J. Meunier, J. Phys.: Condens. Matter, 1996, 8, 49 CrossRef.
- M. J. Hou, M. Kim and D. O. Shah, J. Colloid Interface Sci., 1988, 123, 398 CrossRef.
- J. Lang, A. Jada and A. Malliaris, J. Phys. Chem., 1988, 92, 1946 CrossRef.
- S. Balakrishnan, N. Javid, H. Weingartner and R. Winter, ChemPhysChem, 2008, 9, 2794 CrossRef PubMed.
- R. V. Sharma and K. C. Sharma, Phys. A, 1977, 89, 213 CrossRef.
- E. W. Kaler, J. F. Billman, J. L. Fulton and R. D. Smith, J. Phys. Chem., 1991, 95, 458 CrossRef.
- J. M. Tingey, J. L. Fulton and R. D. Smith, J. Phys. Chem., 1990, 94, 1997 CrossRef CAS.
- J. S. Huang, J. Chem. Phys., 1985, 82, 480 CrossRef CAS.
- A. M. Cazabat, D. Langevin, J. Meunier and A. Pouchelon, J. Phys. Lett., 1982, 43, L89 CrossRef.
- M. Kotlarchyk, S. H. Chen and J. S. Huang, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 28, 508 CrossRef.
- C. Toprakcioglu, J. C. Dore, B. H. Robinson, A. Howe and P. Chieux, J. Chem. Soc., Faraday Trans., 1984, 80, 413 RSC.
- S. H. Chen, J. Rouch, F. Sciotino and P. Tartaglia, J. Phys.: Condens. Matter, 1994, 6, 10855 CrossRef.
- I. Chakraborty and S. P. Moulik, J. Colloid Interface Sci., 2005, 289, 530 CrossRef PubMed.
- M. Gradzielski, D. Langevin, T. Sottmann and R. Strey, J. Chem. Phys., 1996, 104, 3782 CrossRef.
- M. Appel, T. Spehr, R. Wipf and B. Stuhn, J. Colloid Interface Sci., 2012, 376, 140 CrossRef PubMed.
- L. Garcia-Rio, A. Godoy and P. Rodriguez-Dafonte, Eur. J. Org. Chem., 2006, 3364 CrossRef.
- R. A. Day, B. H. Robinson, J. H. Clarke and J. V. Doherty, J. Chem. Soc., Faraday Trans., 1979, 75, 132 RSC.
- J. H. Clarke, J. D. Nicholson and K. N. Regan, J. Chem. Soc., Faraday Trans., 1985, 81, 1173 RSC.
- A. Salabat, J. Eastoe, K. J. Mutch and R. F. Tabor, J. Colloid Interface Sci., 2008, 318, 244 CrossRef PubMed.
- O. Myakonkaya, J. Eastoe, K. J. Mutch, S. Rogers, R. Heenan and I. Grillo, Langmuir, 2009, 25, 2743 CrossRef PubMed.
- R. W. Gale, J. L. Fulton and R. D. Smith, J. Am. Chem. Soc., 1987, 109, 920 CrossRef.
- J. L. Fulton and R. D. Smith, J. Phys. Chem., 1988, 92, 2903 CrossRef.
- J. Eastoe, D. C. Steytler, B. H. Robinson and R. K. Heenan, J. Chem. Soc., Faraday Trans., 1994, 90, 3121 RSC.
- A. A. Padua, J. M. Fareleira, J. C. Calado and W. A. Wakeham, J. Chem. Eng. Data, 1996, 41, 1488 CrossRef.
- W. J. Tay and J. M. Trusler, J. Chem. Thermodyn., 2018, 124, 107 CrossRef.
- E. J. Beckman and R. D. Smith, J. Phys. Chem., 1990, 94, 3729 CrossRef.
- J. Oshitani, S. Takashina, M. Yoshida and K. Gotoh, Langmuir, 2010, 26, 2274 CrossRef PubMed.
- E. Y. Shew, P. L. Nostro, G. Capuzzi and P. Baglioni, Langmuir, 1999, 15, 6671 CrossRef.
- C. M. Dunn, B. H. Robinson and F. J. Leng, Spectrochim. Acta, Part A, 1990, 46, 1017 CrossRef.
- J. Eastoe, G. Fragneto, D. C. Steytler, B. H. Robinson and R. K. Heenan, Physica B, 1992, 180, 555 CrossRef.
- J. Eastoe, D. C. Steytler, B. H. Robinson, R. K. Heenan, A. N. North and J. C. Dore, J. Chem. Soc., Faraday Trans., 1994, 90, 2497 RSC.
- J. Eastoe, T. F. Towey, B. H. Robinson, J. Williams and R. K. Heenan, J. Phys. Chem., 1993, 97, 1459 CrossRef CAS.
- J. Tanori, T. G. Krzywicki and M. P. Pileni, Langmuir, 1997, 13, 632 CrossRef CAS.
- P. Brown, C. Butts, R. Dyer, J. Eastoe, I. Grillo, F. Guittard, S. Rogers and R. K. Heenan, Langmuir, 2011, 27, 4563 CrossRef CAS.
- (a) J. Eastoe, B. H. Robinson and R. K. Heenan, Langmuir, 1993, 9, 2820 CrossRef CAS; (b) R. E. Riter, E. P. Undiks and N. P. Levinger, J. Am. Chem. Soc., 1998, 120, 6062 CrossRef CAS; (c) J. Texter, L. Ge, T. H. Mourey and T. G. Bryan, Langmuir, 2004, 20, 11288 CrossRef CAS; (d) F. M. Pavel and R. A. Mackay, Langmuir, 2000, 16, 8568 CrossRef CAS.
- A. Czajka, C. Hill, J. Peach, J. C. Pegg, I. Grillo, F. Guittard, S. E. Rogers, M. Sagisaka and J. Eastoe, Phys. Chem. Chem. Phys., 2017, 19, 23869 RSC.
- S. Prevost, M. Gradzielski and T. Zemb, Adv. Colloid Interface Sci., 2017, 247, 374 CrossRef CAS.
- D. G. Peck, R. S. Schechter and K. P. Johnston, J. Phys. Chem., 1991, 95, 9541 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1941, 9, 660 CrossRef CAS.
- H. Reiss, W. K. Kegel and J. Groenwold, Ber. Bunsen-Ges., 1996, 100, 279 CrossRef CAS.
- E. Negro, R. Latsuzbaia, A. H. de Vries and G. M. Koper, Soft Matter, 2014, 10, 8685 RSC.
- C. A. Bearchell and D. M. Heyes, Phys. Chem. Chem. Phys., 2001, 3, 5255 RSC.
- Y. Fu, S. Xiao, S. Liu, Y. Chang, R. Ma, Z. Zhang and J. He, Langmuir, 2022, 38, 3129 CrossRef CAS.
- B. Lukanov and A. Firoozabadi, Langmuir, 2016, 32, 3100 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |