Open Access Article
Open Access ArticleFormation and fluctuation of two-dimensional dodecagonal quasicrystals†
Uyen Tu
Lieu
 *a and
Natsuhiko
Yoshinaga
*a and
Natsuhiko
Yoshinaga
 *ab
*ab
aMathematics for Advanced Materials-OIL, AIST, 2-1-1 Katahira, Aoba, 980-8577 Sendai, Japan. E-mail: uyen.lieu@aist.go.jp
bWPI-Advanced Institute for Materials Research (WPI-AIMR), Tohoku University, 2-1-1 Katahira, Aoba, 980-8577 Sendai, Japan. E-mail: yoshinaga@tohoku.ac.jp
First published on 26th September 2022
Abstract
The self-assembly of two-dimensional dodecagonal quasicrystals (DDQCs) from patchy particles is investigated by Brownian dynamics simulations. The patchy particle has a five-fold rotational symmetry pattern described by the spherical harmonics Y55. From the formation of the DDQC obtained by an annealing process, we find the following mechanism. The early stage of the dynamics is dominated by hexagonal structures. Then, nucleation of dodecagonal motifs appears by particle rearrangement, and finally the motifs span the whole system. The transition from the hexagonal structure into the dodecagonal motif is coincident with the collective motion of the particles. The DDQC consists of clusters of dodecagonal motifs, which can be classified into several packing structures. By the analyses of the DDQC under fixed temperature, we find that the fluctuations are characterised by changes in the network of the dodecagonal motifs. Finally we compare the DDQCs assembled from the patchy particle system and isotropic particle system. The two systems share a similar mechanism of the formation and fluctuation of DDQCs.
1 Introduction
Quasicrystals (QCs) are ordered structures lacking periodic translational symmetry.1,2 Different from crystals which possess 2-, 3-, 4-, and 6-fold rotational symmetry, QCs may have 5-, 8-, 10-, 12-, and 18-fold rotational symmetry. QCs can be applied in various applications, such as advanced coatings, reinforced composites, optics, photovoltaics, magnetism,3 superconductivity,4 and bandgap materials in photonic devices.5 The appearance of QCs and approximants has been observed in different length scales, from intermetallics1,6 to meso-scale.7–11 Recently, quasicrystalline structures have been found in soft materials, such as block copolymers,12,13 surfactants,14 colloids,15 and dendrimers.16The quasiperiodic self-assembly has been obtained mainly by three types of mechanisms: isotropic interactions between particles, anisotropic interactions between particles, or polydispersity. In the first case, the isotropic interaction potential depends only on the distance between particles, but has at least two length scales.17–22 For example, the Lennard-Jones–Gauss potentials can produce decagonal QCs or dodecagonal QCs (DDQCs),17 or the hard-core/square-shoulder potentials22 create a family of QC structures with 10-, 12-, 18- and 24-fold bond orientational order. Continuum description has also been proposed in ref. 23–25. The three-well oscillating pair potential is able to form a three-dimensional icosahedral QC in non-atomic systems.18
In the second case of anisotropic interactions between particles, the interactions depend on their mutual orientation while the distance-dependence has only one length scale. For example, the five-patch particles, whose five sticky patches are equally distributed around the equator of the sphere, can arrange into a two-dimensional DDQC;26–29 hard tetrahedra create a three-dimensional DDQC.30
In the third type of systems, DDQCs and approximant structures are realised in polydisperse systems,8,31,32 such as binary nanoparticles with two different sizes,8 and bidisperse pentavalent and hexavalent patchy particles.31 Recently icosahedral QCs have been built from a mixture of patchy particles.33
Despite intensive studies on the structural characterisation of QCs, the kinetics and dynamics of QC growth, are still incomplete.34–37 It is not clear how the QCs appear from a liquid or crystalline state, what is happening at the periphery of QCs during their growth, and how local structures change under thermal fluctuation after QC formation. It is also of interest whether the dynamics and kinetics of QCs are dependent or not on the three aforementioned mechanisms. Most of the previous studies focused on the analysis of the structures. In ref. 26 and 27, stable DDQCs were generated via Monte-Carlo simulations of the five-patch particles. In ref. 28, the growth of DDQCs was studied by particle deposition on a prepared quasicrystalline substrate. The growth of a three-dimensional DDQC was studied in ref. 34, and it was suggested that characteristic structures (icosahedra in that system) preferentially appear around the nucleus of DDQCs. The growth of a two-dimensional DDQC was also studied in ref. 38. Nevertheless, what kind of local structures preferentially appear near the nucleus of QCs in other systems remains unknown. Also, it is of relevance to clarify how those structures are transformed as a part of DDQCs by particle displacements.
To clarify those issues, it is necessary to analyse the dynamics of local structures. We carry out the analyses in different scales: local structures based on neighbours, (dodecagonal) motifs consisting of several particles, and packing of the motifs. These structural changes have not been studied in the previous studies.
In this study, we investigate the kinetics and dynamics of DDQCs by computer simulations. The majority of reported QCs in soft materials are DDQCs. Therefore, we focus on the formation of DDQCs. We have developed a model for the interaction of a pair of anisotropic particles whose surface pattern is described by spherical harmonics Ylm.39,40 Using the five-fold symmetry patchy particles, we are able to assemble the DDQC. We investigate the formation of the DDQC from a bulk phase, and the local structural changes (fluctuation) after the DDQC is formed. The same procedure is applied to the DDQC assembled from the isotropic particle system. We compare the kinetics and dynamics of the DDQCs from the patchy particle system and the isotropic particle system.
2 Methods
2.1 Numerical simulation
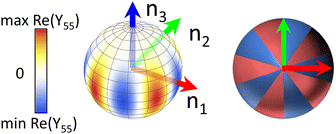
We consider the patchy particle with five-fold symmetry, composed of ten alternating patches of two different types (Fig. 1). The pattern on a spherical particle is described by spherical harmonics Y55.39,40The pairwise interaction of the particles includes a Weeks–Chandler–Andersen (WCA) term preventing the overlap and a Morse-like, orientation-dependent term. The details of the anisotropic potential are given in Appendix A. Fig. 2 illustrates the potential used in the study at different particle configurations.
 | ||
| Fig. 2 Pairwise potential of patchy particles at different configurations. The red arrows indicate the orientations of the patchy particles. | ||
The assembly of patchy particles is performed by Brownian dynamics simulations.41 The positions r and orientations Ω of the particles after the time step Δt are updated according to the equations
 | (1) |
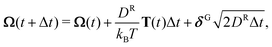 | (2) |
The spherical particles are confined to a two-dimensional plane while rotating freely in three dimensions. The initial condition of the simulation is a random distribution of positions in a periodic box of size Lx × Ly with random orientations. The number of particles is N = 1024. The density is defined as area fraction ρa = πN/(LxLy).
The numerical simulations are conducted in two temperature settings: annealing and fixed temperature. In the annealing, the temperature starts from disordered states at high temperature and gradually decreases to lower temperatures at which crystalline states are stable. For the system at a fixed temperature, the system under the random initial condition is suddenly quenched at the temperature T, and the structures are relaxed at the fixed T. We choose the schedule of annealing as the temperature decreases from Tmax = 1.2 to Tmin = 0.4 with intervals of ΔT = 0.0125. At each temperature the number of steps is 0.1 × 106, and the total steps are 6.5 × 106. The time step is set at Δt = 0.5 × 10−3T, and thus the total time of the annealing simulation is t = 2600. We have checked that the annealing schedule is slow enough to make stable QCs.
For the system at a fixed temperature, we conduct simulations at temperature T ∈ [0.5,1.1]; the number of simulation steps is 5 × 106 and the simulation time at each temperature is t = 2500T.
Note that we use the term annealing in the sense of simulated annealing, consisting of melting and successive cooling.42 In our system, the initial condition is a disordered state and the initial temperature Tmax = 1.2 is high enough to get large thermal fluctuation. Therefore, we do not need a process to increase the temperature during annealing.
To analyse the fluctuation of the DDQC, simulations are performed with the parameters area fraction ρa = 0.75, fixed temperature T = 0.8 and 50 × 106 steps, which are approximately 10 times longer and slightly less dense than the annealing simulations. For five independent simulations, the DDQC is formed from a rich hexagonal phase after the first 5 × 106 steps. The fluctuation of the DDQC is reported after it is formed. We also investigate the DDQC assembled from the isotropic interacting particles. The details of the potential and simulation condition are given in Appendix B.
2.2 Structural analysis
The types of local structures of each particle are determined by the connection of the nearest neighbours of a particle. The local environments in a DDQC are σ, H, and Z26 as given in Fig. 3. These local structures are based on the number of common neighbours of the neighbouring particles analogous to the Frank–Kasper phases. For example, a σ particle has five neighbours. One of them has two common neighbours, and four of them have only one common neighbour. Therefore the local structure of a σ particle is identified as {21111}. The other local structures are H {22110}, Z {222222}, D1 {22211}, and D2 {222211}. In this study, the new local structures D1 and D2 result from fluctuating Z particles, where they form a diamond shape as shown in Fig. 3. A particle which does not fall into these categories is considered as undefined U. The number of unidentified particles is only ≲5% of the total number of particles in the system.The local structure of the particle varies with time. The interchange of a given local structure to/from other local structures is determined between two consecutive snapshots different by 104 time steps, for each local structure. The purpose of this calculation is to identify the relevant “reaction” of the local structures during the growth of DDQCs. For example, we can calculate the interchange rate between Z and σ, which includes the amount of Z becoming σ and the amount of σ becoming Z during the two snapshots. If the amount of Z → σ is greater than that of σ → Z, then the transformation of Z to σ is dominant. By the analyses of the reactions between two local structures, we may also quantify how the interchange of Z ↔ σ (both Z → σ and σ → Z) occurs more frequently than other pairs of local structures, such as D1 ↔ D2.
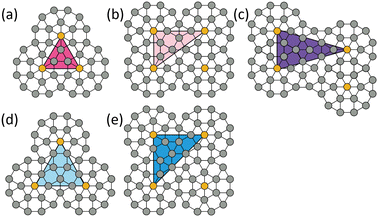
The DDQC has a characteristic dodecagonal motif7,27 (see Fig. 5(e)). The motif is made of one Z particle at the centre, six σ particles on the first ring, and twelve σ particles on the second ring. Fig. 4 shows several ways of packing the motifs. These dodecagonal motifs are identified by the network of Z particles in each snapshot of simulations. The Z particles are the centres of each dodecagonal ring. We describe the motif packing by the triangular tiles in the network of Z particles obtained from Delaunay triangulation. Different clusters of motifs are shown in different colours. Each cluster is characterised by the distance between the centres of the dodecagonal motifs. For example, the dodecagonal motifs can interpenetrate in Fig. 4(a), share a common edge in Fig. 4(d) and (e), or connect via extra σ particles in Fig. 4(c). The criteria of the clusters are based on the edge lengths of the triangular tiles; e.g. the edge lengths of the perfect cluster in Fig. 4(a) are  ; a simulated cluster is of this type if the edge lengths lsim satisfy |lsim − l| < 0.1l. We will discuss how the structure of the clusters of motifs changes over time. The time-dependent network structure during [t, t + δt] is visualised by overlapping the images at [t,…,t + δt] (see Fig. 11 and 12).
; a simulated cluster is of this type if the edge lengths lsim satisfy |lsim − l| < 0.1l. We will discuss how the structure of the clusters of motifs changes over time. The time-dependent network structure during [t, t + δt] is visualised by overlapping the images at [t,…,t + δt] (see Fig. 11 and 12).
 | ||
| Fig. 5 Change in local structures during annealing simulations at ρa = 0.78. (a) Ratio of the local structure in time; the line represents the data of a simulation, and the shaded area corresponds to 95% confidence intervals of 10 independent simulations. The growth of the DDQC is divided into three stages. (b–d) The snapshots and their Fourier transformation; the colour of the particle indicates the local structure as shown in the legend and Fig. 3. (e) Illustration of two kinds of dodecagonal motifs in the boxes in (d); they are interchangeable by rotating the particles on the first ring ±30°. (f) The packing of the dodecagonal motifs of the structure in (d). (g) Orientations of the tiling edges connected by the particle positions of the structure in (d); the colours of the edges correspond to the six unit vectors shown above. | ||
3 Results of the patchy particle system
3.1 The formation of the DDQC
The dynamical self-assembly using the five-fold symmetric patchy particles under annealing is investigated. Fig. 5 shows the change in the ratios of local structures during the formation of the DDQC and the representative snapshots with the colour coded according to local structures σ, Z, D1, and D2 (Fig. 3). Dynamical formation of a DDQC can be decomposed into three stages. At stage I, the majority of particles are Z type, with a ratio of around 0.7. The ratios of both D1 and D2 are around 0.1. The snapshot of this stage is a Z-rich structure with clear hexagonal spots in its Fourier transform. The D1 and D2 particles often appear in pairs as a diamond shape surrounded by Z particles. Stage II corresponds to the growth of the QC where the ratios of Z, D1, and D2 decrease, while that of σ increases. A σ-rich region is formed in the bulk of Z particles. The σ-rich region contains a few Z particles inside. The D1 and D2 particles accumulate at the boundary between this region and the ‘bulk’ Z particles. Finally at stage III, when the expansion of σ reaches the system size, all the ratios maintain constant values with fluctuations. The σ-rich region spans the whole system and a DDQC is assembled, as we can observe the twelve-fold rotational symmetry in the Fourier space.7,26There are several dodecagonal motifs in the QC structure. The motif contains one Z particle at the centre and six σ particles on the first ring and twelve σ particles on the second ring (see Fig. 5(e)). There are two types of motifs which are different by 30° degrees of the first ring. The QC structures consist of the two types of dodecagonal motifs (Fig. 5(e)) packed in different ways as shown in Fig. 4. The four structures in which the Z particles of the motif centres form either an equilateral triangle (Fig. 4(a) and (d)) or a right angle triangle (Fig. 4(b) and (e)) were obtained in ref. 26 using patchy particles with five-fold or seven-fold symmetry. In our simulations, aside from these packings, we also obtain the structure in which the Z particles form an isosceles triangle (Fig. 4(c)). Approximants can be obtained by repeating each packing structure in Fig. 4. Higher-order approximants may also be obtained by combining two or more packing types in Fig. 4, and repeating the unit structure.31,43 DDQCs do not have any periodicity and should appear as a limit of an infinitely large unit cell. The spatial distribution of these packing structures of the dodecagonal motifs at stage III is illustrated in Fig. 5(f). There are several packing types and no periodicity in these packing types is observed.
Here, we discuss the quasicrystallinity of the obtained structures. In Fig. 5(g), a square triangle tiling whose vertices are the particles of the snapshot in Stage III is shown. The edges of the tiles are along the 12 directions at intervals of 30°. The probability of the direction of the edge along the 6 directions shown in the figure is almost identical in the range of (0.16, 0.17). This uniformity of the edge direction suggests that the structures are close to the perfect 12-fold symmetry. Next, we measure the ratio of the number of triangles to squares, and it is 983/424 ≈ 2.31 for the structure in Fig. 5(g) (it is 2.42 ± 0.065 for 10 independent snapshots). This value is comparable to the ratio  of the ideal DDQC made by inflation.44 This ratio appears also for the random tiling of triangles and squares at maximum entropy. Finally, following the method of ref. 45 and 46, we calculate the linear phason strain tensor. To do this, we focus on the region of the well-defined square-triangle tiles in Fig. 5(g), and lift the vertices of the square-triangle tiling to 4d space. The perpendicular space x⊥ is expressed by the physical space x‖ as x⊥ = A·x‖ + b, where b is the residual. From the invariants in the matrix A under rotation, we may estimate the phason strain. The obtained three invariants for the matrix of the linear phason strain (|α| ∼ 0.02, |β| ∼ 0.02, and
of the ideal DDQC made by inflation.44 This ratio appears also for the random tiling of triangles and squares at maximum entropy. Finally, following the method of ref. 45 and 46, we calculate the linear phason strain tensor. To do this, we focus on the region of the well-defined square-triangle tiles in Fig. 5(g), and lift the vertices of the square-triangle tiling to 4d space. The perpendicular space x⊥ is expressed by the physical space x‖ as x⊥ = A·x‖ + b, where b is the residual. From the invariants in the matrix A under rotation, we may estimate the phason strain. The obtained three invariants for the matrix of the linear phason strain (|α| ∼ 0.02, |β| ∼ 0.02, and 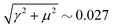 ) are close to the values of the ideal dodecagonal quasiperiodic tiling (
) are close to the values of the ideal dodecagonal quasiperiodic tiling ( ).45 The values of the phason strain are also far from known periodic approximants.45 With these analyses, it is fair to call the obtained structures DDQCs, although they contain defects and are neither an ideal DDQC nor random square-triangle tiling. We should also note that the simulations are performed under the periodic boundary condition, and therefore, the size of the unit cell is bounded by the system size. In this study, by DDQCs we mean the structures discussed in this paragraph.
).45 The values of the phason strain are also far from known periodic approximants.45 With these analyses, it is fair to call the obtained structures DDQCs, although they contain defects and are neither an ideal DDQC nor random square-triangle tiling. We should also note that the simulations are performed under the periodic boundary condition, and therefore, the size of the unit cell is bounded by the system size. In this study, by DDQCs we mean the structures discussed in this paragraph.
The ratio in Fig. 5(a), however, cannot show the “reaction” of each local structure changing to/from other local structures. Fig. 6 shows the interchange among Z, D1, D2, and σ. During stage I, a majority of Z particles change to and from D1 and D2 as the “reactions” are comparable in both forward and backward directions. In stage II, the particles Z, D1, and D2 change to σ faster than the backward direction. This suggests that the relevant ingredients for the formation of the σ particle, or the dodecagonal motif, are the Z, D1, and D2 particles.
We propose that there is a relation between Z, D1, D2, and σ. Specifically, the particles D1 and D2 play an intermediate role in the formation and expansion of the DDQC from a Z-rich structure. Fig. 7(a) shows the decomposition of the D1 and D2 particles in terms of the bulk Dbulk and the boundary Dboundary amounts. Dboundary represents D particles (D1 and D2) neighbouring the σ particles, while the rest are defined as Dbulk. The bulk D fluctuates around a constant value, and then decreases to zero as the QC occupies all the space. Fig. 7(b) shows the relation between the bulk D particles and Z particles. For the bulk particles, the amount of D1 and D2 is almost the same as they often appear as pairs (see snapshots in Fig. 5 and 7), and linearly increases with Z. We fit the data in Fig. 7(b) by linear regression, and find the slope of 6.6−1. In Fig. 3 we illustrate a diamond shape made of four Dbulk in twelve Z. In this case, the ratio of D1 and D2 to Z is equal to 6−1. This argument supports a picture in which D1 and D2 particles appear as fluctuations of Z particles and appear in pairs.
Regarding the D particles at the boundary, as given in Fig. 7(a), these particles occupy a small amount before the growth of the σ-rich domain, then increase during the growth, and eventually decrease to a plateau. Before the QC is formed, the number of stable D particles is small and they appear stochastically associated with σ particles; then when the QC is expanded, the number of boundary D particles increases. The decrease of the boundary D is because of the limit of the finite system size. Moreover, the number of D1 particles is higher than the number of D2 particles, suggesting that there is extra D1 which may contribute to the transformation from D1 to σ or Z.
The larger number of D1 than D2 may be due to the anisotropy of the boundary; one side is dominated by σ particles whereas the other side is dominated by Z particles. Fig. 7(c) shows that Dboundary grows linearly with σ0.5. This is because the growing QC has the area ∝ Nσ and the circumference  .
.
We seek a simple mechanism of DDQC growth. In the simulation, the particles fluctuate locally and change their local structures continuously. However, we observe a typical local rotation of the particle during the growth of DDQCs. Fig. 8 suggests a mechanism from a Z-rich structure (stage I) to a DDQC (stage III). In the schematic of Fig. 8(a), from a hexagonal lattice, the first ring of the hexagonal lattice rotates by 15° either clockwise or anticlockwise. Simultaneously some particles of the second ring displace and eventually a dodecagonal motif is formed. The D1 and D2 particles also appear during this local rotation, and become σ or Z as the dodecagonal motif grows. We can calculate the rotation of the first neighbours of a centre particle (see Appendix C) from the displacements of the particles between two snapshots in Fig. 8(b). Fig. 8(c) shows that around the centres of the DDQC motif (roughly the Z particles in the DDQC), there are rotations for the particles on the first ring. The histogram in Fig. 8(d) approximately has two peaks at ±15°.
To summarise, the mechanism of the self-assembled DDQC from patchy particles can be proposed as follows: (i) initially the structure is rich in Z particles and thermal fluctuation induces the pairs of D1 and D2 in the bulk of Z, (ii) at the right temperature, the σ particles are formed and they cluster together to form dodecagonal motifs. (iii) The DDQC rapidly expands at the boundary where the transformation Z → (D1, D2) → σ occurs. Around the centre of the dodecagonal motifs, local rotations of the nearest neighbours take place.
3.2 Temperature dependence of DDQC formation
In this section, the effect of temperature on the DDQC is investigated. Fig. 9 shows the dependence of the local structure ratio on temperature for annealing simulations and fixed temperature simulations. In both cases, there are two phases: Z-rich and σ-rich, separated by a critical temperature T* ≈ 0.8. The Z-rich phase corresponds to T > T*, where the structure is dominated by Z particles and some D1 and D2 particles due to the strong thermal fluctuation. In this case, the global structure is hexagonal. The σ-rich region appears at T < T*, where the structure is dominated by σ particles. There is a slight difference in T* of the annealing case and the fixed temperature case. This is expected because the onset of the QC, i.e. the growth from the first dodecagonal motif, depends on both temperature and time, and these two parameters cannot be directly compared in the two simulation procedures. For example, at T ≈ T*, the onset of the annealing QC is in a uniform manner, whereas it is more scattered for the fixed temperature QC. As a result, among ten independent simulations at fixed temperature T = 0.825, three of them are DDQCs and the remaining seven are Z-rich. Regarding the quality of the QC of fixed temperature simulation, the ratio of σ particles decreases as T decreases. The fixed temperature simulation is equivalent to very fast quenching before fixing the temperature. The small ratio of σ at the low temperature is due to particles that are kinetically trapped; hence the structure is more disordered and contains more defects. Such a behaviour is not observed in the slow annealing case, as the ratio of σ is independent of temperature. The results reveal that the patchy particle DDQC can be obtained by annealing more easily than fixed temperature when T ≤ T*. The self-assembly of high quality DDQCs corresponds to the annealing scheme or fixed temperature at T = T*.3.3 Local fluctuation after the DDQC is formed
After the DDQC is formed, we have observed local structural changes when it is subjected to thermal fluctuation. The QC structures consist of two types of dodecagonal motifs packed in different ways as shown in Fig. 4. We focus on a network of the dodecagonal motifs, which is evaluated from the network of the Z particles because the Z particles are the centres of the dodecagonal motifs (see Section 2.2).The structural changes are analysed by comparing snapshots at time t and t + δt. We show the change of the network in both short (δt = 105 in Fig. 10) and long (δt = 106 in Fig. 11) timescales.
 | ||
| Fig. 10 Two types of changes of the dodecagonal motif network at T = 0.8. (a) A snapshot and (b) its corresponding dodecagonal motif network of Z particles at t. The coloured dots in (a) represent particle positions and particle types based on the colours in Fig. 3. Coloured triangles in (b) are different packing of dodecagonal motifs in Fig. 4. The white triangles are packing structures that cannot be classified by the structures in Fig. 4. (c and d) Change of the motif network of the boxed area in (a and b) after δt = 105 steps. At t + δt, the displacements of the particles from t are given by red arrows. Here, we show only the large displacements satisfying |r(t + δt) − r(t)| ≥ 0.5a. For the box with a dashed line in (c), the particles rotate but the local dodecagonal network is unchanged. For the box with a solid line in (d), several particles exhibit chain-like displacement and the local dodecagonal network changes. | ||
In the short timescale, Fig. 10 shows the analysed snapshot, its corresponding Z particle network by Delaunay triangulation, and two types of network rearrangement within a time scale of δt = 105 steps. (i) In Fig. 10(c), although a few particles move, the local motif network does not change. The displacements of these particles show that the whole first ring of the centre Z rotates 30° and eventually this dodecagonal motif is still maintained (see Fig. 5 for the two motifs). (ii) On the other hand, in Fig. 10(d), a few particles move and the local motif network changes. When those particles move, their local structures also change, e.g. σ particles become Z particles, and therefore the network of Z also alters. This process may continue as a chain. We observe that the displacements occur for the particles neighbouring Z (centre of the dodecagonal motif). The rearrangement of the network is coincident with the displacement.
We have analysed the phason strain using the same method as in Section 3.1. The phason strain changes by the change of the local structure in Fig. 10(d); for example, one invariant of the phason strain |β| changes ≈0.02. This change is significant compared with the error in the evaluation of the phason strain ≲0.001 when the network rearrangement does not occur. The results suggest that the change of the network is associated with phason flips.
In Fig. 11, we show the fluctuation of the dodecagonal motif network observed in a longer time scale (δt = 106 steps) by means of the packing of motifs for the whole simulated structure. The small panels in Fig. 11(a) are the structures between [t, δt], while the big panel is the superposition of those small panels (see a video in the ESI†). In some regions, for example, bottom and left in Fig. 11(a), the network structure does not change, whereas in other regions, rearrangement of the network occurs. These snapshots are superposed in the big panel of Fig. 11(a). The deeper colour indicates that the network of Z particles is maintained. The region with lighter colours and overlapping edges indicates a network rearrangement. The network rearrangement has two features: first, there is a collective motion of the particles along the place where rearrangement of the network of the dodecagonal motifs occurs. Second, the network contains different types of packing structures of the dodecagonal motifs, and the displacements of the particles seem to occur between two different packing types. The chain of such collective motion is longer than the one in Fig. 10. The readers may refer to Fig. 12 for clearer visualisation of the maintained network and network rearrangement. We perform the same analysis of rotational displacement as in Section 3.1. The rotation angles of the displaced particles around the Z particles (centre of the dodecagonal motif) are around ±30° as depicted in Fig. 11(b). The structural change of the dodecagonal motif network is associated with the local rotation of the first neighbours of the motif's centre. Such rotations seem to appear at the border of different types of packing of dodecagonal motifs. During the structural changes associated with network rearrangement of dodecagonal motifs, the energy is fluctuating around a constant value as shown in Fig. 11(c).
4 Results of the isotropic particle system
As mentioned in the Introduction, the DDQC can be assembled also from isotropic particles. We perform the same analysis with the isotropic DDQC. The details of the potential and simulation parameters can be found in Appendix B.Fig. 12 presents the formation and fluctuation of the isotropic DDQC. In Fig. 12(a–d), similar to the formation of the annealed patchy particle DDQC, the isotropic DDQC also starts with a Z-rich structure with some D1 and D2 particles generated due to fluctuation of Z. The dodecagonal motif is then organised and expanded, in which the D1 and D2 particles are accumulated at the boundary of the cluster of the dodecagonal motif and the Z-rich bulk. The resulting DDQC consists of dodecagonal motifs packed in different ways (Fig. 4). Regarding the mechanism of the transformation from Z-rich structures to DDQCs, the first neighbours of the dodecagonal motif centres rotate by ±15° (Fig. 12(c) and (d)). The fluctuation of the DDQC is investigated by performing simulations at a fixed temperature of T = 0.7. Fig. 12(e) illustrates the fluctuations of isotropic DDQCs in terms of the network of the dodecagonal motifs. The change in the network is also associated with the collective rotation by ±30° of the first neighbours of the motif centres (Fig. 12(f)). For a detailed comparison with the patchy particle system in Fig. 5, 6 and 9, the corresponding analyses for the isotropic particle system are given in Fig. S1–S3 in the ESI.†
However, there are differences between the DDQCs made of patchy particles and isotropic particles. In general, the isotropic DDQC (Fig. 12(e)) has less defects as the network has more well-defined packing structures than that of the patchy particle DDQC (Fig. 11).
In a dodecagonal motif of the DDQC, the Z particle of the isotropic system has the lowest energy whereas the energy of Z particle of the patchy particle DDQC is the highest (see Fig. 15). For the patchy particle case, the orientation of the Z particle at the centre is incompatible with the six σ neighbours. The energy of this hexagonal particle is expected to be higher than that of the σ particle, and hence σ-dominant structures are expected at low density. The patchy particle system requires fine tuning of density to assemble a DDQC, whereas the DDQC in the isotropic particle system works even under low density conditions (Fig. 16). Additional data can be found in Fig. 15 and 16 in Appendix D.
Although the DDQCs in both systems consist of dodecagonal motifs, the network of the motifs is different. In the DDQC made by the particles with the two-length-scale isotropic interaction shown in Fig. 12(e), the distance between the motifs is smaller, namely, the distance between two Z particles at the centres of two dodecagonal motifs (Fig. 5(e)) is shorter. Therefore, there are many small triangles among the packing structures, such as those of Fig. 4(a) and (b). These packing types appear less in the patchy particle DDQC, which rather consists of the packing structures of Fig. 4(c)–(e) (see Fig. 5(f) and 11(a)). We should note that the packing structures of Fig. 4(a) and (b) have triangles with shorter edges (reddish colour), whereas those of Fig. 4(d) and (e) have triangles with longer edges (bluish colour). The difference of the motif arrangement is possibly due to the potentials used in the two particle systems. As discussed above, the patchy particles prefer σ particles, whereas the isotropic particles prefer Z particles. Because Z particles are located at the centre of the dodecagonal motifs and play the role of vertices in the network of packing structures, smaller triangles tend to appear when more Z particles exist.
5 Discussion and conclusions
We have investigated the formation of DDQCs from the patchy particles with five-fold symmetry. From a Z-rich hexagonal structure, fluctuations of positions of patchy particles generate intermediate structures D1 and D2. After the dodecagonal motif is formed, the motif rapidly expands and the D1 and D2 particles are accumulated as a boundary between the cluster of the dodecagonal motif and the hexagonal structure. The DDQC contains many dodecagonal motifs packed in different ways. The formation of the DDQC is driven by the local fluctuations of the particles. The fluctuation is characterised by rotation of the first ring in the dodecagonal motif. After the DDQC is formed, the dodecagonal motif network changes when thermal fluctuation causes large displacements of the particles. The change of the network is associated with rotation of the nearest neighbours of the centres of the motifs.Regarding the formation of the DDQC, the transformation from a Z-rich structure to a DDQC is observed in both the patchy particle system and isotropic particle system. Superposition of a hexagonal lattice and a dodecagonal motif reveals the difference in the position of the first ring, which is manifested by a circular rotation of 15° around the motif's centre. Such displacements of the particles on the first rings of the dodecagonal motifs are confirmed in our simulations. This may be the reason why the DDQCs of patchy particles and isotropic particles both share the same mechanism although the interactions are completely different.
Compared with the growth of the DDQC from a Z-rich phase in the annealing simulation, the reversal process, i.e. the DDQC to Z-rich phase, shows similar behaviours despite the large hysteresis in the structural transitions. A cluster of Z particles appears and then spans the whole system. Transformation from σ to Z reveals a rotation of around 15° of the first ring of the dodecagonal motif (see the schematic in Fig. 8). Further details can be found in Appendix E.
The DDQC comprises different types of packing of dodecagonal motifs (see Fig. 4). These packing structures can be constructed from the network of centres of dodecagonal motifs. The packing is divided into several characteristic structures (Fig. 4). In the obtained DDQCs, different types of packing structures coexist, and they do not show periodicity. We have observed that the DDQC continues to fluctuate in the sense that the relative positions of some particles change. Two types of displacement are considered. (i) In the case of individual displacement, the particles on the first ring of the dodecagonal motif quickly rotate. Despite the particle displacements, the whole dodecagonal motif remains intact. (ii) Collective displacement of particles can bring about rearrangement of the DDQC network. Such changes appear at the border of different types of packing structures, i.e. some dodecagonal motifs are disintegrated and new motifs are generated. The displacement of the particle mostly occurs at the first ring of the dodecagonal motifs, and at short length scale like (i). However such displacements can propagate to the neighbouring motifs, and the whole DDQC network eventually changes.
There is another type of DDQC made of isotropic particles17 where the high-symmetry dodecagonal motif has five particles on the inner ring (compared to six particles for the DDQC in our study) and twelve particles on the second ring. The kinetics and dynamics of those DDQCs may be different from those in this study. We leave the analyses of such different DDQCs as a future study.
The patchy particle DDQC in our study is in agreement with other works using the five-fold symmetry patchy particle system, such as the particle with five equally distributed patches on the equator.26 The Y55 patchy particle in our study also has five-fold symmetry, but the number of patches and the interaction are different. This particle has ten patches in red and blue, where the interaction of red–red/blue–blue patches is considered attractive and that of red–blue patches repulsive. In the assembled DDQC, the orientation of the patchiness of the σ particle and its neighbours (Fig. 3) is found to be similar to the one in ref. 26. Moreover, the ratios of the Z and σ particles of the DDQC in the Monte-Carlo simulations in ref. 26 are about 0.07 and 0.8, respectively, which are comparable to our system in Fig. 5.
A DDQC can be formed by a bidisperse DNA system in simulation31 or experimentation.32 The two DNA tiles can be considered as 5- and 6-point-star particles. The self-assembly of the patchy particle DDQC at different densities in our study is somewhat analogical to that of bidisperse DNA systems.32 When the ratio of the 5- to 6-point-star particle increases, the resultant structures change. A low ratio leads to σ phase structures. A medium ratio forms DDQCs of which many dodecagonal motifs are observed. At a high ratio, the hexagonal structures dominate the dodecagonal motifs. Such changes are also observed in our study when the density of the patchy particle increases.
We have investigated the formation and fluctuation of DDQCs in the patchy particle system and the isotropic particle system. It may help to predict and design the two-dimensional DDQCs in different soft matter systems. The fluctuation of the DDQC may relate to the properties of the QC, e.g. heat capacity. An analogical study is still required for, for example, octagonal QCs and decagonal QCs to know how the other QCs behave.
Author contributions
U. L. performed the simulations and analysed the data. N. Y. designed the research. All the authors were involved in the evaluation of the data and the preparation of the manuscript.Conflicts of interest
There are no conflicts to declare.Appendix
A Potential of the patchy particle system
The potential for a pair of patchy particles is| V = VWCA(r) + VM(r)Ξ(Ω), | (A1) |
The details of the isotropic Week–Chandler–Anderson potential VWCA preventing the overlapping of particles and the Morse potential VM in eqn (A1) are given as
 | (A2) |
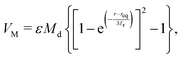 | (A3) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) = r/r, ε is the potential well depth, req is the Morse potential equilibrium position (req = 1.878a), and Md = 2.294a and Mr = a are the Morse potential depth and range, respectively.39,40,47
= r/r, ε is the potential well depth, req is the Morse potential equilibrium position (req = 1.878a), and Md = 2.294a and Mr = a are the Morse potential depth and range, respectively.39,40,47
The anisotropic interaction is calculated based on the mutual orientation of a pair of particles i and j. Let n(i)m and n(j)m with m = 1, 2, 3 be local bases of particles i and j, and ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) is the unit distance vector between particle centres. The anisotropic interaction
is the unit distance vector between particle centres. The anisotropic interaction 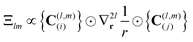 estimates the angular dependence of a pair of particles Ylm as
estimates the angular dependence of a pair of particles Ylm as 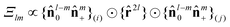 , where
, where ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) 0 = n3 and
0 = n3 and 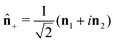 . For example,
. For example,  for a pair of particles Y10, and
for a pair of particles Y10, and  for a pair of particles Y20.
for a pair of particles Y20.
B Isotropic particle system
The isotropic potential is a Lennard-Jones Gauss potential17,19,28,48: | (B1) |
The simulation parameters are almost identical to those of the patchy particle system. The number of particles is N = 1024. In the annealing simulations, the temperature decreases from T = 1.2 to T = 0.4 with an interval of ΔT = 0.0125. There are 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps at each value of temperature, making a total of 65 × 100
000 steps at each value of temperature, making a total of 65 × 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps.
000 steps.
C Determination of neighbouring rotation
The particle configuration is known at every time step. Let r(t1) and r(t2) be the particle position at time t1 and t2, respectively, and d = r(t2) − r(t1) the particle displacement from t1 to t2. Consider that the particle i has Ni nearest neighbours {j1,j2,…,jNi} in a clockwise order. At t1, we define êjk the unit vector from jk to jk+1 of the polygon made of {j1,j2,…,jNi}. The displacement of the neighbour particle is determined from t1 to t2; for example, dj1 is the displacement of the particle j1 (Fig. 14). The rotation of the neighbours of particle i is defined as | (C1) |
Note that the relative displacement to the centre particle is considered as  .
.
D Energy of local structure and density dependence
We compare the energy of each local structure during the growth of the DDQC assembled from the patchy particles and isotropic particles. In each snapshot, for example, the energy of the Z particle is the mean energy of all Z particles. The data are calculated from the annealing simulations of Fig. 5 and Fig. S1 in the ESI.†The energy of each local structure during annealing is given in Fig. 15. The DDQC is steadily formed when the ratio of the local structure is in stage III. Regarding the local structure of the DDQC, the lowest energy particle is the σ particle in the patchy DDQC, while it is the Z particle in the isotropic DDQC. This is due to the difference in the two particle systems. The five-fold patchy particle prefers five nearest neighbours. Therefore, the local structure σ is expected to have the lowest energy. Then the self-assembly of patchy particles at low densities results in a σ-rich structure instead of a DDQC. In contrast, the Z particle in the isotropic DDQC has the lowest energy, and therefore the DDQC structure is formed at low densities. The decrease of energy with time when the DDQC reaches stable stage III is mainly due to lowering of temperature in annealing. As a result, the thermal fluctuation is reduced and the energy decreases.
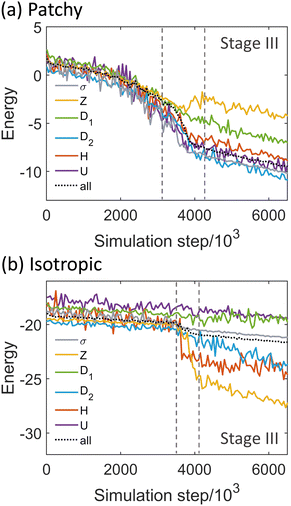 | ||
| Fig. 15 Energy of local structures during annealing simulation from T = 1.2 to T = 0.4 for the (a) patchy particle system and (b) isotropic particle system. The colours of local structures are given in Fig. 3, and the black dotted line shows the average energy of all particles. The vertical dashed lines define the three stages of the growth of the DDQC (see Fig. 5). | ||
We investigate the effect of density on the formation of DDQCs by patchy particles and isotropic particles. Annealing simulations are conducted at different values of the area fractions of the particles. The simulation parameters and results are given in Table 1 and Fig. 16.
| ρ a | T max | T min | ΔT | Total simulation steps | |
|---|---|---|---|---|---|
| Patchy particles | |||||
| (a) | 0.45 | 1.0 | 0.2 | 0.0125 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × 103 000 × 103 |
| (b) | 0.84 | 1.2 | 0.4 | 0.0125 | 6500 × 103 |
| Isotropic particles | |||||
| (c) | 0.30 | 1.2 | 0.2 | 0.0125 | 8500 × 103 |
| (d) | 0.87 | 1.2 | 0.2 | 0.0125 | 8500 × 103 |
 | ||
| Fig. 16 Changes in the ratio of local structures of patchy particle (a and b) and isotropic particle (c and d) self-assemblies at low and high values of area fractions. The snapshots are taken at the last steps of the annealing simulations. The area fractions ρa of the simulations (a-d) are 0.45, 0.84, 0.30, and 0.87, respectively. The details of simulation parameters are given in Table 1. | ||
There are different phases depending on the area fraction. For the patchy particle system, the suitable density for the assembly of the DDQC is limited around 0.69 ≲ ρa ≲ 0.81. At low density ρa < 0.69, the structure contains clusters of σ particles and undefined particles at the interfaces. The dodecagonal motif is hardly observed (Fig. 16(a)). At high density ρ > 0.81 the hexagonal structure is dominant (Fig. 16(b)).
For the isotropic particle system, the DDQC more easily forms as ρa ≲ 0.84. Even at the low density, clusters of the dodecagonal motif are clearly observed inside the interfaces (Fig. 16(c)). At high density ρ > 0.84 the hexagonal structure is also dominant (Fig. 16(d)).
E Structural change in the reverse process
In comparison with the growth of a DDQC from a Z-rich phase in the annealing simulation, the reversal process, i.e. the transformation of a DDQC to a Z-rich phase, is simulated. In this simulation, the parameters are identical to those of the annealing simulation except that the temperature is set to increase.Fig. 17 displays the structural change and the growth of a cluster of Z particles for the patchy particle system. In the annealing simulation, the Z-rich phase transforms to a σ-rich phase at T∼ 0.8. In the simulation, the σ-rich phase transforms to a Z-rich phase at T ∼ 0.95. Regarding the possible mechanism, in the schematic in Fig. 8 for annealing simulation, we illustrate the transformation of a hexagonal lattice to a dodecagonal motif, which can be obtained by a 15° rotation of the first neighbours of a Z particle. Analogically, in this reverse simulation, a region of Z particles is formed and then spans the whole system. At the periphery of the Z-rich domain, particles rotate 15°. This rotation is a reverse process of the rotation that occurs in the transformation from Z to σ particles for the annealing simulations. Similar hysteresis and mechanism are observed for the isotropic particle system. We also show the result in Fig. S4 in the ESI.†
Acknowledgements
The authors acknowledge the support from JSPS KAKENHI Grant number JP20K14437 to U. T. L., and JP20K03874 and JP20H05259 to N. Y.References
- D. Shechtman, I. Blech, D. Gratias and J. W. Cahn, Phys. Rev. Lett., 1984, 53, 1951–1953 CrossRef CAS.
- D. Levine and P. J. Steinhardt, Phys. Rev. Lett., 1984, 53, 2477–2480 CrossRef CAS.
- J. I. Urgel, D. Écija, G. Lyu, R. Zhang, C.-A. Palma, W. Auwärter, N. Lin and J. V. Barth, Nat. Chem., 2016, 8, 657–662 CrossRef CAS PubMed.
- K. Kamiya, T. Takeuchi, N. Kabeya, N. Wada, T. Ishimasa, A. Ochiai, K. Deguchi, K. Imura and N. K. Sato, Nat. Commun., 2018, 9, 154 CrossRef CAS PubMed.
- W. Steurer and D. Sutter-Widmer, J. Phys. D: Appl. Phys., 2007, 40, R229–R247 CrossRef CAS.
- L. Bindi, P. J. Steinhardt, N. Yao and P. J. Lu, Science, 2009, 324, 1306–1309 CrossRef CAS PubMed.
- S. Förster, K. Meinel, R. Hammer, M. Trautmann and W. Widdra, Nature, 2013, 502, 215–218 CrossRef PubMed.
- D. V. Talapin, E. V. Shevchenko, M. I. Bodnarchuk, X. Ye, J. Chen and C. B. Murray, Nature, 2009, 461, 964–967 CrossRef CAS PubMed.
- J. Mikhael, J. Roth, L. Helden and C. Bechinger, Nature, 2008, 454, 501–504 CrossRef CAS PubMed.
- T. Dotera, Isr. J. Chem., 2011, 51, 1197–1205 CrossRef CAS.
- H. Takagi, R. Hashimoto, N. Igarashi, S. Kishimoto and K. Yamamoto, J. Phys.: Condens. Matter, 2017, 29, 204002 CrossRef.
- A. P. Lindsay, R. M. Lewis, B. Lee, A. J. Peterson, T. P. Lodge and F. S. Bates, ACS Macro Lett., 2020, 9, 197–203 CrossRef CAS PubMed.
- K. Hayashida, T. Dotera, A. Takano and Y. Matsushita, Phys. Rev. Lett., 2007, 98, 195502 CrossRef PubMed.
- K. Yue, M. Huang, R. L. Marson, J. He, J. Huang, Z. Zhou, J. Wang, C. Liu, X. Yan, K. Wu, Z. Guo, H. Liu, W. Zhang, P. Ni, C. Wesdemiotis, W.-B. Zhang, S. C. Glotzer and S. Z. D. Cheng, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14195–14200 CrossRef CAS.
- S. Fischer, A. Exner, K. Zielske, J. Perlich, S. Deloudi, W. Steurer, P. Lindner and S. Förster, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1810–1814 CrossRef CAS PubMed.
- X. Zeng, G. Ungar, Y. Liu, V. Percec, A. E. Dulcey and J. K. Hobbs, Nature, 2004, 428, 157–160 CrossRef CAS PubMed.
- M. Engel, M. Umezaki, H.-R. Trebin and T. Odagaki, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 134206 CrossRef.
- M. Engel, P. F. Damasceno, C. L. Phillips and S. C. Glotzer, Nat. Mater., 2015, 14, 109–116 CrossRef CAS.
- K. Barkan, M. Engel and R. Lifshitz, Phys. Rev. Lett., 2014, 113, 098304 CrossRef CAS.
- P. F. Damasceno, S. C. Glotzer and M. Engel, J. Phys.: Condens. Matter, 2017, 29, 234005 CrossRef.
- M. Dzugutov, Phys. Rev. Lett., 1993, 70, 2924–2927 CrossRef CAS.
- T. Dotera, T. Oshiro and P. Ziherl, Nature, 2014, 506, 208–211 CrossRef CAS.
- R. Lifshitz and D. M. Petrich, Phys. Rev. Lett., 1997, 79, 1261–1264 CrossRef CAS.
- P. Subramanian, A. J. Archer, E. Knobloch and A. M. Rucklidge, Phys. Rev. Lett., 2016, 117, 075501 CrossRef CAS.
- N. Yoshinaga and S. Tokuda, 2020, arXiv:2006.06125 [cond-mat, physics:nlin].
- M. N. van der Linden, J. P. K. Doye and A. A. Louis, J. Chem. Phys., 2012, 136, 054904 CrossRef PubMed.
- A. Reinhardt, F. Romano and J. P. K. Doye, Phys. Rev. Lett., 2013, 110, 255503 CrossRef PubMed.
- A. Gemeinhardt, M. Martinsons and M. Schmiedeberg, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 126 CrossRef CAS PubMed.
- A. Gemeinhardt, M. Martinsons and M. Schmiedeberg, EPL, 2019, 126, 38001 CrossRef CAS.
- K. Je, S. Lee, E. G. Teich, M. Engel and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2011799118 CrossRef CAS PubMed.
- A. Reinhardt, J. S. Schreck, F. Romano and J. P. K. Doye, J. Phys.: Condens. Matter, 2017, 29, 014006 CrossRef PubMed.
- L. Liu, Z. Li, Y. Li and C. Mao, J. Am. Chem. Soc., 2019, 141, 4248–4251 CrossRef CAS PubMed.
- E. G. Noya, C. K. Wong, P. Llombart and J. P. K. Doye, Nature, 2021, 596, 367–371 CrossRef CAS PubMed.
- A. S. Keys and S. C. Glotzer, Phys. Rev. Lett., 2007, 99, 235503 CrossRef PubMed.
- W. Steurer, Acta Crystallogr., Sect. A: Found. Adv., 2018, 74, 1–11 CrossRef CAS PubMed.
- U. Grimm and D. Joseph, 1999, arXiv:cond-mat/9903074.
- T. Janssen, G. Chapuis and M. de Boissieu, Aperiodic Crystals, Oxford University Press, 2018, vol. 1 Search PubMed.
- C. V. Achim, M. Schmiedeberg and H. Löwen, Phys. Rev. Lett., 2014, 112, 255501 CrossRef CAS PubMed.
- U. T. Lieu and N. Yoshinaga, Soft Matter, 2020, 16, 7667–7675 RSC.
- U. T. Lieu and N. Yoshinaga, J. Chem. Phys., 2022, 156, 054901 CrossRef CAS PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 2017, vol. 1 Search PubMed.
- S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, Science, 1983, 220, 671–680 CrossRef CAS PubMed.
- T. Dotera, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 155–167 CrossRef CAS.
- T. Ishimasa, Isr. J. Chem., 2011, 51, 1216–1225 CrossRef CAS.
- C. Xiao, N. Fujita, K. Miyasaka, Y. Sakamoto and O. Terasaki, Nature, 2012, 487, 349–353 CrossRef CAS PubMed.
- P. W. Leung, C. L. Henley and G. V. Chester, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 446–458 CrossRef.
- R. A. DeLaCruz-Araujo, D. J. Beltran-Villegas, R. G. Larson and U. M. Córdova-Figueroa, Soft Matter, 2016, 12, 4071–4081 RSC.
- M. Martinsons and M. Schmiedeberg, J. Phys.: Condens. Matter, 2018, 30, 255403 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Simulation results for isotropic particles. See DOI: https://doi.org/10.1039/d2sm00798c |
| This journal is © The Royal Society of Chemistry 2022 |