The role of disorder in the motion of chiral active particles in the presence of obstacles

Abstract

The presence of obstacles is intuitively expected to hinder the diffusive transport of active particles. However, for chiral active particles, a low density of obstacles near a surface can enhance their diffusive behavior. Here, we study numerically the role that disorder plays in determining the transport dynamics of chiral active particles on surfaces with obstacles. We consider different densities of regularly spaced obstacles and distinct types of disorder: noise in the dynamics of the particle, quenched noise in the positions of the obstacles as well as obstacle size polydispersity. We show that, depending on the type and strength of the disorder, the presence of obstacles can either enhance or hinder transport, and discuss implications for the control of active transport in disordered media.

---

1 Introduction

In the last two decades, active matter has become an increasingly important focus of research. On small length scales, active matter describes micron-sized entities such as motile cells and artificial swimmers including Janus particles and active droplets.¹ Typically an active particle or micro-swimmer is represented as an active Brownian particle, or a particle undergoing run-and-tumble dynamics.²

Some active particles, with chiral shapes or with chiral surface properties move in chiral trajectories, typically along circles (2D) or helices (3D).³ For example, due to hydrodynamic interactions, several micro-swimmers trace circular trajectories when swimming near a substrate.^4–6 Significant progress has been made in capturing the behavior of chiral active particles in homogeneous environments. Present tools include agent based models and various stochastic descriptions.^7–10

Biological and man-made chiral active particles, however, rarely move in homogeneous environments, but rather encounter heterogeneity, such as domain walls, pores and obstacles.¹ To address this, recent research efforts have been directed at understanding the underlying (bio)physical mechanisms of chiral active particles in heterogeneous environments.¹¹ From a fundamental perspective, this is interesting to understand and optimise search strategies in realistic environments.^12,13 From a practical perspective, such an understanding is crucial to explain and control biomedically relevant processes, such as bio-film formation. In addition, there remains significant yet unexploited potential to enable novel nanotechnological applications, including smart self-propelled cargo carriers with uses in drug-delivery in tissue or contamination removal in porous soil, among others.^14–18

A first approach to control the dynamics of active particles in heterogeneous environments relies on designing the topography of the environment by carefully placing obstacles or structures on a substrate. Another approach would be to design an active particle that is able to navigate a complex environment in a controlled manner.¹⁹ This requires control over the reorientation of the particle, which has to date been achieved only in a limited number of cases.^20,21

Experimental observations show that the topography of the environment can strongly influence the dynamics of active particles, and in non-intuitive ways. Recent evidence indicates that the presence of porous micro-structures generally hinders the diffusive transport of active particles.^22,23 Interestingly, for chiral active particles, contrasting phenomenology has also been observed. For example, a significantly enhanced propagation on surfaces, due to randomly placed obstacles, has been reported in theoretical studies in ref. 24 and 25 and experimentally for E. coli in ref. 26. Furthermore, experiments tracking E. coli navigating a colloidal crystal found that the colloids rectified the trajectory of bacteria, resulting in enhanced transport.^27–30

A common feature of natural and man-made heterogeneous environments is the presence of disorder or noise in the surface topography. Disorder can occur in the form of spatial positioning and size of obstacles or pores. Also the motion of active particles contains disorder in the reorientation, typically in the form of flagellar noise or rotational Brownian diffusion.^20,21,31,32

The simplest interaction between chiral active particles and obstacles is a purely repulsive interaction. In this article, we examine numerically the effect of disorder (from here on referred to as ‘noise’) in the steric interactions on the dynamics of chiral active particles exploring a periodic arrangement of obstacles, where we introduce noise in a controlled manner. We first consider a chiral active particle that does not experience any rotational Brownian diffusion in a periodic array of obstacles. Distinct types of noise are then introduced independently: ‘dynamic noise’ determining the reorientation of the particle and two types of ‘quenched noise’, the first being disorder in the positions of the obstacles, and the second being polydispersity in the sizes of the obstacles.

To quantify the effect of the different types of noise on the transport properties of the active particle, we computed its effective diffusion coefficient (diffusivity) for a wide range of obstacle area fractions (densities) and noise strengths. We find that the diffusivity of a chiral active particle is strongly non-monotonic for increasing density of obstacles. At lower densities, the transport of a chiral active particle is rectified due to the interaction of the particle with the obstacles, affecting the orbits, and allowing the particle to explore space. At higher densities, the particle is unable to perform chiral motion due to constant interactions with the obstacles and the diffusivity is reduced until the conditions are right for the motion to be channeled in the lattice. When the strength of dynamic noise is increased, the diffusivity is enhanced for all but high densities, which we attribute to the randomization of the chiral orbits. Moreover, the ability of the particle to better explore space becomes less dependent on the obstacles. At high densities, dynamic noise suppresses guided transport through channels. Quenched noise introduces disorder in the spatial arrangement of the obstacles, resulting in erratic motion, preempting fixed orbits, and perturbing guided motion through channels.

2 Model

We consider a spherically shaped chiral active particle of diameter σ (for E. coli typically 1–2 μm) on a surface containing N_o fixed obstacles also of diameter σ. The amount of obstacles is expressed as the percentage of the surface that is covered by the obstacles: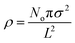 (× 100%), with L being the edge size of the square simulation box. Interactions between the particle and the obstacles are defined by the Weeks–Chandler–Anderson potential obtained by truncating a Lennard–Jones potential at its minimum:where r_i is the distance between the particle and obstacle i. The initial position of the particle is randomly chosen in the box while guaranteeing that it does not overlap with any obstacle. The trajectory of the particle is then obtained by integrating the following equations:where x, y denote the position of the particle, v and ϕ are its speed and direction, and F_x and F_y are the x and y components of the force F = −∇V. The angular velocity ω results in periodic orbiting motion of the particle that is counterclockwise for ω > 0 and D_R defines the rotational diffusion constant. The stochastic term ξ_ϕ represents independent white noise with zero mean and unitary variance. The model reproduced well the experimental data for E. coli in ref. 26. The time evolution of the position of the particle is obtained with a second order Runge–Kutta scheme, to guarantee stability at high obstacle densities. As a reference particle, we consider an ‘ideal chiral active particle’ with v = 3σ and ω = 1, representing a chiral active particle that moves in perfect circles of radius R_o = v/ω = 3σ when moving in a homogeneous environment (no obstacles and D_R = 0) as in Fig. 1(a). As reference surface topography, we consider obstacles placed in a square lattice arrangement (Fig. 1b).

Fig. 1 (a) Schematic depiction of an ‘ideal chiral active particle’ and its trajectory with orbit radius R_o. (b) Schematic depiction of four obstacles in a square lattice with lattice periodicity l_c. (c) Schematic depiction of the trajectory of a chiral active particle with low dynamic noise. (d) Lattice with quenched noise in the form of randomly perturbed obstacle positions. The arrows denote the change in position of the obstacles (dark blue circles) due to the positional quenched noise, relative to their original lattice position marked by the immediately lighter shade of blue. The lightest shade of blue marks the area from which a new position was chosen randomly. (e) Lattice with quenched noise in the form of obstacle polydispersity.

Two types of noise are then introduced independently: dynamic noise in the dynamics of the particle (D_R ≠ 0) (Fig. 1c) and quenched noise either in the positions of the obstacles (Fig. 1d) or in the form of obstacle size polydispersity (Fig. 1e). For positional quenched noise, the strength is set by ξ_q, which defines the radius of a circular disk centered at the position of the obstacle; the perturbed obstacles are placed at a new random position chosen uniformly in this disk. For the obstacle size polydispersity, the size distribution follows a Gaussian with mean σ, and dispersion σ_s. For each obstacle, the diameter d is drawn from the size distribution, if d ≤ 0 a new diameter is drawn from the distribution until a diameter d > 0 is obtained.

In this work the effects due to inertia have been neglected. However, recent studies indicate that for macroscopic active particles, inertial effects become increasingly relevant and require careful consideration.^33–35

In the following we will express distances in terms of the dimensionless obstacle radius σ/2 and time in terms of σ/v. A simulation typically includes N_o = 400 obstacles. Finally, the step size in the simulation is Δt = 10⁻⁴ and a simulation lasts for t = 4800 σ/v.

3 Results

To characterize the transport properties of the chiral active particle, we computed the mean square displacement:

MSD(t) = 〈[R(t) − R(0)]²〉, (3)

with R(t) denoting the position of the particle at time t. The brackets 〈·〉 indicate an ensemble average over 4000 particle trajectories, each beginning at a position selected uniformly at random. For positional quenched noise or size polydispersity, the average is performed over 100 obstacle configurations, with 40 particle trajectories per configuration. At long times, the mean squared displacement is expected to scale with the effective diffusion constant D or diffusivity,

MSD(t) ∼ 4Dt, t→∞ (4)

which we extracted through a linear regression in the interval 3600σ/v < t < 4800σ/v. The diffusivity is measured for obstacle densities ranging from ρ = 0% representing a homogeneous environment (Fig. 2(a) for ρ = 0%) to ρ = 21.0%, where the particle rapidly gets stuck in between obstacles (caged) and is unable to explore space (Fig. 2(a) for ρ = 21.0%).

Fig. 2 (a) Example trajectories (green) of the active particle (red) navigating the square lattice of obstacles (faint blue) for increasing densities. The blue arrows indicate the direction of propagation of the ‘translating orbits’. (b) Diffusivity D vs. density of obstacles ρ for the ‘ideal chiral active particle’ and the ‘ideal straight moving particle’, which has been rescaled such that for ρ = 0, D = 40.0. The inset displays the diffusivity vs. the lattice periodicity l_c normalized by the orbit radius R_o. The dashed lines mark the densities for which diffusion occurs for the ‘ideal chiral active particle’.

3.1 Ideal chiral active particle

In the case of an ‘ideal chiral active particle’ (D_R = 0) in a homogeneous environment (without obstacles), the particle moves in a circular orbit of radius R_o = 3σ. More interesting behaviour emerges for a heterogeneous environment. A defining feature of the ‘ideal chiral active particle’ is that its space exploration is deterministic and a result of being scattered by the obstacles. The spatial distribution of obstacles alone governs its dynamics.

When an ‘ideal chiral active particle’ navigates a square lattice, the particle performs periodic orbits in between or around obstacles at most obstacle densities and is limited to exploring a small part of the system (or ‘localized’), meaning that it does not perform long time diffusion. Example trajectories of ‘localized’ particles are presented in Fig. 2(a) for ρ = 0%, ρ = 4.0%, ρ = 8.5%, ρ = 10.0%, ρ = 15.0% and a caged particle for ρ = 21.0%. For a small number of intermediate densities the particle explores space, performing long time ‘diffusive’ behaviour. Examples of diffusive behaviour are shown in Fig. 2(a) for ρ ≈ 8.0%, ρ ≈ 9.5%, ρ ≈ 10.2% and 20%. In Fig. 2(b), the diffusivity D of the ‘ideal chiral active particle’ vs. ρ, is presented.

The sharp peak in the diffusivity at ρ = 9.5% is a consequence of space exploration in the form of regular periodic motion. For densities around ρ = 9.5%, the distance in between neighbouring obstacles (the lattice periodicity, Fig. 1b) l_c approximates the radius of the orbit R_o causing the particle to collide frequently with the surrounding obstacles. Around density ρ = 9.5%, where R_o ≈ l_c (Fig. 2b), the particle collides with an obstacle before it completes an orbit, and it is scattered forward towards the next row of obstacles. This ‘translating orbit’ (a term we borrow from skyrmion, where a similar effect was observed for Vizarim et al.,³⁶) is repeated for each row of obstacles, and results in the particle efficiently traversing the system. In Fig. 2(a), an example trajectory is presented for ρ = 9.5%. The blue arrow indicates the direction of propagation of the ‘translating orbit’. At the two much smaller neighbouring peaks, for densities ρ = 8.0% (Fig. 2a) and ρ = 10.2% (Fig. 2a), the particle is scattered by the obstacles and traces mostly erratic trajectories with occasional laps of periodic behaviour. For higher densities, at ρ = 20.0%, the particle is unable to trace chiral trajectories due to constant interactions with the closely spaced obstacles. Instead, it is guided through channels in the lattice, a trajectory traces a ‘translating orbit’ as the ‘ideal chiral active particle’ moves through the lattice (Fig. 2a). Efficient transport in the form of ‘translating orbits’, resulting from a crowded topography, strongly contrasts with the behaviour of ‘ideal straight moving particles’ (particles with D_R = 0 and ω = 0), for which increasing the obstacle density monotonically hinders space exploration (Fig. 2b).

3.2 Noise in the dynamics

When a chiral active particle exhibits noisy dynamics (D_R ≠ 0), the circular trajectory is perturbed allowing the particle to explore space. For a chiral active particle experiencing rotational diffusion with strength D_R, τ_R = D_R⁻¹ sets the typical time for the particle to decorrelate from its initial direction of motion in free space.

Let us now consider a chiral active particle moving through a square lattice of obstacles. In Fig. 3(a–c) some example particle trajectories are presented for different densities of obstacles. The noise in the dynamics is represented by the vertical axis (D_R/vσ⁻¹). In Fig. 4(a) the diffusivity is presented for different noise amplitudes D_R. The dashed line indicates the diffusivity for the chiral active particle in a homogeneous environment (without obstacles); by comparing the diffusivity for a given noise strength to the homogeneous case D(D_R,ρ = 0), we can determine the effect of the obstacles on the diffusivity. When a diffusivity curve dips below the dashed line, the presence of obstacles hinders diffusion.

Fig. 3 Example trajectories as a function of the different types of noise, for three increasing values of obstacle density: (a) ρ = 9.5%, (b) ρ = 15.0% and (c) ρ = 20.0%. The particle (red) traces a trajectory (green) moving among the obstacles (faint blue). In the middle, in the ellipsoid shape, the trajectory for the ‘ideal chiral active particle’ (D_R = 0) in a square lattice, with no quenched noise, is shown as reference. The axes indicate the three different noise types: the vertical axis indicates the dynamic noise (D_R), the axis to the left the positional quenched noise (ξ) for a particle with D₀ ≡ D_R/vσ⁻¹ = 0.002, and the axis to the right quenched noise in the form of size polydispersity (σ_s).

Fig. 4 Diffusivity D vs. density of obstacles: (a) for different dynamic noise amplitudes D_R, (b) with D_R/vσ⁻¹ = D₀ = 0.002 for different lattice perturbation amplitudes ξ_q, (c) with D_R/vσ⁻¹ = D₀ = 0.002 for different amplitudes of size polydispersity σ_s. The inset displays the diffusivity vs. the lattice periodicity l_c for the obstacles, for a non perturbed lattice, normalized by the orbit radius R_o. The dashed lines indicate the diffusivity for a system without obstacles, and serve as a guide for the eye. The straight moving particle in (a) represents an active particle with velocity v = 3σ/s, ω = 0 and D₀, and has been rescaled such that, for ρ = 0, it matches the curve with D_R/vσ⁻¹ = 0.080. The random system in (b) represents a regular chiral active particle with D₀, in a system with randomly placed non overlapping obstacles.

For the smallest noise strength (D₀ ≡ D_R/vσ⁻¹ = 0.002), the diffusivity profile is clearly non-monotonic with increasing obstacle density (Fig. 4a). The noise perturbs the localized orbits of the ‘ideal chiral active particle’, resulting in diffusive behaviour for all densities ρ < 20.5%. For higher densities, the particle is caged by the obstacles and the diffusivity vanishes. A fine structure with four peaks emerges, around densities ρ = 2.0%, ρ = 4.5%, ρ = 9.5% and ρ = 20.0%. Less pronounced minima occur at ρ = 2.5%, ρ = 6.0% and ρ = 15.0%. For densities ρ < 7.5%, the fine structure does not qualitatively change the behaviour of the particle, only resulting in a small enhancement or suppression of the diffusion. The fine structure is a result of the chiral active particle interacting with the periodic lattice, and disappears if the lattice is sufficiently perturbed, which will be explored in depth in Section 3.3.

To understand the main features of the diffusivity (Fig. 4a), we can look at the number of orbits a particle typically completes (in a homogeneous environment) before its orientation is randomized by the dynamic noise, as suggested by ref. 25. For the small noise strength (D_R/vσ⁻¹ = 0.002), we obtain n = 159, implying that the particle still largely traces a circular trajectory if it does not interact with the obstacles. In this case, the increased diffusion can be attributed to efficient scattering by obstacles, rectifying the orbits, and enhancing the particle's diffusion. This mechanism dominates for intermediate densities, especially around ρ = 9.5% where the radius of the orbit R_o approximates the spacing between obstacles l_c, such that l_c/R_o ≈ 1 (Fig. 4a inset). Some example trajectories are presented along the vertical axis (D_R/vσ⁻¹) in Fig. 3(a.1–3). The suppression of the diffusion for densities around ρ = 15.0% results from the particle becoming intermediately trapped in trajectories that orbit around a few obstacles. Due to the interactions with the obstacles, the particle keeps moving in a fixed orbit until, driven by dynamic noise, it hops (diffuses) to the next row of obstacles. Similar orbits were also observed for the ‘ideal chiral active particle’ for densities around ρ = 15.0%, but since the ‘ideal chiral active particle’ does not experience dynamic noise, it remains trapped indefinitely (Fig. 2 for ρ = 15%). In Fig. 3(b.3), an example trajectory is presented of a particle that hopped to a new orbit once. At higher densities the channels narrow further; now a small deviation in the trajectory more readily results in the particle hopping across rows, enhancing diffusion. Around density ρ = 20.0% (the highest densities before caging occurs), the frequent interactions with the closely spaced obstacles prevent the particle from moving in circular orbits. Instead, the particle is guided through channels in the lattice, in an erratic way, efficiently exploring space. In Fig. 3(c.1–3) some example trajectories of a particle with dynamic noise navigating a dense system with ρ = 20.0% are presented. For higher densities ρ ≥ 20.5%, the particle is fully caged in the lattice.

Now that the general behaviour of a noisy chiral active particle is outlined, we can examine the effect of increasing the noise strength D_R (Fig. 4a). As a reference, we take the previous case of a particle with D_R = D₀. For a small increase in the noise strength to D_R/vσ⁻¹ = 0.004, and n = 80, the behaviour is similar to the reference case. When the noise is increased to D_R/vσ⁻¹ = 0.016, we obtain n = 20; now the presence of obstacles enhances the diffusivity for all densities in a more uniform manner, but still peaks around ρ = 9.5%, before flattening out. Limited enhancement is observed for densities ρ > 15% until it vanishes for ρ ≥ 20.5%. In this case, the noise is too strong for the particle to remain trapped in fixed periodic orbits for an extended period of time. Instead, the particle moves across the lattice in an erratic way, along with intermittent periods of orbiting around (multiple) obstacles (Fig. 3(a–c.2)). The diffusion of such erratic motion is not very sensitive to the density; the diffusivity varies little for ρ > 15.0%, until it vanishes at ρ = 20.5% as the particle becomes caged by the obstacles.

For still larger noise strengths (D_R/vσ⁻¹ = 0.040 and D_R/vσ⁻¹ = 0.080), the noise increasingly perturbs the orbiting motion, the particle's motion is markedly less chiral, typically only able to perform n = 8 orbits (D_R/vσ⁻¹ = 0.040) and n = 4 orbits (D_R/vσ⁻¹ = 0.080) before its orientation is fully decorrelated. In this case, the particle traces strongly erratic trajectories for all densities, which are not very sensitive to the density. Some example trajectories are presented in Fig. 3(a–c.1) for D_R/vσ⁻¹ = 0.040. Scattering by obstacles enhances diffusion only marginally for low densities ρ < 9.5% (D_R/vσ⁻¹ = 0.040) and ρ < 3.0% (D_R/vσ⁻¹ = 0.080). Moreover, the diffusivity varies little with the density for ρ < 9.5% (D_R/vσ⁻¹ = 0.040) and ρ < 3.0% (D_R/vσ⁻¹ = 0.080). For higher densities, similarly to the ‘straight moving particle’ (black curve in Fig. 4a), a monotonic decrease in diffusivity for increasing density is retrieved, vanishing for ρ ≥ 20.5% where the particle is caged in the lattice.

3.3 Randomness in the positions of the obstacles

When a chiral active particle with D₀ explores a lattice with noise in the positions of the obstacles, the diffusivity is markedly affected for large strengths of noise. In Fig. 4(b), the diffusivity is presented for different amplitudes of the noise ξ_q, alongside the diffusivity of a configuration with randomly placed non-overlapping obstacles. The largest noise strength (ξ_q/σ = 1.00) corresponds to configurations where the contact between obstacles at density ρ = 20.0% is still low, with typically less than 10.0% of the obstacles touching. In Fig. 3, noise in the positions is represented by the left axis (ξ/σ + D₀).

For the smallest noise strength (ξ_q/σ = 0.05), at low densities (ρ < 7.0%), the fine structure is little affected. The diffusivity profile is affected for high densities (ρ > 17.0%), with the peak around ρ = 20.0% being significantly suppressed and shifted towards lower density values with respect to the ordered lattice (ξ_q/σ = 0). The shift in the position of the peak around ρ = 20.0% is a result of the obstacles guiding the particle through (disordered) channels, leading to a small local maximum in the diffusivity for densities around ρ = 19.5%. For higher densities, the randomness combined with the densely spaced obstacles perturbs the channels, and introduces significant backtracking of the trajectories, reducing the diffusivity when compared to the ordered lattice (Fig. 3(c.4)). At the highest densities ρ > 19.5%, the obstacles are closely spaced; even a small perturbation of the channels introduces bottlenecks a particle can not pass through, limiting diffusion.

When the noise is increased to ξ_q/σ = 0.25, the peak is shifted towards lower densities, channels are randomized further and bottlenecks occur at lower densities. Now, the disordered obstacles preempt the particle from getting trapped for long in intermittently stable orbits around a number of obstacles, as observed in the ordered lattice for densities around ρ = 15.0% (Fig. 3(b.4) and for the ‘ideal chiral active particle’ 2a). The particle is scattered randomly and diffuses more efficiently (Fig. 3(b.5)), reducing the depth of the local minimum in the diffusivity. As the lattice perturbation is increased, bottlenecks occur at lower densities (ρ > 18.0%). An example trajectory is presented in Fig. 3(c.5).

For large amplitudes of positional noise (ξ_q/σ = 0.50 and ξ_q/σ = 1.00), with the average random displacement comparable to the obstacle size, the lattice is strongly perturbed. This results in a smoothing out of the fine structure of the diffusivity profile for all densities. In the limit of large positional quenched noise, a random topography is retrieved, and the diffusivity exhibits a single flattened peak, centered around ρ = 10.0% (black curve in Fig. 4b). Due to the positional disorder, the distance between obstacles becomes irregular. This leads to suppression of the diffusion for densities around ρ = 9.5%, as the disordered arrangement preempts regular motion where the particle moves from one row of obstacles to another, instead it is scattered randomly. As the lattice is further perturbed, this effect becomes increasingly pronounced (Fig. 3(a.4–6)). Even for a fully random arrangement, the diffusion is enhanced for densities ρ < 17.0%, indicating that for all but high densities of randomly placed obstacles, the rectification of orbits by obstacles leads to enhanced diffusion. For large amplitudes of positional noise (and the random configuration), and increasing densities ρ > 17.0%, the strongly disordered and densely packed arrangements increasingly contain pockets of obstacles that trap the particle, limiting diffusion. A trajectory of a particle in a strongly disordered lattice that ultimately becomes trapped in a fixed orbit is displayed in Fig. 3(c.6).

3.4 Non-uniform size distribution

For a non-uniform obstacle size distribution, σ_s sets the strength of the obstacle size polydispersity. In Fig. 4(c), the diffusivity is presented for different σ_s. Here the limit of large polydispersity (σ_s/σ = 0.50) corresponds to configurations with about 20.0% of obstacles, typically the largest, touching at density ρ = 20.0%. The right axis in Fig. 3 represents the size polydispersity (σ_s/σ + D₀).

When navigating a surface with polydisperse obstacles, the diffusivity profile for a particle with D₀ is affected similarly to the system with positional quenched noise. For the smallest polydispersity (σ_s/σ = 0.05), at densities ρ < 17.0%, the fine structure is little affected, as the particle traverses the system in an erratic way (Fig. 3(a.7) provides an example for ρ = 9.5%). For higher densities ρ > 17.0%, similar to the positional noise, the shift in the position of the peak around ρ = 20.0% is a result of the obstacles guiding the particle through channels of irregularly sized obstacles (similar to Fig. 3(c.7)). This leads to a local maximum in the diffusivity for densities around ρ = 19.0%. For still higher densities bottlenecks and pockets form that trap the particle. When the polydispersity is increased slightly to σ_s/σ = 0.10, the effect of intermittent trapping in orbits for densities around ρ = 15.0% is reduced (Fig. 3(b.8)) and the peak is smeared out and shifted to lower densities.

For polydispersity σ_s/σ = 0.25, the fine structure is smoothed out for ρ > 12.0% as the particle explores the system efficiently tracing erratic trajectories, until it increasingly becomes trapped for ρ > 18.0% and the diffusivity vanishes (Fig. 3(c.8)). When the polydispersity is increased to σ_s/σ = 0.50, the fine structure is smoothed out for all densities, the peak around ρ = 9.5% is shifted to slightly lower densities and is reduced as the trajectories are randomized and periods of intermittent trapping in orbits occur (Fig. 3(a.9)). The shifting of the peak can be explained by the larger total surface covered by the obstacles due to the size polydispersity (what is gained by the obstacles that increase in size is not offset by what is lost by the obstacles that become smaller). For σ_s/σ = 0.50 the diffusivity is suppressed relatively to σ_s/σ = 0.25, for almost all densities. This is a result of some of the obstacles becoming increasingly larger; for ρ > 8.0% the large obstacles form clusters that trap the particle, as well as walls that subdivide the system and prevent the particle from accessing parts of it. For ρ > 15.0%, the diffusivity vanishes rapidly as the particle becomes caged in pockets of obstacles. In Fig. 3(a–c.9), some example trajectories are displayed for noise amplitudes σ_s/σ = 0.50. When the polydispersity is further increased (σ_s/σ > 0.50), some obstacles become much larger than the particle; in this limit particle–obstacle interactions become more important, and our simplified model is no longer expected to accurately capture the dynamics.^37,38

4 Conclusions

We have investigated the dynamics of a chiral active particle on a surface with obstacles. Different densities of obstacles as a fraction of the surface area were considered. We introduced distinct types of disorder: noise in the dynamics of the particle and noise in the positions of the obstacles, as well as obstacle size polydispersity.

A noiseless chiral active particle in an environment without obstacles gets trapped in circular orbits and does not explore space. When navigating an array of regularly spaced obstacles, for most densities, space exploration of a chiral active particle is limited to fixed orbits. Efficient long time transport, in the form of a ‘translating orbit’, occurs when the distance between the obstacles approximates the orbit radius of the particle, or the spacing between the obstacles approximates the size of the particle. Less efficient long time transport occurs for a few densities, with the particle tracing an erratic trajectory.

A chiral active particle that experiences dynamic noise performs long time transport for all densities, except for very high densities when it becomes trapped by the obstacles. The presence of low to intermediate densities of obstacles enhances the transport of a chiral active particle, by rectifying orbits. Especially when the distance between the obstacles approximates the radius of the orbit, this effect is pronounced. For higher densities, obstacles can enhance transport by guiding the particle through open channels in the lattice.

When the strength of the dynamic noise is increased, the chiral trajectories are more strongly perturbed. This reduces the tendency of the particle to move in circles, enhancing transport for all densities, and reducing the effect of scattering by obstacles on the transport. For large noise amplitudes, the particle is effectively no longer chiral. In this case, the presence of obstacles hinders transport, which is in agreement with previously published results for non-chiral active particles.^22,23

Positional noise and obstacle size polydispersity result in a disordered environment, which enhances transport by preempting fixed orbits in between or around obstacles. Additionally, scattering of the particle by the disordered obstacles results in erratic motion. For densities where the inter-obstacle distance approximates the radius of the particle's orbit, such motion perturbs the otherwise efficient rectification of orbits, and suppresses transport.

For high densities, quenched noise perturbs channels, limiting, and suppressing transport. For high densities and large quenched positional disorder or size polydispersity, pockets of obstacles form that trap the particle, strongly hindering transport. In the limit of large positional noise, the presence of a low or intermediate density of obstacles enhances transport. When the obstacle size polydispersity is increased, the dynamics is increasingly hindered by a few very large obstacles that form pockets that trap the particle, inhibiting long term transport. These findings are in line with a recent experimental and numerical study of (non chiral) active particles exploring a complex micro structure,³⁹ where the authors found a coupling between the active force and the topography of the micro structure that strongly influences the effective diffusivity of the particles. In the future, this effect could be explored further for chiral active particles. In addition, differently shaped (non spherical) obstacles could be considered, and depending on the shape, these might promote the emergence of a preferred direction of motion or the trapping for the active particles.

We solely considered steric (repulsive) interactions. For wet active systems, as e.g. microswimmers, hydrodynamic interactions with the obstacles are also likely to affect the dynamics. For example, in ref. 26 it has been shown that for E. coli, hydrodynamic interactions with obstacles (forward scattering) are the key mechanism responsible for an enhancement in the diffusion for an optimal density of random obstacles. Here, we show that in the absence of hydrodynamic interactions, diffusion of a chiral active particle is also enhanced, although through a different physical mechanism. Future works might include the role of hydrodynamic effects in the particle–obstacle interaction, such effects can introduce an attractive interaction that deflects the particle in the absence of a particle–obstacle collision.^37,38 Moreover, in the case of a strong attraction, the particle might get trapped by the obstacles due to the attraction alone, potentially introducing new localized states.

An interesting extension of this work would be to investigate the effect of spatial arrangement and disorder on the dynamics of interacting chiral active particles. Previous work encountered motility induced phase separation, commensuration effects and frustrated states for a simple model of interacting non-chiral particles in a similar square lattice of obstacles.⁴⁰ Another possibility would be to consider moving obstacles. The bronchus in the lungs are lined with respiratory cilia: microscopic, periodically beating hairs that clear inhaled debris and microbes from the conducting airways.⁴¹ By introducing a periodic motion in the obstacles, the dynamics governing the transport of (chiral) microbes in the cilia could be explored. From a very different perspective, simulation studies of circular ac driven skyrmions on a square lattice of obstacles encountered behaviours similar to our findings for the ‘ideal chiral active particle’.³⁶ It could be interesting to see how such systems respond to noise. Although this work is limited to surface topography, extending it to three dimensions would also be interesting. Recently a geometric criterion for the optimal transport of run and tumble polymers in a porous medium was uncovered, which emerges when their run lengths are comparable to the longest straight path available in the porous medium.³⁰ In addition to a fundamental understanding of the dynamics of chiral active particles in complex environments, these findings can be employed to guide the future design of active searchers capable of optimal navigation in complex environments, or the development of micro-structured surfaces that can control and prevent bacterial adhesion.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge financial support by the European Commissions Horizon 2020 research and innovation program under the Marie Sklodowska-Curie Grant Agreement No. 812780 and from the Portuguese Foundation for Science and Technology (FCT) under Contracts No. PTDC/FIS-MAC/28146/2017 (LISBOA-01-0145-FEDER-028146), UIDB/00618/2020, and UIDP/00618/2020.

Notes and references

1. C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006.
2. S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345.
3. B. Liebchen and D. Levis, Chiral Active Matter, 2022, https://arxiv.org/abs/2207.01923.
4. E. Lauga, W. R. DiLuzio, G. M. Whitesides and H. A. Stone, Biophys. J., 2006, 90, 400–412.
5. A. Bukatin, I. Kukhtevich, N. Stoop, J. Dunkel and V. Kantsler, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 15904–15909.
6. A. S. Utada, R. R. Bennett, J. C. N. Fong, M. L. Gibiansky, F. H. Yildiz, R. Golestanian and G. Wong, Nat. Commun., 2014, 5, 4913.
7. L. Caprini and U. Marini Bettolo Marconi, Soft Matter, 2019, 15, 2627–2637.
8. S. van Teeffelen, U. Zimmermann and H. Löwen, Soft Matter, 2009, 5, 4510–4519.
9. F. J. Sevilla, Phys. Rev. E, 2016, 94, 062120.
10. S. van Teeffelen and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 020101.
11. N. A. M. Araújo, L. M. C. Janssen, T. Barois, G. Boffetta, I. Cohen, A. Corbetta, O. Dauchot, M. Dijkstra, W. M. Durham, A. Dussutour, S. Garnier, H. Gelderblom, R. Golestanian, L. Isa, G. H. Koenderink, H. Löwen, R. Metzler, M. Polin, C. P. Royall, A. Šarić, A. Sengupta, C. Sykes, V. Trianni, I. Tuval, N. Vogel, J. M. Yeomans, I. Zuriguel, A. Marin and G. Volpe, Steering self-organisation through confinement, 2022, https://arxiv.org/abs/2204.10059.
12. G. Volpe and G. Volpe, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11350–11355.
13. E. Perez Ipiña, S. Otte, R. Pontier-Bres, D. Czerucka and F. Peruani, Nat. Phys., 2019, 15, 1–6.
14. J. Li, B. E. de Avila, W. Gao, L. Zhang and J. Wang, Sci. Robot., 2017, 2, eaam6431.
15. W. Gao and J. Wang, ACS Nano, 2014, 8, 3170–3180.
16. J. Zhang, Z. Chen, R. K. Kankala, S.-B. Wang and A.-Z. Chen, Int. J. Pharm., 2021, 596, 120275.
17. P. Erkoc, I. C. Yasa, H. Ceylan, O. Yasa, Y. Alapan and M. Sitti, Adv. Ther., 2018, 2, 1800064.
18. J. S. Adadevoh, S. C. Triolo, C. A. Ramsburg and R. M. Ford, Environ. Sci. Technol., 2016, 50(1), 181–187.
19. G. Volpe, I. Buttinoni, D. Vogt, H.-J. Kümmerer and C. Bechinger, Soft Matter, 2011, 7, 8810–8815.
20. T. Mano, J.-B. Delfau, J. Iwasawa and M. Sano, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E2580–E2589.
21. M. A. Fernandez-Rodriguez, F. Grillo, L. Alvarez, M. Rathlef, I. Buttinoni, G. Volpe and L. Isa, Nat. Commun., 2020, 11, 4223.
22. A. Dehkharghani, N. Waisbord and J. S. Guasto, Self-transport of swimming bacteria is impaired by porous microstructure, 2022, https://arxiv.org/abs/2201.03059.
23. M. Zeitz, K. Wolff and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2017, 40, 1–10.
24. O. Chepizhko and T. Franosch, Soft Matter, 2019, 15, 452–461.
25. O. Chepizhko and T. Franosch, New J. Phys., 2020, 22, 073022.
26. S. Makarchuk, V. Braz, N. Araujo, L. Ciric and G. Volpe, Nat. Commun., 2019, 10, 4110.
27. A. T. Brown, I. D. Vladescu, A. Dawson, T. Vissers, J. Schwarz-Linek, J. S. Lintuvuori and W. C. K. Poon, Soft Matter, 2016, 12, 131–140.
28. A. Weber, M. Bahrs, Z. Alirezaeizanjani, X. Zhang, C. Beta and V. Zaburdaev, Front. Phys., 2019, 7, 148.
29. M. Brun-Cosme-Bruny, E. Bertin, B. Coasne, P. Peyla and S. Rafaï, J. Chem. Phys., 2019, 150, 104901.
30. C. Kurzthaler, S. Mandal, T. Bhattacharjee, H. Löwen, S. Dattaf and H. Stone, Nat. Commun., 2021, 12, 7088.
31. D. Clausznitzer and R. Endres, BMC Syst. Biol., 2011, 5, 151.
32. M. Polin, I. Tuval, K. Drescher, J. P. Gollub and R. E. Goldstein, Science, 2009, 325, 487–490.
33. H. Löwen, J. Chem. Phys., 2020, 152, 040901.
34. O. Dauchot and V. Démery, Phys. Rev. Lett., 2019, 122, 068002.
35. D. Breoni, M. Schmiedeberg and H. Löwen, Phys. Rev. E, 2020, 102, 062604.
36. N. P. Vizarim, C. J. O. Reichhardt, P. A. Venegas and C. Reichhardt, J. Phys. Commun., 2020, 4, 085001.
37. D. Takagi, J. Palacci, A. Braunschweig, M. Shelley and J. Zhang, Soft Matter, 2014, 10, 1784–1789.
38. S. E. Spagnolie, G. R. Moreno-Flores, D. Bartolo and E. Lauga, Soft Matter, 2015, 11, 3396–3411.
39. K. J. Modica, Y. Xi and S. C. Takatori, Front. Phys., 2022, 10, 869175.
40. C. Reichhardt and C. J. O. Reichhardt, Phys. Rev. E, 2021, 103, 022602.
41. R. G. Crystal, S. H. Randell, J. F. Engelhardt, J. Voynow and M. E. Sunday, Proc. Am. Thorac. Soc., 2008, 5, 772–777.

---