Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Critical behavior of quorum-sensing active particles
Nicoletta
Gnan
 *ab and
Claudio
Maggi
*ab and
Claudio
Maggi
 *bc
*bc
aISC-CNR, Institute for Complex Systems, Piazzale A. Moro 2, I-00185, Roma, Italy. E-mail: nicoletta.gnan@cnr.it
bDipartimento di Fisica, Università di Roma “Sapienza”, I-00185, Roma, Italy
cNANOTEC-CNR, Institute of Nanotechnology, Soft and Living Matter Laboratory-Piazzale A. Moro 2, I-00185, Roma, Italy. E-mail: claudio.maggi@cnr.it
First published on 9th September 2022
Abstract
It is still a debated issue whether all critical active particles belong to the same universality class. Here we numerically study the critical behavior of quorum sensing active particles that represents the archetypal model for interpreting motility-induced phase separation. Mean-field theory predicts that this model should undergo a full phase separation if particles slow-down enough when sensing the presence of their neighbors and that the coexistence line terminates in a critical point. By performing large-scale numerical simulations, we confirm this scenario, locate the critical point and use finite-size scaling analysis to show that the static and dynamic critical exponents of this active system substantially agree with those of the Ising universality class.
Introduction
Quorum sensing (QS) is a widely exploited communication strategy among microorganisms which allows a single cell to sense the concentration of the population and act accordingly via gene expression.1 A famous example is that of the bacterium Aliivibrio fischeri2 which is capable of emitting bioluminescence depending on the density of the colony. More recently, it has been shown that QS is implicated in several other biological processes, such as virulence3 or biofilm formation4 and that QS can be used by cells to regulate their motility.5In recent years, scientists have been questioning how to mimic biology by designing synthetic active particles able to display collective behaviors similar to QS. These artificial self-propelled particles are typically phoretic colloids exploiting self-generated chemical6 or temperature gradients7 to achieve autonomous locomotion. Advances in the control of these active particles have allowed to create nano- and micro-robots capable of accomplishing some particular tasks8 and also to realize active systems with controllable interactions. This is the case of light-activated Janus particles whose speed is controlled by the intensity of the impinging radiation. In these systems QS-type interaction is achieved thanks to a real-time particle-detection algorithm which calculates the density field from particles position and adjusts their speed accordingly via light-modulation.9 A similar technique has been employed to implement active particles capable of adjusting their velocities depending on the direction of their peers.10 In both cases it has been observed that particles may act collectively by forming dense clusters.
These aggregation phenomena can be generally rationalised within the so-called motility induced phase separation (MIPS) scenario that has attracted a deep interest in the active matter community.11 MIPS broadly indicates phase separation occurring in active particles which slow down when the local density is high. These active particles thus further accumulate in slow regions causing a positive feedback loop triggering condensation. It has been also shown that such a condensation process, at the mean-field level, is completely analogous to the standard gas–liquid phase separation. Moreover, the MIPS framework has been used to explain the condensation observed in active particles interacting via purely repulsive interaction potentials. In such systems inter-particle collisions are responsible for the dynamic slow-down and, in the modelling, it is assumed that the net effect of pairwise interactions can be mapped into a density-dependent particle speed that decreases when local density increases, as in QS models. More recently, also a formalism including both QS and pairwise interactions, has been proposed12 to describe MIPS.
Besides the interest in studying fully phase-separated active particles, the attention of the community has been recently turned to the study of active systems close to the ending point of the MIPS curve i.e., in the vicinity of the “motility-induced critical point”. However these studies have reached different conclusions about the universality class of these systems. For instance, it has been shown that Active Ornstein–Uhlenbeck particles (AOUPs) in two dimensions, interacting with pairwise repulsion, have static and dynamic critical exponents that agree with those of the Ising universality class.13,14 Differently, results for active Brownian particles (ABPs) are controversial: some in-lattice simulations point towards Ising15 while other in- and off-lattice simulations provide critical exponents deviating considerably from the Ising ones and suggest that some active systems may belong to a different universality class.16,17 It is important to mention that the evaluation of critical exponents in these off-equilibrium systems is highly challenging, since one cannot use the same tools routinely employed in the study of critical equilibrium systems such as grand-canonical simulations. Moreover it has been pointed out that these systems develop additional (non-universal) correlations13 associated with the formation of hexatic microdomains18 and of clusters of particles with aligned velocities.19 Since these correlations play a role at intermediate time and length scales, one should use large system sizes for observing the scaling regime in critical active systems.
All these results have been obtained for model systems with pairwise repulsive interactions, while no study has focused so far on critical QS active particles. In this work we fill this gap by investigating the critical behavior of a minimal model of AOUPs with short-ranged QS interactions in two dimensions (d = 2). AOUPs possibly represent the simplest model for active particles since, as detailed below, the active propulsion force is produced by a linear stochastic process whose analytical properties have allowed to derive numerous theoretical results.20–23 Moreover it has been recently shown that QS AOUPs undergo MIPS if the model's control parameters are varied appropriately.24 We first study the model at the mean field-level showing that the system phase separates when the parameter controlling the particles’ slowing down is varied. Moreover, we show that the spinodal line terminates in a critical point. By performing computer simulations in d = 2 we find that the mean-field theory is in qualitative agreement with the numerical results. By performing a detailed finite-size-scaling analysis we locate the critical point and estimate, independently from each other, the static critical exponents ν, γ, β and η finding that these substantially agree with the Ising exponents. Lastly, we characterize the critical dynamics by studying the density fluctuations at large scales and their relaxation frequencies. We find that also the dynamic exponent z is compatible with the Ising value.
Theory
Here we show that our minimal model of QS AOUPs has a mean-field phase diagram characterized by a spinodal line ending in a critical point. As we will see in the following, the control parameter that can be varied to induce the transition is the speed variation that a particle undergoes when it “senses” a local density change.We start by considering one single AOUP having position x and subject to a space-dependent scalar speed-field  (here x = (x1,…, xd) in a d-dimensional space). The equations of motion of such an AOUP are given by:
(here x = (x1,…, xd) in a d-dimensional space). The equations of motion of such an AOUP are given by:
 | (1) |
τ![[capital Psi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e13b.gif) = −ψ + η = −ψ + η | (2) |
 | (3) |
 . Eqn (3) has been recently derived, specifically for AOUPs, in ref. 28 by using the so called “velocity representation” and solving the Fokker–Planck equation stemming from eqn (1) and (2).
. Eqn (3) has been recently derived, specifically for AOUPs, in ref. 28 by using the so called “velocity representation” and solving the Fokker–Planck equation stemming from eqn (1) and (2).
We now assume that the speed of the probe particle in x is determined by the positions xj of the other N particles in the system, i.e. we set  in eqn (3). Note that, in this approximation, the degrees of freedom xj are considered as if they were frozen parameters. We further assume that the individual xj contribute additively to the speed in xvia some function g:
in eqn (3). Note that, in this approximation, the degrees of freedom xj are considered as if they were frozen parameters. We further assume that the individual xj contribute additively to the speed in xvia some function g:
 | (4) |
The function g is chosen to depend only on the distance between the particle in x and its neighbor in xj, i.e. g(x,xj) = g(|x − xj|). If, for example, d = 2 and
| g(|x − xj|) = Θ(R − |x − xj|)/(πR2) | (5) |
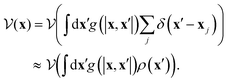 | (6) |
Note that, to obtain eqn (6), we have used the mean-field approximation by which the instantaneous density field  is replaced by the trajectory-averaged density field, i.e.
is replaced by the trajectory-averaged density field, i.e. . Moreover, the gradient expansion of (6) is29
. Moreover, the gradient expansion of (6) is29
 | (7) |
 and
and  are constants independent on x. From now on we assume for simplicity that g0 = 1 (as in the example (5)). Since, for identical particles Np(x) = N〈δ(x − xj)〉 = ρ(x), by taking the log of eqn (3), we obtain the self-consistency equation:
are constants independent on x. From now on we assume for simplicity that g0 = 1 (as in the example (5)). Since, for identical particles Np(x) = N〈δ(x − xj)〉 = ρ(x), by taking the log of eqn (3), we obtain the self-consistency equation: | (8) |
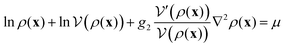 | (9) |
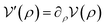 .
.
Assuming a homogeneous density field ρ(x) = ρeqn (9) reduces to the fundamental equation describing MIPS at the mean-field level30,31
 | (10) |
Note that eqn (10) could have also been directly derived by assuming a homogeneous density in (3). Eqn (9) consistently shows that density gradients can also be neglected after the expansion.
For the choice of  we now require that (i)eqn (10) admits a positive solution (ρ > 0) for any number of particles 0 < N < ∞ (i.e. for −∞ < μ < ∞) and that (ii)eqn (10) admits more than one positive solution, at least in some parameters range. A possible choice for
we now require that (i)eqn (10) admits a positive solution (ρ > 0) for any number of particles 0 < N < ∞ (i.e. for −∞ < μ < ∞) and that (ii)eqn (10) admits more than one positive solution, at least in some parameters range. A possible choice for  , which satisfies (i) and (ii), is:
, which satisfies (i) and (ii), is:
 | (11) |
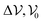 and ρ0 are positive parameters which control the response of the particle's speed to the density. According to (11) when a particle “perceives” a density much lower than the threshold density ρ0 it moves fast (close to maximum speed
and ρ0 are positive parameters which control the response of the particle's speed to the density. According to (11) when a particle “perceives” a density much lower than the threshold density ρ0 it moves fast (close to maximum speed  ), while it moves almost at minimum speed (
), while it moves almost at minimum speed ( ) when ρ ≫ ρ0. Property (i) is clearly satisfied by (11) since ln
) when ρ ≫ ρ0. Property (i) is clearly satisfied by (11) since ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ ranges from −∞ to ∞ (as ρ varies between 0 and ∞) while
ρ ranges from −∞ to ∞ (as ρ varies between 0 and ∞) while 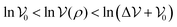 stays finite. Property (ii) is fulfilled if ∂ρμ < 0, i.e. if
stays finite. Property (ii) is fulfilled if ∂ρμ < 0, i.e. if  (which is the condition for MIPS30). Assuming that
(which is the condition for MIPS30). Assuming that 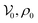 are fixed in (11), while
are fixed in (11), while  is the control parameter, the system undergoes spinodal decomposition when
is the control parameter, the system undergoes spinodal decomposition when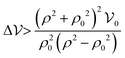 | (12) |
Moreover, by solving
 | (13) |
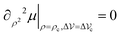 | (14) |
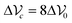 as sketched in Fig. 1(a).
as sketched in Fig. 1(a).
Interestingly the theory suggests that when particles react moving faster in low-density regions (i.e. when  is increased above
is increased above 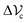 ) the system may phase separate, while particles always maintain a non-zero minimum speed
) the system may phase separate, while particles always maintain a non-zero minimum speed 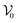 also in the dense phase. Moreover an expansion of eqn (10) around the critical point shows that the latter belongs to the (mean-field) Ising universality class in full analogy with the condensation of van der Waals fluids.29 In the following sections we will compare this scenario with the results of direct particle simulations in d = 2.
also in the dense phase. Moreover an expansion of eqn (10) around the critical point shows that the latter belongs to the (mean-field) Ising universality class in full analogy with the condensation of van der Waals fluids.29 In the following sections we will compare this scenario with the results of direct particle simulations in d = 2.
Numerical model and methods
Our microscopic model for QS is implemented by integrating eqn (1) and (2) for N identical point-like AOUPs (i.e., without excluded volume interactions). The speed of the i-th particle is computed as (see eqn (11)):
of the i-th particle is computed as (see eqn (11)):where the function g(x) is defined in eqn (5) and measures the local density within the cut-off distance R (which sets the range of the interaction). We fix all parameters of the active force to unity D = τ = 1, and the parameters of the QS interactions to ρ0 = 1,
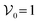 and R = 1.3. The parameter
and R = 1.3. The parameter 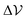 , determining the speed change, will be varied to induce the phase separation and hence, together with density, it represents a control parameter of the system. Particles move in a rectangular box with periodic boundary conditions and with sides Lx = 3 × Ly. To apply the finite-size scaling analysis for the study of the critical point, we simulate different system sizes with N = (3.5, 7.5, 15, 30) × 103. The equations of motion have been integrated numerically using the Euler scheme with a time step Δt = 10−3 up to Nt = 3 × 108 time steps for the largest system size. To reach the stationary state a preliminary run has been performed for a comparable amount of steps, starting from a configuration in which particles are randomly distributed. As in ref. 13 we have checked that the auto-correlation function of density fluctuations relaxes for all system sizes within the simulation time window. Moreover, for each state point investigated, the whole procedure has been repeated five times starting from independent configurations.
, determining the speed change, will be varied to induce the phase separation and hence, together with density, it represents a control parameter of the system. Particles move in a rectangular box with periodic boundary conditions and with sides Lx = 3 × Ly. To apply the finite-size scaling analysis for the study of the critical point, we simulate different system sizes with N = (3.5, 7.5, 15, 30) × 103. The equations of motion have been integrated numerically using the Euler scheme with a time step Δt = 10−3 up to Nt = 3 × 108 time steps for the largest system size. To reach the stationary state a preliminary run has been performed for a comparable amount of steps, starting from a configuration in which particles are randomly distributed. As in ref. 13 we have checked that the auto-correlation function of density fluctuations relaxes for all system sizes within the simulation time window. Moreover, for each state point investigated, the whole procedure has been repeated five times starting from independent configurations.
To characterize the critical behavior of our model, we will rely on the finite-size scaling ansatz according to which any observable  can be rewritten in terms of a dimensionless scaling function
can be rewritten in terms of a dimensionless scaling function  :
:
 | (15) |
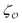 is the critical exponent associated with the observable
is the critical exponent associated with the observable  and ν is the exponent characterizing the divergence of the correlation length ξ, as the control parameter gets close to its critical value. As suggested by the mean-field theory described above, the speed change parameter
and ν is the exponent characterizing the divergence of the correlation length ξ, as the control parameter gets close to its critical value. As suggested by the mean-field theory described above, the speed change parameter  can be used as a control parameter to tune the system at criticality and thus we assume
can be used as a control parameter to tune the system at criticality and thus we assume 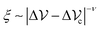 . Note that the scaling ansatz (15) implies that, when the quantity
. Note that the scaling ansatz (15) implies that, when the quantity  is plotted as a function of
is plotted as a function of  , for different system sizes, all data should collapse onto the scaling function.
, for different system sizes, all data should collapse onto the scaling function.
We are interested in measuring observables  related to density fluctuations both for locating the critical point and estimating the critical exponents. These fluctuations are calculated using an improved version of the “block-density-distribution method” initially proposed by Binder and coworkers.32–35 The technique represents an alternative to grand-canonical simulations (where the particle density fluctuates) to characterize density fluctuations in the canonical ensemble (where the overall density is fixed). The main idea is to divide the simulation box into small sub-boxes of linear size L that exhibit, to a good approximation, the same density fluctuations of the grand-canonical ensemble. In each sub-box one measures the particles number density ρ = Nb/L2, where Nb is the number of particles found in a sub-box, and compute the density variance 〈Δρ2〉 = 〈(Nb/L2) − (〈Nb/L2〉)2〉 and its fourth moment 〈Δρ4〉 = 〈(Nb/L2) − (〈Nb/L2〉)4〉. From these quantities one then computes the “Binder cumulant”
related to density fluctuations both for locating the critical point and estimating the critical exponents. These fluctuations are calculated using an improved version of the “block-density-distribution method” initially proposed by Binder and coworkers.32–35 The technique represents an alternative to grand-canonical simulations (where the particle density fluctuates) to characterize density fluctuations in the canonical ensemble (where the overall density is fixed). The main idea is to divide the simulation box into small sub-boxes of linear size L that exhibit, to a good approximation, the same density fluctuations of the grand-canonical ensemble. In each sub-box one measures the particles number density ρ = Nb/L2, where Nb is the number of particles found in a sub-box, and compute the density variance 〈Δρ2〉 = 〈(Nb/L2) − (〈Nb/L2〉)2〉 and its fourth moment 〈Δρ4〉 = 〈(Nb/L2) − (〈Nb/L2〉)4〉. From these quantities one then computes the “Binder cumulant”  for which one expects that the ansatz (15) reduces to the simple form
for which one expects that the ansatz (15) reduces to the simple form  and thus, at the critical point,
and thus, at the critical point,  is size independent since
is size independent since  This suggests that one could locate the critical point by finding the value of the control parameter at which the
This suggests that one could locate the critical point by finding the value of the control parameter at which the  curves, for different sizes, cross. Unfortunately it has been shown that this procedure fails (the
curves, for different sizes, cross. Unfortunately it has been shown that this procedure fails (the  -curves do not cross) even for the equilibrium two-dimensional lattice gas in the canonical ensemble (which is equivalent to the Ising model with conserved magnetization).16,35 The failure of this scheme can be attributed to the fact that the grand-canonical fluctuations cannot be well reproduced in the sub-boxes due to the large contribution coming from the interface between the two phases.
-curves do not cross) even for the equilibrium two-dimensional lattice gas in the canonical ensemble (which is equivalent to the Ising model with conserved magnetization).16,35 The failure of this scheme can be attributed to the fact that the grand-canonical fluctuations cannot be well reproduced in the sub-boxes due to the large contribution coming from the interface between the two phases.
To overcome this problem, a modified version of the method has been proposed in ref. 16 and successfully applied both to critical equilibrium systems and active systems.13,15–17 The basic idea of the modified method is that the system centre of mass can be used to locate the dense phase excluding the interfaces from the analysis. More specifically, for each particle configuration the x-coordinate of the systems’ centre of mass is always shifted to x = 3Lx/4 and density fluctuations are then evaluated far from the interface, by selecting only four squared sub-boxes of size L = Ly/2: two sub-boxes centred around x= 3Lx/4 (dense phase) and the other two in x = Lx/4 (dilute phase). The same procedure is then repeated for different system sizes to find the crossing of the cumulants  and thus locate the critical point. It has been shown that this technique yields the correct critical point in d = 2 in the case of equilibrium square-lattice gas16 and the triangular-lattice gas.13
and thus locate the critical point. It has been shown that this technique yields the correct critical point in d = 2 in the case of equilibrium square-lattice gas16 and the triangular-lattice gas.13
Note that by combining the sub-box method with the finite-size scaling formula (15) we can also obtain the values of the critical exponents. To this aim we employ the data-collapse optimization technique that has been previously exploited to extract critical exponents in various spin models.36,37 To use this approach one first measures the variable  at different values of the control parameter and of the system size. All collected measurements form a set of M data-points, where
at different values of the control parameter and of the system size. All collected measurements form a set of M data-points, where  represent the i-th data point. If (15) holds, and the correct values of
represent the i-th data point. If (15) holds, and the correct values of  ,
,  and ν are known, the following quantity should be zero
and ν are known, the following quantity should be zero
 | (16) |
 . Note that the “error function” (16) is positive (i.e.
. Note that the “error function” (16) is positive (i.e. , since it is a sum of squares) and attains its minimum
, since it is a sum of squares) and attains its minimum  in the ideal case in which the critical parameters
in the ideal case in which the critical parameters  ,
,  and ν have their exact values. This implies that if we knew
and ν have their exact values. This implies that if we knew  we could also minimize (16), with respect to
we could also minimize (16), with respect to 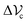 ,
,  and ν to find their correct values, which is the basic principle that we will use in the data-analysis presented below. Although we generally do not know
and ν to find their correct values, which is the basic principle that we will use in the data-analysis presented below. Although we generally do not know  , we can still approximate it from the
, we can still approximate it from the  data. To this aim we divide the
data. To this aim we divide the 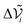 values in a set of W windows (with M > W) and average the values of the data-points
values in a set of W windows (with M > W) and average the values of the data-points  lying within the same window. The value of
lying within the same window. The value of  appearing in (16) can then be calculated by a linear interpolation of the window-averaged
appearing in (16) can then be calculated by a linear interpolation of the window-averaged  . With this technique the function
. With this technique the function  can be then minimized to obtain the parameters
can be then minimized to obtain the parameters  , ν and
, ν and  .
.
Results
Before focusing on the critical behavior we start by discussing how simulations results compare with the mean-field picture explained above. We first numerically locate the boundaries of the MIPS-region, by performing a numerical scan in ρ and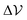 for the smallest system size (N = 3500) distinguishing those state points in which phase-separation occurs from those in which the system is homogeneous. This has been done by checking whether the density distribution (computed over all sub-boxes) has two detectable peaks. The resulting coarse phase-diagram is reported in Fig. 1(b). Already from this data we can approximately locate the critical point to be at
for the smallest system size (N = 3500) distinguishing those state points in which phase-separation occurs from those in which the system is homogeneous. This has been done by checking whether the density distribution (computed over all sub-boxes) has two detectable peaks. The resulting coarse phase-diagram is reported in Fig. 1(b). Already from this data we can approximately locate the critical point to be at  and ρc ≈ 3. Visual inspection of configurations immediately confirms that, upon increasing
and ρc ≈ 3. Visual inspection of configurations immediately confirms that, upon increasing  , QS active particles undergo a transition from a homogeneous state (Fig. 1(e)) to phase separation (Fig. 1(c)), with large fluctuations at intermediate
, QS active particles undergo a transition from a homogeneous state (Fig. 1(e)) to phase separation (Fig. 1(c)), with large fluctuations at intermediate  -values (Fig. 1(d)). The overall picture confirms that the microscopic model follows qualitatively the mean-field scenario discussed above, albeit with significant quantitative differences. In particular, we observe that the MIPS of the numerical model occurs at significantly higher
-values (Fig. 1(d)). The overall picture confirms that the microscopic model follows qualitatively the mean-field scenario discussed above, albeit with significant quantitative differences. In particular, we observe that the MIPS of the numerical model occurs at significantly higher  and ρ-values. However, the shape of the numerical coexistence curve is reminiscent of the theoretical spinodal line which is slightly asymmetric with the dense-fluid branch less steep than the gaseous one. To precisely locate the critical point we proceed as in ref. 13 calculating the Binder parameter
and ρ-values. However, the shape of the numerical coexistence curve is reminiscent of the theoretical spinodal line which is slightly asymmetric with the dense-fluid branch less steep than the gaseous one. To precisely locate the critical point we proceed as in ref. 13 calculating the Binder parameter  , introduced in the previous Section, as a function of ρ and at fixed
, introduced in the previous Section, as a function of ρ and at fixed  , i.e. near the critical
, i.e. near the critical  . According to ref. 34,
. According to ref. 34, 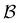 should exhibit a maximum at ρ = ρc when plotted as a function of the density at fixed
should exhibit a maximum at ρ = ρc when plotted as a function of the density at fixed 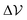 . We perform this analysis for the smallest system size and, fitting the data with a parabola, we get the critical density ρc = 2.821(0.041) as shown in the inset of Fig. 2(a) (we report the fit error in the brackets). Since we are interested in the critical behavior of the system, from now on we will fix ρ = ρc for our analysis. To determine accurately the value of
. We perform this analysis for the smallest system size and, fitting the data with a parabola, we get the critical density ρc = 2.821(0.041) as shown in the inset of Fig. 2(a) (we report the fit error in the brackets). Since we are interested in the critical behavior of the system, from now on we will fix ρ = ρc for our analysis. To determine accurately the value of  and of the exponent ν we first compute
and of the exponent ν we first compute  at different values of
at different values of  and L (simulation data are shown in Fig. 2(a)) and we minimize (16) with respect to ν and
and L (simulation data are shown in Fig. 2(a)) and we minimize (16) with respect to ν and  (which are considered as free fitting parameters). The optimization yields
(which are considered as free fitting parameters). The optimization yields  and ν = 1.040(0.045). We note that the exponents ν is close to the Ising value and that, when we use these parameters to scale data, we obtain a good collapse as shown in Fig. 2(b). Note also that, the obtained
and ν = 1.040(0.045). We note that the exponents ν is close to the Ising value and that, when we use these parameters to scale data, we obtain a good collapse as shown in Fig. 2(b). Note also that, the obtained  corresponds, to a good approximation, with the value at which the Binder cumulants cross, as shown by the vertical line in Fig. 2(a). The common crossing point of the Binder parameters at different L-values confirms that scale-invariance holds and thus that a critical point exists.32
corresponds, to a good approximation, with the value at which the Binder cumulants cross, as shown by the vertical line in Fig. 2(a). The common crossing point of the Binder parameters at different L-values confirms that scale-invariance holds and thus that a critical point exists.32
We now proceed to determine independently the exponents γ and β. To this aim, we fix the values of ν and  to those found previously, letting
to those found previously, letting 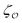 as a free parameter in the optimization. To estimate γ we consider the susceptibility χ = 〈(Nb − 〈Nb〉)2〉/〈Nb〉 at different
as a free parameter in the optimization. To estimate γ we consider the susceptibility χ = 〈(Nb − 〈Nb〉)2〉/〈Nb〉 at different  and L-values, as shown in Fig. 2(c). We then minimize (16) with respect to
and L-values, as shown in Fig. 2(c). We then minimize (16) with respect to  finding that γ = 1.763(0.070) (the error on ν is propagated), which is compatible with the Ising value. Data are well collapsed using this exponent as shown in Fig. 2(d). For estimating β we consider the order parameter m = ρdens − ρdil, defined as the difference between the densities of the dense (ρdens) and dilute (ρdil) phases.16 The values of m, collected at several
finding that γ = 1.763(0.070) (the error on ν is propagated), which is compatible with the Ising value. Data are well collapsed using this exponent as shown in Fig. 2(d). For estimating β we consider the order parameter m = ρdens − ρdil, defined as the difference between the densities of the dense (ρdens) and dilute (ρdil) phases.16 The values of m, collected at several  and L, are shown in Fig. 2(e). The minimization of the error-function (16) with
and L, are shown in Fig. 2(e). The minimization of the error-function (16) with  gives β = 0.116(0.013) (which is close to the Ising β = 0.125) and a scaling of data with this β provides a good collapse as shown Fig. 2(f). To conclude the analysis of the static critical exponents we now estimate the exponent η which controls the behavior of the critical static structure factor S(q) at low wave-vectors q. We consider
gives β = 0.116(0.013) (which is close to the Ising β = 0.125) and a scaling of data with this β provides a good collapse as shown Fig. 2(f). To conclude the analysis of the static critical exponents we now estimate the exponent η which controls the behavior of the critical static structure factor S(q) at low wave-vectors q. We consider  , where ρq is the real part of the Fourier transform of the density field at time t:
, where ρq is the real part of the Fourier transform of the density field at time t: 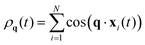 , where q = 2π(nx/Lx,ny/Ly) represents the wave-vector (nx,y ∈
, where q = 2π(nx/Lx,ny/Ly) represents the wave-vector (nx,y ∈ ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) ). Here we assume that rotational and time-translational invariance hold so that S(q) is averaged over all q with the same modulus q = |q| and over all times t. Moreover, the prefactor
). Here we assume that rotational and time-translational invariance hold so that S(q) is averaged over all q with the same modulus q = |q| and over all times t. Moreover, the prefactor 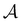 is chosen such that S(q → ∞) = 1. The S(q), calculated for the largest system size, is shown in Fig. 3 for two different
is chosen such that S(q → ∞) = 1. The S(q), calculated for the largest system size, is shown in Fig. 3 for two different  -values across the transition. While far from the critical point the S(q) flattens at low q, close to
-values across the transition. While far from the critical point the S(q) flattens at low q, close to  the structure factor exhibits a power-law behavior. By fitting the low-q data with S(q) ∼ q−2 +η we obtain 2 − η = 1.765(0.012), which is close to the Ising value (2 − η = 1.75). Note that the slope of the fit is appreciably different from the typical mean-field decay S(q) ∼ q−2 which is also reported Fig. 2.
the structure factor exhibits a power-law behavior. By fitting the low-q data with S(q) ∼ q−2 +η we obtain 2 − η = 1.765(0.012), which is close to the Ising value (2 − η = 1.75). Note that the slope of the fit is appreciably different from the typical mean-field decay S(q) ∼ q−2 which is also reported Fig. 2.
Finally, we focus on the critical dynamics of the QS system. As in ref. 14, we compute the time auto-correlation function C(q,t) = 2N−1〈ρ−q(t + s)ρq(s)〉 to characterize the dynamics of spontaneous fluctuations at different time- and length-scales. The C(q,t) is computed for various q-s and at the near-critical value  . From correlations we compute the spectra
. From correlations we compute the spectra  . The functions ωC(q,ω) are shown in Fig. 4(a). We observe that ωC(q,ω) grows in amplitude upon lowering q and its peak shifts towards lower frequencies revealing the characteristic slowing-down of the system's dynamics at large length-scales. As discussed in ref. 14 the value of ω at which ωC(q,ω) reaches its maximum (denoted as ωmax) can be associated with the system's relaxation frequency at that q. Moreover in ref. 14 it was shown that AOUPs may exhibit deviations from the scaling regime at frequencies as high as the relaxation rate of the active force τ−1 (appearing in the equations of motions (1) and (2)). For this reason, we restrict our analysis to q-values that are low enough so that ωmax ≪ 2π/τ.
. The functions ωC(q,ω) are shown in Fig. 4(a). We observe that ωC(q,ω) grows in amplitude upon lowering q and its peak shifts towards lower frequencies revealing the characteristic slowing-down of the system's dynamics at large length-scales. As discussed in ref. 14 the value of ω at which ωC(q,ω) reaches its maximum (denoted as ωmax) can be associated with the system's relaxation frequency at that q. Moreover in ref. 14 it was shown that AOUPs may exhibit deviations from the scaling regime at frequencies as high as the relaxation rate of the active force τ−1 (appearing in the equations of motions (1) and (2)). For this reason, we restrict our analysis to q-values that are low enough so that ωmax ≪ 2π/τ.
Within this q-range we first characterize the shape of ωC(q,ω). This is an interesting feature to consider since it is know38 that, at the critical point, the relaxation spectrum C(q,ω) could be rewritten in terms of a universal scaling function 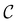 as follows:
as follows:
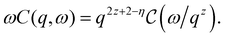 | (17) |
 . In Fig. 4(b) we check this by plotting data of Fig. 4(a) rescaled by their maxima, finding a good superposition. Moreover, since
. In Fig. 4(b) we check this by plotting data of Fig. 4(a) rescaled by their maxima, finding a good superposition. Moreover, since  should be a universal scaling function we plot on top of our data the scaled ωC(q,ω) of the critical two-dimensional lattice gas in equilibrium (see ref. 14 and 39 for details). We find that the data of the QS active system follow quite well the correlator of the lattice gas simulations (especially at large ω/ωmax). Data are also compared with the result of the dynamical Gaussian field-theory38 which yields ωC(q,ω) ∼ ω/(ω2 + ωmax2). Fig. 4(b) shows that this formula (which should be valid only for d > 4) sensibly deviates from the data-points. As mentioned above we expect that the peak position follows ωmax ∼ qz and this allows us to estimate the dynamic critical exponent z. In Fig. 4(c) we show ωmax as a function of q and the direct fit with a power-law giving z = 3.640(0.073) which is also compatible with z = 3.75 of the Ising model, with conserved magnetization and in d = 2. All exponents estimated in the present work are summarized in Table 1.
should be a universal scaling function we plot on top of our data the scaled ωC(q,ω) of the critical two-dimensional lattice gas in equilibrium (see ref. 14 and 39 for details). We find that the data of the QS active system follow quite well the correlator of the lattice gas simulations (especially at large ω/ωmax). Data are also compared with the result of the dynamical Gaussian field-theory38 which yields ωC(q,ω) ∼ ω/(ω2 + ωmax2). Fig. 4(b) shows that this formula (which should be valid only for d > 4) sensibly deviates from the data-points. As mentioned above we expect that the peak position follows ωmax ∼ qz and this allows us to estimate the dynamic critical exponent z. In Fig. 4(c) we show ωmax as a function of q and the direct fit with a power-law giving z = 3.640(0.073) which is also compatible with z = 3.75 of the Ising model, with conserved magnetization and in d = 2. All exponents estimated in the present work are summarized in Table 1.
| Exponent | Ising value | Fitted value | Fit error |
|---|---|---|---|
| ν | 1 | 1.040 | 0.045 |
| γ | 1.75 | 1.763 | 0.070 |
| β | 0.125 | 0.116 | 0.013 |
| η | 0.25 | 0.235 | 0.011 |
| z | 3.75 | 3.640 | 0.073 |
Conclusions
In this work we have investigated the critical behavior of an active system interacting via QS. In the model each particle senses the number of neighbors, within a given cut-off distance, and then varies its speed according to a specific rule. Mean-field theory suggests that this model has a spinodal line ending in a critical point. To check the validity of the theoretical picture we have performed large-scale numerical simulations on GPU, finding that the system does phase-separate and that the coexistence region terminates in a motility induced critical point. To address the problem of the universality class, we have used finite-size scaling analysis to measure static and dynamic critical exponents. We have found that these exponents are in substantial agreement with those of the two-dimensional Ising model with conserved magnetization.We stress that, the QS system studied here interacts differently from the repulsive AOUPs of ref. 13. QS particles slow-down whenever they get close (independently of their orientation), which is different from repulsive active particles which slow-down (or even stop) only when pointing towards each other. Despite these differences the results for the critical fluctuations are nearly identical in these systems (which is the landmark of universality). We recall also that finite-size-scaling analysis has been applied to off-lattice16 and in-lattice simulations15 of repulsive ABPs with some controversial results. In particular the off-lattice simulations seem to lead to non-Ising exponents16 while on-lattice simulations seems to point towards the Ising universality class.15 Such an intense research motivates our present work on QS active particles for which a systematic study of the critical point has not been performed so far.40 Our results on critical QS particles are also consistent with recent field theoretical developments.41–43 Indeed, according to the derivation in ref. 42, only the presence of repulsive interactions, together with a density-dependent speed, could generate field-theoretical terms that may destabilize the critical point.
Our study also opens different possibilities for future investigations on critical active systems. It would be useful to understand if and how the QS interaction rules could be changed to possibly induce micro-phase separation. Moreover, it would be helpful to understand if and how the fluctuation dissipation theorem could be violated by critical QS particles. In particular, it could be to understand whether the breakdown of the theorem differs from the one observed for purely repulsive AOUPs.14 Finally, from a more general perspective, it would be interesting to compare the critical behavior of our QS system with the one of model systems interacting via chemotaxis,44 in the presence of aligning45,46 and/or steric interactions,47 and in mixtures of active and passive particles.48,49
Conflicts of interest
There are no conflicts of interest to declare.References
- M. B. Miller and B. L. Bassler, Annu. Rev. Microbiol., 2001, 55, 165–199 CrossRef CAS PubMed.
- K. H. Nealson, T. Platt and J. W. Hastings, J. Bacteriol., 1970, 104, 313–322 CrossRef CAS PubMed.
- J. Zhu, M. Miller, R. Vance, M. Dziejman, B. L. Bassler and J. J. Mekalanos, Proc. Natl. Acad. Sci. U. S. A., 2002, 99(5), 3129–3134 CrossRef CAS PubMed.
- B. Hammer and B. Bassler, Mol. Microbiol., 2003, 50(1), 101–104 CrossRef CAS.
- R. Daniels, J. Vanderleyden and J. Michiels, FEMS Microbiol. Rev., 2004, 28, 261–289 CrossRef CAS PubMed.
- J. R. Gomez-Solano, S. Samin, C. Lozano, P. Ruedas-Batuecas, R. van Roij and C. Bechinger, Sci. Rep., 2017, 7, 14891 CrossRef PubMed.
- H.-R. Jiang, N. Yoshinaga and M. Sano, Phys. Rev. Lett., 2010, 105, 268302 CrossRef.
- C. Maggi, J. Simmchen, F. Saglimbeni, J. Katuri, M. Dipalo, F. De Angelis, S. Sanchez and R. Di Leonardo, Small, 2016, 12, 446–451 CrossRef CAS PubMed.
- T. Bäuerle, A. Fischer, T. Speck and C. Bechinger, Nat. Commun., 2018, 9, 1–8 CrossRef.
- F. Lavergne, H. Wendehenne and B. C. Bäuerle, Science, 2019, 364(6435), 70–74 CrossRef CAS PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- A. P. Solon, J. Stenhammar, M. E. Cates, Y. Kafri and J. Tailleur, Phys. Rev. E, 2018, 97, 020602 CrossRef CAS PubMed.
- C. Maggi, M. Paoluzzi, A. Crisanti, E. Zaccarelli and N. Gnan, Soft Matter, 2021, 17, 3807–3812 RSC.
- C. Maggi, N. Gnan, M. Paoluzzi, E. Zaccarelli and A. Crisanti, Commun. Phys., 2022, 5, 55 CrossRef.
- B. Partridge and C. F. Lee, Phys. Rev. Lett., 2019, 123, 068002 CrossRef CAS.
- J. T. Siebert, F. Dittrich, F. Schmid, K. Binder, T. Speck and P. Virnau, Phys. Rev. E, 2018, 98, 030601 CrossRef CAS.
- F. Dittrich, T. Speck and P. Virnau, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 1–10 CrossRef PubMed.
- C. B. Caporusso, P. Digregorio, D. Levis, L. F. Cugliandolo and G. Gonnella, Phys. Rev. Lett., 2020, 125, 178004 CrossRef CAS PubMed.
- L. Caprini, U. M. B. Marconi, C. Maggi, M. Paoluzzi and A. Puglisi, Phys. Rev. Res., 2020, 2, 023321 CrossRef CAS.
- U. M. B. Marconi, M. Paoluzzi and C. Maggi, Mol. Phys., 2016, 114, 2400–2410 CrossRef CAS.
- E. Fodor, C. Nardini, M. E. Cates, J. Tailleur, P. Visco and F. van Wijland, Phys. Rev. Lett., 2016, 117, 038103 CrossRef PubMed.
- U. Marini Bettolo Marconi, C. Maggi and M. Paoluzzi, J. Chem. Phys., 2017, 147, 024903 CrossRef PubMed.
- S. Dal Cengio, D. Levis and I. Pagonabarraga, Phys. Rev. Lett., 2019, 123, 238003 CrossRef CAS PubMed.
- D. Martin, J. O’Byrne, M. E. Cates, É. Fodor, C. Nardini, J. Tailleur and F. van Wijland, Phys. Rev. E, 2021, 103, 032607 CrossRef CAS.
- H. Risken, The Fokker-Planck Equation, Springer, 1996, pp. 63–95 Search PubMed.
- C. W. Gardiner, et al., Handbook of stochastic methods, Springer, Berlin, 1985, vol. 3 Search PubMed.
- P. Hänggi and P. Jung, Adv. Chem. Phys., 1995, 89, 239–326 Search PubMed.
- L. Caprini, U. M. B. Marconi, R. Wittmann and H. Löwen, Soft Matter, 2022, 18, 1412–1422 RSC.
- N. G. van Kampen, Phys. Rev., 1964, 135, A362–A369 CrossRef.
- J. Tailleur and M. E. Cates, Phys. Rev. Lett., 2008, 100, 218103 CrossRef CAS PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- K. Binder, Z. Phys. B: Condens. Matter, 1981, 43, 119–140 CrossRef.
- M. Rovere, D. Hermann and K. Binder, EPL, 1988, 6, 585 CrossRef.
- M. Rovere, D. W. Heermann and K. Binder, J. Condens. Matter Phys., 1990, 2, 7009 CrossRef.
- M. Rovere, P. Nielaba and K. Binder, Z. Phys. B: Condens. Matter, 1993, 90, 215–228 CrossRef.
- S. M. Bhattacharjee and F. Seno, J. Phys. A: Math. Gen., 2001, 34, 6375 CrossRef CAS.
- J. Houdayer and A. K. Hartmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 014418 CrossRef.
- U. C. Täuber, Critical dynamics: a field theory approach to equilibrium and non-equilibrium scaling behavior, Cambridge University Press, 2014 Search PubMed.
- L. Caprini, F. Cecconi, C. Maggi and U. M. B. Marconi, Phys. Rev. Res., 2020, 2, 043359 CrossRef CAS.
- J. Stenhammar, arXiv, 2021, preprint, arXiv:2112.05024.
- F. Caballero, C. Nardini and M. E. Cates, J. Stat. Mech.: Theory Exp., 2018, 2018, 123208 CrossRef.
- C. Nardini, É. Fodor, E. Tjhung, F. Van Wijland, J. Tailleur and M. E. Cates, Phys. Rev. X, 2017, 7, 021007 Search PubMed.
- T. Speck, Phys. Rev. E, 2022, 105, 064601 CrossRef CAS.
- E. J. Marsden, C. Valeriani, I. Sullivan, M. Cates and D. Marenduzzo, Soft Matter, 2014, 10, 157–165 RSC.
- F. Farrell, M. Marchetti, D. Marenduzzo and J. Tailleur, Phys. Rev. Lett., 2012, 108, 248101 CrossRef CAS PubMed.
- M. Paoluzzi, D. Levis and I. Pagonabarraga, arXiv preprint arXiv:2205.15643, 2022.
- M. Paoluzzi, M. Leoni and M. C. Marchetti, Soft Matter, 2020, 16, 6317–6327 RSC.
- J. Stenhammar, R. Wittkowski, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2015, 114, 018301 CrossRef CAS PubMed.
- D. R. Rodriguez, F. Alarcon, R. Martinez, J. Ramírez and C. Valeriani, Soft Matter, 2020, 16, 1162–1169 RSC.
| This journal is © The Royal Society of Chemistry 2022 |