Open Access Article
Open Access ArticleDense packings of geodesic hard ellipses on a sphere†
Andraž
Gnidovec
 *a,
Anže
Božič
*a,
Anže
Božič
 b and
Simon
Čopar
b and
Simon
Čopar
 a
a
aUniversity of Ljubljana, Faculty of Mathematics and Physics, SI-1000 Ljubljana, Slovenia. E-mail: andraz.gnidovec@fmf.uni-lj.si
bDepartment of Theoretical Physics, Jožef Stefan Institute, SI-1000 Ljubljana, Slovenia
First published on 29th September 2022
Abstract
Packing problems are abundant in nature and have been researched thoroughly both experimentally and in numerical models. In particular, packings of anisotropic, elliptical particles often emerge in models of liquid crystals, colloids, and granular and jammed matter. While most theoretical studies on anisotropic particles have thus far dealt with packings in Euclidean geometry, there are many experimental systems where anisotropically-shaped particles are confined to a curved surface, such as Pickering emulsions stabilized by ellipsoidal particles or protein adsorbates on lipid vesicles. Here, we study random close packing configurations in a two-dimensional model of spherical geodesic ellipses. We focus on the interplay between finite-size effects and curvature that is most prominent at smaller system sizes. We demonstrate that on a spherical surface, monodisperse ellipse packings are inherently disordered, with a non-monotonic dependence of both their packing fraction and the mean contact number on the ellipse aspect ratio, as has also been observed in packings of ellipsoids in both 2D and 3D flat space. We also point out some fundamental differences with previous Euclidean studies and discuss the effects of curvature on our results. Importantly, we show that the underlying spherical surface introduces frustration and results in disordered packing configurations even in systems of monodispersed particles, in contrast to the 2D Euclidean case of ellipse packing. This demonstrates that closed curved surfaces can be effective at introducing disorder in a system and could facilitate the study of monodispersed random packings.
1 Introduction
Anisotropy in the interactions between building blocks on the nanoscale can arise due to a plethora of reasons: surface patchiness, branching, chemical ordering, roughness, or simply the aspect ratio or faceting of the particle shape.1,2 Not only do the shape and interaction anisotropy of particles extend the possibilities of their assembly, packing, and jamming properties,2–5 they also allow for a more apt description of various systems in biological physics, soft matter, and pharmaceutical and food sciences, where the more symmetric circular and spherical shapes are often not a sufficient approximation. Anisotropic shape of building blocks has been shown to alter macroscopic behavior of granular matter6 and influence mechanical properties of nanoparticle assemblies,7 and can be exploited in the design of self-assembled structures and materials with desired properties.8In particular, packing of anisotropic hard objects in Euclidean geometries has been extensively studied during the last two decades, with development of theoretical models9–11 and research on different particle shapes,12,13 effects of confinement,14–17 and new methods to describe structural properties of jammed states18,19 continuing to this day. In comparison to packings of spherical particles, anisotropy introduces additional degrees of freedom into the system and in turn allows for denser packing configurations for all aspherical shapes in three dimensions,10,20 with asphericity in general influencing the packing density in a non-monotonic way.21 One of the prototypical cases for studying the effects of anisotropy on particle packing are systems of ellipsoids, the most simple aspherical shapes that are routinely used to model particles in a variety of soft matter, granular, and molecular systems. They are known to improve the density of jammed disordered states22–25 and can form unusually dense crystal packings,26,27 with numerous investigations highlighting the mechanical properties of jammed configurations of hard ellipsoids and ellipses.19,24,28–32 Additionally, ellipses were found to maximize the packing fraction of random sequential adsorption in two dimensions among the set of shapes of smoothed n-mers and spherocylinders.33
Besides particle shape, confinement also significantly affects packing properties—most notably its density—both for spherical particles34,35 and anisotropic particles such as rods and ellipses.16,17,36,37 In two dimensions, one can consider systems on a sphere as a peculiar case of confinement that arises due to the compactness of the spherical surface, replete with obligatory topological defects.38,39 The question of optimal packing of circles on the sphere was first posed by Tammes already in 193040 and has been well-researched since,41–44 with studies of jamming having been extended to different surfaces with positive curvature.45 However, investigations into the packing of anisotropic objects on spherical surfaces have to date been mostly limited to systems of hard rods.46,47 There, it was observed that in contrast to their optimal flat-plane packing, short rods adapt to the spherical geometry more efficiently than both spheres and longer rods, demonstrating the significant interplay between curvature and particle shape.
Only very recently have some works started to explore also the packings of ellipsoids on curved surfaces such as sphere.48 Packing of ellipses on the sphere is fundamentally different compared to their 2D packings in Euclidean space. Monodispersed systems of ellipses always crystallize in the plane when simulated by conventional packing algorithms and their packing fraction ϕC will be the same as for the hexagonal packing of circles (ϕC ≈ 0.9069), with ellipse and circle packings directly connected by an affine transformation.49 Analysis of disordered ellipse packings in flat plane therefore requires introducing bidispersity into the system in order to suppress crystallization. However, the closed surface of the sphere and its topological requirement for lattice defects preclude any periodic packing solutions, so in this sense, every configuration of ellipses on the sphere can be considered globally disordered.
In this work, we study a natural extension of the Tammes problem from circles to purely 2D spherical ellipses of arbitrary aspect ratios. The ellipses are defined as having a constant sum of geodesic distances to two foci, which also corresponds to having elliptical orthogonal projections onto a plane.50 We first introduce the model and explain the packing simulation procedure used to generate jammed configurations of spherical ellipses. We then present packing results, demonstrating that the packing fraction depends non-monotonously on the ellipse aspect ratio and can change with system size. We further analyze the generated packings by calculating the structure factor and tensor harmonic expansion to better understand the ordering of spherical ellipses. Finally, we compare our results to previous investigations of similar systems.
2 Model and methods
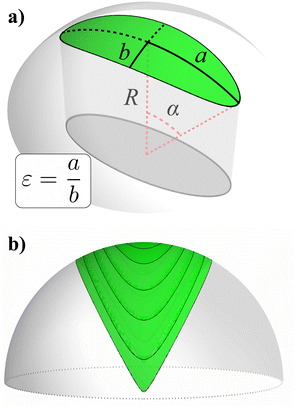
We consider a monodispersed system of N spherical ellipses on a sphere of radius R that satisfy the conventional definition as a set of points with a constant sum of geodesic distances to two focus points on the sphere. The aspect ratio of the ellipses is ε = a/b, where a and b are the semi-major and semi-minor ellipse axes (measured geodesically along the spherical surface; a,b < πR/2, see Fig. 1(a)). The area of such an ellipse is| A = 2πR2(1 − Λ0(ψ,k)), | (1) |
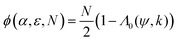 | (2) |
It is important to consider that the shape of spherical ellipses depends on their size α and therefore on the number of particles in a random close packing (RCP). The definition of a spherical ellipse can be satisfied by taking the intersection of a sphere and an elliptical cylinder with semiaxes x1 = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α and x2 = R
α and x2 = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α/ε. The details of this description are given in ref. 50. As α → π/2, the semi-major axis of this ellipsoid approaches R, resulting in a sharper and sharper vertex of the spherical ellipse (see Fig. 1(b)). At α = π/2, the spherical ellipse becomes the shape of a lemon wedge. This shape-changing effect is intrinsic to the purely 2D spherical ellipse model and is more pronounced at larger α (lower N in RCPs) and higher ε. As an alternative to keeping ε of the spherical ellipse constant for different particle sizes α, one could conserve the aspect ratio x1/x2 of the elliptical cylinder that defines the ellipse; however, this does not address the shape-changing effect. Additionally, in this case small changes in cylinder semiaxes close to x1 = R result in large changes of α, which is unfavorable for the iterative packing simulation described below. However, in physically relevant systems, N will be large enough for these shape effects to be negligible.
α/ε. The details of this description are given in ref. 50. As α → π/2, the semi-major axis of this ellipsoid approaches R, resulting in a sharper and sharper vertex of the spherical ellipse (see Fig. 1(b)). At α = π/2, the spherical ellipse becomes the shape of a lemon wedge. This shape-changing effect is intrinsic to the purely 2D spherical ellipse model and is more pronounced at larger α (lower N in RCPs) and higher ε. As an alternative to keeping ε of the spherical ellipse constant for different particle sizes α, one could conserve the aspect ratio x1/x2 of the elliptical cylinder that defines the ellipse; however, this does not address the shape-changing effect. Additionally, in this case small changes in cylinder semiaxes close to x1 = R result in large changes of α, which is unfavorable for the iterative packing simulation described below. However, in physically relevant systems, N will be large enough for these shape effects to be negligible.
In contrast to the Euclidean space where the bulk of packing research is focused on understanding system properties in the thermodynamic limit N → ∞, systems on a sphere are intrinsically of a finite size. The characteristic length scale, given by the semi-major axis a, and the sphere radius R can be varied independently, thus changing the effect of curvature on system behavior. We therefore focus on studying the interplay between finite-size effects and curvature that is most prominent at smaller system sizes (N ≤ 1000). In the thermodynamic limit, one should recover the 2D Euclidean results, as discussed in Section 4.
As packings in nature are not necessarily ordered in the most dense configuration, we do not focus solely on finding the optimal packing solution but rather on analyzing the general properties of jammed configurations of ellipses. That is, we adopt an ensemble-based approach to analyzing packings where the packing simulation is run repeatedly from random initial conditions to gather a statistical sample of jammed configurations with different packing densities, weighted by the probability of occurrence. The generated packings can be related to the concept of RCP, where “randomness” stems from initialization and is not necessarily quantified for end configurations.52–54 This is fundamentally different from the approach based on individual configurations, used to study the mathematically rigorously defined maximally random jammed (MRJ) packings, determined as packings that minimize a chosen order metric (among other requirements).55 As we discuss in Section 4, finding an appropriate order metric to quantify randomness in packings of spherical ellipses proves to be elusive because it is not clear what the ordered phase should be in the first place.
We generate the packings by a compression–decompression algorithm similar to the method used previously to study RCP of spheres and ellipses.29,34,52,56 The procedure requires a measure of overlap to be defined as the system energy; however, conventional overlap parameters used for measuring distances between ellipsoids in Euclidean geometries57–59 do not work for purely 2D ellipses on a sphere. We therefore use a recently developed algorithm by Gnidovec et al.50 to determine the overlap function λ between two spherical ellipses. This algorithm is based on calculating the eigenvalues of a linear interpolation between quadratic forms that define spherical ellipses, and returns λ < 1 if two ellipses overlap. The energy for a pair of ellipses is then defined as E(λ) = 1/λ + λ − 2 for overlapping ellipses and E(λ) = 0 otherwise. Note that the first nonzero term in the expansion of energy around λ = 1 on the overlapping side is the harmonic term (1 − λ)2.
The packing simulation is initialized with random positions and orientations of ellipses on the sphere at a packing fraction ϕ ≈ 0.5. The size of the particles α is then increased step-wise and the configuration is relaxed using energy minimization after each iteration to eliminate overlaps. As we approach a jammed configuration, step size is decreased and, additionally, a decrease of ellipse sizes is permitted if overlaps cannot be removed by translations and rotations of particles. We stop the simulation once the energy falls in the interval E0 < E < 2E0, with E0 = 10−8. It follows that the packing fraction of generated configurations is precise within 10−4, which is sufficient for our analysis. Note that the initial particle growth rate can be set arbitrarily in the algorithm and can impact the density of generated packings. We choose a value of Δϕ ∼ 10−3, which is small enough to prevent significant “unphysical” rearrangements that follow large overlaps of particles while also providing satisfactory time performance of the simulation.
Our simulation procedure technically considers spherical ellipses as soft particles, and some caution is required before classifying the resulting states as equivalent to jammed configurations of hard particles. It can be shown, however, that configurations with locally minimal energy always correspond to jammed states for repulsive interparticle potentials.60,61 What is more, in the limit of zero external forces and pressures on the system (as is the case for our method), the resulting configurations can be closely related to collectively jammed packings of hard ellipses.24,52,62 Here, we adopt the classification of jamming from ref. 63. Note that the more demanding jamming categories, namely, the strictly jammed and metric jammed definitions (the latter proposed by Burke45), cannot be applied to spherical systems, as the underlying surface cannot be deformed. We also expect that alternative algorithms for generating packings of hard particles, such as the Lubachevsky–Stillinger algorithm64 or the Zinchenko algorithm,65 would produce qualitatively similar packings.62
3 Results
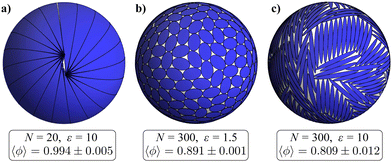
For each combination of parameters (N, ε) we perform 60 packing simulations, starting from independent random initial conditions to obtain statistical samples of jammed configurations. For every sampled point in the parameter space we then determine the packing fraction 〈ϕ〉, with brackets denoting the average over all 60 samples. The packing fraction for three different values of N is presented in Fig. 2(a) as a function of the ellipse aspect ratio ε. As we deviate from circles (ε = 1) towards higher values of ε, packing fraction first increases and reaches a peak of ϕmax ≈ 0.89 around ε ≈ 1.5 for all system sizes, which is close to the theoretical planar limit ϕC ≈ 0.9069. A representative configuration for this densest case at N = 300 is shown in Fig. 3(b). The increase in efficiency of random packing as we go from circles to ellipses is in line with observations from both 2D and 3D random ellipse packings22,31,66,67 and is a direct consequence of introducing an additional degree of freedom per particle into the system. (Note again that Euclidean 2D random packings only emerge in polydispersed systems.) Increasing the aspect ratio of the ellipses further, exclusion volume effects prevail and packing fraction decreases monotonically in the simulated range of ε, at least for large enough system sizes (N ≳ 50). This can be clearly seen in Fig. 3(c) for N = 300 and ε = 10. For low N and high ε, the relative size of the ellipses α becomes larger than 1 (a > R) and their curvature is significant. This decreases the available space between two parallel ellipses and in turn increases the packing efficiency (see the curve for N = 30 in Fig. 2(a)). As α approaches π/2, the densest packing will be the configuration where the ellipses are positioned along the equator, each parallel to their respective neighbors, i.e., in a lemon wedge configuration. It is even possible to achieve a perfect packing of ϕ = 1 for ellipses with aspect ratios ε = N/2. In Fig. 3(a), we show a configuration that closely approaches this perfect packing for N = 20 and ε = 10. Here, it must be kept in mind that while ellipses in these perfect packings satisfy the spherical ellipse definition, they deviate strongly from the idea of ellipses in 2D Euclidean space.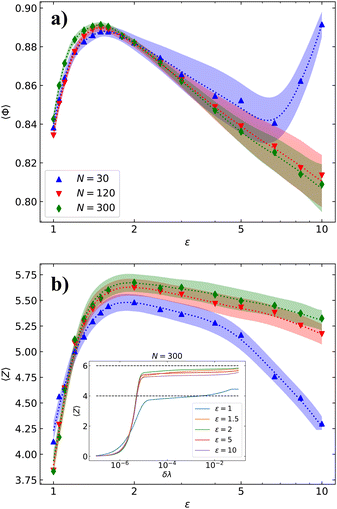 | ||
| Fig. 2 (a) Average packing fraction 〈ϕ〉 and (b) number of contacts 〈Z〉 as functions of the ellipse aspect ratio ε. Dotted curves do not represent a model fit and serve only as guides to the eye, with the shadowed areas around the curves indicating the scale of errorbars. The detailed distribution of packing densities around the plotted averages is shown in Fig. 4. Inset in panel (b) shows the dependence of 〈Z〉 on contact tolerance δλ. A small number of particles, called rattlers, can be underconstrained and able to move within the cage of the surrounding particles. These are also included in the calculation of 〈Z〉. | ||
Jammed configurations of particles must also satisfy force and torque balance that is already implied in our packing generation algorithm. As a requirement to achieve mechanical stability, the isocounting conjecture was proposed, which states that in static packings of frictionless particles, the number of contacts between particles needs to be equal to the number of degrees of freedom (DOF) in the system. It follows that the mean number of contacts per particle is Ziso = 2df − 2/N, where df is the number of DOF per particle. The second term is a consequence of confinement and finite size (configurations are invariant to two global rotations), and becomes small for large systems. On a spherical surface and in 2D in general this results in Ziso = 4 for circles and Ziso = 6 for ellipses. While random packings of spheres in a flat space are indeed isostatic, packings of anisotropic particles such as ellipses and ellipsoids are stable also when hypoconstrained with Z < Ziso, as has been demonstrated both in simulations and experiments.22,24 The missing contacts were shown to belong to quartic modes in the spectrum of the dynamical (Hessian) matrix, describing collective rotational motions of particles.24,29
In Fig. 2(b), we show the dependence of the mean number of contacts per particle 〈Z〉 on the aspect ratio ε, averaged again over all generated configurations at each point in the parameter space. In the simulated packings, contacts are determined between pairs of ellipses if |λ − 1| < δλ, as λ represents the area scaling factor required to reach exact tangency. The value of tolerance is chosen to be δλ = 10−4, where the curves of 〈Z〉 as a function of (δλ) are almost flat over the entire range of simulated ε, as shown in the inset of Fig. 2(b) and similar to what has been observed for ellipsoid packings.68 Our results show that for most circle packings on a sphere we have 〈Z〉 < 4, but there are exceptions with higher contact numbers, such as N = 30, where the average configuration is hyperconstrained (〈Z〉 > 4). As particle shape starts to deviate from a perfect circle, the mean contact number steeply increases as the introduced additional degrees of freedom in the system need to be balanced to reach stability of the configuration. It reaches a maximum at ε ≈ 2, which notably differs from the value where the peak in the packing fraction is attained (ε ≈ 1.5). In 3D packings of ellipsoids, these two extrema are closer together.22 Another difference with 3D results is the subsequent decrease in the mean contact number, as it stays mostly constant for ellipsoid packings after reaching the maximum value. This decrease at high ε could be connected to local crystallization in packings on the sphere (ordered local domains) where many particles only have four contacts. We discuss this more thoroughly in the ESI† (see Fig. S1). Finally, the system with N = 30 particles exhibits consistently lower mean number of contacts than other presented cases at all values of ε > 1. For such small system sizes, the effect of confinement to a compact surface that lowers the number of degrees of freedom in the system (2/N term) becomes significant. Additionally, at high ε, the interplay between ellipse shape and curvature that drives the increase in packing fraction also promotes parallel ordering of neighboring ellipses and consequently domain formation, which amplifies the effect observed at large system sizes.
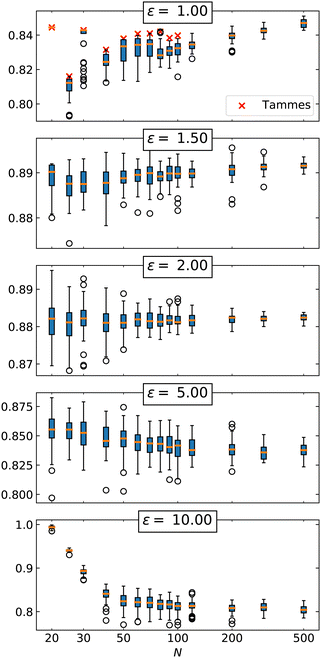
We further study the dependence of packing fraction on system size in Fig. 4, where we use boxplots to show how the results of distinct simulation runs are distributed. Orange lines represent the average values at the respective points. For circular particles at ε = 1, 〈ϕ〉 is non-monotonic, with large variations especially at small system sizes where curvature and compactness of the spherical surface can lead to highly frustrated local arrangements of circles. These variations are not surprising—the best packing configurations closely follow the Tammes solutions (densest circle packings, marked by red crosses in Fig. 4), which exhibit the same property.42 Note that all generated packings at N = 20 and most of those at N = 30 return the respective Tammes configurations. A slight increasing trend in 〈ϕ〉 can be observed as we move towards large system sizes. The packing fraction for circles on the sphere should converge to the planar case ϕC ≈ 0.9069; however, it has been demonstrated that this convergence is very slow.69 In general, the distribution of packing fraction within the ensemble is centered below the maxima dictated by the Tammes solutions and becomes approximately Gaussian for N ≳ 80, which is found to be true also for distributions at other values of ε (with a few exceptions, all distributions pass the normality test). As the aspect ratio ε is increased above 1, any notable differences in packing densities between configurations with different N begin to disappear. This is a direct consequence of adding additional degrees of freedom to the system, resulting in ellipse packings that are less frustrated than the packings of circles. Further details on the transition from circles to ellipses are available in ESI.† For aspect ratios around the peak of the packing fraction (ε ≈ 1.5), the packing efficiency remains approximately constant with respect to N, as indicated already in Fig. 2(a). Increasing the aspect ratio further, the effects of particle curvature at small system sizes that increase the packing fraction (as already mentioned in the discussion of Fig. 2) become evident. Whereas the decrease of 〈ϕ〉 with N is relatively gradual at ε = 5, it is significantly more pronounced at ε = 10 where the case for N = 20 satisfies the condition perfect for packing (the average generated packing has a packing fraction of ϕ = 0.994 (Fig. 3(a))). Average packing fraction then steeply decreases with N until the slope flattens at around N = 50 and continues to decrease more gradually.
4 Discussion
4.1 Harmonic expansion of ellipse positions and orientations
To analyze the generated packings further, we expand their positional order over spherical harmonics and calculate the spherical structure factor39 at each combination of parameters (N, ε),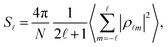 | (3) |
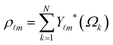 for spherical harmonics Y
for spherical harmonics Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m and the positions of ellipses in the packing in spherical coordinates Ωk = (ϑk,φk); the sum runs over all particles in the system. Additionally, we take the average over the generated configurations to smooth out the variations in the structure factor and amplify the common properties of the packings. The results are presented in Fig. 5 for N = 120 and ε ∈ [1,3]. Sharp peaks in the structure factor for the packing of circles (ε = 1) get smoothed out with increasing ε as the interval [2α/ε,2α] of possible distances between the centers of neighboring ellipses expands. The edge points of this interval can be mapped to “critical values” of
m and the positions of ellipses in the packing in spherical coordinates Ωk = (ϑk,φk); the sum runs over all particles in the system. Additionally, we take the average over the generated configurations to smooth out the variations in the structure factor and amplify the common properties of the packings. The results are presented in Fig. 5 for N = 120 and ε ∈ [1,3]. Sharp peaks in the structure factor for the packing of circles (ε = 1) get smoothed out with increasing ε as the interval [2α/ε,2α] of possible distances between the centers of neighboring ellipses expands. The edge points of this interval can be mapped to “critical values” of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) where the structure factor would have the first peak if all neighbor distances dn.n. were equal. Using the relation
where the structure factor would have the first peak if all neighbor distances dn.n. were equal. Using the relation ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≈ 2π/dn.n. gives us an envelope (dashed lines in Fig. 5) that closely matches the observed widening of spectral peaks, with the left and right branches corresponding to dn.n. = 2α and dn.n. = 2α/ε, respectively. At fixed N, this envelope functionally depends only on ε, and we show in ESI† that
≈ 2π/dn.n. gives us an envelope (dashed lines in Fig. 5) that closely matches the observed widening of spectral peaks, with the left and right branches corresponding to dn.n. = 2α and dn.n. = 2α/ε, respectively. At fixed N, this envelope functionally depends only on ε, and we show in ESI† that 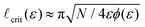 for high N (small α). We note again that, because the configurations are jammed, the ellipse size α depends on the number of particles in the system and, more importantly, on the aspect ratio ε.
for high N (small α). We note again that, because the configurations are jammed, the ellipse size α depends on the number of particles in the system and, more importantly, on the aspect ratio ε.
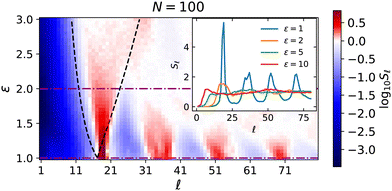 | ||
Fig. 5 Heatmap of the decimal logarithm of the spherical structure factor [eqn (3)] for N = 100 at different aspect ratios ε and wave numbers ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , averaged over all generated configurations. Expansion coefficients vanish when , averaged over all generated configurations. Expansion coefficients vanish when ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) → 0 for all ε. Dashed lines show the theoretical envelope for widening of the first spectral peak, → 0 for all ε. Dashed lines show the theoretical envelope for widening of the first spectral peak, 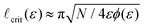 . The inset shows S . The inset shows S![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for a few selected ε (horizontal cross-sections over the heatmap, for ε = 1 and ε = 2 shown as dash-dotted lines). for a few selected ε (horizontal cross-sections over the heatmap, for ε = 1 and ε = 2 shown as dash-dotted lines). | ||
In Euclidean space, jamming is conjectured to be related to hyperuniformity, i.e., the suppression of density fluctuations at large distances described by a vanishing Euclidean structure factor S(k) as |k| → 0 or—for some systems of aspherical particles—vanishing spectral density.70–72 The notion of hyperuniformity was recently expanded to spherical surfaces, where ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) assumes the role of k, and by connecting the spherical structure factor to the spherical cap density, one can show that the hyperuniformity criterion on the sphere corresponds to the limit
assumes the role of k, and by connecting the spherical structure factor to the spherical cap density, one can show that the hyperuniformity criterion on the sphere corresponds to the limit 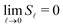 .39Fig. 5 demonstrates that this condition is satisfied up to a small residual on the order of 10−3, at least for the range of aspect ratios shown in the figure. Some larger deviations were observed at high ε, particularly at ε = 10 as seen also in the inset of Fig. 5, where this residual is between one and two orders of magnitude higher (more significantly so at small N). We also calculated the asimptotic expansion coefficients AN for the cap number variance as another way to establish hyperuniformity on the sphere.39,73 The coefficients AN are on the order of 10−3 or smaller for all ensemble samples in the inset of Fig. 5, including ε = 10, which demonstrates that number density fluctuations vanish for larger cap sizes and the systems can be considered hyperuniform. The different extents to which the limit
.39Fig. 5 demonstrates that this condition is satisfied up to a small residual on the order of 10−3, at least for the range of aspect ratios shown in the figure. Some larger deviations were observed at high ε, particularly at ε = 10 as seen also in the inset of Fig. 5, where this residual is between one and two orders of magnitude higher (more significantly so at small N). We also calculated the asimptotic expansion coefficients AN for the cap number variance as another way to establish hyperuniformity on the sphere.39,73 The coefficients AN are on the order of 10−3 or smaller for all ensemble samples in the inset of Fig. 5, including ε = 10, which demonstrates that number density fluctuations vanish for larger cap sizes and the systems can be considered hyperuniform. The different extents to which the limit 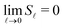 is satisfied for different N and ε is similar to deviations from perfect hyperuniformity that were observed also in Euclidean jammed states and are believed to be related to both imperfections in packings (rattler particles)74 as well as finite size effects, which cannot be avoided on the closed surface of the sphere.
is satisfied for different N and ε is similar to deviations from perfect hyperuniformity that were observed also in Euclidean jammed states and are believed to be related to both imperfections in packings (rattler particles)74 as well as finite size effects, which cannot be avoided on the closed surface of the sphere.
Besides the harmonic expansion of the ellipse positions, further insight into orientational ordering of ellipses in close packings can be obtained by expanding the tensor field 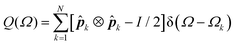 , where unit vectors
, where unit vectors ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) k describe the ellipse orientations, over two orthogonal tangential tensor spherical harmonics on the sphere. Details of this expansion are given in ESI.† In contrast to the scalar structure factor obtained from the positional order, the two tensor structure factors, defined in an analogous fashion from tensor expansion coefficients, do not vanish at small
k describe the ellipse orientations, over two orthogonal tangential tensor spherical harmonics on the sphere. Details of this expansion are given in ESI.† In contrast to the scalar structure factor obtained from the positional order, the two tensor structure factors, defined in an analogous fashion from tensor expansion coefficients, do not vanish at small ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for any value of ε (Fig. S4 in ESI†). Instead, they have a peak at
for any value of ε (Fig. S4 in ESI†). Instead, they have a peak at ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 (the smallest
= 2 (the smallest ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) where the expansion is defined), which shows that even though the ellipses are not positionally ordered, there exists some trend in the average orientational order over long length scales. The peak is higher at large ε, showing that its magnitude indicates the preference for parallel ellipses during the densification process of the packing simulation, as parallel local structures enable higher packing densities. See ESI† for further tensor expansion results and clarifications.
where the expansion is defined), which shows that even though the ellipses are not positionally ordered, there exists some trend in the average orientational order over long length scales. The peak is higher at large ε, showing that its magnitude indicates the preference for parallel ellipses during the densification process of the packing simulation, as parallel local structures enable higher packing densities. See ESI† for further tensor expansion results and clarifications.
4.2 Comparison to packings of ellipses and ellipsoids
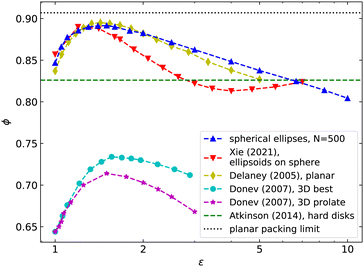
In Fig. 6, we show a comparison of our results for the packing of spherical ellipses to the known packing densities in other anisotropic systems. The most relevant is the comparison with ellipsoid packings on the sphere recently studied by Xie and Atherton.48 One would expect a similar dependence of packing fraction on the aspect ratio for low values of ε, where spherical ellipses are well approximated by intersections of 3D ellipsoids and the surface of the sphere—at least for large system sizes that imply low surface curvature. Nevertheless, the results show significant differences. Ellipsoid packings reach maximal density already at ε ≈ 1.2, followed by a steeper descent with a minimum of ϕ ≈ 0.813 at ε ≈ 4.0 and with the packing density rising again for even higher aspect ratios. This increase at large ε can be attributed to possible overlaps of prolate ellipsoids of revolution as they do not conform to the surface curvature and particles with high anisotropy can stick significantly out of plane relative to the layer thickness (given by the ellipsoid semi-minor axis). The other differences in the packings, namely the maximum at a lower ε and worse packing at intermediate aspect ratios, are more elusive to explain. A possible origin for worse packing can be the usage of Berne–Pechukas overlap parameter57 by Xie and Atherton48 to determine ellipsoid overlaps, as this is merely an approximation that can overestimate the correct touching distance (calculated from the Perram–Wertheim overlap function).59,75 We study this further in ESI† where we compare the geodesic spherical ellipse contact function to both the exact Perram–Wertheim ellipsoid contact function and the Berne–Pechukas approximation. For smaller particle sizes, i.e., large numbers of particles N in RCPs, the 2D spherical ellipse contact function used to generate results in this article closely matches the exact results for ellipsoids. We also demonstrate in panels (c) and (e) of Fig. S5 (ESI†) that the Berne–Pechukas approximation can overestimate the area in the orientation plane where two ellipsoids overlap, which leads to worse packing results. Finally, in Fig. S5f (ESI†) we use a similar argument to show that large spherical ellipses at high values of ε will pack worse than tangential ellipsoids on the sphere.On the other hand, the dependence of packing density on the aspect ratio ε that we obtain for monodispersed spherical ellipses strongly resembles the curve for the bidispersed planar case, not only qualitatively but also quantitatively. The diamond-marked yellow curve in Fig. 6 shows the results obtained by Delaney et al.,66 and other studies of 2D ellipse packings have also observed similar densities.24,31 Just like in the packings of spherical ellipses, the best packing is achieved for ε ≈ 1.5, with the peak being slightly higher in the Euclidean plane. What is more, the decrease in the packing efficiency when ε increases is comparable between the two cases. The strong quantitative resemblance could indicate that there exists a fundamental connection between random packings of ellipses on flat and curved surfaces, even though the mechanism that prevents crystallization is different. As expected, both results also show higher packing densities compared to the elusive monodispersed MRJ packing of hard disks with ϕmono = 0.826, generated by an algorithm designed specifically to avoid crystallization.76
Finally, exploiting curvature as a means of introducing disorder into a system raises the question of the behavior of spherical packings at large system sizes. In the limit of N → ∞ and, consequently, vanishing curvature, one would expect the system to form large domains with crystalline order and with defects concentrated in the grain boundaries, effectively transitioning to the (ordered) planar case where the packing fraction is independent of the ellipse aspect ratio. This is indeed the case for spherical packings of circles, where this transition is continuous as the density of grain boundaries very slowly decreases with increasing system size.69 Similar behavior would be expected for systems of spherical ellipses; however, given the limited range of N studied in our simulations, we are unable to exclude the possibility that the transition from random to crystalline order appears faster around some specific system size. This problem is left for future investigations as it would require a significant computational effort.
5 Conclusions
In this work, we studied the RCP of 2D geodesic ellipses on the surface of the sphere. We have shown that the dependence of packing fraction and mean number of contacts on the ellipse aspect ratio is non-monotonic and qualitatively resembles those from the Euclidean cases of ellipse and ellipsoid packings. However, some fundamental differences have emerged that can be attributed both to the curvature of the system as well as to the fact that the surface of the sphere is closed. These properties of the underlying spherical surface introduce frustration in the system, resulting in disordered packing configurations even in systems of monodispersed particles. This stands in contrast to the packing of ellipses in flat 2D space, where polydispersity is required to routinely suppress crystallization in packing simulations, demonstrating that closed curved surfaces can be effective at introducing disorder into a system and could facilitate the study of monodispersed random packings.In real systems, building blocks of anisotropic shapes are often preferred over spherical ones: for instance, diatom frustules of various adnate diatom species are elliptical with mean aspect ratio ε ≈ 1.7,77 elongated fat particles have been shown to improve the stability (crystallization) of ice cream,78 and using elongated carrier particles in dry powder inhalers can considerably increase the amounts of drug delivered to the lower airway region,79 to name just a few. On spherical surfaces, elliptical particles such as polystyrene ellipsoids can also be used to stabilize Pickering emulsions more efficiently than spherical particles.80,81 They form a dense packing at the spherical liquid–liquid interface, providing a possible realization of packings studied in this work. Similarly, elliptical particles could be used to manipulate properties of liquid marbles.82 In biological systems, our work could help with understanding the packing of adsorbed elliptically-shaped BAR proteins on lipid vesicles.83 These proteins are intrinsically curved and resemble the shape of geodesic spherical ellipses which makes our model preferable compared to the 3D ellipsoid alternatives. However, in all these examples, the interactions between particles and building blocks are more complex than the hard-core repulsion studied in this work. Our model is furthermore purely two-dimensional, which is more suited for thin systems that adhere to the surface, such as structures within biological membranes, but can lead to some discrepancies when describing real systems with three-dimensional ellipsoidal building blocks. We also do not take into account the possible deformations of the underlying spherical surface, or any reshaping of the particles themselves. Each system of interest must therefore be evaluated with regard to whether the geodesic ellipse is a sufficient approximation to the actual shape for the purposes of the investigation.
Some additional challenges still remain. As an ordered reference configuration for the arrangement of ellipses on the sphere does not exist, we are unable to quantify disorder in the system. This essentially precludes us from a detailed analysis of individual configurations, also in terms of finding the MRJ packing density. Additionally, the system sizes studied in this work are relatively limited due to the computational costs involved. In future investigations, more efficient packing algorithms could enable the study of large domain formation that is expected to occur with increasing system size. The model could also be expanded either to non-hard interactions between particles where penetration is possible or to include long-range interactions such as multipolar electrostatic interactions. These more complex models could be used to better describe the behavior of various colloidal or biological systems where building blocks are preferably oblong, or even to enable the design of packings with a desired local structure.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support by Slovenian Research Agency (ARRS) under contracts P1-0099 and J1-9149. The work is associated with the COST action CA17139.References
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562 CrossRef PubMed.
- K. J. Lee, J. Yoon and J. Lahann, Curr. Opin. Colloid Interface Sci., 2011, 16, 195–202 CrossRef CAS.
- V. R. Dugyala, S. V. Daware and M. G. Basavaraj, Soft Matter, 2013, 9, 6711–6725 RSC.
- T. G. Anjali and M. G. Basavaraj, Langmuir, 2018, 35, 3–20 CrossRef PubMed.
- K. Deng, Z. Luo, L. Tan and Z. Quan, Chem. Soc. Rev., 2020, 49, 6002–6038 RSC.
- T. Börzsönyi and R. Stannarius, Soft Matter, 2013, 9, 7401–7418 RSC.
- L. Zhang, G. Feng, Z. Zeravcic, T. Brugarolas, A. J. Liu and D. Lee, ACS Nano, 2013, 7, 8043–8050 CrossRef CAS PubMed.
- S. Sacanna, M. Korpics, K. Rodriguez, L. Colón-Meléndez, S.-H. Kim, D. J. Pine and G.-R. Yi, Nat. Commun., 2013, 4, 1688 CrossRef.
- A. Baule, R. Mari, L. Bo, L. Portal and H. A. Makse, Nat. Commun., 2013, 4, 2194 CrossRef PubMed.
- A. Baule and H. A. Makse, Soft Matter, 2014, 10, 4423–4429 RSC.
- J. Tian, Y. Xu, Y. Jiao and S. Torquato, Sci. Rep., 2015, 5, 16722 CrossRef CAS PubMed.
- T. Marschall and S. Teitel, Phys. Rev. E, 2018, 97, 012905 CrossRef CAS PubMed.
- K. VanderWerf, W. Jin, M. D. Shattuck and C. S. O'Hern, Phys. Rev. E, 2018, 97, 012909 CrossRef.
- E. G. Teich, G. van Anders, D. Klotsa, J. Dshemuchadse and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E669–E678 CrossRef CAS PubMed.
- D. Wang, M. Hermes, R. Kotni, Y. Wu, N. Tasios, Y. Liu, B. de Nijs, E. B. van der Wee, C. B. Murray, M. Dijkstra and A. van Blaaderen, Nat. Commun., 2018, 9, 2228 CrossRef PubMed.
- W. Jin, Y. Wang, H.-K. Chan and Z. Zhong, Phys. Rev. Res., 2021, 3, 013053 CrossRef CAS.
- E. Basurto, P. Gurin, S. Varga and G. Odriozola, J. Mol. Liq., 2021, 333, 115896 CrossRef CAS.
- E. D. Cubuk, S. S. Schoenholz, J. M. Rieser, B. D. Malone, J. Rottler, D. J. Durian, E. Kaxiras and A. J. Liu, Phys. Rev. Lett., 2015, 114, 108001 CrossRef CAS PubMed.
- M. Harrington, A. J. Liu and D. J. Durian, Phys. Rev. E, 2019, 99, 022903 CrossRef CAS.
- Y. Kallus, Soft Matter, 2016, 12, 4123–4128 RSC.
- S. Zhao, N. Zhang, X. Zhou and L. Zhang, Powder Technol., 2017, 310, 175–186 CrossRef CAS.
- A. Donev, I. Cisse, D. Sachs, E. A. Variano, F. H. Stillinger, R. Connelly, S. Torquato and P. M. Chaikin, Science, 2004, 303, 990–993 CrossRef CAS PubMed.
- W. Man, A. Donev, F. H. Stillinger, M. T. Sullivan, W. B. Russel, D. Heeger, S. Inati, S. Torquato and P. M. Chaikin, Phys. Rev. Lett., 2005, 94, 141 CrossRef PubMed.
- A. Donev, R. Connelly, F. H. Stillinger and S. Torquato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 051304 CrossRef.
- Z.-Y. Zhou, R.-P. Zou, D. Pinson and A.-B. Yu, Ind. Eng. Chem. Res., 2011, 50, 9787–9798 CrossRef CAS.
- A. Donev, F. H. Stillinger, P. Chaikin and S. Torquato, Phys. Rev. Lett., 2004, 92, 255506 CrossRef PubMed.
- W. Jin, Y. Jiao, L. Liu, Y. Yuan and S. Li, Phys. Rev. E, 2017, 95, 033003 CrossRef.
- Z. Zeravcic, N. Xu, A. J. Liu, S. R. Nagel and W. van Saarloos, EPL, 2009, 87, 26001 CrossRef.
- M. Mailman, C. F. Schreck, C. S. O'Hern and B. Chakraborty, Phys. Rev. Lett., 2009, 102, 255501 CrossRef PubMed.
- S. Torquato and F. H. Stillinger, Rev. Mod. Phys., 2010, 82, 2633 CrossRef.
- C. F. Schreck, N. Xu and C. S. O'Hern, Soft Matter, 2010, 6, 2960 RSC.
- C. F. Schreck, M. Mailman, B. Chakraborty and C. S. O'Hern, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061305 CrossRef.
- M. Cieśla, G. Pajak and R. M. Ziff, J. Chem. Phys., 2016, 145, 044708 CrossRef PubMed.
- K. W. Desmond and E. R. Weeks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 051305 CrossRef.
- H. Ikeda, Phys. Rev. Lett., 2020, 125, 038001 CrossRef CAS PubMed.
- J. O. Freeman, S. Peterson, C. Cao, Y. Wang, S. V. Franklin and E. R. Weeks, Granular Matter, 2019, 21, 84 CrossRef.
- S. Hashemi, Braz. J. Phys., 2019, 49, 321–332 CrossRef.
- T. L. Hill, Thermodynamics of small systems, Courier Corporation, 1994 Search PubMed.
- A. Božič and S. Čopar, Phys. Rev. E, 2019, 99, 032601 CrossRef PubMed.
- P. Tammes, PhD thesis, University of Groningen, 1930.
- B. W. Clare and D. L. Kepert, Proc. R. Soc. London, Ser. A, 1986, 405, 329 Search PubMed.
- B. W. Clare and D. L. Kepert, J. Math. Chem., 1991, 6, 325–349 CrossRef.
- E. B. Saff and A. B. J. Kuilaars, Math. Intell., 1997, 19, 5 CrossRef.
- A. M. Mascioli, C. J. Burke, M. Q. Giso and T. J. Atherton, Soft Matter, 2017, 13, 7090–7097 RSC.
- C. J. Burke, PhD thesis, Tufts University, 2016.
- F. Smallenburg and H. Löwen, J. Chem. Phys., 2016, 144, 164903 CrossRef PubMed.
- E. Allahyarov, A. Voigt and H. Löwen, Soft Matter, 2017, 13, 8120–8135 RSC.
- Z. Xie and T. J. Atherton, Soft Matter, 2021, 17, 4426 RSC.
- T. Matsumoto and W. Nowacki, Z. Kristallogr., 1966, 123, 401–421 CrossRef.
- A. Gnidovec, A. Božič, U. Jelerčič and S. Čopar, Proc. R. Soc. London, Ser. A, 2022, 478, 20210807 Search PubMed.
- J. T. Conway, Nucl. Instrum. Methods Phys. Res., Sect. A, 2010, 614, 17–27 CrossRef CAS.
- C. S. O’Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011306 CrossRef.
- C. S. O’Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 043302 CrossRef.
- R. D. Kamien and A. J. Liu, Phys. Rev. Lett., 2007, 99, 155501 CrossRef PubMed.
- S. Torquato, T. M. Truskett and P. G. Debenedetti, Phys. Rev. Lett., 2000, 84, 2064–2067 CrossRef CAS PubMed.
- N. Xu, J. Blawzdziewicz and C. S. O'Hern, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061306 CrossRef PubMed.
- B. J. Berne and P. Pechukas, J. Chem. Phys., 1972, 56, 4213–4216 CrossRef CAS.
- J. W. Perram and M. Wertheim, J. Comput. Phys., 1985, 58, 409–416 CrossRef CAS.
- D. J. Cleaver, C. M. Care, M. P. Allen and M. P. Neal, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 559–567 CrossRef CAS PubMed.
- R. Connelly, Invent. Math., 1982, 66, 11–33 CrossRef.
- R. Connelly and W. Whiteley, SIAM J. Discrete Math., 1996, 9, 453–491 CrossRef.
- A. Donev, S. Torquato, F. H. Stillinger and R. Connelly, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 043301 CrossRef.
- S. Torquato and F. H. Stillinger, J. Phys. Chem. B, 2001, 105, 11849–11853 CrossRef CAS.
- B. D. Lubachevsky and F. H. Stillinger, J. Stat. Phys., 1990, 60, 561–583 CrossRef.
- A. Z. Zinchenko, J. Comput. Phys., 1994, 114, 298–307 CrossRef.
- G. Delaney, D. Weaire, S. Hutzler and S. Murphy, Philos. Mag. Lett., 2005, 85, 89–96 CrossRef CAS.
- S. R. Williams and A. P. Philipse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 051301 CrossRef CAS PubMed.
- A. Donev, S. Torquato and F. H. Stillinger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 011105 CrossRef PubMed.
- R. Jullien, J.-F. Sadoc and R. Mosseri, J. Phys. I, 1997, 7, 1677–1692 CrossRef.
- S. Torquato and F. H. Stillinger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 041113 CrossRef PubMed.
- A. Donev, F. H. Stillinger and S. Torquato, Phys. Rev. Lett., 2005, 95, 090604 CrossRef PubMed.
- C. E. Zachary, Y. Jiao and S. Torquato, Phys. Rev. Lett., 2011, 106, 178001 CrossRef PubMed.
- A. Božič, S. Franzini and S. Čopar, Phys. Fluids, 2021, 33, 047109 CrossRef.
- S. Atkinson, G. Zhang, A. B. Hopkins and S. Torquato, Phys. Rev. E, 2016, 94, 012902 CrossRef.
- L. Paramonov and S. N. Yaliraki, J. Chem. Phys., 2005, 123, 194111 CrossRef.
- S. Atkinson, F. H. Stillinger and S. Torquato, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 18436–18441 CrossRef CAS.
- T. Sullivan, Biomimetics, 2019, 4, 29 CrossRef CAS PubMed.
- C. Méndez-Velasco and H. D. Goff, Food Hydrocolloids, 2012, 29, 152–159 CrossRef.
- W. Kaialy, A. Alhalaweh, S. P. Velaga and A. Nokhodchi, Int. J. Pharm., 2011, 421, 12–23 CrossRef CAS PubMed.
- B. Madivala, S. Vandebril, J. Fransaer and J. Vermant, Soft Matter, 2009, 5, 1717 RSC.
- F. Günther, S. Frijters and J. Harting, Soft Matter, 2014, 10, 4977–4989 RSC.
- M. Anyfantakis, V. S. R. Jampani, R. Kizhakidathazhath, B. P. Binks and J. P. F. Lagerwall, Angew. Chem., Int. Ed., 2020, 59, 19260 CrossRef CAS PubMed.
- M. Simunovic, G. A. Voth, A. Callan-Jones and P. Bassereau, Trends Cell Biol., 2015, 25, 780–792 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00624c |
| This journal is © The Royal Society of Chemistry 2022 |