 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Large stress asymmetries of lipid bilayers and nanovesicles generate lipid flip-flops and bilayer instabilities†
Aparna
Sreekumari
and
Reinhard
Lipowsky
 *
*
Theory and Bio-Systems, Max Planck Institute of Colloids and Interfaces, 14424 Potsdam, Germany. E-mail: lipowsky@mpikg.mpg.de; Fax: +49 331 5679602; Tel: +49 331 5679600
First published on 29th July 2022
Abstract
Much effort has been devoted to lipid bilayers and nanovesicles with a compositional asymmetry between the two leaflets of the bilayer membranes. Here, we address another fundamental asymmetry related to lipid densities and membrane tensions. To avoid membrane rupture, the osmotic conditions must be adjusted in such a way that the bilayer membranes are subject to a relatively low bilayer tension. However, even for vanishing bilayer tension, the individual leaflets can still experience significant leaflet tensions if one leaflet is stretched whereas the other leaflet is compressed. Such a stress asymmetry between the two leaflets can be directly controlled in molecular dynamics simulations by the initial assembly of the lipid bilayers. This stress asymmetry is varied here over a wide range to determine the stability and instability regimes of the asymmetric bilayers. The stability regime shrinks with decreasing size and increasing membrane curvature of the nanovesicle. In the instability regimes, the lipids undergo stress-induced flip-flops with a flip-flop rate that increases with increasing stress asymmetry. The onset of flip-flops can be characterized by a cumulative distribution function that is well-fitted by an exponential function for planar bilayers but has a sigmoidal shape for nanovesicles. In addition, the bilayer membranes form transient non-bilayer structures that relax back towards ordered bilayers with a reduced stress asymmetry. Our study reveals intrinsic limits for the possible magnitude of the transbilayer stress asymmetry and shows that the leaflet tensions represent key parameters for the flip-flop rates.
1 Introduction
Lipid bilayers are built up from two leaflets of lipid molecules. These bilayers have a thickness of only 4 to 5 nanometers but form closed vesicles with much larger sizes, varying from tens of nanometers for nanovesicles to tens of micrometers for giant vesicles. Giant vesicles have become versatile research tools for basic membrane science, bioengineering, and synthetic biology.1–3 Nanovesicles provide delivery platforms for pharmaceutics, nutrition, as well as cosmetics and are now used as nanocarriers for the delivery of dermal and transdermal drugs,4,5 of small interfering RNA therapeutics,6,7 and of mRNA vaccines.7,8In addition, lipid bilayers provide the basic building blocks for all cellular membranes including the outer plasma membrane of all cells, the intracellular membranes within eukaryotic cells, as well as extracellular vesicles such as exosomes and microvesicles. Extracellular vesicles are shed off from almost every type of cell9 and are crucial for the chemical communication between cells. Exosomes are released from multivesicular bodies within eukaryotic cells, whereas microvesicles bud off from the outer plasma membranes. Extracellular vesicles have been intensely studied as possible biomarkers for diseases10,11 and as potential drug delivery systems.12,13
The two leaflets of cellular membranes typically differ in their lipid composition.14 Much effort has been devoted to mimick this compositional asymmetry in synthetic vesicles.3,15,16 For giant vesicles, this asymmetry can now be controlled in a systematic and quantitative manner by low densities of membrane-bound proteins.17 For synthetic nanovesicles, several protocols have been developed to produce such vesicles with two bilayer leaflets that differ in their phospholipid composition.16,18–23
Here, we address another fundamental transbilayer asymmetry related to lipid density and membrane tension. Each leaflet of a bilayer membrane experiences a certain leaflet tension which determines how much this leaflet is stretched or compressed. In general, the two leaflet tensions are different and their difference defines the stress asymmetry of the bilayer. So far, stress asymmetries have been largely ignored in experimental studies even though they are relevant for all bilayer membranes. On the other hand, stress asymmetries can be systematically studied in molecular dynamics simulations. Indeed, a few consequences of small leaflet tensions and stress asymmetries have been studied in previous simulations.24–27 Here, we consider an extended range of leaflet tensions and show that large tensions and asymmetries lead to stress-induced flip-flops of lipids from one leaflet to the other and to the formation of transient nonbilayer structures as illustrated in Fig. 1. As described further below, the nonbilayer structures subsequently undergo a self-healing process, which acts to restore the ordered bilayer structure with a lower stress asymmetry. In this way, our study reveals intrinsic stability limits of bilayer membranes which become unstable when the stress asymmetry exceeds certain limiting values.
 | ||
| Fig. 1 Transient nonbilayer structures arising from instabilities of tensionless bilayers and nanovesicles: (a) globular micelle expelled from the highly compressed upper leaflet of a planar bilayer; and (b) cylindrical micelle expelled from the highly compressed outer leaflet of a nanovesicle. These transient conformations decay via lipid flip-flops which lead to a self-healing process that acts to restore the bilayer structure, see later figures further below as well as the time-lapse Movies M1–M3 in the ESI.† The color coding distinguishes the red-green lipids, initially assembled in the upper and outer leaflets, from the purple-blue lipids, initially assembled in the lower and inner leaflets, which facilitates the visualization of flip-flops. | ||
It is important to distinguish the individual leaflet tensions from the bilayer tension which is equal to the sum of the two leaflet tensions. To avoid membrane rupture, the osmotic conditions have to be adjusted in such a way that both cellular and synthetic membranes experience a relatively low bilayer tension. However, even for vanishing bilayer tension, the individual leaflets can still experience significant leaflet tensions if one leaflet is stretched by a positive leaflet tension whereas the other leaflet is compressed by a negative leaflet tension.
In molecular simulations, the stress asymmetry between the two bilayer leaflets can be controlled by the number of lipids that are initially assembled within the leaflets. Both leaflets are tensionless for a unique reference state in which each leaflet is built up from a specific number of lipids. For planar bilayers, this reference state is easy to determine because it is provided by two leaflets with the same number of lipids. For nanovesicles, the reference state is more difficult to identify because it consists of two leaflets with different lipid numbers. Furthermore, the stress-induced flip-flops and bilayer instabilities are shown to depend on membrane size and curvature. To address this dependence, we study both planar bilayers with vanishing mean curvature and spherical nanovesicles with two different diameters and mean curvatures.
When a lipid molecule flips from one leaflet to the other, the hydrophilic head group of the lipid has to move across the hydrophobic core of the bilayer. The corresponding free energy barrier determines the flip-flop rate via an Arrhenius-like law.28,29 The flip-flops change the stress asymmetry between the two leaflets of a bilayer. Indeed, when we start from a tensionless bilayer with one compressed and one stretched leaflet, flip-flops from the compressed to the stretched leaflet act to reduce the stress asymmetry. Vice versa, the stress asymmetry can be increased by reshuffling lipids from one leaflet to the other.
From an experimental point of view, the measurement of flip-flop rates has been quite challenging.15 For phospholipids, a wide range of flip-flop rates has been reported, with the typical time scale for one flip-flop varying from minutes to days.15,30–38 Likewise, the published values for the inverse flip-flop rates of cholesterol and related sterols were observed to vary from seconds39,40 to milliseconds.41 One important conclusion from our simulation study is that the stress asymmetry between the two leaflet tensions of a bilayer membrane represent key parameters for the flip-flop rates. In the experimental studies, these leaflet tensions are difficult to control and play the role of ‘hidden variables’ that contribute to the uncertainty about the experimentally measured flip-flop rates.
Our paper is organized as follows. First, we study the behavior of planar bilayer patches with a constant total number of lipids. We focus on tensionless bilayers and vary the leaflet tensions by reshuffling lipids from one leaflet to the other. For these bilayers, we determine the tension range for which the bilayer remain (meta)stable on the time scale of the simulations. Outside of this tension range, the lipids undergo flip-flops and the bilayers exhibit structural instabilities. To characterize the tension-dependence of the flip-flop rate, we determine the cumulative distribution functions for the statistics of the first flip-flop event. For planar bilayers, this distribution is well fitted by an exponential distribution, which depends only on one fit parameter, the flip-flop rate. We then discuss the structural instabilities of the bilayer and the resulting transient conformations as in Fig. 1a. In the remaining sections, we extend our computational approach to spherical nanovesicles with two different diameters, for which we find qualitatively similar behavior as for planar bilayers as illustrated in Fig. 1b. One notable difference is the statistics for the onset of flip-flops. The corresponding cumulative distribution has a sigmoidal shape which implies that the flip-flop rate increases with the age of the metastable bilayer. At the end, we summarize our results and discuss extensions to bilayers with multiple lipid components and to cellular membranes with membrane proteins that act as lipid pumps.
2 Results and discussion
2.1 Stability of planar bilayers
First, let us consider planar bilayers with vanishing mean curvature. To avoid bilayer poration and membrane rupture, each bilayer is kept at very low bilayer tension by adjusting the total number of lipids assembled in the bilayer to the size of the simulation box. We focus on one-component bilayers with a total number of 1682 lipids assembled in both leaflets. Such a bilayer is symmetric when each leaflet consists of 841 lipids but becomes asymmetric when the two leaflets contain different number of lipids. When the upper leaflet contains Nul = 870 lipids and the lower leaflet Nll = 812 lipids, for example, the upper leaflet is compressed and experiences a negative leaflet tension Σul < 0 whereas the lower leaflet is stretched and subject to a positive leaflet tension Σll > 0, see upper panel of Fig. 2. The computation of the leaflet tensions is based on the stress profile across the bilayer as described in the Methods section and illustrated in Fig. S1 of the ESI.† | ||
| Fig. 2 Stable and unstable states of planar bilayers, assembled from Nul lipids in the upper leaflet and Nll = 1682 − Nul lipids in the lower leaflet. The blue and red data represent the upper and lower leaflet tensions, Σul and Σll, as functions (a) of Nul and (b) of area per lipid, aul. The green data correspond to the bilayer tension Σ = Σul + Σll, which is close to zero. During the run time of 12.5 μs, we observed no flip-flops within the stability regime (white), corresponding to 737 ≤ Nul ≤ 945. The left vertical line at Nul = 957 represents the instability line at which the bilayers become unstable via flip-flops from the compressed upper to the stretched lower leaflet. The right vertical line at Nul = 725 corresponds to the instability line at which the bilayers become unstable via flip-flops from the compressed lower to the stretched upper leaflet. Each data point represents the mean value of three independent simulations. Apart from the left-most data, the error bars are smaller than the size of the symbols used for the data points. The numerical values of the data are given in Table S1 (ESI†). | ||
In Fig. 2a, the leaflet tensions Σul and Σll are plotted as a function of the lipid number Nul in the upper leaflet. In Fig. 2b, the same data are shown as a function of the area per lipid, aul, in the upper leaflet. For both leaflets, the numerical values of lipid numbers, areas per lipid, and leaflet tensions are provided in Table S1 (ESI†). The areas per lipid are in units of d2, the tensions in units of kBT/d2 where d is the diameter of the beads used in our coarse-grained simulation approach and kBT represents the thermal energy, see Methods section. To simplify the mathematical formulas, we will use the short-hand notation γ ≡ kBT/d2 for the basic tension unit.
During the simulation time of 12.5 μs, the lipids did not undergo any flip-flops in the stability regime which is characterized by lipid numbers Nul within the range 945 ≥ Nul ≥ 737 and by upper leaflet tensions Σul with −1.86γ ≤ Σul ≤ + 2.00γ. Flip-flops from the upper to the lower leaflet were observed, however, for Nul ≥ 957, corresponding to the left instability regime in Fig. 2. For Nul = 957, which defines the left instability line in Fig. 2, the upper leaflet was initially compressed with Σul = −2.21γ, which induced flip-flops from the compressed upper to the stretched lower leaflet. As the lipid number in the upper leaflet was increased to Nul > 957, that is, into the left instability regime in Fig. 2, flip-flops became more frequent. On the other hand, for Nul ≤ 725 and Σul ≥ 2.13γ, which defines the right instability region in Fig. 2, lipids underwent flip-flops from the compressed lower leaflet to the stretched upper one.
2.2 Tensionless and asymmetric bilayers
Inspection of Fig. 2 shows that both leaflet tensions vanish for the symmetric bilayer with Nul = Nll = 841 ≡ N0 and the same lipid areas aul = all = 1.271 ≡ a0 in both leaflets. For this tensionless reference state, both leaflets have the same area A0 = N0a0 = 1023.5d2. As we reshuffle lipids from one leaflet to the other, the leaflet areas Aul = Nulaul and All = Nllall remain essentially constant and close to A0 = N0a0. This feature reflects the constraint of vanishing bilayer tension, Σ = Σul + Σll = 0, during the reshuffling of the lipid molecules between the two leaflets and implies the relation all = aulNul/Nll between the lipid areas in the two leaflets. The tensionless bilayer becomes asymmetric when the two leaflets contain different lipid numbers Nul and Nll ≠ Nul. This lipid number asymmetry is equivalent to a density asymmetry as described by different areas per lipid in the two leaflets. In addition, the two leaflet tensions Σul and Σll = −Σul have the same magnitude but opposite signs, corresponding to one stretched and one compressed leaflet. In what follows, we will focus on the case of a compressed upper leaflet and a stretched lower one, corresponding to Nul > N0 and Nll = 1682 − Nul < N0. In this case, the upper leaflet tension Σul is negative and the lower leaflet tension Σll is positive.The stress-asymmetry of a planar bilayer can be described by the difference in the leaflet tensions as given by
| ΔΣpl ≡ Σul − Σll. | (1) |
2.3 Flip-flops in planar bilayers
To determine the kinetic rates of lipid flip-flops, we considered several ensembles of bilayers. Each ensemble consisted of more than 120 bilayers that were assembled from the same lipid numbers Nul and Nll and, thus, experienced the same leaflet tensions as long as they remained in their initial metastable states. More precisely, the bilayers experienced the same initial leaflet tensions until time t1, at which the first flip-flop occurred. The statistics of t1 can be described by the cumulative distribution function Pcdf(t) that represents the probability that the first flip-flop occurs at time t1 ≤ t. From a numerical point of view, the cumulative distribution function Pcdf(t) is more reliable than the probability density function dPexp/dt because, in contrast to the latter function, Pcdf(t) does not require any binning of the data. Furthermore, in the present context, the complementary probability distribution 1 − Pcdf(t) represents the survival probability of the metastable bilayer state without any flip-flops up to time t.The measured distributions Pcdf(t) are displayed in Fig. 3 for planar bilayers with Nul = 986, 1015, and 1073 lipids, corresponding to the black circles, red squares, and blue diamonds, respectively. All three data sets can be well fitted by an exponential distribution of the form
| Pexp(t) = 1 − exp(−ωplt) | (2) |
 | ||
| Fig. 3 Cumulative distribution function Pcdfversus time t, for a planar bilayer with Nul lipids in the upper leaflet and Nll = 1682 − Nul lipids in the lower leaflet. Three sets of data for Nul = 986 (black circles), Nul = 1015 (red squares), and Nul = 1073 (blue diamonds). These data sets are well fitted, using least squares, by an exponential distribution (broken lines) as in eqn (2), which involves only a single fit parameter, the flip-flop rate ωpl. Each data set represents the outcome of more than 120 statistically independent simulations, see Table S2 (ESI†), which also provides the numerical parameter values of the bilayers. Inset: monotonic increase of the flip-flop rate ωpl with the absolute value |ΔΣpl| = |Σul − Σll| of the stress asymmetry between the two leaflets. | ||
In order to undergo a flip-flop, a lipid has to overcome the free energy barrier arising from the hydrophobic core of the bilayer. When we compress the upper leaflet and stretch the lower one, the flip-flop rate increases monotonically with the stress asymmetry as shown in the inset of Fig. 3. In this inset, the observed flip-flop rate ωpl in the planar bilayer is displayed versus the absolute value |ΔΣpl| of the stress asymmetry as defined by eqn (1); the numerical values of stress asymmetry and flip-flop rate are in Table S2 (ESI†). Thus, our simulations imply that the free energy barrier for flip-flops is decreased as we increase the stress asymmetry |ΔΣpl| between the two leaflets of a tensionless bilayer.
2.4 Instability and self-healing of planar bilayers
In addition to the flip-flops of lipid molecules, we also observed structural instabilities of the bilayers as we increased the lipid number Nul in the upper leaflet beyond the left instability line at Nul = 957 in Fig. 2. One example for such a structural instability is shown in Fig. 4 and in the time-lapse Movie M1 (ESI†). In this example, the bilayer was initially assembled with Nul = 986 lipids in the upper leaflet and Nll = 1682 − Nul = 696 lipids in the lower leaflet. The structural instability of the bilayer proceeded by the expulsion of about 100 lipids from the compressed upper leaflet, which then formed a globular micelle. | ||
| Fig. 4 Structural instability and self-healing of a tensionless planar bilayer. At time t = 0, the bilayer is initially assembled from Nul = 986 red-green lipids in the compressed upper leaflet and from Nll = 696 purple-blue lipids in the stretched lower leaflet: (a) at t = 200 ns, the metastable bilayer bulges towards the upper leaflet; (b) at t = 1000 ns, a globular micelle has been formed from about 100 red-green lipids that were expelled from the upper leaflet; (c) at t = 1120 ns, red-green lipids move towards the stretched lower leaflet along the contact line between micelle and bilayer; and (d) this lipid exchange leads to a self-healing process of the bilayer that is completed at t = 1700 ns. At this time point, 93 red-green lipids have moved from the upper to the lower leaflet. The restored bilayer remains stable without flip-flops until the end of the simulations at t = 12.5 μs. For more details on the time course of this process, see time-lapse Movie M1 (ESI†). | ||
The time-lapse Movie M1 (ESI†) can be decomposed into four main stages as shown in Fig. 4. After the initial assembly, the bilayer remains in a metastable state without flip-flops for hundreds of nanoseconds and curves towards the upper leaflet, see the simulation snapshot after 200 ns in Fig. 4a, before it becomes unstable. After 1000 ns, the upper leaflet has expelled some lipids that form a globular micelle, see Fig. 4b. The micelle consists of red-green lipids that were initially assembled in the compressed upper leaflet. Along the contact line between micelle and bilayer segment, we observe frequent exchanges of lipids towards the lower leaflet as can be concluded from Fig. 4c. This lipid exchange increases the number of lipids in the lower leaflet and decreases the number of lipids in the upper leaflet. Finally, after 1700 ns, the conventional bilayer structure has been restored, see Fig. 4d, where the lower leaflet now contains both the blue-purple lipids, from which this leaflet was initially assembled, and 93 red-green lipids that moved from the upper to the lower leaflet. After this self-healing process, the bilayer remained again stable without flip-flops until the end of the simulations at time t = 12.5 μs. Note that the expelled lipids in Fig. 4b form a micelle rather than a bilayer enclosing a certain amount of water, in contrast to the much larger blebs released from the plasma membranes of cells.
In order to study how the lipid flip-flops and bilayer instabilities depend on membrane size and curvature, we extend our simulations to spherical nanovesicles with two different diameters. The larger nanovesicle has a diameter of 23.8d or 19 nm, the smaller one a diameter of 16.3d or 13 nm. The computation of these diameters is described in the Methods section. The mean curvatures of the vesicle membranes are equal to the inverse radii of these vesicles. For both vesicle sizes, we find stable and unstable bilayers of the nanovesicles, in close analogy to the planar bilayers.
2.5 Stability of larger nanovesicles with 19 nm diameter
Next, let us consider the larger nanovesicles with a diameter of 19 nm. The bilayers of the nanovesicles are assembled from a fixed total number of 2875 lipids, with Nil lipids in the inner leaflet and Nol = 2875 − Nil lipids in the outer one. We use the computational approach described in the Methods section to determine the leaflet tensions Σol and Σilviaeqn (6) and the areas per lipid, aol and ail, of the two leaflets viaeqn (9). The computation of the leaflet tensions is again based on the stress profile s(r) across the bilayer which now depends on the radial coordinate r as illustrated in Fig. S2 (ESI†). The radial coordinate measures the distance from the center of the spherical shapes. We focus again on bilayers with bilayer tension Σ = Σol + Σil close to zero.In Fig. 5a, the two leaflet tensions are plotted as a function of the lipid number Nol in the outer leaflet; in Fig. 5b, the same tensions are plotted versus the lipid area aol in the outer leaflet. Inspection of Fig. 5 and the numerical values in Table S3 (ESI†) shows that both leaflet tensions vanish when the outer leaflet contains between 1893 and 1935 lipids. Linear interpolation then leads to tensionless leaflets for Nol,0 = 1921 lipids in the outer leaflet and Nil,0 = 954 lipids in the inner one. Thus, in contrast to planar bilayers, nanovesicles with two tensionless leaflets are now characterized by very different lipid numbers in the outer and inner leaflet. Indeed, for the larger nanovesicles considered here, the lipid number in the tensionless outer leaflet is more than twice as large as the one in the tensionless inner leaflet. Likewise, for these tensionless leaflets, the two areas per leaflet are also quite different with aol,0 = 1.11d2 in the outer leaflet and ail,0 = 1.45d2 in the inner leaflet. Because the area per lipid in the tensionless outer leaflet is smaller than the area per lipid in the tensionless inner leaflet, the latter leaflet is more loosely packed than the tensionless outer leaflet. In fact, inspection of Table S3 (ESI†) reveals that the inequality aol < ail applies to the whole stability regime of the larger nanovesicles which implies that the inner leaflet of such a vesicle is always more loosely packed than the outer leaflet.
 | ||
| Fig. 5 Stable and unstable states of larger nanovesicles, assembled from Nol lipids in the outer leaflet and Nil = 2875 − Nol lipids in the inner leaflet. The vesicles have a diameter of 23.8d or 19 nm. The blue and red data represent the outer and inner leaflet tensions, Σol and Σil, as functions (a) of the lipid number Nol and (b) of the area per lipid, aol, in the outer leaflet. The green data correspond to the bilayer tension Σ = Σol + Σil, which is close to zero. During the run time of 12.5 μs, we observed no flip-flops within the stability regime (white), corresponding to 1775 ≤ Nol ≤ 2095. The left vertical line at Nol = 2105 represents the instability line at which the lipids start to undergo flip-flops from the compressed outer to the stretched inner leaflet. The right vertical line at Nol = 1755 represents the instability line at which the lipids start to undergo flip-flops from the compressed inner to the stretched outer leaflet. Each data point represents the mean value of three independent simulations. The error bars are smaller than the symbols used for the data points. The numerical values of the data are provided in Table S3 (ESI†). | ||
When we start from tensionless leaflets and reshuffle some lipids between these leaflets, we obtain nonzero leaflet tensions Σol and Σil = −Σol. The two leaflets form bilayers that remain stable for the lipid number range 1775 ≤ Nol ≤ 2095 and for the leaflet tension range 1.60γ ≥ Σol ≥ −1.94γ in the outer leaflet, see Fig. 5. Flip-flops from the compressed inner to the stretched outer leaflet are observed for Nol ≤ 1755 and Σol ≥ + 1.78γ, corresponding to the right shaded region in Fig. 5. Flip-flops from the compressed outer to the stretched inner leaflet occur for Nol ≥ 2105 and Σol ≤ −1.97γ, which defines the left shaded region in Fig. 5. Within these two instability regimes with Nol < 1755 and Nol > 2105, we also observe structural instabilities of the lipid bilayers in addition to the flip-flops.
2.6 Stress-asymmetries in nanovesicles
As shown in Fig. 5, the tensionless bilayer of a nanovesicle may experience significant leaflet tensions Σol and Σil = −Σol, corresponding to one compressed and one stretched leaflet. As in the case of planar bilayers, the associated stress asymmetry can be described in two ways. First, by the difference of the two leaflet tensions as given by| ΔΣve ≡ Σol − Σil. | (3) |
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ve of the stress profile s(r), see eqn (11) in the Methods section.
ve of the stress profile s(r), see eqn (11) in the Methods section.
The stress-asymmetries ΔΣve and ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ve become large and negative as we move away from the tensionless leaflets by increasing the lipid number Nol in the outer leaflet and decreasing the lipid number Nil in the inner leaflet. Furthermore, these stress-asymmetries become large and positive as we move away from the tensionless leaflets by decreasing the lipid number Nol in the outer leaflet and increasing the lipid number Nil in the inner leaflet. The numerical values of the stress asymmetries for the larger nanovesicles are included in Table S3 (ESI†).
ve become large and negative as we move away from the tensionless leaflets by increasing the lipid number Nol in the outer leaflet and decreasing the lipid number Nil in the inner leaflet. Furthermore, these stress-asymmetries become large and positive as we move away from the tensionless leaflets by decreasing the lipid number Nol in the outer leaflet and increasing the lipid number Nil in the inner leaflet. The numerical values of the stress asymmetries for the larger nanovesicles are included in Table S3 (ESI†).
2.7 Lipid flip-flops in larger nanovesicles
We now focus on the left shaded region in Fig. 5, corresponding to compressed outer leaflets and stretched inner ones. Within this instability region, the lipids undergo flip-flops from the outer to the inner leaflets. To determine the kinetic rates, we examined again different ensembles of nanovesicles. Each ensemble consisted of more than 60 nanovesicles that were initially assembled from the same lipid numbers Nol and Nil and, thus, experienced the same leaflet tensions as long as they remained in their initial states. More precisely, the bilayers experienced the same initial leaflet tensions until time t1, at which the first flip-flop occurred. As in the case of planar bilayers, the statistics of t1 is again described by the cumulative distribution function Pcdf(t) that represents the probability that the first flip-flop occurs at time t1 ≤ t. This distribution function is depicted in Fig. 6, the numerical values of the data are given in Table S4 (ESI†). | ||
| Fig. 6 Cumulative distribution function Pcdfversus time t for nanovesicles with a diameter of 19 nm, assembled from Nol + Nil = 2875 lipids. Three sets of data are displayed with Nol = 2105 (black circles), Nol = 2125 (red squares), and Nol = 2150 (blue diamonds) lipids in the outer leaflet, which belong to the left instability regime in Fig. 5. The three sets of data are well fitted, using least squares, to Weibull distributions (broken lines) as in eqn (4), which depend on two parameters, the shape parameter k and the rate parameter ωve. The parameter values as obtained from the Weibull plots in Fig. S3 are included in Table S4 (ESI†). Each data set represents the outcome of at least 70 statistically independent simulations, see Table S4 (ESI†), which also provides the numerical parameter values of the vesicles. Inset: monotonic increase of the rate parameter ωve with the absolute value |ΔΣve| of the stress asymmetry as defined by eqn (3). | ||
The cumulative distribution functions in Fig. 6 have a sigmoidal shape with a point of inflection at intermediate times. The sigmoidal shape is qualitatively different from the exponential function in eqn (2) that was used to fit the onset of flip-flops in planar bilayers. Distribution functions with a sigmoidal shape can be obtained by generalizing the exponential distributions in eqn (2) to Weibull distributions as provided by42
| PWei(t) = 1 − exp[−(ωvet)k]. | (4) |
The average first flip-flop time 〈t1〉, which also represents the average life time of the metastable bilayer states, is proportional to the inverse rate parameter ωve−1. As explained in the Methods section, the shape parameter k and the rate parameter ωve can be estimated from so-called Weibull plots of the observed cumulative distribution function.45 The Weibull plots for the larger nanovesicles are displayed in Fig. S3 (ESI†), the numerical values for the shape parameter k and the rate parameter ωve are given in Table S6 (ESI†). In all cases, the parameter k is found to be greater than one which corroborates the sigmoidal shape of the distributions and implies that the instantaneous flip-flop rate increases with the age of the metastable state.
In mathematical statistics, the instantaneous rate is known as the hazard rate and equal to the ratio of the probability density function dPcdf/dt to the survival probability 1 − Pcdf(t).46,47 The only distribution that leads to a constant and age-independent hazard rate is the exponential distribution. Therefore, the sigmoidal shape of the cumulative distribution functions as observed here for the life time of the metastable bilayer states implies ageing of these nanovesicle states.
2.8 Instability and self-healing of larger nanovesicles
When we move beyond the instability lines in Fig. 5, we observe structural instabilities of the bilayers. We focus on the regimes, in which the outer leaflet is significantly compressed by a negative leaflet tension Σol < 0 and the inner leaflet is significantly stretched by a positive leaflet tension Σil > 0. During such a structural instability, the transformation of the nanovesicle proceeds via four stages. One example is displayed in Fig. 7. The details of this shape transformation are displayed in time-lapse Movie M2 (ESI†). | ||
| Fig. 7 Structural instability and self-healing process of larger nanovesicle with a diameter of 19 nm. At time t = 0, the bilayer is assembled from Nol = 2105 and Nil = 770 lipids and the vesicle volume is adjusted in such a way that the bilayer tension is close to zero, which leads to a compressed outer leaflet with negative leaflet tension Σol = −1.97kBT/d2: (a) at t = 780 ns, the compressed outer leaflet exhibits some kinks; (b) at t = 1720 ns, a cylindrical micelle has been formed from about 180 red-green lipids that were expelled from the outer leaflet; (c) at t = 2160 ns, lipids move towards the stretched inner leaflet along the contact line between micelle and bilayer; and (d) at t = 2710 ns, the self-healing process via stress-induced lipid exchange has been completed and 111 red-green lipids have moved to the inner leaflet. The restored bilayer undergoes no further flip-flops until the end of the simulations at t = 12.5 μs. For more details on the time course of this process, see time-lapse Movie M2 (ESI†). Color coding as in Fig. 1. | ||
In Fig. 7, we see typical snapshots of an individual nanovesicle with a diameter of 19 nm. The bilayer of the vesicle is initially assembled from Nol = 2105 lipids in the outer and Nil = 770 lipids in the inner leaflet. The outer leaflet is compressed by the negative leaflet tension Σol= −1.97γ, the inner leaflet is stretched by the positive leaflet tension Σil = 1.94γ. During the first 1300 ns, the bilayer of the vesicle undergoes shape fluctuations that appear to be ‘normal’ until the outer leaflet starts to develop a protrusion by expelling some lipids. This protrusion grows rapidly into a cylindrical micelle, see Movie M2 (ESI†), which reaches its maximal extension after 1720 ns as shown in Fig. 7b. Somewhat later, some lipids move into the inner leaflet, primarily along the contact line between the micelle and the bilayer, see snapshot at 2160 ns in Fig. 7c. This lipid exchange decreases the number of lipids within the compressed outer leaflet and increases the number of lipids within the stretched inner leaflet until 111 red-green lipids have been moved from the outer to the inner leaflet and the ordered bilayer structure has been restored at 2710 ns as shown in Fig. 7d. After this time point, the restored bilayer undergoes no further flip-flops until the end of our simulations at 12.5 μs. Note that the expelled lipids in Fig. 7b form a micelle rather than a bilayer enclosing a certain amount of water, in contrast to the much larger blebs released from the plasma membranes of cells.
2.9 Stability of smaller nanovesicles with 13 nm diameter
To examine membranes with a higher curvature, we now consider smaller nanovesicles with a diameter of 13 nm. The bilayers of these nanovesicles are assembled from a fixed total number of 1317 lipids, with Nil in the inner leaflet and Nol = 1317 − Nil in the outer one. Using the same approach as for the larger nanovesicles, we compute the stress profiles s(r), as illustrated in Fig. S4 (ESI†), from which we obtain the leaflet tensions Σol and Σil with bilayer tension Σ = Σol + Σil close to zero, see Fig. 8 and the numerical values in Table S5 (ESI†). Both leaflet tensions vanish for Nol,0 = 982 and Nil,0 = 335 as obtained by linear interpolation of the data for Nol = 977 and Nol = 987. Note that the tensionless outer leaflet now contains almost three times as many lipids as the tensionless inner leaflet. For these tensionless leaflets, the two areas per leaflet are also quite different with aol,0 = 1.09d2 and ail,0 = 1.71d2, which implies that the tensionless inner leaflet is again more loosely packed compared to the tensionless outer leaflet. In fact, inspection of Table S5 (ESI†) reveals that the inequality aol < ail applies to the whole stability regime of the smaller nanovesicles which implies that the inner leaflet of such a vesicle is always more loosely packed than the outer leaflet. | ||
| Fig. 8 Stable and unstable states of spherical nanovesicles, assembled from 1317 lipids with Nol lipids in the outer leaflet and Nil = 1317 − Nol lipids in the inner leaflet. The vesicles have a diameter of 16.3d or 13 nm. The blue and red data represent the outer and inner leaflet tensions, Σol and Σil, as functions (a) of the lipid number Nol and (b) of the area per lipid, aol, in the outer leaflet. The green data correspond to the bilayer tension Σ = Σol + Σil, which is close to zero. During the run time of 12.5 μs, we observed no flip-flops within the stability regime (white), corresponding to 952 ≤ Nol ≤ 1037. The left vertical line at Nol = 1041 represents the instability line at which the bilayers start to undergo flip-flops from the compressed outer to the stretched inner leaflet. The right vertical line at Nol = 947 represents the instability line at which the bilayers start to undergo flip-flops from the compressed inner to the stretched outer leaflet. Each data point represents the mean value of three independent simulations. The error bars are smaller than the symbols used for the data points. The numerical values of the data are provided in Table S5 (ESI†). | ||
When the lipid numbers assembled in the two leaflets differ from those for the tensionless leaflets, we obtain nonzero leaflet tensions Σol and Σil = −Σol as displayed in Fig. 8. Inspection of this figure and the numerical values in Table S5 (ESI†) shows that the bilayers of the small nanovesicles are stable when the lipid number Nol of the outer leaflet lies within the range 952 ≤ Nol ≤ 1037 and the outer leaflet tension Σol satisfies 0.72γ ≥ Σol ≥ −1.33γ. Note that this Σol-range is now quite asymmetric with respect to Σol = 0, a feature that is directly visible in Fig. 8. The lipid bilayers of the nanovesicles exhibit flip-flops from the compressed inner to the stretched outer leaflet for Nol ≤ 947 and positive outer leaflet tension Σol ≥ + 0.79γ, corresponding to the right shaded region in Fig. 8. Flip-flops from the compressed outer to the stretched inner leaflet occur for Nol ≥ 1041 and negative outer leaflet tension Σol ≤ −1.68γ, which defines the left shaded region in Fig. 8. As we move deeper into the two instability regimes with Nol < 947 and Nol > 1041, we observe structural instabilities of the bilayers in addition to the flip-flops.
2.10 Lipid flip-flops in smaller nanovesicles
We focus on the left-shaded region in Fig. 8, in which the lipids undergo stress-induced flip-flops from the compressed outer leaflet to the stretched inner one. The corresponding cumulative distribution functions Pcdf(t) are displayed in Fig. 9. These distributions have again a sigmoidal shape and look qualitatively similar to those in Fig. 6, as obtained for the larger nanovesicles. Furthermore, the three sets of data in Fig. 9 corresponding to three different stress asymmetries are again well fitted by Weibull functions as determined by the Weibull plots in Fig. S5 (ESI†). The corresponding numerical parameter values are provided in Table S6 (ESI†). | ||
| Fig. 9 Cumulative distribution function Pcdfversus time t for nanovesicles with a diameter of 13 nm, assembled from a total number of Nil + Nol = 1317 lipids: three sets of data for lipid numbers Nol = 1041 (black circles), Nol = 1046 (red squares), and Nol = 1051 (blue diamonds) in the outer leaflets. All three data sets belong to the left instability regime in Fig. 8. These data are well fitted, using least squares, to Weibull distributions as in eqn (4) (broken lines), which depend on two parameters, the shape parameter k and the rate parameter ωve. The parameter values as obtained from the Weibull plots in Fig. S5 (ESI†) are provided in Table S6 (ESI†). Each data set represents the outcome of more than 60 statistically independent simulations, see Table S6 (ESI†), which also provides the numerical parameter values of the vesicles. Inset: Monotonic increase of the rate parameter ωve with the absolute value |ΔΣve| of the stress asymmetry defined by eqn (3). | ||
2.11 Instability and self-healing of smaller nanovesicles
As we move into the instability regimes corresponding to the shaded regions in Fig. 8, the bilayers undergo structural instabilities in addition to the lipid flip-flops. One example is displayed in Fig. S6 and Movie M3 (ESI†). The bilayer of the vesicle is initially assembled from Nol = 1041 lipids in the outer and Nil = 276 lipids in the inner leaflet. The outer leaflet is compressed by the negative leaflet tension Σol = −1.68γ, the inner leaflet is stretched by the positive leaflet tension Σil = 1.71γ. During the first 3400 ns, the bilayer of the vesicle undergoes strong shape fluctuations that have a kinky appearance until the outer leaflet starts to develop a protrusion by expelling some lipids. This protrusion grows into a cylindrical micelle, see Movie M3 (ESI†), which reaches its maximal extension after about 4400 ns as shown in Fig. S6b (ESI†). Somewhat later, some lipids move into the inner leaflet, primarily along the contact line between the micelle and the bilayer, see snapshot at 4800 ns in Fig. S6c (ESI†). This exchange of lipids decreases the number of lipids within the compressed outer leaflet and increases the number of lipids within the stretched inner leaflet. This reshuffling process continues until 57 red-green lipids have been moved from the outer to the inner leaflet and the ordered bilayer structure has been restored after 2710 ns, see Fig. S6d (ESI†). The restored bilayer undergoes no further flip-flops until the end of the simulations at 12.5 μs.2.12 Comparison between different bilayer systems
We now compare the results for the three bilayer systems as provided by the planar bilayer as well as by the larger and smaller nanovesicles. The three bilayer systems also differ in their mean curvature which vanishes for the planar bilayer and has the values (9.5 nm)−1 and (6.5 nm)−1 for the large and small nanovesicles, corresponding to the inverse radii of these vesicles. All three systems exhibit qualitatively similar but quantitatively different behavior.| Left instability line | Stability regime | Right instability line | |
|---|---|---|---|
| Planar bilayers | Σ ul = −2.21γ | −1.86γ ≤ Σul ≤ + 2.00γ | Σ ul = + 2.13γ |
| Large nanovesicles | Σ ol = −1.97γ | −1.94γ ≤ Σol ≤ + 1.60γ | Σ ol = + 1.78γ |
| Small nanovesicles | Σ ol = −1.68γ | −1.33γ ≤ Σol ≤ + 0.72γ | Σ ol = + 0.79γ |
Another quantity by which one can characterize the instability lines and the stability regimes is the first moment of the stress profiles which provides the torque densities, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) pl and
pl and ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ve, as computed viaeqn (10) for the planar bilayers and viaeqn (11) for the nanovesicles. In Table S7 (ESI†), we characterize the stability regime together with the two instability lines in terms of these torque densities, confirming that the stability regime shrinks as we increase the mean curvature of the bilayer system.
ve, as computed viaeqn (10) for the planar bilayers and viaeqn (11) for the nanovesicles. In Table S7 (ESI†), we characterize the stability regime together with the two instability lines in terms of these torque densities, confirming that the stability regime shrinks as we increase the mean curvature of the bilayer system.
Finally, we compare the cumulative distribution functions for the onset of flip-flops in the unstable regimes of the nanovesicles, as displayed in Fig. 6 and 9. We rescale the time t by the rate parameter ωve for the nanovesicles, thereby introducing the dimensionless time s = ωvet. As a result, we obtain the master curve in Fig. S7 (ESI†) which shows that all six data sets for the large and small nanovesicles lie on top of each other, further corroborating the accuracy of the deduced flip-flop rates.
3 Summary and outlook
In summary, we studied the stable and unstable states of three bilayer systems as provided by planar bilayers and nanovesicles with two different diameters. In all three systems, the bilayers were tensionless and characterized by (almost) zero bilayer tension whereas the two leaflets experienced variable leaflet tensions of opposite sign. For each of these systems, we identified a stability regime of low leaflet tensions, in which the bilayers do not undergo flip-flops and retain their ordered bilayer structure during the time scale of our simulations (Fig. 2, 5, and 8). Each of these stability regimes are bounded by two instability lines, at which the bilayers start to undergo stress-induced flip-flops. When the leaflet tensions are increased beyond these instability lines, the bilayers undergo both flip-flops and structural instabilities. Comparison of the results for the three bilayer systems (Table 1) shows that the stability regime is reduced when the bilayer membrane is more strongly curved.The most stable states within the stability regimes are provided by the reference states with two tensionless leaflets. For planar bilayers, these reference states correspond to symmetric bilayers for which the two leaflets contain the same number of lipids and are characterized by the same area per lipid (Fig. 2 and Table S1, ESI†). Both symmetries are lost for nanovesicles, for which the reference states consist of two tensionless leaflets that differ both in their number of lipids and in their area per lipid (Fig. 5 and Table S3 as well as Fig. 8 and Table S5, ESI†) Thus, in contrast to planar bilayers, the most stable bilayer states of nanovesicles with two tensionless leaflets cannot be obtained by symmetry arguments related to the lipid numbers or the areas per lipid.
In all three bilayer systems, the onset of stress-induced flip-flops can be characterized by a cumulative distribution function Pcdf(t), which is complementary to the survival probability of the metastable states of the bilayers as given by 1 − Pcdf(t). For the planar bilayers, the cumulative distribution function is well fitted by an exponential distribution (Fig. 3). For the nanovesicles, the cumulative distribution function has a sigmoidal shape (Fig. 6 and 9), which implies that the instantaneous flip-flop rate is not constant but increases with the age of the metastable bilayer. In the latter case, the cumulative distribution functions are well fitted by a Weibull distribution as described by eqn (4). The flip-flop rates ωpl and ωve deduced from the distribution functions determine the average time scale for the first stress-induced flip-flop that is observed when the bilayer becomes unstable. For the large and small nanovesicles, all six data sets form a single master curve when plotted against the rescaled time s = ωvet (Fig. S7, ESI†). This master curve corroborates the reliability of the deduced flip-flop rates.
In addition, all three bilayer systems undergo structural instabilities that proceed via four main stages (Fig. 4, 7, and Fig. S6, ESI†). When the upper leaflet of a planar bilayer or the outer leaflet of a nanovesicle are highly compressed, these leaflets expel many lipids that form a globular (Fig. 4b) or cylindrical micelle (Fig. 7b and Fig. S6b, ESI†). Subsequently, a self-healing process sets in that is mediated via flip-flops towards the highly stretched lower and inner leaflets. A large fraction of these flip-flops is observed along the contact lines between the micelles and the remaining bilayers (Fig. 4c, 7c, and Fig. S6c, ESI†). As a result of these flip-flops, the micelles are reintegrated into the bilayers, which then remain in a metastable state until the end of the simulations (Fig. 4d, 7d, and Fig. S6d, ESI†).
In this study, we focused on one-component bilayers for the sake of computational simplicity but our results can be directly generalized to multi-component bilayers as well, provided the bilayer leaflets are fluid and have a laterally uniform composition. The latter requirement does not apply to coexistence regions of the phase diagram, in which the bilayers undergo lipid phase separation. On the other hand, in the one-phase regions of the phase diagram, the leaflet tensions describe the local stress within the leaflets, irrespective of the number of molecular components as long as the leaflets remain in a fluid state and do not phase separate. Thus, for a multi-component bilayer, the different components will have different areas per lipid but the average molecular area in each leaflet will again determine the corresponding leaflet tension and vice versa. Furthermore, for a two-dimensional leaflet, the associated leaflet tension plays the same role as the pressure in a three-dimensional liquid. Therefore, in the absence of hydrodynamic flows within the bilayer membranes, the leaflet tensions must be uniform along the membranes and will again govern the flip-flop rates, which will now differ for different lipid components.
Multi-component bilayers can undergo lipid phase separation as observed for nanovesicles containing the two phospholipids DPPC and POPC.18 The inner leaflet of these nanovesicles consisted of a uniform POPC-rich phase whereas the outer leaflet underwent lipid phase separation into a DPPC-rich and a POPC-rich phase. The DPPC-rich phase was not fluid but formed a gel phase. In such a situation, the phase-separated leaflet involves a line tension that arises from the domain boundaries between the DPPC-rich and the POPC-rich phase. Such a line tension would make another contribution to the free energy, of the nanovesicle, in addition to the leaflet tensions, but plays no role for bilayer leaflets with a laterally uniform composition as considered here.
Multi-component bilayers could also be studied in order to measure the cumulative distribution function for the onset of flip-flops experimentally. To prepare a population of vesicles with a significant stress asymmetry, one might use the enzymatic conversion of phospholipid headgroups in the outer leaflet as demonstrated by the conversion of the PS to the PE headgroup21 and of the PC headgroup to the PS and PE headgroups.22 After such a vesicle population has been prepared, one would look for flip-flops and measure the corresponding flip-flop times, which are likely to exceed the flip-flop times observed in our simulations by several orders of magnitude. Studying a dilute dispersion of liposomes and adding local lipid probes to their membranes, it may also be possible to distinguish flip-flops in the same vesicle from those in different vesicles. In this way, one could determine the cumulative distribution function Pcdf(t) experimentally, in close analogy to our simulation study. If this distribution has a sigmoidal shape as in Fig. 6 and 9, the flip-flop rate is not constant but depends on the age of the nanovesicles.
Our results are also relevant for the behavior of biological membranes which contain membrane proteins that change the flip-flop rates of the lipids. Three families of such membrane proteins have been identified. One family of membrane proteins, so-called scramblases, act to reduce the free energy barrier for the flip-flops, thereby facilitating bi-directional and reversible flip-flops between the two bilayer leaflets.14,48–51 In addition, two families of membrane proteins that hydrolyze ATP have also been identified: Flippases actively pump lipids from the exoplasmic to the cytoplasmic leaflet of the membranes whereas floppases hydrolyze ATP to pump lipids in the opposite direction, i.e., from the cytoplasmic to the exoplasmic leaflet.14,52–54
Because the activity of a scramblase is not coupled to ATP hydrolysis, such a membrane protein acts to reduce the stress asymmetry between the two leaflets. In particular, scramblases should further increase the flip-flop rate from a compressed to a stretched leaflet. On the other hand, both flippases and floppases will increase the stress asymmetry. As an example, consider a nanovesicle with reconstituted flippase proteins that move lipids from the inner to the outer leaflet, thereby compressing the outer leaflet and stretching the inner one. When we reach a sufficiently large stress asymmetry between the two leaflets, the nanovesicle is expected to undergo structural instabilities as displayed in Fig. 7 and Fig. S6 (ESI†). Therefore, using nanovesicles with reconstituted flippases, these structural instabilities should become accessible to systematic experimental studies.
4 Methods
4.1 Molecular modelling and interactions
Our coarse-grained simulation approach is provided by the dissipative particle dynamics (DPD) simulation method.55,56 In DPD, the lipid and water molecules are modelled as soft beads that interact with pairwise additive forces. These forces conserve momentum locally, which ensures a reliable description of hydrodynamics. The aqueous liquid consists of water (W) beads that have a diameter d of about 0.8 nm and thus represent small volumes of the liquid. The lipids consist of three headgroup (H) beads and two hydrocarbaon chains, each of which is built up from six chain (C) beads, corresponding to the SH lipids used in our previous simulation study.25 All beads have the same diameter d, which provides the basic length scale and the cut-off for the DPD forces; for further details of our method, see ref. 25. The DPD method has been applied to a large variety of membrane topics including diffusion through membranes.57 We performed all simulations using the MD code LAMMPS (Large Scale Atomic/Molecular Massively Parallel Simulator).584.2 Simulation parameters and bilayer geometry
We study planar bilayers consisting of 1682 lipids in total. The reference state with two tensionless leaflets is provided by the symmetric bilayer with 841 lipids in each leaflet. Asymmetric bilayers are obtained if the upper and lower leaflet contain different lipid numbers Nul and Nll = 1682 − Nul, while keeping the total number of lipids constant. The cubic simulation box has the base area A = LxLy and the height Lz with Lx = Ly varied between 32.0d and 32.2d and the height Lz varied between 46.9d and 46.3d for fixed volume of the box. The lipid areas in the upper and lower leaflet are then obtained via aul = A/Nul and all = A/Nll which implies the relationship all = aulNul/Nll.The larger nanovesicles are assembled from a total number of 2875 lipids, the smaller ones from a total number of 1317 lipids. Tensionless bilayers with Σ = 0 are obtained by adjusting the volume of the vesicles. The inner and outer radii RiH and RoH of the spherical bilayers are estimated from the two maxima of the density profile ρH(r) for the hydrophilic H beads, corresponding to the inner and outer headgroup layers. For the larger nanovesicles, this procedure leads to the inner radius RiH = 9.2d and to the outer radius RoH = 14.2d. For the smaller nanovesicles, we obtain the inner radius RiH = 5.3d and the outer radius RoH = 10.3d.
4.3 Stress profiles, midsurfaces, and leaflet tensions
The stress profile s(z) across a planar bilayer, which depends on the Cartesian coordinate z, is computed as in ref. 59 and 25. The value z = 0 corresponds to the location of the maximum for the density profile of the hydrophobic C beads, which is taken to define the midplane of the bilayer. The leaflet tensions Σul and Σll of the upper and lower leaflet are given by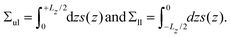 | (5) |
The stress profile s(r) across a spherical nanovesicls, which depends on the radial coordinate r, is obtained as described previously.26 The midsurface of the spherical bilayer is placed at r = Rmid, corresponding to the r-value, at which the density profile of the hydrophobic C beads has its maximum. As a result, we obtain the radius Rmid = 11.88d for the midsurface of the larger nanovesicles and the radius Rmid = 8.13d for the midsurface of the smaller nanovesicles.
The leaflet tensions Σol and Σil of the outer and inner leaflet are
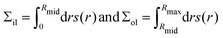 | (6) |
4.4 Midsurfaces of leaflets and areas per lipid
In order to determine the areas per lipid in the two leaflets, we first compute the radii Ril and Rol for the midsurfaces of these leaflets. The inner leaflet is bounded by the inner headgroup layer with radius RiH and the midsurface of the bilayer with radius Rmid. Thus, the midsurface of the inner leaflet has the radius | (7) |
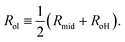 | (8) |
Finally, the areas per lipid, ail and aol, in the inner and outer leaflets are computed by dividing the areas of the midsurfaces of the inner and outer leaflets by the number of lipids assembled within these leaflets, which leads to
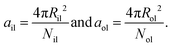 | (9) |
4.5 First moments of stress profiles
For a planar and tensionless bilayer, the first moment of the stress profile s(z) can be interpreted as a torque density,![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) pl, which is directly related to the product of two curvature-elastic parameters, the bending rigidity κ and the spontaneous curvature m. This relationship has the form24,25,60
pl, which is directly related to the product of two curvature-elastic parameters, the bending rigidity κ and the spontaneous curvature m. This relationship has the form24,25,60 | (10) |
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) pl are included in Table S1 (ESI†).
pl are included in Table S1 (ESI†).
For spherical nanovesicles with a tensionless bilayer, the first moment of the stress profile is related to the bending rigidity κ, the spontaneous curvature m, and the radius Rmid of the spherical mid-surface according to26
 | (11) |
4.6 Weibull plots for the onset of flip-flops
The statistics for the onset of flip-flops is encoded in the cumulative distribution function Pcdf(t) which describes the probability that the first flip-flop occurs at time t1 ≤ t. The complementary distribution 1 − Pcdf(t) represents the survival probability for the metastable state without any flip-flops up to time t. In order to fit the simulation data to the Weibull distribution in eqn (4), we rewrite the latter equation asln(−ln[1 − PWei(t)]) = k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln(t) + k ln(t) + k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln(ωve). ln(ωve). | (12) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was conducted within the Max Planck School Matter to Life supported by the German Federal Ministry of Education and Research (BMBF) in collaboration with the Max Planck Society and the Max Planck Institute of Colloids and Interfaces. Open Access funding provided by the Max Planck Society.References
- Physics of Biological Membranes, ed. P. Bassereau and P. Sens, Springer Nature, 2018 Search PubMed.
- The Giant Vesicle Book, ed. R. Dimova and C. Marques, Taylor & Francis, 2020 Search PubMed.
- R. Lipowsky and R. Dimova, Soft Matter, 2021, 17, 214–221 RSC.
- S. Rai, V. Pandey and G. Rai, Nano Rev. Exp., 2017, 8, 1325708 CrossRef PubMed.
- T. Limongi, F. Susa, M. Marini, M. Allione, B. Torre, R. Pisano and E. D. Fabrizio, J. Nanomater., 2021, 11, 3391–3429 CrossRef CAS PubMed.
- J. A. Kulkarni, D. Witzigmann, S. Chen, P. R. Cullis and R. V. D. Meel, Acc. Chem. Res., 2019,(52), 2435–2444 CrossRef CAS PubMed.
- Y. Suzuki and H. Ishihara, Drug Metab. Pharmacokinet., 2021, 41, 100424 CrossRef CAS PubMed.
- M. Chen, X. Hu and S. Liu, Macromol. Chem. Phys., 2022, 223, 2100443 CrossRef CAS.
- E. Woith, G. Fuhrmann and M. F. Melzig, Int. J. Mol. Sci., 2019, 20, 5695 CrossRef CAS PubMed.
- L. Barile and G. Vassalli, Pharmacol. Ther., 2017, 174, 63–78 CrossRef CAS PubMed.
- I. Jalaludin, D. M. Lubman and J. Kim, Mass Spec. Rev., 2021, e21749 Search PubMed.
- I. K. Herrmann, M. J. A. Wood and G. Fuhrmann, Nat. Nanotechnol., 2021, 16, 748–759 CrossRef CAS PubMed.
- L. van der Koog, T. B. Gandek and A. Nagelkerke, Adv. Healthcare Mater., 2022, 11, 2100639 CrossRef CAS PubMed.
- Y. Yang, M. Lee and G. D. Fairn, J. Biol. Chem., 2018, 293, 6230–6240 CrossRef CAS PubMed.
- D. Marquardt, B. Geier and G. Pabst, Membranes, 2015, 5, 180–196 CrossRef CAS PubMed.
- J. R. St. Clair, Q. Wang, G. Li and E. London, The Biophysics of Cell Membranes, Springer Nature Singapore, 2017, vol. 19, pp. 1–27 Search PubMed.
- J. Steinkühler, R. L. Knorr, Z. Zhao, T. Bhatia, S. Bartelt, S. Wegner, R. Dimova and R. Lipowsky, Nature Commun., 2020, 11, 905 CrossRef PubMed.
- F. A. Heberle, D. Marquardt, M. Doktorova, B. Geier, R. F. Standaert, P. Heftberger, B. Kollmitzer, J. D. Nickels, R. A. Dick, G. W. Feigenson, J. Katsaras, E. London and G. Pabst, Langmuir, 2016, 32, 5195–5200 CrossRef CAS PubMed.
- H.-Y. Sun, G. Deng, Y.-W. Jiang, Y. Zhou, J. Xu, F.-G. Wu and Z.-W. Yu, Chem. Commun., 2017, 53, 12762–12765 RSC.
- H.-Y. Guo, H.-Y. Sun, G. Deng, J. Xu, F.-G. Wu and Z.-W. Yu, Langmuir, 2020, 36, 12684–12691 CrossRef CAS PubMed.
- C. Drechsler, M. Markones, J.-Y. Choi, N. Frieling, S. Fiedler, D. R. Voelker, R. Schubert and H. Heerklotz, Biophys. J., 2018, 115, 1509–1517 CrossRef CAS PubMed.
- R. Takaoka, H. Kurosaki, H. Nakao, K. Ikeda and M. Nakano, BBA – Biomembr., 2018, 1860, 245–249 CrossRef CAS PubMed.
- K. Kamiya, T. Osaki and S. Takeuchi, Sens. Actuators, B, 2021, 327, 128917 CrossRef CAS.
- B. Różycki and R. Lipowsky, J. Chem. Phys., 2015, 142, 054101 CrossRef PubMed.
- A. Sreekumari and R. Lipowsky, J. Chem. Phys., 2018, 149, 084901 CrossRef PubMed.
- R. Ghosh, V. Satarifard, A. Grafmüller and R. Lipowsky, Nano Lett., 2019, 19, 7703–7711 CrossRef CAS PubMed.
- M. Miettinen and R. Lipowsky, Nano Lett., 2019, 19, 5011–5016 CrossRef CAS PubMed.
- A. Imparato, J. C. Shillcock and R. Lipowsky, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 11, 21–28 CrossRef CAS PubMed.
- G. Parisio, A. Ferrarini and M. M. Sperotto, Int. J. Adv. Eng. Sci. Appl. Math., 2016, 8, 134–146 CrossRef.
- R. D. Kornberg and H. M. McConnell, Biochemistry, 1971, 10, 1111–1120 CrossRef CAS PubMed.
- B. W. van der Meer, Biomembranes: Physical Aspects, VCH Verlagsgesellschaft, 1993, pp. 97–158 Search PubMed.
- A. V. Victorov, N. Janes, G. Moehren, E. Rubin, T. F. Taraschi and J. B. Hoek, J. Am. Chem. Soc., 1994, 116, 4050–4052 CrossRef CAS.
- J. Liu and J. C. Conboy, Biophys. J., 2005, 89, 2522–2532 CrossRef CAS PubMed.
- M. Nakano, M. Fukuda, T. Kudo, N. Matsuzaki, T. Azuma, K. Sekine, H. Endo and T. Handa, J. Phys. Chem. B, 2009, 113, 6745–6748 CrossRef CAS PubMed.
- J. Liu, K. L. Brown and J. C. Conboy, Faraday Discuss., 2013, 161, 45–61 RSC.
- D. Marquardt, F. A. Heberle, T. Miti, B. Eicher, E. London, J. Katsaras and G. Pabst, Langmuir, 2017, 33, 3731–3741 CrossRef CAS PubMed.
- M. M. Sperotto and A. Ferrarini, The Biophysics of Cell Membranes, 2017, 29–60 CAS.
- L. Porcar and Y. Gerelli, Soft Matter, 2020, 16, 7696–7703 RSC.
- T. L. Steck, J. Ye and Y. Lange, Biophys. J., 2002, 83, 2118–2125 CrossRef CAS PubMed.
- J. A. Hamilton, Curr. Opin. Lipidol., 2003, 14, 263–271 CrossRef CAS PubMed.
- R. J. Bruckner, S. S. Mansy, A. Ricardo, L. Mahadevan and J. W. Szostak, Biophys. J., 2009, 97, 3113–3122 CrossRef CAS PubMed.
- W. Weibull, J. Appl. Mech., 1951, 18, 293–297 CrossRef.
- H. Rinne, The Weibull Distribution – A Handbook, Taylor & Francis, 2008 Search PubMed.
- C.-D. Lai, Generalized Weibull Distributions, Springer, 2014 Search PubMed.
- C. Corsaro, G. Neri, A. M. Mezzasalma and E. Fazio, Polymers, 2021, 13, 2897 CrossRef CAS PubMed.
- D. R. Cox, Renewal Theory, Methuen and Co Ltd, 1962 Search PubMed.
- H. M. Taylor and S. Karlin, An Introduction to Stochastic Modelling, Academic Press, San Diego, 1998 Search PubMed.
- P. Comfurius, P. Williamson, E. F. Smeets, R. A. Schlegel, E. M. Bevers and R. F. A. Zwaal, J. Biol. Chem., 1996, 35, 7631–7634 CAS.
- X. Buton, G. Morrot, P. Fellmann and M. Seigneuret, J. Biol. Chem., 1996, 271, 6651–6657 CrossRef CAS PubMed.
- J. Suzuki, M. Umeda, P. J. Sims and S. Nagata, Nature, 2010, 468, 834–840 CrossRef CAS PubMed.
- E. M. Bevers and P. L. Williamson, Physiol. Rev., 2016, 96, 605–645 CrossRef CAS PubMed.
- P. F. Devaux, FEBS Lett., 1988, 234, 8–12 CrossRef CAS PubMed.
- T. T. Sebastian, R. D. Baldridge, P. Xu and T. R. Graham, Biochim. Biophys. Acta, 2012, 1821, 1068–1077 CrossRef CAS PubMed.
- H. M. Hankins, R. D. Baldridge, P. Xu and T. R. Graham, Traffic, 2015, 16, 35–47 CrossRef CAS PubMed.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- J. C. Shillcock and R. Lipowsky, J. Chem. Phys., 2002, 117, 5048–5061 CrossRef CAS.
- Z. Xu, L. Gao, P. Chen and L.-T. Yan, Soft Matter, 2020, 16, 3869–3881 RSC.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- R. Goetz and R. Lipowsky, J. Chem. Phys., 1998, 108, 7397–7409 CrossRef CAS.
- W. Helfrich, Physics of Defects, North-Holland Publishing Company, Amsterdam, 1981, pp. 715–755 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Supporting Fig. S1–S7, supporting Tables S1–S7, and three Movies M1–M3. See DOI: https://doi.org/10.1039/d2sm00618a |
| This journal is © The Royal Society of Chemistry 2022 |
