Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bio-hybrid micro-swimmers propelled by flagella isolated from C. reinhardtii†
Raheel
Ahmad
 a,
Albert J.
Bae
ab,
Yu-Jung
Su
a,
Samira Goli
Pozveh
a,
Eberhard
Bodenschatz
a,
Albert J.
Bae
ab,
Yu-Jung
Su
a,
Samira Goli
Pozveh
a,
Eberhard
Bodenschatz
 acd,
Alain
Pumir
acd,
Alain
Pumir
 ae and
Azam
Gholami
ae and
Azam
Gholami
 *a
*a
aMax Planck Institute for Dynamics and Self-Organization, Am Fassberg 17, D-37077 Göttingen, Germany. E-mail: azam.gholami@ds.mpg.de
bLewis & Clark College, Portland, Oregon, USA
cInstitute for Dynamics of Complex Systems, University of Göttingen, Göttingen 37077, Germany
dLaboratory of Atomic and Solid-State Physics and Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, New York 14853, USA
eUniv Lyon, Ecole Normale Superieure de Lyon, CNRS, Laboratoire de Physique, F-69342 Lyon, France
First published on 8th June 2022
Abstract
Bio-hybrid micro-swimmers, composed of biological entities integrated with synthetic constructs, actively transport cargo by converting chemical energy into mechanical work. Here, using isolated and demembranated flagella from green algae Chlamydomonas reinhardtii (C. reinhardtii), we build efficient axonemally-driven micro-swimmers that consume ATP to propel micron-sized beads. Depending on the calcium concentration, we observed two main classes of motion: whereas beads move along curved trajectories at calcium concentrations below 0.03 mM, they are propelled along straight paths when the calcium concentration increases. In this regime, they reached velocities of approximately 20 μm s−1, comparable to human sperm velocity in vivo. We relate this transition to the properties of beating axonemes, in particular the reduced static curvature with increasing calcium concentration. Our designed system has potential applications in the fabrication of synthetic micro-swimmers, and in particular, bio-actuated medical micro-robots for targeted drug delivery.
1 Introduction
Bio-actuated micro-swimmers, fabricated by integration of a live biological entity with a synthetic cargo, are the subject of growing interest, in particular for their potential applications in the field of targeted drug delivery or assisted fertilization in vivo.1–3 It is known that an essential aspect in designing bio-hybrid micro-swimmers is to take advantage of biological motors, which are highly efficient in converting chemical energy into mechanical work.4 Therefore, the main goal in the synthesis of bio-hybrid micro-swimmers is to integrate these highly efficient energy conversion modules into bio-compatible nano- and micro-swimmers to realize various tasks. In the past decade, the sensory capabilities and the autonomous motility and power of various bacterial species, mainly E. coli have been extensively utilized as a biological micro-actuator in bio-hybrid micro-swimmers to provide an efficient cargo (e.g. liposomes or coated beads) transport.5–12A wide variety of motility mechanisms exist in nature. This includes the polarized assembly and disassembly of biopolymers for the directional movement of amoeboid cells,13,14 or motility driven by eyelash-shaped cellular protrusions – cilia and flagella – that perform periodic whip-like motion to generate fluid flow and propulsion.15–17 In many organisms, multiple motile cilia coordinate their beating activity to enhance the swimming efficiency or directional fluid transport. Examples are transport of cerebrospinal fluid, which contains physiologically important signaling molecules, through the ventricular cavities of the mammalian's brain,18 mucus clearance in mammalian airways,19 or the bi-flagellated algae Chlamydomonas reinhardtii (C. reinhardtii) which swims in water with its two flagella using a characteristic breaststroke beat pattern.20–24
Cilia and flagella have a tube-shaped structure consisting of a periodic arrangement of nine microtubule doublets (MTDs) at the periphery and two axial singlet microtubules at the center. This 9 + 2 structure, known as axoneme, has a diameter of 200 nm and can be actuated via coordinated collective activity of dynein molecular motors that convert chemical energy released during ATP hydrolysis into mechanical work by sliding neighboring MTDs.25–28 However, the sliding of MTDs is resisted by structural constraints imposed by the nexin linker proteins which mechanically couple outer MTDs, and protein complexes ‘radial spokes’ which extend toward the central pair.29–33 Instead, sliding converts to rhythmic bending deformations that propagate along the axonemal length. Flagella in different species show a variety of beat patterns. In contrast to spermatozoa (typical length 50 μm), flagella isolated from green algae C. reinhardtii (typical length 10 μm) beat by asymmetric bending deformations propagating at a fundamental beat frequency along the axonemal length in a base-to-tip direction.34–38 The observed asymmetric waveform is such that the flagellar shapes over one beat cycle average to a semi-circular arc with a mean curvature of about −0.2 μm−1. This static component of the axonemal curvature leads to a curved swimming trajectory,36,39–41 whereas in the absence of this component, flagella swim along a straight path.34,35 The magnitude of the various components contributing to the flagellar wave pattern depends on the calcium ion concentration, which has been shown to be one of the molecular agents which affects most the motion of the flagella. Bessen et al.34,42 have shown that in axonemes isolated from C. reinhardtii, a high Ca2+ concentration triggers a transition from an asymmetric to a symmetric waveform. A similar calcium-dependent change in wave symmetry has also been observed in ATP-reactivated C. reinhardtii cells, in which two flagella are demembranated using detergents.43 Interestingly, to reverse the direction of wave propagation during a photophobic response to intense light, C. reinhardtii cells change the internal level of Ca2+ ions to switch from an asymmetric forward beating pattern to a symmetric reverse beating mode.35,44–46
In the present work, we demonstrate the feasibility of using isolated and demembranated flagella from C. reinhardtii as a bio-actuator to carry and maneuver micron-sized particles. To the best of our knowledge, there has been no report in the literature on isolated flagella-driven propulsion of cargo. Fig. 1 demonstrates the existence of two different regimes of propulsion. At low calcium concentration, see Fig. 1A, the micro-swimmer is propelled on a highly curved trajectory. At higher calcium concentration, on the other hand, the bead is propelled along an almost straight path, at a velocity of ∼20 μm s−1, comparable to the velocity of human sperm in vivo, see Fig. 1C. The possibility to externally modify flagellar wave components and beating frequency with light or chemical stimuli (such as calcium ions, as in Fig. 1B and D)35,44,47,48 opens interesting perspective to control such a bio-hybrid micro-swimmer. The micro-swimmers, propelled by isolated and reactivated flagella, are potentially attractive to develop minimally invasive devices for medical applications, such as in vivo active cargo transport.7,8
 | ||
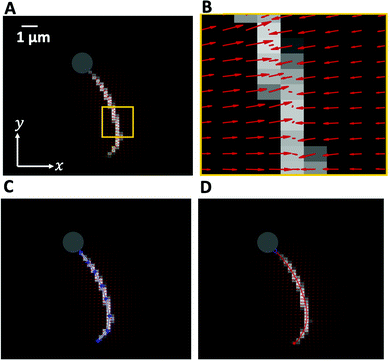
| Fig. 1 Axonemally-driven beads and the effect of calcium ions. (A) An exemplary axoneme at [Ca2+] = 0 mM is attached at the basal end (s = 0) to a bead of diameter 1 μm. The blue trajectory of the bead center shows a curved swimming path at two different time points. (B) The time-projection of the axonemal shapes highlights the counter-clockwise rotation of the axoneme as bending deformations propagate along the contour length. (C) In the presence of 1 mM calcium, the bead is propelled on average along a straight path at the propulsion speed of around 20 μm s−1, which is comparable to the human sperm propulsion speed in mucus. (D) Calcium ions trigger a transition from an ‘asymmetric’ flagellar waveform that rotates counter-clockwise to a ‘symmetric’ waveform that swims along a straight path. In both experiments, the ATP concentration is 200 μM (see Videos S1 and S2, ESI†). | ||
Here, we study systematically the two regimes illustrated in Fig. 1, and elucidate the transition between them. We conclude experimentally that the difference in the nature of the bead trajectory is due to the mean curvature of the beating axonemes. In practice, we combine high-precision high-speed phase contrast microscopy (1000 fps) with image processing techniques to investigate the swimming dynamics of a bead that is propelled by an ATP-reactivated axoneme. We use calcium ions to reduce the static curvature of axonemes by one order of magnitude, thereby34,35 inducing a transition from circular to straight swimming trajectories of axonemal-propelled beads (see Fig. 1).
2 Materials and methods
2.1 Isolation of axonemes from C. reinhardtii and attachment to the beads
Isolation and reactivation of axonemes are done based on a standard protocol described in ref. 49 and 50. Briefly, wild-type C. reinhardtii cells, strain SAG 11-32b, are grown axenically in TAP (tris-acetate-phosphate) medium on a 12 h/12 h day–night cycle. Upon adding dibucaine, cells release their flagella which we purify on a 25% sucrose cushion, and demembranate them using detergent NP-40 in HMDEK solution (30 mM HEPES-KOH, 5 mM MgSO4, 1 mM DTT, 1 mM EGTA, 50 mM potassium acetate, pH 7.4) supplemented with 0.2 mM Pefabloc. The membrane-free axonemes are resuspended in HMDEK buffer plus 1% (w/v) polyethylene glycol (Mw = 20 kg mol−1), 0.2 mM Pefabloc and used freshly after isolation. To perform reactivation experiments, we diluted the axonemes in HMDEKP reactivation buffer (HMDEK plus 1% PEG) supplemented with ATP at different concentrations. Beads (polystyrene microsphere) were washed twice with HMDEKP buffer supplemented with 0.01% SDS and resuspended in the same solution, and sonicated for 5 min before use. For bead attachment, beads are incubated for 20 min with axonemes before being mixed with reactivation buffer and infused into 100 μm deep flow chambers, built from cleaned glass and double-sided tape. The glass slides are treated with casein (2 mg mL−1 in HMDEKP buffer) for 5 min before use to avoid axoneme-substrate attachment.38 For calcium experiments, we added CaCl2 at different concentrations to the HMDEKP reactivation buffer.2.2 Axoneme tracking
We used high-speed phase-contrast microscopy (100× objective, 1000 fps) to capture high-resolution images of fast beating axonemes that propel micron-sized beads and swim parallel to the glass substrate with an approximately planar axonemal beat. This effective confinement to 2D significantly facilitates tracking of flagellar shapes and their analysis. In these images, the bead appears as a bright spot, which interferes with the tracking algorithm of the axoneme. Therefore, the first step is to filter out the bead by applying a threshold to the images (Fig. 2). Next, to increase the signal to noise ratio, we invert the phase-contrast images and subtract the mean-intensity of the time series.38 To smooth the images, we apply a Gaussian filter. Tracking of axonemes is done using a customized MATLAB code (available in the ESI†) which is based on the gradient vector flow (GVF) technique.51–53 In this algorithm, for the first frame, we select a region of interest (ROI) that includes only one actively beating axoneme. We then define an active contour, a snake, as a curve within the ROI that can deform under the influence of internal forces within the curve itself and external forces given by the gradient of the gray-scale map derived from the acquired image (Fig. 2B). To initialize the snake, we draw a line polygon along the contour of the axoneme in the first frame (see Fig. 2C). This polygon is interpolated at N = 30 equally spaced points and used as a starting parameter for the snake. The GVF is calculated as the vector field that minimizes the energy functional defined by eqn (10) of ref. 51 (we took a value of the regularization parameter μ = 0.1, and used 20 iterations). The snake is then deformed according to the GVF where we have adapted the original algorithm by Xu and Prince for open boundary conditions.51,52 The position of axoneme at contour length si and time point t is given by r(si,t) = (x(si,t), y(si,t)). Here s = 0 is the basal end and s = L is the distal tip, where L is the total contour length of the filament. Furthermore, to estimate the systematic error of our tracking algorithm, we generated artificial filaments with known values of mean curvature and used the GVF algorithm to determine the curvature from the tracking algorithm. As shown in Fig. S1 (ESI†), the measured values systematically deviate from the real values at small mean curvatures, but provide a much better estimate when the mean curvature is larger. In other words, our algorithm has a smaller systematic error (less than 4%) for curved filaments with dimensionless mean curvature C0 larger than 0.3.2.3 Principal component analysis
This analysis is based on the method introduced by Stephens et al.54 to characterize the waveforms in C. elegans. We describe the shape of the flagellum by its unit tangent vector t(s) and the unit normal vector n(s) at distance s along the contour.55,56 Instantaneous deformation of flagellum is described by curvature κ(s, t), using the Frenet–Serret formulas54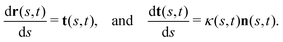 | (1) |
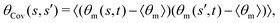 where 〈θm〉 is the spatial average of θm(s,t) at a given time t. The eigenvalues λn and the corresponding eigenvectors Mn(s) of the covariance matrix are given by
where 〈θm〉 is the spatial average of θm(s,t) at a given time t. The eigenvalues λn and the corresponding eigenvectors Mn(s) of the covariance matrix are given by 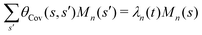 . We show that superposition of the four eigenvectors corresponding to the four largest eigenvalues can describe the flagellum's shape with high accuracy (see Fig. 7C):
. We show that superposition of the four eigenvectors corresponding to the four largest eigenvalues can describe the flagellum's shape with high accuracy (see Fig. 7C):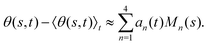 | (2) |
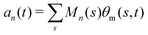 . The fractional variance of flagellum's shape captured by n eigenvectors is calculated as
. The fractional variance of flagellum's shape captured by n eigenvectors is calculated as 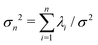 where
where 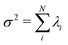 . Here N is the total number of eigenvectors. Fig. S2 (ESI†) shows that already two modes capture 98.6% and four modes capture 99.7% of the total variance.
. Here N is the total number of eigenvectors. Fig. S2 (ESI†) shows that already two modes capture 98.6% and four modes capture 99.7% of the total variance.
3 Results
We fabricated axonemally-based propelled beads, by incubating isolated axonemes from C. reinhardtii (∼10 μm in length) with beads of diameter 1 μm, as described in Materials and methods (see Section 2.1 as well as Fig. 1 and 3). Out of N = 195 bead-axoneme attachments, a single bead attaches to the basal end of the axonemes in 60.5% of the cases. Attachment of beads to the distal tip occurs less frequently in 22.6% of cases, and even less frequently (16.9%) we observed more than one bead attached either to the tip or along the axonemal length. The attachment of the beads to the basal or the distal region of the axonemes is either symmetric, i.e. the tangent vector of the axoneme at the bead-axoneme contact point passes through the bead center, or asymmetric. We emphasize that a limitation of our 2D phase-contrast microscopy is that it is not possible to precisely distinguish a symmetric bead attachment from an asymmetric one and 3D microscopy techniques53 are required to fully determine the bead-axoneme attachment geometry.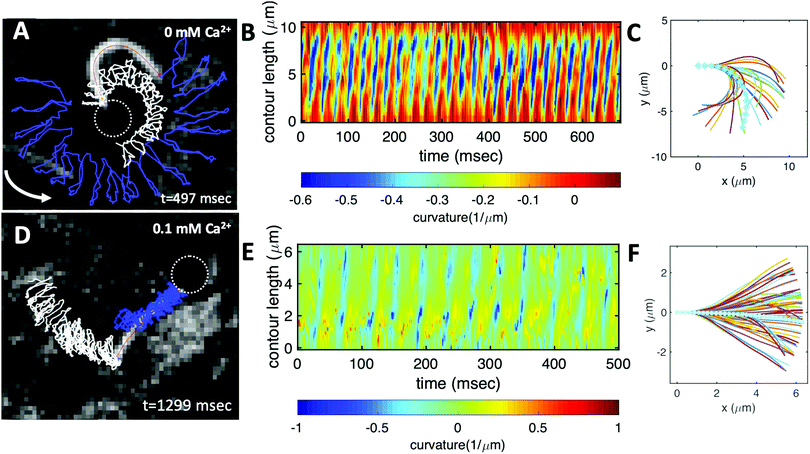 | ||
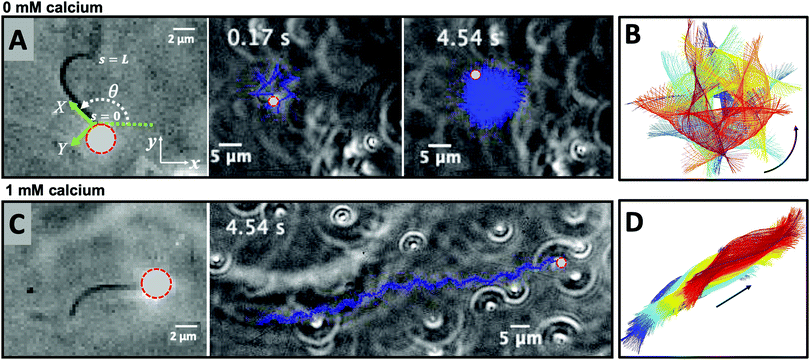
| Fig. 3 Experiments to show the effect of calcium on axonemal waveform. (A) An axonemally-driven bead reactivated at [ATP] = 80 μM and [Ca2+] = 0 mM (see Video S3, ESI†). Tracked axoneme and trajectories of its distal (blue lines) and basal (white lines) ends. Axoneme-bead swimmer rotates counter-clockwise while the bead center follows a spiral-like path (Fig. 5B). (B) Curvature waves as they travel at the frequency of 38.21 ± 0.25 Hz from the proximal region toward the distal tip. (C) Mean shape of the axoneme in cyan color averaged over one beat cycle showing a circular arc with static curvature of ∼− 0.19 μm−1. At different time points, the axoneme is translated and rotated such that the basal end is at (0,0) and the tangent vector at s = 0, which defines the X-axis in the swimmer-fixed frame, is along the x-axis of the laboratory-fixed frame (see Fig. 1A). (D) An axonemally-driven bead reactivated at [ATP] = 80 μM. The reactivation buffer is supplemented with 0.1 mM calcium to reduce the static curvature (see Video S4, ESI†). The axoneme beats at 24.42 ± 0.18 Hz and the bead-axoneme attachment appears to be symmetric. (E) Curvature waves as they travel at the frequency of 24.42 Hz from the basal end toward the distal tip. (F) The axonemal mean shape with static curvature of κ0 ∼ −0.03 μm−1 (filament with cyan color). The mean curvature of axoneme has dropped around ten times in comparison to axonemal shapes in panel (C). This reduction in C0 causes a transition from a circular to a straight swimming trajectory. | ||
The propulsion of axonemally-driven beads is highly sensitive to the axonemal waveform. In our experiments, we use calcium ions at different concentrations to change the axonemal waveform and study the propulsion dynamics. In the following section, we summarize our results without and with calcium ions and show that calcium ions play a crucial role to achieve a directed cargo transport.
3.1 Role of the mean curvature of the axonemes
We return to the striking difference between the two types of bead propulsion illustrated by Fig. 1. Namely, beads can be propelled on a curved trajectory (first regime), or along an almost straight path (second regime). These two distinct modes of propulsion correspond to two different concentrations of calcium ions in the reactivation buffer (0 mM versus 1 mM), which directly affects the axonemal waveform.34,43 As shown in Fig. 1B, in the absence of calcium ions, the time-projection of the ‘asymmetric’ axonemal shapes indicates a counter-clockwise rotation of the axoneme causing a circular swimming trajectory of the bead. However, in the presence of calcium ions, we observe a significant change in the flagellar waveform (Fig. 1C and D) that appears to be ‘symmetric’ and results in a directed bead transport. In the present section, we demonstrate that this difference is a consequence of the existence of a mean curvature of the axonemes in the first regime.Fig. 3 characterizes in more detail the flagellar waveform of the axonemes in the two regimes observed in Fig. 1. Fig. 3A–C shows a representative example of the first regime, where we have tracked the axoneme over time and quantified the curvature waves that propagate along the axonemal length. As seen from Fig. 3B, these bending waves start from the basal end (at s = 0), which is attached to the bead, and propagate at the frequency of f0 ∼ 38.21 ± 0.25 Hz toward the distal tip. Note that the beat frequency of axonemes depends on the ATP concentration, following a Michaelis–Menten kinetics with a linear trend at low amount of ATP and saturation at higher ATP concentrations around 1 mM (see Fig. S4, ESI†).38,47
A remarkable feature of the first propulsion regime is the presence of a mean curvature, κ0, when averaging the flagellar shapes over one beat cycle, with a value κ0 of about −0.19 μm−1 (see the cyan filament in Fig. 3C). The negative sign of κ0 indicates a clockwise bend when moving from the basal end at s = 0 toward the distal tip at s = L. In other words, we can think of the axonemal waveform as a superposition of a traveling wave component which propagates along this circular arc.36,38
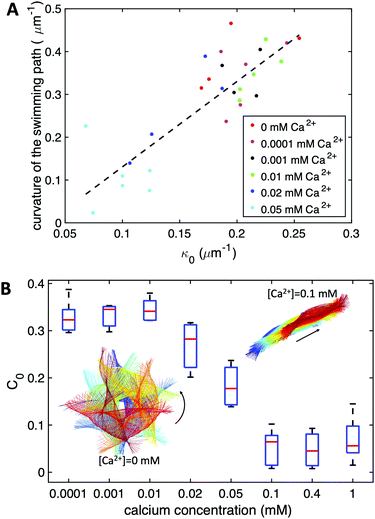
Our experimental results show a clear relation between the averaged curvature of the axoneme over a beat cycle, κ0, and the curvature of its swimming trajectory. Namely, Fig. 4A shows a scatter plot of our experiments, realized at different calcium concentration, as indicated by the different symbols of the legend. Strikingly, we observe an approximately linear relation between the two curvatures, with a coefficient of proportionality approximately equal to 2, see the dashed line in Fig. 4B.38,57 As shown in Fig. 4B, however, the mean curvature of axonemes κ0 is sensitive to the concentration of calcium ions and almost vanishes above a calcium concentration of 0.1 mM.
In very sharp contrast to what happens at low calcium concentration, in the second regime illustrated in Fig. 1C and D, at a calcium concentration of 0.1 mM, the beating pattern shown in Fig. 3D–F corresponds to a condition in which the axonemal curvature averaged over one beat cycle is very low. The observation of a straight trajectory in Fig. 1C is consistent with the trend shown in Fig. 4A. In this case, the axonemal waveform is composed of a propagating wave that travels along an almost straight filament, thereby propelling the axoneme and the cargo along a straight path.
In the absence of mean curvature, axonemes moving in a fluid at low Reynolds number, where viscous drag dominates over inertia, swim along a straight direction. As shown in ref. 39 and 40, a small mean curvature induces a rotational motion of the axonemes, with an angular velocity Ωz. This can be understood by using resistive-force theory,58 which predicts that, to leading order in the mean curvature, κ0, 〈Ωz〉 depends linearly on the dimensionless mean curvature C0 = κ0L/2π. Given the low value of κ0 in the experiments shown in Fig. 1C and D, the motion of the cargo is in practice along a straight trajectory. Remarkably, we observe a mean velocity of about 20 μm s−1 (Fig. 1C), which is slightly slower than the migration speed of the human sperm in mucus (typically 25–45 μm s−1).59
The combination of an overall rotation, at a frequency Ωz, and of a translation, in our experiments without calcium, results in a swimming path along a spiral, clearly seen in Fig. 5. Note that for the exemplary experiment in Fig. 3A, the x–y positions of the bead center exhibit, in addition to the spiraling motion, tiny oscillations at the fast beat frequency of f0 ∼ 38.21 Hz and a secondary slow global rotational frequency around 1.5 Hz (see Fig. 5B).
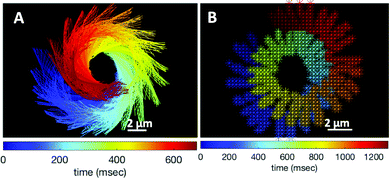 | ||
| Fig. 5 (A) Color-coded time projection of the axonemal shapes of the axoneme presented in Fig. 3A ([Ca2+] = 0 mM). (B) Color-coded trajectory of the bead center from Fig. 3A showing a spiral-like trajectory. The global rotational frequency of the swimmer is around 1.5 Hz (∼1 full rotation in around 650 ms; see Videos S3 and S5, ESI†). | ||
Additionally, in most of our experiments without calcium, the axonemes rotate counter-clockwise in the microscope's field of view with an effective 2D beat pattern, which facilitates the tracking procedure. As an axoneme undergoes planar shape deformations over time, at any instant of time, its motion can be described, aside from its shape deformation, as a solid body with translational and rotational velocities Ux, Uy and Ωz which we measure in the swimmer-fixed frame (Fig. 6).57 These velocities oscillate in time, reflecting the fundamental beat frequency of the axoneme shown in Fig. 3A (∼38.21 Hz) and its higher harmonics. It is worth noticing that the averaged value of Ωz, showed by the horizontal red line in Fig. 6C, appears as very small compared to the recorded excursions of the signal. Nevertheless, the measured value, 〈Ωz〉 = 0.026ω0 indicated by the red line in Fig. 6C, is very close to the angular velocity of the bead along the trajectory in Fig. 3A. In contrast, in our experiments with calcium, axonemal movement often occurs in 3D (see Video S2, ESI†), making tracking of axoneme nearly impossible. The example shown in Fig. 3D is a relatively rare case where the axoneme can be tracked for more than 1 second before swimming out of focus.
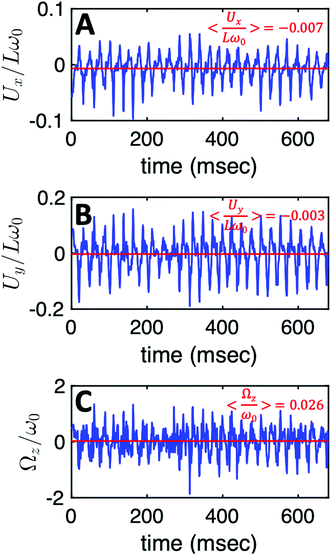 | ||
| Fig. 6 The translational and rotational velocities of the axoneme presented in Fig. 3A, measured in the swimmer-fixed frame, obtained with RFT simulations using the experimental beat pattern as input. The red lines mark the mean values. | ||
3.2 The effect of bead size
To investigate how bead size affects beating frequency and mean curvature of axonemes, we also performed experiments with beads of larger diameter. A summary of the beat frequency and intrinsic curvature of axonemes (all reactivated at [ATP] = 200 μM and [Ca2+] = 0 mM) propelling beads of diameter 1, 2 and 3 micron is given in Table 1. In these experiments, as we increased the bead diameter from 1 μm to 3 μm, we observed a reduction at both the averaged beat frequency (∼12%) and the intrinsic curvature (∼31%) of the axonemes.| Axoneme | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D (μm) | 1 | 2 | 3 | ||||||||||
| f 0 (Hz) | 38.21 | 48.5 | 43.55 | 53.46 | 48.50 | 33.65 | 38.60 | 61.15 | 63.36 | 46.06 | 43.55 | 58.41 | 23.75 |
| 〈f0〉 ± std | 46.44 ± 5.78 | 49.19 ± 15.25 | 42.94 ± 14.35 | ||||||||||
| κ 0 | 0.19 | 0.21 | 0.22 | 0.26 | 0.20 | 0.25 | 0.17 | 0.17 | 0.19 | 0.15 | 0.16 | 0.15 | 0.19 |
| 〈κ0〉 ± std | 0.22 ± 0.03 | 0.19 ± 0.04 | 0.16 ± 0.02 | ||||||||||
3.3 Description of the flagellar shapes
Having stressed the role played by the mean curvature of the axonemes, which determines the curvature of the swimming path of the beads, and the role played by calcium in controlling this curvature, we now focus on a more systematic analysis of the flagellar waveforms. As explained in Section 2.3, our analysis is based on principal component analysis (PCA) of the flagellar motion.39,54Fig. 7A shows the color map of the covariance matrix θCov(s,s′), introduced in Section 2.3, of the axoneme shown in Fig. 3A. This covariance matrix has effectively a reduced dimensionality with only a small number of non-zero eigenvalues. Specifically, we find that the four eigenmodes Mn(s) (n = 1, …, 4) corresponding to the four largest eigenvalues of θCov(s,s′) capture the axonemal waveform with very high accuracy (see Video S6, ESI†). These four eigenvectors are plotted in Fig. 7B. Interestingly, the wavemodes Mn(s) qualitatively appear as a superposition of a few low order Fourier modes, albeit with a wavelength λ that differs from the length of the system, L. To estimate this wavelength, we compute the temporal Fourier transform of the deviation angle θ(s,t) at several fixed values of s, with the convention that θ(s = 0, t) = 0. This allows us to define the phase ϕ(s) of the wave along the axoneme, see Fig. S3 (ESI†). The wavelength is determined as λ ∼ 2πL/(ϕ(L) − ϕ(0)).38 Although ϕ(0) is undefined (since θ (s = 0, t) = 0), the phase gradient, which is the only necessary quantity to define, is determined by fitting the phase dependence along the axonemal length, as indicated by the red line in Fig. S3 (ESI†). In the particular example shown in Fig. 3A, the wavelength λ = 13.19 μm exceeds the length of the axoneme by ∼30%.
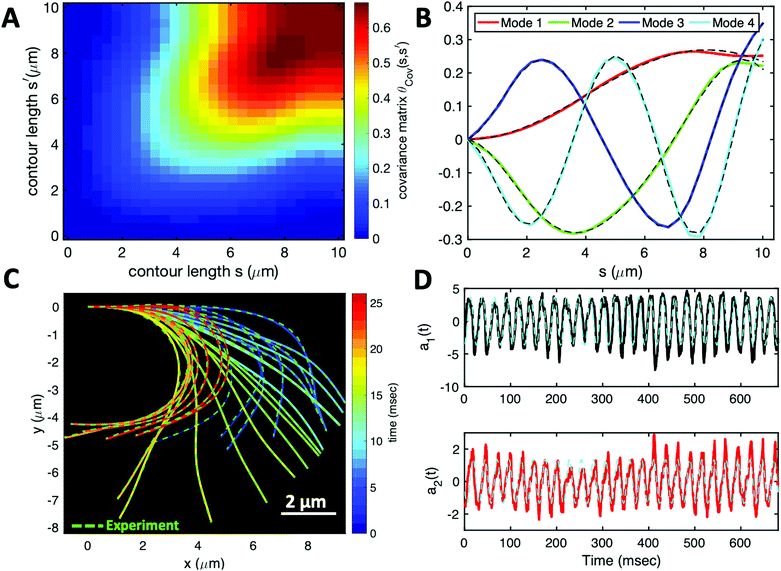 | ||
| Fig. 7 PCA analysis of the axoneme presented in Fig. 3A. (A) The covariance matrix θCov(s,s′) of fluctuations in angle θ(s,t). (B) The four eigenvectors corresponding to the first four largest eigenvalues of θCov(s,s′). (C) The time-projection of the experimental data and the corresponding shapes reconstructed using the four eigenmodes presented in panel (B). (D) The time-dependent motion amplitudes a1(t) and a2(t) as defined in Section 2.3. The black and cyan dashed lines in panels (B) and (D) show the Fourier fits.60 | ||
Finally, we reconstruct the axonemal shapes using the four dominant modes and the corresponding time-dependent motion amplitudes an(t) (n = 1, …, 4) using eqn (2). The reconstructed shapes are presented in Fig. 7C, where the green dashed lines show the experimental data. The contribution of different modes in reconstructing the axonemal shapes is shown in Fig. 8. Please note that higher spatial modes in combination with the corresponding time-dependent motion amplitudes, i.e. a2(t)M2(s), a3(t)M3(s) and a4(t)M4(s), are approximately standing waves.60 The motion amplitudes a1(t) and a2(t), which oscillate at the axonemal beat frequency f0, are shown in Fig. 7D; see also Fig. 9 for a plot of motion amplitudes a1(t) to a4(t) versus each other.
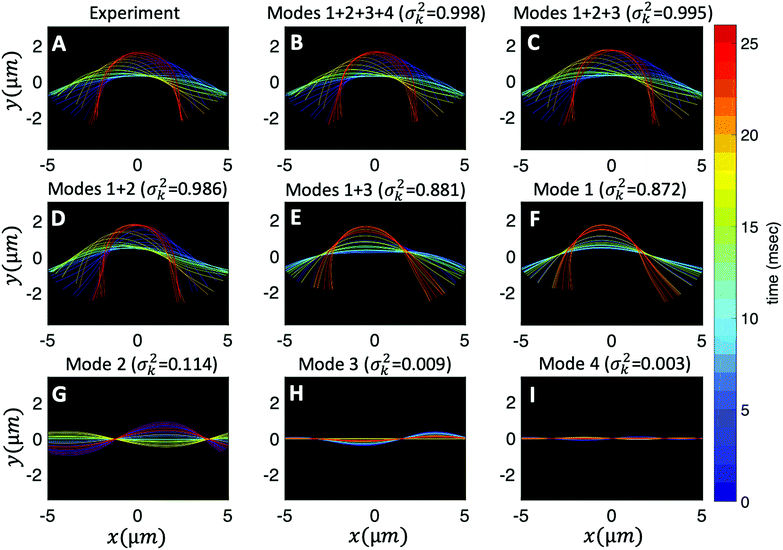 | ||
Fig. 8 Experimental shapes over one beat cycle of the axoneme in Fig. 3A are compared with the axonemal shapes reconstructed using different combination of PCA modes as 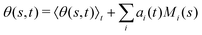 . For each panel, the fraction of the total variance σk2 is also calculated; see Section 2.3 for the definition of σk2. Note that shapes reconstructed using modes 2, 3 and 4 are approximately standing waves. . For each panel, the fraction of the total variance σk2 is also calculated; see Section 2.3 for the definition of σk2. Note that shapes reconstructed using modes 2, 3 and 4 are approximately standing waves. | ||
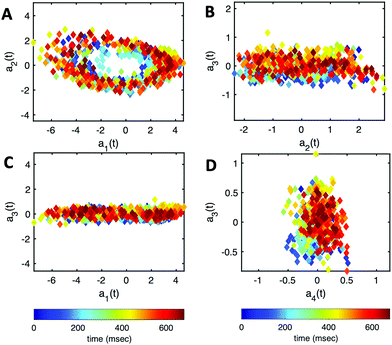 | ||
| Fig. 9 The time-dependent motion amplitudes a1(t) to a4(t) are plotted versus each other for the exemplary axoneme shown in Fig. 3A. | ||
As mentioned above and discussed in details in our recent study,60 the Fourier analysis of PCA modes shows that the traveling curvature waves can be decomposed into a static component C0 and a leading travelling wave component of amplitude C1 coexisting with standing waves at the wavenumber of the travelling waves, and at multiples of this wavenumber (higher harmonics). With this expression of the axoneme waveform, one can apply resistive-force theory58 to determine the translational and rotational velocities of a free axoneme (without cargo) as a function of C0, C1 and the flagellar beat frequency f0 (see also ref. 37 and 40). This analysis shows that at a given beat frequency, up to the leading order, the rotational velocity of an axoneme 〈Ωz〉 is proportional to f0, to C0, and to C12. Thus, 〈Ωz〉/f0 is predominately controlled by the static component of the axonemal waveform C0, which is essential to understand the transition between the two modes of propulsion illustrated in Fig. 1. Once the static component C0 is reduced by the addition of calcium ions, the bead is driven along a straight path with a translational velocity proportional to the size of the axoneme, to the frequency f0, and to the square of the traveling wave component C1.57,61 The extension of this analysis to include the effects of the cargo, and in particular the specificities of the attachment of the flagellum, lead to a semi-quantitative agreement with our measurements of the translational and angular velocities. These results will be the subject of a separate publication. Finally, we note that in contrast to C0, our experiments show that the wave component C1 is less sensitive to the calcium concentration and reduces slightly at high [Ca2+] around 1 mM (see Fig. S5, ESI†).
4 Conclusions and outlook
In this work, we have characterized the motion of a bead (a cargo) propelled by an ATP-reactivated axoneme isolated from the green algae C. reinhardtii. We observed two distinct regimes of bead propulsion depending on the calcium concentration. The first regime describes the bead motion along a curved trajectory which is observed in experiments at zero or very small calcium concentration (less than 0.03 mM). A directed bead propulsion along straight trajectories occurs at higher calcium concentrations where the cargo is propelled at an averaged velocity around 20 μm s−1. This is comparable to the typical human sperm migration speed in mucus.59The role played by calcium in affecting the beating of axonemes, and as a consequence in our experiments, the trajectories of the beads, calls for an explanation at the molecular level. In fact, based on high-resolution structural information obtained by electron cryotomography, Gui et al.62 have proposed that RS (radial spoke) heads and CP (central pair) projections interact via electrostatic forces. In this model, an increase in the electrostatic force with decreasing distance as the axoneme bends causes a tilt of the radial spoke. This tilt is the mechanosignal that is transmitted to the IDAs (inner dynein arms), the N-DRC (nexin–dynein regulatory complex) and, finally, to the ODAs (outer dynein arms). These electron cryotomography data support the idea that calcium may regulate the transmission of these mechanosignals by inducing a conformational change in calmodulin, which is a calcium responsive protein at the interface between RS1 (radial spoke 1) and IDAa (inner dynein arm a). This conformational change in calmodulin can alter directly the wave pattern by affecting RS1–IDAa interaction. An alternative plausible mechanism is that calcium affects a calmodulin-like subunit (LC4) of the ODAs, and consequently influences the dynein behavior.63 Further experiments are required to clarify the mechanism of dynein regulation and the precise role of calcium in shaping the flagellar waveform.
In this paper, we have focused on examples where the axoneme-bead system swims effectively in 2D in the vicinity of the substrate. This greatly facilitates the tracking of axonemes and the data analysis. In our experiments, the axonemes beat with an asymmetric waveform, which resembles the forward swimming motion of flagella in intact cells.24 We extracted the axonemal shapes using gradient vector flow technique51,52 and quantitatively described the beating patterns by the dimensionless curvature C(s,t) at time t and at arc-length s along the axonemal length. Our PCA analysis shows that the axonemal motion is described with a high degree of accuracy, taking into account only the first four dominant eigenmodes corresponding to the first four largest eigenvalues.
It is worth mentioning that we also observed examples where the axoneme-bead swimmer undergoes a tumbling motion in 3D, as shown in the Videos S8–S10 (ESI†). This out of plane swimming dynamics complicates the tracking process of the axonemes. In future studies, 3D microscopy techniques are necessary to capture the full 3D swimming dynamics of the isolated axonemes. In ref. 53, torsional waves are measured in addition to curvature waves, which should be considered in a full modal analysis in 3D, meriting future investigation.
Since the beads in our experiments were incubated with demembranated axonemes, the quantity, spacing and location of beads attached to the axonemes were not controlled. Normally, a small fraction of the beads (less than 10) adheres to the axonemes at random sites preferably at the basal or the distal ends; see ESI,† Videos for examples of having two axonemes attached to one bead (Video S11, ESI†), two beads attached to one axoneme at two opposite ends (Video S12, ESI†), one bead along the contour length (Video S13, ESI†), one bead at the distal tip (Video S14, ESI†), and finally two beads at one end (Video S15, ESI†).
One of the crucial parameters controlling the speed of cargo transport is the beating frequency of axonemes. This frequency can be enhanced by increasing the ATP concentration (Fig. S4, ESI†). A promising method to increase ATP concentration in a controlled manner by an external stimulus (e.g. light), and to maintain it at a constant level, consists in integrating a light-powered ATP-generating energy module composed of functionalized vesicles with our motility module, i.e. axonemes isolated from C. reinhardtii.47 These vesicles (150 nm in size) are co-reconstituted with two transmembrane proteins, bacteriorhodopsin and ATP synthase.64 Upon illumination, bacteriorhodopsin pumps protons into the interior of the vesicles, which drives the activity of ATP synthase, generating ATP from ADP (Fig. 10). The produced ATP is consumed by the axonemal dyneins, that power the oscillatory motion of axonemes. This developed scheme with the cycle of ATP production and consumption can also be integrated into our bio-hybrid flagellum-driven micro-swimmers to provide a continuous source of ATP via illumination. The ATP synthesis rate depends non-linearly on the light intensity showing saturation at higher light intensities, reminiscent of Michaelis–Menten-type kinetics.65Fig. 10 shows a preliminary experiment where the ATP required for the reactivation of axonemes and cargo propulsion is generated via illumination of the functionalized vesicles (see Video S16, ESI†). These light-switchable bio-hybrid microswimmers have potential applications in the biomedical field, where the beating frequency of flagella, hence the propulsion velocity of the cargo, can be controlled via illumination.47
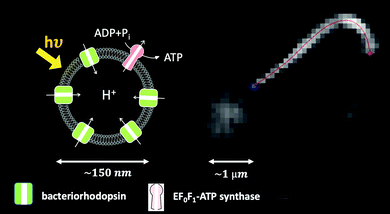 | ||
| Fig. 10 Integration of the light-driven energy module described in ref. 47 with bio-hybrid microswimmers driven by isolated axonemes. The functionalized vesicles are schematically sketched. In this experiment, a bead with a diameter of 1 μm is attached to the distal tip of an axoneme. The ATP concentration is approximately 1 μM, which is generated by illuminating the light-switchable functionalized vesicles with the microscope light (5 watts). The axonemal beat frequency is about 25 Hz (Video S16, ESI†). | ||
In summary, flagella isolated from biological micro-organisms show a variety of waveforms and are promising candidates to provide a reliable power source for motility by an effective conversion of chemical energy from ATP hydrolysis into mechanical work. The C. reinhardtii flagellar-propelled micro-swimmers investigated here have the unique advantage that the beat frequency can be controlled via illumination, as described above,47 and chemical stimuli (e.g. calcium ions) can be used to trigger a transition from a circular to a straight swimming trajectories.34,43 They also serve as an ideal model-swimmer to investigate both experimentally and theoretically the contribution of different wave components in cargo propulsion dynamics. It is our hope that this will open new possibilities in the design and fabrication of micro-swimmers, with interesting applications e.g. for smart drug delivery.
Author contributions
A. G. designed the project. R. A. isolated flagella and performed the experiments. All the authors analyzed the data and discussed and interpreted the results. A. B. wrote the Matlab code to track the axonemes. A. G. wrote the first draft of the manuscript and A. P., E. B. and A. G. wrote the final version.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge J. Molacek, F. Nordsiek, B. Nasouri and unknown referees for valuable comments and S. Romanowsky, M. Müller and K. Gunkel for technical assistance. R. A. acknowledges support from the European Union's Horizon 2020 research and innovation programme under grant agreement MAMI No. 766007. The authors acknowledge the Volkswagen Foundation Initiative LIFE (Project Living Foam) and the MaxSynBio Consortium, which is jointly funded by the Federal Ministry of Education and Research of Germany and the Max Planck Society. The authors also thank M. Lorenz and S. Bank at the Göttingen Algae Culture Collection (SAG) for providing the C. reinhardtii wild type strain SAG 11-32b. Open Access funding provided by the Max Planck Society.Notes and references
- M. M. Stanton, B.-W. Park, A. Miguel-López, X. Ma, M. Sitti and S. Sánchez, Small, 2017, 13, 1603679 CrossRef PubMed.
- K. Higashi and N. Miki, Sens. Actuators, B, 2014, 202, 301–306 CrossRef CAS.
- L. Schwarz, M. Medina-Sánchez and O. G. Schmidt, Appl. Phys. Rev., 2017, 4, 031301 Search PubMed.
- W. Wang, W. Duan, S. Ahmed, T. E. Mallouk and A. Sen, Nano Today, 2013, 8, 531–554 CrossRef CAS.
- A. V. Singh, Z. Hosseinidoust, B.-W. Park, O. Yasa and M. Sitti, ACS Nano, 2017, 11, 9759–9769 CrossRef CAS PubMed.
- Z. Hosseinidoust, B. Mostaghaci, O. Yasa, B.-W. Park, A. V. Singh and M. Sitti, Adv. Drug Delivery Rev., 2016, 106, 27–44 CrossRef CAS PubMed.
- Y. Alapan, O. Yasa, O. Schauer, J. Giltinan, A. F. Tabak, V. Sourjik and M. Sitti, Sci. Robotics, 2018, 3, aar4423 CrossRef PubMed.
- R. W. Carlsen and M. Sitti, Small, 2014, 10, 3831–3851 CrossRef CAS PubMed.
- A. V. Singh and M. Sitti, Adv. Healthcare Mater., 2016, 5, 2325–2331 CrossRef CAS PubMed.
- B. Mostaghaci, O. Yasa, J. Zhuang and M. Sitti, Adv. Sci., 2017, 4, 1700058 CrossRef PubMed.
- P. Prakash, A. Z. Abdulla, V. Singh and M. Varma, Phys. Rev. E, 2019, 100, 062609 CrossRef PubMed.
- P. Prakash, A. Abdulla, V. Singh and M. Varma, Soft Matter, 2020, 16, 9499–9505 RSC.
- D. Pantaloni, C. Le Clainche and M.-F. Carlier, Science, 2001, 292, 1502–1506 CrossRef CAS PubMed.
- T. D. Pollard and G. G. Borisy, Cell, 2003, 112, 453–465 CrossRef CAS PubMed.
- W. Gilpin, M. S. Bull and M. Prakash, Nat. Rev. Phys., 2020, 1–15 Search PubMed.
- J. T. Eggenschwiler and K. V. Anderson, Annu. Rev. Cell Dev. Biol., 2007, 23, 345–373 CrossRef CAS PubMed.
- E. A. Gaffney, H. Gadêlha, D. J. Smith, J. R. Blake and J. C. Kirkman-Brown, Ann. Rev. Fluid Mech., 2011, 43, 501–528 CrossRef.
- R. Faubel, C. Westendorf, E. Bodenschatz and G. Eichele, Science, 2016, 353, 176–178 CrossRef CAS PubMed.
- A. S. Shah, Y. Ben-Shahar, T. O. Moninger, J. N. Kline and M. J. Welsh, Science, 2009, 325, 1131–1134 CrossRef CAS PubMed.
- G. Witman, The Chlamydomonas Sourcebook: Cell Motility and Behavior, Academic Press, 2009, vol. 3 Search PubMed.
- L. Vincensini, T. Blisnick and P. Bastin, Biol. Cell, 2011, 103, 109–130 CrossRef PubMed.
- R. E. Goldstein, Ann. Rev. Fluid Mech., 2015, 47, 343–375 CrossRef PubMed.
- R. E. Goldstein, M. Polin and I. Tuval, Phys. Rev. Lett., 2009, 103, 168103 CrossRef PubMed.
- K. Y. Wan, K. C. Leptos and R. E. Goldstein, J. Royal Soc. Interface, 2014, 11, 20131160 CrossRef PubMed.
- D. T. Chen, M. Heymann, S. Fraden, D. Nicastro and Z. Dogic, Biophys. J., 2015, 109, 2562–2573 CrossRef CAS PubMed.
- D. Nicastro, C. Schwartz, J. Pierson, R. Gaudette, M. E. Porter and J. R. McIntosh, Science, 2006, 313, 944–948 CrossRef CAS PubMed.
- J. Lin and D. Nicastro, Science, 2018, 360 DOI:10.1126/science.aar1968.
- S. M. King, Dyneins: Structure, biology and disease, Elsevier, 2018, pp. 162–201 Search PubMed.
- R. Bower, D. Tritschler, K. VanderWaal, C. A. Perrone, J. Mueller, L. Fox, W. S. Sale and M. Porter, Mol. Biol. Cell, 2013, 24, 1134–1152 CrossRef CAS PubMed.
- G. Pigino, K. H. Bui, A. Maheshwari, P. Lupetti, D. Diener and T. Ishikawa, J. Cell Biol., 2011, 195, 673–687 CrossRef CAS PubMed.
- P. Yang, D. R. Diener, C. Yang, T. Kohno, G. J. Pazour, J. M. Dienes, N. S. Agrin, S. M. King, W. S. Sale and R. Kamiya, et al. , J. Cell Sci., 2006, 119, 1165–1174 CrossRef CAS PubMed.
- T. Heuser, M. Raytchev, J. Krell, M. E. Porter and D. Nicastro, J. Cell Biol., 2009, 187, 921–933 CrossRef CAS PubMed.
- D. Luck, G. Piperno, Z. Ramanis and B. Huang, Proc. Natl. Acad. Sci. U. S. A., 1977, 74, 3456–3460 CrossRef CAS PubMed.
- M. Bessen, R. B. Fay and G. B. Witman, J. Cell Biol., 1980, 86, 446–455 CrossRef CAS PubMed.
- J. S. Hyams and G. G. Borisy, J. Cell Sci., 1978, 33, 235–253 CrossRef CAS PubMed.
- V. F. Geyer, P. Sartori, B. M. Friedrich, F. Jülicher and J. Howard, Curr. Biol., 2016, 26, 1098–1103 CrossRef CAS PubMed.
- P. Sartori, V. F. Geyer, A. Scholich, F. Jülicher and J. Howard, Elife, 2016, 5, e13258 CrossRef PubMed.
- V. Geyer, PhD thesis, Sächsische Landesbibliothek-Staats-und Universitätsbibliothek Dresden, 2013.
- G. Saggiorato, L. Alvarez, J. F. Jikeli, U. B. Kaupp, G. Gompper and J. Elgeti, Nat. Commun., 2017, 8, 1–9 CrossRef CAS PubMed.
- A. Gong, S. Rode, U. B. Kaupp, G. Gompper, J. Elgeti, B. M. Friedrich and L. Alvarez, Philos. Trans. R. Soc., B, 2020, 375, 20190149 CrossRef CAS PubMed.
- Z. Liu, F. Qin, L. Zhu, R. Yang and X. Luo, Phys. Fluids, 2020, 32, 041902 CrossRef CAS.
- D. Eshel and C. J. Brokaw, Cell Motil. Cytoskeleton, 1987, 7, 160–168 CrossRef CAS PubMed.
- C. Omoto and C. Brokaw, Cell Motil., 1985, 5, 53–60 CrossRef CAS PubMed.
- J. A. Schmidt and R. Eckert, Nature, 1976, 262, 713–715 CrossRef CAS PubMed.
- C. J. Brokaw and D. Luck, Cell Motil., 1983, 3, 131–150 CrossRef CAS PubMed.
- R. Eckert and P. Brehm, Ann. Rev. Biophys. Bioeng., 1979, 8, 353–383 CrossRef CAS PubMed.
- R. Ahmad, C. Kleineberg, V. Nasirimarekani, Y.-J. Su, S. Goli Pozveh, A. Bae, K. Sundmacher, E. Bodenschatz, I. Guido, T. Vidakovic-Koch and A. Gholami, ACS Synth. Biol., 2021, 10, 1490–1504 CrossRef CAS PubMed.
- V. F. Geyer, J. Howard and P. Sartori, Nat. Phys., 2022, 1–6 Search PubMed.
- G. B. Witman, Meth. Enzymology, Elsevier, 1986, vol. 134, pp. 280–290 Search PubMed.
- J. Alper, V. Geyer, V. Mukundan and J. Howard, Meth. Enzymology, Elsevier, 2013, vol. 524, pp. 343–369 Search PubMed.
- C. Xu and J. L. Prince, Gradient vector flow: A new externalforce for snakes, IEEE Proc. CVPR, 1997, pp. 66–71, ISBN: 0-8186-7822-4 Search PubMed.
- C. Xu and J. L. Prince, IEEE Trans. Image Process., 1998, 7, 359–369 CrossRef CAS PubMed.
- S. Mojiri, S. Isbaner, S. Mühle, H. Jang, A. J. Bae, I. Gregor, A. Gholami and J. Enderlein, Biomed. Opt. Express, 2021, 12, 3169–3180 CrossRef PubMed.
- G. J. Stephens, B. Johnson-Kerner, W. Bialek and W. S. Ryu, PLoS Comput. Biol., 2008, 4, e1000028 CrossRef PubMed.
- J. Frenet, J. Math. Pures Appl., 1852, 17, 437–447 Search PubMed.
- D. J. Struik, Lectures on classical differential geometry, Courier Corporation, 1961 Search PubMed.
- B. M. Friedrich, I. H. Riedel-Kruse, J. Howard and F. Jülicher, J. Exp. Biol., 2010, 213, 1226–1234 CrossRef CAS PubMed.
- J. Gray and G. Hancock, J. Exp. Biol., 1955, 32, 802–814 CrossRef.
- D. F. Katz, E. Z. Drobnis and J. W. Overstreet, Gamete Res., 1989, 22, 443–469 CrossRef CAS PubMed.
- A. Gholami, R. Ahmad, A. Bae, A. Pumir and E. Bodenschatz, New J. Phys., 2022, 24, 053025 CrossRef.
- E. Lauga, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 041916 CrossRef PubMed.
- M. Gui, M. Ma, E. Sze-Tu, X. Wang, F. Koh, E. D. Zhong, B. Berger, J. H. Davis, S. K. Dutcher and R. Zhang, et al. , Nat. Struct. Mol. Biol., 2021, 28, 29–37 CrossRef CAS PubMed.
- S. M. King and R. S. Patel-King, J. Cell Sci., 1995, 108, 3757–3764 CrossRef CAS PubMed.
- C. Kleineberg, C. Wölfer, A. Abbasnia, D. Pischel, C. Bednarz, I. Ivanov, T. Heitkamp, M. Börsch, K. Sundmacher and T. Vidakovi-Koch, ChemBioChem, 2020, 21, 2149–2160 CrossRef CAS PubMed.
- J. Krupinski and G. G. Hammes, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 4233–4237 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00574c |
| This journal is © The Royal Society of Chemistry 2022 |