 Open Access Article
Open Access ArticleSelf-organization of agitated microspheres on various substrates
Ignaas S. M.
Jimidar
 *ab,
Kai
Sotthewes
*ab,
Kai
Sotthewes
 c,
Han
Gardeniers
c,
Han
Gardeniers
 b,
Gert
Desmet
b,
Gert
Desmet
 a and
Devaraj
van der Meer
a and
Devaraj
van der Meer
 d
d
aDepartment of Chemical Engineering, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussels, Belgium. E-mail: i.s.m.jimidar@utwente.nl
bMesoscale Chemical Systems group, MESA+ Institute and Faculty of Science and Technology, University of Twente, P. O. Box 217, 7500AE Enschede, The Netherlands
cPhysics of Interfaces and Nanomaterials group, MESA+ Institute and Faculty of Science and Technology, University of Twente, P. O. Box 217, 7500AE Enschede, The Netherlands
dPhysics of Fluids group, Max Plank Center Twente for Complex Fluid Dynamics, J. M. Burgers Centre for Fluid Dynamics, MESA+ Institute and Faculty of Science and Technology, University of Twente, P. O. Box 217, The Netherlands
First published on 25th April 2022
Abstract
The vibration dynamics of relatively large granular grains is extensively treated in the literature, but comparable studies on the self-assembly of smaller agitated beads are lacking. In this work, we investigate how the particle properties and the properties of the underlying substrate surface affect the dynamics and self-organization of horizontally agitated monodisperse microspheres with diameters between 3 and 10 μm. Upon agitation, the agglomerated hydrophilic silica particles locally leave traces of particle monolayers as they move across the flat uncoated and fluorocarbon-coated silicon substrates. However, on the micromachined silicon tray with relatively large surface roughness, the agitated silica agglomerates form segregated bands reminiscent of earlier studies on granular suspensions or Faraday heaps. On the other hand, the less agglomerated hydrophobic polystyrene particles form densely occupied monolayer arrangements regardless of the underlying substrate. We explain the observations by considering the relevant adhesion and friction forces between particles and underlying substrates as well as those among the particles themselves. Interestingly, for both types of microspheres, large areas of the fluorocarbon-coated substrates are covered with densely occupied particle monolayers. By qualitatively examining the morphology of the self-organized particle monolayers using the Voronoi approach, it is understood that these monolayers are highly disordered, i.e., multiple symmetries coexist in the self-organized monolayers. However, more structured symmetries are identified in the monolayers of the agitated polystyrene microspheres on all the substrates, albeit not all precisely positioned on a hexagonal lattice. On the other hand, both the silica and polystyrene monolayers on the bare silicon substrates transition into less disordered structures as time progresses. Using Kelvin probe force microscopy measurements, we show that due to the tribocharging phenomenon, the formation of particle monolayers is promoted on the fluorocarbon surface, i.e., a local electrostatic attraction exists between the particle and the substrate.
1 Introduction
Imagine a jar full of marbles (≈12 mm) being emptied inside a box. Intuitively these primary marbles flow from the jar into the box and arrange themselves in an ordered packing. However, when repeating the same experiment at a much smaller scale, namely for an agglomerate comprising multiple primary cohesive spheres with a diameter of d ≤ 10 μm, usually the agglomerate remains intact and rests as a solid block inside the box. This example, albeit simplified, demonstrates that the grain size strongly affects their dynamic behaviour, originating from different dominating forces at various length scales. Inspired by the complexity of the grains' dynamics, a plethora of scientists have devoted their work to granular materials in recent years.1–12In contrast to marbles, cohesive ultrafine powder particles exhibit a relatively large surface to volume ratio, leading to significantly stronger surface over body forces (e.g., gravity), either among these particles or with other surfaces. As a result, the gravity force can often be neglected in this respect. Their interactions are dictated by a delicate competition of different acting forces, such as van der Waals forces, capillary forces, electrostatic forces, and others.1,13,14 The intrinsic properties of the particles, e.g., size, roughness, porosity, composition, charge distribution, determine the dominance of these forces.15,16 Due to these strong interaction forces, the particles tend to cluster and form agglomerates or stick to other surfaces. Consequently, handling micro- or nanoparticles in a dry state can be a daunting task as these forces pose considerable challenges during applications, as exemplified by the very different outcome of the simple experiment described above for large and small grains.
To circumvent the strong interaction forces, micro- or nanoparticles are often suspended in liquids to study the self- or directed organization of these particles on substrates using a variety of techniques, such as manipulation by means of electric and magnetic fields, or solvent evaporation.17–27 In this respect, a profound understanding of the competing interparticle forces and the adhesion force between the particle and substrate is key to attain well-controlled particle patterns20,28,29 which are relevant in various applications, e.g., bio-inspired approaches to materials engineering, paints, photonic crystals, self-cleaning anti-reflective coatings, optical and biological sensors, chemical catalysis, biomimicry.30–34 However, as the wet assembly techniques rely on optimized conditions, such as solvent evaporation rate, surface wettability, pH, it tends to be challenging to attain perfect ordered crystals, without any cracks, on a large scale.35
On the other hand, dry assembly methods such as the rubbing of dry particles, and vacuum-driven assembly of particles from generated clouds, have proven to be promising and faster routes to obtaining assembled particle arrays on surfaces.36–38
In earlier reports, scientists primarily engaged in studying the gravity-dominated pattern formation that emerged when disordered granular packings comprising large, mm-sized spheres or binary grain mixtures on substrates were vibrated in lateral direction.39–45 The well-established concept of vibro-fluidization is commonly applied to mobilize solid granular material or agglomerated powders, i.e., during vigorous horizontal or vertical vibration, granular materials behave in a fluid-like manner.46–50
Inspired by this body of work, we explore in this study if starting from disordered fine powder particles, the microspheres can be arranged in ordered structures, i.e., particle monolayers, using the same concept. These ordered particle structures may ultimately serve as building blocks for ordered packing structures, e.g., photonic band structures, or a platform to assemble particles within microfluidic devices employed as catalytic microreactors or medical sensing devices.
We report on the observation that spontaneous order may also occur in horizontally agitated small particle systems (with diameter d ≤ 10 μm), in spite of the many additional forces that are of relevance in these systems. To the best of our knowledge, this has not been reported yet in literature. We approach this problem by agitating agglomerates comprising 10 μm silica particles in the horizontal direction with an oscillation amplitude A and an angular frequency ω. By exerting a mechanically generated body force Fvib ≤ mparω2A on a particle with mass mpar, the aim is to break or at least mobilize the bonds among the cohesive particles at the surface of the solid agglomerate, leading to the formation of a particle monolayer. This is a very different mechanism than the one causing ordered monolayers for macroscopic grains and can be viewed analogous to a melting ice cube turning into a water layer due to the supplied thermal energy.
In fact, it is not straightforward to break the bonds among these cohesive silica particles as the attractive force among the particles Fad is generally orders of magnitude stronger than the generated force Fvib. Thus, the applied mechanical force due to vibration is generally insufficient to break the bonds between the particles. Nevertheless, instead of breaking, these mutual bonds can be mobilized to obtain assembled particle monolayers.
Our study evidences that it is less challenging to obtain an ordered monolayer of hydrophobic polystyrene than of hydrophilic silica microspheres with diameters d ≤ 10 μm on various substrates when agitated horizontally. These substrates include flat uncoated and CFx-coated silicon surfaces (2 ≤ x ≤ 3) and a micromachined silicon particle tray. The results show that for silica particles a monolayer is only observed on the two flat surfaces, whereas the polystyrene particles organize in a monolayer arrangement on all the investigated surfaces. The self-organization of the agitated microspheres is examined by analyzing the constructed Voronoi diagrams and the hexatic orientational order parameter from images taken of the ordered particle monolayers. It is shown that the microspheres are not perfectly organized in a close hexagonally packed arrangement, i.e., some defects are present in the monolayers. Surprisingly, a higher monolayer packing density of both silica and polystyrene particles was attained on the (hydrophobic) CFx-coated silicon substrates. Using Kelvin probe force microscopy (KPFM),51 we show that this originates from the fact that the particles and CFx layer get tribocharged: a phenomenon typically observed in vibrated granular systems.52–55 To corroborate our observations, a physical mechanism accounting for the friction between particles and substrates is proposed.
In this article, we commence with introducing the experimental setup and methods (Section 2) and briefly discuss the relevant particle interaction forces afterwards (Section 3). What follows is a summary, analysis, and interpretation of the results obtained after agitating the silica and polystyrene particles on the different surfaces (Section 4). Additionally, in Section 4 we elaborate on the friction forces to explain the distinct observations, including the KPFM scan results, supporting the tribocharging hypothesis. Finally, Section 5 contains the concluding remarks.
2 Experimental section
2.1 Setup
Fig. 1 depicts a schematic representation of the experimental setup, in which either silica particles or polystyrene particles are gently deposited on an oscillating substrate mounted between two alumina blocks connected to a shaking device. The device's horizontal sinusoidal vibration is driven via a function generator at frequency f and amplified amplitude A. All experiments were performed under ambient conditions (T = 21.5 °C; relative humidity (RH) = 40–54%).To estimate the acceleration of the oscillating chips, a side-view video of the moving stage was made using a high-speed camera (Photron, FASTCAM SA-X@), allowing to measure the corresponding amplitude A at a set frequency  of the stage. Since the silicon chip is firmly fixed between the two alumina blocks, it is assumed that the silicon chip has the same oscillation parameters. A dimensionless form Γ of the acceleration is defined as:56
of the stage. Since the silicon chip is firmly fixed between the two alumina blocks, it is assumed that the silicon chip has the same oscillation parameters. A dimensionless form Γ of the acceleration is defined as:56
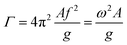 | (1) |
| f [Hz] | A [μm] | Γ | F vib,silica [nN] | F vib,polystyrene [nN] |
|---|---|---|---|---|
| 250 | 82 | 21 | 0.20 | 0.10 |
| 500 | 34 | 34 | 0.33 | 0.18 |
2.2 Materials and methods
All experiments were performed using monodisperse hydrophilic silica particles of diameter (4.89 ± 0.12) and (10.02 ± 0.11) μm, or hydrophobic polystyrene particles of diameter (2.99 ± 0.04) and (10.14 ± 0.12) μm. The mentioned standard deviation (SD) values were specified by the distributor microParticles GmbH (Germany).The particles were deposited on three types of chips: bare polished silicon substrates carrying a native oxide layer of 3 nm, silicon substrates coated with a hydrophobic (CFx) layer of 50–75 nm,36 and a silicon chip carrying a micromachined particle tray. The former two flat chips were diced in pieces of 30 × 30 mm from either the uncoated or CFx-coated silicon wafers (Si-Mat; Germany). The particle tray consists of a circular plateau with a diameter of 18 mm and a depth of 100 μm separated by a wall (thickness = 1 mm) from a larger cavity with depth = ±300 μm and width = 4 mm. Note that as a result of the micromachining, the bottom of the plateau is not perfectly flat, with a larger surface roughness than the polished substrates (see ESI† for further details). Prior to each experiment, all substrates were sonicated for 10 min. in acetone followed by an additional 10 min. of sonication in isopropanol to eliminate any traces of organic contaminants or dust particles from their surfaces.
After agitating the particles, the substrates were inspected using a Zeiss MERLIN HR-SEM to take scanning electron microscopy (SEM) images. SEM inspection was preferred over optical microscopy as the SEM provides a better resolution, ensuing visualization of multiple particle layers without causing any scattering effects.
The Kelvin probe force microscopy (KPFM) experiments were performed to investigate if, due to the tribocharging mechanism, any charge transfer occurred between the particles and substrates during agitation. These KPFM measurements were conducted in a Bruker Icon atomic force microscope (AFM) at ambient conditions with a relative humidity (RH) of 50–55% (measured with a Digital Professional Thermo-Hygrometer KLIMA BEE, TFA, Germany). A Pt–Ir coated heavily n-doped Si-cantilever (resistivity = 0.01–0.025 Ω cm Antimony doped) with a resonance frequency of 75 kHz and a force constant of 3 N m−1 (SCM-PIT-V2, Bruker) was used. The FM-KPFM mode was used in which the topography and the potential landscape are imaged simultaneously. The topography was obtained in tapping mode, where the oscillation amplitude is kept constant, while the potential signal is determined from the frequency shift of the cantilever oscillation due to the change in the electrostatic force gradient.51 The tip scans in a line-by-line fashion (left to right and vice versa for all the images in this work) from which an image is obtained. As the tip was grounded during the KPFM-measurements, the contact potential difference (VCPD) of the sample with respect to the tip is determined by:
 | (2) |
2.3 Structure analysis of particle monolayers
To characterize the structure of the silica or polystyrene monolayers, Voronoi diagrams have been constructed from the SEM images using MATLAB routines. A Voronoi diagram, or so-called tessellation, is constructed by using the centers of the microspheres to partition the space into polygonal cells comprising of points closer to one microsphere center than to all the others.57,58 The shape of each obtained Voronoi cell i can be described by computing a dimensionless quantity ϑi, called shape factor: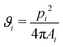 | (3) |
The orientational order of the obtained monolayers can be quantified by computing the local 6-fold bond-orientation, or hexatic, order parameter ψ for each particle which is defined as:59,60
 | (4) |
One can also compute the spatially averaged orientational order parameter ψav of an ensemble of N particles as:
 | (5) |
3 Relevant interaction forces
Before turning to the experimental results, we briefly review the different interparticle and particle substrate forces that may play a role and estimate their magnitude for the particles we used. The interaction forces relevant at the studied scale encompass (i) the van der Waals force, (ii) the contact mechanics force, (iii) the capillary force, and (iv) the electrostatic force.(i) van der Waals force
The van der Waals force stems from the electromagnetic interactions between neutral molecular dipoles. Since we are dealing with macroscopic bodies, the van der Waals force can be calculated using the model proposed by Hamaker.61,62 In the case of two touching bodies, the van der Waals force FvdW is given by: | (6) |
 | (7) |
 .
.
In practice, the separation distance between the touching bodies will be larger when the particles and substrates bear some roughness on their surface, reducing the van der Waals interactions across the bodies. It is noteworthy that the nature of the van der Waals force is always attractive among bodies with identical compositions. Consequently, the cohesion among particles situated in the proximity of each other will be enhanced, promoting the discerned formation of agglomerates.
(ii) Contact mechanics force
As highlighted above, when two bodies approach each other and come in contact, they will experience an attractive van der Waals force. Once in contact, the two solid bodies will inevitably deform their surfaces at their contact area due to their finite elasticity. Consequently, the surface forces acting in this contact area constitute another source of adhesion between the two bodies. In the case of particulate systems, contact mechanics forces between particles and walls may become dominant at low RH levels (up to ±40%) and on hydrophobic materials.14,63 The adhesion force Fcontact resulting from the deformation of a smooth particle with radius R in contact with another surface can be expressed as:| Fcontact = 2πwadhR*. | (8) |
(iii) Capillary force
Recall that water is an indispensable ingredient when shaping rigid sandcastles from dry sand on the beach. The added water forms a liquid meniscus around the contact area between neighbouring grains. As a matter of fact, the liquid meniscus accounts for the onset of the capillary force between the grains, establishing a strong cohesion between wet sand particles. Similarly, water vapour in ambient air inevitably condensates or adsorbs particularly on hydrophilic solid bodies. The liquid meniscus formed between a hydrophilic particle and another hydrophilic surface further enhances the adhesion between these two bodies in humid air.The capillary force Fcap acting between a hydrophilic particle with radius R1 in contact with another hydrophilic body of R2 radius can be approximated as:61,62
Fcap = 2πγLR*(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 + cos θ1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2) θ2) | (9) |
Even though eqn (6), (8) and (9) describe the interaction between perfectly smooth solid bodies, they offer sufficient insight regarding the implications posed by the interaction forces during the experiment. First of all, if the composition of equally-sized particles is identical to the flat substrate, e.g., the silica particles and native oxide present on the flat silicon substrate, the adhesion forces between the particle and flat substrates can be expected to be a factor two higher than between the particles themselves. Secondly, the adhesion force depends linearly on the radius ∼R of the particles, whereas the generated force applied on an agitated particle scales with ∼R3. Consequently, the ratio of the interaction forces and the mechanically generated body force during agitation scales as ∼R−2, implying that the cohesive interactions among the particles are clearly more pronounced as their size is reduced. Hence, it is more demanding to fluidize agglomerates comprising tiny grains.
To estimate the contribution of the different attractive interactions among the employed silica and polystyrene particles, we have computed the three different forces using eqn (6)–(9) and compared them in Table 2. It should be stressed that the absolute values in Table 2 need to be interpreted with caution, as the surface of solid bodies naturally carries some roughness, reducing the adhesion force between bodies. Nonetheless, the values in Table 2 elucidate that the applied body force on the particles (cf.Table 1) is significantly weaker than the interparticle forces between touching particles. Additionally, the van der Waals force can be neglected, in comparison to the much larger contact mechanics forces between the particles. Furthermore, due to the polystyrene particles' hydrophobic nature, no liquid bridges between neighbouring particles will be formed, resulting in a negligible cohesive capillary force.
| Particle | F vdW [nN] | F contact [nN] | F cap [nN] |
|---|---|---|---|
| 5 μm silica | 157 | 785 | 925 |
| 10 μm silica | 315 | 1570 | 1850 |
| 3 μm polystyrene | 99 | 353 | — |
| 10 μm polystyrene | 330 | 1178 | — |
(iv) Electrostatic force
In contrast to the attractive forces reviewed above, the Coulomb force could lead to either attractive or repulsive electrostatic interactions between particles. Two charged particles in close proximity of each other experience an electrostatic force Fe that is described by Coulomb's law:64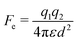 | (10) |
As already mentioned, under ambient conditions, water molecules adsorb on a hydrophilic surface and form a water layer, increasing the electrical conductivity of the particle and the surrounding atmosphere.64 The water layer improves the distribution of charges on the particle and simultaneously enhances the dissipation of static charge from the particle's surface.65 Regarding the latter, Coulomb interactions may not impose a sufficiently dominant attractive or repulsive force for distances less than 20 nm compared to the van der Waals interactions or capillary bridge formation between particulates under humid air conditions.64 Coulomb interactions may however become substantial if particles are subjected to an external electric field or in case of opposite charging of opposing surfaces.16
4 Results and discussion
4.1 The initial state of particles
In light of the aforementioned discussion on interaction forces, the initial state of the hydrophilic silica and hydrophobic polystyrene particles with a diameter of 10 μm is assessed, and the dominant interaction forces between individual particles are (qualitatively) identified. To this end, SEM images of the as-received particles were taken prior to the agitation experiments. It can be readily observed from Fig. 2 that the hydrophilic silica particles (cf.Fig. 2a) contain massive agglomerates, even resembling a crystal-like structure. The latter suggests that cohesive interactions among the hydrophilic silica particles are substantial, presumably resulting from the dominating capillary force among these particles. When this is contrasted with the appearance of the polystyrene particles (cf.Fig. 2b), we observe less and considerably smaller agglomerates. The hydrophobicity of the polystyrene particles, i.e., the absence of capillary forces, in conjunction with their larger surface roughness compared to the silica particles may attribute to the weaker cohesive attraction among the polystyrene particles. In addition, also due to the polystyrene particles' hydrophobic nature, supposedly, a water layer that would screen the surface charge present on the polystyrene particles is absent.54 Thus, the likeliness of the presence of a repulsive Coulomb force acting on particles carrying the same polarity is substantial. Both effects will result in the observed presence of mostly primary and few small clusters of polystyrene particles (cf.Fig. 2b).Please also note from Table 1 that the generated force Fvib on a single silica particle is approximately twice as strong as on a polystyrene particle. All these differences will lead to varying dynamics and distribution of the silica and polystyrene particles on the substrates.
4.2 Global dynamics and distribution of the agitated silica agglomerates
Before elaborating on the microscopic particle distribution on the three different substrates in the following sections, we first visualize the global dynamics manifested by the silica agglomerates during agitation. Fig. 3a–c shows a series of snapshots on the respective substrates at four instances when agitating the silica agglomerates using the same parameters. As the large, solid-like silica particle clusters were agitated, they slowly moved across the substrate while spreading simultaneously, reminiscent of a fluid-like behaviour.41,66 Consequently, it can be observed from Fig. 3a–c that the pattern formation of the agitated silica agglomerates on the substrates includes large clusters, small clusters, and monolayers indicated by green circles, blue squares, and dashed red lines, respectively.On the confined particle tray, the silica agglomerate moved towards the boundary where segregated stripes were formed perpendicular to the oscillating direction (cf.Fig. 3a-3, and a-4). In contrast, from Fig. 3b and c, we infer that the agglomerate tends to leave marked particle traces (a milky layer) as they moved across the two distinct flat substrates parallel to the driving direction. These milky layers in Fig. 3b and c suggest that the flat surfaces were covered by silica particle monolayers, which were, interestingly, even more pronounced on the CFx-coated substrates (cf.Fig. 3d-1).
However, when the less agglomerated polystyrene particles, i.e., loose polystyrene powder, were agitated, they rapidly moved parallel to the oscillating direction on the respective substrates. As a result, and inferred from Fig. 3d-1, a significantly high fraction of all the substrates surfaces were covered with monolayers. Moreover, Fig. 3d-1 shows that the loose polystyrene particles covered the substrates more dominantly than the silica agglomerates with monolayers as time progressed.
Fig. 3d-2 presents the evolution of the three types of coexisting silica or polystyrene particle arrangements covering the fluorocarbon-coated silicon substrate. The data suggests that the cohesion forces among the silica particles are so strong that the agglomerate is mobilized into relatively large and small silica particle clusters. On the other hand, it is less challenging to mobilize the smaller polystyrene particles, even though the generated force Fvib is two times smaller compared to that on a single silica particle. These macroscopic observations support the hypothesis that the competing interaction forces among the particles control the dynamics and obtained particle arrangements on the substrates.
In addition, these findings imply that the chemical composition of the substrate and the physical properties resulting from that, has a pivotal effect on the dynamics and especially the distribution of the agitated particles on the various substrates. The underlying mechanism for these observations could presumably be ascribed to the interaction forces, including the friction force between the particles and substrate.67,68 With this in mind, we introduce a mechanism that entails the friction forces next, and turn to the detailed discussion of the observations afterwards.
4.3 Physical mechanism
To rationalize the distinct observations made on the different substrates, a simplified mechanism accounting for the friction and concomitantly the interaction forces is proposed. This mechanism based on stick-slip motion provides a basic framework to interpret the dynamics of the silica agglomerates on the flat substrates and particle tray.Naturally, a so-called static friction resists the movement of bodies with respect to each other, i.e., the bodies remain in a fixed position during this stick phase. However, when applying a force that exceeds this static friction, the bodies start moving relative to each other, and their motion is retarded by the dynamic friction, during the so-called “slip phase”. Note that the static friction typically exceeds the value of the dynamic friction for a given system, implying that the friction force is reduced when the bodies start moving with respect to each other. On an oscillating body, a transient force is applied (cf.eqn (11) such that a dynamic stick-slip cyclic process might be induced on the body.
Consider, for simplicity, a particle resting on a surface subjected to a harmonic oscillation with amplitude A and frequency f in the horizontal direction:
x = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πft) sin(2πft) | (11) |
Fx = mparA(2πf)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πft). sin(2πft). | (12) |
The friction force on the particles can be modelled using a modified Coulomb friction law and is given by:62,67–69
| Ffric = μ(Lload + Ladh) | (13) |
Here, however, we are dealing with an assemble of agglomerated silica particles (cf.Fig. 2), such that it can be intuitively argued that a particle in the silica agglomerates will not start rolling on the substrate. Owing to this strongly agglomerated state, a complex balance of frictional forces between particles and substrates should be considered to understand their dynamics on the different substrates. In contrast to the example of a primary particle on a substrate with a single frictional contact, a silica particle in the first layer of the depicted agglomerate in Fig. 4, layer (i), inevitably has multiple frictional contacts with neighbouring particles as well as the substrate. The static friction in the latter case is denoted with Ffric,sp, while the static friction between a particle in the first layer and a neighbouring particle layer (ii) is denoted with Ffric,pp.
The visible traces of possible silica particle monolayers (cf.Fig. 3b and c) on the flat substrates suggests that a part of the agitated agglomerate sticks on them. Therefore, we postulate that as the agglomerate is being oscillated, the particles touching the substrate will stick to its surface, while simultaneously its remainder, including layer (ii), slips past the particles in contact with the flat substrates. Presumably, the tangential driving force is insufficiently strong to transcend the static friction with the substrate, but surpasses the static friction acting between the particles in the first and second layer provided that Ffric,pp < Ffric,sp. The latter is indeed plausible as the friction force acting between two silica particles is at least two times smaller than that of the particle and the flat substrate (cf. Section 3).63 Once the second layer starts sliding, the static friction transitions into the dynamic friction, reducing the friction force acting between the first and second layers. This difference in friction force emerging across layer (i) precisely mimics the application of a shear force required to separate the agglomerate from the fixed silica particles in contact with the substrate. Simply put, to ensure that the rest of the agglomerate slips past an arrested monolayer on the substrate, the following condition should be satisfied: Ffric,pp < Fvib < Ffric,sp. During a driving cycle the vibration force Fvib increases until the particles in layer (ii) are mobilized, whereas the particles in layer (i) remain stuck at the substrate, at least for some period of time. In addition, one could argue that the monodispersity of the particles is helping to create a smooth and evenly distributed layer of particles on the substrate on which the remaining particles may slide.
On the particle trays, the agglomerates were sliding as a whole, albeit slowly, on the substrate. Apparently, the friction between layer (i) and the particle tray substrate was insufficient to sustain the tangential driving force, i.e., Fvib > Ffric,sp, resulting in the dynamic friction acting between the tray and the bottom layer of the moving agglomerate. The fact that micromachined structures exhibit a larger surfaces roughness than polished silicon flat substrates offers a simple explanation for the observed results. Owing to the significant surface roughness of the micromachined particle tray, the effective contact area between the silica particles and tray is smaller, presumably leading to a significantly reduced adhesion force.70,71 Inherently, a lower friction force acts between the first layer and the tray compared to the flat substrate's case. In addition, the fact that agglomerates move as a single piece implies that the tangential force did not surpass the static friction acting between the particles of layer (i) and (ii). Thus, it can be safely concluded that on the particle tray Ffric,sp < Fvib < Ffric,pp, implying that the condition for the adherence of a monolayer of particles on the particle tray is not satisfied.
4.4 Agitating silica or polystyrene particles on a micromachined particle tray
Intuition seems to suggest that the boundary of the confined particle tray would ease the disruption of the continuously colliding agglomerate against the wall during agitation, which was the reason for considering such a micromachined particle tray in our experiments. The idea was that the former should result in excess particles spilling over the boundary, while the remaining (primary) particles would form a monolayer on the tray. However, instead of monolayers, Fig. 5a-1 and a-2 reveals that indeed segregated dense layers comprising smaller silica particle clusters were present regardless of the applied frequency and amplitude. As already inferred from Fig. 3a, these segregated stripes were formed perpendicular to the oscillating direction. Similar phenomena are observed in other studies for horizontally agitated larger particles (mm-sized) or granular suspensions,40–42 or Faraday heaps in vertically shaken systems.On the other hand, when the less agglomerated polystyrene particles were employed, Fig. 5b-1 and b-2 clearly show that most primary polystyrene particles tend to form a quasi-monolayer on the tray. Local density variations in the polystyrene particle distribution can be observed with regions densely occupied with ordered structures. These results are reminiscent of the onset of a gas-crystal-like phase transition observed in granular systems comprising mm-sized beads.56 Furthermore, a few polystyrene particles were present on top of the monolayer arrangement, which might be resulting from the higher provided energy to the system. As a result of the particle collisions occurring during agitation, the particles might lose contact with the bottom of the surface, such that a few particles will inevitably expand in the vertical direction.39,56
4.5 Agitating silica particles on flat substrates
To investigate our hypothesis that the substrate's surface chemistry affects the friction force and concomitantly the particle dynamics, we agitated the silica agglomerates on hydrophilic silicon and hydrophobic CFx-coated silicon substrates. In light of these experiments, it is noteworthy that surfaces are traditionally coated with fluorocarbon layers to avoid the formation of a capillary bridge between the particles and substrates in practice. Consequently, the adhesion force is reduced, preventing particles from sticking on these fluorocarbon-coated surfaces.The areas indicated by the red dashed line on the snapshots shown in Fig. 3b and c already suggested that the flat surfaces may be partially covered with monolayers, which is now indeed confirmed by the SEM images displayed in Fig. 6. In addition, it is understood from these findings that the monolayers are solely formed locally on the substrates, as many small and large clusters are still dispersed over the monolayer (cf.Fig. 6b-1). Following the discussion of Section 4.3, it appears that the particles remained sticking to the flat substrates, while simultaneously, the rest of the agglomerate moved past the monolayer, with some particles and small clusters remaining on top of them.
What immediately stands out from both Fig. 3 and 6 is that even though the adhesion force is expected to be reduced on the CFx-coated substrate, the formed monolayers occupied a conspicuously larger area with a higher packing density. Presumably, the silica particles counterintuitively have a higher tendency to adhere on the CFx layer, i.e., they experience a stronger adhesion force. This observation is consistent with previous studies in which silica particles preferentially adhered to the CFx-coated substrates due to the tribocharging phenomenon.36,72 Running the experiments for longer time intervals resulted in larger areas of monolayers prevalent on both types of substrates (cf.Fig. 6a-2 and b-2) but still more pronounced on the CFx-coated substrate. In addition, when comparing the results obtained with a frequency of f = 250 Hz versus f = 500 Hz, it can be inferred from Fig. 6 that the higher amplitude obtained at f = 250 Hz is apparently advantageous to mobilize the silica agglomerates and form monolayers.
Collectively, these results, including those of the particle tray, convincingly show that the surface properties indeed dominate the dynamics as well as the self-organization of the agitated agglomerate on the substrate. This implies that the interaction between the particles and substrate is key to obtain monolayers by agitating silica agglomerates.
4.6 Agitating polystyrene particles on flat substrates
Next, the experiments on the flat substrates were repeated using the polystyrene particles. Similar to our observations in the case of the particle tray, the agitated polystyrene particles moved extensively across the substrates parallel to the oscillating direction, leading to the formation of monolayers. Interestingly, the results in Fig. 7 show a slightly higher density of polystyrene particle monolayers on the CFx-coated substrates than on the bare silicon substrates already after 10 min of agitation. The former is in agreement with the results obtained for the silica particles on these flat substrates. However, a closer inspection of the images shown in Fig. 7a-1 and a-2 reveals that the distance between adjacent particles on the bare silicon substrate progressively became smaller, i.e., the packing density of the particle monolayers increased. Therefore, temporal evolution experiments were performed to study this effect in more detail.Fig. 8 displays the results of polystyrene particles agitated for four different time intervals on the bare and CFx-coated silicon substrates. From these results, it can be inferred that the packing density of polystyrene particle monolayers gradually increased on the bare silicon substrates as fewer voids were apparent in the monolayer. The packing density on the CFx-coated substrates remained approximately constant, but more extensive substrate regions were gradually covered with a monolayer. Thus, even for these loosely packed polystyrene particles, the results indicate that the packing density of the monolayers strongly depends on the surface chemistry and the time interval of the experiment. Note that performing experiments for longer time intervals did not necessarily improve the obtained results.
Overall, taking the discussion on friction forces of Section 4.3 into account, we infer that the active movement of the agitated polystyrene particle across all three types of substrates implies that the driving force acting on the particles exceeded the static friction between the particles and these substrates at some point in the driving cycle, i.e., Fvib > Ffric,pp. Consequently, these particles were at least rolling over the surface, if not sliding. The primary polystyrene particles move and collide against neighbouring particles, eventually forming monolayers that stick to the surface. This can possibly be explained by a mechanism in which the energy of the colliding particles is dissipated in the process, enhanced by the inelastic nature of the collisions. Furthermore, when two particles collide, apart from the already present frictional contact with the substrate, another frictional contact emerges instantaneously at their mutual contact point, suppressing their rolling motion and consequently their angular velocity ω. The latter leads to a situation colloquially referred to as “rotational frustration”.41,73–75 Therefore, in densely occupied regions, particles are less mobile with respect to their neighbours. Eventually, this process yields larger areas covered with dense monolayers as time progresses.
4.7 Agitating smaller particles on flat substrates
Finally, within the set of experiments performed on flat substrates, spherical particles with a smaller diameter than those of the preceding sections were employed. These experiments yielded similar results (cf.Fig. 9) as reported above, with some subtle differences. One deviation from the preceding results (cf.Fig. 5) is the presence of a significant amount of small clusters on top of the silica monolayers that formed in the experiment, as displayed in Fig. 9a1, a2. As already highlighted in Section 3, the cohesive interactions are relatively stronger for smaller grain sizes, implying that the applied body force during agitation was supposedly too weak to mobilize these small clusters from the monolayer. In addition, it is inferred from Fig. 9b1, b2 that the packing density of these smaller polystyrene particles is lower than the larger ones (cf.Fig. 7 and 8), even on the CFx-coated silicon substrates. The relatively stronger cohesive forces suggest that it is more challenging to mobilize these smaller particles, and should therefore result in a higher packing density. As a consequence, the unexpectedly low packing density of small polystyrene particles observed here suggests that an electrostatic repulsive force acts between the agitated polystyrene particles, i.e., that the particles have the same polarity.4.8 Analysis of monolayer structure
The preceding sections elaborated that particle monolayer structures with varying packing densities are prevalent depending on the agitating condition. However, as noticed before, voids and particles present on top of the monolayers appear as topological defects, compromising the organization of the particles in a closely hexagonally packed monolayer structure.To shed light on the morphology of the assembled monolayers, we apply the Voronoi approach to obtain a tessellation of the acquired SEM images from the monolayers attained on the uncoated and coated silicon substrates. Each pattern encountered in the particle monolayer results in a cell of a given shape, forming a so-called Voronoi diagram. Fig. 10a1, a2 and b1, b2 show the Voronoi diagrams constructed from the SEM images of respectively the 10 μm silica and polystyrene microspheres, in which the individual cells i are coloured according to their shape factor ϑi (eqn (3).
 | ||
| Fig. 10 Voronoi diagrams of the 10 μm silica (a) and the 10 μm polystyrene (b) particle monolayers attained after agitating the particles at a frequency of f = 250 Hz and amplitude A = 82 μm for t = 10 min., obtained on the flat bare silicon (1) and CFx-coated silicon substrates (2). The diagrams are constructed from the corresponding SEM image displayed in Fig. 6a2[(a1)], b2[(a2)], 7a2[(b1)] and b2[(b2)]. The Voronoi cells are coloured according to their shapefactor ϑi. The distribution of the normalized shape factor ϑnorm,i of the 10 μm silica (a3) and polystyrene (b3) microspheres monolayers obtained on the respective substrates. At least three SEM images of the monolayers obtained on the uncoated or fluorocarbon-coated silicon substrates were analysed. | ||
First of all, from the constructed Voronoi diagrams, it is understood that the particle arrangements on the flat silicon substrate comprise a higher number of irregularly shaped polygon cells than those on the fluorocarbon-coated silicon substrates. The former is an artefact from the clusters remaining on top of the monolayers on the bare silicon substrates. However, more regularly ordered polygons can be observed on the fluorocarbon-coated silicon substrates, which supports the hypothesis that the monolayer formation of silica or polystyrene microspheres is promoted on these coated substrates.
Although densely packed monolayers are present on the CFx-coated silicon substrates, different symmetry structures are readily noticed from Fig. 10a-2 and b-2, for example, Voronoi cells with a pentagonal shape, as well as a distorted hexagonal shape, i.e., hexagons deviating from regular-shaped hexagons. The former indicates that those particles have only five (instead of the ideal six) nearest neighbours, confirming the presence of voids in the monolayer structure. The irregularities imply that the particles are not positioned on a perfect hexagonal lattice. If the latter were the case, the diagrams would encompass regular hexagons, and the structure would be classified as monocrystalline. It is plausible that particles are carrying the same polarity on their surface and thus experience an electrostatic repulsion from their neighbouring particles; consequently, they are not tightly packed.
To quantify which patterns dominate the monolayer structures on a particular substrate, the distribution of the normalized shape factor ϑnorm,i = ϑi/ϑhex, with ϑhex = 1.1027 for a perfectly hexagonal cell, is determined for the Voronoi diagrams of both the 10 μm-sized silica (Fig. 10a-3) and polystyrene microspheres (Fig. 10b-3) by analyzing at least three SEM images of the obtained monolayer on a respective substrate. Note that ϑnorm = 1 in the case of a perfect hexagonally packed monolayer. It is understood from these results that the peak of the distribution of the normalized shape factor does not coincide with 1, suggesting that self-organized monolayers are indeed not perfectly packed in an ideal hexagonal crystal structure as already concluded from visual inspection of the Voronoi diagrams. However, the results undoubtedly highlight that the obtained monolayer structures are better organized on the fluorocarbon-coated substrates. Apparently, the formation of the hexagonal crystals is significantly enhanced on these substrates, but the spheres are not closely packed as they may repel each other. Furthermore, the data shows that more regular-shaped polygons can be identified in the polystyrene monolayers compared to the silica ones on the silicon substrate, which can be ascribed to the weakly agglomerated state of the polystyrene particles. Consequently, more structured monolayers are attained in the polystyrene case, which are also less covered with clusters.
4.9 Analysis of the orientational order of the monolayer
The Voronoi approach is also applied to get insight into the orientational order within the particle monolayers. Fig. 11a-1 and b-1 show the Voronoi tessellation of the monolayers obtained with respectively 10 μm and 3 μm polystyrene microspheres on the CFx-coated silicon substrates, where the colour of the individual Voronoi cells now indicates the magnitude of the hexatic order parameter (eqn (4), which is between 0 ≤ |ψ| ≤ 1, with |ψ| = 1 for a microsphere positioned in an ideal hexagonal lattice, i.e., with six perfectly positioned nearest neighbours. | ||
| Fig. 11 The respective Voronoi diagrams of the 10 μm (a1) and 3 μm (a2) polystyrene particle monolayers obtained on the flat CFx-coated silicon substrates are constructed from the corresponding SEM image displayed in Fig. 7b-2[(a1)] and 9b-2[(a2)]. The Voronoi cells are coloured according to the magnitude of their hexatic order parameter |ψ|. The distribution of the hexatic order parameter |ψ| of the 10 μm silica and polystyrene particles (b1) and the 5 μm silica and 3 μm polystyrene particles (b2) on the CFx-coated silicon substrates are also provided. (c) The time evolution of the spatially averaged hexatic order parameter ψav. the solid lines represents the data obtained from the 10 μm polystyrene particles, while the dashed lines correspond to the 10 μm silica particles. All experiments were performed at a frequency of f = 250 Hz and amplitude A = 82 μm. | ||
Just as in the previous section, it is inferred that the majority of the individual Voronoi cells deviate from a regular hexagonal shape, which is even more pronounced in the case of the 3 μm particles. That is, monolayers with a lower packing density are obtained with the smaller sized spheres than the 10 μm ones. Next to that, the data depicted in the Voronoi diagrams indicate a significant local disorder in the assembled structures, which is enhanced for the smaller-sized particles. These observations align with the hypothesis that as the interaction forces among the particles are strong relative to the generated vibrated force Fvib, such that it is more challenging to mobilize these small spheres. Considering this, it is suggested that the probability of attaining perfect hexagonal structures tends to be more difficult as the size of the agitated particles decreases.
The symmetry of the obtained monolayers on the fluorocarbon-coated silicon substrates is quantified by finding the distribution of the hexatic order parameter |ψ| of the 10 μm and smaller-sized silica or polystyrene monolayers on these substrates. The results displayed in Fig. 11a-2 and b-2 show that the structures have a low 6-fold positional order, even more significant for the smaller silica and polystyrene microspheres. These results indicate that the monolayers are highly disordered as different symmetries coexist, i.e., the monolayers are not monocrystalline. However, these results highlight that in comparison to the large agglomerates silica particles, a much more regular orientational ordered monolayer can be obtained with the polystyrene microspheres as these weakly agglomerated spheres move more actively across the substrate during agitation.
To understand the temporal evolution of the monolayer structure's order on the bare and fluorocarbon-coated silicon substrate, the spatially averaged bond orientation parameter ψav (eqn 5) has been computed for the 10 μm silica and polystyrene microspheres. As already mentioned in Section 4.6, and now confirmed by computing the local bond order parameter ψav, the packing density and order of the polystyrene particles increased in time on the bare silicon substrates. Also, in the silica particles case, a higher orientational order, although lower than that of the polystyrene spheres, is obtained on the uncoated substrates as time progresses. A more significant amount of the agglomerated powder is possibly mobilized on these substrates as energy is continuously being transferred to them during agitation. As such, more agglomerates move on the substrates and leave particle traces on the substrates. In particular, for the extensively moving polystyrene particles, a steeper increase is observed in the order of the attained monolayers.
Interestingly, for both type of particles, the orientational order of the monolayers remains constant on the fluorocarbon-coated substrates despite the more extensive areas covered with monolayers on these substrates. This suggests that the microspheres are arrested on the substrate as they are being agitated, such that the applied vibration force Fvib is insufficient to mobilize these particles from the substrate. Consequently, the particles stay approximately in the same place, leading to an unaffected spatially averaged order parameter ψav of the densely packed monolayers.
4.10 KPFM Measurements
As mentioned briefly in the previous sections, we hypothesize that the tribocharging mechanism44,52–55,76,77 lies at the heart of the high packing density of both silica and polystyrene particle monolayers attained on the CFx-coated substrates. To verify this hypothesis, we performed Kelvin probe force microscopy (KPFM) measurements using an atomic force microscope (AFM) to measure the surface profile and simultaneously measure the potential difference caused by the surface charge. In this manner we examine if any charge is transferred between the particles and the substrate during agitation. The results of these topography scans together with the contact potential difference (VCPD) measurements between the tip and particles or substrate are presented in Fig. 12 and 13, respectively. Note that the sign of the VCPD-values in these figures are always the opposite of the polarity sign (cf. Section 2.2).Before agitating the microspheres, either the silica or polystyrene particles were gently deposited on a CFx-coated substrate and subsequently scanned to determine the sign (polarity) of their surface charge using KPFM. In Fig. 12a-1 and a-2 we respectively show the topographic map and the simultaneously obtained surface potential map of the 10 μm silica particles prior to agitation, whereas Fig. 12b-1 and b-2 contain the same quantities for the 3 μm polystyrene particles. These results show that, initially, the surface of the silica and polystyrene particles is negatively charged (positive VCPD-value). As already suspected in Section 4.1 and now clearly confirmed by these results, the surface of the polystyrene particles carries more charge relative to the silica particles. With respect to these measurements, it should be mentioned that it proved difficult to scan a large group of particles, as the particles could not be held in place when scanning their surface with the tip, i.e., these particles were less strongly adhered to the CFx-coated substrates before agitation.36 This explains why only a small portion of the surface was scanned prior to agitation in Fig. 10a-1, a-2 and 10b-1, b-2. After agitation, on the other hand, it was less challenging to perform a single scan on a larger group of silica and polystyrene particles as shown in Fig. 10a-3, a-4 and b-3, b-4, respectively.
After being agitated on the CFx-coated substrates in separate experiments, the KPFM measurements reveal that the surface charge of some the silica (cf.Fig. 12a-4) and the majority of the polystyrene particles (cf.Fig. 12b-4) changed from negative to positive. This implies that some negative charge must have been transferred from the particles to the CFx coating during the driving cycles, i.e., the system is in a tribocharged state. In addition, it can be inferred from Fig. 12a-4 that the charge on large part of the silica particles remained unaltered after the experiment, i.e., the polarity remains the same as in Fig. 12a-2 (before agitation). These results corroborate our global observations that the polystyrene particles moved actively across the substrates during agitation, whereas the silica agglomerate slowly slid on the surface, i.e., the polystyrene particles had significantly more opportunities to interact on all sides with the CFx layer; hence, more polystyrene particles acquired a positively tribocharged surface.
To inspect if the underlying CFx-coated silicon substrate is indeed tribocharged by the agitated particles, KPFM measurements were performed on the same substrate before (cf.Fig. 13a) and after (cf.Fig. 13b and c) the agitating experiment. To this end, the silica or polystyrene particles were carefully removed from the CFx-coated substrate using a dry nitrogen gas flow prior to the KPFM measurements. In Fig. 13a the topography and concurrent surface potential map obtained on the CFx-coated coated silicon substrate are presented before agitating the microspheres on them. These initial scans show that the substrate is flat devoid of any inhomogeneities (cf.Fig. 13a-1), and that the substrate has a homogeneous negatively charged surface (cf.Fig. 13a-2). These results are opposed to the scans obtained after agitating either the 5 μm silica or 3 μm polystyrene particles on them shown in Fig. 13b and c, respectively.
From Fig. 13b-2 and c-2 it can be readily observed that the charge on the flat CFx-coated silicon substrates is more unevenly distributed than before (compare with Fig. 13a-2). In particular, after agitation, areas with a higher surface potential on the CFx-coated surface are observed, which implies that locally the substrate is more negatively charged. In fact, this can be ascribed to the movement of the agitated silica agglomerates or polystyrene particles in contact with the substrate during agitation. Furthermore, the surface potential maps of the CFx-coated substrates show a higher contrast in the case of the silica particles compared to the polystyrene ones, implying that the fluorocarbon layer is charged substantially by the silica particles. This observation is supported by a previous study that has reported that due to their mechanical properties the silica particles tend to deform and charge the CFx coating significantly more than the polystyrene particles.72
Next to this, also notice the presence of small craters on the topography and corresponding surface potential maps of the substrate shown in Fig. 13b-1, b-2 and c-1, c-2, implying that some particles impacted on them during agitation. These observations concur with our recent particle impact study,72 in which we reported that only at the point of the craters an increase in surface potential could be observed. Both the movement as well as the impact of particles constitute a local charge transfer between particles and the underlying CFx layer, i.e., the substrate charges more negatively at the point of contact. Thus, the CFx-coated substrate is tribocharged by the silica or polystyrene microspheres as the system is being agitated.
However, as reported in previous studies,36,72 no significant change in surface potential was measured on the surface of the particles or substrate in the case of the bare silicon substrates (not shown). A moderating remark in this respect is that, also in this case, it proved to be challenging to measure the charge on the particles after agitating them on the bare silicon substrate. As the packing of particles on these substrates is less dense, the particles could not be held in place when scanning the surface with the KPFM-tip, i.e., the particles are much less firmly adhered to the bare silicon substrate (weak electrostatic attraction) compared to the CFx-coated substrate after agitation. Thus, it can not be excluded that charge, albeit relatively small, is transferred or even rapidly dissipated on the bare silicon substrates.72
Summarizing, consistent with our previous studies,36,72 the data displayed in both Fig. 12 and 13 jointly show that, as a result of the tribocharging mechanism, the silica or polystyrene particles, independent of their size, and the CFx-coated substrates acquire opposite charges, positive and negative, respectively, after agitating the system. This mechanism induces a significant local electrostatic attraction, promoting the particles to adhere to the CFx-coated substrates. Consequently, gradually more particles remain stuck on the CFx-coated substrates, leading to the conspicuous high packing density of silica or polystyrene particle monolayers on these substrates. In addition, the particles sticking on the surface may repel other particles on top with the same polarity, enhancing the formation of a particle monolayer. Hence, it can be safely concluded that the tribocharging mechanism is a crucial factor in assembling monolayers of microspheres on polymer surfaces.
5 Conclusions
We studied the dynamics and self-organization of horizontally agitated monodisperse dry powder comprising either hydrophilic silica or hydrophobic polystyrene microspheres with diameters of 3–10 μm on various substrates. In particular, the focus has been on the formation of monolayers on three substrates with different surface properties: a micromachined silicon particle tray and two flat silicon substrates, namely an uncoated hydrophilic and a CFx-coated hydrophobic substrate.At first, we established that the silica powder contains massive agglomerates, whereas the polystyrene particles are more loosely packed, consistent with the different dominating interaction forces applicable to the two types of particles, namely the capillary force for the silica particles, and the contact mechanics and electrostatic forces in the case of the polystyrene particles. Consequently, we observed distinct particle and agglomerate migration dynamics: the large agglomerated silica particles moved slowly as a single piece, while the less agglomerated polystyrene particles moved extensively, having ample interactions with the substrate.
We consistently observed that the agitated silica agglomerates partially covered the flat substrates with particle monolayers as they moved across the flat substrates. On the particle trays, on the other hand, segregated bands of silica particles were formed perpendicular to the oscillating direction, which was attributed to their larger surface roughness resulting from the micromachining. As an explanation, a mechanism based on a simple frictional stick-slip motion is proposed.
According to this physical mechanism a monolayer of silica particles will adhere to the substrate if the magnitude of the interparticle friction Ffric,pp is smaller than the vibrational body force Fvib, which in turn should be smaller than the particle-substrate friction Ffric,sp, (Ffric,pp < Fvib < Ffric,sp) during some part of the driving cycle. This is true for the case of the flat substrates on which the bottom layer of the silica agglomerate may stick, but the condition fails for the particle tray which has a rougher surface. As a result of the larger surface roughness, the adhesion and concomitantly the friction force between the silica particles and particle tray is reduced, such that the sticking part of the stick-slip motion between the silica agglomerates and particle tray is absent. The polystyrene particles, on the other hand, formed closely packed monolayers regardless of the substrate. This implies that the applied body force in this case exceeded the static friction, i.e., Fvib > Ffric,sp, such that the polystyrene particles were at least rolling, if not sliding across the substrates.
The morphology and orientational order of the obtained monolayers is examined by employing the Voronoi approach. The results consistently show that better structured, albeit not perfectly hexagonally packed, self-organized polystyrene monolayers can be attained than strongly agglomerated silica particles. However, the order of the monolayers on the silicon substrate can be enhanced by agitating the particles for a longer time.
Despite the hydrophobic nature of the CFx-coated substrates, these substrates were observed to become covered with large areas consisting of densely packed monolayers of silica or polystyrene particles which was attributed to increased tribocharging of the CFx-coated surface. Additionally, the Voronoi analysis supported the observation that more structured monolayers, covered with less clusters, can be obtained on these substrates. KPFM measurements were performed to corroborate these findings. The results show that, due to the tribocharging mechanism, the particles and CFx-coated substrates gain opposite charges, inducing an electrostatic attraction between the particles and substrates. Consequently, this enhances the adhesion of the particles on the CFx-coated substrates during agitation.
Altogether, these results highlight that depending on the substrate and particle properties, different dominating surface interaction forces affect the self-organization of agitated microspheres. Furthermore, it tends to be even more challenging to attain a self-organized monolayer as the size of the microspheres decreases.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge funding from the ERC Advanced Grant “Printpack” (No. 695067). Furthermore, the authors would like to thank Mark Smithers for taking the amazing SEM images.References
- S. Luding and J. Tomas, Granular Matter, 2014, 16, 279–280 CrossRef.
- H. M. Jaeger, S. R. Nagel and R. P. Behringer, Rev. Mod. Phys., 1996, 68, 1259 CrossRef.
- D. Barletta, P. Russo and M. Poletto, Powder Technol., 2013, 237, 276–285 CrossRef CAS.
- S. Tennakoon, L. Kondic and R. Behringer, Europhys. Lett., 1999, 45, 470 CrossRef CAS.
- G. Metcalfe, S. Tennakoon, L. Kondic, D. Schaeffer and R. Behringer, Phys. Rev. E, 2002, 65, 031302 CrossRef.
- R. Amirifar, K. Dong, Q. Zeng and X. An, Soft Matter, 2018, 14, 9856–9869 RSC.
- N. Preud'Homme, G. Lumay, N. Vandewalle and E. Opsomer, Phys. Rev. E, 2021, 104, 064901 CrossRef PubMed.
- P. Kong, P. Wang, L. Zhou and R. Li, Phys. Rev. E, 2022, 105, 014903 CrossRef CAS.
- F. López-González, A. M. Herrera-González and F. Donado, Phys. A, 2022, 590, 126756 CrossRef.
- A. P. Santos, D. S. Bolintineanu, G. S. Grest, J. B. Lechman, S. J. Plimpton, I. Srivastava and L. E. Silbert, Physical Review E, 2020, 102, 032903 CrossRef CAS PubMed.
- L. Jing, J. M. Ottino, R. M. Lueptow and P. B. Umbanhowar, J. Fluid Mech., 2021, 925, A29 CrossRef CAS.
- D. Wang, J. A. Dijksman, J. Barés, J. Ren and H. Zheng, Phys. Rev. Lett., 2020, 125, 138001 CrossRef CAS.
- L. Brendel, J. Török, R. Kirsch and U. Bröckel, Granular Matter, 2011, 13, 777–786 CrossRef.
- R. Jones, H. M. Pollock, J. A. Cleaver and C. S. Hodges, Langmuir, 2002, 18, 8045–8055 CrossRef CAS.
- R. Jones, H. Pollock, D. Geldart and A. Verlinden, Powder Technol., 2003, 132, 196–210 CrossRef CAS.
- S. Beaudoin, P. Jaiswal, A. Harrison, J. Laster, K. Smith, M. Sweat and M. Thomas, Part. Sci. Technol., 2015, 3–79 CAS.
- O. Kruglova, P.-J. Demeyer, K. Zhong, Y. Zhou and K. Clays, Soft Matter, 2013, 9, 9072–9087 RSC.
- S. Nöjd, P. S. Mohanty, P. Bagheri, A. Yethiraj and P. Schurtenberger, Soft Matter, 2013, 9, 9199–9207 RSC.
- J. Byrom and S. L. Biswal, Soft Matter, 2013, 9, 9167–9173 RSC.
- X. Jiang, Q. Zeng, C. Chen and A. Yu, J. Mater. Chem., 2011, 21, 16797–16805 RSC.
- E. M. Furst, Soft Matter, 2013, 9, 9039–9045 RSC.
- G. Malescio and G. Pellicane, Nat. Mater., 2003, 2, 97–100 CrossRef CAS PubMed.
- N. Osterman, D. Babič, I. Poberaj, J. Dobnikar and P. Ziherl, Phys. Rev. Lett., 2007, 99, 248301 CrossRef CAS.
- J. M. Meijer and L. Rossi, Soft Matter, 2021, 17(9), 2354–2368 RSC.
- N. Berneman, I. S. Jimidar, W. Van Geite, H. Gardeniers and G. Desmet, Powder Technol., 2021, 390, 330–338 CrossRef CAS.
- J.-M. Meijer, V. Meester, F. Hagemans, H. N. Lekkerkerker, A. P. Philipse and A. V. Petukhov, Langmuir, 2019, 35, 4946–4955 CrossRef CAS PubMed.
- S. Schyck, J.-M. Meijer, L. Baldauf, P. Schall, A. V. Petukhov and L. Rossi, JCIS Open, 2022, 5, 100037 CrossRef.
- E. Locatelli and E. Bianchi, Soft Matter, 2018, 14, 8119–8136 RSC.
- O. Koshkina, L. T. Raju, A. Kaltbeitzel, A. Riedinger, D. Lohse, X. Zhang and K. Landfester, ACS Appl. Mater. Interfaces, 2021, 14(1), 2275–2290 CrossRef PubMed.
- N. Vogel, M. Retsch, C.-A. Fustin, A. del Campo and U. Jonas, Chem. Rev., 2015, 115, 6265–6311 CrossRef CAS.
- V. Lotito and T. Zambelli, Adv. Colloid Interface Sci., 2017, 246, 217–274 CrossRef CAS.
- V. N. Manoharan, Science, 2015, 349, 1253751 CrossRef.
- J. van der Gucht, Front. Phys., 2018, 6, 87 CrossRef.
- A. Scacchi, S. J. Nikkhah, M. Sammalkorpi and T. Ala-Nissila, Phys. Rev. Res., 2021, 3, L022008 CrossRef CAS.
- B. Perkins-Howard, A. R. Walker, Q. Do, D. I. Senadheera, F. Hazzazi, J. Grundhoefer, T. Daniels-Race and J. C. Garno, J. Phys. Chem. C, 2022, 126(1), 505–516 CrossRef CAS.
- I. Jimidar, K. Sotthewes, H. J. Gardeniers and G. Desmet, Langmuir, 2020, 36, 6793–6800 CrossRef CAS.
- C. Park, T. Lee, Y. Xia, T. J. Shin, J. Myoung and U. Jeong, Adv. Mater., 2014, 26, 4633–4638 CrossRef CAS.
- W. Van Geite, I. S. Jimidar, K. Sotthewes, H. Gardeniers and G. Desmet, Mater. Des., 2022, 216, 110573 CrossRef.
- M. Heckel, A. Sack, J. E. Kollmer and T. Pöschel, Phys. Rev. E, 2015, 91, 062213 CrossRef PubMed.
- R. Moosavi, M. Maleki, M. R. Shaebani, J. C. Ruiz-Suárez and E. Clément, Europhys. Lett., 2014, 107, 34006 CrossRef.
- D. Krengel, S. Strobl, A. Sack, M. Heckel and T. Pöschel, Granular Matter, 2013, 15, 377–387 CrossRef.
- C. Lozano, I. Zuriguel, A. Garcimartn and T. Mullin, Phys. Rev. Lett., 2015, 114, 178002 CrossRef CAS PubMed.
- M. Fujii, A. Awazu and H. Nishimori, Phys. Rev. E, 2012, 85, 041304 CrossRef PubMed.
- K. Polev, V. Visyn, W. Adamkiewicz, Y. Sobolev and B. A. Grzybowski, Soft Matter, 2021, 17, 8595–8604 RSC.
- B. A. Grzybowski, A. Winkleman, J. A. Wiles, Y. Brumer and G. M. Whitesides, Nat. Mater., 2003, 2, 241 CrossRef CAS PubMed.
- J. Yang, T. Zhou and L. Song, Adv. Powder Techn., 2009, 20, 158–163 CrossRef CAS.
- S. Warr, J. M. Huntley and G. T. Jacques, Phys. Rev. E, 1995, 52, 5583 CrossRef CAS.
- K. J. Ford, J. F. Gilchrist and H. S. Caram, Powder Techn., 2009, 192, 33–39 CrossRef CAS.
- Y. Mawatari, M. Tsunekawa, Y. Tatemoto and K. Noda, Powder Technol., 2005, 154, 54–60 CrossRef CAS.
- A. Gnoli, A. Lasanta, A. Sarracino and A. Puglisi, Sci. Rep., 2016, 6, 1–7 CrossRef.
- W. Melitz, J. Shen, A. C. Kummel and S. Lee, Surf. Sci. Rep., 2011, 66, 1–27 CrossRef CAS.
- D. J. Lacks and R. M. Sankaran, J. Phys. D: Appl. Phys., 2011, 44, 453001 CrossRef.
- D. J. Lacks and T. Shinbrot, Nat. Rev. Chem., 2019, 3(8), 465–476 CrossRef CAS.
- A. Schella, S. Herminghaus and M. Schröter, Soft Matter, 2017, 13, 394–401 RSC.
- S. R. Waitukaitis and H. M. Jaeger, Rev. Sci. Instrum., 2013, 84, 025104 CrossRef CAS PubMed.
- G. Straßburger and I. Rehberg, Phys. Rev. E, 2000, 62, 2517 CrossRef PubMed.
- V. Lotito and T. Zambelli, Langmuir, 2018, 34, 7827–7843 CrossRef CAS PubMed.
- V. Lotito and T. Zambelli, Adv. Colloid Interface Sci., 2020, 102252 CrossRef CAS PubMed.
- P. Dillmann, G. Maret and P. Keim, Eur. Phys. J. Spec. Top., 2013, 222, 2941–2959 CrossRef.
- P. Digregorio, D. Levis, L. F. Cugliandolo, G. Gonnella and I. Pagonabarraga, Soft Matter, 2022, 18, 566–591 RSC.
- J. N. Israelachvili, Intermolecular and surface forces, Academic Press, 2011 Search PubMed.
- H.-J. Butt, M. Kappl, et al., Surface and interfacial forces, Wiley Online Library, 2010 Search PubMed.
- L.-O. Heim, J. Blum, M. Preuss and H.-J. Butt, Phys. Rev. Lett., 1999, 83, 3328 CrossRef CAS.
- X. M. Zeng, G. P. Martin and C. Marriott, Particulate Interactions in Dry Powder Formulation for Inhalation, CRC Press, 2000 Search PubMed.
- S. Herminghaus, Wet granular matter: a truly complex fluid, World Scientific, 2013, vol. 6 Search PubMed.
- G. H. Ristow, Pattern formation in granular materials, Springer Science & Business Media, 2000 Search PubMed.
- J. Meyer, R. Fuchs, T. Staedler and X. Jiang, Friction, 2014, 2, 255–263 CrossRef CAS.
- J. Tomas, Chem. Eng. Sci., 2007, 62, 1997–2010 CrossRef CAS.
- J. Gao, W. Luedtke, D. Gourdon, M. Ruths, J. Israelachvili and U. Landman, Frictional forces and Amontons' law: from the molecular to the macroscopic scale, 2004 Search PubMed.
- R. Fuchs, J. Meyer, T. Staedler and X. Jiang, Tribol.-Mater., Surf. Interfaces, 2013, 7, 103–107 CrossRef CAS.
- R. Fuchs, T. Weinhart, J. Meyer, H. Zhuang, T. Staedler, X. Jiang and S. Luding, Granular Matter, 2014, 16, 281–297 CrossRef CAS.
- I. S. Jimidar, K. Sotthewes, H. Gardeniers and G. Desmet, Powder Technol., 2021, 383, 292–301 CrossRef CAS.
- B. Painter and R. Behringer, Phys. Rev. E, 2000, 62, 2380 CrossRef CAS PubMed.
- B. Painter and R. Behringer, Phys. Rev. Lett., 2000, 85, 3396 CrossRef CAS PubMed.
- L. Kondic, Phys. Rev. E, 1999, 60, 751 CrossRef CAS PubMed.
- D. Kumar, A. Sane, S. Gohil, P. Bandaru, S. Bhattacharya and S. Ghosh, Sci. Rep., 2014, 4, 1–9 CAS.
- G. Grosjean, S. Wald, J. C. Sobarzo and S. Waitukaitis, Phys. Rev. Mater., 2020, 4, 082602 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |











