How macromolecules softness affects diffusion under crowding

Abstract

Diffusion in a macromolecularly crowded environment is essential for many intracellular processes, from metabolism and catalysis to gene transcription and translation. So far, theoretical and experimental work has focused on anomalous subdiffusion, and the effects of interactions, shapes, and composition, while the compactness or softness of macromolecules has received less attention. Herein, we use Brownian dynamics simulations to study how the softness of crowders affects macromolecular diffusion. We find that in most cases, soft crowders slow down the diffusion less effectively than hard crowders like Ficoll. For instance, at a 30% occupied volume fraction, the diffusion in Ficoll70 is about 20% slower than in soft crowders of the same size. However, our simulations indicate that elongated macromolecules, such as double-stranded DNA pieces, can diffuse comparably or even faster in hard crowders. We relate these effects to the volume excluded by soft and hard crowders to different tracers. Our results show that the softness and shape of macromolecules are crucial factors determining diffusion under crowding, relevant to diverse intracellular environments.

---

Macromolecular crowding plays an essential role in cellular life,^1–4 affecting protein stability,⁵ chemical equilibria,⁶ gene regulation,⁷ enzymatic reactions^8–11 and diffusion of metabolites and macromolecules.^12–14 Macromolecular diffusion is vital in many intracellular processes, including metabolism, catalysis, signal transduction, transcription and translation.^15,16 Theoretical and experimental work so far has focused on anomalous subdiffusion,^17–20 the effects of hydrodynamic^21,22 and other^23–26 interactions, and on the role of composition^27–30 and macromolecular shapes.^26,31–38

In simulations of macromolecular diffusion and crowding, one often uses coarse-grained or atomistic rigid-molecule models. However, macromolecules generally have flexible, often polymer-branching structures, which determine the interactions between the macromolecules at small separations. Recently, Blanco et al.²⁵ introduced a shoulder-shaped, chain-entanglement softened potential (CESP, the second term in eqn (1); see also Fig. 1) to take into account the macromolecular softness and chain entanglements when modelling Dextran crowders. They found that this model reproduces the experimental data better than the frequently-used hard-sphere-like models. In more recent work, Junker et al.³⁹ used fluorescent correlation spectroscopy (FCS) to investigate the diffusion of variously shaped macromolecules in compact crowders (Ficoll) and in more expanded, softer polyethylene glycol (PEG) and poly(ethylene oxide) (PEO) crowders. The experiments suggested a slower diffusion in PEG/PEO crowders (see, however, below and Fig. S6, ESI†), but we note that the soft and compact crowders had different sizes, which likely affected the macromolecular diffusion too.^24,28

Fig. 1 Model of soft interactions between macromolecules. (a) Schematics of two soft particles (top) and of a soft and a WCA (hard) particle (bottom). The dark spheres represent the hard core and the light grey spheres show the range of the soft shoulder potential given by eqn (1). The light grey spheres can overlap, while the dark cores cannot. (b) Relation between the parameters U₀ and (a_e − a_c)/a_c of the interaction potential, eqn (1), providing the same occupied volume v_occ ≈ 555.6 nm³ as the hard (WCA) particle with the radius a_c = 5.1 nm corresponding to Ficoll70. The occupied volume fractions were calculated based on the Boltzmann weight with the corresponding interaction potentials (Section S1A, ESI†). The symbols indicate the values used in panel (c) with the same color code. (c) Examples of the interaction potentials between two soft particles with the parameters from panel (b) and between two hard (WCA) particles corresponding to Ficoll70. All particles have the same occupied volume v_occ ≈ 555.6 nm³. The thin vertical lines indicate the values of the hard core diameter 2a_c.

Herein, we study with Brownian dynamics (BD) simulations how crowders' softness (or compactness) affects the diffusion in crowded environments. We consider soft and hard particles with the same hydrodynamic radius, effectively occupying the same volume, and ask which particle is a better crowder and how the diffusion slowdown depends on the properties of a tracer.

In our simulations, we used the following total interaction potential between macromolecules

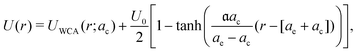where U_WCA is the short-ranged repulsive-only Week–Chandler–Anderson (WCA) type potential adapted for macromolecules⁴⁰ and a_c is the hard-core radius (Section S1C1, ESI†). Parameter U₀ describes the magnitude of the CESP potential,²⁵a_e the extension of entanglement interactions and a sets the length scale (we set in all calculations in line with ref. 25). Potential (1) models the interactions between soft, expanded crowders such as PEG/PEO or Dextran.²⁵ For the interaction between a hard and a soft particle, we took eqn (1) using the same U₀ as for two soft particles and the Lorentz combining rule to calculate a_e and a_c from the corresponding values for the hard and soft particles (assuming a_e = a_c for hard particles). To compare diffusion in soft and hard (i.e., WCA only) crowders, we chose the CESP parameters such that a soft particle occupied the same volume v_occ ≈ 555.6 nm³ as the WCA particle with a radius a_c = 5.1 nm (equal to the hydrodynamic radius a_H), corresponding to Ficoll70. To fix the relation between a_e and a_c, we kept a_e + a_c = 2a_H constant (see eqn (1)), i.e., we assumed that the softness emerges by shrinking the core of the particle and extending its polymer-branching structure to a similar extend (Section S1A, ESI†). We calculated excluded (occupied) volumes with Monte Carlo (MC) simulations by inserting a tracer (point particle) into a simulation box with the probability (Section S3, ESI†). Fig. 1b demonstrates that the strength of the soft interactions (i.e., U₀) increases with decreasing its range (i.e., a_e–a_c) when keeping the occupied volume constant, as one might expect. We note that the same occupied volumes for soft and hard particles imply the same second virial coefficients⁴¹ (Section S3, ESI†). Fig. 1c shows two examples of the CESP potential acting between two soft particles and compares them with the WCA potential for hard particles (no CESP interactions) with the same occupied volume.

To study how diffusion depends on macromolecular softness, we performed BD simulations of mixtures of soft and hard particles, both acting as tracers and crowders. We used a customized version of the package BD_BOX^42,43 with the interaction potential given by eqn (1) and took into account hydrodynamic interactions via the generalized Rotne-Prager-Yamakawa (RPY) tensor.^44–47 While the RPY approach is ubiquitously used in numerous studies, we note that it neglects many body interactions and near-field lubrication forces, which might be important for diffusion in crowded environments.^21,48 We, therefore, restricted our considerations mainly to a relatively low volume fraction of 10% (except for Fig. 2e). We recall that in all simulations, the hydrodynamic radii of soft and hard particles were taken the same (a_H = 5.1 nm), implying the same short-time diffusion coefficients. From the BD trajectories, we calculated time-averaged mean-square displacements TAMSD(t) = 〈|r(t) − r(0)|²〉 of the geometrical center r of the macromolecules and extracted the corresponding long-time diffusion coefficients D as detailed in Section S2D of the ESI.† We note that we used TAMSD instead of ensemble averaged (EA) MSD to get better statistics; in the long-time limit, both TAMSD and EAMSD should give the same results (for recent discussions regarding the relations between time and ensemble averaging, see ref. 49 and 50).

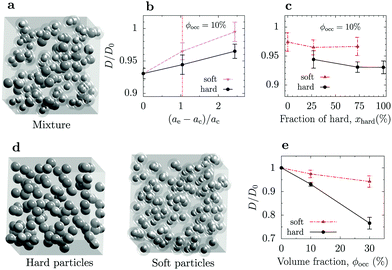Fig. 2 Effect of macromolecule's softness on diffusion. (a) Snapshots from BD simulations of mixture of soft and hard particles. (b) Long-time diffusion coefficients of hard and soft particles as functions of the softness parameter (eqn (1)). The value a_e = a_c corresponds to a hard (WCA) particle. The soft particle occupies the same volume as the hard particle (Fig. 1). Occupied volume fraction ϕ_occ = 10% and molar fraction of hard particles x_hard ≈ 27%. (c) Long-time diffusion coefficients of hard and soft particles as functions of molar fraction of hard particles for occupied volume fraction 10%. (d) Snapshots from BD simulations of two systems containing only soft particles and only hard particles. (e) Long-time diffusion coefficients as functions of the occupied volume fraction for systems consisting of hard particles and soft particles. For radial distribution functions, see Fig. S2–S4 (ESI†). See Table S4 (ESI†) for the number of particles in each system.

We first studied how diffusion depends on the range of entanglement, i.e., a_e–a_c (a_e = a_c corresponds to a compact, hard particle). We simulated a mixture of hard and soft macromolecules of the total occupied volume fraction 10% and molar fraction of hard particles x_hard ≈ 27%. Fig. 2b shows that in this setup, softer crowders provide a weaker slowdown of the macromolecular diffusion. At low excluded volume fractions, the diffusion coefficient can be roughly estimated by^51,52

D(ϕ_occ) = D₀(1 − αϕ_ex(ϕ_occ)), (2)

where D₀ is the diffusion coefficient in infinite dilution, ϕ_ex is the volume fraction excluded to a tracer by the crowders, and α is a constant. Although both crowders effectively occupy the same volume, the soft crowders exclude significantly smaller volumes to tracers because of their softer shells. Indeed, a hard particle excludes a volume of 8v_occ to another hard particle; a soft particle with U₀ = 1.2 (and a_e–a_c ≈ a_c) excludes ≈7.2v_occ to a hard particle and about 7v_occ to a soft particle. Decreasing U₀ (=increasing a_e–a_c) makes excluded volumes even smaller (Table S6, ESI†), enhancing the diffusion.

Our simulations show a relatively weak dependence of the diffusion coefficient on the molar fraction of hard particles in the mixture (Fig. 2c); this is in line with virtually no change in the radial distribution function observed in the same systems (Fig. S3, ESI†). Nevertheless, increasing the fraction of hard particles slightly slowed down the diffusion in all cases. Consistent with Fig. 2b, at all molar fractions, the diffusion of soft particles was faster than the diffusion of hard particles, which is again due to the lower excluded volumes (Table S7, ESI†).

The effect of the total volume fraction in unmixed systems exhibiting self-crowding was more substantial (Fig. 2d). For ϕ_occ = 30%, the self-diffusion in the system with hard particles was about 20% slower than in the system composed of soft particles. The differences between the two systems are also reflected in the radial distribution functions, which show a monotonic to oscillatory behaviour with increasing ϕ_occ for hard particles, but only small quantitative changes in the case of soft ones (Fig. S4, ESI†). Somewhat surprisingly, the difference in the excluded volumes in both systems was only a few per cent (Table S8, ESI†), incompatible with the large difference in the diffusion coefficients. This is reflected in the parameter α in eqn (1). Indeed, fitting this equation to the simulation data gives significantly different values α ≈ 0.24 for hard and α ≈ 0.06 for soft particles. In the calculations of the excluded volumes, we measured the interaction energies in the Boltzmann factor with respect to the infinite separation between the particles. However, in such crowded systems, most macromolecules' repulsive shoulders overlap and the particles experience a lower energy difference when approaching each other from the average distance (determined by the occupied volume fraction) compared to infinite dilution. This shift in the energy level likely reduces the excluded volume as seen by a tracer, providing a faster diffusion.

In addition to the diffusion of hard and soft particles due to self-crowding, we also studied how differently shaped macromolecules diffuse in hard and soft crowders. We chose a cylindrically-shaped, 16 nm-long double-stranded (ds) DNA and Y-shaped Immunoglobulin G (IgG) (Fig. 3a). We modelled a dsDNA as a quasi-rigid charged polymer consisting of eight connected spherical beads, each with the hydrodynamic radius of 1.14 nm (see ref. 26). As in our previous work,²⁶ the dsDNA beads interacted electrostatically with each other via the DLVO potential with the screening length 0.95 nm (all other particles were uncharged). For IgG, we took the model that we introduce in the upcoming article⁵³ (Section S1B, ESI†), developed to reproduce the experimentally measured angle distribution and hydrodynamic radius of IgG.

Fig. 3 Effect of macromolecular shapes and softness on diffusion. (a) Models of dsDNA (≈16 nm long) and Immunoglobulin G (IgG) and snapshots from BD simulations of dsDNA and IgG in hard and soft crowders. Hydrodynamic radii a_H have been obtained from BD simulations of single macromolecules (i.e., in infinite dilution). (b) Long-time diffusion coefficients and (c) excluded volume fractions of dsDNA, IgG and Ficoll70 (hard particle) in soft and hard crowders. See Table S5 in the ESI,† for the number of particles in each system. (d) Difference in the excluded volume fractions Δϕ_ex = ϕ^hard_ex − ϕ^soft_ex for a dsDNA modelled as a quasi-rigid polymer of length [small script l] in hard and soft crowders of the same hydrodynamic radius a_H. a_b is the radius of a dsDNA bead. (e) Comparison of a dsDNA and a quasi-rigid polymer model with two times smaller bead size. (f) Diffusion coefficients of the dsDNA and the smaller polymer (panel f) in soft and hard crowders as functions of a/a_b. The occupied volume fraction is 10%.

Our simulations show that for both crowders, the diffusion coefficients are reduced more significantly for larger tracers (Fig. 3b), in accord with previous studies.^21,30,39 Moreover, both IgG and Ficoll70 diffused considerably faster in soft crowders. This is similar to Fig. 2. In stark contrast, a smaller and more elongated dsDNA was faster (albeit only weakly) in hard crowders. To understand this result, we calculated with MC simulations the volume fractions excluded to these tracers by soft and hard crowders, which showed similar trends (Fig. 3c). We further investigated this effect by calculating the difference in the excluded volumes for hard and soft crowders, Δϕ_ex = ϕ^hard_ex − ϕ^soft_ex, as a function of the crowder size and tracer's aspect ratio. Fig. 3d shows the results in the form of a heatmap and demonstrates well-defined regions of positive and negative Δϕ_ex. We observed a similar behaviour in a wide range of occupied volume fractions (Fig. S5, ESI†). The results show that the excluded volume for an elongated dsDNA is larger in soft crowders, provided the crowder is sufficiently large. In contrast to a hard crowder, a soft crowder can interact repulsively with a few dsDNA beads at the same time, and more than one soft crowder can repel a dsDNA bead if the system is sufficiently crowded. Clearly, these effects increase the excluded volume when the length of a polymer increases or when the size of the polymer bead decreases. Fig. 3d suggests larger differences in the diffusion coefficients in the case of bigger crowders or smaller bead sizes of a polymeric tracer (Fig. 3e). Indeed, Fig. 3f shows that soft crowders slow down the diffusion of a polymer with smaller beads more substantially than hard crowders.

It is instructive to compare our results with FCS measurements by Junker et al.³⁹ who studied the diffusion of variously shaped tracers in Ficoll and polyethylene glycol/poly(ethylene oxide) (PEG/PEO), which are softer, more expanded crowders compared to Ficoll. These authors based their calculations of the occupied volumes on specific molecular volumes and found that the diffusion was faster in Ficoll than in PEG. However, recalculating the occupied volume based on the hydrodynamic radii, as in our simulations, gives a roughly comparable diffusion slowdown (Fig. S6, ESI†), unlike our simulation results. Although the precise reason for this discrepancy is unclear, we note that Ficoll and PEG had different hydrodynamic radii, contributing differently to the diffusion's slowdown.^24,28 In addition, streptavidin (hydrodynamic radius a_H ≈ 3.2 nm) is much smaller than Ficoll70 (a_H ≈ 5.1 nm) used as a tracer in our simulations. Finally, Junker et al.³⁹ considered relatively high occupied volume fractions (above 25% after recalculations), at which polyethylene glycol could form polymeric networks, leading to sieving effects, not captured by the CESP potential of ref. 25 that we utilized in our work. In future work, it will be useful to modify the model to take such effects into account on a computationally inexpensive, coarse-grained level and extend experiments to cover a wider range of occupied volume fractions and macromolecular varieties.

In conclusion, we have studied how macromolecular diffusion is influenced by the softness of crowders. We found that in most cases, soft crowders reduced the tracer diffusion to a much lesser extent than hard crowders of the same size (Fig. 2). However, our BD simulations indicated that cylindrically-shaped macromolecules could diffuse similarly or even faster in hard crowders (Fig. 3). We related these effects to the volume fractions excluded by soft and hard crowders to different tracers. These results are relevant to intracellular environments composed of macromolecules of different shapes and softness, and we hope that our work will motivate further more detailed simulation and experimental studies on the relation between macromolecular structure and diffusion in highly crowded systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by NCN grant No. 2017/25/B/ST3/02456. We thank PLGrid for providing computational resources.

Notes and references

1. S. B. Zimmerman and A. P. Minton, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 27–65.
2. G. Rivas, F. Ferrone and J. Herzfeld, EMBO Rep., 2004, 5, 23–27.
3. J. Herzfeld, J. Mol. Recognit., 2004, 17, 376–381.
4. M. Weiss, Crowding, diffusion, and biochemical reactions, Elsevier Inc., 1st edn, 2014, vol. 307, pp. 383–417.
5. D. Gomez, K. Huber and S. Klumpp, J. Phys. Chem. Lett., 2019, 10, 7650–7656.
6. R. J. Ellis, Trends Biochem. Sci., 2001, 26, 597–604.
7. M. Tabaka, T. Kalwarczyk and R. Hołyst, Nucleic Acids Res., 2014, 42, 727–738.
8. M. G. Norris and N. Malys, Biochem. Biophys. Res. Commun., 2011, 405, 388–392.
9. I. Pastor, L. Pitulice, C. Balcells, E. Vilaseca, S. Madurga, A. Isvoran, M. Cascante and F. Mas, Biophys. Chem., 2014, 185, 8–13.
10. A. Kuzmak, S. Carmali, E. von Lieres, A. J. Russell and S. Kondrat, Sci. Rep., 2019, 9, 455.
11. T. Skóra, M. N. Popescu and S. Kondrat, Phys. Chem. Chem. Phys., 2021, 23, 9065–9069.
12. E. Dauty and A. S. Verkman, J. Mol. Recognit., 2004, 17, 441–447.
13. J. A. Dix and A. S. Verkman, Annu. Rev. Biophys., 2008, 37, 247–263.
14. M. Feig, I. Yu, P. H. Wang, G. Nawrocki and Y. Sugita, J. Phys. Chem. B, 2017, 121, 8009–8025.
15. S. Soh, M. Byrska, K. Kandere-Grzybowska and B. A. Grzybowski, Angew. Chem., Int. Ed., 2010, 49, 4170–4198.
16. P. E. Schavemaker, A. J. Boersma and B. Poolman, Front. Mol. Biosci., 2018, 5, 93.
17. M. Weiss, M. Elsner, F. Kartberg and T. Nilsson, Biophys. J., 2004, 87, 3518–3524.
18. D. S. Banks and C. Fradin, Biophys. J., 2005, 89, 2960–2971.
19. J. Szymanski and M. Weiss, Phys. Rev. Lett., 2009, 103, 038102.
20. F. Höfling and T. Franosch, Rep. Prog. Phys., 2013, 76, 046602.
21. T. Ando and J. Skolnick, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 18457–18462.
22. J. Skolnick, J. Chem. Phys., 2016, 145, 100901.
23. S. R. McGuffee and A. H. Elcock, PLoS Comput. Biol., 2010, 6, e1000694.
24. T. Kalwarczyk, N. Ziebacz, A. Bielejewska, E. Zaboklicka, Koynov, J. Szymański, A. Wilk, A. Patkowski, J. Gapiński, H. J. Butt and R. Hołyst, Nano Lett., 2011, 11, 2157–2163.
25. P. M. Blanco, J. L. Garcés, S. Madurga and F. Mas, Soft Matter, 2018, 14, 3105–3114.
26. T. Skóra, F. Vaghefikia, J. Fitter and S. Kondrat, J. Phys. Chem. B, 2020, 124, 7537–7543.
27. T. Frembgen-Kesner and A. H. Elcock, Biophys. Rev., 2013, 5, 109–119.
28. S. Kondrat, O. Zimmermann, W. Wiechert and E. von Lieres, Phys. Biol., 2015, 12, 046003.
29. M. Grimaldo, H. Lopez, C. Beck, F. Roosen-Runge, M. Moulin, J. M. Devos, V. Laux, M. Härtlein, S. Da Vela, R. Schweins, A. Mariani, F. Zhang, J.-L. Barrat, M. Oettel, V. T. Forsyth, T. Seydel and F. Schreiber, J. Phys. Chem. Lett., 2019, 10, 1709–1715.
30. T. Miyaguchi, Phys. Rev. Res., 2020, 2, 013279.
31. T. Munk, F. Höfling, E. Frey and T. Franosch, EPL, 2009, 85, 30003.
32. J. Balbo, P. Mereghetti, D.-P. Herten and R. C. Wade, Biophys. J., 2013, 104, 1576–1584.
33. M. Długosz and J. M. Antosiewicz, J. Chem. Theory Comput., 2014, 10, 2583–2590.
34. S. Leitmann, F. Höfling and T. Franosch, Phys. Rev. Lett., 2016, 117, 097801.
35. S. Leitmann, F. Höfling and T. Franosch, Phys. Rev. E, 2017, 96, 012118.
36. J. Shin, A. G. Cherstvy and R. Metzler, New J. Phys., 2015, 17, 113028.
37. J. S. Myung, F. Roosen-Runge, R. G. Winkler, G. Gompper, P. Schurtenberger and A. Stradner, J. Phys. Chem. B, 2018, 122, 12396–12402.
38. F. Roosen-Runge, P. Schurtenberger and A. Stradner, J. Phys.: Condens. Matter, 2021, 33, 154002.
39. N. O. Junker, F. Vaghefikia, A. Albarghash, H. Höfig, D. Kempe, J. Walter, J. Otten, M. Pohl, A. Katranidis, S. Wiegand and J. Fitter, J. Phys. Chem. B, 2019, 123, 4477–4486.
40. D. Henderson, D.-M. Duh, X. Chu and D. Wasan, J. Colloid Interface Sci., 1997, 185, 265–268.
41. M. G. Noro and D. Frenkel, J. Chem. Phys., 2000, 113, 2941–2944.
42. M. Długosz and J. Trylska, BMC Biophys., 2011, 4, 3.
43. M. Długosz, P. Zieliński and J. Trylska, J. Comput. Chem., 2011, 32, 2734–2744.
44. J. Rotne and S. Prager, J. Chem. Phys., 1969, 50, 4831–4837.
45. H. Yamakawa, J. Chem. Phys., 1970, 53, 436–443.
46. P. J. Zuk, E. Wajnryb, K. A. Mizerski and P. Szymczak, J. Fluid Mech., 2014, 741, R5.
47. E. Smith, I. Snook and W. Van Megen, Phys. A, 1987, 143, 441–467.
48. P. M. Blanco, M. Via, J. L. Garcés, S. Madurga and F. Mas, Entropy, 2017, 19, 105.
49. K. Klett, A. G. Cherstvy, J. Shin, I. M. Sokolov and R. Metzler, Phys. Rev. E, 2021, 104, 064603.
50. W. Wang, A. G. Cherstvy, H. Kantz, R. Metzler and I. M. Sokolov, Phys. Rev. E, 2021, 104, 024105.
51. M. A. Lauffer, Biophys. J., 1961, 1, 205–213.
52. I. L. Novak, P. Kraikivski and B. M. Slepchenko, Biophys. J., 2009, 97, 758–767.
53. E. Słyk, T. Skóra and S. Kondrat, 2022, in preparation.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00357k

---