 Open Access Article
Open Access ArticleReply to the ‘Comment on “Surface elastic constants of a soft solid”’ by E. Gutman, Soft Matter, 2022, 18, DOI: 10.1039/D1SM01412A
Nicolas
Bain
a,
Stefanie
Heyden
a,
Qin
Xu
 b,
Robert W.
Style
b,
Robert W.
Style
 a and
Eric R.
Dufresne
a and
Eric R.
Dufresne
 *a
*a
aDepartment of Materials, ETH Zürich, 8093 Zürich, Switzerland
bDepartment of Physics, The Hong Kong University of Science and Technology, Hong Kong, China. E-mail: eric.dufresne@mat.ethz.ch
First published on 9th June 2022
We appreciate the interest in our paper “Surface elastic constants of a soft solid”.1 There, we observed a strain-dependent change to the contact-line geometry of a liquid droplet on a soft solid. We interpreted these data as a signature of surface elasticity, and were able to collapse the data using two surface elastic constants.In his comment, Prof. Gutman questions the validity of our interpretation, raising three criticisms. First, he claims that the Shuttleworth equation2 relating the surface energy and surface stress of a solid is invalid. Second, he remarks that the experimental deformations are too large to allow the use of linear surface elasticity. Third, he claims soft solids do not have surface elasticity. We believe these criticisms are unfounded, and address them below.
On the validity of the Shuttleworth equation
Gutman's critique of the Shuttleworth equation appears to be based on a misunderstanding. His analysis is incorrect primarily because it does not distinguish between different measures of the surface energy and surface stress. In particular, the specific surface energy can be expressed as energy per unit area of undeformed surface (i.e. reference configuration), γR, or per unit area of deformed surface (i.e. current configuration), γC. Similarly, surface stress can be expressed as force per unit length of undeformed contact line, ϒRij, or per unit length of deformed contact line, ϒCij. In terms of quantities relative to the undeformed state,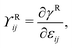 | (1) |
 | (2) |
We recall that the above derivation was conducted on specific, and not total, surface energies. Therefore, there appears to be no contradiction between Gutman's preferred eqn (1) and the Shuttleworth equation. Note that Gutman's critique of the Shuttleworth equation is a reiteration of his earlier published arguments.4 For a thorough rebuttal, see e.g., Section 3.3 of ref. 5.
Prof. Gutman further claims that having a linear term in the surface energy density,
 | (3) |
| ϒij = ϒ0δij + λsδijεkk + 2μsεij, | (4) |
On the use of linear theory
Prof. Gutman further argues that the measured deformations are too large to allow comparison to the linear form of surface stresses, eqn (4). In our paper,1 we observed a linear dependence of the apparent surface stresses as a function of the observed surface strain. This is sufficient justification for our use of a linear constitutive relation.A related, but potentially significant, concern is that large bulk strains due to far-field stretch could have a singular effect on the geometry of the wetting ridge. This would compromise the validity of the Neumann construction and invalidate our measurements of surface stress on stretched substrates. Opposing theories argue for the importance7 or insignificance8 of this effect. We are actively exploring this question, and are developing novel ways to measure surface elasticity that avoid the large deformations associated with contact lines.9,10
On the existence of surface elasticity in soft solids
Finally, Prof. Gutman claims that surface elasticity is not necessary, as it has not been treated by Gibbs or many other works on soft materials. This unusual line of reasoning assumes that anything that has not yet been observed does not exist.Using a completely different approach to ref. 1, we recently showed that the surface mechanics of a patterned silicone gel could not be captured without surface elasticity.10 Measurements of the tensile load carried by an adhesive contact are also suggestive of surface elasticity.11 Thus, diverse lines of evidence suggest that surface elasticity not only exists, but also has a measurable impact on the mechanics of soft solids.
We would like to highlight that surface elasticity is very well established in fluid–fluid interfaces.12 In that case, surface elasticity emerges because of species adsorbed to the fluid interface. In the case of soft solids, we anticipate that surface elasticity could arise either from similar compositional differences or from of variations in the structure of the polymer network near the interface. While the correlation between surface and bulk elasticity has started to be investigated,13 the origins of surface elasticity in soft solids are unknown and demand further investigation.
Conflicts of interest
There are no conflicts to declare.References
- Q. Xu, R. W. Style and E. R. Dufresne, Soft Matter, 2018, 14, 916 RSC.
- R. Shuttleworth, Proc. Phys. Soc., London, Sect. A, 1950, 63, 444 CrossRef.
- R. W. Style, A. Jagota, C.-Y. Hui and E. R. Dufresne, Annu. Rev. Condens. Matter Phys., 2017, 8, 99 CrossRef CAS.
- E. Gutman, J. Phys.: Condens. Matter, 1995, 7, L663 CrossRef CAS.
- D. Kramer and J. Weissmüller, Surf. Sci., 2007, 601, 3042 CrossRef CAS.
- I. S. Sokolnikoff, Mathematical Theory of Elasticity, McGraw-Hill, 1950 Search PubMed.
- R. Masurel, M. Roché, L. Limat, I. Ionescu and J. Dervaux, Phys. Rev. Lett., 2019, 122, 248004 CrossRef CAS PubMed.
- A. Pandey, B. Andreotti, S. Karpitschka, G. Van Zwieten, E. Van Brummelen and J. Snoeijer, Phys. Rev. X, 2020, 10, 031067 CAS.
- S. Heyden, P. M. Vlahovska and E. R. Dufresne, J. Mech. Phys. Solids, 2022, 161, 104786, DOI:10.1016/j.jmps.2022.104786.
- N. Bain, A. Jagota, K. Smith-Mannschott, S. Heyden, R. W. Style and E. R. Dufresne, Phys. Rev. Lett., 2021, 127, 208001, DOI:10.1103/PhysRevLett.127.208001.
- K. E. Jensen, R. W. Style, Q. Xu and E. R. Dufresne, Phys. Rev. X, 2017, 7, 041031 Search PubMed.
- G. G. Fuller and J. Vermant, Annu. Rev. Chem. Biomol. Eng., 2012, 3, 519 CrossRef CAS PubMed.
- W. Zhao, J. Zhou, H. Hu, C. Xu and Q. Xu, Soft Matter, 2022, 18, 507–513 RSC.
| This journal is © The Royal Society of Chemistry 2022 |
