Quantifying cooperative flow of fat crystal dispersions

Abstract

We quantify the cooperative flow behaviour of fat crystal dispersions (FCDs) upon varying crystallization conditions. The latter enabled altering the multiscale microstructure of the FCDs, from the nanometer-sized platelets, and the dispersed fractal aggregates, up to the strength of the mesoscopic weak-link network. To the goal of characterizing strongly-confined flow in these optically-opaque materials, we acquire high-resolution rheo-magnetic-resonance-imaging (rheo-MRI) velocimetry measurements using an in-house developed 500 μm gap Couette cell (CC). We introduce a numerical fitting method based on the fluidity model, which yields the cooperativity length, ξ, in the narrow-gap CC. FCDs with aggregates sizes smaller than the confinement size by an order of magnitude were found to exhibit cooperativity effects. The respective ξ values diverged at the yield stress, in agreement with the Kinetic Elasto-Plastic (KEP) theory. In contrast, the FCD with aggregates sizes in the order of the gap size did not exhibit any cooperativity effect: we attribute this result to the correspondingly decreased mobility of the aggregates. We foresee that our optimized rheo-MRI measurement and fitting analysis approach will propel further similar studies of flow of other multi-scale and optically-opaque materials.

---

Introduction

Flow through sub-mm geometries of complex dispersions, with particle sizes in the order of tens to hundreds micrometers, occurs during production processes and customer use of, e.g., foods, cosmetics or paints.^1–3 It is well known that, under such strongly- confined conditions, flow of particulate dispersions can become cooperative, due to the onset of spatial coupling between plastic events throughout the system.⁵ As a result, the flowing material is macroscopically fluidized and, thus, exhibits higher velocities and larger spatial heterogeneities of viscosity as compared to theoretical predictions in the absence of cooperativity.

Despite many experimental and numerical studies conducted over the last two decades,^6,7 a quantitative and comprehensive characterization of flow cooperativity is still missing, specifically regarding its dependence on microstructural and confinement properties. Thus, predicting cooperativity effects in fundamental soft matter studies, and in industrial applications of complex fluids, remains an open challenge.^4,8–10 To address this, suitable measurement techniques and numerical models must be developed for quantifying and predicting flow cooperativity in non-model, optically-opaque, dispersions.

In the pioneering works of Goyon et al.^10,11 and Bocquet et al.,¹² a quantitative formalism was introduced, centered around the concepts of fluidity, flow cooperativity and a correlation length scale, ξ. Since then, cooperativity effects have been quantified, under confined flow conditions, in emulsions,⁹ microgels,¹³ cellulose dispersions,⁴ and granular materials.¹⁴ In all these studies, cooperativity lengths were consistently found to be several times larger than the sizes of the microstructural constituents, e.g. grains, droplets, or aggregates. Yet, studies of the effect of microstructural properties on the extent of cooperativity have been, thus far, limited to evaluating the dependence on concentration and polydispersity of the dispersed particles. Goyon et al.¹⁰ found that, in flowing model emulsions, ξ increased with both concentration and droplet size, while it decreased with increasing polydispersity. Similar results were found by Géraud et al.^13,15 in flowing microgels. Less well established is the influence of flow confinement on cooperativity. In their same study on concentrated model emulsions, Goyon et al.¹⁰ found that flow cooperativity was independent of both gap size and wall roughness, while Paredes et al.⁹ found that only in rough microchannels flow of emulsions could be described as cooperative, and even as responsible for the apparent wall-slip. In agreement with these works, Derzsi et al.⁸ observed, both experimentally and numerically, enhanced cooperativity effects in concentrated model emulsions flowing through geometries with rough walls. Interestingly, in most of the above-mentioned studies, the authors reported stress-independent ξ values, which is in disagreement with numerical simulations based on the KEP theory.¹² The latter predicts that cooperativity lengths diverge as stresses approach the yield stress of the material. Stress-dependent ξ values are reported only in the numerical simulations of granular materials by Kamrin et al.,⁵ or in the studies of microgels by Geraud et al.¹³ Thus far, extensive studies have been mostly limited to model, optically-transparent, fluids with rather simple colloidal structures.^8–10,16 Consequently, the fundamental understanding of flow cooperativity in multiscale, and typically optically-opaque, complex materials remains elusive, hindering reliable predictions of strongly-confined flow in industrial applications.

As an example, strongly-confined flow of FCDs is encountered during the production and consumption of, e.g. margarine or chocolate. The flow behavior of FCDs depends on the morphology of the multiscale crystal structure, which in turn is strongly dependent on the crystallization conditions, namely applied shear, cooling rate, and temperature.^17–19 These parameters govern the interplay between fat crystallization and network formation processes, in turn affecting the shape, size and fractal dimension of the crystal aggregates, as well as the strength of the interstitial network. The latter has been established to be in the weak-link regime.^20,21 Thus far, the flow of FCDs with varying microstructural properties has been studied only in geometries with cm-sized gaps, exceeding the sizes of crystal aggregates by at least two orders of magnitude, while the respective sub-mm confined flow behavior and the potential presence of cooperativity effects have never been addressed.^17,19

In this work, we study the sub-mm flow of three FCD samples prepared at different crystallization rates, yielding different crystal aggregate sizes, fractal dimensions and strength of the interstitial weak-link network. These microstructural properties were respectively characterized, under static conditions, using light microscopy, wide- and small-angle X-ray diffraction (WAXD and SAXD), ultra-small-angle X-ray scattering (USAXS), and Raman imaging. We study the global flow behavior in both wide- and narrow-gap CCs with classical rheology, and compare the results with spatially-resolved rheo-MRI velocimetry measurements using an in-house developed 500 μm gap CC.²² We find that the presence and spatial extent of cooperative flow depends on the microstructural changes induced by varying crystallization rates. By fitting the data to a numerical fluidity-based model adapted for narrow-gap CC, we show that the flow cooperativity length depends not only on the sizes of the fat crystal aggregates, but also on the inter-particle interactions mediated by the colloidal network.

Materials and methods

Sample preparation

The solid fat blend was mixed with a commercially available sunflower oil (SF) to give a 27 wt% fat-in-oil dispersion, which was heated at 50 °C for 20 min to erase crystal polymorphic history. For each sample, the melt was subjected to a distinct crystallization procedure, to obtain samples with varying microstructures. For an isothermal crystallization (IC) the melt was transferred to a vessel pre-set at 15 °C corresponding to an approximate cooling rate of 5 °C min⁻¹. For rapid crystallization (RC) and slow crystallization (SC), the melt was cooled to 20 °C at a rate respectively of 1 or 0.1 °C min⁻¹. Using the crystallization rates and temperatures as labels, we henceforth refer to the respective samples as IC(15), RC(1) and SC(0.1). All measurements were carried out on FCD samples at room temperature (RT) within 8 h from the completion of their crystallization process, with the exception of USAXS, which was carried out within 3 days of chilled storage and transport since the crystallization.

WAXD

A Bruker D8-Discover diffractometer with a Våntec 500 2D detector and an IμS microfocus X-ray source (CuKα radiation, λ ¼ 0.154 nm) was used in a θ/θ configuration. WAXD data were collected in the range of 7° < 2θ < 55°. The beam cross section at the sample position was about 1 mm. The distance and angle between detector and sample were 32.5 cm and 10°, respectively.

Polarized light microscopy

Optical images of the three samples were obtained using a polarized light microscope (Nikon Eclipse) equipped with a 10× objective lens. The images were acquired with an Olympus DP70 camera and digitalized using a cellSens imaging software. To obtain an estimate of the average crystal aggregate size for each sample, 15 images were acquired at different locations across the measured surface. The mean size and its standard deviation (SD) over 50 randomly chosen aggregates was calculated in ImageJ 1.52.

USAXS and SAXD

USAXS and SAXD measurements were performed at the ID02 beamline at the European Synchrotron Radiation Facility (ESRF) (Grenoble, France). The average crystal thickness was obtained from the first order diffraction peak originating from triglyceride 2L layers using the Scherrer equation.²³ For the determination of the fractal dimension, data processing was conducted in Igor Pro 6.37 software using the Irena SAS 2.57 package. The USAXS signal of the SF oil sample was subtracted before data modelling. The Unified Fit model²⁴ provided the radius of gyration, R_gi, and the Porod slope, P_i, from which information about the crystal surface, morphology and the fractal dimension can be extracted. For P_i < 3 the fractal dimension equals to and relates to a mass fractal. Otherwise, the fractal dimension can be calculated as 6 − P_i and indicates a surface fractal.

Raman imaging

The hyperspectral Raman images were acquired using a WITec confocal Raman (Alpha 300R+) microscope equipped with a Zeiss upright microscope with a 532 nm laser at 25.0 mW, using a 100×/0.9 objective. The Raman spectrometer was coupled to a cooled (−60 °C) EMCCD detector. The obtained Raman spectra were in the range of 100–3800 cm⁻¹. An integration time of 0.05 s was used for imaging a 150 × 150 μm area with a resolution of 1 μm. The raw data were subjected to standard corrections, namely the cosmic ray removal and background subtraction in the Project FIVE 5.2 software after which the true component analysis was performed using the Raman spectra of the pure components to obtain the spatial distribution of solid fat and liquid oil in the three samples.

Rheology

All rheometric measurements were performed using an Anton Paar (MCR 301) rheometer. Global flow curves were acquired using a standard stainless steel CC with the radius of the bob, r_i = 5.25 mm, and the radius of the cup, r_o = 8.75 mm. Sandpaper was glued to the surface of both bob and cup to prevent slip. Each sample was pre-sheared for 3 min at 30 s⁻¹ and, thereafter, exposed to stress measurements under a shear rate sweep from 100 s⁻¹ to 0.01 s⁻¹. A total of 20 points per decade in shear rate were recorded, averaging each stress value over 5 s. Confined flow measurements were carried out using an in-house constructed CC made of polyether ether ketone (PEEK) with the radii of the bob and the cup respectively equal to r_i = 8.5 mm and r_o = 9 mm. This 500 μm CC was designed identically to the one used in rheo-MRI measurements, in order to ensure comparability of the results obtained from the two techniques.

Rheo-MRI

Rheo-MRI velocimetry measurements were performed on a wide-bore Bruker Avance III spectrometer operating at 7 T. Excitation and detection of the ¹H signal was performed using a bird-cage radiofrequency coil with an inner diameter of 25 mm, and the standard microimaging gradient system Micro 2.5 (Bruker Biospin) with maximum gradient intensity of 1.5 T m⁻¹ along all three axes. The magnet was equipped with the standard Bruker rheo-MRI accessory, consisting of a stepper motor and drive shaft, used in combination with a custom-made 500 μm CC (r_i/r_o = 8.5/9 mm) with smooth walls.²²

1D velocity profiles were measured using a Pulsed Gradient Spin Echo (PGSE)²⁵ sequence, within a slice 1 mm thick along two dimensions, echo time T_E = 20 ms and repetition time T_R = 2 s. The duration of the velocity-encoding gradient pulses, and their inter-pulse spacing, were δ = 1 ms and Δ = 13 ms, respectively. To avoid chemical-shift artefacts, a CHEmical Shift Selective (CHESS) suppression module, as implemented by Serial et al.,²⁶ was used in all measurements using three 90° chemically selective pulses with bandwidth of 0.8 kHz and offset of 1.1 kHz. The frequency-encoding read gradient provided a 10 mm-long slice over 1024 pixels, such that the spatial resolution was Δx = 10 μm. Using 512 scans, the total measurement time per velocity profile was 34 min. Each measurement was carried out on a fresh sample batch.

Results and discussion

Multiscale structure

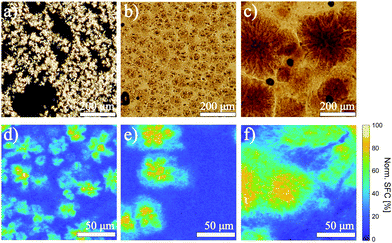
From the melt, FCDs were prepared by isothermal crystallization at 15 °C (IC(15)) and by rapid or slow crystallization at 1 or 0.1 °C min⁻¹, here denoted as RC(1) and SC(0.1), respectively. Irrespective of the applied cooling regime, all fat crystals in the FCDs are in the β′ polymorphic form, as evidenced by the presence of strong diffraction peaks at 19.5 and 23.4 2θ in WAXD spectra (see Fig. S1a in ESI†).²⁷ The different crystallization rates did, however, affect the sizes of the crystal aggregates, yielding samples with aggregates ranging across two orders of magnitude in size, and with varying polydispersity, as shown in the polarized light micrographs in Fig. 1. The isothermal crystallization at 15 °C yielded a sample with aggregates’ mean diameter of 30 ± 13 μm (IC(15)), while crystallization rates of 1 and 0.1 °C min⁻¹ towards 20 °C resulted in dispersions with respective aggregates’ mean diameters of 53 ± 12 μm (RC(1)), and 223 ± 119 μm (SC(0.1)). This trend is in line with studies on microstructures of model and real fat systems crystallized under varying conditions of temperature and shear.^28–31 According to the established theories on crystallization mechanisms in FCDs, lower crystallization rates lead to lower degree of undercooling, which in turn results in a decrease of nucleation rate and thus larger crystallites, which aggregate into fractal networks.³² The increase in crystallite size with decreasing crystallization rates was confirmed by SAXD measurements, which yielded the average crystallite thickness of 54.0 ± 0.3 nm, 60.0 ± 0.3 nm and 80.0 ± 0.3 nm for samples IC(15), RC(1) and SC(0.1), respectively. The fractal nature of the aggregates was confirmed by the USAXS measurements, which yielded fractal dimensions for samples IC(15), RC(1) and SC(0.1) respectively of 2.90 ± 0.03, 2.70 ± 0.03 and 2.40 ± 0.01 (see Fig. S1b in ESI†). The lowest fractal dimension for sample SC(0.1) is in line with the porous and spherulitic appearance of the crystal aggregates visible in the micrograph in Fig. 1c. To gain further insight into the structure and the colloidal network beyond the crystal aggregates, we investigated the spatial distribution of solid fat in the three samples with Raman imaging, with results presented in Fig. 1d–f. As expected, in all samples the solid fat is concentrated within the aggregates. However, the analysis of the Raman spectra (see Fig. S2 in ESI†) corresponding to voxels within interstitial spaces revealed an increasing similarity with the reference spectrum of the pure solid fat component of the FCDs, going from sample IC(15) to SC(0.1). Both the spatially-resolved Raman spectroscopy and SAXD measurements evidence that the weak-link network in the IC(15) and RC(1) samples has a lower solid fat content, and is composed of thinner crystal platelets. In contrast, in the SC(0.1) sample more solid fat is present in the weak-link network, which is composed of less space filling, thicker crystallites.

Fig. 1 Images of the FCD samples IC(15) (left), RC(1) (middle) and SC(0.1) (right) obtained by polarized light microscopy (top) or Raman imaging (bottom). The images were acquired at RT within 3 h after completion of the crystallization process.

Flow characterization

The flow of the FCDs is typically studied globally and described with a local constitutive rheological law, which is insensitive to flow confinement size.^19,21,33 To test whether such theoretical approach is sufficient to capture all aspects of flow of FCDs, we study and compare the global and local flow of each sample, using classical rheology and sub-mm rheo-MRI, respectively.

Global flow

The global flow behaviour of samples IC(15), RC(1) and SC(0.1) under strain-controlled conditions in a 3.5 mm gap CC is shown in Fig. 2a–c (black circles) as measurements of shear stress, σ, at varying shear rates, [small gamma, Greek, dot above], in the range 0.01–100 s⁻¹. The data appear independent of microstructural differences across the samples and can be well described by the Herschel–Bulkley (HB) model: σ = σ_y + A[small gamma, Greek, dot above]ⁿ. Here, σ_y denotes the yield stress, A is a proportionality constant, and n is a power law index.³⁴ The fitted parameters obtained for the three samples are summarised in Table 1. In the ESI,† we include a verification that the wide gap condition, with its intrinsic shear and stress inhomogeneity, doesn’t affect our results.

Fig. 2 Global flow curves of the 27% FCD samples IC(15) (a), RC(1) (b), and SC(0.1) (c), measured with the rheometer from high to low shear rates, using a standard 3.5 mm gap CC with glued sandpaper to prevent slip (open circles). Each flow curve was fitted with a HB model (solid red line). Stress values at chosen shear rates were also measured with a 500 μm gap CC with smooth walls (blue crosses). The plotted values are the mean and the SD of two repeats.

Table 1 Fitting parameters obtained from fitting analysis of the global flow curves of the three FCDs using the HB model

	σ y	A	n
IC (15 °C)	13.7 ± 0.2	3.1 ± 0.1	0.70 ± 0.01
RC (1 °C min^−1)	17.3 ± 0.2	4.4 ± 0.1	0.67 ± 0.01
SC (0.1 °C min^−1)	12.6 ± 0.1	4.1 ± 0.1	0.67 ± 0.01

---

To investigate whether the measured global flow behaviour depends on the size of the flow geometry, we measured the global stress responses of the three FCDs in a 500 μm gap CC at chosen shear rates of [small gamma, Greek, dot above] = 0.5, 0.7, 1, 2, 5, 10 and 30 s⁻¹ (blue crosses in Fig. 2a–c). Comparison between results obtained with the 500 μm and 3.5 mm gap CCs shows that flow in sample SC(0.1), where aggregate sizes are the largest, is independent of the gap size. However, for the other two samples the global stress is markedly lower in the narrow-gap CC. The presence of a gap-size dependence of the rheological properties for samples IC(15) and RC(1) can arise from various flow instabilities, such as shear banding³⁵ and wall slip,⁹ or can indicate cooperative flow behaviour.¹¹ To elucidate the source of the bulk rheological properties observed in Fig. 2, local flow information is needed. Thus, in the next section we study the confined flow in a spatially-resolved manner by rheo-MRI.

Local flow

The local flow behaviour was studied by high-field rheo-MRI using an in-house developed 500 μm gap CC. This cell was designed to enable imposing confined flow while keeping stress inhomogeneity and off-axis wobbling negligible.²² These conditions are essential for observing and quantifying confined flow behaviour, without distortions originating from the rotating geometry. The rheo-MRI velocity profiles of all FCDs, acquired at the same shear rates as the stress measurements by standard rheology (Fig. 2), are shown in Fig. 3a–c. Local shear rates, shown in Fig. 3d–f, were derived from each of the measured velocity profiles using the following equation:where x is the measured position across the gap and v(x) is the respective spatially-dependent velocity. As [small gamma, Greek, dot above](x) values are proportional to the first spatial derivative of v(x), they are expected to better unravel sample-specific deviations from linear flow profiles. It can be seen in Fig. 3 that all samples exhibit non-linear velocity profiles and, thus, non-uniform local shear rates, as confirmed by data in Fig. 3d–f. Furthermore, for samples IC(15) and RC(1) shear banding can be observed only at the lowest [small gamma, Greek, dot above]_app value, while flow in sample SC(0.1) bands over [small gamma, Greek, dot above]_app values up to 1 s⁻¹. Similarly, the percentage of wall slip, averaged across all [small gamma, Greek, dot above]_app values (see Fig. S4 in ESI†) is 35%, 34% and 47% for IC(15), RC(1) and SC(0.1) respectively, indicating a markedly distinct behaviour of the latter sample. With the aim to describe this complex flow behaviour, we compare the rheo-MRI velocity profiles with those calculated from the global HB flow behaviour (solid lines in Fig. 3a–c). We find that the measured velocities are in agreement with the predictions from the HB equation only for sample SC(0.1), while for samples IC(15) and RC(1) they largely exceed the predicted velocities at all shear rates. Hence, our narrow-gap rheo-MRI measurements indicate (i) the failure of the local HB flow model, and the existence of enhanced velocities for FCDs prepared at high crystallization rates, and (ii) the presence of shear-banding and shear-dependent wall slip. In literature, such flow instabilities have been associated with confinement-induced cooperativity effects.^9–11,15 Thus, in the following section we describe and use a non-local rheological model, suitable for the adopted narrow-gap CC, to quantify flow cooperativity for samples IC(15) and RC(1).

Fig. 3 For the FCD samples IC(15), RC(1) and SC(0.1), from left to right: (a–c) ¹H rheo-MRI velocity profiles measured in a 500 μm gap CC (open symbols) and respective calculated velocities from the HB model (solid lines) as a function of the normalized position across the gap, upon varying applied shear rates, [small gamma, Greek, dot above]_app. Measured flow profiles were corrected for slippage by subtracting the slip velocity (see ESI†) determined by extrapolation of the last 10 pixels at the outer wall as done in previous work;⁴ (d–f) corresponding shear rates calculated from each measured velocity profile. The dotted line serves as a guide for the eye.

Characterization of flow cooperativity

Cooperativity effects in the flow of soft particle dispersions can be quantified using a so-called fluidity model. Fluidity, defined as the ratio of the shear rate and the shear stress, , is linked, on a microscopic level, to the local rate of plastic rearrangements across the whole flowing system. If the material exhibits cooperative flow, the plastic rearrangements have non-local character, i.e. they induce further rearrangements of neighbouring particles and lead to complex spatio-temporal variations of the fluidity. In this case, the fluidity is predicted to obey a non-local equation:where f_bulk is the bulk fluidity in the absence of non-local effects, ξ is the cooperativity length, which can be interpreted as the distance over which the plastic events influence the surrounding, and x is the position across the gap. For our samples, whose global flow is well described by the HB model (see Fig. 2), the bulk fluidity is defined as:where is the stress distribution specific to the CC geometry. The latter expression is derived from the momentum balance, where T is the torque exerted on the rotating bob measured at a rheometer, and H is the height of the bob.³⁶ Given the form of the stress distribution in a CC, eqn (2) has no closed, analytical, solution. Hence, to obtain the cooperativity lengths for each sample at varying shear rates, we numerically solve the following system of first-order ordinary differential equations (ODEs), with the shear rates at both inner and outer walls, respectively [small gamma, Greek, dot above]_ri and [small gamma, Greek, dot above]_ro, as boundary conditions:where [small gamma, Greek, dot above]_loc is the local shear rate obtained from rheo-MRI measurements (Fig. 3d–f). We note that our proposed numerical approach for solving the fluidity equation enables easily adapting the model to different flow geometries with radial symmetry, by simply defining the expression of the stress distribution. The stress distribution, along with the definition of bulk fluidity, becomes instead a constraining factor in the commonly used analytical integrations of the fluidity equation,^9,10,13 making the model less general and straightforward. The solution of eqn (4) is numerically integrated to obtain a theoretical velocity profile, which we fit to the measured data using the boundary conditions and the cooperativity length as fitting parameters.

To achieve a robust estimate of all fitting parameters, in particular of the boundary conditions which rely on the derivative of the velocity profiles, high spatial resolution in the measured velocimetry data is a key requirement. This condition is satisfied in our experimental data, where a spatial resolution of 10 μm per pixel could be achieved thanks to our improved design of the new rheo-MRI setup with improved mechanical stability of the rotating elements.^4,37,38

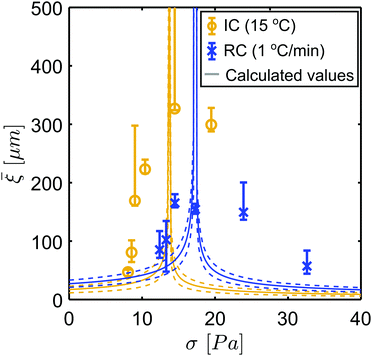
In Fig. 4a and b the experimental velocity profiles, respectively for samples IC(15) and RC(1) as already displayed in Fig. 3a and b, are fitted using the fluidity model. In the ESI,† we include the fitting results using the bulk flow behaviour corrected for the shear rate inhomogeneity of a wide gap geometry. We also attempted fitting the model to the velocity profiles of sample SC(0.1), which yielded either no convergence or cooperativity lengths below the mean particle size (see Fig. S5 in ESI†), further confirming the absence of cooperativity in this FCD sample. For samples IC(15) and RC(1) the mean cooperativity lengths were obtained, at each shear rate, by averaging the fitting results from triplicate measurements (Fig. 4c and d). The calculated mean ξ values were weighed using the fitting error of each repeat, while the error bars represent the maximum and the minimum ξ value obtained from fitting the individual measurements (see Fig. S6 in ESI† for plots of the other fitting parameters, [small gamma, Greek, dot above]_ri and [small gamma, Greek, dot above]_ro). First, we observe that the obtained numerical solutions of eqn (4) are in agreement with the measured velocity profiles, and that all obtained ξ values are in the order of the aggregate sizes in the FCD samples. This is in agreement with the current understanding of flow cooperativity, and in line with findings from previous studies.^4,9,10,15 Interestingly, we observe a decrease in the cooperativity lengths with increasing aggregate sizes, reaching a null cooperativity length in sample SC(0.1), where the largest aggregates are present. The observed differences among the FCDs likely originate from the respective variation in the mesoscopic weak-link network and in the aggregates’ fractality. We hypothesize that in the IC(15) and RC(1) samples the inter-particle weak-link network effectively enables cooperative behaviour. Instead, in the SC(0.1) sample the coarser interstitial network, higher fractality and mean size of the aggregates result in stronger confinement condition and reduction in the mobility of the aggregates during flow. This severly limits the inter-particle interactions in the SC(0.1) sample, resulting in the absence of cooperativity effects. A similar hypothesis was made by Geraud et al. in their study on cooperative flow of microgels.¹³

Fig. 4 For samples IC(15) (a and c) and RC(1) (b and d): experimental and fitted velocity profiles (top row) and mean cooperativity lengths, ξ, (bottom row) obtained using eqn (2) and (3). The ξ values were obtained from three replicate rheo-MRI measurements per [small gamma, Greek, dot above]_app and calculated using the individual fitting errors as weights. The error bars represent the spread of the ξ values. Insets report the obtained ξ values normalized to the respective mean aggregate size, d.

Lastly, Fig. 4d and f unravel a non-monotonic trend of the ξ values as a function of the applied shear rate. This trend is in agreement with the KEP model,¹² which suggests that the cooperativity length should diverge at the yield stress of the material, according to the following equation:

where C is a dimensionless scaling constant, and d is the characteristic length scale of the fluid microstructure, which here we assume to be the determined mean aggregate sizes and their respective SD. In Fig. 5 we show the theoretical cooperativity lengths on the scale of stresses relevant for samples IC(15) and RC(1), calculated using either the respective mean sizes of the aggregates, 30 and 53 μm (solid lines), or the corresponding minimum and maximum values calculated as (30 ± 13) μm and (53 ± 12) μm (dotted lines). We compare these predictions with the ξ values (cross symbols) obtained from the fitted velocity profiles (Fig. 4), plotted in Fig. 5 against the stress values measured in the 500 μm CC by classical rheology (Fig. 2). Although the theoretical and fitted ξ values are not in perfect agreement, it is clear that for both IC(15) and RC(1) samples ξ reaches a maximum around the corresponding yield stress value.

Fig. 5 Theoretical ξ values predicted by the KEP model for samples IC(15) and RC(1) (solid lines) at stresses 1–40 Pa, compared with the mean cooperativity lengths, ξ obtained from fits of the fluidity model, plotted against stresses at the bob, measured by global rheology. Dotted lines are the calculated ξ values for smallest and largest aggregates present in each sample, given the respective polydispersity.

Conclusions

In this work we have studied the flow behaviour of three FCDs prepared at different crystallization rate conditions, that yielded FCDs with average crystal aggregate sizes in the range of 10–10² μm, and with varying colloidal network properties. We have found that the flow of the FCD sample with the largest crystal aggregates is independent of the confinement size, and is well described by a classical rheological HB model. In contrast, the flow of FCDs with smaller crystal aggregates was sensitive to the confinement size, yielding lower stress values in sub-mm confinement than in a wide-gap CC. With sub-mm rheo-MRI CC measurements, we identified cooperativity as the underlying cause of the observed differences in the confined flow between the FCDs. By fitting the measured velocity profiles with our proposed numerical fluidity model, we have quantified the cooperativity length scale, ξ, for samples IC(15) and RC(1). The found ξ values were 1–15 times larger than the respective mean aggregates’ sizes, in line with the previous findings.^9,10,15 In addition, ξ values were found to be dependent on the applied shear rate, diverging at the yield stress of each FCD, in agreement with the theoretical predictions of the KEP model. Finally, sample IC(15), with smallest aggregates and lowest polydispersity, respectively ∼30 μm and 40%, exhibited the highest ξ values at medium shear rates. In contrast, sample SC(0.1), with largest aggregates and highest polydispersity, respectively ∼200 μm and 50%, did not exhibit any cooperativity effects, which we attribute to the decreased mobility of the aggregates, caused by their high fractality and sizes approximating the confinement size.

Thanks to the optimized narrow-gap rheo-MRI setup and numerical modelling approach, we were able to characterize confined flow of the FCDs, and to quantify the dependence of its cooperativity on the adopted crystallization conditions. The obtained results show that the cooperativity length does not necessarily simply scale with particle size. We foresee that our proposed experimental and modelling approach can be used to aid elucidating the dependence of cooperativity on other structural or rheological properties of FCDs, such as particle concentration and shape, confinement size and wall slip. This will ultimately aid in robustly predicting flow cooperativity in FCDs under industrially-relevant conditions.

Author contributions

Conceptualization: C. T., J. A. D. and J. P. M. v. D.; experimental measurements and data analysis: K. W. M.; validation: K. W. M.; formal analysis: K. W. M.; writing – original draft preparation: K. W. M.; writing – review and editing: C. T., J. A. D. and J. P. M. v. D.; visualization: K. W. M.; supervision: C. T., J. P. M. v. D, J. A. D. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

J. P. M. van Duynhoven is employed by a company that manufactures fat-continuous food products. None of the other authors have a conflict of interest to declare.

Acknowledgements

We thank Bruker BioSpin (Germany) for co-sponsoring this project, and Dieter Gross and Thomas Oerther from Bruker BioSpin for useful discussions on the rheo-MRI setup. We thank John Philippi for the design of the rheo-MRI CC. We also acknowledge: Brian Tighe (TU Delft), for fruitful discussions on numerical modelling and data interpretation; Theyencheri Narayanan and Michael Sztucki, for support during experiments on the ID02 beamline at ESRF; Ruud van Adel, for help with the analysis of WAXD, SAXD and USAXS spectra; Arjen Bader, for help with the acquisition of Raman spectra. Upfield (Rotterdam, The Netherlands) is thanked for providing the solid fat blend. We acknowledge the support of NWO for the MAGNEFY centre, which is part of the uNMR-NL national facility. The USAXS experiments were performed at the European Synchrotron Radiation Facility (ESRF), Grenoble, France. C. T. acknowledges funding from the 4TU Precision Medicine Program supported by High Tech for a Sustainable Future.

Notes and references

1. G. Corrieu and C. Béal, in Reference Module in Food Science, ed. G. Smithers, Elsevier, 2016, pp. 617–624.
2. J. Sun, W. Zhou and D. Huang, in Reference Module in Food Science, ed. G. Smithers, Elsevier, 2018, pp. 1–9.
3. L. Xu, L. Gu, Y. Su, C. Chang, J. Wang, S. Dong, Y. Liu, Y. Yang and J. Li, Food Hydrocoll., 2020, 100, 105399.
4. D. W. de Kort, S. J. Veen, H. Van As, D. Bonn, K. P. Velikov and J. P. M. van Duynhoven, Soft Matter, 2016, 12, 4739–4744.
5. K. Kamrin and G. Koval, Phys. Rev. Lett., 2012, 108, 178301.
6. J. A. Dijksman, Front. Phys., 2019, 7, 1–8.
7. K. Kamrin and D. L. Henann, Soft Matter, 2015, 11, 179–185.
8. L. Derzsi, D. Filippi, G. Mistura, M. Pierno, M. Lulli, M. Sbragaglia, M. Bernaschi and P. Garstecki, Phys. Rev. E, 2017, 95, 052602.
9. J. Paredes, N. Shahidzadeh and D. Bonn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 042313.
10. J. Goyon, A. Colin and L. Bocquet, Soft Matter, 2010, 6, 2668–2678.
11. J. Goyon, A. Colin, G. Ovarlez, A. Ajdari and L. Bocquet, Nature, 2008, 454, 84–87.
12. L. Bocquet, A. Colin and A. Ajdari, Phys. Rev. Lett., 2009, 103, 036001.
13. B. Geraud, L. Bocquet and C. Barentin, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 1–13.
14. K. Kamrin, Front. Phys., 2019, 7, 1–7.
15. B. Géraud, L. Jørgensen, C. Ybert, H. Delanoë-Ayari and C. Barentin, Eur. Phys. J. E: Soft Matter Biol. Phys., 2017, 40, 1–10.
16. J. R. Seth, C. Locatelli-Champagne, F. Monti, R. T. Bonnecaze and M. Cloitre, Soft Matter, 2012, 8, 140–148.
17. T. Nikolaeva, R. den Adel, R. van der Sman, K. J. A. Martens, H. Van As, A. Voda and J. P. M. van Duynhoven, Langmuir, 2019, 35, 2221–2229.
18. A. G. Marangoni and M. A. Rogers, Appl. Phys. Lett., 2003, 82, 3239–3241.
19. T. Nikolaeva, R. den Adel, E. Velichko, W. G. Bouwman, D. Hermida-Merino, H. Van As, A. Voda and J. P. M. van Duynhoven, Food Funct., 2018, 9, 2102–2111.
20. S. S. Narine and A. G. Marangoni, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 1908–1920.
21. A. G. Marangoni, J. P. M. van Duynhoven, N. C. Acevedo, R. A. Nicholson and A. R. Patel, Soft Matter, 2020, 16, 289–306.
22. K. W. Milc, M. R. Serial, J. Philippi, J. A. Dijksman, J. P. M. van Duynhoven and C. Terenzi, Magn. Reson. Chem., 2021, 1–9.
23. R. den Adel, K. van Malssen, J. van Duynhoven, O. O. Mykhaylyk and A. Voda, Eur. J. Lipid Sci. Technol., 2018, 120, 1800222.
24. F. Peyronel, J. Ilavsky, G. Mazzanti, A. G. Marangoni and D. A. Pink, J. Appl. Phys., 2013, 114, 234902.
25. P. T. Callaghan, Rep. Prog. Phys., 1999, 62, 599–670.
26. M. R. Serial, T. Nikolaeva, F. J. Vergeldt, J. P. M. van Duynhoven and H. Van As, Magn. Reson. Chem., 2019, 57, 766–770.
27. V. D'Souza, J. M. deMan and L. deMan, J. Am. Oil Chem. Soc., 1990, 67, 835–843.
28. F. Maleky, N. C. Acevedo and A. G. Marangoni, Eur. J. Lipid Sci. Technol., 2012, 114, 748–759.
29. N. Kaufmann, V. De Graef, K. Dewettinck and L. Wiking, Food Biophys., 2012, 7, 308–316.
30. B. Liang, Y. Shi and R. W. Hartel, J. Am. Oil Chem. Soc., 2008, 85, 397–404.
31. R. Campos, S. S. Narine and A. G. Marangoni, Food Res. Int., 2002, 35, 971–981.
32. F. Peyronel, N. C. Acevedo, D. A. Pink and A. G. Marangoni, in Crystallization of Lipids, ed. K. Sato, Wiley, 2018, ch. 5, pp. 143–181.
33. N. C. Acevedo, J. M. Block and A. G. Marangoni, Faraday Discuss., 2012, 158, 171–194.
34. W. H. Herschel and R. Bulkley, Proc., Am. Soc. Test. Mater., 1926, 26, 621–633.
35. S. Lerouge and P. D. Olmsted, Front. Phys., 2020, 7, 1–11.
36. J. M. McKelvey, Polymer Processing, Wiley, New York, 1962.
37. P. Coussot, J. Raynaud, F. Bertrand, P. Moucheront, J. Guilbaud, H. Huynh, S. Jarny and D. Lesueur, Phys. Rev. Lett., 2002, 88, 218301.
38. K. G. Hollingsworth and M. L. Johns, J. Rheol., 2004, 48, 787–803.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d2sm00233g

---