 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modeling the assembly of oppositely charged multi-indented lock- and key-colloids†
Björn
Stenqvist
 *a and
Jérôme J.
Crassous
*a and
Jérôme J.
Crassous
 *ab
*ab
aDivision of Physical Chemistry, Lund University, POB 124, SE-22100 Lund, Sweden. E-mail: bjorn.stenqvist@teokem.lu.se
bInstitute of Physical Chemistry, RWTH Aachen University, Landoltweg 2, 52074, Aachen, Germany. E-mail: crassous@pc.rwth-aachen.de
First published on 10th June 2022
Abstract
The interactions between oppositely charged multi-indented lock- and spherical key-particles are investigated by means of Monte Carlo simulations at low volume fractions. The specificity of the interactions is initially investigated in an excess of either lock- or key-particles, and we find ordered clusters with highly directional bonds. This suggests electrostatics alone to be capable of inducing the assembly of specifically bound clusters. Considering different numbers of indentations and number ratios corresponding to perfect lattices (cubic/hexagonal/diamond), we however only find gel-like structures with no tendency to form dense ordered aggregates or lattices. We conjecture that the high entropic cost that comes with specific binding of several keys to a single lock impedes the spontaneous formation of defined lattices at low volume fractions and “lock” the assembly into disordered gel-like structures.
Nature's ability to assemble seemingly disparate building blocks into well-defined structures has been a wellspring of inspiration for the generation of scientists, as well as a driving force for innovation in many fields. Shape complementarity and selectivity, unified under the lock and key concept,1 are central for such self-organization. Often referred in biology to describe for instance interactions between enzymes and substrates,2,3 lock and key interactions are widely present in many biological processes involving recognition, sorting and signaling. Their application extends to the field of chemistry, where they have become some of the keystones of supramolecular chemistry.4
Spherical particles have been widely employed to create a large variety of assemblies at the colloidal domain, yet they have limitations in producing intrinsically more complex systems.5–7 The association of lock- and key-systems has widen the range of possible assemblies by adding extra directionality to the interactions,8 similar to the development of Janus9 and patchy colloids.10,11 This offers the advantage that the selectivity of the association mostly arises from the shape complementarity, leading to opportunities for different materials to assemble into a predefined design.12,13 Highly specific associations can thus be achieved by relying on excluded volume effects.14–18 Depletion interactions have been widely studied for the lock and key self-assembly of colloidal building blocks, and recent demonstrations show that such an assembly principle could be greatly extended to other types of interactions using responsive microgel systems.19 Introducing systems where dimensions could be altered with temperature allows for the formation of specific and responsive colloidal molecules with tuneable valency. However, using simple indented spheres14 or bowl-shaped particles19 as these lock-particles does not provide enough coordination to go beyond the formation of “simple” colloidal molecules.
This was recently overcome using supramolecular tubules as linkers and microgels as nodes for the design of supracolloidal “atomium-like” frameworks20 with a similar idea to DNA functionalized colloids with flexible joins.21 In both cases, the formation of larger structures is ensured by the mobility of the linkers, which allows the distance between the joining colloids to be precisely set. These two examples point to the importance of flexibility and dynamics for the realization of the defined self-assembly. However, the drawback of these approaches is their lack of directionality, which is essential for the spontaneous self-assembly into periodic structures such as non-closed packed crystals. This is also illustrated by the theoretical phase behavior of particles with limited valence and flexible bonds, for which liquid states may be preferred over a crystalline state.22
It has become obvious that complex assemblies often require complex building blocks. The perfect example for this is the work on “DNA bricks”,23,24 where each brick is especially designed to find its place in the assembly. When this approach could be seen as a puzzle-like assembly, most synthetic approaches rely on far more simplistic strategies where each colloidal building block fulfill one function such as nodes or linkers, following a “construction-kit” scheme. Hereby, the implementation of a strong coordination and directionality has motivated the development of alternative colloidal designs such as patchy particles, colloidal molecules and multi-indented lock-particles.8 In this case, the idea of a colloidal carbon was one of the main inspirations with respect to the potential assembly into a diamond lattice with extraordinary photonic properties. However, besides the successful development of such an advanced design at the single particle level, functionalized colloidal molecules and multi-indented lock particles have been limited to our knowledge for the formation of either colloidal molecules12,19,25–27 or linear assembly.8 Therefore in this work we explore the effects on the self-assembly of introducing further directionality by utilising simulations of multi-indented lock-particles at low densities.
1. Theory
In this section, we will first evaluate the excluded volume effects (rotational entropy) between a multi-indented lock-particle and a key-particle and then extend a previous model for the electrostatic potential from a lock-particle which will be used in simulations. In Fig. 1a, we present a sketch of a key-particle and a lock-particle with three indentations, and introduce essential parameters. From here on, the locks will be denoted as LX, where X is its number of cavities. In this work, the cavity centers of all: L2 particles are antipodal, L3 particles are placed at the corners of an equilateral triangle about a great circle, L4 particles construct a regular tetrahedron, and L6 particles are at the corners of a regular octahedron. For a visual representation, see Fig. 1b. Note however that other cavity positions are possible using the presented approach as long as the cavities are mutually non-overlapping.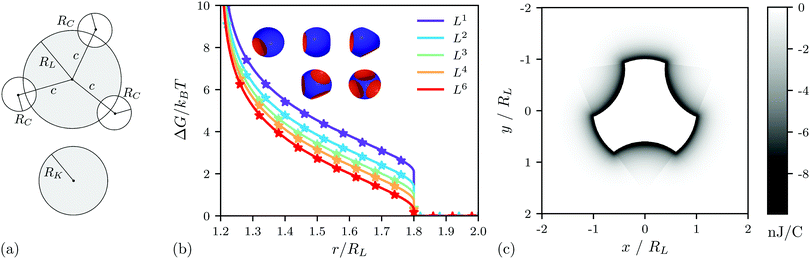 | ||
| Fig. 1 (a) Schematic of a key-particle with a radius RK, and a lock-particle with a radius RL and three indentations, all with the same cavity centers displaced by c from the particle center, and the radius RC. (b) Analytic free energy (see Section S2 in the ESI†) (lines) and simulation (stars) free energy between the lock- and the key-particle using a hard-overlap potential. All cavities were located at c = 1.2RL from the lock-particles center, where RL is the lock radius. The radii of the cavities were RC = RK, where the key particle radius RK = 0.8RL. (c) Electrostatic potential map using an L3 particle and an ionic strength I of 10−5 M (see Section S3 in the ESI†). | ||
1.1 Entropy
In a previous work, an exact analytic expression was given for the excluded volume effects between a single-indented lock-particle and a key-particle.27 By assuming non-overlapping cavities, this approach is straightforward to extend to the excluded volume effects between a multi-indented lock-particle and a key-particle (see Section S1 and Section S2 in the ESI† for details). The resulting free energy for lock-particles with equal cavity sizes is shown in Fig. 1b, where the analytic results (solid lines) are compared and validated against the simulation output (stars, see Section 2, for details). In Fig. 1b, we note a decrease in free energy as the number of cavities increases. The repulsion of the key particle is related to the volume of the lock-particle and as more cavities are introduced the particle volume decreases and so does the repulsion between the lock and key. The results thus suggest that assembly between a single lock and a key is more favorable when using several indentations.1.2 Energy
The electrostatic interactions between a single-indented lock-particle and a key-particle with equal (but oppositely polarized) surface charge density have been modeled in a previous study.27 This approach was based on describing the interactions between the particles with different analytic expressions pending the distance and/or angle between the lock-particle cavity and the key-particle center (see Fig. 3 in ref. 27 for clarity). The scheme used here extends this approach to several indentations, see Fig. S1 (ESI†). As such, we approximate the potential with linear combinations of the exact analytic expressions of single-indented lock-particles. This approximation is valid for electrostatic interactions at length-scales comparable to the particle size or smaller. The electrostatic potential map calculated from an L3 particle under the conditions used later in this work is shown in Fig. 1c. Note that the extent of the potential is fairly short-ranged compared to the particle size.2. Simulations
In order to investigate multi-indented lock particle interactions with key particles, we performed Metropolis Monte Carlo simulations using the Faunus28 software; see Section S7 in the ESI† for more information on the simulation software. The simulations were performed using N = 1000 particles in the canonical ensemble and after equilibration production runs of 5 × 105 steps were executed. For many of the setups, the equilibration was far longer than that of the production run. The equilibration length was determined by analyzing different quantities, among them energies, structural properties such as the radial distribution function, and the configurations themselves. Using translation and rotational moves, in addition to cluster moves,29,30 and non-rejection schemes,31 we were able to sample the system with typical acceptance ratios ranging from a few percent to a few tens of percent, depending on the move. The no-rejection moves used either translational, inverted, or rotational displacement around a single pivot point. The average number of moved particles varied substantially between one and a thousand and was strongly coupled to the specificity of the interactions. Two types of cluster moves were used. The first one selects a particle at random in the system, includes that particle in the cluster, and then includes every other particle within a cutoff distance from the center of the selected particle.29 The second cluster move is initially identical to the previous description, but for every added particle we perform the procedure again. That is, include all particles within a cutoff distance from the center of the later added particles. This allows the second type of clusters to grow and potentially include all particles in the system. Two cutoffs were used, one that only allowed for specifically bound particles to be added to a cluster, and one that also allowed unspecifically bound particles. Specific bonds are defined as particles within a distance r ≤ RX + RY from one another and unspecific bonds as particles within a distance RX + RY < r ≤ 1.1(RX + RY), where X and Y index the two different particles. The number of bound particles is retrieved by integrating the radial distribution function g(r) between locks and keys over the desired intervals, described in the previous sentence, as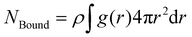 | (1) |
Two key aspects to investigate in this study were the impact from the size and position of the cavity of the locks, and the impact from the charge. In order to maximize the specificity of the interactions we, based on the results from a previous study of single indented lock particles,27 used the parameters RC = RK for the lock and key geometry and an ionic strength I of 10−5 M. We furthermore used RL = 500 nm and a surface charge density |σ0| = 3.183 × 10−4e nm−2, where e is the elementary charge, and a relative permittivity of εr = 80, and temperature T = 293.15 K. The surface charge densities of the locks σL and keys σK were opposite in sign but equal in magnitude, σL = − σK = σ. Systems were investigated using various surface charge densities σ = {0.5,1.0,1.5}σ0, radii of the key RK = {0.8,1.0,1.2,1.4,1.6}RL (and thus implicitly also the radius of the cavity RC of the lock as they are in a one-to-one ratio), distances from the center of the lock to the center of cavities c = {1.2,1.4,1.6,1.8,2.0}RL, and number ratios NK/NL. The choice of this parameter space is based on a previous study27 where the charge density σ = 1.0σ0 was used and gave high specificity for single-indented locks and keys. Moreover, we restrict our study to locks and keys of reasonably similar size, that is the choice of RK. The limitations of the model (no mutual overlap between cavities) further restrict the choice of c. For L2 particles, we use three different number ratios: NK/NL = {1/1,1/2,1/3} which (if optimally specifically bound) should assemble into chains, diamond lattices, or a cubic lattice, respectively. For L{3,4,6} particles, we used NK/NL = {3/2,2/1,3/1} which similarly should assemble into a (2D-)hexagonal, diamond, or cubic lattices. In Section S4 in the ESI,† we derive the number ratios for the different assemblies. Based on the above parameter-space, we perform one simulation for each set of parameters. For example, one simulation with L2 particles, NK/NL = 1/3, RK/RL = RC/RL = 1.6, c/RL = 2.0, and σ = 1.0σ0. A snapshot from the simulation of the described setup is shown in Fig. 5a and quantitative results are highlighted with a red square in Fig. 6, 7a and b.
3. Results
3.1 Excess of one type of particle
In Fig. 2, we present configurations from simulations where different types of locks are interacting with an excess of keys. For all presented cases, the keys are bound by highly specific interactions, i.e., to the cavities of the locks. These colloidal molecules are in many ways similar to the results in a previous study using single indented lock-particles.27 In Section S5 in the ESI,† Fig. S2 (ESI†), we present the corresponding configurations for keys in an excess of locks and see highly specific interactions yet less coordinated satellites compared to those in Fig. 2. | ||
| Fig. 2 {(a),(b),(c),(d)} Typical configuration of L{2,3,4,6} particles in an excess of key-particles using RK = {1.6,1.4,1.0,0.8}RL, c = {2.0,1.8,1.4,1.2}RL, and σ = 1.0σ0. The colored squares in the upper left corner of the figures index the same setup as the system indexed by the corresponding colored squares in Fig. 3. | ||
The specificity of the bonds is quantified in Fig. 3 where we present the average number of specifically bound keys per cavity of the locks. Here, black areas indicate high specificity and light grey index no specificity. The white represent geometries that are not sampled; the upper right white areas give locks where the cavities are shifted completely out of the main particle making the locks spherical, and the lower left areas give mutually overlapping cavities which are not covered by the used model. For the case of an excess of keys (Fig. 3a), we note a marked difference between surface charge densities (indexed at upper axis), giving no or very low specific interactions, at 0.5σ0, and the others which show high and many times exclusively specific interactions. The exception is the upper most right diagonal region using 1.0σ0 which are shallow cavities, making the lock-particle almost spherical. Here, the available volume to enter a cavity is small, as is the surface to which the key can interact specifically. The corresponding results for keys in an excess of locks are presented in Fig. 3b. Here, we see similar trends as previously described but the specificity decreases using smaller keys in combination with lower cavity offset values c (upper left regions), compared to larger keys with higher cavity offset values (lower right regions).
 | ||
| Fig. 3 (a) Average number of specifically bound key particles per lock particle cavity in an excess of key particles. The colored squares index the same setup as the system indexed by the corresponding colored squares in Fig. 2. (b) Average number of specifically bound lock particles per key particle in an excess of the former. Note the different scales on the figure bars. The particles shown on the side of (a) and (b) are conceptual as to give a notion of how the clusters can look like. | ||
3.2 Number ratio dependence
Now we explore systems with optimal number ratios between locks and keys for the production of various structures or lattices. As shown in Fig. 4, the assembly of an equal number of L2 locks and keys leads to the formation of chains or chain-like structures, and also we notice a tendency to assemble in 3D networks. Similar structures are found using this number ratio and various lock/key geometries.The systems with most specific interactions using different geometric parameters and number ratios are presented in Fig. 5. These aggregates are all bound largely by specific bonds. However, it is clear that the specificity is substantially reduced compared to when using an excess of either locks or keys. This is readily seen in Fig. 6 where we have quantified the specificity. There are many similarities to the analysis of the previous paragraph yet the only systems that display the complete specificity (i.e. black color) are type L2 particles with a number ratio NK/NL of 1/1. Moreover, in Fig. 7a, we present the average number of specifically bound particles in clusters. In several cases, the intermediate surface charge density provides the highest specific assembly. Even so, we see no large aggregates that are bound together by specific interactions, instead they merely include a few percentages of the total particles in the system. Fig. 7b shows similar results but for clusters using any bond, specific or otherwise. As the surface charge density increases, so does the size of the clusters, which together with Fig. 7a indicates large mainly unspecifically bound structures. Finally, in Table 1, we provide the geometric parameters leading to the most specific assemblies. Here, we observe that the difference between c and RK is constant 0.4RL. That is, in order to have an effective cavity in terms of specific interactions, the cavity has to have a fairly specific depth. This value is the result of the effects of electrostatics and excluded volume interactions and may thus differ for other attractive/repulsive potentials. Another important observed property of the specificity is the inverse relationship between the number of cavities and the size of the key.
 | ||
| Fig. 5 {(a)–(d)} Typical configuration of L{2,3,4,6} particles in an optimal number ratio to construct lattices using RK = {1.6,1.4,1.0,0.8}RL, c = {2.0,1.8,1.4,1.2}RL, and σ = 1.0σ0. The colored squares in the upper left corner of the figures index the same setup as the system indexed by the corresponding colored squares in Fig. 6, 7a and b. | ||
 | ||
| Fig. 6 Average number of specifically bound key particles per lock particle cavity using the optimal number ratio of lattices. The colored squares index the same setup as the system indexed by the corresponding colored squares in Fig. 5. | ||
 | ||
| Fig. 7 (a) Cluster-size of particles that are bound only by specific interactions. (b) Cluster-size of particles that are specifically and unspecifically bound. The colored squares index the same setup as the system indexed by the corresponding colored squares in Fig. 5. | ||
| R K/RL | c/RL | X |
|---|---|---|
| 1.6 | 2.0 | 2 |
| 1.4 | 1.8 | 3 |
| 1.0 | 1.4 | 4 |
| 0.8 | 1.2 | 6 |
4. Discussion
In the previous section, we have seen that electrostatic interactions between multi-indented locks and spherical keys can induce highly specific bonds. Moreover, the interactions can produce highly coordinated specifically bound multivalent clusters. Similar clusters have been observed in experiments using hollow multi-indented lock-particles.12 At low surface charge densities, we observe no bonds; at intermediate charge densities, we see high specificity; and at the highest surface charge density, we have similar or slightly lower bonding. This agrees with the results in a previous study however there the strength of the electrostatic interactions was tuned instead using the ionic strength.27 In spite of the highly specific bonding, we have not found a single example of higher-order closely packed structures such as lattices. The only type of ordered structures we have found is low-density gel-like networks. These results question the applicability of multi-indented particles for the spontaneously assembly into higher-order structures at low volume-fractions. For high volume fractions, crystallization can be forced32 yet here we are interested in the low-volume limit.There are two main ways of using locks to construct lattices: the first is to use them as bonds (i.e. type L2) and the second as nodes (i.e. types L3, L4, etc.). L2 particles show high specificity to keys yet the coordination in-between the bound satellites is low. This leads to a seemingly random binding orientation and we find bifurcated networks or chains with no tendency for either close-packing nor short-ranged order. These networks inherent a certain mobility, such as the capability to bend, and is therefore entropically less restricted then rigid rod-like clusters which might be preferred from an electrostatic point-of-view. Similar chains have been observed experimentally using multi-indented “golf-ball” particles interacting with spherical particles.33 Tuning the number ratio between locks and keys might slightly affect the packing density, yet we have not observed any providing defined lattices. Clusters or “block-molecules” constructed as (single indented) lock particles confined to the surface of a centered key has in (2D and quasi-3D) simulations demonstrated an ability to reconfigure into a wide array of crystalline structures.17 The self-assembly of these block-molecules was explained by the depletion interaction but similar clusters can also be induced by the electrostatic interaction.27 A key aspect of successfully constructing the complex structures was the ability for the lock satellites to remain bound while still being able to rotate around the centered key,17 a feature which the clusters in Fig. S2 (ESI†) does display. However, a salient difference to our system is their restriction of the particles to 2D or quasi-3D which drastically alter the entropic contributions to the free energy. Based on this comparison, we conjecture that the dimensionality of our system, and implicitly therefore the entropic cost, is responsible for the lack of long-ranged ordered structures.
The second approach is to use locks with more than two indentations as nodes which are linked by key bonds. Here, we also find it possible to induce highly specific interactions between locks and keys by tuning the geometry and surface charge density. Nonetheless, even though we find high coordination between the satellites, there is no short- or long-range order beyond this. Instead of forming a dense crystal, the particles form thick chain-like structures. As the indentations of the locks are pointing in different directions, the chains are not straight but they zig-zag while stretching out, see for example Fig. 5c. This also resembles the earlier mentioned “golf-ball” chains, yet even to a higher degree than by using L2 particles.33 Even the most specifically bound system still gives about one vacant cavity per lock, and this seems enough to prevent, the otherwise theoretical optimal sharing of keys, a closely packed lattice from emerging.
In Fig. 1b, we presented the free energy cost to bind a single key to a lock. Yet if a second key would bind to the lock the cost would be even higher, as the repulsion from the first bound key would decrease the available excess volume. For L3, L4, and L6 particles, the cost would be higher still if a third key would bind, and so forth for more bound keys. Therefore, the cost of building clusters of keys centered around a single lock is entropically more costly for locks with more cavities than lock with fewer ones, see Section S6 (ESI†). This is also true if electrostatics are introduced as the satellites repel one another.
As we have seen earlier, the translational entropic cost for a key to bind to a lock can be overcome by the attractive electrostatic energetic contribution it entails. However, for every mutually shared key between clusters, their translations and/or rotations are severely hindered. For locks with several indentations (and therefore opportunities for more bonds), this cost is higher than for locks with fewer indentations as the final lattice structure would be less flexible for a structure with more average bonds per particle. This brings about a large entropic cost with only the electrostatic energetic compensation of a single specific bond. It would be possible to increase the interaction strength of specific bonds enough to overcome the entropic expense due to spatial restrictions, for example by increasing the surface charge density. Yet this would also result in static bonds with little room for flexibility, the latter of which is a highly needed feature in self-assembly.17 This line of argument is also supported by our results as a higher surface charge density often gives clusters with a low degree of specificity in contrast to results using an intermediate surface charge density. One could argue that the electrostatic repulsion between satellites is the explanation to the lack of ordered structures. Still, for an excess of key particles, we observed all but perfect specific binding which suggests that even though the bonded satellite key particles do come close to one another, their mutual repulsion does not exceed their attractive interaction to the centered lock. As such we infer that the lack of higher order structures is not due to the electrostatic repulsion, but rather arise from large entropic costs inherent to the formation of highly ordered lattices.
5. Conclusions
In this work, we have investigated the assembly of keys with multi-indented lock-particles in dilute systems by means of Monte Carlo simulations. For this purpose, we first extended a previous model of hard-overlap and electrostatic potentials between single indented locks to also include multiple indentations. We found that using a reasonable surface charge density, particles (lock or key) surrounded by an excess or the complementary and oppositely polarized type particles (key or lock) interact through the cavity of the locks to form colloidal clusters. The satellites of these clusters are highly coordinated when the central particle is a lock, and less coordinated when the central particle is a key. While using number ratios between locks and keys that correspond to various perfect lattices we found no such structures but instead gel-like networks or chains. The assembly of higher order structures requires some flexibility of the bonds while forming, which effectively gives an upper bound to the attractive interaction strength. Even so, a high attractive force is needed to overcome the entropic costs that come with the growth of an initially highly specifically bound cluster to a larger lattice-like aggregate. Our results show that the requirement of a strong attractive force to compensate for entropic costs, with the requirement of a weak attractive force that entails flexibility of bonds, is non-compatible. Therefore, in essence, we attribute the lack of higher-order structure to the large entropic costs in the process of assembling complex crystals. The lack of flexibility between the particles within the gel-like assembly for the higher number of indentation however makes these systems appealing to investigate, specifically the related linear and non-linear mechanical properties of such colloidal gels.Our results send us back to former observations made on patchy particles,10 where the precise arrangement of patches combined with patch “recognition” is necessary to direct the particle positioning into complex assemblies. The simple lock and key approach does not allow such a thing with respect to its additional rotational degree of freedom similar to the single covalent bond between atoms. A possibility to implement the equivalence of a double bond would be to design for instance anisotropic (square-like, ellipsoidal) indentation34 in combination with the complementary key-particles. At the synthetic level, it would however be highly challenging as it requires a precise engineering of the lock-particle indentation position and orientation. A less costly but not yet tested possibility would be to at least reduce one of the degree of freedom by polarizing the particles. This could be achieved by using for instance ferromagnetic multivalent lock-particles with a well-defined magnetic moment orientation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank LUNARC in Lund for computational resources and acknowledge financial support from the Knut and Alice Wallenberg Foundation (project grant KAW 2014.0052).Notes and references
- E. Fischer, in Untersuchungen Über Kohlenhydrate und Fermente (1884–1908), Springer Berlin Heidelberg, 1909, pp. 362–376 Search PubMed.
- L. Pauling, Chem. Eng. News, 1946, 24, 1375–1377 CrossRef CAS.
- D. E. Koshland, Angew. Chem., Int. Ed. Engl., 1995, 33, 2375–2378 CrossRef.
- J.-M. Lehn, Chem. Soc. Rev., 2007, 36, 151–160 RSC.
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562 CrossRef PubMed.
- F. Huo, A. Lytton-Jean and C. Mirkin, Adv. Mater., 2006, 18, 2304–2306 CrossRef CAS.
- Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–55 CrossRef CAS PubMed.
- W. Li, H. Palis, R. Mérindol, J. Majimel, S. Ravaine and E. Duguet, Chem. Soc. Rev., 2020, 49, 1955–1976 RSC.
- A. Walther and A. H. E. Müller, Chem. Rev., 2013, 113, 5194–5261 CrossRef CAS PubMed.
- Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407–1413 CrossRef CAS PubMed.
- M. Kamp, B. de Nijs, M. N. van der Linden, I. de Feijter, M. J. Lefferts, A. Aloi, J. Griffiths, J. J. Baumberg, I. K. Voets and A. van Blaaderen, Langmuir, 2020, 36, 2403–2418 CrossRef CAS PubMed.
- Y. Wang, Y. Wang, X. Zheng, G.-R. Yi, S. Sacanna, D. J. Pine and M. Weck, J. Am. Chem. Soc., 2014, 136, 6866–6869 CrossRef CAS PubMed.
- P.-E. Rouet, C. Chomette, E. Duguet and S. Ravaine, Angew. Chem., Int. Ed., 2018, 57, 15754–15757 CrossRef CAS PubMed.
- S. Sacanna, W. T. M. Irvine, P. M. Chaikin and D. J. Pine, Nature, 2010, 464, 575–578 CrossRef CAS PubMed.
- G. Odriozola, F. Jiménez-Ángeles and M. Lozada-Cassou, J. Phys. Chem., 2008, 129, 111101 CrossRef CAS PubMed.
- D. J. Ashton, R. L. Jack and N. B. Wilding, Soft Matter, 2013, 9, 9661 RSC.
- D. Ortiz, K. L. Kohlstedt, T. D. Nguyen and S. C. Glotzer, Soft Matter, 2014, 10, 3541 RSC.
- D. J. Ashton, R. L. Jack and N. B. Wilding, Phys. Rev. Lett., 2015, 114, 237801 CrossRef PubMed.
- A. M. Mihut, B. Stenqvist, M. Lund, P. Schurtenberger and J. J. Crassous, Sci. Adv., 2017, 3, e1700321 CrossRef PubMed.
- J. Cautela, B. Stenqvist, K. Schillén, D. Belić, L. K. MÅnsson, F. Hagemans, M. Seuss, A. Fery, J. J. Crassous and L. Galantini, ACS Nano, 2020, 14, 15748–15756 CrossRef CAS PubMed.
- I. Chakraborty, V. Meester, C. van der Wel and D. J. Kraft, Nanoscale, 2017, 9, 7814–7821 RSC.
- F. Smallenburg and F. Sciortino, Nat. Phys., 2013, 9, 554–558 Search PubMed.
- Y. Ke, L. L. Ong, W. M. Shih and P. Yin, Science, 2012, 338, 1177–1183 CrossRef CAS PubMed.
- W. M. Jacobs, A. Reinhardt and D. Frenkel, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 6313–6318 CrossRef CAS PubMed.
- J. Borovička, S. D. Stoyanov and V. N. Paunov, Nanoscale, 2013, 5, 8560 RSC.
- G. Odriozola and M. Lozada-Cassou, Phys. Rev. Lett., 2013, 110, 105701 CrossRef PubMed.
- B. Stenqvist, M. Trulsson and J. J. Crassous, Soft Matter, 2019, 15, 5234–5242 RSC.
- B. Stenqvist, A. Thuresson, A. Kurut, R. Vácha and M. Lund, Mol. Simul., 2013, 39, 1233–1239 CrossRef CAS.
- D. Wu, D. Chandler and B. Smit, J. Phys. Chem., 1992, 96, 4077–4083 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding molecular simulation: from algorithms to applications., Academic, 2002 Search PubMed.
- J. Liu and E. Luijten, Phys. Rev. Lett., 2004, 92, 035504 CrossRef PubMed.
- M. He, J. P. Gales, É. Ducrot, Z. Gong, G.-R. Yi, S. Sacanna and D. J. Pine, Nature, 2020, 585, 524–529 CrossRef CAS PubMed.
- K. Watanabe, Y. Tajima, T. Shimura, H. Ishii and D. Nagao, J. Colloid Interface Sci., 2019, 534, 81–87 CrossRef CAS PubMed.
- S. Sacanna, M. Korpics, K. Rodriguez, L. Colón-Meléndez, S.-H. Kim, D. J. Pine and G.-R. Yi, Nat. Commun., 2013, 4, 1688 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00182a |
| This journal is © The Royal Society of Chemistry 2022 |

