Open Access Article
Open Access ArticleSlip-stick transitions of soft permeable particles near a repulsive wall
Monica E. A.
Zakhari
 *ab and
Roger T.
Bonnecaze
*ab and
Roger T.
Bonnecaze
 b
b
aDepartment of Mechanical Engineering, Eindhoven University of Technology, PO Box 513, Eindhoven 5600 MB, The Netherlands. E-mail: m.e.a.zakhari@tue.nl
bMcKetta Department of Chemical Engineering, The University of Texas at Austin, Austin, Texas 78712, USA
First published on 9th May 2022
Abstract
The behavior of permeable, elastic particles sliding along a repulsive wall is examined computationally. It is found that particles will stick or slip depending on the interplay of elastohydrodynamic and repulsive forces, and the flow in the porous particle. Particles slip when either the elastohydrodynamic lift or repulsive forces are large and create a supporting lubricating film of fluid. However, for lower values of elastohydrodynamic lift or repulsive forces, the flow within the porous particle reduces the pressure in the thin film, resulting in the particles making contact and sticking to the surface. The criteria for the slip-stick transition is presented, which can be used to design systems to promote or suppress slip for such suspensions.
1 Introduction
Complex fluids are composed of two or more coexisting phases, e.g. solid and fluid in suspensions. Their properties are often viscoelastic, making them useful for many industrial and technological applications such as functional coatings,1–3 pharmaceuticals,4,5 and foods.6–8 The control and design of the desired macroscopic properties are achieved by tailoring the properties of the constituents, often particles of colloidal scale. Exploiting the full potential of complex fluids requires accurate characterization of the constituent-dependent mechanical behavior in order to contrive processing conditions for industrial applications, e.g. 3D printing.9 In both material characterization and processing, deforming colloidal suspensions near rigid surfaces is necessary.10–13 Wall effects are inevitable – whether the material slips or sticks to the bounding rigid surfaces – will decide the fate of the resulting product.Slip is a result of the lack of adhesion between the flowing solutions and the bounding rigid surfaces. When a pure fluid, i.e. no suspended particles, is sheared between solid surfaces such as in a rheometer, the fluid layer nearest to the rigid surface sticks to it and both fluid and surface move at the same velocity. In other words, the relative velocity between the fluid and the rigid surface is vanishing and the flow is considered homogeneous. The viscous fluid properties and the flow characteristics can result in loss of adhesion, i.e. a relative velocity between the fluid and the rigid surfaces. This true slip results in flow instabilities that cause product defects in extruded polymer melts such as sharkskin defects14 and melt fracture.15–17 Surface chemical and physical properties also affect wall-slip behavior. Rough surfaces have been found to suppress slip by disrupting the thin lubricating fluid layer, and hence promoting stick.18 Surface asperities can be realized by sandblasting,10,19,20 machining,18,21 or using serrated tools.22 The success of surface roughness in suppressing slip requires the surface features to be larger than the largest dominating heterogeneity, as discussed in detail in ref. 23 and 24. Surfaces can also be chemically modified to interact with the fluid to favor slip or stick.25–28 Attractive interactions between the flowing solution and the rigid surface result in stick, while repulsive interactions promote slip instead.12,26,27 This begs the question: When is slip desirable over stick and vice versa?
Slip enhances transport efficiency. Several biological systems and natural processes benefit from slip; for example transport of food throughout the digestive tract.29 Several organs are covered with a mucus layer – a biological lubricant – which promotes slip and traps irritants such as dirt and foreign particles from organs such as the eye.30 Motion of red blood cells through microvascular networks is essential for the delivery of oxygen and nutrients. If slip is inhibited in blood vessels, thrombosis can occur.31 In this case, red blood cells stick and cluster at vessel walls and can eventually lead to blood clots which can be fatal if not caught on time. The concept of slip-enhanced transport is exploited in several industrial applications such as microfluidic devices,32–34 sewage treatment,35 oil extraction,36 and food processing.37,38 On the other hand, slip hampers accurate material characterization. The presence of a layer of fluid that is depleted from suspended particles as a result of slip, leads to non-uniform overall properties. Macroscopic flow measurements will inherently detect these heterogeneities and encompass errors, in particular in predictions of the yield stress.11,12,39 These resulting flow gradients in the vicinity of the rigid surface also have considerable impact on processing conditions of these materials.
The intricate coupling between particle properties, fluid and its flow characteristics, and surface properties together with the growing need for control of stick-slip transitions in advanced processing techniques have motivated recent efforts in modelling wall effects in concentrated particle suspensions. These models aim at capturing the essential physics taking into account the particle properties. In suspensions, the properties of the particles influence the properties of the entire suspension near bounding surfaces. Particles that are in close proximity to the rigid surfaces experience higher resistance than particles away from the surface.40 If the system is dilute so that the particles are free to move, particles will steer clear from the rigid surface as a result of the viscous forces from the compressed fluid in the gap between the particle and surface.41,42 In a dilute system of elastic particles, rebound between particle and solid surface will also be accompanied by deformation of the particle surface.43 If the particle density is sufficiently high, the relative motion between particles is inhibited. In this case, hydrodynamic pressure between the elastic particles and the rigid surface leads to asymmetric deformation of the particle surface in order to maintain flow in the gap.10–12 Permeable particle systems, as a model of microgel and star polymer systems, are able to offer an alternative route for the gap fluid to escape, hence reducing the pressure in the gap on the one hand, and reducing the amount of fluid in the gap on the other hand. Consequently, dense permeable particle systems tend to stick rather than slip when sheared against a rigid surface.44 The sticky behavior of permeable particle suspensions to rigid surfaces hints at a permeability-dependent attractive particle–wall interaction, which we investigate in detail in this paper.
Short-range interactions of dense suspensions of impermeable elastic particles with rigid walls have been investigated in detail in Seth et al.26 Bonnecaze and co-workers developed an elastohydrodynamic (EHD) model suitable for concentrated elastic particle suspensions.10–12 The model was later extended to account for short-range interactions with rigid walls.26,27 This extension comprises an additional disjoining pressure that acts to deform the particle surface according to its interaction with the wall. For instance, if the particle–wall interaction is dominated by strong repulsion, then the particle deform in manner that maximizes the distance from the wall and hence minimizing the repulsive force felt from the wall. This deformation, in turn, reduces the hydrodynamic pressure in the gap, since particle deformation is coupled with the latter. Their work is motivated by the fact that typical gap heights (2–10 nm10,11) are in the range where particle–wall interactions become significant.26
Our recent work that extends the EHD-model to permeable, elastic particles, has shown that these particles are remarkably sticky, when sliding near a rigid wall.44 In other words, the gap heights exhibited by permeable particles can be notably smaller than those observed in impermeable particle systems sliding near a rigid wall at the same speed.44 The aim of this paper is to investigate the competition between short-range repulsive interactions with the wall and permeability-induced attractions, and identify the role of flow in this process.
To achieve this goal, the poro-elastohydrodynamics model is generalized to include a disjoining pressure term to account for short-range particle–wall interactions in Section 2. In Section 3, we present the numerical procedure to solving the governing equations, followed by our numerical results and parametric study in Section 4. Finally, we end with a discussion of the results and concluding remarks in Section 5.
2 Theoretical framework
A poro-elastohydrodynamic theory for modeling slip of dense suspensions of permeable particles near a wall is summarized in this section and extended to include a disjoining pressure that accounts for particle–wall interaction forces.2.1 Poro-elastohydrodynamic theory with particle–wall interaction
Consider a suspension of soft permeable particles, each of permeability, κ. The suspensions of interest here are those packed at volume fractions, ϕ, well beyond random close packing (RCP) fraction of hard-sphere systems, i.e. ϕ ≫ 0.64. In this high density regime, soft particles are compressed against each other and form facets at contact as shown in Fig. 1a, hence particle motion and rotation relative to each other can be neglected. The suspension is compressed against a rigid smooth wall, with which the particles interact through a short-range repulsion. Particle–particle interactions are not accounted for explicitly in this paper; here we focus on particle–wall interaction. However, the effect of surrounding particles is embodied in the initial compression h0, where a particle at wall contact forms a circular facet at rest of radius, r0, due to Hertzian contact. By virtue of shear or pressure-driven flow, a relative velocity U between of the particle and the wall develops as shown in Fig. 1b. In this case, a lubricating fluid layer of height δ develops between the particle and the wall. The hydrodynamic pressure in the gap p, measured relative to far-field fluid pressure away from the wall, is not symmetric with respect to the particle center. This pressure in the gap deforms the particle surface facing the wall asymmetrically and the facet is not circular anymore.10,11,26,44The model in its original form10,11 couples Reynolds lubrication equation45 for the dependence of hydrodynamic pressure p on the gap height δ, with the general integral equation for contact mechanics.46,47 We extended the model for the case of permeable particles by taking into account the pressure-gradient driven flow through the internal pores of the particle via Darcy's law as presented in ref. 44. Here, the poro-elastohydrodynamic theory presented in ref. 44 is modified to account for short-range wall interactions in a similar fashion to what was first introduced in ref. 26. The latter is done by means of an additional disjoining pressure, pd, that acts to deform the surface of the particle.12 In the steady-state limit, the coupled set of governing equations is expressed as
| ∇·(δ3∇p) = −6ηsU∂xδ + 12ηsυ(x, y), | (1a) |
 | (1b) |
 | (1c) |
In the steady-state limit, the vertical fluid velocity in the gap υ, according to lubrication theory,45 should vanish since the pressure does not vary in the z-direction. However, fluid can flow through the permeable-particle pores and consequently pressure variations are to be expected inside permeable particles. In this case, to calculate υ at the particle surface, only the pressure-gradient at the particle surface ∂Ω is required, following Darcy's law:48,49
 | (2) |
| ∇2p = 0 for (x, y, z) ∈ Ω. | (3) |
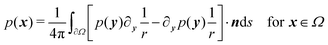 | (4) |
 and r = ‖x − y‖.52 In the derivation of eqn (4), the particle is approximated by a semi-infinite domain and Green's second identity is used. The form of the solution presented in eqn (4) is suitable for Boundary Element Method (BEM)50–52 as described in detail in ref. 44.
and r = ‖x − y‖.52 In the derivation of eqn (4), the particle is approximated by a semi-infinite domain and Green's second identity is used. The form of the solution presented in eqn (4) is suitable for Boundary Element Method (BEM)50–52 as described in detail in ref. 44.
It is convenient to express the governing eqn (1a)–(1c) in a non-dimensional form. Length scales parallel to the wall and derivatives thereof are rescaled by the radius of the flattened surface parallel to the wall at rest, i.e. the contact radius 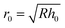 47 (see Fig. 1);
47 (see Fig. 1);
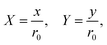 | (5a) |
 | (5b) |
 | (5c) |
 | (5d) |
 | (5e) |
| ∇·(H3∇P) = −∂xH + V, | (6a) |
 | (6b) |
 | (6c) |
Beyond the thin lubrication layer, the solvent flow around the particle follows the solution for a rigid particle moving parallel to a smooth wall,41 and is enforced by setting this solution as the pressure at the boundaries of the computational domain as
 | (6d) |
 | (7) |
Using the scaling in eqn (5) to solve for the vertical velocity, the dimensionless form of the boundary integral eqn (4) is given as
 | (8a) |
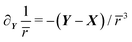 ,
, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = ‖X − Y‖, and dS = ds/r02. The corresponding Darcy's equation for the vertical fluid velocity becomes
= ‖X − Y‖, and dS = ds/r02. The corresponding Darcy's equation for the vertical fluid velocity becomes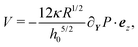 | (8b) |
| P|X∈∂Ω = P(X, Y). | (8c) |
2.2 Origin of short-range repulsive particle–wall interactions
Commonly-realized permeable particles are microgels and star polymers.53,54 Microgels are cross-linked networks of polymer, where the cross-link density dictates the elastic properties and permeability of the microgel.53,55,56 In star polymers, the number of arms attached to a central core and their degree of polymerization govern the particle's elastic properties and its permeability.53,57–59 In both cases, when microgels or star polymers are in close proximity to the wall, short-range interactions with the wall can become significant, the origin of which is described in detail in ref. 26 and summarized briefly in this section. Since the porous nature of the particles makes them sticky44 and can be viewed as attraction to the wall, this paper focuses on the effect of particle–wall repulsion that counteracts the effect of permeability. One or more type of repulsive interactions can be present in a system, henceforth, regardless of the origin of repulsion, we express the repulsive pressure as | (9) |
Particle–wall repulsion can originate from (i) steric hindrance, (ii) hydrophilic polar interactions, and (iii) electrostatic interactions. Steric hindrance emerges from the loose polymer ends at the particle surface, when the fluid gap between the particle and wall is compressed. According to ref. 26 and 60, for microgels with uniform distribution of dangling polymer chains of radius a and surface density d−2, cr = 100kbT/d3 and lr = a/π, where kbT is the thermal energy. Free end chains within the fluid gap lead to particle–wall polar interactions, the net contribution of which can also be cast in the exponential form in eqn (9), with cr = 2πaΔGAB/d2 and lr ≈ lw, where ΔGAB is the free-energy of interaction per unit area, and lw is the characteristic decay length of hydrophobic interactions in water.61 Finally, when the particle or the wall are charged due to for example the particle being polyelectrolytes such as microgels, electrostatic repulsive develops due to the presences of these fixed charges and their counterions in the fluid gap between the particle and the wall. In this case, the repulsion length is the Debye length, and the repulsion strength cr depends on the surface charge density.26 It is to be noted that this type of interaction can be attractive as well with a negative sign for the disjoining pressure in eqn (9). For microgel particles, some estimates of the repulsion parameters cr and lr can be found in Table 1 for the different origins of short-range particle–wall repulsion.
Finally, eqn (9) can be made non-dimensional using the dimensional scaling given in eqn (5). Particularly, lr is scaled with the initial overlap h0, and the pressure is scaled with the characteristic pressure Pc. The non-dimensional repulsive pressure is given as
 | (10) |
2.3 Dimensionless group specification
To model the behavior of suspensions of permeable particles, realistic estimates of the properties of suspension, individual particle, suspending fluid, and wall are required. Similar to our earlier work,44 each simulation is described in terms of the flow parameter λ, and the dimensionless permeability![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) = κ/h02, and for the present work, the strength and length of repulsion {Cr, Lr}, respectively. A summary of system properties and simulation parameters is provided in Table 2.
= κ/h02, and for the present work, the strength and length of repulsion {Cr, Lr}, respectively. A summary of system properties and simulation parameters is provided in Table 2.
| Parameter | Symbol | Physical value |
|---|---|---|
| Solvent viscosity | η s | 1 mPa s |
| Particle modulus | G p | 105 Pa |
| Particle radius | R | 220 nm |
| Initial overlap | h 0 | 22 nm |
| Flow parameter | λ = 6ηsUR/(Gph02) | [0.0001–2] |
| Dimensionless permeability |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) = κ/h02 = κ/h02 |
{0, 0.207, 1.03, 2.07} × 10−3 |
| Repulsion strength | C r = crR1/2/(Gph01/2) | [1–10] |
| Repulsion length | L r = lr/h0 | 0.1 |
A representative dense suspension of microgel particles in water is considered in the present study. Akin to our earlier work,44 a suspension of volume fraction of approximately 0.88 is modeled in the present study. The suspended particles are microgels of radius R = 220 nm. At rest, the density of the system results in an initial compression, h0, of the particles near the wall due to steric effects. This initial compression is calculated according to ref. 63 as
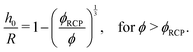 | (11) |
Finally, the repulsive interaction between the particle and wall is described by its strength and its length. Both parameters depend on the origin of repulsion. The repulsion length is usually small compared to h0, and ranges 0.02h0–0.2h0 for steric hindrance of microgels and hydrophilic forces of microgel particles near a silicon surface.26 The length is fixed in our simulations to lr = 0.1h0. The repulsion strength is however varied to cover weak interactions Cr ∼ 1, e.g. electrostatic interaction, and strong interactions Cr ∼ 10, e.g. steric hindrance.
3 Numerical methods and procedure
The coupled system of eqn (6) and (8) are solved numerically for pressure P, gap height H, particle deformation UZ(X, Y)|Z=0, and vertical fluid velocity at the particle surface V. The computational domain is a plane (X, Y) parallel to the wall. The domain is chosen to be large compared to the contact radius r0, so doing ensures that the entire deformed surface of the particle is within the domain and far from the boundaries. At the domain boundaries, particle deformation vanishes UZ(X, Y)|Z=0 = 0 and consequently H = −1 + (X2 + Y2)/2, and the pressure follows boundary condition eqn (6d). The computational domain is discretized into square elements, by dividing the domain uniformly into NX-by-NY elements in each direction.With an initial guess of the pressure field over the entire domain, eqn (6c) is solved for UZ(X, Y)|Z=0, using numerical trapezoidal integration scheme. The solution is used to update the gap height H from eqn (6b). The gap height and the initial guess for the pressure field are used to solve the boundary integral equation (eqn (8)) using Boundary Element Methods (BEM)50,51 for V. This procedure is described in detail in our earlier paper,44 see Section 3.1 therein. The computed V and H are then used to update the pressure field by solving eqn (6a) using finite difference. Solution is said to be converged when the norm of the difference in pressure field (pre- and post-updated) is less than 10−7. Alternatively, convergence is reached when the norm of the drag and lift forces between iterations is constant up to the fifth decimal point. The drag and lift forces are calculated from the particle stresses integrated over the surface as
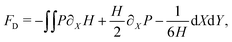 | (12a) |
 | (12b) |
Finally, under-relaxation of UZ(X, Y)|Z=0 is used to ensure smooth convergence and to avoid large particle displacements per iteration step. The calculation of the vertical velocity is the most computationally expensive step in our numerical procedure. In strong flows, this calculation can be performed less often since the particle gap tend to be larger than in the case of weak flows.44 The numerical procedure to compute the vertical velocity is performed every 2 steps in weak to intermediate flows to reduce computational cost, without loss of accuracy.
4 Results
4.1 Short-range wall repulsion sets the slip length of impermeable particles at low flow speeds
Before examining the behavior of soft permeable particles near a repulsive wall, the wall-slip behavior for a soft impermeable particle is summarized. The reader is referred to ref. 26 for a detailed description of the behavior of soft impermeable particles near a repulsive wall.Fig. 2 shows the behavior of a soft impermeable particle sliding against a neutral wall and a repulsive wall, i.e. Cr = 0 and Cr ≠ 0, respectively. When repulsive interactions with the wall are present, the particle surface is nearly flat in weak flows. The particle slips at a distance larger than in the case of a neutral wall, as can be seen in Fig. 2a. The corresponding pressure profiles below the center-line of the particle in Fig. 2b show that the pressure at the lagging side is negative which draws fluid into the gap near both neutral and repulsive walls. At the leading side, the pressure is positive which expels fluid from the gap. However, in the absence of repulsion, the dominant positive pressure at the leading side creates a net hydrodynamic lift force acting on the particle, pushing the particle away from the wall and sustaining the lubricating layer. In the presence of repulsion, the pressure profile beneath the particle is nearly symmetric, hence the net hydrodynamic lift force is negligible. In this case the particle is supported away from the wall almost solely by the repulsive pressure.
The extent by which repulsion influences the lubricating layer depends on the sliding speed, characterized by λ. The gap height at different sliding speeds can be characterized effectively by the closest point to the wall Hmin. Fig. 2c shows Hmin at different λ for a soft impermeable particle sliding against a neutral and a repulsive wall. At large λ, elastohydrodynamics dominates wall-slip; strong flows (i.e. high λ) lead to large net hydrodynamic lift force on the particle and a large gap. Far away from the wall, repulsion is negligible as Pr ∼ exp(−H/Lr). In this regime, Hmin ∼ λ0.5.26,44 At weaker flows (i.e. low λ), the particle gets closer to the wall and, at a distance dictated by the repulsion parameters, {Cr, Lr},26 wall-slip becomes dominated by repulsion. In this regime, Hmin becomes independent of λ and a plateau is reached. The gap height in this case is set by the repulsion strength as can be seen in Fig. 2c; the plateau value increases with increasing the strength of repulsion, Cr. It is to be noted that the repulsion length Lr also affects the slip length in a similar manner as the repulsion strength, Cr. To this end, the former is kept constant in this paper.
The drag force, FD, experienced by the particle as a result of the hydrodynamic pressure in the gap under different flow conditions and different interactions with the wall, i.e. repulsion strength, are shown in Fig. 2d. The drag force is calculated based on eqn (12a). At strong flows, the particle experiences a drag force that is independent of the repulsion strength. At weaker flows, however, the wall-repulsion leads to a thicker gap compared to a neutral wall (see Fig. 2c) at a given sliding speed. As a result, the particle experiences less pressure and consequently less drag force. The stronger the repulsion, the lower the drag force acting on the particle. To summarize, soft impermeable particles slip near a wall at low sliding speeds even in the absence of repulsive interactions with the wall. The thickness of the lubricating layer is set by the sliding speed in the absence of interactions with the wall. The thickness of the lubricating layer is set by repulsion strength in the presence of repulsive interactions with the wall.
4.2 Permeable particles slip instead of stick in the presence of strong short-range wall repulsion
The effect of permeability of soft particles near a neutral wall on their slip behavior is described in detail in ref. 44. The fundamental difference between the wall-slip behavior of impermeable and permeable particles is the fact that the latter stick upon decreasing the sliding speed instead of slip near a neutral wall. In this section, we examine the wall-slip behavior of permeable particles near a repulsive wall. It is noteworthy, that the sticking point observed near a neutral wall is obtained from fitting the minimum gap height as a function of the sliding speed with a power law with exponent that is independent of the permeability value, Hmin ∼ (λ − λs)0.50. The sticking point depends on the permeability as, λs ∼![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) 0.65. The reader is referred to ref. 44 for more detail.
0.65. The reader is referred to ref. 44 for more detail.
Fig. 3 shows the particle profile, hydrodynamic pressure, and vertical fluid velocity beneath the center-line of the particle in the sliding direction at different sliding speeds, λ. The data outlined in red in Fig. 3 correspond to the behavior at flow speeds lower than the sticking point near a neutral wall, i.e. λ < λs. At these flow speeds, a particle with the same permeability sliding near a neutral wall would stick to it. As the sliding speed decreases, repulsion dominates and the particle profile is nearly flat as shown in Fig. 3a. The slip length at weak flows is set by repulsion. Fig. 3b shows that at strong flows the pressure is asymmetric with a dominant positive pressure at the particle leading edge. As the flow becomes weaker, the pressure profile becomes more symmetric leading to less resultant lift force on the particle, and repulsion dominates.
Fig. 3c shows the vertical velocity profile at a permeable-particle surface when sliding near a repulsive wall and different speeds. For all speeds, the positive vertical velocity appears to be dominant which results in a net flow to the particle pores. However, as flow weakens the vertical flow velocity profile becomes more symmetric, reducing the net flow to the particle pores. The small net flow to the particle pores is not enough to counteract the effect of repulsion as evidenced by the particle surface at these flow speeds staying away from the wall (see Fig. 3a).
Flow through permeable particle pores is essentially the origin of their sticky behavior. Flow through particle pores is directly coupled with the gap height and hydrodynamic pressure as depicted by the lubrication eqn (6a). This flow is also indirectly affected by the repulsive pressure; at gap heights where repulsion cannot be neglected, the particle surface deforms due to repulsive pressure and consequently the gap height varies as a result of this repulsion. Next, this indirect dependence of the flow through the particle pores on the repulsion strength is explained in detail in view of the minimum gap height.
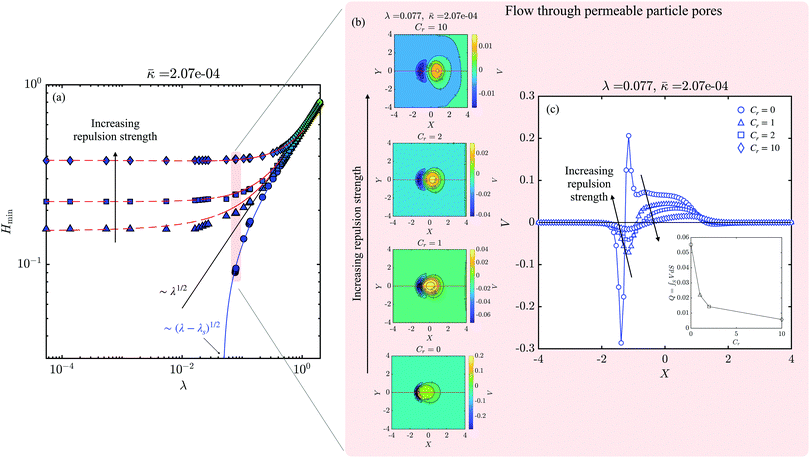
Fig. 4a shows the minimum gap height between a permeable particle near a neutral wall, i.e. Cr = 0, and repulsive walls with different repulsion strengths, i.e. Cr ≠ 0, at different sliding speeds. In the absence of wall repulsion, slip is governed by elastohydrodynamics at high flow speeds and Hmin ∼ λ0.5, as already reported in our earlier work.44 Upon decreasing the flow speed, permeable particles get closer to the wall, and at a critical speed denoted by λs, they stick to the wall in the absence of repulsion. In the remainder of the paper, we will refer to λs as λs|Cr=0 to make explicit the fact that the reference sticking point is relative to the neutral wall case.
In the presence of repulsive interactions with the wall, permeable particles slip independent of repulsion strength at high sliding speeds as shown in Fig. 4a. In this regime, the minimum gap height is also governed by elastohydrodynamics, i.e. Hmin ∼ λ0.5. As flow weakens, permeable particles move away from the repulsive wall compared to their behavior near a neutral wall. In the limit of very weak flows, repulsion dominates and the gap height reaches a plateau value. At intermediate flow speeds, a clear deviation from the previously-described behavior near a neutral wall is observed. The range over which this intermediate regime is observed depends on the repulsion strength and length. It is to be noted that the latter is kept constant for all simulations presented in this paper. In this regime, the minimum gap height achieved by a permeable particle at low non-zero repulsion strength is lower than the minimum gap height of an impermeable particle near a wall of the same repulsion strength (see the corresponding data in red dashed lines in Fig. 4a).
To examine the effect of repulsion on the flow to the particle pores, the vertical flow velocity near the sticking point, λs|Cr=0, is examined for different repulsion strengths, Cr, including Cr = 0. Although the contour plots Fig. 4b are qualitatively similar for all Cr, the magnitude of the vertical flow velocity decreases with increasing the repulsion strength, Cr. The velocity profiles beneath the center-line of the particle (red lines in Fig. 4b) are plotted in Fig. 4c, which confirm that the velocity magnitudes at the lagging and leading edges of the particle, respectively, decrease as repulsion strength increases. In all cases the net flow is to the particle pores as shown in the inset figure in Fig. 4c. At increasing repulsion strength, the gap between the particle and the wall becomes thicker. The thicker the gap is, the lower the hydrodynamic pressure in the gap, which inevitably drives less flow from and to the particle pores as both are driven by hydrodynamic pressure gradients.
The fact that, at intermediate flow strengths, a permeable particle is still able to get close to the wall compared to its impermeable counterpart suggests that, under the right conditions, the ability of permeable particles to get close to the wall can be pronounced enough that the particle would stick instead of slip. We explore this possibility and the underlying conditions in detail in Section 4.3. The close connection between stick/slip behavior and flow to particle pores is rooted in the competition between the ability of the particle to take in and expel the gap fluid, i.e. due to its permeability, and the ability of the wall to keep the particle away from the wall, i.e. due to repulsion. We hypothesize that there is a critical repulsion strength below which permeable particles stick and above which they slip, and that this critical value depends on permeability. We test this hypothesis in the following section, Section 4.3.
4.3 Slip-stick transitions depend on strength of short-range wall repulsion
To test the hypothesis that a critical permeability-dependent repulsion strength exists and moderates the slip-stick transition, we examine the behavior of particles with different permeability values sliding near repulsive walls with varying repulsion strength. Stick and slip behavior is characterized by means of the minimum gap height; a particle slips at finite non-zero minimum gap heights, while it approaches a sticking point when the minimum gap height decreases with decreasing sliding speeds.To identify the critical repulsion strength, denoted hereafter by  , we first revisit the expected behavior of permeable particle near a wall above and below the critical repulsion strength. A particle is expected to slip at
, we first revisit the expected behavior of permeable particle near a wall above and below the critical repulsion strength. A particle is expected to slip at  and to stick at
and to stick at  . One way to identify
. One way to identify  is to perform simulations at varying Cr and λ, until a transition from a stick regime to a slip regime is reached as the repulsion strength is increased. This point is the critical value of repulsion strength,
is to perform simulations at varying Cr and λ, until a transition from a stick regime to a slip regime is reached as the repulsion strength is increased. This point is the critical value of repulsion strength,  . However, this approach is computationally expensive, in particular as numerical solutions become increasingly difficult as the particle gets close to the wall, i.e. close to sticking points. A more efficient approach to tackle this problem is to devise an initial value of the critical repulsion strength, which we denote as
. However, this approach is computationally expensive, in particular as numerical solutions become increasingly difficult as the particle gets close to the wall, i.e. close to sticking points. A more efficient approach to tackle this problem is to devise an initial value of the critical repulsion strength, which we denote as  , then only perform simulations around this initial estimate at varying flow speeds. The procedure to estimate
, then only perform simulations around this initial estimate at varying flow speeds. The procedure to estimate  is based on the idea that if repulsion is strong enough, its effect is to keep the particle away from the wall, i.e. the particle slips, otherwise the particle sticks due to its permeability. Having this in mind, one can conclude that the closest point to the wall prior to sticking has to occur in the absence of repulsion Cr = 0, which is denoted as Hsr. The value of Hsr depends on the particle permeability as can be found in our earlier work.44
is based on the idea that if repulsion is strong enough, its effect is to keep the particle away from the wall, i.e. the particle slips, otherwise the particle sticks due to its permeability. Having this in mind, one can conclude that the closest point to the wall prior to sticking has to occur in the absence of repulsion Cr = 0, which is denoted as Hsr. The value of Hsr depends on the particle permeability as can be found in our earlier work.44
The goal is to design a wall that would repel an impermeable particle a distance Hsr from the wall. In other words, we seek the repulsion strength that leads to a plateau value equivalent to Hsr. To predict the variation of repulsion strength Cr with plateau values of the minimum gap height Hr = Hmin|λ→0, we use the plateau values in Fig. 2c.† This function is found as an exponential function of type
Cr = a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(bHr) + c, exp(bHr) + c, | (13) |
Using the closest point to the wall prior to sticking Hsr from our earlier work44 in eqn (13), an initial estimate of the critical repulsion strength,  , can be calculated. Those values are given in Table 3. These estimated values of
, can be calculated. Those values are given in Table 3. These estimated values of 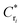 can be considered a lower limit estimate since it is based on the closest point of approach to the wall as described above. Simulations are hence performed at Cr = {0.5, 2, 3} for the permeability values given in the first column of Table 3, respectively.
can be considered a lower limit estimate since it is based on the closest point of approach to the wall as described above. Simulations are hence performed at Cr = {0.5, 2, 3} for the permeability values given in the first column of Table 3, respectively.
| Permeability | Minimum gap height prior to stickinga | Estimated critical repulsion strengthb |
|---|---|---|
a Both values are obtained from Fig. 8 in ref. 44.
b This value is obtained from the exponential fit given by eqn (13):  , see text for more detail. , see text for more detail.
|
||
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif)
|
H sr |
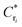
|
| 0.21 × 10−3 | 0.0902 | 0.457 |
| 1.03 × 10−3 | 0.160 | 1.062 |
| 2.07 × 10−3 | 0.225 | 2.114 |
Fig. 5 shows the minimum gap height, as indicator of stick/slip, as a function of sliding speeds characterized by λ for different values of permeability. For all three permeability values and for completeness, we include the behavior of permeable and impermeable particles near a neutral wall Cr = 0 from ref. 44 and near repulsive walls at  . In all panels of Fig. 5, the behavior near the estimated critical repulsion strength is labeled with stars. Near
. In all panels of Fig. 5, the behavior near the estimated critical repulsion strength is labeled with stars. Near 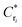 and at all λ that a solution could be reached, the minimum gap height follows Hmin ∼ λ0.5. This trend shows that the behavior of permeable particles near repulsive walls at their corresponding critical strength is governed by elastohydrodynamics. This result suggests that, at the critical repulsion strength, a permeable particle behaves like an impermeable particle near a neutral wall. In other words, the repulsion counteracts the attractive effect of permeability to a great extent. For permeable particles near a repulsive wall at the critical repulsion strength, simulations become increasingly slow as the sliding speed decreases. The numerical resolution of the fluid flow through the particle V is the reason behind this computational difficulty; as the sliding speeds decreases, the lubrication gap narrows. In this case, larger under-relaxation of the surface deformation and frequent calculation of the vertical velocity render the computational cost prohibitive. Adaptive under-relaxation can be an efficient technique that alleviates this numerical limitation, see for example.65Table 4 summarizes the minimum flow speed we could obtain results for at the permeability-dependent critical repulsion strength and the corresponding minimum gap height. Table 4 also shows the corresponding dimensional values of the critical repulsion strength,
and at all λ that a solution could be reached, the minimum gap height follows Hmin ∼ λ0.5. This trend shows that the behavior of permeable particles near repulsive walls at their corresponding critical strength is governed by elastohydrodynamics. This result suggests that, at the critical repulsion strength, a permeable particle behaves like an impermeable particle near a neutral wall. In other words, the repulsion counteracts the attractive effect of permeability to a great extent. For permeable particles near a repulsive wall at the critical repulsion strength, simulations become increasingly slow as the sliding speed decreases. The numerical resolution of the fluid flow through the particle V is the reason behind this computational difficulty; as the sliding speeds decreases, the lubrication gap narrows. In this case, larger under-relaxation of the surface deformation and frequent calculation of the vertical velocity render the computational cost prohibitive. Adaptive under-relaxation can be an efficient technique that alleviates this numerical limitation, see for example.65Table 4 summarizes the minimum flow speed we could obtain results for at the permeability-dependent critical repulsion strength and the corresponding minimum gap height. Table 4 also shows the corresponding dimensional values of the critical repulsion strength,  . Comparing these values to those given in Table 1 for microgel particles, it is noted that the critical values are similar in order of magnitude to the strength of repulsion originating from electrostatic repulsion with the wall. The critical repulsion strength is however dependent on the permeability, that is the higher the particle permeability, the higher the critical repulsion strength.
. Comparing these values to those given in Table 1 for microgel particles, it is noted that the critical values are similar in order of magnitude to the strength of repulsion originating from electrostatic repulsion with the wall. The critical repulsion strength is however dependent on the permeability, that is the higher the particle permeability, the higher the critical repulsion strength.
 and
and  , respectively
, respectively
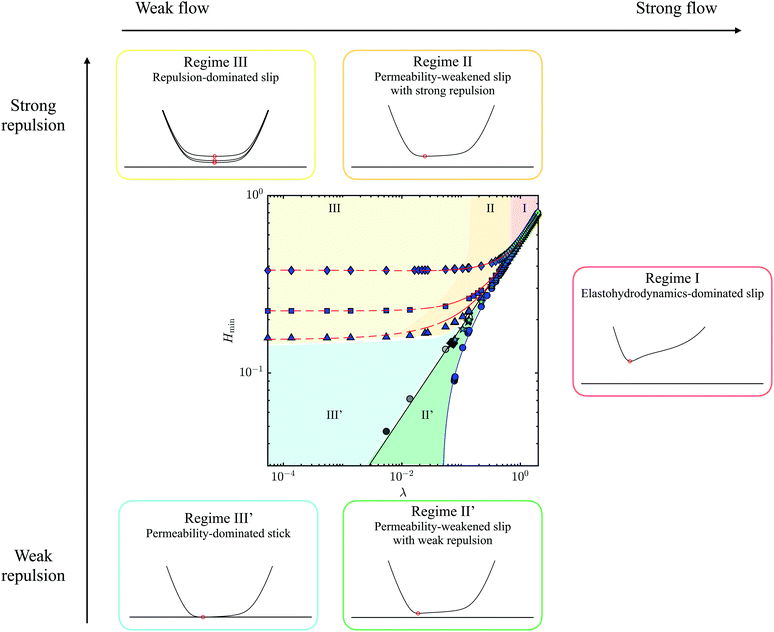
Moreover, Fig. 5 reveals that wall-slip behavior of permeable particles follows one of two paths upon decreasing the flow strength: path (I)–(II)–(III) or path (I)–(II′)–(III′) depending on the strength of particle–wall repulsion. At strong repulsion, permeable – as well as impermeable particles in general – follow (I) an elastohydrodynamics-dominated slip regime, (II) a permeability-weakened slip with strong repulsion regime, followed by (III) a repulsion-dominated slip. At weak repulsion, permeable particles follow (I) the elastohydrodynamics-dominated slip regime, (II′) a permeability-weakened slip with weak repulsion, followed by (III′) permeability-dominated stick.
4.4 Slip mechanism of permeable particles at critical repulsive interactions with a rigid wall
As described in the previous section (Section 4.3), there exists a critical repulsion strength that counteracts the sticky behavior of permeable particles. The mechanism by which this behavior is achieved can be explained by considering a permeable particle near a critically-repulsive wall, i.e. , and an impermeable particle near a neutral wall, i.e. (
, and an impermeable particle near a neutral wall, i.e. (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) = 0, Cr = 0), sliding at the same speed. The comparison is performed in terms of the total surface deformation, UZ|Z=0, and its components, (i) hydrodynamic pressure and (ii) repulsive pressure. The hydrodynamic pressure component implicitly depends on the permeability of the particle since the lubrication equation contains the vertical fluid velocity term.
= 0, Cr = 0), sliding at the same speed. The comparison is performed in terms of the total surface deformation, UZ|Z=0, and its components, (i) hydrodynamic pressure and (ii) repulsive pressure. The hydrodynamic pressure component implicitly depends on the permeability of the particle since the lubrication equation contains the vertical fluid velocity term.
First, the particle profile, is examined for both cases 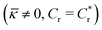 and (
and (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) = 0, Cr = 0) in Fig. 6. Fig. 6 shows that the difference in surface deformation between both cases is insignificant; the curves are almost identical. This observation suggests that, at the critical repulsion strength, the particle-surface deformation is nearly independent of permeability and repulsion strength.
= 0, Cr = 0) in Fig. 6. Fig. 6 shows that the difference in surface deformation between both cases is insignificant; the curves are almost identical. This observation suggests that, at the critical repulsion strength, the particle-surface deformation is nearly independent of permeability and repulsion strength.
To pinpoint the origin of this behavior, the different components of the surface deformation are plotted in Fig. 7a for 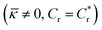 . It is noteworthy that near a neutral wall, i.e. Cr = 0, the total particle–surface deformation is due to hydrodynamic pressure in the gap, while near a repulsive wall, i.e. Cr ≠ 0, there is an additional contribution due to the repulsive pressure. Fig. 7a shows that the repulsive contribution dominates the deformation at the lagging side of the particle, while the hydrodynamic contribution dominates the deformation at the leading side of the particle. Mechanistically, at the lagging side where sticking is observed for permeable particles near neutral walls, repulsion pushes the particle away from the wall hence preventing it from sticking. At the leading side, the gap is thicker compared to the lagging side so the repulsive pressure is lowest. However, to maintain the lubricating layer, fluid from the gap has to flow to beyond the particle and hence hydrodynamic pressure is highest beneath the particle in this region. Since the particle is permeable, this high pressure leads to flow to the particle pores, lowering the hydrodynamic pressure on the leading side compared to the impermeable case (see Fig. 7b and c).
. It is noteworthy that near a neutral wall, i.e. Cr = 0, the total particle–surface deformation is due to hydrodynamic pressure in the gap, while near a repulsive wall, i.e. Cr ≠ 0, there is an additional contribution due to the repulsive pressure. Fig. 7a shows that the repulsive contribution dominates the deformation at the lagging side of the particle, while the hydrodynamic contribution dominates the deformation at the leading side of the particle. Mechanistically, at the lagging side where sticking is observed for permeable particles near neutral walls, repulsion pushes the particle away from the wall hence preventing it from sticking. At the leading side, the gap is thicker compared to the lagging side so the repulsive pressure is lowest. However, to maintain the lubricating layer, fluid from the gap has to flow to beyond the particle and hence hydrodynamic pressure is highest beneath the particle in this region. Since the particle is permeable, this high pressure leads to flow to the particle pores, lowering the hydrodynamic pressure on the leading side compared to the impermeable case (see Fig. 7b and c).
5 Discussion and conclusions
Inspired by the sticky behavior of permeable particles when sheared near rigid walls,44 the present work investigates the competition between permeability-induced attractions and short-range repulsive particle–wall interactions. We introduce a disjoining pressure term to the poro-elastohydrodynamics model, presented initially in ref. 44, to account for short-range interactions between particle and wall. This disjoining pressure acts to deform the particle surface resulting in changes of the gap height, which is in turn coupled with hydrodynamic pressure of the gap fluid and the flow speed through the particle pores. The model is then used to study the interplay between particle properties, flow characteristics, and electrostatic wall affinity, when soft permeable particles are sheared near a repulsive rigid wall.Impermeable particles slip at all sliding speeds when sheared near a repulsive wall with any finite repulsion strength. Two slip regimes can be identified: elastohydrodynamics-dominated slip and repulsion-dominated slip. Under strong flow conditions, slip depends primarily on the flow speed, that is elastohydrodynamics dominates and the slip behavior is independent of repulsion strength. However, for weaker flows, soft impermeable particle slip near a repulsive wall. Repulsion parameters set the minimum gap height between the impermeable particle and the wall – the slip length – at low sliding speeds. These results confirm prior observation in literature, where a gap height plateau is reached in the presence of repulsive interactions between elastic impermeable particles and a rigid wall.26
Permeable particles, however, exhibit repulsion- and permeability-dependent stick-slip transitions. Permeable particles stick at decreasing sliding speeds near a neutral wall at permeability-dependent sticking point.44 This sticky behavior of permeable particles results in an emergent third regime that we identify as a permeability-weakened slip. The extent of this weakening depends on the particle permeability. We define a characteristic permeability-dependent critical repulsive,  . In the presence of strong repulsion, i.e.
. In the presence of strong repulsion, i.e.  , permeable particles slip for all sliding speeds, following three distinct regimes: (I) elastohydrodynamics-dominated slip at strong flows, (II) a permeability-weakened slip approach to the wall with strong repulsion at intermediate flows, and (III) a repulsion-dominated slip plateau at weak flows. In the presence of weak repulsion i.e.
, permeable particles slip for all sliding speeds, following three distinct regimes: (I) elastohydrodynamics-dominated slip at strong flows, (II) a permeability-weakened slip approach to the wall with strong repulsion at intermediate flows, and (III) a repulsion-dominated slip plateau at weak flows. In the presence of weak repulsion i.e. 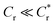 , elastohydrodynamics-dominated slip (regime (I)) still occurs under strong flow conditions, followed by a permeability-weakened slip with weak repulsion (regime (II′)), but this slip is weakened so much to the point of sticking (regime (III′)). In this latter regime, repulsion is not sufficient to overcome the effect of the sticky behavior enabled by permeability. These regimes are summarized in Fig. 8.
, elastohydrodynamics-dominated slip (regime (I)) still occurs under strong flow conditions, followed by a permeability-weakened slip with weak repulsion (regime (II′)), but this slip is weakened so much to the point of sticking (regime (III′)). In this latter regime, repulsion is not sufficient to overcome the effect of the sticky behavior enabled by permeability. These regimes are summarized in Fig. 8.
The mechanism by which repulsion counteracts the effect of permeability is revealed by examining the behavior at the corresponding critical repulsion strength. At the critical repulsion strength and as the sliding speed is decreased, repulsion dominates the surface deformation at the lagging edge of the particle, which prevents it from sticking to the wall. Hydrodynamic pressure, on the other hand, dominates the surface displacement at the leading edge of the particle. The effect of permeability is thence also dominant at the leading edge as its role is coupled with the hydrodynamic pressure via the lubrication equation. This redistribution of surface deformations has a direct consequence on the internal effective solid-phase stress and pore pressure distribution within the particle. The fact that permeability reduces the hydrodynamic pressure in the gap even when their effective behavior resembles that of impermeable particles near a repulsive wall can be leveraged to control the stress distribution at the interior of the particle. Control over the magnitude of internal stresses is great relevance in biological systems, as living cell function is significantly altered when exposed to high stress states.66
The different slip regimes offer ample opportunities to control slip and its extent at any desired sliding speed. At any operating flow speed, slip can be controlled via fluid dynamics, particle internal-structure, and wall affinity, at decreasing sliding speeds, respectively. Even at weak flows, sticky permeable particles can still be released by applying a repulsion that is stronger than the critical repulsion strength. Fostering these ideas can help optimize and improve several technological processes such as extrusion-based additive manufacturing techniques for soft matter such as foods67,68 and biological tissue.9,69
The presented unified model for slip-stick behavior of soft-particle systems near rigid surfaces provides fundamental insights that can be exploited in modeling many permeable-particle systems, see e.g. ref. 70 for spherical particles and ref. 71 for ellipsoidal particles, in a similar fashion to ref. 72 for soft impermeable particle systems. This model can also be adopted in several micro-systems, such as in the field of mechanical phenotyping of cells in microfluidic devices,73 where the inherent cell properties can be used for cell cytometry.
Author contributions
M. Z.: methodology, software, investigation, formal analysis, validation, visualization, data curation, writing – original draft. R. B.: conceptualization, methodology, resources, supervision, funding acquisition, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. Z. and R. T. B. gratefully acknowledge financial support from the National Science Foundation (NSF) (MRSEC under Award No. DMR 1720595).Notes and references
- C. W.-A. Bromley, J. Coat. Technol., 1989, 61, 39–43 CAS.
- N. L. Thomas, Prog. Org. Coat., 1991, 19, 101–121 CrossRef CAS.
- D. Saatweber and B. Vogt-Birnbrich, Prog. Org. Coat., 1996, 28, 33–41 CrossRef CAS.
- J. D. Smart, Adv. Drug Delivery Rev., 2005, 57, 1556–1568 CrossRef CAS PubMed.
- Q. Wang, Y. Zhao, Y. Yang, H. Xu and X. Yang, Colloid Polym. Sci., 2007, 285, 515–521 CrossRef CAS.
- J. R. Stokes and W. J. Frith, Soft Matter, 2008, 4, 1133–1140 RSC.
- P. Burey, B. R. Bhandari, T. Howes and M. J. Gidley, Crit. Rev. Food Sci. Nutr., 2008, 48, 361–377 CrossRef CAS PubMed.
- A. Bouchoux, P.-E. Cayemitte, J. Jardin, G. Gésan-Guiziou and B. Cabane, Biophys. J., 2009, 96, 693–706 CrossRef CAS PubMed.
- C. B. Highley, K. H. Song, A. C. Daly and J. A. Burdick, Adv. Sci., 2019, 6, 1801076 CrossRef PubMed.
- S. P. Meeker, R. T. Bonnecaze and M. Cloitre, Phys. Rev. Lett., 2004, 92, 198302 CrossRef PubMed.
- S. P. Meeker, R. T. Bonnecaze and M. Cloitre, J. Rheol., 2004, 48, 1295–1320 CrossRef CAS.
- M. Cloitre and R. T. Bonnecaze, Rheol. Acta, 2017, 56, 283–305 CrossRef CAS.
- D. Bonn, M. M. Denn, L. Berthier, T. Divoux and S. Manneville, Rev. Mod. Phys., 2017, 89, 035005 CrossRef.
- J.-F. Agassant, D. R. Arda, C. Combeaud, A. Merten, H. Munstedt, M. R. Mackley, L. Robert and B. Vergnes, Int. Polym. Process., 2006, 21, 239–255 CrossRef CAS.
- T. F. Ballenger, I.-J. Chen, J. W. Crowder, G. E. Hagler, D. C. Bogue and J. L. White, Trans. Soc. Rheol., 1971, 15, 195–215 CAS.
- P. Beaufils, B. Vergnes and J. F. Agassant, Int. Polym. Process., 1989, 4, 78–84 CrossRef CAS.
- J. Molenaar and R. J. Koopmans, J. Rheol., 1994, 38, 99–109 CrossRef CAS.
- A. Magnin and J. M. Piau, J. Non-Newtonian Fluid Mech., 1990, 36, 85–108 CrossRef CAS.
- S. A. Khan, C. A. Schnepper and R. C. Armstrong, J. Rheol., 1988, 32, 69–92 CrossRef CAS.
- M. P. Lettinga and S. Manneville, Phys. Rev. Lett., 2009, 103, 248302 CrossRef PubMed.
- S. A. Gulmus and U. Yilmazer, J. Appl. Polym., 2005, 98, 439–448 CrossRef CAS.
- C. S. Nickerson and J. A. Kornfield, J. Rheol., 2005, 49, 865–874 CrossRef CAS.
- B. K. Aral and D. M. Kalyon, J. Rheol., 1994, 38, 957–972 CrossRef CAS.
- G. H. Meeten, Rheol. Acta, 2004, 43, 6–16 CrossRef CAS.
- H. J. Walls, S. B. Caines, A. M. Sanchez and S. A. Khan, J. Rheol., 2003, 47, 847–868 CrossRef CAS.
- J. R. Seth, M. Cloitre and R. T. Bonnecaze, J. Rheol., 2008, 52, 1241–1268 CrossRef CAS.
- J. R. Seth, C. Locatelli-Champagne, F. Monti, R. T. Bonnecaze and M. Cloitre, Soft Matter, 2012, 8, 140–148 RSC.
- M. Christel, R. Yahya, M. Albert and B. Antoine, Soft Matter, 2012, 8, 7365–7367 RSC.
- J. R. Stokes, M. W. Boehm and S. K. Baier, Curr. Opin. Colloid Interface Sci., 2013, 18, 349–359 CrossRef CAS.
- S. K. Lai, Y.-Y. Wang, D. Wirtz and J. Hanes, Adv. Drug Delivery Rev., 2009, 61, 86–100 CrossRef CAS PubMed.
- P. F. Costa, H. J. Albers, J. E.-A. Linssen, H. H.-T. Middelkamp, L. Van der Hout, R. Passier, A. Van den Berg, J. Malda and A. D. Van der Meer, Lab Chip, 2017, 17, 2785–2792 RSC.
- E. Lauga, M. Brenner and H. Stone, Springer Handbooks, Springer, 2007, pp. 1219–1240 Search PubMed.
- C. J. Pipe and G. H. McKinley, Mech. Res. Commun., 2009, 36, 110–120 CrossRef.
- T. Lee, E. Charrault and C. Neto, Adv. Colloid Interface Sci., 2014, 210, 21–38 CrossRef CAS PubMed.
- H. Tabuteau, J.-C. Baudez, F. Bertrand and P. Coussot, Rheol. Acta, 2004, 43, 168–174 CrossRef CAS.
- D. D. Joseph, Powder Technol., 1997, 94, 211–215 CrossRef CAS.
- P. Morell, I. Hernando and S. M. Fiszman, Trends Food Sci. Technol., 2014, 35, 18–31 CrossRef CAS.
- J. Chen, Z. Liu and S. Prakash, Food Hydrocoll., 2014, 42, 100–105 CrossRef CAS.
- H. A. Barnes, J. Non-Newtonian Fluid Mech., 1995, 56, 221–251 CrossRef CAS.
- H. Brenner, Chem. Eng. Sci., 1961, 16, 242–251 CrossRef CAS.
- M. E. O'Neill and K. Stewartson, J. Fluid Mech., 1967, 27, 705–724 CrossRef.
- M. D.-A. Cooley and M. E. O'neill, Mathematika, 1969, 16, 37–49 CrossRef.
- R. H. Davis, J.-M. Serayssol and E. J. Hinch, J. Fluid Mech., 1986, 163, 479–497 CrossRef.
- M. E.-A. Zakhari and R. T. Bonnecaze, Soft Matter, 2021, 17, 4538–4549 RSC.
- L. G. Leal, Advanced transport phenomena: Fluid mechanics and convective transport processes, Cambridge University Press, 2007, vol. 7 Search PubMed.
- W. L. Bargar and J. L. Nowinski, Acta Mech., 1974, 20, 217–231 CrossRef.
- K. L. Johnson, Contact mechanics, Cambridge University Press, 1985 Search PubMed.
- A. Verruijt, An introduction to soil dynamics, Springer Science & Business Media, 2009, vol. 24 Search PubMed.
- J. Bear, Dynamics of fluids in porous media, Dover, 2013 Search PubMed.
- W. S. Hall, The boundary element method, Springer, 1994, pp. 61–83 Search PubMed.
- K.-C. Ang, Int. J. Math. Educ. Sci. Technol., 2008, 39, 505–519 CrossRef.
- P. K. Kythe, An introduction to boundary element methods, CRC Press, 2020 Search PubMed.
- D. Vlassopoulos and M. Cloitre, Curr. Opin. Colloid Interface Sci., 2014, 19, 561–574 CrossRef CAS.
- M. E.-A. Zakhari, P. D. Anderson and M. Hütter, Phys. Rev. E, 2017, 96, 012604 CrossRef PubMed.
- P. A.-L. Fernandes, S. Schmidt, M. Zeiser, A. Fery and T. Hellweg, Soft Matter, 2010, 6, 3455–3458 RSC.
- A. Fernandez-Nieves, H. Wyss, J. Mattsson and D. Weitz, Microgel Suspensions: Fundamentals and Applications, Wiley, Hoboken, NJ, 2011 Search PubMed.
- M. Daoud and J. P. Cotton, J. Phys., 1982, 43, 531–538 CrossRef CAS.
- D. Vlassopoulos, G. Fytas, T. Pakula and J. Roovers, J. Phys.: Condens. Matter, 2001, 13, R855 CrossRef CAS.
- D. Vlassopoulos and G. Fytas, High Solid Dispersions, Springer, 2009, pp. 1–54 Search PubMed.
- J. N. Israelachvili, Intermolecular and surface forces, Academic Press, 2015 Search PubMed.
- C. J. Oss Van, R. J. Good and M. K. Chaudhury, Sep. Sci. Technol., 1987, 22, 1–24 CrossRef.
- S. H. Behrens and D. G. Grier, J. Chem. Phys., 2001, 115, 6716–6721 CrossRef CAS.
- T. G. Mason, M.-D. Lacasse, G. S. Grest, D. Levine, J. Bibette and D. A. Weitz, Phys. Rev. E, 1997, 56, 3150 CrossRef CAS.
- C. A. Grattoni, H. H. Al-Sharji, C. Yang, A. H. Muggeridge and R. W. Zimmerman, J. Colloid Interface Sci., 2001, 240, 601–607 CrossRef CAS PubMed.
- H. Wu, N. Moyle, A. Jagota and C.-Y. Hui, Soft Matter, 2020, 16, 2760–2773 RSC.
- S. Fulda, A. M. Gorman, O. Hori and A. Samali, Int. J. Cell Biol., 2010, 214074 Search PubMed.
- Y. Ma, M. A.-I. Schutyser, R. M. Boom and L. Zhang, Innov. Food Sci. Emerg. Technol., 2021, 73, 102764 CrossRef.
- S. Sridharan, M. B.-J. Meinders, L. M. Sagis, J. H. Bitter and C. V. Nikiforidis, Adv. Funct. Mater., 2021, 2101749 CrossRef CAS.
- C. B. Highley, in 3D Bioprinting Technologies, ed. M. Guvendiren, Springer International Publishing, 2019, pp. 1–66 Search PubMed.
- M. E.-A. Zakhari, M. Hütter and P. D. Anderson, J. Rheol., 2018, 62, 543–557 CrossRef CAS.
- M. Zakhari, P. Anderson and M. Hütter, J. Non-Newton. Fluid Mech., 2018, 259, 23–31 CrossRef CAS.
- J. R. Seth, L. Mohan, C. Locatelli-Champagne, M. Cloitre and R. T. Bonnecaze, Nat. Mater., 2011, 10, 838–843 CrossRef CAS PubMed.
- D. Stoecklein and D. Di Carlo, Anal. Chem., 2018, 91, 296–314 CrossRef PubMed.
Footnote |
| † It is noteworthy that the plateau values are independent of the permeability, and hence can be equivalently obtained from Fig. 4a for example. |
| This journal is © The Royal Society of Chemistry 2022 |