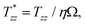Open Access Article
Open Access ArticleTorsional instability of constant viscosity elastic liquid bridges†
San To
Chan
 ,
Stylianos
Varchanis
,
Stylianos
Varchanis
 ,
Simon J.
Haward
,
Simon J.
Haward
 and
Amy Q.
Shen
and
Amy Q.
Shen
 *
*
Okinawa Institute of Science and Technology Graduate University, Onna, Okinawa 904-0495, Japan. E-mail: amy.shen@oist.jp
First published on 7th February 2022
Abstract
By experiment and simulation, we report that viscoelastic liquid bridges made of constant viscosity elastic liquids, a.k.a. Boger fluids, can be effectively destabilized by torsion. Under torsion, the deformation of the liquid bridge depends on the competition between elastocapillarity and torsion-induced normal stress effects. When the elastocapillary effect dominates, the liquid bridge undergoes elastocapillary instability and thins into a cylindrical thread, whose length increases and whose radius decays exponentially over time. When the torsion-induced normal stress effect dominates, the liquid bridge deforms in a way similar to edge fracture, a flow instability characterized by the sudden indentation of the fluid's free surface when a viscoelastic fluid is sheared at above a critical deformation rate. The vertical component of the normal stress causes the upper and lower portions of the liquid bridge to approach each other, and the radial component of the normal stress results in the liquid bridge thinning more quickly than under elastocapillarity. Whether such quick thinning continues until the bridge breaks depends on both the liquid bridge configuration and the level of torsion applied.
1 Introduction
Liquid bridges are formed when liquids are constrained between two (or more) surfaces via the capillary force.1,2 They appear in a wide range of contexts including biology, medicine, and engineering. In the context of biology, liquid bridges enable animals like geckos to adhere to vertical walls.3–5 In medicine, liquid bridges can collapse the lung airway and cause respiratory failure.6 In engineering, industries such as electronic packaging, food engineering, and additive manufacturing often require functional fluids to be dispensed efficiently.7–10 In the latter case, the liquid bridge connecting the dispensing nozzle and the substrate is often viscoelastic in nature and needs to be broken cleanly and quickly.To destabilize liquid bridges, the current mainstream industrial approach is to lift up the dispensing nozzle quickly.10 This elongates the liquid bridge and enlarges the capillary force acting on its surface, hence accelerating the breakup process. The elongation method is simple; however, for viscoelastic fluids it has two serious drawbacks. First, elongation causes high molecular weight polymer chains in the viscoelastic fluid to stretch. This induces extension-hardening of the fluid due to elastic stress in the polymer, which resists the extensional flow and hence delays complete breakup of the liquid bridge. Under these conditions, termed elastocapillarity, the radius of the liquid bridge decays exponentially with a constant (3λ)−1, where λ is the relaxation time of the viscoelastic fluid.11–14 Second, elongation causes secondary droplets15 and a long capillary tail16 to form after the liquid bridge breakup, which may fall randomly and contaminate the dispensing substrate.
Recently, Chan et al.17 propose that the aforementioned two drawbacks of the elongation method can be overcome using torsion, i.e., rotating one end of the viscoelastic liquid bridge while keeping the other end fixed. Using a viscoelastic silicone oil with a characteristic relaxation time of λ ∈ O(1 ms) as the model fluid, they show that when the liquid bridge is subjected to torsion it undergoes edge fracture, a flow instability characterized by the sudden indentation of the fluid's free surface when a viscoelastic fluid is sheared at above a critical rate.17–24 The indent caused by the viscoelastic stresses propagates towards the vertical centerline of the liquid bridge, which creates a horizontal cut and causes the bridge radius to undergo power-law decay, hence resulting in the clean and quick breakup of the liquid bridge.
In this work, we take a step further and show that torsion can effectively destabilize liquid bridges made of constant viscosity elastic liquid (Boger fluid) as well. The Boger fluid we used has a relaxation time of λ ∈ O(1 s), which is 1000 times larger than that of the silicone oil used by Chan et al.17 Hence, elastocapillarity is expected to play a much more pivotal role in the liquid bridge deformation process. In fact, deformation of the liquid bridge under torsion depends on how the elastocapillary effect competes with the torsion-induced normal stress effect. When the elastocapillary effect dominates, the liquid bridge undergoes exponential thinning; the fluid extension-hardens as the liquid bridge becomes increasingly long and slender over time. When the torsion-induced normal stress effect dominates, the liquid bridge thins more quickly. In this case, the liquid reservoirs at either end of the liquid bridge approach each other, thus preventing the viscoelastic fluid from hardening due to the extensional flow. Whether such quick thinning leads to liquid bridge break up depends on both the bridge configuration and the level of torsion applied.
2 Experiments
2.1 Experimental setup
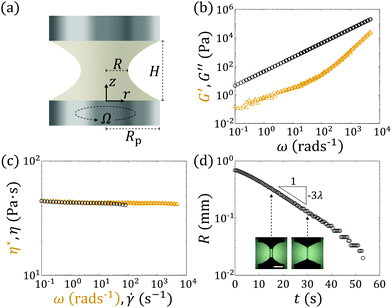
The experimental setup consists of two coaxial circular plates of radius Rp = 3 mm and initially separated by a distance H0 = 0.7 mm (Fig. 1(a)). The plates are installed on a strain-controlled rheometer (ARES-G2, TA instruments). The upper plate can translate vertically and the lower plate can rotate unidirectionally. Between the two plates, viscoelastic fluid of volume V = 20 ± 0.5 μL is injected using a positive displacement pipette (MICROMAN®, Gilson) in order to create a liquid bridge. In each experiment, the liquid bridge is stretched from the initial height H0 to a final height H ≤ 5 mm at a rate of Up = 2.2 mm s−1. When H is reached, the liquid bridge is allowed to relax for 5 s. Then, at t = 0 s, the lower plate is accelerated to a rotational speed Ω within a time span of 0.15 s. The liquid bridge is illuminated using a high intensity light-emitting diode surface light (IHM-108/114, Leimac Ltd) connected to a digital pulse-width modulation controller (IDGB-50M2-24, Leimac Ltd). Videos of the deformation process of the liquid bridge are recorded using a high-speed camera (FASTCAM Mini AX100, Photron USA Inc.) with a frame rate of 50 to 60 fps, a shutter speed of 3000 Hz and a 12× zoom, 12 mm fine focus objective lens (Navitar Inc.).2.2 Liquid bridge radius tracking
The captured videos are analyzed using an in-house developed Matlab (Mathwork, USA) program. The program thresholds each video frame into black and white images, with the black area being the background and the white area being the liquid bridge. The liquid bridge radius is obtained by multiplying the number of horizontal white pixels by the image resolution of 13.6 μm per pixel. The vertical position at which there is the least number of horizontal white pixels is the position at which the liquid bridge radius is minimal. The minimal radius (or neck radius) R is tracked over time t.2.3 Material characterization
The viscoelastic fluid used is a dilute solution (c = 0.025 wt%) of high molecular weight polystyrene (Scientific Polymer Products, Mw = 2.25 × 106 g mol−1) dissolved in oligomeric styrene (Herculus Piccolastic A5 Resin).25 It is a Boger fluid with nearly constant shear viscosity and high elasticity.26 The rheology of the fluid was characterized by a strain-controlled rheometer (ARES-G2, TA instruments) equipped with a 25 mm diameter stainless steel 1° cone-and-plate geometry. The small amplitude oscillatory shear test was performed with a strain amplitude of 5% to obtain the storage modulus G′ and the loss modulus G′′ in a frequency range of 0.01 to 100 rad s−1 and temperature range of 4 to 35 °C. The data obtained at different temperatures were used to construct a master curve at 25 °C (Fig. 1(b)) using the time-temperature superposition principle.27 The steady-shear test was performed at 25 °C to obtain the flow curve in a shear rate range of 0.1 to 80 s−1. Fig. 1(c) shows that both the shear viscosity η and complex viscosity η* are nearly constant with respect to the shear rate![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and oscillation frequency ω. The shear viscosity is approximated to be η = 43.9 ± 2 Pa s; the complex viscosity is approximated to be η* = 42.9 ± 0.7 Pa s. Capillary breakup extensional rheometry (CaBER)11 was performed using the experimental setup shown in Fig. 1(a) with H = 5 mm and Ω = 0 rad s−1. The neck radius of the liquid bridge shows exponential decay (Fig. 1(d)), which signifies elastocapillary instability. The relaxation time λ = 5.29 ± 0.02 s of the Boger fluid was obtained by fitting the function R = A
and oscillation frequency ω. The shear viscosity is approximated to be η = 43.9 ± 2 Pa s; the complex viscosity is approximated to be η* = 42.9 ± 0.7 Pa s. Capillary breakup extensional rheometry (CaBER)11 was performed using the experimental setup shown in Fig. 1(a) with H = 5 mm and Ω = 0 rad s−1. The neck radius of the liquid bridge shows exponential decay (Fig. 1(d)), which signifies elastocapillary instability. The relaxation time λ = 5.29 ± 0.02 s of the Boger fluid was obtained by fitting the function R = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/3λ) to the neck radius R(t) of the liquid bridge. An optical tensiometer (Theta Attension, Biolin Scientific) was used to measure surface tension σ = 40.5 ± 0.02 mN m−1 of the Boger fluid by the pendant drop method28 at 25 °C. The density of the Boger fluid was measured to be ρ = 1000 kg m−3.
exp(−t/3λ) to the neck radius R(t) of the liquid bridge. An optical tensiometer (Theta Attension, Biolin Scientific) was used to measure surface tension σ = 40.5 ± 0.02 mN m−1 of the Boger fluid by the pendant drop method28 at 25 °C. The density of the Boger fluid was measured to be ρ = 1000 kg m−3.
3 Simulations
3.1 Flow geometry
In the numerical simulations, we consider the three-dimensional (3D) axisymmetric flow of a viscoelastic fluid confined between two coaxial cylindrical solid plates of radius Rp = 3 mm (Fig. 1(a)). The initial distance between the two plates is denoted as H0 = 0.7 mm. Cylindrical coordinates (r, θ, z) are employed to describe this axisymmetric problem, where r, θ, and z denote the radial, azimuthal, and axial coordinates, respectively. The velocity in the fluid is denoted as u = [ur(r,z), uθ(r,z), uz(r,z)], where each component of the velocity varies only in the r and z directions because of the axisymmetric flow assumption. Gravity acts along the negative z-direction. The three phase contact lines that are formed by the fluid, the surrounding air, and the solid plates are assumed to be pinned. This means that the contact lines are not allowed to move tangentially to the wall, and the contact angle that is formed by the fluid and the solid is calculated implicitly from the flow field. Initially, the fluid is at rest (u = 0) in a stress-free condition, forming a cylindrical column between the two plates. Then, the upper plate moves in the z-direction, separating from the stationary lower plate, with a constant velocity equal to Up = 2.2 mm s−1 until it reaches a final separation of H = 3 mm. After the elongation process, the liquid bridge is allowed to rest for 5 s. Finally, at t = 0 s the lower plate accelerates abruptly to a constant rotational speed Ω and the torsional process begins. As a side note, in the simulation we have assumed that the lower plate accelerates to its full speed instantaneously. This assumption holds as the actual acceleration time of the lower plate is negligible compared to the relaxation time of the viscoelastic fluid.3.2 Governing equations
The viscoelastic fluid has a constant density ρ and the fluid–air interface has a constant interfacial tension σ. The fluid has a total dynamic viscosity η0 = ηp + ηs, where ηs is the viscosity of the Newtonian solvent and ηp = GΛ is the contribution of the polymer chains to the viscosity. Here, G and Λ denote the elastic modulus and relaxation time of the fluid, respectively. Note that the relaxation time Λ here is labeled uppercase to distinguish it from the experimentally measured λ. The flow of the present viscoelastic fluid is governed by the conservation of mass and momentum, and the extended White–Metzner (eWM) constitutive equation.29 The conservation equations for incompressible fluids are:| ∇·u = 0, | (1) |
 | (2) |
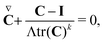 | (3) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a2.gif) = ∇u + (∇u)T is the deformation rate tensor. The material derivative is given as D/Dt, and the trace of the conformation tensor is given as tr(C). Moreover, the inverted triangle
= ∇u + (∇u)T is the deformation rate tensor. The material derivative is given as D/Dt, and the trace of the conformation tensor is given as tr(C). Moreover, the inverted triangle  over the conformation tensor denotes the upper convected derivative. Finally, k is a material parameter of the constitutive equation that governs the degree of shear-thinning and extension-hardening of the fluid.29 Note that when k = 0, the eWM model reduces to the Oldroyd-B model and Λ = λ.
over the conformation tensor denotes the upper convected derivative. Finally, k is a material parameter of the constitutive equation that governs the degree of shear-thinning and extension-hardening of the fluid.29 Note that when k = 0, the eWM model reduces to the Oldroyd-B model and Λ = λ.
3.3 Boundary conditions
In terms of boundary conditions along the free surface, the velocity field satisfies a normal force balance between the surface tension, total stresses in the liquid, and pressure in the inviscid surrounding air. In addition, the liquid–gas interface moves according to the usual kinematic conditions. On the surfaces of the upper and lower plates, the no slip and no penetration velocity conditions are imposed. Finally, flow symmetry is imposed on the axis of symmetry. The interested reader may refer to Varchanis et al.30 for a detailed description of the boundary conditions.3.4 Discretization
The system of the aforementioned partial differential equations is discretized and solved using the Petrov–Galerkin stabilized finite element method for viscoelastic flows (PEGAFEM-V) by Varchanis et al.30–32 The computational grid is provided by the quasi-elliptic mesh generator proposed by Dimakopoulos and Tsamopoulos.33 The element size close to the free surface is he ≈ 3 × 10−5Rp and the time step used is dt = 0.01Ω−1. All simulations are transient and terminate when either the neck radius R becomes smaller than 0.01 mm, or when any structure with radius of curvature smaller than 0.0015 mm appears on the free surface. A detailed description of the mesh and time step convergence tests, together with the simulation results of several test cases, are given in the ESI.†3.5 Parameter fitting of the constitutive model
The rheology of the present viscoelastic solution is described by the eWM model (eqn (3)), which is a thermodynamically acceptable constitutive equation that can describe the rheology of a wide range of viscoelastic fluids.29 We choose this particular model because of its extensional properties. In the simpler Oldroyd-B model, the slope of the exponential elastocapillary thinning is defined only by the value of λ (see Fig. 1(d)).11–14 However, the eWM model predicts a power-law evolution of the steady extensional viscosity versus the extension rate when −1 ≤ k < 0.29 Thus, the slope of the elastocapillary thinning depends both on the values of Λ and k. This property of the eWM model allows us to fit more precisely the elastocapillary regime, and at the same time yields an overall better agreement of the model with the experimental data.Estimation of the material parameters of the model (ηp, Λ, k, ηs) was performed using a similar optimization protocol as that proposed by Varchanis et al.34 Initially, the sum η0 = ηp + ηs is extracted from the flow curve (Fig. 1(c)). Subsequently, ηs can be found from fitting the relation G′′ = ηsω to the experimental curve of G′′ from the frequency sweeps (Fig. 1(b)). Finally, values of Λ and k are found by minimizing the numerical predictions of the 3D model with respect to the experimental data for the evolution of the neck radius R versus time t for H = 3 mm and Ω = 0 rad s−1. The values of the material parameters that are found to give the best match with the experimental data are: ηp = 8.8 Pa s, Λ = 7.86 s, ηs = 35.2 Pa s, and k = −0.1.
4 Dimensional analysis
The deformation of the viscoelastic liquid bridge under torsion will depend on how inertia, elasticity, capillarity, viscous dissipation and gravity interact,14,35 which can be characterized by four main dimensionless parameters. With RΩ being the characteristic velocity, the Reynolds number Re = ρR2Ω/η characterizes the relative importance of inertial and viscous stresses. The Weissenberg number Wi = λΩ characterizes the relative importance of elastic and viscous stresses. The capillary number Ca = ηRΩ/σ characterizes the relative importance of viscous and capillary stresses. With g being gravitational acceleration, the Bond number Bo = ρgR2/σ characterizes the relative importance of gravity and capillary stress.Having the four main dimensionless parameters defined, interpretation of experimental and simulation results can be simplified in two ways. The first way is to compare the magnitudes of the dimensionless parameters. With a typical R = 1 mm and Ω = 1–100 rad s−1, Re ∈ O(10−5–10−3) and Bo ∈ O(0.1) are at least an order of magnitude smaller than Wi, Ca ∈ O(1–102). Hence, effects of Re and Bo can be safely neglected. The second way is to define two additional dimensionless parameters, namely, the elastocapillary number Ec and the recently introduced Tanner number Tn.17 The elastocapillary number Ec ≡ Wi/Ca = λσ/ηR characterizes the combined importance of elastic stress and capillary stress as compared to viscous stress. The Tanner number Tn ≡ WiCa = ληRΩ2/σ characterizes the relative importance of torsion-induced normal stress and capillary stress. Essentially, Ec and Tn represent the same set of dimensional parameters as Wi and Ca. Importantly, however, Ec does not depend on the rotational speed Ω. Thus, by employing the pair of parameters Ec and Tn, the effect of varying Ω can be described with only one dimensionless parameter instead of two.
In fact, simply by inspecting how the neck radius R and the rotational speed Ω affect the magnitudes of Ec and Tn, we can obtain insights into how the viscoelastic liquid bridge may deform under torsion. First, we consider the case where there is no torsion applied, i.e., Ω = 0 rad s−1 and Tn = 0. In this case, the dynamics of the liquid bridge would be solely governed by Ec. For a typical R = 1 mm, Ec ∈ O(1), the liquid bridge dynamics would depend on how the elastic, capillary and viscous effects interact. As the liquid bridge thins, R becomes smaller. This increases Ec and renders the viscous effect less relevant, eventually leaving the elastic and capillary effects in the force balance. As previously discussed, in the elastocapillary regime, a liquid bridge will thin exponentially over time according to the form R ∝ exp(−t/3λ).11–14 Next, we consider the case where there is a moderate level of torsion applied such that Tn and Ec ∈ O(1). This corresponds to a typical R = 1 mm and Ω ∈ O(1 rad s−1). In such a scenario, the torsion applied would cause the viscoelastic liquid bridge be subjected to an additional normal stress. The direction of the normal stress and its effects on the liquid bridge are to be determined by the experiments and simulations that follow below. However, as long as the liquid bridge thins and R becomes small enough, Ec would eventually dominate Tn. The liquid bridge can thus be expected to enter the elastocapillary regime and thin exponentially over time before its breakup. Lastly, we consider the case where torsion governs the liquid bridge dynamics, i.e., Tn ≫ Ec for all observable values of R. This corresponds to a typical Ω ∈ O(100 rad s−1). In such a case, the capillary effect would be insignificant. The liquid bridge would be deformed solely by the torsion-induced normal stress; hence, it would not enter the elastocapillary regime.
5 Results and discussion
5.1 Viscoelastic liquid bridge under torsion
Three patterns of deformation can be observed when a viscoelastic liquid bridge is subjected to different levels of torsion. Fig. 2 shows the liquid bridge configurations at different time t with a fixed height H = 3 mm. When there is no rotation applied to the bottom plate, i.e., Ω = 0 rad s−1, the liquid bridge thins slowly over time (Fig. 2(a)). During the initial stage of the thinning process, say t = 18.1 s, the liquid bridge surface curves like a parabola. The parabolic shape is symmetric over the liquid bridge's horizontal mid-plane, which suggests that gravity is indeed negligible as anticipated since Bo ∈ O(0.1). At a later stage, say t = 54.5 s, a cylindrical fluid thread appears around the liquid bridge center, which signifies elastocapillary instability. Following the onset of the elastocapillary regime, the fluid thread becomes longer and thinner over time.Applying a Ω = 5 rad s−1 rotation results in the liquid bridge thinning more quickly than when no rotation is applied (Fig. 2(b)). The thinning process is similar to the case of Ω = 0 rad s−1, except for in two regards. First, during the initial stage of thinning, the liquid bridge surface is not parabolic but rather more conical. Such a different shape suggests that additional normal stresses develop in the liquid bridge when it is subjected to torsion. Second, the liquid bridge enters the elastocapillary regime faster. For instance, to achieve a similar cylindrical shape (see far right images in Fig. 2(a) and (b)), the case of Ω = 0 rad s−1 needed 62.9 s but the case of Ω = 5 rad s−1 only needed 34.1 s. From this we can deduce that the torsion-induced normal stress has a destabilizing effect on the viscoelastic liquid bridge.
Increasing the rotational speed to Ω = 50 rad s−1 further accelerates the thinning process of the liquid bridge. However, the thinning process is drastically different from that at lower rotational speeds. An obvious difference can be seen at t = 0.48 s when helical wrinkles appear on the cylindrical portion of the liquid bridge. As time proceeds, the liquid reservoirs on the upper and lower plates approach each other along the cylindrical portion and merge at t = 1.36 s. This triggers a subsequent buckling instability at t = 2.58 s, which can dewet the liquid bridge from the experimental setup (see ESI,† Video S3). Because of this, the experiment has to be halted.
At an even higher rotational speed of Ω = 200 rad s−1 (Fig. 2(d)), the thinning process of the liquid bridge is rather similar to the Ω = 50 rad s−1 case. For example, at t = 0.25 s and 0.38 s there are helical winkles appearing on the cylindrical portion. Also, the upper and lower liquid reservoirs approach each other as time proceeds. However, in contrast to the Ω = 50 rad s−1 case, for the Ω = 200 rad s−1 case the liquid bridge thins much faster. As a result, at t = 0.57 s fluid in the cylindrical portion drains out before the upper and lower liquid reservoirs come into close contact. As the two reservoirs make contact, they then touch each other rather irregularly several times without coalescence, which snaps off the small fluid filament connecting them and leads to complete breakup of the liquid bridge (see ESI,† Video S4). The observed irregular contact of the upper and lower liquid reservoirs may be an inherent feature of the liquid bridge thinning process. However, it may also simply be due to the small mechanical noise of the rotating lower plate being amplified at high rotational speed.
To inspect how the viscoelastic liquid bridge deforms under strong torsion more clearly, Fig. 3 contains 6 images showing how the cylindrical portion of the liquid bridge deforms under Ω = 200 rad s−1 in between t = 0.22 s and 0.42 s. At t = 0.22 s when the cylindrical portion just emerges, helical wrinkles which exhibit 2 turns can be seen on the cylindrical surface. As time proceeds, the number of turns increases to 3 at t = 0.25 s and to 4 at t = 0.28 s. Later, at t = 0.35 s the number of turns decreases back to 2, signifying that the upper and lower wrinkles have merged with the liquid reservoirs on the upper and lower plates. After this merging event, the number of wrinkles increases again to 3 at t = 0.38 s and to 4 at t = 0.42 s. The wrinkling-merging process then continues, until the upper and lower liquid reservoirs make contact, undergo irregular touching and cause the liquid bridge to pinch off.
Having described qualitatively how the viscoelastic liquid bridge deforms under torsion, next we describe some of its quantitative features. Fig. 4(a) shows the experimentally measured and simulated neck radius R(t) of the viscoelastic liquid bridge subjected to rotational speeds of Ω ≤ 25 rad s−1. The simulation results (broken lines) will be discussed later in Section 5.3. For now, we shall focus on the experimental results (solid lines). For Ω = 0 rad s−1 where there is no rotation applied, the liquid bridge initially thins slowly over time due to the high viscosity of the fluid. At t ≈ 55 s, the neck radius starts to decay exponentially over time with R(t) ∝ exp(−t/3λ). The onset of exponential decay at t ≈ 55 s coincides with the formation of the cylindrical thread of the liquid bridge, as shown in Fig. 2(a), confirming elastocapillary instability. Increasing the rotational speed to Ω = 1 rad s−1 and 5 rad s−1 results in the liquid bridge entering the elastocapillary regime incrementally faster. Further increasing the speed to Ω = 10 rad s−1 and 25 rad s−1, thinning of the liquid bridge becomes even faster. However, the neck radius no longer decays according to R(t) ∝ exp(−t/3λ) but with a steeper slope, which can no longer be explained by elastocapillary instability. Hence, there must be an additional stress in effect other than the elastic and capillary stresses, the only possible candidate of which is the torsion-induced normal stress.
Fig. 4(b) shows the neck radius R(t) of the liquid bridge subjected to higher rotational speeds of Ω ≥ 50 rad s−1. For these higher speed cases, as the liquid reservoirs on the upper and lower plates tend to approach each other (see Fig. 2(c) and (d)), the true neck radius cannot be resolved precisely. Hence, the curves of R(t) appear to be noisy. Nonetheless, a clear trend can be seen as Ω is increased. For Ω = 50 rad s−1 where there is no breakup, the neck radius first decays over time. Later, at t ≈ 0.5 s, as the upper and lower portions of the liquid bridge make contact with each other, buckling instability occurs, causing the neck radius to increase over time. Increasing the rotational speed to Ω = 120 rad s−1 causes the liquid bridge to break. The neck radius first decays over time with a rate higher than that of Ω = 50 rad s−1. At t ≈ 0.5 s, quasi-periodic oscillation can be seen due to the irregular touching of the upper and lower liquid reservoirs. The oscillation continues until t ≈ 5 s when the liquid bridge pinches off. Further increasing Ω causes the neck radius to decay even faster. For the Ω considered, the corresponding quasi-periodic oscillation starts roughly at the same time at t ≈ 0.5 s (marked by the vertical dashed gray line in Fig. 4(b)). However, the oscillation ends faster as Ω is increased. For instance, for Ω = 150 rad s−1, 200 rad s−1 and 275 rad s−1 the oscillation ends at t ≈ 4 s, 3 s and 2 s, respectively.
5.2 Time evolution of Ec and Tn
In Section 4, we argued by dimensional analysis that the dynamics of the viscoelastic liquid bridge under torsion can be characterized by inspecting the magnitudes of the elastocapillary number Ec and the Tanner number Tn. This urges us to plot Ec and Tn over time t for different rotational speeds Ω, as shown in Fig. 5. For Ω = 5 rad s−1 (Fig. 5(a)), initially Tn is an order of magnitude larger than Ec, implying that the torsion-induced normal stress effect governs the initial deformation process of the liquid bridge. After t ≈ 30 s as Ec becomes an order of magnitude larger than Tn, the elastocapillary effect becomes dominant, explaining why the neck radius decays exponentially with R(t) ∝ exp(−t/3λ). For Ω = 25 rad s−1 (Fig. 5(b)), the crossover of Ec and Tn occurs at a smaller R compared to that of Ω = 5 rad s−1. Also, Ec and Tn are of the same order of magnitude even at the smallest measurable R, which suggests that torsion-induced normal stress effect is significant during the whole liquid bridge thinning process. Because of this, a quicker thinning mode was observed in this case. For Ω = 50 rad s−1, initially Tn ∈ O(104) is four orders of magnitude larger than Ec ∈ O(1), suggesting that the elastocapillary effect is insignificant and deformation of the liquid bridge is solely driven by the torsion-induced normal stress. The normal stress brings the upper and lower liquid reservoirs towards each other. The liquid reservoirs make contact and coalesce before the liquid bridge's neck drains out (see t = 1.36 s, Fig. 2(c)). Effectively, this causes R to remain in the same order of magnitude over time, rendering Ec and Tn to remain in the same order of magnitude over time as well. For Ω = 200 rad s−1, initially Tn ∈ O(105) is five orders of magnitude larger than Ec ∈ O(1). As in the Ω = 50 rad s−1 case, the torsion-induced normal stress brings the upper and lower liquid reservoirs towards each other. However, for Ω = 200 rad s−1 the thinning speed of the liquid bridge's neck is higher. As a result, the liquid bridge is able to thin a significant amount before the liquid reservoirs make contact (see Fig. 2(c)). In effect, R decreases over time, which in turn causes Tn to decrease over time and Ec to increase over time, respectively.5.3 The second normal stress difference N2
When the Tanner number Tn dominates the elastocapillary number Ec, torsion-induced normal stress governs how the viscoelastic liquid bridge deforms. From Fig. 2(c) and (d), we know that the torsion-induced normal stress causes the upper and lower liquid reservoirs to approach each other. To be able to do so, the total stress tensor T = −PI + G(C − I) + ηs![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a2.gif) must contain an axial component Tzz compressive to the liquid bridge free surface. From Fig. 4, we know that torsion causes the liquid bridge radius to decay faster. Hence, T must contain a radial component Trr as well. The above two observations lead us to hypothesize that torsion destabilizes the viscoelastic liquid bridge through the second normal stress difference N2 = Tzz − Trr.
must contain an axial component Tzz compressive to the liquid bridge free surface. From Fig. 4, we know that torsion causes the liquid bridge radius to decay faster. Hence, T must contain a radial component Trr as well. The above two observations lead us to hypothesize that torsion destabilizes the viscoelastic liquid bridge through the second normal stress difference N2 = Tzz − Trr.
We test this hypothesis using axisymmetric viscoelastic flow simulation. Fig. 4(a) shows the simulated (broken lines) and experimentally measured (solid lines) neck radius R(t) of the liquid bridge subjected to rotational speeds of Ω ≤ 25 rad s−1. For all Ω, the simulation and experimental results agree reasonably well. For instance, for Ω = 0 rad s−1, 1 rad s−1 and 5 rad s−1, the simulation is able to capture the elastocapillary thinning behavior of the liquid bridge when R gets small enough. Also, the simulation can reproduce the experimentally observed trend of the liquid bridge thinning behavior when Ω is increased. However, there is one main difference between the simulation and experimental results. For Ω = 10 rad s−1 and 25 rad s−1, the simulation halts when R reaches 0.27 mm and 0.32 mm, respectively (see blue and purple lines). This implies that there is a certain structure with a radius of curvature smaller than 0.0015 mm appearing on the liquid bridge free surface, see Section 3.4. The neck radius R at which this torsion-induced structure appears decreases when Ω is increased; in other words, the torsion-induced structure appears earlier in the liquid bridge thinning process when a higher level of torsion is applied. In fact, a scaling relation between the imposed rotational speed Ω and the liquid bridge thinning speed can be obtained by inspecting the simulated R(t) curves in a log–log plot; interested readers are referred to the ESI.†
The aforementioned torsion-induced structure is hypothesized to be caused by the second normal stress difference N2. Also, its formation is likely to be related to the quicker breakup of viscoelastic liquid bridges subjected to higher rotational speed Ω. To see how the torsion-induced structure looks and how it is related to N2 and the liquid bridge breakup process, we visualize the distributions of the simulated dimensionless radial normal stress 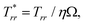 axial normal stress
axial normal stress  shear stress
shear stress  and second normal stress difference
and second normal stress difference  in the liquid bridge at different times t with a fixed height H = 3 mm. To provide a more quantitative picture, and to see how
in the liquid bridge at different times t with a fixed height H = 3 mm. To provide a more quantitative picture, and to see how  together deform the liquid bridge, we also visualize how the dimensionless normal traction distributes on the liquid bridge free surface at different times t. With
together deform the liquid bridge, we also visualize how the dimensionless normal traction distributes on the liquid bridge free surface at different times t. With ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) the outward pointing unit normal vector on the free surface, the dimensionless traction vector has the form τ* =
the outward pointing unit normal vector on the free surface, the dimensionless traction vector has the form τ* = ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ·T* =
·T* = ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ·T/ηΩ. With nr and nz the radial and axial components of
·T/ηΩ. With nr and nz the radial and axial components of ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) , the radial component of the dimensionless traction vector is
, the radial component of the dimensionless traction vector is  and the axial component is
and the axial component is  .
.
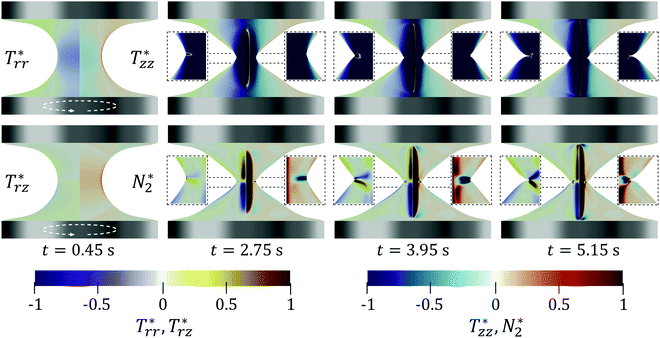
Fig. 6 shows how the dimensionless stresses  are distributed in the liquid bridge for Ω = 1 rad s−1 at different times t. The time evolution of the radial normal stress
are distributed in the liquid bridge for Ω = 1 rad s−1 at different times t. The time evolution of the radial normal stress  and the shear stress
and the shear stress  are rather simple. For
are rather simple. For 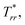 it is negative around the liquid bridge neck for all time t. On the neck surface,
it is negative around the liquid bridge neck for all time t. On the neck surface,  acts towards the negative r-direction and hence facilitates liquid bridge thinning. For
acts towards the negative r-direction and hence facilitates liquid bridge thinning. For  it is positive in the top half and negative in the bottom half of the liquid bridge for all time t. Around the liquid bridge neck,
it is positive in the top half and negative in the bottom half of the liquid bridge for all time t. Around the liquid bridge neck,  acts towards the negative r-direction similar to
acts towards the negative r-direction similar to  ; hence, it tends to facilitate liquid bridge thinning. In the top half of the liquid bridge,
; hence, it tends to facilitate liquid bridge thinning. In the top half of the liquid bridge, 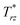 acts towards the positive z-direction; while in the bottom half, it acts towards the negative z-direction. Hence,
acts towards the positive z-direction; while in the bottom half, it acts towards the negative z-direction. Hence,  tends to expand and flatten the free surface. On the other hand, the time evolution of the axial normal stress
tends to expand and flatten the free surface. On the other hand, the time evolution of the axial normal stress  is more complicated. Initially at t = 5.85 s,
is more complicated. Initially at t = 5.85 s, 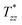 is positive on the whole liquid bridge free surface; it tends to compress and curve the free surface as opposed to
is positive on the whole liquid bridge free surface; it tends to compress and curve the free surface as opposed to  . As time proceeds to t = 15.85 s, the magnitude of
. As time proceeds to t = 15.85 s, the magnitude of  on the free surface decreases. Furthermore, around the liquid bridge vertical centerline, a region of positive
on the free surface decreases. Furthermore, around the liquid bridge vertical centerline, a region of positive  emerges. Here, the liquid bridge is in a state of extensional stress and the fluid undergoes extension-hardening. At t = 31.85 s, the previously positive
emerges. Here, the liquid bridge is in a state of extensional stress and the fluid undergoes extension-hardening. At t = 31.85 s, the previously positive  on the free surface turns negative, it therefore tends to expand and flatten the free surface similar to
on the free surface turns negative, it therefore tends to expand and flatten the free surface similar to  . Also, as the liquid bridge thins, the distance between the free surface and the center positive
. Also, as the liquid bridge thins, the distance between the free surface and the center positive  region becomes shorter. Later at t = 47.85 s, the neck free surface approaches the center positive
region becomes shorter. Later at t = 47.85 s, the neck free surface approaches the center positive  region. The positive, extensional
region. The positive, extensional  stretches the liquid bridge neck into a cylindrical thread. As the free surface of the thread is now parallel to the z-axis,
stretches the liquid bridge neck into a cylindrical thread. As the free surface of the thread is now parallel to the z-axis,  can no longer act on the free surface. Hence, deformation of the cylindrical thread becomes locked in the r-direction. Subtracting
can no longer act on the free surface. Hence, deformation of the cylindrical thread becomes locked in the r-direction. Subtracting  from
from 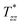 gives the second normal stress difference
gives the second normal stress difference  . Initially at t = 5.85 s,
. Initially at t = 5.85 s,  is positive both on the neck surface and around the vertical centerline of the liquid bridge. Later at t = 15.85 s and 31.85 s, the positive
is positive both on the neck surface and around the vertical centerline of the liquid bridge. Later at t = 15.85 s and 31.85 s, the positive  becomes more and more concentrated around the vertical centerline. On the liquid bridge free surface, close to the upper and lower plates, the magnitude of
becomes more and more concentrated around the vertical centerline. On the liquid bridge free surface, close to the upper and lower plates, the magnitude of 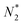 is close to zero. Finally at t = 47.85 s when the liquid bridge neck is turned into a cylindrical thread,
is close to zero. Finally at t = 47.85 s when the liquid bridge neck is turned into a cylindrical thread,  is positive in the entire region of the thread; elsewhere, it is close to zero.
is positive in the entire region of the thread; elsewhere, it is close to zero.
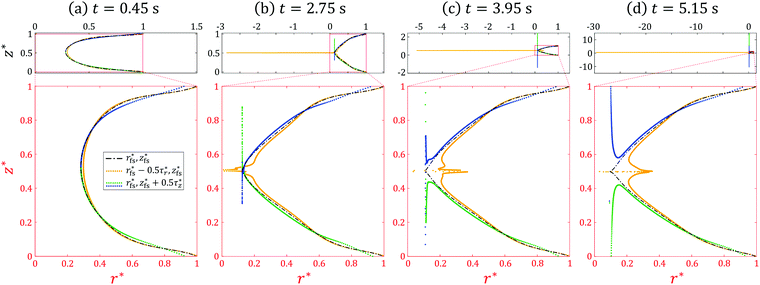
Fig. 7 further shows how the dimensionless traction vector τ* is distributed on the liquid bridge free surface for Ω = 1 rad s−1. The dimensionless radial and axial coordinates of the free surface are  (black broken lines). The radial component
(black broken lines). The radial component 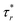 of the traction vector is visualized as
of the traction vector is visualized as  (orange dots). By this visualization scheme, for
(orange dots). By this visualization scheme, for  which acts towards the positive r-direction,
which acts towards the positive r-direction,  will lie on the left hand side of
will lie on the left hand side of  vice versa for
vice versa for  . The axial component
. The axial component  of the traction vector is visualized as
of the traction vector is visualized as  (green and blue dots). The reason of using two colors for
(green and blue dots). The reason of using two colors for 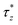 is to distinguish the top and bottom halves of the liquid bridge. For
is to distinguish the top and bottom halves of the liquid bridge. For  which acts towards the positive z-direction,
which acts towards the positive z-direction,  will lie above
will lie above  , and vice versa. Initially at t = 5.85 s (Fig. 7(a)), around the neck of the liquid bridge (0.2 < z* < 0.8),
, and vice versa. Initially at t = 5.85 s (Fig. 7(a)), around the neck of the liquid bridge (0.2 < z* < 0.8), 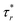 is negative and hence tends to facilitate liquid bridge thinning. Away from the neck,
is negative and hence tends to facilitate liquid bridge thinning. Away from the neck,  is compressive to the liquid bridge free surface; it tends to increase the curvature of the free surface. Later at t = 15.85 s (Fig. 7(b)), for 0.4 < z* < 0.6,
is compressive to the liquid bridge free surface; it tends to increase the curvature of the free surface. Later at t = 15.85 s (Fig. 7(b)), for 0.4 < z* < 0.6,  turns positive and tends to oppose liquid bridge thinning. For 0.1 < z* < 0.9, τz tends to expand and flatten the free surface. At t = 31.85 s (Fig. 7(c)), for 0.4 < z* < 0.6, τr turns negative with its minimum located at the neck of the liquid bridge (z* ≈ 0.5). For 0.1 < z* < 0.9, as before,
turns positive and tends to oppose liquid bridge thinning. For 0.1 < z* < 0.9, τz tends to expand and flatten the free surface. At t = 31.85 s (Fig. 7(c)), for 0.4 < z* < 0.6, τr turns negative with its minimum located at the neck of the liquid bridge (z* ≈ 0.5). For 0.1 < z* < 0.9, as before,  is expansive to the free surface. Its magnitude increases over time, which signifies extension-hardening of the fluid. Finally at t = 47.85 s (Fig. 7(d)), the neck of the liquid bridge (0.3 < z* < 0.7) has turned into a thin cylindrical thread with a dimensionless neck radius R* = R/Rp ≈ 0.014. This implies a dimensionless Laplace pressure of
is expansive to the free surface. Its magnitude increases over time, which signifies extension-hardening of the fluid. Finally at t = 47.85 s (Fig. 7(d)), the neck of the liquid bridge (0.3 < z* < 0.7) has turned into a thin cylindrical thread with a dimensionless neck radius R* = R/Rp ≈ 0.014. This implies a dimensionless Laplace pressure of  where σ* = σ/ηRpΩ is the dimensionless surface tension, matching the magnitude of
where σ* = σ/ηRpΩ is the dimensionless surface tension, matching the magnitude of  observed in Fig. 7(d). On the other hand, the high value of
observed in Fig. 7(d). On the other hand, the high value of  and the extension-hardening of the fluid together result in the much higher magnitude of the expansive
and the extension-hardening of the fluid together result in the much higher magnitude of the expansive  around the liquid bridge neck, as compared to those observed at previous times (see Fig. 7(a)–(c)).
around the liquid bridge neck, as compared to those observed at previous times (see Fig. 7(a)–(c)).
For Ω = 5 rad s−1 (Fig. 8), initially at t = 1.05 s, the shape and stress fields of the liquid bridge are essentially the same as those observed in the case of Ω = 1 rad s−1 (see t = 5.85 s, Fig. 6). However, several previously unobserved features appear later in time. For instance, at t = 10.25 s, the liquid bridge neck is seen to be more curved with a sharp cusp as opposed to smoothly-curving, as observed in the Ω = 1 rad s−1 case. A small region of positive  appears at the cusp; it tends to oppose liquid bridge thinning locally there. Slightly above the cusp
appears at the cusp; it tends to oppose liquid bridge thinning locally there. Slightly above the cusp  is negative, and slight below it is positive. This implies that
is negative, and slight below it is positive. This implies that  tends to oppose liquid bridge thinning at the cusp. Also, it tends to compress and sharpen the cusp even further. As time proceeds to t = 20.25 s, the cusp is sharpened. A positive region of
tends to oppose liquid bridge thinning at the cusp. Also, it tends to compress and sharpen the cusp even further. As time proceeds to t = 20.25 s, the cusp is sharpened. A positive region of  appears around the cusp; similar to
appears around the cusp; similar to 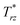 , it tends to compress and sharpen the tip. Finally at t = 30.25 s as the liquid bridge neck turns into a cylindrical thread, stress fields in the bridge once again become similar to that observed in the Ω = 1 rad s−1 case (see t = 47.85 s, Fig. 6). Fig. 9 shows the normal traction t* on the liquid bridge free surface for the case of Ω = 5 rad s−1. At t = 1.05 s (Fig. 9(a)), the distributions of both
, it tends to compress and sharpen the tip. Finally at t = 30.25 s as the liquid bridge neck turns into a cylindrical thread, stress fields in the bridge once again become similar to that observed in the Ω = 1 rad s−1 case (see t = 47.85 s, Fig. 6). Fig. 9 shows the normal traction t* on the liquid bridge free surface for the case of Ω = 5 rad s−1. At t = 1.05 s (Fig. 9(a)), the distributions of both  and
and 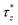 are similar to those observed in the case of Ω = 1 rad s−1 (see Fig. 7(a)), except their magnitudes being smaller. As time proceeds to t = 10.25 s (Fig. 9(b)), the liquid bridge neck is turned into a sharp cusp. Locally at the cusp (z* ≈ 0.5),
are similar to those observed in the case of Ω = 1 rad s−1 (see Fig. 7(a)), except their magnitudes being smaller. As time proceeds to t = 10.25 s (Fig. 9(b)), the liquid bridge neck is turned into a sharp cusp. Locally at the cusp (z* ≈ 0.5),  turns positive. Compared to the Ω = 1 rad s−1 case (see Fig. 7(b)), the magnitude of the positive
turns positive. Compared to the Ω = 1 rad s−1 case (see Fig. 7(b)), the magnitude of the positive  is much larger, and its distribution is much narrower, resembling a singularity. Away from the cusp, the magnitude of the negative
is much larger, and its distribution is much narrower, resembling a singularity. Away from the cusp, the magnitude of the negative 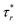 is increased. Meanwhile,
is increased. Meanwhile,  is compressive at the cusp; again, the narrow distribution and large magnitude of
is compressive at the cusp; again, the narrow distribution and large magnitude of  at the cusp resemble a singularity. Away from the cusp,
at the cusp resemble a singularity. Away from the cusp,  becomes expansive to the liquid bridge free surface. Later at t = 20.25 s as the cusp is sharpened further (Fig. 9(c)), the magnitudes of both the positive
becomes expansive to the liquid bridge free surface. Later at t = 20.25 s as the cusp is sharpened further (Fig. 9(c)), the magnitudes of both the positive 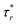 and the compressive
and the compressive  at the cusp are increased. Away from the cusp, the magnitude of the negative
at the cusp are increased. Away from the cusp, the magnitude of the negative  and expansive
and expansive  are also increased. Finally at t = 30.25 s (Fig. 9(d)), the neck of the liquid bridge (0.4 < z* < 0.6) is stretched into a thin cylindrical thread. Because of the high Laplace pressure
are also increased. Finally at t = 30.25 s (Fig. 9(d)), the neck of the liquid bridge (0.4 < z* < 0.6) is stretched into a thin cylindrical thread. Because of the high Laplace pressure  there,
there,  turns negative and
turns negative and  becomes expansive.
becomes expansive.
For Ω = 10 rad s−1 (Fig. 10), the simulation halts when R reaches 0.27 mm (see blue curve, Fig. 6), which implies that there is certain torsion-induced structure appearing in the liquid bridge thinning process. At t = 0.45 s, the shape and stress fields of the liquid bridge are the same as those observed in the Ω = 1 rad s−1 (see t = 5.85 s, Fig. 6) and 5 rad s−1 (see t = 1.05 s, Fig. 8). At t = 2.75 s, just like the case of 5 rad s−1, a small region of positive  and negative
and negative  appear on the cusp of the liquid bridge.
appear on the cusp of the liquid bridge.  turns negative at the cusp, and
turns negative at the cusp, and  is negative slightly above the cusp and positive slightly below the cusp. Later at t = 3.95 s, the stress fields are highly similar to those observed in the Ω = 5 rad s−1 case (see t = 10.25 s, Fig. 8) both in terms of their magnitudes as well as their distributions in the liquid bridge. However, the cusp for the Ω = 10 rad s−1 case is seen to be sharper. Such a difference in the neck curvatures can be rationalized via the dimensionless surface tension σ* = σ/ηRpΩ, the magnitude of which for the Ω = 10 rad s−1 case is 2 times smaller than that for the Ω = 5 rad s−1 case. Given that the stress fields are highly similar in the two liquid bridges, the one having the lower σ* (or higher Tn) would have a lower resistance against deformation. This explains why the cusp for the Ω = 10 rad s−1 case is sharper than that for the Ω = 5 rad s−1 case. Finally at t = 5.15 s, the cusp has developed into a noticeable indent. The previously negative
is negative slightly above the cusp and positive slightly below the cusp. Later at t = 3.95 s, the stress fields are highly similar to those observed in the Ω = 5 rad s−1 case (see t = 10.25 s, Fig. 8) both in terms of their magnitudes as well as their distributions in the liquid bridge. However, the cusp for the Ω = 10 rad s−1 case is seen to be sharper. Such a difference in the neck curvatures can be rationalized via the dimensionless surface tension σ* = σ/ηRpΩ, the magnitude of which for the Ω = 10 rad s−1 case is 2 times smaller than that for the Ω = 5 rad s−1 case. Given that the stress fields are highly similar in the two liquid bridges, the one having the lower σ* (or higher Tn) would have a lower resistance against deformation. This explains why the cusp for the Ω = 10 rad s−1 case is sharper than that for the Ω = 5 rad s−1 case. Finally at t = 5.15 s, the cusp has developed into a noticeable indent. The previously negative  turns positive. Hence, it tends to compress and sharpen the indent together with
turns positive. Hence, it tends to compress and sharpen the indent together with  . Fig. 11 further shows the distribution of the normal traction τ* on the liquid bridge free surface. At t = 0.45 s when the lower plate just started to rotate (Fig. 11(a)) and t = 2.75 s when the cusp just appears at the liquid bridge neck (z ≈ 0.5) (Fig. 11(b)), the distributions of
. Fig. 11 further shows the distribution of the normal traction τ* on the liquid bridge free surface. At t = 0.45 s when the lower plate just started to rotate (Fig. 11(a)) and t = 2.75 s when the cusp just appears at the liquid bridge neck (z ≈ 0.5) (Fig. 11(b)), the distributions of  and
and  are similar to those observed in the case of Ω = 5 rad s−1 (see Fig. 9(a) and (b)). Later, at t = 3.95 s (Fig. 11(c)) as the cusp is sharpened, the distributions of the positive
are similar to those observed in the case of Ω = 5 rad s−1 (see Fig. 9(a) and (b)). Later, at t = 3.95 s (Fig. 11(c)) as the cusp is sharpened, the distributions of the positive  and compressive
and compressive  at the cusp and the negative
at the cusp and the negative 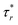 and expansive
and expansive  away from the cusp appear to be narrower compared to the Ω = 5 rad s−1 case (see Fig. 9(c)). Lastly at t = 5.15 s (Fig. 11(d)) when the cusp is developed into an indent, the distribution of the positive
away from the cusp appear to be narrower compared to the Ω = 5 rad s−1 case (see Fig. 9(c)). Lastly at t = 5.15 s (Fig. 11(d)) when the cusp is developed into an indent, the distribution of the positive  at the cusp becomes even narrower, and its magnitude is increased. This can be explained by considering the radius of curvature of the indent. Moments before the simulation halts, the indent has a dimensionless radius of curvature a* = a/Rp ≈ 0.0005, (see ESI,† Video S2). This implies a dimensionless Laplace pressure of
at the cusp becomes even narrower, and its magnitude is increased. This can be explained by considering the radius of curvature of the indent. Moments before the simulation halts, the indent has a dimensionless radius of curvature a* = a/Rp ≈ 0.0005, (see ESI,† Video S2). This implies a dimensionless Laplace pressure of  which matches the magnitude of τr ≈ 60 observed in Fig. 11(d). The high value of
which matches the magnitude of τr ≈ 60 observed in Fig. 11(d). The high value of  also causes the compressive
also causes the compressive  to have a higher magnitude at the cusp as compared to t = 2.75 s and 3.95 s (see Fig. 11(b) and (c)).
to have a higher magnitude at the cusp as compared to t = 2.75 s and 3.95 s (see Fig. 11(b) and (c)).
5.4 Similarity to edge fracture
The indent that we observed in the Ω = 10 rad s−1 case (see t = 4.9 s, Fig. 7(c)) deserves attention. In fact, the critical role of the second normal stress difference N2, the shape of the indent and its associated stress fields closely resemble edge fracture. Edge fracture is a flow instability characterized by the sudden indentation of the fluid's free surface when a viscoelastic fluid is sheared at above a certain critical shear rate.17–24 Historically, Tanner and Keentok18 first realized that the second normal stress difference N2 is important in driving edge fracture. By assuming a semicircular indent of radius a in a second-order fluid with surface tension σ, they derived a criterion of edge fracture which reads |N2| > 2σ/3a. Since then, several experimental, computational and theoretical works have confirmed Tanner and Keentok's postulation.19–23 Of particular interest are the simulation studies of Hemingway and Fielding,22,23 which showed how edge fracture and the curvature of the viscoelastic fluid's free surface are interrelated. When the free surface is concave, normal stress can be localized in the viscoelastic fluid, which then leads to edge fracture. Building on Hemingway and Fielding's findings, Chan et al.17 showed that edge fracture can also occur when a liquid bridge made of viscoelastic silicone oil is subjected to torsion. In that study, the silicone oil had a zero-shear viscosity of η0 ∈ O(10 Pa s), characteristic relaxation time of λ ∈ O(1 ms) and surface tension of σ ∈ O(10 mN m−1). Assuming a neck radius of R = 1 mm, the elastocapillary number Ec ∈ O(10−3) was negligible compared to the Tanner number Tn ∈ O(102). Due to the relatively low values Ec and Tn compared to those in the current study (see Fig. 5(b)–(d) for example values), the indents that Chan et al.17 observed were much rounder than those observed here; they had a more well-defined semicircular tip with a characteristic size of O(0.1 mm). Nonetheless, the distributions of the stress fields observed in both studies share a number of similarities, the most crucial of which is N2 being negative at the indent tip. Hence, we have evidence to believe that the indent formation seen in Fig. 7(c) shares the same physical mechanism as edge fracture. As a side note, since the second normal stress difference of Boger fluids subjected to rheometric flows that approximate the planar Couette flow is generally very close to zero, it had been argued that edge fracture cannot occur in Boger fluids; experiments performed using parallel-plate rheometers (H ≪ Rp) support this view.19 Nonetheless, our results show that as long as the Boger fluid is configured as a liquid bridge with H ≈ Rp, edge fracture is possible. Hence, there is a gap between those earlier attempts to explain edge fracture and the observations in our current study. More works need to be done to fill in this gap.5.5 Effect of the liquid bridge height H
So far, we have been able to describe the viscoelastic liquid bridge thinning problem with only two dimensionless parameters, namely, the elastocapillary number Ec and the Tanner number Tn. However, this is because we have fixed the initial condition of the liquid bridge in all our experiments and simulations. In reality, geometric parameters such as the liquid bridge height H will also affect the liquid bridge thinning dynamics. To summarize our experimental observations, we present a phase diagram showing how the dimensionless height H* = H/Rp and the characteristic Tanner number Tnc = ληRpΩ2/σ together determine the liquid bridge behavior (Fig. 12). To visualize the data points more clearly, is shown instead of Tnc. The liquid bridge behavior is characterized into four regimes. First, there is the stable regime (black squares) in which the liquid bridge does not break up. Second, there is the elastocapillary breakup regime (orange up-triangles) in which the liquid bridge thins into a cylindrical thread before its breakup (see Fig. 2(a) and (b) for example). Third, there is the buckling regime (green circles) in which the liquid reservoirs on the upper and lower plates are brought towards each other by the torsion-induced axial normal traction τz, leading to the buckling of the liquid bridge (see Fig. 2(c) for example). Lastly, there is the quick breakup regime (blue down-triangles) in which the liquid bridge neck drains out before the upper and lower liquid reservoirs approach each other (see Fig. 2(d) for example). For H* = 1, the liquid bridge is unstable, hence the stable regime is not observed. The elastocapillary breakup regime is seen for
is shown instead of Tnc. The liquid bridge behavior is characterized into four regimes. First, there is the stable regime (black squares) in which the liquid bridge does not break up. Second, there is the elastocapillary breakup regime (orange up-triangles) in which the liquid bridge thins into a cylindrical thread before its breakup (see Fig. 2(a) and (b) for example). Third, there is the buckling regime (green circles) in which the liquid reservoirs on the upper and lower plates are brought towards each other by the torsion-induced axial normal traction τz, leading to the buckling of the liquid bridge (see Fig. 2(c) for example). Lastly, there is the quick breakup regime (blue down-triangles) in which the liquid bridge neck drains out before the upper and lower liquid reservoirs approach each other (see Fig. 2(d) for example). For H* = 1, the liquid bridge is unstable, hence the stable regime is not observed. The elastocapillary breakup regime is seen for  the buckling regime is seen for
the buckling regime is seen for  and the quick breakup regime is seen for
and the quick breakup regime is seen for  . Decreasing the height to H* < 1 renders the viscoelastic liquid bridge more resistant to breakup. For instance, the elastocapillary and quick breakup regimes are seen in a narrower range of
. Decreasing the height to H* < 1 renders the viscoelastic liquid bridge more resistant to breakup. For instance, the elastocapillary and quick breakup regimes are seen in a narrower range of  for H* = 0.83, the quick breakup regime even disappears. For H* < 0.93, the stable regime is seen when no rotation is applied
for H* = 0.83, the quick breakup regime even disappears. For H* < 0.93, the stable regime is seen when no rotation is applied  . Also for H* < 0.93, the buckling regime is observed over an increased range of
. Also for H* < 0.93, the buckling regime is observed over an increased range of  . Buckling is facilitated because the same amount of fluid is confined in a shorter column; thus, due to the compressive action of the axial normal traction τz, the upper and lower liquid reservoirs approach each other more easily. On the other hand, increasing the height to H* > 1 does not alter the liquid bridge behavior much. The phase boundaries between different regimes are seen to remain at similar values of
. Buckling is facilitated because the same amount of fluid is confined in a shorter column; thus, due to the compressive action of the axial normal traction τz, the upper and lower liquid reservoirs approach each other more easily. On the other hand, increasing the height to H* > 1 does not alter the liquid bridge behavior much. The phase boundaries between different regimes are seen to remain at similar values of  . Incidentally, we note that the phase diagram depicted in Fig. 12 is only valid for liquid bridges with a dimensionless volume of V* = 3V/4πRp3 ≈ 0.18. It is expected that if V* is decreased, surface tension will drive the liquid bridge to become less stable for the same dimensionless height H*. The areas of those unstable regimes in the phase diagram can hence be expected to enlarge. On the other hand, if V* is increased, the liquid bridge will become more stable. Gravity may start to interfere as the Bond number Bo increases. In such a case, a new axis will have to be introduced to the phase diagram. However, inertia can still be assumed to be negligible due to the small magnitude of the Reynolds number Re.
. Incidentally, we note that the phase diagram depicted in Fig. 12 is only valid for liquid bridges with a dimensionless volume of V* = 3V/4πRp3 ≈ 0.18. It is expected that if V* is decreased, surface tension will drive the liquid bridge to become less stable for the same dimensionless height H*. The areas of those unstable regimes in the phase diagram can hence be expected to enlarge. On the other hand, if V* is increased, the liquid bridge will become more stable. Gravity may start to interfere as the Bond number Bo increases. In such a case, a new axis will have to be introduced to the phase diagram. However, inertia can still be assumed to be negligible due to the small magnitude of the Reynolds number Re.
 | ||
| Fig. 12 A phase diagram based on the experimental observations showing how the dimensionless height H* = H/Rp and the characteristic Tanner number Tnc = ληRpΩ2/σ affect the liquid bridge behavior. Black square: stable regime in which the liquid bridge does not breakup. Orange triangle: elastocapillary breakup regime in which the liquid bridge undergoes elastocapillary thinning before its breakup, as shown in shown in Fig. 2(a) and (b). Green circle: buckling regime in which the liquid bridge undergoes the buckling instability shown in Fig. 2(c). Blue inverted triangle: quick breakup regime in which the liquid bridge undergoes a quicker, non-elastocapillary thinning mode before its breakup, as shown in Fig. 2(d). | ||
6 Conclusions
We have presented a simple method to break viscoelastic liquid bridges quickly and cleanly. By using a viscoelastic fluid with nearly constant shear viscosity (a Boger fluid), we showed by experiment and simulation that applying rotation to one end of the liquid bridge could effectively destabilize the liquid bridge. Destabilization of the liquid bridge depends on how the elastocapillary effect and torsion-induced normal stress effect interact. The elastocapillary effect is quantified by the elastocapillary number Ec, which characterizes the combined importance of elastic stress and capillary stress as compared to viscous stress. The torsion-induced normal stress effect is quantified by the Tanner number Tn, which characterizes the relative importance of torsion-induced normal stress and capillary stress. When the elastocapillary effect dominates (Ec ≫ Tn), as time proceeds, the liquid reservoirs on the upper and lower endplates separate from each other. In effect, this turns the liquid bridge into a cylindrical thread whose radius thins exponentially over time. On the other hand, when the torsion-induced normal stress effect dominates (Tn ≫ Ec), helical wrinkles appear on the liquid bridge surface. As time proceeds, the radial normal stress Trr drives the liquid bridge neck towards the vertical centerline. Also, the vertical normal stress Tzz drives the upper and lower liquid reservoirs towards each other. Hence, deformation of the liquid bridge free surface is driven by the second normal stress difference N2 = Tzz − Trr. Such dependence on N2 points to the possibility that the observed deformation of the free surface shares the same physical mechanism as edge fracture, a flow instability characterized by the sudden indentation of the fluid's free surface when a viscoelastic fluid is sheared at above a critical rate.17–24 However, now it is still unclear how exactly the liquid bridge deformation observed in the current study is related to edge fracture. Also, how the helical wrinkles are formed remains unknown. Future works are to be done to unravel these mysteries.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the support of Okinawa Institute of Science and Technology (OIST) Graduate University with subsidy funding from the Cabinet Office, Government of Japan. S. T. C., S. J. H., and A. Q. S. also acknowledge financial support from the Japanese Society for the Promotion of Science (JSPS) (Grants 21J10517, 21K03884) and the Joint Research Projects supported by the JSPS and the Swiss National Science Foundation. We would also like to thank Prof. Gareth H. McKinley and his group for sharing their Boger fluid for our experiments. We are also grateful for the help and support provided by the Scientific Computing and Data Analysis section of the Research Support Division at OIST.Notes and references
- S. Kumar, Annu. Rev. Fluid Mech., 2015, 47, 67–94 CrossRef.
- J. B. Bostwick and P. H. Steen, Annu. Rev. Fluid Mech., 2015, 47, 539–568 CrossRef.
- W. Sun, P. Neuzil, T. S. Kustandi, S. Oh and V. D. Samper, Biophys. J., 2005, 89, L14–L17 CrossRef CAS PubMed.
- G. Huber, H. Mantz, R. Spolenak, K. Mecke, K. Jacobs, S. N. Gorb and E. Arzt, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 16293–16296 CrossRef CAS PubMed.
- A. P. Russell, A. Y. Stark and T. E. Higham, Integr. Comp. Biol., 2019, 59, 101–116 CrossRef CAS PubMed.
- A. M. Alencar, A. Majumdar, Z. Hantos, S. V. Buldyrev, H. E. Stanley and B. Suki, Phys. A: Stat. Mech. Appl., 2005, 357, 18–26 CrossRef.
- X. B. Chen, Int. J. Adv. Manuf. Technol., 2009, 43, 276–286 CrossRef.
- G. Tabilo-Munizaga and G. V. Barbosa-Cánovas, J. Food Eng., 2005, 67, 147–156 CrossRef.
- M. E. Mackay, J. Rheol., 2018, 62, 1549–1561 CrossRef CAS.
- J. Li and G. Deng, Proceedings of the Sixth IEEE CPMT Conference on High Density Microsystem Design and Packaging and Component Failure Analysis (HDP'04), 2004, pp. 198–205.
- O. Arnolds, H. Buggisch, D. Sachsenheimer and N. Willenbacher, Rheol. Acta, 2010, 49, 1207–1217 CrossRef CAS.
- A. Y. Malkin, A. Arinstein and V. Kulichikhin, Prog. Polym. Sci., 2014, 39, 959–978 CrossRef CAS.
- S. L. Anna and G. H. McKinley, J. Rheol., 2001, 45, 115–138 CrossRef CAS.
- G. H. McKinley, Rheol. Rev., 2005, 3, 1–48 Search PubMed.
- C. Clasen, P. M. Phillips, L. Palangetic and J. Vermant, AIChE J., 2012, 58, 3242–3255 CrossRef CAS.
- B. L. Toh, H. K. Yeoh, W. H. Teoh and L. C. Chin, Int. J. Adv. Manuf. Technol., 2017, 90, 2083–2094 CrossRef.
- S. T. Chan, F. P. van Berlo, H. A. Faizi, A. Matsumoto, S. J. Haward, P. D. Anderson and A. Q. Shen, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104790118 CrossRef CAS PubMed.
- R. I. Tanner and M. Keentok, J. Rheol., 1983, 27, 47–57 CrossRef.
- M. Keentok and S. C. Xue, Rheol. Acta, 1999, 38, 321–348 CrossRef CAS.
- R. R. Huilgol, M. Panizza and L. E. Payne, J. Non-Newtonian Fluid Mech., 1993, 50, 331–348 CrossRef CAS.
- C. S. Lee, B. C. Tripp and J. J. Magda, Rheol. Acta, 1992, 31, 306–308 CrossRef CAS.
- E. J. Hemingway and S. M. Fielding, J. Rheol., 2019, 63, 735–750 CrossRef CAS.
- E. J. Hemingway and S. M. Fielding, J. Rheol., 2020, 64, 1147–1159 CrossRef CAS.
- O. Maklad and R. J. Poole, J. Non-Newtonian Fluid Mech., 2021, 104522 CrossRef CAS.
- S. L. Anna and G. H. McKinley, Rheol. Acta, 2008, 47, 841–859 CrossRef CAS.
- D. F. James, Annu. Rev. Fluid Mech., 2009, 41, 129–142 CrossRef.
- J. D. Ferry, Viscoelastic properties of polymers, John Wiley & Sons, 1980 Search PubMed.
- J. D. Berry, M. J. Neeson, R. R. Dagastine, D. Y. C. Chan and R. F. Tabor, J. Colloid Interface Sci., 2015, 454, 226–237 CrossRef CAS PubMed.
- A. Souvaliotis and A. N. Beris, J. Rheol., 1992, 36, 241–271 CrossRef CAS.
- S. Varchanis, A. Syrakos, Y. Dimakopoulos and J. Tsamopoulos, J. Non-Newtonian Fluid Mech., 2020, 284, 104365 CrossRef CAS.
- S. Varchanis, A. Syrakos, Y. Dimakopoulos and J. Tsamopoulos, J. Non-Newtonian Fluid Mech., 2019, 267, 78–97 CrossRef CAS.
- S. Varchanis and J. Tsamopoulos, Numerical simulations of interfacial and elastic instabilities, 2021, http://pcwww.liv.ac.uk/robpoole/jnnfm/vids/Patras_JNNFM_28042021.mp4.
- Y. Dimakopoulos and J. Tsamopoulos, J. Comput. Phys., 2003, 192, 494–522 CrossRef.
- S. Varchanis, Y. Dimakopoulos, C. Wagner and J. Tsamopoulos, Soft Matter, 2018, 14, 4238–4251 RSC.
- J. Eggers and E. Villermaux, Rep. Prog. Phys., 2008, 71, 036601 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Numerical mesh and time step convergence tests, distributions of stress along the liquid bridge free surface, and the effect of the imposed rotational speed on the liquid bridge thinning speed. See DOI: 10.1039/d1sm01804c |
| This journal is © The Royal Society of Chemistry 2022 |